DOI:
10.1039/C6RA13038K
(Paper)
RSC Adv., 2016,
6, 76813-76823
Acidity analysis of iron ore based on calibration-free laser-induced breakdown spectroscopy (CF-LIBS) combined with a binary search algorithm (BSA)
Received
19th May 2016
, Accepted 7th August 2016
First published on 8th August 2016
Abstract
Calibration-free laser-induced breakdown spectroscopy (CF-LIBS) combined with a binary search algorithm (BSA) is proposed to determine the acidity (CaO/SiO2 mass ratios) of iron ore. It is based on the idea that different samples with a similar matrix ablated in the same conditions have the same plasma temperature. Ca I/Si I molar ratios are obtained by the intercepts on the Boltzmann plots drawn by using corrected spectral lines without self-absorption, and the number concentrations of primary ionization ions of the elements are evaluated by the Saha equation. Furthermore, one standard sample matrix-matched with unknown samples along with BSA is employed to obtain a more accurate plasma temperature. Noteworthily, BSA is a classical search method and utilized to search the optimal plasma temperature for the first time in CF-LIBS. The acidity of the iron ores can be calculated according to the obtained value of Ca/Si molar ratios. The calculated acidity of the unknown samples were close to the certified acidity based on the root mean square error (RMSE) and mean relative error (MRE) which were 0.0145 and 4.01%, respectively. The proposed CF-LIBS method can be used to determine the acidity of iron ores, and it provides a new method and technology for selection and quality control of iron ore.
1. Introduction
Iron ore is the main raw material for the production of iron and steel.1 Its acidity is an important indicator in the mining industry and blast furnaces, and directly determines the proportion of furnace charge.2 The acidity of iron ore can be simply defined as the CaO/SiO2 mass ratio.1 If the value of mCaO/mSiO2 is higher than 1, the iron ore can be classified as alkaline ore. Otherwise, it belongs to the acidic ore classification. The alkaline ore is beneficial to desulfurization and can reduce coke ratio. So lower contents of acidic components in iron ore are required in industry. However, the vast majority of iron ores are acidic because of the high content of SiO2. Therefore, in order to adjust the acidity of iron ore in the metallurgical process, different types and quantities of alkaline flux (limestone, quartzite, etc.) could be added to slag with SiO2 and reduce viscosity of the slag. Under modern conditions of the blast furnace, online analysis of acidity of iron ore could be helpful to quality control in the blast furnace equipment.
In general, the analytical techniques of iron ore include chemical analysis, inductively coupled plasma atomic emission spectrometry (ICP-AES)3 and atomic absorption spectroscopy (AAS).4 However, these approaches require complicated sample preparation and much analysis time, which fails to obtain timely information on the steel product, and even hinders their application for real time and fast analysis. Laser-induced breakdown spectroscopy (LIBS) is an analytical technique of atomic emission spectroscopy (AES) used for qualitative and quantitative analysis. Compared with conventional analytical techniques, the LIBS technique owns some obvious advantages,5–7 such as multi-elemental simultaneous analysis, all types of samples8,9 (solids, liquids, and gases) can be analyzed, a small amount of samples requirement and no need pretreatment of complicated samples. At present, the LIBS technology has been successfully applied to the metallurgical industry including iron ore selection,10 process control,11 iron slag analysis,12–14 and so on.
The main quantitative analytical method for LIBS is calibration curve method, which needs a set of standard samples to construct the relationship between the integrated intensity of the analytical line and the known concentration.12 However, calibration curve method easily suffers from the matrix effect and requires a series of calibration samples with the same matrix to unknown samples. For these reasons, the calibration-free LIBS (CF-LIBS) was proposed by Ciucci et al.15 to determine the concentrations of elements by using the mathematic models that can be used to describe the plasma emission. Hence, it can overcome matrix effects and does not require to construct the calibration curve of standard samples for quantitative analysis. Thus, it is more suitable for field analysis and on-line applications. CF-LIBS has been widely applied for the quantitative analysis of metals and alloys,16 cultural heritage targets,17 geological samples,18 etc. CF-LIBS relies on the assumption of local thermodynamic equilibrium (LTE) and on the plasma parameters (i.e. plasma temperature and electron density). However, the quantitative accuracy of CF-LIBS is poor for absolute theoretical calculation and mathematical model. Hence, several variants of the classical CF-LIBS method developed from two aspects including self-absorption correction and the reliability of essential parameters (i.e. plasma temperature, electron density and so on) to improve the quantitative accuracy. Curve of growth (COG)19 and Internal reference for self-absorption correction (IRSAC)20 have been proposed to correct self-absorption. Compared with the procedure of the self-absorption correction based on COG, the proposed IRSAC method does not require so many theoretical values, and thus it can be more easily implemented. The determination coefficient (R2) and the accuracy of the quantitative results are improved significantly with respect to those obtained without self-absorption correction using IRSAC method. In order to enhance the reliability of essential parameters in CF-LIBS, Cavalcanti et al.21 put forward one-point calibration method by using one standard sample. Furthermore, for the inconsistency of plasma temperature after self-absorption correction, the genetic algorithm (GA) was proposed to obtain optimal plasma temperature.22 However, there are some problems of GA such as precocity that the results easily get into the local optimal solution and poor stability that the obtained results can not be repeated.
Although the researches above have made a great progress in CF-LIBS analysis, there are only few reports on the quantitative analysis for gangue mineral (CaO, SiO2) and acidity of iron ore using CF-LIBS. Herein, based on the ideas of the above authors, an internal reference line without self-absorption effect for each species is selected to correct intensities of other spectral lines with self-absorption effect. The Ca I/Si I molar ratio is calculated using the intercept relationship of Ca I and Si I on the Boltzmann plot. As the energy levels of the ionic lines of Ca and Si elements are very convergent, the number concentrations of primary ionization ions of the Ca and Si are evaluated by the Saha equation. Besides, based on a verified assumption that different samples with similar matrix ablated in the same conditions have the same plasma temperature,23 one standard sample matrix-matched with the unknown samples combined with binary search algorithm (BSA)24 is utilized to search the accurate plasma temperature. Then, the CaO/SiO2 concentration ratio is calculated, and the acidity of iron ore is determined.
2. Methodology
The method consists of (1) self-absorption correction; (2) calculation of electron density and plasma temperature; (3) determining the acidity of iron ores, which will be addressed in details in the following sections.
2.1 Self-absorption correction
In order to improve the accuracy of temperature calculation, a self-absorption coefficient is introduced here, as expressed in eqn (1):| |
 | (1) |
where parameters i and j refer to upper and lower levels of the transition, λ is the wavelength corresponding to the transition between two energy levels (Ei and Ej) of an atomic or ionic species s; I is the integral intensity of spectral line, Cs is the number concentration of the emitting species s, Aij is the transition probability between the two levels, gi is the degeneracy of the i level, Us(T) is the partition function for the emitting species at the plasma temperature T, kB is the Boltzmann constant, F is a constant that is related to the efficiency of the spectral detection system, fbλ is defined as the self-absorption coefficient at the wavelength λ, with the value between 0 and 1 (fbλ = 0 and fbλ = 1 means the spectral line is absolutely reabsorbed along the optical path and not affected by self-absorption effect, respectively). The spectral parameters of Aij, gi and Ei can be obtained from National Institute for Standards and Technology (NIST).25 The values of F, Cs and T can be determined from the experimental data.
The self-absorption effect can be corrected by using the internal reference line. Spectral lines with the lower transition probability and the higher excitation energy level are weakly affected by the self-absorption effect, thus it can be considered to have no influence of self-absorption and selected as internal reference line. The self-absorption coefficient can be calculated by the intensity ratios of emission spectral line to internal reference line as given by eqn (2):
| |
 | (2) |
where

,
λR and
IλRmn are the self-absorption coefficient, wavelength and spectral line intensity of the internal reference line, respectively. The
Amn,
gmn and
Em are the spectral parameters of transition between excitation energy levels of
m and
n. The self-absorption coefficients of all the internal reference lines can be regarded as 1

. Therefore, the corrected spectral line intensities can be expressed as:
| |
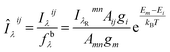 | (3) |
where the corrected spectral line intensities
Îλij can be used to draw a new Boltzmann plot, and then a new plasma temperature can be obtained. By that logic, the iterative correction is running until the convergence of determination coefficient on the Boltzmann plot (
R2 > 0.8). Consequently, a good fitted line will be obtained after the self-absorption correction. However, due to the spectral lines of different species suffer from self-absorption of different degree, the plasma temperatures obtained on the Boltzmann plots are inconsistent. Hence, it is necessary to take further steps to obtain uniform and accurate plasma temperature.
2.2 Calculation of electron density and plasma temperature
Determination of the electron density and temperature is a crucial step in the CF-LIBS process. The electron density can be calculated from the Stark broadening mechanism of the hydrogen Hα line (656 nm).26 The full width at half maximum (FWHM) parameter and the full width at half area (FWHA) parameter are often used to calculate the electron density.27 In this paper, the full width at half area (FWHA) parameter is used because it is much less sensitive to ion dynamics effects than FWHM. Electron density is calculated according to the following equation:| |
 | (4) |
where ne is the electron density (m−3).
The optimal plasma temperature is defined as the one providing the lowest discrepancy between the calculated value and the certified value, namely, the minimum of the Δwt(T)%, Δwt(T)% = abs(wt%cert − wtcalc(T)%)/wt%cert. In Fig. 1, the BSA as a classical and fast search method is utilized to calculate the Δwt(T)% using the middle temperature between the minimum and maximum. If Δwt1(T)% < 0.8%, the optimal plasma temperature is found and the search is finished. If not, the search continues. Compared with the Δwt(T)% calculated by the middle temperatures of two different ranges of Tmin (K)–Tmid (K) and Tmid (K)–Tmax (K), if Δwt2(T)% < Δwt3(T)%, the temperature range of Tmid (K)–Tmax (K) is eliminated and the search continues within the remaining temperature range of Tmin (K)–Tmid (K). This search method can progressively narrow the search range, thus search time is reduced and accuracy is improved.
 |
| | Fig. 1 Flow diagram of the BSA for determining optimal plasma temperature. | |
Based on a confirmed and reasonable assumption23 that different samples with similar matrix ablated in the same conditions have the same plasma temperature, the optimal plasma temperature obtained by the BSA can be applied to the unknown samples to calculate their Ca/Si molar ratios. A flow diagram of the novel method is described in Fig. 2.
 |
| | Fig. 2 Flow diagram of the proposed method. | |
2.3 Determining the acidity of iron ores
The Boltzmann plots are drawn by using the corrected spectral lines intensities. The equations to determine molar ratio of different elements are put forward below:| |
 | (5) |
| |
 | (6) |
| |
 | (7) |
| |
 | (8) |
| |
 | (9) |
| |
 | (10) |
In eqn (5)–(10),  respectively represent the intercept of atoms of element s1 and s2 on the Boltzmann plot, CII and CI are the number concentrations of ions and atoms of the given elements.
respectively represent the intercept of atoms of element s1 and s2 on the Boltzmann plot, CII and CI are the number concentrations of ions and atoms of the given elements.  molar ratio is calculated using the relationship of
molar ratio is calculated using the relationship of  on the Boltzmann plot, which can overcome the restriction that the sum of the relative concentration of all species equal unity for the calculation of the experimental factor F. me is the electron mass (kg), h is Planck's constant (J s), Eion is the energy of first ionization (J). Concerning the oxygen content, it has been calculated by the stoichiometric relation in the mineral oxide of the detected elements. Therefore, the mass ratios of oxides can be calculated using the equation reported below. Then, the acidity of iron ore can be determined.
on the Boltzmann plot, which can overcome the restriction that the sum of the relative concentration of all species equal unity for the calculation of the experimental factor F. me is the electron mass (kg), h is Planck's constant (J s), Eion is the energy of first ionization (J). Concerning the oxygen content, it has been calculated by the stoichiometric relation in the mineral oxide of the detected elements. Therefore, the mass ratios of oxides can be calculated using the equation reported below. Then, the acidity of iron ore can be determined.
| |
 | (11) |
where
Ms1 and
Ms2 are the molar mass of the oxides s
1 and s
2.
The contribution of ionized fraction of the elements is evaluated with the Saha equation. This approach can not only avoid the complexity of selecting emission lines of ions but also reduces the error of the over convergence of the energy levels of the ionic lines.
3. Experimental
3.1 Experimental setup
A schematic representation of the instrument set-up is shown in Fig. 3. All LIBS measurements were carried out with the Nd:YAG laser (Litron, Nano L120-20, UK), which operated at 1064 nm with repetition rate of 5 Hz and pulse energy of 83.9 mJ. The spectral range of 220–800 nm was collected by an Echelle spectrometer (ARYELLE-Butterfly, LTB200, Germany). A intensified charge-coupled device (ICCD) camera (iStar from Andor Technology) combined with the spectrometer was used for detection of the dispersed light, The ICCD detector was operated in the gated mode and the gate width was set to be 100 μs. All spectra were acquired at the delay time of 3.0 μs.
 |
| | Fig. 3 Schematic experimental setup. | |
3.2 Investigated samples
The standard iron ore samples (GBW07822), (GBW07824), (GBW07826), (GBW07828) and (GBW07830) from the Institute of Geo physical and Geo-chemical Exploration (China) were studied. For convenience, the samples were numbered from B-1 to B-5. Moreover, different mass concentration of CaO were added to the standard iron ore sample (GBW07824) to form seven new samples of different acidity, and the new samples were numbered from A-1 to A-7. The standard iron ore samples (GBW07824) as the known sample was used to obtain the optimal plasma temperature and the others were considered as unknown samples. Table 1 lists the mass concentration (wt%) and certified acidity of the investigated samples.
Table 1 Mass composition (wt%) and the acidity of investigated samples
| No. |
SiO2 |
CaO |
Certified acidity |
| A-1 |
33.800 |
2.370 |
0.070 |
| A-2 |
33.580 |
3.020 |
0.090 |
| A-3 |
31.370 |
9.410 |
0.300 |
| A-4 |
28.670 |
17.200 |
0.600 |
| A-5 |
26.400 |
23.760 |
0.900 |
| A-6 |
24.460 |
29.350 |
1.200 |
| A-7 |
22.790 |
34.180 |
1.500 |
| B-1 |
60.860 |
2.840 |
0.050 |
| B-2 |
33.930 |
2.000 |
0.063 |
| B-3 |
11.480 |
1.360 |
0.127 |
| B-4 |
10.930 |
0.180 |
0.018 |
| B-5 |
5.050 |
0.140 |
0.030 |
3.3 Acquisition conditions
Polyvinyl alcohol was used as a binding material. Iron ore powder and polyethylene were pressed into pellets by a hydraulic pressing machine at 40 MPa for 2 minutes. The size of the pellets is Ø 20 × 1.5 mm. A measured spectrum was collected as an accumulation of 30 laser shots per location for the purpose of improving the signal-to-noise ratio, and each of pellet included 15 spectra obtained at 15 different positions of the sample surface. Furthermore, the 15 spectra were averaged to obtained a single spectrum in order to reduce the influence caused by composition inhomogeneity. The data processing and quantitative analysis for iron ore were completed on Matlab (version 2007, Mathworks).
4. Result and discussion
4.1 Selection of analytical lines and internal reference lines for self-absorption correction
All the analytical lines are selected on the basis of NIST database25 and ref. 28. The energy levels of Ca II and Si II spectral lines were all very convergent, and thus the convincing fitted lines of Ca II and Si II could not be built. Therefore, the number concentrations of Ca II and Si II were evaluated by the number concentrations of Ca I and Si I with Saha equation, respectively. In this paper, the analytical lines of Ca I and Si I have been selected according to the criteria.29
The selection of the internal reference line plays a key role in the correction of the self-absorption effect for other spectral lines for each species. The lines with high excitation energies at upper levels and low transition probabilities suffer from negligible self-absorption effect, and thus the lines are preferentially considered. Spectral lines identified in the measured LIBS spectra are summarized in Table 2, and the boldfaced numbers in table represent the internal reference lines.
Table 2 List of the selected emission lines (the boldfaced numbers are the internal reference lines) used for building the Boltzmann plot
| Species |
Wavelength (nm) |
| Ca I |
428.94 |
431.87 |
442.55 |
443.50 |
443.57 |
558.89 |
610.28 |
612.23 |
| 643.92 |
|
|
|
|
|
|
|
| Si I |
243.52 |
251.93 |
263.13 |
288.17 |
298.74 |
390.57 |
|
|
In this paper, the self-absorption effect of Ca I and Si I spectral lines are corrected, and the selected internal reference lines are the same for all the test samples. The Boltzmann plots before and after correction of self-absorption effect with internal reference line for B-2# standard sample are shown in Fig. 4.
 |
| | Fig. 4 Boltzmann plots before (a) and after (b) self-absorption correction for B-2# standard sample. | |
In Fig. 4, the determination coefficients (R2) of Ca I and Si I are improved significantly after correction. R2 of Ca I is improved from 0.5443 to 0.9644 and Si I is improved from 0.3438 to 1.000 after self-absorption correction. Points on the Boltzmann plots show randomly scattered distribution as well as poor linear regression before correction, shown in Fig. 4(a). The reason is the dramatic decrease of the intensities of spectral lines caused by self-absorption, which leads to the decrease of slope and intercept of regression lines for each species. Accordingly, the calculated temperatures exceed the actual temperature significantly, and the concentrations of species are lower than expected, which leads to large errors in the quantitative results. From Fig. 4(b), these points are distributed near the regression line. However, the slope of each regression line is inconsistent, which indicates that the spectral intensities of the different species are suffered from varying degrees of self-absorption. The corrected LIBS spectra can be obtained based on the corrected Boltzmann plots. Fig. 5 shows the comparison between raw spectral intensities and corrected spectral intensities for the selected emission lines of Ca and Si for B-2# standard sample. Spectral line intensities are increased obviously other than internal reference line intensities which keep invariant in Fig. 5.
 |
| | Fig. 5 LIBS spectra before (a) and after (b) self-absorption correction for B-2# standard sample with Ca and Si labelled (the internal reference lines are labelled in red). | |
4.2 Calculation of electron density and plasma temperature with one standard sample
Based on the above formula,4 the value of electron density for B-2# standard sample is 3.87 × 1023 m−3. Besides, electron densities for the unknown samples are the same with the B-2# standard sample.21
The Boltzmann plot provides an individual temperature for Ca I and Si I, respectively, which is 9419 K and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054 K based on the Fig. 4(b). Herein, the optimal plasma temperature which is closest to the real plasma temperature could be obtained by BSA in a range from 9419 K to 11054 K. BSA runs on the B-2# standard sample based on Fig. 1 by eqn (5)–(10). In Fig. 6, the curve shows variation tendency of Δwt(T)% along with the plasma temperature T, and the detail image of optimal plasma temperature is plotted in the inset of figure to highlight the Δwt(T)% trend around the optimal plasma temperature. The search is stopped until the relative error of Ca/Si molar ratio is minimum (Δwt(T)% = 0.6%, less than 0.8%). The optimal plasma temperature searched by BSA is 9440 K, as shown in Fig. 6.
054 K based on the Fig. 4(b). Herein, the optimal plasma temperature which is closest to the real plasma temperature could be obtained by BSA in a range from 9419 K to 11054 K. BSA runs on the B-2# standard sample based on Fig. 1 by eqn (5)–(10). In Fig. 6, the curve shows variation tendency of Δwt(T)% along with the plasma temperature T, and the detail image of optimal plasma temperature is plotted in the inset of figure to highlight the Δwt(T)% trend around the optimal plasma temperature. The search is stopped until the relative error of Ca/Si molar ratio is minimum (Δwt(T)% = 0.6%, less than 0.8%). The optimal plasma temperature searched by BSA is 9440 K, as shown in Fig. 6.
 |
| | Fig. 6 Δwt(T)% of Ca/Si molar ratio vs. T curves for B-2# standard sample with BSA, and the optimal temperature is obtained corresponding to the minimum of Δwt(T)%. The inset is the detail image of the minimum Δwt(T)% vs. T curves. | |
4.3 Acidity measurement of unknown iron ores
Based on the assumption that different samples with similar matrix ablated in the same conditions have the same plasma temperature, the plasma temperature (T = 9440 K) searched by BSA on the B-2# standard sample is considered as the plasma temperature of the unknown samples. Therefore, the obtained temperature can be used to calculate the Ca I/Si I molar ratios of the unknown samples.
The Boltzmann plots after correction for the unknown samples which have the same matrix with the B-2# standard sample are shown in Fig. 7.
 |
| | Fig. 7 Boltzmann plots corrected using the internal reference line for the samples from A-1# to A-7# corresponding to (a)–(g). | |
From Fig. 7, it can be observed that the fitted lines of Ca I and Si I are almost parallel, and the temperature corresponding to the slope is in close proximity to the obtained temperature (T = 9440 K). The intercepts of Ca I and Si I are gradually approaching on Boltzmann plots with the acidity gradually decreasing of the seven samples. The intercepts of Ca I and Si I for the samples from A-1# to A-7# are shown in Table 3.
Table 3 The intercepts of Ca I and Si I for the samples from A-1# to A-7#
| Intercepts |
A-1 |
A-2 |
A-3 |
A-4 |
A-5 |
A-6 |
A-7 |
| Ca I |
−6.026 |
−4.986 |
−4.687 |
−4.451 |
−3.722 |
−3.056 |
−2.933 |
| Si I |
−2.855 |
−2.540 |
−3.193 |
−3.846 |
−3.272 |
−2.697 |
−3.043 |
Fig. 8 shows the comparison between raw spectral intensities and corrected spectral intensities for the selected emission lines of Ca and Si for the unknown samples from A-1# to A-7#.
 |
| | Fig. 8 LIBS spectra before (a) and after (b) self-absorption correction for the samples from A-1# to A-7# with Ca and Si labelled (the internal reference lines are labelled in red). | |
Fig. 9 shows the Boltzmann plots of Ca I and Si I for the unknown samples which have the similar matrix with the B-2# standard sample. The fitted lines of Ca I and Si I are almost parallel, and the plasma temperatures approach to obtained temperature (T = 9440 K).
 |
| | Fig. 9 Boltzmann plots corrected using the internal reference line for the samples from B-1# to B-5# corresponding to (a)–(d). | |
Fig. 10 shows the comparison between raw spectral intensities and corrected spectral intensities for the selected emission lines of Ca and Si for the unknown samples from B-1# to B-5#.
 |
| | Fig. 10 LIBS spectra before (a) and after (b) self-absorption correction for the samples from B-1# to B-5# with Ca and Si labelled (the internal reference lines are labelled in red). | |
From Fig. 7 and 9, Ca I/Si I molar ratios of the unknown samples can be obtained based on the intercepts relationship of Ca I and Si I on the Boltzmann plots. The number concentrations of Ca II and Si II are evaluated by the Saha equation, eqn (9), and Ca/Si molar ratio can be calculated by eqn (9) and (10). Quantitative results of Ca/Si molar ratios for the unknown samples from A-1# to B-5 are shown in Table 4.
Table 4 Quantitative results of Ca/Si molar ratios for the unknown samples from A-1# to B-5
| No. |
Certified value |
Calculated value |
Relative error (%) |
Mean relative error (%) |
| A-1 |
0.075 |
0.076 |
1.333 |
1.800 |
4.903 |
| A-2 |
0.096 |
0.094 |
2.083 |
| A-3 |
0.321 |
0.314 |
2.181 |
| A-4 |
0.643 |
0.647 |
0.622 |
| A-5 |
0.964 |
0.994 |
3.112 |
| A-6 |
1.286 |
1.273 |
1.011 |
| A-7 |
1.607 |
1.643 |
2.240 |
| B-1 |
0.050 |
0.054 |
8.000 |
8.010 |
| B-3 |
0.127 |
0.112 |
11.811 |
| B-4 |
0.018 |
0.017 |
5.556 |
| B-5 |
0.030 |
0.032 |
6.667 |
Table 4 shows the quantitative results of the samples which have the same matrix and the similar matrix with B-2# standard sample. It can be seen that the results of Ca/Si molar ratios are in good agreement with certified values, and the mean relative error (MRE) of the all unknown samples approximates 4.903%. The MRE of the samples with the same matrix to the B-2# standard sample approximates 1.80% which is lower than the similar matrix (MRE = 8.01%). The reason is that the real plasma temperature of the samples which have the same matrix with B-2# standard sample are closer to the searched plasma temperature than the samples which have the similar matrix with B-2# standard sample. mCaO/mSiO2 could be calculated by the stoichiometric relation of Ca/Si molar ratio, and then the acidity of unknown samples can be determined. The acidity of unknown samples are shown in Table 5. The correlation between the certified acidity and predicted acidity of the all unknown samples, shown in Fig. 11, is very good (R2 = 0.9995). Compared with the certified acidity, the root mean square error (RMSE) is 0.0145 and the MRE is 4.01%.
Table 5 The relative error between certified acidity and predicted acidity of unknown samples
| No. |
Certified acidity |
Predicted acidity |
Relative error (%) |
| A-1 |
0.070 |
0.071 |
1.429 |
| A-2 |
0.090 |
0.088 |
2.222 |
| A-3 |
0.300 |
0.293 |
2.333 |
| A-4 |
0.600 |
0.604 |
0.667 |
| A-5 |
0.900 |
0.928 |
3.111 |
| A-6 |
1.200 |
1.188 |
1.000 |
| A-7 |
1.500 |
1.533 |
2.200 |
| B-1 |
0.047 |
0.050 |
6.383 |
| B-3 |
0.119 |
0.105 |
11.765 |
| B-4 |
0.017 |
0.016 |
5.882 |
| B-5 |
0.028 |
0.030 |
7.143 |
 |
| | Fig. 11 Correlation between the certified acidity and predicted acidity of the all unknown samples at the obtained plasma temperature (T = 9440 K). | |
5. Conclusion
In this paper, CF-LIBS combined with BSA is proposed to determine the acidity of iron ore. It is based on a confirmed and reasonable assumption that different samples with similar matrix ablated in the same conditions have the same plasma temperature. Ca I/Si I molar ratios are obtained by the intercepts on the Boltzmann plot drawn by the corrected lines. The number concentrations of primary ionization ions is evaluated by Saha equation. Furthermore, one standard sample is employed to determine the optimal temperature with BSA to improve the reliability of results. The acidity of the iron ores can be calculated according to the obtained value of Ca/Si molar ratios. The calculated acidity of the unknown samples are close to the certified acidity based on the RMSE and MRE which are 0.0145 and 4.01%, respectively. It suggests that CF-LIBS can be a feasible and reliable method to measure the acidity of iron ore in the mineral industry.
Acknowledgements
This research was supported by National Natural Science Foundation of China (no.21375105) and the National Major Scientific Instruments and Equipment Development Projects of China (no. 2011YQ030113).
References
- Z. Q. Hao, C. M. Li, M. Shen, X. Y. Yang, K. H. Li, L. B. Guo, X. Y. Li, Y. F. Lu and X. Y. Zeng, Opt. Express, 2015, 23, 7795–7801 CrossRef CAS PubMed.
- J. H. Luo, K. H. Qiu, Y. C. Qiu and P. C. Zhang, Adv. Mater. Res., 2013, 813, 292–297 CrossRef CAS.
- A. S. Hensler, S. G. Hagemann, C. A. Rosière, T. Angerer and S. Gilbert, Ore Geol. Rev., 2015, 69, 325–351 CrossRef.
- Y. A. Azarova, A. V. Pestov, A. Y. Ustinov and S. Y. Bratskaya, Carbohydr. Polym., 2015, 134, 680–686 CrossRef CAS PubMed.
- D. A. Cremers and R. C. Chinni, Appl. Spectrosc. Rev., 2009, 44, 457–506 CrossRef CAS.
- F. J. Fortes and J. J. Laserna, Spectrochim. Acta, Part B, 2010, 65, 975–990 CrossRef.
- D. W. Hahn and N. Omenetto, Appl. Spectrosc., 2012, 66, 347–419 CrossRef CAS PubMed.
- Q. Lin, Z. Wei, M. Xu, S. Wang, G. Niu, K. Liu, Y. Duan and J. Yang, RSC Adv., 2014, 4, 14392–14399 RSC.
- F. W. Aquino, J. M. Santos, R. R. Carvalho, J. A. Coelho and E. R. Pereira-Filho, RSC Adv., 2015, 5, 67001–67010 RSC.
- P. Yaroshchyk, D. L. Death and S. J. Spencer, J. Anal. At. Spectrom., 2012, 27, 92–98 RSC.
- L. Peter, V. Sturm and R. Noll, Appl. Opt., 2003, 42, 6199–6204 CrossRef CAS PubMed.
- T. Zhang, S. Wu, J. Dong, J. Wei, K. Wang, H. Tang, X. Yang and H. Li, J. Anal. At. Spectrom., 2015, 30, 368–374 RSC.
- V. Sturm, H. U. Schmitz, T. Reuter, R. Fleige and R. Noll, Spectrochim. Acta, Part B, 2008, 63, 1167–1170 CrossRef.
- B. Praher, R. Rössler, E. Arenholz, J. Heitz and J. D. Pedarnig, Anal. Bioanal. Chem., 2011, 400, 3367–3375 CrossRef CAS PubMed.
- A. Ciucci, M. Corsi, V. Palleschi, S. Rastelli, A. Salvetti and E. Tognoni, Appl. Spectrosc., 1999, 53, 960–964 CrossRef CAS.
- M. L. Shah, A. K. Pulhani, G. P. Gupta and B. M. Suri, Appl. Opt., 2012, 51, 4612–4621 CrossRef CAS PubMed.
- F. Colao, R. Fantoni, V. Lazic, L. Caneve, A. Giardini and V. Spizzichino, J. Anal. At. Spectrom., 2004, 19, 502–504 RSC.
- B. Praher, V. Palleschi, R. Viskup, J. Heitz and J. D. Pedarnig, Spectrochim. Acta, Part B, 2010, 65, 671–679 CrossRef.
- D. Bulajic, M. Corsi, G. Cristoforetti, S. Legnaioli, V. Palleschi, A. Salvetti and E. Tognoni, Spectrochim. Acta, Part B, 2002, 57, 339–353 CrossRef.
- L. Sun and H. Yu, Talanta, 2009, 79, 388–395 CrossRef CAS PubMed.
- G. H. Cavalcanti, D. V. Teixeira, S. Legnaioli, G. Lorenzetti, L. Pardini and V. Palleschi, Spectrochim. Acta, Part B, 2013, 87, 51–56 CrossRef CAS.
- J. Dong, L. Liang, J. Wei, H. Tang, T. Zhang, X. Yang, K. Wang and H. Li, J. Anal. At. Spectrom., 2015, 30, 1336–1344 RSC.
- R. Gaudiuso, M. Dell'Aglio, O. De Pascale, S. Loperfido, A. Mangone and A. De Giacomo, Anal. Chim. Acta, 2014, 813, 15–24 CrossRef CAS PubMed.
- H. Bottenbruch, J. Assoc. Comput. Mach., 1962, 9, 161–221 CrossRef.
- http://physics.nist.gov/PhysRefData/Handbook/periodictable.htm.
- A. M. El Sherbini, H. Hegazy and T. M. El Sherbini, Spectrochim. Acta, Part B, 2006, 61, 532–539 CrossRef.
- E. Tognoni, G. Cristoforetti, S. Legnaioli, V. Palleschi, A. Salvetti, M. Mueller, U. Panne and I. Gornushkin, Spectrochim. Acta, Part B, 2007, 62, 1287–1302 CrossRef.
- R. Kurucz, CD-ROM No. 23, Harvard-Smithsonian Center for Astrophysics, 1995 Search PubMed.
- A. De Giacomo, M. Dell'Aglio, O. De Pascale, S. Longo and M. Capitelli, Spectrochim. Acta, Part B, 2007, 62, 1606–1611 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. 

 , λR and IλRmn are the self-absorption coefficient, wavelength and spectral line intensity of the internal reference line, respectively. The Amn, gmn and Em are the spectral parameters of transition between excitation energy levels of m and n. The self-absorption coefficients of all the internal reference lines can be regarded as 1
, λR and IλRmn are the self-absorption coefficient, wavelength and spectral line intensity of the internal reference line, respectively. The Amn, gmn and Em are the spectral parameters of transition between excitation energy levels of m and n. The self-absorption coefficients of all the internal reference lines can be regarded as 1  . Therefore, the corrected spectral line intensities can be expressed as:
. Therefore, the corrected spectral line intensities can be expressed as: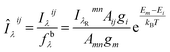







 respectively represent the intercept of atoms of element s1 and s2 on the Boltzmann plot, CII and CI are the number concentrations of ions and atoms of the given elements.
respectively represent the intercept of atoms of element s1 and s2 on the Boltzmann plot, CII and CI are the number concentrations of ions and atoms of the given elements.  molar ratio is calculated using the relationship of
molar ratio is calculated using the relationship of  on the Boltzmann plot, which can overcome the restriction that the sum of the relative concentration of all species equal unity for the calculation of the experimental factor F. me is the electron mass (kg), h is Planck's constant (J s), Eion is the energy of first ionization (J). Concerning the oxygen content, it has been calculated by the stoichiometric relation in the mineral oxide of the detected elements. Therefore, the mass ratios of oxides can be calculated using the equation reported below. Then, the acidity of iron ore can be determined.
on the Boltzmann plot, which can overcome the restriction that the sum of the relative concentration of all species equal unity for the calculation of the experimental factor F. me is the electron mass (kg), h is Planck's constant (J s), Eion is the energy of first ionization (J). Concerning the oxygen content, it has been calculated by the stoichiometric relation in the mineral oxide of the detected elements. Therefore, the mass ratios of oxides can be calculated using the equation reported below. Then, the acidity of iron ore can be determined.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054 K based on the Fig. 4(b). Herein, the optimal plasma temperature which is closest to the real plasma temperature could be obtained by BSA in a range from 9419 K to 11054 K. BSA runs on the B-2# standard sample based on Fig. 1 by eqn (5)–(10). In Fig. 6, the curve shows variation tendency of Δwt(T)% along with the plasma temperature T, and the detail image of optimal plasma temperature is plotted in the inset of figure to highlight the Δwt(T)% trend around the optimal plasma temperature. The search is stopped until the relative error of Ca/Si molar ratio is minimum (Δwt(T)% = 0.6%, less than 0.8%). The optimal plasma temperature searched by BSA is 9440 K, as shown in Fig. 6.
054 K based on the Fig. 4(b). Herein, the optimal plasma temperature which is closest to the real plasma temperature could be obtained by BSA in a range from 9419 K to 11054 K. BSA runs on the B-2# standard sample based on Fig. 1 by eqn (5)–(10). In Fig. 6, the curve shows variation tendency of Δwt(T)% along with the plasma temperature T, and the detail image of optimal plasma temperature is plotted in the inset of figure to highlight the Δwt(T)% trend around the optimal plasma temperature. The search is stopped until the relative error of Ca/Si molar ratio is minimum (Δwt(T)% = 0.6%, less than 0.8%). The optimal plasma temperature searched by BSA is 9440 K, as shown in Fig. 6.








