Recognizing the reactive sites of SnFe2O4 for the oxygen evolution reaction: the synergistic effect of SnII and FeIII in stabilizing reaction intermediates†
Anubha
Rajput
a,
Pandiyan
Sivasakthi
 b,
Pralok K.
Samanta
b,
Pralok K.
Samanta
 *b and
Biswarup
Chakraborty
*b and
Biswarup
Chakraborty
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology Delhi, Hauz Khas, 110016, New Delhi, India. E-mail: cbiswarup@chemistry.iitd.ac.in
bDepartment of Chemistry, Birla Institute of Technology and Science Pilani (BITS Pilani), Hyderabad Campus, Hyderabad-500078, India. E-mail: pralokkumar.samanta@hyderabad.bits-pilani.ac.in
First published on 22nd October 2024
Abstract
Among the reported spinel ferrites, the p-block metal containing SnFe2O4 is scarcely explored, but it is a promising water-splitting electrocatalyst. This study focuses on the reaction kinetics and atomic scale insight of the reaction mechanism of the oxygen evolution reaction (OER) catalyzed by SnFe2O4 and analogous Fe3O4. The replacement of FeIIOh sites with SnIIOh in SnFe2O4 improves the catalytic efficiency and various intrinsic parameters affecting the reaction kinetics. The variable temperature OER depicts a low activation energy (Ea) of 28.71 kJ mol−1 on SnFe2O4. Experimentally determined second-order dependence on [OH−] and the prominent kinetic isotope effect observed during the deuterium labelling study implies the role of hydroxide ions in the rate-determining step (RDS). Using density functional theory, the reaction mechanism on the (001) surface of SnFe2O4 and Fe3O4 is modelled. The DFT simulated free energy diagram for the reaction intermediates shows an adsorbate evolution mechanism (AEM) on both the ferrites' surfaces where the formation of *OOH is the RDS on SnFe2O4 while *O formation is the RDS on Fe3O4. In contrast to other spinel ferrites, where individual metal sites act independently, in case of SnFe2O4, a synergy between FeIIIOh and the neighbouring SnIIOh atoms is responsible for stabilizing the OER intermediates, enhancing the catalytic OER activity of SnFe2O4 as compared to isostructural Fe3O4.
Introduction
Spinel oxides with a common formula AB2O4 exhibit a cubic close-packed lattice with two basic crystallographic sites, namely octahedral (Oh) and tetrahedral (Td) sites. The normal spinel has a configuration of AIITd(BIIIOh)2O4 where A2+ ions occupy the tetrahedral sites, while B3+ ions occupy the octahedral sites, whereas in an inverse spinel with a configuration of BIIITd(AIIOhBIIIOh)O4, the divalent cations occupy half of the octahedral sites.1 The presence of mixed-valence cations with accessible multiple redox states results in high electronic conductivity, favourable for electrocatalytic OER performance.2 In the last decade, cobaltite spinel-oxide MCo2O4 materials (M = Mn, Co, Ni, Zn, etc.) were explored as the anode material for the OER and the CoOh sites were believed to be the reactive sites for the OER.3–5 The inverse-spinel Fe3O4 and metal ferrites such as NiFe2O4 and CoFe2O4 nanoparticles also exhibit remarkable OER activity.6 Bimetallic spinel ferrites have been shown to outperform their monometallic counterparts toward the OER.7 To manifest the experimental difference in the catalytic activity of the bimetallic and monometallic catalysts, computational modelling and an atomistic level understanding of the reaction mechanism are crucial. Theoretical studies performed with NiFe2O4 identified that the nickel sites exposed on the (001) plane are active for the OER and follow a lattice oxygen mechanism (LOM).6 However, on the (001) surface of CoFe2O4, both the cobalt and iron sites participate independently in the OER as individual reactive sites following the adsorbate evolution mechanism (AEM).6 In general, due to poor covalency between the transition metal and oxygen, the OER on the spinel oxides follows the AEM.8 However, a recent experimental study revealed the LOM as the dominant pathway of the OER on NiFe2O4.9 Tin ferrite (SnFe2O4) is another important metal ferrite spinel that has been recently reported as a bi-functional electrode material to perform electrochemical water splitting at very low overpotentials.10 The SnFe2O4 lattice exhibits three potent catalytic sites viz. SnIIOh, FeIIITd, and FeIIIOh, out of which Fe3+ sites were predicted to facilitate the OER. However, to uncover the real OER mechanism and to determine the possible effect of heteroatom doping, a detailed electro-kinetics and computational study is very important.To validate the experimentally obtained electro-kinetic data (intrinsic reaction parameters) and to understand the reaction mechanism of the OER, theoretical studies are also important. Recently, Goddard's group proposed that during the OER, FeIV and NiIV synergistically act in stabilizing the reaction intermediates, to impart excellent activity to NiFe(O)OH.11 Temperature-dependent and electrolyte concentration-dependent electrokinetics on NiFe LDH studied by Hu and co-workers also yielded several intrinsic parameters.12 Carter and co-workers also studied the effect of temperature on the activity of NiFe(O)OH, with a hundred-fold increase in the catalytic current at a fixed potential.13 Driess's group substituted CoII with redox inactive ZnII in Co3O4 and found that ZnII stabilized CoIV, which are the main active sites during the OER.14 Pan and coworkers reported the effect of temperature on the performance of Co3O4.15 Additionally, Boettcher and his group have shown that during alkaline electrolysis, hydroxide anions get adsorbed on the catalyst surface as the major reactant for the OER, and their concentration in the electrolyte determines the overpotential and Tafel slope, i.e. activity and kinetics, respectively, of the OER process.16,17 Besides, certain variables affecting the OER activity of the spinels are the electrolyte, pH, and temperature, which in turn, directly affect the kinetics of the catalytic reaction. Different intrinsic electrochemical parameters like activation energy (Ea), the magnitude of the anodic transfer coefficient (αa), reaction order (m), etc., determine the individual electrokinetic properties of the catalyst, which collectively hints at the reaction mechanism and kinetics on the catalyst surface. Although Chakraborty and coworkers have demonstrated SnFe2O4 as a promising bifunctional electrocatalyst for the OER, the role of tetrahedral and octahedral sites, particularly the role of the p-block metal SnII, and the operating mechanism for the OER on the SnFe2O4 surface is still conspicuous.
Herein, two structurally related inverse-spinels, SnFe2O4 and Fe3O4, have been taken as electrocatalysts to perform the alkaline OER, while temperature-dependent electrocatalysis is performed to obtain important intrinsic parameters that can establish the reaction mechanism. The correlation of temperature-dependent and variable concentration studies provides information about the activation energy, reaction order, and the charge transfer coefficient during the OER. Accompanied by the labelling study with D2O and the kinetic isotope effect (KIE) on the OER, a detailed theoretical study helps to determine the energetics of different reaction steps of the operative AEM for the OER. The introduction of electron-rich Sn in the spinel Fe3O4 and its effect on the OER are understood by performing detailed electrokinetics and in-silico studies. In contrast to the extensive experimental studies, theoretical research on the atomistic OER mechanism in spinel oxide catalysts is still rare, which is a prerequisite to designing efficient electrocatalysts. This study thereby addresses the gap through a combined experimental and theoretical study of the OER mechanism on two isostructural spinels, SnFe2O4 and Fe3O4.
Experimental section
Electrokinetic measurements
To study the electrocatalytic activity, a potentiostat (Gamry Interface 1010E) instrument controlled by Echem Analyst™ software was used. The electrochemical study was done in a three-electrode system using a 1 M KOH electrolyte (pH 13.6) where nickel foam (NF) loaded with catalyst was used as a working electrode (WE), a graphite rod was used as a counter electrode (CE) and an Hg/HgO electrode (E° = 0.098 V vs. RHE) was used as a reference electrode (RE). CV and LSV were performed to study the electrochemical OER. The manual iR compensation (R = resistance of the solution including the test electrode) was 85%, in which the value of uncompensated resistance was obtained from the impedance study. In 1 M KOH, the reference potential with respect to Hg/HgO was converted to potential with reference to the Reversible Hydrogen Electrode (RHE). To study the OER, linear sweep voltammetry (LSV) was performed within a potential range of 1.0 V to 1.8 V (vs. RHE) with a scan rate of 1 mV s−1. The obtained polarographs were used to calculate the overpotential at a fixed current density. A temperature-dependent study was performed by varying the temperature from 303 to 343 K. For the temperature-dependent electrochemical study, the cell temperature was recorded with a thermometer dipped into the cell, and the cell was kept in an oil bath to control the temperature. To determine Ea from the temperature-dependent study, the slope of the Arrhenius plot of j0vs. temperature was found, and the apparent electrochemical activation energy (Ea) was calculated using the Arrhenius relation: | (1) |
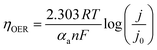 | (2) |
 | (3) |
 | (4) |
The kinetic isotope effect (KIE) was investigated to identify the RDS of the electrocatalytic OER process. For investigating the KIE, 25% D2O solution in water was used for the preparation of the KOH solution, and the resultant electrolyte was used for the electrocatalytic OER study. Substitution of a proton with an isotope (D) has a significant effect on the reaction rate due to the two-fold increase in mass.22 KIE is defined as the ratio of the reaction rate constant when protons are available to the reaction rate constant when deuterium ions are available.
The catalytically inactive alkali and alkali earth metal cations in the electrolyte may affect the activity of the catalyst during the OER. In a different set of experiments, the electrolyte was also varied from 1 M LiOH, 1 M NaOH to 1 M KOH. The double layer capacitance (Cdl) of the catalyst was determined by recording the cyclic voltammogram (CV) of each catalyst in a non-faradaic region of 0.8953 V to 0.9953 V (vs. RHE) in 1 M KOH at varying scan rates (i.e., 10, 25, 50, 100, 150, and 200 mV s−1). To determine Cdl, the charging current was measured from each redox half of the CV curve at midway potential, which was then plotted against the scan rate to obtain a linear slope. This slope represents Cdl at the electrode–electrolyte interface.
The free energy change in these electrochemical oxidation reactions (i.e., the adsorption-free energies of intermediates) has been calculated using the equation proposed by Nørskov and co-workers.23
| ΔG = ΔE + ΔEZPE − TΔS − neU | (5) |
Results and discussion
The cubic phase inverse spinel-type SnFe2O4 and Fe3O4 were synthesized by a well-established method using the appropriate stoichiometry of metal salts. The crystallinity of SnFe2O4 and Fe3O4 has been confirmed by PXRD and other spectro/microscopic techniques.10 The major PXRD reflections were assigned according to JCPDS 11-0614, which confirmed the presence of a cubic phase with the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (Fig. 1a). The bulk morphology and size of the catalysts were viewed through high-resolution transmission electron microscopy (HR-TEM). The SnFe2O4 particles appeared as irregular fragments with an average size of ca. 5 nm (Fig. 1b) and the exposed (311) plane with an interplanar distance of 0.25 nm (Fig. 1b inset). The bulk morphology and composition of the as-synthesized SnFe2O4 particles were verified by field emission scanning electron microscopy (FESEM) imaging and FESEM-energy dispersive X-ray (EDX) elemental mapping. The bulk morphology shows randomly agglomerated semi-spherical nanoparticles (Fig. S1a–S1c†). The FESEM-EDX elemental mapping indicated that composite elements are uniformly distributed over the surface of the catalyst (Fig. S1d–S1f†). The FESEM-EDX elemental ratio for Sn
m (Fig. 1a). The bulk morphology and size of the catalysts were viewed through high-resolution transmission electron microscopy (HR-TEM). The SnFe2O4 particles appeared as irregular fragments with an average size of ca. 5 nm (Fig. 1b) and the exposed (311) plane with an interplanar distance of 0.25 nm (Fig. 1b inset). The bulk morphology and composition of the as-synthesized SnFe2O4 particles were verified by field emission scanning electron microscopy (FESEM) imaging and FESEM-energy dispersive X-ray (EDX) elemental mapping. The bulk morphology shows randomly agglomerated semi-spherical nanoparticles (Fig. S1a–S1c†). The FESEM-EDX elemental mapping indicated that composite elements are uniformly distributed over the surface of the catalyst (Fig. S1d–S1f†). The FESEM-EDX elemental ratio for Sn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe was also found to be ∼1
Fe was also found to be ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, whereas O was found to exceed slightly the expected ratio which is possibly due to the surface adsorbed O from the air (Fig. S1g†). The crystal lattice of inverse spinel SnFe2O4 is composed of [SnIIO6]Oh, [FeIIIO6]Oh, and [FeIIIO4]Td units, where [SnIIO6]Oh occupies half of the octahedral sites, while [FeIIIO6]Oh and [FeIIIO4]Td occupy another half of octahedral and tetrahedral sites, respectively (Fig. 1c). The adjoining multiple-unit cells along the three axes of the cell build up the bulk structure (Fig. 1c). The (001) surface can be created by placing a 2 × 2 supercell of SnFe2O4 layers. The side or top view of the (001) surface points out that the [SnIIO6]Oh and [FeIIIO6]Oh sites are exposed on the surface and positioned alternatively to each other via μ2-oxo bridging. In the case of the isostructural ferrite Fe3O4 (001) surface, [SnIIO6]Oh sites will be replaced by the [FeIIO6]Oh sites.6–9
2, whereas O was found to exceed slightly the expected ratio which is possibly due to the surface adsorbed O from the air (Fig. S1g†). The crystal lattice of inverse spinel SnFe2O4 is composed of [SnIIO6]Oh, [FeIIIO6]Oh, and [FeIIIO4]Td units, where [SnIIO6]Oh occupies half of the octahedral sites, while [FeIIIO6]Oh and [FeIIIO4]Td occupy another half of octahedral and tetrahedral sites, respectively (Fig. 1c). The adjoining multiple-unit cells along the three axes of the cell build up the bulk structure (Fig. 1c). The (001) surface can be created by placing a 2 × 2 supercell of SnFe2O4 layers. The side or top view of the (001) surface points out that the [SnIIO6]Oh and [FeIIIO6]Oh sites are exposed on the surface and positioned alternatively to each other via μ2-oxo bridging. In the case of the isostructural ferrite Fe3O4 (001) surface, [SnIIO6]Oh sites will be replaced by the [FeIIO6]Oh sites.6–9
Temperature-dependent OER and activation energy (Ea)
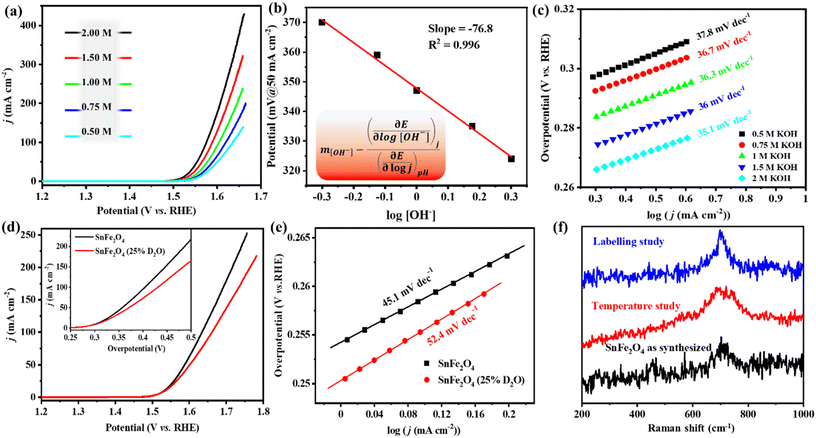
During the OER-LSV study at room temperature (303 K), the polarization curve of the cathodic scan with SnFe2O4/NF and Fe3O4/NF displayed a large current density (j > 300 mA cm−2) at the switching potential (Fig. 2a and S2a†). At a current density of 10 mA cm−2, SnFe2O4 showed an overpotential (η) of 285 mV, while the reference material Fe3O4 showed a larger overpotential of 301 mV (Fig. 2a and S2a†). The effect of temperature on the electrocatalytic OER activity was studied in a 1 M KOH electrolyte with a temperature variation from 303 to 343 K (30 to 70 °C) (Fig. 2a). The effect of temperature on SnFe2O4/NF was compared with Fe3O4/NF as a control material (Fig. S2†). Upon examining the effect of temperature on the OER activity of the catalysts, it could be established that η is inversely proportional to an increase in temperature (Fig. S3†). A plot between overpotential (η) vs. 1/T at different higher current densities of 10, 50, 100, and 200 mA cm−2 shows that a linear relationship holds for Fe3O4 at all temperatures, while for SnFe2O4, a deviation from the linear relationship could be observed (Fig. S3a and S3b†). At a high current of 200 mA, a higher slope of 216 V K for SnFe2O4 indicates greater dependence of SnFe2O4 activity on the temperature (Fig. S3c†). The exchange current density (j0@V ≈ 1.23 V vs. RHE) at different temperatures was calculated from the experimental LSV curves. The Ea values of both catalysts were found using eqn (1). The Ea value of Fe3O4 turns out to be 3 times larger than that of SnFe2O4 (Fig. 2b and S2a inset†). For SnFe2O4, an Ea value of 28.71 kJ mol−1 was comparable to other reports like 25 ± 12 kJ mol−1 for NiFeOx,24 while it is considerably lower than 75 kJ mol−1 reported for spinel NiCo2O4 by Davidson et al.25E a can be further used to find the change in the rate of the reaction upon varying the temperature. The increase in the rate of the reaction on moving from 303 K to 343 K was 3.7 times, clearly exhibiting the role of temperature in improving the activity of SnFe2O4. With the increase in temperature, the charge transfer resistance (Rct) decreases, while it is shown to increase below −10 °C to such an extent that Rct becomes a predominant factor during an electrochemical reaction.26 Upon increasing the temperature, the Rct value decreases in the case of SnFe2O4 as well as Fe3O4, but the effect was more pronounced in the case of SnFe2O4, with a decrease of 1.81 Ω, while only 1.00 Ω for Fe3O4 (Fig. S4†).
The Raman study done after OER-LSV of SnFe2O4 and Fe3O4 at 343 K showed that the prominent Raman peak at 672 cm−1 corresponding to the (A1g) mode of spinels is retained, and no new phase could be observed (Fig. 3f and S6d†). In an earlier report on NiCo2O4 by Zhou et al., it was found that the Raman spectra or the structure of the catalyst was unchanged after 45 °C until the potential was not increased.27 Similarly, Zhang et al. found spinel Co3O4 to be structurally stable up to 75 °C during the oxygen evolution reaction.15 It is found that at lower potentials, the spinel structures serve as the active species of the OER,10,27 unlike the electrochemically (in situ) formed oxyhydroxide active phases in other transition metal-based catalysts.28–30
Tafel analysis and charge transfer coefficient (αa)
The Tafel slope values of the OER within the temperature range of 303–343 K were calculated according to eqn (2). The average Tafel slope of 46 ± 3 mV dec−1 for SnFe2O4 signifies peroxide bond formation as the RDS and 2 electron transfer before this electrochemical step;31 alongside, a small variation of the Tafel slope by 6 mV dec−1 upon temperature variation indicates that the RDS does not change with the temperature (Fig. 2c). The Tafel slope value for SnFe2O4 decreased from 49 mV dec−1 (at 303 K) to 43 mV dec−1 (at 343 K), which was three times higher than Fe3O4, which shows a change of only 2 mV dec−1 on moving from 303 to 343 K (Fig. 2c and S2b†). These results indicate a greater kinetic dependence of SnFe2O4 activity on temperature. Another kinetic parameter, i.e. α, the fraction of potential at the electrode–electrolyte interface, is used to increase the rate of the reaction by lowering the energy barrier of the reaction. Specifically, during the OER, α can be replaced by an anodic charge transfer coefficient (αa), which can be related to the Tafel slope. αa was calculated at the individual temperature in the low current regions (LCR). The average value of αa = 1.35 ± 0.04 was calculated for SnFe2O4, while 1.4 ± 0.03 was calculated for Fe3O4, respectively (Fig. 2d). The knowledge of αa also enables the determination of the symmetry factor β according to eqn (3).19Effect of [OH−] and order of the reaction (m)
The change in the reactant concentration at a constant voltage determines the reaction order (m). To elucidate the order of the OER (m) in the case of SnFe2O4 and Fe3O4, OER-LSV was performed in varying concentrations of KOH solution (Fig. 3a and S5a†). The water activity ([OH−]) was varied between 0.5 M and 2 M, and the OER polarization curves were recorded at 303 K. The m value was determined using eqn (4), where the denominator part of the equation is the Tafel slope, and the numerator part is the slope shown in Fig. 2b and c. With a decrease in the reactant, [OH−], the cell voltage increased, and the limiting current density decreased (Fig. 3a). The logarithmic plots of the overpotential at high current against the logarithmic [OH−] gave a slope of −76.8, yielding a reaction order of ∼2 for SnFe2O4 (Fig. 3b) while ∼1 for Fe3O4 (Fig. S5b†).12 In the case of SnFe2O4 as well as Fe3O4, concentration-dependent Tafel slopes have a linear relationship with an increase in [OH−], and a small change in the Tafel slope from 0.5 M KOH to 2 M KOH indicates that the RDS essentially remains the same, with the numerator part being constant in eqn (4) (Fig. 3c and S5c†).Kinetic isotope effect (KIE) and involvement of protons in the RDS
The difference in the vibrational energies of H and D bonds gives rise to the KIE. The OER-LSV curves of SnFe2O4 and Fe3O4 were studied in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ::
::![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O
D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O mixture of 1 M KOH, and the LSV polarogram was compared with the OER-LSV curve in 1 M KOH (Fig. 3d and S6a†). The KIE was calculated for SnFe2O4 and Fe3O4 in the overpotential ranges of 0.35–0.45 mV and 0.35–0.4 mV, respectively (Fig. S6c†). The variation of the isotope effect (IE) with varying potentials indicates that the IE is a kinetic phenomenon.32 The KIE of SnFe2O4 and Fe3O4 yielded average values of 1.29 and 3.5, respectively. The obtained value (1 < KIE < 2) for SnFe2O4 signifies the secondary KIE where the RDS does not directly involve the breaking of the D–O/H–O bond, while a higher value (2 < KIE < 7) in the case of Fe3O4 indicates the primary KIE, i.e., the bond involving the isotope (D) is being formed or broken.22 In Fe-containing catalysts, the decrease in the OER activity accompanied by an increase in the Tafel slope during alkaline OER in deuterated water may be due to the effect on the interactions of intermediates with adsorbed water. The increase in the Tafel slope observed for SnFe2O4 as well as Fe3O4 on moving from H2O to D2O indicates the variation in the enthalpy of formation of the intermediate in the RDS, i.e., the interaction between *O⋯HO− (the formation of O–O bond) (Fig. 3e and S6b†).33 The exchange of hydrogen with deuterium does not significantly affect the electronic structure or the energetics of the catalyst surface. It primarily affects the reaction rates rather than the surface of the catalyst. To validate this fact, the Raman study of SnFe2O4 and Fe3O4 was done after OER-LSV at 343 K, and the structure of the catalysts was found to be unchanged after the KIE study (Fig. 3f and S6d†).
H2O mixture of 1 M KOH, and the LSV polarogram was compared with the OER-LSV curve in 1 M KOH (Fig. 3d and S6a†). The KIE was calculated for SnFe2O4 and Fe3O4 in the overpotential ranges of 0.35–0.45 mV and 0.35–0.4 mV, respectively (Fig. S6c†). The variation of the isotope effect (IE) with varying potentials indicates that the IE is a kinetic phenomenon.32 The KIE of SnFe2O4 and Fe3O4 yielded average values of 1.29 and 3.5, respectively. The obtained value (1 < KIE < 2) for SnFe2O4 signifies the secondary KIE where the RDS does not directly involve the breaking of the D–O/H–O bond, while a higher value (2 < KIE < 7) in the case of Fe3O4 indicates the primary KIE, i.e., the bond involving the isotope (D) is being formed or broken.22 In Fe-containing catalysts, the decrease in the OER activity accompanied by an increase in the Tafel slope during alkaline OER in deuterated water may be due to the effect on the interactions of intermediates with adsorbed water. The increase in the Tafel slope observed for SnFe2O4 as well as Fe3O4 on moving from H2O to D2O indicates the variation in the enthalpy of formation of the intermediate in the RDS, i.e., the interaction between *O⋯HO− (the formation of O–O bond) (Fig. 3e and S6b†).33 The exchange of hydrogen with deuterium does not significantly affect the electronic structure or the energetics of the catalyst surface. It primarily affects the reaction rates rather than the surface of the catalyst. To validate this fact, the Raman study of SnFe2O4 and Fe3O4 was done after OER-LSV at 343 K, and the structure of the catalysts was found to be unchanged after the KIE study (Fig. 3f and S6d†).
Effect of the electrolyte cation on the OER activity
The OER-LSV curves of Fe3O4 and SnFe2O4 were recorded in 1 M KOH, NaOH, and LiOH, where the metal ions K+, Na+, and Li+, respectively, have ionic radii of 1.38 Å, 1.02 Å, and 0.76 Å (Fig. 4a and b). In the case of SnFe2O4, a significant anodic shift in the onset potential of ca. 100 mV was observed from KOH to LiOH, accompanied by a decrease in the limiting current value. As the size of alkali metal cations decreases, the overpotential increases in the order, KOH (282 mV), NaOH (327 mV), and LiOH (380 mV), which leads to the conclusion that bigger cations help in enhancing the OER activity (Fig. 4a). A similar trend of activity was previously observed in the literature.34,35 The choice of metal ions in the electrolyte affects the OER process in terms of the electrochemical surface area (ECSA), reaction mechanism, intermediate formation, kinetics, etc. Boettcher and co-workers found out that during the OER on the NiO(OH) surface, other alkali earth metals like Mg2+ and Ca2+ in the electrolyte were found to inhibit the activity due to their higher Lewis acidity and strong affinity towards the OER intermediates.34 It is assumed that the electrolyte cation interacts with the peroxo species formed during the acid–base reaction step of the OER process, as shown below:36| M–OO–H + C+ ↔ M–OO−–C+ + H+ |
The resistance in various electrolytes can also be verified by the electrochemical impedance study (EIS) done with SnFe2O4 and Fe3O4 in 1 M each of KOH, NaOH, and LiOH. EIS was also used to determine the capacitance value by the fitting of the equivalent circuits. The EIS study was performed for SnFe2O4 in KOH, NaOH, and LiOH at fixed potentials of 1.54 V, 1.58 V, and 1.62 V (vs. RHE), respectively, and the low-frequency impedance increased in the order, Li > Na > K (Fig. 4e). The charge transfer resistance of the catalyst was the least in the case of KOH (1.9 Ω), followed by NaOH (2.4 Ω) and LiOH (2.66 Ω). The constant phase element (CPR) model was used to fit the corresponding circuits since it also represents the capacitor (double layer) formed at the electrode–electrolyte interface (Fig. 4e inset). The double layer capacitance (Cdl), which is a way to evaluate the electrochemically active surface area, was calculated using the Rct value from the CPE fitting (Fig. S7†). The maximum Cdl value of 9.05 mF was attained for SnFe2O4 in 1 M KOH, which is also validated by the Cdl values obtained by the CV cycles in non-faradaic regions (Fig. S8†). As anticipated, the highest Cdl value of 0.86 mF was obtained for SnFe2O4 in 1 M KOH and a comparable Cdl in NaOH and LiOH using the cyclic voltammetry curves in the non-faradaic region (Fig. S8†). A similar trend of impedance and Cdl was observed in the case of Fe3O4 in 1 M each of KOH, NaOH, and LiOH (Fig. 4f and S9†).
DFT study
DFT calculations were carried out within the (001) plane using a 2 × 2 supercell of inverse spinel SnFe2O4 (a = 17.44 Å, b = 17.44 Å, c = 30.00 Å, and α = β = γ = 90°) (Fig. 1c) to study the OER kinetics. The oxygen evolution reaction (OER) is comprised of the following four elementary steps, each involving the transfer of an electron until OH− is oxidized to water (H2O).23,40| OH− + * → *OH + e− | (1) |
| *OH + OH− → *O + H2O + e− | (2) |
| *O + OH− → *OOH + e− | (3) |
| *OOH + OH− → * + H2O + O2 + e− | (4) |
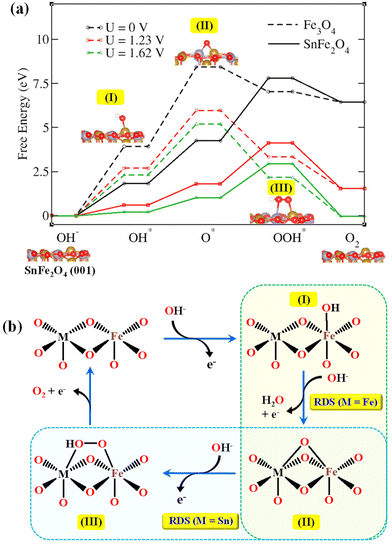
The active site preference during alkaline OER was compared between Fe3O4 and SnFe2O4 spinels. The energy profile diagram (Fig. 5) illustrates an OER pathway at 0 V, 1.23 V, and 1.62 V, the OER overpotential, where the adsorption-free energies of intermediates were calculated using eqn (5). Between SnFe2O4 and Fe3O4, the lowest overall OER free energy change was shown by SnFe2O4 at different potentials (Table S1†). In the case of SnFe2O4, the energetically uphill reaction step, or the RDS, leads to the formation of *OOH, with endothermic free energy of 1.93 eV for an applied overpotential of 1.62 V.41 Fe3O4 exhibits a higher overall OER free energy change with endothermic free energy of 2.89 eV for its rate-determining step of *O formation with an applied overpotential of 1.62 V.
Proposed OER mechanism
The OER is a complex multistep reaction. After prolonged experimental and computational studies, three different OER intermediates, namely Oads, OHads, and OOHads, have been identified during the catalytic mechanism. Rossmeisl et al.42 performed DFT calculations for rutile RuO2, IrO2, and TiO2. The DFT calculations considered the concerted proton-coupled electron transfer (PCET) steps, i.e., one H+ and one e− are transferred in a single kinetic step. Contrary to other mechanisms,43 Rossmeisl's peroxide path (RPP) involves peroxide formation in the third step due to a lesser activation barrier than the direct formation of O2 from Oad.42,44 For a multistep reaction, the overall rate of the reaction is limited to the rate of its slowest step, and the overall rate cannot exceed the rate of the slowest step. Generally, during heterogeneous electrocatalytic reactions, the reaction step involving a single intermediate species and a single type of active site is considered to be the RDS. Either the deprotonation of OHads (OHads = Oads + H+ + e−) or the O–O bond formation (Oads + OH− = OOHads + e−) is often found to be the RDS for heterogeneous systems.45 From the results of the calculated Tafel slope (46 ± 3 mV dec−1) over a temperature range and a reaction order close to 2, the RDS of the metal peroxo bond can be acknowledged. The results of the symmetry factor also complement the hypothesis that step 3 of RPP, i.e. metal peroxo bond, is the rate-determining step of SnFe2O4.To understand the improved OER activity of SnFe2O4 in comparison with Fe3O4, DFT calculations were carried out to understand the atomic scale OER mechanism on the Fe active sites of the (001) surface (Fig. 5a and S10a†). The adsorbed intermediates during the OER, i.e., *OH, *O, and *OOH are stabilized on the (001) catalyst surface by hydrogen bonding with solvent water molecules. The OER process on Fe3O4 (001) was limited by the oxidation of *OH to *O, perhaps due to the weak binding between *O and Fe atoms (Fig. 5b and S10b†). Replacing FeII with SnII ions in the Fe3O4 lattice improves the OER activity of the (001) surface of SnFe2O4 due to the synergistic effect of Fe and Sn in stabilizing the OER intermediates. As a consequence, the rate-limiting step for SnFe2O4 changes to the conversion of *O to *OOH (Fig. 5b). The formation of OOH* on the SnFe2O4 surface is an endothermic process (ΔHf = 3.547 eV) and is facilitated by the applied potential during the electrochemical OER. The direct involvement of the isotopically labelled species in the RDS of Fe3O4, i.e., the deuteration of *OD to form *O, was supported by the primary KIE shown by Fe3O4. Moreover, the secondary KIE shown by SnFe2O4 supported the indirect involvement of O–H/O–D in the RDS.
From the literature studies, it is evident that for spinel ferrites, the (001) surface is most suited for the OER DFT study. Piccinin and coworkers found that on the (001) surface of Fe3O4, both terminal oxygen and bridging oxygen atoms can participate in the OER. While considering the distorted bulk truncated (DBT) model, the OER in Fe3O4 was found to proceed via the terminal oxygen, and the RDS was the dehydrogenation of the *OH group. Upon considering the subsurface cation vacancy (SCV) model, the OER proceeded via the bridging oxygen, and the RDS was the formation of the hydroperoxo species.40 Similarly, a DFT study was performed to understand the OER process on the (001) surface of inverse spinel NiFe2O4 and CoFe2O4. For NiFe2O4, Fe is the main catalytic site where the OER happens preferably by the LOM pathway with O–O as the RDS. In the case of CoFe2O4, Co and Fe can participate in the OER as the active catalytic site. Fe-site favoured the LOM pathway whereas the Co sites preferred the AEM pathway, thus concluding the coexistence of two active sites in CoFe2O4.6 Likewise, in a DFT study performed by Peng et al. on spinel undoped, and Fe- and Ni-doped Co3O4 (001) surfaces, the octahedral Co sites were found to be OER active in all cases. However, the RDS changed from *OH formation in the case of Ni-doped Co3O4 to *OOH formation in the case of Fe-doped Co3O4.46 Interestingly, unlike other metal ferrites, where individual metal sites can act independently in assisting the catalytic OER, in the case of SnFe2O4, FeIII and SnII act in synergy to facilitate the OER on the (001) surface.
Conclusion
Currently, the rational design of electrocatalysts for the OER is limited by the vague understanding of the in-depth kinetic analysis and reaction mechanism, particularly for the OER. In this research, the experimental results, coupled with the computational modelling, could enlighten a path to the detailed understanding and designing of the electrocatalysts, eventually leading to a more efficient electrocatalytic OER. As a contribution towards understanding the OER on the spinel surface and the role of heteroatom substitution in the lattice, the reaction mechanism and electrokinetic parameters were studied on two isostructural inverse spinels, SnFe2O4 and Fe3O4. The experimentally obtained Ea values from the temperature-dependent study of SnFe2O4 and Fe3O4 suggest that the substitution of FeII with SnII in the Fe3O4 lattice decreases the activation energy of the OER by as much as three times. Alongside, the reaction order also changed from 2 in the case of SnFe2O4 to 1 in the case of Fe3O4. These experimental findings were the primary evidence of the change in the RDS during the OER as a result of the substitution of FeII by a heteroatom in the catalyst lattice. A slight change in the Tafel slope with temperature in the case of SnFe2O4 and Fe3O4 substantiated that the rate-determining step, albeit different, was independent of the change in the cell temperature. The DFT study on the (001) surface of SnFe2O4 and Fe3O4 validated that the reaction on both catalysts was limited to the AEM pathway, which was also supported by the experimentally determined intrinsic parameters. On the (001) surface of Fe3O4, the formation of *O was the rate-limiting step, while on SnFe2O4, the metal-peroxo (*OOH) formation became the RDS. From the current research, it can be discerned that the presence of a heteroatom in the spinel ferrite may drastically affect the reaction pathway and, hence, the RDS during the electrocatalytic OER. Conclusively, the change in the reaction mechanism and the RDS upon p-block metal doping in Fe3O4 is the key finding. Therefore, analysis of the role of each catalytic site during the reaction mechanism is critical for engineering the catalyst to further enhance its OER efficiency. Unlike other DFT-modelled spinel catalysts, where individual 3d transition metal centres act independently to catalyze the OER, the FeIIIOh centre in inverse-spinel SnFe2O4 acts synergistically with the SnIIOh unit to facilitate the catalytic OER.Data availability
Characterization of the catalysts by spectroscopic, microscopic, PXRD, and analytical techniques along with the details of the experimental and electrochemical methods are included in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
AR sincerely acknowledges the PMRF scheme of the Gov. of India (ID 1401195) for the fellowship. BC sincerely acknowledges the IIT Delhi seed grant PLN12/04CY. The authors thank the Central Research Facility-IIT Delhi for the microscopic and XPS facilities. PS and PKS acknowledge the computational facilities in the Department of Chemistry at BITS Pilani (Hyderabad campus).References
- R. J. Hill, J. R. Craig and G. V. Gibbs, Phys. Chem. Miner., 1979, 4, 317–339 CrossRef CAS.
- Y. Sun, J. Wang, S. Xi, J. Shen, S. Luo, J. Ge, S. Sun, Y. Chen, J. V. Hanna, S. Li, X. Wang and Z. J. Xu, Nat. Commun., 2023, 14, 2467 CrossRef CAS PubMed.
- C. Wei, R. R. Rao, J. Peng, B. Huang, I. E. L. Stephens, M. Risch, Z. J. Xu and Y. Shao-Horn, Adv. Mater., 2019, 31, 1806296 CrossRef PubMed.
- Y. Zhou, S. Sun, C. Wei, Y. Sun, P. Xi, Z. Feng and Z. J. Xu, Adv. Mater., 2019, 31, 1902509 CrossRef CAS.
- S. Sun, Y. Sun, Y. Zhou, S. Xi, X. Ren, B. Huang, H. Liao, L. P. Wang, Y. Du and Z. J. Xu, Angew. Chem., Int. Ed., 2019, 58, 6042–6047 CrossRef CAS.
- Ö. N. Avcı, L. Sementa and A. Fortunelli, ACS Catal., 2022, 12, 9058–9073 CrossRef.
- V. Jeyavani, S. Manoj and S. P. Mukherjee, ACS Appl. Nano Mater., 2024, 7, 17776–17785 CrossRef CAS.
- Q. Zhang, Y. Hu, H. Wu, X. Zhao, M. Wang, S. Wang, R. Feng, Q. Chen, F. Song, M. Chen and P. Liu, ACS Nano, 2023, 17, 1485–1494 CrossRef CAS.
- R. Chen, Z. Wang, S. Chen, W. Wu, Y. Zhu, J. Zhong and N. Cheng, ACS Energy Lett., 2023, 8, 3504–3511 CrossRef CAS.
- A. Rajput, A. A. Pandey, A. Kundu and B. Chakraborty, Chem. Commun., 2023, 59, 4943–4946 RSC.
- H. Xiao, H. Shin and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5872–5877 CrossRef CAS.
- L. Bai, S. Lee and X. Hu, Angew. Chem., Int. Ed., 2021, 60, 3095–3103 CrossRef CAS.
- A. G. Rajan, J. M. P. Martirez and E. A. Carter, ACS Catal., 2021, 11, 11305–11319 CrossRef.
- B. Chakraborty, A. Indra, P. V. Menezes, M. Driess and P. W. Menezes, Mater. Today Chem., 2020, 15, 100226 CrossRef CAS.
- G. Zhang, H. Wang, J. Yang, Q. Zhao, L. Yang, H. Tang, C. Liu, H. Chen, Y. Lin and F. Pan, Inorg. Chem., 2018, 57, 2766–2772 CrossRef CAS.
- T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Sci. Rep., 2015, 5, 13801–13822 CrossRef PubMed.
- L. Trotochaud, J. K. Ranney, K. N. Williams and S. W. Boettcher, J. Am. Chem. Soc., 2012, 134, 17253–17261 CrossRef CAS PubMed.
- E. Fabbri, A. Habereder, K. Waltar, R. Kötz and T. J. Schmidt, Catal. Sci. Technol., 2014, 4, 3800–3821 RSC.
- T. Schuler, T. Kimura, T. J. Schmidt and F. N. Büchi, Energy Environ. Sci., 2020, 13, 2153–2166 RSC.
- J. O. M. Bockris and Z. Nagy, J. Chem. Educ., 1973, 50, 839 CrossRef CAS.
- L. Negahdar, F. Zeng, S. Palkovits, C. Broicher and R. Palkovits, ChemElectroChem, 2019, 6, 5588–5595 CrossRef CAS.
- T. Y. George, T. Asset, A. Avid, P. Atanassov and I. V. Zenyuk, ChemPhysChem, 2020, 21, 469–475 CrossRef CAS PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- E. Nurlaela, T. Shinagawa, M. Qureshi, D. S. Dhawale and K. Takanabe, ACS Catal., 2016, 6, 1713–1722 CrossRef CAS.
- C. Davidson, G. Kissel and S. Srinivasan, J. Electroanal. Chem. Interfacial Electrochem., 1982, 132, 129–135 CrossRef CAS.
- S. Zhang, K. Xu and T. Jow, J. Power Sources, 2003, 115, 137–140 CrossRef CAS.
- T. Zhou, C. Wang, Y. Shi, Y. Liang, Y. Yu and B. Zhang, J. Mater. Chem. A, 2020, 8, 1631–1635 RSC.
- A. Rajput, P. K. Nayak, D. Ghosh and B. Chakraborty, ACS Appl. Mater. Interfaces, 2024, 16, 28756–28770 CrossRef CAS.
- A. Rajput, M. K. Adak and B. Chakraborty, Inorg. Chem., 2022, 61, 11189–11206 CrossRef CAS.
- M. K. Adak, A. Rajput, D. Ghosh and B. Chakraborty, ACS Appl. Energy Mater., 2022, 5, 13645–13660 CrossRef CAS.
- Y. Hao, Y. Li, J. Wu, L. Meng, J. Wang, C. Jia, T. Liu, X. Yang, Z.-P. Liu and M. Gong, J. Am. Chem. Soc., 2021, 143, 1493–1502 CrossRef CAS PubMed.
- M. K. Adak, L. Mallick, K. Samanta and B. Chakraborty, J. Phys. Chem. C, 2023, 127, 154–168 CrossRef CAS.
- C. Yang, O. Fontaine, J. M. Tarascon and A. Grimaud, Angew. Chem., 2017, 129, 8778–8782 CrossRef.
- J. Zaffran, M. B. Stevens, C. D. Trang, M. Nagli, M. Shehadeh, S. W. Boettcher and M. C. Toroker, Chem. Mater., 2017, 29, 4761–4767 CrossRef CAS.
- J. D. Michael, E. L. Demeter, S. M. Illes, Q. Fan, J. R. Boes and J. R. Kitchin, J. Phys. Chem. C, 2015, 119, 11475–11481 CrossRef CAS.
- A. C. Garcia, T. Touzalin, C. Nieuwland, N. Perini and M. T. Koper, Angew. Chem., Int. Ed., 2019, 58, 12999–13003 CrossRef CAS PubMed.
- X. Chen, I. T. McCrum, K. A. Schwarz, M. J. Janik and M. T. Koper, Angew. Chem., Int. Ed., 2017, 56, 15025–15029 CrossRef CAS PubMed.
- A. Kundu, B. Kumar and B. Chakraborty, J. Phys. Chem. C, 2022, 126, 16172–16186 CrossRef CAS.
- J. A. D. del Rosario, G. Li, M. F. M. Labata, J. D. Ocon and P.-Y. A. Chuang, Appl. Catal., B, 2021, 288, 119981 CrossRef CAS.
- G. Righi, S. Fabris and S. Piccinin, J. Phys. Chem. C, 2021, 125, 18752–18761 CrossRef CAS.
- K. S. Exner and H. Over, ACS Catal., 2019, 9, 6755–6765 CrossRef CAS.
- J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- J. M. Bockris, J. Chem. Phys., 1956, 24, 817–827 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, A. Logadottir, S. Bahn, L. B. Hansen, M. Bollinger, H. Bengaard, B. Hammer, Z. Sljivancanin and M. Mavrikakis, J. Catal., 2002, 209, 275–278 CrossRef.
- Y. Duan, N. Dubouis, J. Huang, D. A. D. Corte, V. Pimenta, Z. J. Xu and A. Grimaud, ACS Catal., 2020, 10, 4160–4170 CrossRef CAS.
- Y. Peng, H. Hajiyani and R. Pentcheva, ACS Catal., 2021, 11, 5601–5613 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03107e |
| This journal is © The Royal Society of Chemistry 2024 |