Water slowing down drives the occurrence of the low temperature dynamical transition in microgels

Abstract

The protein dynamical transition marks an increase in atomic mobility and the onset of anharmonic motions at a critical temperature (T_d), which is considered relevant for protein functionality. This phenomenon is ubiquitous, regardless of protein composition, structure and biological function and typically occurs at large protein content, to avoid water crystallization. Recently, a dynamical transition has also been reported in non-biological macromolecules, such as poly(N-isopropyl acrylamide) (PNIPAM) microgels, bearing many similarities to proteins. While the generality of this phenomenon is well-established, the role of water in the transition remains a subject of debate. In this study, we use atomistic molecular dynamics (MD) simulations and elastic incoherent neutron scattering (EINS) experiments with selective deuteration to investigate the microscopic origin of the dynamical transition and distinguish water and PNIPAM roles. While a standard analysis of EINS experiments would suggest that the dynamical transition occurs in PNIPAM and water at a similar temperature, simulations reveal a different perspective, also qualitatively supported by experiments. From room temperature down to about 180 K, PNIPAM exhibits only modest changes of dynamics, while water, being mainly hydration water under the probed extreme confinement, significantly slows down and undergoes a mode-coupling transition from diffusive to activated. Our findings therefore challenge the traditional view of the dynamical transition, demonstrating that it occurs in proximity of the water mode-coupling transition, shedding light on the intricate interplay between polymer and water dynamics.

---

Introduction

The protein dynamical transition is a long investigated phenomenon which was originally found to occur in hydrated protein suspensions at low temperature.¹ The transition is identified by a clear change in the protein dynamics, namely a steep increase of the atomic mobility which corresponds to the onset of anharmonic motions and local diffusion of groups of atoms at a temperature T_d. The same temperature marks the activation of the protein biological functionality in physiological conditions.^2,3 Motivated by this reason, a continuous effort has been devoted towards a full understanding of the molecular origin of this process. The dynamical transition has been universally observed in proteins, independently on their composition, structure or biological function, including myoglobin,¹ ribonuclease A,⁴ cytochrome c,⁵ purple membrane protein,⁶ lysozyme,^7,8 intrinsically disordered proteins,⁹ and even unstructured polypeptides¹⁰ and amino acids.¹¹ In addition, it was also reported for other types of bio-macromolecules, including RNA,¹² DNA¹³ and lipid bilayers,¹⁴ albeit the T_d value can slightly vary depending on the specific system.

More recently, evidence of the occurrence of a protein dynamical transition was also provided for non-biological macromolecules, i.e. poly(N-isopropyl acrylamide), PNIPAM, microgels^15,16 and linear chains.¹⁷ PNIPAM is a synthetic polymer renowned for its thermoresponsivity, thanks to which the polymer chains undergo a reversible coil-to-globule transition upon increasing temperature. This behavior recalls protein folding and, together with the amphiphilic nature, the presence of amide groups, and the complex energy landscape, evidences strong similarities between PNIPAM and proteins. The measured value of the dynamical transition temperature T_d was found to be ∼225 K for both PNIPAM microgels (cross-linked polymer networks) and linear (not cross-linked) chains, in analogy with proteins and irrespective of macromolecular topology.¹⁷ However, the polymer architecture was shown to have a significant effect on the solution behavior, with microgels being stronger confining agents, able to prevent water crystallization up to a higher water content with respect to linear chains,¹⁸ and also to proteins.¹⁶

While the generality of the protein dynamical transition is well established, a long-standing question concerns the role played by water in the dynamical transition. A hint on the important contribution given by water derives from the observation that the protein dynamical transition is generally suppressed in the absence of water.^2,7 Although onsets of anharmonic motions were also found in dry proteins,^19,20 they are ascribable to motions with a different nature with respect to those that are activated above T_d.²¹ Furthermore, at T_d a parallel activation of the water dynamics was reported in several systems^9,22–26 and was shown to have a characteristic onset temperature independent of the surface nature.²⁷ Finally, some studies related the occurrence of the protein dynamical transition to the underlying liquid–liquid critical point and its related Widom line.^28,29 Altogether, there is a clear evidence of a complex interplay between protein and water dynamics, that is still nowadays largely debated: while several works support the idea that water strongly influences the protein motion,^30–33 others say that biomacromolecules in turn strongly affect water dynamics³⁴ or that water and protein dynamics are decoupled.³⁵

In this work, we aim to investigate the physical origin of the dynamical transition in microgel suspensions by combining atomistic molecular dynamics (MD) simulations and elastic incoherent neutron scattering (EINS) experiments. The atomic motions involved in this phenomenon occur in the picosecond–nanosecond timescale, which is directly accessible with both techniques. To understand the role of water in the dynamical transition we exploit PNIPAM microgels because they were shown to be the most efficient system to avoid water crystallization.^16,18 While our two choices of investigation techniques are quite common, we here combine them by employing on one hand selective deuteration in our experiments and on the other hand by exploiting our recently-developed nanoscale in silico model of PNIPAM network in simulations.¹⁶ The latter is based on the use of one of the most realistic models of water³⁶ and was shown to be capable to quantitatively reproduce the polymer dynamical observables measured in EINS experiments.¹⁵ The use of deuterated microgels is instead validated by recent works, which have shown that they behave qualitatively similar to protiated ones,^37,38 but their clever use in neutron scattering experiments is able to reveal for example individual particle properties under concentrated conditions.^39,40 Thanks to these investigations, we find that, performing the EINS experiments and standard analysis used for protein systems, one would be led to conclude that PNIPAM and water undergo a dynamical transition occurring roughly at the same temperature. Instead, the simulations reveal a completely different story, showing that, while PNIPAM dynamics changes only mildly as temperature decreases from room condition up to about 180 K, the water dynamics slows down by orders of magnitude. This prompts us to adopt a completely different way of looking at the data in order to correctly compare water and PNIPAM dynamics. Based on this perspective, we are able to demonstrate that the protein-like dynamical transition of microgels occurs at roughy the same temperature where water dynamics changes its behavior from diffusive to activated, the so-called mode coupling temperature.

Results and discussion

Water and PNIPAM dynamics from EINS experiments

To access the picosecond–nanosecond timescale, in which the molecular processes involved in the protein dynamical transition take place, EINS experiments were performed on PNIPAM microgels suspensions using the spectrometers IN13 and IN16B of the Institut Laue-Langevin (ILL, Grenoble, France). Microgels suspensions with different isotopic (hydrogen/deuterium) composition were investigated in order to distinguish the contribution of water dynamics from that of the polymer. Indeed, due to the significantly higher neutron incoherent cross-section of hydrogen atoms, the measured integrated elastic intensity I_τ(T) (the integral over the measured Q-range of I(Q, 0) at a given resolution time τ, in ps) gives information on the dynamics of the molecular processes involving the hydrogen atoms. Recent EINS experiments carried out on protiated microgels suspensions in D₂O¹⁵ provided a characterization of the polymer dynamics, showing the occurrence of a dynamical transition at low temperature (T). In this work, to evaluate water behavior, we first investigate deuterated microgels suspensions (D-PNIPAM) in H₂O. Fig. 1a compares the temperature dependence of the I₁₅₀(T) measured on IN13 for three different polymer concentrations, i.e. 45, 50 and 60 wt%. Within the temperature sampling of IN13, the I₁₅₀(T) increases upon cooling and does not show a strong dependence on wt%, except for a more marked decrease between 225 K and 250 K for the less polymer-concentrated samples in analogy with what observed for PNIPAM dynamics.¹⁵Fig. 1b reports the I₁₈₀₀(T) of D-PNIPAM in H₂O measured on IN16B. The higher time resolution and denser temperature sampling of this instrument allows us to detect a sharp discontinuity for all studied wt% at T_m ∼ 265 K as a consequence of melting of a small fraction of ice formed from processes of cold crystallization.^17,18 We now focus for simplicity only on the 60 wt% sample (representative examples of the measured I(Q, 0) are shown in Fig. S1 of the ESI†) in order to minimize the contribution of the discontinuity in the I₁₈₀₀(T), and compare different polymer/solvent isotopic compositions. Fig. 1c reports I₁₈₀₀(T) for deuterated microgels in H₂O, protiated microgels (H-PNIPAM) in H₂O, and protiated microgels in D₂O, thus giving information on the dynamics of water, a combination of water and PNIPAM, and PNIPAM, respectively. For D-PNIPAM in H₂O, in addition to the observed melting, a distinct change of slope in I₁₈₀₀(T) is found also at T_d ∼ 210 K, marking the occurrence of the dynamical transition. On a closer look to the other two samples, we find that a dynamical transition is detected in all cases and the corresponding transition temperatures T_d are summarized in Table S1.† Interestingly, the value of T_d varies among the three samples with constant polymer concentration, but different isotopic composition. Specifically, a dynamical transition temperature of ∼210 K is observed for D-PNIPAM in water, while T_d ∼ 225 K is found for H-PNIPAM both in water and in D₂O. Opposite effects of deuteration on mobility are reported for proteins, with both promotion and damping of biopolymer motions.⁴¹ However, comparing the D-PNIPAM and H-PNIPAM dynamical transition temperatures, a lower T_d value for the former system is consistent with the lower lipophilicity of deuterated aliphatic groups in this polymer as compared to protiated, because of the lessened vibrations of deuterons with respect to protons.^42,43 Considering the significant presence of contacts between aliphatic moieties in the microgel at high PNIPAM concentration, a weaker interaction between hydrophobic groups in D-PNIPAM network favors the harmonic-to-anharmonic transition of segmental motions. Based on the same rationale, PNIPAM deuteration increases the value of the volume phase transition temperature of the microgel in aqueous solution.¹⁸ For completeness, the melting temperatures T_m are also reported in Table S1 of the ESI,† to show that T_m is roughly constant when H₂O is used as a solvent, while it increases with D₂O, thus confirming that the corresponding discontinuity of I₁₈₀₀(T) is originated from ice melting. In agreement with this interpretation, we observe that the intensity drop at T_m is more pronounced for D-PNIPAM in H₂O, consistently with the fact that, in this sample, water provides the largest incoherent scattering contribution. In addition, a recent study based on differential scanning calorimetry measurements¹⁸ indicates that the crystallization degree for protiated microgels with PNIPAM concentration of 60 wt% in both D₂O or H₂O is of the order of ∼0.3%, while for deuterated microgels in H₂O, it increases up to a few percent (∼3%). Notably, the study also shows that melting processes completely disappear for microgel samples at concentration above 60 wt%. Therefore these findings suggest that in the investigated microgels systems practically all water molecules behave as hydration water. In Fig. 1d, we further show the behavior of I₁₈₀₀(T) at 60 wt% upon heating (same data as in Fig. 1c) and cooling. We observe a significant hysteresis of the data, with a shift of T_m of about 20°. This suggests that under cooling the system is able to explore liquid-like states in a more extended range of temperatures up to ∼250 K.

Fig. 1 Integrated elastic intensity as a function of temperature T: (A) I₁₅₀(T) measured on IN13 and (B) I₁₈₀₀(T) measured on IN16B for D-PNIPAM in H₂O at 45 wt%, 50 wt% and 60 wt%; (C) I₁₈₀₀(T) for D-PNIPAM in H₂O, H-PNIPAM in H₂O and H-PNIPAM in D₂O at 60 wt%, acquired upon heating. The dashed lines are linear fits to the data. Data are vertically shifted by 0.05 for clarity. Error bars are within symbol size; (D) I₁₈₀₀(T) for D-PNIPAM in H₂O at 60 wt% acquired upon cooling and heating cycles.

Atomistic insights from MD simulations

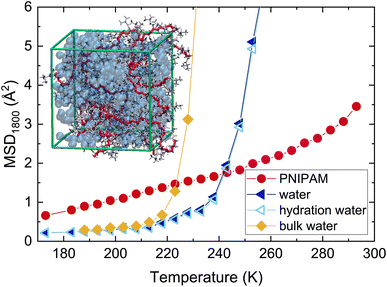
To shed light on the molecular origin of the differences in the values of T_d measured for water and PNIPAM, all-atom molecular dynamics simulations were performed on a PNIPAM network in TIP4P/ICE water.^15,16 A commonly employed observable to track the protein dynamical transition is the mean squared displacement (MSD), which can be directly computed from molecular dynamics simulations. Fig. 2 reports the MSD₁₈₀₀, calculated for PNIPAM hydrogen atoms and for water, respectively, at the resolution time τ = 1800 ps of IN16B for the simulations of PNIPAM 60 wt%. As temperature increases, a notable enhancement of the atomic mobility takes place, characterized by a deviation from the low-T linear dependence, which is compatible with the interpretation that a dynamical transition occurs also for this observable, as shown in Fig. S2 of the ESI† and detected also for PNIPAM linear chains.¹⁷ In the explored temperature interval, the increase of mobility is found to be much more pronounced for water. In Fig. 2 we also perform the additional comparison of the MSD₁₈₀₀ of all water molecules with respect to hydration water ones, the latter defined as those molecules whose oxygen atoms are located within the first minima of the radial distribution functions of water around PNIPAM atoms. We observe no major differences between water and hydration water, due to the fact that, at this high polymer concentration, the vast majority (>90%) of water molecules can be identified as hydration water. Finally, Fig. 2 includes a further comparison with the MSD₁₈₀₀ calculated for an independent simulation of bulk water under the same simulated conditions. In the case of bulk water, a steep increase of the MSD occurs at a much lower temperature with respect to water confined within the polymer network, suggesting that a change in water dynamics takes place also in the absence of the polymer.

Fig. 2 Temperature dependence of the MSD₁₈₀₀ calculated from MD simulations of PNIPAM 60 wt% at 1800 ps, averaged over 200 ns, for PNIPAM hydrogen atoms, all water molecules, and hydration water molecules. A comparison with the MSD₁₈₀₀ calculated for an independent simulation of bulk water is also included. Error bars are within symbol size. The inset reports a snapshot of the microgel network model in which the polymer backbone and side chains are represented in red and gray, respectively, while water molecules are shown with blue spheres.

To further probe the microscopic dynamics of water, we examined in detail the temperature dependence of water self diffusion coefficient, D_w, which can be estimated in the numerical simulations from the long-time limit of the MSD, also shown in Fig. S3 of the ESI.†Fig. 3 shows the Arrhenius plot of D_w, calculated both for water in the system of PNIPAM 60 wt% and for the simulation of bulk water. As the temperature decreases, we observe a slowing down of water dynamics which is strongly enhanced in the presence of PNIPAM. To analyze the effect of water supercooling within the framework of the mode-coupling theory (MCT)^44–46 of glassy dynamics, we apply a power-law fit of D_w following the equation:

D_w = C(T − T_MCT)^γ (1)

where T_MCT is the MCT temperature at which the relaxation time of the system should diverge according to the theory, C is a prefactor, and γ is the power-law exponent. The fits work quite well at relatively high temperatures, where D_w follows the MCT predictions with a critical temperature, T_MCT around 229 K, 227 K and 221 K for water in PNIPAM 60 wt%, PNIPAM 40 wt% and for bulk water, respectively. Robustly, all fits yield an exponent γ ∼ 2.9 in agreement with previous findings,^44–47 including experimental ones.⁴⁸

Fig. 3 Arrhenius plot of water self diffusion coefficient D_w calculated for water molecules in simulations of bulk water, PNIPAM 40 wt%, and PNIPAM 60 wt%. Solid and dashed lines are the MCT and Arrhenius fit, respectively. Error bars are within symbol size. The estimated T_MCT are marked with arrows.

The MCT fits, as expected, are a good description of the numerical data up to intermediate temperatures, below which the behavior of D_w deviates from the MCT power law and instead is found to obey an Arrhenius behavior, with an activation energy E_A of ∼80 kJ mol⁻¹ and ∼55 kJ mol⁻¹ for water in the system of PNIPAM 60 wt% and bulk water, respectively, consistently with previous estimates.¹⁶ Such low-T deviation is typical of glass-forming liquids, which follow the MCT predictions up to roughly the MCT temperature and then avoid the singularity undergoing a change in the dynamical behavior from diffusive-like to activated-like.⁴⁹ The latter regime is dominated by hopping processes, typical of Arrhenius behavior. Fig. 3 also shows that the deviation from the MCT power law behavior takes place at temperatures slightly higher than the MCT temperature of ideal structural arrest, because in reality the hopping processes start to occur just before the system approaches T_MCT, becoming the dominant mechanism of relaxation only below T_MCT. The MCT temperature is thus a precursor of the true glass transition, which takes place at a lower value, not easily accessible in simulations. For example, for TIP4P/2005 bulk water T_MCT is found to change between 180 K and 210 K along different isochores,⁴⁵ while the estimates of the experimental glass transition point to roughly 140 K.⁵⁰ Of course, these temperatures will be higher in the presence of a confining agent, in agreement with experimental studies of water confined in Vycor, which roughly suggest a difference of 20 K in the behavior of bulk and confined water.⁵¹

Altogether, these findings demonstrate that water in PNIPAM 60 wt% undergoes a MCT-like transition upon cooling for T ≲ 230 K, in good agreement with similar estimates of water in nanopores.⁵² Below this temperature, the dynamics becomes activated, rather than diffusive, which is sometimes referred as strong-to-fragile dynamic crossover.^45,52 The MCT temperature signals the onset of slow dynamics and the fact that at even lower temperatures a true glass transition will take place, which is difficult to probe due to the long equilibration times that are required.

Time- and length-scales of water and PNIPAM dynamics

To understand the influence of the time- and length-scales used to track the low temperature dynamical transition, we show in Fig. 4A a direct comparison between the MSD of water calculated from the MD simulations of PNIPAM 60 wt% at the resolution time of both IN13 (MSD₁₅₀) and IN16B (MSD₁₈₀₀), and water self diffusion coefficient D_w. At elevated temperatures the MSDs calculated at both resolution times closely follow the temperature dependence of D_w. However, as the system is cooled down, the MSD₁₅₀ quickly deviates from D_w. Instead, remarkably, the MSD₁₈₀₀ falls on the same curve of D_w, spanning roughly two orders of magnitude of variation of the dynamics, up to ∼235 K. Even though deviations between the two observables occur below this temperature, this happens when the system approaches the MCT transition, so when the system is already becoming glassy. These observations allow us to conclude that the MSD₁₈₀₀ correctly probes the overall system dynamics and is able to signal the onset of dynamical arrest. On the other hand, clearly the MSD₁₅₀ does not provide a good observable for tracking the slow dynamics of the system because of its too-short time scale. Motivated by these findings, we report in Fig. 4B a logarithmic representation of the MSD₁₈₀₀ as a function of temperature. Indeed, while the MSD is the property commonly used to monitor the protein dynamical transition,²¹ its usual observation is carried out in a linear scale, as also previously discussed in Fig. 2. The semi-logarithmic description of Fig. 4B is therefore much more appropriate to monitor a supercooled system and indeed highlights a notably distinct behavior between the polymer network and the water confined within it. Specifically, for the former, the variation in MSD₁₈₀₀ values with temperature is only minor, by roughly a factor of three in the whole temperature region explored, whereas for the latter, the MSD₁₈₀₀ spans approximately two orders of magnitude, mirroring the features exhibited by bulk water. Altogether these findings provide a clear evidence that the slow dynamics of water acts as the driving force behind the low temperature dynamical transition in microgels, which actually seems to take place quite close to the MCT transition temperature.

Fig. 4 (A) Comparison between water MSD calculated from simulations of PNIPAM 60 wt% at the resolution time of IN13 τ = 150 ps (MSD₁₅₀) and of IN16B τ = 1800 ps (MSD₁₈₀₀) and water self diffusion coefficient D_w. Data are normalized to the MSD₁₈₀₀ data by rescaling to the value at 293 K; (B) semilog representation of the numerical MSD for PNIPAM 60 wt% at 1800 ps for PNIPAM hydrogen atoms and water molecules, and for bulk water shown in linear scale in Fig. 2; experimental MSD, obtained through a double well (DW) fit of I(Q) measured on IN16B for D-PNIPAM in H₂O at 60 wt% under heating and cooling cycles, and also obtained from a Gaussian fit (G) of the data measured only upon cooling.

Fig. 4B further compares the numerical MSD₁₈₀₀ with the experimental ones, indirectly obtained by a fit of the measured I(Q) for D-PNIPAM in H₂O at 60 wt%. We first applied a global fitting procedure, similar to what performed in ref. 17, as a function of temperature, scattering vector, and energy resolution, using the widely employed double-well (DW) model. Such a model is the combination of a hopping motion between two adjacent potential wells and a shorter vibrational motion inside one of the two wells. The vibrational term provides harmonic contributions at all temperatures, whereas the hopping term becomes active only above temperatures high enough to allow jumping over the energy barrier between the two wells. As such, the model is well suited to describe the dynamical transition, i.e. a transition from a purely harmonic to a more complex relaxational dynamics, although it encompasses only bound degrees of freedom. Indeed, we find that the employed fitting procedure closely captures the behavior of the MSD of PNIPAM atoms, that are never diffusive at this concentration over the entire temperature range, as shown in Fig. 4B. On the other hand, it is not adequate to separately describe the dynamics of water, that for T ≳ 230 K is diffusive, as seen from the simulations. To confirm that this is the case, we adopted the double-well model to fit also the intensities measured upon cooling, for which the data clearly show a greater ability of the system to explore lower temperatures without the interference of freezing/kinetic arrest down to T > 250 K. To detect the diffusive behavior of water, we thus limit the fits of I(Q) upon cooling only at these high temperatures. As expected, again the double-well model is not able to provide a good estimate of the MSD, likely because the scattering signal of D-PNIPAM in H₂O is dominated by the larger cross-section of water. Hence, we attempt to extract the water diffusive contribution by focusing only on the low-Q part of the data²⁴ and fitting the I(Q) upon cooling for T > 250 K with a simple Gaussian (G) function. Despite the over-simplification of such analysis, we find that the extracted MSD of water for T > 250 K by this simple Gaussian treatment is in surprisingly good agreement with simulations and, qualitatively, of the right order of magnitude with respect to the MSD of the polymer. However, the Gaussian fit overestimates the MSD for T < 250 K. We therefore conclude that, while a more sophisticated model able to capture simultaneously the correct dynamics of both water and polymer is needed, a satisfying phenomenological approach is to adopt the Gaussian fit for water in the diffusive regime and a different model such as the double-well one for the polymer at all temperatures.

Conclusion

In this study we investigated the molecular origin of the low temperature dynamical transition of PNIPAM microgels by examining the individual dynamics of both polymer and water. To this aim, we combined two complementary techniques that allowed us to probe the picosecond–nanosecond time-scale at which this molecular process takes place, i.e. all-atom molecular dynamics simulations and elastic incoherent neutron scattering experiments with isotopic substitution. Indeed, while in the simulations it is directly possible to analyze the individual contributions of PNIPAM and water dynamics, selective deuteration allows to distinguish them also experimentally. The observation of a slope change in the temperature dependence of the integrated elastic intensity reveals a dynamical transition temperature of ∼210 K for D-PNIPAM in water, while a value of T_d ∼ 225 K is found for H-PNIPAM in both H₂O and D₂O. To gain further insights into the microscopic dynamics of water, we used atomistic simulations with a nanoscale in silico model of PNIPAM microgel network embedded in one of the most realistic available water models,³⁶ which was previously shown to quantitatively reproduce the polymer MSD measured in EINS experiments, even at different resolution times.^15,16 Here, we went one step forward in the test of such a model, by comparing simulated water dynamics to the one probed experimentally by investigating deuterated microgels.

As a results of this effort, we are now able to draw several important conclusions. First, we show that the water MSD computed at 1800 ps, measurable by EINS experiments at high energy resolution, is as a robust indicator for the overarching system dynamics in a wide temperature range. As visible in Fig. 4A, the MSD₁₈₀₀ closely follows the self-diffusion coefficient of water for about two orders of magnitude in the diffusive regime. Deviations only occur at low enough T when water dynamics becomes activated. On the other hand, when using MSDs at shorter timescales, such as the 150 ps provided by spectrometers of lower resolution, there is a significant difference. This strongly suggests that EINS experiments at high temporal resolution can be used as a probe for water diffusion, when this is appropriately decoupled e.g. through selective deuteration.

Moving the focus from polymer to water dynamics, we find that the latter spans several orders of magnitude as in systems approaching the glass transition, so that a linear representation of the MSDs temperature dependence, such as that shown in Fig. 2, is no longer adequate. Instead, a logarithmic description is needed, as done in Fig. 3 and 4, allowing us to highlight the distinct dynamics pertaining to the polymer network and the water confined within it. Indeed, water is much more diffusive at high temperatures, but still nearly two orders of magnitude slower than bulk water. This indicates that water is strongly confined and, in agreement with differential scanning calorimetry measurements,¹⁸ reveals that at this high polymer concentration water mainly behaves as hydration water.

Another important point emerging from our study is the direct comparison between experimental and numerical MSDs. We find that PNIPAM dynamics is well-captured by the simulations, when the measured intensities as a function of wavevector are fitted by the commonly employed double-well function. This confirms what previously observed for H-PNIPAM in D₂O both for microgels and for polymer chains. Instead, such a model dramatically fails to describe water dynamics in the diffusive regime, as expected from the fact that its functional form contains only bound motions that, in this regime, do not belong to water. Indeed, while the MSDs of water follow a diffusive regime down to ∼230 K, those of the polymer do show a non-diffusive, more complex behavior that to a first approximation can be that of jumping between two different states as expressed by the double model. Due to the unavailability of a more comprehensive model, we thus simply fitted the high temperature data, where water is diffusive, with a Gaussian function. Despite the rough approximation of this procedure, such a fit qualitatively captures the water MSDs for T > 250 K, thus indicating a much faster dynamics with respect to the polymer, in agreement with simulations. Importantly, at lower temperatures, signatures of water freezing in D-PNIPAM microgels are more accentuated than in H-PNIPAM ones, confirming previous calorimetry experiments,¹⁸ although the amount of existing crystalline nuclei was estimated to be less than 10%. The influence of freezing also manifests by the pronounced hysteresis of the measured intensity. However, upon cooling, we find a clear window of supercooled (non-freezing) states down to 250 K, that we used to compare to numerical MSDs. We remark that crystallization is never observed within the explored time and length scales in the simulations.

Finally, the present analysis allows us to shed light on the nature of the dynamical transition. Indeed, we unambiguously find that for microgels this happens at temperatures close to the MCT-like transition of water diffusion. We estimated T_MCT through a power-law extrapolation of the numerical self-diffusion coefficient, which was previously shown to provide a good description of dynamical arrest in bulk water.^47,53 Below T_MCT, the dynamics of water is well-described by an Arrhenius behavior, also in agreement with previous works.^45,52 Under such regime of activated dynamics, the system is strongly out-of-equilibrium and it is delicate to look at fix timescales, such as those probed experimentally, to draw conclusive observations on the behavior of the system. Therefore, T_MCT ∼ 234 K anticipates the occurrence of water glass transition temperature T_g at the studied PNIPAM concentration, that should take place well below it. According to the estimates for bulk water, the difference between T_MCT and T_g is about 50°.⁴⁵ The anticipation of T_g given by T_MCT and by the onset of activated dynamics turns out to be quite close to the occurrence of the dynamical transition temperature T_d. The present findings in a non-biological system are therefore in agreement with some studies which connected the occurrence of the protein dynamical transition with the strong-to-fragile crossover.⁵⁴ Interestingly, the protein dynamical transition has also been related to the presence of the underlying liquid–liquid critical point (LLCP),²⁸ although there is no evidence to-date that water under the extreme confinement exerted by proteins (or microgels) would still undergo a LLCP. This calls for future investigations.

Our physical interpretation of the dynamical transition is that when water becomes diffusive, also the microgel or the protein becomes more mobile, the latter finally being able to explore configurations compatible with its biological function. Future works, for example by QENS measurements, will be needed to further explore the dynamics of water and polymers/proteins close to the glass transition in the supercooled regime, to provide a comprehensive model of the dynamics of the system, capable to discern the diffusive/non-diffusive contribution of water from the activated dynamics of the suspended polymer. This will have to be carried out taking appropriate care of water crystallization, a ubiquitous problem in supercooled water regime,⁵⁵ that is found to be non-negligible also in the presence of a deuterated confining agent.

In conclusion, the present investigation provides evidence that the low-temperature dynamical transition in PNIPAM microgels is dictated by a change in water dynamics at the MCT temperature. Based on the marked similarities between PNIPAM microgels and proteins in water, these novel insights on the interplay between PNIPAM and solvent dynamics contribute to a deeper understanding of analogous processes in biological macromolecules, and may be extended to other non-biological macromolecular systems.

Methods

Sample preparation

PNIPAM microgels were synthesised by standard precipitation polymerization as previously described in ref. 15 and detailed in the ESI.† For the synthesis of the protiated microgel, NIPAM (0.137 M) was solubilized in 1560 mL of ultrapure water in a 2 L four-neck jacketed reactor in the presence of BIS (1.87 mM) and SDS (7.82 mM). KPS (2.44 mM, previously dissolved in 10 mL of deoxygenated water) was added to start the polymerization, carried out for 4 hours at 343 K. The synthesis of the deuterated microgels was carried by replacing NIPAM with an equimolar amount of NIPAM-d10. For both microgels, non-deuterated BIS was used as crosslinker, by assuming its concentration negligible with respect to the monomer one. The microgels network mesh size is estimated to be 100 ± 20 Å at 25 °C by using small angle neutron scattering experiments (see the ESI†).

Elastic incoherent neutron scattering

EINS experiments were performed at Institut Laue-Langevin (ILL, Grenoble, France) using the spectrometers IN13 and IN16B,^56,57 measuring the scattered neutron intensity I(Q, |E| ≲ ΔE) ≐ I(Q, 0) in a narrow energy window ΔE centered about the elastic peak E = 0, as a function of exchanged momentum Q. I(Q, 0) was measured as a function of T with resolution ΔE = 8 μeV for IN13 in a Q-interval from about 0.2 to 4.5 Å⁻¹, and with resolution ΔE = 0.75 μeV for IN16B in a Q-interval from about 0.2 to 1.9 Å⁻¹, giving access to motions faster than about 150 ps and 1800 ps, respectively. The neutron incoherent cross-section of hydrogen, higher by more than one order of magnitude than the sum of coherent and incoherent cross-sections of all other atoms including deuterium, was exploited to discriminate water and PNIPAM dynamics by preparing samples with selective deuteration. In particular, protiated microgels were dispersed in D₂O to highlight the polymer signal, while deuterated PNIPAM microgels were dispersed in H₂O to detect water contributions. Additional samples of protiated PNIPAM microgels were prepared in H₂O to disentangle the complex interplay between PNIPAM and water dynamics. Dispersions of protiated PNIPAM in H₂O were prepared at 3 different polymer concentrations: 45, 50, and 60 wt%. Isotopically substituted samples were prepared keeping the molar fraction constant. Elastic incoherent neutron scattering experiments were performed in flat aluminium cells (3.0 × 4.0 cm) sealed with an In o-ring. For each sample, the cell thickness was selected to achieve a transmission of about 90% for the relevant incoming wavelength λ_i of the instruments. Sample weights were measured before and after each EINS experiments, without showing any significant change. All data were corrected for background and cell scattering, self absorption and detector efficiency. Examples of raw data are reported in the ESI.†

Molecular dynamics simulations

All-atom molecular dynamics simulations of PNIPAM microgels suspensions were performed using a nanoscale network model, which quantitatively reproduces neutron scattering results.¹⁵ The network model is designed from 12 atactic chains which are connected by 6 BIS cross-links. Two PNIPAM mass fractions of 40 and 60% (w/w) were investigated. Simulations were performed in the range between 293 K and 173 K, every 5 K. At each T, trajectory data were collected for ∼0.5 μs, with a sampling of 0.2 frame per ps. The OPLS-AA force field⁵⁸ with the implementation by Siu et al.⁵⁹ is used to describe PNIPAM, while water is modelled with the Tip4p/ICE force field.⁶⁰ Simulations were carried out using the GROMACS 2020.6 software.^61,62 MD simulations were also carried out for a cubic box containing 1782 Tip4p/ICE water molecules following a similar procedure. Trajectory data were acquired in the NVT ensemble. Pressure was controlled by the Parrinello–Rahman algorithm with time constant of 2 ps. Temperature was controlled with the velocity rescaling thermostat coupling algorithm with a time constant of 0.1 ps. Electrostatic interactions were treated with the smooth particle-mesh Ewald method with a cutoff of non-bonded interactions of 1 nm. Further details are reported in the ESI.†

Data availability

Data are available on the online repository Zenodo (https://doi.org/10.5281/zenodo.11207847).

Author contributions

EZ supervised the research. EB and MB prepared the samples. LT, MZ, MA, FN, and AO performed neutron scattering experiments. LT, EC and EZ performed molecular dynamics simulations. LT and EZ wrote the paper with inputs and suggestions from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank F. Sciortino for fruitful discussions and Y. Gerelli for support in data analysis. LT and EZ acknowledge financial support from ICSC – Centro Nazionale di Ricerca in High Performance Computing, Big Data and Quantum Computing, funded by European Union – NextGenerationEU – PNRR, Missione 4 Componente 2 Investimento 1.4; AO acknowledges funding by the European Union – NextGenerationEU under the Italian Ministry of University and Research (MUR) National Innovation Ecosystem grant ECS00000041 – VITALITY – CUP J97G22000170005. We also acknowledge ILL for beamtime and CINECA-ISCRA for HPC resources.

Notes and references

1. W. Doster, S. Cusack and W. Petry, Nature, 1989, 337, 754–756.
2. M. Ferrand, A. J. Dianoux, W. Petry and G. Zaccai, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 9668–9672.
3. G. Zaccai, Science, 2000, 288, 1604–1607.
4. B. F. Rasmussen, A. M. Stock, D. Ringe and G. A. Petsko, Nature, 1992, 357, 423.
5. A. G. Markelz, J. R. Knab, J. Y. Chen and Y. He, Chem. Phys. Lett., 2007, 442, 413–417.
6. K. Wood, M. Plazanet, F. Gabel, B. Kessler, D. Oesterhelt, D. Tobias, G. Zaccai and M. Weik, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18049–18054.
7. J. H. Roh, V. N. Novikov, R. B. Gregory, J. E. Curtis, Z. Chowdhuri and A. P. Sokolov, Phys. Rev. Lett., 2005, 95, 038101.
8. S. Capaccioli, K. L. Ngai, S. Ancherbak and A. Paciaroni, J. Phys. Chem. B, 2012, 116, 1745–1757.
9. G. Schirò, Y. Fichou, F.-X. Gallat, K. Wood, F. Gabel, M. Moulin, M. Härtlein, M. Heyden, J.-P. Colletier and A. Orecchini, et al. , Nat. Commun., 2015, 6, 6490.
10. Y. He, P. I. Ku, J. R. Knab, J. Y. Chen and A. G. Markelz, Phys. Rev. Lett., 2008, 101, 178103.
11. G. Schirò, C. Caronna, F. Natali, M. M. Koza and A. Cupane, J. Phys. Chem. Lett., 2011, 2, 2275–2279.
12. G. Caliskan, R. M. Briber, D. Thirumalai, V. Garcia-Sakai, S. A. Woodson and A. P. Sokolov, J. Am. Chem. Soc., 2006, 128, 32–33.
13. E. Cornicchi, S. Capponi, M. Marconi, G. Onori and A. Paciaroni, Philos. Mag., 2007, 87, 509–515.
14. J. Peters, J. Marion, F. Natali, E. Kats and D. J. Bicout, J. Phys. Chem. B, 2017, 121, 6860–6868.
15. M. Zanatta, L. Tavagnacco, E. Buratti, M. Bertoldo, F. Natali, E. Chiessi, A. Orecchini and E. Zaccarelli, Sci. Adv., 2018, 4, eaat5895.
16. L. Tavagnacco, E. Chiessi, M. Zanatta, A. Orecchini and E. Zaccarelli, J. Phys. Chem. Lett., 2019, 10, 870–876.
17. L. Tavagnacco, M. Zanatta, E. Buratti, B. Rosi, B. Frick, F. Natali, J. Ollivier, E. Chiessi, M. Bertoldo and E. Zaccarelli, et al. , Phys. Rev. Res., 2021, 3, 013191.
18. E. Buratti, L. Tavagnacco, M. Zanatta, E. Chiessi, S. Buoso, S. Franco, B. Ruzicka, R. Angelini, A. Orecchini and M. Bertoldo, et al. , J. Mol. Liq., 2022, 355, 118924.
19. Z. Liu, J. Huang, M. Tyagi, H. O'Neill, Q. Zhang, E. Mamontov, N. Jain, Y. Wang, J. Zhang, J. C. Smith and L. Hong, Phys. Rev. Lett., 2017, 119, 048101.
20. K. Ngai, L. Hong, S. Capaccioli and A. Paciaroni, J. Mol. Liq., 2019, 286, 110810.
21. G. Schirò and M. Weik, J. Phys.: Condens.Matter, 2019, 31, 463002.
22. M. Tarek and D. J. Tobias, Phys. Rev. Lett., 2002, 88, 138101.
23. J. Roh, J. Curtis, S. Azzam, V. Novikov, I. Peral, Z. Chowdhuri, R. Gregory and A. Sokolov, Biophys. J., 2006, 91, 2573–2588.
24. K. Wood, A. Frölich, A. Paciaroni, M. Moulin, M. Härtlein, G. Zaccai, D. J. Tobias and M. Weik, J. Am. Chem. Soc., 2008, 130, 4586–4587.
25. S.-H. Chen, L. Liu, E. Fratini, P. Baglioni, A. Faraone and E. Mamontov, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9012–9016.
26. Y. Fichou, G. Schirò, F.-X. Gallat, C. Laguri, M. Moulin, J. Combet, M. Zamponi, M. Härtlein, C. Picart and E. Mossou, et al. , Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6365–6370.
27. L. Zheng, Z. Liu, Q. Zhang, S. Li, J. Huang, L. Zhang, B. Zan, M. Tyagi, H. Cheng and T. Zuo, et al. , Chem. Sci., 2022, 13, 4341–4351.
28. P. Kumar, Z. Yan, L. Xu, M. G. Mazza, S. Buldyrev, S.-H. Chen, S. Sastry and H. Stanley, Phys. Rev. Lett., 2006, 97, 177802.
29. M. Bin, R. Yousif, S. Berkowicz, S. Das, D. Schlesinger and F. Perakis, Phys. Chem. Chem. Phys., 2021, 23, 18308–18313.
30. P. W. Fenimore, H. Frauenfelder, B. McMahon and R. Young, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14408–14413.
31. P. W. Fenimore, H. Frauenfelder, B. H. McMahon and F. G. Parak, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 16047–16051.
32. S. Mukherjee, S. Mondal and B. Bagchi, Phys. Rev. Lett., 2019, 122, 058101.
33. M. Bin, M. Reiser, M. Filianina, S. Berkowicz, S. Das, S. Timmermann, W. Roseker, R. Bauer, J. Öström and A. Karina, et al. , J. Phys. Chem. B, 2023, 127, 4922–4930.
34. S. Khodadadi, J. Roh, A. Kisliuk, E. Mamontov, M. Tyagi, S. Woodson, R. Briber and A. Sokolov, Biophys. J., 2010, 98, 1321–1326.
35. A. Benedetto, J. Phys. Chem. Lett., 2017, 8, 4883–4886.
36. P. G. Debenedetti, F. Sciortino and G. H. Zerze, Science, 2020, 369, 289–292.
37. M. Brugnoni, A. C. Nickel, L. C. Kröger, A. Scotti, A. Pich, K. Leonhard and W. Richtering, Polym. Chem., 2019, 10, 2397–2405.
38. M. Cors, L. Wiehemeier, J. Oberdisse and T. Hellweg, Polymers, 2019, 11, 620.
39. A. Scotti, A. R. Denton, M. Brugnoni, J. E. Houston, R. Schweins, I. I. Potemkin and W. Richtering, Macromolecules, 2019, 52, 3995–4007.
40. J. E. Houston, L. Fruhner, A. de la Cotte, J. Rojo González, A. V. Petrunin, U. Gasser, R. Schweins, J. Allgaier, W. Richtering and A. Fernandez-Nieves, et al. , Sci. Adv., 2022, 8, eabn6129.
41. P. J. Nichols, I. Falconer, A. Griffin, C. Mant, R. Hodges, C. J. McKnight, B. Vögeli and L. Vugmeyster, Protein Sci., 2020, 29, 1641–1654.
42. M. Turowski, N. Yamakawa, J. Meller, K. Kimata, T. Ikegami, K. Hosoya, N. Tanaka and E. R. Thornton, J. Am. Chem. Soc., 2003, 125, 13836–13849.
43. D. Wade, Chem.-Biol. Interact., 1999, 117, 191–217.
44. W. Gotze and L. Sjogren, Rep. Prog. Phys., 1992, 55, 241.
45. M. De Marzio, G. Camisasca, M. Rovere and P. Gallo, J. Chem. Phys., 2016, 144, 074503.
46. G. Camisasca, M. De Marzio, D. Corradini and P. Gallo, J. Chem. Phys., 2016, 145, 044503.
47. P. Gallo, F. Sciortino, P. Tartaglia and S.-H. Chen, Phys. Rev. Lett., 1996, 76, 2730.
48. F. Prielmeier, E. Lang, R. Speedy and H.-D. Lüdemann, Phys. Rev. Lett., 1987, 59, 1128.
49. L. Angelani, R. Di Leonardo, G. Ruocco, A. Scala and F. Sciortino, Phys. Rev. Lett., 2000, 85, 5356.
50. G. Johari, A. Hallbrucker and E. Mayer, Nature, 1987, 330, 552–553.
51. J.-M. Zanotti, M.-C. Bellissent-Funel and S.-H. Chen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 3084.
52. S.-H. Chen, F. Mallamace, C.-Y. Mou, M. Broccio, C. Corsaro, A. Faraone and L. Liu, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12974–12978.
53. F. Sciortino, P. Gallo, P. Tartaglia and S.-H. Chen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 6331.
54. F. Mallamace, C. Corsaro, P. Baglioni, E. Fratini and S.-H. Chen, J. Phys.: Condens. Matter, 2012, 24, 064103.
55. P. Gallo, K. Amann-Winkel, C. A. Angell, M. A. Anisimov, F. Caupin, C. Chakravarty, E. Lascaris, T. Loerting, A. Z. Panagiotopoulos and J. Russo, et al. , Chem. Rev., 2016, 116, 7463–7500.
56. L. Tavagnacco, M. Bertoldo, E. Buratti, F. Camerin, B. Frick, J. Ollivier, A. Orecchini, P. Tozzi, E. Zaccarelli and M. Zanatta, Investigation of supercooled water dynamics by confinement in dense microgel suspensions, 2018,  DOI:10.5291/ILL-DATA.9-11-1864.
57. M. Zanatta, M. Bertoldo, E. Buratti, F. Natali, J. Ollivier, A. Orecchini, J. M. Ruiz Franco, L. Tavagnacco and E. Zaccarelli, Low-temperature dynamical transition in polymeric aqueous environments, 2018,  DOI:10.5291/ILL-DATA.9-11-1866.
58. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
59. S. W. I. Siu, K. Pluhackova and R. A. Böckmann, J. Chem. Theory Comput., 2012, 8, 1459–1470.
60. J. L. F. Abascal, E. Sanz, R. G. Fernández and C. Vega, J. Chem. Phys., 2005, 122, 234511.
61. S. Páll, M. J. Abraham, C. Kutzner, B. Hess and E. Lindahl, in Tackling Exascale Software Challenges in Molecular Dynamics Simulations with GROMACS, ed. S. Markidis and E. Laure, Springer International Publishing, Cham, 2015, pp. 3–27.
62. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc02650k

‡ These authors contributed equally to the work.

---