Kinetic–thermodynamic correlation of conformational changes in ammonium complexes of a flexible naphthocage

Abstract

Conformational changes in non-covalent complexes are of fundamental importance to many chemical and biological processes. Yet, these low-energy structural changes are usually fast and difficult to monitor, which poses challenges in their detailed kinetic understanding. The correlation between kinetics and thermodynamics of the conformational change of a model supramolecular system featuring a flexible naphthocage and quaternary ammonium guests is described in this work. Guest binding initially locks the host in two major conformations, which then equilibrates over time to the more stable conformer. The overall rate of the system to attain conformational equilibrium is found to inversely correlate with the thermodynamic stability of the host–guest complexes, and hence not only can the kinetic parameters of the conformational exchange be predicted from the easily obtainable thermodynamic data, but the kinetic profile can also be rationalized by using the structural properties of the different guests.

---

Introduction

Conformational changes in non-covalent complexes, and their underlying thermodynamics and kinetics, are of fundamental importance in many chemical and biological processes such as catalysis, transport, protein–drug interactions, etc.^1–4 For example, many neurodegenerative disorders including Alzheimer's and Parkinson's diseases are due to protein misfolding that can be considered as large-scale conformational changes.⁵ Understanding the relationship between the stability and dynamics of the various conformational states of the proteins is not only essential to the disease pathology, but also valuable to the development of new therapeutic strategies that can intervene in the onset and progression of the diseases.^6–8

While information on thermodynamics is generally more easily available, studies of fast, low-energy conformational changes to obtain rate and other kinetic parameters are however more challenging.^9,10 Indeed, reported studies on conformationally flexible host–guest systems are largely focusing on structures and binding thermodynamics, whereas their kinetic studies remain rare and poorly understood despite also being important to the binding mechanism,¹¹ dynamics,¹² guest selectivity,¹³ and further downstream events.¹⁴ In this regard, appropriate supramolecular systems with systematically varying host/guest structures will be essential to investigate and establish a structure–thermodynamic–kinetic correlation behind the conformational exchange of non-covalent complexes. Kinetic parameters could also be predicted from readily accessible thermodynamics and structural data from such a correlation.

Similar to the linear free energy relationship between reaction rates and equilibrium constants for chemical reactions as described by Hammett and Brønsted plots,¹⁵ we report herein a study on correlating the binding thermodynamics and conformational kinetics of a host–guest system which consists of the conformationally flexible naphthocage NC and a series of quaternary ammonium guests. Upon guest binding, two conformers of the 1 : 1 host–guest complexes are initially obtained, and the thermodynamically less stable conformer is found to convert to the more stable one over time whose kinetics can be followed by ¹H NMR. Kinetic analysis showed that the rate of the conformational conversion is correlated with the stability of the two conformers, and hence the observed rate and kinetic parameters of the conformational change can be rationalized and predicted by the overall and local structural features of the guests (Fig. 1).

Fig. 1 (a) Control of the conformational exchange rate of the naphthocage NC by binding to guests of different affinities and (b) an energy diagram showing the relationship between the thermodynamics and kinetics of the conformal exchange. Models of the host and complexes are created by Spartan 14′ and are for illustration only.

Results and discussion

Structures and thermodynamics of NC complexes

NC is a molecular cage having two 1,3,5-triethylbenzene covers and three (2,6-dibutoxy)-1,5-naphthyl side walls connected via ether linkages (Fig. 2).¹⁶ Quaternary ammonium cations can bind strongly to NC, and a series of quaternary ammoniums of different sizes and functional groups (G1–G24) were studied in the present work. Broad peaks were observed for the naphthyl protons in the ¹H NMR spectrum of free NC, showing that the host exists as multiple exchanging conformations due to the flipping of the flexible naphthyl side walls with an exchange rate similar to that of the NMR time-scale (i.e. ∼10² s⁻¹). Occupying the cage cavity by encapsulating an ammonium guest hindered the flipping motions and gave two major conformers, in which the naphthyl walls are either all in the same relative orientation (NC1), or one of the naphthyl walls orients differently than the other two (NC2).

Fig. 2 (a) Chemical structures of G@NC1 and G@NC2, (b) models of the 2 + 6 type complex for G1, and (c) models of the 6 + 12 type complex for G5. Model of the complexes are created by Spartan 14′ and are for illustration only.

Binding of ammonium guests was followed by ¹H NMR spectroscopy. Addition of the guest to a 1 mM solution of NC in CD₂Cl₂/CD₃CN (v/v = 1 : 1) resulted in two sets of sharp signals assignable to G@NC1 and G@NC2 that are in slow exchange. Concentration of G@NC1 was found to increase at the expense of G@NC2 over time except for G8, G10, G11, G14, G19 and G20. At equilibrium, 85% to 98% of the host–guest complexes were found to be G@NC1, suggesting that the symmetrical conformer is more stable. Depending on the structure of the guests and the overall symmetry of the inclusion complex, different ¹H NMR spectral features were observed. For guests that can be fully encapsulated inside the cage, two doublets were observed for the naphthyl protons of G@NC1 with an overall D₃ symmetry, and six naphthyl doublets were observed for the G@NC2 conformer with an overall C₂ symmetry (“2 + 6” type). For guests with longer substituents that extend to the outside of the cage, the host–guest complexes are less symmetrical, in which G@NC1 will have an overall C₂ symmetry with six naphthyl doublets, and the G@NC2 conformer will have a C₁ symmetry with twelve doublets for the naphthyl protons (“6 + 12” type). Larger ammonium ions such as ⁿPr₄N⁺ and ⁿBu₄N⁺ showed no binding to NC, presumably because the cavity and/or the openings of the cage are not large enough for these larger ions.

The binding constant of these guests to NC was determined by the NMR competitive experiment and the data are summarized in Table 1.¹⁷ Binding constants (K_a1) of the more stable G@NC1 complexes are found to range from 2.4 × 10³ M⁻¹ (for G8) to 2.4 × 10⁷ M⁻¹ (for G9), and are generally related to the structure and bulkiness of the ammonium guests. For example, comparing G2 with G9 to G14, a smaller binding constant is found when more of the methyl groups in the ammonium guests are replaced by the relatively bulkier ethyl and propyl substituents. A similar observation can also be found when comparing the binding constants of G18 and G19, and that of G21 and G22. Also, binding of G17–G24 that feature either a phenyl, cyclohexyl or naphthyl substituent group is also generally weaker than that of other tetraalkylammoniums. G@NC2 is less stable and K_a2 is generally an order of magnitude smaller than K_a1. A plot of ln(K_a1) against ln(K_a2) shows a good positive correlation (Fig. 3), suggesting that there is a similar extent of differential stabilities for the two conformers of these host–guest complexes.

Table 1 Binding constants of guest G1 to G18 (as PF₆⁻ salts) to NC1 (K_a1) and NC2 (K_a2) determined by ¹H NMR competition in CD₂Cl₂/CD₃CN (v/v = 1 : 1). Guests highlighted in purple and red are those that showed no conformational evolution and do not conform to the kinetic model (vide infra) respectively

	K a1/M^−1	K a2/M^−1	Type		K a1/M^−1	K a2/M^−1	Type
G1	1.9 × 10^6	3.9 × 10^4	2 + 6	G13	5.6 × 10^5	9.1 × 10^4	2 + 6
G2	2.0 × 10^7	8.3 × 10^5	2 + 6	G14	1.1 × 10^5	5.3 × 10^4	2 + 6
G3	6.2 × 10^6	6.9 × 10^5	2 + 6	G15	1.0 × 10^7	7.7 × 10^5	2 + 6
G4	2.5 × 10^6	1.6 × 10^5	2 + 6	G16	1.4 × 10^7	2.9 × 10^5	2 + 6
G5	8.6 × 10^5	7.5 × 10^4	6 + 12	G17	1.4 × 10^5	2.1 × 10^4	2 + 6
G6	4.2 × 10^6	4.1 × 10^5	2 + 6	G18	2.1 × 10^5	2.9 × 10^4	6 + 12
G7	1.6 × 10^6	1.6 × 10^5	2 + 6	G19	6.2 × 10^4	5.5 × 10^3	6 + 12
G8	2.4 × 10^3	3.4 × 10^2	2 + 6	G20	3.0 × 10^3	3.0 × 10^2	6 + 12
G9	2.4 × 10^7	1.3 × 10^6	2 + 6	G21	3.8 × 10^4	4.2 × 10^3	6 + 12
G10	1.2 × 10^6	4.6 × 10^6	2 + 6	G22	1.9 × 10^4	1.4 × 10^3	6 + 12
G11	5.9 × 10^5	2.7 × 10^5	2 + 6	G23	1.1 × 10^5	7.0 × 10^3	6 + 12
G12	3.4 × 10^6	7.5 × 10^4	2 + 6	G24	1.6 × 10^5	6.9 × 10^3	6 + 12

---

Fig. 3 A plot of ln(K_a1) against ln(K_a2). Error bars are ±SD (n = 3) from three measurements.

Kinetics of the conformational changes

Kinetics of conformational evolution was studied by monitoring changes in the concentrations of G@NC1 and G@NC2 over time. During the conformational conversion, only resonances corresponding to the two complex conformers were observed, and no free host was detected, suggesting that the guest association was fast relative to the NMR timescale. The time required for the complexes to re-configure their conformations and reach equilibrium varies and ranges from hours to days. In particular, the time to reach conformational equilibrium is extremely slow for G12, and changes in the concentration of the two complex conformers were still observed even after the complex mixture has been analysed for over 8 days. Taking the complex of G1 (a “2 + 6” type) as an example (Fig. 4), two and six doublets in a ratio of 0.38 to 0.62, assignable to G1@NC1 and G1@NC2 respectively, were observed after 5 minutes of addition of the guest to NC (total concentration = 1 mM). Concentration of G1@NC1 gradually increased over time at the expense of G1@NC2, and equilibrium was reached in about four hours with the final concentration of G1@NC1 at 0.98 mM. The absence of observable conformational changes for G8, G10, G11, G14, G19 and G20 could either be due to a very fast or extremely slow conformational change that the timescale of the equilibrium is out of the range of that of the NMR.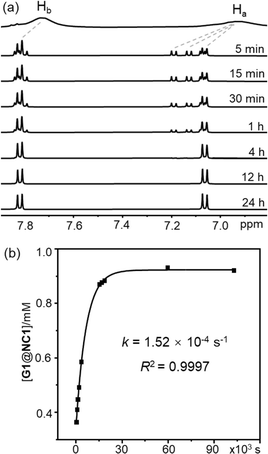

Fig. 4 (a) Partial ¹H NMR spectra (500 MHz, CD₂Cl₂/CD₃CN (v/v = 1 : 1), 298 K) of NC after addition of G1 at different times, and (b) time-dependent changes of G1@NC1 concentration.

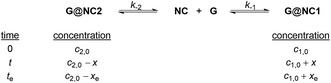
The relatively slow conformational change that allows convenient monitoring is unusual for flexible hosts like NC, which also provides a good opportunity for following the conformational exchange by ¹H NMR spectroscopy that is convenient and sensitive for monitoring subtle structural changes. While UV-vis and other spectroscopic methods with a faster timescale are generally more suitable for studying fast conformational exchanges, it is also necessary for the different conformers of the host, guest, or host–guest complex to possess unique spectroscopic features for efficient differentiation and monitoring, which renders the kinetic study of host–guest systems generally challenging. Nevertheless, since it is less plausible for G@NC2 to convert directly to G@NC1 when the host cavity is occupied by the guest and flipping of the naphthyl walls is inhibited, a “guest dissociation-host conformational change-guest re-association” mechanism involving the unbound NC as a conformationally flexible intermediate is proposed. Although both the conformational exchange of free NC and guest association are fast, the substantial stability of both complex conformers implies that the slower guest dissociation would be the rate-determining step of the observed conformational evolution. As a result, kinetics of the conformational change can be described similarly by using the kinetic rate equation of reversible reactions, and the rate of the net increase in the concentration of G@NC1 is hence the difference between the dissociation rates of the two conformers under a steady-state approximation.^18,19

where c_1,0 and c_2,0 are the concentrations of G@NC1 and G@NC2 at time = 0 respectively; x and x_e are the change in concentration at time = t and equilibrium respectively; and k₋₁ and k₋₂ are the dissociation rate constants of G@NC1 and G@NC2, respectively.

By integrating eqn (1),

at equilibrium,

substituting (5) into (3):

x = −x_ee^−kt + x_e (6)

where k is the observed rate constant and k = k₋₁ + k₋₂.

Fitting the concentration changes of G@NC1 determined by ¹H NMR at different times to the above equation gives the dissociation rate constants k₋₁ and k₋₂, and the initial concentrations c_1,0 and c_2,0. The results are summarized in Table 2, and all the guests that showed conformational evolution were found to conform to the above equation. Several analyses can be made using the obtained data. First, consistent with the proposed mechanism, it is found that k₋₂ has a major contribution to the overall rate k (∼90% or above), showing that the observed rate of conformational evolution is largely dependent on the dissociation of the less stable G@NC2. Second, the relationship between the measured binding constants and dissociation rate constants obtained from the fitting is analysed. Since the binding constant can be expressed as the ratio between the association rate constant and dissociation rate constant,

Table 2 The rate constant for the conformational change and dissociation and the initial concentration and the equilibrium concentration of G@NC1 and G@NC2, as determined by the ¹H NMR (500 MHz, CD₂Cl₂/CD₃CN (v/v = 1 : 1)) experiment and kinetic equation fitting. The total concentration of the host is 1 mM

	From the experiment		From fitting
	c 1,5min/mM	c 1,e/mM	c 1,0/mM	c 2,0/mM	c 1,e/mM	c 2,e/mM	k/s^−1	k −1/s^−1	k −2/s^−1	R ^2
a No conformational change was observed. b The conformational equilibrium was not reached after 8 days and the equilibrium concentration was therefore not measured.
G1	0.38	0.98	0.33	0.67	0.98	0.02	3.0 × 10^−4	4.7 × 10^−6	2.9 × 10^−4	0.9999
G2	0.36	0.95	0.36	0.64	0.96	0.04	2.2 × 10^−5	9.3 × 10^−7	2.1 × 10^−5	0.9998
G3	0.34	0.90	0.34	0.66	0.90	0.10	1.9 × 10^−5	1.9 × 10^−6	1.8 × 10^−5	0.9999
G4	0.33	0.94	0.32	0.68	0.94	0.06	4.7 × 10^−5	2.8 × 10^−6	4.4 × 10^−5	0.9999
G5	0.35	0.90	0.34	0.66	0.92	0.08	1.1 × 10^−4	8.9 × 10^−6	1.1 × 10^−4	0.9996
G6	0.36	0.90	0.36	0.64	0.91	0.09	1.5 × 10^−5	1.3 × 10^−6	1.3 × 10^−5	0.9991
G7	0.35	0.91	0.34	0.66	0.91	0.09	5.3 × 10^−5	4.7 × 10^−6	4.8 × 10^−5	0.9999
G8	0.90	0.90	—	—	—	—	—	—	—	—
G9	0.41	0.93	0.41	0.59	0.95	0.05	2.6 × 10^−6	1.4 × 10^−7	2.4 × 10^−6	0.9999
G10	0.73	0.73	—	—	—	—	—	—	—	—
G11	0.69	0.69	—	—	—	—	—	—	—	—
G12	0.67		0.67	0.33	0.98	0.02	6.0 × 10^−7	1.3 × 10^−8	5.9 × 10^−7	0.9979
G13	0.65	0.85	0.65	0.35	0.86	0.14	6.3 × 10^−6	8.7 × 10^−7	5.4 × 10^−6	0.9992
G14	0.68	0.68	—	—	—	—	—	—	—	—
G15	0.31	0.92	0.31	0.69	0.93	0.07	1.0 × 10^−5	7.1 × 10^−7	9.6 × 10^−6	0.9981
G16	0.31	0.96	0.31	0.69	0.98	0.02	1.3 × 10^−5	3.1 × 10^−7	1.3 × 10^−5	0.9980
G17	0.47	0.84	0.28	0.72	0.87	0.13	8.5 × 10^−4	1.1 × 10^−4	7.4 × 10^−4	0.9965
G18	0.67	0.88	0.67	0.33	0.88	0.12	5.4 × 10^−5	6.7 × 10^−6	4.8 × 10^−5	0.9996
G19	0.92	0.92	—	—	—	—	—	—	—	—
G20	0.89	0.89	—	—	—	—	—	—	—	—
G21	0.68	0.90	0.46	0.54	0.90	0.10	2.4 × 10^−3	2.3 × 10^−4	2.1 × 10^−3	0.9980
G22	0.78	0.93	0.78	0.22	0.93	0.07	1.9 × 10^−4	1.4 × 10^−5	1.8 × 10^−4	0.9836
G23	0.64	0.94	0.50	0.50	0.94	0.06	1.4 × 10^−3	8.4 × 10^−5	1.3 × 10^−3	0.9960
G24	0.54	0.95	0.35	0.65	0.96	0.04	1.2 × 10^−3	5.3 × 10^−5	1.1 × 10^−3	0.9975

---

hence,

ln K_a1 = ln k₁ − ln k₋₁  (8)

ln K_a2 = ln k₂ − ln k₋₂ (9)

Except for G12, G13, G18 and G22, a good inverse linear relationship was found in the ln(K_a1) − ln(k₋₁) and ln(K_a2) − ln(k₋₂) plots for all other guests (Fig. 5). Such an inverse linear relationship shows that these guests have a very similar association rate (i.e. k₁ and k₂) when forming the two complex conformers, implying that these guests bind to NCvia a similar process. In fact, these guests that conform to the inverse linear relationship are mostly trimethylammonium ions. While G9 is only slightly larger with two methyl and two ethyl groups, the 5- and 6-membered rings in G15 and G16 would also be less bulky than comparable linear/branched alkyls. On the other hand, both G12 and G13 contain at least three ethyl groups on the ammonium nitrogen, and G18 and G22 also have one ethyl and a benzyl substituent, making these four guests larger in size than the trimethylammonium ones. Furthermore, for G8, G10, G11, G14, G19 and G20 that showed no conformational evolution, for which the corresponding rate will also not conform to the above linear relationship, their steric bulkiness is even greater due to the presence of the bulky neopentyl (G8), 2-methylbenzyl (G20), two propyl (G10 and G11) or one propyl plus one ethyl/benzyl (G14 and G19) groups on the ammonium nitrogen. Consistent with the structure of these inclusion complexes in which the cationic ammonium portion of the guest is always encapsulated, this steric dependence may suggest that the guest first approaches and enters the host cavity via its ammonium portion during binding. The corresponding structural change of the host (e.g. flipping of the naphthyl walls) and activation barrier for accommodating the guest would hence be similar if the bulkiness around the ammonium nitrogen is similar. Intuitively, while the entry of a guest with a trimethylammonium head (or smaller) may involve a certain extent of naphthyl wall rearrangement, a guest with a larger ammonium head would need a larger opening and a larger extent of naphthyl wall rearrangement when entering the cavity, which would hence result in a higher activation barrier (Fig. 6). In fact, in the ln(K_a1) − ln(k₋₁) and ln(K_a2) − ln(k₋₂) plots, the data points for G12, G13, G18 and G22 are all found to be below the fitted line obtained from other trimethylammonium guests, showing that the corresponding association rate constants (i.e. k₁ and k₂) of these four larger ammonium guests are indeed smaller.

Fig. 5 Plot of (a) ln(k₋₁) against ln(K_a1) and (b) ln(k₋₂) against ln(K_a2). Data points for G12, G13, G18 and G22 are excluded in the fitting of the trend line.

Fig. 6 Models of (a) G2, G5 and G14 approaching NC, in which the opening of the host, and hence the activation barrier is related to the steric hindrance around the ammonium head of the guest, and (b) the three inclusion complexes whose thermodynamic stability is dependent on the overall structure of the guests. The models are created by Spartan 14′ and are for illustration only.

The similar binding mechanisms for most of the studied guests can also be reflected by the similar ratio of the initial concentration of G@NC1 and G@NC2. Statistically, the ratio of c_1,0/c_2,0 would be 1 : 3 if the activation barrier for forming both conformers are the same. Except for G9, G12, G13, G18, G21, G22 and G23, a similar c_1,0/c_2,0 ratio of ∼1 : 2 was found for all other guests. While this similar ratio is again suggestive of a similar binding process, the higher c_1,0/c_2,0 ratio than that statistically expected may indicate a relatively lower activation barrier for forming the symmetrical conformer than that of the unsymmetrical one, which is also consistent with the slightly larger ln(k₁) than ln(k₂) obtained from the ln(K_a1) − ln(k₋₁) and the ln(K_a2) − ln(k₋₂) plots (i.e. the y-intercepts). For the sterically bulkier G12, G13, G18 and G22 that do not conform to the ln(K_a1) − ln(k₋₁) and ln(K_a2) − ln(k₋₂) plots, the corresponding c_1,0/c_2,0 ratio of 1 : 0.3 to 1 : 0.5 is also significantly different than that of the other guests. While for the slightly larger G9 (with two methyl and two ethyl) and G21 (with three methyl and one 3-methylbenzyl), the c_1,0/c_2,0 ratio of 1 : 1.4 and 1 : 1.2, respectively, are closer to the 1 : 2 observed for most other guests, further supporting that the local substituents around the ammonium are playing a more important role in the initial guest association.

Guest dissociation, on the other hand, is correlated with the thermodynamic stability of the complex conformers. Since the guest dissociation barrier is the sum of the guest association barrier and the free energy of guest binding, both the local structure (i.e. related to the association barrier) and the overall structure (i.e. related to the thermodynamic stability) of the guests will be contributing factors in guest dissociation. As mentioned above, both G@NC1 and G@NC2 are conformationally rigid and the observed conformational evolution likely involves the conformationally flexible unbound NC; the dissociation of the less stable G@NC2 would be the rate-determining step. Since guests with similar local structural features bind to NCvia a similar mechanism with a similar association barrier, and K_a1 and K_a2 are positively correlated due to the comparable differential stability of the two complex conformers, for a guest that forms a more stable G@NC1 complex, the corresponding G@NC2 conformer will also be more stable, and therefore the dissociation barrier for G@NC2 will be proportionally higher with a slower guest dissociation rate (Fig. S106†). The overall rate of conformational evolution will therefore be slower which explains the observed time required for the system to reach the conformational equilibrium. In other words, these results show that sufficient time is essential for an evolving, dynamic system to search for the thermodynamically favored product (e.g.G@NC1), especially if it is a highly stable one in which the possible existence of other kinetic products (e.g.G@NC2) of significant stability with slow reverse kinetics cannot be excluded.

Predicting the time required for attaining conformational equilibrium

By applying the established structure–thermodynamic–kinetic correlation for NC and the model ammonium guests, we also sought to predict the conformational equilibration time for the NC complexes of trimethylammonium guests derived from biogenic amines including acetylcholine, glycine, γ-aminobutyric acid, dopamine and tryptamine (i.e.A1–A7). These biogenic amines are important neurotransmitters and their host–guest complexes could find applications in sensing and triggered-release. In addition, a triethylammonium guest (i.e.A8) was also selected as a control. The binding constant of these guests was first determined by a competitive NMR experiment, and the results are summarized in Table 3. These guests were found to bind to NC with ln(K_a1) ranging from 10 to 15, suggesting that their dissociation rate constants would also span across several orders of magnitude.

Table 3 Binding constants of guest A1 to A8 (as PF6-salts) to NC1 (K_a1) and NC2 (K_a2) determined by ¹H NMR competition in CD₂Cl₂/CD₃CN (v/v = 1 : 1)

	K a1/M^−1	K a2/M^−1	Type		K a1/M^−1	K a2/M^−1	Type
A1	3.0 × 10^6	1.7 × 10^5	2 + 6	A5	3.6 × 10^5	3.1 × 10^4	6 + 12
A2	1.3 × 10^6	1.1 × 10^5	6 + 12	A6	7.1 × 10^5	7.6 × 10^4	6 + 12
A3	8.4 × 10^5	1.6 × 10^5	6 + 12	A7	1.3 × 10^5	6.0 × 10^3	6 + 12
A4	3.0 × 10^4	4.0 × 10^3	2 + 6	A8	2.0 × 10^4	4.6 × 10^3	6 + 12

---

With the measured K_a1 and K_a2 for A1 to A7, values of k₋₁ and k₋₂ can be obtained from the ln(k₋₁) − ln(K_a1) and ln(k₋₂) − ln(K_a2) plots (Fig. 5), from which the time required for the complexes to reach conformational equilibrium (t_e) can be predicted (see ESI† for details). The conformational changes in these host–guest complexes were also independently studied by ¹H NMR, and the corresponding dissociation rate constants were determined as previously described (Table 4). A good agreement was found between the predicted and experimentally obtained values of k₋₁, k₋₂ and t_e, demonstrating that the conformational kinetics of the host–guest system can be satisfactorily predicted from the more easily available binding constants. On the other hand, NC complexes of A8 were found to display no conformational exchange.

Table 4 Predicted and experimentally determined dissociation rate constants and time required to reach conformational equilibrium for NC complexes of A1 to A7

	From the experiment			From the prediction
	k −1/s^−1	k −2/s^−1	t e/min	k −1/s^−1	k −2/s^−1	t e/min
A1	2.9 × 10^−6	5.2 × 10^−5	920	2.6 × 10^−6	4.6 × 10^−5	1020
A2	6.7 × 10^−6	7.5 × 10^−5	610	6.4 × 10^−6	6.9 × 10^−5	660
A3	1.0 × 10^−5	5.5 × 10^−5	770	1.1 × 10^−5	5.1 × 10^−5	810
A4	5.0 × 10^−4	3.7 × 10^−3	12	3.7 × 10^−4	2.5 × 10^−3	17
A5	2.7 × 10^−5	3.1 × 10^−4	150	2.5 × 10^−5	2.8 × 10^−4	160
A6	1.1 × 10^−5	9.9 × 10^−5	450	1.2 × 10^−5	1.1 × 10^−4	420
A7	1.0 × 10^−4	2.1 × 10^−3	22	7.6 × 10^−5	1.6 × 10^−3	29

---

Conclusions

In summary, a supramolecular system consisting of the flexible molecular cage NC and a series of quaternary ammonium guests is discovered to be a suitable model for studying conformational kinetics in host–guest binding. Binding of quaternary ammonium guests resulted in two conformers whose stability is positively correlated. After the initial binding, the less stable conformer converts to the more stable one via a “guest dissociation-host conformational change-guest re-association” mechanism, and as such the guest dissociation from the less stable conformer to form the conformationally flexible, unbound host is the rate determining step of the observed conformational evolution, which in turn correlates with the overall thermodynamics of the complexes. As a result, the rate of the fast conformational exchange of the free NC is significantly slowed down from ∼10² s⁻¹ to 10⁻³ s⁻¹ to 10⁻⁷ s⁻¹via binding to ammonium guests with association constants from 10⁴ M⁻¹ to 10⁷ M⁻¹. Applying the established thermodynamic–kinetic correlation also allows the successful prediction of the kinetic parameters from thermodynamic data for another series of guests derived from biogenic amines. Further analysis of the rate and binding data shows that while the complex stability is related to the overall structural features of the guests, kinetics of the guest association is governed by the local steric properties around the ammonium head that first approaches the host during the binding.

The present study demonstrates for the first time the free energy analysis and correlation of the kinetics and thermodynamics of conformational changes in non-covalent complexes. Similar to Hammett analysis that explains and predicts the behaviours and outcomes of chemical reactions from reactant structures, understanding of such a thermodynamics–kinetics relationship of conformational changes will have broad implications in host–guest binding, structural adaption, dynamic assembly and induced motions in different supramolecular systems.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

S. He: conceptualization, methodology, formal analysis, investigation, writing – original draft, writing – review & editing; M. Quan: methodology, formal analysis; L.-P. Yang: methodology; H. Y. Au-Yeung: formal analysis, writing – original draft, writing – review & editing, supervision, funding acquisition; W. Jiang: conceptualization, resources, supervision, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was financially supported by the National Natural Science Foundation of China (No. 22125105 and 22101125), the Shenzhen Science and Technology Innovation Committee (JCYJ20180504165810828), the CAS-Croucher Funding Scheme for Joint Laboratories and the Collaborative Research Fund (CRF) (C7075-21G) from the Research Grant Council of Hong Kong. We are grateful for the technical support from SUSTech-Core Research Facilities.

Notes and references

1. K. Dunker, C. J. Brown, J. D. Lawson, L. M. Iakoucheva and Z. Obradović, Biochemistry, 2022, 41, 6573.
2. (a) W. L. Jorgensen, Science, 1991, 254, 954; (b) M. I. Zavodszky and L. A. Kuhn, Protein Sci., 2005, 14, 1104; (c) L. Cai and H. X. Zhou, J. Chem. Phys., 2011, 134, 105101; (d) Y. Wang, J. M. Martins and K. L. Larsen, Chem. Sci., 2017, 8, 6466.
3. (a) B. H. Havsteen and G. P. Hess, J. Am. Chem. Soc., 1962, 84, 491; (b) G. G. Hammes, Biochemistry, 2002, 41, 8221; (c) R. Callender and R. B. Dyer, Acc. Chem. Res., 2015, 48, 407.
4. (a) D. R. Madden, Nat. Rev. Neurosci., 2002, 3, 91; (b) S. S. Ramaswamy, D. M. MacLean, A. A. Gorfe and V. Jayaraman, J. Bio. Chem., 2013, 288, 35896; (c) S. Talwar and J. W. Lynch, Neuropharmacology, 2015, 98, 3.
5. P. J. Tummino and R. A. Copeland, Biochemistry, 2008, 47, 5481.
6. (a) S. B. Prusiner, Science, 1991, 252, 1515; (b) S. B. Prusiner, Science, 1997, 278, 245.
7. (a) E. H. Corder, A. M. Saunders and W. J. Strittmatter, Science, 1993, 261, 921; (b) J. Poirier, J. Davignon, D. Bouthillier, S. Kogan, P. Bertrand and S. Gauthier, Lancet, 1993, 342, 697; (c) A. M. Saunders, W. J. Strittmatter and D. Schmechel, Neurology, 1993, 43, 1467.
8. (a) Y. Mizuno, N. Hattori and H. Matsumine, J. Neurochem., 1998, 71, 893; (b) H. Shimura, N. Hattori, S. Kubo, Y. Mizuno, S. Asakawa and S. Minoshima, Nat. Genet., 2020, 25, 302.
9. (a) G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334; (b) A. R. Hughes, M. Liu, S. Paul, A. I. Cooper and F. Blanc, J. Phys. Chem. C, 2021, 125, 13370; (c) G. Schreiber, G. Haran and H.-X. Zhou, Chem. Rev., 2009, 109, 839.
10. For examples of reviews on common supramolecular hosts that include discussion on their binding kinetics, see: (a) S. Fa, T. Kakuta, T. Yamagishi and T. Ogoshi, Chem. Lett., 2019, 48, 1278; (b) E. Masson, X. Ling, R. Joseph, L. Kyeremeh-Mensah and X. Lu, RSC Adv., 2012, 2, 1213; (c) T. Ogoshi, T.-A. Yamagishi and Y. Nakamoto, Chem. Rev., 2016, 116, 7937; (d) M. Xue, Y. Yang, X. Chi, Z. Zhang and F. Huang, Acc. Chem. Res., 2012, 45, 1294; (e) K. Hermann, Y. Ruan, A. M. Hardin, C. M. Hadad and J. D. Badjić, Chem. Soc. Rev., 2015, 44, 500.
11. (a) G. G. Hammes, Y. C. Chang and T. G. Oas, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13737; (b) C. M. Hong, D. M. Kaphan, R. G. Bergman, K. N. Raymond and F. D. Toste, J. Am. Chem. Soc., 2017, 139, 8013; (c) L. P. Yang, L. Zhang, M. Quan, J. S. Ward, Y. L. Ma, H. Zhou, K. Rissanen and W. Jiang, Nat. Commun., 2020, 11, 2740; (d) Z. Y. Tang and C. A. Chang, J. Chem. Theory Comput., 2018, 14, 303.
12. (a) H. Tang, D. Fuentealba, Y. H. Ko, N. Selvapalam, K. Kim and C. Bohne, J. Am. Chem. Soc., 2011, 133, 20623–20633; (b) C. Bohne, Chem. Soc. Rev., 2014, 43, 4037; (c) C. Bohne, Langmuir, 2006, 22, 9100.
13. S. Rieth, X. G. Bao, B. Y. Wang, C. M. Hadad and J. D. Badjić, J. Am. Chem. Soc., 2010, 132, 773.
14. (a) H. Zheng, L. Fu, R. Wang, J. Jiao, Y. Song, C. Shi, Y. Chen, J. Jiang, C. Lin, J. Ma and L. Wang, Nat. Commun., 2023, 14, 590; (b) T. Zhao, W. Wu and C. Yang, Chem. Commun., 2023, 59, 11469.
15. L. P. Hammett, Chem. Rev., 1935, 17, 125.
16. (a) F. Jia, H. V. Schröder, L.-P. Yang, C. von Essen, S. Sobottka, B. Sarkar, K. Rissanen, W. Jiang and C. A. Schalley, J. Am. Chem. Soc., 2020, 142, 3306; (b) F. Jia, H. Hupatz, L.-P. Yang, H. V. Schröder, D.-H. Li, S. Xin, D. Lentz, F. Witte, X. J. Xie, B. Paulus, C. A. Schalley and W. Jiang, J. Am. Chem. Soc., 2019, 141, 4468; (c) S. B. Lu, H. X. Chai, J. S. Ward, M. Quan, J. Zhang, K. Rissanen, R. Luo, L. P. Yang and W. Jiang, Chem. Commun., 2020, 56, 888.
17. L. P. Cao, M. Sekutor, P. Y. Zavalij, K. M. Majerski, R. Claser and L. Isaacs, Angew. Chem., Int. Ed., 2014, 53, 988.
18. J. F. Bunnett, Investigation of Rates and Mechanisms of Reactions, John Wiley & Sons, New York, 1986.
19. A. Prabodh, S. Sinn, L. Grimm, Z. Miskolczy, M. Megyesi, L. Biczók, S. Bräse and F. Biedermann, Chem. Commun., 2020, 56, 12327.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc02831g

‡ Deceased 25 December 2022.

---