Small-angle neutron scattering differentiates molecular-level structural models of nanoparticle interfaces

Abstract

The highly anisotropic and nonadditive nature of nanoparticle surfaces restricts their characterization by limited types of techniques that can reach atomic or molecular resolution. While small-angle neutron scattering (SANS) is a unique tool for analyzing complex systems, it has been traditionally considered a low-resolution method due to its limited scattering vector range and wide wavelength spread. In this article, we present a novel perspective on SANS by showcasing its exceptional capability to provide molecular-level insights into nanoparticle interfaces. We report a series of experiments on multicomponent nanoparticles, where we demonstrate the ability of SANS to differentiate between competing structural models with molecular- and Å-scale differences. The results provide accurate quantification of organic ligand chain lengths, nanoparticles’ heterogeneity, and detailed structures of surrounding counter-ion layers in solution. Furthermore, we show that SANS can probe subtle variations in self-assembled monolayer structures in different thermodynamic states. Our findings challenge the conventional view of SANS as a low-resolution technique for nanoparticle characterization and demonstrate its unique potential for providing molecular-level insights into complex nanoparticle surface structures.

---

Zhi Luo

Dr Zhi Luo received his bachelor's degree from Tsinghua University in 2013 and his Ph.D. (with Distinction Award) from EPFL in 2018. He was supported by the ETH Fellow Program as a postdoctoral researcher at ETH Zurich before being appointed as an Associate Professor at the Southern University of Science and Technology (SUSTech) in 2021. Currently, he leads the Laboratory of Bioinspired Medicine and Materials, focusing on biomaterial characterization and polymer drugs.

---

Introduction

Understanding the interfacial structures of nanoparticles is key to the comprehension of a wide spectrum of their physical, chemical, and biological properties.¹ The interfaces, as the boundary between the core and the surrounding media, are characterized by sharp transitions of chemical potentials. Even subtle changes in the interfaces can substantially alter the properties of nanoparticles.² For instance, the surface energy of nanoparticles is found to be nonadditive at the nanoscale,³ and local structural variations can modulate both the charge and hydrophobic profiles of their surfaces.⁴ The importance of interfaces is also manifested in the collective behavior of nanoparticles, such as their self-assembly capability,⁵ and the charge transfer process within the sophisticated superstructures.⁶ Moreover, surface functionalities govern the intermolecular interactions between nanomaterials and small molecules or biomacromolecules, and such an interplay forms the basis for the sensing and biomedical applications of nanoparticles.⁷

Despite the broad impact of nanomaterial surfaces, our knowledge of their detailed structures is inadequate, especially at an atomic or molecular level.⁸ Typically, the surface is a hybrid system that consists of both organic and inorganic components. Hence, it is essential to obtain high-resolution information that contains both spatial and chemical details in order to form a complete picture of the surface.⁸ However, it is often challenging to simultaneously characterize these structures using a single type of technique. For example, transmission electron microscopy (TEM), as the gold standard, is able to capture accurate images of metal nanoparticle structures with sub-Å resolution.⁹ Nevertheless, fine details on the thin organic layer that surrounds the core material's heavy elements are barely detectable. On the other hand, spectroscopic techniques, such as nuclear magnetic resonance (NMR),¹⁰ X-ray photoelectron spectroscopy (XPS),¹¹ Raman spectrometry,¹² and mass spectrometry,¹³ can sensitively probe the molecular identities on the nanoparticles. As a result, spectroscopic and microscopic methods must be combined together to integrate the chemical information into a 3D space, and this can be a formidable task given the distinct working principles of different techniques.¹⁴

Small-angle neutron scattering (SANS) is a unique technique, as it can provide both dimensional and chemical information on complex material systems.^15,16 Although SANS has a lower intensity compared to X-ray scattering, its strength lies in its sensitivity to isotopes. Compared to X-rays, the scattering cross-section of neutrons is not a monotonic function of the atomic number and is sensitive to isotopes. This sensitivity allows for selective deuteration to label organic molecules and highlight them in the presence of heavy elements. The analysis of SANS typically relies on simple form factor models (e.g., core–shell spheres and ellipsoids) and is routinely used to determine the sizes, shapes, and compositions of various nanoparticle systems.¹⁷ For example, Diroll et al. reported a direct quantification of a series of gold nanoparticles protected by ligands with varying lengths and rigidities, ranging from small molecules to dendritic macromolecules.¹⁸ The authors calculated the ligand shell's thickness ratios in solid and solution states, which could be used to define the softness of the nanoparticle interfaces. Furthermore, SANS can locate specific components on complex surfaces through contrast variation.^19,20 As a notable example, Hammouda et al. discovered that the surfactants on gold nanorods are not uniformly distributed, which can be correlated to the retention of ligand molecules on nanoparticles during the nucleation and growth processes.²¹

Although SANS is a highly versatile technique, it has an intrinsically low resolution due to restrictions on the instrument setup, such as wide wavelength spread, limited collimation, area-sensitive detectors, and pinhole geometry.^22,23 Meanwhile, the range of scattering vectors further limits the length scale (typically corresponding to ∼1 nm in real space) that can be covered with SANS. Compared to small-angle X-ray scattering (SAXS), the lower flux of the neutron beam often requires the sacrifice of resolution for higher intensities on the sample. Consequently, SANS has even less resolving power than SAXS, particularly when it comes to recognizing sharp features like scattering maxima and minima.²⁴ However, depending on the desired intensity or power in resolving scattering patterns like peaks or dips, the instrument parameters, such as wavelength spread, collimation and pinhole geometry, can be tuned within rather broad boundaries.²⁵

In recent years, advances in computational methods have made it possible to directly reconstruct 3D models from SANS and SAXS data without the need for additional information.^26,27 Although such methods present inherently low-resolution, they are often used to validate high-resolution structures that have been resolved by cryo-EM, X-ray diffraction, or NMR,²⁸ and can offer important insight into macromolecules’ conformational states in solution.²⁹ When fitting the scattering profiles to these atomic models, explicit atom distances and water molecules are often required to achieve high-quality fitting.³⁰ For protein molecules, the scattering data take into account the hydration layer's excess scattering density (∼10% greater than bulk), and they can be fitted up with a resolving power of about 5 Å.³¹ SANS and SAXS are also the preferred methods for analyzing flexible macromolecules, providing a snapshot of the dynamic ensemble structures in certain thermodynamic states without signal broadening.³² Rambo et al. have proposed the super-resolution concept in SAXS, as the analysis on flexible protein structures can be extended to atomistic models.^33,34 The same authors have also defined a new scattering invariant (the volume of correlation, V_c), which can be used to accurately determine the molecular mass of proteins and RNA, with only an ∼4% average error.³⁵ This calculation has been applied to protein-like metal nanoclusters and offers high precision, with deviations of only a few atoms, as confirmed by crystallographic results.³⁶

In contrast to the conventional view of SANS as a low-resolution technique, herein, we present the potential of SANS in distinguishing between structurally similar models with molecular-level differences. While the absolute resolution of SANS measurements on nanoparticles is limited, we demonstrate that highly accurate information can be extracted from the scattering data and can be utilized to distinguish subtle structural differences at the Å-scale. Our analysis of SANS data reveals that even a difference of only two carbon–carbon bonds in the length of the ligand shell on nanoparticles can be readily captured and interpreted. The resolving power is further highlighted by the possibility to directly probe the detailed structures of the counter-ions that surround nanoparticles in solution. By using the contrast variation technique and simultaneously fitting multiple SANS curves with different contrasts using Monte Carlo-type calculations, we were able to reconstruct 3D models to represent complex morphologies. We further applied this modeling method to examine the structure of self-assembled monolayers on nanoparticles before and after a mild thermo-treatment. These findings emphasize the exceptional resolving power of SANS and highlight its competencies in characterizing the molecular-scale properties of nanoparticles. We believe that such capabilities of SANS are often underestimated and can offer valuable insights for the nanoparticle research field.

Results and discussion

On the resolution, accuracy and precision of SANS analysis

SANS is a powerful spectroscopic technique that provides information on the scattering length density fluctuations within a sample solution (Fig. 1A), making it possible to extract multiple structural parameters. These parameters include the dimensions of the core, shell, and surrounding counter-ion layers, as well as the spatial heterogeneity of the ligand assembly structures (Fig. 1B). However, in practice, SANS analyses are often hindered by low resolution due to limitations in the instrument's performance. Several factors contribute to this problem, including the wavelength spread of monochromators, collimation, area-sensitive detectors, and pinhole geometry.³⁷ Nevertheless, SANS analysis can still provide highly accurate information, particularly for biological systems, such as the hydration and conformational ensemble of protein molecules.^38,39

Fig. 1 A summary of key considerations when conducting SANS experiments. (A) Schematic representation of SANS analysis of nanoparticles. (B) Calculated SANS curves of gold nanoparticles (with a core diameter of 10 nm and a ligand shell thickness of 1.2 nm) with core size polydispersities of 0%, 10%, and 20%. (C) Calculated SANS curves of the same monodisperse gold nanoparticles under different pinhole smearing conditions, i.e., 0%, 10%, and 20% instrumental resolution smearing (dq/q). Fitting parameters are given in Table S1.† (D) Typical surface details of a nanoparticle that can be probed by SANS. We also demonstrate that comparable data quality can be obtained using time-of-flight instruments on spallation sources (Fig. S1B†).

To fully understand the SANS results, it is important to differentiate between the concepts of resolution, accuracy, and precision. In this paper, the resolution in SANS refers to the instrumental resolution, which is the uncertainty of the measured value of momentum transfer q, caused by factors such as wavelength spread and limited collimation.²² The resolution of SANS determines its ability to distinguish sharp features such as maxima and minima and is typically lower than that of SAXS due to the relaxation of these features to gain intensity on the sample. It is important to note that in some studies, the limits of the q-range are also considered a measure of resolution, as it represents the length scale that can be covered with SANS. Accuracy in SANS measurements refers to the degree of agreement between the measured value and the true value. To ensure accurate measurements, calibration of the instrument using standard samples and careful preparation of the sample are required. Precision, on the other hand, refers to the consistency and reproducibility of measurements. Precisely controlled experimental parameters, such as sample homogeneity and temperature, can increase precision to a large extent. By optimizing these parameters, it is possible to retrieve highly accurate and precise structural information from SANS data, even with a limited q-range. Overall, clarifying these concepts is crucial for the proper interpretation and analysis of our SANS measurements.

Furthermore, the quality of scattering data in SANS is also largely dependent on sample quality, including factors such as purity and polydispersity. To illustrate the impact of sample quality on scattering data, we conducted simulations on ligand-protected gold nanoparticles with a core diameter of 10.0 nm and a ligand shell thickness of 1.2 nm, varying the degree of core size polydispersity from 0% to 20% (Fig. 1C). The oscillating patterns typical of spheres became increasingly smeared with higher polydispersity and could even become completely featureless, as shown in Fig. S1A† when nanoparticles with 35% polydispersity were measured. Such effects are similar to those caused by instrument smearing. Using the same gold nanoparticle system with no size dispersity, we calculated SANS curves under varying degrees of pinhole smearing conditions, including 0%, 10%, and 20% dq/q, and obtained fitting parameters from Table S1† (Fig. 1C). As the smearing increased, the resolution of the scattering data deteriorated, similar to the effects caused by sample polydispersity. We also demonstrate that comparable data quality can be obtained using time-of-flight instruments on spallation sources (Fig. S1B†).

In summary, the quality of the scattering data in SANS is significantly affected by both instrument resolution and sample quality. Optimizing both factors can improve the accuracy and precision of SANS measurements, leading to more reliable and informative structural information (Fig. 1D). As a result, prior characterization of nanoparticles using TEM and SAXS is often crucial for accurate SANS analysis, providing additional information that helps prevent misinterpretation of the data. Thus, all the following SANS results are based on highly monodisperse gold nanoparticles with a robust chemical synthesis as model systems, and the SANS experiments were performed on instruments with Δλ/λ = 10% or 20% (as set by the mechanical selector). Other parameters such as the effective sample's diameter (0.2 cm), the collimation setup (6 m) and the sample detector's distance (1.5 m) were also optimized in order to balance the resolution, the q-range, and the scattering signal's intensity.

Å-scale resolving power on the dimension of nanoparticles

To thoroughly demonstrate the capability of SANS in different similar models with an Å-scale accuracy, we prepared two binary ligand-protected gold nanoparticles as model systems. Both nanoparticles were synthesized according to the Stucky protocol in order to obtain highly monodisperse samples (see the Materials and methods in ESI†).⁴⁰ A TEM analysis confirmed that the metal core's size distribution was less than 10% (4.7 ± 0.4 nm, as shown in Fig. S2†). The first binary ligand system is composed of 2-phenylethanethiol (PET) and 1-octanethiol (OT) with a ratio of 2 : 3, as determined by NMR (Fig. S2†). Two batches of nanoparticles with the same core sizes and ligand ratios were synthesized with one fully deuterated ligand in each sample (i.e., dPET–OT and PET–dOT combinations). It should be noted that we add a “d” to the front of the acronyms when we refer to the fully deuterated version of molecules in this manuscript. As all the experiments on PET–OT nanoparticles were performed using deuterated toluene (dTol) to match the deuterated ligands’ contrast, only one ligand component (nondeuterated) is visible by neutrons in each scattering experiment.

As shown in Fig. 2A, in all the SANS measurements, the highest scattering vector q was 0.35 Å⁻¹. This implies that the resolution (in terms of the length scale covered) of the dataset is only ∼1.8 nm. Under such experimental conditions, the recorded scattering patterns of the PET–OT nanoparticles were still significantly different under the two ligand contrasts. Specifically, the first minima of oscillation, which correlated with the size of the spherical objects, shifted from ∼0.13 Å⁻¹ (∼48.3 Å in real space) for the dPET–OT nanoparticles to ∼0.15 Å⁻¹ (∼41.9 Å in real space) for the PET-dOT nanoparticles. This suggests that the overall size of the latter nanoparticles was smaller than the former's, and that the difference arose solely from the length of the two organic molecules’ chains. According to the calculated pair distribution function, P(r), the D_max value of the dPET–OT nanoparticles was 71 Å, while the D_max value of the PET–dOT nanoparticles was 63 Å (Fig. 2B). The D_max values corresponded to the nanoparticles’ diameters, including the ligand shell and the metal core. Since the core's diameter was 4.7 ± 0.4 nm (as was measured by TEM), the organic ligands’ thicknesses were calculated to be 8 Å and 12 Å, indicating that the OT ligand was ∼4 Å longer than the PET ligand on the nanoparticles. As shown in Fig. 2I, the theoretical difference between the fully extended conformation of the OT and PET is approximately two C–C bonds, which agrees well with the above-calculated values. Additionally, by comparing the experimental curves and the simulated curves, subtle changes can be detected based on the shift and size of peaks and the slope of the curve. Therefore, the results demonstrate that SANS is capable of discerning Å-scale variations in ligand length between nanoparticles with similar structures and it also suggests that toluene is a good solvent for the PET–OT nanoparticles since both ligands adopt an extended conformation on the surfaces.

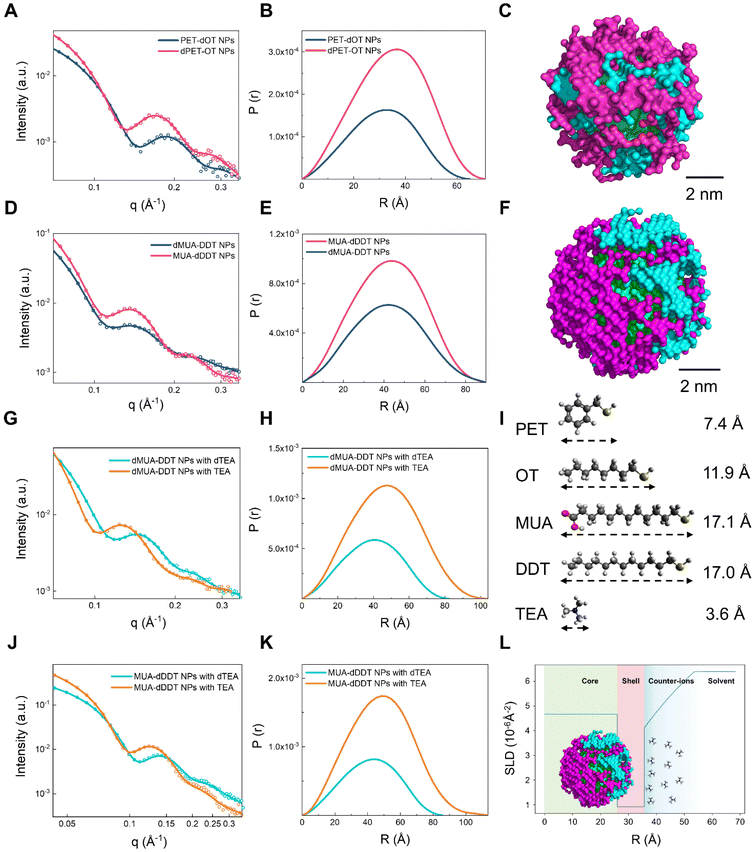Fig. 2 SANS data, P(r) functions, and 3D models of a series of nanoparticles. (A) SANS data and (B) calculated P(r) functions of the dPET–OT (pink solid line) and PET–dOT (dark blue solid line) nanoparticles. In all the SANS plots, the dots represent the experimental data and the full lines show the fitting results. (C) A 3D model of the PET–DDT nanoparticles generated using the MONSA program. The parameters that define instrument resolution are listed in Table S2.† The green, blue, and pink beads represent the gold, PET, and OT phases, respectively. (D) SANS data and (E) calculated P(r) functions of the MUA–dDDT (pink solid line) and dMUA–DDT (dark blue solid line) nanoparticles. (F) A 3D model of the MUA–DDT nanoparticles generated using the MONSA program. The green, blue, and pink beads represent the gold, DDT, and MUA phases, respectively. (G) SANS data and (H) calculated P(r) functions of the dMUA–DDT–dTEA (cyan) and dMUA–DDT–TEA (orange) samples. (I) Chemical structures and lengths of the PET, MUA, TEA, OT and DDT molecules. (J) SANS data and (K) calculated P(r) functions of the MUA–dDDT–dTEA (cyan) and MUA–dDDT–TEA (orange) samples. (L) Scattering length density (SLD) curve representation of TEA counter-ions surrounding the MUA–DDT nanoparticles. “Nanoparticles” are abbreviated as “NPs” in all figures.

To further investigate whether SANS has the ability to differentiate between nanoparticles with similar structures, nearly identical lengths and sizes, we tested another system in which the binary ligands had almost the same chain length, i.e., 11-mercaptoundecanoic acid (MUA)- and 1-dodecanethiol (DDT)-protected nanoparticles. The same as the experiment above, we used two ligand contrast conditions (i.e., dMUA–DDT and MUA–dDDT nanoparticles), and both were measured in deuterated methanol (MeOD). According to Fig. 2D, there was no clear difference in the minima or peak positions of the scattering patterns under the two contrast conditions. The D_max values of both nanoparticles were 90 Å, as was calculated for P(r), which indicates that the overall sizes of the dMUA–DDT and MUA–dDDT nanoparticles were almost identical (Fig. 2E). Also, the TEM images and NMR in Fig. S3† confirm the diameter of the MUA–DDT gold nanoparticles and the ligand ratio of the MUA–DDT gold nanoparticles, respectively. While there was a subtle difference in the length of the chain in DDT (17.0 Å) and MUA (17.1 Å), it was indistinguishable by SANS (Fig. 2G), and the result shows that the two ligands adopted similar conformations in methanol solution.

Unveiling the structure of the counter-ion layer and ligand solvation

An interesting property of the MUA–DDT nanoparticles is that their solubility can be tuned by changing the charge states of the carboxylic acid group of MUA ligands. For example, when we added an organic base, triethylamine (TEA), the nanoparticles became highly soluble under aqueous conditions. Based on the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory,⁴¹ the positively charged TEA molecules, in principle, form a counter-ion layer through electrostatic interactions. This would stabilize the nanoparticles in water. Therefore, we investigated whether SANS could characterize the difference in the presence of the counter-ion cloud that was formed by the small organic base, as well as the difference in the solvation of the ligand shell. The two sets of nanoparticles were mixed with either TEA or its deuterated form (dTEA), and the resulting four samples (i.e., dMUA–DDT–TEA, dMUA–DDT–dTEA, MUA–dDDT–TEA, and MUA–dDDT–dTEA) were all dissolved in D₂O for the SANS experiment. Each of the four sets of contrast conditions highlighted different components in the nanoparticles, e.g., the MUA ligand, the DDT ligand, or the TEA counter-ions (Fig. 2G and J).

As shown in the P(r) plots in Fig. 2H and K, when the dTEA's contrast matched that of the D₂O solvent, the overall sizes (D_max) of the dMUA–DDT and MUA–dDDT nanoparticles were 82 Å and 86 Å, respectively. As discussed above, the D_max values of both nanoparticles in MeOD were ∼90 Å; therefore, the SANS data in D₂O suggest that the MUA–DDT ligand shell adopted a more collapsed conformation (∼2–4 Å thinner) under aqueous conditions. While the two ligands had identical chain lengths in MeOD, a small difference in the D_max value could be observed in D₂O: the DDT molecule is ∼2 Å shorter than the MUA molecule. Considering the hydrophobic nature of DDT and the charged MUA head group, such a subtle variation is reasonable and could be related to the different hydration degrees of the two ligands. Therefore, these results further prove that SANS has the capability to distinguish between closely resembling structures at the Å-scale while simultaneously detecting subtle changes in the conformation of ligand molecules on the surfaces of nanoparticles in various solvent environments.

From the SANS data, it is obvious that for both the dMUA–DDT and MUA–dDDT nanoparticles, when the nondeuterated TEA was used, the valley of oscillation in their scattering patterns shifted toward a lower q region than the dTEA contrast. This indicates that the overall sizes of the nanoparticles significantly increased due to the scattering contribution from the counter-ion TEA. The SANS data were then fitted using a core and multiple shell structure model with the core and the first ligand shell having fixed scattering length density (SLD) values, while the SLD of the second shell features an exponential function of the radius (Fig. 2L). This analysis indicates that the first ligand shell, which is composed of MUA and dDDT, has an average thickness of ∼10 Å. The thickness of the second diffused layer of the counter-ions is found to be ∼18 Å, while within this range, the SLD value gradually increases from 4.1 × 10⁻⁶ Å⁻² to 6.4 × 10⁻⁶ Å⁻². It should be noted that while the electric double layer theory is central to surface science, the direct characterization of its structure is highly challenging with most of the techniques. The present findings provide compelling evidence that the exceptional sensitivity and resolving power of SANS validate physical models that contain molecular-scale details, paving the way for a comprehensive study of the interfacial structures of nanoparticles.

Probing the spatial heterogeneity at the molecular scale

In addition to extracting parameters such as the core–shell's diameter, it has been previously demonstrated that 3D models can be readily reconstructed using programs such as MONSA in the ATSAS package.^19,42 This program utilizes a three-phase bead model (a metal core and two ligands) to represent the structures of the nanoparticles. Starting from randomly assigned phases, the Monte Carlo-type calculation fits multiple SANS curves simultaneously and minimizes the overall discrepancy between the experimental data and the fitting results. A detailed description of the algorithm and the fitting procedure can be found in the ESI.† As shown in Fig. 2C and F, the models that were generated from MONSA allowed the phase separation structure of the binary ligands on nanoparticle surfaces to be directly visualized. Both the PET–OT and MUA–DDT ligand shells featured small phase separation domains that were similar to the ones in previous reports and molecular dynamic simulations.¹⁹ It should be noted that, being a Monte Carlo method, the fitting from each run would generate a different model. Thus, we performed multiple fitting tests, starting from different random configurations, and all the resulting models from the repeated calculations were very similar to each other (Fig. S4†). Furthermore, Fig. S4† shows a direct comparison with theoretical scattering patterns for the ideal stripe-like, patchy or Janus type of morphology, and they clearly deviate from the experimental curves.

The Stuhrmann plot and contrast variation are often used to analyze the inhomogeneity of nanoparticles. As shown in eqn (1), the α coefficient in the Stuhrmann equation describes the relative distribution of scattering length density radially from a particle's center of mass. The α value is positive when regions with a higher density are close to the periphery and vice versa. The value of β is a measure of the distance of the center of mass of the particle to the center of scattering length density of its heterogeneous components. β = 0 when they coincide; otherwise, β ≠ 0.

where Δρ = ρ_m − ρ_solv, which is the difference between the contrast of the scattering object and that of the solvent. R_c is the radius of a particle's gyration at an infinite contrast (i.e. if it were homogeneous).

A series of SANS experiments were conducted under various contrast conditions using a mixture of H₂O and D₂O (100/0, 50/50, 25/75, 0/100), as shown in Fig. 3C. A binary ligand combination of 11-mercapto-1-undecanesulfonate (MUS) and dOT (Fig. 3A) was used (90.9% MUS and 9.1% OT), which resulted in the nanoparticles being highly soluble in water. The OT ligand was fully deuterated but the MUS ligand was nondeuterated so that there would be a sharp contrast between the two ligands. As shown in Fig. 3D, an R_c value of 9.1 nm was obtained, and the values of α and β were −432.7 and 87.6, respectively. The negative and large absolute value of α indicates that the high contrast component was enriched at the core of the nanoparticles, which is in line with the conventional core–shell structure of the nanoparticles. As the metal core of the nanoparticles can be regarded as uniform and symmetric, the value of β reveals the structure of the ligand shell. The non-zero and large value of β indicates that the binary ligand shell had a highly axisymmetric structure in which the particle's center of mass did not correspond to the center of scattering length density. A large degree of eccentricity is also indicated by the narrow parabolic shape of this curve. Therefore, the Stuhrmann plot confirms the overall core–shell structure of the nanoparticles as well as the heterogeneous ligand structure on the surface.

Fig. 3 A normalized Stuhrmann plot, P(r) function, and SANS data of the nanoparticles. (A) Schematic representation of the MUS–OT nanoparticles. (B) 3D models, generated using MONSA, of the MUS–OT nanoparticles. All four phases, i.e., the solvent (white), MUS (pink), OT (blue), and gold (green), are shown. (C) SANS data of the MUS–OT nanoparticles. (D) A normalized Stuhrmann plot of (R_g/R_c)²vs. ρ_m/Δρ at four different contrasts: D₂O/H₂O = 100/0, 75/25, 50/50, and 0/100. (E) Calculated P(r) function of the MUS–dOT nanoparticles at different solvent contrasts. (F) I₀^0.5vs. Δρ at four contrasts: D₂O/H₂O = 100/0, 75/25, 50/50, and 0/100.

Moreover, calculating the Stuhrmann Plot required measuring the particle's radius of gyration at an infinite dilution, and it was measured with at least three different solvents (Fig. 3F). The contrast match point was also measured, and it can be considered an important characteristic of the nanoparticles. The dependence of zero-angle scattering on the contrast is given by eqn (2):

I(0) = (Δρ)²V². (2)

From this equation, a linearization vs. Δρ yields the contrast match point of the particle at I(0) = 0. At this point, ρ_m = ρ_solv. Therefore, the average density level within the particle can be readily determined. The inclination of the line is related to the volume of a particle. As shown in Fig. 3F, the experimentally determined contrast match point was found to be ρ_m = 0.3 × 10⁻⁶ Å⁻² and the inclination was 0.2, agreeing with the ligand ratio measurement from NMR (Fig. S5†).

The D_max value of the MUS–dOT nanoparticles was 9.2 nm, as determined from P(r) in Fig. 3E. The shape of the black curve in the P(r) function deviates slightly from the bell shape, which might be due to the specific combination of the ligand's length and composition as well as the spatial distribution of the ligands that deviate from the random mixing. To further resolve the nanoparticles’ structure, the scattering curves were fitted using MONSA (Fig. 3B), and the ligand shell heterogeneity was visualized using the reconstructed 3D model. As shown in Fig. 3D, the OT ligands seem to form relatively large domains, and the heterogeneity of the ligand shell is large. Nanoparticles that are protected with an amphiphilic ligand shell have many interesting interfacial properties, and similar nanoparticles have shown great potential in various fields such as sensing, drug delivery, and antivirals.^43,44 Thus, the information retrieved from SANS can hopefully help establish their structure–property relationships in biomedical applications.

Distinguishing structures in different thermodynamic states

For the binary self-assembled monolayers on nanoparticles, previous studies have established that various morphologies could arise as a result of the balance between the enthalpy of ligand packing and chain conformational entropy.⁴⁵ Therefore, in principle, the morphology of a binary ligand shell may evolve as it goes through the thermo-treatment process.^46,47 To assess the ability of SANS to differentiate variations in the ligand organization in similar thermodynamic states, dPET–DDT-protected nanoparticles were prepared using the ligand exchange reaction at room temperature (Fig. 4B). Under such conditions, the self-assembled patterns were influenced by the exchange kinetics, and thus nonequilibrium structures could be observed.⁴⁶ A heating treatment was then performed on the nanoparticles’ dTol solution at 50 °C for 24 hours. As shown in Fig. S6,† both NMR and TEM analyses were performed, and they showed that the ligand ratio and core size of the nanoparticles were the same before and after the thermo-treatment process. This was further confirmed by the SANS spectra, which overlapped in the Guinier region (Fig. 4A), suggesting that the R_g value of the nanoparticles remained unchanged. Similarly, the P(r) values (Fig. S7†) of the two nanoparticles appeared almost identical, with the D_max values being 8.2 nm and 8.3 nm respectively.

Fig. 4 SANS data, a scheme of the nanoparticles, and 3D models of the nanoparticles. (A) SANS data (dots) and fitting (full lines) for the PET–DDT nanoparticles before (red) and after (gray) the thermo-treatment. (B) Schematic representation of the PET–DDT nanoparticles. (C) SANS data in a high q region highlighting the subtle changes of the form factors of nanoparticles due to the heating process. (D) 3D models of the PET–DDT nanoparticles under different thermostatic conditions generated using MONSA. All four phases, i.e., the solvent (white), DDT (pink), PET (blue), and gold (green), are shown.

Combined with the information from the other supporting techniques discussed above, the overlapping scattering curves at a low q value confirm that the overall size and composition of the nanoparticles remained constant during the heating process. An observable deviation in the form factor could be seen from 0.08 Å⁻¹ to 0.39 Å⁻¹ (Fig. 4C), as the oscillation features in the scattering profiles became sharper for nanoparticles after thermo-treatment. Such a difference can be attributed to the ligand shell rearrangements on the nanoparticle surfaces. The 3D models were then reconstructed using MONSA fitting with the same procedure described above and are shown in Fig. 4D. Although the overall structures of the binary ligand assembly were similar, the two nanoparticle models differed slightly in terms of the nanoscale domains. The phase separation domains of the PET ligands became thinner after heating. This observation might be explained by the conformational entropy contribution at higher temperatures, which favors smaller and more elongated domain structures. Similar behavior has been reported previously on other binary ligand-protected nanoparticles.⁴⁷ Although further experimental and simulation studies are required to validate the proposed structural models, to the best of our knowledge, SANS is presently the sole technique that can effectively detect such subtle morphological alterations on nanoparticle surfaces.

Conclusions

In summary, this study has demonstrated the exceptional resolving power of SANS in analyzing the surface structures of nanoparticles. Despite being constrained by the range of scattering vectors and instrument resolution, SANS can distinguish similar structural models at the molecular scale. We have shown that SANS is particularly powerful in investigating the dimensions of ligand shells on nanoparticle surfaces, a task challenging for both TEM and X-ray scattering. Moreover, we have demonstrated the capability of SANS to examine the intricate details of the counter-ion layer. Additionally, by utilizing advanced computational tools like MONSA, we can reconstruct 3D models that effectively describe the surface morphologies of nanoparticles in various thermodynamic states. The structural information is crucial for applying nanomaterials across a broad spectrum of fields, including drug delivery, diagnostics, and catalysis, where surface structures and interactions with other molecules are key. Consequently, we believe that SANS is a premier technique and will play an increasingly vital role in nanoscience. Future research should concentrate on developing new, dedicated data analysis algorithms to enhance the interpretation of SANS results for complex nanomaterial systems. Additionally, integrating SANS with other complementary techniques is crucial for fully exploiting its capabilities to probe the dynamic behavior of nanomaterials. This integration will enable more effective in situ and in operando analyses in future studies.

Author contributions

Conceptualization: Z. L. and F. S. Methodology: Y. W., X. L., A. R., L. P., H. J., Y. H., Y. K., T. D., and Z. L. Simulation: Y. W. and Z. L. Supervision: Z. L. Writing – review & editing: Y. W., X. L., A. K. H., and Z. L.

Data availability

All data needed to evaluate the conclusions in the paper are present in the paper and/or its ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Key Research and Development Program of China (No. 2022YFB3804700). Z. L. acknowledges the financial support from the National Natural Science Foundation of China (22272071), the Shenzhen Medical Research Fund (Grant No. A2303062), the Shenzhen Science and Technology Innovation Commission (Grant No. 20220815164435002), and the Large Scientific Facility Open Subject of Songshan Lake, Dongguan, Guangdong (KFKT2022A09). The authors acknowledge the assistance of SUSTech Core Research Facilities and the Materials Characterization and Preparation Center.

References

1. T. Kister, D. Monego and P. Mulvaney, et al., Colloidal Stability of Apolar Nanoparticles: The Role of Particle Size and Ligand Shell Structure, ACS Nano, 2018, 12, 5969–5977.
2. R. Lévy, N. T. K. Thanh and R. C. Doty, et al., Rational and Combinatorial Design of Peptide Capping Ligands for Gold Nanoparticles, J. Am. Chem. Soc., 2004, 126, 10076–10084.
3. C.A. Silvera Batista, R. G. Larson and N. A. Kotov, Nonadditivity of nanoparticle interactions, Science, 2015, 350, 1242477.
4. C. D. Ma, C. Wang and C. Acevedo-Vélez, et al., Modulation of hydrophobic interactions by proximally immobilized ions, Nature, 2015, 517, 347–350.
5. M. Grzelczak, J. Vermant and E. M. Furst, et al., Directed Self-Assembly of Nanoparticles, ACS Nano, 2010, 4, 3591–3605.
6. M. Y. Ben Zion, X. He and C. C. Maass, et al., Self-assembled three-dimensional chiral colloidal architecture, Science, 2017, 358, 633–636.
7. D. F. Moyano and V. M. Rotello, Nano Meets Biology: Structure and Function at the Nanoparticle Interface, Langmuir, 2011, 27, 10376–10385.
8. R. M. Choueiri, E. Galati and H. Thérien-Aubin, et al., Surface patterning of nanoparticles with polymer patches, Nature, 2016, 538, 79–83.
9. Y. Lin, M. Zhou and X. Tai, et al., Analytical transmission electron microscopy for emerging advanced materials, Matter, 2021, 4, 2309–2339.
10. L. E. Marbella and J. E. Millstone, NMR Techniques for Noble Metal Nanoparticles, Chem. Mater., 2015, 27, 2721–2739.
11. C.-K. Wu, M. Yin and S. O'Brien, et al., Quantitative Analysis of Copper Oxide Nanoparticle Composition and Structure by X-ray Photoelectron Spectroscopy, Chem. Mater., 2006, 18, 6054–6058.
12. Q. Zhou, X. Li and Q. Fan, et al., Charge Transfer between Metal Nanoparticles Interconnected with a Functionalized Molecule Probed by Surface-Enhanced Raman Spectroscopy, Angew. Chem., 2006, 118, 4074–4077.
13. L. Yu and A. Andriola, Quantitative gold nanoparticle analysis methods: A review, Talanta, 2010, 82, 869–875.
14. Y. Yang, S. Liao and Z. Luo, et al., Comparative characterisation of non-monodisperse gold nanoparticle populations by X-ray scattering and electron microscopy, Nanoscale, 2020, 12, 12007–12013.
15. S. Mehan, A. J. Chinchalikar and S. Kumar, et al., Small-Angle Neutron Scattering Study of Structure and Interaction of Nanoparticle, Protein, and Surfactant Complexes, Langmuir, 2013, 29, 11290–11299.
16. G. Von White, F. S. Mohammed and C. L. Kitchens, Small-Angle Neutron Scattering Investigation of Gold Nanoparticle Clustering and Ligand Structure Under Antisolvent Conditions, J. Phys. Chem. C, 2011, 115, 18397–18405.
17. J. J. Richards, C. L. Whittle and G. Shao, et al., Correlating Structure and Photocurrent for Composite Semiconducting Nanoparticles with Contrast Variation Small-Angle Neutron Scattering and Photoconductive Atomic Force Microscopy, ACS Nano, 2014, 8, 4313–4324.
18. B. T. Diroll, K. M. Weigandt and D. Jishkariani, et al., Quantifying “Softness” of Organic Coatings on Gold Nanoparticles Using Correlated Small-Angle X-ray and Neutron Scattering, Nano Lett., 2015, 15, 8008–8012.
19. Z. Luo, D. Marson and Q. K. Ong, et al., Quantitative 3D determination of self-assembled structures on nanoparticles using small angle neutron scattering, Nat. Commun., 2018, 9, 1343.
20. Z. Luo, Y. Yang and A. Radulescu, et al., Multidimensional Characterization of Mixed Ligand Nanoparticles Using Small Angle Neutron Scattering, Chem. Mater., 2019, 31, 6750–6758.
21. M. J. A. Hore, X. Ye and J. Ford, et al., Probing the Structure, Composition, and Spatial Distribution of Ligands on Gold Nanorods, Nano Lett., 2015, 15, 5730–5738.
22. J. S. Pedersen, D. Posselt and K. Mortensen, Analytical treatment of the resolution function for small-angle scattering, J. Appl. Crystallogr., 1990, 23, 321–333.
23. M. Nakano, M. Fukuda and T. Kudo, et al., Determination of Interbilayer and Transbilayer Lipid Transfers by Time-Resolved Small-Angle Neutron Scattering, Phys. Rev. Lett., 2007, 98, 238101.
24. T. Vad, W. F. C. Sager and J. Zhang, et al., Experimental determination of resolution function parameters from small-angle neutron scattering data of a colloidal SiO ₂ dispersion, J. Appl. Crystallogr., 2010, 43, 686–692.
25. A. Radulescu, N. K. Székely and S. Polachowski, et al., Tuning the instrument resolution using chopper and time of flight at the small-angle neutron scattering diffractometer KWS-2, J. Appl. Crystallogr., 2015, 48, 1849–1859.
26. J. E. Houston, L. Fruhner and A. de la Cotte, et al., Resolving the different bulk moduli within individual soft nanogels using small-angle neutron scattering, Sci. Adv., 2022, 8, eabn6129.
27. T. Zettl, R. S. Mathew and X. Shi, et al., Gold nanocrystal labels provide a sequence–to–3D structure map in SAXS reconstructions, Sci. Adv., 2018, 4, eaar4418.
28. C. Guo and J. L. Yarger, Characterizing gold nanoparticles by NMR spectroscopy, Magn. Reson. Chem., 2018, 56, 1074–1082.
29. X. Liu, M. Yu and H. Kim, et al., Determination of monolayer-protected gold nanoparticle ligand–shell morphology using NMR, Nat. Commun., 2012, 3, 1182.
30. B. Hammouda, D. Ho and S. Kline, SANS from Poly(ethylene oxide)/Water Systems, Macromolecules, 2002, 35, 8578–8585.
31. A. V. Sokolova, L. Kreplak and T. Wedig, et al., Monitoring intermediate filament assembly by small-angle x-ray scattering reveals the molecular architecture of assembly intermediates, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 16206–16211.
32. F. Spinozzi, G. Ceccone and P. Moretti, et al., Structural and Thermodynamic Properties of Nanoparticle–Protein Complexes: A Combined SAXS and SANS Study, Langmuir, 2017, 33, 2248–2256.
33. R. P. Rambo and J. A. Tainer, Super-Resolution in Solution X-Ray Scattering and Its Applications to Structural Systems Biology, Annu. Rev. Biophys., 2013, 42, 415–441.
34. Z. He, M. Rödel and J. Lütgert, et al., Diamond formation kinetics in shock-compressed C—H—O samples recorded by small-angle x-ray scattering and x-ray diffraction, Sci. Adv., 2022, 8, eabo0617.
35. R. P. Rambo and J. A. Tainer, Accurate assessment of mass, models and resolution by small-angle scattering, Nature, 2013, 496, 477–481.
36. X. Liu, H. Yang and Y. Chen, et al., Quantifying the Solution Structure of Metal Nanoclusters Using Small–Angle Neutron Scattering, Angew. Chem., Int. Ed., 2022, 61, e202209751.
37. D. Franke, M. V. Petoukhov and P. V. Konarev, et al., ATSAS 2.8 : a comprehensive data analysis suite for small-angle scattering from macromolecular solutions, J. Appl. Crystallogr., 2017, 50, 1212–1225.
38. U. R. Shrestha, P. Juneja and Q. Zhang, et al., Generation of the configurational ensemble of an intrinsically disordered protein from unbiased molecular dynamics simulation, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 20446–20452.
39. H. S. Kim, A. Martel and E. Girard, et al., SAXS/SANS on Supercharged Proteins Reveals Residue-Specific Modifications of the Hydration Shell, Biophys. J., 2016, 110, 2185–2194.
40. N. Zheng, J. Fan and G. D. Stucky, One-Step One-Phase Synthesis of Monodisperse Noble-Metallic Nanoparticles and Their Colloidal Crystals, J. Am. Chem. Soc., 2006, 128, 6550–6551.
41. P. Claesson, R. G. Horn and R. M. Pashley, Measurement of surface forces between mica sheets immersed in aqueous quaternary ammonium ion solutions, J. Colloid Interface Sci., 1984, 100, 250–263.
42. D. I. Svergun, Restoring Low Resolution Structure of Biological Macromolecules from Solution Scattering Using Simulated Annealing, Biophys. J., 1999, 76, 2879–2886.
43. A. Bekdemir, S. Liao and F. Stellacci, On the effect of ligand shell heterogeneity on nanoparticle/protein binding thermodynamics, Colloids Surf., B, 2019, 174, 367–373.
44. A. Verma and F. Stellacci, Effect of Surface Properties on Nanoparticle–Cell Interactions, Small, 2010, 6, 12–21.
45. C. Singh, P. K. Ghorai and M. A. Horsch, et al., Entropy-Mediated Patterning of Surfactant-Coated Nanoparticles and Surfaces, Phys. Rev. Lett., 2007, 99, 226106.
46. Z. Luo, J. Hou and L. Menin, et al., Evolution of the Ligand Shell Morphology during Ligand Exchange Reactions on Gold Nanoparticles, Angew. Chem., Int. Ed., 2017, 56, 13521–13525.
47. Z. Luo, A. Murello and D. M. Wilkins, et al., Determination and evaluation of the nonadditivity in wetting of molecularly heterogeneous surfaces, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 25516–25523.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04365k

‡ These authors contributed equally to this work.

---