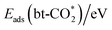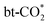Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Scaling relations of CO2 hydrogenation and dissociation on single metal atom doped In2O3 catalysts with promoted oxygen vacancy sites†
Yuanjie Baoab,
Ziqi Tangac,
Yuchen Wang ac and
Shenggang Li
ac and
Shenggang Li *abcd
*abcd
aCAS Key Laboratory of Low-Carbon Conversion Science and Engineering, Shanghai Advanced Research Institute, Chinese Academy of Sciences, 100 Haike Road, Shanghai 201210, P. R. China. E-mail: lisg@sari.ac.cn
bUniversity of Chinese Academy of Sciences, Beijing 100049, P. R. China
cSchool of Physical Science and Technology, ShanghaiTech University, Shanghai 201210, P. R. China
dState Key Laboratory of Low Carbon Catalysis and Carbon Dioxide Utilization, Shanghai Advanced Research Institute, Chinese Academy of Sciences, Shanghai 201210, P. R. China
First published on 12th March 2025
Abstract
In this work, we conducted a computational study on single atom doped In2O3 catalysts with 12 transition metals (Fe–Cu, Ru–Ag, Os–Au) through density functional theory (DFT) calculations, by investigating the dissociation of H2, and the dissociation and hydrogenation of CO2. From the thermodynamic-kinetic scaling relationships such as Brønsted–Evans–Polanyi (BEP) and transition-state scaling (TSS) relations, we establish the descriptors for the energy barriers and improve our understanding of the synergistic catalytic effect of oxygen vacancies and single atoms. We find that the adsorption energy of the H adatom on the perfect surface can serve as an effective descriptor for the dissociation energy barrier of H2 on this surface, and the formation energy of the oxygen vacancy can serve as an effective descriptor for the energy barrier of CO2 hydrogenation to HCOO as well as the energy barrier of CO2 direct dissociation.
1. Introduction
To address the severe environmental issues caused by excessive carbon emissions, technologies for carbon capture, utilization and storage (CCUS) have gained widespread attention.1–3 Much effort has been made for the exploration of the CO2 hydrogenation to methanol reaction4,5 with the aim of simultaneously improving the utilization of renewable energy sources. At present, methanol synthesis at an industrial scale relies much on the conversion of synthesis gas, which is a mixture of CO and H2 with a small amount of CO2 facilitated by the Cu/ZnO/Al2O3 catalysts. Nonetheless, Cu-based catalysts are notably active for the reverse water–gas shift (RWGS) reaction, leading to lower methanol selectivity and catalyst deactivation especially at relatively high reaction temperatures.6–8In2O3 has been regarded as a highly promising catalyst for CO2 hydrogenation to methanol in recent years.9,10 Interestingly, its potential was initially unveiled through density functional theory (DFT) calculations by Ye et al.,11,12 which has been confirmed through follow-up experiments.13 Structural characterization of the In2O3 catalyst by Frei et al.14 evidenced a dominant exposure of the (111) facet, and the CO2 hydrogenation reaction was considered to proceed via the selective and consecutive addition of hydrides and protons. Such a viewpoint was also supported by the DFT calculations of Qin et al.,15 indicating that the heterolytic dissociation of H2 at surface In and O pair sites is kinetically favorable on both the perfect and defective In2O3 surfaces. Martin et al.16 experimentally showed that methanol selectivity could reach 100% using the In2O3/ZrO2 mixed-oxide catalyst under the industrially relevant conditions (T = 473–573 K, P = 10–50 bar, GHSV = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–48
000–48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1). Dang et al.17 found that the threefold oxygen vacancy site on the cubic c-In2O3(111) and hexagonal h-In2O3(104) surfaces favored the linear CO2 physisorption structure and the HCOO pathway, leading to high CH3OH selectivity.
000 h−1). Dang et al.17 found that the threefold oxygen vacancy site on the cubic c-In2O3(111) and hexagonal h-In2O3(104) surfaces favored the linear CO2 physisorption structure and the HCOO pathway, leading to high CH3OH selectivity.
While In2O3 allows for high methanol selectivity by effectively suppressing the rival RWGS reaction, CO2 reactivity is hindered by its relatively low activity for the dissociation of molecular H2.18 To enhance hydrogen activation, a range of metal promoters has been investigated including Pd, Pt, Ag, Ru, Rh, Ir, Ni, Re, and Au.19–27 Several of these studies indicate that highly dispersed metal promoters play a crucial role in enhancing the catalytic activity of In2O3 for the methanol synthesis reaction. To facilitate a direct comparison of the formation and promotional effects of these catalysts, Pérez-Ramírez et al.28 introduced 9 metal promoters into In2O3 at the same loading of 0.5 wt% through flame spray pyrolysis (FSP) as a standardized synthesis method. It was found that atomically dispersed promoters such as Pd, Pt, Rh, Ru and Ir led to the greatest performance improvement, especially Pd and Pt, which significantly promote hydrogen activation while hindering CO formation. Shen et al.27 further demonstrated that at low Re loadings of ≤1 wt%, Re was doped into the In2O3 lattice in a single atom form, which benefits methanol formation. Huang et al.29 designed a bifunctional single atom catalyst (SAC) based on the synergy of atomic Ir and In2O3 and revealed that a Lewis acid–base pair site was formed between the atomic Ir and the adjacent oxygen vacancy (VO) site on In2O3 to form two distinct catalytic centers, which could reduce CO2 to the active intermediates and then facilitated the C–C coupling reaction to form ethanol.
The above studies demonstrate that the atomically dispersed M/In2O3 SAC is promising for the CO2 hydrogenation to methanol reaction. However, due to the difficulty in experimental preparation and characterization of single atoms, the structure–activity relationship of these atom-doped catalysts remains elusive. DFT calculations have been widely used in the field of catalysis for decades, typically for understanding experimental results, elucidating reaction mechanisms, establishing microkinetic models, and predicting structure–activity relationship.30,31 However, complex reaction networks as well as compositional complexity pose a significant challenge. To reduce the computational cost, linear correlations such Brønsted–Evans–Polanyi (BEP) and transition-state scaling (TSS) relations were investigated for the rapid estimation of energy barriers.32,33 The former reflects the relationship between the reaction energy and the energy barrier, whereas the latter suggests a linear relationship between the adsorption energy of the initial or final state and the energy barrier. These scaling relations reveal the factors that affect the catalytic activity of different materials, generally known as descriptors. Zhao et al.30 recently gave an overview of the reactivity descriptors for diverse catalytic systems, encompassing both electronic descriptors such as d-band center of metal and structural descriptors such as coordination numbers (CN) of the active site. It has been generally recognized that the development of effective scaling relationships and descriptors is vital for the rational design of catalytic systems.
Although single atom doped In2O3 catalysts serve as excellent theoretical models, there have been few researches on their scaling relations and descriptors. Chen et al.34 found the relationship between CO2 adsorption energies and the adsorption energies of transition states on 9 single-metal-atom-doped In2O3(110) surfaces. However, the formation energy of oxygen vacancy (Ef,VO) has not been explored as a possible descriptor, which has important influence on the adsorption and activation of CO2 based on previous studies.12,35,36 In addition, previous studies showed that there were differences in the methanol selectivity for different In2O3 facets and the (111) surface was the most stable surface under experimental conditions.17 Previous studies from our group37 found that the single atom-doped In2O3 surface can promote the formation of surface oxygen vacancies, thereby promoting the adsorption and activation of CO2 on the surface and triggering the subsequent RWGS reaction.
In this work, we performed extensive DFT calculations to explore the synergistic effect of single metal atom, oxygen vacancies, and In2O3 for the activations of H2 and CO2, where the metals were selected based on previous experiments.28 By regulating the formation energy of the oxygen vacancy through single metal atom doping, we aim to demonstrate the influence of oxygen vacancies and metal dopants on CO2 reactivity.
2. Computational details
DFT calculations were performed using the Vienna ab initio simulation package (VASP).38,39 The generalized gradient approximation (GGA) with the Bayesian error estimation functional including the van der Waals correction (BEEF-vdW)40 was employed to treat the electron exchange and correlation in the Kohn–Sham theory. The parameters used in this work are similar to those in our previous works.15,17,26,37 A plane wave energy cut-off of 400 eV and the Gaussian smearing width of 0.05 eV were employed. Convergence thresholds for the energy and force were set to 10−4 eV and 0.03 eV Å−1, respectively. Both the climbing image nudged elastic band (CI-NEB) method41,42 and the dimer method43 were used to find the transition states (TS), which were further confirmed through harmonic frequency analysis.Similar to our previous work,44 the c-In2O3(111) surface was built from the optimized primitive unit cell and modeled with a p(1 × 1) slab consisting of 48 In atoms and 72 O atoms distributed in three O–In–O trilayers. The supercell has a dimension of 14.44 Å × 14.44 Å × 17.99 Å, where the bottom layer was fixed and a vacuum layer of 15 Å was inserted between adjacent slabs. The Brillouin zone was sampled using a (3 × 3 × 1) Monkhorst–Pack k-point mesh.35,44 For the Fe, Co and Ni-doped model, spin polarization was enabled.
Substitution of an In atom in the topmost layer of the c-In2O3(111) surface by a transition metal (M) atom (Fe–Cu, Ru–Ag, Os–Au) results in the model denoted as M/In2O3. The adhesive energy (ΔEadh) of the single metal atom is defined in eqn (1):
| ΔEadh = EM/In2O3 − EV_In − EM | (1) |
| ΔEcoh,M = Ebulk,M/nM − EM | (2) |
| ΔEstability = ΔEadh − ΔEcoh,M | (3) |
Definitions of the formation energy of a VO site (ΔEf,VO) and the adsorption energy of an adsorbate A on a slab surface denoted as Eads(A) are similar to our previous works.15,45 Briefly, ΔEf,VO was calculated as the reaction energy of the thermal desorption of molecular O2 from eqn (4):
| ΔEf,VO = Esurface_VO − Eperfect + 1/2 × EO2 | (4) |
| Eads(A) = Etotal − (Eslab + EA) | (5) |
3. Results and discussion
3.1 Thermal stabilities and electronic structures of M/In2O3(111)
The model of In2O3(111) surface is shown in Fig. 1(a). Based on the coordination environments of the In atoms on In2O3(111) surface, they can be classified into six categories,37 namely Ina–Inf, as shown in Fig. 1(b). For the selected transition metals studied in this work as shown in Fig. 1(c), the adhesive energy of the metal dopant (ΔEadh) was calculated for all different In sites. As shown in Fig. 1(d), most of the single metal atom substitutions for the Inb site lead to the lowest energy among the different In sites, which is chosen for metal doping. Previous studies26,28 suggest that Pd, Pt, Rh, Ru, Ni and Ir can be atomically dispersed into In2O3 by co-precipitation and flame spray pyrolysis (FSP). To reveal the stability of the doped structure, ΔEadh is compared with the binding energy of the single metal (ΔEcoh,M) as shown in Fig. 1(e), and ΔEadh is always more negative than ΔEcoh,M, indicating a stronger interaction between the single metal atom and the In2O3(111) surface than that between the single metal atoms, which may prevent the aggregation of the single metal atoms. Values of the calculated ΔEstability for all doped surfaces are shown in Table 1, where more negative values indicate stronger interaction between the single metal atom and the In2O3(111) surface than that between the single metal atoms.| Surface | Fe/In2O3 | Co/In2O3 | Ni/In2O3 | Cu/In2O3 |
| ΔEstability | −4.00 | −4.09 | −7.67 | −6.36 |
| Surface | Ru/In2O3 | Rh/In2O3 | Pd/In2O3 | Ag/In2O3 |
| ΔEstability | −5.55 | −9.20 | −7.61 | −5.41 |
| Surface | Os/In2O3 | Ir/In2O3 | Pt/In2O3 | Au/In2O3 |
| ΔEstability | −5.66 | −11.73 | −11.16 | −7.25 |
As shown in Fig. S1(a),† based on the coordination environment the surface oxygen atoms can be classified into four categories (Oa–Od) when the single metal dopant is at the Inb site. For a better illustration of their interaction, the atoms on the In2O3(111) surface are shown by the 2 × 2 supercell in Fig. S1(b).† The charge depletion of the single atoms at the Inb site is reduced compared to the pristine In2O3(111) surface as shown in Table 2, suggesting a lower valence doping, consistent with previous experimental observations.26,28 Differential charge density analysis shown in Fig. S1(c)† indicates that most of the charge redistributions are concentrated in the single metal atom and adjacent In and O atoms, although there are slight charge redistributions among other surface and subsurface atoms, which are further confirmed by our Bader charge analysis as listed in Table S1.† The average Bader charges of the Oa, Ob, Oc and Od sites are −1.18, −0.97, −1.15 and −1.16|e| for the single atom doped surfaces, compared to those of −1.17, −1.15, −1.15 and −1.17|e| on the pristine In2O3 surface, indicating that the charge reduction of the single atoms decreases the charge of adjacent Ob atoms directly bound to the single metal atoms.
| Surface | q(M)/|e| | ||
|---|---|---|---|
| Clean surface | H-Adsorbed surface | Defect surface | |
| Fe/In2O3 | 1.48 | 1.42 | 1.33 |
| Co/In2O3 | 1.34 | 1.30 | 1.21 |
| Ni/In2O3 | 1.29 | 1.17 | 1.06 |
| Cu/In2O3 | 1.18 | 1.09 | 1.03 |
| Ru/In2O3 | 1.58 | 1.45 | 1.29 |
| Rh/In2O3 | 1.29 | 1.22 | 1.11 |
| Pd/In2O3 | 1.28 | 1.10 | 0.79 |
| Ag/In2O3 | 1.06 | 0.90 | 0.71 |
| Os/In2O3 | 1.85 | 1.70 | 1.51 |
| Ir/In2O3 | 1.51 | 1.40 | 1.21 |
| Pt/In2O3 | 1.40 | 1.41 | 0.81 |
| Au/In2O3 | 1.04 | 1.01 | 0.99 |
| In2O3 | 1.89 | 1.83 | 1.72 |
In addition, there is an apparent linear relation between the Bader charge of the single atom (q(M)) and the formation energy of the Ob vacancy as shown in Fig. S1(d),† indicating the single metal atom can affect the formation of the adjacent oxygen vacancy through charge transfer.
3.2 Scaling relations for H2 dissociative adsorption on the perfect surface
Previous studies14,47 suggested that heterolytic dissociation of H2 that leads to a proton bound to an O atom and a hydride bound to an In atom is easier than homolytic dissociation on the In2O3(111) perfect surface. Due to the lower stability of H adsorbed at the M site on the doped surface, it is easy for the H adatom to migrate to the surrounding oxygen, making it less likely to form the H@M&H@O pair (H@M&H@O refers to co-adsorption of H on M and H on O). Thus, only the H@In&H@O pair is considered. The potential energy surface of H2 heterolysis and further water formation is shown in Fig. 2(a).H2 heterolysis is thermodynamically favorable but on the pristine In2O3 surface incurs a modest energy barrier of 0.88 eV. Single metal doping reduces this energy barrier to 0.56–0.84 eV. In addition, Au, Ag and Cu doping are more favorable for H2 dissociation with lowest energy barriers among the studied elements in the same transition row. The subsequent formation of H2O by the transfer of the hydride from Ine–H to the adjacent hydroxyl group (Ob–H) on most single metal atom doped In2O3 surfaces incurs a higher energy barrier ranging from 1.02 to 1.92 eV than that on the pristine In2O3 surface of 0.96 eV, whereas Au, Ag and Cu doping can promote oxygen vacancy formation because of their much lower energy barrier (from 0.73 to 0.87 eV).
In addition, Table S2† further shows that the adsorption energy of two H adatoms as hydroxyls (−3.7 eV) is much higher than that of H@In&H@O (−0.77 eV) for Ag/In2O3, making it difficult to break one of the O–H bonds to form H2O, consistent with a higher energy barrier of 1.49 eV than that to H2O via H@In&H@O of 0.80 eV as shown in Table S3,† suggesting that the In2O3 surface may be hydroxylated under the typical reaction conditions.14 Contrary to the work of Pérez-Ramírez et al.28 we find that oxygen vacancy formation by H2 reduction is easier for Ag/In2O3 and Au/In2O3 due to their relatively low energy barriers when they are atomically dispersed on the In2O3(111) surface. However, in their experiments, Ag and Au may actually interact with the In2O3 catalyst in the form of metal clusters, so their effect on oxygen vacancy formation may differ from our theoretical predictions.
BEP relations are widely studied for the activation of gas phase species (such as H2) on surfaces of transition metals and their oxide.31 As shown in Fig. 2(b), the BEP relation of H2 dissociation on all doped surfaces is obvious except for Au and Ag doped surfaces and the pristine In2O3 surface. This may be due to that the transition state structures for these surfaces differ significantly from their final state structures, as also noted by a previous study.33 As shown in Table S4,† their In–H bond lengths (2.37 and 2.45 Å) are significantly longer than those of the other surfaces (1.98–2.23 Å). Owing to the weak physisorption of H2 in the initial state, the reaction energy is close to the adsorption energy of the final state, and the transition state scaling (TSS) relation shown in Fig. 2(c) reveals that the adsorption energy of the final state rather than that of the initial state has a more significant impact on the transition state energy. Besides, the adsorption energy of the H adatom at the Ine site (EadsH@In) on the different surfaces remains basically unchanged as shown in Table S2,† so the adsorption energy of the final state is mainly determined by the adsorption energy of H on O (EadsH@O) with a coefficient of determination (R2) of 0.85 as shown in Fig. 2(d). This is consistent with the good linear relation between EadsH@O and the energy barrier with an R2 value of 0.90 as shown in Fig. 2(e).
From the differential charge density analysis of H adsorption on the surface in Fig. 2(f), electron transfer mainly occurs between Ob and the atoms directly bound to it. The changes in the charge of the single metal atom and the Ob atom on the clean and H-adsorbed surfaces shown in Table 2 indicate that the charge carried by the single metal atom decreases while the number of electrons acquired by the Ob atom increases, suggesting that charge transfer occurs between the single metal atom, the Ob atom and the H adatom. Furthermore, EadsH@O scales linearly with the charge carried by the single metal atom (q(M)) as shown in Fig. S2(a),† indicating that the reactivity of the adjacent oxygen site is enhanced because of the higher EadsH@O than that on the pristine In2O3 surface. Besides, EadsH@O also scales linearly with the p-band center of the O site (εp) with a negative slope in Fig. S2(b),† which was previously proposed as a descriptor for the adsorption energies of intermediates involved in the oxygen evolution reaction (OER) reaction on perovskite surfaces.30 In addition, here we construct a descriptor φ by combining the effects of both εd and εp through a multivariate linear regression model as shown in eqn (6):
| φ = −0.1 × εd − 0.77 × εp − 2.73 | (6) |
As shown in Fig. S2(c and d),† there is a linear relation between the energy barrier of TS1 or EadsH@O and the combined value of the O p-band center (εp) and M d-band center (εd). The reason for considering εd is that electrons from the H adatom are transferred to the Ob atom, leading to their subsequent transfer into a vacant d-orbital of the single metal atom on the H-adsorbed surfaces.48 The initial, transition and final state structures for TS1 are shown in Fig. S3(a).† Upon water desorption, the surface oxygen vacancy is formed as shown in Fig. S3(b).†
3.3 Scaling relations for H2 dissociative adsorption on defective In2O3 surfaces
As shown in Fig. 3(a), the dissociative adsorption of H2 at the VO site on the defect In2O3 surfaces can occur via four possible pathways leading to the formation of (1) H@M&H@In, (2) H@M&H@O, (3) H@In&H@In, and (4) H@In&H@O (with the H adsorbed at the top site). Our previous work47 shows that H2 dissociation to form H@In&H@O has a lower energy barrier than that to H@In&H@In. As shown in Table S5,† the adsorption energies of H@In&H@O are similar for all model surfaces and the adsorption energies are approximately 0 eV for the initial state, leading to similar reaction energies (ΔH), so the BEP relation of H2 dissociation to form H@In&H@O may be untenable. This is demonstrated by our calculations for several model surfaces, which yield nearly the same energy barriers and reaction energies as shown in Table S6,† so no further calculations are performed for the pathway leading to H@In&H@O. As for pathway 1, 2 and 4, their initial, transition and final state structures on Ag doped defect surface are shown in Fig. S4.†H2 dissociation via pathway (1) starts from H2 physisorption, and is endothermic on all doped surfaces except for Pt, Os and Ir, resulting in two hydrides both with negative charges. The energy barriers for this pathway on all defect surfaces are shown in the Fig. 3(b), ranging from 0.19 to 1.90 eV. The energy barriers of all defect doped surfaces are lower than the defect undoped surface, and the energy barriers of the defect Au, Ag and Cu doped surfaces are the highest among the elements in the same period, contrary to that on the perfect surfaces. Furthermore, H2 dissociation is easy to occur on the defect Os/In2O3 surface with a low energy barrier of 0.19 eV, and different from the transition state structure for the other doped surfaces, both H adatoms binds the Os sites and the final state is highly stable with an adsorption energy of −0.66 eV. The BEP relation in Fig. 3(c) with a R2 of 0.90 indicates that the transition state structures are more similar to each other except for the defect undoped surface, where one H adatom is located at the bridge site between Inb and Ind in its final state. As the adsorption energy of the initial state is approximately zero, there is a good TSS relation between the energy barrier and the adsorption energy of the final state as shown in Fig. 3(d). The high energy barriers of the defect Au, Ag and Cu doped surfaces are due to the high endothermic adsorption energies in the final state as shown in Table S7.† Due to the fact that single metal atom doping does not notably affects the adsorption energy of the H adatom at the In site (EadsH@In) as shown in Table S5,† the relative energy of the final state has a good linear relation with the adsorption energy of the H adatom at the single metal atom site (EadsH@M) as shown in Fig. S5(a),† which can serve as a descriptor for the energy barrier of H2 dissociation on the defect surfaces. The dissociative adsorption of H2 is more likely to occur with a reduced EadsH@M.
Previous studies suggest that the d-band center of surface metal site can affect the adsorption energy of the H adatom on transition metals and their oxides.49 However, our study shows that the d-band center does not scale linearly with the adsorption energy of the H adatom at the single metal atom site as shown in Fig. S5(b).† We attribute this to the presence of the oxygen vacancy, as the H adatom adsorbed at the top site tends to shift towards the oxygen vacancy, leading to the inclination of both the H–M and H–In bonds. The linear relation shown in Fig. S5(c)† indicates that adsorption of the H adatom at the single metal atom site is enhanced as the oxygen vacancy formation energy increases, which also scales linearly with the energy barrier of H2 dissociation as shown in Fig. S5(d).†
As shown in Fig. 3(b), the energy barriers of H2 dissociation via pathway (2) range from 0.00 to 1.02 eV. This pathway is kinetically more favorable than pathway (1) for all doped surfaces except for Pt and Pd doping. The energy barriers on the defect Pt/In2O3 and Pd/In2O3 are the highest, nearly the same as that on the undoped In2O3. Because H tends to adsorbs at the bridge site between M and Ine in the final state, resulting in a less stable structure than the top site of Pt and Pd after H2 heterolysis. However, on the Ru, Rh, Os and Ir doped surfaces, the energy barrier for H2 heterolysis is lower than 0.1 eV. In addition, no BEP or TSS relation is found in H2 dissociation via pathway (2) due to the significant differences in the transition state structures for all defect doped surfaces. Previous studies17,27,34 suggest that for CO2 hydrogenation, the hydrogen comes from the hydride (H–In), and our results show that H2 dissociation through M–O is more favorable, which may provide a different hydrogen source (H–M).
3.4 CO2 hydrogenation and dissociation on defect surfaces
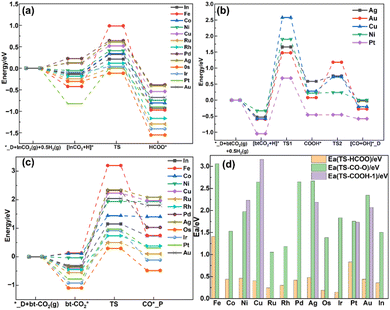
Previous studies suggest that CO2 hydrogenation to methanol on the defect In2O3 surface occurs via the formate route , where the HCOO* specie is the key intermediate during methanol formation from early studies,12,14,15 whereas CO is formed via the RWGS route
, where the HCOO* specie is the key intermediate during methanol formation from early studies,12,14,15 whereas CO is formed via the RWGS route  initiated by CO2 protonation to COOH or CO2 direct dissociation
initiated by CO2 protonation to COOH or CO2 direct dissociation 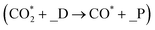 , where _D refers to the defect surface with VO and _P refers to the perfect surface. Thus, the initial conversion of CO2 plays an important role in methanol synthesis activity, and the energy barriers of the elementary reactions involved in the initial conversion of CO2 on all doped surfaces are calculated to reveal the effect of metal doping on the CO2 conversion route, considering that the structure of the single metal atom doped In2O3(111) surface is similar to that of the pure In2O3(111) surface.
, where _D refers to the defect surface with VO and _P refers to the perfect surface. Thus, the initial conversion of CO2 plays an important role in methanol synthesis activity, and the energy barriers of the elementary reactions involved in the initial conversion of CO2 on all doped surfaces are calculated to reveal the effect of metal doping on the CO2 conversion route, considering that the structure of the single metal atom doped In2O3(111) surface is similar to that of the pure In2O3(111) surface.
According to our previous study, there are two distinct CO2 adsorption configurations at the VO-b site on the defective (111) surface, namely the linear CO2  and bent CO2
and bent CO2  .17 For
.17 For  , the C atom is far from the M atom on all surfaces, both the C–O bond lengths are approximately 1.18 Å on all surfaces, which are close to the C–O bond lengths in gas CO2 and nearly no charge transfer occurs between the adsorbate and surface, indicating that CO2 weakly physisorbs above the Ob vacancy site. As shown in Table S8,† the adsorption energy of
, the C atom is far from the M atom on all surfaces, both the C–O bond lengths are approximately 1.18 Å on all surfaces, which are close to the C–O bond lengths in gas CO2 and nearly no charge transfer occurs between the adsorbate and surface, indicating that CO2 weakly physisorbs above the Ob vacancy site. As shown in Table S8,† the adsorption energy of  ranges from −0.48 to −0.27 eV on the different surfaces, which is more negative than that from our previous work due to the inclusion of the van der Waals correction via the BEEF-vdW exchange–correlation functional. The bond length, bond angle, and adsorption energy of
ranges from −0.48 to −0.27 eV on the different surfaces, which is more negative than that from our previous work due to the inclusion of the van der Waals correction via the BEEF-vdW exchange–correlation functional. The bond length, bond angle, and adsorption energy of  are shown in Table 3. No stable structures were found for the
are shown in Table 3. No stable structures were found for the  adsorption configuration on the Ag, Au doped and pristine In2O3 surfaces. For the
adsorption configuration on the Ag, Au doped and pristine In2O3 surfaces. For the  adsorption configuration, the C–M bond length ranges from 1.99 to 2.17 Å, the C–O1 bond length ranges from 1.29 to 1.39 Å, while the C–O2 bond length ranges from 1.19 to 1.22 Å, and the O–C–O angle ranges from 120.6 to 143.4°, where O1 occupies the VO and O2 only binds the C. There is significant charge transfer between CO2 and the surface, as also indicated by the differential charge density analysis shown in Fig. S6.† Thus, the bt-CO2 adsorbate is chemisorbed and activated with an adsorption energy ranging from −1.09 to 0.14 eV. This chemisorption is endothermic for Fe/In2O3 and Co/In2O3, whereas it is more exothermic on Os/In2O3, Ir/In2O3 and Pt/In2O3 than other catalysts. The adsorption energies of the H adatom, the linear and bent CO2 and their co-adsorption are given in Table S8.†
adsorption configuration, the C–M bond length ranges from 1.99 to 2.17 Å, the C–O1 bond length ranges from 1.29 to 1.39 Å, while the C–O2 bond length ranges from 1.19 to 1.22 Å, and the O–C–O angle ranges from 120.6 to 143.4°, where O1 occupies the VO and O2 only binds the C. There is significant charge transfer between CO2 and the surface, as also indicated by the differential charge density analysis shown in Fig. S6.† Thus, the bt-CO2 adsorbate is chemisorbed and activated with an adsorption energy ranging from −1.09 to 0.14 eV. This chemisorption is endothermic for Fe/In2O3 and Co/In2O3, whereas it is more exothermic on Os/In2O3, Ir/In2O3 and Pt/In2O3 than other catalysts. The adsorption energies of the H adatom, the linear and bent CO2 and their co-adsorption are given in Table S8.†
 where O1 occupies the VO and O2 only binds the C
where O1 occupies the VO and O2 only binds the C
| Surface | C–M/Å | C–O1/Å | C–O2/Å | Angle (O1–C–O2)/° | |
|---|---|---|---|---|---|
| Fe/In2O3 | 2.17 | 1.29 | 1.19 | 134.7 | 0.14 |
| Co/In2O3 | 1.99 | 1.34 | 1.20 | 127.3 | 0.11 |
| Ni/In2O3 | 2.07 | 1.29 | 1.19 | 134.3 | −0.03 |
| Cu/In2O3 | 2.07 | 1.25 | 1.19 | 143.4 | −0.08 |
| Ru/In2O3 | 2.01 | 1.37 | 1.22 | 122.7 | −0.55 |
| Rh/In2O3 | 2.00 | 1.37 | 1.21 | 123.3 | −0.45 |
| Pd/In2O3 | 2.10 | 1.30 | 1.20 | 132.9 | −0.32 |
| Os/In2O3 | 2.03 | 1.39 | 1.22 | 120.6 | −1.09 |
| Ir/In2O3 | 2.01 | 1.39 | 1.21 | 121.3 | −0.92 |
| Pt/In2O3 | 2.05 | 1.34 | 1.20 | 126.3 | −0.78 |
In addition, for single Ni atom doped surface, Cannizzaro et al.50 previously predicted CO2 hydrogenation from the H adatom at the O site to have an energy barrier of 1.70 eV, while our group's previous calculation51 found a much lower energy barrier of 0.83 eV for CO2 hydrogenation from the H adatom at the Ine site. Here, we calculated and compared two different hydrogenation pathways on Ag, Ni, Os, Ir, and Pd doped In2O3 surfaces as listed in Table S9.† Two types of hydrides, namely H–In and H–M hydrides, are formed by H2 dissociation as mentioned in Section 3.3. HCOO* is formed by  hydrogenation with a hydride via the Eley–Rideal mechanism,52 where one O of HCOO* fills the oxygen vacancy as shown in Fig. S7.† Our calculations indicate that transfer of the H–M hydride has a higher energy barrier than that of the H–In hydride because of the higher stability of the H–M bond than the H–In bond. Moreover, the hydride in H–M is more favorable for the formation of the monodentate HCOO* (mono-HCOO*), while the hydride in H–In is more favorable for the formation of the bidentate HCOO* (bi-HCOO*), consistent with hydrogenation of the bi-HCOO* to H2COO* from previous studies.12 Therefore, only the hydrogenation of the
hydrogenation with a hydride via the Eley–Rideal mechanism,52 where one O of HCOO* fills the oxygen vacancy as shown in Fig. S7.† Our calculations indicate that transfer of the H–M hydride has a higher energy barrier than that of the H–In hydride because of the higher stability of the H–M bond than the H–In bond. Moreover, the hydride in H–M is more favorable for the formation of the monodentate HCOO* (mono-HCOO*), while the hydride in H–In is more favorable for the formation of the bidentate HCOO* (bi-HCOO*), consistent with hydrogenation of the bi-HCOO* to H2COO* from previous studies.12 Therefore, only the hydrogenation of the  with the H–In was studied in this work, as shown in Fig. 4(a). The energy barrier of CO2 hydrogenation ranges from 0.15 to 0.48 eV, indicating that this process is easy to occur. The high stability of the HCOO* is indicated by the very negative adsorption energy ranging from −4.35 to −3.19 eV. In addition, only for the Ru, Rh, Ir and Os doped surfaces, the energy barrier of this process is lower than that on the pure In2O3 surface of 0.36 eV. Low energy barriers of <0.2 eV were previously reported for Ir–In2O3 by Huang et al.29 and Chen et al.,34 and our results indicate the potential of the Os/In2O3 SAC for CO2 hydrogenation.
with the H–In was studied in this work, as shown in Fig. 4(a). The energy barrier of CO2 hydrogenation ranges from 0.15 to 0.48 eV, indicating that this process is easy to occur. The high stability of the HCOO* is indicated by the very negative adsorption energy ranging from −4.35 to −3.19 eV. In addition, only for the Ru, Rh, Ir and Os doped surfaces, the energy barrier of this process is lower than that on the pure In2O3 surface of 0.36 eV. Low energy barriers of <0.2 eV were previously reported for Ir–In2O3 by Huang et al.29 and Chen et al.,34 and our results indicate the potential of the Os/In2O3 SAC for CO2 hydrogenation.
As shown in Fig. S8,† in the initial structure of the RWGS route, the bt-CO2 is co-adsorbed with a proton at the Oc site followed by the protonation of the bt-CO2. Unfortunately, the COOH* adsorbate is unstable on all these surfaces except for the Ag, Au, Cu, Ni and Pt doped surfaces, leading to its direct dissociation into adsorbed CO and hydroxyl group. Fig. 4(b) shows the potential energy surface for the protonation of CO2 to form CO on the Ag, Au, Cu, Ni and Pt doped In2O3 surfaces. The energy barrier of the protonation step ranges from 1.73 to 3.16 eV, so it is slower than the CO2 hydrogenation to the HCOO* intermediate in terms of both thermodynamics and kinetics. The energy barrier for further dissociation of the COOH* to form CO (TS2) ranges from 0.00 to 1.11 eV, and COOH* should readily occur on these surfaces except for the Au doped surface. Comparing the energy barriers of these two elementary steps in the RWGS route, CO2 protonation is the rate determining step (RDS), consistent with previous predictions.37 In addition, there is a decrease in the energy barrier of TS1 and an increase in the energy barrier of TS2 with the increase in the oxygen vacancy formation energy, indicating that a higher oxygen vacancy formation energy benefits CO2 protonation but not COOH dissociation, so an intermediate value for the oxygen vacancy formation energy should be preferable for the RWGS reaction via the COOH route.
The potential energy surface of CO2 direct dissociation is shown in Fig. 4(c), where the O* generated by CO2 dissociation fills the oxygen vacancy. The energy barrier ranges from 1.05 to 3.06 eV, also significantly higher than that of CO2 hydrogenation to the HCOO* intermediate on all doped surfaces but lower than that of CO2 protonation to the COOH* intermediate on the Cu and Ni doped surfaces. In addition, Fig. 4(d) shows the comparison of these energy barriers for a more intuitive display. Based on the transition state structures of CO2 direct dissociation, there are three types as shown in Fig. 5. Type (I) includes Pd, Os and Ir surfaces, where the transition state actually involves the breaking of both the C–O and C–M bonds in the bt-CO2 as CO does not adsorb on the surface. Type (II) includes Rh, Co, Ni, Ru and Pt doped surfaces, where the transition state involves only the breaking of the C–O bond as the bt-CO2 dissociates from the opposite configuration of type (I) to form the physisorbed CO on surface. Type (III) includes the pristine and Ag, Au, Cu doped surfaces, where the  is the initial state in CO2 dissociation and the transition state involves the breaking of only the C–O bond. The energy barriers of CO2 direct dissociation on the Co, Ru, Rh and Os doped surfaces are lower than that of the pristine surface. Furthermore, the energy barrier of the Ru/In2O3 surface is the lowest (1.05 eV) among all the studied surfaces, and the energy barrier of CO2 hydrogenation to the HCOO* intermediate on this surface is also very low (0.24 eV), thus Ru and Os single atom doped In2O3 catalysts may be excellent SACs for the CO2 hydrogenation to methanol reaction. In contrast, the energy barrier of CO2 direct dissociation on the Fe/In2O3 surface is very high (3.06 eV), and that of CO2 hydrogenation to the HCOO* intermediate is also quite high (1.41 eV), so this surface can be expected to be quite inactive to the CO2 hydrogenation reaction.
is the initial state in CO2 dissociation and the transition state involves the breaking of only the C–O bond. The energy barriers of CO2 direct dissociation on the Co, Ru, Rh and Os doped surfaces are lower than that of the pristine surface. Furthermore, the energy barrier of the Ru/In2O3 surface is the lowest (1.05 eV) among all the studied surfaces, and the energy barrier of CO2 hydrogenation to the HCOO* intermediate on this surface is also very low (0.24 eV), thus Ru and Os single atom doped In2O3 catalysts may be excellent SACs for the CO2 hydrogenation to methanol reaction. In contrast, the energy barrier of CO2 direct dissociation on the Fe/In2O3 surface is very high (3.06 eV), and that of CO2 hydrogenation to the HCOO* intermediate is also quite high (1.41 eV), so this surface can be expected to be quite inactive to the CO2 hydrogenation reaction.
3.5 Scaling relations of CO2 hydrogenation and dissociation on defect surfaces
For hydrogenation to HCOO*, the BEP relationship is poor in the work of Chen et al.34 possibly due to the differences in the transition state structures. However, in this work, obvious BEP relation of this reaction and TSS relation between the energy barrier and the adsorption energy of the final state are found in Fig. 6(a) and (b), but the linear relation between the energy barrier and the adsorption energy of the initial state cannot be established, as the adsorption energy of physiosorbed CO2 in the initial state is approximately 0 eV, and the adsorption energy of H on the Ine site is similar for all the studied surfaces. From the expanded scaling relations in Fig. 6(c) and (d), both the adsorption energy of the HCOO* and the energy barrier of
hydrogenation to HCOO*, the BEP relationship is poor in the work of Chen et al.34 possibly due to the differences in the transition state structures. However, in this work, obvious BEP relation of this reaction and TSS relation between the energy barrier and the adsorption energy of the final state are found in Fig. 6(a) and (b), but the linear relation between the energy barrier and the adsorption energy of the initial state cannot be established, as the adsorption energy of physiosorbed CO2 in the initial state is approximately 0 eV, and the adsorption energy of H on the Ine site is similar for all the studied surfaces. From the expanded scaling relations in Fig. 6(c) and (d), both the adsorption energy of the HCOO* and the energy barrier of  hydrogenation to HCOO* scales linearly with the oxygen vacancy formation energy. Therefore, Ef,VO can be used as a good descriptor for
hydrogenation to HCOO* scales linearly with the oxygen vacancy formation energy. Therefore, Ef,VO can be used as a good descriptor for  hydrogenation to HCOO*, where a higher oxygen vacancy formation energy enhances the stability of the HCOO* and also reduces the energy barrier of
hydrogenation to HCOO*, where a higher oxygen vacancy formation energy enhances the stability of the HCOO* and also reduces the energy barrier of  hydrogenation, as shown in Fig. 6(d). This illustrates the crucial role of the oxygen vacancy formation energy in the CO2 hydrogenation reaction, which can be regulated by single metal atom doping.
hydrogenation, as shown in Fig. 6(d). This illustrates the crucial role of the oxygen vacancy formation energy in the CO2 hydrogenation reaction, which can be regulated by single metal atom doping.
 | ||
Fig. 6 (a) BEP and (b) TSS relations of  hydrogenation to HCOO*, scaling relations between Ef,VO and (c) Eads(HCOO*) and (d) the energy barrier of hydrogenation to HCOO*, scaling relations between Ef,VO and (c) Eads(HCOO*) and (d) the energy barrier of 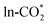 hydrogenation to HCOO*. hydrogenation to HCOO*. | ||
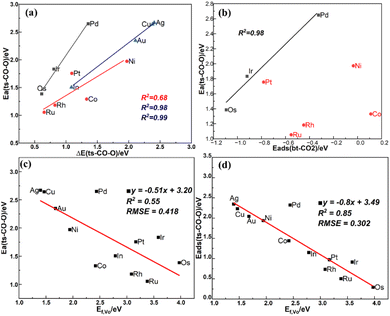
For the bt-CO2 adsorption state, the linear correlation between the oxygen vacancy formation energy and the CO2 adsorption energy is not strong (R2 = 0.74) as shown in Fig. S9(a),† as previously noted by Ye et al.12 From the differential charge density analysis shown in Fig. S6,† there is an obvious charge transfer (Δq) between CO2 and the surface ranging from 0.42 to 0.96e. The charge difference is concentrated in the metal single atom dopant and the surrounding atoms, and the linear correlation between Δq and the CO2 adsorption energy is very poor as shown in Fig. S9(b),† so is the formation energy of the VO. However, as shown in Fig. S9(c),† the Os 5d and C 2p states are strongly hybridized on the defect Os/In2O3 surface, so here we propose a binary descriptor consisting of the d-band center of the single metal atom on the defect surface and the oxygen vacancy formation energy to correlate the adsorption energy of the  . As shown in Fig. S9(d),† a good linear relationship (R2 = 0.87) is found, indicating a synergy of the oxygen vacancy and the single metal atom sites on CO2 adsorption.
. As shown in Fig. S9(d),† a good linear relationship (R2 = 0.87) is found, indicating a synergy of the oxygen vacancy and the single metal atom sites on CO2 adsorption.
The BEP relation for CO2 direct dissociation on all doped surfaces is not strong, but after dividing the transition states into the three types (I, II, III) as mentioned in Section 3.4, the BEP relations are much improved with the R2 values of 0.99, 0.68 and 0.98 as shown in Fig. 7(a), suggesting there are significant difference among the transition state structures of the different types, which affect the BEP relation on the single metal atom doped In2O3 surfaces. Due to the weak CO adsorption in the final state with an essentially zero adsorption energy, there is a good TSS relation between the adsorption energy of the initial state and the energy barrier as shown in Fig. 7(b). The energy barrier of CO2 direct dissociation decreases as the CO2 adsorption becomes stronger, but this trend is not obvious for type (II). The energy barrier of type (I) also scales linearly with the oxygen vacancy formation energy, indicating the crucial role of the oxygen vacancy in  dissociation. Although the linear relation between the oxygen vacancy formation energy (Ef,VO) and the energy barrier for CO2 direct dissociation is poor as shown in Fig. 7(c), the energy of the transition state can be linearly correlated with Ef,VO with a R2 value of 0.85 as shown in Fig. 7(d), indicating that Ef,VO can be used as a descriptor for CO2 direct dissociation.
dissociation. Although the linear relation between the oxygen vacancy formation energy (Ef,VO) and the energy barrier for CO2 direct dissociation is poor as shown in Fig. 7(c), the energy of the transition state can be linearly correlated with Ef,VO with a R2 value of 0.85 as shown in Fig. 7(d), indicating that Ef,VO can be used as a descriptor for CO2 direct dissociation.
For the RWGS reaction via the COOH* pathway, the BEP and TSS relations are both poor due to the significant differences in the transition state structures of  protonation. Nonetheless, as shown in Fig. S10(a),† the energy barrier of
protonation. Nonetheless, as shown in Fig. S10(a),† the energy barrier of  protonation scales linearly with the
protonation scales linearly with the  adsorption energy when Cu/In2O3 is excluded, consistent with a previous study.34 Moreover, a good BEP relation can only be established for COOH* dissociation to CO* and OH* when excluding Ni and Pt doped In2O3 surfaces as the transition state of COOH* dissociation is difficult to locate as shown in Fig. S10(b).†
adsorption energy when Cu/In2O3 is excluded, consistent with a previous study.34 Moreover, a good BEP relation can only be established for COOH* dissociation to CO* and OH* when excluding Ni and Pt doped In2O3 surfaces as the transition state of COOH* dissociation is difficult to locate as shown in Fig. S10(b).†
In addition, Fig. 4(d) shows that CO2 hydrogenation to the HCOO* is easier to occur than the CO2 dissociation via the COOH* and its direct dissociation. However, several recent studies suggest that In2O3 catalysts with Ni and Pt single atom dopants on the surface lead to a high CO selectivity and a low methanol selectivity. As shown in Fig. 6(d) and 7(c), the slopes of the linear relations between the energy barriers of CO2 hydrogenation to HCOO* and direct dissociation of CO2 and the oxygen vacancy formation energy are −0.12 and −0.51, respectively, indicating that CO2 dissociation are more sensitive to the oxygen vacancy formation energy than its hydrogenation to the HCOO*. Based on the calculated energy barriers, the predicted order of the catalytic performance of the 12 single metal atom-doped In2O3 catalysts is shown in Table S10.† For the perfect surfaces, Au/In2O3 exhibits the highest reducibility by H2, leading to the formation of oxygen vacancies. For the surfaces with oxygen defects, Os/In2O3 shows the optimal performance for H2 dissociation, Ir/In2O3 exhibits the highest activity for CO2 hydrogenation to HCOO*, and Ru/In2O3 demonstrates the superior activity for CO2 dissociation to CO. Thus, Ru/In2O3, Ir/In2O3, and Os/In2O3 may be expected to have high catalytic activities for CO2 hydrogenation.
3.6 Discussion
Previously, there have already been some scaling relations for CO2 conversion on oxide-supported single atom catalysts. On single metal doped t-ZrO2(101), Cheula et al.53 have derived linear scaling relations between the formation energy of the transition state and the co-adsorption energy of two H adatoms at the M and O sites in the HCOO* formation step with a R2 value of 0.98. As a similar scaling relation was not found in this work, we replaced the co-adsorption energy of H adatoms with the adsorption energy of HCOO* as mentioned in Section 3.5. In addition, they found the formation energy of the transition state for H2 dissociation was also linearly correlated with the co-adsorption energy of two H adatoms at the M and O site, whereas we found the adsorption energy of H at the O site to be sufficient.Moreover, increasing the coverage of  on the catalyst surface should promote its reaction, so a strong CO2 adsorption will usually benefit the CO2 conversion rate.54 In a previous study,55 comparison of the linear and bent CO2 adsorption energies over the TiO2 with metal adatoms (M/TiO2) surfaces shows that adsorptions of the linear and bent CO2 over the TiO2 surface are much weaker than those on the surfaces with metal adatoms, indicating the likely important role of the metal atom dopant in CO2 adsorption and reduction. Our calculations show that ln-CO2 adsorption is strengthened on most metal doped surfaces except for Ag, Au, Pt, Os, Pd, as shown in Table S8.† In addition, CO2 dissociation is more favorable on early transition metal doped surfaces such as Hf and W rather than late transition metals such as Cu and Pt as the CO2 dissociation energy becomes more negative from the early to late transition metal element in the same period, similar results are also found in this work as shown in Fig. S10(c).† An approximately linear correlation between the CO2 dissociation energy and the bt-CO2 adsorption energy is found with a R2 value of 0.78,55 so capacity for CO2 activation is positively correlated with that of CO2 reduction, and there is a similar but poorer linear correlation between the CO2 dissociation energy and the bt-CO2 adsorption energy as shown in Fig. S10(d)† with a R2 value of 0.57. In order to understand the linear scaling relations between CO2 adsorption strength and its dissociation barrier, correlations between the adsorption energy, dissociation barrier, and excess charge on the surface of TiO2, Al2O3, and CeO2 with single metal atoms (M) are explored.56 The linear relation between the energy barrier of CO2 direct dissociation and the Hirshfeld charge suggests that a more negative charge on the single atom correlates with a lower energy barrier, but a similar correlation cannot be established from our results, as shown in Fig. S9(b).† Systems with stronger CO2 adsorption also have a lower energy barrier for CO2 direct dissociation from their linear scaling relation with a R2 value of 0.73 for M/Al2O3, consistent with our results as shown in Fig. 7(b). In addition, the bt-CO2 adsorption structure is not stable on Ag/CeO2 or Ag/Al2O3, indicating a weaker adsorption and a less activated CO2 adsorbate. They found CO2 adsorption on Cu/Al2O3 and Ag/Al2O3 surfaces to be weaker than the Rh/Al2O3 surface, which is consistent with our results for the corresponding M/In2O3 surfaces (CO2 adsorption energies are −0.32 eV, −0.31 eV, and −0.47 eV for Cu/In2O3, Ag/In2O3 and Rh/In2O3, respectively).
on the catalyst surface should promote its reaction, so a strong CO2 adsorption will usually benefit the CO2 conversion rate.54 In a previous study,55 comparison of the linear and bent CO2 adsorption energies over the TiO2 with metal adatoms (M/TiO2) surfaces shows that adsorptions of the linear and bent CO2 over the TiO2 surface are much weaker than those on the surfaces with metal adatoms, indicating the likely important role of the metal atom dopant in CO2 adsorption and reduction. Our calculations show that ln-CO2 adsorption is strengthened on most metal doped surfaces except for Ag, Au, Pt, Os, Pd, as shown in Table S8.† In addition, CO2 dissociation is more favorable on early transition metal doped surfaces such as Hf and W rather than late transition metals such as Cu and Pt as the CO2 dissociation energy becomes more negative from the early to late transition metal element in the same period, similar results are also found in this work as shown in Fig. S10(c).† An approximately linear correlation between the CO2 dissociation energy and the bt-CO2 adsorption energy is found with a R2 value of 0.78,55 so capacity for CO2 activation is positively correlated with that of CO2 reduction, and there is a similar but poorer linear correlation between the CO2 dissociation energy and the bt-CO2 adsorption energy as shown in Fig. S10(d)† with a R2 value of 0.57. In order to understand the linear scaling relations between CO2 adsorption strength and its dissociation barrier, correlations between the adsorption energy, dissociation barrier, and excess charge on the surface of TiO2, Al2O3, and CeO2 with single metal atoms (M) are explored.56 The linear relation between the energy barrier of CO2 direct dissociation and the Hirshfeld charge suggests that a more negative charge on the single atom correlates with a lower energy barrier, but a similar correlation cannot be established from our results, as shown in Fig. S9(b).† Systems with stronger CO2 adsorption also have a lower energy barrier for CO2 direct dissociation from their linear scaling relation with a R2 value of 0.73 for M/Al2O3, consistent with our results as shown in Fig. 7(b). In addition, the bt-CO2 adsorption structure is not stable on Ag/CeO2 or Ag/Al2O3, indicating a weaker adsorption and a less activated CO2 adsorbate. They found CO2 adsorption on Cu/Al2O3 and Ag/Al2O3 surfaces to be weaker than the Rh/Al2O3 surface, which is consistent with our results for the corresponding M/In2O3 surfaces (CO2 adsorption energies are −0.32 eV, −0.31 eV, and −0.47 eV for Cu/In2O3, Ag/In2O3 and Rh/In2O3, respectively).
4. Conclusions
In this study, we investigated the mechanism of H2 and CO2 activations on single metal atom doped In2O3 catalyst to reveal the effective catalyst descriptors influencing CO2 and H2 activation through scaling relations. For the dissociative adsorption of H2 on the perfect doped surfaces, the formation of In–O pairs through heterolytic dissociation remains feasible and good BEP and TSS relations are found. The adsorption energy of the H adatom at the O site serves as an effective descriptor for the energy barrier of H2 dissociation, which can be further described in terms of the d band center of the single metal dopant and the p band center of the O site. Our calculations further show that single atom catalysts formed by Au, Ag and Cu doping can readily induce the formation of adjacent oxygen vacancies. Secondly, we conducted investigations into the activation of H2 and CO2 on surfaces with oxygen vacancy and identified Os, Ru and Ir/In2O3 as promising single-atom catalysts (SACs) for CO2 hydrogenation. Thirdly, we found that CO2 hydrogenation is significantly easier than protonation and is greatly influenced by the formation energy of oxygen vacancies. The formation energy of oxygen vacancies, acting as a descriptor, negatively scale linearly with energy barriers of both CO2 hydrogenation to HCOO and dissociation to CO and the effect on the latter is greater.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Yuanjie Bao: investigation, data curation, writing – original draft, visualization; Ziqi Tang: investigation, data curation, visualization; Yuchen Wang: methodology, validation, visualization; Shenggang Li: conceptualization, validation, resources, supervision, project administration, funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (22172188, 22293023), Science and Technology Commission of Shanghai Municipality (23ZR1481700), “Frontier Science” program of Shell Global Solutions B.V. (CW373032, CW906044).Notes and references
- A. Goeppert, M. Czaun, J.-P. Jones, G. K. Surya Prakash and G. A. Olah, Chem. Soc. Rev., 2014, 43, 7995–8048 RSC.
- H. Mikulčić, I. Ridjan Skov, D. F. Dominković, S. R. Wan Alwi, Z. A. Manan, R. Tan, N. Duić, S. N. Hidayah Mohamad and X. Wang, Renewable Sustainable Energy Rev., 2019, 114, 109338 CrossRef.
- E. Alper and O. Yuksel Orhan, Petroleum, 2017, 3, 109–126 CrossRef.
- X. Jiang, X. Nie, X. Guo, C. Song and J. G. Chen, Chem. Rev., 2020, 120, 7984–8034 CrossRef CAS PubMed.
- J. Wang, G. Zhang, J. Zhu, X. Zhang, F. Ding, A. Zhang, X. Guo and C. Song, ACS Catal., 2021, 11, 1406–1423 CrossRef CAS.
- M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlögl, Science, 2012, 336, 893–897 CrossRef CAS PubMed.
- A. Álvarez, A. Bansode, A. Urakawa, A. V. Bavykina, T. A. Wezendonk, M. Makkee, J. Gascon and F. Kapteijn, Chem. Rev., 2017, 117, 9804–9838 CrossRef.
- S. Kuld, M. Thorhauge, H. Falsig, C. F. Elkjær, S. Helveg, I. Chorkendorff and J. Sehested, Science, 2016, 352, 969–974 CrossRef CAS.
- T. Bielz, H. Lorenz, P. Amann, B. Klötzer and S. Penner, J. Phys. Chem. C, 2011, 115, 6622–6628 CrossRef.
- L. Wang, Y. Dong, T. Yan, Z. Hu, F. M. Ali, D. M. Meira, P. N. Duchesne, J. Y. Y. Loh, C. Qiu, E. E. Storey, Y. Xu, W. Sun, M. Ghoussoub, N. P. Kherani, A. S. Helmy and G. A. Ozin, Nat. Commun., 2020, 11, 2432 CrossRef.
- J. Ye, C. Liu and Q. Ge, J. Phys. Chem. C, 2012, 116, 7817–7825 Search PubMed.
- J. Ye, C. Liu, D. Mei and Q. Ge, ACS Catal., 2013, 3, 1296–1306 CrossRef.
- K. Sun, Z. Fan, J. Ye, J. Yan, Q. Ge, Y. Li, W. He, W. Yang and C.-j. Liu, J. CO2 Util., 2015, 12, 1–6 CrossRef.
- M. S. Frei, M. Capdevila-Cortada, R. García-Muelas, C. Mondelli, N. López, J. A. Stewart, D. Curulla Ferré and J. Pérez-Ramírez, J. Catal., 2018, 361, 313–321 CrossRef.
- B. Qin, Z. Zhou, S. Li and P. Gao, J. CO2 Util., 2021, 49, 101543 CrossRef.
- O. Martin, A. J. Martín, C. Mondelli, S. Mitchell, T. F. Segawa, R. Hauert, C. Drouilly, D. Curulla-Ferré and J. Pérez-Ramírez, Angew. Chem., Int. Ed., 2016, 55, 6261–6265 CrossRef.
- S. Dang, B. Qin, Y. Yang, H. Wang, J. Cai, Y. Han, S. Li, P. Gao and Y. Sun, Sci. Adv., 2020, 6, eaaz2060 CrossRef PubMed.
- J. Ye, C.-j. Liu, D. Mei and Q. Ge, J. Catal., 2014, 317, 44–53 CrossRef.
- M. S. Frei, C. Mondelli, R. García-Muelas, K. S. Kley, B. Puértolas, N. López, O. V. Safonova, J. A. Stewart, D. Curulla Ferré and J. Pérez-Ramírez, Nat. Commun., 2019, 10, 3377 CrossRef PubMed.
- Z. Han, C. Tang, J. Wang, L. Li and C. Li, J. Catal., 2021, 394, 236–244 CrossRef.
- N. Rui, F. Zhang, K. Sun, Z. Liu, W. Xu, E. Stavitski, S. D. Senanayake, J. A. Rodriguez and C.-J. Liu, ACS Catal., 2020, 10, 11307–11317 CrossRef.
- J. Wang, K. Sun, X. Jia and C.-j. Liu, Catal. Today, 2021, 365, 341–347 CrossRef CAS.
- Q. Wu, C. Shen, N. Rui, K. Sun and C.-j. Liu, J. CO2 Util., 2021, 53, 101720 CrossRef CAS.
- C. Shen, K. Sun, Z. Zhang, N. Rui, X. Jia, D. Mei and C.-j. Liu, ACS Catal., 2021, 11, 4036–4046 CrossRef CAS.
- K. Sun, Z. Zhang, C. Shen, N. Rui and C.-j. Liu, Green Energy Environ., 2022, 7, 807–817 CrossRef CAS.
- Z. Zhou, Y. Wang, Y. Bao, H. Yang, J. Li, C. Chang, S. Li and P. Gao, Sci. China:Chem., 2024, 67, 1715–1728 CrossRef CAS.
- C. Shen, K. Sun, R. Zou, Q. Wu, D. Mei and C.-j. Liu, ACS Catal., 2022, 12, 12658–12669 CrossRef CAS.
- T. Pinheiro Araújo, J. Morales-Vidal, T. Zou, R. García-Muelas, P. O. Willi, K. M. Engel, O. V. Safonova, D. Faust Akl, F. Krumeich, R. N. Grass, C. Mondelli, N. López and J. Pérez-Ramírez, Adv. Energy Mater., 2022, 12, 2103707 CrossRef.
- X. Ye, C. Yang, X. Pan, J. Ma, Y. Zhang, Y. Ren, X. Liu, L. Li and Y. Huang, J. Am. Chem. Soc., 2020, 142, 19001–19005 CrossRef CAS.
- Z.-J. Zhao, S. Liu, S. Zha, D. Cheng, F. Studt, G. Henkelman and J. Gong, Nat. Rev. Mater., 2019, 4, 792–804 CrossRef.
- A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- G. Jones, J. G. Jakobsen, S. S. Shim, J. Kleis, M. P. Andersson, J. Rossmeisl, F. Abild-Pedersen, T. Bligaard, S. Helveg, B. Hinnemann, J. R. Rostrup-Nielsen, I. Chorkendorff, J. Sehested and J. K. Nørskov, J. Catal., 2008, 259, 147–160 CrossRef CAS.
- S. Wang, V. Petzold, V. Tripkovic, J. Kleis, J. G. Howalt, E. Skúlason, E. M. Fernández, B. Hvolbæk, G. Jones, A. Toftelund, H. Falsig, M. Björketun, F. Studt, F. Abild-Pedersen, J. Rossmeisl, J. K. Nørskov and T. Bligaard, Phys. Chem. Chem. Phys., 2011, 13, 20760–20765 RSC.
- D. Yang, H. Lu, G. Zeng and Z.-X. Chen, J. Phys. Chem. C, 2023, 127, 22023–22031 CrossRef CAS.
- B. Qin, Z. Zhou and S. Li, Appl. Surf. Sci., 2021, 542, 148591 CrossRef CAS.
- Z. Wei, S. Li and P. Gao, Phys. Chem. Chem. Phys., 2024, 26, 16449–16453 Search PubMed.
- Y. Wang and S. Li, Phys. Chem. Chem. Phys., 2024, 26, 381–389 Search PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef.
- P. Gao, S. Li, X. Bu, S. Dang, Z. Liu, H. Wang, L. Zhong, M. Qiu, C. Yang, J. Cai, W. Wei and Y. Sun, Nat. Chem., 2017, 9, 1019–1024 CrossRef.
- Z. Zhou, B. Qin, S. Li and Y. Sun, Phys. Chem. Chem. Phys., 2021, 23, 1888–1895 RSC.
- M. Meunier and S. Robertson, Mol. Simul., 2021, 47, 537–539 CrossRef.
- B. Qin and S. Li, Phys. Chem. Chem. Phys., 2020, 22, 3390–3399 RSC.
- Q.-Y. Chang, K.-Q. Wang, Z.-J. Sui, X.-G. Zhou, D. Chen, W.-K. Yuan and Y.-A. Zhu, ACS Catal., 2021, 11, 5135–5147 CrossRef.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef.
- F. Cannizzaro, E. J. M. Hensen and I. A. W. Filot, ACS Catal., 2023, 13, 1875–1892 CrossRef PubMed.
- Y. Wang, Z. Zhou, B. Qin, Q. Chang, S. Dang, Y. Hu, K. Li, Y. Bao, J. Mao, H. Yang, Y. Liu, J. Li, S. Li, D. A. Dixon, Y. Sun and P. Gao, EES Catal., 2025, 3, 106–118 RSC.
- S. Jiao, X. Fu and H. Huang, Adv. Funct. Mater., 2022, 32, 2107651 CrossRef.
- R. Cheula, T. A. M. Q. Tran and M. Andersen, ACS Catal., 2024, 14, 13126–13135 CrossRef.
- Y. Li, S. H. Chan and Q. Sun, Nanoscale, 2015, 7, 8663–8683 RSC.
- S. K. Iyemperumal, T. D. Pham, J. Bauer and N. A. Deskins, J. Phys. Chem. C, 2018, 122, 25274–25289 CrossRef.
- F. Doherty and B. R. Goldsmith, Plasma Sources Sci. Technol., 2023, 32, 034004 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra09111f |
| This journal is © The Royal Society of Chemistry 2025 |