Thermometer or freezer: dual functionality in a 2D mixed-anion terbium(III) oxide carbodiimide

Abstract

Advances in the chemistry of compounds containing the NCN²⁻ complex anion are leading to the discovery of new materials with interesting and promising properties. Here we present a comprehensive investigation of the optical and magnetic properties of the 2D phosphor Tb₂O₂NCN whose structure presents a double layer of Tb-triangular lattices separated from each other by the NCN²⁻ anion, offering a conjunction of luminescent thermometry and magnetocaloric effects. Temperature-dependent luminescence studies reveal the typical behavior of thermal quenching, but when the temperature increases, a mechanism of direct relaxation to the ⁵D₄ levels of Tb³⁺ ions is activated, thereby giving rise to an anti-thermal quenching effect. This peculiar feature has prompted us to explore the characteristics of Tb₂O₂NCN in temperature sensing, using the classical approach of optical ratiometric thermometry as well as an approach based on linear transformations (i.e., principal component analysis). The latter, by employing the entire emission spectrum, offers better sensitivity leading to more accurate temperature values. The magnetic properties of Tb₂O₂NCN reveal a long-range antiferromagnetic ordering below T_N = 6.5 K as well as first-order field-induced metamagnetic transitions. The absence of hysteresis and its high magnetic density make Tb₂O₂NCN a fine candidate for magnetic refrigeration, with a surprisingly large value of −ΔS_M = 11.7 J kg⁻¹ K⁻¹ at 5 T, much more promising than those reported for other Tb-comprising compounds.

---

Introduction

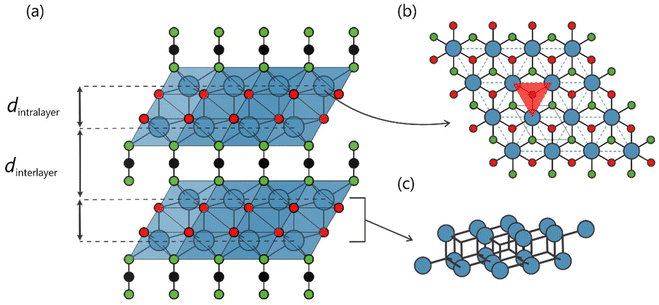
In recent years, layered crystal structures incorporating the NCN²⁻ anion have been shown to display a wide variety of desirable optical properties, as well as finding applications in electrochemistry and photochemistry.¹ Among the most prominent examples are the MNCN (M = Zn, Mn, Fe, Co) binary carbodiimide compounds, which exhibit outstanding performance as anodes in lithium- and sodium-ion batteries, and also silver cyanamide, Ag₂NCN, which has been used as a catalyst for water oxidation.^2–8 One area in which NCN-based compounds stand out is that of luminescence, however, as they are able to incorporate many of the most common activators into their crystal structure, such as lanthanide ions Ln³⁺ (Ln = Ce, Tb, Pr, Eu) or Mn²⁺ and Eu²⁺ divalent cations.^9–20 Several phosphor materials have been synthesized by substitution using as host lattice NCN-based structures such as those based on binary carbodiimides, for example CaNCN:Mn²⁺, SrNCN:Eu²⁺, and Gd₂NCN₃:Tb³⁺, or those synthesized based on ternary cyanamides, such as LiIn(NCN)₂:Tb³⁺ or the recent work on the alkaline-mixed compound Li_xNa_1−xTb(NCN)₂.^21,22 Nonetheless, the mixed-anion oxide carbodiimides, Ln₂O₂NCN, currently constitute the largest family of host lattices suitable for the preparation of luminescent materials.

The crystal structure of Ln₂O₂NCN (Ln = Sm–Yb, P3̄m1) is composed of alternating layers of [Ln₂O₂]²⁺ and NCN²⁻ stacked along the c-axis as shown in Fig. 1.^23,24 The structure of the cationic layer is formed by a block (or double-layer) of Ln³⁺ ions composed of two sheets with a triangular Ln–Ln network extending throughout the ab-plane. The geometry of the crystal sublattice of the Ln³⁺ ions is such that the distance between sheets within the same block, d_intra, is much smaller than the distance between sheets of different blocks, d_inter, so that the distance arrangement between the Ln³⁺ ionic planes is d_intra–d_inter–d_intra–d_inter–… along the stacking axis, making it a structure that can be understood as being two-dimensional. Luminescent materials of this family have been developed, such as the substituted compounds Y₂O₂NCN:Eu³⁺ and Gd₂O₂NCN:Eu³⁺,Tb³⁺.^25,26 As in the case of the other luminescent compounds based on the NCN group, however, the description of the optical properties is limited to the study of the excitation/emission spectra and radiative decay curves but potential uses as a functional material have not yet been explored in depth.

Fig. 1 (a) Crystal structure of Tb₂O₂NCN with two different spacings between layers. (b) The terbium atoms (blue) are arranged in a double-layer consisting of two sheets of triangular nets (in red) of terbium cations. (c) Arrangement of Tb³⁺ ions in shifted triangular lattice layers.

An application field receiving increased attention recently is that of optical thermometry, where the temperature can be determined by the emission characteristics of a luminescent center present in the material hence called “thermometric”.^27–37 Thus, by analyzing thermally induced changes in specific spectroscopic parameters of the phosphor, a direct correlation between said parameters and temperature can be established. Accordingly, luminescent thermometry has been developed on the basis of photoluminescent properties such as the intensity of an emission band, spectral position, bandwidth, radiative decay time, or, most importantly, the ratio of the emission intensity (dubbed “ratiometric”) of two different bands.^27,28,38,39 The latter is the most frequently employed approach, since this type of thermometry is not affected by changes in the experimental conditions under which the emission intensities are obtained.^28,40–42

Typically, in a ratiometric-thermometric material, two luminescent centers with different temperature response are required.^39,43,44 The design usually involves a lanthanide ion (Ln³⁺) acting as a reference and a transition-metal ion (M²⁺) to detect the signal. This type of configuration is particularly effective given the difference in the responsible ions’ thermal quenching mechanism (i.e., how the emission of the centers is affected with respect to temperature).^45–48 In this way, one will obtain thermometers with good accuracy (δT) and thermal sensitivity (S_r). This technique still has some limitations, however, mainly related to the need to spectroscopically resolve the bands involved which is not always simple as there may be band overlap. In addition, a good thermometric material should be as thermally and chemically stable as possible while its preparation process should be robust enough to reproduce the results of luminescence evaluation.^{27,28,31,38,49,50}

Hereby, we present the inorganic solid-state mixed-anion phosphor terbium(III) oxide carbodiimide (Tb₂O₂NCN) as a candidate multifunctional material, coupling magnetism and photosensitivity in the same compound. The temperature-dependent photoluminescence exhibits typical thermal-quenching behavior at low temperatures but reveals, at moderate temperatures, an antithermal-quenching mechanism, so as to establish ratiometric thermometry with only one luminescent center. This peculiar characteristic, together with the fact that Tb₂O₂NCN presents high chemical, thermal and mechanical stability and a facile solid-state synthesis process, make it a promising material for thermal sensing at cryogenic temperatures. In addition, we present an approach to thermometry, which is receiving increasing attention, based on dimensional reduction through principal component analysis (PCA): not only the emission of two bands but the complete data of the emission spectrum (high dimensional space) are considered for the treatment of the information, thus eliminating problems related to spectral overlap or changes in the shape of the emission spectrum.^51–55

Tb₂O₂NCN also exhibits a temperature-dependent magnetic behavior demonstrating a giant magnetocaloric effect (MCE) such that it is also a promising candidate for a low-temperature refrigerant. The large ground-state spin of Tb³⁺ ions and the high magnetic density in Tb₂O₂NCN lead to a large magnetic entropy change (−ΔS_M) manifesting its role for magnetic refrigeration.^56,57 Finally, this compound exhibits slow magnetic relaxation as a consequence of the inherent anisotropy in the ions’ magnetic ordering, thus demonstrating a strong structure–property relation; the geometry of the crystal structure determines the processes related to the energy migration of the photoluminescence as well as the magnetic interaction between the Tb³⁺ ions.

Results and discussion

The fully inorganic 2D Tb₂O₂NCN was synthesized via solid-state metathesis by heating a solid, homogenized mixture of Li₂NCN and TbOCl to 600 °C under argon flow, as described recently.⁵⁸ The powder X-ray diffraction pattern reveals high phase purity (Fig. 2a) with hexagonal lattice parameters a = 3.75 Å and c = 8.20 Å. Details of the Rietveld refinement, crystallographic information and atomic positions are available in the ESI (Fig. S1 and Tables S1, S2†). The structure of Tb₂O₂NCN (P3̄m1, no. 164) is composed of a double-layer of Tb³⁺ ions with a bipyramidal-type coordination environment, i.e., three NCN²⁻ units on one side and three oxygen atoms on the opposite side, plus an additional oxygen atom forming a Tb–O bond along the c-stacking axis (Fig. 2b). Each of the TbN₃O₄ polyhedra shares an edge with six other polyhedra in the same layer and with three others in the next layer. The terbium cations within the double-layer are bridged to each other by O²⁻ anions, while the connection between terbium atoms in different layers relies on NCN²⁻ anions. The arrangement of the Tb³⁺ magnetic ions in each sheet of the double-layer forms an equilateral triangular lattice with distances d_intrasheet ≈ 3.75 Å and d_intralayer ≈ 3.65 Å (Fig. 2b). An important characteristic is that these triangular Tb motifs are displaced from each other in such a way that the Tb³⁺ ion in one layer is above/below the center of the triangle formed by the terbium ions in the next layer of the double-layer, as shown in Fig. 2c. Thus, the triangular layers alternate with the NCN²⁻ anion in a stacking with an AB-NCN-AB-NCN-AB arrangement and an interlayer distance d_interlayer ≈ 5.69 Å, so that we can expect a behavior characteristic for a two-dimensional system.

Fig. 2 (a) Powder X-ray diffraction pattern of Tb₂O₂NCN and simulated reflections based on the previously reported model. (b) Connection between terbium atoms within the double layer revealing two different spacings, d_intrasheet = 3.75 and d_intralayer = 3.65 Å, as well as the communication between atoms of different layers at a distance of d_interlayer = 5.69 Å. (c) Topological arrangement of Tb³⁺ ions highlighting the three most important distances: intrasheet, intralayer and interlayer.

To investigate the optical properties of Tb₂O₂NCN, photoluminescence emission spectra were recorded in the temperature range of 3–320 K (Fig. 3a). Upon excitation at 270 nm the oxide carbodiimide exhibits typical Tb³⁺ luminescence with narrow and well-resolved emission bands. The spectrum consists of multiple bands along five regions centered around 487, 543, 583, 621, and 658 nm corresponding to the [Xe]4f⁸–[Xe]4f⁸ intraconfigurational transitions of the Tb³⁺ ions from the ⁵D₄ level towards the ⁷F_J levels with J = 6, 5, 4, 3, and 2, respectively. The temperature dependence of the emission spectra of Tb₂O₂NCN is provided in Fig. 3b and reveals two types of behavior. First, as the temperature increases from 3 to 140 K, the intensity of the main emission (at 543 nm) decreases to about 55% of the intensity at 3 K, which typically is due to the thermal activation of non-radiative decay mechanisms, an observation well-known as thermal quenching. Quite surprisingly, however, starting at 140 K the intensity increases progressively with temperature up to 320 K, an increase of about 200% compared to the intensity at 140 K, thus demonstrating an anti-thermal quenching behavior.

Fig. 3 (a) Emission spectra of Tb₂O₂NCN under λ_exc = 270 nm in the temperature range between 3 and 320 K, resulting in the transitions ⁵D₄ → ⁷F_J. (b) Temperature-dependent emission spectra showing the anti-thermal quenching effect for the main emission at 543 nm. (c) Temperature-dependence of integrated intensities for the total emission and ⁵D₄ → ⁷F_J transitions, R₁ (J = 6), R₂ (J = 5), R₃ (J = 4), R₄ (J = 3) and R₅ (J = 2). (d) Schematic energy diagram of the cross-relaxation process between ⁵D₃ → ⁷F₀ and ⁷F₆ → ⁵D₄. (e) Suggested configurational coordinate diagram for the anti-thermal quenching process in Tb₂O₂NCN. (f) Decay curves for the transition ⁵D₄ → ⁷F₅ at 100, 300, and 500 K. Inset: temperature-dependence of the experimental radiative lifetime (τ₀). For the excitation spectrum of Tb₂O₂NCN, please see ref. 58.

To facilitate the analysis of the thermal and anti-thermal quenching of the ⁵D₄ → ⁷F_J transitions, we segmented the emission spectrum into five different regions: R₁ (J = 6, 480–500 nm), R₂ (J = 5, 535–555 nm), R₃ (J = 4, 577–602 nm), R₄ (J = 3, 613–629 nm), and R₅ (J = 2, 656–660 nm). The behavior of the intensities (expressed as integrated area) of the five R_i regions with temperature, as well as the total emission, are shown in Fig. 3c. Clearly, the intensity of the regions R₁, R₂ (related to the main emission at 543 nm) and R₃ mirror the thermal and antithermal quenching behavior, although the effect is not as pronounced in the R₁ case. In contrast, the intensity of the R₄ region is not strongly affected by temperature until 200 K at which point the intensity starts to increase up to 150% at T = 320 K compared to the value at 3 K. The R₅ region looks practically unaffected. Thus, the anti-thermal quenching effect becomes dominant in four out of five regions from T = 200 K onwards.

This temperature behavior can be explained by two different processes. A first mechanism takes place at low temperatures, where under excitation at 270 nm the electrons pass directly from the ground state to the 5d levels (Fig. 3d), where by non-radiative processes they populate the ⁵D_J levels and emit light mainly by ⁵D₄ → ⁷F_J transitions. Thus, as the temperature increases, the non-radiative transfer process becomes more dominant and the intensity of the emission decreases, which constitutes the thermal-quenching effect. This is observed in the intensity behavior of regions R₂ and R₃ where the intensity clearly decreases as the temperature increases. Nonetheless, the fact that the intensity in the R₁ region (transition ⁵D₄ → ⁷F₆) is not so strongly affected by temperature can be explained by a compensation effect resulting from Tb–Tb energy transfer through a cross-relaxation mechanism between the ⁵D₃ → ⁷F₀ and ⁷F₆ → ⁵D₄ transitions. At moderate temperatures, as the temperature increases multiple vibration states above the 5d levels are formed. If they are energetically close enough to the Tb-NCN charge-transfer state, the 5d electrons relax directly towards the ⁵D₄ levels, thereby increasing the intensity of all radiative emissions towards the ⁷F_J levels and explaining the anti-thermal quenching effect, as shown in Fig. 3e (violet line). Therefore, in this temperature regime, this second mechanism compensates and exceeds the intensity reduction originating from the intrinsic thermal-quenching effect, so all the intensities of the R_i regions increase. If the temperature continues to increase, i.e., the compound is over-heated, electrons could be thermally induced from the Tb-NCN state to the ground state without light emission, thus increasing the non-radiative energy loss (Fig. 3e yellow line).

To obtain information about the energy transfer process between Tb³⁺ ions, time-dependent luminescence measurements (λ_exc = 270 nm) were carried out for the ⁵D₄ → ⁷F₅ transition in the 100–500 K range, as depicted in Fig. 3f. In all cases, the decay curves do not show mono-exponential behavior but the long-time part follows the mono-exponential decay model: I = I₀ exp(−t/τ₀). By fitting the experimental data with this equation, an experimental radiative lifetime of τ₀ = 13.6 μs at T = 100 K is obtained, which increases to 19.4 μs at 500 K, revealing that the energy migration process slows with temperature and is consistent with the thermal intensity behavior in the emission spectrum. Now, it is known that the probability (or rate) of energy transfer (P) can be expressed as P = C exp(−2R/L), where R is the distance between the luminescent centers, C is an interaction constant between them, and L is the effective average Bohr radius (≈0.30 Å for Tb³⁺ ions). Since in the Tb₂O₂NCN structure the intrasheet distance (≈3.75 Å) is considerably smaller than the interlayer distance (≈5.69 Å) the energy-migration rate is dominant along the Tb³⁺ ion double-layer (P_intrasheet/P_interlayer ≈ 8 × 10⁵). To investigate the nature of these short-distance interactions, the value of the critical transfer distance (R_C) compared to the Tb–Tb distance in the triangular network (d_intrasheet ≈ 3.75 Å) has been evaluated. This very critical distance can be calculated according to where V is the unit-cell volume, n is the number of activators per unit cell, and x_C is the activator concentration (1.0 for Tb₂O₂NCN, a stoichiometric compound fully occupied by Tb³⁺ ions). Thus, one obtains R_C ≈ 4.57 Å > d_intrasheet, indicating that the energy-migration process is favored through an exchange interaction mechanism.

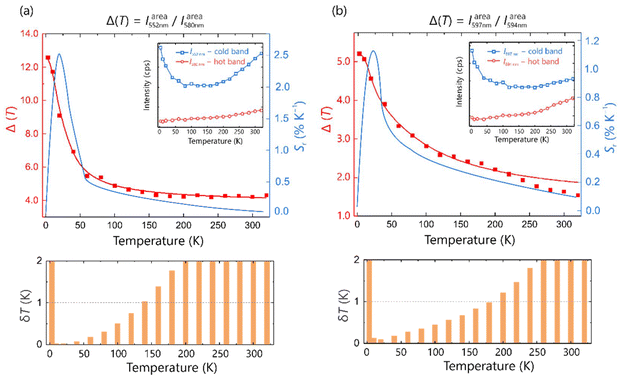
In an attempt to take advantage of the particular thermal behavior of the emission spectrum, Tb₂O₂NCN was tested for ratiometric thermometry. We found that the thermal variation of the intensities (expressed as integrated area, I^area_λ) of the emission peaks in regions R₂ and R₃ provide good combinations suitable for thermometric parameters, . The choice of λ₁ and λ₂ is made so that one of the intensities is strengthened at low temperatures (cold band) while the other is weakened (hot band). In this way, we have explored the temperature behavior of two thermometric parameters Δ_552/580 = I^area_{552 nm}/I^area_{580 nm} and Δ_597/594 = I^area_{597 nm}/I^area_{594 nm} as shown in Fig. 4. The experimental data can be appropriately described according to the Mott–Seitz equation^59,60 according to which Δ_T = Δ₀/[1 + α₁ exp(−ΔE₁/k_B·T) + α₂ exp(−ΔE₂/k_B·T)], where Δ₀, α₁ and α₂ are fitting parameters and ΔE₁ and ΔE₂ are the activation energies for the emissions. Fitting the model yields that for thermometry based on Δ_552/580 only one channel is required (i.e., ΔE₂ ≈ 0) so that ΔE₁ ≈ 37 K while for the thermometric parameter Δ_597/594 values of ΔE₁ ≈ 225 K and ΔE₂ ≈ 38 K (see ESI† for details) are obtained. Small values in the activation energy could be related to a multiphonon quenching mechanism while the higher value would be associated with the thermal crossover mechanism described in Fig. 3. Moreover, as shown in Fig. 4, the values of Δ_552/580 decrease exponentially with temperature, which explains the presence of only one non-radiative decay channel, while Δ_597/594 shows an “S-shaped” decrease, making the presence of two channels ΔE₁ and ΔE₂ with a considerable energy difference understandable.

Fig. 4 Top: thermometric calibration curves Δ(T) involving the integrated areas for the peaks (inset) and relative sensitivity dependence, S_r(T), for (a) the 552/580 nm area-intensity ratio and (b) the 597/594 nm area-intensity ratio. Red squares are experimental data while solid curves are the best fit to the Mott–Seitz model. Bottom: temperature uncertainty curves δT(T).

The performance analysis of both thermometric curves was carried out by inspecting the relative thermal sensitivity, S_r = |∂Δ_T/∂T|/Δ, and temperature uncertainty, δT = |δΔ/Δ|/S_r.^27,28,38 This evaluation reveals that the wavelengths chosen provide good values of S_r and δT (i.e., S_r > 1% K⁻¹ and δT < 1 K) at relatively low temperatures. The thermometric parameter Δ_552/580 offers an operating range between 10 and 140 K with a maximum sensitivity S_r = 2.42% K⁻¹ at 20 K while Δ_597/594 provides a maximum sensitivity S_r = 1.13% K⁻¹ also at 20 K but with a wider temperature reading range between 10 and 180 K. Similar results can also be obtained with the intensities associated with the maximum emission (Fig. S2†). Furthermore, it is possible to establish a direct linear correlation between temperature and the thermometric parameters Δ_594/597 and Δ_580/597, involving wavelengths of the transition ⁵D₄ → ⁷F₄, in addition to Δ_622/597 related to the transitions ⁵D₄ → ⁷F₃ and ⁵D₄ → ⁷F₄, respectively. Hence, the thermometry appears in three different temperature regimes: cryogenic (10–120 K), low (80–200 K) and medium (180–320 K) as shown in Fig. 5. This type of thermometry is simpler, more robust and reliable, and it does not require any additional calibration. In addition, large values in the slopes demonstrate a high sensitivity indicating that Tb₂O₂NCN is an excellent self-referencing luminescent thermometer.

Fig. 5 (a) Relation between thermometric parameters and the temperature ranges offering the best performance for linear thermometry. Temperature-dependence of the ratiometric parameters Δ_594/597 (b), Δ_580/597 (c) and Δ_622/597 (d). Solid squares represent the experimental data and dashed lines correspond to the best fit to a linear equation.

One of the biggest challenges related to ratiometric thermometry is to extract intensities reliably and easily. In the case of Tb₂O₂NCN, the wavelengths offering the best results in sensitivity (S_r) and precision (δT) involve the ⁵D₄ → ⁷F_J transitions (J = 4 and 3), which involve a high degree of complexity due to the splitting of the emissions by the crystal field, and this could hinder a future real application. For this reason, we have explored the option of a thermometry involving, during the analysis, information from the entire emission spectrum and not just part of it, thereby eliminating any error upon intensity extraction. To do so, we propose a multivariant thermometry based on principal component analysis (PCA), a statistical dimensionality-reduction method used to find combinations of variables describing the behavior of large datasets. In this way, the collected data were arranged in a 18 × 251 matrix X where the number of rows corresponds to the number of observations (i.e., the different temperatures in the range 3–320 K) while the number of columns represents the number of variables, in our case the intensities at the wavelengths of the emission spectrum between 450–700 nm. Thus, the PCA was performed on this matrix X, producing a set of new variables, or principal components (PC_i), which are related to the original intensities I(λ_j) at a given temperature, by means of PC_i = ∑c_i(λ_j)I(λ_j) where c_i(λ_j) represents the coefficients describing the behavior of each principal component.^54,55

After applying PCA to our experimental datasets, we found that only three principal components are sufficient to describe more than 90% of the variance of the original data. In addition, the coefficients associated with each of the three principal components reproduce the emission spectrum in considerable detail (Fig. 6a), showing a shape and variability very close to the original information in the regions of interest R_i (that is, where the transitions ⁵D₄ → ⁷F_J occur) while in the areas outside their contribution is basically null, so that our principal components are not only statistically relevant but also have physical meaning. As a result, temperature was related to these new variables by multivariate linear regression, obtaining a good correlation as shown in Fig. 6b. In order to evaluate the performance parameters, the linear regression equation was used as a basis T_calc = β₀ + ∑β_iPC_i obtaining sensitivity values (S_r) well above 1.0% as shown in Fig. 6b and a precision (δT) of ≈1.0 K (see ESI† for details). It is rather obvious that PCA-thermometry offers better performance results since it uses the entire experimental dataset to identify the parameters that correlate with temperature, without the need to pre-select regions or specific thermometric parameters.

Fig. 6 (a) Photoluminescent emission spectrum of Tb₂O₂NCN and the corresponding coefficients for the first three principal components: PC₁ explains 65.7% of the original data's variance while PC₂ and PC₃ have values of 25.29% and 2.06%. (b) Relation between temperature and calculated temperature by multivariate regression using principal components as input. Solid squares represent the experimental data while the dashed line represents the best fit to a linear equation. In addition, the relative sensitivity dependence S_r(T) is shown on the right axis.

The magnetic behavior of μ-crystalline Tb₂O₂NCN was investigated by susceptibility measurements using a SQUID magnetometer. The value of the magnetic susceptibility χ_MT at room temperature is 22.4 cm³ K mol⁻¹ in good agreement with the theoretical value of 23.6 cm³ K mol⁻¹ expected for two isolated Tb³⁺ ions (J = 6, g_L = 3/2).^37,61–63 Upon cooling, χ_MT remains practically constant up to about 150 K, from where, due to the depopulation of the excited levels of the ⁷F₆ ground multiplet, it starts to decrease to a value of 2.1 cm³ K mol⁻¹ at 3 K as shown in Fig. 7a. In the temperature range between 50–300 K the susceptibility χ_M follows the Curie–Weiss law quite well, so that by fitting a 1/χ_Mvs. T curve the parameters θ_CW = −16.6 K and C = 23.75 cm³ K mol⁻¹ are obtained. The negative value of θ_CW indicates predominantly antiferromagnetic interactions between Tb³⁺ ions in the paramagnetic state, while the effective magnetic moment calculated from C yields 13.98μ_B (i.e., 9.70μ_B per Tb³⁺ ion), in agreement with the expected theoretical value .^37,64 Under 50 K, the curve χ(T) clearly shows the characteristic peak for a paramagnetic transition to long-range antiferromagnetic order at T_N ≈ 6.5 K (Fig. 7b). This low ordering temperature reflects the Tb–Tb interactions: as already mentioned, the arrangement of the Tb³⁺ in Tb₂O₂NCN corresponds to three Tb–Tb distances: d_intrasheet ≈ 3.75 Å, d_intralayer ≈ 3.65 Å, and d_interlayer ≈ 5.69 Å. For our analysis we may ignore the intralayer interactions in the same double-layer because (Fig. 7c) this interaction (J₂) should be small since a positional shift in the triangular network frustrates the intralayer magnetic coupling. Therefore, we will limit ourselves to comparing the d_intrasheet (J₁) and d_interlayer (J₃) interactions. Given that the NCN²⁻ anion is between the Tb³⁺ ions in different layers, these are relatively far away from each other, so a small value of J₃ can be expected compared to J₁. In fact, this can be seen if comparing the scale of the dipolar interactions^65–68 (here R is the Tb–Tb distance) from which D₁/D₃ = 6.01 K/1.72 K = 3.49 is obtained, reinforcing the idea of a two-dimensional system with magnetic moments located on the triangular lattice. Furthermore, the frustration index f = |θ_CW/T_N| = 2.55 of Tb₂O₂NCN reflects a geometrically frustrated system according to the criteria established by Ramirez.^69,70 Given that magnetic ordering is observed at low temperature, however, we can conclude that such geometrical frustration does not completely hinder the emergence of magnetic ordering in Tb₂O₂NCN.

Fig. 7 (a) Temperature dependence of χ_MT for Tb₂O₂NCN at H = 200 Oe and 10 kOe. (b) Magnetic susceptibility vs. temperature under an applied field of 200 Oe and 10 kOe. Inset: inverse of susceptibility (χ⁻¹) showing Curie–Weiss behavior. (c) Projection of the double-layer down the c-axis showing only terbium atoms. Empty and filled circles represent the Tb on the different sheets of the double layer, bottom and top, respectively. The unit cell is shown in red. The Tb–Tb intrasheet (J₁) and intralayer (J₂) magnetic interactions are indicated in blue and green, respectively.

Isothermal magnetization measurements (Fig. 8a) in the range of μ₀H = 0–9 T at various temperatures show a lack of saturation, indicative of magnetocrystalline anisotropy. The slow relaxation dynamics of Tb₂O₂NCN was studied by AC susceptibility measurements at 2 K. In a zero DC field with an AC field of 5 Oe in the frequency range of 10–10 000 Hz, a clear dependence of the out-of-phase component of the susceptibility (χ′′) on the frequency is revealed, although without the presence of any maximum in the measurement range. Fitting simultaneously χ′ and χ′′ to a generalized Debye model^71–74 (see ESI† for more details) allows us to extract (Fig. 8b and c) the characteristic magnetic relaxation time of τ₀ ≈ 5.7 μs and a parameter α = 0.01, indicating that the relaxation of the magnetic configurations takes place simultaneously. Additionally, the curves M(H) at temperatures between 2.5–8 K show a slope change at ≈1.8 T that becomes evident when comparing the behavior at low and high magnetic fields, clearly observed in the ∂M/∂H plot of Fig. 8a, which typically suggests a metamagnetic transition. To confirm and determine the nature of the magnetic transition, the M–H data were converted into M²–μ₀H/M curves (Arrott plot) depicted in Fig. 8d. According to the Banerjee criterion,⁷⁵ a negative slope in the Arrott plot would indicate a first-order magnetic transition.

Fig. 8 (a) Field-dependent magnetization curves of Tb₂O₂NCN at various temperatures. The right ordinate axis represents ∂M/∂H as a function of the field, revealing the metamagnetic transition at ≈1.8 T. Frequency dependence of the in-phase, χ′ (b) and out-of-phase, χ′′ (c) magnetic susceptibility at 2 K. Solid lines correspond to the best fit to the Debye generalized model. (d) Arrott plots calculated from the M–H curves.

These characteristics in the behavior of the M(H) curves, together with the fact that Tb₂O₂NCN has a high magnetic density (2 × M_Tb/M_w = 0.82) and is also magnetically reversible (no magnetic hysteresis, see Fig. S3†), make it particularly attractive for magnetic refrigeration applications. The magnetocaloric performance was evaluated by means of the magnetic entropy change (−ΔS_M), calculated from the isothermal magnetization curves using the Maxwell equation .^76–80Fig. 9a depicts the magnetic entropy change curves as a function of temperature in the 1–7 T range. The maximum −ΔS_M at low field (3 T) reaches a value of ≈3.6 J kg⁻¹ K⁻¹ while in high field (7 T) a maximum of ≈21.1 J kg⁻¹ K⁻¹ is observed, but still far from the theoretical maximum of −ΔS_M = nR ln(2J + 1)/M_W ≈ 109.0 J kg⁻¹ K⁻¹ (here, n is the number of magnetic centers, R is the gas constant and M_W represents the formula weight).⁵⁷ A comparison of the magnetocaloric performance of Tb₂O₂NCN with other Tb-based compounds is summarized in Table 1, together with sketches of the magnetic sublattices in Fig. 9b. These compounds can be grouped according to the dimensionality of the connected terbium ions. In the group of compounds with 3D ordering, TbCrO₄ stands out: the TbO₈ polyhedra are arranged in the tetragonal zircon (ZrSiO₄) structure, with Tb–Tb ≈ 3.9 Å and a maximum magnetic entropy change of 16.2 J kg⁻¹ K⁻¹ at 23 K.⁸¹ In turn, in TbBO₃, 2D triangular nets of Tb³⁺ are observed forming monolayers with intra- and inter-layer distances of 3.8 Å and 4.4 Å, respectively, with a value of −ΔS_M of 5.97 J kg⁻¹ K⁻¹ at 2 K.⁸² In LiTbP₄O₁₂, terbium ions form 1D channels with intra- and inter-channel distances of 5.6 Å and 6.4 Å, the maximum value of −ΔS_M being 15.9 J kg⁻¹ K⁻¹ at 2 K.⁸³ Tb₂O₂NCN, however, with a double layer arrangement and intra- and inter-layer distances of 3.75 Å and 5.69 Å, far surpasses all their performances under the same applied field and temperature. Apparently, the effect of magnetic frustration compensation on Tb–Tb interactions in this type of structure plays an important role. We conclude that Tb₂O₂NCN would be an excellent candidate for practical application as a cryogenic refrigerant.

Fig. 9 (a) Magnetic entropy change (−ΔS_M) as a function of temperature at several magnetic field changes in the range 1–7 T. (b) Selected Tb-based magnetic refrigeration materials with Tb–Tb networks showing 1D, 2D, and 3D structural dimensionality.

Table 1 Structural characteristics and magnetic features of selected Tb-based compounds

Material	θ CW (K)	T N (K)	−ΔSM ^a (J kg^−1 K^−1) at 5 T	Tb-arrangement
a At 2 T for LiTb6O6(BO3)3. b This work.
TbCrO4 ^81	—	22.1	16.2 (T = 23 K)	3D framework
TbBO3 ^82	−11.0	<2	5.97 (T = 2 K)	2D layers
LiTbP4O12 ^83	0.86	<2	15.9 (T = 2 K)	1D channels
LiTb6O6(BO3)3 ^84	−12.4	<2	6.58 (T = 4 K)	3D framework
TbMnO3 ^85	—	7.0	6.75 (T = 16 K)	3D framework
Tb2O2NCN^b	−16.6	6.5	11.7 (T = 9 K)	2D double layers

---

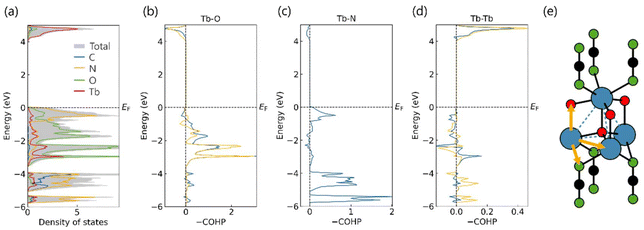
At this point, it is clear that the arrangement of Tb³⁺ ions in the Tb₂O₂NCN structure plays a key role in determining the properties even though it is not only the arrangement: the interatomic communication may perhaps be even more decisive. Hence, the density of states (DOS) and crystal orbital Hamilton population (COHP) for the interactions involving Tb were calculated to analyze the electronic structure of Tb₂O₂NCN (Fig. 10). From the local DOS, the expected, dominant contribution of the N 2p and O 2p levels is seen at the valence band maximum (VBM) between −2.5 and 0 eV, while the conduction band minimum (CBM), between 3.75 and 5 eV, is Tb-centered. The Crystal Orbital Hamilton Populations (COHP) for Tb–X (X = Tb, O, N) interactions shows that Tb–O bonds are stronger than Tb–N bonds (a higher value in the integrated COHP), while, curiously, Tb–Tb interactions show a bonding character in the empty conduction band, unlike Tb–O and Tb–N interactions. This suggests that under excitation at 270 nm (≈4.45 eV) Tb–Tb communication (i.e., the energy migration process in luminescence) would take place directly (attractively in terms of Tb–Tb but not necessarily reducing terbium) and not through O²⁻ or NCN²⁻. In contrast, the strong bonding character of the Tb–N bond near the Fermi level (E_F) indicates that Tb–Tb magnetic interactions will occur through the NCN²⁻ unit, thus explaining the communication of the triangular nets of different layers when long-range magnetic order is established.

Fig. 10 (a) Total and local density of states of Tb₂O₂NCN. The Fermi level (E_F) is set to zero. COHP for Tb–O (b), Tb–N (c) and Tb–Tb (d) interactions. In all cases blue and orange lines represent interactions between nearest and second-nearest neighbours, respectively. (e) Possible communication pathways between terbium atoms: direct or via oxygen or the N of the NCN²⁻ unit.

Conclusions

Both spectroscopic and magnetic investigations on solid-state Tb₂O₂NCN have allowed us to explore its potential for luminescent thermometry and magnetic refrigeration applications at low temperatures. The crystal structure can be understood as a two-dimensional system, formed by alternating layers of the extended NCN²⁻ anion and [Tb₂O₂]²⁺ which, in turn, consist of a double-layer of Tb triangular lattice, all stacked along the [001] direction. Thanks to its anti-thermal quenching behavior, Tb₂O₂NCN is suitable for optical thermometry using appropriate thermometric parameters offering good sensitivity (S_r > 1% K⁻¹) and precision (δT > 1 K). In addition, the option of an instantaneous, linear and simple thermometry has been explored that allows covering a wider temperature range thanks to dimensionality reduction (PCA) offering better performance. In turn, magnetic investigations show that Tb₂O₂NCN contains magnetic frustration between Tb³⁺ ions. This frustration is topological, a consequence of the arrangement geometry, since the Tb-triangular lattices are shifted from each other in the double-layer, separated by the large NCN²⁻ anion. Given the comparatively large Tb³⁺ magnetic moment, however, the frustration is insufficient to suppress the magnetic order observed from T_N = 6.5 K. Furthermore, magnetocalorics of Tb₂O₂NCN was investigated, thanks to first-order metamagnetic transitions taking place at around 1.8 T. The maximum for the magnetic entropy change achieves −ΔS_M ≈ 21.1 J kg⁻¹ K⁻¹ at 7 T. Furthermore, −ΔS_M ≈ 11.7 J kg⁻¹ K⁻¹ at 5 T is considerably larger than those reported for other materials incorporating trivalent terbium under the same magnetic field change and temperature. These excellent results establish that Tb₂O₂NCN is an extremely promising material for applications in thermometry and magnetic refrigeration.

Experimental section

Synthesis

Preparation of Tb₂O₂NCN. The stoichiometric terbium oxide carbodiimide, Tb₂O₂NCN, was prepared on a 0.4 g scale by solid-state metathesis reaction between TbOCl and Li₂NCN in a 2 : 1 molar ratio under argon protective atmosphere. The mixture was homogenized using a mortar and pestle agate, transferred into an open dry glass capillary and loaded into a glass ampoule. The sample was heated in a horizontal tubular furnace at 600 °C under flowing argon for 18 h, with heating and cooling rates of 2 °C min⁻¹. The product is an air-stable powder which was washed several times with water and acetone to remove the LiCl metathesis salt, finally dried in air at 100 °C.

Powder X-ray diffraction analysis

Powder X-ray diffraction data of washed Tb₂O₂NCN were collected employing a STOE STADI-P powder diffractometer with a flat sample holder (Cu–K_α1, linear PSD, 2θ = 4–120° with individual steps of 0.015°). Rietveld refinement was performed using GSAS II.⁸⁶ In the final cycles of least-squares refinement, lattice parameters, fractional coordinates, site-occupancy factors and isotropic thermal displacement parameters (U_iso) were refined for all atoms with a constrained U_iso for chemically reasonable sorts of atoms, in particular all C and N atoms.

Luminescence spectroscopy

Excitation and emission spectra of Tb₂O₂NCN sample were recorded using a fluorescence spectrometer FLS920 (Edinburgh Instruments) equipped with a 450 W xenon discharge lamp (OSRAM) as the radiation source. For the data collection, a R2658P single-photon-counting photomultiplier tube from Hamamatsu was used. For temperature adjustment a cryostat “MicrostatN” from Oxford Instruments had been mounted on the spectrometer. Liquid nitrogen was used as a cooling agent. The photoluminescence decay curves were also recorded on the FLS920 spectrometer, while a 270 nm laser diode from Edinburgh Instruments was used as an excitation source.

Magnetic measurements

Magnetic susceptibility measurements of powderous Tb₂O₂NCN were performed using a Quantum Design SQUID MPMS-XL magnetometer. Samples were placed in PTFE containers and data were recorded in the temperature range 4–300 K in a field of 200 Oe. Magnetization data were collected at several temperatures in the field range 0 ≤ μ₀H(T) ≤ 9. The AC magnetic susceptibility measurements were performed in a PPMS-DynaCool system using the vibrating sample magnetometry option in an oscillating AC field of 5 Oe with frequencies from 10 Hz to 10 kHz in a zero-DC field. The magnetic susceptibilities were corrected for the sample holder and the intrinsic diamagnetic contribution of the compound (χ_M,dia = −1.95 × 10⁻⁴ cm³ mol⁻¹).

Dimensionality reduction

Before performing the PCA, the data in the X matrix (18 observations × 251 wavelengths) were pre-processed. First, each observation (i.e., each row) was normalized using the intensity maximum, and subsequently each column was adjusted to the normal distribution by the transformation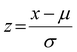 . The resulting matrix Z served as input for PCA. In overall, PCA is a technique that transforms a set of correlated variables p in a new set of independent variables q, denominated as principal components. The first stage involves the calculation of the covariance matrix and then, the eigenvalues and eigenvectors are determined, sorted in descending order according to their eigenvalues. The number of principal components was determined by using the scree plot as criterion (Fig. S4†).

Computational details

Density-functional theory calculations were performed using the Vienna ab initio simulation package (VASP, version 6.1.1).^87,88 Projector augmented wave pseudopotentials with Perdew–Burke–Ernzerhof (PBE)⁸⁹ parameterization were used. The generalized gradient approximation (GGA)⁹⁰ scheme was chosen for treating both electron exchange and correlation. 800 eV was set as the cutoff for the plane-wave basis set. A Γ-centered Monkhorst–Pack k point mesh was used throughout for sampling the first Brillouin zone, the distance between two adjacent k points being always below 2π × 0.02 Å⁻¹. The experimentally obtained structure was first optimized on this level of theory until energy and force differences between consecutive iterations fell below thresholds of 10⁻⁸ eV and 10⁻⁶ eV Å⁻¹, respectively. Gaussian smearing with 0.02 eV as the smearing width was set to treat partial occupancies for each orbital. It is worth noting that, due to the well-known self-interaction errors, the 4f orbitals of Tb were downfolded in the core, and a special “trivalent” GGA potential (designated Tb_3) was used. Following the structure optimization, self-consistent field (SCF) calculations were carried out. Only time-reversal symmetry was considered during the SCF calculations and tetrahedron method with Blöchl corrections⁹¹ was utilized for Brillouin zone integration. Wavefunctions were written out by the end of SCF calculations. Subsequently, a reciprocal space unitary transformation⁹² was performed by using the Local-Orbital Basis Suite Towards Electronic Structure Reconstruction (LOBSTER, version 5.1.1)^93,94 suite to extract both density of states (DOS) and chemical-bonding information. The outputs from LOBSTER were automatically postprocessed by LOBSTER's postprocessor (LOPOSTER).⁹⁵

Author contributions

All authors have accepted responsibility for the entire content of this submitted manuscript and approved the submission.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no conflicts of interest regarding this article.

Acknowledgements

We thank Mr T. Storp for his assistance with PXRD measurements and Ms C. Houben for her assistance with magnetic measurements. J. Medina-Jurado is grateful for the financial support from Deutscher Akademischer Austauschdienst (DAAD). A. Corkett is indebted to the Deutsche Forschungsgemeinschaft (DFG) for funding (project number 441856704).

References

1. A. J. Corkett, O. Reckeweg, R. Pöttgen and R. Dronskowski, Chem. Mater., 2024, 36, 9107–9125.
2. M. Becker and M. Jansen, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, 57, 347–348.
3. X. Liu, M. Krott, P. Müller, C. Hu, H. Lueken and R. Dronskowski, Inorg. Chem., 2005, 44, 3001–3003.
4. X. Liu, R. Dronskowski, R. K. Kremer, M. Ahrens, C. Lee and M.-H. Whangbo, J. Phys. Chem. C, 2008, 112, 11013–11017.
5. X. Liu, L. Stork, M. Speldrich, H. Lueken and R. Dronskowski, Chem. – Eur. J., 2009, 15, 1558–1561.
6. M. Krott, X. Liu, B. P. T. Fokwa, M. Speldrich, H. Lueken and R. Dronskowski, Inorg. Chem., 2007, 46, 2204–2207.
7. S. K. Deb and A. D. Yoffe, Trans. Faraday Soc., 1959, 55, 106–113.
8. M. Becker, J. Nuss and M. Jansen, Z. Naturforsch. B, 2000, 55, 383–385.
9. E. Leysour de Rohello, Y. Suffren, O. Merdrignac-Conanec, O. Guillou, C. Calers and F. Chevire, J. Solid State Chem., 2021, 300, 122240.
10. M. Kubus, C. Castro, D. Enseling and T. Jüstel, Opt. Mater., 2016, 59, 126–129.
11. M. Krings, G. Montana, R. Dronskowski and C. Wickleder, Chem. Mater., 2011, 23, 1694–1699.
12. Y. Masubuchi, S. Nishitani, A. Hosono, Y. Kitagawa, J. Ueda, S. Tanabe, H. Yamane, M. Higuchi and S. Kikkawa, J. Mater. Chem. C, 2018, 6, 6370–6377.
13. D. Dutczak, M. Ströbele, D. Enseling, T. Jüstel and H.-J. Meyer, Eur. J. Inorg. Chem., 2016, 25, 4011–4016.
14. J. Glaser, L. Unverfehrt, H. Bettentrup, G. Heymann, H. Huppertz, T. Jüstel and H.-J. Meyer, Inorg. Chem., 2008, 47, 10455–10460.
15. D. Dutczak, A. Siai, M. Ströbele, D. Enseling, T. Jüstel and H.-J. Meyer, Eur. J. Inorg. Chem., 2020, 41, 3954–3958.
16. E. Säilynoja, M. Lastusaari, J. Hölsä and P. Porcher, J. Lumin., 1997, 72, 201–203.
17. J. Hölsä, R.-J. Lamminmäki, M. Lastusaari, P. Porcher and E. Säilynoja, J. Alloys Compd., 1998, 275, 402–406.
18. J. Hölsä, R.-J. Lamminmäki, M. Lastusaari, E. Säilynoja, P. Porcher, P. Dereń and W. Strȩk, Spectrochim. Acta, Part A, 1998, 13, 2065–2069.
19. M. Takahashi, Y. Hashimoto, S. I. Kikkawa and H. Kobayashi, J. Soc. Mater. Sci., 2000, 11, 1230–1234.
20. T. Takeda, N. Hatta and S. Kikkawa, Chem. Lett., 2006, 9, 988–989.
21. M. Kubus, R. Heinicke, M. Ströbele, D. Enseling, T. Jüstel and H.-J. Meyer, Mater. Res. Bull., 2015, 62, 37–41.
22. J. Medina-Jurado, H. Bourakhouadar, Y. Wang, A. J. Corkett, D. Enseling, T. Jüstel and R. Dronskowski, Chem. Mater., 2025, 37, 2506–2515.
23. Y. Hashimoto, M. Takahashi, S. Kikkawa and F. Kanamaru, J. Solid State Chem., 1996, 125, 37.
24. M. Li, W. Yuan, J. Wang and C. Gu, Powder Diffr., 2007, 22, 59.
25. J. Sindlinger, J. Glaser, H. Bettentrup, T. Jüstel and H.-J. Meyer, Z. Anorg. Allg. Chem., 2007, 633, 1686–1690.
26. L. Wang, S. Yuan, Y. Yang, F. Chevire, F. Tessier and G. Chen, Opt. Mater. Express, 2015, 5, 2616–2624.
27. A. Ansari, A. Parchur, M. K. Nazeeruddin and M. Tavakoli, Coord. Chem. Rev., 2021, 444, 214040.
28. M. D. Dramićanin, J. Appl. Phys., 2020, 128, 040902.
29. Y. Shen, X. Han, S. Wang, H. Yu and H. Zhang, Inorg. Chem., 2025, 64, 133–141.
30. R. M. Diaz-Rodriguez, D. A. Gálico, D. Chartrand, E. A. Suturina and M. Murugesu, J. Am. Chem. Soc., 2022, 144, 912–921.
31. D. K. Amarasinghe and F. A. Rabuffetti, Chem. Mater., 2019, 31, 10197–10204.
32. M. Suta, Ž. Antić, V. Ðorđević, S. Kuzman, M. D. Dramićanin and A. Meijerink, Nanomaterials, 2020, 10, 543.
33. X. Liu, A. Skripka and Y. Lai, et al. , Nat. Commun., 2021, 12, 6401.
34. S. Wang, Y. Xu, T. Chen, W. Jiang, J. Liu, X. Zhang, W. Jiang and L. Wang, Chem. Eng. J., 2021, 404, 125912.
35. P. Dang, W. Wang, H. Lian, G. Li and J. Lin, Adv. Opt. Mater., 2022, 10, 2102287.
36. K. Karachousos-Spiliotakopoulos, V. Tangoulis, N. Panagiotou, A. Tasiopoulos, V. Nastopoulos, E. Moreno-Pineda, W. Wernsdorfer, M. Schulze, A. M. P. Botas and L. D. Carlos, Inorg. Chem., 2022, 61, 18629–18639.
37. J. Wang, J. J. Zakrzewski, M. Zychowicz, Y. Xin, H. Tokoro, S. Chorazy and S.-I. Ohkoshi, Angew. Chem., Int. Ed., 2023, 62, e202306372.
38. C. D. S. Brites, R. Marin, M. Suta, A. N. Carneiro-Neto, E. Ximendes, D. Jaque and L. D. Carlos, Adv. Mater., 2023, 35, 2302749.
39. Y. Ma, A. Aierken, Y. Wang and A. Meijerink, J. Colloid Interface Sci., 2023, 638, 640–649.
40. Y. Wang, L. Lei, R. Ye, G. Jia, Y. Hua, D. Deng and S. Xu, ACS Appl. Mater. Interfaces, 2021, 13, 23951–23959.
41. K. Elzbieciak-Piecka and L. Marciniak, Sci. Rep., 2022, 12, 16364.
42. G. Brunet, R. Marin, M.-J. Monk, U. Resch-Genger, D. A. Gálico, F. A. Sigoli, E. A. Suturina, E. Hemmer and M. Murugesu, Chem. Sci., 2019, 10, 6799–6808.
43. Y. Cui, H. Xu, Y. Yue, Z. Guo, J. Yu, Z. Chen, J. Gao, Y. Yang, G. Qian and B. Chen, J. Am. Chem. Soc., 2012, 134, 3979–3982.
44. X. Shi, Y. Xue, Q. Mao, L. Pei, X. Li, M. Liu, Q. Zhang and J. Zhong, Inorg. Chem., 2023, 62, 893–903.
45. M. Back, J. Ueda, H. Nambu, M. Fujita, A. Yamamoto, H. Yoshida, H. Tanaka, M. Brik and S. Tanabe, Adv. Opt. Mater., 2021, 9, 2100033.
46. J. Stefańska, A. Bednarkiewicz and L. Marciniak, J. Mater. Chem. C, 2022, 10, 5744–5782.
47. Y. H. Wang, S. Yang, Q. F. Xu, C. L. Yang, S. F. Zhang, S. Y. J. Yu and M. M. Jiao, J. Phys. Chem. C, 2022, 126, 15517–15527.
48. P. Du, X. Huang and J. Yu, Inorg. Chem. Front., 2017, 4, 1987–1995.
49. K. M. N. de Souza, R. N. Silva, J. A. B. Silva, C. D. S. Brites, B. Francis, R. A. S. Ferreira, L. D. Carlos and R. L. Longo, Adv. Opt. Mater., 2022, 10, 2200770.
50. Z. Liang, J. Wu and Y. Cui, Light: Sci. Appl., 2023, 12, 36.
51. K. Trejgis, K. Ledwa and K. Maciejewska, et al. , Sci. Rep., 2022, 12, 5847.
52. I. E. Kolesnikov, D. V. Mamonova, M. A. Kurochkin, M. A. Khodasevich, V. A. Medvedev, E. Y. Kolesnikov and A. A. Manshina, J. Mater. Chem. C, 2023, 11, 14814–14825.
53. Š. Dragutin, et al. , Tehnika, 2020, 75, 279–283.
54. E. Ximendes, R. Marin and L. D. Carlos, et al. , Light: Sci. Appl., 2022, 11, 237.
55. A. Rajčić, Z. Ristić, Z. J. Periša, B. Milićević, S. Aldawood, A. N. Alodhayb, Ž. Antić and M. D. Dramićanin, Technologies, 2024, 12, 131.
56. Z. Li, A. Arauzo, J. G. Planas and E. Bartolomé, Dalton Trans., 2024, 53, 8969–8979.
57. B. Wang, X. Liu, F. Hu, J. Wang, J. Xiang, P. Sun, J. Wang, J. Sun, T. Zhao, Z. Mo, J. Shen, Y. Chen, Q. Huang and B. Shen, J. Am. Chem. Soc., 2024, 146, 35016–35022.
58. J. Medina-Jurado, H. Bourakhouadar, A. J. Corkett, D. Enseling, T. Jüstel and R. Dronskowski, Z. Anorg. Allg. Chem., 2025, e202400212.
59. C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millán, V. S. Amaral, F. Palacio and L. D. Carlos, Nanoscale, 2012, 4, 4799–4829.
60. D. V. Lapaev, V. G. Nikiforov, V. S. Lobkov, A. A. Knyazev and Y. G. Galyametdinov, J. Mater. Chem. C, 2018, 6, 9475–9481.
61. C. Ritchie, E. G. Moore, M. Speldrich, P. Kögerler and C. Boskovic, Angew. Chem., Int. Ed., 2010, 49, 7702.
62. K. Katoh, S. Yamashita, N. Yasuda, Y. Kitagawa, B. K. Breedlove, Y. Nakazawa and M. Yamashita, Angew. Chem., Int. Ed., 2018, 57, 9262.
63. H. Wang, Z. Zhu, L. La Droitte, W. Liao, O. Cador, B. Le Guennic and J. Tang, Chem. Sci., 2023, 14, 7208.
64. S. Mugiraneza and A. M. Hallas, Commun. Phys., 2022, 5, 1.
65. N. P. Raju, M. Dion, M. J. P. Gingras, T. E. Mason and J. E. Greedan, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 14489.
66. S. E. Palmer and J. T. Chalker, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 488.
67. M. J. P. Gingras, C. Lacroix, P. Mendels and F. Mila, Introduction to Frustrated Magnetism, Springer, Berlin, 2011.
68. O. A. Petrenko and D. McK Paul, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 024409.
69. V. Biondo, P. C. W. Sarvezuk, F. F. Ivashita, K. L. Silva, A. Paesano Jr. and O. Isnard, Mater. Res. Bull., 2014, 54, 41–47.
70. A. P. Ramirez, Annu. Rev. Mater. Sci., 1994, 24, 453.
71. P. V. Madduri, S. Sen, B. Giri, D. Chakrabartty, S. Manna, S. Parkin and A. Nayak, Phys. Rev. B, 2020, 102, 174402.
72. O. Pastukh, P. Konieczny, M. Laskowska and Ł. Laskowski, Magnetochemistry, 2021, 7, 122.
73. M. Balanda, Acta Phys. Pol. A, 2013, 124, 964.
74. C. V. Topping and S. J. Blundell, J. Phys.: Condens. Matter, 2019, 31, 013001.
75. B. K. Banerjee, Phys. Lett., 1964, 12, 16.
76. K. P. Shinde, S. H. Jang, J. W. Kim, M. Ranot and K. C. Chung, Dalton Trans., 2015, 44, 20386–20391.
77. M. Kumar, L. Li, J. K. Zareba, L. Tashi, S. C. Sahoo, M. Nyk, S. Liu and H. Sheikh, Cryst. Growth Des., 2020, 20, 6430–6452.
78. S.-J. Liu, S.-D. Han, J.-P. Zhao, J. Xu and X.-H. Bu, Coord. Chem. Rev., 2019, 394, 39–52.
79. S.-J. Liu, C. Cao, S.-L. Yao, T.-F. Zheng, Z.-X. Wang, C. Liu, J.-S. Liao, J.-L. Chen, Y.-W. Li and H. R. Wen, Dalton Trans., 2017, 46, 64–70.
80. Y. Wang, H. Zhang, M.-L. Wu, K. Tao, Y.-W. Li, T. Yan, K.-W. Long, T. Long, Z. Pang and Y. Long, Chin. Phys. B, 2016, 25, 127104.
81. E. Palacios, M. Castro, J. Romero de Paz, J. M. Gallardo-Amores and R. Sáez-Puche, J. Solid State Chem., 2022, 314, 123356.
82. P. Mukherjee, Y. Wu, G. I. Lampronti and S. E. Dutton, Mater. Res. Bull., 2018, 98, 173–179.
83. D. N. Petrov, P. T. Long, Y. S. Koshkid'Ko, J. Ćwik and K. Nenkov, J. Phys. D: Appl. Phys., 2020, 53, 495005.
84. Y. Chen, W. Liu, J. Feng, R. Guo, F. Fan, J. Shen, G. Zhang and H. Tu, Cryogenics, 2022, 124, 103476.
85. M. Staruch, K. Luna, A. McDannald and M. Jain, J. Magn. Magn. Mater., 2015, 377, 117–120.
86. B. Toby, J. Appl. Crystallogr., 2001, 34, 210.
87. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
88. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
89. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
90. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
91. P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233.
92. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567.
93. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
94. R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940.
95. Y. Wang, P. C. Müller, D. Schnieders and R. Dronskowski, J. Comput. Chem., under review.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dt01003a

---