 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Real-space Kohn–Sham density functional theory for complex energy applications
Zeyi
Zhang
ab,
Liping
Liu
 d,
Drew M.
Glenna
ac,
Asmita
Jana
a,
Carlos Mora
Perez
a and
Jin
Qian
d,
Drew M.
Glenna
ac,
Asmita
Jana
a,
Carlos Mora
Perez
a and
Jin
Qian
 *a
*a
aChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA. E-mail: jqian2@lbl.gov
bDepartment of Chemistry, University of California, Berkeley, Berkeley, California 94720, USA
cDepartment of Nuclear Engineering & Industrial Management, University of Idaho, Idaho Falls, Idaho 83402, USA
dDepartment of Chemical Engineering, Virginia Polytechnic Institute and State University, Blacksburg, Virginia 24060, USA
First published on 16th June 2025
Abstract
Real-space Kohn–Sham density functional theory (real-space KS-DFT) enables large-scale electronic structure simulations that is particularly well-suited for the modern high-performance computing (HPC) architectures. This feature article reviews its theoretical foundations, highlights the algorithmic advances and recent developments, and showcases applications in complex nano systems. We aim to provide a perspective on the trajectory of real-space KS-DFT as an emerging tool for computational chemistry and materials science in the exascale era.
1 Introduction
KS-DFT, commonly referred to as DFT, is a powerful and widely used computational framework for modeling electronic structure. It has been instrumental in unraveling fundamental insights at the atomistic level, which in turn govern macroscopic properties. For a comprehensive review of the theoretical and applied aspects of DFT and its extended electronic structure methods, we refer readers to the paper by Marzari et al.1When discussing DFT, one's implicit assumption often involves traditional implementations based on either the atomic orbitals or plane-wave basis sets. These methods, as implemented in widely used software packages such as Q-Chem,2 Gaussian,3 or VASP,4,5 and Quantum Espresso,6 have been highly successful but typically scale to systems containing only a few hundred atoms. This limitation arises from the computational cost of solving the KS equations in non-localized bases, where the Hamiltonian matrix is dense and diagonalization becomes a bottleneck.
To address the growing need for simulating increasingly complex chemical systems – such as gas–liquid–solid interfaces and large-scale nanostructures (e.g., from ∼100 to ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms), we introduce the latest advances in real-space KS-DFT. Unlike conventional approaches, real-space KS-DFT discretizes the KS Hamiltonian directly on finite-difference (FD) grids in real, physical space.7,8 This results in a large but highly sparse eigenproblem matrix, enabling massive parallelization with minimal communication overhead, making real-space KS-DFT particularly well-suited for the modern HPC architectures.
000 atoms), we introduce the latest advances in real-space KS-DFT. Unlike conventional approaches, real-space KS-DFT discretizes the KS Hamiltonian directly on finite-difference (FD) grids in real, physical space.7,8 This results in a large but highly sparse eigenproblem matrix, enabling massive parallelization with minimal communication overhead, making real-space KS-DFT particularly well-suited for the modern HPC architectures.
In recent years, several computational breakthroughs have demonstrated the scalability and efficiency of real-space KS-DFT. The PARSEC team9 successfully simulated a 20 nm spherical Si nanocluster containing over 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, solving the electronic structure problem in parallel across 8192 nodes.10 The ARES team performed extensive benchmarking studies, demonstrating the accuracy of real-space KS-DFT for metallic, semiconductor, and insulating systems directly by comparing the results against CASTEP,11 and also showcased a demonstration of simulating aluminum systems with 10
000 atoms, solving the electronic structure problem in parallel across 8192 nodes.10 The ARES team performed extensive benchmarking studies, demonstrating the accuracy of real-space KS-DFT for metallic, semiconductor, and insulating systems directly by comparing the results against CASTEP,11 and also showcased a demonstration of simulating aluminum systems with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms for scalability.12 The RESCU team has simulated Si and Al systems containing thousands of atoms.13 The OCTOPUS team has contributed significantly to time-dependent developments and applications.14,15 The SPARC team enabled not only static but also dynamic solutions,16,17 while the DFT-FE team developed an all-electron (AE) solution projected on a finite-element (FE) basis.18,19
000 atoms for scalability.12 The RESCU team has simulated Si and Al systems containing thousands of atoms.13 The OCTOPUS team has contributed significantly to time-dependent developments and applications.14,15 The SPARC team enabled not only static but also dynamic solutions,16,17 while the DFT-FE team developed an all-electron (AE) solution projected on a finite-element (FE) basis.18,19
Despite the these achievements, real-space KS-DFT is still in a developmental stage, with most of its applications focused on model systems.8,10,20–22 In computational chemistry and materials science, practical demonstrations of its advantages remain limited, and further benchmarks are needed for spectroscopic validation and comparison with experimental observables.23–26
In this article, we introduce the theoretical foundations and algorithmic innovations of real-space KS-DFT. We first review key theoretical background, including the KS equation, pseudopotentials (PPs), and FD discretization. Then we discuss computational acceleration techniques such as subspace filtering,27,28 Rayleigh–Ritz diagonalization,29 and space-filling curves for parallelization.30 To bridge the gap between theory and experiments, we developed a PP based method within the real-space KS-DFT framework to predict X-ray photoelectron spectroscopy (XPS) core electron binding energy (CEBE).24,26 Following this, we discuss recent applications from our group, including studies on complex nanodroplet interactions with gas-phase species and carbon capture near the direct air capture (DAC) limit. These examples illustrate cases where real-space KS-DFT provides unique insights as well as instances where conventional DFT remains sufficient, respectively. For completeness, alternative methods for simulating large systems, such as orbital-free DFT (OF-DFT) and linear scaling DFT, are also reviewed. Finally, we provide an outlook on the future of real-space KS-DFT, emphasizing its potential for exascale computing and its evolving role in computational materials science and chemistry. Current status quo, challenges and gaps, along with potential solutions, are summarized in this section, in detail. By evaluating both its strengths and limitations, we aim to provide a clear perspective on the trajectory of real-space KS-DFT as an emerging computational tool in chemistry and materials science.
2 Theory
2.1 KS equation
Real-space KS-DFT is fundamentally based on the KS equation:31,32 | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is the wavefunction or eigenfunction, Ei is the energy or eigenvalue, and
) is the wavefunction or eigenfunction, Ei is the energy or eigenvalue, and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) is the position. ρ(
is the position. ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) represents the charge density and is defined as:
) represents the charge density and is defined as: | (2) |
V[ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), ),![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ] = VH[ρ( ] = VH[ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )] + Vion( )] + Vion(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) + Vxc[ρ( ) + Vxc[ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )] )] | (3) |
∇2VH[ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )] = −4πρ( )] = −4πρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) ) | (4) |
V
ion is the ionic potential, and Vxc is the exchange–correlation potential, which can be approximated by local density approximation (LDA),32 generalized gradient approximation (GGA),33 other LDA/GGA variants,34–37 or higher rungs in the Jacob's ladder.38 After solving the KS equation self-consistently, we obtain the KS orbitals, which give the charge density, where additional properties can then be derived. The standard scaling for KS-DFT calculation is ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (Na3) for GGA, where Na is the number of atoms.1,39
(Na3) for GGA, where Na is the number of atoms.1,39
2.2 PP theory
In most practical electronic structure calculations, the PP approach is preferred over the AE methods due to its substantial computational advantages. By replacing the strong Coulomb potential of the nucleus and tightly bound core electrons with a smoother effective potential, PPs eliminate the need to resolve the rapidly oscillating core wavefunctions, which require extremely fine grids or large basis sets. Since core electrons are usually chemically inert, this approximation introduces little loss in accuracy for most materials properties. As a result, PPs significantly reduce the computational cost and improve numerical stability. Consequently, we choose to introduce real-space KS-DFT in this article with a particular focus on the FDPP approach.We show the basic idea here. For an atom, we assume one valence wavefunction can be replaced by a pseudo-wavefunction and core wavefunctions:
 | (5) |
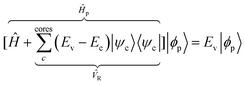 | (6) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) R is the repulsive potential energy operator. Incidentally, a PP is obtained:
R is the repulsive potential energy operator. Incidentally, a PP is obtained:| Vp|ϕp〉 = (V + VR)|ϕp〉 | (7) |
In principle, if we were able to solve eqn (6), the pseudo-wavefunction and PP can be obtained. However, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) R is a nonlocal operator which has a dependency on Ev, resulting in an energy-dependent Hamiltonian that is impractical to solve. Therefore, in practice, PPs are not solved from this theorem but are constructed from the KS equation, as discussed below.
R is a nonlocal operator which has a dependency on Ev, resulting in an energy-dependent Hamiltonian that is impractical to solve. Therefore, in practice, PPs are not solved from this theorem but are constructed from the KS equation, as discussed below.
(1) The eigenvalue for ϕp should be identical to ψv with Ep = Ev;
(2) Pseudo-wavefunctions should be nodeless, leading to ϕp > 0;
(3) The pseudo-wavefunction should be equal to the AE wavefunction beyond a chosen core radius rc, that is ϕp = ψv, when r > rc.
Based on (3), if ϕp is normalized, the corresponding PP is said to be “norm-conserving (NC)”, which encloses the same charge density within the core region:  .
.
There are PPs that do not meet the NC condition, such as ultrasoft PPs45 and PAW.46 However, in the FDPP method, NC-PPs are commonly used, especially through the Martins–Troullier form of pseudo-wavefunctions:44,47
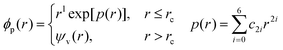 | (8) |
 | (9) |
The index i in the expression indicates the state-dependent character, which means that PPs are different for s-, p-, and d-electrons in different shells.
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) totion,p, which describes the interactions between valence electrons and pseudo-ionic cores in the system, can then be separated into a local part and a nonlocal part:48
totion,p, which describes the interactions between valence electrons and pseudo-ionic cores in the system, can then be separated into a local part and a nonlocal part:48 | (10) |
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) a is the nucleus position of it. ϕap,lm is the pseudo-wavefunction corresponding to the angular momentum number l,m for the a-th atom. Vap,l is the PP generated by eqn (9), whereas Valoc,p is the local PP part of Vap,l's. In practice, the choice of the local part can be arbitrary. For example, choosing either the 2s or 2p as the local PP is allowed for 2nd row elements. If 2p is selected as the local PP, then the 2p component must be subtracted from the 2s component when constructing the nonlocal potential. It is often convenient to use the highest l-component of interest, which simplifies the projection operators. To improve upon the accuracy, this choice can be tested by benchmarking the results from different components and assessing the overall solutions. However, two things need to be emphasized. First, all PPs outside the core region are the same, which are set to the real AE Vion. This indicates that there is no nonlocal contribution outside the core region, meaning the nonlocal potential is a short-range interaction. Second, the summation of l,m should be interpreted as the inclusion of all valence orbitals. Fig. 1 shows an example of PPs for the O atom and O1s1 atom, meaning that one 1s core–hole (CH) is created for XPS. The cancellation of the strong potential in the core region can be seen from the shape of the lines. Instead of a −Zeff/r-shape curve (Zeff is the effective core charge imposed on an electron), the PPs go to some finite values at r = 0, showing a weak potential character. The nonlocality can be recognized by the fact that, within the same shell, different subshells have different PPs (as seen by the differences between the red and black lines in Fig. 1).
a is the nucleus position of it. ϕap,lm is the pseudo-wavefunction corresponding to the angular momentum number l,m for the a-th atom. Vap,l is the PP generated by eqn (9), whereas Valoc,p is the local PP part of Vap,l's. In practice, the choice of the local part can be arbitrary. For example, choosing either the 2s or 2p as the local PP is allowed for 2nd row elements. If 2p is selected as the local PP, then the 2p component must be subtracted from the 2s component when constructing the nonlocal potential. It is often convenient to use the highest l-component of interest, which simplifies the projection operators. To improve upon the accuracy, this choice can be tested by benchmarking the results from different components and assessing the overall solutions. However, two things need to be emphasized. First, all PPs outside the core region are the same, which are set to the real AE Vion. This indicates that there is no nonlocal contribution outside the core region, meaning the nonlocal potential is a short-range interaction. Second, the summation of l,m should be interpreted as the inclusion of all valence orbitals. Fig. 1 shows an example of PPs for the O atom and O1s1 atom, meaning that one 1s core–hole (CH) is created for XPS. The cancellation of the strong potential in the core region can be seen from the shape of the lines. Instead of a −Zeff/r-shape curve (Zeff is the effective core charge imposed on an electron), the PPs go to some finite values at r = 0, showing a weak potential character. The nonlocality can be recognized by the fact that, within the same shell, different subshells have different PPs (as seen by the differences between the red and black lines in Fig. 1).
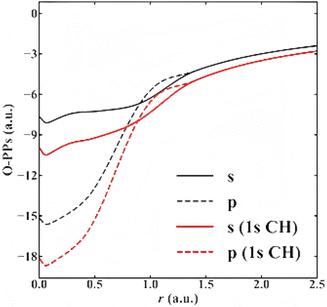 | ||
| Fig. 1 An illustration of PPs for s and p orbitals for O atom and O1s1 atom. Red lines are PPs for the first shell, and black lines are PPs for the second shell. Figure is reproduced with permission from ref. 24 under a Creative Commons License CC BY 4.0. | ||
2.3 FD method
The FD method lies at the heart of the real-space DFT framework. Instead of relying on the atomic or plane-wave basis set, real-space KS-DFT represents the Hamiltonian matrix in terms of grids in real space. We can write the 3D Laplacian, which is the kinetic part of the Hamiltonian, in terms of wave function values at these FD grids:7,8 | (11) |
| Order | C 0 | C ±1 | C ±2 | C ±3 | C ±4 | C ±5 |
|---|---|---|---|---|---|---|
| N = 1 | −2 | 1 | ||||
| N = 2 | −5/2 | 4/3 | −1/12 | |||
| N = 3 | −49/18 | 3/2 | −3/20 | 1/90 | ||
| N = 4 | −205/72 | 8/5 | −1/5 | 8/315 | −1/560 | |
| N = 5 | −5269/1800 | 5/3 | −5/21 | 5/126 | −5/1008 | 1/3150 |
For isolated or non-periodic cases, we need to specify a cutoff radius Rcut that contains the entire system and is large enough to capture the accurate electron density. The wavefunction values are forced to be zero outside the domain defined by Rcut. This is called Dirichlet boundary condition (DBC). A typical geometry for a FD domian with DBC is illustrated in Fig. 2.
 | ||
| Fig. 2 An example for the real-space grids representation, where Rcut is shown by the blue sphere. The wave function is set to zero outside the sphere. Figure is reproduced with permission from ref. 24 under a Creative Commons License CC BY 4.0. | ||
With these FD grids as a “basis set”, we can now analyze the sparsity of the discretized Hamiltonian matrix. For the kinetic energy component, it is a near-diagonal matrix, and the width of the diagonal nonzero lines will depend on the order of expansion. For the potential energy component, the VH and Vxc matrices are strictly diagonal because of the locality. As for the Vion part, the local term is diagonal, and the nonlocal terms will only be nonzero around the core region for each atom due to the short-range character. Therefore, the relatively small width (usually with an expansion order N = 12–15) of nonzero diagonal elements in the kinetic matrix compared to the high dimension of the total matrix, the locality of VH, Vxc, Vloc,p, and the short-range character of the nonlocal ionic PP lead to a sparse Hamiltonian matrix. An example of the Hamiltonian sparsity analysis for CH4 is illustrated in Fig. 3. Here, we set N = 8, and h = 0.4 a.u. as an example. The darker near-diagonal elements correspond to the Laplacian, and the light off-diagonal elements come from the nonlocal ionic PP contribution. The cutoff is set to 10−7 a.u. One can anticipate that lower thresholds will give even sparser matrix form.
2.4 Algorithmic considerations
Suppose we have the following set of grids-based wavefunctions:
 | (12) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) k) is the wavefunction value for the j-th eigenvalue at the grid point rk, and N is the number of grids in the domain. We can then construct a projection operator using a Hamiltonian form of polynomials and apply it to one column of wavefunctions:
k) is the wavefunction value for the j-th eigenvalue at the grid point rk, and N is the number of grids in the domain. We can then construct a projection operator using a Hamiltonian form of polynomials and apply it to one column of wavefunctions: | (13) |
If the factor ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (El) is close to zero for eigenvalues above a specific state and stays large for the remaining ones, we then “filter out” the components that have higher energies and only keep the states we are interested in. An ideal design for such a polynomial is shown in Fig. 4.
(El) is close to zero for eigenvalues above a specific state and stays large for the remaining ones, we then “filter out” the components that have higher energies and only keep the states we are interested in. An ideal design for such a polynomial is shown in Fig. 4.
 | ||
| Fig. 4 Illustration of the ideal polynomial that enhances the wanted spectrum region and suppresses the unwanted spectrum region. | ||
A very common and popular choice that satisfies the requirement mentioned above is called the Chebyshev polynomials:9,27,28
 | (14) |
The Chebyshev polynomials stay close to zero within [−1,1] while having large values outside [−1,1], and these polynomials are easy to expand to higher orders by the recursion relation.
The next step is to map the unwanted states in the energy spectrum to the range [−1,1]. Suppose that the full spectrum of the Hamiltonian H, denoted as σ(H), spans within [a0,b], and we only want the states in the range [a0,a](a0 < a < b). So, we need to map [a,b] to [−1,1] by:
 | (15) |
In practice, the lower bound a is obtained from a previous iteration, and the upper bound b is estimated using 4 or 5 Lancozos steps.52
 | (16) |
Gram-Schmit procedure53 is common for orthogonalization, but Cholesky QR54 can be a more efficient alternative.
Suppose that the original full space wavefunction Ψ and the projected subspace wavefunction Φ are linked by a transformation matrix Q. Then the KS equations are satisfied as such:
| HΨ = EΨ ⇔ H(ΦQ) = E(ΦQ) = (ΦQ)E | (17) |
| (Φ†HΦ)Q = (Φ†Φ)QE = QE | (18) |
We note Ĥ = Φ†HΦ as the projected Hamiltonian. After solving this projected eigenvalue problem, we can get the transformation matrix Q to obtain the original full space wavefunction Ψ:
| Ĥ = Φ†HΦ → ĤQ = QE → Ψ = ΦQ | (19) |
SFCs are mathematical constructs that map multi-dimensional space onto a one-dimensional path while preserving locality and self-similarity.60,61 Traditional Cartesian partitioning often leads to poor load balancing and excessive inter-processor communication. SFC-based partitioning solves this by reordering grid points into a structured sequence, improving memory access, and reducing data transfer costs.62,63 Among various SFCs, the Hilbert curve stands out due to its superior locality preservation.60 The locality preservation means that grids that are spatially close will remain adjacent along the SFC. This minimizes communication between processors, improving efficiency. Additionally, Hilbert SFCs coupled with blockwise operations enhance vector processing capabilities by grouping multiple grid points, and further optimizing computational performance.64,65Fig. 5 illustrates the two-dimensional versions of the Hilbert SFCs that convert all grids into one dimension.
 | ||
| Fig. 5 Examples of Hilbert SFCs that map the two-dimensional grids into a one-dimensional curve and preserve the locality and self-similarity. | ||
With the help of Hilbert SFCs, the computations are remarkably accelerated. Compared to the normal Cartesian partition, blockwise Hilbert SFCs achieved a 6-time speedup and the scalability went up to 512 processors, whereas traditional methods struggle beyond 100 processors.30 These improvements enabled PARSEC's simulation of silicon nanocrystals with over 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, while accurately capturing Van Hove singularities in the density of states.30 These results demonstrate the importance of Hilbert SFCs in large-scale real-space electronic structure calculations and suggest their potential application in other computational fields requiring efficient grid partitioning.
000 atoms, while accurately capturing Van Hove singularities in the density of states.30 These results demonstrate the importance of Hilbert SFCs in large-scale real-space electronic structure calculations and suggest their potential application in other computational fields requiring efficient grid partitioning.
2.5 Predicting experimental XPS CEBE through PPs development
Within the PP framework, our group developed a method to predict the XPS CEBE,24 which connects the real-space FDPP method with real observables in experiments.XPS CEBE (Eb) is defined as:
| Eb = EN−1[nF] − EN[nI] | (20) |
 | (21) |
| Core | Element | AE | AE | AE | PP | PP |
|---|---|---|---|---|---|---|
| PBE | SCAN | B3LYP | PBE | PBE(B3LYP) | ||
| 1s | B | 0.27 | 0.06 | 0.23 | 0.11 | |
| C | 0.38 | 0.12 | 0.20 | 0.18 | ||
| N | 0.14 | 0.12 | 0.15 | 0.14 | ||
| O | 0.11 | 0.10 | 0.11 | 0.12 | ||
| S | 0.65 | 0.22 | 0.70 | 0.20 | ||
| P | 0.30 | 0.09 | 0.32 | 0.19 | ||
| 2s | S | 0.38 | 0.26 | 0.40 | 0.23 | |
| P | 0.24 | 0.49 | 0.22 | 0.65 | ||
| 2p3/2 | S | 0.32 | 0.16 | 0.33 | 0.14 | |
| P | 0.25 | 0.13 | 0.31 | 0.15 | ||
In addition, the results from two different boundary conditions, the periodic boundary condition (PBC) and DBC, are compared. To converge the energy of the charged system, PBC requires a much larger supercell size than DBC due to its unavoidable inclusion of strong electrostatic interactions between supercells.24 However, if the electron holes are not delocalized,78 one can use the Makov–Payne equation79 to correct the core–hole interactions75 by setting a sufficiently large supercell.26 To test the applicability of the real-space KS-DFT PP method for large-scale systems, the O-1s CEBE shifts in protonated water clusters [H3O+⋯(H2O)n, n ≤ 20],24 and the Si-2p CEBE shifts of HZSM5 as well as its deprotonated counterparts26 with respect to ZSM580–82 were also investigated.
3 Applications
3.1 Characterizing air–water interactions in nanodroplets with real-space KS-DFT
Understanding ion behavior at the air–water interfaces is crucial for diverse chemical and environmental processes, with potential impacts ranging from atmospheric aerosol chemistry,83–85 uptake of gases at the ocean surface,86 and myriad biological processes. Here, we showcase our work of CO2 dissolution in the NaCl nanodroplets (see Fig. 6). Insights gained from this study can be applied to ocean acidifcation and mammalian respiration physiology. Classical electrostatic theory87 predicts that doubly charged carbonate ions (CO32−) should have much higher solvation energies than singly charged bicarbonate ions (HCO3−). As a result, carbonate ions are expected to reside predominantly in the bulk, where they can be fully solvated, while bicarbonate ions, with their lower charge and solvation energy, are more likely to populate the interface. However, recent experimental work by Devlin et al.88 employing resonantly enhanced deep-UV second-harmonic generation (DUV-SHG) spectroscopy revealed counterintuitive behaviors at these interfaces, such as the enhanced concentration of carbonate anions over bicarbonate anions at the air–water interface, contradicting the classical electrostatic expectations. This unexpected surface affinity demands additional characterization validation and mechanistic insights beyond conventional atomistic models. | ||
| Fig. 6 Schematic of the experimental design for probing a carbonate cluster residing near the liquid water surface. Figure is reproduced with permission from ref. 88, Copyright 2023 American Chemical Society and licensed under a Creative Commons License CC BY 4.0, respectively. | ||
Simulating such complex interfaces poses significant challenges for traditional DFT methods due to the sheer number of atoms (on the order of thousands) required in the simulation box to capture local variances and long-range phenomena. Real-space KS-DFT addresses these challenges by providing a framework that naturally handles nonperiodicity, disorder, and efficient parallelization of large-scale simulations, making it uniquely suited for exploring heterogeneous environments like nanodroplets. Furthermore, the recent development of surface-sensitive XPS prediction capabilities within the real-space KS-DFT framework24,26 offers a new avenue for directly linking computational results to experimental observables.
Accelerated molecular dynamics (MD) simulations were initially performed by Jamnuch et al.,88 which were used to generate snapshots for the electronic structure calculations. Each set of simulations had representative structures of the targeted carbon containing chemical species at the air–water interface and in the bulk. Then, we calculated the C 1s CEBE shifts for carbonate and bicarbonate at the air–water interface using real-space KS-DFT code ARES. Due to the enormous computational cost associated, a novel PBE(B3LYP) one-shot strategy was developed in ARES to further accelerate these calculations while maintaining a desired accuracy that is comparable to AE-B3LYP.24 This entails non-SCF calculations at the B3LYP level based on the converged PBE charge density. As a result, all calculations reported were performed at this PBE(B3LYP) level. As shown in Fig. 7(a), our calculations reveal that the XPS spectra were invariant to the displacement of the anion relative to the air–water interface as well as to the coordination number of the carbonate species. In Fig. 7(b), the surface-sensitive AP-XPS spectra measured by Lam et al.89 are reproduced. The relative shift between the experimental carbonate/bicarbonate spectral signatures agrees well with the shift in the calculated binding energies, with a difference of only 0.1 eV, indicating indeed that the spectral fitting and relative concentrations reported by Lam et al.89 are of the distinct carbonate/bicarbonate peaks and not some convolution of the two due to spectral shifts. By tuning the incident photon energy, the experiments can explore different attenuation lengths of the emitted photoelectron with a depth profiling as shallow as ∼2 nm, therefore gaining interfacial concentration information for the different ions presented in the system. Finally, these calculations support the hypothesis that strong ion pairing of CO32− with Na+ counterions leads to the formation of near neutral agglomerates, which are more surface affinity than their singly charged bicarbonate counterparts.
 | ||
| Fig. 7 (a) Simulated XPS CEBEs for C(1s) excitation of carbonate and bicarbonate at the air–water interface. Individual data points indicate the calculated CEBE and the associated coordination number with the anion. Calculated binding energies are “energy-aligned” to the experimental carbonate peak at 289.1 eV. (b) C(1s) XPS binding energies with an incident photon energy of 490 eV from 0.5 M solutions of NaHCO3 and Na2CO3 and their CEBE shift estimated from the real-space PP methods. Reproduced with permission from ref. 88, Copyright 2023 American Chemical Society and licensed under a Creative Commons License CC BY 4.0, respectively. | ||
3.2 Studying carbon capture near the DAC limit with real-space KS-DFT
The rising concentration of atmospheric CO2 has intensified the search for effective carbon capture strategies,90–92 with DAC emerging as an intriguing avenue due to its potential for negative emissions. However, capturing CO2 directly from air presents unique challenges, stemming from its low concentration (∼400 ppm) and the weak adsorption characteristics of CO2, a linear molecule with high kinetic stability. Consequently, DAC systems require adsorbents capable of both effective CO2 capture under these dilute conditions and efficient release during regeneration to minimize energy costs.93Our vision, as shown in Fig. 8, is to couple carbon-based solid sorbents with a steam-assisted temperature vacuum swing desorption (TVSD) process for energy- and cost-effective carbon capture and release. Activated carbon (AC)-based sorbents, derived from abundant and economical resources like wood and biochar, offer a promising pathway for scalable DAC. These materials can be chemically and structurally engineered to preferentially adsorb CO2 over other atmospheric gases like N2 and O2, while high-temperature steam aids desorption by driving CO2 into a collection reservoir. Integrating these materials into a dynamic energy supply has the potential to further reduce the overall cost of carbon capture. To identify optimal AC-based adsorbents for DAC applications, Glenna et al.94 proposed a hierarchical selection criterion integrating experimental insights and computational techniques. The primary criterion focuses on the CO2 adsorption energy, Eads, which determines the balance between strong binding for effective capture and weak binding for energy-efficient desorption. Eads is defined as:
| Eads = Egrapheneder+CO2 − (Egrapheneder + ECO2) | (22) |
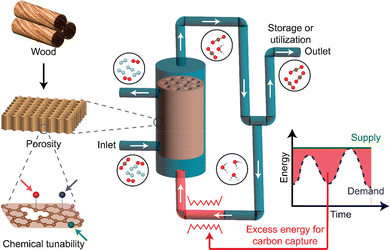 | ||
| Fig. 8 Schematic showing the steam-assisted temperature vacuum swing desorption process with wood-derived AC as the CO2 adsorbent. Graphene-derived materials are suitable templates for evaluating AC-based materials. Integrating with a dynamic energy supply results in energy- and cost-effective solutions for carbon capture. Figure is reproduced with permission from ref. 94 under a Creative Commons License CC BY 4.0. | ||
A critical question that arose from this framework was whether Eads changes when system size increases to reflect the near-zero surface coverage relevant to DAC conditions. Traditional DFT methods, constrained by scaling limitations, cannot easily probe these effects, making it difficult to assess adsorption behavior at ultra-low coverages. Real-space KS-DFT, however, addresses this gap by enabling simulations at the scale required to explore such regimes, leveraging favorable parallelization.
To study coverage effects, the Langmuir isotherm model was applied to predict CO2 coverage on graphene:
 | (23) |
Using ARES, real-space KS-DFT calculations were performed to predict CO2 adsorption on PG sheets containing 36, 252, 780, and 1152 carbon atoms (Fig. 9). Importantly, the result for the 36-carbon atom system was validated against an exemplary Quantum Espresso calculation at the same level of theory, confirming the accuracy of the real-space KS-DFT approach. Results showed that Eads converges rapidly even with relatively small simulation boxes, as shown in Table 3. Importantly, the adsorption energy remained consistent across different system sizes, indicating that enthalpy alone does not significantly affect coverage. As such, conventional DFT methods are likely sufficient to accurately capture thermodynamic properties like Eads for AC-based DAC materials.
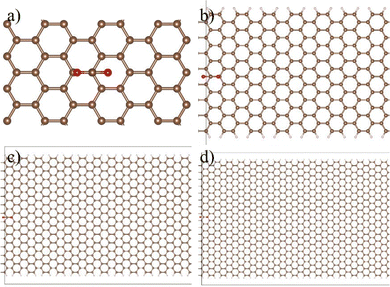 | ||
| Fig. 9 Single point configuration of CO2 on PG in 36 (a), 252 (b), 780 (c), and 1152 (d) C atom sheets using ARES. Figure is reproduced with permission from ref. 94 under a Creative Commons License CC BY 4.0. | ||
| CO2 concentration (ppm) | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3520 | 1135 | 768 |
| # C atoms/CO2 molecule | 36 | 252 | 780 | 1152 |
| PG (ARES) | −0.201 | −0.194 | −0.196 | −0.192 |
4 Alternative methods for large-scale simulations
In addition to the real-space DFT techniques, recent years witnessed exciting booming in other method developments for large-scale simulations.Orbital-free DFT (OF-DFT) bypasses the need to compute Kohn–Sham orbitals and instead approximates the total energy directly as a functional of the electron density. This enables formally linear scaling with system size, making OF-DFT attractive for large-scale simulations.96–101 However, a key limitation of OF-DFT lies in the construction of accurate orbital-free kinetic energy functionals (KEFs).96,102 Additionally, by design, OF-DFT does not yield wavefunctions, and as such, it cannot be directly used to compute spectroscopic properties. Machine learning (ML) approach103 can be useful, but usually with a total energy focus and at high cost in terms of physics and explainability. Therefore, while OF-DFT and ML approaches represent powerful additions to the computational toolbox for large-scale materials simulations, they often complement rather than replace the capabilities of real-space KS-DFT, especially in scenarios where electronic structure solution and spectroscopic accuracy are critical, such as in the example of nanodroplet. In this case, the absence of explicit wavefunctions in OF-DFT makes it unsuitable for spectroscopic simulations such as XPS, where access to orbital information is essential for accurately predicting CEBE. By contrast, real-space KS-DFT provides direct access to the electronic structure, enabling reliable and accurate spectroscopic predictions in such complex, inhomogeneous environments. Moreover, for systems like graphene with delocalized character, the construction of accurate KEFs becomes particularly problematic, while real-space DFT overcomes this limitation.
Likewise, other linear-scaling DFT frameworks have been developed to reduce the computational complexity of electronic structure simulations by avoiding explicit diagonalization of the Kohn–Sham Hamiltonian. These methods rely on the locality of the electronic density matrix and typically reformulate DFT in terms of localized orbitals or sparse density matrices by truncation, enabling formal linear scaling with system size. Examples include ONETEP, which uses variationally optimized non-orthogonal generalized Wannier functions (NGWFs);104,105 CONQUEST, which employs localized support functions with density matrix minimization;106,107 and BigDFT, which leverages wavelet bases to capture real-space locality efficiently.108,109 While these methods are powerful for modeling large insulating and semiconducting systems, it remains challenging to construct a single and generalizable scheme that yields accurate and transferable descriptions of metals, molecules, and heterogeneous systems. In particular, linear-scaling DFT techniques often require strict localization of orbitals or density matrices, which breaks down for delocalized states or systems with long-range interactions. As such, while linear-scaling DFT methods complement conventional and real-space KS-DFT in certain regimes, they do not fully replace them, particularly in charged, metallic, or highly delocalized systems, like the absorption of CO2 on graphene. For graphene, the delocalized π-electron structure poses a significant challenge to linear-scaling DFT approaches, which depend on strict localization of orbitals or density matrices. In contrast, real-space KS-DFT handles both localized adsorption interactions and extended delocalized states without imposing localization constraints, making it better suited for such systems. Likewise, the nanodroplet involves long-range ion–ion interactions, which violate the locality assumptions required for density matrix truncation or localized orbitals, whereas real-space KS-DFT can capture both short- and long-range interactions without enforcing localization.
5 Outlook
As energy applications grow increasingly complex, the need for computational tools capable of accurately simulating large, disordered systems with unbalanced charge is becoming more evident. Real-space KS-DFT has shown promise in addressing these challenges, as demonstrated by its application to the air–water interface in nanodroplets and carbon capture near the DAC limit. In both cases, real-space KS-DFT enabled simulations of large, non-periodic systems and captured subtle interfacial effects that conventional DFT methods and other linear-scaling techniques could yet resolve. These examples highlight the method's ability to provide valuable insights into complex chemical environments at scales relevant to practical applications. As research continues to tackle more intricate problems in energy storage, conversion, and environmental remediation, real-space KS-DFT is poised to become an increasingly important tool for computational chemistry and materials science.From a computational perspective, the transition into the exascale era presents new opportunities for leveraging HPC infrastructure. For example, Oak Ridge National Laboratory's Frontier supercomputer110 – the first to break the exascale barrier – performs over a quintillion calculations per second, enabling simulations at unprecedented scales. Real-space KS-DFT's inherently parallelizable structure aligns well with large-scale HPC environments, making it particularly suited for heterogeneous CPU–GPU architectures. As computational power grows, improving the efficiency of distributed algorithms – particularly for operations and memory management – will be crucial to realizing the full potential of this method. The increasing complexity of modern simulations calls for the continued adoption and development of real-space KS-DFT to address scientific challenges that demand large-scale modeling.
Recently, the real-space DFT community has made notable progress, and various codes now support a broad range of applications. For instance, OCTOPUS enables real-time and linear-response time-dependent DFT (TDDFT) calculations,111 making it well suited for computing optical absorption spectra, dielectric functions, and photoelectron spectra.112 DFT-FE and SPARC now support CPU–GPU heterogeneous architectures,19,113 further advancing real-space DFT toward the exascale era. PARSEC has also implemented more efficient subspace filtering techniques and eigenvalue solvers, enhancing its computational performance.114–116 In addition, PARSEC provides real-space implementations for systems with general or partial periodicity by directly incorporating Bloch's theorem into the Kohn–Sham equations.117 Combined with appropriate k-point sampling techniques, this enables calculations of band structures and densities of states (DOS).
Despite its strengths, real-space DFT also faces key challenges that currently limit its broader adoption. One major issue is that, compared to traditional basis-based methods, it is much more memory-intensive, especially when using fine grids. A powerful strategy to address this is the use of matrix-free methods, where the Hamiltonian is never stored explicitly but applied on-the-fly during matrix-vector multiplications. The Laplacian-vector products can be computed directly using FD stencils or FE operators.118 This drastically reduces memory usage and enables highly scalable matrix-vector operations. Similar strategies can be used to handle the nonlocal part of the Hamiltonian as well. Moreover, adaptive mesh refinement (AMR)50,51 can be employed to concentrate grid resolution near nuclei or chemical interfaces while using coarser grids elsewhere, reducing the number of required grid points for systems with high spatial heterogeneity. Another major issue is the computational cost of diagonalizing the sparse Hamiltonians. Even though advanced techniques such as Chebyshev subspace filtering and Rayleigh–Ritz projection are under active development to reduce this bottleneck by focusing only on the eigenspace near occupied levels, further algorithmic implementations for sparse-matrix eigensolvers119,120 or alternative strategies towards linear-scaling are worth exploring. One possible idea is to gain inspiration from density matrix purification121,122 that avoids the direct diagonalization of the Hamiltonian. Additionally, the Hartree potential evaluation step is often time-consuming for large systems. Therefore, efficient Poisson solvers123–125 for both periodic and non-periodic systems are critical for accelerating the simulations.
In terms of status quo, certain capabilities remain more mature in conventional plane-wave and localized basis set codes. For example, hybrid functional calculations involving exact exchange are not yet fully implemented in real-space DFT frameworks due to the significant computational cost associated with the nonlocal nature of Fock exchange. However, strategies such as projection schemes have been proposed,126,127 and the ARES team has implemented a one-shot B3LYP (double hybrid functional) strategy based on the wavefunctions from PBE calculations.24,26 The SPARC team also has made notable progress in this area recently.128 Features such as phonon calculations, density functional perturbation theory (DFPT) or double hybrid, and response properties like Raman and dielectric tensors are also less commonly implemented in real-space frameworks compared to well-established packages like VASP or Quantum Espresso. Furthermore, real-space codes often rely on norm-conserving PPs and may lack support for PAW, ultrasoft PPs or relativistic effects, which are important for transition metals and heavy elements. Finally, compared to mainstream DFT codes, real-space codes currently offer limited support for high-throughput workflows, automated job management, and integration with materials databases. A more mature ecosystem will be essential for accelerating discovery and enabling complex, multi-step simulations, particularly in large-scale screening and materials design efforts. Bridging this gap will be important for broadening the adoption of real-space methods and ensuring their accessibility to a wider research community.
Looking ahead, further methodological developments are needed to keep pace with the hardware advancements.129,130 Establishing new protocols for modularization and interoperability will help real-space KS-DFT integrate more seamlessly into broader computational frameworks. Additionally, advancements in exchange–correlation functionals,38 post-DFT methods,19,107,109 excited-state techniques,131,132 and fast molecular dynamics133,134 will remain essential to enhancing predictive accuracy and expanding the method's applicability. Importantly, as real-space KS-DFT matures, identifying unique applications where its massive parallelization capabilities are truly warranted will help ensure its continued impact in both method development and scientific discovery. The path forward lies not only in scaling computations but also in finding the right questions to answer with this powerful approach.
Conclusions
Real space KS-DFT has emerged as a compelling computational framework capable of meeting the increasing demands of modern electronic structure problems. This article reviewed the foundational theories, algorithmic developments, and recent applications that illustrate the method's potential for tackling large, complex, and disordered systems. Through a FDPP approach, real-space KS-DFT enables scalable, accurate simulations of complicated systems while naturally integrating with HPC architectures. We demonstrated the predictive power of real-space KS-DFT in chemically and environmentally relevant systems. From capturing the nuanced behavior of carbonates at air–water interfaces to modeling CO2 adsorption in carbon-based sorbents under DAC conditions, the method proves effective in bridging quantum-scale phenomena with experimental observables. Notably, innovations such as real-space XPS predictions and efficient algorithmic strategies (e.g., subspace filtering and space-filling curve partitioning) further enhance the method's capability and performance. Looking forward, as computational chemistry continues to scale into the exascale era, real-space KS-DFT is poised to play an important role through its parallelization capability. Continued progress in methodological development, especially in exchange–correlation approximations, excited-state modeling, and real-time dynamics, will be essential to fully realize its impact. Ultimately, real-space KS-DFT represents not just a technical advancement, but a versatile toolset for exploring the frontiers of chemical and materials discovery.Author contributions
J. Q. acquired funding for, and led the project. Z. Z. and J. Q. conceptualized the project and wrote the first manuscript. All authors contributed to reviewing and editing the manuscript under the supervision of J. Q.Code availability
The ARES code cited in the paper is currently proprietary. The first real-space code PARSEC from James R. Chelikowsky's group is available on Github: https://github.com/PARSEC-real-space-code/PARSEC. The Matlab version of PARSEC is also available on Github: https://github.com/PARSEC-real-space-code/Matlab_Real_Space.Data availability
The data mentioned in this article can be found in corresponding references. There are no extra data associated with this article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Early Career Research Award Program from the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division, through Contract No. DE-AC02-05CH11231.References
- N. Marzari, A. Ferretti and C. Wolverton, Nat. Mater., 2021, 20, 736–749 CrossRef CAS PubMed.
- E. Epifanovsky, A. T. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons and A. L. Dempwolff, et al. , J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsujiet al.Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. R. Chelikowsky, N. Troullier and Y. Saad, Phys. Rev. Lett., 1994, 72, 1240 CrossRef CAS PubMed.
- J. R. Chelikowsky, N. Troullier, K. Wu and Y. Saad, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 11355 CrossRef CAS PubMed.
- L. Kronik, A. Makmal, M. L. Tiago, M. Alemany, M. Jain, X. Huang, Y. Saad and J. R. Chelikowsky, Phys. Status Solidi B, 2006, 243, 1063–1079 CrossRef CAS.
- M. Dogan, K.-H. Liou and J. R. Chelikowsky, J. Chem. Phys., 2023, 158, 244114 CrossRef CAS PubMed.
- M. Segall, P. J. Lindan, M. A. Probert, C. J. Pickard, P. J. Hasnip, S. Clark and M. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717 CrossRef CAS.
- Q. Xu, S. Wang, L. Xue, X. Shao, P. Gao, J. Lv, Y. Wang and Y. Ma, J. Phys.: Condens. Matter, 2019, 31, 455901 CrossRef CAS PubMed.
- V. Michaud-Rioux, L. Zhang and H. Guo, J. Comput. Phys., 2016, 307, 593–613 CrossRef CAS.
- M. A. Marques, A. Castro, G. F. Bertsch and A. Rubio, Comput. Phys. Commun., 2003, 151, 60–78 CrossRef CAS.
- X. Andrade, D. Strubbe, U. De Giovannini, A. H. Larsen, M. J. Oliveira, J. Alberdi-Rodriguez, A. Varas, I. Theophilou, N. Helbig and M. J. Verstraete, et al. , Phys. Chem. Chem. Phys., 2015, 17, 31371–31396 RSC.
- Q. Xu, A. Sharma, B. Comer, H. Huang, E. Chow, A. J. Medford, J. E. Pask and P. Suryanarayana, SoftwareX, 2021, 15, 100709 CrossRef.
- B. Zhang, X. Jing, Q. Xu, S. Kumar, A. Sharma, L. Erlandson, S. J. Sahoo, E. Chow, A. J. Medford and J. E. Pask, et al. , Software Impacts, 2024, 20, 100649 CrossRef.
- P. Motamarri, S. Das, S. Rudraraju, K. Ghosh, D. Davydov and V. Gavini, Comput. Phys. Commun., 2020, 246, 106853 CrossRef CAS.
- S. Das, P. Motamarri, V. Subramanian, D. M. Rogers and V. Gavini, Comput. Phys. Commun., 2022, 280, 108473 CrossRef CAS.
- M. Lopez del Puerto, M. L. Tiago, I. Vasiliev and J. R. Chelikowsky, Phys. Rev. A:At., Mol., Opt. Phys., 2005, 72, 052504 CrossRef.
- S. J. Sahoo, X. Jing, P. Suryanarayana and A. J. Medford, J. Phys. Chem. C, 2022, 126, 2121–2130 CrossRef CAS.
- S. J. Sahoo, Q. Xu, X. Lei, D. Staros, G. R. Iyer, B. Rubenstein, P. Suryanarayana and A. J. Medford, ChemPhysChem, 2024, 25, e202300688 CrossRef CAS PubMed.
- J. Qian, A. Baskin, Z. Liu, D. Prendergast and E. J. Crumlin, J. Chem. Phys., 2020, 153, 044709 CrossRef CAS PubMed.
- Q. Xu, D. Prendergast and J. Qian, J. Chem. Theory Comput., 2022, 18, 5471–5478 CrossRef CAS PubMed.
- J. Qian, E. J. Crumlin and D. Prendergast, Phys. Chem. Chem. Phys., 2022, 24, 2243–2250 RSC.
- L. Liu, Q. Xu, L. dos Anjos Cunha, H. Xin, M. Head-Gordon and J. Qian, J. Chem. Theory Comput., 2024, 20, 6134–6143 CrossRef CAS PubMed.
- Y. Zhou, Y. Saad, M. L. Tiago and J. R. Chelikowsky, J. Comput. Phys., 2006, 219, 172–184 CrossRef CAS.
- Y. Zhou, Y. Saad, M. L. Tiago and J. R. Chelikowsky, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2006, 74, 066704 CrossRef PubMed.
- J. MacDonald, Phys. Rev., 1933, 43, 830 CrossRef.
- K.-H. Liou, A. Biller, L. Kronik and J. R. Chelikowsky, J. Chem. Theory Comput., 2021, 17, 4039–4048 CrossRef CAS PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Kümmel and J. P. Perdew, Phys. Rev. B:Condens. Matter Mater. Phys., 2003, 68, 035103 CrossRef.
- V. I. Anisimov, F. Aryasetiawan and A. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767 CrossRef CAS.
- M. Cococcioni and S. De Gironcoli, Phys. Rev. B:Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- H. J. Kulik, M. Cococcioni, D. A. Scherlis and N. Marzari, Phys. Rev. Lett., 2006, 97, 103001 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- R. M. Martin, Electronic structure: basic theory and practical methods, Cambridge University Press, Cambridge, 2nd edn, 2020 Search PubMed.
- H. Hellmann, J. Chem. Phys., 1935, 3, 61 CrossRef.
- J. C. Phillips and L. Kleinman, Phys. Rev., 1959, 116, 287 CrossRef CAS.
- M. H. Cohen and V. Heine, Phys. Rev., 1961, 122, 1821 CrossRef CAS.
- D. Hamann, M. Schlüter and C. Chiang, Phys. Rev. Lett., 1979, 43, 1494 CrossRef CAS.
- N. Troullier and J. L. Martins, Phys. Rev. B:Condens. Matter Mater. Phys., 1991, 43, 1993 CrossRef CAS PubMed.
- D. Vanderbilt, Phys. Rev. B:Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- G. Kerker, J. Phys. C, 1980, 13, L189 CrossRef CAS.
- L. Kleinman and D. Bylander, Phys. Rev. Lett., 1982, 48, 1425 CrossRef CAS.
- B. Fornberg, SIAM Rev., 1998, 40, 685–691 CrossRef.
- M. J. Berger and P. Colella, J. Comput. Phys., 1989, 82, 64–84 CrossRef.
- M. J. Berger and J. Oliger, J. Comput. Phys., 1984, 53, 484–512 CrossRef.
- C. Lanczos, J. Res. Natl. Bur. Stand., 1950, 45, 255–282 CrossRef.
- W. Cheney and D. Kincaid, Aust. Math. Soc., 2009, 110, 544–550 Search PubMed.
- C. Benoit, Bull. Geod., 1924, 2, 67–77 CrossRef.
- L. N. Trefethen and D. Bau, Numerical linear algebra, SIAM, Philadelphia, 25th Anniversary edn, 2022 Search PubMed.
- H. Sagan, Space-filling curves, Springer Science & Business Media, New York, 2012 Search PubMed.
- J. K. Lawder and P. J. King, British National Conference on Databases, 2000, pp. 20–35.
- P. Xu and S. Tirthapura, ACM Trans. Database Syst., 2014, 39, 1–27 CrossRef.
- A.-J. N. Yzelman and D. Roose, IEEE Trans. Parallel Distrib. Syst., 2013, 25, 116–125 Search PubMed.
- B. Moon, H. V. Jagadish, C. Faloutsos and J. H. Saltz, IEEE Trans. Knowl. Data Eng., 2001, 13, 124–141 CrossRef.
- S. P. Sastry, E. Kultursay, S. M. Shontz and M. T. Kandemir, Eng. Comput., 2014, 30, 535–547 CrossRef.
- R. Borrell, J. C. Cajas, D. Mira, A. Taha, S. Koric, M. Vázquez and G. Houzeaux, Comput. Fluids, 2018, 173, 264–272 CrossRef.
- S. Schamberger and J.-M. Wierum, Future Gener. Comput. Syst., 2005, 21, 759–766 CrossRef.
- K. P. Lorton and D. S. Wise, ACM SIGARCH Comput. Archit. News, 2007, 35, 6–12 CrossRef.
- C. Yount, J. Tobin, A. Breuer and A. Duran, 2016 Sixth International Workshop on Domain-Specific Languages and High-Level Frameworks for High Performance Computing (WOLFHPC), 2016, pp. 30–39.
- M. Fuchs and M. Scheffler, Comput. Phys. Commun., 1999, 119, 67–98 CrossRef CAS.
- P. S. Bagus, Phys. Rev., 1965, 139, A619 CrossRef.
- J. Q. Broughton and D. L. Perry, J. Chem. Soc., Faraday Trans. 2, 1977, 73, 1320–1327 RSC.
- P. Bagus and M. Seel, Phys. Rev. B:Condens. Matter Mater. Phys., 1981, 23, 2065 CrossRef CAS.
- P. Bagus, A. Rossi and P. Avouris, Phys. Rev. B:Condens. Matter Mater. Phys., 1985, 31, 1722 CrossRef CAS PubMed.
- C. Flynn and N. Lipari, Phys. Rev. B, 1973, 7, 2215 CrossRef CAS.
- M. Segala, Y. Takahata and D. P. Chong, J. Electron Spectrosc. Relat. Phenom., 2006, 151, 9–13 CrossRef CAS.
- D. P. Chong, J. Chem. Phys., 1995, 103, 1842–1845 CrossRef CAS.
- D. P. Chong, O. V. Gritsenko and E. J. Baerends, J. Chem. Phys., 2002, 116, 1760–1772 CrossRef CAS.
- J. M. Kahk, G. S. Michelitsch, R. J. Maurer, K. Reuter and J. Lischner, J. Phys. Chem. Lett., 2021, 12, 9353–9359 CrossRef CAS PubMed.
- A. T. Gilbert, N. A. Besley and P. M. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171 CrossRef CAS PubMed.
- D. Hait and M. Head-Gordon, J. Chem. Theory Comput., 2020, 16, 1699–1710 CrossRef CAS PubMed.
- J. M. Kahk and J. Lischner, J. Chem. Theory Comput., 2023, 19, 3276–3283 CrossRef CAS PubMed.
- G. Makov and M. C. Payne, Phys. Rev. B:Condens. Matter Mater. Phys., 1995, 51, 4014 CrossRef CAS PubMed.
- M. S. Hossain, G. S. Dhillon, L. Liu, A. Sridhar, E. J. Hiennadi, J. Hong, S. R. Bare, H. Xin, T. Ericson and A. Cozzolino, et al. , Chem. Eng. J., 2023, 475, 146096 CrossRef CAS.
- V. Van Speybroeck, K. Hemelsoet, L. Joos, M. Waroquier, R. G. Bell and C. R. A. Catlow, Chem. Soc. Rev., 2015, 44, 7044–7111 RSC.
- S. Kim, M.-S. Lee, D. M. Camaioni, O. Y. Gutiérrez, V.-A. Glezakou, N. Govind, T. Huthwelker, R. Zhao, R. Rousseau and J. L. Fulton, et al. , J. Am. Chem. Soc. Au, 2023, 3, 2487–2497 CAS.
- A. M. Jubb, W. Hua and H. C. Allen, Acc. Chem. Res., 2012, 45, 110–119 CrossRef CAS PubMed.
- A. M. Prophet, K. Polley, G. J. Van Berkel, D. T. Limmer and K. R. Wilson, Chem. Sci., 2024, 15, 736–756 RSC.
- C. Weeraratna, C. Amarasinghe, W. Lu and M. Ahmed, J. Phys. Chem. Lett., 2021, 12, 5503–5511 CrossRef CAS PubMed.
- T. L. Tarbuck and G. L. Richmond, J. Am. Chem. Soc., 2006, 128, 3256–3267 CrossRef CAS PubMed.
- L. Onsager and N. N. Samaras, J. Chem. Phys., 1934, 2, 528–536 CrossRef CAS.
- S. W. Devlin, S. Jamnuch, Q. Xu, A. A. Chen, J. Qian, T. A. Pascal and R. J. Saykally, J. Am. Chem. Soc., 2023, 145, 22384–22393 CrossRef CAS PubMed.
- R. K. Lam, J. W. Smith, A. M. Rizzuto, O. Karslıoğlu, H. Bluhm and R. J. Saykally, J. Chem. Phys., 2017, 146, 094703 CrossRef.
- R. A. Kerr, Science, 2007, 316, 188–190 CrossRef CAS PubMed.
- C. B. Field and V. R. Barros, Climate change 2014–Impacts, adaptation and vulnerability: Regional aspects, Cambridge University Press, Cambridge, 2014 Search PubMed.
- A. Rafiee, K. R. Khalilpour, D. Milani and M. Panahi, J. Environ. Chem. Eng., 2018, 6, 5771–5794 CrossRef CAS.
- D. W. Keith, Science, 2009, 325, 1654–1655 CrossRef CAS PubMed.
- D. M. Glenna, A. Jana, Q. Xu, Y. Wang, Y. Meng, Y. Yang, M. Neupane, L. Wang, H. Zhao and J. Qian, et al. , J. Phys. Chem. Lett., 2023, 14, 10693–10699 CrossRef CAS PubMed.
- T. M. McDonald, J. A. Mason, X. Kong, E. D. Bloch, D. Gygi, A. Dani, V. Crocella, F. Giordanino, S. O. Odoh and W. S. Drisdell, et al. , Nature, 2015, 519, 303–308 CrossRef CAS PubMed.
- Y. A. Wang and E. A. Carter, Theoretical methods in condensed phase chemistry, 2000, vol. 5, pp. 117–184 Search PubMed.
- M. Chen, X.-W. Jiang, H. Zhuang, L.-W. Wang and E. A. Carter, J. Chem. Theory Comput., 2016, 12, 2950–2963 CrossRef CAS PubMed.
- V. V. Karasiev and S. B. Trickey, Adv. Quantum Chem., Elsevier, 2015, vol. 71, pp. 221–245 Search PubMed.
- W. C. Witt, B. G. Del Rio, J. M. Dieterich and E. A. Carter, J. Mater. Res., 2018, 33, 777–795 CrossRef CAS.
- X. Shao, K. Jiang, W. Mi, A. Genova and M. Pavanello, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2021, 11, e1482 CAS.
- V. Gavini, K. Bhattacharya and M. Ortiz, J. Mech. Phys. Solids, 2007, 55, 697–718 CrossRef CAS.
- J.-D. Chai and J. D. Weeks, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 75, 205122 CrossRef.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- C.-K. Skylaris, P. D. Haynes, A. A. Mostofi and M. C. Payne, J. Chem. Phys., 2005, 122, 084119 CrossRef PubMed.
- J. C. Prentice, J. Aarons, J. C. Womack, A. E. Allen, L. Andrinopoulos, L. Anton, R. A. Bell, A. Bhandari, G. A. Bramley and R. J. Charlton, et al. , J. Chem. Phys., 2020, 152, 174111 CrossRef CAS PubMed.
- D. Bowler, R. Choudhury, M. Gillan and T. Miyazaki, Phys. Status Solidi B, 2006, 243, 989–1000 CrossRef CAS.
- A. Nakata, J. S. Baker, S. Y. Mujahed, J. T. Poulton, S. Arapan, J. Lin, Z. Raza, S. Yadav, L. Truflandier and T. Miyazaki, et al. , J. Chem. Phys., 2020, 152, 164112 CrossRef CAS PubMed.
- S. Mohr, L. E. Ratcliff, L. Genovese, D. Caliste, P. Boulanger, S. Goedecker and T. Deutsch, Phys. Chem. Chem. Phys., 2015, 17, 31360–31370 RSC.
- L. E. Ratcliff, W. Dawson, G. Fisicaro, D. Caliste, S. Mohr, A. Degomme, B. Videau, V. Cristiglio, M. Stella and M. D’alessandro, et al. , J. Chem. Phys., 2020, 152, 194110 CrossRef CAS PubMed.
- S. Atchley, C. Zimmer, J. Lange, D. Bernholdt, V. Melesse Vergara, T. Beck, M. Brim, R. Budiardja, S. Chandrasekaran, M. Eisenbachet al. Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, 2023, pp. 1–16.
- A. Castro, H. Appel, M. Oliveira, C. A. Rozzi, X. Andrade, F. Lorenzen, M. A. Marques, E. Gross and A. Rubio, Phys. Status Solidi B, 2006, 243, 2465–2488 CrossRef CAS.
- N. Tancogne-Dejean, M. J. Oliveira, X. Andrade, H. Appel, C. H. Borca, G. Le Breton, F. Buchholz, A. Castro, S. Corni and A. A. Correa, et al. , J. Chem. Phys., 2020, 152, 124119 CrossRef CAS PubMed.
- A. Sharma, A. Metere, P. Suryanarayana, L. Erlandson, E. Chow and J. E. Pask, J. Chem. Phys., 2023, 158, 204117 CrossRef CAS PubMed.
- K.-H. Liou, C. Yang and J. R. Chelikowsky, Comput. Phys. Commun., 2020, 254, 107330 CrossRef CAS.
- Y. Zhou, J. R. Chelikowsky and Y. Saad, J. Comput. Phys., 2014, 274, 770–782 CrossRef.
- G. Schofield, J. R. Chelikowsky and Y. Saad, Comput. Phys. Commun., 2012, 183, 497–505 CrossRef CAS.
- A. Natan, A. Benjamini, D. Naveh, L. Kronik, M. L. Tiago, S. P. Beckman and J. R. Chelikowsky, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 78, 075109 CrossRef.
- W. H. Press, Numerical recipes: The art of scientific computing, Cambridge University Press, Cambridge, 3rd edn, 2007 Search PubMed.
- V. Hernandez, J. Roman, A. Tomas and V. Vidal, Universitat Politecnica De Valencia, SLEPs technical report STR-6, 2009.
- F. Rabbi, C. S. Daley, H. M. Aktulga and N. J. Wright, International Workshop on Accelerator Programming Using Directives, 2019, pp. 66–88 Search PubMed.
- A. H. Palser and D. E. Manolopoulos, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 58, 12704 CrossRef CAS.
- D. Bowler and M. Gillan, Comput. Phys. Commun., 1999, 120, 95–108 CrossRef CAS.
- L. Genovese, T. Deutsch, A. Neelov, S. Goedecker and G. Beylkin, J. Chem. Phys., 2006, 125, 074105 CrossRef PubMed.
- L. Genovese, T. Deutsch and S. Goedecker, J. Chem. Phys., 2007, 127, 054704 CrossRef PubMed.
- A. Cerioni, L. Genovese, A. Mirone and V. A. Sole, J. Chem. Phys., 2012, 137, 134108 CrossRef PubMed.
- I. Duchemin and F. Gygi, Comput. Phys. Commun., 2010, 181, 855–860 CrossRef CAS.
- N. M. Boffi, M. Jain and A. Natan, J. Chem. Theory Comput., 2016, 12, 3614–3622 CrossRef CAS PubMed.
- X. Jing, A. Sharma, J. E. Pask and P. Suryanarayana, arXiv, 2025, preprint, arXiv:2501.16572 DOI:10.48550/arXiv.2501.16572.
- V. Gavini, S. Baroni, V. Blum, D. R. Bowler, A. Buccheri, J. R. Chelikowsky, S. Das, W. Dawson, P. Delugas and M. Dogan, et al. , Modell. Simul. Mater. Sci. Eng., 2023, 31, 063301 CrossRef.
- V. Blum, R. Asahi, J. Autschbach, C. Bannwarth, G. Bihlmayer, S. Blügel, L. A. Burns, T. D. Crawford, W. Dawson and W. A. de Jong, et al. , Electron. Struct., 2024, 6, 042501 CrossRef CAS.
- A. Gulans, S. Kontur, C. Meisenbichler, D. Nabok, P. Pavone, S. Rigamonti, S. Sagmeister, U. Werner and C. Draxl, J. Phys.: Condens. Matter, 2014, 26, 363202 CrossRef PubMed.
- M. Govoni and G. Galli, J. Chem. Theory Comput., 2015, 11, 2680–2696 CrossRef CAS PubMed.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt and F. Schiffmann, et al. , J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- F. Gygi, IBM J. Res. Dev., 2008, 52, 137–144 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |







