Nanophotonics of mid-infrared plasmon-polaritons at interfaces between metals and two-dimensional crystals†
Flávio H.
Feres
 *a,
Ingrid D.
Barcelos
*a,
Ingrid D.
Barcelos
 a,
Dario A.
Bahamon
bc,
João E.
Levandoski
a,
Dario A.
Bahamon
bc,
João E.
Levandoski
 d,
Andrea
Mancini
d,
Andrea
Mancini
 e,
Thiago M.
dos Santos
e,
Thiago M.
dos Santos
 a,
Rafael A.
Mayer
a,
Rafael A.
Mayer
 af,
Davi H. S.
Camargo
g,
Carlos C. B.
Bufon
h,
Adrian
Cernescu
i,
Stefan A.
Maier
af,
Davi H. S.
Camargo
g,
Carlos C. B.
Bufon
h,
Adrian
Cernescu
i,
Stefan A.
Maier
 jk,
Raul de O.
Freitas
jk,
Raul de O.
Freitas
 a and
Francisco C. B.
Maia
a and
Francisco C. B.
Maia
 *a
*a
aBrazilian Synchrotron Light Laboratory (LNLS), Brazilian Center for Research in Energy and Materials (CNPEM), Zip Code 13083-970, Campinas, Sao Paulo, Brazil. E-mail: flavio.feres@lnls; francisco.maia@lnls.br
bMackGraphe – Graphene and Nanomaterials Research Institute, Mackenzie Presbyterian University, São Paulo – 01302-907, Brazil
cSchool of Engineering, Mackenzie Presbyterian University, São Paulo – 01302-907, Brazil
dDepartment of Materials and Bioprocesses Engineering, School of Chemical Engineering, University of Campinas, Campinas, Brazil
eChair in Hybrid Nanosystems, Nanoinstitute Munich, Ludwig-Maximilians-Universität Munich, Königinstrasse 10, 80539 Munich, Germany
fPhysics Department, Gleb Wataghin Physics Institute, University of Campinas (Unicamp), 13083-859 Campinas, Sao Paulo, Brazil
gBrazilian Laboratory of Nanotechnology (LNNano), Brazilian Center for Research in Energy and Materials (CNPEM), Zip Code 13083-970, Campinas, Sao Paulo, Brazil
hInstitute of Geosciences and Exact Sciences, São Paulo State University (UNESP), Rio Claro, Brazil
iAttocube Systems AG, 85540, Haar-Munich, Germany
jSchool of Physics and Astronomy, Monash University, Clayton, 3800, VIC, Australia
kBlackett Laboratory, Imperial College London, London, SW7 2AZ, UK
First published on 23rd April 2025
Abstract
The optical response of metal/dielectric interfaces is largely influenced by surface plasmon-polariton (SPP) modes. In the mid-infrared (IR) range, SPPs can probe the inner physicochemical properties of metal/dielectric systems, including interfaces with mid-IR polaritonic 2D crystals. Using advanced nanoscopy techniques, we characterize mid-IR SPP modes at air/gold and hexagonal boron nitride (hBN) 2D crystal/gold interfaces via synchrotron infrared nanospectroscopy (SINS) and scattering-scanning near-field optical microscopy (s-SNOM) imaging. SPPs in these systems show micrometer-sized wavelengths and propagation lengths over 20 micrometers at room temperature. In hBN/Au, both SPPs and hyperbolic phonon polaritons (HPhPs) coexist, creating SPP–HPhP wave superposition. The experimental momentum and damping of the SPP waves are determined from the s-SNOM imaging and the SINS spatio-spectral linescan. Thereby, we retrieve the experimental frequency–momentum dispersion relation, presenting excellent agreement with theory. Furthermore, we characterize an anti-crossing of the SPP dispersion near the in-plane transverse optical phonon frequency of hBN, indicating that SPP modes and phonon form a coupled system interacting in the strong coupling regime. Such an interaction of SPPs with phonons can be further explored to enhance the sensibility of mid-IR nanospectroscopy techniques.
Surface plasmon-polaritons (SPP),1,2 quasi-particles originating from the coupling of photons to collective oscillations of free charge carriers, are intrinsically two-dimensional (2D) modes confined to the interface between a material of metallic character and a dielectric one. Such ultimate 2D confinement originates from the fact that while SPPs are propagative modes in the interface plane, they are evanescent along the interface normal direction. Being genuinely photon-charge coupled modes intrinsic to the optical near-field electromagnetic zone, SPP waves possess intertwined optical and electronic properties, leading to their exploitation from the ultraviolet-visible to near-infrared (IR) ranges in waveguiding,3 plasmonic circuits,3,4 sensing,5 lasing,6–8 light harvesting5 and for quantum information processing.9 In the mid-IR, SPPs have been studied in metallic structures engineered to achieve high confinement of electromagnetic modes as IR nanofocusing in tapered transmission line waveguides.10–12 Moreover, mid-IR SPPs are found as stationary and localized modes in antennas10,13–15 and resonators16,17 of semiconducting18 and metallic19 micro- and nanostructures. Furthermore, mid-IR SPPs are theoretically predicted to allow for accessing and retrieving invaluable information from physicochemical properties of general dielectric/metal (D/M) interfaces associated with molecular vibrations, electronic transitions, and room temperature thermodynamical reactions.17 In the pursuit of such great conceptual potential, we present here a thorough characterization of mid-IR SPP waves at D/M interfaces, using scattering-type scanning near-field optical microscopy (s-SNOM)20 and synchrotron infrared nanospectroscopy (SINS).21 Our study not only reveals fundamental nanophotonic properties of SPPs but also demonstrates that these waves can deeply probe matter through strong coupling (SC) with phonons. SC phenomena in nanophotonics have garnered significant attention due to their potential to reach and manipulate new hybrid quantum states22 as recently shown from SC interaction between polaritons of van der Waals (vdW) crystals and vibrational modes of organic molecules.23 Additionally, new polaritonic modes arising from SC between hyperbolic phonon polaritons (HPhPs) in hetero-bicrystals have been observed, enabling exquisite optical phenomena such as negative refraction and negative group velocity.24,25 Interactions between SPPs and phonons have also been documented in graphene hexagonal boron nitride (hBN)26,27 and carbon nanotubes–hBN28 heterostructures. Here we aim to expand the understanding of SC phenomena in 2D systems by reporting, for the first time, the SC regime between long-range SPPs on gold (Au) and optical phonons in hyperbolic crystals.
In this work a full characterization of SPPs at mid-IR frequencies is achieved by investigating the D/M interfaces: (i) Au/SiO2, a 90 nm thick film of Au sputtered onto a 2 μm-thick layer of SiO2 and (ii) hBN/Au, a hBN 2D crystal deposited onto Au surface (see the Experimental Methods section for details on techniques and sample construction). The s-SNOM images and SINS spectral linescans provide a complete data set permitting us to quantify the complex momentum qSPP, where qSPP = qSPP + iγSPP, (mqSPP is the propagative momentum part and γSPP is the damping) for each excitation frequency (ω). This analysis produces the experimental frequency–momentum dispersion relation, ω−qSPP, governing the SPP waves. Moreover, s-SNOM and SINS nanoimagings also reveal the superposition of SPP and HPhP waves of hBN. The phenomenon is observed for different ω values in the hBN upper Reststhralen (RS) band, which is defined as that in between the transversal (TO), ωTO = 1365 cm−1, and the longitudinal optical (LO) phonons, ωLO = 1610 cm−1.29–32 The wave superposition results from the interference between high momenta HPhPs (qHPhP ∼ 105 cm−1)14,29–32 and low momenta SPPs (qSPP ∼ 104 cm−1). We remark that HPhP modes in metallic substrates have been referred to as hyperbolic image polaritons (HIP)33,34 formed due to the coupling of the mode in the polaritonic medium with its image in the metal. As observed, the HIPs present larger confinement (higher momentum) than the analogues formed when the polaritonic medium lies on dielectric substrates.30
To understand these polariton modes, we compute the theoretical dispersion by solving the Maxwell equations at the D/M interface.35 The calculations yield a parameter-free ω−qSPP dispersion in good quantitative agreement with the experimental observations. Moreover, both theoretical and experimental dispersions feature an anti-crossing (AC) effect near the hBN ωTO. Our analysis demonstrates that the AC arises from the interaction of SPP waves with the hBN phonon in the SC regime as evaluated from a coupled oscillator model.23,28
The s-SNOM and SINS experimental schemes and the hBN (60 nm)/Au (90 nm)/SiO2 (2 μm) sample architecture are sketched in Fig. 1a (see the Experimental Methods for details). The scheme also features the SPP–HPhP wave superposition representing the main polariton modes herein discussed. Fig. 1b presents the AFM topography of the sample that, concisely, was constructed by transferring the hBN crystal onto the Au film which was deposited by an electron beam onto the SiO2/Si surface. Part of the hBN flake is suspended over a 2.5 μm-width groove made by lithography in the Au film. An Au disk-like antenna resides atop the hBN crystal. In Fig. 1c and d, we present s-SNOM images of the third harmonic amplitude (S3) signal using a quantum cascade laser (QCL) as the excitation source. These measurements were performed by tuning the QCL at ω = 1470 cm−1, which is inside the upper RS band of hBN, and at ω = 1200 cm−1, which is outside any hBN RS band. They reveal distinguishable optical patterns on hBN/Au/SiO2 and Au/SiO2, stemming from HPhP and SPP waves of different wavelengths, which are discussed in detail in Fig. 2.
 | ||
| Fig. 1 s-SNOM and SINS schematics and interferometric measurements of polariton modes. (a) s-SNOM and SINS experimental schemes probing a SPP–HPhP wave in hBN/Au/SiO2. Both techniques use an asymmetric Michelson interferometer, formed by a beamsplitter (BS) and a scanning mirror (SM), and a mercury-cadmium-telluride (MCT) detector (further details in the Experimental Methods section). The thicknesses of each material layer are given. (b) Sample topography. (c) and (d) s-SNOM third harmonic amplitude (S3) images at ω = 1470 cm−1 and ω = 1200 cm−1, respectively. The gray squares in (c) and (d) indicate regions examined in Fig. 2. Scale bars: 5 μm. | ||
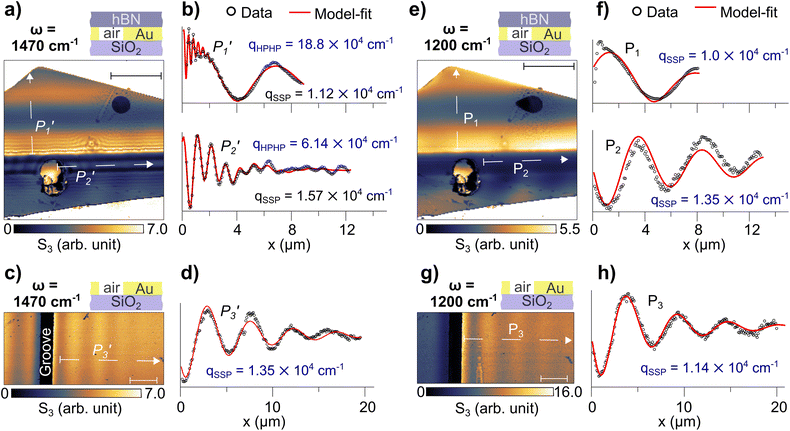 | ||
Fig. 2 Imaging of SPP and HPhP waves. (a) S3 image at ω = 1470 cm−1 from the area indicated in Fig. 1c (gray square). (b)  and and  polariton profiles, extracted from locations shown in (a), with the corresponding model-fits (red curves) and the obtained qSPP and qHPhP. (c) S3 image at ω = 1470 cm−1 of the Au/SiO2 interface and (d) the polariton profile polariton profiles, extracted from locations shown in (a), with the corresponding model-fits (red curves) and the obtained qSPP and qHPhP. (c) S3 image at ω = 1470 cm−1 of the Au/SiO2 interface and (d) the polariton profile  , extracted from (c) with the corresponding model-fit (red curve) and qSPP value. (e–h) Comparative images for excitation at ω = 1200 cm−1. Scale bars: 5 μm. , extracted from (c) with the corresponding model-fit (red curve) and qSPP value. (e–h) Comparative images for excitation at ω = 1200 cm−1. Scale bars: 5 μm. | ||
As seen in Fig. 2a, polaritonic patterns are produced by the interference between SPP and HPhP waves launched both by the disk-like antenna and by the groove edge. The corresponding polaritonic profiles are plotted in Fig. 2b. The profile  permits good visualization of the SPP–HPhP superposition: the SPP wave of lower momentum (qSPP) interfering with the HPhP wave of higher momentum (qHPhP). All scans were performed orthogonally to the groove, ensuring consistency with the conditions described in ref. 36–40. Further details on data extraction and SPP momenta calculations, based on the illumination geometry, are discussed in the ESI.† To obtain quantitative information, we model the resultant polaritonic field (E) as a superposition of SPP (EeSPP) and HPhP (EeHPhP) waves in the form of damped plane waves:
permits good visualization of the SPP–HPhP superposition: the SPP wave of lower momentum (qSPP) interfering with the HPhP wave of higher momentum (qHPhP). All scans were performed orthogonally to the groove, ensuring consistency with the conditions described in ref. 36–40. Further details on data extraction and SPP momenta calculations, based on the illumination geometry, are discussed in the ESI.† To obtain quantitative information, we model the resultant polaritonic field (E) as a superposition of SPP (EeSPP) and HPhP (EeHPhP) waves in the form of damped plane waves:
 | (1) |
This equation consists of the summation over HPhP and SPP complex fields and a complex non-propagative background C. In the analytical form, each damped plane wave is defined by the parameters: amplitude Aα, momentum qα and damping γα, with α = SPP or HPhP. For generalization, a relative phase difference θ between the SPP and HPhP waves is considered. These parameters are determined by fitting eqn (1) to experimental profiles. It is noteworthy that our model includes only edge- and antenna-launched waves. In our data, there is no experimental evidence of tip-launched waves that would introduce half-wavelength contributions from reflected polariton waves at crystal edges.29,31,41,42
The model fit to the profile  (Fig. 2b) yields qSPP = 1.12 × 104 cm−1 and qHPhP = 18.8 × 104 cm−1. Since the wavelength λ = 2π/q, it is verified that λSPP > λHPhP in
(Fig. 2b) yields qSPP = 1.12 × 104 cm−1 and qHPhP = 18.8 × 104 cm−1. Since the wavelength λ = 2π/q, it is verified that λSPP > λHPhP in  as stated above. For the profile
as stated above. For the profile  , extracted from the hBN region onto the groove (Fig. 2a), we determine qHPhP = 6.14 × 104 cm−1 and qSPP = 1.57 × 104 cm−1. It is important to comment that the SPP wave in this profile is created propagate in the groove orthogonal edges, forming an SPP slit waveguide.43 Moreover, in agreement with the literature on HPhP modes of the upper RS band of hBN lying on metallic and dielectric substrates,30,31,33,34,41,44 our analysis finds a larger value of qHPhP on Au in the
, extracted from the hBN region onto the groove (Fig. 2a), we determine qHPhP = 6.14 × 104 cm−1 and qSPP = 1.57 × 104 cm−1. It is important to comment that the SPP wave in this profile is created propagate in the groove orthogonal edges, forming an SPP slit waveguide.43 Moreover, in agreement with the literature on HPhP modes of the upper RS band of hBN lying on metallic and dielectric substrates,30,31,33,34,41,44 our analysis finds a larger value of qHPhP on Au in the  than that in air in the
than that in air in the  . To estimate the accuracy of our approach, we calculate the expected qHPhP values using the Fresnel coefficients for p-polarized modes.32 The theoretically predicted momentum values for HPhP are 19.6 × 104 cm−1 on Au and 7 × 104 cm−1 in air. Such calculations are reasonably close to the model-determined ones from the
. To estimate the accuracy of our approach, we calculate the expected qHPhP values using the Fresnel coefficients for p-polarized modes.32 The theoretically predicted momentum values for HPhP are 19.6 × 104 cm−1 on Au and 7 × 104 cm−1 in air. Such calculations are reasonably close to the model-determined ones from the  and
and  experimental profiles, respectively: 18.8 × 104 cm−1 on Au and 6.14 × 104 cm−1 in air. To complement this discussion, we plot in Fig. 2c the S3 image at ω = 1470 cm−1 of edge-launched SPP waves in Au/SiO2 without hBN. The model-fit to the profile
experimental profiles, respectively: 18.8 × 104 cm−1 on Au and 6.14 × 104 cm−1 in air. To complement this discussion, we plot in Fig. 2c the S3 image at ω = 1470 cm−1 of edge-launched SPP waves in Au/SiO2 without hBN. The model-fit to the profile  (Fig. 2d) yields qSPP = 1.35 × 104 cm−1. In the ESI,† Fourier analyses of these investigated profiles clearly distinguish the SPP and HPhP momenta components, thus, corroborating our modelling results.
(Fig. 2d) yields qSPP = 1.35 × 104 cm−1. In the ESI,† Fourier analyses of these investigated profiles clearly distinguish the SPP and HPhP momenta components, thus, corroborating our modelling results.
To compare, Fig. 2e and h present S3 images of the sample illuminated at ω = 1200 cm−1 where no HPhPs are excited in hBN as the frequency lies outside the upper RS band. Hence, only SPP waves are visualized in the profiles P1 and P2 (Fig. 2f). To fit these profiles, the eqn (1) model is used with one propagative term ascribed to the SPP wave, as confirmed by Fourier transform analysis (ESI†). In Fig. 2g, we observe edge-launched SPP waves in Au/SiO2, with qSPP = 1.14 × 104 cm−1 as determined from the model-fit to P3 (Fig. 2h).
To further our analyses, we inspect the SPP waves in a broader range by a spatio-spectral linescan from SINS technique (Fig. 1a). This measurement consists of a distance × ω map built by plotting a set of SINS spectra acquired along a defined trajectory.45 In Fig. 3a, we present the spatio-spectral linescan of the second harmonic amplitude, S2(ω, x), signal on hBN/Au normalized by the SINS spectrum on a clean Au surface. For better visualization of different polaritons fringes, we re-normalized the measurement by the spectrum at x = 20 μm, which removes signal saturation due to the high reflectivity at the ωTO phonon resonance. The scanned path begins at the groove edge and extends up to x = 20 μm on the 2D crystal as denoted in Fig. 1a. It is displayed the 1320–1420 cm−1 range, including part of the hBN upper RS band (above 1365 cm−1). One can see the fringes of high-momentum HPhP modes (indicated by the white arrow in Fig. 3a) propagating from the groove edge up to x ≈ 3 μm. The SPP modes rise (blue arrows in Fig. 3a) across the entire spectral range, emphasizing their broadband character, and reach x = 20 μm. Intriguingly, near the hBN ωTO = 1365 cm−1, we note a spatio-spectral variation of the SPP modes. The correlation of such distortion with the ωTO is noted from the correspondence with the phonon resonance of the in-plane hBN permittivity εhBN⊥ plotted on the right panel of Fig. 3a. Moreover, the feature is not found in the Au/SiO2 linescan for the same spectral range (see the ESI†). To retrieve quantitative information from this phenomenon, we analyzed SPP profiles extracted near the phonon peak at ω = 1408 cm−1, 1363 cm−1, and 1326 cm−1 (Fig. 3b). Eqn (1) fittings to these data reveal that the 1363 cm−1 profile, which is closer to ωTO, possesses larger damping, γSPP = 0.41 × 104 cm−1, than that of the other frequencies. This is a characteristic behavior of anti-crossing (AC) effect that can be ascribed to the phonon–SPP interaction. In analogy to the reported HPhPs coupled to molecular modes, the phonon–SPP interaction leads to significant modification of qSPP and a considerable increase in γSPP.23
To elucidate such effect, we compute the SPP experimental ω−q dispersion, from the linescan data, employing the expression
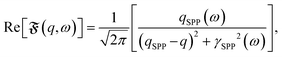 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where θ is the angle between the illumination and the tip) and qSPP (see the ESI†). Our analyses are in concordance with previous studies36–40 considering θ = π/3, where the measured period of the fringes (λeff) is given by
θ, where θ is the angle between the illumination and the tip) and qSPP (see the ESI†). Our analyses are in concordance with previous studies36–40 considering θ = π/3, where the measured period of the fringes (λeff) is given by  .
.
Considering this correction, the experimental ω−q dispersion of SPP modes is plotted in Fig. 4a.
To compare the experimental dispersion with theory, we calculate the theoretical qSPP and γSPP for hBN/Au from.
 | (3) |
In the absence of external sources, eqn (3) is derived from Maxwell's equations in the D/M system (considering both media as being semi-infinite) accounting for the boundary conditions at all interfaces.35 The terms εhBN⊥ and εhBN∥ are the in- and out-of-plane components of the hBN electrical permittivity tensor, εAu is the Au permittivity and k0 is the momentum of light in free space. Hence, we use the theoretical qSPP and γSPP from eqn (3) as inputs to eqn (2) to plot the theoretical dispersion shown in Fig. 4b.
Comparing Fig. 4a and b we note that experiment and theory quantitatively agree regarding momenta and damping values. The AC effect also consistently appears around ωTO in both analyses.
A further evaluation of the SPP–phonon interaction, cause of the AC effect, is given by the classical model of coupled harmonic oscillators.23,28,46 This model can be described by the pair of coupled equations of motion
 | (4) |
 . The solution of eqn (4), setting the approximation FSPP = FP ∼ 0, leads to the upper ω+ and lower ω− eigen-frequencies (eqn (5)) of the coupled modes.
. The solution of eqn (4), setting the approximation FSPP = FP ∼ 0, leads to the upper ω+ and lower ω− eigen-frequencies (eqn (5)) of the coupled modes. | (5) |
 | (6) |
From that, the coupling strength Ω is determined by the smallest difference between ω+ and ω−. When the strict condition η = 2Ω/(ΓSPP − ΓPP) > 1 is fulfilled,23,28,46 the interaction is classified in the SC regime. Following the method adopted in ref. 23, we determine the coupling parameters by fitting the extinction coefficient Cext(qSPP,ω) (eqn (6)) to the experimental iso-momentum spectra near the AC region, which correspond to vertical profiles extracted from the experimental dispersion (green and black vertical lines in Fig. 4a). In this approach, it is assumed that the experimental  is proportional to the dissipated power of the coupled system:
is proportional to the dissipated power of the coupled system:  . Fig. 4c presents iso-momenta data for qSPP = 1.3 × 104 cm−1 and qSPP = 1.5 × 104 cm−1 and the corresponding fittings from Cext (qSPP,ω) (eqn (6)). Using the obtained fitting parameters (Ω = 41 cm−1, ΓSPP = 71 cm−1 and ΓPP = 6 cm−1) we compute the ω+ and ω− dispersion branches, which are displayed as red circles in Fig. 4d. This analysis shows that the SC criterion is fulfilled for the SPP–phonon interaction: η = 2Ω/(ΓSPP − ΓPP) = 1.26 satisfying the condition η > 1. Thereby, the interaction between SPP waves on Au and in-plane ωTO phonon of the hexagonal boron nitride (hBN) occurs within the SC regime.
. Fig. 4c presents iso-momenta data for qSPP = 1.3 × 104 cm−1 and qSPP = 1.5 × 104 cm−1 and the corresponding fittings from Cext (qSPP,ω) (eqn (6)). Using the obtained fitting parameters (Ω = 41 cm−1, ΓSPP = 71 cm−1 and ΓPP = 6 cm−1) we compute the ω+ and ω− dispersion branches, which are displayed as red circles in Fig. 4d. This analysis shows that the SC criterion is fulfilled for the SPP–phonon interaction: η = 2Ω/(ΓSPP − ΓPP) = 1.26 satisfying the condition η > 1. Thereby, the interaction between SPP waves on Au and in-plane ωTO phonon of the hexagonal boron nitride (hBN) occurs within the SC regime.
In summary, here we fully characterize the nanophotonic properties of mid-IR SPP waves at the interface formed between hBN 2D crystal and Au surface using s-SNOM and SINS nanoscopies. In the hBN upper RS polaritonic band, we see the interference between SPP waves on the metal layer and HPhP waves in the 2D crystal, creating an SPP–HPhP wave superposition. In contrast to graphene–hyperbolic crystal systems,44,47,48 where momentum matching forms hybrid waves of one component, SPP–HPhP superposition in hBN/Au arises from interference between polaritons with distinct momenta scales (qSPP ∼ 104 cm−1 and qHPhP ∼ 105 cm−1), generating a wave with two clearly discernible components.42,45,46 This effect can be useful for inducing spatial frequency modulation in 2D polariton waves as observed from the fact that the HPhP constitutes a high spatial frequency modulation onto the SPP wave. We also display and quantitatively evaluate the SC regime of the interaction between mid-IR SPP waves with the hBN in-plane ωTO phonon. Provided the large spectral coverage of SPPs in the IR molecular fingerprint, this ability of the SPP waves to couple with phonons can be exploited for enhanced sensing of other systems including organic and biological materials. Moreover, our study paves the way to future research on the SPP wave properties in interfaces with other 2D materials,47 with phonon and polaritonic activities in the mid-infrared to the terahertz (THz), including anisotropic hyperbolic crystals49–54 that might influence the SPP's directionality.
Experimental Methods
Scattering-type scanning near-field optical microscopy (s-SNOM)
The s-SNOM (neaSNOM from Neaspec, attocube systems AG) uses a metallic tip of an atomic force microscope (AFM) as an optical nanoprobe to measure the optical near-field. The AFM operates in semi-contact mode wherein a metallic tip, with a 25 nm-large apex radius, is electronically driven to vibrate at its natural mechanical frequency (Ω). The IR illumination is focused on the tip–sample region by a parabolic mirror. As a result, a highly confined optical field rises at the tip apex and causes a local effective polarizability to the tip–sample system due to the lightning rod effect.55–57 The back-scattered light (S) from the tip–sample interaction is collected by the same parabolic mirror and directed to a mercury-cadmium-telluride (MCT) detector. This scattered signal is composed of a mixture of the optical near-field scattering, originating from the local effective polarizability, and high-intensity far-field component (background). To suppress the background, S is demodulated in harmonics (n) of Ω, by a lock-in based electronic scheme, and it is used for pseudo-heterodyne (PS-het) detection.58 Authentic optical near-field measurements are given by high harmonic signals, n ≥ 2, in combination with PS-het detection. Quantum cascade lasers (QCL) were employed as the illumination sources. Due to the high near-field intensity confined at the tip apex, it becomes an optical nanoprobe of high spatial resolution, approximately equal to the radius, and high momenta capable of exciting HPhP modes.Synchrotron infrared nanospectroscopy (SINS)
SINS operates based on s-SNOM principles, particularly, regarding optical near-field excitation and the use of a similar detection scheme. In SINS, an s-SNOM microscope is combined with highly brilliant broadband IR radiation emitted by a synchrotron as the illumination source. The scattered light (S) is then directed into an asymmetric Michelson interferometer (Fig. 1a), where it interferes with the reference arm's beam. Analogous to s-SNOM, lock-in detection electronics captures the optical near-field interferograms from the higher harmonics of S (n ≥ 2). Through Fourier transform, the mid-infrared near-field spectrum is obtained. In this study, SINS experiments were conducted at the Imbuia beamline of Sirius, the Brazilian Synchrotron Light Laboratory (LNLS),21 using an MCT detector to measure the optical near-field in the range of 650 to 3000 cm−1.Sample construction
The groove was created by standard photolithography onto SiO2 (2 μm thick)/Si substrates followed by deposition of a 90 nm thick Au film by the electron beam. The hBN flakes were then transferred onto the Au groove using a PDMS-assisted technique.26 Before hBN transfer, the flakes were exfoliated by the standard scotch tape method on the PDMS stamp and were selected based on optical contrast. After the hBN transfer, the Au disk-like antenna, with an average height of 150 nm and an elliptical basis measuring ∼2.4 and ∼3.9 μm for the short and long axes respectively, was designed atop the transferred hBN and at the edge of the groove by a new photolithography step, followed by the deposition of a 90 nm thick Au film by electron beam and lift-off.Data availability
All data that support the findings of this study are included within the article and its ESI.†Conflicts of interest
“The authors declare the following financial interests/personal relationships, which may be considered potential competing interests: Adrian Cernescu is employed by attocube systems AG, a company that manufactures s-SNOM and nano-FTIR spectroscopy instruments”.Acknowledgements
All Brazilian authors thank the Brazilian Synchrotron Light Source (LNLS) for providing beamtime for SINS and s-SNOM experiments at the Imbuia Beamline of Sirius (Proposal 20232881). NeaSpec GmbH is acknowledged for its technical assistance. F. H. F. and R. O. F. acknowledge FAPESP support through the postdoc grant 2023/09839-5. F. C. B. M., and I. D. B. acknowledge financial support from the FAPESP (2022/02901-4). I. D. B., R. O. F. and F. C. B. M. acknowledge the CNPq through research grants 311327/2020-6, 311564/2018-6, and 306170/2023-0, respectively. R. O. F. acknowledges the support from the FAPESP Young Investigator grant 2019/14017-9. I. D. B. acknowledges the financial support from the Brazilian Nanocarbon Institute of Science and Technology (INCT/Nanocarbono). D. A. B. acknowledges support from CAPES-PRINT (88887.310281/2018-00) and Mackpesquisa. The authors also thank the Brazilian Nanotechnology National Laboratory (LNNano) and LNLS, both part of the Brazilian Centre for Research in Energy and Materials (CNPEM), a private non-profit organization under the supervision of the Brazilian Ministry for Science, Technology, and Innovations (MCTI), for sample preparation and characterization.References
-
S. A. Maier, Plasmonics: Fundamentals and Applications, Springer US, New York, NY, 2007 Search PubMed
.
- Z. Han and S. I. Bozhevolnyi, Radiation guiding with surface plasmon polaritons, Rep. Prog. Phys., 2013, 76(1), 016402 CrossRef PubMed
.
- V. G. Achanta, Surface waves at metal-dielectric interfaces: Material science perspective, Rev. Phys, 2020, 5, 100041 CrossRef
.
- Y. Fang and M. Sun, Nanoplasmonic waveguides: towards applications in integrated nanophotonic circuits, Light:Sci. Appl., 2015, 4(6), e294–e294 CrossRef CAS
.
- H. Yu, Y. Peng, Y. Yang and Z.-Y. Li, Plasmon-enhanced light–matter interactions and applications, npj Comput. Mater., 2019, 5(1), 45 CrossRef
.
- Y. J. Lu, J. Kim, H. Y. Chen, C. Wu, N. Dabidian, C. E. Sanders, C. Y. Wang, M. Y. Lu, B. H. Li, X. Qiu, W. H. Chang, L. J. Chen, G. Shvets, C. K. Shih and S. Gwo, Plasmonic nanolaser using epitaxially grown silver film, Science, 2012, 337(6093), 450–453 CrossRef CAS PubMed
.
- R. Chandrasekar, Z. Wang, X. Meng, S. I. Azzam, M. Y. Shalaginov, A. Lagutchev, Y. L. Kim, A. Wei, A. V. Kildishev, A. Boltasseva and V. M. Shalaev, Lasing Action with Gold Nanorod Hyperbolic Metamaterials, ACS Photonics, 2017, 4(3), 674–680 CrossRef CAS
.
- D. J. Bergman and M. I. Stockman, Surface Plasmon Amplification by Stimulated Emission of Radiation: Quantum Generation of Coherent Surface Plasmons in Nanosystems, Phys. Rev. Lett., 2003, 90(2), 027402 CrossRef PubMed
.
- T. J. Davis, D. E. Gómez and A. Roberts, Plasmonic circuits for manipulating optical information, Nanophotonics, 2016, 6(3), 543–559 Search PubMed
.
- M. Schnell, P. Alonso-González, L. Arzubiaga, F. Casanova, L. E. Hueso, A. Chuvilin and R. Hillenbrand, Nanofocusing of mid-infrared energy with tapered transmission lines, Nat. Photonics, 2011, 5(5), 283–287 CrossRef CAS
.
- P. Sarriugarte, M. Schnell, P. Alonso-González, L. Arzubiaga, F. Golmar, F. Casanova, L. E. Hueso and R. Hillenbrand, Propagation and nanofocusing of infrared surface plasmons on tapered transmission lines: Influence of the substrate, Opt. Commun., 2012, 285(16), 3378–3382 CrossRef CAS
.
- P. Sarriugarte, M. Schnell, A. Chuvilin and R. Hillenbrand, Polarization-Resolved Near-Field Characterization of Nanoscale Infrared Modes in Transmission Lines Fabricated by Gallium and Helium Ion Beam Milling, ACS Photonics, 2014, 1(7), 604–611 CrossRef CAS
.
- P. Pons-Valencia, F. J. Alfaro-Mozaz, M. M. Wiecha, V. Biolek, I. Dolado, S. Vélez, P. Li, P. Alonso-González, F. Casanova, L. E. Hueso, L. Martín-Moreno, R. Hillenbrand and A. Y. Nikitin, Launching of hyperbolic phonon-polaritons in h-BN slabs by resonant metal plasmonic antennas, Nat. Commun., 2019, 10(1), 3242 CrossRef CAS PubMed
.
- Y. Zhang, C. Hu, B. Lyu, H. Li, Z. Ying, L. Wang, A. Deng, X. Luo, Q. Gao, J. Chen, J. Du, P. Shen, K. Watanabe, T. Taniguchi, J.-H. Kang, F. Wang, Y. Zhang and Z. Shi, Tunable Cherenkov Radiation of Phonon Polaritons in Silver Nanowire/Hexagonal Boron Nitride Heterostructures, Nano Lett., 2020, 20(4), 2770–2777 CrossRef CAS PubMed
.
- X. Chen, X. Liu, X. Guo, S. Chen, H. Hu, E. Nikulina, X. Ye, Z. Yao, H. A. Bechtel, M. C. Martin, G. L. Carr, Q. Dai, S. Zhuang, Q. Hu, Y. Zhu, R. Hillenbrand, M. Liu and G. You, THz Near-Field Imaging of Extreme Subwavelength Metal Structures, ACS Photonics, 2020, 7(3), 687–694 CrossRef CAS
.
- K. Aleshire, I. M. Pavlovetc, R. Collette, X.-T. Kong, P. D. Rack, S. Zhang, D. J. Masiello, J. P. Camden, G. V. Hartland and M. Kuno, Far-field midinfrared superresolution imaging and spectroscopy of single high aspect ratio gold nanowires, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(5), 2288–2293 CrossRef CAS PubMed
.
- R. Stanley, Plasmonics in the mid-infrared, Nat. Photonics, 2012, 6(7), 409–411 CrossRef CAS
.
- T. Taliercio and P. Biagioni, Semiconductor infrared plasmonics, Nanophotonics, 2019, 8(6), 949–990 CrossRef CAS
.
- Y. Zhong, S. D. Malagari, T. Hamilton and D. Wasserman, Review of mid-infrared plasmonic materials, J. Nanophotonics, 2015, 9(1), 093791 CrossRef CAS
.
- X. Chen, D. Hu, R. Mescall, G. You, D. N. Basov, Q. Dai and M. Liu, Modern Scattering-Type Scanning Near-Field Optical Microscopy for Advanced Material Research, Adv. Mater., 2019, 31(24), 1804774 CrossRef PubMed
.
- R. A. Mayer, F. H. Feres and R. O. Freitas, Synchrotron infrared nanospectroscopy as a game changer in nanophotonics, in 2021 SBFoton International Optics and Photonics Conference (SBFoton IOPC), IEEE, 2021, pp. 1–6.
- D. S. Dovzhenko, S. V. Ryabchuk, Y. P. Rakovich and I. R. Nabiev, Light–matter interaction in the strong coupling regime: configurations, conditions, and applications, Nanoscale, 2018, 10(8), 3589–3605 RSC
.
- A. Bylinkin, M. Schnell, M. Autore, F. Calavalle, P. Li, J. Taboada-Gutièrrez, S. Liu, J. H. Edgar, F. Casanova, L. E. Hueso, P. Alonso-Gonzalez, A. Y. Nikitin and R. Hillenbrand, Real-space observation of vibrational strong coupling between propagating phonon polaritons and organic molecules, Nat. Photonics, 2021, 15(3), 197–202 CrossRef CAS
.
- A. J. Sternbach, S. L. Moore, A. Rikhter, S. Zhang, R. Jing, Y. Shao, B. S. Y. Kim, S. Xu, S. Liu, J. H. Edgar, A. Rubio, C. Dean, J. Hone, M. M. Fogler and D. N. Basov, Negative refraction in hyperbolic hetero-bicrystals, Science, 2023, 379(6632), 555–557 CrossRef CAS PubMed
.
- L. Wehmeier, S. Yu, X. Chen, R. A. Mayer, L. Xiong, H. Yao, Y. Jiang, J. Hu, E. Janzen, J. H. Edgar, X. Zheng, T. F. Heinz, D. N. Basov, C. C. Homes, G. Hu, G. L. Carr, M. Liu and J. A. Fan, Tunable Phonon Polariton Hybridization in a van der Waals Hetero-Bicrystal, Adv. Mater., 2024, 36(33), 2401349 CrossRef CAS PubMed
.
- I. D. Barcelos, A. R. Cadore, L. C. Campos, A. Malachias, K. Watanabe, T. Taniguchi, F. C. B. Maia, R. Freitas and C. Deneke, Graphene/h-BN plasmon–phonon coupling and plasmon delocalization observed by infrared nano-spectroscopy, Nanoscale, 2015, 7(27), 11620–11625 RSC
.
- I. J. Luxmoore, C. H. Gan, P. Q. Liu, F. Valmorra, P. Li, J. Faist and G. R. Nash, Strong Coupling in the Far-Infrared between Graphene Plasmons and the Surface Optical Phonons of Silicon Dioxide, ACS Photonics, 2014, 1(11), 1151–1155 CrossRef CAS
.
- G. Németh, K. Otsuka, D. Datz, Á. Pekker, S. Maruyama, F. Borondics and K. Kamarás, Direct Visualization of Ultrastrong Coupling between Luttinger-Liquid Plasmons and Phonon Polaritons, Nano Lett., 2022, 22(8), 3495–3502 CrossRef PubMed
.
- S. Dai, J. Quan, G. Hu, C.-W. Qiu, T. H. Tao, X. Li and A. Alù, Hyperbolic Phonon Polaritons in Suspended Hexagonal Boron Nitride, Nano Lett., 2019, 19(2), 1009–1014 CrossRef CAS PubMed
.
- F. H. Feres, R. A. Mayer, I. D. Barcelos, R. O. Freitas and F. C. B. Maia, Acceleration of Subwavelength Polaritons by Engineering Dielectric-Metallic Substrates, ACS Photonics, 2020, 7(6), 1396–1402 CrossRef CAS
.
- S. Dai, Q. Ma, T. Andersen, A. S. Mcleod, Z. Fei, M. K. Liu, M. Wagner, K. Watanabe, T. Taniguchi, M. Thiemens, F. Keilmann, P. Jarillo-Herrero, M. M. Fogler and D. N. Basov, Subdiffractional focusing and guiding of polaritonic rays in a natural hyperbolic material, Nat. Commun., 2015, 6(1), 6963 CrossRef CAS PubMed
.
- S. Dai, Z. Fei, Q. Ma, A. S. Rodin, M. Wagner, A. S. McLeod, M. K. Liu, W. Gannett, W. Regan, K. Watanabe, T. Taniguchi, M. Thiemens, G. Dominguez, A. H. C. Neto, A. Zettl, F. Keilmann, P. Jarillo-Herrero, M. M. Fogler and D. N. Basov, Tunable Phonon Polaritons in Atomically Thin van der Waals Crystals of Boron Nitride, Science, 2014, 343(6175), 1125–1129 CrossRef CAS PubMed
.
- J. Duan, R. Chen, J. Li, K. Jin, Z. Sun and J. Chen, Launching Phonon Polaritons by Natural Boron Nitride Wrinkles with Modifiable Dispersion by Dielectric Environments, Adv. Mater., 2017, 29(38), 1702494 CrossRef PubMed
.
- F. H. Feres, I. D. Barcelos, R. A. Mayer, T. M. dos Santos, R. O. Freitas, M. B. Raschke, D. A. Bahamon and F. C. B. Maia, Dipole modelling for a robust description of subdiffractional polariton waves, Nanoscale, 2019, 11(44), 21218–21226 RSC
.
- S. G. Menabde, J. T. Heiden, J. D. Cox, N. A. Mortensen and M. S. Jang, Image polaritons in van der Waals crystals, Nanophotonics, 2022, 11(11), 2433–2452 CrossRef CAS PubMed
.
- S. G. Menabde, S. Boroviks, J. Ahn, J. T. Heiden, K. Watanabe, T. Taniguchi, T. Low, D. K. Hwang, N. A. Mortensen and M. S. Jang, Near-field probing of image phonon-polaritons in hexagonal boron nitride on gold crystals, Sci. Adv., 2022, 8(28), eabn0627 CrossRef CAS PubMed
.
- J. Jacob, A. Babu, G. Mathew and V. Mathew, Propagation of surface plasmon polaritons in anisotropic MIM and IMI structures, Superlattices Microstruct., 2008, 44(3), 282–290 CrossRef CAS
.
- A. Mancini, L. Nan, F. J. Wendisch, R. Berté, H. Ren, E. Cortés and S. A. Maier, Near-Field Retrieval of the Surface Phonon Polariton Dispersion in Free-Standing Silicon Carbide Thin Films, ACS Photonics, 2022, 9(11), 3696–3704 CrossRef CAS
.
- F. Walla, M. M. Wiecha, N. Mecklenbeck, S. Beldi, F. Keilmann, M. D. Thomson and H. G. Roskos, Anisotropic excitation of surface plasmon polaritons on a metal film by a scattering-type scanning
near-field microscope with a non-rotationally-symmetric probe tip, Nanophotonics, 2018, 7(1), 269–276 CrossRef
.
- A. Ambrosio, M. Tamagnone, K. Chaudhary, L. A. Jauregui, P. Kim, W. L. Wilson and F. Capasso, Selective excitation and imaging of ultraslow phonon polaritons in thin hexagonal boron nitride crystals, Light:Sci. Appl., 2018, 7(1), 27 CrossRef PubMed
.
- A. Andryieuski, V. A. Zenin, R. Malureanu, V. S. Volkov, S. I. Bozhevolnyi and A. V. Lavrinenko, Direct Characterization of Plasmonic Slot Waveguides and Nanocouplers, Nano Lett., 2014, 14(7), 3925–3929 CrossRef CAS PubMed
.
- F. C. B. Maia, B. T. O'Callahan, A. R. Cadore, I. D. Barcelos, L. C. Campos, K. Watanabe, T. Taniguchi, C. Deneke, A. Belyanin, M. B. Raschke and R. O. Freitas, Anisotropic Flow Control and Gate Modulation of Hybrid Phonon-Polaritons, Nano Lett., 2019, 19(2), 708–715 CrossRef CAS PubMed
.
- I. D. Barcelos, H. A. Bechtel, C. J. S. de Matos, D. A. Bahamon, B. Kaestner, F. C. B. Maia and R. O. Freitas, Probing Polaritons in 2D Materials with Synchrotron Infrared Nanospectroscopy, Adv. Opt. Mater., 2020, 8(5), 1901091 CrossRef CAS
.
- M. Autore, P. Li, I. Dolado, F. J. Alfaro-Mozaz, R. Esteban, A. Atxabal, F. Casanova, L. E. Hueso, P. Alonso-González, J. Aizpurua, A. Y. Nikitin, S. Vélez and R. Hillenbrand, Boron nitride nanoresonators for phonon-enhanced molecular vibrational spectroscopy at the strong coupling limit, Light:Sci. Appl., 2017, 7(4), 17172–17172 CrossRef PubMed
.
- S. Dai, Q. Ma, M. K. Liu, T. Andersen, Z. Fei, M. D. Goldflam, M. Wagner, K. Watanabe, T. Taniguchi, M. Thiemens, F. Keilmann, G. C. A. M. Janssen, S.-E. Zhu, P. Jarillo-Herrero, M. M. Fogler and D. N. Basov, Graphene on hexagonal boron nitride as a tunable hyperbolic metamaterial, Nat. Nanotechnol., 2015, 10(8), 682–686 CrossRef CAS PubMed
.
- Y. Zeng, Q. Ou, L. Liu, C. Zheng, Z. Wang, Y. Gong, X. Liang, Y. Zhang, G. Hu, Z. Yang, C.-W. Qiu, Q. Bao, H. Chen and Z. Dai, Tailoring Topological Transitions of Anisotropic Polaritons by Interface Engineering in Biaxial Crystals, Nano Lett., 2022, 22(10), 4260–4268 CrossRef CAS PubMed
.
- I. D. Barcelos, A. R. Cadore, A. B. Alencar, F. C. B. Maia, E. Mania, R. F. Oliveira, C. C. B. Bufon, Â. Malachias, R. O. Freitas, R. L. Moreira and H. Chacham, Infrared Fingerprints of Natural 2D Talc and Plasmon–Phonon Coupling in Graphene–Talc Heterostructures, ACS Photonics, 2018, 5(5), 1912–1918 CrossRef CAS
.
- W. Ma, P. Alonso-González, S. Li, A. Y. Nikitin, J. Yuan, J. Martín-Sánchez, J. Taboada-Gutiérrez, I. Amenabar, P. Li, S. Vélez, C. Tollan, Z. Dai, Y. Zhang, S. Sriram, K. Kalantar-Zadeh, S.-T. Lee, R. Hillenbrand and Q. Bao, In-plane anisotropic and ultra-low-loss polaritons in a natural van der Waals crystal, Nature, 2018, 562(7728), 557–562 CrossRef CAS PubMed
.
- F. H. Feres, R. A. Mayer, L. Wehmeier, F. C. B. Maia, E. R. Viana, A. Malachias, H. A. Bechtel, J. M. Klopf, L. M. Eng, S. C. Kehr, J. C. González, R. O. Freitas and I. D. Barcelos, Sub-diffractional cavity modes of terahertz hyperbolic phonon polaritons in tin oxide, Nat. Commun., 2021, 12(1), 1995 CrossRef CAS PubMed
.
- J. Taboada-Gutiérrez, G. Álvarez-Pérez, J. Duan, W. Ma, K. Crowley, I. Prieto, A. Bylinkin, M. Autore, H. Volkova, K. Kimura, T. Kimura, M.-H. Berger, S. Li, Q. Bao, X. P. A. Gao, I. Errea, A. Y. Nikitin, R. Hillenbrand, J. Martín-Sánchez and P. Alonso-González, Broad spectral tuning of ultra-low-loss polaritons in a van der Waals crystal by intercalation, Nat. Mater., 2020, 19(9), 964–968 CrossRef PubMed
.
- R. A. Mayer, L. Wehmeier, M. Torquato, X. Chen, F. H. Feres, F. C. B. Maia, M. Obst, F. G. Kaps, A. Luferau, J. M. Klopf, S. N. Gilbert Corder, H. A. Bechtel, J. C. González, E. R. Viana, L. M. Eng, S. C. Kehr, R. O. Freitas and I. D. Barcelos, Paratellurite Nanowires as a Versatile Material for THz Phonon Polaritons, ACS Photonics, 2024, 4323–4333 CAS
.
- S.-J. Yu, H. Yao, G. Hu, Y. Jiang, X. Zheng, S. Fan, T. F. Heinz and J. A. Fan, Hyperbolic Polaritonic Rulers Based on van der Waals α-MoO 3 Waveguides and Resonators, ACS Nano, 2023, 17(22), 23057–23064 CrossRef CAS PubMed
.
- F. Keilmann and R. Hillenbrand, Near-field microscopy by elastic light scattering from a tip, Philos. Trans. R. Soc., A, 2004, 362(1817), 787–805 CrossRef CAS PubMed
.
- F. G. Kaps, S. C. Kehr and L. M. Eng, Polarization Sensitivity in Scattering-Type Scanning Near-Field Optical Microscopy—Towards Nanoellipsometry, Appl. Sci., 2023, 13(18), 10429 CrossRef CAS
.
- R. Hillenbrand and F. Keilmann, Complex Optical Constants on a Subwavelength Scale, Phys. Rev. Lett., 2000, 85(14), 3029–3032 CrossRef CAS PubMed
.
- N. Ocelic, A. Huber and R. Hillenbrand, Pseudoheterodyne detection for background-free near-field spectroscopy, Appl. Phys. Lett., 2006, 89(10), 101124 CrossRef
.
- T. M. Santos, S. Lordano, R. A. Mayer, L. Volpe, G. M. Rodrigues, B. Meyer, H. Westfahl Jr and R. O. Freitas, Synchrotron infrared nanospectroscopy in fourth-generation storage rings, J. Synchrotron Radiat., 2024, 31(3), 547–556 CrossRef CAS PubMed
.
- R. Cunha, A. Cadore, S. L. L. M. Ramos, K. Watanabe, T. Taniguchi, S. Kim, A. S. Solntsev, I. Aharonovich and L. M. Malard, Second harmonic generation in defective hexagonal boron nitride, J. Phys.: Condens. Matter, 2020, 32(19), 19LT01 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04543b |
| This journal is © The Royal Society of Chemistry 2025 |




