Machine learning modeling of electronic spectra and thermodynamic stability for a comprehensive chemical space of melanin

Abstract

Melanin as a bio-optoelectronic material holds immense potential. However, the understanding of its exact molecular structure has been stalling for decades due to difficulties in experiments, which hinders uncovering its structure–property relationship. Conventional theoretical modeling is also limited due to the huge size of its chemical space resulting from millions of possible oligomer structures. Here, we design a comprehensive virtual chemical space of melanin oligomers and develop a machine learning-based approach for predicting their entire UV-visible spectra and thermodynamic stability using fingerprint input. We also show the similarity of our predicted Boltzmann-weighted average spectrum with the experimental spectrum and discuss their potentiality towards bio-optoelectronics.

---

1 Introduction

Optical devices and materials based on organic molecules are a significant area of research in materials engineering due to their design versatility and cost-effective production, especially when compared to traditional electronics.^1,2 The quest has been for designing materials with improved optoelectronic applications such as sunscreens with broad UV light absorption,^3,4 organic solar cells,^5–7 photovoltaics,^8,9etc. The field advances with two key aspects: maximizing absorption of the solar spectrum and efficiently converting solar energy into other forms of usable energy or functional properties. To achieve the first goal, one needs materials that absorb light over a wide range of wavelengths and can be synthesized using sustainable practices and green chemistry. With recent advancements in experimental and computational techniques, melanin and melanin-like molecular motifs have emerged as some of the leading candidates for bio-optoelectronic applications.^10–15 However, progress in this direction has been stymied by the lack of knowledge about their structure–property relationship. This is mainly due to the sheer volume of the chemical space resulting from various combinations of monomer units, connectivity patterns, and oxidation states, ultimately leading to combinatorial explosion.¹⁶ Realizing the computational aspects of this problem, we aim to address the aforementioned bottleneck by leveraging machine learning (ML).

Structural models of melanin have been developed as early as 2006 by Kaxiras and co-workers.¹⁷ Although these model structures successfully reproduced the broad and featureless electronic absorption spectrum displayed in experiments, the exact structure–spectra correlation and which structural feature corresponds to the different spectral regions remain elusive. Furthermore, UV-IR hole-burning experiments have revealed the presence of common vibrational fingerprints across the UV-vis range, suggesting that various absorbers in melanin consist of similar IR active groups.^18,19 Very recently, there has been development in melanin crystal structure elucidation using solid-state NMR.²⁰ Despite continuous efforts, an efficient design strategy for melanin-based bio-optoelectronic materials is still lacking. It requires forecasting the complete optical and thermodynamic properties of potential model structures from a vast pool.

The modeling of electronic absorption covering a large wavelength range can be done by computing a large number of electronically excited states. While computer simulations of electronically excited states employ quantum chemistry methods, they are restricted to molecules of moderate size or focus mainly on a few of the lowest excitations. Time-dependent density functional theory (TDDFT) is a powerful tool that is used to model such electronic excitations.^21,22 When solved iteratively using Davidson,²³ Lanczos,²⁴etc. algorithms, it still has a computational complexity of kO(N_e³) ∼ kO(N_e⁴) (k is the number of desired excited states and N_e is the number of electrons in the molecule). Recently, ML has demonstrated that ground-state properties, such as atomization energy,^25,26 hydration free energy,^27,28etc., can be accurately mapped to the structural information of molecules (also known as ML input descriptors). Despite the growing success, ML for excited state chemistry is challenging, and this area is still in its early stage of development.^29,30 ML modeling of molecular electronic absorption spectra deals with training two main properties based on quantum chemistry data: electronic excitation energies (peak positions) and the corresponding transition dipoles or oscillator strengths (peak intensities). Training of these properties is restricted only to a small number of low-lying excitations,^31,32 and their applicability is predominantly confined within learning the spectral broadening of a single molecule by sampling a large number of conformers from a certain distribution (classical molecular dynamics, Wigner distribution, etc.). However, in designing molecules and materials for optoelectronic applications with tailored spectral peak positions and intensities, it is desirable to predict the entire electronic absorption spectra across the chemical space containing potential molecules. This is where the limitations of conventional ML become apparent. In a structurally diverse chemical space such as melanin, the substructure (or the chromophore) responsible for electronic excitations varies arbitrarily. Transition intensities, which are related to the transition between two electronic states, are more sensitive to this variation when one tries to map it to the ground state minimum geometry of the molecules.^33,34 This limits the ability to learn absorption intensities, thereby hindering the reconstruction of the complete spectral shape.

In this work, we constructed a comprehensive chemical space of melanin containing ∼124k model oligomers and trained a kernel ridge regression (KRR) based ML (KRR-ML) model with <10% of the entire space for predicting their entire electronic absorption spectra. We have shown that the trainability problem of absorption intensities is overcome by predicting the spectra within a finite bin resolution. Such binning has been demonstrated to accurately capture the shape of the deep-UV spectra for small organic molecules.³⁵ Furthermore, as a measure of synthetic accessibility, we also predicted the thermodynamic stabilities of the molecules.

2 Results and discussion

2.1 Chemical space design

The chemical space of melanin oligomers is generated combinatorially, considering all possible connectivities at the available polymerization sites and the oxidation states of the hydroxyl oxygens. There are countably millions of large oligomers that can be generated, but we restricted our dataset to tetramers. Our dataset contains 123 559 unique tetramers, which can be broadly categorized into linear, branched, and cyclic structures. See Section 4.1 for more details on the structure generation technique. A small subset of tetramers was chosen randomly to perform their quantum chemical calculations. This is a two-step process. In the first step, geometries were optimized using DFT, and then TDDFT was employed to calculate excitation energies and oscillator strengths for the lowest 60 singlet excited states (see Section 4.2 for more details).

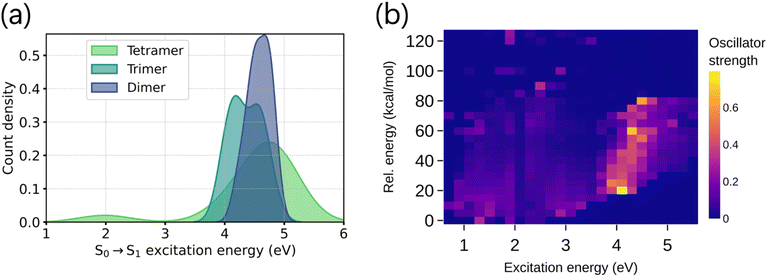
It is noteworthy that the tetramers show significantly different electronic absorptions compared to the dimers and trimers. Unlike the dimers and trimers, the S₀ → S₁ excitation energies of tetramers are distributed over a wider range (Fig. 1a), suggesting larger variations of the tetrameric chromophores. To design tailored optoelectronic materials, it is essential to understand how various properties of the molecules in the chemical space can be tuned. This is illustrated in Fig. 1b. Low-lying electronic excitation energies are shown against the relative energy of the molecules, where the color bar codes the oscillator strengths of the corresponding excitations. We notice variations in the absorption intensities of molecules across different excitation energy and stability domains. This is due to the varying oxidation states of the monomer building blocks and their connectivity patterns to form oligomers, which alters the chromophoric natures. Because of this reason, modeling the excitation energy of only one particular excited state (say S₁), regardless of its absorption intensity value, will not provide the complete spectral nature.³⁶ It is also worth mentioning that there is no clear correlation between stability and optical properties (Fig. 1), which further highlights the need to model both properties independently.

Fig. 1 (a) Distribution of S₀ → S₁ excitation energies (in eV) of dimers, trimers and tetramers. (b) Optical and thermodynamic properties calculated for random 10k tetramer molecules from the chemical space. S₁, S₂, … up to S₁₀ electronic excitation energies (in eV, along the X-axis) vs. relative energy (in kcal mol⁻¹, along the Y-axis). The color bar represents the oscillator strength for the corresponding excited state.

2.2 Model architecture and evaluations

In this section, we briefly describe the construction of the KRR-ML model, which learns the absorption spectra across the entire UV-visible range (200–800 nm) using data from quantum chemistry calculations. This allows us to predict the complete spectral shape of these promising optoelectronic molecules for further exploration of their potential. Besides, the predictive power of our model is assessed for the stability of the individual molecule. For the theoretical details of training and prediction with KRR-ML, see Section 4.3.

2.2.1 Codification of fingerprints. Although molecules in our dataset differ globally, their local structures (i.e. the monomer backbone) are similar. Thus, our ML model can benefit from fingerprint-like input descriptors, which are much simpler and easier to explain than descriptors derived from three-dimensional coordinates of the molecules. In an oligomer molecule, the positions through which the monomers are connected to the other are codified by ‘1’ while the remaining positions are codified by ‘0’. Besides, we codify the oxidation states of the oxygen atoms in each monomer; the nature of the oligomer (linear, branched, etc.); and geometrical isomerism about specific torsional angles. Together, these elements are converted into a bit string that uniquely and unambiguously encodes the oligomer structure. We illustrated this with an example in Fig. 2 and discussed it in more detail in the ESI.†

Fig. 2 Fingerprint generation technique. This involves stepwise codification of structural information such as connectivity patterns, the oxidation state of the monomer oxygens, oligomer type, and geometrical (cis/trans) isomerism about some specific torsional angles. Bit string fragments are also shown at each step used to produce the final fingerprint.

Since the fingerprint descriptor here is based on the connectivity patterns, oxidation states, and geometrical isomerism in molecules, this is very similar to the molecular graphs in graph neural networks (GNNs). Recent studies have also shown that learning the molecular descriptors obtained from GNNs performs better than fixed molecular fingerprints.^37,38 However, these models typically demand significantly larger training datasets (often millions) due to the increased complexity in mapping input descriptors to target properties.^39,40 Quantum mechanically (QM) calculated descriptors are sometimes incorporated in GNNs to enhance the performance when data are limited.⁴¹ The optimal selection of such QM descriptors depends on the specific task, and quantities such as transition densities between ground and excited states have been speculated as QM descriptors for modeling oscillator strengths.^33,34 However, their calculation adds extra computational cost. This suggests the preference of fingerprint descriptors when the training data are limited.

2.2.2 Learning molecular spectral properties. We used fingerprint representation as input for training two separate KRR models: one for the excitation energies and the other for the corresponding oscillator strengths. Here it is important to mention that we trained the models with the lowest 60 singlet excited states. Within the framework of KRR, multi-output modeling simply extends the linear equation solver as:

[α₁, α₂, …, α_k] = [K + λ1]⁻¹[y₁, y₂, …, y_k] (1)

where y₁, y₂, …, y_k are the property vectors of interest (excitation energy or oscillator strength) for different excited states. K is the kernel matrix and λ is the regularization strength. For the effective generalization of multi-output models, the test error of each target output should exhibit a decreasing trend when the training dataset size increases. However, this becomes more complicated when the output data involve excited state properties that are not low-lying. This is shown in Fig. 3, where we represented the individual excited states along the X-axis and the amount of training data along the Y-axis. The test errors for prediction over a hold-out dataset are shown in the color bars. It is seen that the excitation energies of more or less all the excited states exhibit satisfactory learning trends (upper panel in Fig. 3a). Furthermore, the errors in low-lying excited states are relatively higher than those in the higher excited states. This occurs because the excitation energies of the low-lying excited states are relatively sparse, whereas the excitation energies of the higher excited states tend to form a more continuous spectrum. However, the oscillator strengths show little to no learning (lower panel in Fig. 3a). We also tested inputs, such as SLATM (Spectrum of London and Axilrod–Teller–Muto potential) and the Coulomb matrix, which are derived from DFT-optimized three-dimensional coordinates of the molecules. SLATM is particularly adept at mapping structure–property relationships in quantum chemistry due to its robust many-body formulation.⁴² Nonetheless, we did not observe any improvements in the learning trends of oscillator strengths (see ESI Fig. S3†). This is because the melanin oligomeric chromophores responsible for electronic transitions vary non-systematically across the chemical space and oscillator strengths are very sensitive to this variation. Moreover, the higher excited states in TDDFT are not well defined due to numerous root flips.

Fig. 3 Training and evaluation of KRR-ML models for predicting the electronic absorption spectra and relative energies of melanin tetramers using fingerprint input. (a) Learning excitation energies and oscillator strengths of the lowest 60 excited states. The test errors calculated over a hold-out dataset are shown by color bars. The X-axis represents the individual excited states, and the Y-axis represents the training dataset size. (b) Same as (a), but the learning is shown for individual bin intensities. Three plots (from top to bottom) are for bin resolutions of 25 nm, 50 nm and 100 nm across the 200–800 nm spectral range, resulting in 24, 12 and 6 uniform bins, respectively. (c) Learning curves with Gaussian and Laplacian kernel functions shown using relative error (left) and the overlap metric (right) as the accuracy measure. The vertical error bars correspond to the uncertainty over 20 independent runs. (d) Learning curve showing the overlap metric for 25 nm, 50 nm and 100 nm bin resolutions. (e) Learning curve showing the MAE (in kcal mol⁻¹) for relative energies at the B3LYP/6-31G(d) level.

2.2.3 Binning of absorption intensities. To overcome the non-learnability discussed above, we adopt a different approach to train the absorption intensities by dividing the entire UV-visible range into some finite number of bins. This is similar to the feature discretization technique used in statistics and ML. The multi-output KRR-ML (eqn (1)) is used to train the individual bin intensitieswhere k is the bin index and f_i are the oscillator strengths of all the excited states that fall within that bin range.

We uniformly divided the 200–800 nm wavelength range into 24, 12, and 6 bins, resulting in bin widths of 25, 50, and 100 nm, respectively. Learning improves significantly when we train on individual bin intensities across the UV-visible range compared to training on the oscillator strengths of individual states. This demonstrates a more robust generalization, as the test error for each target output (i.e. individual bin intensity) consistently decreases with an increase in training dataset size (see Fig. 3b). Furthermore, within TDDFT formalism, modeling bin intensities is more reliable than modeling individual excited states as there will be uncertainties for higher excited states due to the approximations in hybrid DFT functionals.

The natural transition orbitals (NTOs) were calculated to analyze the nature of the excited states within each bin. The bins in 200–400 nm wavelength regions consist of all kinds of excitations: local excitation (LE), charge transfer (CT) and mixed LE and CT states (mixed). However, the bins in 400–800 nm regions are found to consist of pure LE or CT states (see ESI Table S5†). As the bin intensity value already offers some insights into whether it consists of LE or CT states, we did not explicitly include the nature of the excited states in the learning process.

2.2.4 Measurement of accuracy for multi-output KRR-ML. For the accuracy measure of our multi-output KRR-ML, we used relative error and discrete overlap between predicted and reference spectra. The relative error is calculated aswhere m and n are the number of molecules in the test dataset and the number of bins as target outputs, respectively. a_i,j is the intensity value for j-th bin of the i-th molecule in the dataset. For j-th bin, Δa_j refers to the spread of the intensity values in the training dataset. To calculate the discrete overlap between the predicted and TDDFT reference spectra, we first normalize both the spectra for every molecule in the test dataset:where is a vector with elements a_i,j and is the norm of the vector. Then, the mean overlap over all the molecules in the test dataset is calculated aswhere m is the number of molecules in the test dataset. We evaluated the effectiveness of Gaussian and Laplacian kernel functions in training our multi-output KRR-ML models using the above-mentioned accuracy metrics, as shown in Fig. 3c. The accuracy measure for our multi-output KRR-ML for the prediction of bin absorption intensities decreases for relative error and increases for discrete overlap. It is apparent that the learning curve for the Laplacian kernel is steeper than that for the Gaussian kernel and can continue to improve with an increasing training dataset size. This is shown for a bin width of 50 nm, where the overlap between predicted and reference spectra is almost 0.8. The prediction power of our fingerprint input is also compared to that of the SLATM and Coulomb matrix input in ESI Fig. S4.†

However, the learning is not consistent for different bin widths, as shown in Fig. 3d. The learning is compromised when the bin width is decreased, or in other words, the spectral resolution is increased. For a given amount of training data, the overlap for different bin widths shows the following trend: 100 nm > 50 nm > 25 nm. This occurs because narrower bin widths attempt to capture minor shifts in TDDFT sticks, which affects learning as the bin width goes beyond the uncertainty in hybrid DFT functionals compared to high-level quantum chemistry methods. Therefore, it is important to consider the trade-off between the accuracy of the DFT functional and the requirement for high-resolution spectra.

2.2.5 Learning relative energy. In the quest to discover new materials, one objective is to identify those with high thermodynamic stability. As the dataset includes molecules with varying stoichiometries caused by different oxidation states of monomer units, the ground state energies were calculated using stoichiometrically balanced formulae. The stoichiometry of monomers with different oxidation states are balanced as

Using eqn (7), the energy of tetramers with different stoichiometries is compared by calculating the below quantity:

where E refers to the ground state energy and n is the number of monomers in a tetramer that are in oxidized form. Finally, the relative energies of the tetramers are calculated w.r.t. the most stable tetramer. A single-output KRR-ML model is trained to predict the relative energies using the fingerprint descriptor mentioned above. The relative energies show satisfactory learning, achieving a MAE ∼ 3 kcal mol⁻¹ with only 5k training data, as demonstrated in Fig. 3e.

To probe the efficacy of our KRR-ML model trained on DFT relative energies, we also performed DLPNO-CCSD(T)/cc-pVDZ calculations with the resolution-of-identity (RI) approximation on a few molecules. We observe a similar trend between DLPNO-CCSD(T) and ML-predicted values of relative energies (see ESI Fig. S6†).

2.3 Final applications

In this section, we show the construction of the final spectra of individual oligomers from the ML-predicted bin intensities. We also discuss the role of thermodynamic stabilities on the nature of the final spectrum for heterogeneous melanin. Potential application domains with efficient bio-optoelectronic material design are also explored.

2.3.1 Predicted UV-visible spectra of melanin tetramers. Our multi-output KRR-ML model predicts the absorption intensity value of each bin across the 200–800 nm spectral range. In Fig. 4a, we show the predicted UV-visible spectra of two random tetramers not present in the training dataset. The position of the vertical lines refers to the midpoint of each bin with a 50 nm width, and the height (marked by circles) of each line is the intensity value of that bin. Predicted and TDDFT reference intensities are shown in green and black color, respectively. As seen in Fig. 4a, different intensity distributions across the wavelength are well captured by the model, which was trained using simple fingerprint input. This indicates an ideal generalization of a model. More examples of predicted spectra are provided in the ESI.†

Fig. 4 ML prediction of UV-visible absorption spectra and relative energies. (a) UV-visible absorption spectra of two random tetramer molecules predicted using the multi-output KRR-ML model trained on a 10k dataset with fingerprint input. The vertical lines with circles on the top refer to the bin intensity values, and the curves are Gaussian broadening with FWHM equal to the bin resolution (i.e. 50 nm). (b) Scatter plot of DFT (B3LYP/6-31G(d)) versus predicted relative energies using the KRR-ML model trained on a 5k dataset with fingerprint input. The identity line (solid black) is also provided for comparison. (c) The Boltzmann-weighted average spectrum of DHI-melanin showing broad absorption across the UV-visible wavelength.

With the trained model, predicting the spectra of any molecule in the highly diverse melanin chemical space becomes straightforward. This ability to predict the full UV-visible spectra of ∼124k molecules marks a significant speedup compared to TDDFT calculations of a large number of excited states.

For application in dye-sensitized solar cells, the short-chain oligomers (e.g. the tetramers) are preferred over the aggregated form of melanin.⁴³ However, the individual tetramers do not absorb over a broad wavelength range. Using the spectra predicted by our model, one can identify tetramer pairs that exhibit strong absorption in specific regions while maintaining minimal spectral overlap with each other. The tetramers obtained in pairs can be connected in a “tandem” architecture to design tandem organic solar cells, which can offer a broader absorption range than single-junction organic solar cells.

2.3.2 Guide to stable material designing. Thermodynamic stability provides important insights into the structural information, such as planarity, the ratio of oxidized to reduced monomers in the tetramer structures, etc. Prediction of relative energies can help exclude a huge overload of unstable molecules before their spectral prediction.

The DFT vs. predicted relative energy scatter plot is provided in Fig. 4b, which shows an even distribution of the points around the identity line, suggesting a robust generalization of the model.

The stability analysis also reveals the predominance of oxidized monomers in the tetramers. This is vital from a synthesis standpoint, as the ratio of oxidized to reduced monomers is regulated by the pH and other factors in the reaction medium. DFT vs. predicted relative energy scatter plots for tetramers containing different proportions of oxidized and reduced monomers are provided in the ESI Fig. S7† as a guideline for stable material synthesis.

2.3.3 Broadband absorption spectrum of melanin. Natural melanin is known for its role in skin photoprotection, which is reflected through its broad and featureless absorption spectrum across the UV-visible range. However, the individual tetramers alone cannot produce the broad nature of the melanin spectrum (see Fig. 4a). Using the KRR-ML model, we made predictions of stabilities and spectra for the entire chemical space. Based on the predicted properties, the Boltzmann-weighted average spectrum is produced by calculatingwhere 〈A_k〉 is the Boltzmann-weighted average intensity value for the k-th bin, A_k,i is the intensity value for the k-th bin of the i-th molecule in the chemical space, N is the total number of molecules and p_i is the probability factor obtained from the relative energies (ΔG_i) asWe used T = 300 K and ML-predicted values for A_k,i and ΔG_i. The Boltzmann-weighted average spectrum shows broad absorption across the UV-visible range, as given in Fig. 4c. There are three major peaks at around 226 nm, 324 nm and 524 nm, which closely resemble the experimental spectrum of DHI-melanin.^18,44,45 This highlights the significance of the Boltzmann-weighted average of the individual tetramers in accurately predicting the spectral nature, as opposed to using the simple arithmetic average. While our predicted spectra are based on gas-phase conditions, the influence of solvent polarity has been found to be minimal, resulting in only slight shifts in peak positions.⁴⁵

The computational cost of our KRR-ML method is based on the cost of data generation and model training. The most costly part of data generation is TDDFT spectra calculation, which has a scaling k·O(N_e³) ∼ k·O(N_e⁴), where k is the number of desired excited states and N_e is the number of electrons in the molecule. Hence, the total data generation cost is N_train·k·O(N_e³) ∼ N_train·k·O(N_e⁴), where N_train is the number of training data. The cost of KRR model training depends on the Cholesky factorization of the kernel matrix K, which is an N_train × N_train matrix (see Section 4.3). This factorization has a computational cost m·O(N_train³),⁴⁶ where m is the number of target properties that are trained, e.g. the number of bins. Although the data generation cost depends on the system size, only a small subset of the data (here, <10% of the total chemical space) is needed to build the model. In the case of model training, the cost does not depend on the system size. Therefore, our model is scalable to larger systems, provided that a small subset of the chemical space's electronic absorption spectra is available for training.

3 Conclusions

In summary, we have designed a comprehensive chemical space of DHI-melanin oligomers. Using a simple fingerprint input representation, our multi-output KRR-ML method predicts the entire UV-visible absorption spectra of these oligomers. Through this method, we also demonstrated why predicting the intensities of bins with finite resolution is more beneficial than the excitation energies and oscillator strengths of a large number of TDDFT excited states.

Predicted UV-visible spectra showed good accuracy in terms of the overlap (∼80%) with TDDFT reference spectra. Our model, trained on less than 10% of the total molecules in the chemical space, offers substantial acceleration in predicting both the electronic absorption spectra and the thermodynamic stability of these large biomolecules. It is worth noting that the prediction of full spectra, which is closely equal to the lowest 60 TDDFT excited states, as well as B3LYP-level relative energies, can be achieved using only fingerprint-based input. This input is based on connectivity patterns and oxidation states which does not require geometry optimization, unlike those based on three-dimensional geometry.

In the final step, we compute the Boltzmann-weighted average spectrum based on the predictions made by the model. It correctly produces the broad spectrum of DHI-melanin observed in the experiments, lending support to the chemical heterogeneity hypothesis.

4 Methods

4.1 Combinatorial structure generation

The vastness of the chemical space arises due to a large number of possible connectivity patterns together with different oxidation states in the monomer units, which leads to a combinatorial explosion (see Fig. 5a). We progressively generated the oligomer structures using a combinatorial approach, as illustrated in Fig. 5b. Starting from parent monomers, we generated dimers, trimers and tetramers in 3 consecutive steps by attaching substituents at the available site of polymerization. By substituents, we refer to the three monomers of melanin with the available polymerization sites marked with colored arrows (see Fig. 5b).

Fig. 5 Data generation and data assessment for machine learning. (a) Combinatorial explosion in the melanin chemical space design: the number of all possible combinations increases exponentially. (b) Step-wise oligomer generation starting from monomers to sequentially generate dimers, trimers and tetramers. At each step, the alignment operation (illustrated in the upper-right corner) is performed on the parent and the substituent. (c) MAE (in eV) in excitation energies for the lowest 60 excited states calculated with TD-B3LYP and TD-CAM-B3LYP w.r.t. the SOS-CIS(D) method. The circles refer to the MAE for individual excited states, and the horizontal dashed lines refer to the MAE over all 60 states.

At each step, some geometric alignment is done along the coordinate axes. The bond of the molecule through which oligomerization occurs is aligned along the z-axis, and the molecular σ_h plane is aligned to the xz-plane. We performed this rotation operation for the parent and substituent, but their bond vectors are kept in opposite directions along the z-axis (see the upper-right of Fig. 5b). The corresponding oligomerization sites are kept 1.45 Å apart by removing the valence hydrogens. This produces 100 576 linear and 22 962 branched tetramers. A few of these tetramer structures, along with some cyclic tetramers, are shown in the ESI.† It is also important to note that during the structure generation process, we excluded oligomerization sites that would lead to steric clashes between substituents.

Given the limited number of cyclic tetramers, they were excluded from the ML modeling, as their spectra can be readily obtained via TDDFT. Additionally, the different connectivity patterns of cyclic tetramers necessitate a redefinition of the fingerprint representation, and training a separate ML model for cyclic tetramers would suffer from insufficient data.

4.2 Quantum chemistry calculations

We randomly select a small subset of the structures to perform quantum chemistry calculations, which generates the data needed to train and test our ML model. Given the large size of the tetramer molecules in our dataset, which contains 44 heavy atoms (CNO), we first relaxed the geometries with the universal force field (UFF) using OpenBabel.⁴⁷ This addresses any inconsistencies in the geometry, thereby preventing failures in the DFT (B3LYP/6-31G(d)) geometry optimization in the subsequent step using the Gaussian16 suite of the program.⁴⁸

The DFT-optimized geometries are then used to calculate the LR-TDDFT excitation energies and corresponding oscillator strengths with CAM-B3LYP/6-31G(d) using the Q-Chem software package.⁴⁹ The lowest 60 singlet excited states are computed to ensure coverage of the entire UV-visible spectrum range (200–800 nm). The DLPNO-CCSD(T)/cc-pVDZ calculations were performed using the ORCA quantum chemistry package.⁵⁰

The excitation energy calculation of the lowest bright state of the DHI monomer unit suggests that B3LYP is much closer to the experimental value (Table 1). However, given that we are calculating a large number of states, CAM-B3LYP is a more suitable option in our case.^53,54 We compared the performance of B3LYP and CAM-B3LYP with respect to SOS-CIS(D) in computing the 60 lowest excited states of the tetramers. The mean absolute error (MAE) for each excited state calculated over a small benchmark set is shown in Fig. 5c. We have also included the CAM-B3LYP/6-31G(d) spectrum of the DHI monomer in ESI Fig. S9,† which shows good agreement with the experimental spectrum.⁵¹

Table 1 Excitation energy (in eV) of the lowest bright excited state of a DHI monomer in its fully reduced form

Experiment^51	EOM-CCSD/6-31++G(d,p)^52	SOS-CIS(D)/6-31G(d)	TD-B3LYP/6-31G(d)	TD-CAM-B3LYP/6-31G(d)
4.13	4.55	4.62	4.62	4.79

---

4.3 Kernel ridge regression

KRR approximates the target excited state properties of a query input molecular descriptor (x_query) as a linear combination of the kernel function:Here, the kernel function, k(x_query, x_i), is a pairwise measure of similarity between the query molecule (x_query) and all N_train training molecules (x_i). The obvious way to find the regression coefficients (α_i) is to minimize the squared error loss function with an added regularization (λ)where is the norm of y^pred in the kernel Hilbert space.^55,56 This is done by solving the normal equation, which has a closed-form solution

α = [K + λI]⁻¹y (13)

where K is called the kernel matrix with elements K_ij = k(x_i, x_j) and y is the vector with elements y^ref_i. A non-zero λ always makes [K + λI] a positive-definite, and hence invertible. Utilizing the positive-definite nature of [K + λI], we employed Cholesky factorization to solve eqn (13) for single-output KRR and eqn (1) for multi-output KRR. The Python code can be found on the GitHub repository.

Among the most widely used kernel functions, we assessed the performance of the below functions. The Gaussian or radial basis kernel function is given by

with ‖·‖₂ being the L² norm and σ being the length scale of the kernel and the Laplacian kernel function is given bywith ‖·‖₁ being the L¹ norm.

The model hyperparameters, namely regularization strength (λ) and kernel parameter (σ), are evaluated via 5-fold cross-validation. This was done as follows. First, we have chosen 1250 molecules from the training dataset and divided them into 5 subsets, each containing 250 molecules. Then we trained the model using 4 subsets (1000 molecules) and tested it on 1 leave-out set (250 molecules). This is repeated 5 times, taking each subset as the test set and all other 4 subsets as the training set. This procedure was iterated for all possible combinations of λ and σ from the below array:

Finally, for each hyperparameter combination, we calculate the average error over the 5 fold and the combination which gives the lowest error was taken as the optimum hyperparameter for final model training. The optimum hyperparameter values are given in the ESI.†

Data availability

All the ML input, output data and relevant codes used to train our KRR-ML model are publicly available on GitHub (https://github.com/arpanchoudhury/mlspectra-DHI_melanin).

Author contributions

D. G. conceived of the project, A. C. and D. G. developed the algorithm and A. C. performed the calculations and models. All authors discussed and contributed to the manuscript writing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. C. thanks DST-INSPIRE and IACS for the senior research fellowship and research associateship. D. G. thanks SERB (SPF/2021/000194 and CRG/2023/001806) for funding.

Notes and references

1. S. R. Forrest and M. E. Thompson, Chem. Rev., 2007, 107, 923–925.
2. O. Ostroverkhova, Chem. Rev., 2016, 116, 13279–13412.
3. L. A. Baker, B. Marchetti, T. N. Karsili, V. G. Stavros and M. N. Ashfold, Chem. Soc. Rev., 2017, 46, 3770–3791.
4. C.-T. Chen, C. Chuang, J. Cao, V. Ball, D. Ruch and M. J. Buehler, Nat. Commun., 2014, 5, 3859.
5. H. Hoppe and N. S. Sariciftci, J. Mater. Res., 2004, 19, 1924–1945.
6. R. Kroon, M. Lenes, J. C. Hummelen, P. W. Blom and B. De Boer, Polym. Rev., 2008, 48, 531–582.
7. S. Mathew, A. Yella, P. Gao, R. Humphry-Baker, B. F. Curchod, N. Ashari-Astani, I. Tavernelli, U. Rothlisberger, M. K. Nazeeruddin and M. Grätzel, Nat. Chem., 2014, 6, 242–247.
8. J. Hachmann, R. Olivares-Amaya, S. Atahan-Evrenk, C. Amador-Bedolla, R. S. Sánchez-Carrera, A. Gold-Parker, L. Vogt, A. M. Brockway and A. Aspuru-Guzik, J. Phys. Chem. Lett., 2011, 2, 2241–2251.
9. H. Yao, L. Ye, H. Zhang, S. Li, S. Zhang and J. Hou, Chem. Rev., 2016, 116, 7397–7457.
10. M. d'Ischia, A. Napolitano, A. Pezzella, P. Meredith and T. Sarna, Angew. Chem., Int. Ed., 2009, 48, 3914–3921.
11. E. Vahidzadeh, A. P. Kalra and K. Shankar, Biosens. Bioelectron., 2018, 122, 127–139.
12. W. Xie, E. Pakdel, Y. Liang, Y. J. Kim, D. Liu, L. Sun and X. Wang, Biomacromolecules, 2019, 20, 4312–4331.
13. M. d'Ischia, A. Napolitano, A. Pezzella, P. Meredith and M. Buehler, Angew. Chem., Int. Ed., 2020, 59, 11196–11205.
14. A. Choudhury and D. Ghosh, Chem. Commun., 2020, 56, 10481–10484.
15. A. Choudhury, R. Ramakrishnan and D. Ghosh, Chem. Commun., 2024, 60, 2613–2616.
16. C.-T. Chen, F. J. Martin-Martinez, G. S. Jung and M. J. Buehler, Chem. Sci., 2017, 8, 1631–1641.
17. E. Kaxiras, A. Tsolakidis, G. Zonios and S. Meng, Phys. Rev. Lett., 2006, 97, 218102.
18. C. Grieco, F. R. Kohl, A. T. Hanes and B. Kohler, Nat. Commun., 2020, 11, 4569.
19. F. R. Kohl, C. Grieco and B. Kohler, Chem. Sci., 2020, 11, 1248–1259.
20. K. Vinod, R. Mathew, C. Jandl, B. Thomas and M. Hariharan, Chem. Sci., 2024, 15, 16015–16024.
21. C. A. Ullrich, Time-Dependent Density-Functional Theory: Concepts and Applications, OUP Oxford, 2011.
22. M. E. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323.
23. E. R. Davidson, J. Comput. Phys., 1975, 17, 87–94.
24. C. Lanczos, Applied Analysis, Dover, New York, 1988.
25. M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. Von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301.
26. F. A. Faber, L. Hutchison, B. Huang, J. Gilmer, S. S. Schoenholz, G. E. Dahl, O. Vinyals, S. Kearnes, P. F. Riley and O. A. Von Lilienfeld, J. Chem. Theory Comput., 2017, 13, 5255–5264.
27. C. Rauer and T. Bereau, J. Chem. Phys., 2020, 153, 014101.
28. J. Weinreich, N. J. Browning and O. A. von Lilienfeld, J. Chem. Phys., 2021, 154, 134113.
29. J. Westermayr and P. Marquetand, Chem. Rev., 2020, 121, 9873–9926.
30. A. Choudhury and D. Ghosh, J. Comput. Chem., 2025, 46, e70038.
31. S. Ye, W. Hu, X. Li, J. Zhang, K. Zhong, G. Zhang, Y. Luo, S. Mukamel and J. Jiang, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 11612–11617.
32. B.-X. Xue, M. Barbatti and P. O. Dral, J. Phys. Chem. A, 2020, 124, 7199–7210.
33. R. Ramakrishnan, M. Hartmann, E. Tapavicza and O. A. Von Lilienfeld, J. Chem. Phys., 2015, 143, 084111.
34. E. Tapavicza, G. F. von Rudorff, D. O. De Haan, M. Contin, C. George, M. Riva and O. A. Von Lilienfeld, Environ. Sci. Technol., 2021, 55, 8447–8457.
35. P. Kayastha, S. Chakraborty and R. Ramakrishnan, Digital Discovery, 2022, 1, 689–702.
36. D. Bosch, J. Wang and L. Blancafort, Chem. Sci., 2022, 13, 8942–8946.
37. J. Guo, M. Sun, X. Zhao, C. Shi, H. Su, Y. Guo and X. Pu, J. Chem. Inf. Model., 2023, 63, 1143–1156.
38. Y.-J. Duan, L. Fu, X.-C. Zhang, T.-Z. Long, Y.-H. He, Z.-Q. Liu, A.-P. Lu, Y.-F. Deng, C.-Y. Hsieh and T.-J. Hou, et al. , J. Chem. Inf. Model., 2023, 63, 2345–2359.
39. Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing and V. Pande, Chem. Sci., 2018, 9, 513–530.
40. J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203.
41. S.-C. Li, H. Wu, A. Menon, K. A. Spiekermann, Y.-P. Li and W. H. Green, J. Am. Chem. Soc., 2024, 146, 23103–23120.
42. B. Huang and O. A. von Lilienfeld, Nat. Chem., 2020, 12, 945–951.
43. N. Al-Shamery, J.-H. Park, S. R. Kim, F. Heppner, S. Y. Yoon, T. Bredow, T.-H. Kwon and P. S. Lee, Mater. Adv., 2025 10.1039/D5MA00081E.
44. R. Micillo, L. Panzella, M. Iacomino, G. Prampolini, I. Cacelli, A. Ferretti, O. Crescenzi, K. Koike, A. Napolitano and M. d'Ischia, Sci. Rep., 2017, 7, 41532.
45. X. Wang, L. Kinziabulatova, M. Bortoli, A. Manickoth, M. A. Barilla, H. Huang, L. Blancafort, B. Kohler and J.-P. Lumb, Nat. Chem., 2023, 15, 787–793.
46. L. N. Trefethen and D. Bau, Numerical Linear Algebra, SIAM, 2022.
47. N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 1–14.
48. M. e. Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson, H. Nakatsuji, et al., Gaussian 16, 2016.
49. Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng, et al. , Mol. Phys., 2015, 113, 184–215.
50. F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 73–78.
51. M. Gauden, A. Pezzella, L. Panzella, A. Napolitano, M. d'Ischia and V. Sundstrom, J. Phys. Chem. B, 2009, 113, 12575–12580.
52. P. Ghosh and D. Ghosh, J. Phys. Chem. B, 2017, 121, 5988–5994.
53. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
54. Z.-L. Cai, M. J. Crossley, J. R. Reimers, R. Kobayashi and R. D. Amos, J. Phys. Chem. B, 2006, 110, 15624–15632.
55. M. Rupp, Int. J. Quantum Chem., 2015, 115, 1058–1073.
56. A. Dawid, J. Arnold, B. Requena, A. Gresch, M. Płodzień, K. Donatella, K. A. Nicoli, P. Stornati, R. Koch, M. Büttner, et al., arXiv, 2022, preprint, arXiv:2204.04198,  DOI:10.48550/arXiv.2204.04198.

---

Footnote

† Electronic supplementary information (ESI) available: Fingerprint generation, ML hyperparameters, predicted spectra, and DFT vs. predicted relative energy. See DOI: https://doi.org/10.1039/d5sc00046g

---