An investigation of contributors to the spin exchange interactions in organic pentacene–radical dyads using quasi-degenerate perturbation theory†
Philip S.
Weiss
 a,
Amiel S.
Paz
abc and
Claudia E.
Avalos
a,
Amiel S.
Paz
abc and
Claudia E.
Avalos
 *a
*a
aDepartment of Chemistry, New York University, New York, New York 10003, USA. E-mail: claudia.avalos@nyu.edu
bNYU Shanghai, 567 West Yangsi Road, Shanghai 20012, China
cNYU-ECNU Center for Computational Chemistry at NYU Shanghai, 3663 North Zhongshang Road, Shanghai 200062, China
First published on 7th March 2025
Abstract
Chromophore–radical (C–R) dyads are a promising class of molecules with potential applications in magnetometry, nuclear magnetic resonance and quantum sensing. Given the vast chemical space that is possible in these systems, computational studies are vital to aid in the rational design of C–R molecules with desired electronic and spin properties. Multireference perturbation theory (MRPT) calculations have been shown to be useful for rationalizing spin correlations in C–R dyads. In this work we apply quasi-degenerate perturbation theory, specifically QD-NEVPT2, for the prediction of vertical transition energies (VTEs) as well as spin-correlation parameters in three-spin-center pentacene–radical dyads containing up to 153 atoms. We find that QD-NEVPT2 performs well in the prediction of JTR, the magnetic coupling parameter between the excited-state triplet and the radical, but underestimates VTEs; this underestimation is attributed to variational averaging over different spin states and active space limitations, and we show that addressing these shortcomings reduces error. The calculated magnitudes and signs of JTR are rationalized through molecular symmetry, coupling distance, and π-structure considerations. The predicted signs of JTR are consistent with and explained via mechanisms of kinetic and potential spin-exchange, allowing for future functional design of magnetic organic molecules. The role of active space choice on VTE accuracy and predicted magnetic coupling is additionally explored.
1 Introduction
Systems that exhibit optically induced spin polarization have applications in optically detected magnetometry,1 nanoscale nuclear magnetic resonance,2 and quantum sensing.3 The characterization and optimization of the spin properties of such systems is a growing field and is one that encompasses a variety of molecular systems, including point defects in solids, as well as organic and inorganic chromophore–radical (C–R) dyads. Photoexcitation of organic chromophore–radical dyads has been shown to lead to electron spin polarization (ESP) of the tethered radical following the spin-selective decay of a polarized triplet formed via intersystem crossing (ISC).4–6 In general, whether a C–R system exhibits ESP following excitation depends on the spin-coupling parameters of the chromophore and radical, as well as the efficiency of the photophysical processes that convert optically bright states to spin-polarized states, dictated in large part by the ordering and spacing of the excited states. One such photophysical process that chromophore–radical dyads have been known to exhibit, and which often leads to ESP, is radical-enhanced intersystem crossing (EISC).4,7–9 In EISC, strong coupling between the radical moiety and chromophore leads to the rapid formation of a spin polarized triplet state on a picosecond timescale. The extent of mixing between the chromophore triplet and radical doublet states further determines whether this process may be accompanied by the formation of a spin polarized ground state.The spin Hamiltonian for a triplet–radical system is shown below:4
 | (1) |
The combined triplet–radical spin system can be described in terms of a product basis, where the state mixing is defined by the δ and γ mixing coefficients.4 As described in ref. 4 and 11 and reproduced here, we can define these states at high-field as follows:
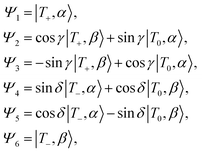 | (2) |
 state, β denotes an electron in the
state, β denotes an electron in the  state, and T+,T−, and T0 stand for the three triplet chromophore states |αα〉, |ββ〉, and
state, and T+,T−, and T0 stand for the three triplet chromophore states |αα〉, |ββ〉, and  ), respectively.
), respectively.
The magnitude of the exchange coupling constant compared to that of the uniaxial zero-field splitting (ZFS) parameter DT and Zeeman terms allows for the distinction of the three coupling regimes. At zero-field, when  is much less than, about equal to, or much greater than 1, these are known as the weak, intermediate, and strong coupling regimes respectively.4 The hyperfine term (eqn (1)) for the systems here is on the order of ∼10−3 cm−1, and is comparable in magnitude to the other terms only in the most weakly coupled cases.
is much less than, about equal to, or much greater than 1, these are known as the weak, intermediate, and strong coupling regimes respectively.4 The hyperfine term (eqn (1)) for the systems here is on the order of ∼10−3 cm−1, and is comparable in magnitude to the other terms only in the most weakly coupled cases.
In the presence of a magnetic field, the coupling regime is defined by comparing the magnitude of the exchange interaction, JTR, relative to the difference in the Zeeman energies of the two spin systems, (gT − gR)μBB0, as well as considering the relative magnitudes of the Zeeman energy of the spin system and the zero-field splitting parameters of the triplet.11 We do not consider the contribution of the dipolar interaction as it is much smaller than the zero-field splitting in the structures studied here.
In the limit of no-coupling we have the triplet–doublet product states:
 | (3) |
In the strong coupling limit these states transform as:
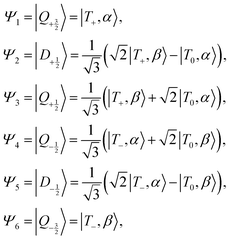 | (4) |
In the limit of strong exchange coupling, JTR ≫ |gT − gR| μBB0 and μBB0gT, μBB0gR ≫ DT, the eigenfunctions are pure quartet and doublet states.11 In the zero-field case, where JTR is the dominant interaction, we can categorize the coupling regimes for chromophore–radical species based on the ratio  .
.
Following the production of a polarized triplet, the evolution of ESP on the radical has been attributed to at least two different processes, the reverse quartet mechanism (RQM) for the case of strong coupling, and the electron spin polarization transfer (ESPT) mechanism for the case of weak coupling.12–14 The sign and magnitude of the observed ESP evolution depends in part on the sign and magnitude of JTR. Accurate modeling of the excited state energies and spin coupling properties in chromophore–radical dyads is essential for increasing our understanding of the spin polarization mechanisms at play, as well as for narrowing down design rules. Molecular design motifs such as radical–triplet distance, conjugation, and the presence of heavy atoms all play a major role in determining the coupling parameters and resulting photophysical behavior.4,15 In this work, we calculate the excited state energies and spin exchange parameters of a class of organic C–R dyads based on pentacene chromophores. We use these results to rationalize the experimentally observed photophysics in a set of pentacene–radicals found in an intermediate coupling regime that exhibit both strong and weak coupling behavior.5
Types of exchange coupling. The spin-exchange interaction can be broadly understood as the potential between spin centers that determines the energetic ordering of a high-spin and low-spin state. As this magnetic interaction is weak compared to the Coulomb interaction, the coupling is very sensitive to the nature of magnetic orbital (i.e. singly-occupied orbital) overlap. For example, while magnetically active orbitals may be in close proximity, constructive versus destructive interference of probability amplitudes as well as structural barriers to π-delocalization can result in entirely different coupling signs.16 Quantum chemistry methods are thus particularly useful as it allows for the detailed study of these orbital interactions.
In the calculation of spin exchange interactions, a popular choice of methodology is broken-symmetry density functional theory (BS-DFT),17 in which spin exchange coupling constants are calculated using an energy difference of a high-spin and a broken-symmetry determinant. However, this method exhibits variance in numerical accuracy based on choice of functional and spin projection scheme. BS-DFT also overestimates exchange interactions due to spurious delocalization of magnetic orbitals.18,19 In turn, multireference methods such as the complete active space self-consistent field (CASSCF)20,21 in tandem with multireference perturbation theory (MRPT) avoid the limitations of BS-DFT and provide reliable excited state exchange couplings.22
Recently, Franz et al. used a particular flavor of MRPT – quasi-degenerate n-electron valence perturbation theory (QD-NEVPT2)23,24 – with a Heisenberg–Dirac–van-Vleck (HDVV) effective Hamiltonian to calculate JTR in perylene-tethered radicals and found good agreement between calculated and experimentally determined signs of JTR.22 We thus apply their procedure to our own set of C–R systems.
We note that other variants of MRPT have been found to be successful in the prediction of spectra of single organic molecules, particularly extended multistate complete active space second-order perturbation theory (XMS-CASPT2).25,26 We therefore performed additional benchmarking calculations using this method in the BAGEL v1.2.2 quantum chemistry package,27 the results for which are given in the ESI.† Important contributors to the sign of the exchange coupling are illustrated in the two-center Hubbard Hamiltonian for spin-1/2 particles28–31 expressed here in the second quantization form:
 | (5) |
 | (6) |
The third term on the RHS of eqn (5) is the energetic contribution from potential exchange and as indicated by the negative sign of this term (since Kij is always positive), stabilizes the high-spin state. This term therefore favors a ferromagnetic coupling in the excited state. It will be shown that many of the calculated BDPA-tethered pentacene structures were found to exhibit excited-state ferromagnetic coupling (ESFC) which can be explained when considering the predictors outlined by Goodenough and Kanamori.33–35 These rules state that ferromagnetic coupling in a system can be expected when the interacting magnetic orbitals are close enough to experience each others’ potentials, but the nature of orbital overlap is such that the bonding character is negligible. For example, this would arise in cases where one has coupling between electrons occupying same-site orthogonal p orbitals (e.g. px, py) or an s orbital overlapping symmetrically on either side of the nodal plane of a π orbital, such that overlap with either lobe is equal and opposite, and the overlap integral  . In contrast to the potential exchange, Kij, there is a kinetic exchange interaction which instead favors antiferromagnetic coupling.33–35 When orbital interference favors the formation of a bonding/anti-bonding molecular orbital pair, the presence of configuration state functions where two electrons are spin-paired in a single orbital can deliver greater energetic stability (i.e. the pairing energy) than is offered by Kij. These configurations are known as ionic determinants, as opposed to neutral determinants in which each spin center contains at most one electron. This energetic stability from pairing is captured in the first term on the RHS of eqn (5), i.e. the hopping integral, tij. The balance between the magnitudes of these terms tij, Ui, and Kij determines the relative stability, and thus ordering, of high- and low-spin states, and therefore the sign of J. Electrons of the same spin cannot benefit from pairing interactions due to the Pauli exclusion principle, and the pairing stabilization from an ionic state is offset by the energetic tax of two electrons occupying the same space.
. In contrast to the potential exchange, Kij, there is a kinetic exchange interaction which instead favors antiferromagnetic coupling.33–35 When orbital interference favors the formation of a bonding/anti-bonding molecular orbital pair, the presence of configuration state functions where two electrons are spin-paired in a single orbital can deliver greater energetic stability (i.e. the pairing energy) than is offered by Kij. These configurations are known as ionic determinants, as opposed to neutral determinants in which each spin center contains at most one electron. This energetic stability from pairing is captured in the first term on the RHS of eqn (5), i.e. the hopping integral, tij. The balance between the magnitudes of these terms tij, Ui, and Kij determines the relative stability, and thus ordering, of high- and low-spin states, and therefore the sign of J. Electrons of the same spin cannot benefit from pairing interactions due to the Pauli exclusion principle, and the pairing stabilization from an ionic state is offset by the energetic tax of two electrons occupying the same space.
In pursuit of clarity, we will take a moment to differentiate two different types of “overlap.” “Orbital overlap” (or “wavefunction overlap”) implies that one is discussing the interference of the probability amplitudes of two or more molecular orbitals. “Density overlap” on the other hand, describes the extent to which the orbitals share regions of significant non-zero probability density, where the probability density is defined as ρa(r) = |ψa(1)|2, and the density overlap as  . It is possible (and indeed is often the case) that orbitals for which Sab = 0 also exhibit Πab > 0.
. It is possible (and indeed is often the case) that orbitals for which Sab = 0 also exhibit Πab > 0.
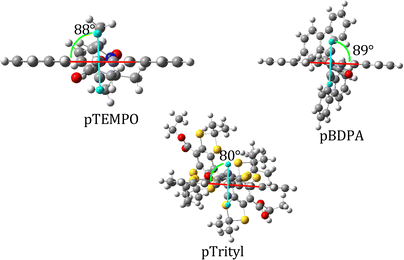
The remainder of the paper is organized as follows. Following a methods overview, we first evaluate the performance of the QD-NEVPT2 method for the reproduction of experimentally known vertical excitation energies and qualitative spin coupling magnitudes in pentacene–radical systems. This is followed by a detailed study of the effect of molecular functionalization on the sign and magnitude of the triplet–radical exchange coupling parameter JTR. In particular, we study the effects of changing the key dihedral angles, bridge modifications, breaking of molecular symmetry, emergent effects of cross conjugation, and strengthening of π interactions between the spin centers. Finally, we revisit these effects using a larger active space. The principal aims of this work are to understand patterns in the sign and magnitude of JTR in pentacene–radical systems and to explain the observation of EISC and electron spin polarization (ESP) in triisopropylsilyl (TIPS)/pentacene-tethered tetrathiaryl trityl (pTrityl) and the absence of EISC and ESP in similarly coupled systems 2,2,6,6-tetramethylpiperidine 1-oxyl (pTEMPO) and α,γ-bisdiphenylene-β-phenylallyl (pBDPA).5 These structures are labeled as 1a (pTEMPO), 1b (pBDPA) and 1c (pTrityl) in Fig. 2.
 | ||
| Fig. 2 The three radical moieties used in this study are labeled as a, b, c. The distinct binding site and bridge structures are labeled 1–11, with R indicating one of the three radicals. | ||
2 Methods
2.1 Geometry optimization
Geometry optimizations utilized the TeraChem v1.9 (development version) quantum chemistry package.36,37 The unrestricted ωPBEh functional38,39 was used with the cc-PVDZ basis.40 For TEMPO and BDPA, an additional optimization step using the aug-cc-PVDZ basis was performed. No auxiliary basis sets were used. Example input files are given in the ESI.†2.2 QD-NEVPT2
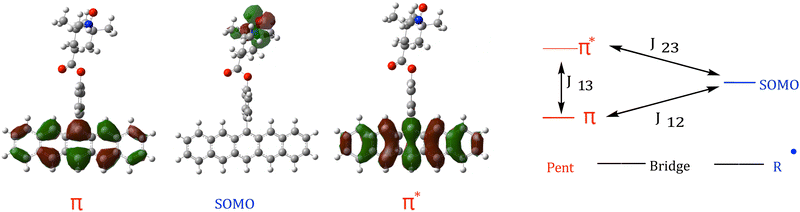
QD-NEVPT2 calculations were carried out in the ORCA 5.0.4 package41,42 and followed the procedure outlined in ref. 22. Briefly, strongly-contracted NEVPT2 (SC-NEVPT2) calculations were performed with the def2-TZVP basis using the RIJK resolution of identity approximation (choice of def2/JK for both the AuxC and AuxJK fitting basis) and a quasi-degenerate van Vleck effective Hamiltonian.43 Calculations were initially performed using a minimal πpent/radical/ (3,3) active space, as shown in Fig. 3. Default convergence criteria for ORCA 5.0.4 was employed for the CASSCF module, and a corresponding example input file is given in the ESI.† Guess orbitals were generated via an unrestricted Kohn–Sham procedure as part of a TD-DFT calculation, utilizing the same choice of basis set and resolution of identity approximations, and the default integration grid. Since these orbitals are from an unrestricted calculation, they are then transformed to the corresponding set of quasi-restricted orbitals, and are then inspected for active space orbital selection. Example input files are given in the ESI.†
(3,3) active space, as shown in Fig. 3. Default convergence criteria for ORCA 5.0.4 was employed for the CASSCF module, and a corresponding example input file is given in the ESI.† Guess orbitals were generated via an unrestricted Kohn–Sham procedure as part of a TD-DFT calculation, utilizing the same choice of basis set and resolution of identity approximations, and the default integration grid. Since these orbitals are from an unrestricted calculation, they are then transformed to the corresponding set of quasi-restricted orbitals, and are then inspected for active space orbital selection. Example input files are given in the ESI.†
Various expansions of this active space were also carried out to target possible sources of missing static electron correlation, including allowing for radical-localized π → π* excitations or expanding the description of the pentacene π subspace. In addition, higher energy sing-doublet states above the main excitation and doublet/quartet manifold were requested due to the possibility of EISC via resonant energy transfer.44
In addition to excitation energies, J-exchange parameters (as shown in Fig. 3) were calculated. For a complete review of the technique one may refer to ref. 22, but concisely, one can extract J-exchange parameters J12, J23, and J13 (Fig. 3) via the Heisenberg–Dirac–van Vleck effective Hamiltonian:
 | (7) |
In addition, JTR can be solved for directly from the computed state energies:
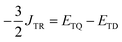 | (8) |
This equation is valid for the case where J13 ≥ JTR, as is the case for the systems studied here. ETD is the energy of the trip-doublet state associated with the D/Q manifold, |D+1/2〉, and ETQ is the energy of the corresponding trip-quartet state, |Q+3/2〉.
After localizing the active-space orbitals with a Foster–Boys procedure, the QD-NEVPT2 state vectors were projected onto the neutral determinant basis |ααβ〉, |αβα〉, |βαα〉.
The trip-quartet state, |Q+3/2〉, represented in this neutral determinant basis is:
 | (9) |
The new neutral determinant coefficient matrix was then renormalized and orthogonalized via a Löwdin orthogonalization.45 The original Hamiltonian (a diagonal matrix with calculated state energies on the diagonal, re-scaled to set ETQ = 0) rotated into the basis of the orthogonal neutral determinant coefficient matrix has one-to-one correspondence with the Heisenberg–Dirac–van Vleck Hamiltonian, and therefore expressions for J12, J23, and J13 can be determined.
3 Results and discussion
Quasi-degenerate SC-NEVPT2 calculations with the canonical van Vleck treatment were carried out on structures 1a–c. A minimal 3-electron, 3-orbital (3,3) active space was used, including only the π and π* orbitals of the pentacene moiety, and the singly occupied molecular orbital (SOMO) of the radical, as shown in Fig. 3 for pTEMPO 1a. The corresponding orbitals for pBDPA 1b and pTrityl 1c are shown in Fig. S3 (ESI†). The calculated VTEs, oscillator strengths, and JTR values are presented in Table 1 for structures 1a–c. Collected results including all structures which will be discussed later in this section, are given in Table 2. The D0 → D2 transition has the most significant oscillator strength among the lowest-lying doublet transitions in all three systems, suggesting (and confirmed by inspection of state configurations) that it is the main S0 → S1 excitation of pentacene. When compared to experimental values, calculated VTEs differed by −0.50, −0.59, and −0.50 eV for 1a, 1b, and 1c, respectively. Underestimations were expected, as variational optimization to a state-averaged energy of doublet and quartet states during the CASSCF step destabilizes the doublet ground state. Further error can be attributed to the high dimensionality (Nelec) of the system, requiring the use of a strongly-contracted scheme for NEVPT2, as well as the limitations of a minimal pentacene active space.| State | pTEMPO [1a] (eV) | f | pBDPA [1b] (eV) | f | pTrityl [1c] (eV) | f |
|---|---|---|---|---|---|---|
| Q 0 | 1.299 | 0.000 | 1.258 | 0.000 | 1.293 | 0.000 |
| D 1 | 1.299 | 0.000000 | 1.258 | 0.000 | 1.293 | 0.000 |
| D 2 | 1.506 | 0.2215 | 1.413 | 0.1275 | 1.497 | 0.2230 |
| D 3 | 2.128 | 0.000979 | 1.843 | 0.000 | 2.120 | 0.000828 |
| J TR (cm−1) | −0.001250 | −0.0009760 | −0.003733 | |||
| D 1 (eV) | D 2 (eV) | D 3 (eV) | Q 0 (eV) | J TR (cm−1) | |
|---|---|---|---|---|---|
| 1a | 1.299 | 1.506 | 2.128 | 1.299 | −0.001250 |
| 1a* | 1.288 | 1.488 | 2.125 | 1.288 | −0.004123 |
| 1b | 1.258 | 1.413 | 1.843 | 1.258 | −0.0009760 |
| 1b* | 1.243 | 1.401 | 1.738 | 1.243 | 0.01601 |
| 1c | 1.293 | 1.497 | 2.120 | 1.294 | −0.003733 |
| 1c* | 1.282 | 1.480 | 2.114 | 1.282 | −0.8535 |
| 2a | 1.301 | 1.505 | 2.128 | 1.301 | −0.004723 |
| 2b | 1.159 | 1.302 | 1.697 | 1.159 | 0.3224 |
| 2c | 1.294 | 1.491 | 2.111 | 1.294 | −0.6253 |
| 2d | 1.222 | 1.427 | 2.125 | 1.222 | −0.01628 |
| 3a | 1.301 | 1.502 | 2.129 | 1.301 | −0.003994 |
| 3b | 1.265 | 1.412 | 1.765 | 1.265 | −0.006103 |
| 3c | 1.295 | 1.488 | 2.113 | 1.295 | −0.03963 |
| 4a | 1.291 | 1.633 | 2.227 | 1.291 | −0.002394 |
| 4b | 1.260 | 1.561 | 2.192 | 1.260 | −0.1341 |
| 4c | 1.284 | 1.626 | 2.215 | 1.284 | −0.2433 |
| 5a | 1.289 | 1.631 | 2.223 | 1.289 | −0.002471 |
| 5b | 1.260 | 1.560 | 2.189 | 1.260 | 0.02946 |
| 5c | 1.281 | 1.625 | 2.213 | 1.282 | −1.010 |
| 6a | 1.244 | 1.477 | 2.124 | 1.244 | 0.06732 |
| 6b | 1.179 | 1.330 | 1.361 | 1.181 | 10.49 |
| 6c | 1.006 | 1.212 | 1.843 | 1.100 | −509.7 |
| 6d | 1.223 | 1.439 | 2.102 | 1.222 | 2.941 |
| 7a | 1.221 | 1.420 | 2.154 | 1.221 | 0.02960 |
| 7b | 1.171 | 1.440 | 1.658 | 1.171 | −0.3387 |
| 7c | 1.195 | 1.334 | 2.075 | 1.199 | −22.48 |
| 8a | 1.287 | 1.630 | 2.215 | 1.287 | 0.006775 |
| 8b | 1.256 | 1.555 | 1.834 | 1.256 | 1.769 |
| 8c | 1.263 | 1.606 | 2.185 | 1.275 | −68.48 |
| 8d | 1.287 | 1.626 | 2.213 | 1.222 | 0.3747 |
| 9b | 1.304 | 1.503 | 1.775 | 1.304 | −0.005186 |
| 9c | 0.1374 | 1.431 | 1.622 | 1.431 | 0.03532 |
| 10b | 1.307 | 1.498 | 1.698 | 1.307 | −0.03765 |
| 10c | 0.03933 | 1.323 | 1.510 | 1.323 | 0.06960 |
| 11b | 1.228 | 1.431 | 1.753 | 1.228 | −0.5977 |
| 11c | 0.04325 | 1.260 | 1.459 | 1.260 | 1.450 |
| 12a | 1.225 | 1.431 | 2.097 | 1.225 | 0.01563 |
| 12d | 1.301 | 1.498 | 2.092 | 1.301 | 0.2501 |
| 13a | 1.265 | 1.416 | 2.063 | 1.265 | 1.376 |
| 14a | 0.09897 | 0.1076 | 0.4522 | 0.1076 | −0.002875 |
In all three structures 1a–cD1 was found to be the trip-doublet state, with configuration coefficients ΨD1 = 0.82|αβα〉 + 0.41|ααβ〉 + 0.41|βαα〉, in agreement with eqn (4).
QD-NEVPT2 performs well in capturing the expected magnitude of JTR for weakly-coupled systems 1a–c and is reasonably consistent with what has been observed in transient ESR measurements.4,5 The (trip-doublet) D1 and (trip-quartet) Q0 states were calculated to be degenerate to at least two decimal places (in eV), reflecting the expected weak triplet–radical coupling in molecules 1a, 1b and 1c. While pTrityl displayed the greatest |JTR| among the three structures, the calculated magnitude is weaker than expected.5 Previously published experimental results indicate either an intermediate regime or a distribution of JTR parameters. For pentacene in a p-terphenyl matrix, the zero-field splitting parameter has previously been found to be DT = 0.046509 cm−1.46 In order to be in the strong coupling regime, we would expect our calculated JTR magnitude to be more than an order of magnitude greater than this, or approximately equal for the intermediate case. The same sign of JTR was predicted for all three systems (JTR < 0), and if one considers the JTR/DT ratio, the three pentacene–radicals are in a weak-to-intermediate coupling regime.
Lastly, in addition to the electronic states shown in Fig. 1, a configuration corresponding to a higher energy state D3 was also predicted in the structures 1a–c. The D3 state in 1a and 1c exhibits the character of a double excitation in the pentacene from the HOMO to LUMO, resulting in a doubly occupied  orbital. In pBDPA (1b) the D3 state is instead dominated by a πpent → πSOMO charge-transfer configuration forming pent˙+–PhCOO–BDPA˙− (where πSOMO denotes the radical-localized π orbital containing the unpaired electron in the single-determinant ground state (SDGS) configuration).
orbital. In pBDPA (1b) the D3 state is instead dominated by a πpent → πSOMO charge-transfer configuration forming pent˙+–PhCOO–BDPA˙− (where πSOMO denotes the radical-localized π orbital containing the unpaired electron in the single-determinant ground state (SDGS) configuration).
We note that the magnitudes of JTR predicted in structure 1 molecules, which are on the order of 10−3 cm−1, correspond to energy differences of ∼10−9 Hartrees, which is smaller than the default CASSCF convergence energy change tolerance of 10−6 Hartrees. For this reason, calculations for 1a,b,c were repeated using the “VeryTightSCF” convergence settings, corresponding to an energy change tolerance of 10−9 Hartrees. With these updated convergence settings, JTR was found to be −0.001112, −0.0009657, and −0.003730 cm−1 respectively for structures 1a, 1b, and 1c. These values deviate from those found with default convergence criteria by 11%, 1.1%, and 0.08% respectively. We believe the consistency of the JTR values under much stricter convergence criteria (on the same order of magnitude as the present calculated exchange coupling) provides sufficient evidence for the (careful) interpretation of these results. Keeping in mind the small magnitudes of these splittings, however, precise coupling magnitudes will be interpreted for the most part within the context of this study, i.e. we are interested in relative sign and magnitude changes as a function of molecular functionalization rather than evaluation of the accuracy of our JTR values in comparison to experiment. Indeed, the difficulty in obtaining these experimental values accurately is a primary reason we are pursuing this work. For the sake of completion we also calculated values of JTR for these systems after geometry optimization under a different functional, this time the ωB97X-D3 functional.47,48 Results were consistent and can be found in the ESI† “Consistency of results after geometry optimization with an alternate functional.”
3.1 Addressing the error in the main excitation of pentacene
Expanding the active space to include more π-type orbitals is known to improve the accuracy of calculated VTEs in conjugated systems, assuming the additional orbital(s) are relevant contributors to the excitation of interest. For example, mean absolute errors in the SC-NEVPT2 calculation of π → π* vertical singlet excitation energies in small organic molecules of 0.16 eV49 and 0.23 eV50 have previously been reported with active spaces as large as 12 electrons in 9 orbitals. While it is possible to better describe the main excitation by increasing the active space to include pentacene-localized π-orbitals energetically neighboring the HOMO and LUMO, this was not done across all structures due to the increase in computational cost given that our primary goal was to accurately model JTR. However, to ease the conscience regarding the errors in the S0 → S1 excitation, QD-NEVPT2 calculations were carried out on lone pentacene using the same perturbation parameters with the (2,2) and (6,6) active spaces with and without a quartet state requested, to test whether the method itself or the minimal active space was a greater contributor to the large error exhibited here. Experimental measurements on isolated pentacene in a neon matrix report a 542.7 nm (2.28 eV) transition energy from the ground to first excited state.51 In the case of a (2,2) minimal active space, requesting three singlets and one triplet, the S0 → S1 excitation is predicted to be 1.69 eV, and improves to 1.84 eV when the triplet state is not requested (errors of −0.59 and −0.44 eV, respectively). Using a (6,6) active space and requesting four singlet states and two triplet states, a 1.92 eV S0 → S1 excitation is predicted, which improves to 2.07 eV when only three singlet and no triplet states are requested (errors of −0.36 and −0.21 eV, respectively). The (6,6) active space calculations therefore, while still systematically underestimating this excitation energy, demonstrated a significant improvement on the prediction compared to the (2,2) active space. Coto et al.52 using CASPT2 (14,14) predicted an S0 → S1 excitation energy of 2.31 eV, with an error of only 0.03 eV. Thus, the accuracy of the QD-NEVPT2 methods applied here can likely be further improved upon via further inclusion of excitation-relevant orbitals in the pentacene-localized subspace of the active space.Calculations on structures 1a,b,c requesting only doublet states with a (3,3) minimal active space gave  excitation energies of 1.64, 1.63, and 1.62 eV respectively, improving on errors from simultaneous quartet/doublet calculation by 0.14, 0.22, and 0.12 eV.
excitation energies of 1.64, 1.63, and 1.62 eV respectively, improving on errors from simultaneous quartet/doublet calculation by 0.14, 0.22, and 0.12 eV.
3.2 Adjustment of the pentacene/phenyl and phenyl/carbonyl dihedral angles
Previously obtained transient electron spin resonance measurements of pTrityl 1c showed signals of both weakly and strongly coupled systems which is characteristic of an intermediate regime.5 In particular, both quartet and triplet signals were observed. In the study,5 pTrityl molecules were dissolved in a glass forming a matrix which is then flash frozen. One hypothesis that was proposed as an explanation for the appearance of both signals was that upon flash freezing, the distribution of bridge/pentacene dihedral conformations gives rise to differing coupling regimes. In order to test this hypothesis, a structural study was carried out by manually adjusting the pentacene/phenyl and phenyl/carbonyl dihedral angles in structures 1a–c, in order to investigate how the magnitude and sign of JTR change under a reasonable molecular torsion. These structures are labeled by an asterisk (i.e.1a*) in Table 2. The pentacene/phenyl dihedral angle in each aug-cc-PVDZ optimized structure was set to 55° and the phenyl/carbonyl angle to 37°, as shown in Fig. 4. Of particular note was the significant increase in JTR for pTrityl relative to pTEMPO and pBDPA following angle-adjustment, and importantly its shift from a weak/intermediate to strong coupling regime (|JTR| ≫ DT ≈ 0.045 cm−1). These results are consistent with angle-adjusted pTrityl being found in a strong/intermediate coupling regime. JTR for pTEMPO increased by less than an order of magnitude, in pBDPA by one order of magnitude, and in pTrityl by two orders of magnitude (results shown in Table 3). Furthermore, the JTR of pBDPA changed sign. The relative changes in magnitude can be attributed to the presence of π-system interactions between the radical and pentacene subunits in pBDPA and pTrityl as contrasted with the π-system interruption in the TEMPO moiety. This effect can be highlighted by noting that |JTR| in pTrityl 1c was 299% larger than that for 1a at equilibrium, and was 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 697% larger after the angle adjustment. From these results it can be seen that angle adjustment had a much more significant effect on 1c than 1a. These results provide a promising explanation for the appearance of EISC and a spin polarized ground state in 1c. The significant response in the |JTR| of pTrityl compared to pBDPA and pTEMPO, in addition to its shift to a strong coupling regime, could suggest that upon experimental flash freezing of the sample in ref. 5 a torsion of the bridge promoting greater pentacene/bridge planarity could lead to a distribution of JTR values causing some population to be in the weak coupling regime and some in the strong coupling regime. For the case of pTEMPO, 1a, upon changing the dihedral angle, |JTR| did not increase to the order of the zero-field splitting parameter DT. In the case of pBDPA 1b*, JTR changed sign and increased by an order of magnitude as compared to 1b and in 1b*JTR > DT. The flip in the sign of J could disrupt the EISC mechanism, vis à vis a switch in which state in the D/Q manifold neighboring sing-doublets interact more strongly with, since the trip-quartet state is now lowest in energy, and thus this result would still be consistent with experiment.
697% larger after the angle adjustment. From these results it can be seen that angle adjustment had a much more significant effect on 1c than 1a. These results provide a promising explanation for the appearance of EISC and a spin polarized ground state in 1c. The significant response in the |JTR| of pTrityl compared to pBDPA and pTEMPO, in addition to its shift to a strong coupling regime, could suggest that upon experimental flash freezing of the sample in ref. 5 a torsion of the bridge promoting greater pentacene/bridge planarity could lead to a distribution of JTR values causing some population to be in the weak coupling regime and some in the strong coupling regime. For the case of pTEMPO, 1a, upon changing the dihedral angle, |JTR| did not increase to the order of the zero-field splitting parameter DT. In the case of pBDPA 1b*, JTR changed sign and increased by an order of magnitude as compared to 1b and in 1b*JTR > DT. The flip in the sign of J could disrupt the EISC mechanism, vis à vis a switch in which state in the D/Q manifold neighboring sing-doublets interact more strongly with, since the trip-quartet state is now lowest in energy, and thus this result would still be consistent with experiment.
| pTEMPO [1a] | pBDPA [1b] | pTrityl [1c] | |
|---|---|---|---|
| Equil. JTR (cm−1) | −0.001250 | −0.000976 | −0.003732 |
| Partial Ang. Adj. JTR (cm−1) | −0.002821 | 0.004561 | −0.06846 |
| Ang. Adj. JTR (cm−1) | −0.004123 | 0.01601 | −0.8535 |
In order to verify that the results found here are derived from the angle adjustment and not from another emergent interaction gained at significant angle distortion, calculations on structures 1a–c with a more moderate angular perturbation were performed. In this case, the pentacene/phenyl angle was adjusted to 70°. Indeed, the expected pattern was seen: pTEMPO produced the least significant shift in exchange magnitude from its equilibrium geometry, with JTR = −0.002821 cm−1 as shown in Table 3. The exchange interaction in pBDPA once again exhibited a change in sign with JTR = 0.004561 cm−1. The 70° angle-adjusted pBDPA has a lower magnitude than in the full angle adjustment, suggesting an angle-dependent ferromagnetic interaction propagated by a π network. In the case of pTrityl, JTR increased in magnitude without a change in sign (JTR = −0.06846 cm−1), though to a lesser extent than in the full angle adjustment, as would be indicative of a steady increase in π overlap with a shrinking dihedral angle.
To again check the reproducibility of these results when stricter convergence criteria are used, we resubmitted structures 1a*,b*,c* under “VeryTightSCF” criteria as was done for 1a,b,c. JTR was found to be −0.004110 cm−1 for 1a*, 0.01623 cm−1 for 1b*, and −0.8551 cm−1 for 1c*. All calculated signs of JTR remain consistent, with magnitudes differing by 3.1%, 1.3%, and 1.9% respectively.
3.3 Removal of the carboxylate linker
Calculated JTR magnitudes for the pentacene-based C–R dyads presented above are an order of magnitude smaller than those calculated with QD-NEVPT2 for perylene–radical analogs.22 One explanation could be the shorter bridge length in these systems, having only a phenyl bridge linker rather than a phenyl and carboxylate. Therefore, QD-NEVPT2 calculations were carried out using a shortened linker without the carboxylate (Fig. 2 structures 2a–c. Results are shown in Table 2. All magnitudes of JTR increased relative to the carboxylate-containing bridge systems: 2a by less than an order of magnitude, and 2b,c by two orders magnitude. No significant change in pentacene π-orbital penetration into the phenyl linker was found after removal of the carboxylate (as shown in the spin density maps in Fig. 5a). Therefore, this increase in |JTR| was attributed to a combination of the shortening of the linker, and the absence of π-network disruption following the removal of the cross-conjugated carbonyl and the sp3-hybridized oxygen. The JTR of the trityl derivative, 2c, is still largest in magnitude in the 2-series, however it is still an order of magnitude smaller than the perylene–phenyl–trityl system reported in ref. 22; this is attributed to both differences in the electron density distribution in perylene versus pentacene, and the asymmetry of the trityl–phenyl–perylene system as compared to 2c. Contribution of molecular asymmetry to the magnitude of JTR is further discussed in the Section 3.5. Fig. 6 highlights the greater spin penetration into the phenyl bridge in peri-perylene tethered TEMPO, noting the presence of spin density on the phenyl carbon para- to the pentacene, which was not seen in structures 2a–c. It should be noted that when we performed calculations on the same (peri-)perylene–phenyl–trityl structure, a JTR of −0.126 cm−1 was found, showing the same sign and on the same order as was found for our calculations on structure 2c, however, this value is an order of magnitude lower than what was calculated in ref. 22. | ||
| Fig. 6 Spin density plot resulting from (3,3) QD-NEVPT2 calculations performed on perylene–phenyl–TEMPO. | ||
Given that π interactions are favored by lower dihedral angles in conjugated systems, useful information on the strength of π interactions in a given system can be gleaned by comparing dihedral angles of the pentacene and phenyl groups upon structural (and therefore electronic) modification. In the case of 1a,b,c, the planes of the pentacene and phenyl are nearly orthogonal due to steric effects between γ-hydrogens on the pentacene and phenyl; the optimized structures of 1a,b,c were found to have dihedral angles of 88°, 89°, and 80° respectively (as shown in Fig. 7). For the case of 2a,b,c, structures with only a phenyl linker, the dihedral angle of the pentacene/phenyl moieties were calculated to be 89°, 74°, and 89° respectively. A significant change in the pentacene–phenyl angle upon removal of the carboxylate was only seen for the case of 2b, the BDPA-tethered structure. The slight increase in the dihedral angle in 2c as compared to 1c is likely due to increased coulombic repulsion between the bulky sulfur-groups on the trityl moiety and the pentacene. The BDPA group, by comparison, contains an additional phenyl group to space out the bulky lobes of the BDPA moiety from the pentacene, and thus 2b adopts a smaller pentacene/phenyl dihedral angle favoring π interactions.
Despite the 15° reduction in the dihedral angle upon removal of the carboxylate in 2b, the penetration of triplet spin density into the bridge did not change significantly, as can be seen from spin density plots (Fig. 5a and Fig. S5, ESI†) and the data provided in Table 4. Löwdin spin density53 values obtained from the ORCA output files revealed little to no change in spin density on the phenyl moiety for structures with (1a–c) and those without (2a–c) the carboxylate linker. Regardless, JTR of 2c was found to increase by two orders of magnitude as compared to the carboxylate-containing 1c analog. It was thus concluded that an additional orbital penetration is not the driving force in 2c for larger |JTR|, but rather the shortened distance between the pentacene and radical moieties. This is likely still the case for the increased |JTR| in 2b, however the decreased pentacene/phenyl dihedral angle and the switch to ferromagnetic coupling as compared to 1b are suggestive of stronger π interactions.
| TEMPO (a) | BDPA (b) | Trityl (c) | |
|---|---|---|---|
| With carboxylate (1) | 0.01655 | 0.01912 | 0.01692 |
| Without carboxylate (2) | 0.01649 | 0.02045 | 0.01660 |
3.4 Ferromagnetic coupling in pentacene–BDPA radicals
A sign flip in JTR was calculated for BDPA structure 1b upon changing the pentacene/phenyl dihedral angle as well as upon changing the length of the bridging linker (2b). The BDPA radical moiety, labeled as b, in Fig. 2 exhibits resonance structures that allow the radical to be localized on either side of the central carbon connecting the two BDPA lobes, but never on the central carbon itself, as shown in Fig. 5b. This leads to a potential exchange interaction (Kij) between the π system of the bridge and the radical due to the inability of the radical to delocalize into the bridge π-system, which leads to limited molecular orbital overlap between the two systems. This set of resonance structures in BDPA points to the presence of cross-conjugation, whereby in a system of three connected π-hybridized atom centers, only two may interact at any given time, with the third center being isolated. This has been shown to have significant effects on the coupling sign of two magnetic centers.54,55 Cross-conjugation in 2b therefore leads to the stabilization of the trip-quartet state relative to the trip-doublet state and a positive JTR. As shown in Fig. 8, the πSOMO orbital of BDPA is equal and opposite in phase on either lobe, i.e. it is antisymmetric with respect to the mirror plane bisecting the BDPA. Given that the π system localized on the BDPA phenyl is symmetric with respect to this plane, the total overlap with either lobe of the BDPA would cancel, giving rise to ferromagnetic coupling.16 | ||
| Fig. 8 Visualization of BDPA radical-character orbital in structure 2b, visualized with GaussView 6. | ||
In the contrasting case of the trityl group, a resonance structure exists in which the electron density of the radical can extend to and overlap directly with the bridge. In 2c, this overlap leads to the delocalization of the radical spin density onto the phenyl bridge, and it thus exhibits kinetic exchange interactions with the pentacene π system. In the case of TEMPO, the pentacene/radical interactions are weak and the system exhibits antiferromagnetic coupling. This preference for excited-state antiferromagnetic coupling (ESAFC) in very weakly coupled systems could be due to the multi-determinantal nature of the trip-doublet state, as opposed to the single-determinant nature of the quartet state, observed in a (3,3) active space. The trip-doublet is therefore stabilized via non-dynamical correlation correction.
One can further rationalize that more significant consequences on the sign and magnitude of |JTR| are to be expected in 2b,c as compared to 2a when the carboxylate group (which contains a cross-conjugated carbonyl and an sp3 hybridized oxygen) is removed from the bridge, due to the extended π systems present in both BDPA and trityl.
The reader will recall that in pBDPA (1b) the D3 state has dominating character of a πpent → πSOMO charge-transfer configuration forming pent˙+–PhCOO–BDPA˙−. This may be surprising given that cross-conjugation acts to sever π (and thus CT) networks.54–57 It is therefore pertinent to note that the oscillator strength for the D0 → D3 transition in 1b is 2.7 × 10−8 (given in Table S26, ESI†), as compared to magnitudes on the order of 10−4 for the double excitation D0 → D3 in 1a and 1c or 10−1 for the main pentacene excitation in all three structures 1a,b,c; this is in line with expected behavior of cross-conjugation in BDPA.
3.5 Contribution of asymmetry to JTR: attachment of linker and radical to 2-position of pentacene
Deconvolution and interpretation of the J-exchange parameters. Implementing the procedure for the J-exchange deconvolution, J12, J23 and J13 parameters (indexed as shown in Fig. 3) were calculated. The results for structures 1–11 are shown in Tables 5 and 6. As expected, J13 is by far largest in magnitude in all cases, as the pentacene π and π* are significantly closer in space to one another than to the radical moiety. If J13 ≥ JTR, as it is in the systems presented here, then JTR can be approximated as the average of J12 and J23,22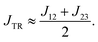 | (10) |
| pTEMPO [1a] (cm−1) | pBDPA [1b] (cm−1) | pTrityl [1c] (cm−1) | |
|---|---|---|---|
| J 12 | 0.004699 | 0.001378 | −0.01705 |
| J 23 | −0.006929 | −0.003300 | 0.009597 |
| J 13 | 1668 | 1251 | 1642 |
| J TR | −0.001250 | −0.0009759 | −0.003733 |
| J 12 (cm−1) | J 23 (cm−1) | J 13 (cm−1) | J 12 + J23 (cm−1) | ‖J12| − |J23‖ (cm−1) | J TR (cm−1) | |
|---|---|---|---|---|---|---|
| 1a | −0.005342 | 0.002840 | 1668 | −0.002502 | 0.002502 | −0.001250 |
| 1a* | 0.002726 | −0.01097 | 1616 | −0.008244 | −0.008244 | −0.004123 |
| 1b | 0.001378 | −0.003300 | 1251 | −0.001952 | 0.001952 | −0.0009759 |
| 1b* | −0.06880 | 0.1008 | 1274 | 0.03200 | 0.03200 | 0.01601 |
| 1c | −0.01705 | 0.009597 | 1642 | −0.007453 | 0.007453 | −0.003733 |
| 1c* | −0.4852 | −1.222 | 1596 | 1.707 | 0.7368 | −0.8535 |
| 2a | −0.02962 | 0.02018 | 1643 | −0.009446 | 0.009446 | −0.004723 |
| 2b | 0.3286 | 0.3162 | 1153 | 0.6448 | 0.0124 | 0.3224 |
| 2c | −0.6008 | −0.6498 | 1591 | −1.251 | 0.6730 | −0.6253 |
| 3a | 0.01816 | −0.02608 | 1617 | −0.00792 | 0.007986 | −0.003995 |
| 3b | 0.009416 | −0.02161 | 1187 | −0.01219 | 0.01219 | −0.006100 |
| 3c | −0.06241 | −0.016849 | 1562 | −0.07926 | 0.04556 | −0.03963 |
| 4a | 0.01890 | −0.02346 | 2760. | −0.004560 | 0.004560 | −0.002394 |
| 4b | −0.6237 | 0.3560 | 2430. | −0.2677 | 0.2677 | −0.1341 |
| 4c | 0.2612 | −0.7498 | 2765 | −0.4886 | 0.4886 | −0.2432 |
| 5a | 0.01206 | −0.01700 | 2761 | −0.004940 | 0.004940 | −0.002471 |
| 5b | 2.365 | −2.303 | 2424 | 0.06200 | 0.06200 | 0.02946 |
| 5c | −0.04361 | −1.976 | 2765 | −2.020 | 1.932 | −1.010 |
| 6a | 0.1075 | 0.02713 | 1877 | 0.08037 | 0.07034 | 0.06732 |
| 6b | 12.37 | 8.621 | 1462 | 20.99 | 3.749 | 10.49 |
| 6c | −333.1 | −669.2 | 1137 | −1002 | 336.1 | −509.7 |
| 7a | 0.08777 | −0.02857 | 1599 | 0.05920 | 0.05920 | 0.02960 |
| 7b | 0.2859 | −0.9631 | 2166 | −0.6772 | 0.6502 | −0.3387 |
| 7c | −7.666 | −37.09 | 1101 | −44.76 | 29.42 | −22.48 |
| 8a | −0.03407 | 0.04738 | 2763 | 0.01331 | 0.01331 | 0.006774 |
| 8b | 6.033 | −2.488 | 2408 | 3.545 | 3.545 | 1.769 |
| 8c | −37.36 | −99.24 | 2698 | −136.6 | 61.88 | −68.48 |
| 9b | −0.001366 | −0.009004 | 1604 | −0.01037 | 0.007638 | −0.005186 |
| 9c | −0.2554 | 0.3261 | 1542 | 0.0707 | −0.0707 | 0.03532 |
| 10b | 0.04882 | −0.1241 | 1540. | −0.07528 | −0.07528 | −0.03765 |
| 10c | −3.583 | 3.731 | 1501 | 0.1480 | 0.148 | 0.06960 |
| 11b | −0.6657 | −0.5297 | 1635 | −1.1954 | 0.136 | −0.5977 |
| 11c | 1.185 | 1.715 | 1605 | 2.900 | 0.5300 | 1.450 |
Therefore, in order to maximize the magnitude of JTR in such a system, J12 and J23 must either (i) exhibit the same sign or (ii) if their signs differ they must be significantly different in magnitude. The former is more difficult to guarantee, as interpretation (and therefore prediction) of the relative sign of each J component is unclear though likely related to the symmetry relationship of the magnetically active orbitals. The latter can be achieved by reducing the molecular symmetry as a whole, e.g. via asymmetric molecular functionalization.
Remembering that J13 is the exchange parameter between the two π electrons localized on pentacene, one may gain some insight into the quality of these calculated parameters by comparing J13 to the exchange parameter of pure pentacene. Tiago et al.58 used a first-principle Green's function approach to calculate the electronic and optical properties of solid pentacene, and found an excited singlet/triplet energy gap of 0.8 eV. The exchange parameter J between two electrons can be given by:22
| 2J = ES − ET. | (11) |
Introducing asymmetry: comparing 2-position and 6-position attachment. As previously discussed in Sections 3.2 and 3.3, the distance between the chromophore and the radical as well as the dihedral angle of the pentacene and bridge contribute to the magnitude and sign of JTR. In this section, we investigate how JTR changes upon introduction of structural asymmetry into the pentacene–radical structure by attaching a phenyl carboxyl bridge to the 2-position of pentacene, as shown in structures 4a,b,c (Fig. 2). These phenyl–carboxylate bridged structures with a 2-position attachment produce a reduced average dihedral angle of 41° between the pentacene and phenyl bridge as compared to the average dihedral for 6-position attachment structures 1a,b,c, 86°. The reduction in the average dihedral angle in the 2-position structure is likely driven by a favorable π overlap with reduced steric hindrance. Results of the QD-NEVPT2 calculations are shown in Table 2. If we compare the substitutions of the TEMPO radical in the 2- and 6-positions (1a and 4a), |JTR| increased, but only by less than an order of magnitude, when attached at the 2-position. In the case of trityl (1c and 4c) and BDPA (1b and 4b), |JTR| increased by two orders of magnitude at the 2-position. However, despite the reduction in the dihedral angle between pentacene and the phenyl bridge when bonded at the 2-position, Löwdin spin density populations showed reduced spin density on the bridging phenyl α-carbon when compared to the 6-position case, as shown in Table 7 and visualized in Fig. 9.
| pTEMPO | pBDPA | pTrityl | |
|---|---|---|---|
| 6-Position [1] | 0.01655 | 0.01913 | 0.01693 |
| 6-Position (no carboxylate) [2] | 0.01649 | 0.02045 | 0.01660 |
| 2-Position [4] | 0.002531 | 0.002798 | 0.002583 |
| 2-Position (no carboxylate) [5] | 0.002547 | 0.002844 | 0.002683 |
 | ||
| Fig. 9 Spin density plots of structures 4a,b,c and 5a,b,c from QD-NEVPT2 calculations using a (3,3) active space. | ||
The calculated increase in JTR can be explained by eqn (10): a large difference in the magnitude of J12 and J23 (when opposite in sign) leads to an increase in JTR. In the case of the 6-position, |J12| − |J23| values for structures 1a,b,c, were found to be 0.003, 0.002, and 0.006 cm−1, respectively (from Table 6). Upon attachment at the 2-position for structures 4a,b,c these differences increased to 0.005, 0.27 and 0.49 cm−1, respectively. Further calculations were carried out on structures containing a phenyl bridge attached at the 2-position of pentacene rather than a phenyl–carboxylate, 5a,b,c (Fig. 2). |JTR| in 5b decreased by an order of magnitude upon removal of the carboxylate, while it remained constant in 5a and increased by less than an order of magnitude in 5c. This is in contrast to the removal of the carboxylate in the 6-position case in which |JTR| increased for all three cases upon shortening of the linker (1a,b,c compared to 2a,b,c). Investigation of the spin density plots of the 2- and 6-positions revealed lower pentacene triplet electron density at the 2-position as seen in Fig. 9 and Fig. S6 (ESI†). The weaker interactions are consistent with the smaller changes in |JTR| for the 2-position case upon shortening of the bridge as compared to the 6-position. It is interesting to note that the significantly more planar pentacene–phenyl dihedral angle in the 2-position is not sufficient to offset this weakening of the interaction.
Phenyl-bridged radicals at the 2-position, 5a and 5b, were also calculated to have a smaller JTR as compared to the corresponding phenyl-bridged 6-position structures 2a,b. However, in the case of the trityl structure 5c, a slight increase (less than an order of magnitude) in |JTR| as compared to 2c was found. This is consistent with a greater delocalization of the trityl radical as compared to BDPA or TEMPO, since it seems to more readily reap the benefits of the reduced bridge pentacene/phenyl dihedral angle in going from 2c to 5c, though we would be cautious to not overinterpret given the small magnitude of the change. Interestingly, the trip-doublet and trip-quartet states of the BDPA system (5b) once again exhibited excited-state ferromagnetic coupling, as opposed to the excited-state anti-ferromagnetic coupling in 4b, despite the exhibited decrease in the coupling strength. This reaffirms the importance of the cross-conjugation in the BDPA radical combined with favorable π interactions as a driving factor for ESFC.
It is worth noting that J13 is significantly larger in 2-position structures 4, 5, and 8, as shown in Table 6. This is attributed to the reduced penetration of the pentacene π system into the bridge, resulting in an increased electron density localized on the pentacene.
3.6 Contribution of π delocalization to the sign of JTR
To investigate the effects of spin delocalization on JTR, TEMPO, BDPA, and trityl structures attached at the 6- and 2-position via an alkyne bridge (6a,b,c/8a,b,c) were studied, in addition to the structures shown and labeled in Fig. 10, with results reported in Table 8. Molecules containing ‘eTEMPO’ in Fig. 10, labeled with “d”, have an additional double bond on the radical moiety which allows for closer interaction of πpent and the nitroxide radical in conjugated bridges, as well as delocalization of radical spin density towards the bridge. | ||
| Fig. 10 TEMPO/eTEMPO variations: 2-eTAP [8d] (top left), 6-eTAP [6d] (top right), 6-TAPhP [12a] (bottom left), 6-eTAPhP [12d] (bottom center), 6-eTPhP [2d] (bottom right). | ||
| [2d] (eV) | [8d] (eV) | [6d] (eV) | [12a] (eV) | [12d] (eV) | |
|---|---|---|---|---|---|
| Q 0 | 1.222 | 1.287 | 1.222 | 1.225 | 1.301 |
| D 1 | 1.222 | 1.287 | 1.223 | 1.225 | 1.301 |
| D 2 | 1.427 | 1.626 | 1.439 | 1.431 | 1.4987 |
| D 3 | 2.125 | 2.213 | 2.102 | 2.097 | 2.092 |
| J TR (cm−1) | −0.01628 | 0.3747 | 2.941 | 0.01563 | 0.2501 |
The switch to an alkyne bridge gave rise to excited-state ferromagnetic coupling (ESFC) in all systems except pTrityl, 6c/8c, as shown in Table 2. 6b exhibits cross-conjugation at the BDPA radical, whereas 6c displays an extended uninterrupted π network connecting and including pentacene and the radical group that is mediated by the alkyne linker, allowing for a strong kinetic exchange interaction. 6a,b,c all displayed higher magnitude JTR values as compared to 1a,b,c, and all exhibited the expected sign as would be predicted by the Goodenough and Kanamori rules. 6a exhibits ESFC since the pentacene triplet extends further into the bridge towards the nitroxide radical without significant overlap with the radical orbital, making potential exchange the dominating interaction. Structures 8a,b,c,d (attached at the 2-position) displayed JTR values an order of magnitude less than their corresponding 6-position structures 6a,b,c,d. This is consistent with reduced π delocalization into the bridge due to the reduced amplitude of the π orbital, and therefore spin density, at the 2-position of the pentacene moiety. In contrast, structures which contain a phenyl–carboxylate bridge attachment (1a,b,c (6-position) and 4a,b,c (2-position)), showed an increased |JTR| at the 2-position which was attributed to molecular asymmetry. Based on these results, if π delocalization dominates the pentacene-bridge-radical coupling, then attachment at the 2-position leads to a decreased JTR magnitude compared to the 6-position. In the case where the π-system is less delocalized across the bridge and thus π-propagated interactions are weak, breaking of the molecular symmetry will be a more significant contributor, and attachment at the 2-position will give an increased JTR.
The 2-position and 6-position alkyne–eTEMPO (6d, 8d) structures displayed JTR values two orders of magnitude larger than those for the alkyne–TEMPO structures (6a, 8a). This is consistent with the extension of the pentacene π system in 6d closer to the radical which further stabilizes the ferromagnetic exchange interaction as compared to 6a. Assignment of this effect to a greater π-delocalization towards the radical was supported by the calculations of JTR of 12a and 12d structures which contain an alkyne–phenyl bridge. Despite the large chromophore–radical distance, the alkyne–phenyl bridge also leads to a positive JTR; the addition of an alkyne linker between the pentacene and phenyl leads to an equilibrium structure where the phenyl group is in plane with the pentacene chromophore, as contrasted with structure 2, and thus the integrity of the π conjugation is maintained. In the case of eTEMPO with a phenyl bridge, 2d, the phenyl group is perpendicular to the pentacene, and QD-NEVPT2 calculations supported ESAFC due to far weaker interactions between the π system and radical, as was expected.
In order to isolate the effects of π-system extension and triplet/radical distance, two additional TEMPO/chromophore structures (Fig. 11) were studied (13a, 14a). We note that the input DFT orbitals for structure 14a were calculated on the anionic form of the molecule. It was found that direct attachment of the TEMPO radical to the pentacene moiety leads to a positive JTR (Table 2), whereas extension of the π-system away from the radical does not. Therefore one can confidently say that in 6a the ferromagnetism results from a strengthening of the potential exchange interaction via a reduction of the triplet–radical distance, rather than from the triplet delocalization alone.
 | ||
| Fig. 11 Structures and calculated JTR values for TEMPO directly attached to pentacene (left) and TEMPO with phenyl–carboxylate bridge attached to an extended chromophore moiety (right). | ||
In addition, configurational contributions to the trip-doublet states of the alkyne bridge structure 6c were compared to the phenyl–carboxylate bridge structure 1c. It was found that in structure 1c, the coefficients associated with the trip-doublet state reflected the expected weighting based on eqn (4):  ;
;  ; and accordingly
; and accordingly  . This is not maintained in the trip-doublet state of 6c, which exhibits C|T+,β〉 = −0.411,
. This is not maintained in the trip-doublet state of 6c, which exhibits C|T+,β〉 = −0.411,  , and
, and  , with
, with 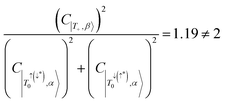 , deviating from the expression shown in eqn (4). We propose that the deviation of this ratio from 2 can be used as a quantitative measure of the isolation of the D/Q manifold from nearby states. Values closer to 2 indicate a well-isolated spin manifold, and deviation is indicative of state mixing of the spin manifold with neighboring states. For example, in the case of 6c (where the ratio is 1.19) charge transfer configurations significantly contribute to the description of the trip-doublet, with a weighting coefficient of −0.59 associated with a
, deviating from the expression shown in eqn (4). We propose that the deviation of this ratio from 2 can be used as a quantitative measure of the isolation of the D/Q manifold from nearby states. Values closer to 2 indicate a well-isolated spin manifold, and deviation is indicative of state mixing of the spin manifold with neighboring states. For example, in the case of 6c (where the ratio is 1.19) charge transfer configurations significantly contribute to the description of the trip-doublet, with a weighting coefficient of −0.59 associated with a  CT configuration, and 0.24 associated with the reverse πpent → πSOMO. These configurations do not contribute to the trip-doublet or trip-quartet states in the case of 1c where the ratio is 2. A ratio of slightly less than 2 (i.e. ∼1.99) was observed in structures 1c*, 2c, 6b, 7b, 7c, see Table S14 (ESI†). The disparity between
CT configuration, and 0.24 associated with the reverse πpent → πSOMO. These configurations do not contribute to the trip-doublet or trip-quartet states in the case of 1c where the ratio is 2. A ratio of slightly less than 2 (i.e. ∼1.99) was observed in structures 1c*, 2c, 6b, 7b, 7c, see Table S14 (ESI†). The disparity between 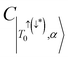 and
and 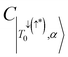 in 6c reflects preferential excitation of the β-spin on the chromophore, and is an artifact of the computational model which assumes a priori the radical is in the α-state when the triplet is in |T0〉. This allows for spin pairing of the chromophore π* β-electron and the radical α-electron, consistent with a strong kinetic exchange interaction.
in 6c reflects preferential excitation of the β-spin on the chromophore, and is an artifact of the computational model which assumes a priori the radical is in the α-state when the triplet is in |T0〉. This allows for spin pairing of the chromophore π* β-electron and the radical α-electron, consistent with a strong kinetic exchange interaction.
3.7 Cross-conjugation studies
To study the effects of cross-conjugation, the exchange coupling in pentacene–radical structures with a phenyl linker (2a,b,c) were compared to those with a phenyl–carbonyl linker (3a,b,c). In addition, structures with an alkyne linker (6a,b,c) were compared to an alkyne–carbonyl linker (7a,b,c). Results are shown in Table 2. In both comparisons, we find that the addition of the carbonyl reduces |JTR|. This result is consistent with a longer linker as well as a disruption of the π interactions dominating the coupling, as shown in the spin density plots in Fig. 12. The inclusion of the carbonyl linker also leads to a sign switch, from ESFC to ESAFC, for BDPA systems (2b, 6b (JTR > 0) to 3b, 7b (JTR < 0)). The π system linking the pentacene and BDPA is disrupted by the carbonyl, which reduces the contribution of potential exchange to JTR and leads to a change in the sign of JTR. A sign change was not observed in the corresponding TEMPO (3a, 7a) or trityl (3c, 7c) structures. Unlike TEMPO and trityl structures, BDPA structures contain an inherent cross-conjugation point at the central carbon which acts to further disrupt the π system. | ||
| Fig. 12 Spin density plots (visualized in GaussView 6) for structures 6a, 6b, 6c and 7a, 7b, 7c from QD-NEVPT2 calculations with a (3,3) active space. | ||
The calculated exchange coupling, JTR in TEMPO structures 2a/3a is negative while for structures 6a/7a it is positive. The positive JTR in 7a is attributed, similar to the 6a case, to the greater π delocalization on the alkyne bridge as compared to the phenyl bridge 2a/3a. In both TEMPO cases, the coupling is weak and the cross conjugation imposed by the carbonyl in 3a and 7a does not significantly affect the magnitude or sign of JTR, presumably because the shift in the interaction distance is only from a Csp3–Csp bond length to a Csp3–Csp2 bond length. In the case of trityl structures 2c/3c, 6c/7c, JTR was calculated to be negative. In 2c and 6c the kinetic exchange dominates, due to a stronger JTR and non-zero overlap between the triplet and radical π systems. The addition of the carbonyl has the effect of reducing |JTR| by an order of magnitude for both alkyne and phenyl bridge structures, consistent with a longer bridge and disruption of the π network. The sign remains the same for 3c and 7c, however this result was unexpected as the addition of the carbonyl was predicted to give rise to ESFC in 7c, as presumably it would allow the delocalization of the πpent and πSOMO up to the carbonyl cutoff without allowing bonding overlap. It will be shown in Section 3.9 that upon increasing the active space to allow for local radical excitations, this sign flips. This could suggest that the ESAFC calculated for 7c could be an artifact of the limitations of a small active space, and a more systematic study finding a limiting value for the sign and magnitude of the exchange with increasing active space is worth pursuing in the future.
Destructive quantum interference (DQI) effects leading to reduced charge transport in molecules through a m-phenyl structural motif are consistent with the similar DQI effects observed in cross-conjugated structures.57 In order to probe the effects of cross-conjugation and quantum interference effects across the π network we investigated structures with a BDPA or trityl radical tethered at the meta-position of a 6-position bridging phenyl group. ESFC was obtained for all trityl-tethered meta-structures 9c, 10c, 11c, and ESAFC for all BDPA-tethered meta-structures 9b, 10b, 11b.
It is particularly interesting that ESFC was observed in the cases of very weak coupling in 9c and 10c, particularly after ESAFC was observed in 7c. An ESFC interaction in 7c would require a strong potential exchange interaction between the pentacene/radical magnetic orbitals at the carbonyl, whereas in 9c and 10c the ferromagnetism can be attributed to the absence of triplet spin density at the (3,5-) phenyl positions (as seen for structure 11c in Fig. 13). This difference in behavior for the meta- and para-bonded systems is a well-known driver of selectivity rules in electrophilic aromatic substitution, and is known to have consequences on magnetic coupling.59
 | ||
| Fig. 13 (3,3) QDNEVPT2 spin density plots (visualized in GaussView 6) for structure 11c (right) and its para-attachment counterpart (left), along with the associated sign of JTR. | ||
This effect is highlighted in structure 11c, where there is extensive delocalization across the bridge with no overlap (STR ∼ 0) between the triplet and radical wavefunctions. In this case, potential exchange becomes the dominating interaction. As a proof of concept, additional (3,3)-QDNEVPT2 calculations were performed on the para-analog of 11c (shown in Fig. 13), which led to the negative |JTR| as expected.
The increased exchange coupling magnitude seen in 2c upon removal of the carboxylate group of 1c was no longer seen in the 9c and 10c analogs, which is consistent with a disruption of a π-mediated exchange effect via meta-attachment. As with the para-tethered analogs, 1c and 2c, the phenyl group is orthogonal to the pentacene in structures 9c, 10c.
If we now consider the BDPA radical, as mentioned in the cases of 3b and 7b, due to the cross-conjugation inherent to the group, propagation of radical spin density towards the bridge is limited. The same argument applies to structures 9b and 10b where the potential exchange interaction is too weak to lead to ESFC, and is highlighted by the change in the sign of JTR when BDPA attachment to a phenyl bridge is changed from the para- to meta-position, going from positive in 2b to negative in 10b.
3.8 The sign of J12 and J23
As described previously, under the condition that J13 ≫ JTR, the magnitude of JTR depends on the sum of J12 and J23. Thus, |JTR| depends on the relative sign of both of these terms. However, the physical interpretation of the sign of J12 and J23 is unclear.22 Of the thirty molecules studied with a (3,3) active space, we identified thirteen cases where the sign of both of these terms remained the same: 1c* (angle-adjusted 6-phenyl–carboxylate), 2b/2c (6-phenyl), 3c (6-phenyl–carbonyl), 5c (2-phenyl), 6a/6b/6c (6-alkyne), 7c (6-alkyne–carbonyl), 8c (2-alkyne), 9b (6-m-phenyl–carboxylate, and 11b/c (6-alkyne–m-phenyl). Two notable patterns emerge: structures which exhibit bridges promoting π-orbital delocalization and strong π–radical interactions are more likely to exhibit the same sign in J12 and J23, as well as structures which are tethered at the more symmetric 6-position. Except for 6a (6-alkyne), all TEMPO-based structures demonstrated the J12 and J23 values of opposing sign. This suggests that J12 and J23 tend to exhibit similar sign in the presence of strong πpent/radical interactions. With the exceptions of structures 5c and 8c, all TEMPO, BDPA, and trityl structures with radical attachment at the 2-position exhibited J12 and J23 values of opposite signs. This may be attributed to both reduced πpent bridge penetration, as well as a reduced molecular symmetry.In addition, there seems to be a preference for similar coupling signs of J12 and J23 in trityl-tethered structures as compared to BDPA structures. In all BDPA structures where J12 has the same sign as J23, trityl likewise exhibits this behavior. However, for structures with a weaker pentacene–radical coupling, specifically series 1, 5, 8, the trityl structures 1c*, 5c, 8c maintain sign(J12) = sign(J23), whereas BDPA structures 1b*, 5b, 8b do not. Coupling between the pentacene system and the BDPA radical is largely derived from potential exchange via non-bonding interactions between the π system and radical. Trityl, on the other hand, is capable of forming a continuous π system with conjugated bridges and thus maintains strong π–radical interactions. As mentioned previously, symmetric pentacene–radical structures are more likely to exhibit the same sign of J12 and J23. However, the presence of sign(J12) = sign(J23) in structures 8c, 11b, and 11c suggest that this may also be observed in asymmetric structures when π-conjugation is significant. When we compare the J components of 1c to 1c*, JTR is an order of magnitude smaller in 1c and the sign(J12) ≠ sign(J23). In the case of 1c*JTR is two orders of magnitude larger, and sign(J12) = sign(J23). This comparison gives rise to the question of whether the relative sign of J12 and J23 could have important mechanistic consequences for the emergence of EISC and ESP.
3.9 Expansion of the radical active space
Intramolecular charge-transfer states that are close in energy to the excited sing-doublet state may assist in quartet formation via spin–orbit coupling.60 In order to probe for the presence of these states, QD-NEVPT2 calculations with a (5,5) active space were carried out on tethered-BDPA and -trityl structures to allow for electronic excitations from and into the π/π* orbitals localized on the radical moiety energetically above and below the SDGS SOMO. In order to emphasize that these orbitals are borne of the radical moiety, we will label these orbitals the πSOMO±1, and the orbital singly-occupied in the SDGS the πSOMO; however, these orbitals may be singly-, doubly-, or un-occupied. This labeling scheme is shown for systems 1b and 1c in Fig. 14. The results of these calculations are given in Table 9. The tethered-TEMPO structures were not considered, as inspection of (3,3) CASSCF frontier orbitals revealed no occupied or virtual orbitals of the nitroxide radical energetically near the SDGS SOMO or π/π* of pentacene. | ||
| Fig. 14 (5,5) active space orbitals of (a) pBDPA [structure 1b] and (b) pTrityl [structure 1c]. SDGS = “single-Determinant Ground State”. | ||
| D 1 (eV) | D 2 (eV) | D 3 (eV) | D 4 (eV) | Q 0 (eV) | J TR (cm−1) | |
|---|---|---|---|---|---|---|
| a Convergence not achieved at CASSCF step. | ||||||
| 1b | 1.256 | 1.287 | 2.296 | 3.583 | 1.287 | −0.1247 |
| 1b* | 1.260 | 1.271 | 2.295 | 3.566 | 1.271 | −0.2426 |
| 1c | 0.2111 | 1.301 | 1.319 | 2.371 | 1.301 | −0.1382 |
| 1c* | 1.250 | 1.272 | 1.759 | 3.031 | 1.273 | −1.371 |
| 2b | 1.137 | 1.181 | 2.287 | 3.466 | 1.181 | 0.5227 |
| 2c | 0.1327 | 1.428 | 1.435 | 2.416 | 1.428 | −1.048 |
| 4b | 1.295 | 1.458 | 2.297 | 3.593 | 1.295 | −0.08554 |
| 4c | 0.3156 | 1.623 | 1.823 | 2.649 | 1.623 | −0.6330 |
| 5b | 1.301 | 1.476 | 2.278 | 3.577 | 1.301 | 0.2021 |
| 5c | ||||||
| 6b | 1.215 | 1.275 | 2.277 | 3.446 | 1.210 | 26.80 |
| 6c | 0.9795 | 1.095 | 1.821 | 2.837 | 1.073 | −501.8 |
| 7b | 1.210 | 1.362 | 2.316 | 3.510 | 1.210 | 1.299 |
| 7c | 0.4986 | 0.6132 | 1.180 | 1.397 | 1.171 | 46.28 |
| 8b | 1.300 | 1.471 | 2.281 | 3.574 | 1.299 | 4.008 |
| 8c | ||||||
| 9b | 1.263 | 1.291 | 2.293 | 3.583 | 1.291 | −0.1131 |
| 9c | 1.233 | 1.280 | 1.769 | 3.050 | 1.280 | −0.4448 |
| 10b | 1.273 | 1.293 | 2.286 | 3.579 | 1.293 | −0.3247 |
| 10c | 0.1437 | 1.438 | 1.440 | 2.424 | 1.438 | −3.213 |
| 11b | 1.206 | 1.261 | 2.293 | 3.496 | 1.206 | −0.3661 |
| 11c | 0.1316 | 1.338 | 1.407 | 2.423 | 1.338 | 1.148 |
It is important to note that in the present case an increase in the active space does not necessarily imply an increase in accuracy. While this is the case in the limit of an active space encompassing the entirety of the MO space (coinciding with full configuration interaction), in the case of smaller active spaces, inclusion of an additional orbital has significant consequences on the description of the target state(s), and the resulting space must be carefully inspected.
The sign of JTR stays consistent going from a (3,3) active space to a (5,5) active space in three out of four structure 1 moieties tested (1b, 1b*, 1c, 1c*), with the exception being 1b*, suggesting that a minimal active space may be sufficient to predict the sign in very weakly coupled systems. For these structures, all values of |JTR| are larger than in their (3,3) counterparts. In fact, this increase in |JTR| is maintained in all (5,5) calculations. This is consistent with a reduced separation between interacting spin centers, suggesting that correlation of the pentacene triplet with the excited states of the tethered radical is a significant contributor to the strength of the triplet/radical magnetic interactions for the BDPA and trityl systems examined here. In these structures, the πSOMO±1 orbitals exhibit greater amplitude near the bridge than the SDGS πSOMO orbitals do, as shown in Fig. 14. Thus, when an electron in the πSOMO−1 and/or πSOMO is locally excited, the πSOMO−1 and/or πSOMO+1 may contain an unpaired electron and thus would become a magnetically active orbital. Due to the delocalized π-character of the SOMO±1 orbitals, the strength of the exchange interaction increases due to a decrease in the interaction distance between magnetic orbitals. This can be seen in the spin density plots of 1b and 1c in Fig. 15, when compared with those in Fig. 5.
 | ||
| Fig. 15 Spin density plots (visualized in GaussView 6) for structures 1b, 2b, 3b and 1c, 2c, 3c from QD-NEVPT2 calculations with a (5,5) active space. | ||
The ground state of 1c is found to be closely neighbored by a state dominated by a πSOMO−1 → πSOMO radical excitation. This state lies 0.2 eV above D0 and the transition from D0 to this state is found to have a nonzero oscillator strength, suggesting that it is an important contributor to the description of the radical. A simplified molecular orbital diagram for this configuration is shown in Fig. 16a (left) for the case of 2c. The change in calculated coupling sign for 1b* upon expanding from a (3,3) to a (5,5) active space may be attributed to the contribution of similar πSOMO−1 → πSOMO(+1) configurations to the description of the radical electronic structure. The phenyl group on the BDPA moiety that is bonded to the bridge bears the πSOMO−1 orbital and becomes magnetically active after the πSOMO−1 → πSOMO excitation, and does not exhibit the same cross-conjugated nature as the BDPA lobes. This would allow for constructive overlap between magnetic orbitals on the BDPA and the pentacene π system. Spin density plots of 1b* resulting from a (3,3) versus a (5,5) active space are given in the ESI† (Fig. S7), and show the appearance of significant β-spin density on the cross-conjugated carbon only in the (5,5) calculation, further suggesting emergent magnetic activity on the central fragment of the BDPA moiety after radical excitations are included in the active space.
Trityl structures 2c (6-phenyl), 4c (2-phenyl–carboxylate), 7c (6-alkyne–carbonyl), 10c (6-m-phenyl), and 11c (6-alkyne–m-phenyl) likewise exhibited the mixing of low-energy states with a radical-localized πSOMO−1 → πSOMO sing-doublet state configuration. In all of these structures, the sing-doublet state is dominated by πSOMO−1 → πSOMO configuration and is nearly degenerate with and mixes with the SDGS configuration. The D0 and D1 states exhibit mirroring proportions of each configuration, e.g. for 1c: ψD0 = (0.96) × |22α00〉 + (0.15) × |α2200〉 + … and ψD1 = (0.15) × |22α00〉 + (0.95) × |α2200〉 + …, where the basis vector is  with 2 indicating double occupation and 0 indicating non-occupation.
with 2 indicating double occupation and 0 indicating non-occupation.
In structures 2c, 4c, 10c, and 11c, this πSOMO−1 → πSOMO sing-doublet even drops below the SDGS-dominated state, with proportions shown in Fig. 16a for the case of 2c.
The state most well-represented by the πSOMO−1 → πSOMO configuration in BDPA systems is relatively high in energy when compared with the trityl analogs; e.g. this state lies 2.30 eV above the ground state in 1bversus 0.26 eV in 1c. As a result, there is minimal mixing between this configuration and the SDGS ground-state configuration. This destabilization in the BDPA radical excitation πSOMO−1 → πSOMO is predicted to be a consequence of the cross-conjugated nature of the BDPA radical: not only is the same-site Coulomb repulsion of a doubly-occupied πSOMO larger due to the cross-conjugation inhibiting delocalization, but also the opposite relative phase of the two BDPA lobe π orbitals results in a destructive interference between the lobes. Taking a symmetry perspective, the πSOMO−1 and  (shown in Fig. 14) are symmetric with respect to the mirror plane bisecting the radical, whereas the πSOMO is antisymmetric, and thus a mixing between these orbitals to allow the SOMO to extend closer towards the bridge is symmetry-forbidden.
(shown in Fig. 14) are symmetric with respect to the mirror plane bisecting the radical, whereas the πSOMO is antisymmetric, and thus a mixing between these orbitals to allow the SOMO to extend closer towards the bridge is symmetry-forbidden.
We also consider the effect of including these radical excitations on the state-ordering of the pentacene–radical systems. Calculations utilizing a (5,5) active space predict that the pentacene excited sing-doublet state in 1c lies 0.02 eV above the D/Q manifold neighboring the trip-quartet state, whereas in 1c* it is found 0.02 eV below the D/Q manifold neighboring the trip-doublet state. While this state ordering change can have significant impact on the relaxation pathway, we find after calculating with an increased pentacene active space (adding an additional πpent and  orbital each to the present (5,5) space, creating a (7,7) active space overall) the main excitation remains above the D/Q manifold. Further calculations exploring the active space are therefore necessary.
orbital each to the present (5,5) space, creating a (7,7) active space overall) the main excitation remains above the D/Q manifold. Further calculations exploring the active space are therefore necessary.
If we now consider the spin density plots shown in Fig. 15, there is a greater spin density on the radical group aromatic ring connecting to the bridge in structures 1c, 2c, 3c as compared to 1b, 2b, 3b. This suggests stronger kinetic exchange coupling, and is in line with the mechanistic explanation of Quintes et al.,4 who proposed that the likely path for quartet formation involves a spin-conserving flip of the radical and an electron of the singly excited pentacene, forming a triplet on the pentacene with an antiparallel radical doublet, and would require a spin-pairing interaction between the pentacene and radical electrons.
The (3,3) QD-NEVPT2 calculations of alkyne–carbonyl systems (7b and 7c) predict negative JTR (ESAFC). When a (5,5) active space is implemented, a change to a positive JTR is predicted for both structures. As can be seen from spin density plots of 7b, 7c resulting from a (5,5) active space (Fig. 17 and 18), the radical can more effectively extend to, but not beyond, the carbonyl; this allows for close proximity without constructive overlap, characteristic of potential exchange. A minimal active space does not allow for as significant delocalization towards the carbonyl, presumably leading (due to a larger distance of interaction) to negligible potential exchange contribution and therefore a negative JTR for both the trityl and BDPA cases. This nodal behavior is highlighted in Fig. 18a, where in the case of structure 6c (6-alkyne), the spin density extends uninterrupted along the conjugated system, connecting the pentacene and trityl moiety. Similarly shown in Fig. 17a, delocalization from the pentacene through the bridge and into the BDPA moiety up to the cross-conjugation on BDPA itself is observed, at which point the positive spin density sharply stops and the cross-conjugated carbon exhibits negative spin density. In structures 7b,c (6-alkyne–carbonyl) a nodal point is introduced at the carbonyl carbon in the bridge, and both structures exhibit ESFC. This is further evidenced for 7c by the active space molecular orbitals shown in Fig. 18b and c. Fig. 18b shows an active molecular orbital resulting from a (5,5) calculation on structure 6c, and indeed the orbital is delocalized across the length of the molecule, with significant amplitude on the pentacene, bridge, and radical moieties consistent with the calculated negative sign of JTR. This is seen in none of the resulting active orbitals for structures 7b,c, with each orbital being greatly delocalized but constrained to the locus of either the pentacene/bridge system or radical, consistent with the calculated positive sign of JTR.
As part of our investigation of the role of radical excitations on these systems, structures with attachment points at the meta-position of the phenyl group were once again investigated to explore the relationship between bridge cross-conjugation and larger active spaces.
C–R structures featuring a meta-phenyl linker group again exhibit ESAFC in BDPA structures 9, 10, 11b when using a (5,5) active space, as was calculated in with a (3,3) active space. Again a change in the sign of JTR from positive in 2b (para-attachment) to negative in 10b (meta-attachment) was seen. As explained in Section 3.7, introduction of cross-conjugation by meta-attachment at the phenyl disrupts the π system coupling the radical and pentacene groups. Due to the existence of cross-conjugation already on the radical, BDPA did not exhibit as strong of a magnetic orbital extension towards the bridge when the active space is increased (as evidenced by the lack of low-lying πSOMO−1 → πSOMO states in BDPA structures). The additional cross-conjugation leads only to a further weakening of π-propagated potential exchange interactions and leads to ESAFC.
Unlike in calculations that use a minimal active space, calculations using a (5,5) active space did not predict ESFC in all of structures 9, 10, 11c.
In the calculations performed by Gorgon et al.,60 it was found that a charge-transfer state lying close to the quartet manifold was likely to be responsible for the appearance of ESP in their chromophore-tethered radicals. Among the molecules originally studied by Avalos et al.,5 a charge-transfer state near the quartet manifold was found only for 1b and 1b*, and only in the (3,3) set of calculations, where in both cases D3 is a state that is dominated by the CT configuration πpent → πSOMO.
In the (3,3) calculations of trityl structures 10c and 11c an extremely low-lying (<0.05 eV) D1 state was predicted, where this state is dominated by the πpent → πSOMO CT configuration in 11c and in 10c both D0 and D1 are approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of this configuration and the SDGS configuration. However, upon increasing the active space to (5,5), these charge-transfer states are no longer observed. This difference is shown in Fig. 19 for the case of 1b. In Fig. 19, only the most significant contributors to D3 are shown for the (5,5) calculations, however there was no contribution from a CT configuration in D3 or D4. Out of all (5,5)-calculated structures, only trityl structures 6c and 7c showed the states with significant CT-character, which highlights the disconnected nature of the BDPA radical from the bridge π-network. The appearance of charge-transfer states in the (5,5) calculations of structures 6c and 7c may also provide insight to the nature of the exchange coupling, given that a charge-transfer determinant may be considered a type of ionic determinant, which is characteristic of kinetic exchange. In general, calculations of cross-conjugated pBDPA structures using a (5,5) active space indicated no significant contributions from ionic configurations, consistent with the presence of ionic determinants as a predictor of antiferromagnetic interactions.
1 mixtures of this configuration and the SDGS configuration. However, upon increasing the active space to (5,5), these charge-transfer states are no longer observed. This difference is shown in Fig. 19 for the case of 1b. In Fig. 19, only the most significant contributors to D3 are shown for the (5,5) calculations, however there was no contribution from a CT configuration in D3 or D4. Out of all (5,5)-calculated structures, only trityl structures 6c and 7c showed the states with significant CT-character, which highlights the disconnected nature of the BDPA radical from the bridge π-network. The appearance of charge-transfer states in the (5,5) calculations of structures 6c and 7c may also provide insight to the nature of the exchange coupling, given that a charge-transfer determinant may be considered a type of ionic determinant, which is characteristic of kinetic exchange. In general, calculations of cross-conjugated pBDPA structures using a (5,5) active space indicated no significant contributions from ionic configurations, consistent with the presence of ionic determinants as a predictor of antiferromagnetic interactions.
 | ||
| Fig. 19 D 3 state contributions for structure 1b in the (3,3) versus (5,5) active space calculations. Red/blue electron arrows indicate electrons which are in the pentacene/radical in the single-determinant ground state. Left diagram orbitals (as numbered in Fig. 14a) from bottom to top: 212, 213, 214. Right diagram orbitals (as numbered in Fig. 14a) from bottom to top: 211, 212, 213, 214, 215. | ||
To explain why ESFC is predicted for 11c in the (5,5) case but not in the (3,3) case, one may consider the contribution of the πSOMO±1 orbitals. These trityl π orbitals extend towards the (1,2,4,5)-tetrathiophenyl group that is directly bound to the bridge and can interact more closely, but does not overlap, with the pentacene π system. In 11c the phenyl is in the same plane as the pentacene and the pentacene π system extends through the phenyl bridge. The cross-coupling introduced by the meta-attachment of the radical prevents a continuous π network with the trityl moiety and gives rise to ESFC. This can be seen in the spin-density plot of 11c in Fig. 20, which shows zero spin density on the m-carbon where the trityl moiety is attached. Thus, the π and trityl radicals can interact closely but not via a bonding interaction. This mechanism dominates over through-bond interactions, and the excited-state interaction is ferromagnetic with JTR = 1.14 cm−1. Calculations on the same structure with para-attachment of the trityl radical produced ESAFC with JTR = −9.16 cm−1, consistent with the proposed hypothesis.
These results agree with the recent results published by Shinozuka et al.,61 which demonstrated that bridging and radical moieties which favor strong uninterrupted radical/pentacene overlap result in a large trip-doublet/trip-quartet gap for the pentacene frontier orbitals, and thus a large |JTR|, whereas a smaller trip-doublet/trip-quartet gap (and thus smaller |JTR|) is observed in systems where the radical cannot overlap significantly with the pentacene π system, such as in the cross-conjugation of BDPA or the π-network interruption of TEMPO. Indeed, as is especially apparent in the (5,5) calculations with the use of an alkyne linker, the strong π network connecting the pentacene frontier orbitals with the radical of trityl results in a much larger |JTR| as compared to in the analogous BDPA or TEMPO systems.
4 Conclusions
Herein was reported the calculation of the excited state energies and J-exchange parameters in large radical-tethered pentacene systems using quasidegenerate perturbation theory (QD-NEVPT2).Using QD-NEVPT2, structural studies exploring the effects of various conjugation, distance, and symmetry motifs on the nature of exchange coupling in these systems were additionally performed. We also compared the effect of introducing local radical excitations on the magnitude and sign of JTR by increasing the active space to include radical localized π orbitals above and below the (single-determinant ground state) SOMO. We found that our state-averaged QD-NEVPT2 (3,3) calculations underestimate the  transition energy. This is in part due to a systematic destabilization of the doublet ground-state due to state averaging across the different electronic states as well as the use of a minimal active space. QD-NEVPT2 (3,3) reproduced the expected relative JTR magnitudes of structures 1a,b,c, with pTrityl showing the greatest |JTR|, however all three of these structures were found to be in a weak coupling regime which was inconsistent with experiment.5 Considering distortion of the pentacene/phenyl dihedral angles, we found that the trityl structure 1c exhibits the greatest response in |JTR| after angle adjustment when compared to the analogous BDPA and TEMPO structures. More importantly, the response of |JTR| in pTrityl to reasonable angle adjustments was consistent with the coexistence of both weak and strong coupling regimes present, while the exchange coupling of the TEMPO and BDPA systems remained consistent with a weak coupling regime or exhibited an inversion of magnetic state ordering, respectively.
transition energy. This is in part due to a systematic destabilization of the doublet ground-state due to state averaging across the different electronic states as well as the use of a minimal active space. QD-NEVPT2 (3,3) reproduced the expected relative JTR magnitudes of structures 1a,b,c, with pTrityl showing the greatest |JTR|, however all three of these structures were found to be in a weak coupling regime which was inconsistent with experiment.5 Considering distortion of the pentacene/phenyl dihedral angles, we found that the trityl structure 1c exhibits the greatest response in |JTR| after angle adjustment when compared to the analogous BDPA and TEMPO structures. More importantly, the response of |JTR| in pTrityl to reasonable angle adjustments was consistent with the coexistence of both weak and strong coupling regimes present, while the exchange coupling of the TEMPO and BDPA systems remained consistent with a weak coupling regime or exhibited an inversion of magnetic state ordering, respectively.
From the 6-position structures that were explored in this study, the shortening of the bridge linker generally leads to an increase in the predicted |JTR| as does an extended π delocalization of the pentacene triplet across a conjugated bridge. However, the results for 2-position structures indicate that asymmetry in the contribution of individual J interactions can in some cases dominate changes in |JTR| over the effect of distance and π delocalization. We also found that greatly extended delocalization of the pentacene π-system towards the radical gives rise to ESFC (JTR > 0) in the absence of direct overlap of the π system and radical orbitals, this is seen across multiple structures for BDPA which has an inherent cross-conjugation motif. However, when magnetic orbitals are highly localized, the introduction of cross-conjugation into the bridge can limit the extended delocalization of the π system and results in a switch from ESFC to ESAFC (JTR < 0) due to weakened π interactions.
QD-NEVPT2 (5,5) calculations that included the radical-localized orbitals above and below the SOMO of trityl and BDPA structures maintain the sign of JTR in almost all structure 1 systems when compared to their QD-NEVPT2 (3,3) counterparts. Exceptions arise in cases where the introduction of the additional radical-localized π orbitals to the active space contribute to a description of the radical that is more delocalized. This can lead to a case where the type of exchange that more significantly contributes to the sign of J (potential or kinetic) can change. This is an important result, as it highlights that a minimal active space in C–R dyads may not be suitable when the radical has an extended π system as is the case for trityl. The role of the individual J-components was also explored and we found that the signs of J12 and J23 match in structures where the bridge encourages strong π-delocalization and π–radical interaction, as well as in structures of greater symmetry (i.e. 6-position attachment rather than 2-position). We note that angle-adjusted trityl 1c* exhibits a change in relative signs of the J components from opposite to same sign as compared to 1c. Given that 1c* shows a large enough JTR to be in the strong coupling regime while 1c does not, these sign changes may have mechanistic implications for the experimental appearance of EISC and ESP. However, drawing any strong conclusions about the contribution of the relative sign of the individual components likely requires further systematic studies.
The accurate prediction of exchange interactions via electronic structure calculations is a persistent challenge in quantum chemistry. Based on both (3,3) and (5,5) active space calculations, for the systems studied here, we can confidently report that the calculated sign of JTR in our structures can be well explained by invoking the rules set forth by Kanamori and Goodenough.33–35 This consistency allows a strong predictive power guided by employing these principles to determine the dominant type of exchange coupling (kinetic vs. potential) taking place. We’d also like to note a recent work62 which applied a difference-dedicated perturbation theory (DDPT2) to separate distinct contributions of the exchange interaction through careful consideration of the weight of ionic determinants in the optimization step of CASSCF.
Obtaining accurate calculations of the magnitude and sign of exchange interactions as well as the origin of these interactions in C–R dyads would aid in their design for applications in quantum sensing and dynamic nuclear polarization, as the coupling regimes could be tuned to be compatible with strong or weak-coupling regimes depending on a given magnetic field.
Future studies aim to perform multiconfigurational pair density functional theory calculations in conjunction with nonadiabatic statistical theory63 calculations in order to explore the nature of minimum energy crossing points and conical intersections in the present systems. For example, Varganov et al. have demonstrated the use of nonadiabatic statistical theory in the study of SOC-mediated intersystem crossing rates.63–66
Author contributions
Philip S. Weiss: implementation, quantum calculations, investigation, methodology, analysis, writing – original draft; Amiel S. Paz: implementation, writing – review and editing; Claudia E. Avalos: conceptualization, project administration, supervision, writing – review and editing, funding acquisition.Data availability
The input and log files from this study have been uploaded to the following Zenodo data repository: https://doi.org/10.5281/zenodo.14885112.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Prof. William Glover and Yuquan Cao at NYU Shanghai for helpful conversations and initial assistance with excited state calculations. This study is based upon work supported by the National Science Foundation under Grant No. 2339355. This work was supported in part through the NYU IT High Performance Computing resources, services, and staff expertise. The authors would also like to extend particular thanks to Shenglong Wang of the NYU HPC team who provided his expertise and support for setting up and maintaining calculations on the NYU HPC systems.Notes and references
- C. S. Shin, C. E. Avalos, M. C. Butler, D. R. Trease, S. J. Seltzer, J. Peter Mustonen, D. J. Kennedy, V. M. Acosta, D. Budker and A. Pines, et al. , J. Appl. Phys., 2012, 112, 124519 CrossRef.
- S. J. DeVience, L. M. Pham, I. Lovchinsky, A. O. Sushkov, N. Bar-Gill, C. Belthangady, F. Casola, M. Corbett, H. Zhang and M. Lukin, et al. , Nat. Nanotechnol., 2015, 10, 129–134 CrossRef CAS PubMed.
- M. Maylander, S. Chen, E. R. Lorenzo, M. R. Wasielewski and S. Richert, J. Am. Chem. Soc., 2021, 143, 7050–7058 CrossRef PubMed.
- T. Quintes, M. Mayländer and S. Richert, Nat. Rev. Chem., 2023, 7, 75–90 CrossRef PubMed.
- C. E. Avalos, S. Richert, E. Socie, G. Karthikeyan, G. Casano, G. Stevanato, D. J. Kubicki, J. E. Moser, C. R. Timmel and M. Lelli, et al. , J. Phys. Chem. A, 2020, 124, 6068–6075 CrossRef CAS PubMed.
- E. T. Chernick, R. Casillas, J. Zirzlmeier, D. M. Gardner, M. Gruber, H. Kropp, K. Meyer, M. R. Wasielewski, D. M. Guldi and R. R. Tykwinski, J. Am. Chem. Soc., 2015, 137, 857–863 CrossRef CAS PubMed.
- X. Zhang, X. Chen, Y. Sun and J. Zhao, Org. Biomol. Chem., 2024, 22, 5257–5283 RSC.
- E. M. Giacobbe, Q. Mi, M. T. Colvin, B. Cohen, C. Ramanan, A. M. Scott, S. Yeganeh, T. J. Marks, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2009, 131, 3700–3712 CrossRef CAS.
- Y. Kandrashkin and A. van der Est, Chem. Phys. Lett., 2003, 379, 574–580 CrossRef CAS.
- S. Richert, C. E. Tait and C. R. Timmel, J. Magn. Reson., 2017, 280, 103–116 CrossRef CAS PubMed.
- A. van der Est, M. Asano-Someda, P. Ragogna and Y. Kaizu, J. Phys. Chem. A, 2002, 106, 8531–8542 CrossRef CAS.
- V. Rozenshtein, A. Berg, E. Stavitski, H. Levanon, L. Franco and C. Corvaja, J. Phys. Chem. A, 2005, 109, 11144–11154 CrossRef CAS PubMed.
- E. Sartori, A. Toffoletti, C. Corvaja and L. Garlaschelli, J. Phys. Chem. A, 2001, 105, 10776–10780 CrossRef CAS.
- M. T. Colvin, R. Carmieli, T. Miura, S. Richert, D. M. Gardner, A. L. Smeigh, S. M. Dyar, S. M. Conron, M. A. Ratner and M. R. Wasielewski, J. Phys. Chem. A, 2013, 117, 5314–5325 CrossRef CAS.
- Y. Qiu, A. Equbal, C. Lin, Y. Huang, P. J. Brown, R. M. Young, M. D. Krzyaniak and M. R. Wasielewski, Angew. Chem., Int. Ed., 2023, 62, e202214668 CrossRef CAS PubMed.
- A. Bencini and D. Gatteschi, Electron paramagnetic resonance of exchange coupled systems, Springer-Verlag, Berlin, 1990, pp. 20–47 Search PubMed.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- C. J. Cramer, Computational Chemistry: Theories and Models, 2004 Search PubMed.
- A. Bajaj and M. E. Ali, J. Phys. Chem. C, 2019, 123, 15186–15194 Search PubMed.
- B. O. Roos, P. R. Taylor and P. E. Sigbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- P. Siegbahn, A. Heiberg, B. Roos and B. Levy, Phys. Scr., 1980, 21, 323 CAS.
- M. Franz, F. Neese and S. Richert, Chem. Sci., 2022, 13, 12358–12366 CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CAS.
- C. Angeli, S. Borini, M. Cestari and R. Cimiraglia, J. Chem. Phys., 2004, 121, 4043–4049 CAS.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 Search PubMed.
- T. Shiozaki, W. Györffy, P. Celani and H.-J. Werner, J. Chem. Phys., 2011, 135, 081106 Search PubMed.
- T. Shiozaki, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1331 Search PubMed.
- M. C. Gutzwiller, Phys. Rev. Lett., 1963, 10, 159 Search PubMed.
- J. Kanamori, Prog. Theor. Phys., 1963, 30, 275–289 Search PubMed.
- J. Hubbard, Proc. R. Soc. London, Ser. A, 1963, 276, 238–257 Search PubMed.
- J. Hubbard, Proc. R. Soc. London, Ser. A, 1964, 281, 401–419 Search PubMed.
- B. Kaduk, T. Kowalczyk and T. Van Voorhis, Chem. Rev., 2012, 112, 321–370 CrossRef CAS PubMed.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564 CrossRef CAS.
- J. B. Goodenough, J. Phys. Chem. Solids, 1958, 6, 287–297 CrossRef CAS.
- J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98 CrossRef CAS.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed.
- A. V. Titov, I. S. Ufimtsev, N. Luehr and T. J. Martinez, J. Chem. Theory Comput., 2013, 9, 213–221 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- I. Shavitt and L. T. Redmon, J. Chem. Phys., 1980, 73, 5711–5717 CrossRef CAS.
- Y. E. Kandrashkin and A. van der Est, J. Phys. Chem. Lett., 2021, 12, 7312–7318 CrossRef CAS PubMed.
- J. G. Aiken, J. A. Erdos and J. A. Goldstein, Int. J. Quantum Chem., 1980, 18, 1101–1108 CrossRef CAS.
- T.-C. Yang, D. J. Sloop, S. Weissman and T.-S. Lin, J. Chem. Phys., 2000, 113, 11194–11201 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- Y.-S. Lin, G.-D. Li, S.-P. Mao and J.-D. Chai, J. Chem. Theory Comput., 2013, 9, 263–272 CrossRef CAS PubMed.
- R. Sarkar, P.-F. Loos, M. Boggio-Pasqua and D. Jacquemin, J. Chem. Theory Comput., 2022, 18, 2418–2436 CAS.
- I. Schapiro, K. Sivalingam and F. Neese, J. Chem. Theory Comput., 2013, 9, 3567–3580 CrossRef CAS PubMed.
- T. M. Halasinski, D. M. Hudgins, F. Salama, L. J. Allamandola and T. Bally, J. Phys. Chem. A, 2000, 104, 7484–7491 CAS.
- P. B. Coto, S. Sharifzadeh, J. B. Neaton and M. Thoss, J. Chem. Theory Comput., 2015, 11, 147–156 CrossRef CAS PubMed.
- P.-O. Löwdin, J. Chem. Phys., 1950, 18, 365–375 CrossRef.
- M. L. Kirk, D. A. Shultz, D. E. Stasiw, D. Habel-Rodriguez, B. Stein and P. D. Boyle, J. Am. Chem. Soc., 2013, 135, 14713–14725 CrossRef CAS PubMed.
- D. A. Shultz, R. M. Fico, S. H. Bodnar, R. K. Kumar, K. E. Vostrikova, J. W. Kampf and P. D. Boyle, J. Am. Chem. Soc., 2003, 125, 11761–11771 CrossRef CAS PubMed.
- P. A. Limacher and H. P. Lüthi, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 477–486 CAS.
- H. Valkenier, C. M. Guédon, T. Markussen, K. S. Thygesen, S. J. van der Molen and J. C. Hummelen, Phys. Chem. Chem. Phys., 2014, 16, 653–662 RSC.
- M. L. Tiago, J. E. Northrup and S. G. Louie, Phys. Rev. B:Condens. Matter Mater. Phys., 2003, 67, 115212 CrossRef.
- R. V. Viesser, L. C. Ducati, C. F. Tormena and J. Autschbach, Chem. Sci., 2017, 8, 6570–6576 RSC.
- S. Gorgon, K. Lv, J. Grüne, B. H. Drummond, W. K. Myers, G. Londi, G. Ricci, D. Valverde, C. Tonnelé and P. Murto, et al. , Nature, 2023, 620, 538–544 CrossRef CAS PubMed.
- T. Shinozuka, D. Shimizu and K. Matsuda, New J. Chem., 2024, 48, 8683–8689 RSC.
- M. Franz, F. Neese and S. Richert, Phys. Chem. Chem. Phys., 2024, 26, 25005–25020 RSC.
- R. R. Zaari and S. A. Varganov, J. Phys. Chem. A, 2015, 119, 1332–1338 CrossRef CAS PubMed.
- A. O. Lykhin, D. S. Kaliakin, G. E. DePolo, A. A. Kuzubov and S. A. Varganov, Int. J. Quantum Chem., 2016, 116, 750–761 CrossRef CAS.
- V. D. Dergachev, M. Rooein, I. D. Dergachev, A. O. Lykhin, R. C. Mauban and S. A. Varganov, New Horizons in Computational Chemistry Software, 2022, pp. 79–103 Search PubMed.
- I. D. Dergachev, V. D. Dergachev, M. Rooein, A. Mirzanejad and S. A. Varganov, Acc. Chem. Res., 2023, 56, 856–866 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04908j |
| This journal is © the Owner Societies 2025 |