i-Motif DNA in isolated hemiprotonated cytosine dimers, studied using IR spectroscopy and theoretical calculations

Abstract

This study provides a comprehensive investigation of the structural and vibrational properties of protonated cytosine monomers and dimers. Experimental IRPD spectroscopy, combined with theoretical calculations, revealed distinct behaviors for monomers and dimers. We find that protonated cytosine monomers predominantly adopt the enol form in the gas phase, with a contribution from the keto form between 25% and 33%. For dimers, our computations predict a keto–enol configuration to be more stable than the keto–keto form by 1.5 kcal mol⁻¹. However, experimentally, the keto–keto form emerged as the dominant structure. The theoretically most stable keto–enol configuration undergoes a structural reorganization in MD simulations with explicit methanol, forming the dynamically unstable neutral-keto–protonated–keto complex. This reorganization highlights the role of environmental factors in modulating tautomer populations.

---

1. Introduction

The i-motif is a unique, four-stranded DNA secondary structure stabilized by intercalated, hemiprotonated cytosine–cytosine (C·CH⁺) base pairs, which forms under slightly acidic conditions, common in cellular environments. Found in cytosine-rich sequences such as telomeric DNA and gene promoters, i-motifs have garnered attention due to their potential roles in cellular processes such as gene regulation, genome stability, telomere maintenance, and implications in various diseases.^1–3 For example, the presence of i-motifs in promoter regions of oncogenes such as c-myc, Bcl-2, and VEGF underscores their potential regulatory role in gene expression, as it suggests they may function as molecular switches modulating transcriptional activity, making them attractive targets for therapeutic interventions.^4–6 Telomeric DNA, which also adopts i-motif structures, is crucial for the stability and function of telomeres, with significant implications for cellular aging and cancer, and it could influence transcriptional activities.^7–9 Moreover, i-motifs may regulate genes related to neurological functions, suggesting broader impacts on neurological health.¹⁰ Their distinct structure also makes them promising targets for drug development, where ligands that stabilize or destabilize i-motifs could modulate oncogene expression, opening new avenues for cancer treatment.^11,12 Additionally, i-motifs may influence the progression of infectious diseases by regulating genes involved in immune responses.²

Despite their biological relevance, the intrinsic factors governing i-motif stability are not fully understood. The tautomeric forms of the cytosine building blocks in the hemiprotonated dimers influence hydrogen bonding and structural stability. Studying these interactions in the gas phase provides an opportunity to explore the details of their intrinsic interactions, free from solvent or ionic interferences. At the same time, gas-phase studies using electrospray ionization (ESI) have shown that i-motif structures can maintain their integrity under specific conditions, offering insights into their molecular behavior in solution.^13,14

The nature of hydrogen bonds in protonated cytosine dimer base pairs has been elucidated through various spectroscopic techniques, including NMR.¹⁵

Salpin and co-workers studied a protonated cytosine monomer (CH⁺) and its monohydrated complexes, produced with electrospray ionization (ESI) in a quadrupole ion trap.^16,17 Employing infrared multiphoton dissociation (IRMPD) in the 1000–2000 cm⁻¹ and 2700–3750 cm⁻¹ spectral ranges, they concluded that CH⁺ forms in the keto (M1 Fig. 1) and in the enol (M2 and M3 in Fig. 1) tautomer conformations under the electrospray conditions, with the enol forms the most populated. Broquier et al., while investigating the excited state dynamics of CH⁺, reported UV photodissociation spectra showing keto (M3 in Fig. 1) and enol tautomers.¹⁸ The enol signal was significantly stronger, although an absolute abundance ratio could not be determined. Yang et al. studied protonated cytosine dimers using infrared multiphoton dissociation (IRMPD) spectroscopy in the spectral range of (3400–3600 cm⁻¹) and concluded that they observed exclusively the i-motif.¹⁹

Fig. 1 Most stable protonated cytosine monomer structures (M1), (M2) and (M3) and their relative energies (ΔE) optimized in the gas phase at the MP2/cc-pVTZ level. Atomic color code representation: grey – carbon, red – oxygen, blue – nitrogen, and white – hydrogen.

In the i-motif, both cytosines are in the keto-tautomeric form, while the monomers are predominantly in the enol form. This discrepancy makes the selective formation of a keto–keto tautomeric dimer challenging to explain and raises the question of whether the occurrence of the i-motif in DNA is an intrinsic property of the protonated dimer or primarily influenced by the macromolecular environment. To address these issues, we present here a structural analysis of both protonated cytosine monomers and protonated cytosine dimers using infrared (IR) spectroscopy, including isomer-selective hole-burning IR spectroscopy in combination with advanced theoretical calculations.

2. Methodology

2.1 Experimental

We measured the infrared spectra using a cryogenic ion trap setup combined with an electrospray ion source and a time-of-flight mass spectrometer (ToF-MS), as depicted in Fig. S1 (ESI†) and described in detail previously.²⁰ Briefly, we prepared a 10⁻⁵ M solution of cytosine in methanol with 0.5% formic acid which was electrosprayed (ESI) from an emitter using N₂ as the sheath gas to guide fine droplets toward a glass capillary. The capillary was heated to 80 °C to facilitate solvent evaporation from the droplets, introducing protonated cytosine monomers (C–H⁺) and dimers (CC–H⁺) into the gas phase.

Mass-selected ions were filtered sequentially through a quadrupole mass filter (Q-MS1) and a second quadrupole mass spectrometer (QMS2). These ions were trapped in a cryogenic quadrupole ion trap (QIT) at 4 K, allowing for high-resolution spectroscopy.

To measure the infrared photo-dissociation (IRPD) spectra of the target ions in the gas phase, we employed a hydrogen tagging method, where H₂ molecules were introduced as a buffer gas in the QIT to attach to target ions. A tunable IR laser (OPO/OPA: Laser Vision) irradiated the trapped ions. Upon resonance with a vibrational mode of the tagged ions, the IR laser detached H₂, and we monitored the resulting bare ions with a ToF-MS. IRPD spectra were generated by tracking the increase in bare ion signal as a function of IR wavelength.

We obtained the isomer-selected IR spectra of specific cytosine-H⁺ conformers employing IR–IR double resonant spectroscopy, as shown in Fig. S2 (ESI†). First, the IRPD signal is measured at a fixed resonance wavelength, vibrationally selecting a specific isomer. A burn laser pulse, scanned across wavelengths of interest, was applied 1 ms before the probe pulse, selectively decreasing the IRPD signal whenever its wavelength is resonant with a vibrational mode of the same isomer. The burn laser pulses are chopped at 5 Hz by an optical chopper to produce a difference signal. By applying a tickle RF pulse, fragment ions from the burn laser were eliminated, isolating the probe-generated ions. Monitoring the depletion of fragment signal by the probe laser as a function of burn laser wavelength produces an IR spectrum for each conformer selected by the probe laser.

2.2 Theoretical

We performed molecular dynamics (MD) simulations at T = 100 K, using ORCA 5.0.3 code²¹ and visualized by VMD 1.9.2 visualization software,²² to investigate the structural stability of cytosine–cytosineH⁺ complexes, prepared from optimized cytosine and cytosineH⁺ monomers. The monomers were first subjected to optimization, harmonic frequency calculations, and natural bond orbital (NBO) analyses using density functional theory (DFT) at the PBE0-D3/def2-TZVP level with Gaussian 16.²³ These optimized monomer structures were subsequently reoptimized at the MP2/cc-pVTZ level, including harmonic frequency calculations and NBO analyses. The monomer energies obtained from these calculations were used as a reference for evaluating the interaction energies and free energies of all the optimized dimers.

Using the optimized monomer structures, we generated six candidate cytosine–cytosineH⁺ complexes for further investigation. We performed MD simulations for these dimer structures at the PBE0-D3BJ/def2-SVP level of theory, with a Nose–Hoover Chain thermostat and a high-order Yoshida integrator^24,25 (20 fs time constant) to control the temperature. Simulations ran for 10 ps with a 1 fs time step, and the resulting trajectories were visualized with VMD 1.9.2 software. Structurally and periodically selected snapshots from these MD trajectories were then subjected to geometry optimization, harmonic frequency calculations, and NBO analyses at the PBE0-D3/def2-TZVP level, using Gaussian 16.²³ We further reoptimized these optimized dimer structures at the MP2/cc-pVTZ level, accompanied by harmonic frequency calculations and NBO analyses.

The interaction energies and free energies of the cytosine–cytosineH⁺ complexes were determined using the calculated energies of both the dimer structures and their corresponding monomers. All optimized structures and minimum energy configurations were analyzed using GaussView 6.0.16 for visualization, ensuring accuracy in interpreting the structural and energetic properties of the systems.

Interaction energies (ΔE) and free energies (ΔG) were calculated using:

ΔE = E_complex − E_monomer1 − E_monomer2 (1)

ΔG = G_complex − G_monomer1 − G_monomer2 (2)

The interaction energies (ΔE) and the binding free energies (ΔG) were determined using the rigid rotor–harmonic oscillator–ideal gas approximation at the same computational level. Binding free energies will be presented throughout with a positive sign indicating stabilization.

Throughout this work, the calculated spectra are scaled by a scaling factor of 0.945 for the 3μ range (3000–3800 cm⁻¹) and 0.956 for the 6μ range (1400–1900 cm⁻¹).

In contrast to previous studies that often relied on the lower level B3LYP/6-31G* method—limited by its lack of dispersion correction and insufficient treatment of long-range interactions—our theoretical calculations incorporate dispersion forces through high-level theoretical methodologies. Specifically, we use PBE0-D3/def2-TZVP and MP2/cc-pVTZ, for all the calculations including harmonic frequency calculations, providing greater accuracy and reliability for the cluster model analyses.

The H₂ tagging technique employed in this study represents a form of IR action spectroscopy, offering a sensitive and selective method for probing vibrational modes. While IR multiphoton dissociation spectroscopy of untagged ions can provide analogous information, it necessitates significantly higher photon fluxes, making the tagging technique a gentler and more precise alternative. However, we must account for the potential influence of cluster dissociation on the observed IR spectra. Specifically, the monitored M⁺ ion could result from the dissociation of larger clusters containing additional H₂ molecules, following the pathway M⁺(H₂)_n → M⁺ + nH₂. To evaluate whether this phenomenon impacts the accuracy of the observed spectra, we calculated the IR frequencies of hemiprotonated dimer clusters with multiple H₂ tags. These calculations confirm the robustness of the tagging technique, ensuring that the reported spectra accurately reflect the intrinsic vibrational characteristics of the target ions.

3. Results

3.1. Protonated cytosine monomer

3.1.1 Experimental IRPD spectrum of protonated cytosine monomers. Fig. 2(a)–(c) show experimental IR spectra for the protonated cytosine monomer in the 3-micron range (3250–3700 cm⁻¹). Fig. 2(a) displays the IRPD spectrum representing the total vibrational spectrum of coexisting species. Fig. 2(b) and (c) display isomer-specific IR–IR hole-burning spectra, with probe frequencies fixed at 3513 cm⁻¹ and 3533 cm⁻¹, respectively.

Fig. 2 Comparison spectra of (a) experimental IRPD, (b) and (c) IRIR hole burning spectra with probe at 3513 cm⁻¹ (b), and 3533 cm⁻¹ (c). (d)–(i) Computational spectra for the tautomer forms shown in Fig. 1 with different hydrogen tag structures, shown in the figure and labeled as or . The calculated spectra have a scaling factor 0.945.

The hole burning spectra reveal the presence of two distinct species contributing to the IRPD spectrum in Fig. 2(a). The bands at 3384 cm⁻¹ and 3513 cm⁻¹ in Fig. 2(a) correspond exclusively to the species probed at 3513 cm⁻¹ in Fig. 2(b). The band at 3533 cm⁻¹ uniquely characterizes the single species in Fig. 2(c), as it doesn’t appear in Fig. 2(b). Both species, exhibit a shared vibrational mode at 3415 cm⁻¹, which appears prominently in the IRPD spectrum due to the contributions from both isomers.

3.1.2 Computational analysis. To assign the experimental peaks, we optimized the geometries and calculated IR spectra of protonated cytosines at the MP2/cc-pVTZ level. Fig. 1 depicts the most stable isolated protonated cytosine structures (M1, M2, and M3). Protonation at the N3 position induces notable structural shifts, with a shortened N3–C4 bond and an elongated C4–N4 bond, reflecting electron density redistribution. Among these, structures M2 and M3 represent two enol rotamers with near-identical vibrational spectra (see Fig. S3(g) and (h), ESI†).

To enable a meaningful comparison with the experimental data, which were obtained with H₂ tagging, we optimized the geometries and calculated the IR spectra for the H₂-tagged versions of the structures M1–M3. For each tautomer we found two optimized hydrogen tagged structures, labeled as and , respectively. Fig. 2(d)–(i) show the tagged structures and their calculated IR spectra, with a scaling factor of 0.945 (for the 6-micron range, shown in Fig. S3, we used a scaling factor of 0.956, ESI†).

We attribute the IR–IR spectra shown in panel (b) to either M1′ or M1′′ or a combination of those two. For the keto structures, the H₂ molecule is tagged to the N1–H bond in M1′ and to the amino group in M1′′. This positional difference in H₂ tagging alters the vibrational modes associated with N–H and C–H stretches. Specifically, M1′ exhibits a prominent N–H stretching mode at ∼3350 cm⁻¹ and a C–H vibrational mode at 3513 cm⁻¹, both of which closely match the experimental spectrum in Fig. 2(b). In contrast, M1′′ shows slightly shifted vibrational modes due to the amino-side tagging, but these shifts are not distinguishable in the experimental data, and the theoretical calculations show similar energies and frequencies, thus preventing conclusive differentiation between M1′ and M1′′.

For the enol structures, the H₂ molecule is tagged at the hydroxyl group in M2′ and M3′, while in M2′′ and M3′′ it is tagged at the amino group. This distinction impacts the O–H stretching modes. M2′ features a red-shifted O–H stretching mode at ∼3533 cm⁻¹ due to intramolecular hydrogen bonding, matching the experimental spectrum in Fig. 2(c). M2′′, on the other hand, exhibits a free O–H stretch at ∼3626 cm⁻¹, which is absent in the experimental data, indicating that the amino-side tagged enol tautomer (M2′′) is not observed under these experimental conditions. M3′ also shows a red-shifted O–H stretch frequency, relative to the amino-side tagged M3′′. However, both M3 spectra form a poor fit with the experimental data, so, although bare M3 is more stable than bare M2 by 8 kcal mol⁻¹, it appears that M3 is not observed in the experiment, which reflects the more stable complexes formed with H₂ tagging.

Fig. S3 (ESI†) compares the experimental IRPD spectrum with calculated vibrational spectra for both tagged and untagged protonated cytosine structures across the 3-micron (3000–3800 cm⁻¹) and 6-micron (1400–2000 cm⁻¹) regions. The H₂-tagged spectra (M1′–M2′, Fig. S3(b)–(d)) align closely with the experimental data, confirming peak assignments to specific tautomers. This also matches prior IRMPD observations by Salpin et al., where the enol tautomer was predominantly assigned.¹⁶ Key differences between the tagged (M1′–M2′′) and untagged (M1–M3) structures illustrate the subtle shifts induced by the H₂ tag, particularly in the 3-micron region where the interactions with functional groups (carbonyl, amino, hydroxyl) are prominent. The keto forms exhibit strong N–H and C–H stretching modes (∼3384 cm⁻¹ and ∼3513 cm⁻¹), while the enol forms feature an O–H stretching mode (∼3533 cm⁻¹).

We conclude that the IRPD peaks at 3513 cm⁻¹ and 3533 cm⁻¹ are unique for the keto and enol tautomeric forms, respectively. Therefore, we can use these peaks to calculate the relative abundances of these two tautomers in our experiment, using the following equation:

where S_a and S_b are the areas of the peaks in the IRPD spectrum, and I_a, I_b are the corresponding calculated IR intensities. For this type of action spectroscopy, we adopt the assumption that the IR induced H₂ loss rate is the same for all modes. Since we cannot experimentally distinguish between the two keto structures (d) and (e) we separately calculated the abundance ratio for each case. Assuming (d) as the keto structure, this calculation provides a relative abundance of 25% for the keto form and 75% for the enol form. Assuming (e) as the keto, structure the abundance ratio would be 33% for the keto form and 67% for the enol form. A mixture would have a ratio between these two values, so we bracket the keto population between 25% and 33%. In either case, these results indicate that the enol tautomer is dominant in this mixture.

3.2. Protonated cytosine dimer

3.2.1 Experimental IRPD spectrum of protonated cytosine dimers. The experimental IRPD spectrum of protonated cytosine dimers, presented in Fig. 3(a), spans the 3-micron and 6-micron regions. In the 6-micron range, distinct bands appear between 1600 cm⁻¹ and ∼1800 cm⁻¹. In the 3-micron range, dominant peaks appear near ∼3200 cm⁻¹ and ∼3450 cm⁻¹, with two additional weaker features around ∼3500 cm⁻¹. Compared to previously reported IRMPD spectra obtained at room temperature,²⁶ the sharper peaks observed in this study result from the colder experimental conditions (∼10 K) achieved using our cryogenic ion trap setup. These low-temperature conditions reduce thermal broadening, enabling more precise spectral assignments.

Fig. 3 Comparison of the measured IRPD spectrum (a) with the calculated vibrational spectra of the most stable protonated cytosine dimer structures (b)–(e) in the 3-micron (3000–3800 cm⁻¹) and 6-micron (1400–2000 cm⁻¹) regions. Panels (b)–(e) correspond to the D1 (b), D2 (c), D3 (d), and D4 (e) structures, with calculated spectra scaled by a factor of 0.945 for the 3-micron range and 0.956 for the 6-micron range.

3.2.2 Computational analysis. To explore the structural diversity of protonated cytosine dimers, six initial configurations were generated by combining optimized monomers of neutral cytosine (C) and protonated cytosine (CH⁺) in both keto and enol forms. These starting configurations included planar, stacked, and T-shaped conformations in both keto–keto and keto–enol arrangements. Experimentally, the sample is released from the ESI capillary at ∼350 K and trapped in the ion trap at 4 K. Within that range, it is rather difficult to specify the temperature at which proton transfer may occur in the dimer. While higher temperatures could facilitate, it is important to establish the possibility of proton transfer at lower temperature. Therefore, we performed molecular dynamics simulations at T = 100 K in the gas phase at the PBE0/def2-SVP level, followed by structural optimizations at the PBE0-D3/def2-TZVP level and reoptimized at the MP2/cc-pVTZ level along with vibrational analysis at both levels. These results revealed that cytosine–cytosineH⁺ dimers preferentially adopt planar configurations, as shown in Fig. 4. Stacked conformations were found to be unstable and did not converge to minima, highlighting the structural preference for planar arrangements under the given conditions.

Fig. 4 Optimized geometries of the most stable hemiprotonated cytosine dimer structures (D1)–(D4) calculated at the MP2/cc-pVTZ level, their interaction energies (ΔE) and binding free energies (ΔG) with a positive sign indicating stabilization, are presented above each structure. Color code: grey = carbon, red = oxygen, blue = nitrogen, white = hydrogen.

Fig. 4 provides the optimized geometries of the four most stable dimer configurations (D1–D4), highlighting key structural features and their calculated interaction energies (ΔE) and binding free energies (ΔG) at T = 100 K (positive number indicates stabilization). D1 (planar keto–keto) and D2 (planar keto–enol) represent the dominant configurations, with strong hydrogen bonding interactions accounting for their stability. D1 and D2 exhibit the lowest interaction energies (ΔE = −48.3 kcal mol⁻¹ and ΔE = −49.1 kcal mol⁻¹, respectively) and binding free energies (ΔG = 43.1 kcal mol⁻¹ and ΔG = 44.6 kcal mol⁻¹). These configurations are energetically favorable and practically isoenergetic, with additional stability stemming from strong hydrogen bonding interactions.

3.2.3 Comparison of theoretical and experimental spectra. The IR spectra of the four most stable dimer configurations (D1–D4) were calculated at the MP2/cc-pVTZ level with scaling factors of 0.945 (3-micron region) and 0.956 (6-micron region). These calculated spectra, accompanied by their molecular structures, are shown in Fig. 3(b)–(e).

The keto–keto structure D1 exhibits excellent agreement with experimental data across both frequency ranges. In the 6-micron range, the experimental IRPD spectrum displays a peak at 1762 cm⁻¹ that agrees with the vibrational band from the D1 keto–keto isomer corresponding to the C=O stretch of the dimer complex. In the 3-micron region, all observed bands can be assigned to the D1 isomer. With the superscripts ⁰ and ^p describing the neutral and protonated cytosine, we can make the following assignments: the symmetric (NH₂)⁰ stretch at 3250 cm⁻¹, the (N1–H)⁰ and (N1–H)^p stretch at 3450 cm⁻¹, the asymmetric (NH₂)^p stretch at 3485 cm⁻¹, and the asymmetric (NH₂)⁰ stretch at 3525 cm⁻¹. The doublet structure of the peak at 3420 cm⁻¹ is likely due to the contributions of the N1–H stretches from both cytosines, which only differ by a few wavenumbers. This not fully resolved combination also explains the larger intensity of this peak in the experimental spectrum. There could be a small contribution to this peak from the peak at 3445 cm⁻¹ in D2, which arises from the symmetric NH₂ stretches of both cytosines (split by 3 cm⁻¹), however, since we do not observe the 3560 cm⁻¹ peak (from the antisymmetric NH₂ stretches on both cytosines) and the 6-micron range for D2 does not match well, this contribution cannot be significant. These observations establish D1 as the primary contributor to the experimental spectrum.

The keto–keto D3 exhibits poor agreement with the experimental spectrum in both regions. Its calculated modes do not correspond to the dominant experimental features, particularly in the 6-micron range. Consequently, D3 is excluded as a meaningful contributor. The keto–enol structure D4 initially appears promising in the 3-micron region, where its calculated peaks near ∼3400 cm⁻¹ and ∼3500 cm⁻¹ align with experimental features. However, its poor agreement in the 6-micron range excludes it as a significant contributor.

While a precise quantitative population analysis cannot be performed with the current data, the strong agreement between the experimental spectrum and the calculated spectra for D1 suggests that this keto–keto configuration is the major contributor to the population of protonated cytosine dimers in the gas phase, although D2 is energetically more stable by 1.5 kcal mol⁻¹, according to the computations. These results reveal a significant shift in tautomer preference between monomers and dimers: while protonated cytosine monomers predominantly favor the enol configuration, dimerization stabilizes the keto tautomer through robust hydrogen bonding. This shift highlights the importance of dimerization in reshaping tautomer stability and sets the stage for further investigation of how environmental factors, such as solvent interactions, modulate these populations.

To further refine the spectral assignments and explore the effects of hydrogen tagging, additional configurations of D1 and D2 were generated. Fig. S4 (ESI†) illustrates the structural variations of D1 and D2 under hydrogen tagging, showing configurations with either one hydrogen molecule tagging (D1′ and D2′) or multiple hydrogen molecule tagging (D1′′, D1′′′, and D2′′). Despite the added hydrogen molecules, all tagged structures retained their planar geometries and strong hydrogen bonding interactions. These findings emphasize that the intrinsic stability of D1 and D2 is preserved even under these modified experimental conditions, further supporting their relevance as key configurations in the gas phase. Comparison between theoretical and experimental spectra without tagging is shown Fig. S5 in ESI.†

4. Discussion

While these gas phase measurements provide structural detail at the isolated molecular level, we need to consider to what extent they represent structures in solution. There is ample evidence that structures emerging from electrospray ionization sources, such as ours, can correspond to a large degree to the nascent solution structures.^27–29 This correspondence is especially plausible for the cytosine dimers observed in our study, given the known predominance of the i-motif dimer structure in solution.^7,30 The likelihood of dimer formation occurring solely in the gas phase is low because non-covalent complex formation during the ESI process is energetically unfavorable. The removal of solvent molecules during ionization requires substantial energy, making recombination of a protonated cytosine monomer with a neutral molecule in the gas phase improbable. Consequently, the cytosine dimer observed following ESI is most likely already formed and protonated in solution, where protonation predominantly occurs at the N3 site. As Rajabi et al. pointed out, the preservation of solvent-phase structures in small species is preserved in gas-phase studies.²⁷ It also implies that theoretical modeling should incorporate solvent effects rather than be limited to isolated gas-phase calculations, as the structures must predict the gaseous ions born in solution, such as those from an electrospray source.²⁷ Indeed, Cruz-Ortiz et al. demonstrated that the experimentally observed isomers of small molecular systems, such as cytosine dimers, align more closely with calculated structures in solution than in the gas phase. Their work also showed that the relative populations of isomers estimated experimentally are in better agreement with solution-phase models, both at 298 K and under polar solvent conditions.³¹ Thus, these findings underscore the necessity of considering solvent effects when interpreting structural assignments derived from gas-phase experimental spectra and calculations. Our study employs solvent-phase optimizations and MD simulations to address this limitation and refine our understanding of cytosine dimer configurations.

Together, these analyses emphasize the critical role of D1 and D2 as dominant gas-phase configurations of protonated cytosine dimers. However, the observed structural stabilization of the keto–keto configuration (D1) raises questions about how dimerization and tautomer stability might be influenced by environmental factors, such as solvent effects. The strong preference for the keto form in the dimer compared to the enol dominance in monomers, even as it is not the energetically most stable form, highlights the need to investigate how solvent interactions reshape these equilibria, particularly under biologically relevant conditions.

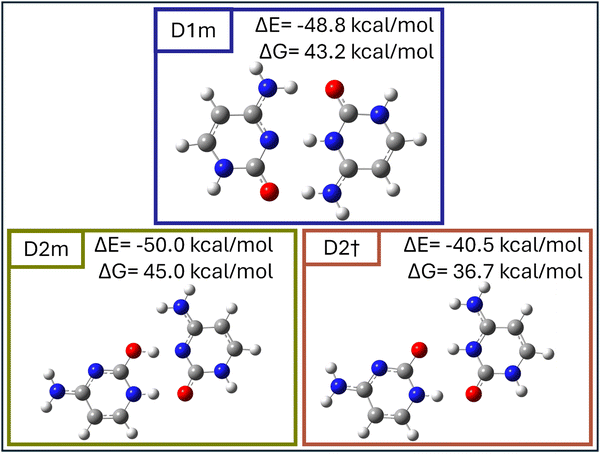
To investigate the influence of solvent on the stability and structural preferences of hemiprotonated cytosine dimers, we performed density functional theory (DFT) calculations for D1 and D2 in a methanol solvent environment. Optimizations were performed at the PBE0-D3/def2-TZVP level using a continuum solvation model (COSMO, ε = 32.7), obtaining the structures D1M and D2M. Here, ε = 32.7 corresponds to the dielectric constant of methanol solvent. These geometries were retained for subsequent single-point energy calculations in the gas phase to evaluate their energy without further re-optimization. Notably, vibrational frequency calculations were performed separately for the solvent-optimized and gas-phase models, revealing distinct IR spectra for these complexes in the solvent environment (Fig. 6D1M and D2M) compared to the gas phase, following solvent evaporation (Fig. 6D1m and D2m). These calculations were complemented with vibrational and natural bond orbital (NBO) analyses, allowing for a comprehensive evaluation of the structural dynamics and stability of the dimers under solvent conditions. Energies, hydrogen-bond distances, and vibrational frequencies for these configurations are summarized in Table 1. Even in these high-level theoretical calculations, the enol–keto dimer conformation (D2 and related structures) shows comparable stability to the keto–keto dimer.

Table 1 Interaction energies (ΔE) and binding free energies (ΔG) with a positive sign indicating stabilization, distances of various H-bonds, and their corresponding vibrational frequencies of hemiprotonated cytosine dimer structures optimized in methanol before (D1M and D2M), and after (D1m and D2m) evaporation of the solvent, and D2m after rearrangement before (D2†M) and after solvent evaporation (D2†). For the complex with methanol, the first number is the vibrational frequency corresponding to geometry optimized in methanol, second number corresponds to the frequency in gas phase for the optimized geometry in methanol and the third number corresponds to the frequency of gas phase optimized geometry. Energies are given in kcal mol⁻¹, with distances of various hydrogen bonds (H-bonds) provided in Å, alongside corresponding vibrational frequencies in cm⁻¹

System	ΔE (kcal mol^−1)	ΔG (kcal mol^−1)	OH⋯N (Å) (cm^−1)	NH⋯O (Å) (cm^−1)	NH⋯N (Å) (cm^−1)	O⋯HN (Å) (cm^−1)
D1m	−48.8	43.2		1.892 (3437)	1.709 (2592)	1.609 (2862)
D1M	−16.4	12.0		1.918 (3461/3450/3437)	1.780 (2777/2779/2592)	1.701 (3046/3042/2862)
D2m	−50.0	45.0	1.569 (2497)	1.644 (2924)
D2M	−20.1	16.9	1.539 (2087/2169/2497)	1.665 (2936/2970/2924)
D2†M	−11.6	7.6		1.581 (2632/2588/1862 + 1787 + 1765)		1.872 (3345/3375/3378)
D2†	−40.5	36.7		1.326 (1862 + 1787 + 1765) combination due to repulsion		1.914(3378)

---

Fig. 5 presents the optimized structures of D1m and D2m in methanol after solvent evaporation, highlighting their distinct hydrogen bonding arrangements and stability in the solvent environment.

Fig. 5 Optimized structures of the most stable hemiprotonated cytosine dimers in methanol after solvent evaporation and their subsequent rearrangements. D1m and D2m represent D1 and D2 dimers, respectively, optimized in methanol solvent after evaporation. D2† depicts the structure of D2m after rearrangement. Their respective interaction energies (ΔE) and binding free energies (ΔG) with a positive sign indicating stabilization are given above each structure.

To understand the inconsistency between the experimental domination of the keto–keto dimer and theoretically similar stabilities of keto–keto and enol–keto dimers, we conducted molecular dynamics (MD) simulations at T = 100 K using both implicit methanol and an explicit solvent model with 18 methanol molecules. In the implicit solvent model, both complexes rapidly destabilized and disintegrated within a few hundred steps (step size = 1.0 fs), highlighting the limitations of this approach in capturing accurate solvation effects. In contrast, the explicit solvent model provided a more reliable theoretical description (see Fig. 6), revealing that D1M, stabilized by three hydrogen bonds, remained intact and exhibited greater stability than D2M throughout the simulation.

Fig. 6 MD simulation snapshots of D1M and D2M in explicit methanol at T = 100 K, showing starting structures (left), transition state at ∼200 fs where the proton transfer occurs, and final configurations after 10 000 steps (right). D1M (keto–keto) remains stable with three hydrogen bonds, while D2M undergoes proton transfer, forming D2†, a neutral-keto–protonated–keto configuration. These results suggest D1M as the predominant dimer and D2M as dynamically unstable in methanol. Atomic color code: grey – carbon, red – oxygen, blue – nitrogen, white – hydrogen.

D1M (keto–keto configuration) retains its planar geometry, stabilized by three hydrogen bonds involving the amine and carbonyl groups. This structure remains energetically favorable in a polar solvent environment, with the same intermolecular interactions as the ones observed in the gas-phase interactions.

For D2M, we observed a significant structural transformation: the hydrogen atom on the protonated enol's hydroxyl group transferred to the nitrogen atom of the neutral keto molecule, resulting in the formation of a new complex, D2†, as shown in Fig. 5. This proton transfer marks a transition to the neutral-keto–protonated–keto configuration, which persisted as stable for 10 000 simulation steps. This behavior indicates that in methanol, the cytosine dimer predominantly exists in the D1M (keto–keto) form, with D2M being dynamically unstable. Furthermore, the results suggest that D2M may transition to D1M via proton transfer and subsequent rotation. These findings demonstrate the exclusion of the enol–keto configuration (D2M) in methanol and confirm the dominance of D1M. A minor population of D2† (neutral-keto–protonated–keto) may also coexist, as supported by MD simulations. Snapshots illustrating the behavior of D1M and D2M during the MD simulations are shown in Fig. 6.

The interaction and binding free energies (ΔE and ΔG) calculated for these configurations further underscore the preference for D1M. While D2M undergoes structural reorganization in methanol, D1M demonstrates robust stability, retaining its three hydrogen bonds even under solvent conditions.

Fig. 7 compares the experimental IRPD spectrum of protonated cytosine dimers with calculated vibrational spectra of D1 and D2 in various environments, providing further insights into the solvent effects. D1 and D2 in the gas-phase (panels b and e) are displayed again in this figure for reference. The methanol-optimized structure of D1 (D1M, panel c) exhibits spectral shifts compared to gas-phase D1, particularly in the 6-micron region. These shifts are primarily associated with changes in hydrogen bonding patterns due to the polar methanol environment, which alters the C=O stretching modes. Upon solvent evaporation, the spectrum of D1m (panel d) transitions back toward that of the isolated gas-phase D1 (panel b). While D1m does not fully recover the gas-phase spectral features of D1, this behavior reflects the inherent structural stability of D1 and its ability to adapt back to its equilibrium gas-phase configuration. These findings highlight D1's robustness and dominance across varying environmental conditions.

Fig. 7 Comparison of the experimental IRPD spectrum of the hemiprotonated cytosine dimer (a) with calculated spectra for D1 and D2 in various environments: (b) D1 in the gas phase, (c) D1 optimized in methanol (D1M), (d) D1 after solvent evaporation (D1m), (e) D2 in the gas phase, (f) D2 optimized in methanol (D2M), (g) D2 after solvent evaporation (D2m), and (h) rearranged D2† after solvent evaporation. Vibrational modes are scaled by 0.945 (3-micron range) and 0.956 (6-micron range). The spectra illustrate the stability of D1 across environments and the rearrangement of D2 into D2† upon solvent evaporation.

The methanol-optimized spectrum of D2 (D2M, panel f) is characterized by vibrational shifts similar to those observed for D1 upon solvent optimization. However, upon solvent evaporation, D2m (panel g) retains many features of D2M, suggesting that D2m does not fully relax to the gas-phase equilibrium geometry. Instead, D2m appears “frozen” in a configuration resembling the solvent-optimized form, reflecting D2's lower stability and reduced tendency to equilibrate in the gas phase. After further relaxation in the gas phase, D2m undergoes a proton transfer and structural rearrangement, resulting in the neutral-keto–protonated–keto configuration labeled D2† (panel h). The spectrum of D2† diverges significantly from D2m, exhibiting new vibrational features in both the 6-micron and 3-micron regions. Notably, the emergence of D2† suggests that D2's keto–enol configuration is dynamically unstable in the absence of solvent, further reinforcing D1's dominance. These results suggest that in a methanol environment, cytosine dimer complexes exist predominantly as the stable D1m (keto–keto form) and, to a much lower extent, as D2† in the neutral-keto–protonated–keto configuration. This evidence indicates that D2m in its original keto–enol form is unlikely to persist, and instead, rearrangement towards D1m may occur through proton transfer and rotation. The transition of D2m to D2† highlights the dynamic nature of dimer configurations in solvent and underscores the stabilizing role of strong hydrogen bonding in the D1m structure.

5. Conclusion

This study provides a comprehensive investigation of the structural and vibrational properties of protonated cytosine monomers and dimers, highlighting how tautomer stability shifts under varying environmental conditions. Experimental IRPD spectroscopy, combined with theoretical calculations, revealed distinct behaviors for monomers and dimers.

Our experimental and theoretical results agree that protonated cytosine monomers predominantly adopt the enol form in the gas phase, with a contribution from the keto form between 25% and 33%. For dimers, our computations predict the keto–enol configuration (D2) to be more stable than the keto–keto form (D1) by 1.5 kcal mol⁻¹. Experimentally, D1 emerged as the dominant structure. The theoretically most stable keto–enol configuration (D2) undergoes a structural reorganization in MD simulations with explicit methanol, forming the dynamically unstable D2† (neutral-keto–protonated–keto). This reorganization reinforces the dominance of D1 and highlights the role of environmental factors in modulating tautomer populations.

These findings advance our understanding of tautomerism and non-covalent interactions in protonated biomolecular systems, bridging the gap between gas-phase and solution-phase dynamics. They also provide a framework for exploring the structural behavior of cytosine-rich sequences in biologically relevant environments. Future studies could extend this work by investigating a wider range of solvents, pH conditions, and dynamic environments to elucidate the impact of external factors on the stability and behavior of cytosine-based systems.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Prof. Gilles Gregoire, Dr. Satchin Soorkia at U. Paris-Saclay and Gustavo A. Pino at the National University of Cordoba for stimulating and insightful discussions. AP was supported by the Japan Society for the Promotion of Science (JSPS) through the Postdoctoral Fellowships for Research in Japan program. The author acknowledges the support received as a JSPS International Research Fellow at Tokyo Institute of Technology. This article has been produced with the financial support of the European Union under the REFRESH – Research Excellence for Region Sustainability and High-tech Industries project number CZ.10.03.01/00/22_003/0000048 via the Operational Programme Just Transition (P. H.). This work has been supported by the National Science Foundation under CHE-2154787. YO, KH, SI and MF were supported in part by KAKENHI (JP20H00372, JP21H04674, JP21K14585) and the Core-to-core program of JSPS (JPJSCCA20210004, JPJSCCA2024002), World Research Hub Initiative in the Institute of Science Tokyo, the Cooperative Research Program of the ‘‘Network Joint Research Center for Materials and Devices’’ from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan.

References

1. P. Fojtík and M. Vorlícková, The fragile X chromosome (GCC) repeat folds into a DNA tetraplex at neutral pH, Nucleic Acids Res., 2001, 29(22), 4684–4690,  DOI:10.1093/nar/29.22.4684 (acccessed 6/11/2024).
2. X. Luo, J. Zhang, Y. Gao, W. Pan, Y. Yang, X. Li, L. Chen, C. Wang and Y. Wang, Emerging roles of i-motif in gene expression and disease treatment, Front. Pharmacol., 2023, 14, 1136251,  DOI:10.3389/fphar.2023.1136251 From NLM.
3. J. Dai, A. Ambrus, L. H. Hurley and D. Yang, A Direct and Nondestructive Approach To Determine the Folding Structure of the I-Motif DNA Secondary Structure by NMR, J. Am. Chem. Soc., 2009, 131(17), 6102–6104,  DOI:10.1021/ja900967r.
4. C. E. Kaiser, N. A. Van Ert, P. Agrawal, R. Chawla, D. Yang and L. H. Hurley, Insight into the Complexity of the i-Motif and G-Quadruplex DNA Structures Formed in the KRAS Promoter and Subsequent Drug-Induced Gene Repression, J. Am. Chem. Soc., 2017, 139(25), 8522–8536,  DOI:10.1021/jacs.7b02046 From NLM.
5. S. Kendrick, H.-J. Kang, M. P. Alam, M. M. Madathil, P. Agrawal, V. Gokhale, D. Yang, S. M. Hecht and L. H. Hurley, The Dynamic Character of the BCL2 Promoter i-Motif Provides a Mechanism for Modulation of Gene Expression by Compounds That Bind Selectively to the Alternative DNA Hairpin Structure, J. Am. Chem. Soc., 2014, 136(11), 4161–4171,  DOI:10.1021/ja410934b.
6. S. Takahashi, S. Bhattacharjee, S. Ghosh, N. Sugimoto and S. Bhowmik, Preferential targeting cancer-related i-motif DNAs by the plant flavonol fisetin for theranostics applications, Sci. Rep., 2020, 10(1), 2504,  DOI:10.1038/s41598-020-59343-2.
7. M. Zeraati, D. B. Langley, P. Schofield, A. L. Moye, R. Rouet, W. E. Hughes, T. M. Bryan, M. E. Dinger and D. Christ, I-motif DNA structures are formed in the nuclei of human cells, Nat. Chem., 2018, 10(6), 631–637,  DOI:10.1038/s41557-018-0046-3.
8. S. Sedghi Masoud and K. Nagasawa, i-Motif-Binding Ligands and Their Effects on the Structure and Biological Functions of i-Motif, Chem. Pharm. Bull., 2018, 66(12), 1091–1103,  DOI:10.1248/cpb.c18-00720.
9. H. Abou Assi, M. Garavís, C. González and M. J. Damha, i-Motif DNA: structural features and significance to cell biology, Nucleic Acids Res., 2018, 46(16), 8038–8056,  DOI:10.1093/nar/gky735.
10. S. Benabou, A. Aviñó, R. Eritja, C. González and R. Gargallo, Fundamental aspects of the nucleic acid i-motif structures, RSC Adv., 2014, 4(51), 26956–26980,  10.1039/C4RA02129K.
11. J. Amato, N. Iaccarino, A. Randazzo, E. Novellino and B. Pagano, Noncanonical DNA secondary structures as drug targets: the prospect of the i-motif, ChemMedChem, 2014, 9(9), 2026–2030,  DOI:10.1002/cmdc.201402153 From NLM.
12. H. A. Day, P. Pavlou and Z. A. E. Waller, i-Motif DNA: structure, stability and targeting with ligands, Bioorg. Med. Chem., 2014, 22(16), 4407–4418,  DOI:10.1016/j.bmc.2014.05.047.
13. F. Rosu, V. Gabelica, L. Joly, G. Grégoire and E. De Pauw, Zwitterionic i-motif structures are preserved in DNA negatively charged ions produced by electrospray mass spectrometry, Phys. Chem. Chem. Phys., 2010, 12(41), 13448–13454,  10.1039/C0CP00782J.
14. J. Gao, G. Berden, M. T. Rodgers and J. Oomens, Interaction of Cu+ with cytosine and formation of i-motif-like C–M⁺–C complexes: alkali versus coinage metals, Phys. Chem. Chem. Phys., 2016, 18(10), 7269–7277.
15. A. L. Lieblein, M. Krämer, A. Dreuw, B. Fürtig and H. Schwalbe, The nature of hydrogen bonds in cytidine···H⁺ ···cytidine DNA base pairs, Angew. Chem., Int. Ed., 2012, 51(17), 4067–4070,  DOI:10.1002/anie.201200549 From NLM.
16. J. Y. Salpin, S. Guillaumont, J. Tortajada, L. MacAleese, J. Lemaire and P. Maitre, Infrared spectra of protonated uracil, thymine and cytosine, ChemPhysChem, 2007, 8(15), 2235–2244,  DOI:10.1002/cphc.200700284.
17. J. M. Bakker, J.-Y. Salpin and P. Maître, Tautomerism of cytosine probed by gas phase IR spectroscopy, Int. J. Mass Spectrom., 2009, 283(1), 214–221,  DOI:10.1016/j.ijms.2009.03.014.
18. M. Broquier, S. Soorkia, G. Pino, C. Dedonder-Lardeux, C. Jouvet and G. Grégoire, Excited State Dynamics of Cold Protonated Cytosine Tautomers: Characterization of Charge Transfer, Intersystem Crossing, and Internal Conversion Processes, J. Phys. Chem. A, 2017, 121(34), 6429–6439,  DOI:10.1021/acs.jpca.7b06423.
19. B. Yang, R. R. Wu, G. Berden, J. Oomens and M. T. Rodgers, Infrared Multiple Photon Dissociation Action Spectroscopy of Proton-Bound Dimers of Cytosine and Modified Cytosines: Effects of Modifications on Gas-Phase Conformations, J. Phys. Chem. B, 2013, 117(46), 14191–14201,  DOI:10.1021/Jp405105w.
20. S.-I. Ishiuchi, H. Wako, D. Kato and F. Masaaki, High-cooling-efficiency cryogenic quadrupole ion trap and UV-UV hole burning spectroscopy of protonated tyrosine, J. Mol. Spectrosc., 2017, 332, 45–51,  DOI:10.1016/j.jms.2016.10.011.
21. F. Neese, Software update: The ORCA program system—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1606,  DOI:10.1002/wcms.1606.
22. W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38,  DOI:10.1016/0263-7855(96)00018-5 , 27-38From NLM.
23. Gaussian 16 Rev. C.01, Wallingford, CT, 2016.
24. G. J. Martyna, M. L. Klein and M. Tuckerman, Nosé–Hoover chains: the canonical ensemble via continuous dynamics, J. Chem. Phys., 1992, 97(4), 2635–2643,  DOI:10.1063/1.463940 (acccessed 6/11/2024).
25. G. J. Martyna, M. E. Tuckerman, D. J. Tobias and M. L. Klein, Explicit reversible integrators for extended systems dynamics, Mol. Phys., 1996, 87(5), 1117–1157,  DOI:10.1080/00268979600100761.
26. B. Yang, R. R. Wu and M. T. Rodgers, Base-Pairing Energies of Proton-Bound Homodimers Determined by Guided Ion Beam Tandem Mass Spectrometry: Application to Cytosine and 5-Substituted Cytosines, Anal. Chem., 2013, 85(22), 11000–11006,  DOI:10.1021/ac402542g.
27. K. Rajabi, K. Theel, E. A. L. Gillis, G. Beran and T. D. Fridgen, The Structure of the Protonated Adenine Dimer by Infrared Multiple Photon Dissociation Spectroscopy and Electronic Structure Calculations, J. Phys. Chem. A, 2009, 113(28), 8099–8107,  DOI:10.1021/Jp9033062.
28. F. Rosu, V. Gabelica, L. Joly, G. Gregoire and E. De Pauw, Zwitterionic i-motif structures are preserved in DNA negatively charged ions produced by electrospray mass spectrometry, Phys. Chem. Chem. Phys., 2010, 12(41), 13448–13454,  10.1039/c0cp00782j From NLM Medline.
29. A. F. Cruz-Ortiz, F. L. Molina, P. Maitre and G. A. Pino, Guanine Tautomerism in Ionic Complexes with Ag⁺ Investigated by IRMPD Spectroscopy and Mass Spectrometry, J. Phys. Chem. B, 2021, 125(26), 7137–7146,  DOI:10.1021/acs.jpcb.1c03796.
30. A. T. Phan, M. Guéron and J. L. Leroy, The solution structure and internal motions of a fragment of the cytidine-rich strand of the human telomere, J. Mol. Biol., 2000, 299(1), 123–144,  DOI:10.1006/jmbi.2000.3613.
31. A. F. Cruz-Ortiz, F. L. Molina, P. Maitre and G. A. Pino, Guanine Tautomerism in Ionic Complexes with Ag(+) Investigated by IRMPD Spectroscopy and Mass Spectrometry, J. Phys. Chem. B, 2021, 125(26), 7137–7146,  DOI:10.1021/acs.jpcb.1c03796 From NLM.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00657k

‡ Equal first author contribution.

---