Metal intercalation induced magnetic modulation in VS2 bilayers: a first principles study†
Dantong
Li
,
Xiaocheng
Zhou
*,
Yu
Wang
 and
Yafei
Li
and
Yafei
Li
 *
*
Key Laboratory of Numerical Simulation for Large Scale Complex Systems (Ministry of Education of PRC), School of Chemistry and Materials Science, Nanjing Normal University, Nanjing 210023, China. E-mail: xczhou@njnu.edu.cn; liyafei@njnu.edu.cn
First published on 1st April 2025
Abstract
Two-dimensional (2D) magnetic materials have emerged as highly promising candidates for spintronic applications owing to their unique properties. However, they tend to exhibit antiferromagnetic coupling when stacked, which limits their broader applications. It is of critical importance to manipulate the magnetic coupling and explore their applications in low-energy-consumption spintronic devices. Here, we theoretically investigated the electronic and magnetic properties of VS2 bilayers intercalated with transition metals (TMs) using density functional theory (DFT) computations and the nonequilibrium Green's function (NEGF) method. It is revealed that metal intercalation can significantly enhance the ferromagnetic exchange interaction. The TM-intercalated VS2 bilayers (TM–VS2) exhibit diverse electronic and magnetic properties, which can be precisely tuned via controlling the type and concentration of intercalated metals. The spin-polarized transport calculations demonstrate that the TM–VS2 bilayer with half-metallicity exhibits pronounced spin filtering properties. Our theoretical study provides a promising route to design and modulate the magnetic properties of 2D ferromagnets for their applications in advanced spintronic devices.
1. Introduction
Two-dimensional (2D) materials have attracted great attention due to their novel properties and potential applications. Their unique quantum confinement effect helps them effectively overcome the short-channel effect in miniaturized electronic devices.1–3 Among them, 2D magnetic materials have attracted extensive attention and demonstrated promising applications beyond conventional semiconductors with the introduction of spin freedom.4–6 The spin state of electrons can be used for information generation, storage, and transmission, which is essential for low power spintronic technologies. Ideally, spintronic devices can generate pure spin currents, substantially reducing Joule heating and achieving ultra-high circuit integration density.7 However, most of the 2D materials do not have inherent magnetism, which limits their widespread application in spintronics. Previously, several approaches were used to successfully introduce magnetism into 2D materials, such as atomic doping, defect engineering, and edge effects.8–10 However, the induced magnetism is often highly localized and weak, bringing challenges for their widespread application in practical devices.11 Therefore, it is imperative to discover 2D ferromagnets with strong magnetic anisotropy and ordered long-range magnetic exchange interaction. In recent years, several 2D magnetic materials were obtained experimentally, such as ferromagnetic (FM) CrI3,12 Cr2Ge2Te6,13 Fe3GeTe2,14 MnSe2,6 and VX215,16 and antiferromagnetic (AFM) FePS317 and NiPS3.18In two-dimensional magnetic materials, interlayer magnetic coupling plays a crucial role in determining magnetic properties. For instance, the CrI3 monolayer exhibits intrinsic intralayer ferromagnetism. When two layers of CrI3 are stacked, they tend to exhibit interlayer antiferromagnetic coupling in monoclinic stacking and ferromagnetic coupling in rhombohedral stacking.19 It has been revealed that the stacking-dependent magnetism originates from the interlayer orbital hybridization and charge accumulation. Still, most of the 2D magnets possess weak coercive fields due to the relatively weak magnetocrystalline anisotropy. Consequently, it is necessary to explore effective strategies to enhance and tune the magnetism of 2D magnets. Intercalation of atoms into the van der Waals (vdW) gap is a feasible approach for tuning and enhancing magnetism in 2D materials due to the induced interfacial charge redistribution and long-range spin-exchange interaction. So far, various atoms have been intercalated into 2D materials with controlled concentration and order. For example, Li intercalation in layered Fe3GeTe2 remarkably enhances the ferromagnetism and increases the ferromagnetic transition temperature.20 The intercalation of Fe and Cr into NbS2 and TaS2 leads to distinct magnetic behaviors, depending on the type of intercalant and the intercalation concentration.21 In addition, self-intercalation was also successfully achieved in a broad class of 2D materials, such as layered materials (TMDs), which provides a powerful method for tuning and controlling magnetism.22
As a typical member of transition metal dichalcogenides, VS2 has two possible phases: octahedral coordinated (T-phase) and trigonal prismatic (H-phase).15 They have quite different electronic and magnetic properties. The T-phase VS2 monolayer has been widely studied due to its high conductivity, excellent electrocatalytic activity, and ferromagnetism. However, the H-phase VS2 is a ferromagnetic semiconductor with a large magnetic moment.23 Notably, when two layers of H-phase VS2 are stacked together, they show antiferromagnetic interlayer coupling with a zero net magnetic moment.24 Although antiferromagnetic spintronics has been successfully used in various fields,25 effective regulation of magnetic coupling is still desired for satisfying different requirements of spintronic devices.
Here, we performed density functional theory (DFT) and non-equilibrium Green's function (NEGF) calculations to study the electronic and magnetic properties of transition metal intercalated H-phase VS2 bilayers (TM–VS2) for their applications in spintronic nanodevices. The geometries, ground state energies, band structures, and magnetic behaviors of VS2 bilayers with different intercalation configurations, metals and concentrations have been investigated. The results demonstrated that the VS2 bilayers exhibit a rich variety of magnetic properties depending on the type of intercalation. Notably, the self-intercalated V–VS2 bilayer exhibits the half-metallic characteristic, which is crucial for achieving spin filtering effects. Our results indicate that metal intercalation offers a powerful approach to design 2D spintronic devices with tunable magnetic functionalities.
2. Computational methods
Our calculations are based on density functional theory (DFT), implemented using the Vienna ab initio simulation package (VASP).26 The exchange–correlation interaction is described using the Perdew–Burke–Ernzerhof (PBE) functional27 based on the generalized gradient approximation (GGA).28 To avoid interactions between adjacent layers, a vacuum of 15 Å along the z-direction is used. The energy cut-off is set to be 450 eV and the convergence criterion for energy is 10−5 eV. Geometry optimization is performed until the force acting on each atom is less than 0.02 eV Å−1. The Brillouin zone was sampled with a 5 × 5 × 1 k-mesh grid. Ab initio molecular dynamics (AIMD) simulations were performed for 10 ps at 500 K with a time step of 1 fs. The temperature was controlled using the Nosé–Hoover method.29 To appropriately describe the strongly correlated electrons in d orbitals of TM atoms, we use the PBE+U method30 with the effective U values of 3.0 eV for V, Co, and Mn atoms and 2.0 eV for the Cr atom.5,23,31–33We further designed the device based on TM–VS2 to investigate its potential applications in spintronics. The spin-polarized transport simulations were implemented via the NANODCAL package,34 which combines DFT with the non-equilibrium Green's function. A cutoff energy of 3000 eV is adopted and the convergence criterion for both the Hamiltonian and the density matrix is set to 10−4 eV. The k-point grid meshes are 1 × 3 × 1 and 100 × 3 × 1 for the center region and the electrode, respectively. The Landauer–Buttiker formula is used to calculate the probability of incoming electrons transferred from one electrode to another with the specific energy (E) as follows:
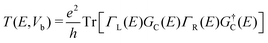 | (1) |
 are the retarded and advanced Green's functions, respectively.35,36
are the retarded and advanced Green's functions, respectively.35,36
3. Results and discussion
3.1. Structure and stability of TM–VS2
To investigate the properties of VS2 with intercalated transition metals, we started from the atomic structures of the pristine VS2 bilayer with different stacking geometries. The most stable stacking geometry is shown in Fig. 1a. The relaxed lattice constants of the 2√3 × 2√3 × 1 supercell are a = b = 11.02 Å, and the corresponding V–S bond length and the distance between two VS2 layers are 2.38 Å and 3.26 Å, respectively. Our calculations show that the VS2 monolayer is ferromagnetic while the VS2 bilayer prefers antiferromagnetic interlayer coupling (which is energetically lower than the FM interlayer coupling by 26 meV per supercell), agreeing well with previous studies.24 The calculated electronic properties presented in Fig. 1b indicate that the AFM VS2 bilayer is semiconducting with a direct bandgap of 0.61 eV.Owing to the layered structure, intercalation of transition metal atoms into the bilayer gap is experimentally feasible.37 It has emerged as an effective method to modulate the properties of 2D materials. To systematically explore the effect of intercalated atoms on magnetic coupling, we considered possible intercalation sites for transition metals in the VS2 bilayer and fully relaxed the structures to identify the optimal intercalation position (Fig. S1, ESI†). It turned out that the most energetically favorable site for an intercalant is at the top of the V atom, where the intercalated atom bonds with six S atoms to form an octahedral coordination in the vdW gap (Fig. 1c). This site preference may be attributed to the geometric characteristics of octahedral coordination, which provides a more favorable six-fold coordination environment and requires minimal structural reorganization. Compared with the pristine bilayer structure, the lattice constants of the intercalated bilayer are almost unchanged, while the interlayer distances are decreased from 3.26 Å to 3.11 Å, indicating the enhanced interactions within the bilayer. To evaluate the energetic stability of intercalated atoms, we define the intercalation energy as follows:
| Ei = (Etot − Ebilayer − nETM)/n | (2) |
3.2. Magnetic properties of TM–VS2
After intercalation, the intralayer ferromagnetic coupling remains robust, while the interlayer magnetic coupling of the VS2 bilayer will be affected. Importantly, the intercalated TM atoms also exhibit various magnetic states, which will decisively influence the overall properties of the systems. To figure out the magnetic ground states of the systems, we calculated the energy difference defined as follows:| E = EAFM − EFM | (3) |
 , e′(dxy, dx2 − dy2), and e′′(dxz, dyz), and the
, e′(dxy, dx2 − dy2), and e′′(dxz, dyz), and the 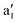 orbital is the lowest level. The single electron in the 3d1 configuration occupies one of the spin-polarized dz2 orbitals. This is consistent with our calculations that each V atom exhibits a magnetic moment of about 1 μB. The interlayer AFM coupling of the VS2 bilayer is facilitated by the direct V–V exchange interaction. The d orbitals of intercalated transition atoms are divided into two groups, t2g(dxy, dxz, dyz) and eg(dz2, dx2 − dy2). The interlayer magnetic coupling almost remains antiferromagnetic for V, Cr, and Co intercalation but becomes ferromagnetic for Mn intercalation. This difference arises primarily from the distinct d-electron configurations of the metals, which influence their interactions with the V atoms in the pristine bilayer. The eventual interlayer magnetic coupling is a consequence of the competition between direct and indirect exchange interactions. As shown in Fig. 2, the calculated local magnetic moments on each intercalated V, Cr, Mn, and Co atoms are approximately 2, 3, 4, and 2μB, respectively. The spin configurations of one and three intercalated atoms are obviously ferromagnetic, whereas those of two and four intercalated atoms depend on the type and concentration of the metals. In the case of two intercalated atoms, we found that only 2V tend to adopt the FM configuration, while 2Cr, 2Mn, and 2Co prefer the AFM configuration. When four atoms are intercalated, 4V, 4Cr, and 4Co favor the AFM configuration, and only 4Mn exhibits the FM configuration. Considering diverse spin configurations of intercalated atoms, our results demonstrate that TM–VS2 systems exhibit a rich variety of properties, including ferromagnetic metals, ferromagnetic half-metals, ferromagnetic semiconductors, antiferromagnetic metals, and antiferromagnetic semiconductors.
orbital is the lowest level. The single electron in the 3d1 configuration occupies one of the spin-polarized dz2 orbitals. This is consistent with our calculations that each V atom exhibits a magnetic moment of about 1 μB. The interlayer AFM coupling of the VS2 bilayer is facilitated by the direct V–V exchange interaction. The d orbitals of intercalated transition atoms are divided into two groups, t2g(dxy, dxz, dyz) and eg(dz2, dx2 − dy2). The interlayer magnetic coupling almost remains antiferromagnetic for V, Cr, and Co intercalation but becomes ferromagnetic for Mn intercalation. This difference arises primarily from the distinct d-electron configurations of the metals, which influence their interactions with the V atoms in the pristine bilayer. The eventual interlayer magnetic coupling is a consequence of the competition between direct and indirect exchange interactions. As shown in Fig. 2, the calculated local magnetic moments on each intercalated V, Cr, Mn, and Co atoms are approximately 2, 3, 4, and 2μB, respectively. The spin configurations of one and three intercalated atoms are obviously ferromagnetic, whereas those of two and four intercalated atoms depend on the type and concentration of the metals. In the case of two intercalated atoms, we found that only 2V tend to adopt the FM configuration, while 2Cr, 2Mn, and 2Co prefer the AFM configuration. When four atoms are intercalated, 4V, 4Cr, and 4Co favor the AFM configuration, and only 4Mn exhibits the FM configuration. Considering diverse spin configurations of intercalated atoms, our results demonstrate that TM–VS2 systems exhibit a rich variety of properties, including ferromagnetic metals, ferromagnetic half-metals, ferromagnetic semiconductors, antiferromagnetic metals, and antiferromagnetic semiconductors.
 | ||
| Fig. 2 A summary of the magnetic properties of TM–VS2 bilayers with the intercalation concentrations of (a) 8.3%, (b) 16.7%, (c) 25%, and (d) 33.3%. | ||
3.3 Electronic properties of TM–VS2
Considering the diverse properties of VS2 systems induced by intercalated TM atoms, we take Cr–VS2 as a representative example to conduct the in-depth analysis. In Fig. 3a, the spin-polarized band structures of 1Cr–VS2 reveal that the system is converted into half-metallic, suggesting its potential to achieve the spin filtering effect. As observed from the band structures, intercalation shifts the Fermi level upwards, resulting in the bands crossing the EF in the spin-up channel while retaining the semiconducting feature in the spin-down channel. The spin density shown in Fig. 3b indicates that the V atoms in the bilayer favor FM intralayer coupling and AFM interlayer coupling. The asymmetric spin-up and spin-down projected densities of states (PDOS) confirm the ferromagnetic ground state of 1Cr–VS2. The localized state around the Fermi level is primarily contributed by the Cr_d orbitals, which contributes to the flat bands. It can be observed that there is a significant overlap between the Cr_d and V_d orbitals around the Fermi level, indicating the strong orbital hybridization between them. This is consistent with our charge density difference (Fig. S5a, ESI†) and Bader charge analysis calculations, which show that about 1.2 electrons are transferred from Cr to the VS2 bilayer and lead to an electron doping effect. These interactions are primarily contributed by the dxz and dyz orbitals of the Cr atom. The above results demonstrated that the intercalation of Cr can enhance the hybridization between Cr_d and V_d orbitals and induce the spin redistribution, thereby achieving effective regulation of magnetic properties.To further investigate the effect of intercalation concentration on magnetic coupling, we computed the band structures and PDOS of Cr–VS2 at the concentrations of 16.7%, 25%, and 33.3%. When two Cr atoms (16.7%) are intercalated into the vdW gap, they tend to form an AFM spin configuration. As shown in Fig. 4a, the V atoms in the bilayer maintain AFM interlayer coupling, and the two Cr atoms between layers present spin densities in opposite directions. The 2Cr–VS2 exhibits metallic behavior, which is primarily contributed by the Cr_d orbitals near the Fermi level. As the intercalation concentration increases to 25% and 33.3%, the intercalated Cr atoms induce FM half-metallic and AFM semiconducting characteristics, respectively. The spin densities presented in Fig. 4b and c indicate that three Cr atoms in the bilayer gap align with the same spin orientation, whereas four Cr atoms adopt an AFM spin configuration. Notably, although the VS2 bilayer exhibits AFM interlayer coupling, the spin configurations of the intercalated Cr atoms significantly influence the magnetic states and moments of V atoms. As seen from the PDOS, 1Cr and 3Cr intercalations produce similar electronic states of VS2. It is obviously that the enhanced V_d density of states appear in the majority spin channel near the Fermi level due to the FM state of Cr in the interlayer gap. Conversely, 2Cr and 4Cr intercalations generate a distinct type of electronic states of VS2, where the AFM Cr intercalations influence the electronic states of VS2 primarily by introducing two spin-polarized peaks below the Fermi level. Particularly, when the doping concentration reaches 33%, the magnetic states of the V atoms adjacent to the intercalated atoms are significantly affected. The four V atoms adjacent to Cr exhibit spin configurations opposite to those of the intercalated atoms, driving the system into the lowest energy state. These findings confirm the significant impact of intercalation concentration and the spin configurations of Cr atoms on the electronic and magnetic properties of Cr–VS2 systems.
The type of intercalated metal is another critical factor in influencing the magnetic properties of the TM–VS2 systems. For V and Co intercalations, the TM–VS2 systems exhibit AFM interlayer coupling between VS2 layers. Consequently, the PDOS of V–VS2 and Co–VS2 are similar to that of Cr–VS2, with electronic states near the Fermi level predominantly contributed by the TM_d orbitals (Fig. S6 and S8, ESI†). The overlap between TM_d and V_d orbitals indicates significant orbital hybridization. The electronic and magnetic properties of the systems are ultimately determined by the type and concentration of the intercalated atoms. Analysis of the PDOS and spin density reveals that for systems with 1–3 V atoms intercalated, the intercalated V atoms exhibit FM coupling. Among them, 1V–VS2 and 3V–VS2 systems demonstrate FM metallic behavior, while the 2V–VS2 system exhibits the FM semiconducting characteristic, with the conduction band minimum and valence band maximum primarily contributed by the intercalated atoms. When four V atoms are intercalated, they tend to adopt an antiferromagnetic configuration. The combined effects of the intercalated and intrinsic V atoms drive the 4V–VS2 system toward metallic behavior. The 1Co- and 3Co–VS2 systems adopt FM configurations, whereas 2Co- and 4Co–VS2 systems favor AFM configurations. Regardless of the concentration, all Co–VS2 systems consistently display metallic behaviors, driven by the strong orbital hybridization between Co_d and V_d orbitals near the Fermi level. In contrast, Mn atoms possess unique half-filled d-orbitals, which may alter the spin state of the V atoms and activate direct exchange interactions mediated by the V_d orbitals. This can be corroborated by the PDOS of the Mn–VS2 system (Fig. S7, ESI†), where the PDOS near the Fermi level is dominated by V_d orbitals, while the contributions from Mn_d orbitals are at deeper energy levels. Consequently, the VS2 bilayer exhibits ferromagnetic interlayer coupling in the Mn-intercalated system. Taken together, we suggest that intercalation of transition metal atoms with different types and concentrations can significantly modulate the electronic and magnetic properties of VS2 bilayers, providing theoretical insights for designing functional 2D materials with diverse properties.
3.4. Spin transport properties of the V self-intercalated bilayer
The above results demonstrate that tuning the type and concentration of intercalated transition metal atoms can yield TM–VS2 systems with diverse electronic properties and magnetic states, which makes them highly promising candidates for various spintronic applications. The intercalated atoms create chemical binding with the intrinsic bilayer, which could facilitate the carrier transfer between layers and effectively regulate the spin transport. Notably, self-intercalation can be achieved by controlling the metal chemical potential during the material growth process,39 avoiding the harsh reaction conditions typically required for foreign atom intercalation.To investigate the spin transport properties of the system, we constructed a dual-probe system for calculations using non-equilibrium Green's function method. As illustrated in Fig. 5a, the dual-probe model consists of three regions: semi-infinite left and right electrode regions composed of pristine bilayer VS2 and a central device region formed by V–VS2 (5.6%). The computed spin-polarized transmission spectrum reveals a pronounced spin polarization property. Specifically, at the Fermi level, the transmission spectrum exhibits a pronounced peak in the spin-up channel, while in the spin-down channel it is negligible. The transmission coefficient at the Fermi level reflects the probability of electron transfer through the conductance channel. To evaluate whether the device can be applied in spin filters, the spin polarization (SP) is defined as SP = (Tup − Tdown)/(Tup + Tdown), where Tup and Tdown are the spin-up transmission and spin-down transmission at the Fermi level, respectively.40 We found that the SP of the device can reach up to 96% at a bias voltage of 0.2 V, indicating its potential application as a spin filter by facilitating current through the spin-up channel.
4. Conclusions
In summary, we have systematically investigated the strategy of modulating the electronic and magnetic properties of the VS2 bilayer via metal intercalation based on the combination of DFT and NEGF calculations. Our results reveal that the interlayer coupling in bilayer VS2 is affected by the type of intercalated metal; intercalation of V, Cr, and Co preserves the AFM interlayer coupling, whereas Mn intercalation induces a transition to FM interlayer coupling. Moreover, the magnetic characteristics of the TM–VS2 systems are determined by both the type and concentration of the intercalated atom. Adjusting these parameters could effectively modulate the charge transfer between the intercalants and the VS2 bilayer, thereby altering orbital occupation and magnetic exchange interactions, which enables diverse tunable electronic and magnetic properties, spanning from ferromagnetic to antiferromagnetic, as well as metallic, half-metallic, and semiconducting behaviors. Furthermore, our spin transport calculations confirm that the half-metallic system exhibits obvious spin-polarized transmission spectra and spin filtering capability. This study deepens our understanding of the role of metal intercalation in magnetic modulation and provides theoretical guidance for the tailored design of spintronic devices with specific functionalities.Author contributions
This manuscript was written through contributions from all authors. All authors have given approval to the final version.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors are grateful for funding support from the Natural Science Foundation of China (No. 12202209, No. 22173048, and 22425302), and the Natural Science Foundation of Jiangsu Province (BK20220379).References
- N. Tombros, C. Jozsa, M. Popinciuc, H. T. Jonkman and B. J. V. Wees, Nature, 2007, 448, 571–574 CrossRef CAS PubMed.
- E. C. Ahn, npj 2D Mater. Appl., 2020, 4, 17 CrossRef CAS.
- A. L. Friedman, O. M. J. V. Erve, C. H. Li, J. T. Robinson and B. T. Jonker, Nat. Commun., 2014, 5, 3161 CrossRef PubMed.
- A. Avsar, J. Y. Tan, M. Kurpas, M. Gmitra, K. Watanabe, T. Taniguchi, J. Fabian and B. Özyilmaz, Nat. Phys., 2017, 13, 888–893 Search PubMed.
- M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M.-H. Phan and M. Batzill, Nat. Nanotechnol., 2018, 13, 289–293 CrossRef CAS PubMed.
- D. J. O’Hara, T. Zhu, A. H. Trout, A. S. Ahmed, Y. K. Luo, C. H. Lee, M. R. Brenner, S. Rajan, J. A. Gupta, D. W. McComb and R. K. Kawakami, Nano Lett., 2018, 18, 3125–3131 CrossRef PubMed.
- Y. Hu, S. Liu, J. Huang, X. Li and Q. Li, Nano Lett., 2023, 23, 7890–7896 CrossRef CAS PubMed.
- K. Zhang, S. Feng, J. Wang, A. Azcatl, N. Lu, R. Addou, N. Wang, C. Zhou, J. Lerach, V. Bojan, M. J. Kim, L.-Q. Chen, R. M. Wallace, M. Terrones, J. Zhu and J. A. Robinson, Nano Lett., 2015, 15, 6586–6591 CrossRef CAS PubMed.
- O. V. Yazyev, Phys. Rev. Lett., 2008, 101, 037203 CrossRef PubMed.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347–349 CrossRef CAS PubMed.
- R. R. Nair, M. Sepioni, I.-L. Tsai, O. Lehtinen, J. Keinonen, A. V. Krasheninnikov, T. Thomson, A. K. Geim and I. V. Grigorieva, Nat. Phys., 2012, 8, 199–202 Search PubMed.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273 CrossRef CAS PubMed.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269 CrossRef CAS PubMed.
- Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen and Y. Zhang, Nature, 2018, 563, 94–99 CrossRef CAS PubMed.
- H. Zhang, L.-M. Liu and W.-M. Lau, J. Mater. Chem. A, 2013, 1, 10821 RSC.
- M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M.-H. Phan and M. Batzill, Nat. Nanotechnol., 2018, 13, 289–293 CrossRef CAS PubMed.
- J.-U. Lee, S. Lee, J. H. Ryoo, S. Kang, T. Y. Kim, P. Kim, C.-H. Park, J.-G. Park and H. Cheong, Nano Lett., 2016, 16, 7433–7438 CrossRef CAS PubMed.
- K. Kim, S. Y. Lim, J.-U. Lee, S. Lee, T. Y. Kim, K. Park, G. S. Jeon, C.-H. Park, J.-G. Park and H. Cheong, Nat. Commun., 2019, 10, 345 CrossRef PubMed.
- B. Niu, T. Su, B. A. Francisco, F. Kargar, X. Huang, M. Lohmann, J. Li, Y. Xu, T. Taniguchi, K. Watanabe, D. Wu, A. Balandin, J. Shi and Y.-T. Cui, Nano Lett., 2020, 20, 553–558 CrossRef CAS PubMed.
- X. Huang, J. Xu, R. Zeng, Q. Jiang, X. Nie, C. Chen, X. Jiang and J.-M. Liu, Appl. Phys. Lett., 2021, 119, 012405 CrossRef CAS.
- L. S. Xie, S. Husremovic, O. Gonzalez, I. M. Craig and D. K. Bediako, J. Am. Chem. Soc., 2022, 144, 9525–9542 CrossRef CAS PubMed.
- K. Niu, G. Qiu, C. Wang, D. Li, Y. Niu, S. Li, L. Kang, Y. Cai, M. Han and J. Lin, Adv. Funct. Mater., 2023, 33, 2208528 CrossRef CAS.
- M. Kan, B. Wang, Y. H. Lee and Q. Sun, Nano Res., 2015, 8, 1348–1356 CrossRef CAS.
- X. Liu, A. P. Pyatakov and W. Ren, Phys. Rev. Lett., 2020, 125, 247601 CrossRef CAS PubMed.
- T. Jungwirth, X. Marti, P. Wadley and J. Wunderlich, Nat. Nanotechnol., 2016, 11, 231–241 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- S. Sarkar and P. Kratzer, Phys. Rev. B, 2021, 103, 224421 CrossRef CAS.
- T. O. Wehling, A. I. Lichtenstein and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 235110 CrossRef.
- X. Zhang, Z. Bao, X. Ye, W. Xu, Q. Wang and Y. Liu, Nanoscale, 2017, 9, 11231 RSC.
- J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245407 CrossRef.
- P. Panigrahi, P. K. Panda, Y. Pal, H. Bae, H. Lee, R. Ahuja and T. Hussain, ACS Appl. Nano Mater., 2022, 5, 2984–2993 CrossRef CAS.
- J. Prasongkit, E. de Freitas Martins, F. A. L. de Souza, W. L. Scopel, R. G. Amorim, V. Amornkitbamrung, A. R. Rocha and R. H. Scheicher, J. Phys. Chem. C, 2018, 122, 7094–7099 CrossRef CAS.
- S. Husremović, C. K. Groschner, K. Inzani, I. M. Craig, K. C. Bustillo, P. Ercius, N. P. Kazmierczak, J. Syndikus, M. V. Winkle, S. Aloni, T. Taniguchi, K. Watanabe, S. M. Griffin and D. K. Bediako, J. Am. Chem. Soc., 2022, 144, 12167–12176 CrossRef PubMed.
- K. J. Koski, J. J. Cha, B. W. Reed, C. D. Wessells, D. Kong and Y. Cui, J. Am. Chem. Soc., 2012, 134, 7584–7587 CrossRef CAS PubMed.
- X. Zhao, P. Song, C. Wang, A. C. Riis-Jensen, W. Fu, Y. Deng, D. Wan, L. Kang, S. Ning, J. Dan, T. Venkatesan, Z. Liu, W. Zhou, K. S. Thygesen, X. Luo, S. J. Pennycook and K. P. Loh, Nature, 2020, 581, 171–177 CrossRef CAS PubMed.
- H. Bai, Q. Wu, H. Ai, D. Liu, J. Feng, L. K. Ang, Y. Lu, M. Yang and H. Pan, Adv. Electron. Mater., 2022, 8, 2200209 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00869g |
| This journal is © the Owner Societies 2025 |




