BC2N monolayer as a high-performance anode material for potassium-ion batteries†
Jingguo
Wang
a,
Wenyuan
Zhang
b,
Yanling
Si
 *a and
Guochun
Yang
*a and
Guochun
Yang
 *b
*b
aSchool of Environmental and Chemical Engineering, Yanshan University, Qinhuangdao 066004, P. R. China. E-mail: siyl@ysu.edu.cn
bState Key Laboratory of Metastable Materials Science & Technology and Hebei Key Laboratory of Microstructural Material Physics, School of Science, Yanshan University, Qinhuangdao 066004, P. R. China. E-mail: yanggc468@nenu.edu.cn
First published on 25th April 2025
Abstract
As global energy demand rises and fossil fuel resources dwindle, the exploration of sustainable energy alternatives has become imperative. Rechargeable metal-ion batteries, particularly potassium-ion batteries (KIBs), are a key focus in this effort. Graphene, a leading two-dimensional carbon material, has limitations as an anode due to low ion mobility and dendrite formation. Doping graphene with boron and nitrogen can enhance its performance by leveraging the distinct electronegativities of these elements. In this study, we propose a BC2N monolayer with a honeycomb configuration to assess its potential as an anode for KIBs. The BC2N monolayer demonstrates a low K-ion migration barrier of 0.13 eV, a theoretical capacity of 1094.10 mA h g−1, and an average open circuit voltage of 0.31 V. The strong hybridization between K s orbitals and B/C/N pz orbitals facilitates K ion adsorption, boosting storage capacity. The configurations show inherent metallicity, ensuring high electron conductivity. Our findings highlight the BC2N monolayer as a breakthrough anode material for high performance KIBs, offering valuable insights for future battery development.
1. Introduction
Technological advancements and societal progress have driven an increasing demand for energy in recent years. As fossil fuel resources continue to deplete, the quest for sustainable energy alternatives has become paramount. Renewable energy sources such as wind, solar, tidal, biomass, and geothermal sources offer promising solutions, but their intermittent nature necessitates the development of efficient energy storage systems to fully capitalize on these resources.1 In this context, rechargeable metal-ion batteries have emerged as a central focus within the scientific community. Among metal-ion batteries, lithium-ion batteries (LIBs) stand out due to their long cycle life, portability, compact size, high energy density, and substantial storage capacity. These characteristics have led to their widespread use in a range of applications, from smartphones to electric vehicles.2–7 Nonetheless, LIBs are not devoid of challenges. The geographic concentration of lithium and cobalt—key elements in LIBs—renders the supply chain vulnerable to disruptions and price volatility.8 Moreover, LIBs carry inherent safety risks, such as thermal runaway and explosions, which can occur due to dendrite formation at the electrode–electrolyte interface.9To overcome these limitations, researchers are exploring alternative metal-ion batteries that can replace or complement LIBs.10 In recent years, potassium-ion batteries (KIBs) have garnered significant attention as a viable alternative. Potassium is abundantly available on Earth, and K-ions can reversibly intercalate into graphite electrodes, similar to lithium ions.11,12 Additionally, KIBs offer the advantage of high power density due to the rapid diffusion of K-ions, a result of weaker interaction with solvents and anions.10 These unique features make KIBs promising candidates for replacing LIBs, particularly in terms of cost-effectiveness and resource availability.
The pursuit of high-performance anode materials is essential to enhancing the efficiency of KIBs. Two-dimensional materials, including graphene,13 transition metal dichalcogenides (e.g., MoS2),14 transition metal oxides (e.g., MnO215 and TiO216),17 MXenes (e.g., Ti3C2,18 Ti2C,19 and TiC320), and phosphides (e.g., PC621), have demonstrated considerable promise as electrode materials in metal-ion batteries. Due to their high specific surface area and unique geometric structures, these materials exhibit enhanced reversible capacities and improved charge/discharge rates.22 Among them, graphene, a two-dimensional carbon-based material, stands out for its high theoretical capacity. However, it also faces significant challenges, such as low-rate capabilities,23 voltage hysteresis,24 and dendrite formation,25 which can lead to short circuits. To overcome these issues, researchers have explored doping graphene with boron and nitrogen atoms. This doping enhances graphene's chemical properties, offering improved physical and chemical characteristics.26,27 For example, boron doping increases lithium adsorption energy, while nitrogen doping accelerates charge transfer.28–30 In this context, co-doping graphene with equal proportions of boron (B) and nitrogen (N) not only maintains its isoelectronic nature but also induces charge redistribution. This feature opens up new possibilities for optimizing the performance of graphene-based anode materials.
On the other hand, the BC2N material family with a graphene-like layered structure has been successfully synthesized through chemical vapor deposition (CVD).31,32 Due to the varying distributions of B and N, the BC2N monolayers exhibit a range of possible structures, each displaying distinct electronic properties.33,34 The BC2N monolayer with a large bandgap (2.0 eV) has been predicted to exhibit high carrier mobility,35 along with strong in-plane thermal transport anisotropy, where in-plane phonon modes dominate the thermal transport process.36,37 Additionally, Chen et al. investigated the optical properties of BC2N and proposed its potential as an infrared window material,38 while Shi et al. predicted that the BC2N monolayer could serve as a promising anchoring material for lithium–sulfur batteries, with defects and doping further enhancing its performance.39 Our work focuses on the graphene-like BC2N monolayer with inversion symmetry, which features a mirror-symmetric B–N distribution and an ultra-narrow bandgap of 0.04 eV. Using first-principles calculations, we systematically studied the adsorption behavior of K-ions on its surface, and calculated the migration barriers for K-ions. Additionally, the thermal stability of the BC2N monolayer was confirmed through ab initio molecular dynamics (AIMD) simulations. Our results indicate that the BC2N monolayer possesses excellent electrical conductivity, high theoretical capacity, low K-ion migration barrier, and a favorable open-circuit voltage, making it a highly promising candidate for KIB anodes.
2. Computational methods
In this work, we conduct structural relaxation and property calculations utilizing the Vienna Ab initio Simulation Package (VASP),40,41 which is based on density functional theory (DFT).42 The electron–ion interactions are described using the projector augmented wave (PAW) pseudopotential,41,43 while the exchange–correlation potentials are represented by the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE).41,44 To account for van der Waals (vdW) interactions, we incorporate the semi-empirical DFT-D2 method with a vdW correction for damping. The cut-off energy of the plane wave basis function is set to 600 eV. To prevent interactions between neighboring layers, a vacuum layer with a thickness of 30 Å is introduced in the perpendicular direction of each model. Additionally, we employ Monkhorst–Pack k-meshes with a density of 2π × 0.03 Å−1 for our calculations.To explore the adsorption and diffusion of potassium on the BC2N monolayer, we expand the original unit cell to the 2 × 2 × 1 supercell for structural relaxation. We optimize both the lattice constants and atomic coordinates until the force convergence reaches 0.03 eV Å−1 and energy convergence attains 10−5 eV. The density of states (DOS) and band structure are computed using the PBE functional. For the calculation of phonon dispersion, we employ the Phonopy code on a 2 × 2 × 1 supercell of BC2N.44 The thermal stability at 300 K within the NVT ensemble is assessed45 using the Nosé–Hoover thermostat method with a simulation duration of 5 ps and a time step of 1.0 fs.46 The formation energy (Ef) of the BC2N monolayer is determined using the following equation:47
| Ef = EBC2N − μB − 2μC − μN | (1) |
 | (2) |
| Ead = EK+BC2N − EBC2N − EK | (3) |
 | (4) |
 | (5) |
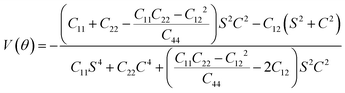 | (6) |
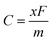 | (7) |
 | (8) |
3. Results and discussion
3.1. Structure, stability, and electronic properties of the BC2N monolayer
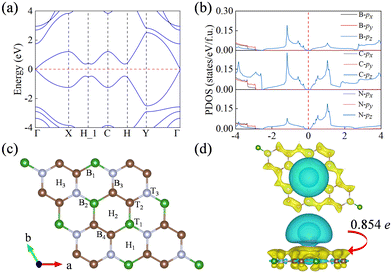
The BC2N monolayer, upon relaxation, exhibits a planar honeycomb configuration possessing Cmmm symmetry (Fig. 1a), which aligns with previous findings.33 The bond lengths within this structure, specifically 1.53 Å for B–C, 1.46 Å for B–N, and 1.41 Å for C–C, are comparable to those observed in BC3,57 h-BN,58 and graphene,59 respectively. The strong covalent nature of all the bonds in the BC2N monolayer is evident from the electronic localization function, as shown in Fig. 1b. Additionally, we calculated the formation energy for the BC2N monolayer (−2.02 eV f.u.−1) and the exfoliation energies of graphene and the BC2N monolayer (20 meV Å−2 and 15 meV Å−2, respectively) on graphite substrate. The calculated exfoliation energy of graphene aligns with the findings of Rico Friedrich et al.48 The acceptable formation/exfoliation energy of the BC2N monolayer indicates its potential preparation under appropriate conditions.31,32 To evaluate the structural stability of the BC2N monolayer, we started by computing its phonon dispersion curve. The absence of significant imaginary frequencies in the phonon spectra, as illustrated in Fig. 2a, verifies the dynamic stability of the BC2N monolayer. Additionally, ab initio molecular dynamics (AIMD) simulations were conducted at 300 K and 350 K for a duration of 5 ps. The results, presented in Fig. 2b and Fig. S1 (ESI†), demonstrate minimal structural changes alterations without any changes in bonding patterns or significant geometric reconfigurations, thereby confirming the thermal stability of the BC2N monolayer at room temperature.The BC2N monolayer, when considered as an anode material for metal-ion batteries, exhibits strong resistance to deformation, which is advantageous for battery recycling. Our calculations of its mechanical properties revealed that elastic constants satisfy Born's criterion:60C11C22–C122 > 0, C66 > 0, confirming its mechanical stability. The Young's modulus and Poisson's ratio in any angular plane can be determined using independent elastic constants C11, C12, C22, C44 and θ. Notably, the Young's modulus of the BC2N monolayer ranges from 274.45 to 291.68 N m−1, while the Poisson's ratio varies from 0.19 to 0.22, indicating obvious anisotropy. These values are comparable to those of h-BN (Ys = 279.20 N m−1, v = 0.22),61 showing the high stiffness of BC2N. Overall, the BC2N monolayer exhibits excellent mechanical properties, rendering it resilient to deformation and damage during the charging and discharging cycles of batteries.
The calculated electronic band structure and the projected density of states (PDOS) of the BC2N monolayer (Fig. 3a and b), determined using generalized PBE functionals, reveal that this material is a direct bandgap semiconductor with a narrow bandgap of 0.04 eV. The valence band maximum primarily originates from the pz orbital contributions of B, C, and N atoms. Furthermore, strong hybridization between the px and py orbitals of these atoms contributes to the enhanced structural stability of the BC2N monolayer.
3.2. Metal ion adsorption and diffusion on the BC2N monolayer
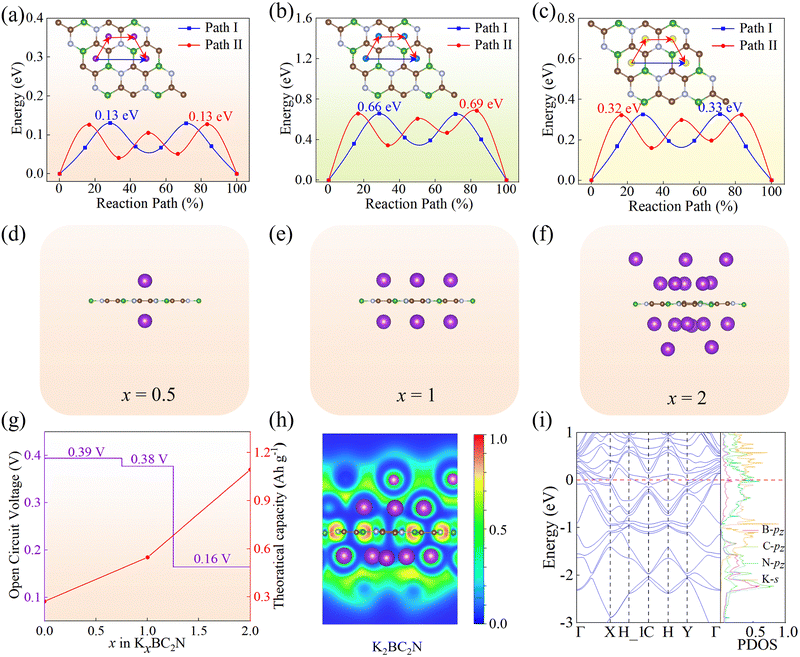
The adsorption capability of an anode material for K ions is crucial for the stable operation and storage capacity of KIBs. To assess the suitability of the BC2N monolayer as an anode in KIBs, we constructed a 2 × 2 × 1 supercell and identified 10 highly symmetric potential adsorption sites based on the material's geometric symmetry (Fig. 3c). These sites encompass positions above B, C, and N atoms (labeled as T1, T2, and T3), vacancies within B2C2N2, B2C4, and C4N2 six-membered rings (denoted as H1, H2, and H3), and the bridging sites between BC, BN, CN, and CC (marked as B1, B2, B3, and B4). Upon structural relaxation, the K ions originally adsorbed at the B1, B2, B3, and B4 sites shift to the H2, H1, H3, and H3 positions, respectively. This migration can be attributed to the larger radius of the K atom, which experiences minimal repulsion in the hollow positions of the six-membered rings composed of the B, C, and N atoms in the BC2N monolayer. Consequently, six stable adsorption sites on the BC2N monolayer were identified, with their corresponding adsorption energies listed in Table S2 (ESI†). Notably, the H2 site exhibited the most stable adsorption for K ions on the BC2N monolayer, with an adsorption energy of −0.61 eV, which surpassed that of other sites.To explore the adsorption mechanism of the K atom on the BC2N monolayer, we performed differential charge density calculations and Bader charge analysis. As shown in Fig. 3d, two electron depletion regions (blue area) are observed near the K ions and in the in-plane bonding direction of BC2N, while electron accumulation (yellow area) is seen in the out-of-plane π bonds of BC2N, especially on both sides of the B2C4 six-membered rings. This observation suggests that B, C, and N atoms transfer a small amount of in-plane σ electrons to the pz orbitals of BC2N. Additionally, by Bader charge analysis, it is found that each K atom transfers 0.854e to the BC2N surface.
Charge and discharge rates are another critical factor influencing the performance of rechargeable batteries, with higher rate capacities enabling faster charge and discharge processes. These rates largely depend on the migration rate of adsorbed metal ions and the conductivity of the anode material. To evaluate the BC2N monolayer as a potential anode material for KIBs, we employed the CI-NEB method to calculate the diffusion barrier of K ions on the BC2N monolayer, a parameter directly linked to rate performance. Two possible migration paths between the most stable adsorption sites, labeled as path I and path II (Fig. 4a), were analyzed. Path I proceeds along the H2–H2 direction, while path II follows the H2–H3–H1–H2 direction. These pathways were selected based on the observation that K adsorption is most stable at the hollow positions within the six-membered rings, which facilitates efficient K-ion transport. Our calculations reveal that the migration barriers for K ions along both path I and path II are 0.13 eV (Fig. 4a), indicating stable K-ion migration on the BC2N monolayer. Furthermore, we observed that the polar bond strength within the BC2N monolayer during K-ion migration significantly impacts the migration barriers, with higher barriers across BC bonds compared to CN bonds. Notably, the predicted migration barriers for BC2N are comparable to or even lower than those reported for other 2D materials, such as Ti3C2 (0.103 eV),62 PC6 (0.260 eV),63 MoN2 (0.490 eV),64 SnSe (0.160 eV),65 BP monolayer (0.155 eV),66 and TiS2 (0.440 eV).67 Additionally, we determined the migration barriers of Li and Na ions on the BC2N monolayer (Fig. 4b and c) to be 0.66 eV and 0.33 eV, respectively. Interestingly, the actual migration path of Li ions differs from the initially labeled paths (Fig. 4b). Specifically, in path I, Li ions exhibited a deviation from the B atom upon crossing the B–C bond, rather than migrating in a straight line. Similarly, in path II, Li ions shifted towards the C and N atoms when crossing the B–C and C–N bonds, respectively. In contrast, K and Na ions did not display such deviations, potentially due to their larger atomic radius and higher atomic mass compared to Li. The stronger electronegativity of C and N, relative to B, led to a stronger attraction of Li ions towards these atoms when crossing the polar B–C and C–N bonds, accounting for the observed deviations. Overall, among the ions studied, K ions exhibited the lowest migration barriers on the BC2N monolayer, rendering it a favorable material for enhancing the rate capacity of KIBs.
3.3. Capacity and open-circuit voltage of the BC2N monolayer as the anode
For rechargeable metal-ion batteries, key performance characteristics of anode materials encompass high storage capacity, low average open-circuit voltage, and stable voltage distribution. The storage capacity of these batteries is primarily governed by the number of ions adsorbed onto the anode material—a higher number of adsorbed ions translates to a higher theoretical capacity. Herein, we investigated the K adsorption behavior using a 2 × 2 × 1 supercell and observed that as the number of adsorbed K atoms increases, the adsorption energy decreases, ultimately reaching a maximum adsorption concentration when the adsorption energy approaches zero. We calculated the formation energies at different adsorption concentrations (i.e., KxBC2N, x = 0.5, 1, 1.25, 1.5, and 2) and plotted the convex hull. From Fig. S2 (ESI†), it can be observed that the configurations obtained at K concentrations of 0.5, 1, and 2 are thermodynamically stable (i.e., KxBC2N, x = 0.5, 1, 2), with their structure as illustrated in Fig. 4d–f. In particular, the theoretical storage capacity (TSC) increases with K-ion content (Fig. 4g), peaking at 1094.10 mA h g−1, which significantly surpasses that of other 2D materials such as Ti3C2 (191.80 mA h g−1),62 Ti2N (242.00 mA h g−1),68 and PC6 (781.00 mA h g−1).63 Subsequently, the BC2N monolayer in the saturated adsorption state (K2BC2N) was subjected to AIMD simulations at 300 K for a duration of 5 ps. The results, as shown in Fig. S3 (ESI†), revealed minor structural changes with no significant geometric reconstruction, thereby confirming the thermal stability of the BC2N monolayer in the saturated adsorption state at room temperature.During charging and discharging, the half-cell reaction of the BC2N monolayer as the anode for KIBs can be expressed as:
| BC2N + xK+ + xe− ↔ KxBC2N |
Using eqn (8), we estimated the OCV of the BC2N monolayer in KIBs and calculated the corresponding voltage profile. As shown in Fig. 4g, the calculated OCV decreases gradually with an increase in the concentration of K ions. The average OVC of the BC2N monolayer is 0.31 V, which falls well within the standard range (0–1 V)69 for anode materials in metal-ion batteries. This low OCV reduces the risk of dendrite growth in the cell,70 highlighting the BC2N monolayer as a promising anode material for KIBs.
3.4. Absorption mechanism and electronic properties of KxBC2N
To delve into the origin of the high TSC, we analyzed the interlayer distances of the K-ion adsorbed layers on the BC2N substrate and the electron localization function (ELF) of KxBC2N (x = 0.5, 1, and 2), as depicted in Fig. S4, S5 (ESI†) and Fig. 4h. It can be observed that as multilayer adsorption proceeds, the distance from the substrate gradually increases, with the distances for one-layer and two-layer K adsorption being 2.86 Å and 5.79 Å, respectively, similar to the MB4 results.71 After adsorption in the first layer, the valence electrons from the K atoms migrate to the surface of the K1BC2N monolayer, accumulating around the K atoms to form an electron cloud. This negative electron cloud is crucial for stabilizing the multilayer adsorption process,20 as it helps to alleviate Coulomb repulsion between K ions. When the maximum K-atom adsorption is achieved, the negative electron cloud becomes uniformly distributed around the K ions, enhancing the overall stability of the adsorption layer by fostering static attractive interactions between the ions and minimizing the Coulomb repulsion.The electronic energy bands and DOS of KxBC2N (x = 0.5, 1, and 2) are shown in Fig. S6 (ESI†) and Fig. 4i. The metallic characteristics of KxBC2N, evident from multiple bands crossing the Fermi level, stands in stark contrast to the semiconducting behavior of the pristine BC2N monolayer, which features a narrow direct band gap. The metallic nature of KxBC2N (x = 0.5, 1, and 2) facilitates rapid electron transfer, thereby enhancing cycling stability. In addition, the PDOS diagrams reveal significant overlap below the Fermi energy level between the pz orbitals of B, C, and N atoms, as well as the s orbital of K. This prominent s–p hybridization implies stronger interactions between the K atoms and the BC2N monolayer.
4. Conclusions
In this work, we propose the BC2N monolayer as a highly promising anode material for KIBs based on first-principles calculations. The monolayer demonstrates excellent dynamic, thermal, and mechanical stability. The stable adsorption of K atoms on the BC2N surface is enhanced by boron's electron-deficient nature, which boosts surface reactivity. The strong electronegativity of nitrogen efficiently modulates charge distribution within the six-membered rings of boron and carbon, resulting in highly stable adsorption sites. Furthermore, the polar covalent C–N bonds reduce the migration barrier for K ions, facilitating faster ion migration compared to C–C bonds. Consequently, the BC2N monolayer outperforms current anode materials for KIBs in terms of storage capacity, diffusion barrier, and open-circuit voltage, underscoring its potential for superior battery performance.Author contributions
Jingguo Wang: writing – original draft, visualization, methodology, investigation, and conceptualization. Wenyuan Zhang: resources and formal analysis. Yanling Si: supervision, conceptualization, project administration, and writing – review & editing. Guochun Yang: resources, project administration, methodology, funding acquisition, conceptualization, and writing – review & editing.Data availability
Data will be made available on request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grants No. 22372142, 12304028, 12404027, and U23A20537, the Foreign Expert Introduction Program (G2023003004L), the Central Guiding Local Science and Technology Development Fund Projects (236Z7605G), the Natural Science Foundation of Hebei Province (Grant No. B2024203051, A2024203023, and A2024203002), the Science and Technology Project of Hebei Education Department (Grants No. JZX2023020), and the Innovation Capability Improvement Project of Hebei province (22567605H).References
- D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS.
- J. Deb, R. Ahuja and U. Sarkar, ACS Appl. Nano Mater., 2022, 5, 10572–10582 CrossRef CAS.
- H. Dua, J. Deb, D. Paul and U. Sarkar, ACS Appl. Nano Mater., 2021, 4, 4912–4918 CrossRef CAS.
- G. Assat and J.-M. Tarascon, Nat. Energy, 2018, 3, 373–386 CrossRef CAS.
- D. Lin, Y. Liu and Y. Cui, Nat. Nanotechnol., 2017, 12, 194–206 CrossRef CAS.
- J. B. Goodenough and K. S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS.
- A. Yoshino, Angew. Chem., Int. Ed., 2012, 51, 5798–5800 CrossRef CAS PubMed.
- S. Dhir, S. Wheeler, I. Capone and M. Pasta, Chem, 2020, 6, 2442–2460 CAS.
- K. V. Kravchyk, C. Seno and M. V. Kovalenko, ACS Energy Lett., 2020, 5, 545–549 CrossRef CAS.
- T. Hosaka, K. Kubota, A. S. Hameed and S. Komaba, Chem. Rev., 2020, 120, 6358–6466 CrossRef CAS.
- Z. Jian, W. Luo and X. Ji, J. Am. Chem. Soc., 2015, 137, 11566 CrossRef CAS PubMed.
- S. Komaba, T. Hasegawa, M. Dahbi and K. Kubota, Electrochem. Commun., 2015, 60, 172–175 CrossRef CAS.
- S. Mukherjee, Z. Ren and G. Singh, Nano-Micro Lett., 2018, 10, 70 CrossRef CAS.
- M. Chhowalla, H. S. Shin, G. Eda, L. J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263–275 CrossRef.
- M. V. Reddy, G. V. Subba Rao and B. V. Chowdari, Chem. Rev., 2013, 113, 5364–5457 CrossRef CAS PubMed.
- S. Paul, M. A. Rahman, S. B. Sharif, J. H. Kim, S. E. Siddiqui and M. A. M. Hossain, Nanomaterials, 2022, 12, 2034 CrossRef CAS PubMed.
- J. Jiang, Y. Li, J. Liu, X. Huang, C. Yuan and X. W. Lou, Adv. Mater., 2012, 24, 5166–5180 CrossRef CAS PubMed.
- Q. Tang, Z. Zhou and P. Shen, J. Am. Chem. Soc., 2012, 134, 16909–16916 CrossRef CAS PubMed.
- Y. Wang, M. Zhou, L. C. Xu, W. Zhao, R. Li, Z. Yang, R. Liu and X. Li, J. Power Sources, 2020, 451, 227791 CrossRef CAS.
- T. Yu, Z. Zhao, L. Liu, S. Zhang, H. Xu and G. Yang, J. Am. Chem. Soc., 2018, 140, 5962–5968 CrossRef CAS PubMed.
- T. Yu, Z. Zhao, Y. Sun, A. Bergara, J. Lin, S. Zhang, H. Xu, L. Zhang, G. Yang and Y. Liu, J. Am. Chem. Soc., 2019, 141, 1599–1605 CrossRef CAS PubMed.
- J. Lin, T. Yu, F. Han and G. Yang, WIREs Comput. Mol. Sci., 2020, 10, e1473 CrossRef CAS.
- J. Xu, J. Mahmood, Y. Dou, S. Dou, F. Li, L. Dai and J. B. Baek, Adv. Mater., 2017, 29, 1702007 CrossRef PubMed.
- R. Raccichini, A. Varzi, S. Passerini and B. Scrosati, Nat. Mater., 2015, 14, 271–279 CrossRef CAS PubMed.
- M. Winter, J. O. Besenhard, M. E. Spahr and P. Novák, Adv. Mater., 1998, 10, 725–763 CrossRef CAS.
- T. Zhang, Z. Chen, J. Zhao and Y. Ding, Diamond Relat. Mater., 2018, 90, 72–78 CrossRef CAS.
- T. Jian, X. Chen, S. D. Li, A. I. Boldyrev, J. Li and L. S. Wang, Chem. Soc. Rev., 2019, 48, 3550–3591 RSC.
- N. A. Jaber, Z. T. Abed, M. M. Kadhim, Y. Yaseen, W. M. Khazaal, H. A. Almashhadani, A. M. Rheima and A. Mohamadi, Mater. Chem. Phys., 2023, 294, 126926 CrossRef CAS.
- Y. Qie, J. Liu, S. Wang, S. Gong and Q. Sun, Carbon, 2018, 129, 38–44 CrossRef CAS.
- A. Bafekry, Phys. E, 2020, 118, 113850 CrossRef CAS.
- J. Kouvetakis, T. Sasaki, C. Shen, R. Hagiwara, M. Lerner, K. M. Krishnan and N. Bartlett, Synth. Met., 1989, 34, 1–7 CrossRef CAS.
- M. O. Watanabe, S. Itoh, K. Mizushima and T. Sasaki, J. Appl. Phys., 1995, 78, 2880–2882 CrossRef CAS.
- A. Y. Liu, R. M. Wentzcovitch and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 1760–1765 CrossRef CAS PubMed.
- H. Nozaki and S. Itoh, J. Phys. Chem. Solids, 1996, 57, 41–49 CrossRef CAS.
- J. Xie, Z. Y. Zhang, D. Z. Yang, D. S. Xue and M. S. Si, J. Phys. Chem. Lett., 2014, 5, 4073–4077 CrossRef CAS PubMed.
- B. Mortazavi, I. S. Novikov and A. V. Shapeev, Carbon, 2022, 188, 431–441 CrossRef CAS.
- C. Lin, X. Zhang and Z. Rao, Nano Energy, 2017, 38, 249–256 CrossRef CAS.
- L. Jiao, M. Hu, Y. Peng, Y. Luo, C. Li and Z. Chen, J. Solid State Chem., 2016, 244, 120–128 CrossRef CAS.
- Y. Shao, Q. Wang, L. Hu, H. Pan and X. Shi, Carbon, 2019, 149, 530–537 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Xiao, F. Shi, T. Glossmann, C. Burnett and Z. Liu, Nat. Energy, 2023, 8, 329–339 CrossRef.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- W. Li, et al. , Nano Energy, 2019, 61, 594–603 CrossRef CAS.
- T. Barnowsky, A. V. Krasheninnikov and R. Friedrich, Adv. Electron. Mater., 2023, 9, 2201112 CrossRef CAS.
- X. Zhang, J. Hu, Y. Cheng, H. Y. Yang, Y. Yao and S. A. Yang, Nanoscale, 2016, 8, 15340–15347 RSC.
- H.-B. Cao, X.-H. Wang, X. Xiong, C.-S. Liu and X.-J. Ye, Appl. Phys. Lett., 2024, 124, 073908 CrossRef CAS.
- S. Thomas, E. B. Nam and S. U. Lee, ACS Appl. Mater. Interfaces, 2018, 10, 36240–36248 CrossRef CAS PubMed.
- A. Urban, D.-H. Seo and G. Ceder, npj Comput. Mater., 2016, 2, 16002 CrossRef CAS.
- S. Luo, J. Zhao, Y. Wang, Y. Zhang, Y. Xiong, N. Ma and J. Fan, J. Phys. Chem. C, 2023, 127, 12484–12491 CrossRef CAS.
- Q.-H. Qiu, S.-Y. Wu, G.-J. Zhang, L. Yan and Z.-T. Wei, Comput. Mater. Sci., 2023, 216, 111868 CrossRef CAS.
- Y. Xiao and W. Zhang, Appl. Surf. Sci., 2020, 513, 145883 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- L. Zhao, Y. Li, G. Zhou, S. Lei, J. Tan, L. Lin and J. Wang, Chin. Chem. Lett., 2021, 32, 900–905 CrossRef CAS.
- R. Beiranvand and S. Valedbagi, Diam. Relat. Mater., 2015, 58, 190–195 CrossRef CAS.
- M. F. Budyka, T. S. Zyubina, A. G. Ryabenko, S. H. Lin and A. M. Mebel, Chem. Phys. Lett., 2005, 407, 266–271 CrossRef CAS.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- Q. Peng, W. Ji and S. De, Comput. Mater. Sci., 2012, 56, 11–17 CrossRef CAS.
- D. Er, J. Li, M. Naguib, Y. Gogotsi and V. B. Shenoy, ACS Appl. Mater. Interfaces, 2014, 6, 11173–11179 CrossRef CAS PubMed.
- K. Dou, Y. Ma, T. Zhang, B. Huang and Y. Dai, Phys. Chem. Chem. Phys., 2019, 21, 26212–26218 RSC.
- X. Zhang, Z. Yu, S.-S. Wang, S. Guan, H. Y. Yang, Y. Yao and S. A. Yang, J. Mater. Chem. A, 2016, 4, 15224–15231 RSC.
- Q. Peng, J. Rehman, M. K. Butt, S. A. Shafiee, Z. Yang, M. Ouladsmane, J. Liu, M. ullah and Z. Li, J. Phys. Chem. C, 2023, 127, 15730–15737 CrossRef CAS.
- H. R. Jiang, W. Shyy, M. Liu, L. Wei, M. C. Wu and T. S. Zhao, J. Mater. Chem. A, 2017, 5, 672–679 RSC.
- Z. Zhang, M. Yang, N. Zhao, L. Wang and Y. Li, Phys. Chem. Chem. Phys., 2019, 21, 23441–23446 RSC.
- D. Wang, Y. Gao, Y. Liu, D. Jin, Y. Gogotsi, X. Meng, F. Du, G. Chen and Y. Wei, J. Phys. Chem. C, 2017, 121, 13025–13034 CrossRef CAS.
- X. Lu, J. Qi, J. Ren, J. Li, H. Xue, F. Tang and X. Guo, Vacuum, 2023, 218, 112655 CrossRef CAS.
- P. Xiang, S. Sharma, Z. M. Wang, J. Wu and U. Schwingenschlögl, ACS Appl. Mater. Interfaces, 2020, 12, 30731–30739 CrossRef CAS PubMed.
- M. K. Masood, J. Wang, J. Song and Y. Liu, J. Mater. Chem. A, 2024, 12, 22945–22959 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00900f |
| This journal is © the Owner Societies 2025 |