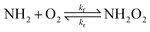Formation of the aminoperoxyl radical in the atmospheric oxidation of ammonia

Abstract

Atmospheric oxidation of ammonia is initiated by its reaction with the hydroxyl radical, producing the aminyl radical (NH₂). Thus far, it has been believed that the subsequent fate of NH₂ is to react bimolecularly with other atmospheric trace gases like NO, NO₂, or O₃. Its reaction with O₂ has been considered insignificant under atmospheric conditions. However, this is based on a rate coefficient that is orders of magnitude smaller than those known for analogous reactions of O₂ with carbon-, sulfur-, and other nitrogen-centered radicals. We demonstrate by multireference calculations and kinetic modelling that the reaction of NH₂ and O₂ leading to the formation of the aminoperoxyl radical (NH₂O₂) occurs with a rate coefficient similar to those of the aforementioned analogous radicals. We show that the previously estimated small rate coefficient is due to an unimolecular rate limiting step in the formation of measured products rather than the initial NH₂ + O₂ reaction. The lack of experimental detection of NH₂O₂ in the existing literature is likely due to the experiments being conducted at either high temperature or low pressure. We show that the atmospheric presence of NH₂O₂ depends greatly on atmospheric conditions. Its formation is an important, yet previously overlooked pathway in atmospheric ammonia oxidation, especially at low temperatures.

---

1 Introduction

Ammonia (NH₃) is one of the most abundant nitrogen-containing compounds in the atmosphere. It is emitted into the atmosphere from agricultural activities, wild fires, and in polar regions also from penguin and seabird colonies, with a current estimated annual global emission of 58 Tg N.^1–5 Ammonia has an atmospheric lifetime from hours to a few days.^6–8 Its most significant loss mechanisms are acid–base reactions, wet deposition, and gas-phase oxidation reactions.^7,9 The branching of these routes is uncertain, but the lifetime of NH₃ with respect to oxidation is estimated to be ten times longer than its other loss mechanisms.¹⁰ This suggests that only a minor fraction of ammonia is oxidized in the gas phase. However, at high altitudes, above the boundary layer, this oxidation is likely more important. Moreover, because the transient concentration of NH₃ is high, NH₃ oxidation may lead to significant production of NO_x and other nitrogen-containing species in the atmosphere.

The atmospheric oxidation reactions of ammonia are known to be initiated via hydrogen abstraction by the OH radical^11,12 or by halogen radicals,¹³ yielding the aminyl radical (NH₂). The NH₂ radical is known to react bimolecularly with NO₂, NO, O₃, and O₂.¹⁴ The reactions with NO₂ and NO are believed to be dominant since the IUPAC recommended rate coefficient for its reaction with O₂ is smaller than 6 × 10⁻²¹ cm³ per molecule per s.¹⁴ It has been argued in earlier literature that if the rate coefficient of the NH₂ + O₂ reaction is larger than 3 × 10⁻¹⁸ cm³ per molecule per s, then it would be the dominant bimolecular reaction of NH₂ under atmospheric conditions.¹⁵

A wide range of rate coefficients for the NH₂ + O₂ reaction (10⁻¹⁵–10⁻²¹ cm³ per molecule per s) have been determined using different experimental setups.^15–21 The largest rate coefficient (10⁻¹⁵ cm³ per molecule per s) was determined in 1972 by measuring the NH₂ decay, which was revised in 1979 to 10⁻¹⁷ cm³ per molecule per s by the same authors.¹⁹ The basis of the current IUPAC recommendation is a more recent experimental study from 1991,¹⁵ where the rate coefficient was inferred indirectly by measuring the NO_x and N₂O formation in experiments of NH₂ in excess molecular oxygen with and without added NO. The product distributions were explained by the known kinetics of other competing reactions in their reaction system; therefore, the rate coefficient was given as an upper limit.

For methane, CH₄, the reaction with OH and O₂ leads to the formation of CH₃O₂, which is the most abundant alkylperoxyl radical in the atmosphere.²² This peroxyl radical has been detected in laboratory experiments by e.g. cavity ring down spectroscopy.²³ As far as we know, clear evidence of the formation of the corresponding peroxyl radical, NH₂O₂, has not been reported in any of the experimental studies of NH₃ oxidation.^15–21

The thermostability of the aminoperoxyl radical, NH₂O₂, has been investigated theoretically in multiple studies.^24–28 These previous studies give a somewhat conflicting picture of the reaction enthalpy for the NH₂O₂ radical formation. According to earlier studies, the formation of NH₂O₂ is endothermic by 10 kcal mol⁻¹, while later studies found it to be exothermic by 3–6 kcal mol⁻¹.^24–28 The latter assessments are likely more reasonable for the radical addition reaction. These types of reactions are usually exoergic processes, because the reaction only involves the formation of a bond and does not require breaking of any covalent bonds. Despite the discrepancies between the available values, the NH₂ + O₂ → NH₂O₂ reaction appears to be close to thermoneutral. This suggests that unless the reaction is prevented by an insurmountable barrier, the reaction is reversible; thus, the branching between NH₂ + O₂ and NH₂O₂ is sensitive to the accuracy of the value of the reaction enthalpy and also likely to the specific reaction conditions.

In this work, we study the NH₂ + O₂ ⇋ NH₂O₂ reaction using multireference electronic structure methods. The interacting NH₂ + O₂ system consists of three unpaired electrons, coupled to an overall doublet state, so multireference methods are necessary to obtain reasonable predictions of the shape of the reaction potential. We assess the reversibility of this reaction and estimate the branching ratios between NH₂ + O₂ and NH₂O₂ under a broad set of relevant atmospheric conditions. We estimate the high pressure limit reaction rate coefficient using canonical variational theory (CVT)²⁹ and model the temperature- and pressure-dependent rate coefficients with Rice–Ramsberger–Kassel–Marcus (RRKM/ME)³⁰ and inverse Laplace transform (ILT/ME) master equation models.³¹ We also apply the multireference methodologies to the analogous CH₃ + O₂ → CH₃O₂ reaction for comparison.

2 Methods

We obtained the starting geometries for various multireference calculations by carrying out geometry optimizations at the ωB97X-D3/aug-cc-pVTZ level.^32–34 In some instances, we also used B3LYP(D3BJ),^35–37 M06-2X,³⁸ and CAM-B3LYP³⁹ functionals for comparison purposes. All DFT calculations were done using ORCA version 5.0.3.,^40,41 in which the used DFT functionals were implemented with analytical energy gradients for geometry optimizations, while the second derivatives of the potentials (Hessian) were calculated numerically.

In all multireference calculations, we used the complete active space self-consistent field (CASSCF) method for constructing the zeroth-order wave functions for the subsequent multireference calculations.⁴² The used active spaces are denoted using the general n-electrons in m-orbitals, CAS(ne,mo) notation, where the configuration state function space is constructed from the Full-CI expansion within the CAS subspace. We used the perturbation-based Super-CI SCF optimizer [SuperCI(PT)] in the CASSCF calculations.⁴³ The natural orbitals corresponding to the optimized CAS orbitals for each relevant obtained stationary structure are visualized in the ESI (Section S8).† All CASSCF and subsequent multireference (MR) calculations were done using the aug-cc-pVTZ basis set.

In the calculations with the NH₂O₂ molecule and related bimolecular reactants, we used two active spaces. The first, which was used for all the geometry optimizations and frequency calculations, is a CAS(13e,11o) space, which includes all valence orbitals, except the 2s orbitals of the oxygen atoms and the lone pair of the nitrogen atom. The second active space CAS(19e,14o) corresponds to the full-valence CAS of NH₂O₂ and was used in single-point energy correction calculations. Calculations concerning the NH₂ and O₂ separately were done using full-valence CAS, which are CAS(7e,6o) and CAS(12e,8o), respectively.

In the calculations of further unimolecular reactions of NH₂O₂, the geometries and frequencies of all intermediate species were obtained using the CAS(13e,11o) active space, but the electronic energies were corrected with the full-valence CAS(19e,14o) active space. The HNO, OH, NO, and H₂O calculations were done with their respective full-valence active spaces.

For geometry optimizations and frequency calculations concerning the CH₃O₂ molecule and related bimolecular reactants, we used a CAS(13e,9o) active space, which consists of all oxygen valence orbitals, as well as the C–O bonding and antibonding orbitals, and the C–H bonding and antibonding orbitals are not included in the CAS. The geometry and frequencies of the isolated CH₃ molecule were calculated using the full-valence CAS(7e,7o) active space.

We used N-electron valence state second-order perturbation theory (NEVPT2)^44,45 to treat the dynamical electron correlation in the studied systems. All NEVPT2 calculations in this work were done using the fully internally contracted (FIC) variants of theory (in earlier literature, they were referred to as partial contraction, PC). Strict pre-screening criteria were used for higher order reduced density matrices, 3-RDM and 4-RDM (1 × 10⁻¹⁶ cutoff for configuration weights), to prevent false intruder states arising from approximated RDM.^46,47 NEVPT2 geometry optimizations and frequency calculations were done with ORCA-5.0.3,⁴¹ using numerical gradients and numerical Hessians. We studied the NH₂ + O₂ → NH₂O₂ reaction also with CASPT2 and CASPT2-IPEA methods.^48,49 The results obtained with these methods are discussed in the ESI Section S6.†

We also carried out benchmark calculations with the complete basis set extrapolated CCSD(T),^50–53 using two-point extrapolation with cc-pVTZ and cc-pVQZ basis sets,⁵⁴ denoted as CCSD(T)/CBS. Additionally, we conducted W2X and W3X-L composite method calculations,⁵⁵ using Molpro and MRCC programs.^56,57 The W2X extends the CCSD(T)/CBS method by also considering core–valence correlation and scalar-relativistic effects, upon which the W3X-L method further adds post-CCSD(T) contributions up to CCSDT(Q).

2.1 Thermodynamics and kinetics

In the thermochemical analyses, standard approaches were used for obtaining rigid-rotor, translation, and electronic contributions to their respective thermodynamic quantities. By default, all vibrational analyses were based on the harmonic approximation, but at non-stationary points of potential energy surfaces the vibrations were obtained orthogonal to the gradient of the energy (see ESI Section S2.1.1† for details). The entropy contributions from low-frequency modes were scaled with the qRRHO method,⁵⁸ using 100 cm⁻¹ reference value for the weighting function between vibrational and rotational entropies. Furthermore, the vibration corresponding to the internal rotation around the N–O bond in NH₂⋯O₂ was treated with a one-dimensional rigid hindered rotor model (details are provided in the ESI Section S2.1.2†).

We used three methodologies to assess the kinetics of the studied reaction systems: canonical variational theory for the high-pressure limit thermal rate coefficients, k^CVT_∞(T) (CVT details are provided in ESI Section S2†), and Rice–Ramsberger–Kassel–Marcus (RRKM/ME) and inverse Laplace transform (ILT/ME) master equation models to calculate temperature- and pressure-dependent rate coefficients k(p, T).^30,31 The CVT rate coefficient equation is given by

where κ is the tunneling coefficient, k_B is the Boltzmann constant, T is the absolute temperature, h is the Planck constant, p^Θ is the reference pressure of 1 bar, M is the reaction molecularity, ΔG(s)^‡,CVT is the quasi-thermodynamic Gibbs energy of activation, and s is the reaction coordinate. The tunneling coefficient κ was assumed as one, except for the NH₂O₂ → HNOOH isomerization reaction, where the coefficient was calculated using the Eckart potential approximation.⁵⁹ For the most part, the CVT rate coefficient equation is identical to the conventional transition state theory rate coefficient equation. The only difference is the ΔG(s)^‡,CVT term, which is defined as the energy difference of the maximum of the Gibbs energy along the minimum energy path of reaction coordinate and the Gibbs energy of the reactants (G_reac):

The Gibbs energy of activation for the 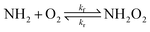association reaction (ΔG^‡,CVT_f) was calculated indirectly from the reaction Gibbs energy change (ΔG) and the reverse dissociation Gibbs energy of activation (ΔG^‡,CVT_r):

ΔG^‡,CVT_f = ΔG + ΔG^‡,CVT_r (3)

where

ΔG = G(NH₂O₂) − G(NH₂ + O₂) (4)

and

ΔG^‡,CVT_r = G^‡,CVT_TS − G(NH₂O₂) (5)

We believe that W3X-L is the most accurate method in the present study for estimating the reaction energy [E(NH₂) + E(O₂) − E(NH₂O₂)]. Thus, we calculated the ΔG from the W3X-L electronic energies of NH₂, O₂, and NH₂O₂ and combined with the thermodynamic corrections obtained at full-valence NEVPT2 for NH₂ and O₂ and at NEVPT2(13e,11o) for NH₂O₂. We were not able to calculate the W3X-L energy in the transition state geometry, so the ΔG^‡,CVT_r was calculated using NEV-PT2(19e,14o) electronic energies with thermodynamic corrections obtained at the NEVPT2(13e,11o) level.

In both the RRKM/ME and ILT/ME calculations, we used a temperature independent collisional energy transfer model, where the average energy lost due to collisions with the N₂ bath was set to 〈ΔE〉_d = 100 cm⁻¹. The high-pressure limit Arrhenius parameters, E_a and A, which are required for the ILT/ME simulations, were derived from Arrhenius plots of the k^CVT_∞(T) values at different temperatures (see ESI Section S3†). We used the standard Arrhenius equation with a temperature independent pre-exponential factor in the fitting of the k^CVT_∞(T) against the temperature:

k^CVT_∞(T) = A × e^−E_a/RT (6)

In the RRKM/ME calculations, the NH₂ + O₂ reaction is assumed to form a pre-reactive complex NH₂⋯O₂ with a collision limited rate coefficient (10⁻¹⁰ cm³ per molecule per s in our calculations), whereafter the isomerization of the complex through a transition state to the NH₂O₂ minimum was calculated with RRKM. In RRKM/ME and ILT/ME simulations, the rate coefficients of the reverse dissociation (k_r) were obtained from the equilibrium constant (K_eq) and the forward reaction pseudo-first order rate coefficient with the following detailed balance condition:

All ILT/ME and RRKM/ME simulations were done using the MESMER program version 7.0.⁶⁰ The MESMER simulations are discussed in more detail in the ESI Section S3.†

3 Results and discussion

The formation of peroxyl radicals from alkyl radicals reacting with O₂ is well known.^61,62 Small peroxyl radicals like CH₃O₂ have been observed with cavity ring-down experiments.^23,63 In contrast, the observation of the analogous NH₂O₂ radical has been elusive. In light of this, we have investigated the NH₂ + O₂ → NH₂O₂ reaction. First, the potential energy surface (PES) is explored, second the kinetics of the reaction, third the formation of NH₂O₂ under different atmospheric conditions, and finally we discuss the lack of detection of NH₂O₂ in previous experiments.

3.1 Potential energy surface of NH₂ + O₂

In Fig. 1, we show that formation of the peroxyl radical is exoergic for both the CH₃ and NH₂ radicals reacting with O₂. Both the CH₃O₂ and NH₂O₂ formation reactions proceed via a barrierless potential, with the alkyl peroxyl radical bound much stronger. Thus, it appears that NH₂O₂ formation is not hindered or prevented by unfavorable reaction energetics. A similar potential has also been found for the CH₃S + O₂ → CH₃SO₂ reaction.⁶⁴

Fig. 1 Electronic potential energy curves of the R + O₂ → RO₂ reactions as a function of the R–O₂ distance for R=CH₃ (dashed) and R=NH₂ (solid), obtained with NEVPT2(13e,9o)/aug-cc-pVTZ and NEVPT2(19e,14o)/aug-cc-pVTZ, respectively.

In Fig. 2, we show the reaction potential of the NH₂ + O₂ → NH₂O₂ reaction with different methods. The potential energy surface of the NH₂ + O₂ → NH₂O₂ reaction was obtained in reverse via dissociation of NH₂O₂ to NH₂ and O₂ by using the N–O distance as the reaction coordinate and carrying out a relaxed scan with respect to this coordinate from 1.45 Å to 3.00 Å distance with a step size of 0.05 Å (Fig. 2a). The geometries along the reaction potential were optimized at the multireference NEVPT2(13e,11o) level (black line in Fig. 2a), which were further corrected with full-valence NEVPT2(19e,14o) single-point energy calculations (red line in Fig. 2a). The relative energy difference between NH₂ + O₂ and NH₂O₂ was obtained by increasing the distance between NH₂ and O₂ to 30 Å and optimizing the geometry of the resulting structure with respect to this distance constraint and then comparing the energy with that of the minimum. In addition, the relative energy of the reactants with respect to NH₂O₂ was calculated with a range of other methods. These results are shown on the left-side of Fig. 2a by the scattered symbols at the ∞ mark on the horizontal axis.

Fig. 2 Minimum energy path of the NH₂ + O₂ → NH₂O₂ reaction as a function of the H₂N–O₂ distance. (a) Electronic potential energy surface with NEVPT2(13e,11o) geometry optimizations (black) and NEVPT2(19e,14o) single-point energy corrections (red). The black ★ symbols correspond to stationary points obtained at the NEVPT2(13e,11o) level, and the blue ★ is calculated with W3X-L. (b) The Gibbs energy surface of the reaction around the Gibbs energy saddle point, at 298 K and 1 atm, with electronic energies calculated at the NEVPT2(19e,14o) level and thermodynamic corrections at the NEVPT2(13e,11o) level. The orange ★ highlights the position of the NEVPT2(13e.11o) saddle point.

The relative energy at the NEVPT2(19e,14o) level was obtained by optimizing the NH₂ and O₂ geometries separately at their respective full-valence active space NEVPT2 levels, summing up their energies, and then subtracting the NEVPT2(19e,14o)//NEVPT2(13e,11o) energy of NH₂O₂. The NEVPT2(13e,11o) and NEVPT2(19e,14o) reaction potentials show ca. 3 kcal mol⁻¹ difference in the estimated association energies (Fig. 2a). The relative energies obtained with other methods are scattered between the NEVPT2(13e,11o) and NEVPT2(19e,14o) relative energies. W3X-L may be regarded as the most accurate method used in the present work, and therefore the NEVPT2(19e,14o) relative energies and PES appear more reasonable than the NEVPT2(13e,11o) energies.

The NEVPT2(13e,11o) reaction curve (black line in Fig. 2a) shows a pre-reactive van der Waals complex and a shallow submerged barrier at around 2.65 Å and 2.2 Å N–O distances, respectively (★ symbols in Fig. 2a). Despite the presence of the saddle point in the NEVPT2(13e,11o) PES, the height of the barrier is very low and is not present in the NEVPT2(19e,14o) corrected surface (red line in Fig. 2a). This means that using this point as a transition state may be inaccurate. The region around this point was inspected more closely in the corresponding Gibbs energy surface (Fig. 2b) to better define the location of the transition state of the reaction. Details of how the Gibbs energy surface was obtained are discussed in the ESI Section S2.1.† There are three distinct features in the Gibbs energy surface compared to the PES: the saddle point is more pronounced, it is shifted to a shorter N–O distance, and the pre-reactive complex is absent from the Gibbs energy surface.

Overall, the NH₂ + O₂ → NH₂O₂ reaction does not appear to be prevented by potential energy barriers; in contrast, the reaction PES shows either a negligible barrier or no barrier. The reaction is exoergic but considerably less than the analogous CH₃ + O₂ → CH₃O₂ reaction (Fig. 1), so a smaller fraction of the NH₂O₂ product is expected to be present under ambient conditions compared to CH₃O₂, due to a faster back reaction. At finite temperature, the entropy penalty associated with two molecules reacting to form one molecule introduces a clear saddle point in the Gibbs energy surface of the NH₂ + O₂ → NH₂O₂ reaction, which controls the rate of the reaction.

3.2 Kinetics of NH₂ + O₂

We have estimated the kinetics of the reaction with CVT, ILT/ME, and RRKM/ME (Table 1). The thermal high-pressure limit (HPL) rate coefficients k_∞(T) for the forward association (k_f) and reverse dissociation (k_r) were calculated with the CVT method, using the maximum of the Gibbs energy surface as the transition state structure (Fig. 2b). The k_∞(298 K) value, 1.1 × 10⁻¹³ cm³ per molecule per s, is eight orders of magnitude larger than the current IUPAC recommended value (10⁻²¹ cm³ per molecule per s). However, reactions involving small molecules often do not exhibit HPL kinetics at ambient pressure.⁶⁵ Therefore, we studied the pressure and temperature dependence of the reaction system with the ILT and RRKM master equation models. As expected, the ILT/ME and RRKM/ME rate coefficients at 298 K and 1 atm are smaller than the HPL values obtained with CVT. The pressure dependence of k_f at varying temperatures, obtained with the ILT/ME method, is illustrated in Fig. S7.† At 298 K and 1 atm, the ILT/ME and RRKM/ME rate coefficients are roughly 10⁻¹⁵ cm³ per molecule per s, suggesting the rapid formation of NH₂O₂ under atmospheric conditions.

Table 1 Calculated rate coefficients of the NH₂ + O₂ ⇋ NH₂O₂ reaction at 298 K

	CVT (HPL)	ILT/ME (1 atm)	RRKM/ME (1 atm)
k f (cm^3 per molecule per s)	1.1 × 10^−13	1.7 × 10^−15	2.5 × 10^−15
k r (s^−1)	8.6 × 10^6	1.3 × 10^5	1.8 × 10^5

---

Based on our ME calculations, we find that the rate coefficient at 1 atm pressure is about two orders of magnitude lower, and at 0.1 atm pressure about 3 orders of magnitude lower, than the HPL value (Table 1) (ESI Section S3).†

Independent of the methodology used, our calculated rate coefficients of NH₂O₂ formation are larger than those obtained by experimentally measuring the NH₂ decay rate^18–21 and several orders of magnitude larger than the currently recommended rate coefficient value for the NH₂ + O₂ reaction by IUPAC.^15,66 We hesitate to give absolute recommendations for the rate coefficient because the methods and approximations we have used also have their uncertainties. However, we carried out various sensitivity tests (ESI Section S3†) and found the rate coefficients to vary by less than two orders of magnitude.

In addition, we performed similar multireference electronic structure calculations and ME simulations for the analogous CH₃ + O₂ → CH₃O₂ system (see ESI Sections S1 and S3†), for which a lot of experimental kinetics data are available (see ref. 66 for example). Our k(p, T) values for that system are in reasonable agreement with the currently recommended values.^66–68 The experimental rate coefficient for the CH₃ + O₂ → CH₃O₂ reaction at 298 K and 1 atm is 8.1 × 10⁻¹³ cm³ per molecule per s,⁶⁸ while our calculated values under these conditions are 2.1 × 10⁻¹³ and 1.1 × 10⁻¹² cm³ per molecule per s, with ILT/ME and RRKM/ME, respectively (ESI Table S2†), both of which are in good agreement with the experimental value.

3.3 Atmospheric presence of NH₂O₂

Whether formation of NH₂O₂ has any effect on atmospheric processes depends on the stability of NH₂O₂ with respect to back-dissociation, i.e. its fraction at equilibrium compared with the loss rates of NH₂ and NH₂O₂ with respect to other competing reactions.

The competition of bimolecular reactions of NH₂ with NO, NO₂, and O₃ can be estimated by comparing the pseudo-first order rate coefficients of these reactions. An upper limit for these competing bimolecular reactions would be that they occur with a rate coefficient near the collision limit of around 10⁻¹⁰ cm³ per molecule per s and that the combined concentration of these reactants is 40 ppb, which leads to a pseudo-first order rate coefficient of 100 s⁻¹.⁶⁹ The actual pseudo-first order rate coefficient is likely much smaller than this upper limit.

The reactions of NH₂ with NO_x and O₃ are considerably faster than the reaction with O₂, but the concentration of O₂ is substantially higher than the NO_x and O₃ concentrations. With our calculated rate coefficients in Table 1 (2 × 10⁻¹⁵ cm³ per molecule per s) and the atmospheric O₂ concentration, the pseudo-first order rate coefficient of NH₂ + O₂ → NH₂O₂ is 10⁴ s⁻¹, thus the reaction is much faster than other bimolecular reactions. The back reaction NH₂O₂ → NH₂ + O₂ is even faster than the forward reaction (Table 1). This suggests that the NH₂ + O₂ ⇋ NH₂O₂ equilibrium is established before the competing bimolecular reactions start consuming either NH₂ or NH₂O₂. Even if the calculated rate coefficients in Table 1 were 1–2 orders of magnitude too high, this would still hold.

Then, if the NH₂ + O₂ ⇋ NH₂O₂ reaction has reached equilibrium and there are no reactions affecting the equilibrium, the fraction of NH₂O₂ can be easily calculated. At equilibrium, k_f[NH₂][O₂] = k_r[NH₂O₂], hence the ratio [NH₂O₂]/[NH₂] = (k_f/k_r)[O₂]. Our calculations with ILT/ME and RRKM/ME suggest that at 298 K and 1 atm (with 21% O₂ partial pressure), the fraction of NH₂O₂ is 6.4%. We carried out ILT/ME simulations of NH₂ + O₂ ⇋ NH₂O₂ with a broad set of conditions to show how the equilibrium fraction of NH₂O₂ varies with temperature and pressure. In Fig. 3a, we show the fraction of NH₂O₂ as a function of temperature (230–330 K) at four total pressures: 700, 570, 400, and 200 torr, with 21% O₂ partial pressure. Fig. 3b shows the NH₂O₂ equilibrium fraction as a function of altitude (0–10 km), for global (288 K, solid)⁷⁰ and polar (263 K, dashed) average surface temperatures. The temperatures and pressures at various altitudes were calculated with the barometric formula, using the temperature lapse rate of −6.5 K km⁻¹ (ESI Section S4†).

Fig. 3 Fraction of NH₂O₂ under typical tropospheric conditions: (a) at total pressures of 200 torr (black dotted line), 400 torr (blue dotted line), 570 torr (red dotted line), and 760 torr (orange dotted line), in the temperature range 230–330 K; (b) as a function of altitude of 0–10 km, with the global average surface temperature 288 K (solid line) and polar average surface temperature 263 K (dashed line). All calculations were carried out with 21% O₂ concentration, using the ILT/ME method.

The formation of NH₂O₂ is more pronounced at lower temperatures and higher pressures, which is explained by the entropy effect (Fig. 3a). The average temperature of Earth's atmosphere at the ground level is 288 K, where 10% of formed NH₂ will add O₂ forming NH₂O₂ (Fig. 3b). In polar regions, where the mean surface temperature is 263 K, the NH₂O₂ fraction is much larger at the ground level (32%); therefore, it is likely an important pathway in NH₃ oxidation. At high altitudes (Fig. 3b), where both the temperature and pressure are low, the fraction of NH₂O₂ becomes substantial.

3.4 Unimolecular reactions of NH₂O₂

It is critical to assess whether there are any unimolecular reactions of NH₂O₂ that would affect the NH₂ + O₂ ⇋ NH₂O₂ equilibrium. In previous literature, it has been demonstrated that the most exothermic products of the NH₂ + O₂ reaction would be NO + H₂O and HNO + OH, the prior being the thermodynamically preferred product channel.¹⁵ We calculated the unimolecular reaction pathways that connect the NH₂O₂ to these product channels. The Gibbs energy profile of these reactions at 298 K and 1 atm is shown in Fig. 4. We also validated some of the calculated energy asymptotes in Fig. 4 against reaction enthalpies in the Active Thermochemical Tables database⁷¹ (see ESI Section S7† for details).

Fig. 4 Gibbs energy diagram of the unimolecular reactions of NH₂O₂, including those leading to HNO and NO formation, calculated at the NEVPT2 level (see details in the Methods section), at 298 K and 1 atm. Red = oxygen, blue = nitrogen, and gray = hydrogen. Zero energy corresponds to the Gibbs energy of NH₂O₂.

After the initial association of NH₂ and O₂, the formed NH₂O₂ has three accessible unimolecular reactions: the reverse dissociation to NH₂ + O₂, isomerization to the HNOOH radical via intramolecular hydrogen atom transfer, and dissociation to the aminoxyl radical and atomic oxygen (NH₂O + O). The last reaction has been deemed unlikely to be competitive under ambient conditions,²⁸ which is also supported by our findings: the reaction is endergonic by 31.4 kcal mol⁻¹ at 298 K and 1 atm (Fig. 4). The isomerization of NH₂O₂ to HNOOH, which ultimately leads to the formation of NO and HNO, occurs via a tight transition state, with a Gibbs energy barrier height of 28.5 kcal mol⁻¹ (Fig. 4).

The hydrogen atom transfer reaction (H-shift) is accelerated by quantum mechanical tunneling, which we estimated using the Eckart potential approximation.⁵⁹ We simulated the hydrogen atom transfer reaction at 298 K and 1 atm pressure using RRKM/ME and determined a rate coefficient of 7.6 × 10⁻⁶ s⁻¹ including tunneling. The effective rate coefficient for the overall reaction from NH₂ + O₂ to HNOOH, which we use as a proxy for NO production, is calculated by combining ILT/ME for the NH₂ + O₂ → NH₂O₂ reaction with a RRKM/ME for the NH₂O₂ → HNOOH reaction. This gives 5.8 × 10⁻²⁵ cm³ per molecule per s at 298 K and 1 atm. Thus, this pathway is insignificant under ambient conditions. This small rate coefficient is in qualitative agreement with the IUPAC recommendation.^15,66

It is evident that under atmospheric conditions, the only plausible reactions of NH₂O₂ are the reverse dissociation back to NH₂ + O₂ or further bimolecular reactions. In this work, we did not explicitly model any of these further bimolecular reactions. Because NH₂O₂ is a peroxyl radical, its most likely further bimolecular reactions are with NO, NO₂, HO₂, and other RO₂. If we estimate that the bimolecular rate coefficients of NH₂O₂ are comparable to those of alkyl RO₂, which are known to be in the range of 10⁻¹⁰–10⁻¹³ cm³ per molecule per s,⁷² the lifetimes of NH₂ (excluding the reaction with O₂) and NH₂O₂ are similar.

It is known that peroxyl radicals (RO₂) can react bimolecularly with NO₂, NO, HO₂ and other RO₂ to form e.g. peroxy nitrates (ROONO₂), organic nitrates (RONO₂), hydroperoxides (ROOH), alcohols (ROH), carbonyl compounds (R–H=O), alkoxyl radicals (RO), and organic peroxides (ROOR).⁷² For the aminoperoxyl radical NH₂O₂, the corresponding products would be NH₂OONO₂, NH₂ONO₂, NH₂OOH, NH₂OH, and NH₂OOR, which are different compound classes to those currently expected as products of NH₃ oxidation (NO, N₂O, and N₂).⁹ The bimolecular reactions of NH₂O₂ will likely also produce the NH₂O radical, which is also known to form in the bimolecular reactions of NH₂ with O₃, NO₂, and HO₂.^14,21,73 Therefore, the substantial branching ratio of NH₂O₂ may lead to previously undiscovered nitrogen-containing compounds in the atmosphere and influence the current atmospheric modeling.

3.5 Previous experiments

There have been several experimental investigations of the reaction between NH₂ and O₂ by measuring the NH₂ decay rate in the presence of O₂, and the results suggest that the reaction between NH₂ and O₂ is negligible. However, these experiments have been conducted largely under either low-pressure or high-temperature conditions, where the reaction between NH₂ and O₂ forming NH₂O₂ is not expected to play a substantial role based on our calculations. The calculated fraction of NH₂O₂ under different experimental conditions is given in the ESI Section S5.†

The pulse radiolysis experiments of NH₃ by Pagsberg et al.¹⁹ showed that, at 350 K, the NH₂ decay rate is independent of O₂ concentration, even at their highest O₂ concentration experiment (42% O₂ at 705 torr). In agreement, our results show that the fraction of NH₂O₂ is 1.5% under these conditions (ESI Table S4†), and thus the decay of NH₂ would be largely independent of O₂.

Cheskis and Sarkisov¹⁸ carried out room temperature flash photolysis experiments of NH₃ at 100 and 570 torr total pressures, with varying O₂ percentage. They observed significant enhancement in the NH₂ decay at 1 torr O₂ partial pressure and 570 torr total pressure (≈0.2% O₂) compared to a similar experiment without oxygen. The authors explained that the increased decay rate was unlikely to be due to the reaction between NH₂ and O₂ but instead was due to their experimental setup. In the experiment, the NH₂ radicals were generated via NH₃ photolysis, yielding H radicals that can react with O₂ to form HO₂, which reacted irreversibly with NH₂, resulting in the decay of NH₂. This is in agreement with our results, which show that at such low O₂ percentage, the formation of NH₂O₂ was insignificant (0.05%, ESI Table S4†). However, no increase in the NH₂ decay rate was observed when further increasing the O₂ pressure to 100 and 570 torr in the experiments (18% and 100% O₂ at 570 torr total pressure). These observations are in contrast to our calculations, which suggest that the fraction of NH₂O₂ was 4% and 20% under these conditions, respectively (ESI Table S4†), which would affect the NH₂ decay rate. The NH₂ decay was saturated because significant NH₂ decay rate was also observed upon increasing the N₂ pressure from 100 torr to 570 torr without any O₂ in the experiments.

Patrick and Golden²¹ conducted experiments in the temperature range 272–348 K where NH₂ was generated via O₃ photolysis forming atomic O, which reacted with NH₃ to form NH₂. The experiments with O₂ were carried out at low total pressures of 230–240 torr and O₂ partial pressures of only 0–14 torr (max. 6% O₂). Our calculations show that the NH₂O₂ fraction is less than 3% at such low O₂ pressures (ESI Table S4†). No significant reactivity between NH₂ and O₂ was observed in the experiments, in agreement with our results. Experiments with higher O₂ partial pressures cannot be conducted in this setup because the reaction between O₂ and atomic O would suppress the formation of NH₂.

4 Conclusions

We have carried out high-level multireference calculations and kinetic modeling for studying the formation of the NH₂O₂ radical via the association reaction between NH₂ and O₂, which is a crucial step in the atmospheric oxidation of NH₃. We find that the association reaction is much faster than the current IUPAC estimate and that NH₂ + O₂ is the dominant bimolecular reaction of NH₂ in the atmosphere. Our calculations encompass a broad range of atmospherically relevant conditions, and we show that NH₂O₂ formation can play an important role in NH₃ oxidation, especially under low-temperature and high-pressure conditions, where a substantial equilibrium fraction of NH₂O₂ is expected to be present. We encourage laboratory experiments to directly detect the NH₂O₂ radical and determine the rate of the NH₂ + O₂ reaction under relevant conditions.

Data availability

Calculation output files related to the study are available in the ESI† and at http://doi.org/10.5281/zenodo.12657070.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Research Council of Finland Centre of Excellence: Virtual Laboratory for Molecular-Level Atmospheric Transformations (grant 346369), the Jane and Aatos Erkko (JAES) Foundation, and the Villum Fonden (VIL50443) for funding. We also thank the CSC – IT Center of Science (Finland) for providing the supercomputing platforms and computational resources.

References

1. L. Liu, W. Xu, X. Lu, B. Zhong, Y. Guo, X. Lu, Y. Zhao, W. He, S. Wang and X. Zhang, et al. , Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2121998119.
2. R. Zhu, J. Sun, Y. Liu, Z. Gong and L. Sun, Antarct. Sci., 2011, 23, 78–92.
3. J. Lindaas, I. B. Pollack, J. J. Calahorrano, K. O'Dell, L. A. Garofalo, M. A. Pothier, D. K. Farmer, S. M. Kreidenweis, T. Campos and F. Flocke, et al. , J. Geophys. Res.: Atmos., 2021, 126, e2020JD033730.
4. S. Riddick, T. Blackall, U. Dragosits, F. Daunt, M. Newell, C. Braban, Y. Tang, J. Schmale, P. Hill and S. Wanless, et al. , Atmos. Environ., 2016, 134, 40–50.
5. J. Plautz, Science, 2018, 361, 1060–1063.
6. R. Pinder, A. Gilliland and R. Dennis, Geophys. Res. Lett., 2008, 35, L12808.
7. S. N. Behera, M. Sharma, V. P. Aneja and R. Balasubramanian, Environ. Sci. Pollut. Res., 2013, 20, 8092–8131.
8. N. Evangeliou, Y. Balkanski, S. Eckhardt, A. Cozic, M. Van Damme, P.-F. Coheur, L. Clarisse, M. W. Shephard, K. E. Cady-Pereira and D. Hauglustaine, Atmos. Chem. Phys., 2020, 2020, 1–41.
9. S. J. Pai, C. L. Heald and J. G. Murphy, ACS Earth Space Chem., 2021, 5, 1674–1685.
10. J. M. Roberts, A. O. Langford, P. D. Goldan and F. C. Fehsenfeld, J. Atmos. Chem., 1988, 7, 137–152.
11. R. D. Stephens, J. Phys. Chem., 1984, 88, 3308–3313.
12. C. P. Ennis, J. R. Lane, H. G. Kjaergaard and A. J. McKinley, J. Am. Chem. Soc., 2009, 131, 1358–1359.
13. M. Monge-Palacios and J. Espinosa-Garcia, J. Phys. Chem. A, 2010, 114, 4418–4426.
14. R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Atmos. Chem. Phys., 2004, 4, 1461–1738.
15. G. Tyndall, J. Orlando, K. E. Nickerson, C. Cantrell and J. Calvert, J. Geophys. Res.: Atmos., 1991, 96, 20761–20768.
16. H. Gesser, J. Am. Chem. Soc., 1955, 77, 2626–2629.
17. R. Jayanty, R. Simonaitis and J. Heicklen, J. Phys. Chem., 1976, 80, 433–437.
18. S. Cheskis and O. Sarkisov, Chem. Phys. Lett., 1979, 62, 72–76.
19. P. B. Pagsberg, J. Eriksen and H. Christensen, J. Phys. Chem., 1979, 83, 582–590.
20. W. Hack, O. Horie and H. G. Wagner, J. Phys. Chem., 1982, 86, 765–771.
21. R. Patrick and D. M. Golden, J. Phys. Chem., 1984, 88, 491–495.
22. R. L. Caravan, M. A. H. Khan, J. Zádor, L. Sheps, I. O. Antonov, B. Rotavera, K. Ramasesha, K. Au, M.-W. Chen and D. Rösch, et al. , Nat. Commun., 2018, 9, 4343.
23. M. B. Pushkarsky, S. J. Zalyubovsky and T. A. Miller, J. Chem. Phys., 2000, 112, 10695–10698.
24. C. Pouchan and M. Chaillet, Chem. Phys. Lett., 1982, 90, 310–316.
25. C. F. Melius and J. S. Binkley, ACS Symp. Ser., 1984, 103–115.
26. J. W. Bozzelli and A. M. Dean, J. Phys. Chem., 1989, 93, 1058–1065.
27. R. Sumathi and S. D. Peyerimhoff, J. Chem. Phys., 1998, 108, 5510–5521.
28. S. J. Klippenstein, L. B. Harding, P. Glarborg and J. A. Miller, Combust. Flame, 2011, 158, 774–789.
29. J. L. Bao and D. G. Truhlar, Chem. Soc. Rev., 2017, 46, 7548–7596.
30. R. A. Marcus, J. Chem. Phys., 1952, 20, 359–364.
31. J. W. Davies, N. J. Green and M. J. Pilling, Chem. Phys. Lett., 1986, 126, 373–379.
32. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
33. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
34. R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
35. A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160.
36. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
37. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101.
38. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
39. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
40. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
41. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
42. B. O. Roos, P. R. Taylor and P. E. Sigbahn, Chem. Phys., 1980, 48, 157–173.
43. C. Kollmar, K. Sivalingam, B. Helmich-Paris, C. Angeli and F. Neese, J. Comput. Chem., 2019, 40, 1463–1470.
44. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264.
45. C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153.
46. Y. Guo, K. Sivalingam and F. Neese, J. Chem. Phys., 2021, 154, 214111.
47. C. Kollmar, K. Sivalingam, Y. Guo and F. Neese, J. Chem. Phys., 2021, 155, 234104.
48. K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488.
49. G. Ghigo, B. O. Roos and P.-Å. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149.
50. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
51. S. Zhong, E. C. Barnes and G. A. Petersson, J. Chem. Phys., 2008, 129, 184116.
52. F. Neese and E. F. Valeev, J. Chem. Theory Comput., 2011, 7, 33–43.
53. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646.
54. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
55. B. Chan and L. Radom, J. Chem. Theory Comput., 2015, 11, 2109–2119.
56. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, I. Miller, F. Thomas, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107.
57. M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and Á. Ganyecz, J. Chem. Phys., 2020, 152, 074107.
58. S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964.
59. R. L. Brown, J. Res. Natl. Bur. Stand., 1981, 86, 357–359.
60. D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560.
61. P. D. Lightfoot, R. Cox, J. Crowley, M. Destriau, G. Hayman, M. Jenkin, G. Moortgat and F. Zabel, Atmos. Environ., Part A, 1992, 26, 1805–1961.
62. J. J. Orlando and G. S. Tyndall, Chem. Soc. Rev., 2012, 41, 6294–6317.
63. A. Bossolasco, E. P. Faragó, C. Schoemaecker and C. Fittschen, Chem. Phys. Lett., 2014, 593, 7–13.
64. J. Chen, J. R. Lane, K. H. Bates and H. G. Kjaergaard, Environ. Sci. Technol., 2023, 57, 21168–21177.
65. B. M. Wong, D. M. Matheu and W. H. Green, J. Phys. Chem. A, 2003, 107, 6206–6211.
66. R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi, J. Troe and IUPAC Subcommittee, Atmos. Chem. Phys., 2006, 6, 3625–4055.
67. R. X. Fernandes, K. Luther and J. Troe, J. Phys. Chem. A, 2006, 110, 4442–4449.
68. J. B. Burkholder, S. P. Sander, J. Abbatt, J. R., C. Cappa, J. D. Crounse, T. S. Dibble, R. E. Huie, C. E. Kolb, M. J. Kurylo, V. L. Orkin, C. J. Percival, D. M. Wilmouth and P. H. Wine, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, JPL Publication, Jet Propulsion Laboratory, Pasadena, 19, 2019.
69. J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, John Wiley & Sons, 2016.
70. Atmospheric Administration and United States Committee on Extension to the Standard Atmosphere, US Standard Atmosphere, National Oceanic and Atmospheric Administration, 1976.
71. B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszevski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Chem. Phys. A, 2004, 108, 9979–9997.
72. F. Bianchi, T. Kurtén, M. Riva, C. Mohr, M. P. Rissanen, P. Roldin, T. Berndt, J. D. Crounse, P. O. Wennberg, T. F. Mentel, J. Wildt, H. Junninen, T. Jokinen, M. Kulmala, D. R. Worsnop, J. A. Thornton, N. Donahue, H. G. Kjaergaard and M. Ehn, Chem. Rev., 2019, 119, 3472–3509.
73. P. Glarborg, H. Hashemi, S. Cheskis and A. W. Jasper, J. Phys. Chem. A, 2021, 125, 1505–1516.

---

Footnote

† Electronic supplementary information (ESI) available: Further details and discussion of the CH₃ + O₂ → CH₃O₂ calculations, CVT calculations, Gibbs energy surface calculations, master equation simulations and sensitivity tests, NH₂ + O₂ → NH₂O₂ reaction potentials calculated with CASPT2 and CASPT2-IPEA methods, structural parameters and visualizations of CAS orbitals of relevant structures obtained at the NEVPT2 level of theory, and xyz-coordinates of the studied molecules. See DOI: https://doi.org/10.1039/d5ea00042d

---