Beyond lithium lanthanum titanate: metal-stable hafnium perovskite electrolytes for solid-state batteries

Abstract

Perovskite-type electrolytes (PTEs) exhibit high room-temperature ionic conductivity (∼1 mS cm⁻¹) but suffer from poor stability against metal anodes, limiting their application in metal all-solid-state batteries. We investigated alternatives to the prototypical PTE, lithium lanthanum titanate (LLTO), to identify PTE compositions with improved stability against metal-anodes and electrolyte performance. We evaluated composition–stability relationships of PTEs using DFT calculations of thermodynamic and electrochemical stabilities, diffusion barriers, and mechanical properties. Substituting Ti with Zr (LLZrO) and Hf (LLHfO) resulted in promising metastability against metallic Li anodes, although their diffusion barriers (0.188–0.576 eV) generally exceed those of LLTO. Unlike LLZrO, which lacks mechanical stability, LLHfO is predicted to be mechanically stable with balanced elasticities, high hardness, good ductility, low anisotropy, and the potential to suppress dendrite formation. These characteristics make LLHfO a promising Li-metal-compatible alternative to LLTO with strong overall performance metrics. Analogous Na-PTEs are stable against Na-metal; however, their high Na⁺ diffusion barriers (>0.85 eV) must be lowered to achieve practical ionic conductivity.

---

Broader context

The research situates itself within the effort to enhance the performance of metal all-solid-state batteries by addressing the stability limitations of perovskite-type electrolytes (PTEs). While conventional electrolytes like lithium lanthanum titanate (LLTO) offer high ionic conductivity at room temperature, their instability against metal anodes restricts their wider application. By leveraging density functional theory (DFT), the study explores alternative PTE compositions that could offer improved compatibility with lithium and sodium metal anodes. In particular, substituting titanium with zirconium (LLZrO) and hafnium (LLHfO) reveals that although these alternatives exhibit higher diffusion barriers compared to LLTO, LLHfO shows promising mechanical stability—combining high hardness, good ductility, and low anisotropy—to potentially suppress dendrite formation. For sodium-based batteries, however, the high diffusion barriers remain a critical challenge, indicating the need for further compositional or defect engineering. Overall, this systematic investigation not only identifies LLHfO as a promising candidate for lithium-metal batteries but also lays the groundwork for future modifications aimed at optimizing PTEs for high-performance energy storage applications.

Lithium-ion batteries (LIBs) are the leading commercial rechargeable (secondary) battery technology, widely used across various applications due to their high energy and power densities, and excellent cycling stability.¹ However, the energy density and safety of LIBs still fall short of meeting the increasingly ambitious demands of electric vehicles and grid-scale energy storage.^2,3 To overcome these limitations, the development of metal all-solid-state batteries (MASSBs) has become a central focus of battery research, offering the promise of higher energy density and enhanced safety.⁴ To develop MASSBs, researchers have investigated a range of inorganic crystalline solid-state electrolytes (SSEs), including LISICON-like materials,⁵ argyrodites,⁶ garnets,⁷ NASICON-like structures,⁸ nitrides,⁹ hydrides,¹⁰ halides,¹¹ thio-LISICON,¹² and perovskites.¹³ Among these SSE families, perovskites represent a mature and well-established material class.¹⁴ Often called the “inorganic chameleon”, they exhibit exceptional compositional and structural flexibility, making them attractive for a wide range of applications, including photovoltaics and batteries.^13–15

Since its first synthesis by Inaguma et al. in 1993, lithium lanthanum titanate (LLTO) has become the archetypal perovskite-type electrolyte (PTE).^13,16 Despite its high room-temperature bulk ionic conductivity (∼1 mS cm⁻¹),¹⁷ LLTO suffers from poor stability against Li metal anodes, limiting its use as an SSE in MASSBs.¹⁸ The general formula of LLTO is Li_3xLa_2/3−x□_1/3−2xTiO₃, where □ represents A-site vacancies. PTEs are typically aliovalent substitutional solid solutions with A-site deficiencies, formed by substituting a lower-valent A-site cation (e.g., Sr²⁺) with a higher-valent one (e.g., La³⁺). The resulting A-site vacancies preserve charge neutrality via ionic compensation.¹⁹ To enable vacancy-mediated ion diffusion, a fraction of the A-site vacancies accommodates Li⁺, while the remainder serve as hopping sites for Li⁺.⁷ The transition state (TS) for Li⁺ diffusion is the 3c site, which is located between neighboring A-sites and consists of four oxygen ions in the perovskite octahedral channel.⁸ The composition of PTE takes the general formula A′_mA′′_n□_oBX₃, where A′, A′′, □, B, and X are the working-ion, large-ionic-radius cation, A-site vacancy, small-ionic-radius cation, and anion, respectively.²¹ m, n, and o represent the concentrations of the working-ion, the large-ionic-radius cation, and the A-site vacancy, respectively. For a monovalent working-ion, compositions can be categorized as working-ion-poor or working-ion-rich. Working-ion-poor compositions typically exhibit lower and more anisotropic ionic conductivity, while working-ion-rich compositions provide higher, isotropic ionic conductivity.²⁰

Each crystallographic site in the SSE, along with the overall composition, plays a distinct role in performance by influencing geometric constraints, ion redox activity, the diffusion energy landscape of the working-ion, and the local bonding environment.^4,22 Achieving electrochemical stability in PTEs requires avoiding multivalent elements that are susceptible to reduction or oxidation.¹⁷ Enhancing ionic conductivity in PTEs is guided by two key design strategies: first, the working-ion octahedral diffusion channels can be expanded by incorporating large-radius cations, ensuring that the A′′-site cation is larger than the B-site cation, which is critical for maintaining perovskite structural stability.^4,20 Second, interactions at the hopping TS can be reduced by strengthening the B–X bond, which weakens the A′–X interaction,^20,24 and selecting X-site elements with high polarizability.⁴ However, because highly polarizable X-site elements are often multivalent, their use must be carefully considered. To improve PTE performance, previous work leveraged several strategies including tuning Li⁺ concentrations in LLTO,¹⁷ incorporating polymers,^17,24 and doping or alloying elements at the A, B, and X sites in both LLTO and other PTEs.^17,20 However, these efforts improved ionic conductivity, but to date, no PTE has demonstrated stability against metal anodes. Notably, the search for pristine, metal-stable alternatives to LLTO has largely been neglected. Instead, most studies have focused on directly doping or alloying non-LLTO PTEs, often without a comprehensive evaluation of SSE performance of their pristine compositions.

In this work, we aim to identify pristine PTE compositions that are stable against metal anodes and to elucidate key factors governing SSE performance. To this end, we studied how PTE composition influences stability against metal anodes. To benchmark performance, we selected PTE compositions composed of elements with relatively stable oxidation states, similar to those found in LLTO. For the A′-site, we primarily focused on Li⁺ and extended our investigation to Na⁺ in cases where the composition showed stability with Li⁺. For the A′′-site, we selected La³⁺, the largest trivalent ion with a relatively stable oxidation state. For the B-site, we examined two groups of elements in addition to the benchmark Ti case. First, we investigated Zr and Hf, which are in the same group as Ti in the periodic table and share similar characteristics. Notably, Hf⁴⁺ and Zr⁴⁺ exhibit more stable oxidation states, larger ionic radii, and lower electronegativities than Ti, all of which are anticipated to strengthen the B–X bonds.^25–27 Second, we examined Sn and Pb, both p-block (post-transition) metals with comparatively large ionic radii. Sn has a relatively stable 4+ oxidation state,^25–27 while Pb is a well-known B-site element for a variety of applications.²⁸ We considered the chalcogens O, S, Se, and Te as potential X-site anions, assuming each to adopt the 2⁻ oxidation states. Although heavier chalcogens (S, Se, and Te) can exhibit multiple oxidation states, they may enhance ionic conductivity if their 2⁻ oxidation state is maintained.⁴ Sulfur, in particular, enables the high-energy-density anion-redox chemistry that underpins low cost metal–sulfur batteries.²⁹

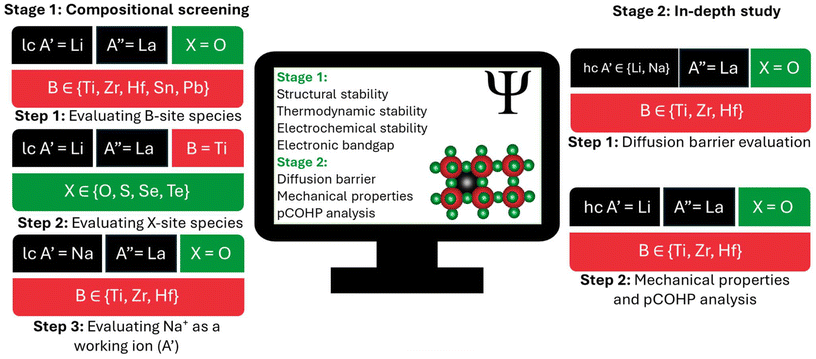
For the studied PTE compositions, we first evaluated a broad set of compositions (Fig. 1) to determine their structural, thermodynamic, and electrochemical stabilities. We also calculated electronic bandgaps to assess electronic conductivity. Finally, we conducted an in-depth analysis (Fig. 1) by computing the diffusion barriers, mechanical properties, and Projected Crystal Orbital Hamilton Population (pCOHP) of promising candidates. Detailed structural models and computational details are provided in the ESI.† We analyzed two distinct regimes: a computationally efficient low working-ion concentration (lc) model (A′_0.125A′′_0.625□_0.25B₁X₃) for compositional screening, and a high working-ion concentration (hc) model (A′_0.3125A′′_0.5625□_0.125B₁X₃) for in-depth analysis.

Fig. 1 Schematic of the two-stage computational workflow: compositional screening and in-depth analysis. In the screening stage, structural, thermodynamic, and electrochemical stability, along with electronic bandgap, were evaluated for lc compositions. Compositions with bandgaps >2 eV and sufficient stability advanced to the in-depth study stage, where diffusion barriers, mechanical properties, and pCOHP analysis were computed, primarily for hc compositions. The screening focused on varying B-site elements, with Li, La, and O occupying the A′-, A′′-, and X-sites, respectively. Separately, a range of X-site elements was assessed with Li, La, and Ti occupying the A′-, A′′-, and B-sites. For compositions with B- and X-site elements that were predicted to be stable, Na⁺ was also evaluated as a working-ion, along with corresponding hc variants.

We evaluated the perovskite structural stability using the Goldschmidt tolerance factor (t, eqn (S1)†), the octahedral factor (μ, eqn (S2)†), and the machine-learned tolerance factor τ (eqn (S3)†), which all utilize Shannon ionic radii. Additionally, we used the weighted average effective ionic A-site radius (, eqn (S4)†) to assess A-site size compatibility. Stability was defined within the ranges 0.75 < t < 1, μ > 0.414, and τ < 4.18.^{23,25,30–32} Table 1 shows that all studied compositions were structurally stable, except those containing heavier chalcogens (S, Se, and Te) at the X-site. This instability is attributed to their large ionic radii, which lower μ below 0.414 and raise τ above 4.18, thereby destabilizing the octahedral framework.

Table 1 Summary of compositional screening results, including evaluations of structural, thermodynamic, and electrochemical stability, and electronic bandgaps. t is the Goldschmidt tolerance factor, μ the octahedral factor, τ a machine-learned tolerance factor, E_f the formation energy, E_D the decomposition energy, E_w the electrochemical stability window relative to the working-ion, and E_g the electronic bandgap computed using the HSE DFT functional

Structure	t	μ	τ	Ef (eV per atom)	ED (eV per atom)	Ew (eV)	Eg (eV)	Comment
a Denotes metastable electrochemical stability, indicating that the reduction potential onset is metastable.
Step 1: Evaluating B-site elements
lc-LLTO	0.98	0.43	3.86	−3.50	−5.50	[1.53, 3.45]	3.69	Benchmark
lc-LLZrO	0.92	0.51	3.87	−3.71	−5.69	[0, 3.19]^a	5.27	Passed
lc-LLHfO	0.93	0.51	3.85	−3.80	−5.92	[0, 3.28]^a	5.68	Passed
lc-LLSnO	0.94	0.49	3.83	−2.51	−4.58	Unstable	3.06	Excluded
lc-LLPbO	0.90	0.55	4.03	−2.00	−4.61	[2.95, 3.20]	0.73	Excluded
Step 2: Evaluating X-site elements
lc-LLTS	0.93	0.33	4.59	−1.78	−4.84	Unstable	1.33	Excluded
lc-LLZrS	0.89	0.39	4.48	−1.99	−5.03	Unstable	2.23	Excluded
lc-LLHfS	0.89	0.39	4.47	−2.00	−5.31	Unstable	2.45	Excluded
lc-LLTSe	0.92	0.31	4.82	−1.59	−4.45	Unstable	0.93	Excluded
lc-LLTTe	0.90	0.27	5.20	−1.12	−4.19	Unstable	0.01	Excluded
Step 3: Evaluating Na^+ as a working-ion (A′)
lc-NLTO	0.98	0.43	3.84	−3.50	−5.49	[0, 3.03]^a	3.55	Passed
lc-NLZrO	0.93	0.51	3.83	−3.72	−5.69	[0, 2.68]	5.23	Passed
lc-NLHfO	0.93	0.51	3.81	−3.80	−5.94	[0, 2.26]	5.63	Passed

---

Due to the disordered solid-solution nature of PTEs, we employed Pymatgen's OrderDisorderedStructureTransformation module to generate symmetry distinct atomic configurations within the lc and hc models.³³ We applied the Ewald summation (Coulomb) method to calculate electrostatic energies to rank configurations.³⁴ DFT calculations were performed on the ten lowest-energy configurations (LECs) to identify the most probable configuration for the lc and hc compositions. Formation and decomposition energies were then calculated using the DFT energies of the LEC's, Pymatgen's PhaseDiagram module,³³ and data from the materials project (MP) repository.³⁵ Results are reported in Table 1. All studied compositions exhibited negative decomposition and formation energies, indicating thermodynamic stability against decomposition into competing compounds and elemental phases.

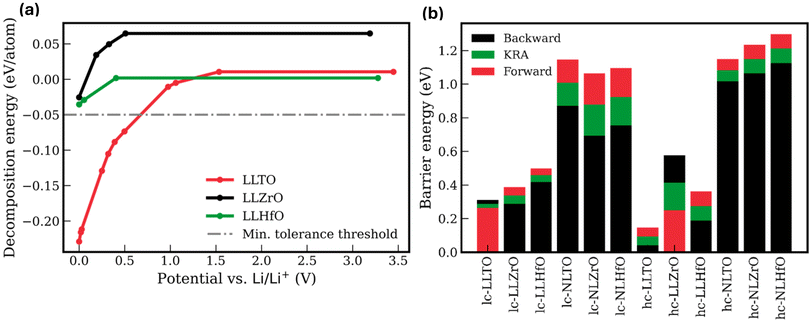
We defined the electrochemical stability window (E_w) as the potential range over which a given phase has decomposition energies ≥−50 meV per atom, as described in eqn (S8)† and illustrated in Fig. 2(a). This threshold accounts for both the DFT margin of error affecting calculated formation energies and the metastability arising from kinetic stabilization effects.³⁶ Ideally, the electrochemical stability window of a given composition should span a wide potential range relative to the metal anode reference. It should start with a reduction potential onset at 0 V to ensure stability against metal anodes and extend to a high oxidation potential onset (i.e., >3 V) to support high-voltage cathode chemistries. Under grand canonical ensemble conditions relevant to battery environments, the computed E_w values in Table 1 indicate that six compositions are largely unstable, exhibiting low thermodynamic favorability relative to decomposition into competing phases. Notably, LLZrO, LLHfO, and NLTO (with Na⁺ as the working-ion) exhibit reasonable metastability against metal anodes along with high oxidation potential onset, as shown in Fig. 2(a). NLZrO and NLHfO also showed stability against metal anodes, as shown in Fig. S1(b).† To assess the electronic insulation, a key requirement of SSEs, we used the HSE06 hybrid DFT functional to compute electronic bandgaps.³⁷ Table 1 shows that only four compositions had bandgaps <2 eV, with LLTTe exhibiting a near-zero bandgap, indicative of poor electronic insulation. During compositional screening, B-site substitution with Zr and Hf combined with O on the X-site yielded promising results for both Li⁺ and Na⁺ compositions, as summarized in Table 1. The hc composition results closely mirror those of the lc variants during compositional screening (see Tables 1 and S1†).

Fig. 2 (a) Electrochemical stability of LLTO, LLZrO, and LLHfO. LLZrO and LLHfO demonstrate reasonable metastability against Li metal with high oxidation potential onsets. (b) Diffusion barriers for lc and hc compositions for LLTO, LLZrO, LLHfO, NLTO, NLZrO, and NLHfO. While LLZrO and LLHfO exhibit moderate diffusion barriers, these remain consistently higher than those of LLTO. In contrast, the studied PTEs are predicted to be unsuitable for Na all-solid-state batteries due to Na⁺ diffusion barriers exceeding 0.85 eV.

We calculated the working-ion diffusion barriers for the stable lc and hc compositions using the climbing-image solid-state nudged elastic band (CI SS-NEB) method (see ESI†) and report the results in Fig. S2(a–d).† As a solid solution, PTE exhibits configurational disorder. Consequently, working-ions in PTEs diffuse along site-to-site trajectories with asymmetric activation barriers that strongly depend on the local atomic arrangement surrounding the diffusing ion. This leads to direction-dependent hopping barriers. To account for this variability, we employed the kinetically-resolved activation (KRA) barrier, which is defined as the average of all the diffusion barriers referenced to the end points of a given ion hop.^38,39 The results are summarized in Fig. 2(b) and Table S2.† Generally, for disordered materials, diffusion barriers from a single configuration do not yield quantitative predictions of ionic conductivity, which requires extensive sampling and statistical mechanics analysis.³⁸ Furthermore, the uncertainty of the DFT-calculated diffusion barriers is ∼0.1 eV.⁴⁰ Nonetheless, diffusion barrier calculations provide valuable information about the relative ion transport kinetics in PTEs. In addition to their promising metastability against metallic Li anodes, LLZrO and LLHfO exhibited Li⁺ diffusion barriers between 0.188–0.576 eV, only moderately higher than those of LLTO (0.040–0.311 eV). This implies a lower room-temperature ionic conductivity, potentially by an order of magnitude, assuming Arrhenius behavior. In contrast, the analogous diffusion barriers for Na⁺ exceed 0.85 eV. Therefore, despite their favorable metastability against Na anodes, these PTEs are unlikely to be viable for Na all-solid-state batteries without further modifications to lower their diffusion barriers. The high barrier is attributed to the large ionic diameter of Na⁺ (2 Å), which is nearly twice the size of the steric opening at the TS (bottleneck) in both lc and hc structures (see Table S2†).²⁵

Mechanical properties are crucial in SSEs for safe, durable and reliable battery handling and operation. The stress–strain method, based on the generalized Hooke's law, was employed to calculate the elastic constants using VASPKIT.⁴¹ The LECs for LLTO and LLHfO were mechanically stable, satisfying all the Born stability criteria, as described in the ESI.† However, for LLZrO, the LEC showed a negative C₅₅ and one negative elastic tensor eigenvalue, suggesting either a structural distortion or configurational shift. We instead evaluated the second most stable configuration that has an energy 3 meV per atom above the LEC. This was more tractable than attempting to predict a mechanically stable distorted phase and found that it satisfied the mechanical stability criteria. The mechanical properties of the three studied compositions, reported in Table 2, were used to assess the elastic stability of PTEs. High bulk modulus (B), Young's modulus (E), and Debye temperature increase SSE stiffness and reduce compressibility, though excessively high values may deteriorate ionic conductivity.^42–44 Accordingly, LLHfO and LLZrO exhibited more favorable elastic properties than LLTO due to their moderate and balanced stiffness.^45,46 According to the Pugh criterion (B/G > 1.75, where G is the shear modulus), LLTO, LLZrO, and LLHfO are all ductile,⁴⁷ making them robust under battery operating conditions and manufacturing-friendly. According to Monroe and Newman's linear elasticity model, G of an SSE must be at least twice that of lithium metal to suppress dendrite propagation.^48,49 All three compositions have higher computed values of G than that required to suppress dendrite formation, as discussed in the ESI.† ⁵⁰ The computed Poisson ratios (v) predict that all three compositions are highly rigid. Vickers hardness reflects the strength of the bonds of a material and serves as an indicator of its structural integrity under mechanical stress. We found that LLHfO and LLZrO have higher Vickers hardness than LLTO and are thus likely to be more mechanically stable against stress during battery operation. In SSEs, anisotropy affects ionic conductivity and mechanical stability. The universal anisotropy number (UAN) quantifies the degree of anisotropy, where a UAN greater than 1 indicates significant directional dependence.⁵¹ LLTO and LLHfO's computed UANs of 0.14 and 0.11 suggest more uniform mechanical behavior and ionic conductivity than LLZrO, which has a UAN of 0.99. LLHfO shows the best combination of isotropy and stiffness, whereas LLZrO, while softer (lower E, B) than LLTO, has a significantly higher anisotropy, which could influence crack propagation or ionic percolation in a real polycrystal.

Table 2 Summary of the mechanical properties of hc compositions for LLTO, LLZrO, and LLHfO

Mechanical property, unit	LLTO	LLZrO	LLHfO
Bulk modulus (B), GPa	277.54	115.60	135.92
Young's modulus (E), GPa	251.46	150.21	186.44
Shear modulus (G), GPa	93.20	58.52	73.32
Poisson's ratio (v)	0.35	0.28	0.27
Pugh's ratio (B/G)	2.98	1.98	1.85
Vickers hardness, GPa	4.88	6.70	8.91
Universal anisotropy number (UAN)	0.14	0.99	0.11
Debye temperature, K	609.40	438.80	427.40

---

We used Lobster⁵² to perform pCOHP analysis on the Li–O and transition metal (TM)–O bonds in the studied compositions to examine the interaction between the working-ion (A′) and the X-site anion. The analysis was performed on both the initial (Li@A-site) and TS (Li@TS) configurations, extracted from the NEB images shown in Fig. S3.† The Li–O peaks are considerably weaker than the TM–O peaks, confirming their greater ionicity and weaker bonding. Notably, the Li–O anti-bonding peak for LLTO lies higher than those of LLZrO and LLHfO, indicating stronger Li–O bonding in LLTO than in LLZrO and LLHfO. For Zr–O bonds, the presence of anti-bonding interactions below the Fermi level highlights their tendency to dissociate under stress or elevated temperatures. This observation aligns with the results from mechanical stability analyses. Conversely, the small bonding peaks in the anti-bonding contribution of Li–O bonds in LLTO are negligible and positioned far above the Fermi level, indicating minimal influence on its bonding nature. Additionally, the Integrated Crystal Orbital Hamilton Population (ICOHP) was used to quantify the Li–O and TM–O bond strengths, with higher (−ICOHP) values indicating stronger bonds. As shown in Fig. 3(a), the results indicate that Zr and Hf form stronger bonds with oxygen due to their lower electronegativity relative to Ti, which slightly weakens the Li–O bonds in LLZrO and LLHfO relative to LLTO. To examine the Li–O bonding changes upon diffusion, the average −ICOHP values for Li–O bonds of the diffusing Li⁺ were calculated at the Li@TS configurations. As shown in Fig. 3(b), the Li–O bonds of LLZrO and LLHfO are slightly weaker than those in LLTO, reducing the interaction of oxygen with the diffusing Li⁺, as intended. Nonetheless, the persistence of high diffusion barriers in LLZrO and LLHfO despite weaker Li–O bonding (A′–X interaction) indicates that factors such as the lattice deformation energy may dominate diffusion kinetics, suggesting that this design principle may need to be revisited in future studies.

Fig. 3 (a) The comparative −ICOHP for the studied compositions for the Li@TS configurations. (b) The average −ICOHP of the diffusing Li⁺ in the studied compositions for the Li@TS configurations. −ICOHP refers to the negative integrated Crystal Orbital Hamilton Population, used to evaluate bond strength between the diffusing Li⁺ and surrounding atoms at the transition state (TS).

Conclusions

This study systematically explores the composition–stability relationship of PTEs, assessing their structural, thermodynamic, and electrochemical stabilities, as well as their working-ion diffusion barriers and mechanical properties. In the compositional screening, La (A′′-site), Zr and Hf (B-site), and O (X-site) showed promise for both Li⁺ and Na⁺. In-depth analysis revealed that while LLZrO and LLHfO exhibit reasonable diffusion barriers (0.188–0.576 eV) and metastability against metallic Li anodes, their barriers remain generally higher than LLTO (0.040–0.311 eV). However, for Na⁺, the significantly higher diffusion barriers (>0.85 eV) render these PTEs unsuitable for sodium metal all-solid-state batteries. Mechanical analysis confirmed the stability of LLHfO. LLHfO and LLZrO exhibit good ductility, high Vickers hardness, and balanced elasticity, which enhance their manufacturability and operational durability. All compositions surpassed the shear modulus threshold for dendrite suppression, with LLHfO showing lower mechanical anisotropy and a favorable Debye temperature. Thus, LLHfO emerges as a promising Li-metal-compatible alternative to LLTO, which is unstable against Li-metal. Importantly, experimental evaluation is essential to confirm the viability of LLHfO as a PTE, particularly its ionic conductivity and metal-anode compatibility. If the ionic conductivity of LLHfO is indeed lower than that of LLTO, it could still be useful for applications that do not require fast cycling, such as renewable energy grid storage. Alternatively, doping modifications could be explored to enhance its ionic conductivity while retaining LLHfO's stability advantages. For Na⁺, the small bottlenecks in the studied PTEs require compositional (e.g., defect and anion) engineering to accommodate Na⁺. Another approach is to explore PTE compositions with different oxidation states, such as halide perovskites. This study provides a pathway for PTE design and engineering, laying the groundwork for future development of high-performance metal all-solid-state batteries.

Data availability

The data that supports the findings of this study are available in the ESI† of this article.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

We gratefully acknowledge the support from the National Science Foundation, Award No. NSF CBET-2323065. The views expressed in this article do not necessarily represent the views of the National Science Foundation nor the U.S. Government. This work used the NSF Anvil CPU at Purdue University through allocation MAT240100 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by NSF grants 2138259, 2138286, 2138307, 2137603, and 2138296.

References

1. M. Dixit, N. Muralidharan, A. Parejiya, R. Amin, R. Essehli and I. Belharouak, Current Status and Prospects of Solid-State Batteries as the Future of Energy Storage, in Management and Applications of Energy Storage Devices, ed. K. E. Okedu, IntechOpen, 2022.  DOI:10.5772/intechopen.98701.
2. M. Fichtner, K. Edström, E. Ayerbe, M. Berecibar, A. Bhowmik, I. E. Castelli, S. Clark, R. Dominko, M. Erakca, A. A. Franco, A. Grimaud, B. Horstmann, A. Latz, H. Lorrmann, M. Meeus, R. Narayan, F. Pammer, J. Ruhland, H. Stein, T. Vegge and M. Weil, Rechargeable Batteries of the Future—The State of the Art from a BATTERY 2030+ Perspective, Adv. Energy Mater., 2022, 12(17), 2102904,  DOI:10.1002/aenm.202102904.
3. D. Bresser, K. Hosoi, D. Howell, H. Li, H. Zeisel, K. Amine and S. Passerini, Perspectives of Automotive Battery R&D in China, Germany, Japan, and the USA, J. Power Sources, 2018, 382, 176–178,  DOI:10.1016/j.jpowsour.2018.02.039.
4. J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Inorganic Solid-State Electrolytes for Lithium Batteries: Mechanisms and Properties Governing Ion Conduction, Chem. Rev., 2016, 116(1), 140–162,  DOI:10.1021/acs.chemrev.5b00563.
5. A. R. Rodger, J. Kuwano and A. R. West, Li⁺ Ion Conducting γ Solid Solutions in the Systems Li₄XO₄-Li₃YO₄: X = Si, Ge, Ti; Y = P, As, V; Li₄XO₄-LiZO₂: Z = Al, Ga, Cr and Li₄GeO₄-Li₂CaGeO₄, Solid State Ionics, 1985, 15(3), 185–198,  DOI:10.1016/0167-2738(85)90002-5.
6. H.-J. Deiseroth, S.-T. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiß and M. Schlosser, Li₆PS₅X: A Class of Crystalline Li-Rich Solids With an Unusually High Li⁺ Mobility, Angew. Chem., Int. Ed., 2008, 47(4), 755–758,  DOI:10.1002/anie.200703900.
7. V. Thangadurai, S. Narayanan and D. Pinzaru, Garnet-Type Solid-State Fast Li Ion Conductors for Li Batteries: Critical Review, Chem. Soc. Rev., 2014, 43(13), 4714–4727,  10.1039/C4CS00020J.
8. A. Martínez-Juárez, C. Pecharromán, J. E. Iglesias and J. M. Rojo, Relationship between Activation Energy and Bottleneck Size for Li⁺ Ion Conduction in NASICON Materials of Composition LiMM′(PO₄)₃; M, M′ = Ge, Ti, Sn, Hf, J. Phys. Chem. B, 1998, 102(2), 372–375,  DOI:10.1021/jp973296c.
9. H. Yamane, S. Kikkawa and M. Koizumi, Preparation of Lithium Silicon Nitrides and Their Lithium Ion Conductivity, Solid State Ionics, 1987, 25(2), 183–191,  DOI:10.1016/0167-2738(87)90119-6.
10. M. Matsuo and S. Orimo, Lithium Fast-Ionic Conduction in Complex Hydrides: Review and Prospects, Adv. Energy Mater., 2011, 1(2), 161–172,  DOI:10.1002/aenm.201000012.
11. H. D. Lutz, P. Kuske and K. Wussow, Ionic Motion of Tetrahedrally and Octahedrally Coordinated Lithium Ions in Ternary and Quaternary Halides, Solid State Ionics, 1988, 28–30, 1282–1286,  DOI:10.1016/0167-2738(88)90371-2.
12. R. Kanno, T. Hata, Y. Kawamoto and M. Irie, Synthesis of a New Lithium Ionic Conductor, Thio-LISICON–Lithium Germanium Sulfide System, Solid State Ionics, 2000, 130(1), 97–104,  DOI:10.1016/S0167-2738(00)00277-0.
13. Y. Inaguma, C. Liquan, M. Itoh, T. Nakamura, T. Uchida, H. Ikuta and M. Wakihara, High Ionic Conductivity in Lithium Lanthanum Titanate, Solid State Commun., 1993, 86(10), 689–693,  DOI:10.1016/0038-1098(93)90841-A.
14. A. K. Jena, A. Kulkarni and T. Miyasaka, Halide Perovskite Photovoltaics: Background, Status, and Future Prospects, Chem. Rev., 2019, 119(5), 3036–3103,  DOI:10.1021/acs.chemrev.8b00539.
15. L. Ortega-San-Martin, 1 - Introduction to Perovskites, in Perovskite Ceramics, ed. J. L. C. Huamán and V. A. G. Rivera, Elsevier Series in Advanced Ceramic Materials, Elsevier, 2023, pp. 3–29.  DOI:10.1016/B978-0-323-90586-2.00015-2.
16. N. J. Szymanski and C. J. Bartel, Computationally Guided Synthesis of Battery Materials, ACS Energy Lett., 2024, 9(6), 2902–2911,  DOI:10.1021/acsenergylett.4c00821.
17. J. Lu and Y. Li, Perovskite–type Li–ion Solid Electrolytes: A Review, J. Mater. Sci.: Mater. Electron., 2021, 32(8), 9736–9754,  DOI:10.1007/s10854-021-05699-8.
18. Y. Harada, T. Ishigaki, H. Kawai and J. Kuwano, Lithium Ion Conductivity of Polycrystalline Perovskite La_0.67−xLi_3xTiO₃ with Ordered and Disordered Arrangements of the A-Site Ions, Solid State Ionics, 1998, 108(1), 407–413,  DOI:10.1016/S0167-2738(98)00070-8.
19. A. R. West, Solid State Chemistry and Its Applications, Wiley, Chichester, West Sussex, UK, 2nd edn, Student edn, 2014.
20. Y. Sun, P. Guan, Y. Liu, H. Xu, S. Li and D. Chu, Recent Progress in Lithium Lanthanum Titanate Electrolyte towards All Solid-State Lithium Ion Secondary Battery, Crit. Rev. Solid State Mater. Sci., 2019, 44(4), 265–282,  DOI:10.1080/10408436.2018.1485551.
21. Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier, M. Armand and L. Chen, New Horizons for Inorganic Solid State Ion Conductors, Energy Environ. Sci., 2018, 11(8), 1945–1976,  10.1039/C8EE01053F.
22. C. S. Sunandana, Introduction to Solid State Ionics: Phenomenology and Applications, CRC Press, 2015.  DOI:10.1201/b19496.
23. V. M. Goldschmidt, Die Gesetze der Krystallochemie, Naturwissenschaften, 1926, 14(21), 477–485,  DOI:10.1007/BF01507527.
24. H. Yang, K. Tay, Y. Xu, B. Rajbanshi, S. Kasani, J. Bright, J. Boryczka, C. Wang, P. Bai and N. Wu, Nitrogen-Doped Lithium Lanthanum Titanate Nanofiber-Polymer Composite Electrolytes for All-Solid-State Lithium Batteries, J. Electrochem. Soc., 2021, 168(11), 110507,  DOI:10.1149/1945-7111/ac30ad.
25. R. D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., Sect. A, 1976, 32(5), 751–767,  DOI:10.1107/S0567739476001551.
26. Periodic Table - Ptable. https://ptable.com/?lang=en (accessed 2025-01-02).
27. Shannon Radii. https://abulafia.mt.ic.ac.uk/shannon/ptable.php (accessed 2025-02-27).
28. M. V. Kovalenko, L. Protesescu and M. I. Bodnarchuk, Properties and Potential Optoelectronic Applications of Lead Halide Perovskite Nanocrystals, Science, 2017, 358(6364), 745–750,  DOI:10.1126/science.aam7093.
29. X. Yang, J. Luo and X. Sun, Towards High-Performance Solid-State Li–S Batteries: From Fundamental Understanding to Engineering Design, Chem. Soc. Rev., 2020, 49(7), 2140–2195,  10.1039/C9CS00635D.
30. C. Li, K. C. K. Soh and P. Wu, Formability of ABO3 Perovskites, J. Alloys Compd., 2004, 372(1), 40–48,  DOI:10.1016/j.jallcom.2003.10.017.
31. D. H. Ji, S. L. Wang, X. Z. Ge, Q. Q. Zhang, C. M. Zhang, Z. W. Zeng and Y. Bai, The Maximum Predicted Content of Cation Vacancies in Inorganic and Organic–Inorganic Perovskites: The Role of the Tolerance Factor, Phys. Chem. Chem. Phys., 2017, 19(26), 17121–17127,  10.1039/C7CP01792H.
32. C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, New Tolerance Factor to Predict the Stability of Perovskite Oxides and Halides, Sci. Adv., 2019, 5(2), eaav0693,  DOI:10.1126/sciadv.aav0693.
33. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (Pymatgen): A Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314–319,  DOI:10.1016/j.commatsci.2012.10.028.
34. M. Ataya, E. McCalla and R. Z. Khaliullin, Machine Learning for High-Throughput Configuration Sampling of Li–La–Ti–O Disordered Solid-State Electrolyte, J. Phys. Chem. C, 2024, 128(34), 14149–14157,  DOI:10.1021/acs.jpcc.4c01221.
35. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation, APL Mater., 2013, 1(1), 011002,  DOI:10.1063/1.4812323.
36. W. Sun, S. T. Dacek, S. P. Ong, G. Hautier, A. Jain, W. D. Richards, A. C. Gamst, K. A. Persson and G. Ceder, The Thermodynamic Scale of Inorganic Crystalline Metastability, Sci. Adv., 2016, 2(11), e1600225,  DOI:10.1126/sciadv.1600225.
37. J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid Functionals Based on a Screened Coulomb Potential, J. Chem. Phys., 2003, 118, 8207–8215,  DOI:10.1063/1.1564060.
38. A. Van Der Ven, G. Ceder, M. Asta and P. D. Tepesch, First-Principles Theory of Ionic Diffusion with Nondilute Carriers, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64(18), 184307,  DOI:10.1103/PhysRevB.64.184307.
39. Z. Jadidi, T. Chen, P. Xiao, A. Urban and G. Ceder, Effect of Fluorination and Li-Excess on the Li Migration Barrier in Mn-Based Cathode Materials, J. Mater. Chem. A, 2020, 8(38), 19965–19974,  10.1039/D0TA06415G.
40. G. Henkelman, Methods for Calculating Rates of Transitions with Application to Catalysis and Crystal Growth, 2001.
41. V. Wang, N. Xu, J. C. Liu, G. Tang and W. T. Geng, VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code, Comput. Phys. Commun., 2021, 267, 108033,  DOI:10.1016/J.CPC.2021.108033.
42. H. Chen and T. Hong, First-Principles Investigation of the Mechanical and Thermodynamic Properties of the Metal-Borohydrides as Electrolytes for Solid-State Batteries, J. Electrochem. Soc., 2019, 166(4), A493–A500,  DOI:10.1149/2.0071904JES/XML.
43. C. Li and Z. Wang, Computational Modelling and Ab Initio Calculations in MAX Phases – I, in Advances in Science and Technology of Mn⁺¹AX_n Phases, Elsevier, 2012, pp. 197–222.  DOI:10.1533/9780857096012.197.
44. T. Tohei, A. Kuwabara, F. Oba and I. Tanaka, Debye Temperature and Stiffness of Carbon and Boron Nitride Polymorphs from First Principles Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(6), 064304,  DOI:10.1103/PhysRevB.73.064304.
45. M. Wu, B. Xu, X. Lei, K. Huang and C. Ouyang, Bulk Properties and Transport Mechanisms of a Solid State Antiperovskite Li-Ion Conductor Li₃OCl: Insights from First Principles Calculations, J. Mater. Chem. A, 2018, 6(3), 1150–1160,  10.1039/c7ta08780b.
46. S. Sradhasagar, S. Pati and A. Roy, Computational Design of an Affordable, Lightweight Solid Electrolyte for All-Solid-State Lithium-Ion Batteries, J. Phys. Chem. C, 2024, 37, 15242–15254,  DOI:10.1021/acs.jpcc.4c03260.
47. J. E. Antonio, J. L. Rosas-Huerta, J. M. Cervantes, J. León-Flores, M. Romero, E. Carvajal and R. Escamilla, Li/Na Atoms’ Substitution Effects on the Structural, Electronic, and Mechanical Properties of the CaSnO₃ Perovskite for Battery Applications, Comput. Mater. Sci., 2023, 219, 112006,  DOI:10.1016/j.commatsci.2022.112006.
48. C. Monroe and J. Newman, The Impact of Elastic Deformation on Deposition Kinetics at Lithium/Polymer Interfaces, J. Electrochem. Soc., 2005, 152(2), A396,  DOI:10.1149/1.1850854.
49. M. Jiang, Z. W. Chen, A. Rao, L. X. Chen, P. Adeli, P. Mercier, Y. Abu-Lebdeh and C. V. Singh, Effects of Neutral Point Defects on the Solid-State Electrolyte Li₃ScBr₆, J. Mater. Chem. C, 2024, 12(13), 4885–4896,  10.1039/d3tc03266c.
50. Z. Wan, X. Chen, Z. Zhou, X. Zhong, X. Luo and D. Xu, Atom Substitution of the Solid-State Electrolyte Li₁₀GeP₂S₁₂ for Stabilized All-Solid-State Lithium Metal Batteries, J. Energy Chem., 2024, 88, 28–38,  DOI:10.1016/j.jechem.2023.09.001.
51. K. S. Nagy and D. J. Siegel, Anisotropic Elastic Properties of Battery Anodes, J. Electrochem. Soc., 2020, 167(11), 110550,  DOI:10.1149/1945-7111/aba54c.
52. R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, LOBSTER: Local Orbital Projections, Atomic Charges, and Chemical-Bonding Analysis from Projector-Augmented-Wave-Based Density-Functional Theory, J. Comput. Chem., 2020, 41(21), 1931–1940,  DOI:10.1002/jcc.26353.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5eb00089k

---