 Open Access Article
Open Access ArticleCurrent distribution simulation of parallel-connected modules using degraded lithium-ion battery cells
Jusuke Shimura *ab,
Kanta Onoderab,
Hikari Watanabe
*ab,
Kanta Onoderab,
Hikari Watanabe b,
Isao Shitanda
b,
Isao Shitanda b and
Masayuki Itagakib
b and
Masayuki Itagakib
aMurata Manufacturing Co., Ltd, 1-10-1 Higashikotari, Nagaokakyo-shi, Kyoto 617-8555, Japan. E-mail: jusuke.shimura@murata.com
bDepartment of Pure and Applied Chemistry, Faculty of Science and Technology, Tokyo University of Science, 2641 Yamazaki, Noda-shi, Chiba 278-8510, Japan
First published on 3rd June 2025
Abstract
This study introduces a method for determining current distribution during the charging of modules composed of parallel-connected lithium-ion battery cells exhibiting varying levels of degradation. The proposed method was validated by examining current distribution in two- and three-cell parallel modules containing both new and degraded cells, demonstrating that the calculated charging currents were highly consistent with experimental measurements, with discrepancies between 1.1% and 2.2%. Furthermore, an overdistribution phenomenon was observed, where degraded cells received excessive current toward the end of the charging process. Investigation attributed this phenomenon to a rapid alteration in the internal resistance balance during charging. The proposed methodology is extendable to configurations with more than three cells through recursive calculations, highlighting its applicability in designing large-scale energy storage systems and strategies for repurposing used batteries.
Broader contextThe global shift toward renewable energy and a low-carbon future depends on effective and safe energy storage solutions. Lithium-ion batteries are essential for powering electric vehicles and large-scale energy storage systems, yet their performance degrades over time, creating challenges in safely reusing aging battery modules. Our research focuses on understanding and predicting how charging current divides among battery cells with different levels of degradation—a critical issue because uneven charging can lead to premature cell failure, safety hazards, and compromised system reliability. By developing a novel simulation method that accurately reflects real-world charging behavior, our work advances the ability to repurpose used batteries, reducing waste and mitigating the environmental impact of battery production. This approach not only supports the transition to sustainable energy systems but also provides valuable insights for policy makers, industry leaders, and researchers looking for safer, more efficient energy storage designs. Ultimately, our findings contribute to a more resilient and sustainable energy infrastructure, addressing pressing global issues such as energy security, resource conservation, and climate change. |
1. Introduction
In recent years, the use of lithium-ion batteries has broadened to encompass large-scale applications such as electric vehicles and energy storage systems (ESSs).1–5 Given that lithium-ion batteries rely on scarce metals like cobalt, the reutilization of battery modules has gained attention for optimizing resource use.6–10 Reusing battery modules in different applications than their original purpose is termed “repurposing”, while utilizing them within the same application category is known as “reusing”.11,12 For instance, when constructing an ESS using low-capacity battery modules through repurposing, multiple battery modules need to be combined with varying degrees of degradation. Each battery module experiences distinct types and degrees of degradation influenced by its usage history. Consequently, directly connecting these modules in parallel without proper management leads to complex current distribution dynamics.4,5,7,9–11 This can result in certain degraded modules experiencing unforeseen rapid charging. Such rapid charging accelerates the early degradation of lithium-ion batteries and heightens the risk of thermal runaway and fires in degraded battery modules.4,9,13,14 To mitigate these issues and ensure the safety and durability of repurposed battery modules, it is essential to comprehensively understand these complex current distribution phenomena and develop appropriate methods for combining modules.Previous studies on parallel-connected battery groups under unmanaged conditions have documented instantaneous current distribution behaviors.15–20 For instance, Zabara et al. developed a highly accurate method to predict current distributions and voltage responses in hybrid battery/supercapacitor systems by utilizing differential evolution optimization algorithms based on electrochemical impedance spectroscopy (EIS) data.16 However, their approach is limited in simulation accuracy for extrapolated EIS measurement regions, particularly in extremely high- or low-frequency domains.
In this study, we have developed a simulation method that employs reference data obtained from direct-current charging at zero frequency to calculate long-term current distribution behavior across the full range from fully discharged to fully charged states. Additionally, we explore methods for simulating distributions involving three or more cells.
2. Theory
Instead of directly addressing the issue of the current distribution in an ESS composed of multiple battery modules, we employed a downscaling approach in which the fundamental aspects of the problem remain unchanged.2.1 Current distribution ratio
In this study, we introduced the current distribution ratio ij as a metric representing the proportion of the total current allocated to each cell j in a parallel-connected module comprising n cells.
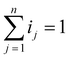 | (1) |
For example, consider two cells (n = 2) connected in parallel, as illustrated in Fig. 1. In this configuration, the total current I flowing through the module can be expressed using current distribution ratios i1 and i2:
| i1I + i2I = I | (2) |
 | ||
| Fig. 1 Current distribution in a two-parallel-module configuration. i1 and i2 represent the current distribution ratios, expressed as proportions. | ||
Furthermore, let us denote the open-circuit voltage (OCV) of each cell as VOC,j, its internal resistance as Rj, and overvoltage as ηj. As all the cells in a parallel connection share an equal cell voltage V, they satisfy the following relationship:
| VOC,1 + η1 = VOC,2 + η2 = V | (3) |
The overvoltage of each cell can thus be expressed as ηj = RjijI. Substituting this expression into the above equation and solving the resulting simultaneous equations yields explicit expressions for the current distribution ratios i1, i2 of each cell.
 | (4) |
The first term on the right-hand side of these equations represents the contribution of the OCV differences between the cells, whereas the second term accounts for the balance of their internal resistances.
2.2 Simulation of constant current charging in a two-cell parallel module
We outline the procedure for calculating the evolution of current distribution ratios i1(t) and i2(t) over time during constant-current (CC) charging of a parallel module consisting of two cells. The calculated current distribution ratios are discrete values obtained at specific time steps t = 0, Δt, 2Δt,⋯.Before starting the calculations, two types of experimental reference data were prepared for each cell. The first dataset comprises the OCV VOC,j as a function of charge capacity Qj, commonly referred to as the charging curve. The second dataset includes internal resistance Rj as a function of the charge capacity Qj. Importantly, these internal resistance measurements account for all resistance components during charging, including concentration polarization with exceptionally large time constants, thereby reflecting real-world charging conditions. Internal resistance was determined by subtracting VOC,j from the cell voltage Vj measured during CC charging and then dividing the result by the applied current. Although both datasets consisted of discrete experimental points, continuous functions were necessary for subsequent analyses, necessitating appropriate interpolation of these discrete data.
The time evolution of the current distribution ratios was calculated using the following process: Initially, at t = 0, both cells were assumed to be fully discharged with initial charge capacities Q1(t) = Q2(t) = 0. Subsequently, based on their respective charge capacities, Qj(t), OCV VOC,j and internal resistances Rj were retrieved from the corresponding reference datasets (*). Utilizing the parameters defined in eqn (4), the current distribution ratios i1(t) and i2(t) were then calculated to determine the proportion of the charging current flowing into each cell. Assuming these currents remain constant over an interval Δt, the incremental increases in charge capacities ΔQ1(t) and ΔQ2(t) can be expressed as follows:
 | (5) |
By adding these increments to their respective existing charge capacities at each step, we obtain updated charge capacities Q1(t + Δt) and Q2(t + Δt) at time step t + Δt. From this point onward, starting again at step (*), the process is iteratively repeated to obtain simulation results over consecutive time intervals.
Although cells 1 and 2 are connected in parallel, it should be noted that in most cases both their charge capacities and their states of charge (SoCs) do not remain identical during charging. Unless the reference data for both cells are completely identical, discrepancies in OCV differences or internal resistance ratios prevent equal current distribution. As charging progresses, these differences accumulate over time, leading to conditions where Q1(t) ≠ Q2(t) for most cases when t > 0. Moreover, no constraint exists to enforce the alignment of the SoCs which are defined as the ratio of the current charge capacity to the full charge capacity.
2.3 Current distribution in modules with three or more cells
For modules with three or more parallel-connected cells, calculations can be performed by recursively grouping two cells into a single equivalent cell. For example, consider a module with three parallel-connected cells: cells 1, 2, and 3. First, cells 1 and 2 are conceptually grouped into a two-cell parallel module, and the current distribution is calculated under CC charging conditions. This calculation enables the derivation of composite reference data for this virtual two-cell module, specifically the composite OCV VOC,1+2 and the composite internal resistance R1+2. These values are defined as follows:
 | (6) |
The composite charge capacity Q1+2(t) is the sum of the charge capacities of cells 1 and 2. The composite internal resistance R1+2(t) is calculated as the equivalent resistance of the two parallel resistors, based on the internal resistances of cells 1 and 2 at their respective charge capacities. Finally, the composite OCV VOC,1+2(t) was obtained by subtracting the overvoltage of the virtual two-cell module from the average cell voltage derived from the OCVs and the overvoltage of both cells. The reference data for this virtual two-cell module Q1+2(t), R1+2(t), VOC,1+2(t) consist of discrete values recorded at a specific time interval Δt. Similar to individual cell reference data, appropriate interpolation is necessary to ensure continuity for subsequent calculations. Fig. 2 provides a flowchart of the overall simulation procedure for clarity. An example figure to clarify how cells are grouped and current values are calculated is shown in Fig. 3.
3. Experimental
3.1 Battery cells
In this study, three cylindrical lithium-ion battery cells (US18650FTC1, Murata Manufacturing Co., Ltd) were employed. These cells utilized LiFePO4 (LFP) as the positive electrode active material, graphite as the negative electrode active material, and had a rated capacity of 1.05 Ah. Among the three cells, two were stored in isothermal chambers at 80 °C and 90 °C for 25 days. The unused cell is designated as “cell N”, while the cells stored at 80 °C and 90 °C are referred to as “cell D1” and “cell D2”, respectively.3.2 Charging tests for parallel-connected modules
Charging experiments were conducted using a parallel two-cell module comprising cell N and cell D2. Each cell was individually connected to a potentio/galvanostat (Bio-Logic, SP-240), placed in an isothermal chamber maintained at 23 °C, and discharged at a constant current of 0.2C-rate (210 mA). Discharging was terminated when the voltage reached 2.0 V, herein referred to as the fully discharged state.After both cells N and D2 were individually drained to their fully discharged states, they were connected in parallel to form a two-cell parallel module. To measure the charging current for each cell within the module, two clamp-type current probes (Yokogawa Electric Corp., Model 701917) were attached to each cell's negative-terminal wiring, and data were recorded using a Yokogawa DL950 ScopeCorder® data logger. The two-cell parallel module was then placed in an isothermal chamber maintained at 23 °C and charged at a constant 1C-rate (2.1 A) using a potentio/galvanostat.
Subsequently, charging experiments were performed on all three cell types (cell N, cell D1, and cell D2) by assembling a three-cell parallel module. Prior to connection, each cell was individually fully discharged. Three clamp-type current probes were installed to separately measure the charging current entering each cell. This three-cell parallel module was then placed in an isothermal chamber at 23 °C and charged at a constant 1C-rate (3.15 A) (Fig. 4).
3.3 Preparation of reference data
For cell N, cell D1, and cell D2, two sets of reference data were prepared as outlined in the previous section: the OCV VOC,j as a function of charge capacity Qj and the internal resistance Rj as a function of charge capacity.To obtain the OCV, each cell was first fully discharged and then subjected to CC charging at a 0.02C-rate (21 mA). During the CC charging process, the cell voltage was measured and recorded as VOC,j. To determine the internal resistance Rj, the overvoltage at various charge capacities was initially calculated by subtracting the corresponding VOC,j from the measured cell voltage during CC charging at a 1C-rate (1.05 A). The internal resistance was then derived by dividing this overvoltage by the current at the 0.98C-rate (1.029 A).
Both reference datasets comprise discrete values obtained experimentally for specific charge capacities. However, because continuous functions were necessary for the simulations, these discrete datasets were transformed into continuous functions by applying a non-rational, uniform, cubic B-spline implemented via a custom Excel VBA function.
3.4 Current distribution calculation for parallel-connected modules
Utilizing the reference data for cells N, D1, and D2, current distribution simulations during CC charging were conducted following the procedure outlined in the previous section. The simulations were performed for two configurations: a two-cell parallel module consisting of cells N and D2, and a three-cell parallel module consisting of cells N, D1, and D2.A time step Δt of 15 s was employed in all simulations. During the simulations, both factors contributing to the current imbalance—the ODD (OCV difference dependent) term and the RBD (resistance balance dependent) term from eqn (4)—were calculated separately to evaluate their respective impacts on current distribution. All simulations were performed using Microsoft Excel for Office 365 (MSO). The B-spline approximation was implemented with a custom VBA function. Correct operation was confirmed by visually comparing interpolated curves against raw data.
4. Results and discussion
4.1 Reference data
Fig. 5 presents the reference data for cells N, D1, and D2. Based on the OCV measurements conducted at a 0.02C-rate, the charge capacities were determined to be 1110, 1010, and 990 mA h for cells N, D1, and D2, respectively. Based on the measured values, the capacity loss for D1 and D2 were determined to be 10% and 12%, respectively.Regarding the shapes of the charging curves, cells N, D1, and D2 exhibited nearly identical profiles except near full charge. The lithium-ion batteries in this study utilized LixFePO4 as the cathode material. When x is between 0.032 and 0.962, LiFePO4 and FePO4 coexist as two distinct phases, resulting in a nearly constant open-circuit potential.21 Therefore, the non-uniform behavior observed in the OCV in Fig. 5 is attributed primarily to variations in anode potential. Since this behavior remained largely consistent, high-temperature storage did not significantly affect anode capacity. The overall capacity loss may result from cathode degradation or other mechanisms such as loss of lithium inventory and electrode slippage; definitive attribution would require further half-cell or materials analyses.
Subsequently, internal resistance was examined and found to increase in the following order: cell N, cell D1, and cell D2. Regarding the timing of internal resistance fluctuations during charging, all three cells displayed nearly identical patterns in the first half of charging, reaching a minimum at ∼130 mA h and a maximum at ∼230 mA h. Although the timing of the variations in the first half was almost identical across the cells, differences in behavior became apparent in the latter half. In all cases, internal resistance sharply increased just before full charging; however, the timing of this surge differed—with cell D2 exhibiting the increase first, followed by cell D1, and then cell N.
Considering that the anode capacity hardly declined, and that capacity loss is mainly caused by cathode degradation, the uniform behavior in the first half is primarily attributed to the anode, whereas the variations in the latter half are attributed to the cathode. In addition, the sudden surge in internal resistance in the latter half is interpreted as resulting from lithium extraction from the LFP cathode.
4.2 Current distribution
Fig. 6(a) displays the experimentally observed current distribution for cells N and D2 connected in parallel, while Fig. 6(b) shows the calculated current distribution based on the reference data for these cells. Fig. 6(c) illustrates the ODD and RBD term values for cell N derived from the calculations. We emphasize that the simulation relies exclusively on measured OCV and internal resistance curves (ODD and RBD term values) and does not attempt to model internal physical phenomena such as temperature gradients or spatially varying reaction rates.Initially, the root-mean-square error (RMSE) between the measured currents in Fig. 6(a) and the calculated currents in Fig. 6(b) was calculated. The RMSE for the charging currents of cell N and cell D2 were 13.3 mA and 13.4 mA, respectively, which correspond to errors of 1.2% and 1.4% relative to the average measured current. These low RMSE values indicate that the calculated results closely match the experimental measurements.
Thereafter, the experimental data presented in Fig. 6(a) are analyzed. Despite charging the two-cell module at a constant current of 2.1 A, the current was unevenly distributed between cells N and D2, and the distribution ratio varied throughout the charging process. In detail, with respect to the charging current for cell N, the minimum and maximum values were observed at 5.5 min (point A) and 9.5 min (point B), and another set of minimum and maximum values at 19.5 min (point C) and 31.5 min (point D). Furthermore, up to 54 minutes (point E), a larger current flowed into cell N compared to cell D2. However, at point E, this pattern reversed, resulting in a greater current being delivered to cell D2 thereafter.
The calculated current variations closely matched the experimental results, except during the initial approximately 1.5 minutes period (Fig. 6(b)). Specifically, the extrema corresponding to points A, B, C, and D—represented as A′, B′, C′, and D′ in the simulations—were observed, and the current-reversal phenomenon at point E (corresponding to E′ in the simulation) was also reproduced. The discrepancy during the initial 1.5 minutes is attributed to the voltage difference between fully discharged cell N and cell D2; due to differences in internal resistance, the voltage of fully discharged cell D2 is higher than that of cell N. In the experiments using the real cells, when the cells are connected in parallel, a balancing current flows to adjust the voltage, but such an adjustment is not incorporated in the simulation. As a result, an instantaneous large current is estimated to have flowed into the lower-voltage cell N at the beginning of the simulation.
Fig. 6(c) portrays that the ODD term remains negative throughout the charging process, indicating that the OCV of cell N is consistently higher than that of cell D2. Since the OCV increases monotonically during charging, this suggests that the SoC of cell N was always higher than that of cell D2, meaning that cell N was being charged ahead of cell D2. Additionally, the RBD term stays above 0.5, indicating that the internal resistance of cell N remains consistently lower than that of cell D2. Although the internal resistance varied considerably near full charge (Fig. 5), the internal resistance of cell D2 remained higher than that of cell N.
Subsequently, the origins of the extrema were examined to determine whether they arose from differences in OCV or internal resistance. In the simulation near point A, the RBD term exhibits an upward convex profile, whereas the ODD term shows a downward convex profile. This indicates that the minimum charging current at point A is predominantly attributable to the OCV difference. Similarly, around point B, the RBD term displays a downward convex profile, and the ODD term presents an upward convex profile, suggesting that the maximum charging current at point B is also primarily due to the OCV difference. At point C, the simulation demonstrates that the charging current for cell N decreases monotonically from point B to point C, reaches a minimum at point C, and then increases monotonically up to point D. Furthermore, the simulation reveals that the overall variation from point B to point D is largely driven by the ODD term, with only the region near point C significantly influenced by the RBD term. Therefore, although the resistance balance partially affects the minimum at point C, the dominant factor across the range from points B–D is the OCV difference. Similarly, the maximum charging current for cell N observed at point D is primarily ascribed to the OCV difference between cell N and cell D2 at that time.
Because extrema at points A, B, C, and D were observed during the first half of the charging process, they were considered attributable to the anode. Graphite, utilized as the anode material, undergoes alterations in its staging structure during charging, leading to intricate variations in both the solid-state diffusion coefficient of lithium within the graphite particles and the anode potential.22,23 In this experiment, the charging of cell N consistently preceded that of cell D2, and the staging transitions occurred at different times. Consequently, if discrepancies in the solid-state diffusion coefficient emerged from these timing mismatches, they manifested as peaks associated with the RBD term, while potential discrepancies appeared as peaks related to the ODD term.
4.3 Overdistribution phenomenon in degraded cell D2
As illustrated in Fig. 6(a), when the module comprising cells N and D2 was connected in parallel and subjected to CC charging, an overdistribution phenomenon was observed near the end of charging (after point E), where the current flowing into cell D2 exceeded that flowing into cell N. This section examines this phenomenon in detail.The primary cause was the rapid changes in the internal resistance balance. Notably, Fig. 5 shows that each cell's internal resistance rises sharply near full charge during single-cell charging; we infer that the rapid resistance increase of cell N in the parallel module has the same origin. As depicted in Fig. 6(c), the RBD term experienced a sharp decline near point E′. Consequently, the excessive current overdistribution to cell D2 observed at the end of charging in actual cells was largely influenced by this shift in the internal resistance balance. However, as the RBD value consistently remained above 0.5 and the internal resistance of cell D2 did not fall below that of cell N, the variations in the internal resistance alone cannot completely account for this phenomenon.
Furthermore, the ODD term remains consistently negative, signifying that the SoC of cell N persistently surpasses that of cell D2, which is critical. Under these circumstances, an OCV difference develops between the two cells, resulting in a tendency to allocate more current to cell D2. Moreover, as charging nears its end, the internal resistance of cell N—which, owing to its higher SoC, reaches full charge sooner—surges sharply before that of cell D2, abruptly upsetting the resistance balance and causing an overdistribution phenomenon in which cell D2 receives more current than cell N.
In summary, the overdistribution to cell D2 is considered to occur when two conditions are met: first, during charging, cell N's SoC remains higher than that of cell D2 (ODD < 0), and second, under these conditions, cell N reaches the charging endpoint earlier with a rapid increase in internal resistance.
4.4 Current distribution in a three-cell module
Fig. 7(a) displays the measured current distribution from cells N, D1, and D2 connected in parallel, whereas Fig. 7(b) shows the calculated current distribution based on reference data. The RMSE for the charging currents of cells N, D1, and D2 were 24.8 mA, 16.8 mA, and 11.0 mA, corresponding to error rates of 2.2%, 1.6%, and 1.1% relative to their respective average measured charging currents. These results confirm that the simulation achieved highly accurate predictions even in a three-cell configuration. Furthermore, a concentration of charging current in cells D1 and D2 near the end of charging was observed experimentally and successfully replicated by the simulation.Additionally, qualitative features, such as the number of extrema in the current profiles, were consistent between the experimental and simulation results. The success of accurately simulating the current distribution behavior in this three-cell module validates the effectiveness of the recursive approach described in Section 2 for combining two or more cells into equivalent composite units for modeling purposes. By iteratively applying this recursive method, modules containing four or more cells can be simulated with comparable accuracy. Error accumulation arising from measurement equipment specifications and environmental conditions has not been considered in this recursive grouping approach and is beyond the scope of this study.
5. Conclusion
In this study, we developed a precise method for simulating the charging current distribution in modules composed of multiple parallel-connected lithium-ion battery cells with varying levels of degradation and validated its accuracy by comparing the calculated values with experimental measurements. The charging currents calculated using the proposed method closely matched the measured values, thereby demonstrating its effectiveness in predicting the performance of parallel-connected lithium-ion battery modules. Furthermore, this method can be recursively applied to configurations with three or more cells arranged in complex patterns, highlighting its potential for large-scale system deployment. We introduced a current distribution ratio, comprising ODD and RBD terms, as indices to analyze the factors contributing to non-uniform current distribution. Analysis using these parameters revealed that the overdistribution phenomenon observed at the end of charging—where excessive current is delivered to degraded cells—resulted from a combination of two factors: differences in OCV and changes in internal resistance. Specifically, it became clear that a rapid shift in the internal resistance balance during charging acted as a direct trigger for the overdistribution of current to the degraded cells. Such overdistribution phenomena in degraded batteries are considered to be critical issues with respect to safety and long-term operational durability.The present findings will significantly contribute to the design of ESS by repurposing used batteries. When assembling an ESS by integrating various lithium-ion battery modules with differing levels of degradation, the proposed method can predict whether excessive current will be directed to the degraded modules without the necessity of physically connecting them in parallel and measuring the charging current. For example, once the reference data for the selected battery modules are measured and stored in a database, the optimal combination of used batteries can be calculated on a server, thereby facilitating the efficient assembly of the ESS. Details of database standardization and real-time simulation performance are left for future implementation work. These results will potentially aid in establishing a scientific foundation for advancing the reuse of used batteries and the development of a safe and sustainable energy society.
Author contributions
Jusuke Shimura: conceptualization, funding acquisition, methodology, resources, software, writing – original draft. Kanta Onodera: data curation, formal analysis, investigation, validation, visualization. Hikari Watanabe: writing – review & editing. Isao Shitanda: project administration. Masayuki Itagaki: supervision.Data availability
The raw data of this study is not publicly available without the consent of Murata Manufacturing Co., Ltd. Licensing details can be obtained from the corresponding author, J.S., upon request.Conflicts of interest
There are no conflicts to declare.References
- X. Chang, Y.-M. Zhao, B. Yuan, M. Fan, Q. Meng, Y.-G. Guo and L.-J. Wan, Solid-state lithium-ion batteries for grid energy storage: opportunities and challenges, Sci. China: Chem., 2024, 67, 43–46 CrossRef CAS.
- B. Dunn, H. Kamath and J.-M. Tarascon, Electrical energy storage for the grid: a battery of choices, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- D. Larcher and J.-M. Tarascon, Towards greener and more sustainable batteries for electrical energy storage, Nat. Chem., 2015, 7, 19–29 CrossRef CAS.
- A. Gharehghani, M. Rabiei, S. Mehranfar, S. Saeedipour, A. M. Andwari, A. García and C. M. Reche, Progress in battery thermal management systems technologies for electric vehicles, Renewable Sustainable Energy Rev., 2024, 202, 114654 CrossRef.
- M. Jiang, D. Li, Z. Li, Z. Chen, Q. Yan, F. Lin, C. Yu, B. Jiang, X. Wei, W. Yan and Y. Yang, Advances in battery state estimation of battery management system in electric vehicles, J. Power Sources, 2024, 612, 234781 CrossRef CAS.
- T. K. Sankar, Abhilash and P. Meshram, Environmental impact assessment in the entire life cycle of lithium-ion batteries, Rev. Environ. Contam. Toxicol., 2024, 262, 5 CrossRef CAS.
- X. Qiu, C. Wang, Y. Chen, Z. Du, L. Xie, Q. Han, L. Zhu, X. Cao and X. Ji, Potential-regulated design for direct recycling of degraded LiFePO4 Cathode, Small, 2024, 20, 2402278 CrossRef CAS.
- X. Zhang, L. Li, E. Fan, Q. Xue, Y. Bian, F. Wu and R. Chen, Toward sustainable and systematic recycling of spent rechargeable batteries, Chem. Soc. Rev., 2018, 47, 7239–7302 RSC.
- Y. Miao, P. Hynan, A. von Jouanne and A. Yokochi, Current Li-ion battery technologies in electric vehicles and opportunities for advancements, Energies, 2018, 12, 6 CrossRef.
- Y. Hua, S. Zhou, Y. Huang, X. Liu, H. Ling, X. Zhou, C. Zhang and S. Yang, Sustainable value chain of retired lithium-ion batteries for electric vehicles, J. Power Sources, 2020, 478, 228753 CrossRef CAS.
- M. Philippot, D. Costa, M. S. Hosen, A. Senécat, E. Brouwers, E. Nanini-Maury, J. Van Mierlo and M. Messagie, Environmental impact of the second life of an automotive battery: reuse and repurpose based on ageing tests, J. Cleaner Prod., 2022, 366, 132872 CrossRef.
- C. White, B. Thompson and L. G. Swan, Repurposed electric vehicle battery performance in second-life electricity grid frequency regulation service, J. Energy Storage, 2020, 28, 101278 CrossRef.
- Y. Liu, Y. Zhu and Y. Cui, Challenges and opportunities towards fast-charging battery materials, Nat. Energy, 2019, 4, 540–550 CrossRef.
- A. Tomaszewska, Z. Chu, X. Feng, S. O'Kane, X. Liu, J. Chen, C. Ji, E. Endler, R. Li, L. Liu, Y. Li, S. Zheng, S. Vetterlein, M. Gao, J. Du, M. Parkes, M. Ouyang, M. Marinescu, G. Offer and B. Wu, Lithium-ion battery fast charging: A review, etransportation, 2019, 1, 100011 CrossRef.
- T. Bruen and J. Marco, Modelling and experimental evaluation of parallel connected lithium ion cells for an electric vehicle battery system, J. Power Sources, 2016, 310, 91–101 CrossRef CAS.
- M. A. Zabara, C. B. Uzundal and B. Ülgüt, Performance modeling of unmanaged hybrid battery/supercapacitor energy storage systems, J. Energy Storage, 2021, 43, 103185 CrossRef.
- M. P. Klein and J. W. Park, Current distribution measurements in parallel-connected lithium-ion cylindrical cells under non-uniform temperature conditions, J. Electrochem. Soc., 2017, 164, A1893 CrossRef CAS.
- Q. Qin, X. Li, Z. Wang, J. Wang, G. Yan, W. Peng and H. Guo, Experimental and simulation study of direct current resistance decomposition in large size cylindrical lithium-ion battery, Electrochim. Acta, 2023, 465, 142947 CrossRef CAS.
- X. Liu, W. Ai, M. N. Marlow, Y. Patel and B. Wu, The effect of cell-to-cell variations and thermal gradients on the performance and degradation of lithium-ion battery packs, Appl. Energy, 2019, 248, 489–499 CrossRef.
- M. J. Brand, M. H. Hofmann, M. Steinhardt, S. F. Schuster and A. Jossen, Current distribution within parallel-connected battery cells, J. Power Sources, 2016, 334, 202–212 CrossRef CAS.
- A. Yamada, H. Koizumi, N. Sonoyama and R. Kanno, Phase change in LixFePO4, Electrochem. Solid-State Lett., 2005, 8, A409–A413 CrossRef CAS.
- T. Zheng, J. N. Reimers and J. R. Dahn, Effect of turbostratic disorder in graphitic carbon hosts on the intercalation of lithium, Phys. Rev. B:Condens. Matter Mater. Phys., 1995, 51, 734 CrossRef CAS.
- Z. Ogumi and M. Inaba, Electrochemical lithium intercalation within carbonaceous materials: intercalation processes, surface film formation, and lithium diffusion, Bull. Chem. Soc. Jpn., 1998, 71, 521–534 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |







