Recent advances in using severe plastic deformation for the processing of nanomaterials

Abstract

The grain size is an important structural parameter in polycrystalline materials contributing to the strength of the material and the ability to achieve a superplastic forming capability. Grain refinement is especially important because small grains lead to stronger materials and they provide more opportunities for attaining superplastic flow. Traditionally, the grain size was modified through the use of various thermo-mechanical treatments but this had a significant limitation because it was not possible to produce materials with grain sizes smaller than a few micrometers. The situation has changed over the last forty years with the demonstration that much smaller grain sizes may be produced by processing through the application of severe plastic deformation (SPD) where a high strain is imposed without causing any significant change in the overall dimensions of the sample. This report summarizes the principles of the main SPD processing techniques and then demonstrates the significance of producing submicrometer grain sizes.

---

Terence G. Langdon

Terence G. Langdon graduated from the University of Bristol in 1961 and obtained a Ph.D. from Imperial College in 1965. He was at the University of Southern California from 1971 to 2012 and then at the University of Southampton until 2025. His awards include the Blaise Pascal Medal from the European Academy of Sciences, the Lee Hsun Award from the Chinese Academy of Sciences, the Honorary Medal “De Scientia et Humanitate Optime Meritis” from the Academy of Sciences of the Czech Republic and the Acta Materialia Gold Medal. On Google Scholar he has 106 000 citations and an h-index of 157.

---

1. Introduction

When a polycrystalline solid is subjected to an external stress, the nature of the flow behaviour is dependent upon the microstructural characteristics of the material. This is equally true for metals, ceramics, minerals and geological materials and in practice the most important microstructural feature is the grain size, d. Thus, the measured flow stress, σ, will follow the conventional and well-established Hall–Petch relationship^1,2 which is given by

σ = σ₀ + Kd^−1/2 (1)

where σ₀ is the threshold stress and K is a constant of yielding. It follows directly from eqn (1) that a reduction in grain size will lead to a higher flow stress and therefore to a stronger material. This prediction is consistent with a very wide range of experimental results and comprehensive analyses published over a period of many years.^3–10

In practice, eqn (1) is especially important for examining the properties of materials at low temperatures, typically below ∼0.4 T_m where T_m is the absolute melting temperature of the material, whereas at high temperatures it is necessary to examine the flow properties under creep conditions where the crystalline solid is subjected to an applied stress which is lower than the fracture stress but sufficiently high to produce a nonrecoverable plastic strain which gradually builds up with time. This flow at high temperatures is generally examined by applying a constant stress to the sample and then recording the strain as a function of time. Experiments of this type date back for just over 100 years¹¹ and typically they lead to a creep curve of strain, ε, against time, t, as shown in Fig. 1.¹² Thus, there is an initial instantaneous strain, ε₀, a primary stage (region I) where the creep rate decreases with increasing time, a region of secondary or steady-state creep (region II) where the creep rate remains essentially constant and finally a tertiary stage (region III) where the creep rate increases rapidly to final fracture. In both laboratory experiments and practical situations, much of the flow occurs in the steady-state region so that a major emphasis is generally placed on measuring the creep rate in region II. In creep experiments the steady-state creep rate, , is usually plotted logarithmically against the stress, σ, and the slope of the plot then gives the stress exponent, n, in the relationship

where B₁ is a constant incorporating the dependence on temperature and grain size. Alternatively, tests may be conducted at high temperatures using a testing machine to apply a constant strain rate and then the measured flow stress is given bywhere B₂ is again the appropriate constant and m is termed the strain rate sensitivity. It follows from inspection of eqn (2) and (3) that the stress exponent and the strain rate sensitivity are related since n = 1/m and these two types of testing lead to typical plots as illustrated schematically in Fig. 2.¹³

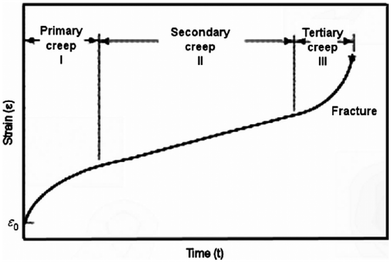Fig. 1 A typical creep curve of strain against time showing the three regions of flow.¹²

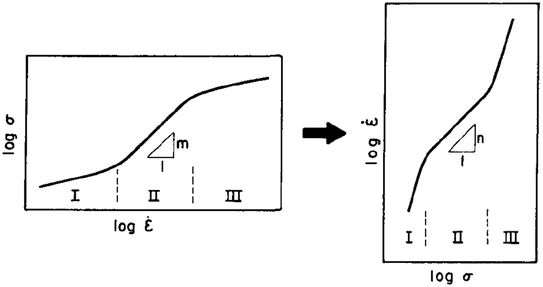Fig. 2 Typical logarithmic plots of stress against strain rate and strain rate against stress showing the meaning of the exponents m and n.¹³

Various creep mechanisms may occur at elevated temperatures including superplasticity which relates to achieving exceptionally high strains without failure. Specifically, superplasticity is defined as a flow mechanism that produces a tensile elongation prior to failure of at least 400% and with a measured strain rate sensitivity close to ∼0.5 so that the stress exponent is n ≈ 2.¹⁴ This flow mechanism is fundamental in industrial superplastic forming operations^15–17 but in practice laboratory experiments show that superplastic elongations are generally achieved only when testing at temperatures of at least 0.5 T_m using crystalline materials having grain sizes smaller than ∼10 μm.¹³ For many years this grain size requirement led to a critical restriction in the ability to achieve superplastic flow so that it became preferable to use two-phase alloys where grain growth was limited by the presence of the separate phases or to incorporate the presence of a fine dispersion of a second phase to act as a grain refiner. The following section outlines the principles of superplastic experiments and the subsequent sections describe recent advances demonstrating that it has become possible, over the last forty years, to produce materials with nanostructured grain sizes.

2. The fundamental principles of superplastic flow

A very early analysis showed that the ductility achieved in tensile testing was dependent upon the value of the strain rate sensitivity and specifically, as shown in Fig. 3,¹³ these very high elongations required a value of m close to ∼0.5 and therefore n ≈ 2.^18–20 This result is important because there are several dislocation mechanism that may control the plastic flow in creep and these mechanisms have different values for n. For example, creep controlled by dislocation climb requires a value of n ≈ 5²¹ whereas creep controlled by dislocation glide has n ≈ 3.²² In practice, this relatively low value for n for dislocation glide leads to the potential for achieving tensile elongations up to more than 300%²³ but this is not true superplasticity and it is more correctly defined as “enhanced ductility”.²⁴ On the contrary, control by dislocation glide led to the development of the Quick Plastic Forming (QPF) technology as developed by General Motors in the United States where this is a hot blow-forming process that was employed in the production of the large aluminum panels that are required in numerous automotive applications.²⁵

Fig. 3 Variation of strain rate sensitivity with elongation to failure¹³ showing results for a range of materials.^18–20

An example of true superplastic flow is shown in Fig. 4 where a Pb-62% Sn alloy with an initial grain size of 11.6 μm was pulled in tension at a temperature of 413 K and exhibited a total elongation of 7550% when using an initial strain rate of 2.1 × 10^–4 s⁻¹: for comparison purposes, an untested specimen is also shown.²⁶ It is readily apparent from inspection of Fig. 4 that, as required for true superplastic flow, this type of deformation leads to the development of an essentially uniform strain with the occurrence of no visible necking within the gauge length.²⁷

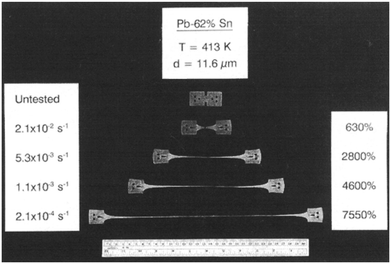Fig. 4 An example of superplasticity in a Pb-62% Sn alloy with an elongation of 7550% at a strain rate of 2.1 × 10^–4 s⁻¹.²⁶

Although the superplastic forming industry was developed extensively over a period of many years, there was a significant limitation within the industry because of the requirement to initially produce a material have a grain size of the order of only a few micrometers. In practice this was achieved using thermo-mechanical processing but these procedures were unable to produce grain sizes that were smaller than ∼2–4 μm. This situation changed dramatically in 1988 with the publication in the Soviet Union of a report demonstrating the potential for achieving a grain size as small as 0.3 μm in a superplastic Al-4% Cu-0.5% Zr alloy.²⁸ It is important to note that the composition of this alloy was almost identical to the superplastic Al-6% Cu-0.5% Zr alloy which was used for production of the commercial Supral-100 alloy by the New Jersey Zinc Company in the U.S. but the American alloy typically had a grain size of ∼3–4 μm and this was one order of magnitude larger than the alloy described in the Russian report. Furthermore, there was no obvious method of reducing the grain size of the U.S. alloy to the submicrometer level. It was therefore important to examine the precise experimental procedure used in Russia in the production of the 0.3 μm material.

The Russian alloy was initially processed at room temperature using the procedure now known as high-pressure torsion (HPT) where the material, in the form of a thin disk, is held between massive anvils, subjected to a high applied pressure and then one anvil is rotated to impose a torsional strain on the disk. In this way, the disk is subjected to a high plastic strain but without imposing any significant change in the overall dimensions of the sample. This type of processing, now designated HPT, was first developed by Professor Percy W. Bridgman at Harvard University in the 1930s and 1940s^29,30 and this and other similar research led to Bridgman receiving the Nobel Prize in physics in 1946 for his work on the application of high pressures to solid materials. Nevertheless, this ground-breaking research received only minor attention in the west but later extensive research on HPT processing was conducted in Russia^31,32 and this led ultimately to the demonstration of the exceptional grain refinement in the Al–Cu–Zr alloy.

Processing by HPT is unusual because, unlike conventional tensile or compressive testing, it can impose an exceptionally high strain but without introducing any significant change in the dimensions of the sample. This and other similar methods are now known as processing through the application of severe plastic deformation (SPD) and these various procedures have provided the impetus which has led to the development of SPD processing facilities and the production of crystalline materials with submicrometer and even nanometer grain sizes at many laboratories around the world. The principles of these various SPD processing methods are described in the following section and a relatively new procedure for SPD processing is described in detail in the next section.

3. Principles of processing through the application of severe plastic deformation

Processing by SPD refers to any process that imposes a very large strain but without incurring any significant change in the overall dimensions of the sample. Basically, there are four traditional methods of SPD processing and each method has additional and newer modifications that are designed to improve some aspect of the processing. This review is designed to summarize the main characteristics of each method but without making any attempt to include information on the various later modifications that have been developed for these procedures. A fifth and more recent SPD processing method is also now available but, since this is a new process that is not generally known to many practitioners using SPD processing to achieve exceptional grain refinement, it is dealt with separately in the following section. It is important to note that comprehensive information on different aspects of the various SPD techniques is now available in several review articles.^33–44

First, HPT is a fundamental SPD processing method and it has four major advantages over the other SPD processing techniques which may be listed as follows: (i) the total processing can be conducted in a single operation even to exceptionally high torsional strains, (ii) the imposition of a large hydrostatic pressure prevents the development of segmentation and cracking in hard-to-process materials such as magnesium alloys,⁴⁵ (iii) the HPT processing provides a capability of producing materials having grain sizes that are generally smaller than may be produced with other SPD procedures^46,47 and (iv) HPT processing produces an ultrafine-grained material containing, by comparison with other SPD techniques, a higher fraction of grain boundaries having high angles of misorientation⁴⁸ where this latter characteristic serves to enhance the superplastic capabilities of the materials. A comprehensive review is also available describing many aspects of the HPT process.⁴⁹

Second, equal-channel angular pressing (ECAP) is a procedure whereby a bar or rod is pressed through a die constrained within a channel that is bent through an abrupt angle near the center of the die. This type of processing is now used extensively in many laboratories around the world but it was first developed in the Soviet Union in the country now known as Belarus.^50,51 An advantage of ECAP is that it can be conducted fairly easily by adopting an appropriate press but there is a disadvantage because only a limited strain is imposed on a single passage through the die. In practice, this strain is dependent upon the angle of bend of the channel within the die and also, to a lesser extent, by the outer arc of curvature where the two parts of the channel intersect. An equation is available for this strain and, typically, the strain is close to ∼1 when the channel angle is equal to 90° but the strain decreases with increasing values of the channel angle.⁵² The effect of using dies with different channel angles has been investigated in several experiments.^53,54 In practice, high strains are achieved by removing the sample from the die and then repetitively pressing through multiple passes and this means that the processing is labour-intensive and requires a continuous monitoring to remove and replace the sample in the die. Again, a comprehensive review is available describing the various aspects of ECAP processing.⁵⁵

Third, accumulative roll-bonding (ARB) describes a processing operation in which a plate is rolled to one-half thickness, cut in half, degreased and cleaned by wire brushing, then stacked so that one piece is placed upon the other and rolled again so that the total process is repeated numerous times.^56–58 This process is again labour-intensive so that it is also a time-consuming procedure. Furthermore, there is the problem that the microstructure produced by ARB consists of a pancake-like structure that tends to be elongated along the rolling direction so that the procedure is generally less effective by comparison with HPT and ECAP. Reports are available making a direct comparison between materials processed by ECAP and ARB⁵⁹ and examining the mechanical behaviour of multi-layered composites processed by ARB.⁶⁰ A recent review of ARB is also now available.⁶¹

Fourth, there is the SPD process of multi-directional forging (MDF)^62–64 which, although easy to perform using any simple compression testing facility, has attracted less attention than HPT, ECAP and ARB and therefore needs a more detailed explanation. This processing is also known as multi-axial forging (MAF)⁶⁵ and multi-axial compression (MAC)^66–69 and it denotes a procedure whereby a prismatic specimen is subjected, in repetitive steps, to compression along each of three mutually perpendicular directions as illustrated schematically in Fig. 5 for three separate passes. This processing is also often designated abc deformation and again, as with ECAP and ARB, it is a labour-intensive process since the specimen must be rotated between each pass. Nevertheless, this processing operation promotes good grain refinement and therefore improved strength and it can be readily adapted for use in many industrial applications. Furthermore, recent reviews on MDF are also now available.^70,71

Fig. 5 The principle of multi-directional forging or abc deformation.

4. SPD processing using tube high-pressure shearing (t-HPS)

The processing technique of tube high-pressure shearing (t-HPS) was introduced as a new SPD procedure in 2012⁷² and more recent experiments show that it is capable of producing materials with exceptional properties and microstructural features. The fundamental objective of this technique is to use a specimen in the form of a tube and to introduce a tangential shear strain in the wall of the tube under the imposition of a high pressure. The principle of this concept is shown in Fig. 6 where r is the radius of the disk or tube, h is the height and there is a displacement at the outer rim through an angle of θ.⁷² In the upper illustration at (a), there is a solid disk and the displacement simply illustrates the conventional situation in HPT where the top surface is rotated relative to the bottom surface. In the second illustration in (b) there is a combined torsion and twisting but now it is applied to a tube. Finally, in the lower illustration at (c) the outer rim is displaced relative to the central point of the tube and thus, whereas (a) and (b) show conventional HPT, (c) depicts the new procedure of t-HPS.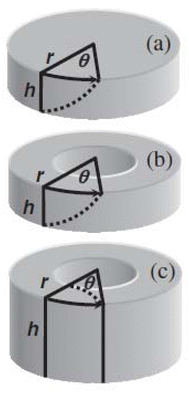

Fig. 6 Comparison of the principles of (a) HPT, (b) tube torsion/twist and (c) t-HPS.⁷²

The processing in t-HPS is conducted by fixing a mandrel, placing a sample in the form of a tube which is situated around the mandrel and held in place by pressure rings, then placing an outer cylinder around everything and rotating the cylinder in order to produce a high hydrostatic pressure in the tube wall. This produces a result that is consistent with (c) in Fig. 6 but which is different from the combined torsion and twist as shown in Fig. 6(b).

This type of processing has the advantage that it achieves significant grain refinement as required in SPD processing but it is also ideal for producing multi-layered gradient structures⁷³ where these structures are now becoming of increasing interest in fundamental research in materials science.^74,75 Similar multi-layered laminates may be achieved also by processing using ARB but the latter procedure is labour-intensive requiring many separate operations and multiple surface cleanings. By contrast, in t-HPS there are no additional surface cleanings after the initial clean and the final laminated microstructure is achieved in a single step without the potential for any surface contamination because of contact with the environment. An example of the grain refinement achieved by t-HPS in a tube of high-purity aluminum is shown in Fig. 7 where the initial grain size before SPD processing was ∼1 mm and microstructures are shown after π/4 to 2π turns where a rotation of π corresponds to a shear strain of ∼8.37.⁷⁶ Separate illustrations are presented for the inner, middle and outer regions of the tube and it is apparent that the grain size is reduced to a final value of ∼0.6–0.7 μm which is similar to the saturation grain sizes reported for similar materials processed by ECAP⁷⁷ or HPT.⁷⁸ It is also consistent with reported trends that there is an overall saturation in both grain size and hardness when processing samples using SPD techniques.^79–86

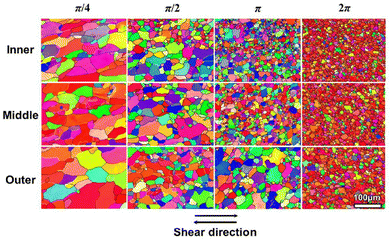Fig. 7 Grain refinement in high-purity aluminum at the inner, middle and outer regions of the tube after processing by t-HPS through different numbers of turns.⁷⁶

Fig. 8 shows an example of the excellent superplastic properties that may be achieved by processing using t-HPS where an elongation of 2320% was reported in a Bi-43% Sn alloy after processing through 100 turns at room temperature (RT) and then pulling to failure at RT (298 K) at an initial strain rate of 1.0 × 10^–4 s⁻¹.⁸⁷ This specimen shows, as also for the Pb–Sn alloy in Fig. 4, an absence of any visible necking within the gauge length. It is interesting to note that the maximum elongation of 2320% is higher than the report of a tensile elongation of 1950% as documented in the earliest experiments on superplasticity using a Bi–Sn eutectic alloy and pulling in tension at RT.⁸⁸ These results confirm, therefore, the opportunities for achieving excellent superplastic elongations using the t-HPS processing method.

Fig. 8 An example of superplasticity in a Bi-43% Sn alloy after processing by t-HPS.⁸⁷

5. Discussion

The preceding sections describe the early inability to achieve, through conventional thermo-mechanical processing, average grain sizes smaller than a few micrometers in crystalline solids and the more recent developments using SPD processing where grain sizes may be attained within the submicrometer and even the nanometer ranges. In order to appreciate the significance of these developments, it is first necessary to examine the basic characteristics of superplastic flow.

Early investigations of superplasticity were generally conducted by using a single specimen, measuring the initial grain size and then pulling the sample in tension at different strain rates to measure the flow stresses under these various conditions. In practice, however, this testing technique is quick and easy to conduct but it fails to incorporate the occurrence of any grain growth that may take place during the testing operation and therefore the results from these tests are not truly representative of a single well-defined grain size. This problem was recognized and then overcome in early experiments on the Zn-22%Al eutectoid alloy by testing a separate sample at each selected strain rate and pulling each sample to failure to measure both the flow stress and the total elongation.^19,89 Results of this type provided a clear demonstration that superplasticity occurs over a limited range of strain rates, typically covering about two orders of magnitude, and the elongations are then reduced at both faster and slower strain rates.

It is convenient to plot these experimental data in the form of deformation mechanism maps where the normalized grain size, d/b, is plotted on logarithmic axes against the normalized stress, σ/G, for any selected temperature where b is the relevant Burgers vector and G is the shear modulus.⁹⁰ In high temperature creep the grains of a polycrystal become divided into subgrains where the subgrain boundaries have low angles of misorientation. Extensive experiments show that in creep the average subgrain size, λ, is given by the relationship⁹¹

where B₃ is a constant having a value of ∼20. The relationship shown in eqn (4) applies not only to metals⁹² but also to ceramics⁹³ and a wide range of rocks and minerals.^94–97 Assuming, therefore, that the grain size of the material is equal to the equilibrium subgrain size, it is feasible to superimpose the subgrain size predicted by eqn (4) onto these deformation mechanism maps and the results show that superplastic flow requires a grain size that is equal to or smaller than the average subgrain size.⁹⁸

The results from this analysis show that in conventional creep the grains become divided into an inner core of subgrains which is surrounded by an outer mantle of subgrains lying immediately next to the grain boundary.⁹⁹ In order to make use of this interpretation, it is first noted that superplasticity represents a flow process where large elongations are achieved but the individual grains retain an essentially equi-axed appearance. This means that superplastic flow occurs through deformation by grain boundary sliding (GBS)¹⁰⁰ and this can be modelled by a dislocation process in which grain boundary dislocations move along a grain boundary to pile up at a triple point and this is accommodated by slip in the next grain.¹⁰¹ In practice, the dislocations in this slip will either pile-up and climb into the first subgrain boundary as in GBS in conventional creep or, in the absence of any subgrains as in superplastic flow, the dislocations will pile up and climb into the opposite grain boundary. The former process corresponds to normal GBS and is well documented in an earlier detailed review which shows that GBS then divides into the co-called Rachinger sliding which is accommodated by the intragranular movement of dislocations and Lifshitz sliding which accommodates diffusion creep¹⁰² whereas the latter process represents GBS in superplastic flow. For the latter process, it can be shown that the rate of GBS in superplasticity, , is given by a relationship of the form¹⁰¹

where D_gb is the coefficient for grain boundary diffusion, k is Boltzmann's constant, T is the absolute temperature, A_sp is a constant having a value of ∼10 and the exponents of both the stress and the inverse grain size are equal to ∼2.

Eqn (5) relates to conventional high temperature GBS which is appropriate for use in commercial superplastic forming operations but GBS may also occur at low temperatures. This latter process may be modelled by permitting the build up of a supersaturation of vacancies during the sliding operation to give a rate equation that no longer has a constant value for the stress exponent n.⁶ The model for low temperature GBS has been subjected to a detailed analysis which supports the concept of this type of flow¹⁰ but nevertheless it is not important for commercial forming operations.

In conventional industrial superplastic forming, a plate is placed in a furnace, heated to temperature and then formed into the desired shape at a strain rate of the order of ∼10^–3 s⁻¹ with the whole process taking a total time of about 20 minutes. This slow forming rate leads to the production of a limited range of low-volume high-value components. However, eqn (5) shows that the strain rate in superplasticity varies inversely with the grain size raised to the power of 2 and this means that the strain rate for optimum superplasticity can be increased by making a substantial reduction in the grain size. This suggests, therefore, that it may be possible to use SPD processing to achieve high strain rate superplasticity (HSR SP) which is defined as attaining superplastic elongations at strain rates at or above 10^–2 s⁻¹.¹⁰³

The first example of this capability was presented in 1997 when exceptional superplastic elongations were achieved when testing in tension at 623 K an Al-5.5% Mg-2.2% Li-0.12% Zr alloy processed by ECAP to a total strain of ∼12 to give an average grain size of ∼1.2 μm. The result is shown in Fig. 9 where there is an elongation of 1180% without failure at an imposed strain rate of 10^–2 s⁻¹ and an elongation to failure of 910% at the faster strain rate of 10^–1 s⁻¹.¹⁰⁴ These exceptional elongations at these very rapid strain rates are excellent examples of the occurrence of HSR SP.

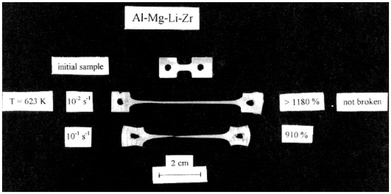Fig. 9 An example of high strain rate superplasticity in an Al–Mg–Li–Zr alloy processed by ECAP to a grain size of ∼1.2 μm and tested in tension at 623 K.¹⁰⁴

Although there is very good evidence for excellent superplastic flow as documented in Fig. 9, it is important to demonstrate in the laboratory the potential for achieving an industrial superplastic forming capability through the use of a simple gas-pressure forming facility. Accordingly, experiments were conducted using an Al-3% Mg-0.2% Sc alloy which was processed by ECAP to a strain of ∼8 to give a grain size of ∼0.2 μm. Small disks were cut from the rod after pressing and these disks were inserted individually into a biaxial gas-pressure forming facility where they were clamped around the edge, heated to 673 K and then subjected to a constant pressure of an argon gas from one side for times up to a maximum of 1 minute. Typical results are shown in Fig. 10 where the disk at (a) is untested and the other two disks were subjected to a gas pressure of 10 atmospheres for times of (b) 30 seconds and (c) 1 minute, respectively. It is readily apparent that these disks have blown out into smooth domes at very rapid strain rates.¹⁰⁵

Fig. 10 Disks of an Al–Mg–Sc alloy processed by ECAP to a grain size of ∼0.2 μm and then subjected to biaxial gas-pressure forming at a pressure of 10 atmospheres at 673 K: (a) untested and after (b) 30 seconds and (c) 1 minute.¹⁰⁵

In order to evaluate the uniformity of deformation at these rapid rates, the disks at (b) and (c) were sectioned and then measurements were taken to determine the local thicknesses at various angular increments around the deformed disks. The results are shown in Fig. 11 where 0° corresponds to the centre of each disk, 90° corresponds to the outer edges and the final measurements were taken at 85° which is close to the edge on either side of each disk.¹⁰⁵ These plots demonstrate that for both domes, and especially after processing for 1 minute, the deformation is remarkably uniform. These measurements confirm the validity of this approach for use in industrial superplastic forming operations and it is readily apparent that the deformation has occurred without the development of any cracking within the samples. Thus, these results provide a clear demonstration of the validity of using SPD processing for achieving a material that may be used for the rapid forming of complex parts.

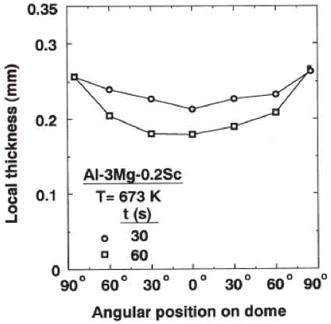Fig. 11 The local thicknesses measured around the two deformed domes in Fig. 10 subjected to a pressure of 10 atmospheres for times of 30 and 60 seconds, respectively.¹⁰⁵

Although the preceding review deals exclusively with the application of SPD to metals, it is important to note that the same techniques of SPD processing may be applied also to other non-metallic materials. A detailed description of the relevant experiments is beyond the scope of the present review but nevertheless it should be noted that there are reports of SPD processing with ceramics,^106–108 including not only with existing ceramics but in the synthesis of new types of ceramics such as high-entropy ceramics and metastable high-pressure ceramics,¹⁰⁹ polymers,¹¹⁰ polymer-based nanocomposites¹¹¹ and geological materials.^112–114 An examination of the available results with non-metals suggests the potential for using this approach to produce different materials having unusual and useful properties.

Finally, it should be noted that the major emphasis in this review concerned the development of new opportunities for achieving superplastic properties in metals but there are also many other potential industrial applications for materials produced by SPD processing as outlined in detail in several recent comprehensive reports.^115–118 For example, there are reports of the use of SPD processing for the production of a range of materials for various biomedical and orthopaedic applications,^119–123 for dental implants,^124–126 for materials used in Zn, Li, Mg and Al-based batteries¹²⁷ and for the production of sputtering targets for the electronics industry.¹²⁸ These developments confirm the many potential uses that become available through the processing of ultrafine-grained materials using SPD techniques.

6. Summary and conclusions

1. The grain size of a polycrystalline material is an important parameter because it controls many of the physical properties. Thus, a reduction in grain size to the submicrometer level has the advantage of increasing the strength of the material and introducing a potential for achieving a superplastic forming capability.

2. Different grain sizes are generally achieved through the use of thermo-mechanical processing but this has the limitation that it cannot be used to refine the grain size below the level of a few micrometers. Over the last forty years it has been possible to attain submicrometer or even nanometer grains by using severe plastic deformation (SPD) processing where a solid is subjected to a high strain without producing any significant changes in the overall dimensions of the sample.

3. Five major SPD processing techniques are now available and these are high-pressure torsion, equal-channel angular pressing, accumulative roll-bonding, multi-directional forging and the new process of tube high-pressure shearing. Each of these processes is capable of producing significant grain refinement but high-pressure torsion is especially attractive because it produces smaller grain sizes, higher fractions of high angle boundaries and it can be performed in a single operation so that it is not labour-intensive.

4. By introducing very significant grain refinement through SPD processing, it is possible to achieve superplastic flow at high strain rates thereby providing the potential for achieving rapid superplastic forming operations in industry.

Author contributions

The author is responsible for the concept, methodology and writing of the paper.

Conflicts of interest

The author has no competing interests.

Data availability

All data are available in the appropriate references.

Acknowledgements

This report is based on the opening Plenary Lecture given at the NANO-2024 conference in Abu Dhabi, UAE, on 4 November, 2025. The author is grateful to Professor Daniel Choi of Khalifa University for the invitation to make this presentation.

References

1. E. O. Hall, Proc. Phys. Soc., London, Sect. B, 1951, 64, 747.
2. N. J. Petch, J. Iron Steel Inst., 1953, 174, 25.
3. A. Loucif, R. B. Figueiredo, T. Baudin, F. Brisset, R. Chemam and T. G. Langdon, Mater. Sci. Eng., A, 2012, 532, 139.
4. P. Bazarnik, Y. Huang, M. Lewandowska and T. G. Langdon, Mater. Sci. Eng., A, 2015, 626, 9.
5. N. Balasubramanian and T. G. Langdon, Metall. Mater. Trans. A, 2016, 47, 5827.
6. R. B. Figueiredo and T. G. Langdon, J. Mater. Res. Technol., 2021, 14, 137.
7. F. H. Duan, Y. Naunheim, C. A. Schuh and Y. Li, Acta Mater., 2021, 213, 116950.
8. N. Q. Chinh, D. Olasz, A. Q. Ahmed, G. Sáfrán, J. Lendvai and T. G. Langdon, Mater. Sci. Eng., A, 2023, 862, 144419.
9. S. Dangwal, K. Edalati, R. Z. Valiev and T. G. Langdon, Crystals, 2023, 13, 413.
10. R. B. Figueiredo, M. Kawasaki and T. G. Langdon, Prog. Mater. Sci., 2023, 137, 101131.
11. F. T. Trouton and A. O. Rankine, Philos. Mag., 1904, 8, 538.
12. T. G. Langdon, Adv. Eng. Mater., 2020, 22, 1900442.
13. T. G. Langdon, Metall. Trans. A, 1982, 13, 689.
14. T. G. Langdon, J. Mater. Sci., 2009, 44, 5998.
15. A. J. Barnes, J. Mater. Eng. Perform., 2007, 16, 440.
16. T. G. Langdon, Solid State Phenom., 2020, 306, 1.
17. J. Wongsa-Ngam and T. G. Langdon, Metals, 2022, 12, 1921.
18. D. A. Woodford, Trans. ASME, 1969, 62, 291.
19. F. A. Mohamed, M. M. I. Ahmed and T. G. Langdon, Metall. Trans. A, 1977, 8, 933.
20. M. M. I. Ahmed and T. G. Langdon, Metall. Trans. A, 1977, 8, 1832.
21. J. Weertman, J. Appl. Phys., 1955, 26, 1213.
22. J. Weertman, J. Appl. Phys., 1957, 28, 1185.
23. M. Otsuka, S. Shibasaki and M. Kikuchi, Mater. Sci. Forum, 1997, 233–234, 193.
24. E. M. Taleff, D. R. Lesuer and J. Wadsworth, Metall. Mater. Trans. A, 1996, 27, 343.
25. P. E. Krajewski and J. G. Schroth, Mater. Sci. Forum, 2007, 551–552, 3.
26. Y. Ma and T. G. Langdon, Metall. Mater. Trans. A, 1994, 25, 2509.
27. T. G. Langdon, Met. Sci., 1982, 16, 175.
28. R. Z. Valiev, O. A. Kaibyshev, R. I. Kuznetsov, R. Sh. Musalimov and N. K. Tsenev, Dokl. Akad. Nauk SSSR, 1988, 301, 864.
29. P. W. Bridgman, Phys. Rev., 1935, 48, 825.
30. P. W. Bridgman, J. Appl. Phys., 1943, 14, 273.
31. D. I. Tupitsa, V. P. Pilyugin, R. I. Kuznetsov, G. G. Taluts and V. A. Teplov, Fiz. Met. Metalloved., 1986, 61, 325.
32. N. A. Smirnova, V. I. Levit, V. P. Pilyugin, R. I. Kuznetsov and M. V. Degtyarev, Fiz. Met. Metalloved., 1986, 62, 566.
33. R. Z. Valiev, R. K. Islamgaliev and I. V. Alexandrov, Prog. Mater. Sci., 2000, 45, 103.
34. R. Z. Valiev, Y. Estrin, Z. Horita, T. G. Langdon, M. J. Zehetbauer and Y. T. Zhu, JOM, 2006, 58(4), 33.
35. R. Z. Valiev and T. G. Langdon, Adv. Eng. Mater., 2010, 12, 677.
36. Y. Estrin and A. Vinogradov, Acta Mater., 2013, 61, 782.
37. T. G. Langdon, Acta Mater., 2013, 61, 7035.
38. R. Z. Valiev, A. P. Zhilyaev and T. G. Langdon, Bulk Nanostructured Materials: Fundamentals and Applications, Wiley/TMS, Hoboken, NJ, USA, 2014.
39. K. Edalati and Z. Horita, Mater. Sci. Eng., A, 2016, 652, 325.
40. R. Z. Valiev, Y. Estrin, Z. Horita, T. G. Langdon, M. J. Zehetbauer and Y. T. Zhu, JOM, 2016, 68, 1216.
41. R. Z. Valiev, Y. Estrin, Z. Horita, T. G. Langdon, M. J. Zehetbauer and Y. T. Zhu, Mater. Res. Lett., 2016, 4, 1.
42. K. Edalati, A. Bachmaier, V. A. Beloshenko, Y. Beygelzimer, V. D. Blank, W. J. Botta, K. Bryła, J. Čížek, S. Divinski, N. A. Enikeev, Y. Estrin, G. Faraji, R. B. Figueiredo, M. Fuji, T. Furuta, T. Grosdidier, J. Gubicza, A. Hohenwarter, Z. Horita, J. Huot, Y. Ikoma, M. Janeček, M. Kawasaki, P. Král, S. Kuramoto, T. G. Langdon, D. R. Leiva, V. I. Levitas, A. Mazilkin, M. Mito, H. Miyamoto, T. Nishizaki, R. Pippan, V. V. Popov, E. N. Popova, G. Purcek, O. Renk, Á. Révész, X. Sauvage, V. Sklenicka, W. Skrotzki, B. B. Straumal, S. Suwas, L. S. Toth, N. Tsuji, R. Z. Valiev, G. Wilde, M. J. Zehetbauer and X. Zhu, Mater. Res. Lett., 2022, 10, 163.
43. R. Z. Valiev, B. Straumal and T. G. Langdon, Annu. Rev. Mater. Res., 2022, 52, 357.
44. K. Edalati, A. Q. Ahmed, S. Akrami, K. Ameyama, V. Aptukov, R. N. Asfandiyarov, M. Ashida, V. Astanin, A. Bachmaier, V. Beloshenko, E. V. Bobruk, K. Bryła, J. M. Cabrera, A. P. Carvalho, N. Q. Chinh, I. C. Choi, R. Chulist, J. M. Cubero-Sesin, G. Davdian, M. Demirtas, S. Divinski, K. Durst, J. Dvorak, P. Edalati, S. Emura, N. A. Enikeev, G. Faraji, R. B. Figueiredo, R. Floriano, M. Fouladvind, D. Fruchart, M. Fuji, H. Fujiwara, M. Gajdics, D. Gheorghe, L. Gondek, J. E. González-Hernández, A. Gornakova, T. Grosdidier, J. Gubicza, D. Gunderov, L. He, O. F. Higuera, S. Hirosawa, A. Hohenwarter, Z. Horita, J. Horky, Y. Huang, J. Huot, Y. Ikoma, T. Ishihara, Y. Ivanisenko, J. il Jang, A. M. Jorge, M. Kawabata-Ota, M. Kawasaki, T. Khelfa, J. Kobayashi, L. Kommel, A. Korneva, P. Kral, N. Kudriashova, S. Kuramoto, T. G. Langdon, D. H. Lee, V. I. Levitas, C. Li, H. W. Li, Y. Li, Z. Li, H. J. Lin, K. D. Liss, Y. Liu, D. M. M. Cardona, K. Matsuda, A. Mazilkin, Y. Mine, H. Miyamoto, S. C. Moon, T. Müller, J. A. Muñoz, M. Y. Murashkin, M. Naeem, M. Novelli, D. Olasz, R. Pippan, V. V. Popov, E. N. Popova, G. Purcek, P. de Rango, O. Renk, D. Retraint, Á. Révész, V. Roche, P. Rodriguez-Calvillo, L. Romero-Resendiz, X. Sauvage, T. Sawaguchi, H. Sena, H. Shahmir, X. Shi, V. Sklenicka, W. Skrotzki, N. Skryabina, F. Staab, B. Straumal, Z. Sun, M. Szczerba, Y. Takizawa, Y. Tang, R. Z. Valiev, A. Vozniak, A. Voznyak, B. Wang, J. T. Wang, G. Wilde, F. Zhang, M. Zhang, P. Zhang, J. Zhou, X. Zhu and Y. T. Zhu, J. Alloys Compd., 2024, 1002, 174667.
45. Y. Huang, R. B. Figueiredo, T. Baudin, F. Brisset and T. G. Langdon, Adv. Eng. Mater., 2012, 14, 1018.
46. A. P. Zhilyaev, B.-K. Kim, G. V. Nurislamova, M. D. Baró, J. A. Szpunar and T. G. Langdon, Scr. Mater., 2002, 46, 575.
47. A. P. Zhilyaev, G. V. Nurislamova, B.-K. Kim, M. D. Baro, J. A. Szpunar and T. G. Langdon, Acta Mater., 2003, 51, 753.
48. J. Wongsa-Ngam, M. Kawasaki and T. G. Langdon, J. Mater. Sci., 2013, 48, 4653.
49. A. P. Zhilyaev and T. G. Langdon, Prog. Mater. Sci., 2008, 53, 893.
50. V. M. Segal, V. I. Reznikov, A. E. Drobyshevsky and I. Kopylov, Russ. Metall., 1981, 1, 115.
51. V. M. Segal, Mater. Sci. Eng., A, 1995, 197, 157.
52. Y. Iwahashi, J. Wang, Z. Horita, M. Nemoto and T. G. Langdon, Scr. Mater., 1996, 35, 143.
53. K. Nakashima, Z. Horita, M. Nemoto and T. G. Langdon, Acta Mater., 1998, 46, 1589.
54. R. B. Figueiredo, I. J. Beyerlein, A. P. Zhilyaev and T. G. Langdon, Mater. Sci. Eng., A, 2010, 527, 1709.
55. R. Z. Valiev and T. G. Langdon, Prog. Mater. Sci., 2006, 45, 103.
56. Y. Saito, N. Tsuji, H. Utsunomiya, T. Sakai and R. G. Hong, Scr. Mater., 1998, 39, 1221.
57. Y. Saito, H. Utsunomiya, N. Tsuji and T. Sakai, Acta Mater., 1999, 47, 579.
58. N. Tsuji, Y. Saito, H. Utsunomiya and S. Tanigawa, Scr. Mater., 1999, 40, 795.
59. A. A. C. Asselli, D. R. Leiva, J. Huot, M. Kawasaki, T. G. Langdon and W. J. Botta, Int. J. Hydrogen Energy, 2015, 40, 16971.
60. C. Ding, J. Xu, X. Li, D. Shan, B. Guo and T. G. Langdon, Adv. Eng. Mater., 2020, 22, 1900702.
61. S. M. Ghalehbandi, M. Malaki and M. Gupta, Appl. Sci., 2019, 9, 3627.
62. O. R. Valiakhmetov, R. M. Galeyev and G. A. Salishchev, Fiz. Met. Metalloved., 1990, 10, 204.
63. R. M. Galeyev, O. R. Valiakhmetov and G. A. Salishchev, Russ. Metall., 1990, 4, 97.
64. S. V. Zherebtsov, G. A. Salishchev, R. M. Galeyev, O. R. Valiakhmetov, S. Yu. Mironov and S. L. Semiatin, Scr. Mater., 2004, 51, 1147.
65. R. Kapoor, A. Sarkar, R. Yogi, S. K. Shekhawat, I. Samajdar and J. K. Chakravartty, Mater. Sci. Eng., A, 2013, 560, 404.
66. B. Cherukuri, T. S. Nedkova and R. Srinivasan, Mater. Sci. Eng., A, 2005, 410–411, 394.
67. X. Xu, Q. Zhang, N. Hu, Y. Huang and T. G. Langdon, Mater. Sci. Eng., A, 2013, 588, 280.
68. C. G. de Faria, N. G. S. Almeida, M. T. P. Aguilar and P. R. Cetlin, Mater. Lett., 2016, 174, 153.
69. C. G. de Faria, N. G. S. Almeida, F. de C. Bubani, K. Balzuweit, M. T. P. Aguilar and P. R. Cetlin, Mater. Lett., 2018, 227, 149.
70. N. A. N. da Silva, P. C. A. Flausino, M. T. P. Aguilar and P. R. Cetlin, Comprehensive Materials Processing, ed. M. S. J. Hashmi, Elsevier, Oxford, UK, 2024, vol. 3, pp. 130–156.
71. M. Şahbaz, Current Studies in Materials Science and Engineering, ed. H. Gokmese, S. Bulbul and Y. Uzon, ISRES Publishing, Meram, Turkey, 2024, pp. 113–127.
72. J. T. Wang, Z. Li, J. Wang and T. G. Langdon, Scr. Mater., 2012, 67, 810.
73. Z. Li, P. F. Zhang, H. Yuan, K. Lin, Y. Liu, D. L. Yin, J. T. Wang and T. G. Langdon, Mater. Sci. Eng., A, 2016, 658, 367.
74. X. L. Wu, P. Jiang, L. Chen, J. F. Zhang, F. P. Yuan and Y. T. Zhu, Mater. Res. Lett., 2014, 2, 185.
75. X. L. Wu, P. Jiang, L. Chen and Y. T. Zhu, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 7197.
76. Z. Li, L. Y. Li, Y. B. Zhu, K. Lin, Z. T. Ren, Y. Yang, Y. Liu, J. T. Wang and T. G. Langdon, Sci. Rep., 2022, 12, 17901.
77. A. P. Zhilyaev, D. L. Swisher, K. Oh-ishi, T. G. Langdon and T. R. McNelley, Mater. Sci. Eng., A, 2006, 429, 137.
78. M. Kawasaki, R. B. Figueiredo and T. G. Langdon, Acta Mater., 2011, 59, 308.
79. R. Pippan, S. Scheriau, A. Taylor, M. Hafok, A. Hohenwarter and A. Bachmaier, Annu. Rev. Mater. Res., 2010, 40, 319.
80. M. Hafok and R. Pippan, Int. J. Mater. Res., 2010, 101, 1097.
81. A. P. Zhilyaev, S. Swaminathan, A. I. Pshenichnyuk, T. G. Langdon and T. R. McNelley, J. Mater. Sci., 2013, 48, 4626.
82. S. Sabbaghianrad, J. Wongsa-Ngam, M. Kawasaki and T. G. Langdon, J. Mater. Res. Technol., 2014, 3, 319.
83. S. Sabbaghianrad and T. G. Langdon, J. Mater. Sci., 2015, 50, 4357.
84. S. Sabbaghianrad and T. G. Langdon, Lett. Mater., 2015, 5, 335.
85. A. Bachmaier, R. Pippan and O. Renk, Adv. Eng. Mater., 2020, 22, 2000879.
86. H. Azzeddine, D. Bradai, T. Baudin and T. G. Langdon, Prog. Mater. Sci., 2022, 125, 100886.
87. C. T. Wang, Z. Li, J. T. Wang and T. G. Langdon, Mater. Res. Proc., 2023, 32, 3.
88. C. E. Pearson, J. Inst. Met., 1934, 54, 111.
89. H. Ishikawa, F. A. Mohamed and T. G. Langdon, Philos. Mag., 1975, 32, 1269.
90. F. A. Mohamed and T. G. Langdon, Metall. Trans., 1974, 5, 2339.
91. J. E. Bird, A. K. Mukherjee and J. E. Dorn, Quantitative Relation Between Properties and Microstructure, ed. D. G. Brandon and A. Rosen, Israel Universities Press, Jerusalem, Israel, 1959, pp. 255–342.
92. S. V. Raj and G. M. Pharr, Mater. Sci. Eng., 1986, 81, 217.
93. W. R. Cannon and T. G. Langdon, J. Mater. Sci., 1988, 23, 1.
94. R. J. Twiss, PAGEOPH, 1977, 115, 227.
95. M. Toriumi, Contrib. Mineral. Petrol., 1979, 68, 181.
96. S. White, Contrib. Mineral. Petrol., 1979, 70, 193.
97. R. M. Goddard, L. N. Hansen, D. Wallis, M. Stipp, C. W. Holyoke, K. M. Kumamoto and D. L. Kohlstedt, Geophys. Res. Lett., 2020, 47, e2020GL090056.
98. F. A. Mohamed and T. G. Langdon, Scr. Mater., 1976, 10, 759.
99. T. G. Langdon, Mater. Sci. Eng., A, 1991, 137, 1.
100. T. G. Langdon, Mater. Sci. Eng., A, 1994, 174, 225.
101. T. G. Langdon, Acta Metall. Mater., 1994, 42, 2437.
102. T. G. Langdon, J. Mater. Sci., 2006, 41, 597.
103. K. Higashi, M. Mabuchi and T. G. Langdon, ISIJ Int., 1996, 36, 1423.
104. R. Z. Valiev, D. A. Salimonenko, N. K. Tsenev, P. B. Berbon and T. G. Langdon, Scr. Mater., 1997, 37, 1945.
105. Z. Horita, M. Furukawa, M. Nemoto, A. J. Barnes and T. G. Langdon, Acta Mater., 2000, 48, 3633.
106. K. Edalati, M. Arimura, Y. Ikoma, T. Daio, M. Miyata, D. J. Smith and Z. Horita, Mater. Res. Lett., 2015, 3, 216.
107. K. Edalati, Adv. Eng. Mater., 2019, 21, 1800272.
108. P. Edalati, M. Fuji and K. Edalati, Rare Met., 2023, 42, 3246.
109. K. Edalati, J. Hidalgo-Jiménez, T. T. Nguyen, H. Sena, N. Enikeev, G. Rogl, V. I. Levitas, Z. Horita, M. J. Zehetbauer, R. Z. Valiev and T. G. Langdon, Annu. Rev. Mater. Res., 2025, 55, 89.
110. V. Beloshenko, Iu. Vozniak, Y. Beygelzimer, Y. Estrin and R. Kulagin, Mater. Trans., 2019, 60, 1192.
111. M. Fattahi, C. Y. Hsu, A. O. Ali, Z. H. Mahmoud, N. P. Dang and E. Kianfar, Heliyon, 2023, 9, e22559.
112. D. T. Griggs, J. Geol., 1936, 44, 541.
113. P. W. Bridgman, J. Geol., 1936, 44, 653.
114. M. S. Paterson and D. L. Olgaard, J. Struct. Geol., 2000, 22, 1341.
115. R. Z. Valiev, I. Sabirov, A. P. Zhilyaev and T. G. Langdon, JOM, 2012, 64, 1134.
116. T. C. Lowe, R. Z. Valiev, X. Li and B. R. Ewing, MRS Bull., 2021, 46, 265.
117. I. P. Semenova, R. Z. Valiev, A. M. Smyslov, M. V. Pesin and T. G. Langdon, Adv. Eng. Mater., 2021, 23, 2100145.
118. R. Z. Valiev, I. V. Alexandrov, M. Kawasaki and T. G. Langdon, Ultrafine-Grained Materials, TMS/Springer Nature, Cham, Switzerland, 2024.
119. L. Mishnaevsky, E. Levashov, R. Z. Valiev, J. Segurado, I. Sabirov, N. Enikeev, S. Prokoshkin, A. V. Solov'yov, A. Korotitskiy, E. Gutmanas, I. Gotman, E. Rabkin, S. Psakh'e, L. Dluhoš, M. Seefeldt and A. Smolin, Mater. Sci. Eng., R, 2014, 81, 1.
120. A. V. Polyakov, G. S. Dyakonov, I. P. Semenova, G. I. Raab, L. Dluhos and R. Z. Valiev, Adv. Biomater. Dev. Med., 2015, 2, 63.
121. I. P. Semenova, G. V. Klevtsov, N. A. Klevtsova, G. S. Dyakonov, A. A. Matchin and R. Z. Valiev, Adv. Eng. Mater., 2016, 18, 1216.
122. R. Z. Valiev, E. V. Parfenov and L. V. Parfenova, Mater. Trans., 2019, 60, 1356.
123. K. Bryła and J. Horky, Mater. Trans., 2023, 64, 1709.
124. C. N. Elias, J. H. C. Lima, R. Valiev and M. A. Meyers, JOM, 2008, 60(3), 46.
125. R. B. Figueiredo, E. R. de C. Barbosa, X. Zhao, X. Yang, X. Liu, P. R. Cetlin and T. G. Langdon, Mater. Sci. Eng., A, 2014, 619, 312.
126. A. V. Polyakov, L. Dluhoš, G. S. Dyakonov, G. I. Raab and R. Z. Valiev, Adv. Eng. Mater., 2015, 17, 1869.
127. M. Zohrevand, N. Hassanzadeh, R. Alizadeh and T. G. Langdon, J. Mater. Sci., 2024, 59, 5651.
128. S. Ferrasse, V. M. Segal, F. Alford, J. Kardokus and S. Strothers, Mater. Sci. Eng., A, 2008, 493, 130.

---