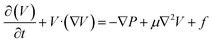DOI:
10.1039/D4RE00481G
(Paper)
React. Chem. Eng., 2025, Advance Article
Reactor intensification on glycerol-to-acrylic acid conversion: a modelling study†
Received
4th October 2024
, Accepted 15th April 2025
First published on 16th April 2025
Abstract
This work presents a numerical analysis for glycerol dehydration & acrolein oxidation to produce acrylic acid and determine the optimal process conditions combining computational fluid dynamics (CFD) with response surface methodology (RSM) techniques. For glycerol dehydration, optimum conditions are found at 623 K, 5731.6 h−1 GHSV, and a glycerol mass fraction of 0.32, resulting in a glycerol conversion of 94.2% and an acrolein selectivity of 79.6%. Further, the simulations with optimized conditions for two proposed configurations have insignificant glycerol conversion and acrolein selectivity suggesting that alternative reactor configurations have limited improvement. In the case of the acrolein selective oxidation process, an optimum temperature of 583.5 K, a GHSV of 1600 h−1, and an oxygen-to-acrolein molar ratio of 5.73 result in an acrylic acid yield and a selectivity of 80.9% and 87.5%, respectively. In the case of a membrane reactor with distributed oxygen feeding, the acrylic acid yield reached 85.9% and it exhibits a remarkable selectivity of 97.1%.
1. Introduction
The continuous utilization of fossil fuels and the environmental concerns of increasing CO2 and climate change have driven the chemical industry to explore alternative pathways for producing various bulk and speciality chemicals.1,2 Acrylic acid is an essential chemical with huge applications in industries such as coating & adhesive, medical hygiene products, polymers, paints & finishers, synthetic rubber, and consumer products.3,4 Currently, it is synthesized industrially by the oxidation of propylene (via fossil fuels) in a two-step catalytic packed bed reactor (PBR).5 The rising demand for acrylic acid and climate issues necessitate sustainable methods such as bio-derived feedstocks.5,6 Biodiesel production via the transesterification process generates glycerol as a by-product, which can be used as a feedstock for the production of acrylic acid.7 The glycerol dehydration (step 1) to acrolein and subsequent oxidation (step 2) to acrylic acid is a two-step cost-effective alternative for acrylic acid production compared to traditional methods.8
Numerous studies focused on the synthesis of efficient catalysts for gas-phase glycerol dehydration to produce acrolein (intermediate) and its further oxidation to acrylic acid.9 In recent years, Talebian-Kiakalaieh et al.10 proposed a kinetic model for step 1 in a PBR using 0.5 g of HSiW–ZrO2 catalyst, tested at 280–340 °C & GHSV 4000 h−1. Park et al.11 conducted a comprehensive kinetic study on dehydration using HZSM-5 and ASPN-40 catalysts at 250–300 °C for 120 h. The study revealed that HZSM-5 with a narrow pore structure accelerates coke precursor condensation and deactivates quickly. In contrast, ASPN-40 exhibited delayed deactivation due to fewer condensed carbonaceous species. For the oxidation process i.e. step 2, catalysts typically comprise transition metal oxides, primarily molybdenum (Mo) and vanadium (V).12 The Mo–V–oxide-based catalyst is notable for its activity and selectivity towards acrylic acid. Chen et al.13 discussed four pure crystalline phase structures of Mo3–V–Ox, finding that the heptagonal micropore channel affects catalytic performance and product selectivity. Miller et al.14 performed an isothermal catalytic reaction in a recirculating gas-phase batch reactor at 498 K and 120–130 kPa using 4.2 mg of Mo–V–Ox catalyst. Drochner et al.15 presented a steady-state transient kinetic analysis & model for acrolein oxidation using 50 mg of Mo–V–W, and a 315 to 375 °C range at 0.1 MPa pressure. To enhance acrylic acid selectivity, it is necessary to control the O2 amount and maintain lower partial pressure by decreasing oxygen concentration since it also produces CO2 and CO.16 In contrast, both the process dehydration and oxidation have limited kinetic data in the literature, with only a few mentioned kinetic mechanisms having reaction rates, activation energy, and frequency factors.
The utilization of computational fluid dynamics (CFD) has become crucial for anticipating experimental campaigns, designing effective experiments, and understanding theoretical process aspects through rigorous analysis.17 Furthermore, recent advancements in process intensification have focused on the development and scale-up of membrane reactors (MRs).18,19 The adoption of higher pressure holds potential for improving the reaction rate, reducing the equipment size, and lowering the energy demand. A viable approach to achieve these benefits is utilizing a MR, capable of selectively removing water and shifting the reaction equilibrium towards product formation allowing higher conversions compared to a PBR. The industrial application of H2O perm-selective membranes is limited by their stability at high temperatures and is not suitable for this purpose. Amorphous membranes degrade above 250 °C and they are hence unstable,20 zeolite membranes such as hydroxy sodalite (H-SOD) can withstand higher temperatures and their stability is affected by thermal expansion and structural changes.21 Rohde,20 Khajavi et al.22 tested H-SOD for steam pervaporation in which a thin defect-free film with a 2 μm layer thickness was synthesized via hydrothermal methods and exhibited a remarkable perm-selectivity of 75 for H2O/H2. They presented supported H-SOD membranes on α-alumina disks that demonstrated exceptional thermal, mechanical, and operational stability. Wang et al.23 prepared supported SOD membranes by a two-step repeated hydrothermal synthesis. They exhibited enhanced stability, making them suitable for steam removal in a MR alongside other species like H2, CH4, and CO2 present in the feed or retentate. In another study, Lafleur et al.24 optimized and fabricated SOD membranes achieving H2O/N2, H2O/CO2, and H2O/H2 ideal gas perm-selectivities of 5.1, 4.8, and 1.4 at 250 °C, while providing a high water permeance (1.26 × 10−7 mol Pa−1 m−2 s−1). The feeding and distribution of oxygen inside the reactor is crucial since the oxidation step is kinetically limited.25,26 Kuerten et al. demonstrated that a partial oxidation system achieves product selectivity exceeding 92% during the oxidative dehydrogenation of methanol to formaldehyde.27 Similarly, Mazloom et al. highlighted that incorporating a membrane significantly enhances product selectivity in the conversion of propane to acrolein and acrylic acid.28 In such circumstances, to enhance the selectivity towards acrylic acid the controlled amount of oxygen maintaining lower partial pressure by decreasing oxygen concentration is necessary because the reaction of acrolein also produces CO2 & CO. Hence, a membrane is a viable solution to distribute the controlled amount of oxygen inside the reactor.
Despite lots of research having been devoted to developing more effective catalysts, little or no literature is available on reactor performance and optimisation for the glycerol-to-acrylic acid pathway. This work aims to cover this gap by attempting for the first time an optimisation at the reactor level. The study is carried out focusing on the reactor operating conditions and also the reactor configuration study using CFD simulation coupled with response surface methodologies. The novelty of this study is represented by the intensification of the two-step process by integrating membranes for water removal and selective oxidation and their conceptual assessment in terms of performance.
2. Materials and methods
Using COMSOL Multiphysics 6.1 software, a 2D non-isothermal model was developed to explore the flow dynamics and chemical reactions involved in glycerol dehydration to acrolein and acrolein oxidation to acrylic acid. Response surface methodology (RSM) analysis, a statistical-based approach, generates a polynomial or linear model that aids in the experimental design process and establishes the relationship between input and output parameters, enabling effective modelling and optimization of the system.29,30 Further, the CFD model is integrated with RSM, and the CFD-RSM model is designed to evaluate the interaction between operating parameters and their effect on system performance. Thus, the optimal conditions for the system can be monitored with a series of simulations. This optimised solution is also applied to the CFD-RSM analysis of the membrane reactor.
2.1. Model configuration and assumptions
In the present study, the PBR model configuration is based on the experimental setup conditions used by Talebian-Kiakalaieh et al.10 for dehydration and Knoche et al.31 for the oxidation process. The general approach was to conduct a baseline CFD analysis for a PBR of 300 mm in length and 11 mm of I.D. The PBR schematic is shown in Fig. 1(a); the two other configurations, SMPBR in Fig. 1(b) and MBPR in Fig. 1(c), are also illustrated. These schemes evaluate the effectiveness of water removal through the sodalite membrane in the SMPBR configuration and the effectiveness of multi-bed versus single bed catalysts in the MBPR configuration during glycerol dehydration. To maintain a consistent GHSV, we reduced both the catalyst volume and feed flow rate by 25% in the SMPBR and MVPR configurations.
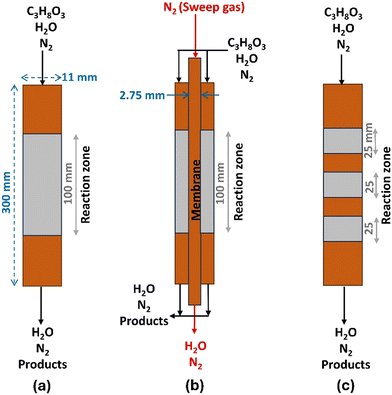 |
| | Fig. 1 Three simulated packed bed reactor schemes for the process of glycerol dehydration: (a): packed bed reactor (PBR), (b): sodalite membrane packed bed reactor (SMPBR), and (c): multi-bed packed reactor (MBPR). | |
Model validation has been carried out concerning the experimental results presented by Talebian-Kiakalaieh et al.,10,32 using a vertical packed-bed quartz reactor including a 0.5 g SiW20–Al/Zr10 catalyst, at atmospheric pressure, using 2 mL h−1 flow rate of a 10 wt% glycerol aqueous solution.
The computational domain of the PBR was discretized using structured rectangular meshes, chosen for their superior mesh quality and ability to ensure convergence during calculations.33 While the present study does not address modelling scale up and process implementation in industry, it provides the necessary background for comparative analysis and research hypothesis confirmation of different intensified reactors using experimental evidence following the same approach in ref. 34–36.
In the case of acrolein oxidation to acrylic acid, Fig. 2(a) shows a schematic representation of the PBR, and Fig. 2(b) includes the additional membrane needed to allow distributed oxygen feeding to the permeate side. The common approach remains the same to conduct a baseline CFD analysis for a PBR of 300 mm in length and 11 mm of I.D. Hence, a gas-phase oxidation of acrolein is taken from the experimental work by Knoche et al.31,37 They used a 0.5 g Mo–V–W mixed oxide catalyst at a temperature of 613 K, operating under atmospheric pressure with a total flow rate of 20 mL min−1.
 |
| | Fig. 2 Two simulated reactor schemes for the process of acrolein oxidation: (a) PBR and (b) MR. | |
Refinement of local meshes near the wall and catalyst bed was implemented while increasing the overall mesh size to enhance numerical accuracy and stability. Although more mesh elements can improve simulation precision, they also increase computational time and cost. To address this, a mesh independence analysis was conducted to determine the optimal number of grid elements, with results presented in the ESI.† Thus, the mesh size is calibrated to balance computational efficiency and numerical precision.
The main assumptions considered in the model are: i) steady-state conditions; ii) the reaction occurs only at the catalyst surface (https://www.sciencedirect.com/topics/engineering/catalyst-surface), hence enabling mass transfer resistance between the bulk gas and the catalyst surface; iii) pseudo-homogeneous conditions in the reaction zone in the reactor and also in the case of the membrane reactor; iv) the perm-selectivity values of the ceramic membranes are assumed to be similar to actual selectivity values.
2.2. Kinetic model
2.2.1. Dehydration process (step 1). Recently, numerous catalysts were developed for the dehydration process, including zeolite-based, metal oxide, heteropoly acid-based, and phosphate-based catalysts.9,38 However, due to the lack of limited kinetic data, just a few explain kinetic mechanisms with reaction rates having activation energy and frequency factors. The reaction mechanism proposed for glycerol dehydration to acrolein and other products, employing a supported solid acid catalyst (SiW20–Al/Zr10), is depicted in Fig. 3. According to previous studies by Talebian-Kiakalaieh and Park,10,11 the proposed mechanism elucidates that acrolein is formed through two consecutive glycerol dehydration steps. The first dehydration step produces two independent products: 3-HPA (3-hydroxypicolinic acid) and acetol, which follow separate pathways. However, due to its high reactivity, 3-HPA readily undergoes conversion into acrolein during the dehydration step (R1). It is worth noting that although 3-HPA is an intermediate product not explicitly included in the suggested mechanism, its significant reactivity towards acrolein is acknowledged.
 |
| | Fig. 3 The reaction pathway of the dehydration of glycerol over solid acid catalysts such as SiW20–Al/Zr10 used in the CFD model.10,11 | |
Fig. 3 illustrates the potential generation of various by-products during glycerol conversion. The suggested mechanism10 proposes a set of independent reactions (R1–R5) as depicted. The dehydration of glycerol to acrolein is represented by eqn (1) (R1), while eqn (2) (R2) is glycerol dehydration to acetol. Eqn (3) (R3) shows glycerol dehydration to acetaldehyde and formaldehyde. The conversion of acrolein to formaldehyde and carbon is represented by eqn (4) (R4), and finally eqn (5) (R5) denotes the dehydration of acetol to acetaldehyde.
| |
 | (1) |
| |
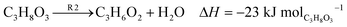 | (2) |
| |
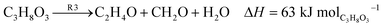 | (3) |
| |
 | (4) |
| |
 | (5) |
Table 1 reports the activation energies and the frequency factors of applied reactions (
eqn (1)–(5)). It should be noted that the reaction rate of each species is obtained according to
eqn (6)–(12).
| | |
RC3H8O3 = ρcatalyst × (−R1 − R2 − R3)
| (6) |
| | |
RC3H4O = ρcatalyst × (+R1 − R4)
| (7) |
| | |
RC3H6O2 = ρcatalyst × (+R2 − R5)
| (8) |
| | |
RC2H4O = ρcatalyst × (+R3 + R4 + R5)
| (9) |
| | |
RH2O = ρcatalyst × (+2R1 + R2 + R3)
| (10) |
| | |
RCH2O = ρcatalyst × (+R3 + R5)
| (11) |
| |
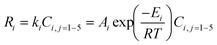 | (12) |
Table 1 Kinetic parameters for the 1st order reactions over the SiW20–Al/Zr10 catalyst in glycerol dehydration10
| Rate constant (ki) (m3 kgcatalyst−1 s−1) |
Activation energy (Ei) (kJ mol−1) |
Frequency factor (Ai) (m3 kgcatalyst−1 s−1) |
| k1 |
46.0 |
20.7 |
| k2 |
53.3 |
12.1 |
| k3 |
5.0 |
6.3 × 10–5 |
| k4 |
6.1 |
1.8 × 10–4 |
| k5 |
46.6 |
2.6 |
2.2.2. Oxidation process (step 2). Fig. 4 illustrates the proposed reaction mechanism for acrolein (C3H4O) oxidation to obtain acrylic acid (C3H4O2). It also includes by-products CO2, CO and H2O. The catalyst used in the reaction is a mixed oxide Mo–V–W. This mechanism was adopted with reference to the work of Drochner et al.15,39
 |
| | Fig. 4 Simplified scheme of the acrolein oxidation to acrylic acid on Mo–V–W-mixed oxides. | |
The reaction kinetics certainly depends on the interaction and involvement of oxygen molecules bound to the catalyst surface. When acrolein and oxygen (isotope 18, 18O2) are exposed for extended periods, it was reported that additional products devoid of 18O2 are still generated. This explains the exchange of oxygen atoms attached to the catalyst surface with the carbonyl oxygen of acrolein, resulting in the complete oxidation of acrolein to CO2, CO, and H2O. The simplified and generalized equations (eqn (13)–(17)) are elucidated below; these do not include the capability of isotope splitting.
| | |
C3H4O + 1/2O2 → C3H4O2 ΔH = −265.3 kJ molC3H4O−1
| (13) |
| | |
C3H4O + 7/2O2 → 3CO2 + 2H2O ΔH = −1594 kJ molC3H4O−1
| (14) |
| | |
C3H4O + 2O2 → 3CO + 2H2O ΔH = −744.5 kJ molC3H4O−1
| (15) |
| | |
C3H4O2 + 3O2 → 3CO2 + 2H2O ΔH = −1329 kJ molC3H4O2−1
| (16) |
| |
 | (17) |
Drochner
et al.15 originally proposed this mechanism and the kinetics of the reaction. In the literature, it was found that a first-order reaction is postulated for acrolein oxidation to acrylic acid and for all the other products, based on the Langmuir–Hinshelwood–Hougen–Watson (LHHW) model.
40 The reaction rate based on
Fig. 4 is described below.
| | |
RC3H4O = (−R1 − R2 − R3)
| (18) |
| | |
RC3H4O2 = (−R4 − R5)
| (19) |
| | |
RH2O = (2 R2 + 2 R3 + 2 R4 + 2 R5)
| (22) |
| | |
RO2 = (−0.5 − 3.5 R2 − 2 R3 − 3 R4 − 1.5 R5)
| (23) |
The reaction rate of individual species is derived by incorporating all the reactions described in
eqn (13)–(17).
Table 2 illustrates the activation energies and frequency factors for all the reactions concerning eqn (24)
| |
 | (24) |
Table 2 Kinetic parameters over the Mo–V–W mixed oxide catalyst for the acrolein oxidation reaction
| Rate constant (ki) (m3 mol−1 s−1) |
Activation energy (Ei) (kJ mol−1) |
Frequency factor (Ai) (m3 mol−1 s−1) × 107 |
| k1 |
108 |
3 |
| k2 |
153 |
2 × 103 |
| k3 |
158 |
3 × 103 |
| k4 |
153 |
20 |
| k5 |
158 |
30 |
2.3. Governing equations
2.3.1. Momentum and continuity equations for the gas phase. The general continuity equation for mass conservation in fluid dynamics considers a porous medium that occupies a fraction of the total volume (i.e., porosity, ε).
Considering a steady state system, the derivative term vanishes, and the continuity equation simplified for the reaction and inert parts is given in eqn (25).The general momentum equation for a fluid flow is:
Considering porosity, the term is modified with inertial and viscous terms. Also, considering a steady-state system, the derivative term becomes zero. Assuming incompressible flow and a Newtonian fluid, the equations can be further simplified.
where
f is the drag force modelled using the Darcy–Forchheimer equation, which includes viscous drag (Darcy term ∼

) and inertial drag (Forchheimer term ∼

).
Eqn (26) is the governing equation for the momentum of gas components in the reaction zone.
| |
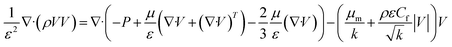 | (26) |
where
ε is the porosity,
ρ is the density,
V is the velocity in the gas phase,
P indicates the operating pressure,
μ is the dynamic viscosity,
κ represents the permeability of the catalytic bed and
Cf is the Forchheimer drag coefficient.
41 Eqn (26) is commonly referred to as the Forchheimer equation, which describes the non-Darcy flow regime. The bed porosity, permeability, and Forchheimer drag coefficient are derived utilizing the Ergun equation.
42| |
 | (27) |
| |
 | (28) |
| |
 | (29) |
The equation of momentum for the inert zone of the reactor is presented as follows:
| |
 | (30) |
It should be noted that
eqn (30) also has been used for the permeate side in the SMPBR case.
2.3.2. Species transport equation for the gas phase. The general species conservation equation for a fluid mixture is
where mi is the mass faction of species i, Ji is the diffusive flux of species i, and Ri is the rate of production or consumption of species i due to chemical reactions.Considering steady state conditions and porosity, the equation is modified as below:
| ∇·(ρεV) = −∇·(ρDi,e∇·mi) + (1 − ε)Ri + Si |
expressing
Ri in terms of molar quantities
Finally, the governing equation for mass transfer in the reaction zone (catalyst bed) is as follows:
| |
 | (31) |
The mass transfer equation for the inert zone is as follows:
| | |
∇·(ρεV) + ∇·(ρDi,e∇·mi) = Si
| (32) |
Here,
Si for oxidation is the oxygen flux term for the components of the MR whereas in the case of dehydration, it is considered as the source/sink term for the element of the sodalite membrane in the SMPBR case. For other cases, this term should be considered as zero. This term that accounts for the molar flow of species across the sodalite membrane is given in
eqn (33), wherein the details of steam flux through the sodalite membrane are given by Iwakiri
et al.43 as follows:
| |
 | (33) |
| |
 | (34) |
where

and

are the partial pressures for steam in the retentate and permeate sides, respectively,
EH2O is the apparent activation energy (
EH2O = 0.684 kJ mol
−1) and
Pe0 is the pre-exponential factor (
Pe0 = 7.86 × 10
−8 mol m
−2 s
−1 bar
−1).
2.3.3. Heat transfer equation for the gas phase. The general energy equation for a fluid (without radiation and viscous dissipation) is
Considering steady state conditions, the effective thermal conductivity λeff combines solid and fluid phases in a porous medium. Hence, eqn (35) describes the governing equation for heat transfer at the reaction side.| | |
ρCpV∇T − ∇·(λeff∇T) + QR = 0
| (35) |
| |
 | (36) |
where Hi and Cp are the molar enthalpy and the heat capacity at constant pressure, respectively, calculated using the seven-coefficient NASA polynomials.44 Also, λeff and QR refer to the effective thermal conductivity of the catalyst bed and the reaction heat, respectively. Indeed, the QR value was assumed to be zero for the inert zone.
2.3.4. Boundary conditions and post-processing definitions. Table 3 presents the boundary conditions for the inlet and outlet sides of the reactor.
Table 3 Boundary conditions used for both processes in the CFD model are listed below
| Position/equations |
Mass equations |
Momentum and continuity equations |
Thermal equation |
| Inlet (Z = 0) |
CGly, CH2O, CN2 |
Vz |
Ti |
| CAcr, CO2, CHe |
| Outlet (Z = L) |
— |
Pgauge = 0 |
— |
| Wall (r = R) |
— |
— |
Ts |
The following formulas are defined to describe the reactor systems during the process:
| |
 | (37) |
| |
 | (38) |
where
X1 is the glycerol conversion for the dehydration process
i.e. step 1 and
X2 is the acrolein conversion for the oxidation process step 2,
CGly-in and
CGly-out are the glycerol concentrations at the inlet and outlet of reactors, and
CAcr-in and
CAcr-out are the acrolein concentrations at the inlet and outlet of reactors, respectively.
| |
 | (39) |
| |
 | (40) |
| |
 | (41) |
| |
 | (42) |
Here,
Y1 is the acrolein yield,
Y2 the acrylic acid yield,
S1 the acrolein selectivity,
S2 the acrylic acid selectivity and
CAcr-out the acrolein concentration in the outlet of the studied reactors.
2.4. Numerical procedure and mesh independency
The CFD package in this study employs a 2D configuration and relies on the finite element method for mathematical calculations. The semi-implicit method for pressure linked equations (SIMPLE) algorithm was implemented to ensure accurate pressure–velocity correction.
Preliminary simulations were conducted using different mesh numbers: 2056, 4019, 8036, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972, 20
972, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467, and 40
467, and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 129 to assess the mesh independence of the CFD model for the dehydration process. Meanwhile, for the oxidation process, the mesh densities were varied from 2056 to 41
129 to assess the mesh independence of the CFD model for the dehydration process. Meanwhile, for the oxidation process, the mesh densities were varied from 2056 to 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 326 elements for more details please refer to ESI† sections A.1. and B.1.
326 elements for more details please refer to ESI† sections A.1. and B.1.
2.5. CFD model validation
The accuracy of CFD results was verified for dehydration and oxidation via experimental studies conducted by Talebian-Kiakalaieh et al.10 and Knoche et al.31,45 respectively by reproducing the same system and operating conditions for a PBR operated at 1 atm and GHSV = 4000 h−1. Also for the oxidation, a distinguished comparison has been made between acrolein conversion and acrylic acid selectivity as a function of reaction temperature. While verifying all the necessary parameters, they resembled the literature and maintained a pressure of 1 bar with a GHSV of 2000 h−1. The ESI† provides more insight with graphs in sections A.2. and B.2.
2.6. Experimental design procedure
This study used a fast-running approximation of the CFD analysis to develop the RSM model. The independent input variables considered in the study are reaction temperature, GHSV, and glycerol mass fraction, as indicated in ESI† sections A.3. and B.3. The three operating parameters were combined using the Box–Behnken design framework, a commonly used approach that resulted in 15 simulation runs. Instead of using experimental data, a CFD-RSM analysis was conducted to fit the CFD simulation runs. The response factors considered in the optimisation analysis were the highest acrolein yield, acrolein selectivity, and glycerol conversion values.
The study used RSM with deterministic CFD simulations, so repeated experiments were not feasible. Instead, sensitivity analysis, ANOVA, and the Box–Behnken design ensured model reliability.46–48 Grid independence tests and optimized parameter selection prevented data redundancy. Full statistical details (R2, p-values) are shown in the ESI.†49
The acrolein selectivity, acrolein yield, and glycerol conversion for dehydration and acrolein conversion, acrylic acid yield, and acrylic acid selectivity were calculated based on the CFD results. Further, preceding calculations were subjected to the analysis of variance method ANOVA. This method illuminates the interconnection between dependent (response) and independent process variables. The quality estimation of the ANOVA analysis was evaluated using the coefficient of determination R2adj and R2. The statistical magnitude was assessed through the F-test, P-values, and ratio of adequate precision. The Design-Expert v13.1.2 software was used to analyse the data for this sensitivity analysis study and regression coefficients.
3. Results and discussion
3.1. Glycerol dehydration process
3.1.1. Evaluation of the reaction temperature effect. The impact of reaction temperature on PBR performance in glycerol dehydration to acrolein was assessed, considering glycerol conversion, acrolein yield, and selectivity using equations presented in section 2.3.4. Boundary conditions and post-CFD-RSM results, obtained at 1 bar pressure, varying glycerol mass fractions (0.1, 0.3, and 0.5), and GHSV values (1500 h−1, 8250 h−1, and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1), showed that as the reaction temperature increases from 543 K to 623 K, the glycerol conversion increased due to the endothermic nature of the reaction as shown in 2D contours in Fig. 5(a). This effect was more pronounced at lower GHSV values (1500 h−1) compared to higher ones (15
000 h−1), showed that as the reaction temperature increases from 543 K to 623 K, the glycerol conversion increased due to the endothermic nature of the reaction as shown in 2D contours in Fig. 5(a). This effect was more pronounced at lower GHSV values (1500 h−1) compared to higher ones (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1), owing to longer residence times. Conversely, acrolein yield exhibited a similar trend in Fig. 5(b), while acrolein selectivity slightly increased with temperature across all GHSV values in Fig. 5(c).
000 h−1), owing to longer residence times. Conversely, acrolein yield exhibited a similar trend in Fig. 5(b), while acrolein selectivity slightly increased with temperature across all GHSV values in Fig. 5(c).
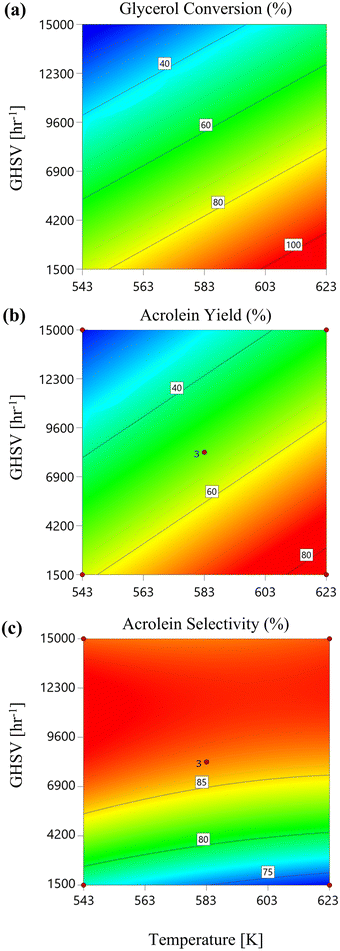 |
| | Fig. 5 Glycerol conversion (a), acrolein yield (b), and acrolein selectivity (c) versus reaction temperature at different GHSV values (at 1 bar reaction pressure and a mass fraction of glycerol of 0.3). | |
The higher activation energy values in the side reaction (eqn (3)) of acrolein conversion to other by-products, forming acetaldehyde and formaldehyde at high temperatures, diminish acrolein selectivity. These observations align with the experimental findings of Kirsten Schuh et al.50 In Fig. 6, response factors in terms of glycerol conversion, acrolein yield, and selectivity versus reaction temperature are obtained at GHSV = 1500 h−1 and GHSV = 8250 h−1. In terms of yield, acrolein production increases with temperature at GHSV = 8250 h−1, while an optimum value is seen at GHSV = 1500 h−1. This is explained by the fact that at higher GHSV the temperature effect on side reaction formation is insignificant since it has less residence time to form other by-products. However, acrolein selectivity in Fig. 6 demonstrates and confirms that increasing reaction temperature enhances the production of other components via side reactions (eqn (2)–(5)) across all GHSV values.
 |
| | Fig. 6 Glycerol conversion, acrolein yield, and acrolein selectivity versus reaction temperature at GHSV = 1500 h−1 (a) and GHSV = 8250 h−1 (b) (at 1 bar reaction pressure and a mass fraction of glycerol of 0.3). | |
Further results on the effect of GSHV on key reaction indicators are also presented in ESI† section A.5.
3.1.2. Evaluation of glycerol concentration. The glycerol content in the aqueous feed solution ranged from 0.1 to 0.5 weight fraction. Fig. 7 depicts response factors with increasing glycerol mass fraction at 583 K and a GSHV of 8250 h−1. Glycerol concentration minimally impacts glycerol conversion and has a limited effect on acrolein yield due to first-order kinetics (eqn (1)–(5)) since the variation of reaction rate is in the same proportion of glycerol concentration change. However, increasing glycerol concentration adversely affects acrolein selectivity, favouring side reactions and increasing by-product formation.
 |
| | Fig. 7 Glycerol conversion, acrolein yield, and acrolein selectivity versus glycerol concentration (at 1 bar, 583 K and 8250 h−1). | |
In Fig. 8, the 2D colour contours show this achievement more clearly at (a) different reaction temperatures and (b) GHSV values. The results show that higher values of acrolein selectivity can be achieved by decreasing the reaction temperature and increasing GHSV values at lower glycerol mass fraction ranges.
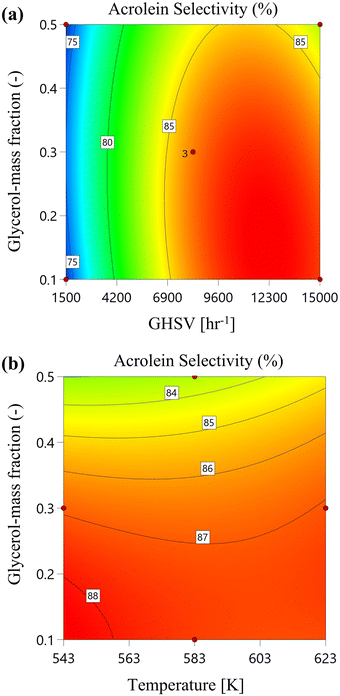 |
| | Fig. 8 Acrolein selectivity versus glycerol mass fraction at 1 bar reaction pressure: (a) by increasing reaction temperature and (b) by increasing GHSV value. | |
3.1.3. Optimisation and sensitivity analysis. According to the CFD-RSM model, the optimal input conditions to maximize glycerol conversion, acrolein yield, and acrolein selectivity in the PBR are 623 K, 5731.6 h−1, and a glycerol mass fraction of 0.316.Under the mentioned previous conditions, the model predicted a maximum glycerol conversion of 94.2%, an acrolein yield of 74.25%, and an acrolein selectivity of 79.62%. The analysis of 2D response surface contours further confirmed these optimum parameter values (as shown in Fig. 9).
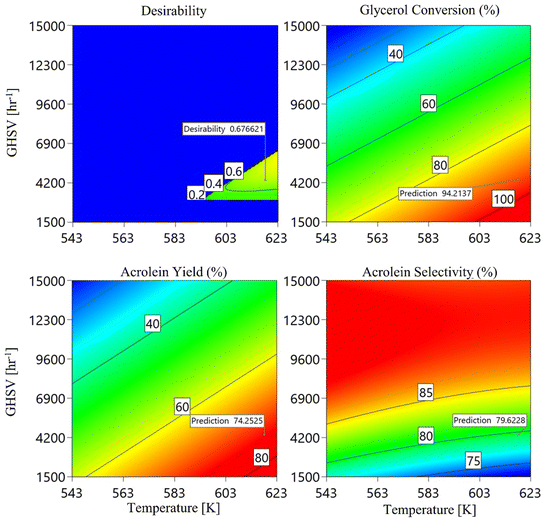 |
| | Fig. 9 The 2D response surface contours for glycerol conversion, acrolein yield, and acrolein selectivity (effects of reaction temperature and GHSV values). | |
The suggested conditions were established concerning minimum acceptable boundaries, considering results from experimental studies10,11 as benchmarks.
3.1.4. Analysis of other reactor configurations over a simple PBR. In this section, two proposed configurations (MBPR and SPBMR) were simulated, analysed, and compared with the PBR system. The theoretical analysis suggests that SPBMRs, incorporating a sodalite membrane for water removal from the reaction zone, may enhance glycerol conversion by shifting the reaction equilibrium towards products. Conversely, the application of MBPRs appears to enhance mass and heat transfer rates by creating an intermittent, turbulent flow regime along the reactor length, potentially improving reaction efficiency.Fig. 10 shows substantially that acrolein selectivity remains lower across all scenarios, indicating consistent behaviour with the previous configuration. Consequently, both MBPR and SPBMR configurations did not yield significant improvements in acrolein yield. These results can be explained by the first-order reaction kinetics. However, to assess the impact of this critical parameter, the kinetic correlation was manipulated to understand its effect on the SMPBR and MBPR performances compared to the PBR.
 |
| | Fig. 10 Acrolein yield versus increasing reaction temperature for three cases (PBR, MBPR, and SMPBR; at 5731.6 h−1, P = 1 atm and a glycerol mass fraction of 0.316). | |
Hence, the reaction rate was adjusted by varying the reaction order (n = 0.5, n = 1, and n = 2) while modifying the pre-exponential factor to achieve exact conversion under the optimal conditions calculated in section 3.1.3. Optimisation and sensitivity analysis. Subsequently, the same kinetic model was employed to simulate the SMPBR and MBPR cases for comparison. Such analysis is crucial for screening potential new kinetic mechanisms amid the uncertainties associated with developing glycerol dehydration catalysts and ongoing research.51
Fig. 11 demonstrates that glycerol conversion, which improved by 7.8% by removing steam through the reaction zone, particularly stands out for a reaction order of n = 2. However, this enhancement diminishes to 2.7% for a reaction order of n = 0.5. Conversely, the use of the MBPR case does not yield higher glycerol conversion breakthroughs, regardless of the kinetics mechanism (i.e., reaction orders).
 |
| | Fig. 11 Glycerol conversion versus different reaction orders of reaction for configurations of the SMPBR, MBPR, and PBR (at 623 K, 0.316 glycerol mass fraction and 5731.6 h−1). | |
3.2. Acrolein oxidation process
3.2.1. Evaluating the effect of reaction temperature. The altering effect of reaction temperature on the PBR for acrolein oxidation to acrylic acid was analysed with respect to the equation mentioned in section 2.3.4. Boundary conditions and post-processing definitions The reaction conditions were oxygen to acrolein molar ratios (0.5, 3.25, 6), with distinct GHSV values (1600 h−1, 8800 h−1, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1), and temperature ranging from 523 K to 623 K operating under a constant pressure of 1 bar. Despite the exothermic nature of the oxidation process, Fig. 12(a) shows 2D contours where acrolein conversion increased with temperature, especially noticeable at GHSV 8800 h−1, signifying a non-equilibrium kinetic nature. Similarly, in Fig. 12(b) acrylic acid yield exhibited a rising trend with temperature, while selectivity decreased due to increased side product formation associated with higher activation energy, hence leading to a higher CO and CO2 selectivity at elevated temperatures.
000 h−1), and temperature ranging from 523 K to 623 K operating under a constant pressure of 1 bar. Despite the exothermic nature of the oxidation process, Fig. 12(a) shows 2D contours where acrolein conversion increased with temperature, especially noticeable at GHSV 8800 h−1, signifying a non-equilibrium kinetic nature. Similarly, in Fig. 12(b) acrylic acid yield exhibited a rising trend with temperature, while selectivity decreased due to increased side product formation associated with higher activation energy, hence leading to a higher CO and CO2 selectivity at elevated temperatures.
 |
| | Fig. 12 Acrolein conversion (a), acrylic acid yield (b), and acrylic acid selectivity (c) versus reaction temperature at different oxygen/acrolein molar ratios (at 1 bar and a GHSV of 8800 h−1). | |
3.2.2. Evaluating the GHSV effect. The feed flow rate or GHSV is a key parameter significantly impacting reactor performance. The variation of GHSV was from 1600 h−1 to 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1 at a constant temperature of 573 K with different oxygen/acrolein molar ratios. At increased GSHV, the acrylic acid yield decreases because the acrolein conversion decreases due to the reduced residence time, Fig. 13(b). However, a slight improvement of the selectivity is recorded to partly mitigate the drop in the single-step conversion indicating the smaller influence of side reactions (to produce CO and CO2).
000 h−1 at a constant temperature of 573 K with different oxygen/acrolein molar ratios. At increased GSHV, the acrylic acid yield decreases because the acrolein conversion decreases due to the reduced residence time, Fig. 13(b). However, a slight improvement of the selectivity is recorded to partly mitigate the drop in the single-step conversion indicating the smaller influence of side reactions (to produce CO and CO2).
 |
| | Fig. 13 Acrolein conversion (a), acrylic acid yield (b), and acrylic acid selectivity (c) versus reaction GHSV at different oxygen/acrolein molar ratios (at 1 bar and 573 K). | |
3.2.3. Optimization and sensitivity analysis. According to the CFD-RSM model, optimal conditions were found at 583.5 K, a GHSV of 1600 h−1, and an oxygen/acrolein molar ratio of 5.7. Under these conditions, 2-D response surface contours were generated, resulting in a maximum acrolein conversion of 99.7%, an acrylic acid yield of 71.8%, and an acrylic acid selectivity of 75.7%, as shown in Fig. 14.
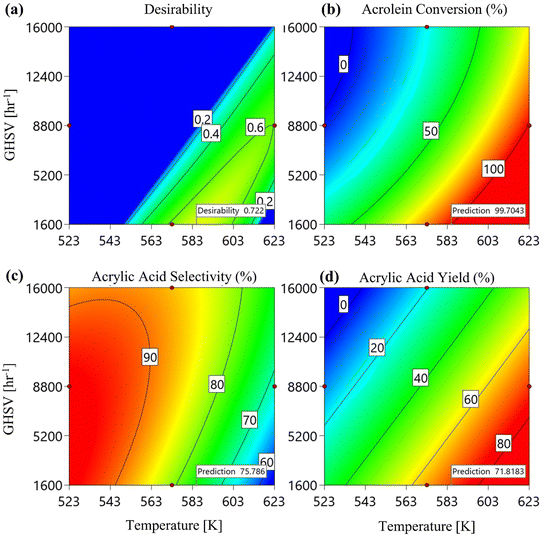 |
| | Fig. 14 The 2D response surface contours for (a) desirability, (b) acrolein conversion, (c) acrylic acid yield, and (d) acrylic acid selectivity. | |
3.2.4. Analysis of ceramic MR performance over a simple PBR. This section discusses the performance of the MR setup in two different permeation fluxes, MR1 and MR2, with simulation done using MR2 having 10 times greater permeation flux than MR1. To ensure that enough oxygen is fed to the reaction, in MR1 only 20% of the oxygen content was supplied in the radial direction (via membrane) and the rest is fed along with acrolein as for the PBR. In the case of MR2, since the permeation is 10× higher, the amount of oxygen fed via the membrane is 50% of the total.Results are compared and analysed with PBR system operation under similar optimized conditions. It was anticipated that applying a membrane reactor would enhance mass transfer by controlling flow regime and pore size distribution, thus increasing velocity to reduce boundary layer thickness and enhance convective mass transfer. Additionally, heat transfer rates can be improved by altering flow conditions and enhancing phase interaction. Fig. 15 illustrates acrolein conversion, acrylic acid yield, and selectivity for PBR, MR1, and MR2 under optimized conditions (T = 583.5 K, GHSV = 1600 h−1, and oxygen/acrolein molar ratio 5.7). This shows slight improvements in both acrolein conversion and acrylic acid yield with MR usage, confirming the hypothesis that distributing oxygen via side streams reduces the selectivity towards CO and CO2. At an increased permeation rate, the acrylic acid selectivity increased by 11.1% and yield by 6%.
 |
| | Fig. 15 Acrolein conversion, acrylic acid yield, and acrylic acid selectivity for three cases PBR, MR1, and MR2 (at temperature 583.5 K, GHSV 1600 h−1, and oxygen/acrolein molar ratio of 5.7). | |
ESI† provides insight into the dispersion of significant components, including acrolein, acrylic acid, oxygen, carbon dioxide, and steam, arranged from left to right in the plots. Additionally, oxygen distribution is represented on both sides of the permeate and retentate streams.
3.3. Overall optimal conditions for glycerol-to-acrylic acid
Given the performance of the two-step conversion of glycerol to acrylic acid with different reactor configurations, a matrix that would combine the two systems together is presented in Table 4 in terms of glycerol to acrylic acid conversion. This calculation does not consider any heat integration or unreacted stream recycling (since only once-through conversion is considered). Moreover, no effects of efficiency of separation and purification are taken into account which would require a more comprehensive and dedicated study. However, Table 4 indicates the effectiveness of the combined processes by using different combinations of the reactor configurations that were studied in this work. As expected, by using 0.624 mol m−3 s−1 glycerol for the dehydration process and 0.468 mol m−3 s−1 acrolein for the selective oxidation, a maximum amount of 0.506 kg of AA per kg of glycerol can be produced which is the optimum case. Instead, using packed bed reactors for both cases (the standard reactor configuration), the maximum acrylic acid production is limited to 0.469 kg of AA per kg of glycerol.
Table 4 The acrylic acid yield values by acrolein selective oxidation for different configurations (PBR, MR1, and MR2) are determined using glycerol dehydration reactor outputs as a feed resource
| Gly-to-AA |
Gly-to-Acr PBR |
Gly-to-Acr SMPBR |
Gly-to-Acr MBPR |
| Acr-to-AA PBR |
81.1% |
80.4% |
80.8% |
| Acr-to-AA MR1 |
82.6% |
81.8% |
82.3% |
| Acr-to-AA MR2 |
86.2% |
85.3% |
85.7% |
4. Conclusion
This work presented comprehensive CFD study simulations of a PBR configuration for glycerol dehydration and acrolein oxidation processes.
In the case of dehydration, the optimized conditions are 623 K, 5731.6 h−1 GHSV, and a glycerol mass fraction of 0.316 resulting in a maximum glycerol conversion of 94.2%, acrolein yield of 74.25%, and acrolein selectivity of 79.62%, which seems promising. The two alternative configurations did not show significant evidence of improved performance primarily because of the reaction order considered for glycerol dehydration.
In the case of oxidation, the optimum values obtained are: a temperature of 583.5 K, a GHSV of 1600 h−1, and an oxygen/acrolein molar ratio of 5.7. Following this, a maximum acrolein conversion of 95.9%, an acrylic acid yield of 80.9%, and an acrylic acid selectivity of 87.5% were obtained. Here, the use of a membrane to distribute the oxygen at the permeate side exhibited improved performance compared to the standard configuration with 11.1% higher acrylic selectivity and 6% higher acrylic acid yield.
This study confirmed the hypothesis that the glycerol-to-acrylic acid conversion can be theoretically improved using intensified reactors. The performance needs to be validated with experimental results to gain confidence in catalyst and membrane technologies applied to these specific processes. Furthermore, process modelling could be used to assess the techno-economic performance of the glycerol-to-acrylic acid process to account for other units and their implication in terms of cost, safety and energy requirements. Finally, a more detailed study should consider the opportunity to operate the two steps in a single reactor unit increasing the level of thermal integration.
Acronyms
| ANOVA | Analysis of variance |
| CFD | Computational fluid dynamics |
| GHSV | Gas hour space velocity |
| LHHW | Langmuir–Hinshelwood–Hougen–Watson |
| MBPR | Multi-bed packed reactor |
| PBR | Packed bed reactor |
| RSM | Response surface methodology |
| R&D | Research and development |
| SMPBR | Sodalite membrane packed bed reactor |
Symbols
| Ai | Frequency factor (m3 kgcatalyst−1 s−1) |
| Ei | Activation energy for kinetic correlations (kJ mol−1) |
| Ki | Permeability of the catalytic bed (m−2) |
| P | Operating pressure (bar) |
| R | Universal gas constant (J mol−1 K−1) |
| T | Operating temperature (K) |
| V | Velocity of the gas phase (m s−1) |
| Cf | Forchheimer drag coefficient (—) |
| Ci | Molar concentration (mol m−3) |
| Cp | Heat capacity at constant pressure (J kg−1 K−1) |
| db | Reactor diameter (m) |
| dp | Catalyst particle diameter (m) |
| Di,e | Effective diffusivity (m2 s−1) |
| EH2O | Apparent activation energy in the membrane flux |
| Hj | Molar enthalpy (J mol−1) |
| JH2O | Water molar flux (mol m−2 s−1) |
| MH2O | Molecular weight of steam (kg mol−1) |
| Mi | Molecular weight (kg mol−1) |
 | Partial pressure for steam in the retentate side (bar) |
 | Partial pressure for steam in the permeate side (bar) |
| Pe0 | Pre-exponential factor in the membrane flux |
| QR | Heat source of reaction (J m−3 s−1) |
| Rb | Reactor radius (m) |
| Ri | Reaction rate (m) |
| SH2O | Source/Sink terms of steam for the SMPBR case (J m−3 s−1) |
| Si | Oxygen flux term for the component of the membrane reactor (J m−3 s−1) |
| Zij | Stoichiometry coefficient (—) |
| B | ANOVA coefficient (—) |
| ε | Catalyst bed porosity (—) |
| k | Permeability of the catalytic bed (—) |
| μ | Dynamic viscosity of the gas phase (kg m−1 s−1) |
| λeff | Effective thermal conductivity of the catalytic bed (W m−1 K−1) |
| ρcat | Catalyst density (kg m−3) |
| ρ | Gas density (kg m−3) |
Data availability
The data that support the findings of this study are available within the article and the ESI.†
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors acknowledge the financial support from the EPSRC “Sustainable Production of ACrylic acId from reNewable waste Glycerol” project, EP/V026089/1. Prashant Pawanipagar would like to acknowledge the Social Welfare Department, Government of Maharashtra, India.
References
- N. Abas, A. Kalair and N. Khan, Review of Fossil Fuels and Future Energy Technologies, Futures, 2015, 69, 31–49, DOI:10.1016/j.futures.2015.03.003.
- S. Koch and R. Klitzman, Reliance on Fossil Fuels: Ethical Implications for Intensivists, Intensive Care Med., 2023, 49(3), 330–333, DOI:10.1007/s00134-023-06994-0.
- A. Abdullah, A. Abdullah, M. Ahmed, U. Okoye and M. Shahadat, A Review on Bi/Multifunctional Catalytic Oxydehydration of Bioglycerol to Acrylic Acid: Catalyst Type, Kinetics, and Reaction Mechanism, Can. J. Chem. Eng., 2022, 100, 2956–2985, DOI:10.1002/cjce.24295.
- A. Chieregato, M. D. Soriano, F. Basile, G. Liosi, S. Zamora, P. Concepción, F. Cavani and J. M. López Nieto, One-Pot Glycerol Oxidehydration to Acrylic Acid on Multifunctional Catalysts: Focus on the Influence of the Reaction Parameters in Respect to the Catalytic Performance, Appl. Catal., B, 2014, 150–151, 37–46 CrossRef CAS.
- A. Sandid, E. Jesús, C. D'Agostino and V. Spallina, Process Assessment of Renewable-Based Acrylic Acid Production from Glycerol Valorisation, J. Cleaner Prod., 2023, 418, 138127, DOI:10.1016/j.jclepro.2023.138127.
- U. C. Abubakar, Y. Bansod, L. Forster, V. Spallina and D. Carmine, Conversion of Glycerol to Acrylic Acid: A Review of Strategies, Recent Developments and Prospects, React. Chem. Eng., 2023, 1819–1838, 10.1039/d3re00057e.
- D. Sun, Y. Yamada, S. Sato and W. Ueda, Glycerol as a Potential Renewable Raw Material for Acrylic Acid Production, Green Chem., 2017, 19(14), 3186–3213, 10.1039/c7gc00358g.
- A. C. Dimian and C. S. Bildea, Sustainable Process Design for Manufacturing Acrylic Acid from Glycerol, Chem. Eng. Res. Des., 2021, 166, 121–134, DOI:10.1016/J.CHERD.2020.12.002.
- A. Abdullah, A. Zuhairi Abdullah, M. Ahmed, J. Khan, M. Shahadat, K. Umar and M. A. Alim, A Review on Recent Developments and Progress in Sustainable Acrolein Production through Catalytic Dehydration of Bio-Renewable Glycerol, J. Cleaner Prod., 2022, 341, 130876, DOI:10.1016/j.jclepro.2022.130876.
- A. Talebian-Kiakalaieh and N. A. S. Amin, Kinetic Study on Catalytic Conversion of Glycerol to Renewable Acrolein, Chem. Eng. Trans., 2017, 56, 655–660, DOI:10.3303/CET1756110 , SE-Research Articles.
- H. Park, Y. S. Yun, T. Y. Kim, K. R. Lee, J. Baek and J. Yi, Kinetics of the Dehydration of Glycerol over Acid Catalysts with an Investigation of Deactivation Mechanism by Coke, Appl. Catal., B, 2015, 176–177, 1–10, DOI:10.1016/J.APCATB.2015.03.046.
- T. Katou, D. Vitry and W. Ueda, Structure Dependency of Mo-V-O-Based Complex Oxide Catalysts in the Oxidations of Hydrocarbons, Catal. Today, 2004, 91–92, 237–240, DOI:10.1016/j.cattod.2004.03.039.
- C. Chen, N. Kosuke, T. Murayama and W. Ueda, Single-Crystalline-Phase Mo3VOx: An Efficient Catalyst for the Partial Oxidation of Acrolein to Acrylic Acid, ChemCatChem, 2013, 5(10), 2869–2873, DOI:10.1002/cctc.201300268.
- J. H. Miller and A. Bhan, Kinetic Modeling of Acrolein Oxidation Over a Promoted Mo−V Oxide Catalyst, ChemCatChem, 2018, 10(23), 5511–5522, DOI:10.1002/cctc.201801029.
- A. Drochner, P. Kampe, N. Menning, N. Blickhan, T. Jekewitz and H. Vogel, Acrolein Oxidation to Acrylic Acid on Mo/V/W-Mixed Oxide Catalysts, Chem. Eng. Technol., 2014, 37(3), 398–408, DOI:10.1002/ceat.201300797.
- J. H. Miller and A. Bhan, Reaction Pathways in Acrolein Oxidation over a Mixed-Oxide Catalyst, ChemCatChem, 2018, 10(22), 5242–5255, DOI:10.1002/cctc.201801027.
- K. Ghasemzadeh, N. Jafar Harasi, A. Iulianelli and A. Basile, Theoretical Evaluation of Various Configurations of Silica Membrane Reactor in Methanol Steam Reforming
Using CFD Method, Int. J. Hydrogen Energy, 2020, 45(12), 7354–7363 CrossRef CAS.
- K. Ghasemzadeh, M. Khosravi, S. M. Sadati Tileban, A. Aghaeinejad-Meybodi and A. Basile, Theoretical Evaluation of PdAg Membrane Reactor Performance during Biomass Steam Gasification for Hydrogen Production Using CFD Method, Int. J. Hydrogen Energy, 2018, 43(26), 11719–11730, DOI:10.1016/j.ijhydene.2018.04.221.
- F. Gallucci, Packed Bed Membrane Reactor, in Encyclopedia of Membranes, ed. E. Drioli and L. Giorno, Springer Berlin Heidelberg, Berlin, Heidelberg, 2015, pp. 1–2, DOI:10.1007/978-3-642-40872-4_436-1.
- M. P. Rohde, G. Schaub, S. Khajavi, J. C. Jansen and F. Kapteijn, Fischer–Tropsch Synthesis with in Situ H2O Removal – Directions of Membrane Development, Microporous Mesoporous Mater., 2008, 115(1–2), 123–136, DOI:10.1016/J.MICROMESO.2007.10.052.
- B. Ilić and S. G. Wettstein, A Review of Adsorbate and Temperature-Induced Zeolite Framework Flexibility, Microporous Mesoporous Mater., 2017, 239, 221–234, DOI:10.1016/J.MICROMESO.2016.10.005.
- S. Khajavi, J. C. Jansen and F. Kapteijn, Application of Hydroxy Sodalite Films as Novel Water Selective Membranes, J. Membr. Sci., 2009, 326(1), 153–160, DOI:10.1016/j.memsci.2008.09.046.
- N. Wang, Y. Liu, A. Huang and J. Caro, Supported SOD Membrane with Steam Selectivity by a Two-Step Repeated Hydrothermal Synthesis, Microporous Mesoporous Mater., 2014, 192, 8–13, DOI:10.1016/J.MICROMESO.2013.08.013.
- M. Lafleur, F. Bougie, N. Guilhaume, F. Larachi, P. Fongarland and M. C. Iliuta, Development of a Water-Selective Zeolite Composite Membrane by a New Pore-Plugging Technique, Microporous Mesoporous Mater., 2017, 237, 49–59, DOI:10.1016/J.MICROMESO.2016.09.004.
- A. Cruellas, J. Heezius, V. Spallina, M. van Sint Annaland, J. A. Medrano and F. Gallucci, Oxidative Coupling of Methane in Membrane Reactors; A Techno-Economic Assessment, Processes, 2020, 8(3), 274, DOI:10.3390/pr8030274.
- A. Cruellas, T. Melchiori, F. Gallucci and M. Van Sint Annaland, Oxidative Coupling of Methane: A Comparison of Different Reactor Configurations, Energy Technol., 2020, 8(8), 1900148, DOI:10.1002/ente.201900148.
- U. Kuerten, M. van Sint Annaland and J. Kuipers, Oxygen Distribution in Packed Bed Membrane Reactors For Partial Oxidation Systems and Its Effect On Product Selectivity, Int. J. Chem. React. Eng., 2004, 2, 1–24 Search PubMed.
- G. Mazloom and S. M. Alavi, Different Catalytic Reactor Technologies in Selective Oxidation of Propane to Acrylic Acid and Acrolein, Part. Sci. Technol., 2018, 36(1), 61–71, DOI:10.1080/02726351.2016.1209264.
- M. A. Ali and M. A. Talib, High Performance of Magnetic Mesoporous Modification for Loading and Release of Meloxicam in Drug Delivery Implementation, Mater. Today Commun., 2020, 23, 100890, DOI:10.1016/j.mtcomm.2019.100890.
- A. Yusra and M. A. Talib, Employing Sodium Hydroxide in Desulfurization of the Actual Heavy Crude Oil: Theoretical Optimization and Experimental Evaluation, Process Saf. Environ. Prot., 2020, 136, 334–342, DOI:10.1016/j.psep.2020.01.036.
- S. Knoche, M. Heid, N. Gora, D. Ohlig, A. Drochner, C. Hess, B. Etzold and H. Vogel, Mechanistic Study on the Selective Oxidation of Acrolein to Acrylic Acid: Identification of the Rate-Limiting Step via Perdeuterated Acrolein, ChemCatChem, 2019, 11(14), 3242–3252, DOI:10.1002/cctc.201900549.
- A. Talebian-Kiakalaieh and N. A. S. Amin, Kinetic Modeling, Thermodynamic, and Mass-Transfer Studies of Gas-Phase Glycerol Dehydration to Acrolein over Supported Silicotungstic Acid Catalyst, Ind. Eng. Chem. Res., 2015, 54(33), 8113–8121, DOI:10.1021/acs.iecr.5b02172.
- K. Ghasemzadeh, M. Ghahremani, T. Yousefi Amiri, A. Basile and A. Iulianelli, Hydrogen Production by Silica Membrane Reactor during Dehydrogenation of Methylcyclohexane: CFD Analysis, Int. J. Hydrogen Energy, 2021, 46(37), 19768–19777, DOI:10.1016/j.ijhydene.2020.05.046.
- J. Ortega-Casanova, Application of CFD on the Optimization by Response Surface Methodology of a Micromixing Unit and Its Use as a Chemical Microreactor, Chem. Eng. Process., 2017, 117, 18–26, DOI:10.1016/J.CEP.2017.03.012.
- J. Sajedifar, S. B. Mortazavi and H. A. Mahabadi, Performance Analysis, Statistical Modeling, and Multiple Response Optimization of a Novel Fixed-Bed Quartz Reactor Packed with Ba-Pt@γ-AL2O3 Using Response Surface Methodology, Heliyon, 2024, 10, e38087, DOI:10.1016/j.heliyon.2024.e38087.
- S. Gao, J. Li, X. Qiu, X. Zheng, M. Jin, Y. Liu and H. Mao, Numerical Simulation and Response Surface Analysis of Esterification of Monobutyl Chlorophosphate with N-Butanol in a Microchannel Reactor, Process, 2024, 12(10), 2116, DOI:10.3390/PR12102116.
- M. Heid, S. Knoche, N. Gora, D. Ohlig, A. Drochner, B. J. M. Etzold and H. Vogel, Dynamics of Bulk Oxygen in the Selective Oxidation of Acrolein, ChemCatChem, 2017, 9(12), 2390–2398, DOI:10.1002/cctc.201700124.
- T. Ma, M. Yin, C. Su, N. Guo, X. Huang, Z. Han, Y. Wang, G. Chen and Z. Yun, Recent Developments in the Field of Dehydration of Bio-Renewable Glycerol to Acrolein over Molecular Sieve Catalysts, J. Ind. Eng. Chem., 2023, 117, 85–102, DOI:10.1016/j.jiec.2022.10.043.
- J. Kunert, A. Drochner, J. Ott, H. Vogel, H. Fueß, K. Jan, D. Alfons, O. Jörg, V. Herbert, F. Hartmut, J. Kunert, A. Drochner, J. Ott, H. Vogel and H. Fueß, Synthesis of Mo/V Mixed Oxide Catalysts via Crystallisation and Spray Drying—a Novel Approach for Controlled Preparation of Acrolein to Acrylic Acid Catalysts, Appl. Catal., A, 2004, 269(1–2), 53–61, DOI:10.1016/J.APCATA.2004.03.050.
- P. Kampe, L. Giebeler, D. Samuelis, J. Kunert, A. Drochner, F. Haaß, A. H. Adams, J. Ott, S. Endres, G. Schimanke, T. Buhrmester, M. Martin, H. Fuess and H. Vogel, Heterogeneously Catalysed Partial Oxidation of Acrolein to Acrylic Acid—Structure, Function and Dynamics of the V–Mo–W Mixed Oxides, Phys. Chem. Chem. Phys., 2007, 9(27), 3577–3589, 10.1039/b700098g.
- O. Mohammad, S. Faryar and H. Ali, Optimization and Improvement of a Conventional Tri-Reforming Reactor to an Energy Efficient Membrane Reactor for Hydrogen Production, Chem. Eng. Process., 2022, 175, 108933, DOI:10.1016/j.cep.2022.108933.
- H. S. Fogler, Elements of Chemical Reaction Engineering, 4th edn, 2006 Search PubMed.
- I. G. I. Iwakiri, C. V. Miguel and L. M. Madeira, Modeling and Simulation of a Steam-Selective Membrane Reactor for Power-to-Methanol, Comput. Chem. Eng., 2022, 156, 107555, DOI:10.1016/J.COMPCHEMENG.2021.107555.
- A. Burcat, Third Millennium Ideal Gas and Condensed Phase Thermochemical Database for Combustion, 2002, No. Technion Aerospace Engineering (TAE) Report # 867, January 2001 Search PubMed.
- S. Knoche, M. Heid, N. Gora, D. Ohlig, A. Drochner, B. Etzold and H. Vogel, Mechanistic Study on the Selective Oxidation of Acrolein to Acrylic Acid Concerning the Role of Water, ChemCatChem, 2020, 12(13), 3560–3575, DOI:10.1002/cctc.201902348.
- J. Rahmannezhad and S. A. Mirbozorgi, CFD Analysis and RSM-Based Design Optimization of Novel Grooved Micromixers with Obstructions, Int. J. Heat Mass Transfer, 2019, 140, 483–497, DOI:10.1016/J.IJHEATMASSTRANSFER.2019.05.107.
- A. M. Awad, I. A. Hussein, M. S. Nasser, S. A. Ghani and A. O. Mahgoub, A CFD-RSM Study of Cuttings Transport in Non-Newtonian Drilling Fluids: Impact of Operational Parameters, J. Pet. Sci. Eng., 2022, 208, 109613, DOI:10.1016/J.PETROL.2021.109613.
- P. Chimchom, A. Matthujak, T. Sriveerakul, S. Sucharitpwatskul, C. Nuntadusit and S. Phongthanapanich, CFD and RSM Assist in Reducing the LPG Consumption of Burners for Agarwood Oil Production in Thailand, Combust. Sci. Technol., 2024, 00(00), 1–23, DOI:10.1080/00102202.2024.2380085.
- B. Jabbari, E. Jalilnejad, K. Ghasemzadeh and A. Iulianelli, Modeling and Optimization of a Membrane Gas Separation Based Bioreactor Plant for Biohydrogen Production by CFD–RSM Combined Method, J. Water Process Eng., 2021, 43, 102288, DOI:10.1016/J.JWPE.2021.102288.
- K. Schuh, W. Kleist, M. Høj, V. Trouillet, P. Beato, A. D. Jensen, G. R. Patzke and J. D. Grunwaldt, Selective Oxidation of Propylene to Acrolein by Hydrothermally Synthesized Bismuth Molybdates, Appl. Catal., A, 2014, 482, 145–156, DOI:10.1016/J.APCATA.2014.05.038.
- I. P. Rosas, J. L. Contreras, J. Salmones, C. Tapia, B. Zeifert, J. Navarrete, T. Vázquez and D. C. García, Catalytic Dehydration of Glycerol to Acrolein over a Catalyst of Pd/LaY Zeolite and Comparison with the Chemical Equilibrium, Catalysts, 2017, 7(3), 1–29, DOI:10.3390/catal7030073.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab and
Vincenzo Spallina
ab and
Vincenzo Spallina *a
*a


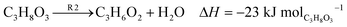
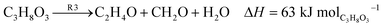


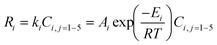


 ) and inertial drag (Forchheimer term ∼
) and inertial drag (Forchheimer term ∼  ).
).
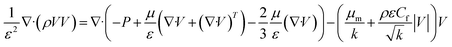







 and
and  are the partial pressures for steam in the retentate and permeate sides, respectively, EH2O is the apparent activation energy (EH2O = 0.684 kJ mol−1) and Pe0 is the pre-exponential factor (Pe0 = 7.86 × 10−8 mol m−2 s−1 bar−1).
are the partial pressures for steam in the retentate and permeate sides, respectively, EH2O is the apparent activation energy (EH2O = 0.684 kJ mol−1) and Pe0 is the pre-exponential factor (Pe0 = 7.86 × 10−8 mol m−2 s−1 bar−1).







![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972, 20
972, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467, and 40
467, and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 129 to assess the mesh independence of the CFD model for the dehydration process. Meanwhile, for the oxidation process, the mesh densities were varied from 2056 to 41
129 to assess the mesh independence of the CFD model for the dehydration process. Meanwhile, for the oxidation process, the mesh densities were varied from 2056 to 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 326 elements for more details please refer to ESI† sections A.1. and B.1.
326 elements for more details please refer to ESI† sections A.1. and B.1.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1), showed that as the reaction temperature increases from 543 K to 623 K, the glycerol conversion increased due to the endothermic nature of the reaction as shown in 2D contours in Fig. 5(a). This effect was more pronounced at lower GHSV values (1500 h−1) compared to higher ones (15
000 h−1), showed that as the reaction temperature increases from 543 K to 623 K, the glycerol conversion increased due to the endothermic nature of the reaction as shown in 2D contours in Fig. 5(a). This effect was more pronounced at lower GHSV values (1500 h−1) compared to higher ones (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1), owing to longer residence times. Conversely, acrolein yield exhibited a similar trend in Fig. 5(b), while acrolein selectivity slightly increased with temperature across all GHSV values in Fig. 5(c).
000 h−1), owing to longer residence times. Conversely, acrolein yield exhibited a similar trend in Fig. 5(b), while acrolein selectivity slightly increased with temperature across all GHSV values in Fig. 5(c).



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1), and temperature ranging from 523 K to 623 K operating under a constant pressure of 1 bar. Despite the exothermic nature of the oxidation process, Fig. 12(a) shows 2D contours where acrolein conversion increased with temperature, especially noticeable at GHSV 8800 h−1, signifying a non-equilibrium kinetic nature. Similarly, in Fig. 12(b) acrylic acid yield exhibited a rising trend with temperature, while selectivity decreased due to increased side product formation associated with higher activation energy, hence leading to a higher CO and CO2 selectivity at elevated temperatures.
000 h−1), and temperature ranging from 523 K to 623 K operating under a constant pressure of 1 bar. Despite the exothermic nature of the oxidation process, Fig. 12(a) shows 2D contours where acrolein conversion increased with temperature, especially noticeable at GHSV 8800 h−1, signifying a non-equilibrium kinetic nature. Similarly, in Fig. 12(b) acrylic acid yield exhibited a rising trend with temperature, while selectivity decreased due to increased side product formation associated with higher activation energy, hence leading to a higher CO and CO2 selectivity at elevated temperatures.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1 at a constant temperature of 573 K with different oxygen/acrolein molar ratios. At increased GSHV, the acrylic acid yield decreases because the acrolein conversion decreases due to the reduced residence time, Fig. 13(b). However, a slight improvement of the selectivity is recorded to partly mitigate the drop in the single-step conversion indicating the smaller influence of side reactions (to produce CO and CO2).
000 h−1 at a constant temperature of 573 K with different oxygen/acrolein molar ratios. At increased GSHV, the acrylic acid yield decreases because the acrolein conversion decreases due to the reduced residence time, Fig. 13(b). However, a slight improvement of the selectivity is recorded to partly mitigate the drop in the single-step conversion indicating the smaller influence of side reactions (to produce CO and CO2).