Open Access Article
Open Access ArticleByproduct-free curing of a highly insulating polyethylene copolymer blend: an alternative to peroxide crosslinking†
Massimiliano
Mauri
*a,
Anna
Peterson
 a,
Ayça
Senol
a,
Khalid
Elamin
ab,
Antonis
Gitsas
c,
Thomas
Hjertberg
d,
Aleksandar
Matic
b,
Thomas
Gkourmpis
d,
Oscar
Prieto
d and
Christian
Müller
a,
Ayça
Senol
a,
Khalid
Elamin
ab,
Antonis
Gitsas
c,
Thomas
Hjertberg
d,
Aleksandar
Matic
b,
Thomas
Gkourmpis
d,
Oscar
Prieto
d and
Christian
Müller
 *a
*a
aDepartment of Chemistry and Chemical Engineering, Chalmers University of Technology, 41296 Göteborg, Sweden. E-mail: mmauri@chalmers.se; christian.müller@chalmers.se
bDepartment of Physics, Chalmers University of Technology, 41296 Göteborg, Sweden
cInnovation & Technology, Borealis Polyolefine GmbH, 4021 Linz, Austria
dInnovation & Technology, Borealis AB, 44486 Stenungsund, Sweden
First published on 11th October 2018
Abstract
High-voltage direct-current (HVDC) cables are a critical component of tomorrow's power grids that seamlessly integrate renewable sources of energy. The most advanced power cable technology uses crosslinked polyethylene (XLPE) insulation, which is produced by peroxide crosslinking of low-density polyethylene (LDPE). Peroxide crosslinking gives rise to hazardous byproducts that compromise the initially excellent purity and cleanliness of LDPE, and hence increase the electrical conductivity of the insulation material. Therefore, a byproduct-free curing process, which maintains the processing advantages and high electrical resistivity of LDPE, is in high demand. Here, we demonstrate a viable alternative to peroxide crosslinking that fulfils these requirements. Click chemistry reactions between two polyethylene copolymers allow the design of a curing process that is additive-free and does not result in the release of any byproducts. The thermoplastic copolymer blend offers a broad processing window up to 140 °C, where compounding and shaping can be carried out without curing. At more elevated temperatures, epoxy and acrylic acid functional groups rapidly react without byproduct formation to form an infusible network. Strikingly, the crosslinked copolymer blend exhibits a very low direct-current (DC) electrical conductivity of 2 × 10−16 S cm−1 at a typical cable operating temperature of 70 °C, which is on par with values measured for both ultra-clean LDPE and commercial XLPE. Hence, the use of polyethylene copolymer blends opens up the possibility to replace peroxide crosslinking with click chemistry type reactions, which may considerably expand the versatility of the most common type of plastic used today.
1. Introduction
Worldwide, we are currently witnessing an accelerating shift from fossil energy sources to renewables driven by the urgent need to reduce carbon emissions. Wind, solar and hydro power is most abundant in places far away from the end user, which necessitates the efficient transport of electricity over long distances. Alternative grid designs are needed that complement high-voltage alternating current (HVAC) cables – which form the backbone of traditional energy grids – with high-voltage direct current (HVDC) cables.1,2 The decisive reduction in transmission losses that can be achieved with HVDC cables allows the reach of power grids to be expanded from hundreds to thousands of kilometers.When power is to be transmitted across large bodies of water or densely populated areas, HVDC cables must be submerged or buried underground. Such cables need to be surrounded by an insulation layer, which is required to be of exceptional quality to withstand the very high transmission voltage of hundreds of kilovolts (the current record is 640 kV).2 The insulation material must be characterized by a very low direct-current (DC) electrical conductivity on the order of σDC ∼ 10−16 S cm−1.3,4 The insulation of the most advanced type of HVDC cable consists of low-density polyethylene (LDPE), which (in contrast to other grades of polyethylene) can be produced with a high degree of both physical and chemical cleanliness, resulting in the required low conductivity. Several strategies such as blending with high-density polyethylene (HDPE)3 and the addition of metal oxide nanoparticles4–8 or reduced graphene oxide9 have been proposed as means to further reduce the conductivity.
One major disadvantage of LDPE is the low onset of melting and low peak melting temperature Tm of 110 °C or less. HVDC cables typically operate at a temperature of 50 to 70 °C, but they can briefly experience temperatures higher than Tm under overload conditions such as a lightning strike.10,11 Therefore, LDPE must be crosslinked to prevent creep and ultimate failure. The most widely used crosslinking process is based on peroxides and in particular dicumyl peroxide (DCP),11–13 which produces volatile and hazardous byproducts such as water, methane, acetophenone, cumyl alcohol and α-methyl styrene.14,15 These unwanted byproducts must be removed by means of a time and energy consuming degassing step.16 Since even traces of the remaining impurities can increase the electrical conductivity of polyethylene, any reduction in the amount of peroxide tends to improve the overall quality of the insulation material.17–19 Evidently, it would be highly desirable if peroxide crosslinking could be replaced altogether with a curing process that completely avoids the release of any harmful byproducts.
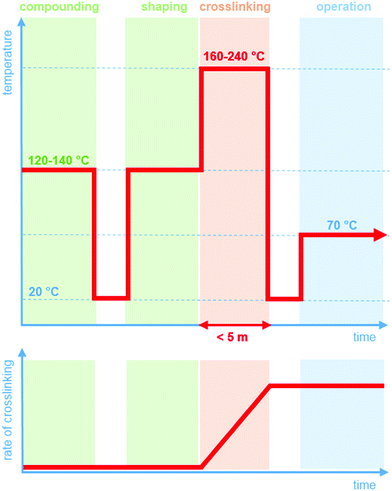
Crosslinking chemistry must fulfil a number of requirements. Prior to the actual curing step, it should be possible to compound and shape the LDPE resin without the occurrence of the crosslinking reaction (Fig. 1). Since LDPE is typically extruded at 120 to 140 °C, it is critical that across this processing window, the crosslinking agent is inactive. In contrast, at more elevated temperatures of typically 160 to 240 °C, the curing reaction must be rapid so that an infusible network is obtained within a short period of time, i.e. commonly five minutes or less. This demanding combination of a distinct processing and crosslinking window is the reason why, despite its shortcomings, peroxide crosslinking continues to be the method of choice to obtain an infusible network of crosslinked polyethylene (XLPE). The development of a byproduct-free curing process would significantly broaden the scope of LDPE based insulation materials.
One intriguing way to crosslink polyethylene is through the incorporation of functional comonomers, which can on-demand react to cure the polymer. One example is silane crosslinking, where crosslinking via the comonomer vinyltrimethoxysilane (VTMS) is initiated by water,11–13,20 which, however, prevents its use for high-voltage applications. We as well as others have recently explored the viability of a click chemistry type curing of polyethylene copolymers that feature epoxy functional groups as part of a glycidyl methacrylate comonomer.21–23 Such ethylene–glycidyl methacrylate copolymers are widely used for reactive processing – a common tool for the compatibilization of polymer blends – which, however, requires that the degree of crosslinking is kept low in order to not compromise the flow properties of the resin.24–28 A variety of functional groups such as amines, carboxylic acids and phenols can react with oxirane rings,29 which opens up the possibility for crosslinking with bifunctional curing agents. We have demonstrated that an ethylene–glycidyl methacrylate copolymer can be readily cured with 1,8-diaminooctane, leading to a high degree of gel formation in about 10 min at 200 °C.22 In another study, we reduced the curing time at 200 °C to only 2 min by combining a phenol-based crosslinking agent with a titanium-based Lewis acid.23 The electrical conductivity of click-chemistry cured copolymers has not yet been characterized. Even though the glycidyl methacrylate comonomer reduces the purity of the insulation material, the polar groups are not necessarily harmful and, in some cases, can even improve the electrical properties.30 However, the use of small-molecular crosslinking agents is not ideal since any molecule that does not participate in a curing reaction may migrate in the insulation material and act as a charge carrier, which would increase the electrical conductivity.
Here, we establish a novel concept for the preparation of a highly insulating XLPE based on blending of two polyethylene copolymers. In particular, we explore a blend that consists of a statistical ethylene–glycidyl methacrylate copolymer, p(E-stat-GMA), and a statistical ethylene–acrylic acid copolymer, p(E-stat-AA). We are able to extrude the copolymer blend at 120 to 140 °C whilst avoiding the curing reaction, which offers a sufficiently broad processing window for compounding and shaping. Once we increase the temperature to more than 160 °C, rapid curing occurs. The click chemistry nature of the here explored curing concept is byproduct-free, and therefore it meets all processing requirements that an LDPE resin must fulfil. Moreover, we find that the crosslinked copolymer resin features a promisingly low DC electrical conductivity of 2 × 10−16 S cm−1, which is on par with commercial high-voltage insulation materials.
2. Results and discussion
We chose to work with two branched grades of p(E-stat-GMA) and p(E-stat-AA) that feature a similar weight fraction of the comonomers, i.e. 8 wt% and 7 wt%, which translates into an ethylene-to-comonomer ratio of 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 35
1 and 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. The neat copolymers feature a peak melting temperature of about 105 and 98 °C. The average thickness of the crystalline lamellae, lc, can be calculated from the melting temperatures using the Gibbs–Thomson equation:
1, respectively. The neat copolymers feature a peak melting temperature of about 105 and 98 °C. The average thickness of the crystalline lamellae, lc, can be calculated from the melting temperatures using the Gibbs–Thomson equation: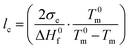 | (1) |
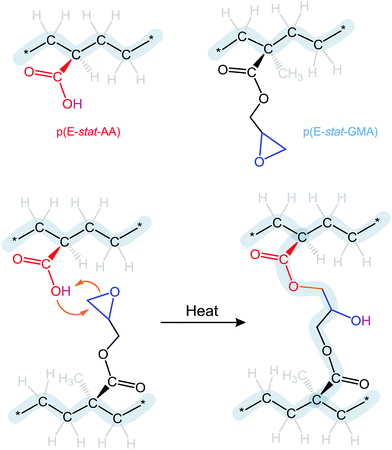
The choice of blend stoichiometry is likely to influence the type of crosslinks that can form. The uncatalyzed reaction of epoxy and carboxyl groups will yield (1) the ester of the primary hydroxyl group, which will covalently link the two polymers, and (2) a hydroxyl group that appears due to opening of the epoxy ring (Fig. 2). Excess of either comonomer may result in a follow-up reaction involving the latter, provided that the temperature is sufficiently high. Excess carboxylic acid may react with the hydroxyl group leading to complete esterification and the release of water as a byproduct. Instead, an excess amount of glycidyl methacrylate may react with the hydroxyl group, resulting in ether formation and no byproducts. We therefore chose to work with a 1.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 p(E-stat-GMA):p(E-stat-AA) blend stoichiometry so that an equal amount of each comonomer is present. To examine if side reactions may have occurred, we carried out Fourier-transform infrared (FTIR) spectroscopy on a series of films crosslinked at 200 °C for different amounts of time, and we compared the height of the fitted peak at 1705 cm−1, arising from the unreacted carboxylic acid group, with the height of the peak at 911 cm−1, associated with C–O deformation of the oxirane ring (ESI,† Fig. S1). We observed that the epoxy and carboxylic acid are consumed at the same rate, which suggests that the two groups react with each other and that the above mentioned side reactions are largely absent. Further, we ruled out esterification because of the absence of the prominent water absorption band in the region between 3500 and 3700 cm−1, associated with the symmetric and asymmetric stretching of the O–H groups (ESI,† Fig. S2), which we would expect if water was produced as a side product. To further test for the presence of water and other volatile byproducts, we performed thermogravimetric analysis (TGA). We selected a TGA heating profile that mimics the curing process (15 minutes at 180 °C in this case) and compared a 1.7
1 p(E-stat-GMA):p(E-stat-AA) blend stoichiometry so that an equal amount of each comonomer is present. To examine if side reactions may have occurred, we carried out Fourier-transform infrared (FTIR) spectroscopy on a series of films crosslinked at 200 °C for different amounts of time, and we compared the height of the fitted peak at 1705 cm−1, arising from the unreacted carboxylic acid group, with the height of the peak at 911 cm−1, associated with C–O deformation of the oxirane ring (ESI,† Fig. S1). We observed that the epoxy and carboxylic acid are consumed at the same rate, which suggests that the two groups react with each other and that the above mentioned side reactions are largely absent. Further, we ruled out esterification because of the absence of the prominent water absorption band in the region between 3500 and 3700 cm−1, associated with the symmetric and asymmetric stretching of the O–H groups (ESI,† Fig. S2), which we would expect if water was produced as a side product. To further test for the presence of water and other volatile byproducts, we performed thermogravimetric analysis (TGA). We selected a TGA heating profile that mimics the curing process (15 minutes at 180 °C in this case) and compared a 1.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 p(E-stat-GMA):p(E-stat-AA) blend with an LDPE crosslinked using 2 wt% DCP (ESI,† Fig. S3). No release of byproducts could be detected for the 1.7
1 p(E-stat-GMA):p(E-stat-AA) blend with an LDPE crosslinked using 2 wt% DCP (ESI,† Fig. S3). No release of byproducts could be detected for the 1.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 p(E-stat-GMA):p(E-stat-AA) blend, while DCP crosslinking gave rise to a weight loss of 1.5%.
1 p(E-stat-GMA):p(E-stat-AA) blend, while DCP crosslinking gave rise to a weight loss of 1.5%.
We compounded the two copolymers by co-extrusion at 120 °C (see the Experimental section for details) and obtained a visually homogeneous extrudate. We used an extruder where the melt is recirculated several times before exiting the die, and we noted that the pressure inside the barrel did not change with the dwell time, indicating that no appreciable crosslinking occurred. It can be anticipated that a certain degree of miscibility is required to facilitate the proximity of the glycidyl methacrylate and acrylic acid comonomers throughout the blend, which is a prerequisite for them to undergo a crosslinking reaction. We therefore analyzed the phase behavior using FTIR spectroscopy and thermal analysis.
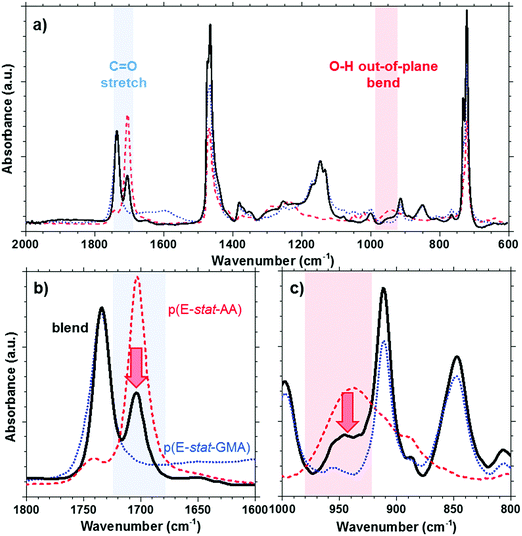
The acrylic acid units are located in the amorphous phase. At room temperature, most acid groups are dimerized.31 By collecting the FTIR spectra of p(E-stat-AA) while stepwise increasing the temperature, we concluded that the acid groups are predominantly present in the dimerized state up to at least 90 °C, which is close to the peak melting temperature of the polymer (see the ESI,† Fig. S4). For the here studied copolymer blend, the presence of dimers can be discerned by the prominent FTIR peaks at 1705 cm−1 (out-of-plane C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching in the dimer31) and 940 cm−1 (O–H out-of-plane bend in the dimer32), which we readily observe for neat p(E-stat-AA) at ambient temperature (Fig. 3). In the case of a strongly phase-separated blend, we would expect that the relative amount of acid dimers, normalized with regard to the fraction of p(E-stat-AA), would not be affected by the presence of the second blend component. Instead, we observe that the relative amount of acid dimers strongly decreases upon blending. We integrated the FTIR signal at 1705 cm−1 to estimate the relative amount of acid dimers and found that blending at a 2
O stretching in the dimer31) and 940 cm−1 (O–H out-of-plane bend in the dimer32), which we readily observe for neat p(E-stat-AA) at ambient temperature (Fig. 3). In the case of a strongly phase-separated blend, we would expect that the relative amount of acid dimers, normalized with regard to the fraction of p(E-stat-AA), would not be affected by the presence of the second blend component. Instead, we observe that the relative amount of acid dimers strongly decreases upon blending. We integrated the FTIR signal at 1705 cm−1 to estimate the relative amount of acid dimers and found that blending at a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 copolymer ratio reduces the number of dimers by more than 50%. Since acid dimers reside only in the amorphous phase,33,34 we ascribe the observed reduction in the degree of dimerization to at least partial miscibility of the two copolymers in the amorphous phase.
1 copolymer ratio reduces the number of dimers by more than 50%. Since acid dimers reside only in the amorphous phase,33,34 we ascribe the observed reduction in the degree of dimerization to at least partial miscibility of the two copolymers in the amorphous phase.
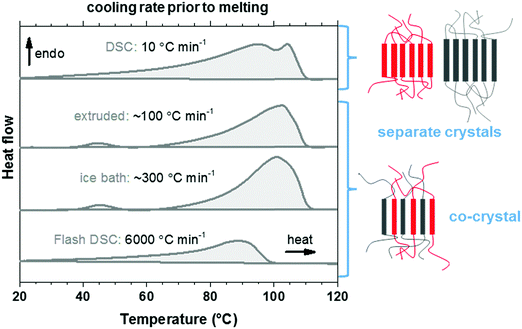
We used thermal analysis to confirm that the here studied copolymer blend is miscible, using co-crystallization as an indicator. A set of differential scanning calorimetry (DSC) heating thermograms of the blend cooled at different rates from the melt at 120 °C was recorded. Polyethylene blends that are miscible in the melt tend to phase-separate upon crystallization, leading to two populations of crystalline lamellae and therefore two distinct melting endotherms. Co-crystallization can occur if the blend components do not have time to phase-separate, i.e. the blend solidifies rapidly from the melt. The presence of a single broad melting endotherm when reheating quenched material is evidence for co-crystallization in the melt-miscible polyethylene blends.35–37 Quenching of p(E-stat-GMA):p(E-stat-AA) by submerging the molten material in an ice bath, or by means of fast scanning chip calorimetry, resulted in a material that displayed a single broad melting endotherm upon reheating (Fig. 4), which indicates co-crystallization. The extruded material displayed comparable behavior. However, the material that was cooled more slowly, i.e. at 10 °C min−1, featured two distinct melting endotherms. We therefore conclude that the copolymer blend is (at least in part) melt-miscible but phase-separates upon crystallization when cooled slowly. This conclusion is supported by scanning electron microscopy (SEM) images of the stochiometric p(E-stat-GMA):p(E-stat-AA) blend, in which no distinct, phase-separated domains can be detected (ESI,† Fig. S5).
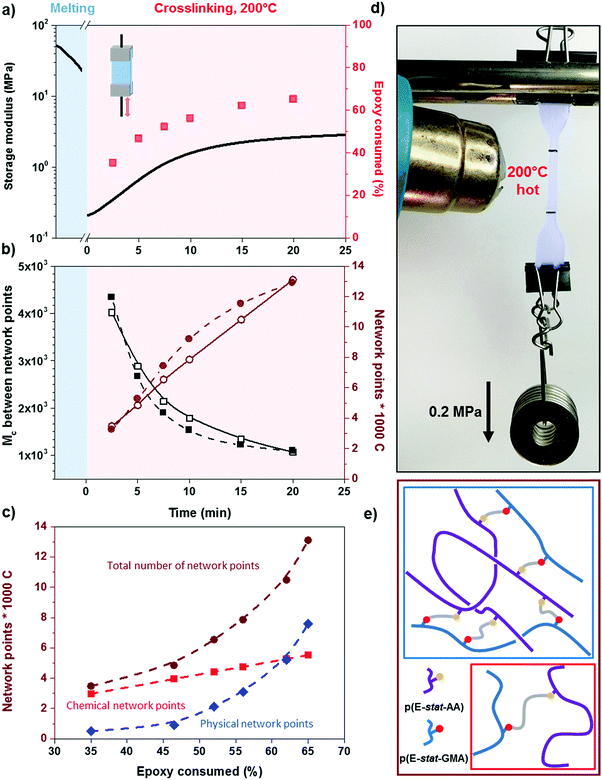
We went on to study the rate of crosslinking of the 1.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 p(E-stat-GMA):p(E-stat-AA) blend at different temperatures. For the compounding and shaping window, i.e. 120 to 140 °C (Fig. 1), we used rheology to monitor the increase in modulus with time. From the storage modulus G′, we were able to calculate the number of network points via the molecular weight between crosslinks Mc according to:
1 p(E-stat-GMA):p(E-stat-AA) blend at different temperatures. For the compounding and shaping window, i.e. 120 to 140 °C (Fig. 1), we used rheology to monitor the increase in modulus with time. From the storage modulus G′, we were able to calculate the number of network points via the molecular weight between crosslinks Mc according to:
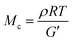 | (2) |
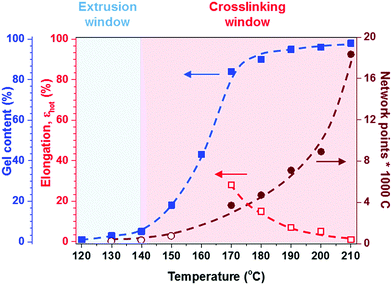 | ||
Fig. 5 Effect of temperature on hot set elongation ( ), number of network points per 1000 C atoms ( ), number of network points per 1000 C atoms ( from hot set, from hot set,  from rheology), and gel content ( from rheology), and gel content ( ) for a 1.7 ) for a 1.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric p(E-stat-GMA):p(E-stat-AA) blend cross-linked for 5 minutes; note that industrial standards for electrical insulation demand a hot set elongation of εhot = λhot − 100% < 75% for σ = 0.2 MPa.42 1 stoichiometric p(E-stat-GMA):p(E-stat-AA) blend cross-linked for 5 minutes; note that industrial standards for electrical insulation demand a hot set elongation of εhot = λhot − 100% < 75% for σ = 0.2 MPa.42 | ||
At a more elevated curing temperature of 150 °C, the gel content increases rapidly, reaching more than 90% at 180 °C and above, which confirms that an infusible network has formed (Fig. 5). Evidently, a broad range of temperatures exists where curing of the copolymer blend can be carried out. We used hot set elongation measurements (see the Experimental section for details) to estimate the number of network points. We obtained this value by calculating the molecular weight between crosslinks Mc as given by the affine network model, which is applicable to elastomers:38
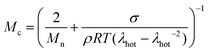 | (3) |
To gain insight into the speed of the curing process, in a further set of experiments, we studied network formation as a function of time at a fixed temperature of 200 °C (ESI,† Fig. S6). We used two techniques to calculate the number of network points, (1) hot set elongation measurements (cf.eqn (3)) and (2) dynamic mechanical analysis (DMA). To realize the latter, we positioned a slightly crosslinked sample that had been cured for 5 minutes at 150 °C (∼0.7 crosslinks per 1000 carbon atoms) in a DMA instrument. The sample was then quickly heated to 200 °C at a rate of 20 °C min−1. At this temperature, we monitored the gradual increase in storage modulus G′ during an isothermal measurement for 25 minutes at a torsion frequency of 0.5 Hz and 1% strain (Fig. 6a). We calculated the molecular weight between crosslinks Mc once again according to eqn (2), using a value of ρ = 0.754 g cm−3 for the density of LDPE at 200 °C. The values for Mc and hence the number of network points that we obtained from hot set elongation measurements and DMA are in good agreement (Fig. 6b). After a curing time of only 2.5 min at 200 °C, we estimate that about 4 network points are present per 1000 carbons, which favorably compares with DCP crosslinking for which 3 network points per 1000 carbons are achieved under the same conditions (data not shown). For comparison, in our previous studies, we achieved a comparable number of network points only after curing for 10 and 20 min at 200 °C in the case of crosslinking of p(E-stat-GMA) with amines22 and phenols.23 We conclude that the here studied copolymer blend rapidly reacts to form an infusible network, resulting in a material that does not change shape even far above its melting temperature (Fig. 6d).
In the crosslinked blend, two types of network points exist in the molten state, (1) covalent crosslinks due to the reaction between the glycidyl methacrylate and acrylic acid comonomers and (2) trapped entanglements. To elucidate the extent to which each type contributes to the overall number of network points, which we measured with DMA and hot set elongation measurements (cf.Fig. 6b), we followed the epoxy ring consumption with FTIR spectroscopy. Each epoxy ring opening gives rise to one covalent crosslink. We observed two peaks at 3050 and 911 cm−1 that are characteristics of the oxirane ring, which we attribute to the C–H tension of the methylene bridge of the epoxy ring and C–O deformation of the oxirane group, respectively. Since the first signal is located close to a prominent O–H absorption band, we used the C–O peak to follow the curing reaction. The C–O peak intensity gradually decreased with increasing consumption of the epoxy ring by the curing reaction, which allowed us to quantify the number of covalent crosslinks (we used the carbonyl peak at 1750 cm−1 for normalization). Comparison between the number of covalent crosslinks (from FTIR spectroscopy) and the total number of network points (from DMA and hot set elongation) indicates that the trapped entanglements become more prominent as soon as more than half the epoxy rings are consumed. For an epoxy consumption of 65%, we note that trapped entanglements are the dominating type of network point, which indicates that one way to further adjust the thermo-mechanical properties of the cured copolymer blends is through changes in the molecular weight and the degree of branching.
We now turn our attention to the electrical properties of the copolymer blend. To determine the DC electrical conductivity, we carried out a series of broadband dielectric spectroscopy (BDS) measurements. Initially, we characterized an LDPE grade that we have investigated previously at a high field of 30 kV mm−1 and 70 °C, yielding a value of σDC ∼ 10−16 S cm−1.3 The conductivity measured with BDS shows a marked frequency dependence (ESI,† Fig. S7). At high frequencies, energy loss associated with dispersion of the dielectric constant results in a steady increase in conductivity with frequency. In this regime, the dielectric response of the material is dominated by dipole relaxation mechanisms. Instead, at sufficiently low frequencies, the conductivity is only determined by the migration of charge carriers and it approaches a constant value. We use this plateau value as a proxy for σDC. For our reference LDPE, we measured a value of σDC ∼ 1.8 × 10−16 S cm−1 at 70 °C (Table 1; ESI,† Fig. S7), which is in good agreement with our previous report.37 Here, we must note that the values of σDC reported previously were measured at high fields, whereas the values reported in this work were measured at significantly lower fields with BDS. This implies that the measurements reported previously were located on the non-linear part of the conductivity–field strength regime. In that region, the charge conduction (ionic movement and hoping of electrons/holes) exhibits both a temperature and field dependence.39 In contrast, the measurements reported in this work are obtained at low field strengths (∼10–100 V mm−1) and fall within the linear (ohmic) regime. Despite these differences, we can see that the conductivity values are similar, which we explain with the exceptionally low amount of charge carriers in the system under investigation. Furthermore, we note that due to the frequency dependence of the conductivity, the initiation of the frequency plateau is outside the investigated frequency window at temperatures below 50 °C. Therefore, we were only able to extract a value for the DC electrical conductivity at elevated temperatures. Finally, it is worth noting that despite the apparent plateau of the measured electrical conductivity, minute changes still occur due to leakage currents. However, those are overshadowed by the nature of the conductivity mechanism that is dominated by migration of charges and not the chain mobility.
| Cured | Stoichiometry | Copolymer 1 | Comonomer content | Copolymer 2 | Comonomer content | Polymer 3 | σ DC at 70 °C (10−16 S cm−1) | σ DC at 90 °C (10−16 S cm−1) |
|---|---|---|---|---|---|---|---|---|
| a Commercial XLPE grade. | ||||||||
| No | 1.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
p(E-stat-GMA) | 8 wt% GMA | p(E-stat-AA) | 7 wt% AA | — | 1.3 | 8.2 |
| Yes | 1.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
p(E-stat-GMA) | 8 wt% GMA | p(E-stat-AA) | 7 wt% AA | — | 2.1 | 16 |
| No | — | — | — | — | — | LDPE | 1.8 | 23 |
| Yes | — | — | — | — | — | XLPEa | 2.2 | 5.2 |
| Yes | 1.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.7 2.7 |
p(E-stat-GMA) | 8 wt% GMA | p(E-stat-AA) | 7 wt% AA | LDPE | 2.8 | 16 |
| Yes | 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
p(E-stat-GMA) | 4.5 wt% GMA | p(E-stat-AA) | 3 wt% AA | — | 0.7 | 1.8 |
| Yes | 2.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
p(E-stat-GMA) | 2 wt% GMA | p(E-stat-AA-stat-TBA) | 5 wt% AA + 5 wt% TBA | — | 0.7 | 1.9 |
We went on to study the p(E-stat-GMA):p(E-stat-AA) copolymer blend. For both the thermoplastic and crosslinked blend (cured at 200 °C for 5 min), we observe a DC plateau at low frequencies for temperatures of 70 °C and above, which allowed us to extract the DC electrical conductivity (Fig. 7). We measured one copolymer blend three times in order to confirm that our BDS analysis yields reproducible results and found a σDC error of ∼4%. At a temperature of 70 °C, we found values of σDC ∼ 1.3 × 10−16 S cm−1 and 2 × 10−16 S cm−1 for the thermoplastic and crosslinked copolymer blend, respectively (Table 1), which are on par with the σDC of LDPE. Our measurements at higher temperatures (e.g. 90 °C; see Table 1) are likewise in excellent agreement. It appears that despite the presence of polar comonomers, the conductivity of the here studied copolymer blend is not negatively affected.
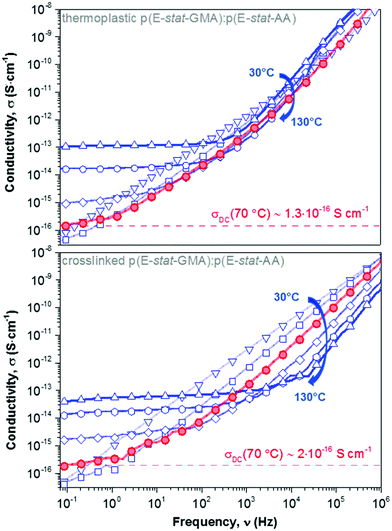 | ||
Fig. 7 DC electrical conductivity measured at different temperatures, ranging from 30 to 130 °C in 20 °C steps, for a 1.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric p(E-stat-GMA):p(E-stat-AA) blend crosslinked at 200 °C for 5 minutes; note that we were not able to construct Master curves because the copolymer gradually melts above 60 °C (cf.Fig. 4). 1 stoichiometric p(E-stat-GMA):p(E-stat-AA) blend crosslinked at 200 °C for 5 minutes; note that we were not able to construct Master curves because the copolymer gradually melts above 60 °C (cf.Fig. 4). | ||
We evaluated our BDS data in more detail to extract information about the charge transport dynamics of the insulation material. Assuming that charge transport is temperature activated and is dominated by nearest-neighbor hoping, we can estimate the activation energy Ea from an Arrhenius plot of the DC electrical conductivity at different temperatures T:
| σ = σ0e−Ea/kT | (4) |
| σ = μne | (5) |
Master curves of the electrical conductivity can be generated by so-called Summerfield scaling (see the ESI,† Fig. S9).40 The crossover frequency vc, which marks the transition from the DC plateau to a frequency-dependent conductivity, corresponds to the characteristic time τc = 1/2πvc needed for the motion of charge carriers. We find that vc, which gradually increases with temperature, for 70 to 130 °C, is located at a notably higher frequency in the case of the crosslinked copolymer blend (Fig. 7 and ESI,† Fig. S9). We explain this behavior with the presence of crosslinks, which act as bridges that assist the motion of charges. Further, the characteristic time and the diffusion coefficient D are related according to the Einstein–Smoluchowski equation:
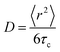 | (6) |
To benchmark the exceptional electrical behavior of the here studied copolymer blends, we also evaluated a crosslinked commercial LDPE (XLPE) grade, which is currently used for high voltage applications, and we found a value of σDC ∼ 2.2 × 10−16 S cm−1. Evidently, the here proposed byproduct free crosslinking concept readily reaches DC conductivity values that are on par with commercial materials.
In a final set of experiments, we explored the versatility of the here explored crosslinking concept. It would be desirable if the comonomer content can be tuned without compromising the mechanical and electrical properties. To demonstrate that this is readily feasible, we chose two approaches: (1) the addition of 50 wt% LDPE to the copolymer blend, thus creating a ternary blend, and (2) a blend of two copolymers that contain a lower content of glycidyl methacrylate and acrylic acid comonomer of 4.5 wt% and 3 wt%, respectively. Both types of formulations feature a high gel content above 70% after curing at 200 °C for 2.5 min, and a hot set elongation of ∼70% (which corresponds to 2.9 crosslinks per 1000 carbons), suggesting that in both cases, an infusible thermoset readily forms. We measured the DC electrical conductivity and found that both the addition of LDPE as well as the reduction of the comonomer content do not markedly influence the value of σDC (Table 1). Further, we explored a different type of copolymer blend, consisting of one copolymer that contains glycidyl methacrylate groups p(E-stat-GMA) with 2 wt% GMA content and a second one, p(E-stat-AA-stat-TBA), containing 5 wt% AA and 5 wt% tert-butyl acrylate (TBA) groups, which release tert-butyl alcohol at elevated temperature to form an acrylic acid group that can cure epoxy functionalities (ESI,† Fig. S10). Again, we find a comparable DC conductivity of 0.7 × 10−16 S cm−1 at 70 °C (Table 1). Evidently, click chemistry crosslinking of an epoxy and an acrylic acid bearing copolymer is a generic concept that leads to infusible polyethylene materials with a low DC electrical conductivity on the order of 10−16 S cm−1, which is comparable to values measured for both ultra-clean LDPE and a commercial XLPE grade.
3. Conclusions
We have studied the crosslinking of a copolymer blend of p(E-stat-GMA) and p(E-stat-AA). At low temperatures of 120 to 140 °C, the material can be melt processed (extruded) without onset of the curing reaction. Instead, at temperatures above 150 °C, the epoxy and acrylic acid groups readily react without the release of byproducts. An infusible network containing at least 4 crosslinks per 1000 C rapidly forms for curing times as low as 2.5 min. A combination of rheology, thermomechanical analysis and FTIR spectroscopy revealed that for low degrees of crosslinking, the network points predominately consist of covalent bonds that form because of reaction of the comonomers. However, with increasing curing, trapped entanglements start to dominate the network behavior. Both the thermoplastic and crosslinked copolymer blends exhibit a very low DC electrical conductivity on the order of 10−16 S cm−1, a value which is on par with values measured for both ultra-clean LDPE as well as a commercial XLPE grade. We conclude that the here explored byproduct-free crosslinking concept opens up the possibility to replace peroxide crosslinking with click chemistry type reactions.4. Experimental section
Materials
The ethylene–glycidyl methacrylate copolymer p(E-stat-GMA) with a GMA content of 8 wt%, a melt flow index MFI ∼ 5 g/10 min (190 °C/2.16 kg, provided by supplier), and a density of 0.94 g cm−3 was obtained from Arkema (Lotader series). The p(E-stat-GMA) copolymer had a weight-average molecular weight Mw ∼ 85 kg mol−1 and a polydispersity index PDI ∼ 7, determined with size exclusion chromatography (SEC) using an Agilent PL-GPC 220 system, in 1,3,4-trichlorobenzene at 150 °C; calibrated with Universal standards. The ethylene–acrylic acid copolymer p(E-stat-AA) with an AA content of 7 wt%, a MFI ∼ 8 g/10 min (190 °C/2.16 kg, provided by supplier), and a density of 0.93 g cm−3 was obtained from DOW (Primacor series). LDPE with a MFI ∼ 2 g/10 min (190 °C/2.16 kg) was obtained from Borealis AB (Mw ∼ 117 kg mol−1, PDI ∼ 9, and number of long-chain branches ∼1.9). The ethylene–glycidyl methacrylate copolymer p(E-stat-GMA) with a GMA content of 4.5 wt%, a melt flow index MFI ∼ 2 g/10 min (190 °C/2.16 kg, provided by supplier), and a density of 0.93 g cm−3 was obtained from Arkema (Lotader series). p(E-stat-AA) containing 3.1 wt% AA and a MFI ∼ 10.6 g/10 min (190 °C/2.16 kg, provided by supplier) was obtained from SK Primacor Europe. A commercial XLPE grade, as well as p(E-stat-GMA) containing 2 wt% AA and p(E-stat-TBA), with a comonomer content of 5 wt% AA and 5 wt% TBA, was provided by Borealis AB (MFI ∼ 2 g/10 min, 190 °C/2.16 kg, provided by supplier).Compounding, crosslinking and sample preparation
Copolymer formulations were compounded through extrusion for 10 minutes at 120 °C using a Haake Minilab Micro Compounder. The extruded material was first melted at 120 °C in a hot press, followed by crosslinking at 170 to 210 °C and a pressure of 25 bar for 2 to 20 min, resulting in 1.5 mm thick plates. Thin 0.5 mm films for FTIR spectroscopy were prepared by melt pressing.Hot set test
Dumbbell-shaped, crosslinked copolymer samples with an initial length of L0 ∼ 75 mm were elongated for 10 min at 200 °C by applying a weight that corresponded to a stress of σ ∼ 0.2 MPa. The final length Lhot was measured to calculate the hot set extension λhot = Lhot/L0 and hot set elongation εhot = λhot − 100%. After the measurement was performed, the weight was removed and the samples were allowed to recover in an oven for 5 minutes, and then at room temperature for 1 hour.Gel content
The gel content of the crosslinked samples was determined gravimetrically using a solvent extraction technique. The samples (∼150 mg) were placed in pre-weighed 100 mesh stainless steel baskets and extracted by refluxing in 1.1 dm3 decalin for 6 h. An antioxidant, 10 g of Irganox 1076 from Ciba-Geigy, was added to the solvent to prevent degradation. Then, the solvent was exchanged with 0.9 dm3 of additive-free, preheated decalin and the extraction was continued for 1 h. Finally, the samples were dried first at ambient temperature overnight and then under vacuum for about 8 hours at 50 °C. After this period, the non-soluble fraction that remained in the basket reached a constant weight, which was used to calculate the gel content.Differential scanning calorimetry (DSC)
DSC measurements were carried out under nitrogen between −50 and 150 °C at a scan rate of 10 °C min−1, using a Mettler Toledo DSC2 calorimeter equipped with a HSS7 sensor and a TC-125MT intercooler. The sample weight was 3–4 mg. Samples for DSC were cooled from the melt at different cooling rates, prior to the DSC heating scan. Fast scanning chip calorimetry (Flash DSC) measurements were performed using a Mettler-Toledo Flash DSC 1 instrument. The samples (in the weight range of ng) were placed on a Mettler-Toledo MultiSTAR UFS1 sensor and subjected to heating–cooling cycles at 6000 °C min−1.Thermogravimetric analysis (TGA)
TGA was carried out under nitrogen using a Mettler Toledo TGA/DSC 3+.Attenuated total reflectance Fourier-transform infrared (ATR FTIR) spectroscopy
IR spectra were recorded using a PerkinElmer FTIR spectrophotometer. For measurements at room temperature, an Attenuated Total Reflectance (ATR) attachment GladiATR from Pike Technologies was used. For variable-temperature measurements, an electrical heating jacket from Specac was used. Scans in the range of 4000–400 cm−1 with a resolution of 2 cm−1 and a scanning interval of 0.5 cm−1 were repeated 20 times. Measurements were conducted at 298 K in air.Dynamic mechanical analysis (DMA)
Samples with a size of 15 × 5 × 1.25 mm were cut from melt-pressed films. DMA was carried out from 40 to 200 °C at a heating rate of 20 °C min−1, and then with an isotherm at 200 °C for 25 minutes at a frequency of 0.5 Hz and 1% strain using a TA Q800 DMA instrument.Scanning electron microscopy (SEM)
Samples for SEM were cryofractured and subsequently etched for 80 min using a solution of 1 wt% potassium permanganate in a mixture of sulfuric acid, ortho-phosphoric acid and water, followed by cleaning with hydrogen peroxide, water and methanol.41 The etched surfaces were sputtered with gold and imaged using a Leo Ultra 55 SEM instrument, with an acceleration voltage of 2.5 to 5 kV.Rheology
Rheology was carried out using a DHR-3 instrument from TA instruments equipped with an environmental test chamber (ETC kit DHR), at temperatures ranging from 130 to 150 °C. The frequency was set to 6.28 rad s−1 and the strain was 0.5%. The geometry used was a parallel plate of 25 mm and the gap was set to 1000 μm, applying a normal force of approximately 1 N.Dielectric spectroscopy
Measurements were performed using a Novocontrol Alpha spectrometer in the frequency range of 10−2 to 107 Hz, at different temperatures in the range of 20–130 °C with an error of ±0.1 °C, at atmospheric pressure and under a nitrogen atmosphere. The sample cell consisted of two silver-coated electrodes of 40 mm in diameter and the sample with a thickness of 0.1 mm. Each measurement was carried out six times, and the average values were recorded. The complex conductivity σ* = σ′ + iσ′′, the real part of which is used for the analysis herein, can be deducted from the complex dielectric permittivity ε* as σ* = iωε0ε*, where ε0 is the permittivity of free space.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge Borealis AB and the Swedish Foundation for Strategic Research (grant agreements FFL15-0147 and GMT14-0036) for funding. We thank Anders Mårtensson for help with SEC measurements, and Anna Ström for help with rheology experiments.References
- G. Mazzanti and M. Marzinotto, Extruded Cables for High-Voltage Direct-Current Transmission, Wiley, Hoboken, 2013 Search PubMed.
- G. C. Montanari, P. H. F. Morshuis, M. Zhou, G. C. Stevens, A. S. Vaughan, Z. Han and D. Li, IET High Volt., 2017, 90–95 Search PubMed.
- M. G. Andersson, J. Hynynen, M. R. Andersson, V. Englund, P. O. Hagstrand, T. Gkourmpis and C. Müller, ACS Macro Lett., 2017, 6, 78–82 CrossRef CAS.
- A. M. Pourrahimi, R. T. Olsson and M. S. Hedenqvist, Adv. Mater., 2018, 30, 1703624 CrossRef PubMed.
- T. J. Lewis, IEEE Trans. Dielectr. Electr. Insul., 2014, 21, 497–502 CAS.
- A. S. Vaughan, Nanodielectrics: The Role of Structure in Determining Electrical Properties, in Controlling the Morphology of Polymers, ed. G. R. Mitchell and A. Tojeira, Springer, Switzerland, 2016 Search PubMed.
- A. M. Pourrahimi, T. A. Hoang, D. M. Liu, L. K. H. Pallon, S. Gubanski, R. T. Olsson, U. W. Gedde and M. S. Hedenqvist, Adv. Mater., 2016, 28, 8651–8657 CrossRef CAS PubMed.
- L. K. H. Pallon, A. T. Hoang, A. M. Pourrahimi, M. S. Hedenqvist, F. Nilsson, S. Gubanski, U. W. Gedde and R. T. Olsson, J. Mater. Chem. A, 2016, 4, 8590–8601 RSC.
- M. Wåhlander, F. Nilsson, R. L. Andersson, A. Carlmark, H. Hillborg and E. Malmström, Macromol. Rapid Commun., 2017, 38, 1700291 CrossRef PubMed.
- E. Peschke and R. von Olshausen, Cable Systems for High and Extra-High Voltage: Development, Manufacture, Testing, Installation and Operation of Cables and Their Accessories, Publicis MCD Verlag, 1999 Search PubMed.
- I. Chodak, Prog. Polym. Sci., 1995, 20, 1165–1199 CrossRef CAS.
- M. Lazar, R. Rado and J. Rychly, Adv. Polym. Sci., 1990, 95, 149–197 CrossRef.
- R. Patterson, A. Kandelbauer, U. Müller and H. Lammer, Crosslinked thermoplastics. in Handbook of Thermoset Plastics, ed. H. Goodman and H. Dodiuk-Kenig, Elsevier, San Diego, 2014, pp. 697–737 Search PubMed.
- A. Smedberg, T. Hjertberg and B. Gustafsson, Polymer, 1997, 38, 4127–4138 CrossRef CAS.
- J. Sahyoun, A. Crepet, F. Gouanve, L. Keromnes and E. Espuche, J. Appl. Polym. Sci., 2017, 134, 44525 CrossRef.
- T. Andrews, R. N. Hampton, A. Smedberg, D. Wald, V. Waschk and W. Weissenberg, IEEE Electr. Insul. Mag., 2006, 22, 5–16 Search PubMed.
- J. C. Fothergill, S. J. Dodd, L. A. Dissado, T. Liu and U. H. Nilsson, IEEE Trans. Dielectr. Electr. Insul., 2011, 18, 1544–1553 CAS.
- V. Englund, J. Andersson, J.-O. Boström, V. Eriksson, P.-O. Hagstrand, J. Jungqvist, W. Loyens, U. H. Nilsson and A. Smedberg, Proc. CIGRE, 2014, D1.104 Search PubMed.
- U. H. Nilsson, J. Andersson, V. Englund, V. Eriksson, P.-O. Hagstrand and A. Smedberg, IEEE Ann. Rep. Conf. Electr. Insul. Dielectr. Phen., 2015, 31–34 Search PubMed.
- T. Hjertberg, M. Palmlöf and B.-Å. Sultan, Polymer, 1991, 42, 1185–1192 CAS.
- R. D. B. Garcia, L. Keromnes, Y. Goutille, P. Cassagnau, F. Fenouillot and P. Chaumont, Eur. Polym. J., 2014, 61, 186–196 CrossRef.
- M. Mauri, N. Tran, O. Prieto, T. Hjertberg and C. Müller, Polymer, 2017, 111, 27–35 CrossRef CAS.
- M. Mauri, L. Svennigsson, T. Hjertberg, L. Nordstierna, O. Prieto and C. Müller, Polym. Chem., 2018, 9, 1710–1718 RSC.
- N. Torres, J. J. Robin and B. Boutevin, J. Appl. Polym. Sci., 2001, 81, 2377–2386 CrossRef CAS.
- V. Chiono, S. Filippi, H. Yordanov, L. Minkova and P. Magagnini, Polymer, 2003, 44, 2423–2432 CrossRef CAS.
- Q. Wei, D. Chionna, E. Galoppini and M. Pracella, Macromol. Chem. Phys., 2003, 204, 1123–1133 CrossRef CAS.
- Q. Wei, D. Chionna and M. Pracella, Macromol. Chem. Phys., 2005, 206, 777–786 CrossRef CAS.
- Y. W. Xu, J. Loi, P. Delgado, V. Topolkaraev, R. J. McEneany, C. W. Macosko and M. A. Hillmyer, Ind. Eng. Chem. Res., 2015, 54, 6108–6114 CrossRef CAS.
- Epoxy Polymers, New Materials and Innovations, ed. J.-P. Pascault and R. J. J. Williams, Wiley-VCH, Weinheim, 2010 Search PubMed.
- J. He and Y. Zhou, Progress in Eco-friendly High Voltage Cable Insulation Materials, 12th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Xi’an, China, 2018.
- E. P. Otocka and T. K. Kwei, Macromolecules, 1968, 1, 244–249 CrossRef CAS.
- D. Hadži and N. Sheppard, Proc. R. Soc. London, Ser. A, 1953, 216, 247–266 CrossRef.
- A. Taubert and K. I. Winey, Macromolecules, 2002, 35, 7419–7426 CrossRef CAS.
- K. Wakabayashi and R. A. Register, Macromolecules, 2006, 39, 1079–1086 CrossRef CAS.
- G. D. Wignall, J. D. Londono, J. S. Lin, R. G. Alamo, M. J. Galante and L. Mandelkern, Macromolecules, 1995, 28, 3156–3167 CrossRef CAS.
- G. D. Wignall, R. G. Alamo, J. D. Londono, L. Mandelkern, M. H. Kim, J. S. Lin and G. M. Brown, Macromolecules, 2000, 33, 551–561 CrossRef CAS.
- M. G. Andersson, J. Hynynen, M. R. Andersson, P. O. Hagstrand, T. Gkourmpis and C. Müller, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 146–156 CrossRef CAS.
- J. P. Flory, Networks, in Encyclopedia of Polymer Science and Engineering, ed. H. F. Mark, N. M. Bikales, C. G. Overberger and G. Menges, Wiley, New York, 1987, vol. 10, pp. 95–112 Search PubMed.
- S. A. Boggs, IEEE Trans. Dielectr. Electr. Insul., 1995, 2, 97–106 CrossRef CAS.
- S. Summerfield, Philos. Mag. B, 1985, 52, 9–22 Search PubMed.
- M. M. Shahin, R. H. Olley and M. J. Blissett, J. Polym. Sci., Part B: Polym. Phys., 1999, 37, 2279–2286 CrossRef CAS.
- International Electrochemical Commission, IEC 60811-507:2012 Electric and optical fibre cables – test methods for non-metallic materials, 2012.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8tc04494e |
| This journal is © The Royal Society of Chemistry 2018 |