DOI:
10.1039/D0SC01328E
(Edge Article)
Chem. Sci., 2020,
11, 7813-7822
Predicting the chemical reactivity of organic materials using a machine-learning approach†
Received
5th March 2020
, Accepted 2nd July 2020
First published on 3rd July 2020
Abstract
Stability and compatibility between chemical components are essential parameters that need to be considered in the selection of functional materials in configuring a system. In configuring devices such as batteries or solar cells, not only the functionality of individual constituting materials such as electrodes or electrolyte but also an appropriate combination of materials which do not undergo unwanted side reactions is critical in ensuring their reliable performance in long-term operation. While the universal theory that can predict the general chemical reactivity between materials is long awaited and has been the subject of studies with a rich history, traditional ways proposed to date have been mostly based on simple electronic properties of materials such as electronegativity, ionization energy, electron affinity and hardness/softness, and could be applied to only a small group of materials. Moreover, prediction has often been far from accurate and has failed to offer general implications; thus it was practically inadequate as a selection criterion from a large material database, i.e. data-driven material discovery. Herein, we propose a new model for predicting the general reactivity and chemical compatibility among a large number of organic materials, realized by a machine-learning approach. As a showcase, we demonstrate that our new implemented model successfully reproduces previous experimental results reported on side-reactions occurring in lithium–oxygen electrochemical cells. Furthermore, the mapping of chemical stability among more than 90 available electrolyte solvents and the representative redox mediators is realized by this approach, presenting an important guideline in the development of stable electrolyte/redox mediator couples for lithium–oxygen batteries.
Introduction
The production and storage of sustainable energies are now regarded as two of the most urgent objectives of modern science. For coping with such a demand, extensive research efforts have been devoted to developing novel energy generation and storage devices with high efficiency and stability.1–4 While various technical breakthroughs in this field have been recently made, which led to various new energy devices, one of the persisting concerns is how one can extend the lifespan of energy devices and achieve prolonged high efficiency of these devices.1,4,5 The current challenges in securing the stability partly arise from the fact that most of the energy devices operate based on a system containing multiple chemical interfaces among different constituting components, which serve as a source of side reactions. For example, a lithium–air battery (LAB), one of the most promising next-generation battery systems, can deliver a remarkably high specific energy density and far outperform state-of-the-art lithium ion batteries; however, its stability over time and electrochemical cycles is seriously hampered by various complicated side reactions occurring between components involving air-electrode materials, lithium metal, electrolyte, and catalyst materials,.1,4,6–8 thus being the main obstacle for further development. Similar issues have been commonly observed in a range of energy storage/generation systems, particularly the ones based on electrochemical reactions, such as dye-sensitized solar cells (DSSCs), which have the issue of long-term stability attributable to unwanted reactions among the electrolyte, substrate materials, sensitizers, and redox mediators (RMs).5,9,10 In addressing these challenges and identifying the optimal combinations of components, the capability to predict/estimate the chemical stability (or reactivity) between cell components in advance would offer one of the imperative missing pieces in the rational design of advanced energy devices with stability, and would serve as a basis for data-driven new material discovery.
With regard to the prediction of the reactivity of materials, theoretical methods such as those based on the reaction activation barrier11–14 or reaction indices (e.g. hardness/softness and electron affinity)15–18 have been traditionally developed and widely adopted. Nevertheless, these indices have not been capable of offering a high-enough accuracy of prediction and failed to cover a wide range of reaction chemistries. As the material discovery using big data is expected to become more important in the near future, the need for the general tool of the reactivity index cannot be overstated. In this study, based on a machine learning approach combined with conventional reaction indices, we developed a new regression model which successfully predicts the general chemical stability of molecules, and can thus be applied to various types of reactions involving them. The trained model illustrates that a high precision of reactivity prediction is achievable considering the collective data of molecular and electronic structures of reactants. Using the trained model, as a showcase, we demonstrate that the chemical stability of cell components in lithium oxygen systems is successfully reproduced, which is in agreement with previous experimental evidence. Moreover, based on our new model, stabilities of more than 90 potential electrolyte solvents are quantitatively analyzed/predicted in the presence of other cell components in lithium–oxygen batteries, which would provide important information for the rational design of new electrochemical systems. It is our belief that the machine learning approach proposed in this study not only serves as a new tool to predict chemical stability with relatively low computational cost, but also provides insights into the general relationship between transferable properties and reactivity of molecules.
Computational methodology
Density functional theory calculations
Geometry optimization, total energy evaluation, and partial spin density calculations of molecules were performed using the Gaussian 09 quantum chemistry package.19 Spin-unrestricted density functional theory (DFT) calculations were conducted for all molecules exploiting the Becke–Lee–Yang–Parr (B3LYP) hybrid exchange-correlation functional20–22 and the triple-zeta valence polarization (TZVP) basis set.23 The solvation effect of electrolytes was considered using the implicit solvation methodology, i.e., the polarizable continuum model (PCM) scheme available in the Gaussian 09 package. The dielectric constants used for each solvent are provided in Table S1.†
Traditional reaction indices
Various reaction indices were tested to estimate electrophilicity and nucleophilicity, which are defined based on the experimental reaction kinetics (i.e. reactivity) according to Mayr et al.'s scheme:24–27| | | log10(kreaction) = SN(E + N), | (1) |
where kreaction is the rate constant for the second-order reaction at 20 °C, SN is the sensitivity determined by a nucleophile, E is the electrophilicity, and N is the nucleophilicity. In this study, hardness/softness, electron affinity/ionization energy, electronegativity/electropositivity, and the E-index/N-index were comparatively adopted as reference reaction indices for the prediction of electrophilicity/nucleophilicity.
Hardness can be expressed as follows using the finite difference approximation:18,28
| | 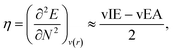 | (2) |
where vIE and vEA refer to the vertical ionization energy and vertical electron affinity, respectively. Softness was introduced as the inverse of hardness:
| | 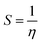 | (3) |
The vertical ionization energy and vertical electron affinity were estimated from the following equations using DFT energy calculations:
| | | vIE = (E(N) − E(N − 1))v(r) | (4) |
| | | vEA = (E(N + 1) − E(N))v(r), | (5) |
where
E(
N),
E(
N − 1), and
E(
N + 1) represent the DFT energy for a given structure with
N,
N − 1, and
N + 1 electrons, respectively, and the subscript
v(
r) indicates that the structures were fixed to the optimized
N-electron (neutral charge state) structure. In the case where IE was employed as the reaction index, we used the referenced-IE (rIE) to obtain a positive value relationship with nucleophilicity:
16| | | referenced vIE = vIE(TCE) − vIE, | (6) |
where vIE(TCE) represents the vertical ionization energy of tetracyanoethylene, which has been revealed to exhibit the largest ionization energy. This referencing makes the IE values positive, thereby preventing unphysical local reactivity indices, as will be introduced later. The electronegativity was derived from DFT calculations as well, by finite difference approximation:
29–31| | 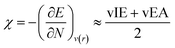 | (7) |
and electropositivity was simply defined as the negative value of electronegativity, −
χ. The
E-index, which refers to the maximum energy gain from the vertical electron injection, was evaluated as
| | 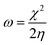 | (8) |
and the
N-index is the reciprocal of the
E-index, 1/
ω.
32 The original names are the ‘electrophilicity index’ and ‘nucleophilicity index’; herein, we designate these indices as the ‘
E-index’ and ‘
N-index’, respectively, to avoid confusion with the experimental electrophilicity and nucleophilicity. We also evaluated the adiabatic ionization energy and adiabatic electron affinity using DFT calculations:
| | | aIE = E(N)v(r) − E(N − 1)v*(r) | (9) |
| | | aEA = E(N + 1)v**(r) − E(N)v(r) | (10) |
Here,
v*(
r) and
v**(
r) refer to the optimized (
N − 1)- and (
N + 1)-electron structure, respectively, indicating the energy difference between a neutral molecule and a fully relaxed molecule with hole/electron injection. Similar to vIE, aIE was also referenced to aIE(TCE),
16| | | referenced aIE = aIE(TCE) − aIE | (11) |
for use as a reaction index.
Proposed new reaction index, GRI
We proposed a new reaction index, the ‘global reactivity index’ (GRI), which is the global sum of local reactivities, and used it to predict the experimental reactivity, under the assumption that the reaction occurs simultaneously and cumulatively at all local sites in the reactant molecule. The new proposed index, GRI, for the electrophilicity/nucleophilicity prediction was defined as a log sum of exponential local indices:| | 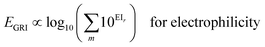 | (12) |
| | 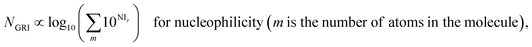 | (13) |
where EIr and NIr, the local indices for electrophilicity and nucleophilicity at atom r of a molecule, respectively, were obtained from a modified Parr function as follows. The Parr function is the measure of the spin density of each r atom in a charged molecule:33,34| | | P−(r) = ρrcs(r) = |ρsn(r) − ρsn+1(r)| for electrophilicity | (14) |
| | | P+(r) = ρras(r) = |ρsn(r) − ρsn−1(r)| for nucleophilicity | (15) |
ρrcs(r) and ρras(r) are the atomic spin densities of the radical cation and anion, respectively, where the atomic spin densities are calculated for all atoms of a molecule. Because the atomic spin densities can be zero for non-radical molecules, we modified the original Parr function to a general form, exploiting the atomic spin density difference before and after electron or hole injection, where ρsn(r), ρsn+1(r), and ρsn−1(r) refer to the atomic spin density at the rth atom of a molecule with n, n + 1, and n − 1, respectively, in order to extend the local indices methodology to non-radical molecules. Based on the modified Parr function, the local indices at the r atom of a molecule were expressed by| | | EIr = P−(r) × EI for electrophilicity | (16) |
| | | NIr = P+(r) × NI for nucleophilicity. | (17) |
Here, EI and NI represent global indices such as IE/EA, η, χ, or ω. Accordingly, the overall reaction rate was expressed as a sum of the local reaction rates at each site according to Mayr et al.'s scheme:| | | kreaction ∝ 10EGRI for electrophilicity | (18) |
| | | kreaction ∝ 10NGRI for nucleophilicity. | (19) |
Machine-learning model
To predict the experimental electrophilicity and nucleophilicity of a molecule from its electronic and structural properties, a machine-learning approach was adopted. After optimization of the architecture (Tables S2–S9†), a neural network with two hidden layers with a 400 × 400 neuron size was trained using the Adam optimizer35 through a learning rate of 10−3 and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 learning steps. To mitigate overfitting, a dropout rate of 0.8 and an L2 regularization parameter of 10−3 were used. The 30 largest local reactivities (components of the GRI) were used for each molecule as an electronic property feature, and 1024-bit Morgan FP36 and MACCS keys generated using the RDKit software37 were employed as a structural feature for electrophilicity and nucleophilicity, respectively. The effective dimensionality of the features was examined using the Pearson correlation. A majority of the 50 largest electronic features showed a Pearson correlation >0.1 for both electrophilicity and nucleophilicity cases, implying that even the local reactivities of less active sites can be meaningful to the prediction (Fig. S1†). The performance of the model was evaluated by averaging 40 test-set R-square values (loss values) of an independently trained model with identical hyperparameters based on the Monte Carlo cross-validation scheme.38 The sample size is predicted to be higher than the VC dimension of the final model, based on learning curves39 (Fig. S2†). A training set and a test set were randomly selected at a 9
000 learning steps. To mitigate overfitting, a dropout rate of 0.8 and an L2 regularization parameter of 10−3 were used. The 30 largest local reactivities (components of the GRI) were used for each molecule as an electronic property feature, and 1024-bit Morgan FP36 and MACCS keys generated using the RDKit software37 were employed as a structural feature for electrophilicity and nucleophilicity, respectively. The effective dimensionality of the features was examined using the Pearson correlation. A majority of the 50 largest electronic features showed a Pearson correlation >0.1 for both electrophilicity and nucleophilicity cases, implying that even the local reactivities of less active sites can be meaningful to the prediction (Fig. S1†). The performance of the model was evaluated by averaging 40 test-set R-square values (loss values) of an independently trained model with identical hyperparameters based on the Monte Carlo cross-validation scheme.38 The sample size is predicted to be higher than the VC dimension of the final model, based on learning curves39 (Fig. S2†). A training set and a test set were randomly selected at a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of the total dataset. To minimize an extrapolated prediction, a random selection of training/test sets was iterated until the differences in both the average and standard deviation of experimental values between the training and test sets become less than 1%. The source codes of the final model can be found at https://github.com/petitcloud/2020_reactivity_ML.
1 ratio of the total dataset. To minimize an extrapolated prediction, a random selection of training/test sets was iterated until the differences in both the average and standard deviation of experimental values between the training and test sets become less than 1%. The source codes of the final model can be found at https://github.com/petitcloud/2020_reactivity_ML.
Selecting the target reactions and the reactivity prediction methodology
Organic molecules have been chosen for the focus of this study, exploiting the abundant experimental/theoretical studies and databases in the literature.40,41 Intrinsic chemical reactivity was considered excluding the extrinsic factors such as mass transport and physical contact between reactants, which are affected by various experimental processes.42,43 As irreversible reactions that permanently degrade electrochemical devices are of particular interest to researchers in the electrochemistry field, plausible side reactions in electrochemical devices were carefully scrutinized in this study. It is noted that the reactivities of irreversible reactions are known to be primarily controlled by the reaction kinetics17,26,27 as illustrated in Fig. 1a. An irreversible reaction can be classified by the reaction order, i.e., first-order, second-order, or third- or higher order reactions. As it is difficult for third- or higher order reactions to occur because of the relatively small possibility of simultaneous collision of three or more species, first- and second-order reactions have been mainly observed and studied.44 A first-order reaction involves a reversible self-reaction generating intermediate species, which should be analyzed by examining their thermodynamic properties, e.g., pKa, bond dissociation energies, whereas the kinetics of most second-order reactions can be described using the electrophilicity/nucleophilicity concept.17,26 We focused on the prediction of second-order reactions to investigate the compatibility between cell components that can potentially undergo side reactions.
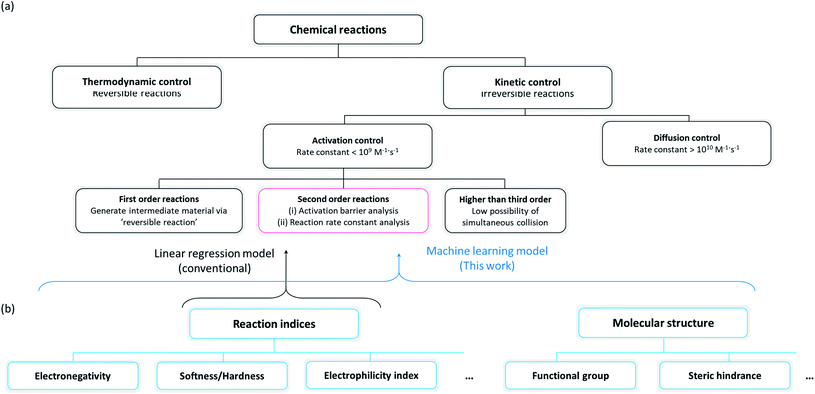 |
| | Fig. 1 (a) Classification scheme of chemical reactions and their governing factors, and (b) classification scheme of the reaction indices, which can predict the rate constant of second-order reactions. | |
Conventionally, two approaches have been suggested for predicting the reaction kinetics, as depicted in a red box in Fig. 1a: (i) evaluation of the activation energy of the target reaction according to the Marcus theory,45 which generally requires a high level of experimental46,47 or computational11–14 effort, or (ii) prediction of the reaction rate constant by building a mathematical relationship with the reaction indices where the selection of the indices is critical in the precision of prediction. We selected the second approach for the reactivity prediction, which was more suitable for fast screening of a large number of reactions and to draw a general chemical insight regarding side reactions occurring in an electrochemical cell (Fig. 1b).15–18 Accordingly, a number of molecules were evaluated with respect to reaction indices as key descriptors determining the reactivity.
To verify the reliability of reaction indices suggested in the literature and in this work, the experimental database constructed by Mayr et al.24–27 was used. In quantifying the reactivity of a molecule (kreaction), an electrophilicity/nucleophilicity scale based on the second-order rate constant of reactions between the reference electrophile/nucleophile molecule was considered as described earlier.24–27kreaction is the rate constant for the second-order reaction at 20 °C. Because reactions with a second-order rate constant lower than 10−5 M−1 s−1 hardly occur at room temperature, it is regarded that N + E < −5 is a metric for stability (i.e. no reactivity) against a target reaction, approximating SN ≈ 1.27
Results and discussion
Limitations of conventional reaction indices for general organic reactions
Intensive theoretical studies have been previously dedicated to evaluating reactivities using electronic properties of reactant molecules, e.g., hardness/softness, electronegativity, E-index/N-index, etc.16,48–52 These conventional indices were often used as a measure to predict the electrophilicity (E) and/or nucleophilicity (N), which are the parameters that determine the reaction kinetics according to eqn (1). Earlier studies revealed that various indices could exhibit linear relationships with E and/or N particularly for molecules possessing a similar functional group, and thus could be reliably employed for the prediction of E and/or N, and subsequently the reaction rate (kreaction).16,48–52 Nevertheless, to the best of our knowledge, these reaction indices have not been tested over a wide chemical space, and the generality of predictions remains unconfirmed. Herein, in order to verify their general prediction capability, we considered a variety of molecules from Mayr's database including 216 electrophiles and 726 nucleophiles, to obtain the reaction indices (see the Computational methodology section for details on calculations of each index from DFT). Then, the efficacy of each index was compared with respect to the prediction capability of E and/or N for all the molecules considered.
In Fig. 2a, the linear correlation between E and each index is presented by R-square, Pearson correlation and root mean square error (RMSE) values obtained from the linear regression of the index versus E, while that for N is shown in Fig. 2b. Fig. 2 along with Fig. S3a and S4a in the ESI† illustrates that hardness (η)/softness (1/η), well-known parameters in the HSAB theory, hardly exhibits a linear relationship with experimental electrophilicity/nucleophilicity. It displays R-square and Pearson correlation values that are way lower than unity along with large RMSE values for both E and N. This finding suggests that hardness/softness cannot be employed to predict the general reaction kinetics for organic molecules, which, to some extent, agrees with previous studies discussing the inefficacy of the HSAB theory in kinetically controlled reactions.17,26 The electronegativity (χ) also shows only a rough correlation with the experimental electrophilicity of molecules, with a low R-square value of 0.539 (Fig. 2a and S3b†), and, moreover, the electropositivity (−χ) fails with the prediction of N (Fig. 2b and S4b†).
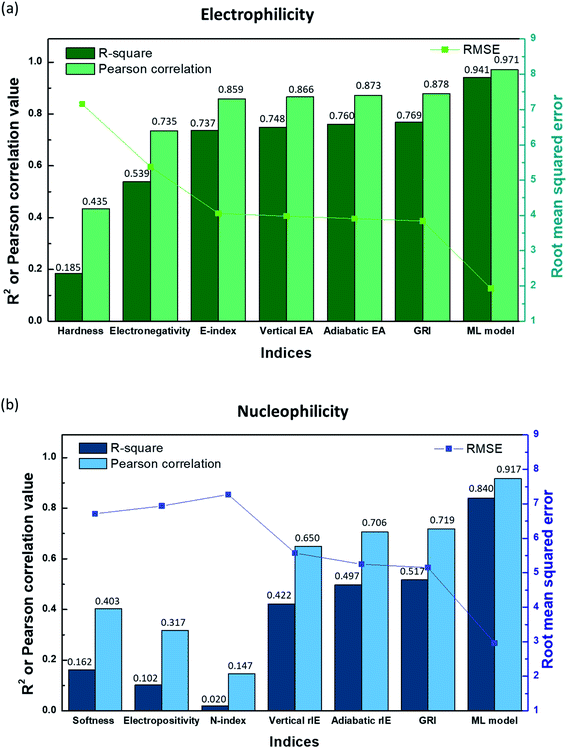 |
| | Fig. 2
R-square, Pearson correlation, and RMSE values obtained from linear regression analysis of (a) the experimental electrophilicity, and (b) experimental nucleophilicity vs. the reaction indices. | |
The E-index (ω), which was suggested as a reaction descriptor by Parr et al.53 and widely exploited17,50–52 to explain the electrophilic reactivity, displays a slightly better correlation with E (Fig. 2a and S3c†), with a higher R-square value (0.737). Nevertheless, the counter index, N-index (1/ω) was not successful in presenting the N (Fig. 2b and S4c†). The generally poorer description of N using a modified form of electronegativity (χ) or E-index (ω) implies that nucleophilicity is not likely to be a dependent variable of electrophilicity and thus cannot be estimated from the negative or reciprocal of electrophilicity (Fig. S5 and S6†). Domingo et al.54 proposed alternative reaction indices, vertical EAs and IEs for electrophilicity and nucleophilicity, respectively, demonstrating that they could deliver more accurate prediction than other indices for a certain chemical space.16,54 We also found that a better linearity with E and N could be presented by vertical EAs and IEs. And, they could display improved R-square values of 0.748 and 0.422, respectively (Fig. 2, S3d and S4d†). However, the high RMSE values for each case (3.98 and 5.57, respectively) suggest that it would be difficult to obtain high prediction accuracy. Adiabatic EAs/IEs were also tested as reaction indices, which resulted in better quality R-square values of 0.760 and 0.497 for E and N, respectively. While these values are the highest, and adiabatic EAs/IEs offer the most reliable prediction results among the reaction indices investigated here, they still do not present dramatic improvements (Fig. 2, S3e and S4e†).
By analyzing the above results, we found that most of the underestimated outliers in the plot of adiabatic IEs vs. nucleophilicity (Fig. S4e†) exhibit particularly uneven electron/spin distributions in molecules, while overestimated outliers generally show delocalized electron/spin distributions (Fig. S7 and S8†), suggesting the potential role of electronic distribution in the molecule. In this respect, we devised a new reaction index, the GRI (global reactivity index), which can take into account the local electronic structure of the molecule. It was assumed that the local reactivity of the site in the reactant molecule cumulatively contributes to the overall reaction rate. Accordingly, the GRI was defined as a sum of the local reactivities, based on adiabatic EAs and IEs embedded with the local reactivities (see the Computational Methodology section for details). While local indices have been traditionally exploited to analyze the preferred reaction site (i.e., stereoselectivity)15,18,50,51 within a molecule, we believed that they could also serve as a good indicator of the local property in defining the reactivity index. Fig. 2 and S3f† show that the predictions of E and N become more reliable with the local reactivity consideration, and the GRI could yield the improved R-square (or Pearson correlation) values of 0.769 (0.878) and 0.517 (0.719), respectively, which record a higher accuracy than any other reaction indices investigated. This suggests the importance of the cumulative approach of the local electronic structure in the reactivity. Nevertheless, it is observed that it is still insufficient, and the RMSE of the predicted N + E is as large as ∼9, indicating that the error range of the predicted rate constant kreaction would be ∼109 M−1 s−1 (eqn (1)). This strongly implies that these regression approaches relying on a simple linear function of the electronic properties of a molecule would not serve as a reliable indicator for the general chemical reactivities.
A machine-learning approach to correlate molecular properties and reactivities
In order to address the complexity in the relationship between the properties of molecules and reactivities, a machine-learning method was applied as an alternative strategy. Among the prevailing machine learning models, e.g. LASSO regression55 (Table S10†), ridge regression56 (Table S11†), Gaussian process regression57 (Table S12†), support vector machine classification58 (Table S13†), and random forest classification59 (Table S14†), the artificial neural network (ANN) model was employed because it exhibited the best performance (see the Computational Methodology section for details).60,61 The ANN model (2 hidden layers, each having 80 neurons) was trained using the 30 largest local indices as a feature and the electrophilicities/nucleophilicities of 216/726 molecules in Mayr's database as a label. The optimization process of hyperparameters is summarized in ESI Tables S2–S9.† The initial performance of the model after the machine-learning training revealed that the averaged test-set R-square (or Pearson correlation) values could increase to 0.864 (0.930) and 0.674 (0.821) for electrophiles and nucleophiles with RMSE values of 2.95 and 4.23, respectively, as verified by a Monte Carlo cross-validation. The prediction performance was notably improved compared with those of the linear regression models, and, in particular, the improvement in the nucleophilicity is remarkable. This suggests the efficacy of the machine-learning scheme in the description.
We believed that a further improvement in the reliability can be potentially made over this initial trial, taking into consideration the intrinsic limitations in reaction indices that only consider the electronic properties, especially omitting the structural features of molecules. Structural factors, e.g., steric hindrance, are often found to be important in governing the chemical reactivity of molecules.62 Nevertheless, it has been difficult to incorporate the molecular structural features in conventional reaction indices because of (i) the challenges in expressing structural factors as a numeric index and (ii) the lack of appropriate reaction indices that can simultaneously contain electronic and structural information. It should be noted that, due to this challenge, most of the previous studies on reaction index methodologies have been carried out within a limited chemical space, i.e., a class of molecules possessing a similar functional group, to minimize the effect of structural differences on the reactivity.16,48–52
In this respect, we attempted to additionally employ structural features in the initial machine-learning scheme, considering our choice of molecules from the wide chemical space. Indeed, the prior difficulties in the implementation could be successfully resolved by taking advantage of the versatile input structures of machine-learning models. Firstly, molecular fingerprinting (FP) methods36,37 were implanted in the machine-learning to express the molecular structure in the numeric index. FP methods could convert structural information of molecules into a simple data form (e.g., binary bits vector), which could serve as inputs. Secondly, by exploiting the machine-learning algorithms, the electronic and structural properties could be simultaneously expressed as a single feature vector, simply by merging two vectors. With these two changes in the scheme, we trained ANN models again, and the resulting performance is presented in Table 1. Markedly, the new model, trained using both structural and electronic features, resulted in R-square values of 0.919 and 0.810 for electrophiles and nucleophiles, respectively, corresponding to an N + E RMSE value of 5.5. This signifies an outstanding improvement over R-square values of 0.864 and 0.674 for E and N, respectively, obtained from the previous ANN model, indicating the decisive role of structural features in the reactivity.
Table 1 Test set R-square and RMSE values of the models trained with different expressions of electronic features and structural features
| Features (electronic) |
Local reactivity |
— |
Local reactivity |
Adiabatic EA/IE |
Adiabatic EA/IE, Parr function |
| Features (structural) |
Fingerprint |
Fingerprint |
— |
Fingerprint |
Fingerprint |
|
Electrophilicity prediction
|
| Performance, test set R2 |
0.919 |
0.811 |
0.864 |
0.839 |
0.864 |
| RMSE |
2.28 |
3.48 |
2.95 |
3.21 |
2.95 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
Nucleophilicity prediction
|
| Performance, test set R2 |
0.810 |
0.646 |
0.674 |
0.707 |
0.757 |
| RMSE |
3.23 |
4.41 |
4.23 |
4.01 |
3.65 |
We could also verify the importance of structural features combined with the local indices by comparatively altering machine-learning schemes, as summarized in Table 1. When simply adopting either structural features (FP) or the local indices, the R-square values of the model after the machine-learning remained significantly lower than the combined case, which were 0.811 (electrophilicity) and 0.646 (nucleophilicity) for FP only and 0.864 and 0.674 for local indices only. Moreover, when excluding the local indices, the R-square values of the models trained with the utilization of FP were significantly low: 0.839 (or 0.864) and 0.707 (or 0.757) for electrophiles and nucleophiles, respectively, in the case of adiabatic EA/IE or the merging of adiabatic EA/IE with the Parr function (see Table S15† for more details). These results not only demonstrate the effectiveness of our local reactivity expressions but also indicate that structural information should be combined with the local reactivity information. They also emphasize that an appropriate expression of features can improve a machine-learning model even if the same amount of information is provided.
In addition to feature selection and processing, we carefully optimized other hyperparameters such as the ANN structure, the number of local indices, the size of FP vectors, the learning rate, and the dropout rate. Detailed values and discussions are provided in the Computational methodology section and Tables S2–S9.† As a result, we achieved significantly higher R-square (Pearson correlation) values of 0.941 (0.971) and 0.840 (0.917) for electrophiles and nucleophiles, respectively, with the RMSE of the N + E value corresponding to 4.89 (mean absolute error (MAE) of the N + E value of 3.38) as depicted and labeled with the ML model in Fig. 2. It is expected that, now by utilizing the obtained machine-learned model, highly reactive materials can be screened out prior to experiments, accelerating the materials development process in practical applications.
Predicting chemical stabilities in lithium–oxygen batteries using the ML model
As an example of showing the validity of our prediction model, the potential side reactions occurring in lithium–oxygen batteries were investigated. In advanced lithium–oxygen batteries, redox mediators (RM) play a key role and participate in intermediate reactions for electron or hole transport.4,63 This process involves the reversible redox reaction of RM being solvated and freely diffusing in an electrolyte.4,63 Under practical operation conditions, however, a charged RM molecule, i.e., RM+ or RM−, can be vulnerable to side reactions particularly with the electrolyte molecules.1,4,63 Previous experimental results on the side reactions between various RMs and electrolytes are summarized in Table 2, including the gas analysis.1 Since the deviation from the e−/O2 = 2 in the gas analysis indicates the degree of side reactions, DMPZ (5,10-dimethylphenazine) and TTF (tetrathiafulvalene) were found to be stable with the TEGDME (tetraethylene glycol dimethyl ether) electrolyte, whereas NDA (1,5-naphthalenediamine), TMA (4,N,N-trimethylaniline), and PPD (1-phenylpyrrolidine) underwent a significant degree of side reactions with the electrolyte (e−/O2 > 2). Our machine-learning model could easily reproduce these trends of the reactivities between the RM+s and TEGDME, simply from the sum of the predicted electrophilicity of RM+ (E) and the nucleophilicity of TEGDME (N). It should be noted that higher values of N + E indicate high reactivity and subsequent side reactions, and, when it is apart from the reaction border value (N + E = −5) by 4.36 (i.e. −5 ± 4.36, and MAE + 2σ = 4.36), the accuracy of the prediction is >95%. As tabulated in Table 2, with an accuracy of >95% for the reactivity, our model successfully demonstrates that DMPZ+ is stable against TEGDME, whereas PPD+ and TMA+ are substantially unstable with high values of N + E, in good agreement with the experimental results. Moreover, the trend of the observed reactivity for different RMs, that is, PPD (e−/O2 = 5.50) > TMA (e−/O2 = 4.51) > NDA (e−/O2 = 3.00), is well-matched with that of the predicted N + E value, i.e., PPD (1.67) > TMA (−0.56) > NDA (−7.96). These results indicate that the machine-learning model can be effectively utilized for fast screening of the relative magnitude of the reactivity as well as for classifying a stable/unstable combination of component materials.
Table 2 Predicted and reported stabilities of TEGDME against charged redox mediators. We designated −9.36 < predicted N + E < −0.64 as the “uncertain region” in which a reaction cannot be statistically classified as reactive or not
| Redox mediators (RM) |
DMPZ |
TTF |
PPD |
TMA |
NDA |
|
E (RM+) |
−9.82 |
−6.84 |
3.57 |
1.31 |
−6.09 |
|
E + N (TEGDME) |
−11.68 |
−8.71 |
1.67 |
−0.56 |
−7.96 |
| Stability (predicted) |
Stable |
Uncertain |
Unstable |
Unstable |
Uncertain |
| Stability (exp.)1 |
Stable |
Stable |
Unstable |
Unstable |
Unstable |
| e−/O2 (exp.)1 |
2.08 |
2.08 |
5.50 |
4.51 |
3.00 |
Inspired by the above results, we further constructed a reactivity map for 93 available solvents against the electrophilic/nucleophilic attack of DMPZ+ and/or DMPZ from the machine-learning model as depicted in Fig. 3. The x-axis corresponds to the N + E value, i.e., the logarithm of the rate constant log10(kreaction) from eqn (1), for the electrophilic attack of DMPZ+ with a solvent molecule. The y-axis corresponds to that for the nucleophilic attack of neutral DMPZ with a solvent molecule. Higher values along the x-axis and y-axis indicate a high possibility of the instability of a solvent molecule with charged DMPZ and neutral DMPZ, respectively. A full list of the N + E values predicting the reactivity of solvents against DMPZ and DMPZ+ is provided in Table S16.† From the reactivity map, we identified 20 solvents that are stable against both DMPZ and DMPZ+ with more than 95% accuracy: 2-butanol, 2-pentanol, 2-pentanone, 2-methyl-2-butanol, 3-methyl-2-butanone, 4-methyl-2-pentanone, 33-dimethyl-2-butanone, 24-dimethyl-3-pentanone, 12-dimethoxyethane, ethyl acetate, tetrahydrofuran, diethyl-carbonate, ethoxybenzene, t-butyl methyl ether, diethyl ether, di-n-propyl ether, n-pentane, ethyl benzene, diisopropyl ether and n-butyl acetate. This list includes 12-dimethoxyethane (DME), which was previously reported to be stable against highly oxidative species such as an oxygen radical.11,64–66 The list also covers well-known electrolytes with high electrochemical stability,67 such as tetrahydrofuran (THF) and diethyl carbonate (DEC). In the stability map, 12 solvents were predicted to undergo a reaction with DMPZ and DMPZ+ with more than 95% probability, implying that these solvents should not be used together with DMPZ. Solvents such as alcohols and ethers were predicted to be chemically stable with the DMPZ species; however, these solvents cannot be used as an electrolyte in electrochemical cells because of other issues such as a low dielectric constant, a narrow electrochemical window or poor thermal properties. This implies that appropriate selection criteria, other than chemical stability against specific materials, should be additionally applied for each application.
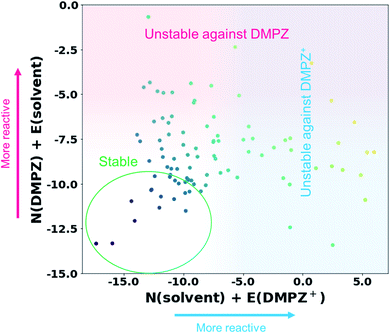 |
| | Fig. 3 Reactivity map showing N + E values, i.e., log10(kreaction) values, of 93 solvents against the electrophilic attack of DMPZ+ and the nucleophilic attack of DMPZ. | |
Despite its usefulness, our prediction model has several limitations, which will be further addressed in future work. First, as observed in Fig. 3 and Table S11,† a large portion of solvents (61 out of 93) were in the “uncertain region”, i.e., −9.36 < predicted N + E < −0.64. This error range is larger than the experimental error (typically lower than ±2),27 which needs to be further improved. We believe that the improvement can be achieved in two ways: (i) larger size of training samples (experimental results). As can be seen in the learning curves of the final model (Fig. S2†), the performance can be improved if there are a larger number of training data. (ii) A more sophisticated ML model and data processing. In this study, it is shown that the appropriate choice of the ML model and data-processing based on scientific knowledge could enhance the prediction performance, suggesting room for more improvement. Second, the model cannot cover the whole chemical space, and is limited by the diversity of Mayr's database,27 which covers nucleophiles with C-, H-, O-, N-, S- and P-reaction centers and electrophiles with C-, N-, Cl-, F- and S-reaction centers. Fortunately, most of the organic molecules reported are composed only of these species (77%, 63 million out of 82 million molecules according to the Chemspider database41) and a large portion of electrolytes, salts and additives used in energy devices also consist only of these elements. We believe that the reactivity of the remaining 23% of compounds can also be evaluated if the reaction centers, i.e. atoms with high local reactivity, are one of the abovementioned elements. Indeed, the molecules containing metal atoms (which are not reaction centers) are also contained in Mayr's database. However, when using our model for reactivity prediction, one should be careful if the atom with a large spin density (Parr function) is not one of the abovementioned elements. Third, although the time and resources required for the reactivity prediction were remarkably reduced compared with those needed for conventional methods that estimate reaction barriers,11–14 our method still requires some degree of DFT calculations for each prediction to calculate electronic information, besides the machine-learning itself. Fourth, as shown in Fig. 1, the reactivity of first-order reactions which comprise another important class of chemical reactions and diffusion-controlled reactions could not be considered in our method. First-order reactions generally involve reversible self-decomposition reactions such as bond dissociation or acidic reactions; therefore, a method evaluating bond dissociation energies or pKa values should be established to predict the reactivity of first-order reactions. For prediction of diffusion-controlled reactivity, the relationship between mass transfer properties, e.g. viscosity, wettability, and ion diffusivity, and the reactivity should be studied. Fifth, we only considered reactions between organic molecules in this work; however, side reactions can be initiated with the interaction between the molecule and other solid species, such as electrodes and conductive agents, i.e. catalytic effect of solid materials. We believe that this can also be predicted using the electrophilicity–nucleophilicity scheme, because it is known that the local reactivity concept (in detail, the Fukui function or the Parr function concept) also works for metals or other solid crystals.68 At the end of the day, this kind of reaction can be analyzed by our model, when we have a high-quality and high-quantity database regarding the reaction between organic materials and solid materials. Finally, the reactivity of excited molecules cannot be predicted with our model, because there is no experimental result involving excited molecules in our database. Furthermore, IE and EA cannot be defined in the excited state, requiring a new reaction index expression which can be generally applicable to both ground and excited states, to construct a general theory for reactivity.
Conclusion
In this study, we developed a new, fast and low-cost screening model for predicting the reactivity of organic molecules, by employing a machine-learning approach. Exploiting conventional reaction indices for reactivity predictions over a wide chemical space proved to be statistically frustrating, and even introducing local indices resulted in only marginal enhancement. Applying a machine-learning approach to this was demonstrated to remarkably improve the prediction capability of reaction indices methodologies, especially when both electronic information and structural information were simultaneously provided for training. The optimized model resulted in test set RMSE values of 1.93 and 2.96 for electrophilicity and nucleophilicity prediction, respectively, representing outstanding results compared with those obtained from the conventional reaction indices methodology. Furthermore, the model accurately predicted the experimental results for the reaction between known electrolytes and redox mediators in lithium–oxygen batteries. For further demonstration, we constructed a reactivity map visualizing the reactivity between 93 available electrolytes and a representative redox mediator material, which could guide the rational design of the lithium–oxygen battery system. We believe that the machine-learning model suggested in this work will not only help accelerate the screening of materials for electrochemical systems that contain various chemical interfaces but also provide general insights into the relationship between molecular properties and reactivity. Finally, this work demonstrates that a machine-learning approach can be a useful tool for drastically improving the performance of an empirical model, suggesting its future potential applicability.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No. 2018R1A2A1A05079249); Project Code (IBS-R006-A2); and the Creative Materials Discovery Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (NRF-2017M3D1A1039553).
References
- H.-D. Lim, B. Lee, Y. Zheng, J. Hong, J. Kim, H. Gwon, Y. Ko, M. Lee, K. Cho and K. Kang, Nat. Energy, 2016, 1, 16066 CrossRef CAS
 .
.
- M. A. Green, K. Emery, Y. Hishikawa, W. Warta and E. D. Dunlop, Prog. Photovoltaics Res. Appl., 2015, 23, 1–9 CrossRef
 .
.
- P. K. Nayak, S. Mahesh, H. J. Snaith and D. Cahen, Nat. Rev. Mater., 2019, 4, 269–285 CrossRef CAS
 .
.
- H.-D. Lim, B. Lee, Y. Bae, H. Park, Y. Ko, H. Kim, J. Kim and K. Kang, Chem. Soc. Rev., 2017, 46, 2873–2888 RSC
 .
.
- T. Daeneke, T.-H. Kwon, A. B. Holmes, N. W. Duffy, U. Bach and L. Spiccia, Nat. Chem., 2011, 3, 211 CrossRef CAS PubMed
 .
.
- D. Aurbach, B. D. McCloskey, L. F. Nazar and P. G. Bruce, Nat. Energy, 2016, 1, 16128 CrossRef CAS
 .
.
- M. Asadi, B. Sayahpour, P. Abbasi, A. T. Ngo, K. Karis, J. R. Jokisaari, C. Liu, B. Narayanan, M. Gerard, P. Yasaei, X. Hu, A. Mukherjee, K. C. Lau, R. S. Assary, F. Khalili-Araghi, R. F. Klie, L. A. Curtiss and A. Salehi-Khojin, Nature, 2018, 555, 502 CrossRef CAS PubMed
 .
.
- D. J. Lee, H. Lee, Y.-J. Kim, J.-K. Park and H.-T. Kim, Adv. Mater., 2016, 28, 857–863 CrossRef CAS PubMed
 .
.
- G. Niu, X. Guo and L. Wang, J. Mater. Chem. A, 2015, 3, 8970–8980 RSC
 .
.
- N. A. Ludin, A. M. Al-Alwani Mahmoud, A. Bakar Mohamad, A. A. H. Kadhum, K. Sopian and N. S. Abdul Karim, Renewable Sustainable Energy Rev., 2014, 31, 386–396 CrossRef CAS
 .
.
- V. S. Bryantsev, J. Uddin, V. Giordani, W. Walker, D. Addison and G. V. Chase, J. Electrochem. Soc., 2013, 160, A160–A171 CrossRef CAS
 .
.
- H. Park, H.-D. Lim, H.-K. Lim, W. M. Seong, S. Moon, Y. Ko, B. Lee, Y. Bae, H. Kim and K. Kang, Nat. Commun., 2017, 8, 14989 CrossRef PubMed
 .
.
- H. C. Kwon, M. Kim, J.-P. Grote, S. J. Cho, M. W. Chung, H. Kim, D. H. Won, A. R. Zeradjanin, K. J. J. Mayrhofer, M. Choi, H. Kim and C. H. Choi, J. Am. Chem. Soc., 2018, 140, 16198–16205 CrossRef CAS
 .
.
- Q. Luo, Z. Shi, D. Li, C. Zhu and M. Wang, Chem. Phys. Lett., 2017, 687, 158–162 CrossRef CAS
 .
.
- S. Pratihar and S. Roy, J. Org. Chem., 2010, 75, 4957–4963 CrossRef CAS
 .
.
- L. R. Domingo and P. Pérez, Org. Biomol. Chem., 2011, 9, 7168–7175 RSC
 .
.
- P. K. Chattaraj, S. Giri and S. Duley, Chem. Rev., 2011, 111, PR43–PR75 CrossRef
 .
.
- R. L. Domingo, M. Ríos-Gutiérrez and P. Pérez, Molecules, 2016, 21, 748 CrossRef
 .
.
-
M. J. Frisch, http://www.gaussian.com/
 .
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS
 .
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
 .
.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS
 .
.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef
 .
.
- H. Mayr and A. R. Ofial, Pure Appl. Chem., 2005, 77, 1807–1821 CAS
 .
.
- H. Mayr and A. R. Ofial, J. Phys. Org. Chem., 2008, 21, 584–595 CrossRef CAS
 .
.
- H. Mayr, M. Breugst and A. R. Ofial, Angew. Chem., Int. Ed., 2011, 50, 6470–6505 CrossRef CAS PubMed
 .
.
- H. Mayr, Tetrahedron, 2015, 71, 5095–5111 CrossRef CAS
 .
.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS
 .
.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS
 .
.
-
R. G. Parr, Density Functional Theory of Atoms and Molecules, in, Horizons of Quantum Chemistry, ed. K. Fukui and B. Pullman, Académie Internationale Des Sciences Moléculaires Quantiques/International Academy of Quantum Molecular Science, Springer, Dordrecht, 1980, vol. 3 Search PubMed
 .
.
- L. R. Domingo, E. Chamorro and P. Pérez, Org. Biomol. Chem., 2010, 8, 5495–5504 RSC
 .
.
- P. K. Chattaraj and B. Maiti, J. Phys. Chem. A, 2001, 105, 169–183 CrossRef CAS
 .
.
- L. R. Domingo, P. Pérez and J. A. Sáez, RSC Adv., 2013, 3, 1486–1494 RSC
 .
.
- E. Chamorro, P. Pérez and L. R. Domingo, Chem. Phys. Lett., 2013, 582, 141–143 CrossRef CAS
 .
.
-
D. P. Kingma and J. Ba, 2014, eprint arXiv:1412.6980, arXiv:1412.6980.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed
 .
.
-
G. Landrum, RDKit: Open-Source Cheminformatics Software, 2016, http://www.rdkit.org/, https://github.com/rdkit/rdkit Search PubMed
 .
.
- J. Shao, J. Am. Stat. Assoc., 1993, 88, 486–494 CrossRef
 .
.
-
S. Shalev-Shwartz and S. Ben-David, Understanding machine learning: From theory to algorithms, Cambridge university press, 2014 Search PubMed
 .
.
- S. Kim, P. A. Thiessen, E. E. Bolton, J. Chen, G. Fu, A. Gindulyte, L. Han, J. He, S. He, B. A. Shoemaker, J. Wang, B. Yu, J. Zhang and S. H. Bryant, Nucleic Acids Res., 2015, 44, D1202–D1213 CrossRef PubMed
 .
.
- H. E. Pence and A. Williams, J. Chem. Educ., 2010, 87, 1123–1124 CrossRef CAS
 .
.
- W. Gomes, Nature, 1961, 192, 865–866 CrossRef CAS
 .
.
-
A. W. Adamson, Physical chemistry of surfaces, Wiley, New York u.a., 3rd edn, 1976 Search PubMed
 .
.
-
K. J. Laidler and J. Keith, Chemical kinetics, McGraw-Hill, New York, 1965 Search PubMed
 .
.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 979–989 CrossRef CAS
 .
.
- C. L. Haynes, Y.-M. Chen and P. B. Armentrout, J. Phys. Chem., 1995, 99, 9110–9117 CrossRef CAS
 .
.
- P. M. Futerko and A. Fontijn, J. Chem. Phys., 1993, 98, 7004–7011 CrossRef CAS
 .
.
- R. Contreras, J. Andres, V. S. Safont, P. Campodonico and J. G. Santos, J. Phys. Chem. A, 2003, 107, 5588–5593 CrossRef CAS
 .
.
- Z. Zhou and R. G. Parr, J. Am. Chem. Soc., 1990, 112, 5720–5724 CrossRef CAS
 .
.
- P. Pérez, A. Toro-Labbé, A. Aizman and R. Contreras, J. Org. Chem., 2002, 67, 4747–4752 CrossRef PubMed
 .
.
- P. Pérez, J. Org. Chem., 2003, 68, 5886–5889 CrossRef PubMed
 .
.
- P. R. Campodónico, P. Fuentealba, E. A. Castro, J. G. Santos and R. Contreras, J. Org. Chem., 2005, 70, 1754–1760 CrossRef PubMed
 .
.
- R. G. Parr, L. v. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS
 .
.
- L. R. Domingo, E. Chamorro and P. Pérez, J. Org. Chem., 2008, 73, 4615–4624 CrossRef CAS PubMed
 .
.
- R. Tibshirani, J. Roy. Stat. Soc. B, 1996, 58, 267–288 Search PubMed
 .
.
-
A. N. Tikhonov, Solutions of ill-posed problems, ed. A. N. Tikhonov and V. Y. Arsenin, translation editor, Fritz John, Winston ; distributed solely by, Halsted Press, Washington: New York, 1977 Search PubMed
 .
.
-
C. K. I. Williams and C. E. Rasmussen, Gaussian processes for machine learning, MIT press Cambridge, MA, 2006 Search PubMed
 .
.
- C. Cortes and V. Vapnik, Mach. Learn., 1995, 20, 273–297 Search PubMed
 .
.
- H. Tin Kam, IEEE Trans. Pattern Anal. Mach. Intell., 1998, 20, 832–844 CrossRef
 .
.
- W. S. McCulloch and W. Pitts, Bull. Math. Biophys., 1943, 5, 115–133 CrossRef
 .
.
-
M. Minsky and S. A. Papert, Perceptrons: An introduction to computational geometry, MIT press, 2017 Search PubMed
 .
.
-
M. B. Smith and J. March, March's advanced organic chemistry: reactions, mechanisms, and structure, John Wiley & Sons, 2007 Search PubMed
 .
.
- Y. Ko, H. Park, B. Kim, J. S. Kim and K. Kang, Trends Chem., 2019, 1, 349–360 CrossRef
 .
.
- A. Khetan, A. Luntz and V. Viswanathan, J. Phys. Chem. Lett., 2015, 6, 1254–1259 CrossRef CAS PubMed
 .
.
- B. D. McCloskey, D. S. Bethune, R. M. Shelby, T. Mori, R. Scheffler, A. Speidel, M. Sherwood and A. C. Luntz, J. Phys. Chem. Lett., 2012, 3, 3043–3047 CrossRef CAS PubMed
 .
.
- V. S. Bryantsev, V. Giordani, W. Walker, M. Blanco, S. Zecevic, K. Sasaki, J. Uddin, D. Addison and G. V. Chase, J. Phys. Chem. A, 2011, 115, 12399–12409 CrossRef CAS PubMed
 .
.
- A. Ponrouch, E. Marchante, M. Courty, J.-M. Tarascon and M. R. Palacin, Energy Environ. Sci., 2012, 5, 8572–8583 RSC
 .
.
- K. Fukui, Science, 1982, 218, 747–754 CrossRef CAS PubMed
 .
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc01328e |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *abc
*abc
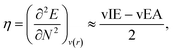
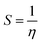
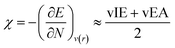
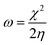
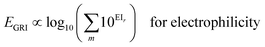
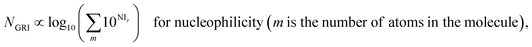
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 learning steps. To mitigate overfitting, a dropout rate of 0.8 and an L2 regularization parameter of 10−3 were used. The 30 largest local reactivities (components of the GRI) were used for each molecule as an electronic property feature, and 1024-bit Morgan FP36 and MACCS keys generated using the RDKit software37 were employed as a structural feature for electrophilicity and nucleophilicity, respectively. The effective dimensionality of the features was examined using the Pearson correlation. A majority of the 50 largest electronic features showed a Pearson correlation >0.1 for both electrophilicity and nucleophilicity cases, implying that even the local reactivities of less active sites can be meaningful to the prediction (Fig. S1†). The performance of the model was evaluated by averaging 40 test-set R-square values (loss values) of an independently trained model with identical hyperparameters based on the Monte Carlo cross-validation scheme.38 The sample size is predicted to be higher than the VC dimension of the final model, based on learning curves39 (Fig. S2†). A training set and a test set were randomly selected at a 9
000 learning steps. To mitigate overfitting, a dropout rate of 0.8 and an L2 regularization parameter of 10−3 were used. The 30 largest local reactivities (components of the GRI) were used for each molecule as an electronic property feature, and 1024-bit Morgan FP36 and MACCS keys generated using the RDKit software37 were employed as a structural feature for electrophilicity and nucleophilicity, respectively. The effective dimensionality of the features was examined using the Pearson correlation. A majority of the 50 largest electronic features showed a Pearson correlation >0.1 for both electrophilicity and nucleophilicity cases, implying that even the local reactivities of less active sites can be meaningful to the prediction (Fig. S1†). The performance of the model was evaluated by averaging 40 test-set R-square values (loss values) of an independently trained model with identical hyperparameters based on the Monte Carlo cross-validation scheme.38 The sample size is predicted to be higher than the VC dimension of the final model, based on learning curves39 (Fig. S2†). A training set and a test set were randomly selected at a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of the total dataset. To minimize an extrapolated prediction, a random selection of training/test sets was iterated until the differences in both the average and standard deviation of experimental values between the training and test sets become less than 1%. The source codes of the final model can be found at https://github.com/petitcloud/2020_reactivity_ML.
1 ratio of the total dataset. To minimize an extrapolated prediction, a random selection of training/test sets was iterated until the differences in both the average and standard deviation of experimental values between the training and test sets become less than 1%. The source codes of the final model can be found at https://github.com/petitcloud/2020_reactivity_ML.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

