Ballistic ΔS = 2 intersystem crossing in a cobalt cubane following ligand-field excitation probed by extreme ultraviolet spectroscopy

Abstract

Femtosecond M_2,3-edge X-ray absorption near-edge structure (XANES) spectroscopy is used to probe the excited-state dynamics of the cobalt cubane [Co^III₄O₄](OAc)₄(py)₄ (OAc = acetate, py = pyridine), a model for water oxidation catalysts. After ligand-field excitation, intersystem crossing (ISC) to a metal-centered quintet occurs in 38 fs. 30% of the hot quintet undergoes ballistic back-ISC directly to the singlet ground state, with the remainder relaxing to a long-lived triplet.

---

Introduction

The realization of renewable solar fuels on a global scale requires the development of earth-abundant water oxidation catalysts. The tetrametallic oxo-cluster, [Co^III₄O₄](OAc)₄(py)₄ (OAc = acetate, py = pyridine), henceforth “Co₄O₄”, is a promising molecular compound that has attracted significant interest due to its provocative “cubane” structure which bears a strong resemblance to the active core of the oxygen-evolving complex (OEC) of photosystem II in plants. Co₄O₄ (shown in Fig. 1A) also exhibits water oxidation activity in several homogeneous photocatalytic systems,^1–3 as well as in heterogeneous studies where it has been incorporated into photoanodes of TiO₂, Fe₂O₃, and BiVO₄.^4–8 Under the high intensity irradiation conditions of photocatalysis, Co₄O₄ excited states may be populated either through direct absorption or via energy transfer from a photosensitizer.

Fig. 1 (A) Structure of Co₄O₄. (B) Ground state M-edge XANES spectrum. The ligand field multiplet (LFM) simulation and sticks are shown in red. (C) Correlation diagram showing transitions between the 3p₆3d₆ ground state and 3p₅3d₇ core-hole excited state as a function of ligand-field strength 10Dq.

The excited-state dynamics of Co(III) complexes have received fairly little study, especially compared to their isoelectronic Fe(II) counterparts.^9,10 Optical transient absorption spectroscopy of amine-coordinated Co(III) complexes such as Co(ethylenediamine)₃³⁺ indicate picosecond relaxation to quintet metal-centered (⁵MC) states after ligand-to-metal charge transfer (LMCT) excitation, whereas Co(acac)₃ was proposed to relax to triplet MC states (³MC) in 10–20 fs followed by vibrational relaxation on the triplet surface.^11,12

In this work, we use femtosecond M_2,3-edge X-ray Absorption Near Edge Structure (XANES) spectroscopy to measure a cascade of intersystem crossing events in Co₄O₄ after ligand-field excitation, including a surprisingly efficient ΔS = 2 crossing between the hot ⁵T₂ state and the ¹A₁ ground state. M_2,3-edge XANES probes 3p → 3d transitions in the extreme ultraviolet (XUV) spectral region (40–100 eV) and is a sensitive reporter of spin state, oxidation state, and ligand field symmetry. This technique been previously used to examine excited state dynamics, including ISC, in metal oxides,^13–15 semiconductors,^16–19 and molecular complexes.^20–22

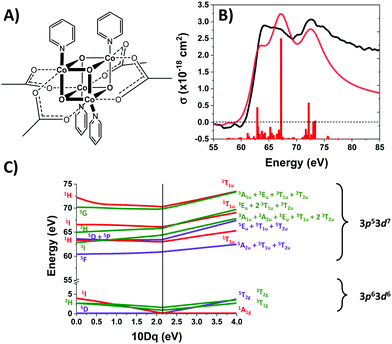
Co₄O₄ consists of four low-spin d⁶ Co³⁺ atoms, each of which is in an approximately octahedral ligand field. The UV-Visible spectrum of Co₄O₄ (Fig. S1, ESI†) exhibits three features in the 300–1000 nm range (note that all oscillator strengths are reported per cubane molecule, not per cobalt atom). A prominent feature at 364 nm has been assigned as a O^2-(2p) → Co³⁺(e_g) LMCT band based on its strength (∼10⁴ L mol⁻¹ cm⁻¹) and by comparison to other compounds bearing Co–O bonds.^14,23,24 The two lower energy features (451 nm and 646 nm) are consistent with d–d transitions, which in the limit of O_h symmetry correspond to ¹A₁ → ¹T₂ and ¹A₁ → ¹T₁ transitions. Analysis of the d⁶ Tanabe–Sugano (TS) diagram yields a ligand field splitting 10Dq of 2.1 eV and predicts ³T_1g as the lowest energy excited state (see ESI†). This 10Dq is consistent with published values for octahedral Co³⁺ complexes bearing aquo, carbonato, or oxalato ligands which present an electronic environment similar to that of Co₄O₄.²⁵ Rigorously speaking, cobalt sites in Co₄O₄ are not of O_h symmetry due to the lone axial pyridine. Tetragonal distortion likely contributes to the relatively high molar absorptivity (∼500 L mol⁻¹ cm⁻¹) of the d–d transitions.

Methods

M_2,3-edge XANES spectra of Co₄O₄ were acquired from thin film samples of the complex deposited upon polymer membranes.²⁶ Details of its synthesis are described in the supporting information. The extreme ultraviolet probe continuum was produced by high-harmonic generation in a tabletop instrument using a Ti:sapphire driving laser (800 nm, 4 mJ, 35 fs, 1 kHz) focused into a ∼100 torr neon gas cell.²⁷ Time-resolved experiments utilized the focused ∼2.5 mJ cm⁻² 550 nm pump output of a noncollinear optical parametric amplifier driven from a 0.65 mJ portion of the same laser. Absolute time zero was determined and corrected for by periodic measurement of the instrument-response limited onset of Fe₂O₃ signal after 550 nm excitation,¹³ with the instrument response function (IRF) found to be 48 fs FWHM. The spectrometer energy resolution is 0.3 eV, calibrated using the atomic absorption lines of ionized xenon and the XUV absorptions of Fe₂O₃, NiO, and Al.

Results

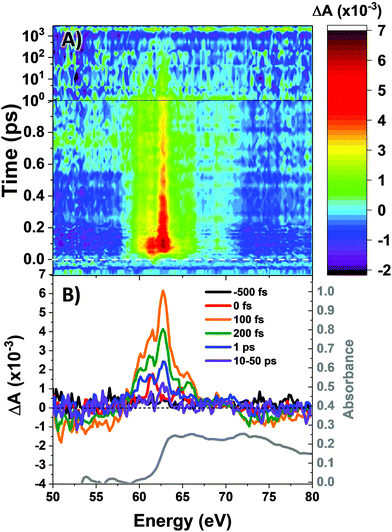
The M_2,3-edge XANES spectrum of Co₄O₄, shown in Fig. 1B, exhibits features at 64.2, 66.2, and 72.3 eV. This three-peaked structure is in accordance with the predictions of crystal field theory for low-spin d⁶ complexes and corroborates previous studies.^22,27 In an analogy to Tanabe–Sugano diagrams, the 3p⁶3d⁶ → 3p⁵3d⁷ transitions probed here can be analysed as shown in the correlation diagram of Fig. 1C. In the weak-field limit, parent states are assigned Russel–Saunders term symbols and ordered by Hund's rules, giving a ⁵D ground state. Moving to the right of the diagram, octahedral symmetry is imposed and the newly split states are described by Mulliken term symbols. As ligand-field strength (10Dq) increases the low-spin states become favoured. Transition energies vary with ligand-field strength and spin state, making M_2,3-edge XANES spectroscopy a powerful probe of electronic structure. Situated on the right-hand side of the diagram, Co₄O₄ exhibits three transitions from its ¹A_1g to ¹T_1u states. Spin–orbit coupling is neglected in this simple picture, but included in ligand field multiplet (LFM) simulations performed with the program CTM4XAS, as detailed in the supplemental information. These simulations reproduce the position of the three features, though the height of the middle peak is overestimated. In addition to the singlet transitions important in the ground state of Co₄O₄, the analysis is useful for predictions of triplet and quintet excited states.

The transient M_2,3-edge XANES response after d–d excitation at 550 nm is shown in Fig. 2A, with spectral slices at selected delay times in Fig. 2B. A short-lived signal is apparent at time zero, exhibiting two sharp positive peaks at 61.6 and 64.6 eV and weak ground state bleaches at energies below 58 eV and above 71.4 eV. This initial spectrum transforms within 100 fs to a longer-lived spectrum characterized by a strong absorption at 62.8 eV, a smaller secondary peak at 65.6 eV, and the same ground state bleaches as the initial signal. The signal subsequently undergoes a loss in intensity without change in shape until ∼1 ps where the spectral shape begins to again evolve: the main 62.8 eV feature diminishes further while the bleach near 72.5 eV has instead become positive. Finally, the signal decays away over hundreds of picoseconds completely disappearing by 3 ns.

Fig. 2 (A) Contour plot of time-resolved M-edge XANES spectra. Time zero is indicated in the dashed white line. (B) Selected spectral slices with the ground state Co₄O₄ spectrum in grey for comparison. The data are binned to 0.2 eV intervals.

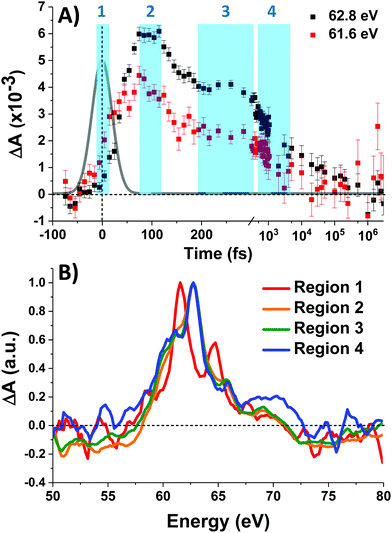
Fig. 3A shows the time traces at 61.6 and 62.8 eV corresponding to the maxima of the initial short-lived spectrum and its immediate successor. Notable features visible in this plot include the ∼35 fs delay from time zero between the two signal traces, and a significant and abrupt drop in magnitude between 100 and 200 fs. Four regions of interest were selected and their averaged and normalized spectra are shown in Fig. 3B. These are: region 1 (−15 to 15 fs) where the first short-lived spectrum appears, region 2 (75 to 115 fs) the high plateau, region 3 (200 to 300 fs) a flat valley immediately after the abrupt drop, and region 4 (900 fs to 5 ps) where the system appears to decay exponentially. The assignment of the dominant states comprising these regions is now discussed.

Fig. 3 (A) Time traces (data points). Error bars are ± the standard error. Data traces are integrated ±0.2 eV from the listed value. Four integration regions (light blue) are defined. The 48 fs instrument response function is plotted in grey. (B) Normalized and smoothed (5-point [1.0 eV] Savitzky–Golay) time-averaged regions.

Photoexcitation into the ¹T₁/¹T₂ states populates antibonding e_g orbitals and induces bond expansion which propels the system towards an intersection with nearby low-lying triplet and quintet states,^28,29 any of which are plausible candidates for the singlet's relaxation products. LFM simulated difference spectra of these states are shown in Fig. 4A. The simulated ¹T₁ difference spectrum exhibits two positive features near 60 and 65 eV with a negative feature between them near 62.5 eV. The energy of these features is a good match to the spectrum of Region 1 in Fig. 3B, although the height of the positive features is underestimated. The ¹T₁ and ¹T₂ spectra are similar, though the latter bears a bleach at 65 eV unlike Region 1. The Region 1 spectrum transforms sequentially into the spectra of Regions 2 and then 3, whose difference spectra are almost identical in shape and thus likely represent the same electronic state. These are characterized by a strong positive absorption at 62.8 eV, two positive shoulders at 65.6 eV and 69.0 eV, and a broad bleach at energies greater than 71.4 eV. A broad bleach also occurs prior to the edge near 57 eV. These features are reproduced in the simulated quintet ⁵T₂ difference spectrum in Fig. 4A, whereas the simulated triplets in contrast are a poor match. In particular, the triplet simulations predict a positive signal above ∼70 eV instead of the bleach predicted for the quintet. The lack of a high-energy bleach in the triplet spectrum can be understood by inspection of the correlation diagram in Fig. 1C, which shows several high-energy triplet transitions that nearly overlap with those of the singlet. The spectrum in Regions 2 and 3 is therefore assigned as ⁵T₂, suggesting that the singlet excited state undergoes rapid two-electron intersystem crossing to the quintet state. If an intermediate triplet state were involved it would have to be extremely short-lived (<30 fs). Finally, the weak transient signal of Region 4 emerges. Relative to Region 3, the spectrum of Region 4 bears a broadened positive absorption near 62.8 eV and the 72.5 eV bleach has become a positive excited state absorption – features characteristic of the ³T₁ triplet simulation.

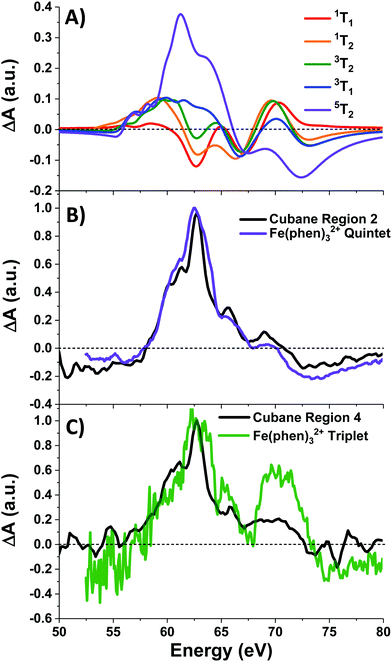Fig. 4 (A) LFM simulations of cubane excited states, and (B) normalized quintet difference spectra of Fe(phen)₃²⁺ (from ref. 22) compared with that of cubane Region 2, and (C) triplet intermediate spectrum (ibid.) compared with cubane Region 4. Fe(phen)₃²⁺ spectra have been blue-shifted 5.5 eV.

Further corroboration of these assignment is achieved by comparison with Fe(II) spin-crossover complexes,^22,28–30 which are isoelectronic to the d⁶ metal centers in the cubane. A recent transient M_2,3-edge XANES study found that Fe(phen)₃²⁺ (phen = o-phenanthroline), after pumping into its metal-to-ligand charge transfer (MLCT) band at 535 nm, relaxes to an intermediate ³T₁ state and then into a metastable ⁵T₂ state.²² The difference spectra associated with these two states are reproduced in Fig. 4B-C along with the spectra of Regions 2 and 4 of cubane. With a +5.5 eV shift applied to the Fe(phen)₃²⁺ data to account for the increased 3p binding energy of cobalt, the spectra are a good match in the case of the triplet, and essentially superimposable for the quintet. To summarize: excitation of the d–d transitions in Co₄O₄ yields an initial ¹T₁ state that rapidly transforms into the ⁵T₂ state, presumably through the unobserved ³T₂ intermediate. The ⁵T₂ state relaxes into a metastable ³T₁ state which eventually settles to the ground state. Note that this sequence is consistent with the state orderings predicted both from the TS diagram and from DFT calculations (see ESI†).

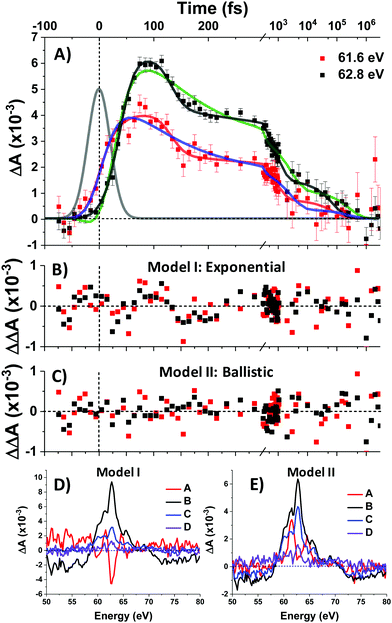
To complement the above qualitative analysis the data were subjected to global analysis under two different models (I and II), each consisting of four states visited sequentially before returning to the ground state: A → B → C → D → GS. Model I imposes single exponential (first-order) kinetics upon each transition and yielded time constants τ₁ = 30 ± 2 fs, τ₂ = 108 ± 20 fs, τ₃ = 2.9 ± 0.7 ps, and τ₄ = 285 ± 114 ps. Both this fit and that of Model II below are convolved with the IRF. Fit traces for the 61.6 eV and 62.8 eV features are shown in Fig. 5A and the extracted component spectra are shown in Fig. 5D. The component spectra in Fig. 5D correspond well with the spectra of Regions 1–4 (Fig. 3B) except for Component A, which exhibits a much stronger bleach at 62.8 eV and makes it better match the simulated ¹T₁ spectrum (Fig. 4A). However, the exponential kinetics of Model I fail to capture the dynamics between 100 and 200 fs, where an abrupt ∼30% decrease in signal intensity is observed. Indeed, residuals for the fit (Fig. 5B) at early times (to 1 ps) exhibit undulatory deviations indicative of inadequacy in the model. Moreover, the rapidity of the spectral evolution for the first two state transitions (30 fs and 108 fs respectively) suggest a process faster than is physically reasonable for exponential (first-order) kinetics.

Fig. 5 Global analysis of transient M_2,3-edge XANES spectroscopy cubane data. A) Data points are shown with error bars (±1 standard error) and a Gaussian profile corresponding to the 48 fs IRF is shown in gray. Fits to the data are shown in solid lines: Model I (exponential) in green and blue, Model II (ballistic) in black and red. Residuals in each model are shown in (B and C) with the same x-axis. Component spectra are shown in (D and E).

Exponential kinetics arise when the transitions between states derive from the probabilistic overtopping of a reaction barrier between those states, with the barrier height described by the activation energy. In contrast, low-barrier or barrierless crossings between appropriately situated potential energy surfaces (PES) results in high-probability curve crossings events. The kinetics are then controlled not by the barrier but rather by the time it takes a population to ballistically traverse the PES from its initial entry point to the curve crossing, and this traversal time can be very short—on the order of a quarter period of the vibrational mode associated with the PES.^28,31

Model II replaces τ₁ and τ₂ with ballistic traversal time constants ω₁ and ω₂, yielding fit values of ω₁ = 38 ± 2 fs, ω₂ = 94 ± 5 fs, τ₃ = 794 ± 345 fs, and τ₄ = 83 ± 14 ps), with component spectra in Fig. 5E. As can be seen qualitatively in Fig. 5A, Model II is better able to capture the rise and fall of the data; Model II residuals (Fig. 5C) do not exhibit the palpably patterned deviations of Model I. Goodness-of-fit between Models I and II was quantitatively assessed and found to favour Model II at the 95% confidence level. The details of this error analysis are described in the supporting information.

Discussion

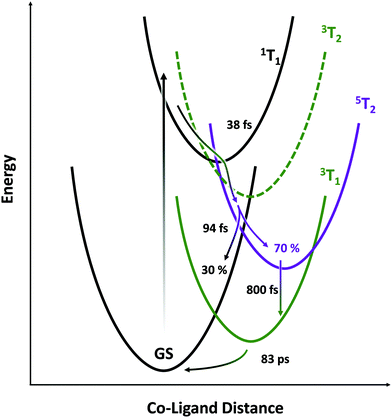
The picture that emerges (illustrated schematically in Fig. 6) is consistent with the state orderings predicted from both the TS diagram and DFT calculations (see ESI†). After ligand-field excitation into the singlet, the system rapidly (38 fs) follows a ballistic trajectory into the quintet manifold. Descending on the quintet surface, it encounters a crossing with the singlet GS after a further 94 fs and loses 30% of its population there. The remaining 70% cools on the quintet surface, then converts into the lowest energy triplet over several picoseconds. The LFM simulations in Fig. 4A predict that the triplet transient should be ∼25% the strength of the quintet, which is seen here experimentally. If the calculations underestimate this ratio, then the loss in intensity accompanying ⁵T₂ → ³T₁ conversion can be explained by an additional parallel exponential decay pathway to the GS. Finally, the metastable triplet relaxes with exponential kinetics back to the ground state in 83 ps.

Fig. 6 Schematic representing potential energy surfaces in the proposed model.

The rapid ΔS = 2 intersystem crossing from the ¹T₁ state to the ⁵T₂ state may be understood in the context of extensive research on Fe(II) chromophores. After ¹MLCT excitation, intersystem crossing to the ³MLCT and internal conversion to a ³T state occur in 100–150 fs, followed by ³T → ⁵T ISC in ∼50 fs. These inverted kinetics led to early controversy^30,32 over the presence of the ³T state, but the brief occupation of this state was later confirmed using spin-sensitive core-level spectroscopy.^22,28 This model was supported by theoretical work which rationalized this possibility by re-evaluating the effective spin–orbit coupling between those states—finding it highly geometry dependent—and showed the importance of molecular vibrations on the magnitude of spin-vibronic coupling.^33–36 Predicted ISC rates are often over 10¹³ s⁻¹, with the doublet-to-quartet process in Fe–Co Prussian-blue analogues calculated to be as little as 20 fs.³⁷ Intersystem crossing between metal-centered states with ΔS = 1 occurs with essentially 100% quantum yield at the crossing point between electronic PESs, as shown by work combining X-ray emission spectroscopy and X-ray scattering.²⁸

In the present work, the relatively slow ³MLCT → ³T step is avoided by directly exciting the ¹T₁ d–d state. Similarly, in an Fe(II) complex, d–d excitation was shown to populate the ⁵T state in as little as 70 fs, leading to enhanced 80 cm⁻¹ coherent oscillations on the quintet surface due to lack of dephasing in the MLCT state.²⁹ The 635 cm⁻¹ IR band of Co₄O₄ has been assigned to Co–O stretching vibrations involving the Co₃(μ₃-O) core, with a short (53 fs) period.³⁸ This frequency is significantly higher than the ∼250 cm⁻¹ (∼133 fs) mode in most Fe–N₆ complexes and is likely the primary determinant for the consequentially rapid 38 fs ΔS = 2 process in Co₄O₄. Hence, the limiting factor is not the magnitude of spin–orbit coupling matrix element, but rather the frequency of M–L stretching modes on the PESs.

The most surprising result of this study is the high (30%) yield of back-ISC upon a single crossing of the ⁵T₂/¹GS surfaces, as shown by the IRF-limited drop in the intensity of the ⁵T₂ spectrum at 130 fs. While the ΔS = 2 forward-ISC could be rationalized as two subsequent ΔS = 1 processes that are unresolved given the time resolution of this study, there is no intermediate triplet in this portion of the quintet PES. To first order, the spin–orbit coupling matrix element for the double spin–flip is zero. However, second-order SOC can lead to significant coupling between singlet and quintet states, and mediates the back-ISC from the ⁵T₂ state in molecules such as Fe(bpy)₃²⁺, on ∼ns timescales.³⁹ The second-order coupling is especially significant in the presence of large distortions from the equilibrium geometry as are found in vibrationally hot states. For example, Sousa et al. calculated a spin–orbit coupling matrix element of up to 67 cm⁻¹ for the ¹MLCT → ⁵T₂ crossing in Fe(bpy)₃²⁺, only a factor of 3–5 less than the maximum coupling for ³T → ⁵T₂ transitions. Given the ∼100% quantum yield of the ³T → ⁵T₂ process found in Fe(II) complexes, a 30% efficient ΔS = 2 process becomes increasingly plausible. While our treatment thus far has considered all of the photophysics to occur at a single Co center, the four cobalt atoms within the cubane cluster exhibit significant electronic delocalization and metal–metal interactions,⁴⁰ which would enhance any heavy-atom effects on ISC rate.^41,42

Further theoretical work will be required to map the excited-state potential energy surfaces and the coupling between them, though the presence of four metal centers will be a considerable computational challenge. The Co₄O₄ cubane itself presents a flexible platform for substitution of its ligands⁴³ and incorporation of heterometals into its core,⁴⁴ potentially providing insights into the factors affecting ultrafast ISC. We note that the high cross-section of M-edge XANES transitions results in a strong transient signal even with low excitation density (4% per cubane, 1% per Co), avoiding multiple excitation of a single cubane and simplifying the analysis.

Conclusions

Time resolved M_2,3-edge XANES spectroscopy was used to probe the metal-centered dynamics of the cobalt cubane Co₄O₄ after pumping its d–d transitions at 550 nm. This revealed the presence of a short-lived singlet state that rapidly undergoes intersystem crossing into the quintet state within 38 fs. This quintet was identified by comparison with LFM simulations and with the M_2,3-edge XANES signal of the known quintet in the isoelectronic Fe(phen)₃²⁺ system. Ballistic back-intersystem crossing returns 30% of the quintet to the singlet ground state in 94 fs. The remainder of the quintet progresses into a metastable triplet state which then relaxes back to the ground state in 83 ps. This work highlights the aptitude of M_2,3-edge XANES spectroscopy towards the characterization of short-lived metal-centered states in transition metal complexes, and shows that single-step ΔS = 2 ISC is a viable decay pathway in such systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC0018904. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-1746047. The XUV instrument was built with partial support from the Air Force Office of Scientific Research under AFOSR Award No. FA9550-14-1-0314.

References

1. A. Genoni, G. La Ganga, A. Volpe, F. Puntoriero, M. Di Valentin, M. Bonchio, M. Natali and A. Sartorel, Faraday Discuss., 2015, 185, 121–141.
2. H. Liu and H. Frei, ACS Catal., 2020, 10, 2138–2147.
3. S. Berardi, G. La Ganga, M. Natali, I. Bazzan, F. Puntoriero, A. Sartorel, F. Scandola, S. Campagna and M. Bonchio, J. Am. Chem. Soc., 2012, 134, 11104–11107.
4. W. Jiang, X. Yang, F. Li, Q. Zhang, S. Li, H. Tong, Y. Jiang and L. Xia, Chem. Commun., 2019, 55, 1414–1417.
5. J. Li, Y. Jiang, Q. Zhang, X. Zhao, N. Li, H. Tong, X. Yang and L. Xia, RSC Adv., 2017, 7, 4102–4107.
6. B. Zhang, F. Li, F. Yu, X. Wang, X. Zhou, H. Li, Y. Jiang and L. Sun, ACS Catal., 2014, 4, 804–809.
7. Y. Wang, F. Li, X. Zhou, F. Yu, J. Du, L. Bai and L. Sun, Angew. Chem., Int. Ed., 2017, 56, 6911–6915.
8. S. Ye, C. Ding, R. Chen, F. Fan, P. Fu, H. Yin, X. Wang, Z. Wang, P. Du and C. Li, J. Am. Chem. Soc., 2018, 140, 3250–3256.
9. O. S. Wenger, Chem. – Eur. J., 2019, 25, 6043–6052.
10. J. K. McCusker, Science, 2019, 363, 484–488.
11. J. K. McCusker, K. N. Walda, D. Magde and D. N. Hendrickson, Inorg. Chem., 1993, 32, 394–399.
12. L. Ferrari, M. Satta, A. Palma, L. Di Mario, D. Catone, P. O’Keeffe, N. Zema, T. Prosperi and S. Turchini, Front. Chem., 2019, 7, 348.
13. J. Vura-Weis, C. M. Jiang, C. Liu, H. Gao, J. M. Lucas, F. M. F. De Groot, P. Yang, A. P. Alivisatos and S. R. Leone, J. Phys. Chem. Lett., 2013, 4, 3667–3671.
14. C. M. Jiang, L. R. Baker, J. M. Lucas, J. Vura-Weis, A. P. Alivisatos and S. R. Leone, J. Phys. Chem. C, 2014, 118, 22774–22784.
15. A. Cirri, J. Husek, S. Biswas and L. R. Baker, J. Phys. Chem. C, 2017, 121, 15861–15869.
16. M. A. Verkamp, J. Leveillee, A. Sharma, A. Schleife and J. Vura-Weis, J. Am. Chem. Soc., 2021 DOI:10.1021/jacs.1c07817.
17. S. K. Cushing, A. Lee, I. J. Porter, L. M. Carneiro, H. T. Chang, M. Zürch and S. R. Leone, J. Phys. Chem. C, 2019, 123, 3343–3352.
18. E. Principi, E. Giangrisostomi, R. Mincigrucci, M. Beye, G. Kurdi, R. Cucini, A. Gessini, F. Bencivenga and C. Masciovecchio, Phys. Rev. B, 2018, 97, 174107.
19. S. K. Cushing, I. J. Porter, B. R. de Roulet, A. Lee, B. M. Marsh, S. Szoke, M. E. Vaida and S. R. Leone, Sci. Adv., 2020, 6, eaay6650.
20. E. S. Ryland, K. Zhang and J. Vura-Weis, J. Phys. Chem. A, 2019, 123, 5214–5222.
21. R. Ash, K. Zhang and J. Vura-Weis, J. Chem. Phys., 2019, 151, 104201.
22. K. Zhang, R. Ash, G. S. Girolami and J. Vura-Weis, J. Am. Chem. Soc., 2019, 141, 17180–17188.
23. T. C. Davenport and T. D. Tilley, Dalton Trans., 2015, 44, 12244–12255.
24. S. A. Chavan, D. Srinivas and P. Ratnasamy, J. Catal., 2001, 204, 409–419.
25. A. R. Riordan, A. Jansma, S. Fleischman, D. B. Green and D. R. Mulford, Chem. Educ., 2005, 10, 115–119.
26. Y. Shari’ati and J. Vura-Weis, J. Synchrotron Radiat., 2021, 28, 1850–1857.
27. K. Zhang, M. F. Lin, E. S. Ryland, M. A. Verkamp, K. Benke, F. M. F. De Groot, G. S. Girolami and J. Vura-Weis, J. Phys. Chem. Lett., 2016, 7, 3383–3387.
28. K. S. Kjær, T. B. Van Driel, T. C. B. Harlang, K. Kunnus, E. Biasin, K. Ledbetter, R. W. Hartsock, M. E. Reinhard, S. Koroidov, L. Li, M. G. Laursen, F. B. Hansen, P. Vester, M. Christensen, K. Haldrup, M. M. Nielsen, A. O. Dohn, M. I. Pápai, K. B. Møller, P. Chabera, Y. Liu, H. Tatsuno, C. Timm, M. Jarenmark, J. Uhlig, V. Sundstöm, K. Wärnmark, P. Persson, Z. Németh, D. S. Szemes, É. Bajnóczi, G. Vankó, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, D. Sokaras, S. E. Canton, H. T. Lemke and K. J. Gaffney, Chem. Sci., 2019, 10, 5749–5760.
29. S. Zerdane, M. Cammarata, O. Iasco, M. L. Boillot and E. Collet, J. Chem. Phys., 2019, 151, 171101.
30. G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629–633.
31. N. A. Miller, A. Deb, R. Alonso-Mori, J. M. Glownia, L. M. Kiefer, A. Konar, L. B. Michocki, M. Sikorski, D. L. Sofferman, S. Song, M. J. Toda, T. E. Wiley, D. Zhu, P. M. Kozlowski, K. J. Kubarych, J. E. Penner-Hahn and R. J. Sension, J. Phys. Chem. A, 2018, 122, 4963–4971.
32. C. Bressler, C. Milne, V.-T. Pham, A. ElNahhas, R. M. van der Veen, W. Gawelda, S. Johnson, P. Beaud, D. Grolimund, M. Kaiser, C. N. Borca, G. Ingold, R. Abela and M. Chergui, Science, 2009, 323, 489–492.
33. W. Baker and M. Van Veenendaal, Phys. Rev. B, 2021, 104, 014407.
34. J. Chang, A. J. Fedro and M. Van Veenendaal, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 075124.
35. C. Sousa, A. Domingo and C. de Graaf, Chem. – Eur. J., 2018, 24, 5146–5152.
36. C. Sousa, M. Llunell, A. Domingo and C. De Graaf, Phys. Chem. Chem. Phys., 2018, 20, 2351–2355.
37. M. Van Veenendaal, Sci. Rep., 2017, 7, 6672.
38. R. Chakrabarty, S. J. Bora and B. K. Das, Inorg. Chem., 2007, 46, 9450–9462.
39. A. Britz, W. Gawelda, T. A. Assefa, L. L. Jamula, J. T. Yarranton, A. Galler, D. Khakhulin, M. Diez, M. Harder, G. Doumy, A. M. March, É. Bajnóczi, Z. Németh, M. Pápai, E. Rozsályi, D. Sárosiné Szemes, H. Cho, S. Mukherjee, C. Liu, T. K. Kim, R. W. Schoenlein, S. H. Southworth, L. Young, E. Jakubikova, N. Huse, G. Vankó, C. Bressler and J. K. McCusker, Inorg. Chem., 2019, 58, 9341–9350.
40. R. G. Hadt, D. Hayes, C. N. Brodsky, A. M. Ullman, D. M. Casa, M. H. Upton, D. G. Nocera and L. X. Chen, J. Am. Chem. Soc., 2016, 138, 11017–11030.
41. C. M. Marian, Annu. Rev. Phys. Chem., 2020, 72, 617–640.
42. Y. Shimizu and T. Azumi, J. Phys. Chem., 1982, 86, 22–26.
43. A. I. Nguyen, J. Wang, D. S. Levine, M. S. Ziegler and T. D. Tilley, Chem. Sci., 2017, 8, 4274–4284.
44. A. I. Nguyen, D. L. M. Suess, L. E. Darago, P. H. Oyala, D. S. Levine, M. S. Ziegler, R. D. Britt and T. D. Tilley, J. Am. Chem. Soc., 2017, 139, 5579–5587.

---

Footnote

† Electronic supplementary information (ESI) available: Details concerning the synthesis of cobalt cubane, sample preparation, LFM and density functional theory simulations, and the M-edge XANES spectrometer. See DOI: 10.1039/d1cp04136c

---