Troubleshooting unstable molecules in chemical space

Abstract

A key challenge in automated chemical compound space explorations is ensuring veracity in minimum energy geometries—to preserve intended bonding connectivities. We discuss an iterative high-throughput workflow for connectivity preserving geometry optimizations exploiting the nearness between quantum mechanical models. The methodology is benchmarked on the QM9 dataset comprising DFT-level properties of 133 885 small molecules, wherein 3054 have questionable geometric stability. Of these, we successfully troubleshoot 2988 molecules while maintaining a bijective mapping with the Lewis formulae. Our workflow, based on DFT and post-DFT methods, identifies 66 molecules as unstable; 52 contain –NNO–, and the rest are strained due to pyramidal sp² C. In the curated dataset, we inspect molecules with long C–C bonds and identify ultralong candidates (r > 1.70 Å) supported by topological analysis of electron density. The proposed strategy can aid in minimizing unintended structural rearrangements during quantum chemistry big data generation.

---

The central focus of all explorations in the chemical compound space (CCS)—designed using mathematical graphs without any bias—is to establish property trends across it, to steer efforts towards synthesis and experimental characterization of molecules with desired properties.¹ Even a tiny fraction of CCS spanned by small organic molecules, is too vast² to exhaustively cover with the conventional “one-molecule-at-a-time” simulation paradigm. To tackle such hard problems, high-throughput computation^3,4 combined with big data analytics^5,6 and machine learning techniques^6–10 promises novel strategies—influencing nearly all aspects of ab initio molecular modelling. At the inception of molecular big data, it is crucial to ensure that equilibrium geometries are faithfully mapped to their desired Lewis formulae.^11–13

A previous high-throughput study presented density functional theory (DFT) level geometries and static properties of the QM9 dataset with 133 885 (134 k) closed-shell organic molecules comprising up to nine C, O, N and F atoms.⁴ As of yet, 2.3% of this dataset—amounting to 3054 (3 k) molecules—remains “uncharacterized”, where the reported geometries are not in line with the intended Lewis structures encoded in their original SMILES (Simplified Molecular Input Line Entry System, denoted as SMI, henceforth) descriptors. This structural ambiguity stems from the fact that the initial atomic coordinates have undergone rearrangements during DFT treatment due to their intrinsic geometric metastability.¹⁴ Hence, the 3 k subset was excluded from other data-intensive explorations.^15–18 Given that the QM9 CCS is generated using graphs abiding the Lewis octet formula, ambiguous DFT-level geometric stabilities reported in ref. 4 can be attributed to three factors: (i) an inherent chemical signature, (ii) initial geometries, and (iii) limitations of the choice of the DFT model.

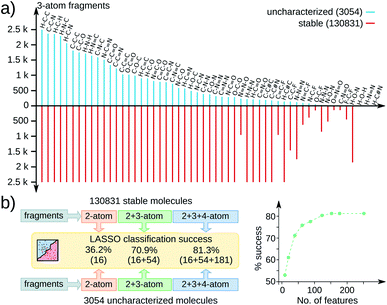
To identify a dominant chemical signature influencing stabilities across the QM9 molecules, we performed statistical analysis based on 251 acyclic fragments with up to 4 atoms (see Fig. 1). These feature vectors span a complete space including all common functional groups; complete list is in the ESI.† All substructures contained in the 3 k set are adequately represented in the stable set, as exemplified by the 3-atom fragment distribution in Fig. 1a. Hence, the geometric instability of the 3 k molecules cannot be attributed to a single structural aspect. To find the most relevant features out of 251, we performed a sparse regression analysis based on the least absolute shrinkage selection operator (LASSO),¹⁹ more details in the ESI.† Since only 433 molecules from the 131 k set are zwitterions while the 3 k set contains 1262 such entries, we performed LASSO analysis only on the remaining 1792 non-zwitterionic subset combined with another set of the same size and identical stoichiometries sampled from the 131 k set.

Fig. 1 Substructure analysis of QM9 molecules: (a) distribution of 3-atom fragments in 3054 uncharacterized (cyan) and 130 831 stable (red) molecules; the upper bound set to 2.5 k. (b) LASSO classification success (in %) using 2, 3, and 4-atom fragment fingerprints for 1792 non-zwitterionic molecules from both sets with stoichiometric stratification; feature vector size in parentheses. % success with increasing features on the right.

The performance of LASSO is quantified via percentage success defined as 100 × (score − base)/(100 − base), where the score is the fraction of entries correctly labeled by LASSO. For a binary classification of data uniformly distributed over both labels, a score of 50 is the base. Fig. 1b presents LASSO classification scores with an increasing number of features reaching up to 81.3% success (> 150 features). The gradual increase in the success rate with increasing features indicates a non-trivial joint occurrence of multiple features to influence geometric stability. Since the number of possible structural variations leads to a combinatorial catastrophe, it is desirable to prevent unwanted geometric rearrangements in high-throughput CCS explorations from a context independent of chemical factors.

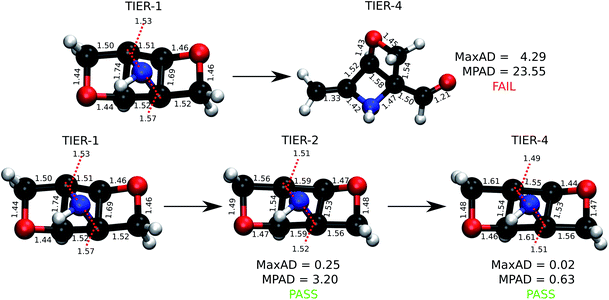
Probing the role of initial geometries and the corresponding theory used requires a robust protocol for efficient geometry refinements. To this end, we propose and benchmark an automated workflow for connectivity preserving geometry optimizations (ConnGO) using multiple tiers of quantum mechanical approximations suitable for high-throughput explorations. The proposed approach, illustrated in Fig. 2, was tested for a multitude of control parameters—the choice of force fields (Fig. S1 & S2†), optimizers (Fig. S3†), and combinations of methodological tiers (Fig. S4†) —and only the best performing set up is discussed here, more details in the ESI.† ConnGO takes a file containing the SMI as the input which is converted to 3D Cartesian coordinates in the SDF format using Openbabel 2.3.2.²⁰ These initial coordinates are relaxed with the Merck molecular force field (MMFF94)²¹via the steepest descent minimizer enforcing a tight threshold of 10⁻⁸ kcal mol⁻¹ for energy convergence. Henceforth, we denote these settings as tier-1 in ConnGO; in Fig. S3† we show this setup to yield superior performance over other variations. Geometries relaxed at tier-1 are stored in the SDF format, with the same bonding connectivities encoded in the corresponding SMI. All tier-1 geometries are further relaxed at tier-2; for this purpose, Hartree–Fock (HF) with a minimal basis set has been identified as suitable among several methods (see Fig. S4†). To probe for geometric rearrangements or dissociation, we use 2 metrics: the maximum absolute deviation (MaxAD) of bond lengths corresponding to covalent connectivities and their mean percentage absolute deviation (MPAD). In order to not rule out the possibility of unusual structures, those with MPAD <5% and MaxAD >0.2 Å are deemed pass in tier-2 if their tier-1 geometries have bond lengths >1.70 Å.

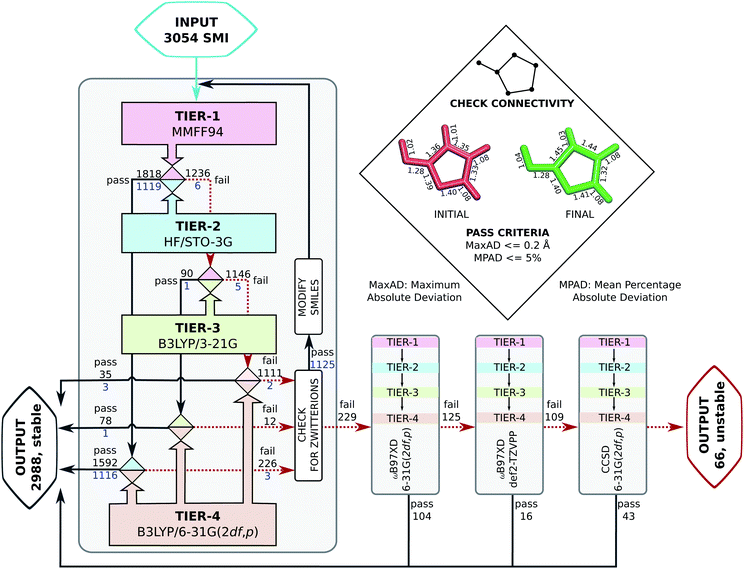Fig. 2 Automated workflow for connectivity preserving geometry optimizations (ConnGO). The scheme is illustrated for the 3 k set with pass/fail statistics. Geometries from hierarchically improved methods (tiers) are checked for connectivity conservation using the criteria highlighted in the inset (top, right). At every tier, the final minimum energy geometry is compared with the initial one. Here, ConnGO takes 3054 SMIs as the input and converges 2825 as the local minima when the tier-4 is B3LYP/6-31G(2df,p), while 163 molecules are subsequently stabilized with better tier-4 options. Numbers in black denote pass/fail statistics when starting with unmodified smiles taken from the QM9 dataset. Numbers in blue stand for failed zwitterionic molecules re-entering the ConnGO flow with a modified, neutral SMILES (see the right side of Fig. S5†).

Geometries converging at tier-2—fulfilling tier-1 vs. tier-2 pass criteria—are sent directly to tier-4 with the target DFT-level, B3LYP/6-31G(2df, p), while those that fail enter the intermediate tier-3, B3LYP/3-21G, starting with the tier-1 geometries. Final optimized geometries from each tier are compared with those from the previous tier and checked for changes in connectivities. In addition, geometries are verified at tiers-2/3/4 for being a local minimum on the potential energy hypersurface through vibrational analysis. SMIs of molecules failing tier-4 are checked for zwitterionic character; when detected, such SMIs are converted to their neutral forms that enter another iteration of ConnGO. All tier-2/3/4 calculations were performed using the Gaussian16 suite of programs.²² The documentation and examples collected at https://github.com/salinisenthil/ConnGO show how ConnGO can be modified to use with other software packages and methods beyond those utilized in the present work.

For the stable 131 k set, we generated tier-1 geometries that in comparison with previously reported⁴ DFT-level geometries pass the ConnGO criteria. Hence, in this study, we only focus on the remaining 3 k set. To maintain uniformity in the quality of the 3 k final geometries with respect to that of the 131 k set studied before, we use the same DFT settings for tier-4. The preference for this theory was motivated by the fact that the Gn series of composite methods²³ depend on minimum energy geometries and scaled harmonic frequencies at this very level. To illustrate the need for iterative geometry optimizations for reliable high-throughput generation of molecular structures, we identified molecules for which a direct target tier-4 optimization starting with tier-1 geometry failed to converge. This is often the case when equilibrium structures at both levels differ substantially, as illustrated in Fig. 3. Such situations benefit from the hierarchical treatment in ConnGO that exploits the nearness in the theoretical models and introduces levels of intermediate rigour. The cornerstones of quantum chemistry modelling, Pople diagrams²⁴ and Perdew's Jacob's ladder,²⁵ have also benefited from the nearness heuristic.

Fig. 3 An example molecule from the 3 k set undergoing rearrangement during DFT optimization while starting with a force field geometry. Successful optimization of the same molecule with the ConnGO workflow using an intermediate tier is also illustrated. Bond lengths and MaxAD are in Å.

Upon analysis, we found 1262 entries of the 3 k set to be zwitterions, of which 1125 failed in the first round of the ConnGO flow (see Fig. 2). These molecules re-entered the workflow, starting with the corresponding neutral SMI; pass/fail statistics are reported in Fig. S5.† Overall, the methodology proposed in this study decreases the number of equivocal molecular cases from 3054 to 229. In view of potential limitations of the B3LYP method to treat complex bonding situations, these 229 molecules were subjected to ConnGO based on the improved tier-4 settings: ωB97XD/6-31G(2df,p), ωB97XD/def2-TZVPP and CCSD/6-31G(2df,p), further decreasing the number of unstable molecules to only 66.

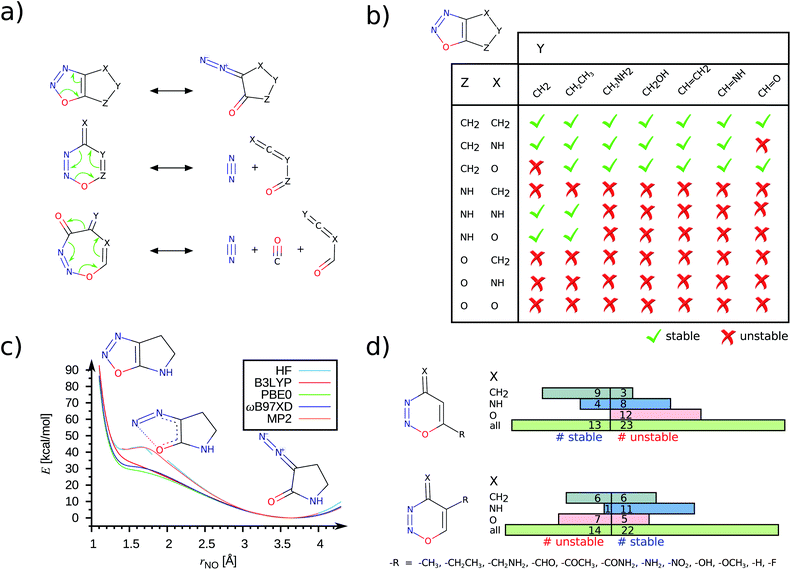
Demonstrating the chemical stability of this 66-set will require more advanced treatments incurring prohibitive computational costs. To facilitate future explorations, SMIs of the unstable set are provided in List S1.† Among the 66 dynamically unstable molecules, 52 are heterocycles containing an –NNO– moiety. Further analysis identifies them to have 5-, 6-, or 7-membered rings that dissociate via the pathways illustrated in Fig. 4a. In all cases, the final structure displays a broken NO bond; their lability must arise from a subtle combination of the ring structure and substitutions as there are 185 stable –NNO– systems in the 2988 newly characterized set featuring conventional NO distances (see Fig. S6†).

Fig. 4 Stability trends across –NNO– containing heterocycles: (a) Mechanistic pathways for ring-opening or fragmentation are shown for 5/6/7-membered ring systems. (b) Effect of regio-selective substitutions on the dynamic stability of 5-membered heterocycles. During geometry optimizations, the unstable structures (red crosses) undergo valence-tautomeric rearrangements to form the diazo-keto product. (c) Ring-opening reaction path for an example 5-membered system. For a given r_NO, all other internal coordinates are relaxed and the corresponding potential energies (E) are plotted for various levels of theory. (d) Effect of regio-selective substitutions on the dynamic stability of 6-membered heterocycles. All results are from the ωB97XD/def2-TZVPP level unless stated otherwise.

It has been previously noted that the simplest –NNO– 5-ring, 1,2,3-oxadiazole, undergoes ring-opening to form its diazo-keto valence-tautomer.²⁶ An earlier study²⁷ based on a small basis set predicted 1,2,3-oxadiazole to be unstable in the gas phase. The same molecule fused with a benzene ring, 1,2,3-benzoxadiazole, has been characterized in an argon matrix using infrared (IR) spectroscopy at 15 K.²⁸ In Fig. S7,† using DFT methods we show both these compounds to be dynamically stable. In this study, we identify several bicyclic 5-ring compounds to be dynamically unstable, resulting in NO σ-bond cleavage. In Fig. 4, we present a consolidated stability map of combinatorially generated –NNO– containing 5/6-rings. While only some of the molecules presented in this analysis feature in the QM9 set, the others were generated afresh for a complete coverage. We find the combination of functional groups at X, Y and Z positions to modulate the stability of the bicyclic rings; the unstable ones undergo ring-opening valence-tautomerism to stabilize the diazo-keto isomer (see Fig. 4a, b). When the group at the Z-position is –CH₂–, which is inductively electron-donating (+I), the –NNO– ring is stabilized, Fig. 4b. Replacing the methylene group with isoelectronic variants –NH– or –O–, containing electronegative centers, promotes ring opening. When the Z group is oxo, the choices at X and Y have no effect. The trends noted here are mostly independent of the DFT methods. To demonstrate this, we have plotted the reaction path for ring-opening modelled at the HF, MP2 levels and with selected DFT methods in Fig. 4c. Both HF and MP2 metastable profiles show a small barrier (<3 kcal mol⁻¹) at r_NO ≈ 1.70 Å preventing the molecule to escape to its dissociated form. On the other hand, DFT methods show a vanishing curvature at r_NO ≈ 1.40 Å indicating an inadequate well-depth to host vibrational bound states for the ring structure. More conclusive characterization of stability will require post-MP2 level treatments that become prohibitively expensive for high-throughput explorations.

The 6/7-ring compounds undergo electrocyclic ring-opening to dissociate into dienes and dienophiles (Fig. 4a). The regio-selective stabilization of the 6-ring as a function of X, Y and Z groups in the ring is illustrated in Fig. 4d. For fixed X and Z, we probed how the modulation of the ring current by + I groups at Y- and Z-terminals will facilitate the retro Diels–Alder reaction. Of the 36 compounds selected with variations at the Y-position, we find 14 to be unstable following a dissociation path. However for variations made at the Z-position, the number of stable compounds decreased indicating perturbation in the environment of the O atom of the –NNO– group to have a role in diminishing the stability of the 6-ring. Of the 52 unstable –NNO– systems, 3 are 7-rings dissociating into diene, N₂ and CO molecules as shown in Fig. 4a.

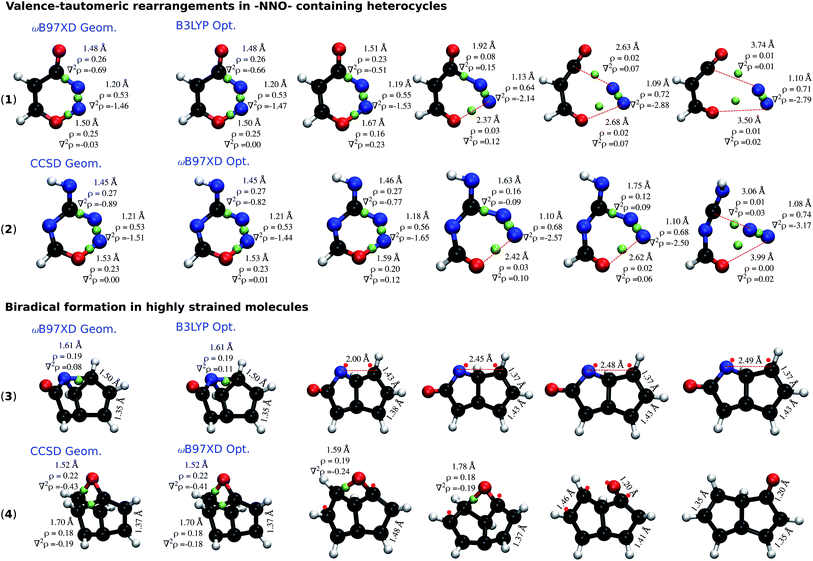
To understand the dependence of the covalent bonding lability on the rigour of the theoretical method employed, we performed topological analysis of electron density²⁹ using the Multiwfn software.³⁰Fig. 5 presents the cases of 2 –NNO– containing rings: 4H-1,2,3-oxadiazin-4-one (1) and 4H-1,2,3,5-oxatriazin-4-imine (2); and 2 highly-strained molecules: 2-azatricyclo[3.3.0.0^2,8]octa-4,6-dien-3-one (3) and 2-oxatetracyclo[4.2.1.0^1,4.0^3,9]nona-5,7-diene (4). In each category, one of the molecules is stabilized at the CCSD level, but undergo ring-cleavage at the DFT-level. The other molecule is stable at the ωB97XD level, while unstable at the B3LYP level. Although it has been argued that the existence of a bond critical point (BCP) is not direct evidence of bonding,^31,32 qualitative conclusions can be drawn from the electron density (ρ) and its Laplacian (∇²ρ) at the BCP.

Fig. 5 Dissociation trajectories of the selected molecules during optimization at a lower level where the initial structures are a higher-level minima. –NNO– containing molecules (top) and highly strained molecules (bottom): (1) & (3) are ωB97XD minima dissociating at the B3LYP level; (2) & (4) are CCSD minima dissociating at the ωB97XD level. BCPs are marked by green spheres; ρ and ∇²ρ at BCPs are reported in e/bohr³ and e/bohr⁵, respectively. Red dots denote radical sites. All results are obtained with the 6-31G(2df,p) basis set.

Molecule (1) when relaxed at the ωB97XD-level exhibits a stable structure. The local minimum from the ωB97XD level, when further relaxed with B3LYP, fragments to 3-oxoprop-2-enal and N₂. Similarly, (2) that is stable at CCSD, fragments to N-carboximidoylformamide and N₂ when treated with ωB97XD. The dissociation of both molecules follows the pathway shown in (Fig. 4a), highlighting 3 bond-breaking and 3 bond-making processes. Molecule (1), at the ωB97XD geometry shows quantitatively similar ρ and ∇²ρ at B3LYP and ωB97XD, indicating the electron density distribution to be very similar; nevertheless the structure is a local minimum in only one of the methods. B3LYP relaxation progresses with a gradual accumulation of ρ along the NN bond, which is also reflected by the corresponding ∇²ρ becoming more negative. In contrast, ρ and ∇²ρ of the NO and CN bonds consistently drop during relaxation, finally vanishing upon fragmentation.

Bond dissociation in the strained cases (3) and (4) are marked by unusually long single bonds that are adequately treated only when the theoretical level captures long-range effects of electron correlation. Structural rearrangements in (3) and (4) are driven by long CN (r = 1.61 Å) and CC bonds (r = 1.70 Å), respectively. In both cases, the end product is a biradical stabilized by an allylic conjugation. Topological analysis indicates an increase in ∇²ρ to mark the onset of structural rearrangements. While it may be argued that the unfavourable description of the electron distribution, ∇²ρ ≥ 0, at the BCP of a covalent bond—NO in (1) and (2), and CN/CC in (3) and (4)—is a factor driving the dissociation, based on the evidence tendered above their close dependence on the theoretical level remains vague.

As a data-mining exercise to reveal structural diversity across the curated QM9 dataset, we search for candidate molecules with ultralong CC single bonds (r_CC > 1.70 Å). Fig. 6 presents the distributions of CC bond lengths for r_CC > 1.60 Å; the results for the entire range are presented in Fig. S8 & S9.† Even though the search for long CC bonds is not new, the principles guiding the detection of such evasive bonding remains largely unknown.³³ One of the longest alkane bond lengths ever reported (1.704 Å) is obtained by coupling a diamantane with a triamantane.³⁴ While other reports have suggested longer bond lengths, the exact classification of their characteristics—based on the fraction of charge transfer/ionic/biradical interactions—requires further investigations. Fig. 6 illustrates r_CC > 1.60 Å and highlights the Top-10 candidates with a BCP; their geometries are shown in List S2.† The structural variation across the systems show that accruing a long CC bond is system-specific and requires a careful balance between stabilizing and destabilizing interactions within a molecule. Remarkably, all systems showcased in Fig. 6 contain at most 9 heavy atoms compared to those identified in previous studies, which contain several main group atoms. Furthermore, we identified 8 molecules in the curated 3 k set with r_CC > 1.90 Å (not shown in Fig. 6). Due to the absence of a BCP along these long CC distances, we believe the corresponding molecules to be of biradical nature with a reduced bond order.

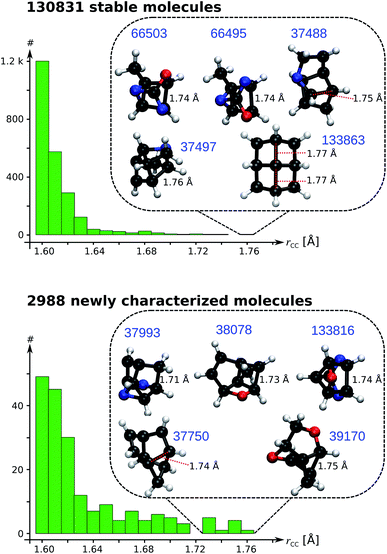Fig. 6 Distribution of long CC bond lengths (r_CC) in the 131 k set (top) and curated 3 k set (bottom). The insets show candidate molecules with ultralong r_CC with their QM9 indices in blue.

The longest bond length in Fig. 6 is noted for the pyramidal conformer (point group, C_4v) of fenestrane, at the B3LYP/6-31G(2df,p) level, with r_CC = 1.77 Å agreeing with a previous report.³⁵ The same study also reported the CC distance dropping to r_CC = 1.49 Å for the competing pyramidal conformer (point group, D_2d)—establishing that the thermodynamic stability of these conformers goes beyond the scope of the present study. In the curated 3 k set, the top candidate is 5,8-dioxatricyclo[4.3.0.0^3,9]nonane with r_CC = 1.75 Å. To understand the sensitivity of r_CC to the theory, we studied the top-10 cases with B3LYP and ωB97XD using a large basis set; the SMI and results from other methods are shown in Table S4.† The corresponding bond lengths along with ρ and ∇²ρ calculated at the BCPs are shown in Table 1. In general, bond lengths predicted with B3LYP are overestimated compared to the ωB97XD values. This trend is also reflected by the diminished values of ρ and its ∇²ρ with B3LYP. Nevertheless, at the more accurate ωB97XD, a number of molecules exhibit r_CC > 1.70 Å warranting further investigations using more rigorous methods for quantitative modelling of vibrational spectra, thermodynamic stability and competing rearrangement reaction pathways, suggesting directions towards experimental detection.

Table 1 Long CC bonds (in Å) for the top-10 molecules highlighted in Fig. 6, computed by B3LYP and ωB97XD methods with the def2-TZVPP basis set. In parenthesis are ρ (in e/bohr³) and ∇²ρ (e/bohr⁵) values at the bond critical points. Missing values indicate dissociating molecules

Index	r CC (ρ, ∇^2ρ)
	B3LYP	ωB97XD
37 488	1.750 (0.161, −0.200)	1.700 (0.178, −0.268)
37 497	1.783 (0.153, −0.187)	1.712 (0.176, −0.277)
37 750		1.757 (0.155, −0.156)
37 993	1.716 (0.169, −0.239)	1.692 (0.177, −0.270)
38 078	1.746 (0.158, −0.169)	1.703 (0.173, −0.228)
39 170		1.751 (0.161, −0.188)
66 495	1.734 (0.174, −0.249)	1.705 (0.183, −0.289)
66 503	1.732 (0.174, −0.253)	1.704 (0.184, −0.292)
133 816	1.737 (0.256, −0.585)	1.699 (0.185, −0.300)
133 863	1.797 (0.130, −0.077)	1.735 (0.150, −0.145)

---

In conclusion, an iterative scheme for automated geometry optimization addresses the difficulties associated with conserving covalent bonding connectivities in high-throughput chemical space explorations. Out of 3054 molecules with structural ambiguities, we curated 2988 using the workflow proposed in this study; the remaining 66 molecules are deemed dynamically unstable. Of the newly characterized molecules, 2825 converged with B3LYP/6-31G(2df, p) tier-4. In the remaining 163 converged with improved tier-4 settings, only five converged with a subsequent B3LYP/6-31G(2df, p)-level geometry optimization. Including these 2830 entries, the QM9 dataset now contains 133 661 optimized structures modeled at a uniform level of theory, consistent with their intended Lewis formulae. For small molecules studied here, the computational overhead associated with preconditioning the geometry using the ConnGO workflow is about 3% of tier-4.

It is important to note that a conclusive diagnosis of the unstable molecules as –NNO– heterocycles or those with pyramidal sp² C—in combination with their unique chemical environment—requires an accuracy better than that of DFT. The unique balance between stabilizing and destabilizing bonding factors makes the –NNO– containing 6- or 7-ring metastable molecules potential candidates for high-energy materials;³⁶ the 6-ring maybe preferred—for; its only side product is N₂. Future studies can also tailor small organic molecule with an ultralong CC bond, through rational modifications of the systems presented in this work. While a universal approach to characterize, a priori, whether a molecular structure will dissociate or rearrange is still lacking, automated determination of BCP characteristics at the initial-guess geometry could provide a remedy incurring additional computational costs. Further benchmarking of the strategy proposed here can also begin with force fields containing anharmonic terms,^37,38 suitable for describing unusually long covalent bonds. Big data initiatives must pay close attention to molecules failing to converge and inspect their properties rather than discarding them—as the factors behind their unusual behaviour may stem from prospective chemical trends as of yet unexplored.

Author contributions

All authors designed and performed research, and wrote the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

SS is grateful to TIFR for Visiting Students' Research Programme (VSRP) and junior research fellowships. We acknowledge support of the Department of Atomic Energy, Government of India, under Project Identification No. RTI 4007. All calculations have been performed using the Helios computer cluster, which is an integral part of the MolDis Big Data facility, TIFR Hyderabad (https://moldis.tifrh.res.in/).

Notes and references

1. P. Kirkpatrick and C. Ellis, Nature, 2004, 432, 823.
2. L. Ruddigkeit, R. Van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875.
3. E. O. Pyzer-Knapp, C. Suh, R. Gómez-Bombarelli, J. Aguilera-Iparraguirre and A. Aspuru-Guzik, Annu. Rev. Mater. Res., 2015, 45, 195–216.
4. R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data, 2014, 1, 140022.
5. I. V. Tetko, O. Engkvist, U. Koch, J.-L. Reymond and H. Chen, Mol. Inf., 2016, 35, 615–621.
6. R. Gómez-Bombarelli and A. Aspuru-Guzik, Handbook of Materials Modeling: Methods: Theory and Modeling, 2020, pp. 1939–1962.
7. O. A. von Lilienfeld, Angew. Chem., Int. Ed., 2018, 57, 4164–4169.
8. O. A. von Lilienfeld and K. Burke, Nat. Commun., 2020, 11, 1–4.
9. B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365.
10. A. Tkatchenko, Nat. Commun., 2020, 11, 1–4.
11. G. N. Lewis, J. Am. Chem. Soc., 1916, 38, 762–785.
12. G. H. Purser, J. Chem. Educ., 1999, 76, 1013.
13. G. H. Purser, J. Chem. Educ., 2001, 78, 981.
14. W. J. Lauderdale, J. F. Stanton and R. J. Bartlett, J. Phys. Chem., 1992, 96, 1173–1178.
15. B. Narayanan, P. C. Redfern, R. S. Assary and L. A. Curtiss, Chem. Sci., 2019, 10, 7449–7455.
16. R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096.
17. A. S. Christensen, L. A. Bratholm, F. A. Faber and O. A. von Lilienfeld, J. Chem. Phys., 2020, 152, 044107.
18. N. Dandu, L. Ward, R. S. Assary, P. C. Redfern, B. Narayanan, I. T. Foster and L. A. Curtiss, J. Phys. Chem. A, 2020, 124, 5804–5811.
19. R. Tibshirani, J. Roy. Stat. Soc. B, 1996, 58, 267–288.
20. N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33.
21. T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision C.01, Gaussian Inc. Wallingford CT, 2016, https://gaussian.com.
23. L. A. Curtiss, P. C. Redfern and K. Raghavachari, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 810–825.
24. J. A. Pople, Rev. Mod. Phys., 1999, 71, 1267.
25. J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 1–20.
26. J. A. Joule and K. Mills, Heterocyclic chemistry, John Wiley & Sons, 2013, p. 569.
27. M. T. Nguyen, A. F. Hegarty and J. Elguero, Angew. Chem., Int. Ed., 1985, 24, 713–715.
28. R. Schulz and A. Schweig, Angew. Chem., 1984, 96, 494–495.
29. R. Bader, T. T. Nguyen-Dang and Y. Tal, Rep. Prog. Phys., 1981, 44, 893.
30. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
31. S. Shahbazian, Chem. - Eur. J., 2018, 24, 5401–5405.
32. C. R. Wick and T. Clark, J. Mol. Model., 2018, 24, 142.
33. L. Howes, Chem. Eng. News, 2019, 97, 24.
34. P. R. Schreiner, L. V. Chernish, P. A. Gunchenko, E. Y. Tikhonchuk, H. Hausmann, M. Serafin, S. Schlecht, J. E. Dahl, R. M. Carlson and A. A. Fokin, Nature, 2011, 477, 308–311.
35. J. M. Schulman, M. L. Sabio and R. L. Disch, J. Am. Chem. Soc., 1983, 105, 743–744.
36. F.-f. He, X.-y. Zhang and Y.-h. Ding, RSC Adv., 2015, 5, 46648–46653.
37. N. L. Allinger, J.-H. Lii and H. F. Schaefer III, J. Chem. Theory Comput., 2016, 12, 2774–2778.
38. R. Shannon, B. Hornung, D. Tew and D. Glowacki, J. Phys. Chem. A, 2019, 123, 2991–2999.

---

Footnote

† Electronic supplementary information (ESI) available: Technical details, benchmarks, geometries and further analyses. See DOI: 10.1039/d0sc05591

---