Open Access Article
Open Access ArticleSelf-assembled cationic organic nanosheets: role of positional isomers in a guanidinium-core for efficient lithium-ion conduction†
Ananta
Dey
 ab,
Vishwakarma Ravikumar
Ramlal
ab,
Selvasundarasekar Sam
Sankar
c,
Subrata
Kundu
*c,
Amal Kumar
Mandal
*ab and
Amitava
Das
ab,
Vishwakarma Ravikumar
Ramlal
ab,
Selvasundarasekar Sam
Sankar
c,
Subrata
Kundu
*c,
Amal Kumar
Mandal
*ab and
Amitava
Das
 *bd
*bd
aAnalytical and Environmental Science Division, Centralized Instrument Facility, CSIR-Central Salt and Marine Chemicals Research Institute, Bhavnagar, Gujarat-364002, India. E-mail: akmandal@csmcri.res.in
bAcademy of Scientific and Innovative Research (AcSIR), CSIR – Human Resource Development Centre (HRDC) Campus, Sector 19, Kamla Nehru Nagar, Ghaziabad, Uttar Pradesh-201 002, India
cElectrochemical Process Engineering (EPE) Division, CSIR-Central Electrochemical Research Institute (CECRI), Karaikudi, Tamil Nadu 630003, India. E-mail: skundu@cecri.res.in
dDepartment of Chemical Sciences, Indian Institute of Science Education and Research Kolkata, Mohanpur 741 246, West Bengal, India. E-mail: amitava@iiserkol.ac.in
First published on 22nd September 2021
Abstract
The growing energy demand with the widespread use of smart portable electronics, as well as an exponential increase in demand for smart batteries for electric vehicles, entails the development of efficient portable batteries with high energy density and safe power storage systems. Li-ion batteries arguably have superior energy density to all other traditional batteries. Developing mechanically robust solid-state electrolytes (SSEs) for lithium-ion conduction for an efficient portable energy storage unit is vital to empower this technology and overcome the safety constraints of liquid electrolytes. Herein, we report the formation of self-assembled organic nanosheets (SONs) utilizing positional isomers of small organic molecules (AM-2 and AM-3) for use as SSEs for lithium-ion conduction. Solvent-assisted exfoliation of the bulk powder yielded SONs having near-atomic thickness (∼4.5 nm) with lateral dimensions in the micrometer range. In contrast, self-assembly in the DMF/water solvent system produced a distinct flower-like morphology. Thermodynamic parameters, crystallinity, elemental composition, and nature of H-bonding for two positional isomers are established through various spectroscopic and microscopic studies. The efficiency of the lithium-ion conducting properties is correlated with factors like nanostructure morphology, ionic scaffold, and locus of the functional group responsible for forming the directional channel through H-bonding in the positional isomer. Amongst the three different morphologies studied, SONs display higher ion conductivity. In between the cationic and zwitterionic forms of the monomer, integration of the cationic scaffold in the SON framework led to higher conductivity. Amongst the two positional isomers, the meta-substituted carboxyl group forms a more rigid directional channel through H-bonding to favor ionic mobility and accounts for the highest ion conductivity of 3.42 × 10−4 S cm−1 with a lithium-ion transference number of 0.49 at room temperature. Presumably, this is the first demonstration that signifies the importance of the cationic scaffold, positional isomers, and nanostructure morphologies in improving ionic conductivity. The ion-conducting properties of such SONs having a guanidinium-core may have significance for other interdisciplinary energy-related applications.
Introduction
Recent reports reveal that two-thirds of the global greenhouse gas emissions arise from energy production and are a primary contributor to environmental pollution and the most widely discussed issue of climate change.1 To meet the climate goals, affordable and efficient processes for generating renewable energy, ‘smart’ technologies that are benign to the environment, are crucial. This situation is further complicated by the diminishing fossil-fuel resources.2–4 The growing demand for clean energy, use of smart portable electronics, and rapid growth in the demand for efficient batteries for portable battery-powered products, such as electric vehicles, necessitate the development of efficient portable batteries with high energy density and safe power storage systems.5–9 Among various storage systems developed to date, lithium-ion batteries (LIBs) have emerged as the most promising candidate for the next generation of portable energy storage units.10–12 Unfortunately, conventional electrolytes are usually volatile and flammable liquids. This contributes to undesired incidents like fire/explosions,13,14 and batteries having such electrolytes generally have issues complying with the required safety norms for portable devices, electric vehicles, etc. Efforts to use flame-retardant solvents in electrolytes have been futile. However, such solvents often fail to passivate carbonaceous anodes suitably, and these efforts have resulted in compromised battery performance.15 It has been argued that mechanically robust solid-state electrolytes as lithium-ion conductors are critical for overcoming this constraint. Such electrolytes could be integrated into the process for further scientific and commercial exploitation.16–20 More recently, research is primarily focused on using inorganic ceramics/glass or organic polymer-based materials as solid-state electrolytes (SSEs) for viable solid-state batteries.21,22 Although inorganic electrolytes offering high ionic conductivity (10−4 to 10−2 S cm−1) are generally brittle, limiting their commercial use.23–25 Furthermore, the reactivity between solid-state electrolytes and electrode materials is poorly understood and adds to the limitation for practical application.21 Excellent flexibility and easy processability of organic polymers such as poly(ethylene oxide) (PEO), poly(vinyl chloride), and poly(vinylidene fluoride) (PVDF) make them promising materials for SSEs. Despite such advantages, low ionic conductivity (10−8 to 10−5 S cm−1) at room temperature restricts their practical application.26,27 To avoid the canonical trade-off between ionic conductivity and the mechanical properties in SSEs, it is crucial to slot in material abundance by developing new functional materials capable of producing and storing energy and favorable for improving the device efficiencies.Self-assembled organic nanosheets (SONs) are defined as a periodic network of repeating organic units shaped through reversible noncovalent interactions. Such SONs have received considerable attention as a new type of material for use as SSEs.28,29 Some of the key features that favor the use of SON based SSEs are (1) flexibility in the design and synthesis of the purpose-built target molecule(s) with an option to fine-tune the ion conductivity, interface stability, and electrochemical performances through the incorporation of a new synthetically accessible functionality in the molecule, (2) purpose-built molecules as the building blocks offer the possibility of having an appropriate host material with adaptable one-dimensional nanochannels for efficient lithium-ion transport, (3) the flexible nature of SONs allows the maximum electrode and electrolyte contact, which stimulates ion transport kinetics,30,31 and (4) incorporation of a cationic scaffold in the SON framework could offer the possibility to restrict the anion movement, as well as to counter the coulombic interactions to favor a facile free cation movement. In addition, their graphene-like geometric shape and enhanced surface area, along with their flexible nature, light weight, and adaptable nature, make them an important class of materials for designing efficient SSEs.32–35 Despite their significance, systematic design approaches for monomers and convenient methods to prepare SONs are scarce in the literature. Subsequently, attaining the desired SONs through the self-assembly process is a challenging issue owing to the associated intricacy in governing multiple noncovalent interactions in a changing environment.
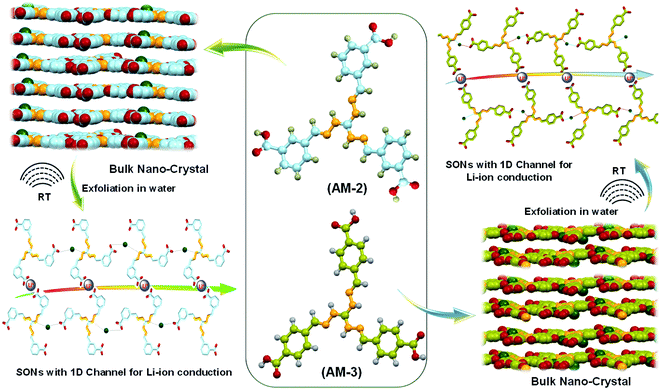
The lithium-ion conductivity primarily relies on two factors, such as free lithium-ion concentration and ionic mobility along the directional channel.36 An appropriate strategy that stimulates ion-pair dissociation and ionic mobility is expected to improve the ionic conductivity. The high propensity of the lithium-ion to form ion pairs or ionic aggregates results in a low free lithium-ion concentration and low ionic conductivity in a solid conductor.37–39 Metal oxide-based fillers favor ion-pair dissociation, though dispersion of the filler through the directional channel adversely affects the energy density and introduces new challenges.40,41 Integration of ionic scaffolds into the covalent or metal–organic frameworks or polymer based SSEs is reported to improve the lithium-ion conductivity by favoring the ion-pair dissociation.42–44 Recently, our group developed cationic guanidinium derivatives having a three-fold symmetry to generate nanostructures through self-assembly.45 The zwitterion form of the guanidinium derivatives self-assembles to produce an organic nanosheet with arrays of a one-dimensional channel. The presence of the directional channel favors the lithium-ion transport with an ion conductivity of 5.14 × 10−5 S cm−1 at room temperature.34 To improve the ion conductivity further, we forestall that, instead of the zwitterion form, incorporation of a positive center on the SON framework would escalate ion-pair dissociation to enhance free lithium-ion concentration. Additionally, altering the size and locus of the directional channel with positional isomers would influence the ionic mobility on the SON framework. In this work, we present a new class of SONs as solid-state lithium-ion conductors by espousing the strategy to boost ion-pair dissociation and ionic mobility. Two positional isomers of the carboxyl derivative (meta-substituted AM-2 and para-substituted AM-3) of the guanidinium moiety (Fig. 1) are used for generating the SONs. Ultrasound-induced liquid-phase exfoliation of the bulk-powder of AM-2 and AM-3 in water was used to construct the cationic SON framework with well-defined directional channels (Fig. 1). These SONs display high crystallinity with an overall planar structure having a width of a few micrometers and thickness of a few nanometres. In the SON framework, the cationic unit favored the ion-pair dissociation of the lithium salts, while the varying positions of the carboxyl functional group enabled the formation of an H-bonded one-dimensional channel with variable size and shape of the directional channel responsible for ionic mobility. Interestingly, the resulting SONs exhibit improved lithium-ion conductivity (up to 3.42 × 10−4 S cm−1) at room temperature. Presumably, this is the first demonstration to articulate the design strategy of the role of positional isomers in influencing the lithium-ion conductivity in SON based SSEs. Additionally, in an N,N-dimethyl formamide (DMF)/water solvent system, these two positional isomers self-assembled to yield a distinct nanoflower morphology. The lithium-ion conductivity of these two isomers reveals a seven-fold higher value for nanosheets in comparison with the nanoflower morphology.
Results and discussion
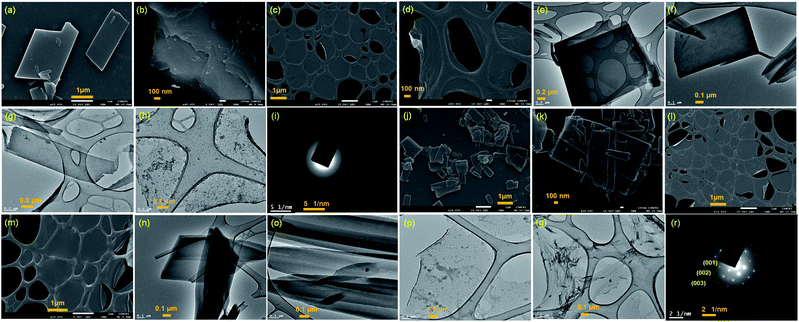
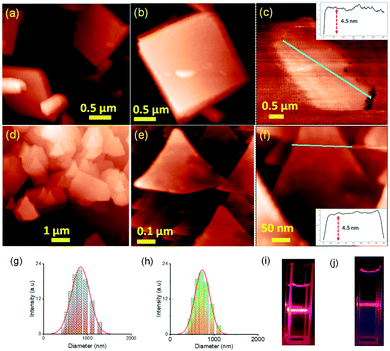
Two positional isomers of tripodal guanidinium derivatives AM-2 and AM-3 were synthesized following a two-step process (Fig. S1 in the ESI†). All the synthesized compounds were characterized using standard analytical techniques (Fig. S2–S7 in the ESI†). To prepare the SONs through solvent-assisted exfoliation, the bulk powder of AM-2 and AM-3 (1 mg ml−1) was sonicated for thirty minutes in water. During the exfoliation process, the cationic center in the guanidinium unit mitigated the repulsive interlayer interactions and favored ultrasonic waves to overcome the interlayer interactions between the layered structures of the bulk sample. As a result, the layers gradually peeled off to produce thin nanosheets. An aliquot of this suspension was drop-cast on the transmission electron microscopy (TEM) grid and dried at room temperature. The morphology of the exfoliated samples with sonication time was envisaged through field-emission scanning electron microscopy (FE-SEM) and TEM. Images from both techniques indicate that the stepwise exfoliation of the bulk sample from nanoplates to nanosheets ensues with increasing sonication time (Fig. 2). The visualized images display the consistent formation of two-dimensional sheet-like structures with lateral sizes of several micrometers from both techniques for both compounds. Interestingly, the staircase-like morphology at the edge of the nanoplate indicates the layered structure of the bulk materials (Fig. 2b). The nanoplate and sheet-like morphology with micrometer scale lateral dimensions of the as-prepared SONs was further confirmed through tapping mode atomic force microscopy (AFM) measurement (Fig. 3). Fig. 3a–f display the nanoplate and nanosheet morphology of the as-prepared SONs obtained from AM-2 and AM-3, respectively. For both isomers, the cross-sectional profile unveils considerable flatness of the surface with uniformity in the thickness of about 4.5 nm (Fig. 3c and f). A dynamic light scattering (DLS) study discloses a size distribution of 1–1.5 μm for the as-prepared SONs obtained from both isomers (Fig. 3g and h). Tyndall scattering of laser light confirms the colloidal stability of these as-prepared SONs (Fig. 3i and j).Self-assembly processes for two positional isomers (AM-2 and AM-3) were investigated in a (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
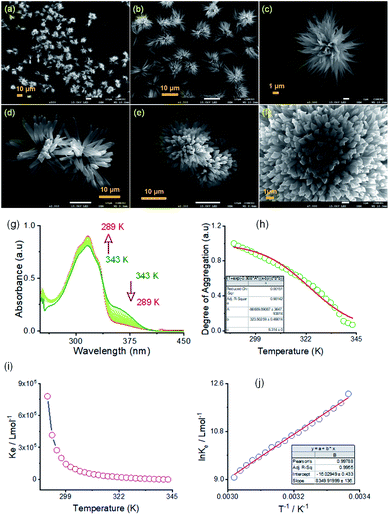
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) DMF/water solvent system at room temperature through FE-SEM experiments. The details of the sample preparation are outlined on ESI Page 7.† An aliquot of this self-assembled suspension was drop cast on a silicon wafer surface and dried at room temperature. FE-SEM images show flower-like microstructures growing radially from one center (Fig. 4a–f). Details examination revealed that collective alignments of thin petals with a diameter of 0.2–0.5 nm and length of several micrometers produced this flower-like structure. The thermodynamic parameters of this self-assembly process were evaluated using temperature-dependent UV-vis spectroscopy upon cooling the solution from 343 K to 289 K at a cooling rate of 2 K per five minutes (Fig. 4 and S8 in the ESI†). For AM-2, upon cooling, the solution absorption was found to increase at 316 nm, decreasing at 365 nm. The trend of spectral change with a distinct isosbestic point at 336 nm points to the transformation from a monomeric state to an aggregate state in the cooling process (Fig. 4g). The distinct feature of the plot of change of absorbance and degree of aggregation (αagg) at 316 nm as a function of temperature indicates that the self-assembly process follows an isodesmic aggregation model (Fig. 4h and S8 in the ESI†).46,47
1, v/v) DMF/water solvent system at room temperature through FE-SEM experiments. The details of the sample preparation are outlined on ESI Page 7.† An aliquot of this self-assembled suspension was drop cast on a silicon wafer surface and dried at room temperature. FE-SEM images show flower-like microstructures growing radially from one center (Fig. 4a–f). Details examination revealed that collective alignments of thin petals with a diameter of 0.2–0.5 nm and length of several micrometers produced this flower-like structure. The thermodynamic parameters of this self-assembly process were evaluated using temperature-dependent UV-vis spectroscopy upon cooling the solution from 343 K to 289 K at a cooling rate of 2 K per five minutes (Fig. 4 and S8 in the ESI†). For AM-2, upon cooling, the solution absorption was found to increase at 316 nm, decreasing at 365 nm. The trend of spectral change with a distinct isosbestic point at 336 nm points to the transformation from a monomeric state to an aggregate state in the cooling process (Fig. 4g). The distinct feature of the plot of change of absorbance and degree of aggregation (αagg) at 316 nm as a function of temperature indicates that the self-assembly process follows an isodesmic aggregation model (Fig. 4h and S8 in the ESI†).46,47
An aggregation association constant (Kiso) of 1.8 × 105 M−1 is estimated at 298 K by fitting this curve with an isodesmic aggregation model (Fig. 4i). The thermodynamic parameters of the aggregation process are derived from the van't Hoff plot of the logarithm of Kiso with the reciprocal temperature (Fig. 4j). The estimated values of standard enthalpy (ΔH°) and entropy (ΔS°) are −69.4 kJ mol−1 and −133.2 J mol−1 K−1. Likewise, for AM-3, an aggregation association constant (Kiso) of 4.5 × 104 M−1 at 298 K is derived from the variable temperature UV-vis measurements.45 The estimated values of standard enthalpy and entropy are ΔH° = −67.6 kJ mol−1 and ΔS° = −135.1 J mol−1 K−1. For both isomers, the negative values of ΔH° and ΔS° indicate the enthalpy-driven self-assembly process with many solvent molecules involved in the aggregation process.
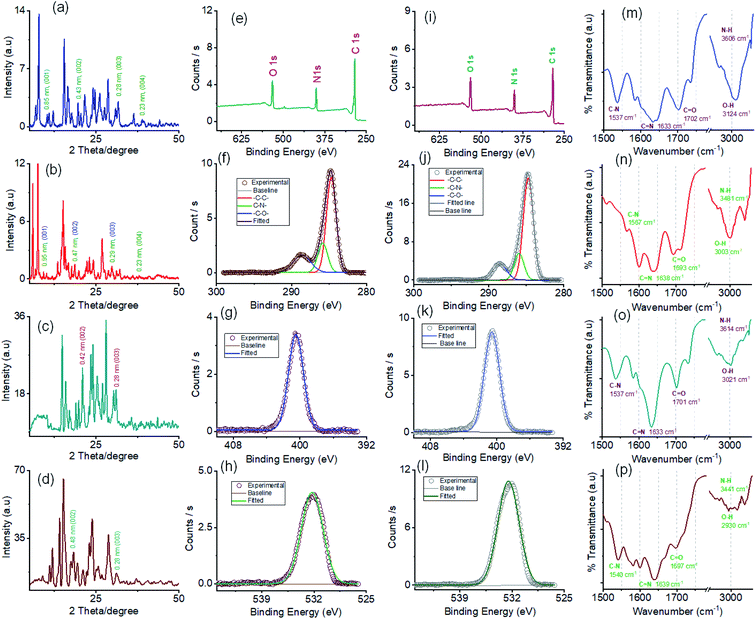
The powder X-ray diffraction (PXRD) pattern was recorded on sedimentation of the self-assembled materials to acquire information about the molecular arrangements in SONs and nanoflower morphology. For both cases, the well-defined sharp, intense Bragg peaks clearly confirm the crystalline nature of the materials (Fig. 5a–d). For SONs of AM-3, d-spacing values of 9.53 Å, 4.75 Å, 2.99 Å, and 2.36 Å correspond to the characteristic reflection peaks at 2θ = 9.27°, 18.67°, 29.83°, and 38.04°, respectively, defining diffraction from the (001), (002), (003) and (004) planes signifying the ordered lamellar packing (Fig. 5b). Excitingly, the d-spacing values corresponding to the reflection of the (001), (002), and (003) planes match well with the selected area electron diffraction pattern (SAED) of the stacked nanosheets (Fig. 2r). In addition, the reflection peak at 2θ = 18.67° with d = 4.75 Å associated with the diffraction of the (002) plane agrees well with the interplanar distance of 4.62 Å (ESI Fig. 9a†). A good correlation between the results of these three techniques confirms the lamellar packing of the SON framework and its structure is retained in the powder form. Likewise, for SONs of AM-2, the characteristic reflection peaks at 2θ = 10.37°, d = 8.52 Å (001), 2θ = 20.45°, d = 4.34 Å (002), 2θ = 31.70°, d = 2.82 Å (003) and 2θ = 38.84°, d = 2.31 Å (004) suggest the layered crystal packing (Fig. 5a). For both SONs, the d-spacing value of 16.66 Å matches well with the molecular length (16.47 Å) obtained from single-crystal data (Fig. S9b in the ESI†). Compared with the AFM measured thickness (∼4.5 nm), the obtained result indicates that three layers are present on the observed SONs. The well-defined sharp, intense PXRD pattern of the nanoflower morphology also indicates the crystalline nature of the materials (Fig. 5c and d). Compared with the PXRD pattern of the SON morphology, a distinct contrast in the number of peaks and peak position is witnessed in the nanoflower morphologies. The characteristic reflection peaks at 2θ = 20.97°, d = 4.23 Å, and 2θ = 31.02°, d = 2.88 Å, corresponding to the diffraction of the (002) and (003) planes, suggest the lamellar packing of the nanoflower morphology of AM-2. Similarly, the distinctive reflection peaks at 2θ = 18.34°, d = 4.83 Å, and 2θ = 31.10°, d = 2.87 Å, consistent with the diffraction of the (002) and (003) planes, are observed for the nanoflower morphology of AM-3. No such distinct peak position corresponding to the lamellar packing was observed from the PXRD pattern of the bulk powder of AM-2 and AM-3 (Fig. S10†). To envision the solvent interactions in the nano-flower morphology of the two positional isomers AM-2 and AM-3, we conducted thermogravimetric analysis (TGA). For both cases, a three-step weight loss was observed in the TGA profile. For AM-2, approximately 14.6% initial weight loss was witnessed due to the expulsion of H-bonded DMF molecules (Fig. S11a†). The subsequent weight loss with temperature is due to the expulsion of the chloride ions (37.7%) and decomposition of AM-2 (20.8%). A similar trend of the TGA profile was observed for the nanoflower morphology of AM-3. Approximately 15.3% initial weight loss corresponding to the H-bonded DMF molecules, followed by 36.0% and 20.9% weight loss corresponding to the loss of chloride ions and decomposition of AM-3 was observed with increasing temperature (Fig. S11b†).
X-ray photoelectron spectroscopy (XPS) studies were carried out to understand the elemental composition and chemical environment of the SON framework for both AM-2 and AM-3 (Fig. 5e–l). The XPS survey spectra confirm the existence of constitutive elements like carbon, nitrogen, and oxygen (Fig. 5e and i). The peak area correction by the photoionization cross-section yielded nitrogen-to-oxygen abundance ratios of 14.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15.9 and 14.9
15.9 and 14.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16.9 for the SONs of AM-2 and AM-3, respectively. Given an accompanying error of 10%, the experimental value agreed well with the estimated value from the molecular structure of AM-2 and AM-3.
16.9 for the SONs of AM-2 and AM-3, respectively. Given an accompanying error of 10%, the experimental value agreed well with the estimated value from the molecular structure of AM-2 and AM-3.
The high-resolution C 1s spectrum of AM-2 was deconvoluted into three Gaussian curves with binding energies of 284.7 eV, 285.8 eV, and 288.6 eV, corresponding to contributions from –C–C–, –C–N– and –C–O–, respectively (Fig. 5f). Similarly, the C 1s core-level spectrum of AM-3 was deconvoluted into three peaks with binding energies of 284.7 eV (–C–C–), 285.9 eV (–C–N–), and 288.5 eV (–C–O–), respectively (Fig. 5j). In addition, the high-resolution XPS spectra unveil peaks with binding energies of 400.5 eV and 532.2 eV for AM-2 and 400.6 eV and 532.0 eV for AM-3, corresponding to the core level spectra of N 1s and O 1s, respectively (Fig. 5g, h, k and l).
Fourier transform infrared spectroscopy (FT-IR) was used as a tool to obtain information about the H-bonding interactions in the assembled structure (Fig. 5m–p). SONs of AM-2 display peaks located at 1537 cm−1, 1633 cm−1, 1702 cm−1, 3124 cm−1, and 3606 cm−1 assigned to the stretching vibrations of C–N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, O–H, and N–H, respectively (Fig. 5m). Interestingly, the blue shifts (125 cm−1 and 121 cm−1) of the transmittance peak were attributed to N–H and O–H stretching vibrations, responsible for the formation of the H-bonding network witnessed for the positional isomer of AM-3 (Fig. 5n). The peak positions for C
O, O–H, and N–H, respectively (Fig. 5m). Interestingly, the blue shifts (125 cm−1 and 121 cm−1) of the transmittance peak were attributed to N–H and O–H stretching vibrations, responsible for the formation of the H-bonding network witnessed for the positional isomer of AM-3 (Fig. 5n). The peak positions for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and C
N and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations remain almost the same, though a redshift of 30 cm−1 is observed for the C–N vibration. This result demonstrates that the position of the –COOH group has an important role in governing the directional H-bonded network as well as the framework structure. In the nanoflower morphology, the position of the peaks remains the same, while the decrease in transmittance suggests the strengthening of H-bonding interactions contributed by solvent–solute interactions (Fig. 5o and p).
O stretching vibrations remain almost the same, though a redshift of 30 cm−1 is observed for the C–N vibration. This result demonstrates that the position of the –COOH group has an important role in governing the directional H-bonded network as well as the framework structure. In the nanoflower morphology, the position of the peaks remains the same, while the decrease in transmittance suggests the strengthening of H-bonding interactions contributed by solvent–solute interactions (Fig. 5o and p).
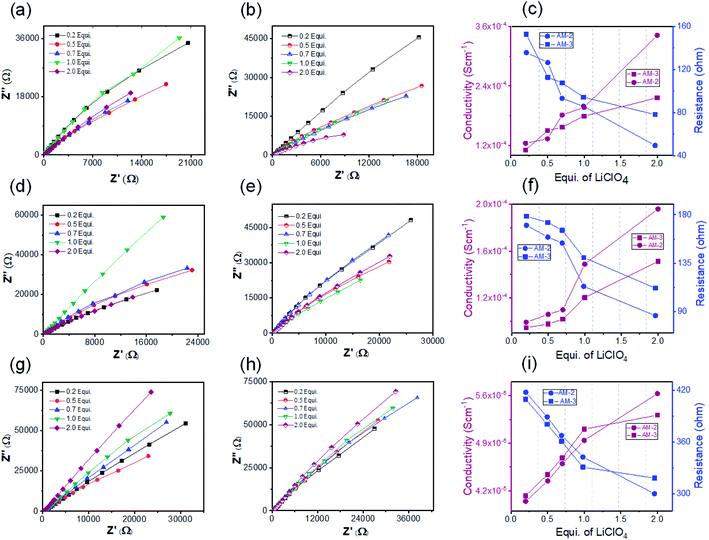
The crystalline nanostructure from both positional isomers with the built-in cationic unit in the monomer enthused us to study the lithium-ion conductivity. To prepare the nanostructure for the conductivity study, the self-assembly and exfoliation process was carried out in the presence of varying concentrations of LiClO4 (ESI Page 10†). The microscopic study indicated that the morphology remained intact after lithium-ion incorporation for both cases (ESI Fig. S12†). The lithium-ion conductivity was measured through a recently established method, where a homogeneous dispersed solution of the nanostructures was drop-cast on the surface of a Whatman filter membrane separator (ESI Page 10†) and allow to dried. After that, the dried separator was sandwiched in between a stainless-steel electrode.48 The thickness (d = 0.026 cm) of the separator was calculated using the screw gauge method. The ionic conductivity was measured by ac impedance spectroscopy under ambient conditions using a stainless-steel electrode. The stainless-steel electrode's radius (7 mm) yielded an electrode area (A) of 1.5386 cm2. To obtain information about the role of the positional isomers in determining ionic conductivity, we prepared three sets of samples with different morphologies: SONs, nanoflowers, and bulk powders of AM-2 and AM-3, with varying equivalents of LiClO4. The Nyquist plots obtained from ac impedance measurements, with a clear Warburg line, indicate a diffusion-controlled process mainly governed by mass transfer (Fig. 6).49,50 Hence, the charge transfer is minimal. The corresponding admittance plots of these three sets of samples revealed the same (Fig. S13 in the ESI†). As the admittance plot is inverse to the Z value, the kinetics resembles the predominantly produced characteristic feature with a distorted semicircle. The resistance (R) values acquired from the Nyquist plot and the lithium-ion conductivity (σ) were calculated by using the equation σ = d/RA. Fig. 6 displays the corresponding plots of ion conductivity and resistance with varying equivalents of LiClO4 and the corresponding data are shown in Table 1 (ESI Tables S1–S6†). For all three sets of samples, a systematic upsurge of ion conductivity was observed with increasing LiClO4 concentration under the same conditions. For the SON morphology of AM-2, a three-fold increase in the conductivity value from 1.24 × 10−4 S cm−1 to 3.42 × 10−4 S cm−1 was observed with increasing the LiClO4 concentration from 0.2 to 2.0 equivalents (Fig. 6c and ESI Table S1†). Noticeably, a two-fold boost of ion conductivity with a maximum value of 2.16 × 10−4 S cm−1 was witnessed with increasing LiClO4 concentration for SONs of AM-3 under identical conditions (ESI Table S2†). Ion conductivities of 1.95 × 10−4 S cm−1 and 1.51 × 10−4 S cm−1 were observed for the bulk-powder of AM-2 and AM-3, in the presence of 2.0 equivalents of LiClO4 (Fig. 5f and Tables S3 and S4 in the ESI†). Under identical conditions, in the presence of 2.0 equivalents of LiClO4, ion conductivities of 5.63 × 10−5 S cm−1 and 5.31 × 10−5 S cm−1 were measured for the nanoflower morphologies of AM-2 and AM-3 (Fig. 6i and ESI Tables S5 and S6†). Fascinatingly, going from the nanoflower to the SON morphology, six-fold and four-fold increases of ion conductivity were observed for AM-2 and AM-3 (Table 1). Strikingly, a 1.6-fold increase in ion conductivity was noticed for the SON morphology of AM-2 in comparison with that of AM-3. In contrast, the ion conductivity values remain almost the same for the bulk-powder and nanoflower morphologies (Table 1). Excitingly, the observed highest ion conductivity value of 3.42 × 10−4 S cm−1 is 6.6-fold higher than that of our recently reported zwitterionic organic nanosheets of a positional isomer of AM-2.34 The observed ion conductivity value is much higher than those of the previously reported self-assembled organic nanosheets and found to be comparable with those of the best-reported covalent and metal–organic frameworks. A comparison chart of the best-reported materials with ion conductivity values is presented in Table S7 in the ESI.† The Bruce–Vincent method was used for the calculation of the Li-ion transference number.51,52 The details of the measurement with relevant plots are shown on ESI Page 14 (Fig. S14 and S15).† In the presence of 2.0 equivalents of LiClO4, the SON morphologies of AM-2 and AM-3 display lithium-ion transference numbers of 0.49 and 0.15 at room temperature respectively (Table S8†). Notably, the higher transference number of the positional isomer AM-2 emphasizes the structural superiority of the meta-substituted –COOH group, in comparison with para-substitution in AM-3. The measured transference numbers are comparable with some previously reported porous crystalline and supramolecular polymer ion conductors.18,42,53–55 To investigate the electrochemical stability, we performed the linear sweep voltammetry (LSV) measurement for SONs of AM-2 and AM-3. The sweep rate was fixed at 0.1 mV s−1 with a fixed voltage window (−0.5 V to 6 V vs. Li/Li+) at room temperature. An electrochemical stability window of ca. 6 V is observed for both SONs of AM-2 and AM-3 (Fig. S16†).
| Morphology | Equivalents of LiClO4 (mM) | Resistance (R) (ohm) | Conductivity (σ) (S cm−1) | |
|---|---|---|---|---|
| AM-2 | SONs | 2.0 | 49.42 | 3.42 × 10−4 |
| Bulk-powder | 2.0 | 86.30 | 1.95 × 10−4 | |
| Nanoflowers | 2.0 | 299.8 | 5.63 × 10−5 | |
| AM-3 | SONs | 2.0 | 78.12 | 2.16 × 10−4 |
| Bulk-powder | 2.0 | 111.80 | 1.51 × 10−4 | |
| Nanoflowers | 2.0 | 317.9 | 5.31 × 10−5 |
Free lithium-ion concentration and ionic mobility are two dominant factors that govern the lithium-ion conductivity of SSEs. For solid conductor, ion-pair dissociation and the facile movements of these dissociated ions are crucial to improve ionic conductivity. In general, the high tendency of lithium-ions to form ion pairs or ionic aggregates creates the possibility to generate free lithium ions. In this study, the integration of a guanidinium-cored cationic scaffold in the nanostructure favors the ion pair splitting of the lithium salt to generate free mobile ions. In addition, the different positions (meta- and para-) of the peripheral carboxyl group are responsible for forming a directional channel through H-bonding, providing the pathway for transport of free ions.
Among the three different morphological nanostructures (SONs, nanoflowers, and bulk powder), the well-defined directional channel formed through H-bonding in the SON framework is responsible for the observed six-fold and four-fold high lithium-ion conductivity values. Under identical conditions, the higher ion conductivity of SONs and bulk-powder in comparison with that of the nanoflower morphology indicates that the solvent system for lithium-ion incorporation plays an important role in determining the conductivity value. Water as a solvent favors the significant release of lithium-ions by hydration in comparison with the DMF/water (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) solvent system which is also responsible for the higher conductivity value.56 Interestingly, the observed ion conductivity value is higher for AM-2 in the three different morphologies between the two positional isomers. The trend of the result suggests that the meta-substitution of the carboxyl group in AM-2 favors the formation of a rigid, well-defined directional channel in comparison with the para-substituted carboxyl group in AM-3. The 6.6-fold higher value of SONs of AM-2 compared with the zwitterionic ortho-substituted positional isomer further supports the importance of ion-pair dissociation and the directional channel for lithium-ion conductivity. Therefore, the result suggests that among the two positional isomers, the meta-substituted carboxyl group forms a well-defined rigid directional channel that favors fast lithium-ion migration. In addition, the combined effect of the integrated cationic scaffold, high lithium-ion hydration in water, and fast ionic mobility through the directional channel are responsible for the higher ionic conductivity value of the SONs of AM-2.
1 v/v) solvent system which is also responsible for the higher conductivity value.56 Interestingly, the observed ion conductivity value is higher for AM-2 in the three different morphologies between the two positional isomers. The trend of the result suggests that the meta-substitution of the carboxyl group in AM-2 favors the formation of a rigid, well-defined directional channel in comparison with the para-substituted carboxyl group in AM-3. The 6.6-fold higher value of SONs of AM-2 compared with the zwitterionic ortho-substituted positional isomer further supports the importance of ion-pair dissociation and the directional channel for lithium-ion conductivity. Therefore, the result suggests that among the two positional isomers, the meta-substituted carboxyl group forms a well-defined rigid directional channel that favors fast lithium-ion migration. In addition, the combined effect of the integrated cationic scaffold, high lithium-ion hydration in water, and fast ionic mobility through the directional channel are responsible for the higher ionic conductivity value of the SONs of AM-2.
Conclusions
By our effort to develop functional organic materials through self-assembly of cationic guanidinium derivatives having a three-fold symmetry, we have successfully developed supramolecular cationic 2D organic nanosheets as SSEs for effective lithium-ion conduction. We could establish that positional isomers and nanostructure morphologies are important to improve ion conduction. Presumably, this is the first such demonstration. In particular, the presence of a cationic scaffold in the nanostructure framework and the attachment sites of the functional group responsible for forming the directional channel through H-bonding are crucial. Solvent-assisted exfoliation of the bulk-powder yielded SONs with near-atomic thickness with lateral dimensions in the micrometer range. At the same time, self-assembly in a DMF/water solvent system produced a distinct flower-like morphology. The dispersion stability and freestanding nature were revealed by DLS and Tyndall light scattering. The thermodynamic parameter and the association constant for the self-assembly process were derived from the temperature-dependent UV-vis study. The highly crystalline nature of the SONs was revealed by PXRD and SAED patterns. XPS and FT-IR revealed the elemental composition and nature of H-bonding in the SON framework for the two positional isomers. Finally, the lithium-ion conducting properties were explored in terms of three factors, nanostructure morphology, ionic scaffold, and positional isomer. Amongst three different morphologies studied, SONs displayed a higher ion conductivity. Amongst the two positional isomers, the meta-substituted carboxyl group forms a more rigid directional channel through H-bonding, favouring ionic mobility and achieving the highest ion conductivity of 3.42 × 10−4 S cm−1 at room temperature. The ion-conducting properties of such SONs having a guanidinium-core could be further exploited for exploring the great possibilities offered by the modular structural design and synthetic ease. We believe that the described strategy could be utilized to boost the ion conductivity for designing other organic nanostructured materials for efficient conduction of ions like Na+, K+, and Al3+, and energy/electron/hole transfer for other energy storage applications.Data availability
All necessary datasets supporting this article have been uploaded as part of the ESI.†Author contributions
Ananta Dey: scholar associated with synthesis, characterization, physicochemical studies of all guanidinium ion derivatives, microscopic images, studies with soft materials. Viswakarma Ravikumar Ramlal: associated with the studies of soft materials. Selvesundarasekar Sam Sankar: performing all electrochemical studies. Subrata Kundu: interpretation of all results of the electrochemical studies and writing up that part. Amal Kumar Mandal: interpretation of all characterization data and results of the soft material. Data correlation and writing up of this article. Amitava Das: interpretation and data correlation. Overall coordination and the writing up of the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author AD acknowledges funding through SERB (India) grants (CRG/2020/000492 & J.C.B./2017/000004), and AKM acknowledges funding through SERB (India) grant SB/2019/F/6229-2020. We also thank the Analytical & Environment Science Division & Centralized Instrument Facility of CSIR-CSMCRI, Bhavnagar, for assistance with different analytical and spectroscopic measurements. SK wishes to acknowledge Dr A. M. Stephan, Dr S. T. Nishanthi and his students in CSIR-CECRI for extending their help with conductivity and transference number measurements. CSIR CSMCRI communication number CSIR-CSMCRI-127/2021.Notes and references
- S. Chu and A. Majumdar, Nature, 2012, 488, 294–303 CrossRef CAS PubMed
.
- D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed
.
- X. Zhang, L. Li, E. Fan, Q. Xue, Y. Bian, F. Wu and R. Chen, Chem. Soc. Rev., 2018, 47, 7239–7302 RSC
.
- E. Fan, L. Li, Z. Wang, J. Lin, Y. Huang, Y. Yao, R. Chen and F. Wu, Chem. Rev., 2020, 120, 7020–7063 CrossRef CAS PubMed
.
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 16141 CrossRef
.
- M. Li, J. Lu, Z. Chen and K. Amine, Adv. Mater., 2018, 30, 1800561 CrossRef PubMed
.
- T. M. Gür, Energy Environ. Sci., 2018, 11, 2696–2767 RSC
.
- J. W. Choi and D. Aurbach, Nat. Rev. Mater., 2016, 1, 16013 CrossRef CAS
.
- T. Zhang, W. He, W. Zhang, T. Wang, P. Li, Z. Sun and X. Yu, Chem. Sci., 2020, 11, 8686–8707 RSC
.
- A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 16103 CrossRef CAS
.
- B. Liu, J.-G. Zhang and W. Xu, Joule, 2018, 2, 833–845 CrossRef CAS
.
- D. Lin, Y. Liu and Y. Cui, Nat. Nanotechnol., 2017, 12, 194–206 CrossRef CAS PubMed
.
- J. Wang, Y. Yamada, K. Sodeyama, C. H. Chiang, Y. Tateyama and A. Yamada, Nat. Commun., 2016, 7, 12032 CrossRef CAS PubMed
.
- N.-S. Choi, Z. Chen, S. A. Freunberger, X. Ji, Y.-K. Sun, K. Amine, G. Yushin, L. F. Nazar, J. Cho and P. G. Bruce, Angew. Chem., Int. Ed., 2012, 51, 9994–10024 CrossRef CAS PubMed
.
- J. Wang, Y. Yamada, K. Sodeyama, E. Watanabe, K. Takada, Y. Tateyama and A. Yamada, Nat. Energy, 2018, 3, 22–29 CrossRef CAS
.
- R. Schmuch, R. Wagner, G. Hörpel, T. Placke and M. Winter, Nat. Energy, 2018, 3, 267–278 CrossRef CAS
.
- K. Borzutzki, J. Thienenkamp, M. Diehl, M. Winter and G. Brunklaus, J. Mater. Chem. A, 2019, 7, 188–201 RSC
.
- D. G. Mackanic, X. Yan, Q. Zhang, N. Matsuhisa, Z. Yu, Y. Jiang, T. Manika, J. Lopez, H. Yan, K. Liu, X. Chen, Y. Cui and Z. Bao, Nat. Commun., 2019, 10, 5384 CrossRef PubMed
.
- W. Zhao, J. Yi, P. He and H. Zhou, Electrochem. Energy Rev., 2019, 2, 574–605 CrossRef CAS
.
- M. Pasta, D. Armstrong, Z. L. Brown, J. Bu, M. R. Castell, P. Chen, A. Cocks, S. A. Corr, E. J. Cussen, E. Darnbrough, V. Deshpande, C. Doerrer, M. S. Dyer, H. El-Shinawi, N. Fleck, P. Grant, G. L. Gregory, C. Grovenor, L. J. Hardwick, J. T. S. Irvine, H. J. Lee, G. Li, E. Liberti, I. McClelland, C. Monroe, P. D. Nellist, P. R. Shearing, E. Shoko, W. Song, D. S. Jolly, C. I. Thomas, S. J. Turrell, M. Vestli, C. K. Williams, Y. Zhou and P. G. Bruce, J. Phys.: Energy, 2020, 2, 032008 CAS
.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed
.
- L. Fan, S. Wei, S. Li, Q. Li and Y. Lu, Adv. Energy Mater., 2018, 8, 1702657 CrossRef
.
- V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714–4727 RSC
.
- W. Liu, N. Liu, J. Sun, P.-C. Hsu, Y. Li, H.-W. Lee and Y. Cui, Nano Lett., 2015, 15, 2740–2745 CrossRef CAS PubMed
.
- X. Wang, H. Zhai, B. Qie, Q. Cheng, A. Li, J. Borovilas, B. Xu, C. Shi, T. Jin, X. Liao, Y. Li, X. He, S. Du, Y. Fu, M. Dontigny, K. Zaghib and Y. Yang, Nano Energy, 2019, 60, 205–212 CrossRef
.
- S. Ramesh and A. K. Arof, J. Power Sources, 2001, 99, 41–47 CrossRef CAS
.
- X. Zhang, S. Wang, C. Xue, C. Xin, Y. Lin, Y. Shen, L. Li and C.-W. Nan, Adv. Mater., 2019, 31, 1806082 CrossRef PubMed
.
- J. Sakamoto, J. van Heijst, O. Lukin and A. D. Schlüter, Angew. Chem., Int. Ed., 2009, 48, 1030–1069 CrossRef CAS PubMed
.
- S.-L. Cai, W.-G. Zhang, R. N. Zuckermann, Z.-T. Li, X. Zhao and Y. Liu, Adv. Mater., 2015, 27, 5762–5770 CrossRef CAS PubMed
.
- L. A. Wehner, N. Mittal, T. Liu and M. Niederberger, ACS Cent. Sci., 2021, 7, 231–244 CrossRef CAS PubMed
.
- L. Kong, C. Tang, H.-J. Peng, J.-Q. Huang and Q. Zhang, SmartMat, 2020, 1, 1 CrossRef
.
- F. Yang, S. Cheng, X. Zhang, X. Ren, R. Li, H. Dong and W. Hu, Adv. Mater., 2018, 30, 1702415 CrossRef PubMed
.
- X. Zhuang, Y. Mai, D. Wu, F. Zhang and X. Feng, Adv. Mater., 2015, 27, 403–427 CrossRef CAS PubMed
.
- A. Dey, V. R. Ramlal, S. S. Sankar, T. S. Mahapatra, E. Suresh, S. Kundu, A. K. Mandal and A. Das, ACS Appl. Mater. Interfaces, 2020, 12, 58122–58131 CrossRef CAS PubMed
.
- T. Singha Mahapatra, A. Dey, H. Singh, S. S. Hossain, A. K. Mandal and A. Das, Chem. Sci., 2020, 11, 1032–1042 RSC
.
- M. Park, X. Zhang, M. Chung, G. B. Less and A. M. Sastry, J. Power Sources, 2010, 195, 7904–7929 CrossRef CAS
.
-
K. Izutsu, in Electrochemistry in Nonaqueous Solutions, 2009, pp. I–XVI, DOI:10.1002/9783527629152.fmatter
.
- I. Kosuke, in Electrochemistry in Nonaqueous Solutions, 2009, pp. 27–61, DOI:10.1002/9783527629152.ch2.
- N. Yanai, T. Uemura, S. Horike, S. Shimomura and S. Kitagawa, Chem. Commun., 2011, 47, 1722–1724 RSC
.
- C. Yuan, J. Li, P. Han, Y. Lai, Z. Zhang and J. Liu, J. Power Sources, 2013, 240, 653–658 CrossRef CAS
.
- S. S. Moganty, N. Jayaprakash, J. L. Nugent, J. Shen and L. A. Archer, Angew. Chem., Int. Ed., 2010, 49, 9158–9161 CrossRef CAS PubMed
.
- H. Chen, H. Tu, C. Hu, Y. Liu, D. Dong, Y. Sun, Y. Dai, S. Wang, H. Qian, Z. Lin and L. Chen, J. Am. Chem. Soc., 2018, 140, 896–899 CrossRef CAS PubMed
.
- K. Jeong, S. Park, G. Y. Jung, S. H. Kim, Y.-H. Lee, S. K. Kwak and S.-Y. Lee, J. Am. Chem. Soc., 2019, 141, 5880–5885 CrossRef CAS PubMed
.
- Y. Hu, N. Dunlap, S. Wan, S. Lu, S. Huang, I. Sellinger, M. Ortiz, Y. Jin, S.-h. Lee and W. Zhang, J. Am. Chem. Soc., 2019, 141, 7518–7525 CrossRef CAS PubMed
.
- A. Dey, A. Maity, T. Singha Mahapatra, E. Suresh, A. K. Mandal and A. Das, CrystEngComm, 2020, 22, 5117–5121 RSC
.
- M. Ogasawara, X. Lin, H. Kurata, H. Ouchi, M. Yamauchi, T. Ohba, T. Kajitani, T. Fukushima, M. Numata, R. Nogami, B. Adhikari and S. Yagai, Mater. Chem. Front., 2018, 2, 171–179 RSC
.
- M. M. J. Smulders, M. M. L. Nieuwenhuizen, T. F. A. de Greef, P. van der Schoot, A. P. H. J. Schenning and E. W. Meijer, Chem.–Eur. J., 2010, 16, 362–367 CrossRef CAS PubMed
.
- S. Suriyakumar, A. M. Stephan, N. Angulakshmi, M. H. Hassan and M. H. Alkordi, J. Mater. Chem. A, 2018, 6, 14623–14632 RSC
.
- B. Ellis, P. Subramanya Herle, Y. H. Rho, L. F. Nazar, R. Dunlap, L. K. Perry and D. H. Ryan, Faraday Discuss., 2007, 134, 119–141 RSC
.
- S. M. Oh, S. B. Patil, X. Jin and S.-J. Hwang, Chem.–Eur. J., 2018, 24, 4757–4773 CrossRef CAS PubMed
.
- J. Evans, C. A. Vincent and P. G. Bruce, Polymer, 1987, 28, 2324 CrossRef CAS
.
- M. Siekierski, M. Bukat, M. Ciosek, M. Piszcz and M. Szerszen, Polymers, 2021, 13, 895 CrossRef CAS PubMed
.
- S. Zugmann, M. Fleischmann, M. Amereller, R. M. Gschwind, H. D. Wiemhöfer and H. J. Gores, Electrochim. Acta, 2011, 56, 3926 CrossRef CAS
.
- H. Zhang, C. Li, M. Piszcz, E. Coya, T. Rojo, L. M. Rodriguez-Martinez, M. Armand and Z. Zhou, Chem. Soc. Rev., 2017, 46, 797–815 RSC
.
- G. Girard, X. Wang, R. Yunis, D. R. MacFarlane, A. J. Bhattacharyya, M. Forsyth and P. C. Howlett, Batteries Supercaps, 2019, 2, 1–12 CrossRef
.
- J. H. Park, S. Jung, Y. H. Song, N. R. Aluru, T. Kim, S. B. Lee, U. H. Choi and J. Lee, ACS Appl. Energy Mater., 2020, 3, 10119–10130 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc04017k |
| This journal is © The Royal Society of Chemistry 2021 |