Recent advances in layered Ln2NiO4+δ nickelates: fundamentals and prospects of their applications in protonic ceramic fuel and electrolysis cells†
Artem P.
Tarutin
 ab,
Julia G.
Lyagaeva
ab,
Julia G.
Lyagaeva
 ab,
Dmitry A.
Medvedev
ab,
Dmitry A.
Medvedev
 *ab,
Lei
Bi
*ab,
Lei
Bi
 *c and
Aleksey A.
Yaremchenko
*c and
Aleksey A.
Yaremchenko
 *d
*d
aLaboratory of Electrochemical Devices Based on Solid Oxide Proton Electrolytes, Institute of High Temperature Electrochemistry, Yekaterinburg 620137, Russia. E-mail: dmitrymedv@mail.ru
bUral Federal University, Yekaterinburg 620002, Russia
cDepartment of Environmental Science and Engineering, School of Resource Environment and Safety Engineering, University of South China, Hengyang 421001, China. E-mail: lei.bi@usc.edu.cn
dCICECO – Aveiro Institute of Materials, Department of Materials and Ceramic Engineering, University of Aveiro, 3810-193 Aveiro, Portugal. E-mail: ayaremchenko@ua.pt
First published on 8th December 2020
Abstract
In the past decade, intensive research on proton-conducting oxide materials has provided a basis for the development of intermediate-temperature protonic ceramic electrochemical cells, which constitute a real alternative to conventional cells based on oxygen-conducting electrolytes. To achieve both high efficiency and excellent performance, not only electrolytes but also electrode materials should be carefully selected considering their functional properties. Compared to the traditional ABO3 perovskite electrode materials, Ln2NiO4+δ with a layered structure has unique advantages (high chemical stability, mechanical compatibility, improved oxygen transport, and hydration ability), and thus is now becoming a hot topic in this field, offering both scientific and practical interests. However, a comprehensive and in-depth review is still lacking in the literature to date. Accordingly, this work presents a comprehensive overview of the prospects of layered nickelates (Ln2NiO4+δ, where Ln = La, Nd, and Pr) as one of the most attractive oxygen (steam) electrode materials for protonic ceramic electrochemical cells. In particular, the crystalline features, defect structure, stability, chemical properties, and mechanical compatibility of this class of materials, contributing to their transport functionality, are discussed with the primary emphasis on revealing the relationship between the composition of the materials and their properties. The presented systematic results reveal the main strategies regarding the utilisation of Ln2NiO4+δ-based electrodes and existing gaps related to fundamental and applied research aspects.
1. Introduction
The ever-increasing demand for the development of highly efficient, environmentally friendly, technologically straightforward and economically expedient energy systems has stimulated rapid progress in the hydrogen and electrochemical energy fields.1–4 Accordingly, research and development related to solid oxide electrochemical cells are widespread due to the higher efficiency, flexibility and variety of these cells for use in energy conversion processes compared with other electrochemical cells.5–7 Although conventional solid oxide electrochemical cells have some disadvantages due to their high operating temperatures, the existing problems can be overcome by replacing the oxygen-ionic conductive electrolytes with proton-conducting counterparts. The improved transfer behaviour of the latter is realised due to the greater mobility of the proton charge carriers, which also exhibit a low migration barrier.8–11 Consequently, energy can be efficiently converted in solid oxide electrochemical cells based on proton-conducting electrolytes below 700 °C, and at this temperature, degradation and compatibility issues become less problematic.Among the different types of electrochemical cells, protonic ceramic fuel cells (PCFCs) and protonic ceramic electrolysis cells (PCECs) are of special interest as systems for converting chemical energy into electricity and vice versa.12–14 These two types of operations can be combined in reversible protonic ceramic cells (rPCCs), which enable power generation or energy conversion depending on the necessary (momentary) requirements. However, although very promising performances have recently been achieved for both PCFCs and PCECs,15–20 their long-term operation under multiple cycles of temperature or steam and oxygen partial pressure requires further improvement. Problems associated with degradation phenomena may also occur for these systems, where instead of fast microstructural changes, cationic interdiffusion, segregation and poisoning occur at high temperatures,21–24 chemical and thermal incompatibilities in the electrode/electrolyte pair play a key role in maintaining the integrity of PCFCs, PCECs and rPCCs.
Although the transport properties of the corresponding electrochemical devices are regulated by a proton-conducting membrane, other functional materials also affect their target electrochemical characteristics (power density, hydrogen production rate, etc.). In particular, the selection of suitable oxygen electrodes is currently of great importance for fabricating low- and intermediate-temperature electrochemical systems, including PCFCs, PCECs and rPCCs.25–27 There is a significant number of publications on the design of suitable oxygen electrodes, as systematically detailed in the following works.28–31 Among the various classes of electrodes, herein, we focus on the interesting group of oxides based on lanthanide nickelates.
The oxide Ln2NiO4+δ (Ln = La, Nd, and Pr) materials having a layered structure belong to the Ruddlesden–Popper (RP) family with the general formula An+1BnO3n+1, where n ≥ 1, A is a rare-earth or alkaline-earth element and B is a transition metal.32 The properties of Ln2NiO4+δ such as excellent oxygen diffusion coupled with high surface exchange coefficients and reduced thermal expansion coefficients (TECs) have resulted in their wide application in solid oxide electrochemical cells, including that based on ZrO2,33,34 CeO2,35,36 and LaGaO3 (ref. 37 and 38) oxygen-conducting electrolytes, and proton-conducting analogues. It should be noted that Ln2NiO4+δ oxides are considered to show triple-conducting behaviour when protonic transport exists simultaneously with oxygen-ionic and electronic transportation.39 Since this feature can affect the target parameters of electrochemical systems based on proton-conducting electrolytes, it should be analysed in detail. Therefore, this review work is devoted to revealing the application peculiarities of nickelates in PCECs, PCFCs and rPCCs and identifying future strategies for the improvement of their efficiency and performance.
2. Structure and defect chemistry of Ln2NiO4+δ
2.1. Crystal structure and oxygen nonstoichiometry
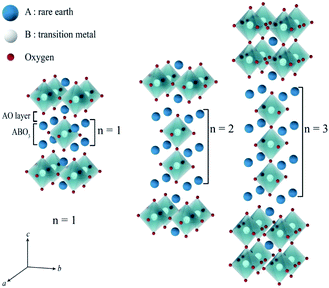
Ln2NiO4+δ nickelates belong to a series of perovskite-related layered compounds with the general formula An+1BnO3n+1, which are referred to as Ruddlesden–Popper (RP) phases.40,41 The RP structure is built of consecutive perovskite-type (ABO3)n blocks alternating with rock-salt-type AO layers along the c crystallographic axis (Fig. 1). Its formula can be represented as (AO)(ABO3)n, where n is the number of connected layers of vertex-sharing BO6 octahedra. Ln2NiO4+δ and its derivatives are n = 1 members of the homologous RP-type nickelate series. Due to their structural similarities, this type of material is also referred to as K2NiF4-type phases. In the stoichiometric Ln23+Ni2+O42− compounds, the A-site Ln cations positioned at the boundary of two types of layers are coordinated by 9 oxygen ions, while the B-site Ni cations are located in the center of octahedra formed by 6 oxygen anions. The NiO6 octahedra share corners in the a–b plane, forming a 2-dimensional network.The characteristic feature of the Ln2NiO4+δ phases is the possibility to accommodate variable oxygen excess of up to δ ∼ 0.25–0.30 in the case of Ln = La,42,43 which is required for the stabilization of the RP-type A2BO4 structure. The structural stability of A2BO4 phases is governed by the bond length matching between the perovskite and rock-salt-type layers, which can be rationalized by the Goldschmidt tolerance factor:41,42,44–47
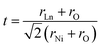 | (1) |
Empirically, the tetragonal RP-type A2BO4 (or K2NiF4-type) structure is stable over the approximate range of 0.85 < t < 1.00.41,44–46 The perfect matching of two layer types will yield a tolerance factor of t = 1, while any deviation in the t value implies a buildup of internal stress in the a–b plane of the crystal lattice.42,45,47 The ionic radii of rare-earth cations are smaller than the ideal rA of ∼1.56 Å (estimated employing Shannon's radii).48 The calculated t = 0.885 in the case of stoichiometric La2NiO4+δ means that the La–O bonds are under tensile stress and the Ni–O bonds are under compressive stress. Incorporation of interstitial oxygen ions into the rock-salt-type LaO layers relaxes the structure due to several factors as follows:42,47,49,50 (i) an increase in the average Ln–O bond length as a result of an increase in the Ln cation coordination; (ii) electrostatic repulsion of intercalated oxygen ions, leading to the same effect; and (iii) shortening of the average Ni–O bond length due to the partial oxidation of nickel cations as a result of the following charge compensation:
 | (2) |
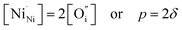 | (3) |
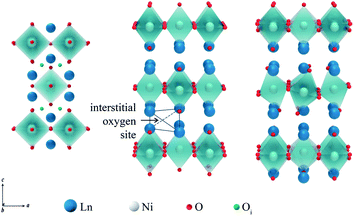
Due to geometric constraints, only three rare-earth cations can form RP-type Ln2NiO4+δ compounds in the undoped form, i.e. lanthanum, praseodymium and neodymium. The oxygen excess, δ, in these phases reversibly decreases on heating or reducing the oxygen partial pressure as a result of oxygen release from the lattice and reduction of Ni cations via reverse reaction (2), but is frozen at temperatures below ∼350 °C (ref. 51–54) due to kinetic reasons. High-temperature pO2–T–δ diagrams and their analysis can be found in ref. 55–65. At elevated temperatures, Ln2NiO4+δ has a tetragonal structure with the space group I4/mmm55,66,67 (Fig. 2) and interstitial oxygen ions in the 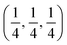 positions in the unit cell.68 A common view is that on cooling in air, the effect of intercalation of interstitial oxygen ions becomes insufficient for the release of internal strains in the tetragonal lattice due to the different thermal expansion of the Ln–O and Ni–O bonds. Consequently, the mismatch between the bond lengths in the perovskite and rock-salt-type layers is additionally released by titling the NiO6 tetrahedra, leading to a symmetry reduction to orthorhombic symmetry (or even monoclinic).69,70 Aspera et al.71 suggested that increasing the concentration of interstitial oxygen in rock-salt-type LnO layers may be a major factor contributing to the change in structure: the interstitial oxygen ions repulse the neighboring apical oxygen ions in the perovskite layers, thus causing tilting of the octahedra. Different space groups have been proposed to describe the orthorhombic lattice of air-equilibrated nickelates (Fig. 2), including Fmmm53,67,68,70,72–74 for La2NiO4+δ, Fmmm73–75 and Bmab72,75 for Pr2NiO4+δ, and Fmmm,72,76–78Abma76 and Bmab53,79 for Nd2NiO4+δ. Although praseodymium exists in a mixed 3+/4+ oxidation state in binary PrOx oxides under oxidizing conditions, analysis of the XANES spectra collected at 25–700 °C demonstrated that the Pr cations retain only the 3+ state in the Pr2NiO4+δ structure in air.80
positions in the unit cell.68 A common view is that on cooling in air, the effect of intercalation of interstitial oxygen ions becomes insufficient for the release of internal strains in the tetragonal lattice due to the different thermal expansion of the Ln–O and Ni–O bonds. Consequently, the mismatch between the bond lengths in the perovskite and rock-salt-type layers is additionally released by titling the NiO6 tetrahedra, leading to a symmetry reduction to orthorhombic symmetry (or even monoclinic).69,70 Aspera et al.71 suggested that increasing the concentration of interstitial oxygen in rock-salt-type LnO layers may be a major factor contributing to the change in structure: the interstitial oxygen ions repulse the neighboring apical oxygen ions in the perovskite layers, thus causing tilting of the octahedra. Different space groups have been proposed to describe the orthorhombic lattice of air-equilibrated nickelates (Fig. 2), including Fmmm53,67,68,70,72–74 for La2NiO4+δ, Fmmm73–75 and Bmab72,75 for Pr2NiO4+δ, and Fmmm,72,76–78Abma76 and Bmab53,79 for Nd2NiO4+δ. Although praseodymium exists in a mixed 3+/4+ oxidation state in binary PrOx oxides under oxidizing conditions, analysis of the XANES spectra collected at 25–700 °C demonstrated that the Pr cations retain only the 3+ state in the Pr2NiO4+δ structure in air.80
The ionic radius of the Ln3+ cations decreases in the sequence La > Pr > Nd,50 leading to a corresponding increase in oxygen excess content necessary to compensate the structural strain under identical conditions,53,81–83 and also a shift of the orthorhombic–tetragonal transition to a higher temperature. For air-equilibrated Ln2NiO4+δ, the reported values of δ at room temperature increase from 0.15–0.18 for Ln = La43,49,66,67,72,73,84,85 to 0.20–0.24 for Ln = Pr49,54,72,73,84 and to 0.22–0.28 for Ln = Nd.49,72,76,77,86,87 The orthorhombic-to-tetragonal transition on heating in air was reported to occur at ∼50–150 °C in air-equilibrated La2NiO4+δ,53,66,67,72,84 420–450 °C in Pr2NiO4+δ,49,54,72,84 and 520–620 °C in Nd2NiO4+δ.49,53,72,76,78,86,88,89 In the case of Pr2NiO4+δ and Nd2NiO4+δ, this reversible structural transformation is accompanied by a discrete change in the oxygen nonstoichiometry and occurs when δ in the orthorhombic modification is decreased to a certain level by 0.175–0.20 for Pr2NiO4+δ(ref. 54, 72 and 90) and 0.135–0.155 for Nd2NiO4+δ.72,91 Consequently, the temperature of the transition decreases with reducing pO2.54,72,76,88,90,91 In La2NiO4+δ (δ ≥ 0.15), an orthorhombic-to-tetragonal transition occurs at reduced temperatures when oxygen exchange is kinetically frozen, but the temperature of this transition increases with an increase in the frozen-in δ value.55,66
In addition to interstitial oxygen ions, oxygen defects important for transport and electrocatalytic properties include oxygen vacancies in the perovskite layers of the RP-type structure. Oxygen vacancies may form due to intrinsic Frenkel-type disorder
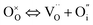 | (4) |
2.2. A-site deficiency and Ln2NiO4+δ-based solid solutions
Similar to ABO3 perovskites, the RP-type A2BO4 structure is very flexible to the introduction of A-site cation deficiency and various substitutions in both sublattices, with effects on structural properties, oxygen nonstoichiometry, ionic and electronic transport, electrocatalytic activity, and other relevant properties. The reported solubility of selected cations in the A and B sublattices of Ln2NiO4+δ is summarized in Table 1. However, the existing range of Ln2NiO4+δ-based solid solutions is not limited to individual doping in the Ln or Ni sites, but also includes a variety of co-substitutions in one or both sublattices.| Ln2−xAxNiO4±δ | Ln = La | Ln = Pr | Ln = Nd | |||
|---|---|---|---|---|---|---|
| x | Ref. | x | Ref. | x | Ref. | |
| a “Max” indicates the identified solubility limit in a given report. | ||||||
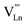
|
0.15 (max) | 51 | 0.30 | 92 | 0.10 | 53 |
| La | — | 2.0 | 73, 83 and 93 | 2.0 | 89 | |
| Pr | 2.0 | 73, 83 and 93 | — | 2.0 | 74 and 94–96 | |
| Nd | 2.0 | 89 | 2.0 | 74 and 94–96 | — | |
| Sm | 1.1 | 97 | ||||
| Ca | 0.6 (max) | 98 | 0.7 | 101 | 0.6 (max) | 79 |
| 0.3 < x(max) < 0.4 | 99 and 100 | 0.5 (max) | 102 | 0.5 (max) | 78 | |
| 1.0 | 103 | |||||
| Sr | 1.6 (max) | 104 and 105 | 1.6 | 106 and 107 | 1.6 | 108 |
| 1.5 (max) | 98 | 1.67 | 104 | |||
| Ba | 1.0 | 109 | 0.4 | 110 | 0.6 (max) | 79 |
| 1.1 (max) | 98 | |||||
| Ln2Ni1−yMyO4+δ | Ln = La | Ln = Pr | Ln = Nd | |||
|---|---|---|---|---|---|---|
| y | Ref. | y | Ref. | y | Ref. | |
| Cu | 1.0 | 111–114 | 0.4 (max) | 111 | 0.3 (max) | 115 and 116 |
| 0.5 | 45 | |||||
| Co | 0.20 (max) | 97 and 117 | 0.1 | 118 | 0.1 | 119 |
| Fe | 0.10 | 120 and 121 | 0.1 | 52 | 0.1 | 119 |
| Mn | ∼0.1 | 119 | ||||
An increase in the concentration of Ln vacancies was reported to gradually decrease the oxygen hyperstoichiometry in the lattice,51,75,85,87,126 eventually leading to oxygen deficiency even in air.51,53 However, room-temperature neutron diffraction studies of Pr2−xNiO4+δ demonstrated that an increase in praseodymium deficiency results in an increase in the concentration of oxygen vacancies in the perovskite layer, in the equatorial and, preferentially, apical positions, while the concentration of interstitial oxygen remains essentially unchanged.75 Thus, the introduction of cation vacancies into the A-sublattice of Ln2NiO4+δ is charge compensated preferentially by the formation of oxygen vacancies, implying the importance of Frenkel disorder in these phases, and the full electroneutrality condition can be expressed as
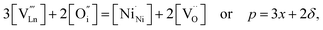 | (5) |
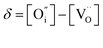 , and
, and 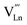 denotes Ln vacancy.
denotes Ln vacancy.
 | (6) |
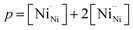 ,
, 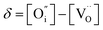 , and
, and 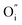 and
and 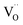 prevail for small and large A-cation fractions, respectively.
prevail for small and large A-cation fractions, respectively.
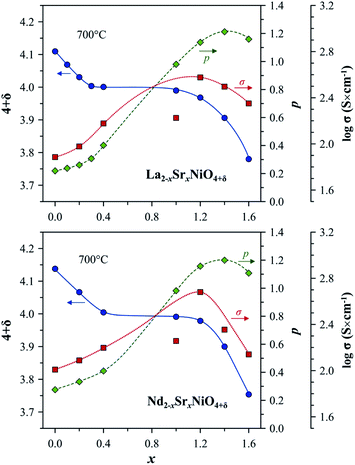 | ||
| Fig. 3 Trends in the variation of oxygen nonstoichiometry 4 + δ, electron–hole concentration, p, and electrical conductivity, σ, with strontium content, x, in Ln2−xSrxNiO4+δ systems at 700 °C. The experimental data on oxygen nonstoichiometry and electrical conductivity are from ref. 56, 59, 108, 142, 145 and 148. The electron–hole concentration is calculated using eqn (6). Note that σ of the Sr-rich compositions is undervalued due to the porosity of samples and microcracking effects.108,145 | ||
The solubility of alkaline-earth cations decreases in the sequence Ca < Ba < Sr (Table 1), in agreement with considerations of the tolerance factor, t, (eqn (1)) and stability of the A2BO4 structure.98 Sr2+ has a slightly higher ionic radius than that of Ln3+ (coordination number of A-site cations in the idealized Ln2NiO4 structure is 9).48 Therefore, the incorporation of strontium into the Ln sites effectively releases the tensile stress in the Ln–O bonds, and Sr cations may occupy up to ∼5/6 sites in the A sublattice of Ln2−xAxNiO4+δ. The ionic radius of Ca2+ is between that of La3+ and Nd3+ and is similar to the ionic radius of Pr3+ (ref. 50), thus having the opposite, but comparatively small steric effect on the RP lattice for different Ln. In combination with the shortening of the Ni–O bond lengths due to gradual Ni2+ → Ni3+ oxidation, this results in the comparatively limited solubility of calcium in the A-sublattice. Finally, large Ba2+ cations48 are even more effective than Sr2+ for releasing the tensile stress in the rock-salt-type layers; however, the tolerance factor reaches the upper limit of t = 1 at a lower concentration compared to the Sr-substituted counterparts.
The level of A-site doping and, consequently, the level of oxygen content has an impact on the variations of oxygen nonstoichiometry with temperature and pO2 within the phase stability domain of RP-type Ln2−xAxNiO4+δ phases at temperatures above ∼400 °C as follows:56–59,81,106,108,131,139,140,142,145,153–155
(i) Oxygen-hyperstoichiometric phases (δ > 0 in air). These compositions behave similarly to the parent nickelates. The oxygen content decreases on heating and with a reduction in oxygen partial pressure, but the materials maintain oxygen excess.
(ii) Oxygen-stoichiometric and nearly stoichiometric phases (δ ∼ 0 in air). These materials demonstrate negligible δ variations upon thermal and pO2 cycling under oxidizing conditions, but tend to exhibit moderate temperature-dependent oxygen deficiency at reduced oxygen pressures. Specifically, increasing x suppresses the formation of interstitial oxygen under oxidizing conditions and promotes the formation of oxygen vacancies under reducing conditions.
(iii) Oxygen-deficient solid solutions (δ < 0 in air). Oxygen deficiency increases on heating and with a decrease in oxygen partial pressure. These phases tend to exhibit a structural transformation to a distorted orthorhombic structure (space group Immm) under moderately reducing conditions (e.g. pO2 ∼ 10−5 atm) accompanied by ordering in the oxygen sublattice and substantial dimensional changes.108,155 Besides, A-rich phases exhibit strongly anisotropic thermochemical expansion, which complicates high-temperature ceramic processing.108,138,145
Other transition metal cations (such as Co, Fe, Mn, Cr, and Ti) tend to exhibit higher oxidation states in oxide compounds under oxidizing conditions, and therefore have very limited (if any) solubility in the nickel sublattice of Ln2NiO4+δ. The solid solubility range of cobalt in La2Ni1−yCoyO4+δ was found to be limited to y = 0.2 in air,97,117,160 although it can be extended under reducing conditions.97,117 The confirmed solubility of cobalt cations in Ln2Ni1−yCoyO4+δ (Ln = Pr and Nd) and iron cations in Ln2Ni1−yFeyO4+δ (Ln = La, Pr, and Nd) is only 10 at%.52,60,118–121,161 Miyoshi et al.162 reported the results of oxygen permeation studies of La2Ni0.8Fe0.2O4+δ and Pr2Ni0.8M0.2O4+δ (M = Co, Fe, and Mn), but did not present a detailed analysis of the XRD data, and thus their phase purity is questionable. Phase impurities were detected in the XRD patterns of Nd2Ni0.9Mn0.1O4+δ,119 La2Ni0.9M0.1O4+δ (M = Ta and V),163,164 and La2Ni1−yMoyO4+δ (y = 0.0125–0.05).165
The impact of partial substitution of nickel by cobalt or iron in Ln2NiO4+δ in terms of defect chemistry is an increase in the concentration of interstitial oxygen and electron holes.60–62,97,120,121,160,161 The corresponding electroneutrality condition is
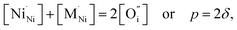 | (7) |
 .
.
In the La2Ni0.9M0.1O4+δ series, δ was found to increase in the sequence M = Cu < Ni < Co < Fe.61,62,65,120,121 A similar tendency was observed for B-site-doped Pr2NiO4+δ.52
The solid solubility of transition metal cations in the nickel sublattice of Ln2NiO4+δ under oxidizing conditions can be substantially expanded by co-substitutions with alkaline earth-cations into the Ln sublattice. In that case, donor-type doping into the B sublattice is partially charge-compensated by acceptor-type doping in the A sublattice. This leads to a complex interplay between the cation composition, oxygen nonstoichiometry, transport and electrochemical properties. The reported examples of co-substitutions include La2−xSrxNi1−yMyO4+δ (M = Co, Fe, Mn, Ti, and Mo),45,165–174 La2−xCaxNi1−yMyO4+δ (M = Fe),131 Nd2−xSrxNi1−yMyO4+δ (M = Cu and Co),175,176 and Pr2−xSrxNi1−yMyO4+δ (M = Co, Mn).177,178 The solubility of the transition metal typically increases with an increase in the fraction of alkaline-earth cation in the A-sublattice, and in the case of Co or Fe, may reach the entire range of B-site concentrations.170,172,174–176
The synthesis of Cr-doped (Ln,A)2Ni1−yCryO4+δ (A – alkaline-earth cation) is only possible at reduced oxygen pressures, under an argon atmosphere.179–184 As an exception, Ishihara et al.185 reported the preparation of Pr2Ni0.75Cu0.20M0.05O4+δ (M = Cr and V) in air, but without accurate structural studies.
Ye and Hertz186 reported that Mg2+ can substitute into the nickel sublattice up to y = 0.3 in La2Ni1−yMgyO4+δ and y = 0.2 in La1.85Ni1−yMgyO4+δ, and that the solubility can be further extended by strontium co-substitution into the lanthanum sublattice. Zhang et al.38 confirmed that La2Ni1−yMgyO4+δ is formed at least in the range 0 ≤ y ≤ 0.1. The formation of La1.7Sr0.3Ni1−yMgyO4+δ (y = 0–0.5) was reported by Meeporn et al.187 On the other hand, Klande et al.163 failed to prepare single-phase La2Ni0.9Mg0.1O4+δ.
Ganguli et al.123 reported the formation of Zn-substituted La1.9Ni0.9Zn0.1O4+δ and La1.9Sr0.1Ni0.9Zn0.1O4+δ, while Silva et al.188 claimed the zinc solubility of up to 40 at% in the nickel sublattice.
The confirmed solubility of aluminum in La2Ni1−yAlyO4+δ corresponds to 5 at% in the nickel sublattice,189,190 while La2Ni0.9Al0.1O4+δ was reported to comprise of secondary phases.163 Surprisingly, donor-type doping by Al3+ was found to reduce the oxygen excess in La2Ni0.95Al0.05O4+δ compared to the parent nickelate.189
The formation of the full range of LaSrNi1−yGayO4±δ (y = 0–1.0) solid solutions with a tetragonal structure was reported by Reinen et al.,191 whereas the solid solubility of scandium in LaSrNi1−yScyO4+δ was found to be limited to y = 0.2.192 Zhang et al.193 also reported the formation of single-phase La1.9Ni0.45Cu0.45Sc0.1O4±δ.
The synthesis of La2Ni0.9Zr0.1O4+δ was attempted in ref. 163 but the product contained La2Zr2O7 impurity.
The membrane screening tests by Miyoshi et al.162 included oxygen permeation studies of Pr2Ni0.8Zn0.2O4+δ and Pr2Ni0.9M0.1O4+δ (M = Mg, Al, and Ga), but the reported information is insufficient to conclude about the phase purity of the samples. A number of works focused on investigating the oxygen permeability or electrochemical properties of co-substituted phases in the (Ln1−xAx)2−aNi1−y−zCuzMyO4+δ (Ln = Pr or Nd; A = La or Sr; M = Al, Ga, In, Zr; x = 0–1.0, a = 0–0.10, y = 0–0.10)185,194–200 series. The compositions were claimed to be phase-pure or to contain minor phase impurities, which were ignored. In most cases, again, the quality of the provided XRD data is not sufficient to accurately conclude about the solid solubility limits of the dopant cations M.
Sm2−xLaxNiO4+δ solid solutions with a tetragonal structure were reported to form in the concentration range of 0.9 ≤ x ≤ 2.0.97 Changing the lanthanum content was observed to have a negligible impact on the low-temperature oxygen nonstoichiometry: for all the compositions, δ varied between 0.11 and 0.13 at room temperature.
Sm2−xSrxNiO4+δ solid solutions exist in a wide range of strontium contents from x = 0.4–0.5 up to x = 1.67 (i.e. 5/6 sites in the Sm sublattice).104,143,201–204 As in the case of other Ln series, increasing the Sr content decreases the temperature of the orthorhombic-to-tetragonal transition. At room temperature, the structure changes from orthorhombic for x = 0.5–0.7 to tetragonal for x = 0.8–1.67.104,143,204 Under these conditions, Sm2−xSrxNiO4+δ is nearly oxygen-stoichiometric for x = 0.5–1.0 and tends to exhibit oxygen deficiency at higher Sr concentrations, while the average Ni oxidation state increases monotonically with x.202
3. Thermodynamic and chemical stability of Ln2NiO4+δ
The thermal stability of the phases in the pseudobinary La2O3–NiO system (Fig. 4) increases in the sequence LaNiO3−δ < La4Ni3O10−δ < La3Ni2O7−δ < La2NiO4+δ,210,215–217 consistent with the reduction in the average oxidation state of the Ni cations from 3+ for LaNiO3 to 2+ for La2NiO4. La2NiO4+δ is the only stable compound in this system at atmospheric oxygen pressure at temperatures above ∼1250 °C (ref. 210 and 215–217) and exists up to the melting point of 1670–1750 °C.210 Although La2NiO4+δ easily forms in air, and once formed can maintain a phase-pure state at different temperatures, RP-type Lan+1NinO3n+1 (n = 2 or 3) and perovskite-like LaNiO3−δ appear to be thermodynamically more favorable at temperatures below 900–1100 °C under ambient pO2. The corresponding pO2-T stability ranges can be found in available phase diagrams.210,216,217 However, the transformation of La2NiO4+δ into other La–Ni–O phases at temperatures below 1100 °C is kinetically suppressed.211,217 While it can be promoted by thermal treatments at elevated oxygen pressures (>150 bar) at 825–850 °C,156,216 no evidence of phase decomposition can be observed after heating La2NiO4+δ for 100 h in ambient air at different temperatures in the range of 600–1100 °C.21 However, Amow et al.97,218 demonstrated that La2NiO4+δ does undergo phase decomposition during a longer term: the formation of a secondary phase (presumably La3Ni2O7−δ) was detected after heating at 900 °C for two weeks in air. Later, Gauquelin et al.219 observed the segregation of nickel-rich La4Ni3O10−δ and La3Ni2O7−δ phases on the surface of La2NiO4+δ single crystals after annealing in air at 1000 °C for 13 days. Furthermore, it was found that the decomposition of La2NiO4+δ into higher-order RP-type nickelates is catalyzed and strongly facilitated by contact with Pt at temperatures ≥ 800 °C,220,221 thus raising concerns about the impact of Pt current collectors on the results of electrochemical studies of La2NiO4+δ-based electrodes. No such an effect was observed in contact with Au current collectors under similar conditions.220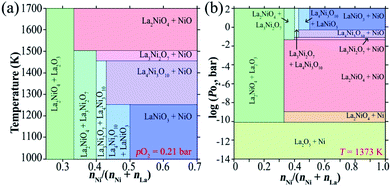 | ||
| Fig. 4 T- (a) and pO2- (b) based phase diagrams in the NiO–LaO1.5 oxide systems. Reproduced with permission.210 Copyright 2004, Elsevier. | ||
The stability boundary of La2NiO4+δ at reduced oxygen partial pressures at 600–1300 °C was determined in ref. 56, 211 and 212 and corresponds to pO2 ∼ 10−17–10−15 atm at 800 °C (Fig. 5). A decrease in oxygen chemical potential below this boundary results in a reduction to La2O3 and metallic Ni. Moderate substitutions (5–20 at%) in the B-sublattice by other transition metal cations (Fe, Co, and Cu)120,121,213,214 or aluminum189 have a rather minor effect of the low-pO2 stability limits at 600–1000 °C (Fig. 5). Nakamura et al.56 studied the La2−xSrxNiO4±δ (x = 0–0.4) system at 600–900 °C and observed only a slight shift in the low-p(O2) stability boundary towards more oxidizing conditions caused by Sr doping for x = 0.2–0.4. Similar results were obtained by Kim et al.153 for La1.9Sr0.1NiO4+δ and La0.9Ca0.1NiO4+δ at 800–1000 °C.
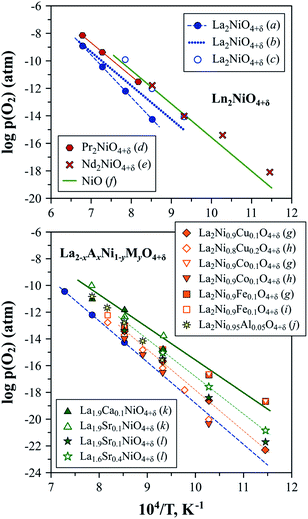 | ||
| Fig. 5 Low-pO2 stability boundaries of Ln2NiO4+δ and La2−xAxNi1−yMyO4+δ nickelates. Literature sources: (a) ref. 212, (b) ref. 211, (c) ref. 63, (d) ref. 222, (e) ref. 58, (f) ref. 223, (g) ref. 120, (h) ref. 214, (i) ref. 121, (j) ref. 189, (k) ref. 153 and (l) ref. 56. | ||
No information on the possible instability of Nd2NiO4+δ under oxidizing conditions can be found in the literature. Petrov et al.211 indicated that the low-pO2 stability limits of Nd2NiO4+δ are close to the NiO/Ni boundary. Later, Nakamura et al.58 evaluated the Nd2−xSrxNiO4+δ (x = 0–0.4) system at 600–900 °C and confirmed that the stability boundary of undoped Nd2NiO4+δ is close to that of nickel oxide (Fig. 5), and, similar to the La2−xSrxNiO4±δ system, the substitution of Nd by Sr has no substantial effect on the stability limits under reduced oxygen pressures.
Thus, electrode materials derived from Ln2NiO4+δ (Ln = La or Nd) can be expected to remain tolerant towards reductive decomposition under the typical conditions of oxygen electrode operation, even under very high cathodic polarisation.
The low-p(O2) stability boundary of Pr2NiO4+δ (Fig. 5) is between that of La2NiO4+δ and Nd2NiO4+δ,222 while partial substitutions in the nickel sublattice were reported to shift the stability limits of Pr2Ni0.9Fe0.1O4+δ and Pr2Ni0.8Cu0.2O4+δ to more oxidising conditions.52 Contrary to its La- and Nd-based counterparts, the Pr2NiO4+δ phase easily decomposes in the high-p(O2) region. Sullivan et al.222 were the first to show that Pr2NiO4+δ undergoes a transformation into Ruddlesden–Popper Pr4Ni3O10±δ and PrOy when exposed to oxidising conditions below a certain temperature (e.g. below ∼1030 °C in pure oxygen) (Fig. 6). The instability of the Pr2NiO4+δ lattice at higher oxygen pressures was confirmed and assessed in more detail in subsequent studies.52,75,224–229 Pr2NiO4+δ, which is stable in air at T ≥ 925 °C, can be rapidly quenched down to low temperatures.52,225 Thermal treatments at T ≤ 900 °C result in a reversible decomposition into a mixture of praseodymium oxide PrOy, Ruddlesden–Popper Pr4Ni3O10±δ and perovskite-like PrNiO3. Ruddlesden–Popper Pr4Ni3O10±δ is a dominant nickel-containing product at 800–900 °C,75,224–226 while PrNiO3 forms preferentially at lower temperatures ≤ 700 °C.228,229 Although the decomposition kinetics is very slow at 580–600 °C (lowest temperature at which the oxidative decomposition was observed),75,228,229 it accelerates with temperature, particularly above 700 °C.96
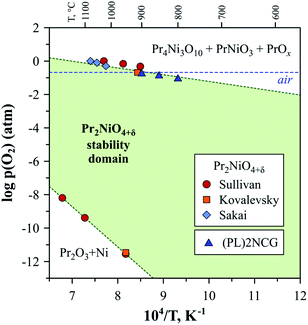 | ||
| Fig. 6 Approximate stability domain of RP-type Pr2NiO4+δ. The literature data on low- and high-pO2 stability limits was taken from Sullivan,222 Kovalevsky52 and Sakai.95 The data on the high-pO2 stability boundary of (Pr0.9La0.1)2Ni0.74Cu0.21Ga0.05O4+δ ((PL)2NCG) was from Xue.230 | ||
The stability field boundary of the Pr2NiO4+δ lattice is interrelated with the overstoichiometric oxygen content. Partial substitution of nickel by copper was found to decrease δ and expand the stability field in air to lower temperatures, while doping by iron in the Ni sublattice led to the opposite effect.52 However, B-site substitutions have a rather negligible effect on the stability from a practical point of view.52,111,118,199,230 A more effective approach, involving the suppression of excess oxygen and stabilisation of the Pr2NiO4+δ phase under oxidising conditions, is the substitution of praseodymium by alkaline-earth cations. In particular, Pr2−xCaxNiO4+δ solid solutions are reported to be stable in air when x ≥ 0.3 for at least 250 h at 850 °C.101 Moreover, no evidence of phase separation under oxidizing conditions was observed for Pr1.35Sr0.65Ni0.75Co0.25O4+δ (ref. 177) and heavily Sr-doped Pr2−xSrxNiO4+δ (x = 1.0–1.6).106,107 The incorporation of cation vacancies into the praseodymium sublattice was suggested as a possible alternative to decrease the oxygen excess and expand the stability field.230 Yet another strategy involves the substitution of praseodymium by lanthanum or neodymium with the formation of (Pr1−xLnx)2NiO4+δ solid solutions.94–96,228,229 However, it was found that full stabilisation requires the substitution of up to 75% of praseodymium cations.96,228,229 Although the intermediate compositions with x ∼ 0.5 were reported to be stable in the short term (≤100 h scale),94,95 they decomposed in the course of long-term thermal treatments (a month scale).96,228,229
Ln2NiO4+δ-derived ceramic materials demonstrate good stability in the presence of steam or carbon dioxide in the gas phase at elevated temperatures. In particular, no degradation of the electrical conductivity of Ln2NiO4+δ (Ln = La, Pr, and Nd) and LaSrNiO4 ceramics in moist air, pH2O = 0.03 atm, was observed at 25–630 °C.81 Water partial pressures of up to 0.3 atm were reported to have no detrimental effect on the conductivity of Pr2NiO4+δ ceramics at temperatures ≤ 700 °C.231 Li et al.232 reported the phase stability of Pr2NiO4+δ powder in a 40% steam/60% air mixture at 700 °C (24 h) and the absence of degradation of electrical conductivity of Pr2NiO4+δ ceramics in a 60% steam/40% air atmosphere at 700 °C (>7 h test). The TGA-MS experiments performed by Egger et al.86 did not reveal any significant influence of humidity or carbon dioxide on the oxygen exchange properties of Nd2NiO4+δ in air containing ∼1% of H2O or 5% of CO2 at 500–900 °C. Upasen et al.233 exposed Ln2NiO4+δ (Ln = La, Pr, and Nd) ceramics to harsher treatment conditions, consisting of high steam pressure of 40 bar, both with and without CO2 gas dissolved in water, at 550 °C for 5 days. The presence of secondary phases originating from undesirable hydroxylation and carbonation in the course of the treatment was detected only in the near-surface layers, while the Nd2NiO4+δ ceramics exhibited the highest structural, mechanical and chemical stability under these conditions. When pure CO2 was used as the sweep gas, the phase stability upon exposure to CO2 and the absence of oxygen permeation flux degradation through mixed-conducting Ln2NiO4+δ-based ceramic membranes were demonstrated in numerous studies conducted at 750–950 °C.163,234–239 At the same time, excessive doping by alkaline-earth cations into the Ln sublattice may deteriorate the stability of CO2, as was demonstrated in the case of (La1−xCax)2(Ni0.75Cu0.25)O4+δ for x ≥ 0.2.237
In addition to chemical stability with respect to the components of the gas phase, electrode materials should preferably exhibit good tolerance towards poisoning by volatile contaminants originating from chromium-based interconnects and silica-based glass-ceramic sealants. The available studies show that Ln2NiO4+δ electrodes exhibit fairly good tolerance with respect to Cr240–244 or Cr + Si245,246 poisoning in a dry atmosphere. Lee et al.240 reported that despite La2NiO4+δ and Cr2O3 readily reacting at 1000 °C with the formation of LaNiO3 and LaCrO3, the polarisation resistance of La2NiO4+δ electrodes at 520–800 °C is insensitive to chromium introduced by solution infiltration for Cr concentrations of up to 0.6 wt%. The Nd2NiO4+δ electrodes did not show an appreciable increase in polarisation resistance in the presence of gaseous chromium species at 850 °C and current density of 500 mA cm−2 during 800 h of testing.241 Oxygen surface exchange and electrochemical studies demonstrate the better stability of Ln2NiO4+δ compared to Sr-containing perovskite-type electrode materials242,243,245 due to chromium poisoning being correlated with the formation of strontium chromate at the surface. At the same time, deterioration of the electrode performance was observed due to the acceleration of Cr/Si poisoning as a result of humidity;243–246 moreover, the negative effect of humidity becomes stronger when the temperature decreased from 800 °C to 700 °C.245,246
4. Electrical transport properties of Ln2NiO4+δ-based ceramics
4.1. Electronic conductivity
As expected for a layered structure, the electrical properties of Ln2NiO4+δ nickelates are highly anisotropic.71,259–261 Bassat et al.260 demonstrated that the electrical conductivity of La2NiO4+δ single crystals along the a–b plane is more than 3 orders of magnitude higher than that along the c-axis at room temperature. Anisotropic electrical properties were obtained for textured Nd2NiO4+δ ceramics:262 the conductivity along and across the a–b plane at 500 °C was 270 and 16 S cm−1, respectively, compared to 117 S cm−1 for ceramics with randomly oriented grains.
The electronic conductivity of Ln2NiO4+δ is p-type and decreases with a reduction in the oxygen partial pressure due to oxygen release from the lattice and corresponding decrease in the concentration of electron holes according to eqn (2).52,57,63,139,140,142,148,258,263 Although there is some scattering in the reported conductivity values, which is apparently due to different synthesis techniques and porosity of ceramics, the electrical conductivity of Ln2NiO4+δ ceramics generally vary in the range of 40–120 S cm−1 in air at 500–900 °C.51,53,57,81,82,86,93,96,97,116,140,144,148,247–250,252,253 Considering the relationship between oxygen nonstoichiometry and concentration of electronic charge carriers, eqn (3), the conductivity of Ln2NiO4+δ can be expected to increase in the sequence La < Pr < Nd. This was confirmed, in particular, by Pikalova et al.,82 although different relationships were reported in some other works,53,81,96 as shown in Fig. 7.
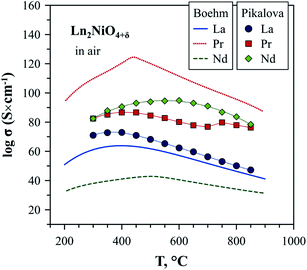 | ||
| Fig. 7 Electrical conductivity of Ln2NiO4+δ ceramics in air. The data is from Boehm53 and Pikalova.82 | ||
It is necessary to highlight that due to the phase instability in air at 700–900 °C, the reported data on the transport properties of Pr2NiO4+δ in this temperature range are mostly compromised. In fact, phase decomposition to a mixture of Pr4Ni3O10±δ and PrOx on cooling from higher temperatures was found to result in a sharp increase in electrical conductivity due to the superior conductivity of RP-type Pr4Ni3O10±δ nickelate.52 Thus, one may expect that reliable data on the electrical properties of undoped Pr2NiO4+δ in air include measurements done using fresh samples within the stability domain (≥925 °C in air) or quenched samples in a metastable region (up to 600–700 °C in air). The same considerations relate to solid solutions derived from Pr2NiO4+δ and their respective stability fields.
In the case of Sr-rich compositions (x ≥ 1.0), the electron–hole concentration and electronic conductivity in the high-temperature range reaches the maximum for x = 1.2 (Fig. 3), with conductivity values in the range of 340–470 S cm−1 at 700 °C, and then declines due to an increase in oxygen vacancy concentration.106–108,145 However, the strong anisotropic expansion of the Ln2−xSrxNiO4+δ (x > 1.0) crystal lattice results in microcracking effects in ceramics and, consequently, in an apparent hysteresis in dilatometric and conductivity curves on temperature cycling.106,108,138,145
Similar to undoped nickelates, Ln2−xAxNiO4+δ are p-type electronic conductors. Variations in the electrical conductivity as a function of the oxygen partial pressure is directly correlated with the changes in oxygen nonstoichiometry. A decrease in oxygen content with a reduction in pO2 is accompanied by a decrease in electrical conductivity for compositions with a moderate (x ≤ 0.3) and large (x ≥ 1.0) substitutional level, while solid solutions with intermediate dopant contents demonstrate nearly pO2-independent oxygen nonstoichiometry (δ ∼ 0) and electronic conductivity at 600–900 °C and pO2 in the range of 10−5 to 1.0 atm.57,106,108,139,142,145,148,154,269 A reduction of Sr-rich La2−xSrxNiO4+δ (x ≥ 1.0) at pO2 ∼ 10−5 atm and associated structural changes were observed to result in a localization of electronic charge carriers and a transition to semiconducting behavior at T ≤ 1000 °C under mildly reducing conditions.152,155
Shen et al.266 reported that the electrical conductivity of La2−xAxNiO4+δ (x = 0.1, 0.3) is higher for A = Sr compared to A = Ba, while the electronic transport in La1.7A0.3NiO4+δ was found to increase in the sequence A = Sr ∼ Ba < Ca.253,267 It should also be noted that the conductivity of Sm1.4Sr0.6NiO4+δ ceramics was reported to be only slightly lower compared to their Pr-based analog,73 which seems to imply that the trends in the Sm2−xSrxNiO4+δ system should be similar to other A-site-doped series.
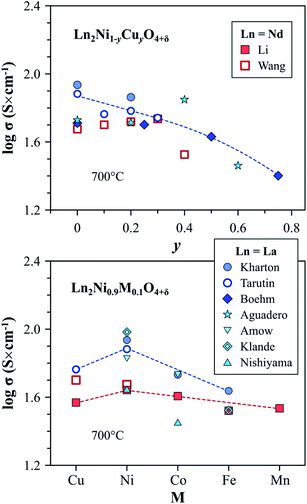 | ||
| Fig. 8 Trends in the variation of electronic conductivity in the Ln2Ni1−yCuyO4+δ and Ln2Ni0.9M0.1O4+δ series at 700 °C in air. Literature sources: Kharton,60,214 Tarutin,157 Boehm,113 Aguadero,114 Amow,97 Klande,270 Nishiyama,250 Wang,116 and Li.119 | ||
Although substitution by cobalt or iron has a contrary effect on the δ and concentration of electron holes, as shown in eqn (7), electronic conductivity of Ln2Ni1−yCoyO4+δ (ref. 60, 97, 118, 119 and 250) and Ln2Ni1−yFeyO4+δ (ref. 52, 60, 119 and 270) decreases on doping. This is attributed to the hole localization and trapping of p-type charge carriers by the dopant cations, forming stable Co3+ and Fe3+ states.60–62,121,271
Upon comparing the effect of different transition metal dopants, the electrical conductivity at 700 °C in air was reported to decrease from 44 to 33 S cm−1 in the sequence M = Ni > Co > Cu > Fe ∼ Mn for the Nd2Ni0.9M0.1O4+δ series119 and from 87 to 44 S cm−1 in the sequence M = Ni > Co > Fe for La2Ni0.9M0.1O4+δ solid solutions60 (Fig. 8). As in the case of the parent praseodymium nickelate, the data on the electrical conductivity of the doped Pr2NiO4+δ can be strongly affected by the instability of the lattice under oxidizing condition: the decomposition into Pr4Ni3O10±δ and PrOx phases was observed to result in a sharp increase in the conductivity of Pr2Ni0.9Fe0.1O4+δ and Pr2Ni0.9Cu0.1O4+δ on cooling in air.52
B-site doping by transition metal cations is also known to suppress electronic transport in A-site co-doped compositions. The corresponding high-temperature conductivity data is available for La1.9Sr0.1Ni1−yFeyO4+δ (y = 0.02–0.10),272,273 La2−xSrxNi1−yFeyO4+δ (x = 0.5–0.8, y = 0–0.5),168,172 LaSrNi1−yMnyO4−δ (y = 0–0.3),171 La1.8Sr0.2Ni1−yMoyO4+δ (y = 0–0.05),165 La1.6Ca0.4Ni1−yCuyO4+δ (y = 0–0.3),131 La1.6Ca0.4Ni1−yFeyO4+δ (y = 0–0.2),131 Nd0.8Sr1.2Ni1−yMyO4−δ (M = Co, Fe, y = 0–0.2),274 La2−2xSr2xNi1−xTixO4+δ,45 and La2−2xSr2xNi1−xMnxO4+δ (x = 0–0.3)169 systems. On the contrary, Shen et al.275 reported an increase in electrical conductivity with an increase in copper content in La1.7Ca0.3Ni1−yCuyO4+δ (y = 0.1–0.3) series.
4.2. Oxygen-ionic transport
Ln2NiO4+δ-based oxide materials are considered mixed ionic-electronic conductors. However, the oxygen-ionic conductivity (σO) in these phases is 3 or more orders of magnitude lower compared to electronic conductivity at 500–1000 °C (Table 2). In addition to σO, the important parameters used to describe oxygen transport processes include the oxygen diffusion coefficient, D, and oxygen surface exchange coefficient, k (Table 3). The diffusion coefficient is the measure of the oxygen diffusion rate in the oxide bulk and is interrelated with the oxygen-ionic conductivity via the Nernst–Einstein equation (for predominantly electronic conductors) as follows:190,286,299,307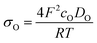 | (8) |
| Composition | σ O, S cm−1 | t O (800 °C) | E a , eV | Ref. | ||
|---|---|---|---|---|---|---|
| 900 °C | 800 °C | 700 °C | ||||
| a pO2 = 0.1 atm. b Calculated using Arrhenius model, σ = (A0/T)exp(−Ea/(kT)). | ||||||
| La2NiO4+δ | — | 0.037 | 0.015 | 8.0 × 10−4 | 0.87 | 53, 85 and 277 |
| La2NiO4+δ | 0.130 | 0.053 | 0.013 | 7.0 × 10−4 | 1.15 | 263 |
| La2NiO4+δa | 0.062 | 0.046 | — | 8.4 × 10−4 | 278 | |
| La2NiO4+δ | — | 0.010 | 3.7 × 10−3 | 1.6 × 10−4 | 1.07 | 100 |
| La1.95NiO4+δ | — | 0.019 | 8.7 × 10−3 | — | 0.77 | 85 |
| La1.9Sr0.1NiO4+δ | — | 0.012 | — | 1.3 × 10−4 | 154 | |
| La1.9Sr0.1NiO4+δa | 0.017 | 0.010 | — | 7.8 × 10−5 | 0.63 | 279 |
| La1.5Sr0.5NiO4+δ | 3.2 × 10−4 | 5.8 × 10−5 | — | — | 1.90 | 280 |
| La1.5Sr0.5Ni0.8Co0.2O4+δ | 1.9 × 10−4 | 3.6 × 10−5 | 6.0 × 10−6 | — | 1.69 | 280 |
| La1.5Sr0.5Ni0.6Co0.4O4+δ | 1.3 × 10−4 | 3.4 × 10−5 | 4.8 × 10−6 | — | 1.86 | 280 |
| La1.5Sr0.5Ni0.9Fe0.1O4+δ | 3.6 × 10−4 | 1.5 × 10−4 | — | 1.2 × 10−6 | 1.21 | 172 and 281 |
| La1.5Sr0.5Ni0.6Fe0.4O4+δ | 9.7 × 10−4 | 2.1 × 10−4 | 3.7 × 10−5 | 1.3 × 10−5 | 1.58 | 172 and 281 |
| La1.9Ca0.1NiO4+δa | 0.038 | 0.022 | — | 1.7 × 10−4 | 0.74 | 279 |
| La1.9Ca0.1NiO4+δ | — | 0.022 | 9.5 × 10−3 | 2.8 × 10−4 | 0.86 | 100 |
| La1.7Ca0.3NiO4+δ | — | 4.9 × 10−3 | 2.7 × 10−3 | 4.2 × 10−5 | 0.62 | 100 |
| La1.7Ca0.3NiO4+δ | — | 8.4 × 10−4 | 3.0 × 10−4 | 1.0 × 10−4 | 1.04 | 282 |
| La2Ni0.5Cu0.5O4+δ | — | — | 7 × 10−3 | — | — | 283 |
| La2Ni0.9Fe0.1O4+δ | 0.258 | — | — | — | — | 60 |
| La2Ni0.95Al0.05O4+δa | 0.109 | 0.085 | — | 2.5 × 10−3 | — | 190 |
| La2Ni0.95Al0.05O4+δa | 2.7 × 10−3 | — | — | — | 284 | |
| Pr2NiO4+δ | — | 0.047 | 0.024 | 5.0 × 10−4 | 0.70 | 53 and 277 |
| Pr2NiO4+δ | — | 0.057 | 0.026 | 7.3 × 10−4 | 0.84 | 282 |
| Pr1.7Ca0.3NiO4+δ | — | 7.9 × 10−4 | 3.0 × 10−4 | 9.4 × 10−6 | 0.96 | 282 |
| Pr1.9Ni0.75Cu0.25O4+δ | — | 0.075 | 0.040 | — | 0.65 | 276 |
| Pr1.9(Ni0.75Cu0.25)0.95Ga0.05O4+δ | — | 0.099 | 0.061 | — | 0.59 | 276 |
| Nd2NiO4+δ | — | 0.045 | 0.015 | 1.3 × 10−3 | 1.06 | 53 and 277 |
| Nd2NiO4+δa | 2.0 × 10−3 | 1.1 × 10−3 | 4.4 × 10−4 | — | 0.76 | 286 |
| Nd2NiO4+δ | — | 0.076 | 0.017 | 9.1 × 10−4 | 1.46 | 282 |
| Nd1.7Ca0.3NiO4+δ | — | 6.8 × 10−4 | 2.2 × 10−4 | 6.0 × 10−6 | 1.08 | 282 |
| Nd1.9Ba0.1NiO4+δ | — | 0.040 | 9.4 × 10−3 | 4.1 × 10−4 | 1.28 | 207 |
| Nd1.9Ba0.1NiO4+δF0.05 | — | 0.081 | 0.023 | 9.7 × 10−4 | 1.17 | 207 |
| Composition | Methoda | D chem, cm2 s−1 | k chem, cm s−1 | E a, eV | Ref. | |||
|---|---|---|---|---|---|---|---|---|
| 600 °C | 700 °C | 600 °C | 700 °C | D chem | k chem | |||
| a Abbreviations: ECR – electrical conductivity relaxation; EIS – electrochemical impedance spectroscopy analysis; IEDP/SIMS – isotope exchange depth profiling combined with secondary ion mass-spectrometry; and IE-GPE – isotope exchange with gas phase equilibration. | ||||||||
| La2NiO4+δ | ECR | 3.9 × 10−5 | 8.3 × 10−5 | 2.8 × 10−5 | 2.6 × 10−5 | 0.53 | 1.36 | 287 |
| La2NiO4+δ | EIS | — | — | — | 8.6 × 10−7 | — | 1.21 | 169 |
| La2NiO4+δ | ECR | — | 2.1 × 10−6 | — | 1.2 × 10−6 | 2.82 | 1.99 | 258 |
| La2NiO4+δ | EIS | — | — | 1.6 × 10−7 | 8.6 × 10−7 | — | 1.21 | 288 |
| La2NiO4+δ | ECR | 4.4 × 10−6 | 2.1 × 10−5 | 1.2 × 10−4 | 8.2 × 10−4 | 1.06 | 1.68 | 289 |
| La2Ni0.95Al0.05O4.025+δ | ECR | 7.9 × 10−6 | 2.1 × 10−5 | 1.7 × 10−5 | 4.4 × 10−5 | 0.92 | 0.84 | 190 |
| La1.8Sr0.2NiO4+δ | EIS | — | — | 4.0 × 10−8 | 2.7 × 10−7 | — | 1.31 | 288 |
| La1.6Sr0.4NiO4+δ | EIS | — | — | — | 1.7 × 10−7 | — | 1.40 | 288 |
| La1.8Sr0.2Ni0.95Mo0.05O4+δ | ECR | 8.0 × 10−6 | 12.6 × 10−6 | — | 2.0 × 10−4 | 0.51 | 1.31 | 165 |
| Nd2NiO4+δ | ECR | — | — | 3.2 × 10−8 | 1.3 × 10−7 | — | 1.10 | 286 |
| Nd2NiO4+δ | ECR | — | — | — | 1.2 × 10−4 | — | — | 295 |
| Nd2NiO4+δ | EIS | 1.8 × 10−8 | 5.6 × 10−8 | 3.0 × 10−6 | 1.8 × 10−7 | 0.90 | 1.43 | 296 |
| Pr2NiO4+δ | ECR | — | — | 2.9 × 10−6 | 4.7 × 10−5 | — | 1.84 | 118 |
| Pr2Ni0.9Co0.1O4+δ | ECR | — | — | 3.1 × 10−5 | 9.9 × 10−5 | — | 0.83 | 118 |
| Composition | Methoda | D*, cm2 s−1 | k*, cm s−1 | E a, eV | Ref. | |||
|---|---|---|---|---|---|---|---|---|
| 600 °C | 700 °C | 600 °C | 700 °C | D* | k* | |||
| La2NiO4+δ | IEDP/SIMS | 1.3 × 10−8 | 3.0 × 10−8 | 2.8 × 10−8 | 1.9 × 10−7 | 0.59 | 1.24 | 160 |
| La2NiO4+δ | IE-GPE | — | 5.5 × 10−10 | — | 7.7 × 10−5 | 1.04 | 1.04 | 82 |
| La2NiO4+δ | IE-GPE | 1.2 × 10−9 | 1.1 × 10−8 | 1.5 × 10−8 | 1.4 × 10−7 | 1.34 | 1.39 | 130 |
| La2NiO4+δ | IEDP/SIMS | — | 3.4 × 10−8 | — | 1.8 × 10−7 | 0.85 | 1.61 | 290 |
| La2NiO4+δ | IE-GPE | 1.1 × 10−9 | 9.6 × 10−9 | — | 1.4 × 10−8 | 1.41 | 1.43 | 291 |
| La2NiO4+δ | IEDP/SIMS | — | 4.8 × 10−8 | — | 2.1 × 10−7 | 0.88 | 0.42 | 53 |
| La2Ni0.9Fe0.1O4+δ | IEDP/SIMS | — | 3.5 × 10−8 | — | 4.5 × 10−7 | 0.99 | 1.17 | 53 |
| La2Ni0.9Co0.1O4+δ | IEDP/SIMS | 1.0 × 10−8 | 2.6 × 10−8 | 5.9 × 10−7 | 6.4 × 10−7 | 0.69 | 0.57 | 160 |
| La2Ni0.8Co0.2O4+δ | IEDP/SIMS | 1.3 × 10−8 | 4.0 × 10−8 | 7.3 × 10−7 | 1.4 × 10−6 | 0.62 | 0.50 | 160 |
| La2Ni0.5Co0.5O4+δ | IEDP/SIMS | 2.6 × 10−8 | 4.7 × 10−8 | 7.1 × 10−7 | 1.4 × 10−6 | 0.62 | 0.26 | 160 |
| La2Ni0.75Cu0.25O4+δ | IEDP/SIMS | — | 3.5 × 10−8 | — | 1.3 × 10−6 | 0.62 | 1.24 | 113 |
| La2Ni0.5Cu0.5O4+δ | IEDP/SIMS | — | 3.0 × 10−8 | — | 6.0 × 10−7 | 0.51 | 1.24 | 113 |
| La1.9Sr0.1NiO4+δ | IEDP/SIMS | — | 1.0 × 10−8 | — | 1.7 × 10−7 | 0.57 | 1.29 | 290 |
| La1.8Sr0.2NiO4+δ | IEDP/SIMS | — | 6.1 × 10−10 | — | 1.2 × 10−7 | 0.60 | 1.06 | 293 |
| La1.8Sr0.3NiO4+δ | IE-GPE | — | 1.4 × 10−9 | — | 6.1 × 10−6 | 1.04 | 1.24 | 267 |
| La1.9Ca0.1NiO4+δ | IE-GPE | — | 1.6 × 10−10 | — | 1.5 × 10−7 | 1.75 | 0.71 | 291 |
| La1.7Ca0.3NiO4+δ | IE-GPE | — | 1.5 × 10−9 | — | 6.0 × 10−6 | 1.04 | 1.24 | 82 |
| La1.7Ba0.3NiO4+δ | IE-GPE | — | 3.3 × 10−9 | — | 1.5 × 10−5 | 1.04 | 1.24 | 267 |
| Nd2NiO4+δ | IE-GPE | — | 4.5 × 10−8 | — | — | 1.45 | — | 82 |
| Nd2NiO4+δ | IEDP/SIMS | — | 4.5 × 10−8 | — | 3.4 × 10−7 | 1.06 | 0.77 | 53 |
| Nd1.95NiO4+δ | IEDP/SIMS | — | 3.5 × 10−8 | — | 9.0 × 10−7 | 0.65 | 0.94 | 53 |
| Nd1.8Ca0.2NiO4+δ | IEDP/SIMS | — | 1.0 × 10−8 | — | 1.9 × 10−7 | 0.72 | 0.74 | 53 |
| Nd1.7Ca0.3NiO4+δ | IE-GPE | — | 6.3 × 10−10 | — | — | 1.09 | — | 82 |
| Pr2NiO4+δ | IE-GPE | — | 7.0 × 10−8 | — | 9.5 × 10−5 | 0.83 | 1.19 | 82 |
| Pr2NiO4+δ | IEDP/SIMS | — | 7.2 × 10−8 | — | 1.4 × 10−6 | 0.73 | 1.34 | 53 |
| Pr1.7Ca0.3NiO4+δ | IE-GPE | — | 7.6 × 10−10 | — | 2.4 × 10−4 | 0.93 | 1.35 | 82 |
| Pr1.9Ni0.75Cu0.25O4+δ | IEDP/SIMS | 4.9 × 10−8 | 1.1 × 10−7 | 1.8 × 10−7 | 5.0 × 10−7 | 0.64 | 0.77 | 276 |
| Pr1.9Ni0.71Cu0.24Ga0.05O4+δ | IEDP/SIMS | 4.3 × 10−8 | 2.2 × 10−7 | — | — | 0.72 | 297 | |
| Pr1.9(Ni0.75Cu0.25)0.95Ga0.05O4+δ | IEDP/SIMS | 4.2 × 10−8 | 1.8 × 10−7 | 2.8 × 10−7 | 1.9 × 10−6 | 0.57 | 0.62 | 276 |
| Pr0.85La0.85Ca0.3NiO4+δ | IE-GPE | — | 5.1 × 10−10 | — | 7.6 × 10−5 | 1.04 | 1.24 | 267 |
Three main experimental techniques are employed to study oxygen transport in RP-type nickelates:
(i) Isotope exchange depth-profiling with secondary ion mass-spectrometry (IEDP/SIMS) is based on analysis of the concentration profile of traced 18O ionic species in an oxide sample (polycrystalline ceramics,160,276,290,292,294,298–301 single crystals277,302,303 or thin films)304 after exposure to an environment enriched with an 18O isotopic tracer (18O2/16O2 gas mixtures) at different temperatures. This method yields the oxygen tracer diffusion (D*) and surface exchange (k*) coefficients. The oxygen tracer and self-diffusion coefficients are related as follows:85,282,283,289,299
| D* = f × DO | (9) |
(ii) The electrical conductivity relaxation (ECR) method involves the analysis of the transient change in the conductivity of the sample (ceramics86,87,92,118,227,286,289,299,305–307 or thin films308,309) induced by an instant change in pO2 at a constant temperature. The oxygen chemical diffusion (![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) O or Dchem) and surface exchange (kchem) coefficients are obtained by fitting the relaxation data. The chemical diffusion coefficient, Dchem, is interrelated with the self-diffusion coefficient, DO, via the thermodynamic enhancement factor, γO:190,286,289,299,306,307
O or Dchem) and surface exchange (kchem) coefficients are obtained by fitting the relaxation data. The chemical diffusion coefficient, Dchem, is interrelated with the self-diffusion coefficient, DO, via the thermodynamic enhancement factor, γO:190,286,289,299,306,307
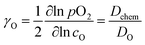 | (10) |
(iii) Oxygen permeability (OP) studies represent the measurements of oxygen permeation flux, jO2, through a dense ceramic membrane under an applied gradient of oxygen chemical potential. The jO2 values obtained under similar conditions can be used as a measure for the rough comparative analysis of the oxygen transport in mixed-conducting ceramics.162,163,185,194,195 The oxygen-ionic conductivity, σO, oxygen self-diffusion coefficient, DO, and surface exchange coefficient, kO, can be extracted from the oxygen permeation data employing the Wagner equation for bulk diffusion and considering the surface exchange kinetics.65,154,263,280,281,283,297,301,310,311 For a mixed conductor with predominately p-type electronic conductivity, the exchange coefficients obtained by different methods are related by:286,306,307
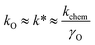 | (11) |
The other less commonly used experimental techniques are the electrochemical ion/electron blocking cell methods,100,207,279–281,284,312 mass92 or lattice parameter92,305,313,314 relaxation after instant p(O2) change, analysis of electrochemical impedance spectroscopy (EIS) and distribution of relaxation times (DRT) data,169,296,315,316 and different methods based on the oxygen isotope exchange with the gas phase, including isotope exchange with the gas phase equilibration (IE-GPE),130,291,317,318 pulse isotopic exchange (PIE),227,319 and temperature-programmed isotope exchange (TPIE) with 18O2 or C18O2.82,102,276,282,317
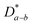 values were found to be comparable (slightly higher) to that of the bulk polycrystalline samples, implying that oxygen transport in Ln2NiO4+δ ceramics is governed by the oxygen diffusion along the basal plane. A large anisotropy was also observed for the surface exchange coefficient with higher k values for the a–b plane.277,302–304
values were found to be comparable (slightly higher) to that of the bulk polycrystalline samples, implying that oxygen transport in Ln2NiO4+δ ceramics is governed by the oxygen diffusion along the basal plane. A large anisotropy was also observed for the surface exchange coefficient with higher k values for the a–b plane.277,302–304
Oxygen hyperstoichiometry of Ln2NiO4+δ phases under oxidizing conditions implies that oxygen migration in these materials may involve either oxygen interstitials or oxygen vacancies, or both. Furthermore, interstitial oxygen ions are highly mobile. Temperature-programmed oxygen desorption studies demonstrate that the release of weakly bonded interstitial oxygen on heating in inert gas starts at temperatures as low as ∼200 °C, while desorption processes associated with the formation of oxygen vacancies in the perovskite layers occur at ≥700 °C (ref. 129, 140, 317 and 320) (except Sr-rich oxygen-deficient Ln2−xSrxNiO4−δ with the onset of oxygen loss from the perovskite layers at lower temperatures).108,140,155 This agrees with the results of the TPIE investigations, also showing that the exchange of interstitial oxygen initiates at ∼200 °C.82,102,267
Several mechanisms of oxygen migration in Ln2NiO4+δ lattice were considered and modeled employing static lattice simulations (SLS),321–324 molecular dynamics simulations (MDS),324–327 and density functional theory (DFT) calculations.47,328–332
(A) Direct interstitial diffusion pathway involving direct jumps of interstitial oxygen ions between vacant adjacent interstitial sites within rock-salt-type LnO layers. SLS and DFT calculations showed that this pathway is characterized by an excessive energy barrier of 1.2–1.4 eV,47,324 and therefore, is least probable compared to other mechanisms of diffusion along the a–b plane.
(B) Interstitialcy mechanism, also referred to as a push–pull or cooperative mechanism. In this mechanism, the oxygen interstitial displaces an apical oxygen ion from the NiO6 octahedron, which in turn move to an adjacent oxygen interstitial site. Oxygen diffusion in the a–b plane by the interstitialcy mechanism is considered as the main pathway of oxygen transport in Ln2NiO4+δ phases.321,324–327 The calculated Ea values for oxygen migration by this mechanism were reported to be in the range of 0.50–0.65 eV for La2NiO4+δ and Pr2NiO4+δ in the high-temperature range,324,325,327 which is in good agreement with the oxygen diffusion activation energy values obtained experimentally in most works (Table 3). The interstitialcy diffusion pathway in the a–b plane is also supported by the results of high-temperature neutron diffraction experiments combined with the analysis by the maximum-entropy method.328,333,334
(C) Vacancy diffusion mechanism involving oxygen vacancies in equatorial and/or apical oxygen positions in the perovskite layers. Anion Frenkel disorder, as shown by eqn (4), was predicted to be a dominant intrinsic defect formation mechanism in La2NiO4, with oxygen vacancies at the equatorial sites of the NiO6 octahedra energetically more favorable than that at the apical sites.321,323,329 Cleave et al.323 performed static lattice simulations of La2NiO4 and reported that all the considered vacancy mechanisms exhibited lower activation energies than the direct interstitial process, and that oxygen anion diffusion between the equatorial positions is energetically most preferable with the calculated Ea = 0.55 eV. However, the formation of oxygen vacancies in the perovskite layers of oxygen-hyperstoichiometric La2NiO4+δvia Frenkel disorder is likely to be suppressed due to the saturation of oxygen interstitials. The thermodynamic analysis of the pO2–T–δ diagrams of undoped and B-site-substituted La2NiO4+δ (ref. 61, 62 and 271) showed that the vacancy formation processes under thermodynamic equilibrium conditions are statistically insignificant when δ ≥ 0. Furthermore, the MD simulations carried out on stoichiometric La2NiO4 and Nd2NiO4 demonstrated insignificant oxygen diffusivities in the high-temperature range.325,326 Nonetheless, the vacancy mechanism must be involved in oxygen diffusion across the perovskite layers (along the c axis).277,303 A limited vacancy transport mechanism was identified along the c axis in the MD simulations of Pr2NiO4+δ.327 Furthermore, the role of oxygen vacancies is expected to increase as a result of acceptor-type A-site substitutions in Ln2−xAxNiO4+δ (A = alkaline-earth cation) accompanied by a reduction in the overall oxygen content and a gradual transition to oxygen deficiency with an increase in x (ref. 145 and 329) and with a reduction in pO2.335 This seems to be supported by the results of TPIE studies, which were interpreted as an indication of two distinguishable oxygen diffusion pathways in some Ln2−xAxNiO4+δ nickelates.82,102,276,282,330
In addition to O2− transport, the involvement of interstitial peroxide O− ions in different diffusion mechanisms is considered.277,321,329,331 In particular, the DFT calculations predict that Oi− species may be more stable compared to Oi2− ions and oxygen vacancies at certain strontium contents in La2−xSrxNiO4+δ,329,331 while the diffusion of Oi− by the interstitialcy mechanism may be more energetically favorable.321,331
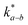 , which is 0.5–1.0 orders of magnitude higher than
, which is 0.5–1.0 orders of magnitude higher than 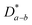 .302,303 Similar trends are generally observed for undoped polycrystalline Ln2NiO4+δ.53 The ionic conductivity of Ln2NiO4+δ ceramics is around 0.05 S cm−1 at 800 °C in air (Table 2). Furthermore, La2NiO4+δ and Pr2NiO4+δ ceramic membranes show similar oxygen permeability at ≥900 °C.52,225
.302,303 Similar trends are generally observed for undoped polycrystalline Ln2NiO4+δ.53 The ionic conductivity of Ln2NiO4+δ ceramics is around 0.05 S cm−1 at 800 °C in air (Table 2). Furthermore, La2NiO4+δ and Pr2NiO4+δ ceramic membranes show similar oxygen permeability at ≥900 °C.52,225
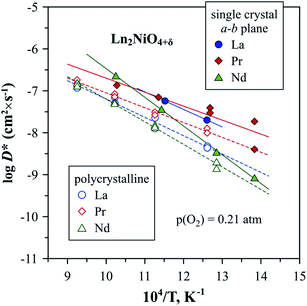 | ||
| Fig. 9 Temperature dependence of oxygen tracer diffusion coefficient, D*, reported for Ln2NiO4+δ single crystals (a–b plane) and polycrystalline samples.53,302,303 | ||
Compared to the oxygen diffusion coefficients, there is a substantially larger variation in the reported values of k and corresponding activation energies, as noted in a number of works.53,300,302 It was highlighted that the scattering in measured surface exchange coefficients can be caused by the differences in surface chemistry (surface termination, near-surface rearrangement, and presence of extrinsic impurities) as a result of different thermal pre-history.302 Generally, the oxygen diffusion and surface exchange coefficients of Ln2NiO4+δ ceramics are higher compared to many perovskite systems, such as La0.6Sr0.4Fe0.8Co0.2O3−δ and La0.6Sr0.4Fe0.8Ni0.2O3−δ, but lower compared to the best (La,Sr)CoO3−δ mixed conductors.53,113,290,307,317
Since interstitial oxygen ions are the dominant ionic charge carriers in Ln2NiO4+δ under oxidizing conditions, the ionic conductivity,65,263,278,279,286,307,311 oxygen diffusion coefficient278,279,301,307,311,312 and surface exchange coefficient286,301,307 decrease with a reduction in pO2 due to the decrease in the interstitial oxygen concentration, as shown by eqn (2).
The instability of the RP-type Pr2NiO4+δ lattice under oxidizing conditions has a strong impact on the experimentally measured ionic transport parameters in the temperature range of 700–900 °C. In particular, it has been demonstrated that the decomposition of Pr2NiO4+δ ceramics into Pr4Ni3O10+δ, PrOx and PrNiO3 at 750 °C in air results in an increase in the oxygen permeation flux and apparent values of oxygen diffusion and surface exchange coefficients by 1–2 orders of magnitude within 120 h.227 A similar increase in the oxygen permeability of Pr2NiO4+δ membranes with time caused by phase decomposition at temperatures below 900 °C was reported in ref. 52 and 225. On the contrary, phase separation resulted in a deterioration of the oxygen permeation flux through (Pr0.9La0.1)2−xNi0.74Cu0.21Ga0.05O4+δ membranes at 800–900 °C.230 Berger et al.118 observed the exsolution of PrOx particles on the surface of Pr2NiO4+δ and Pr2Ni0.9Co0.1O4+δ ceramic samples in the course of ECR at 600–800 °C and pO2 = 10−3 atm, and correlated this with an increase in the measured oxygen exchange coefficients upon temperature cycling.
Contrary to other works, Shen et al.100 reported that the ionic conductivity of La2−xCaxNiO4+δ (x = 0–0.3) at 600–800 °C increases with moderate Ca doping (x = 0.1), despite the decrease in oxygen overstoichiometry, and then declines upon further doping. However, it should be noted that the value of σO obtained for undoped La2NiO4+δ in that work is lower compared to other literature data (Table 2). Zhu et al.339 found that substitution of 5 at% of lanthanum by bismuth enhances the oxygen chemical diffusion and surface exchange coefficient of La1.65Bi0.1Sr0.25NiO4+δ by a factor of 2–3 compared to La1.75Sr0.25NiO4+δ at 700–800 °C. This was attributed to the minor increase in oxygen excess with bismuth doping and higher oxygen diffusivity in the doped material associated with the high polarizability of bismuth cations.
Moderate copper doping was found to be favorable for oxygen transport in Pr2NiO4+δ. In particular, Miyoshi et al.162 reported that the oxygen permeability of Pr2Ni1−yCuyO4+δ (y = 0.1–0.5) ceramic membranes at 600–1000 °C reached the maximum at y = 0.2 and declines upon further doping. IEDP/SIMS studies revealed that the oxygen tracer diffusion coefficient, D*, and ionic conductivity, σO, of copper-doped Pr1.9Ni0.75Cu0.25O4+δ at 730–800 °C is ∼2 times higher compared to undoped praseodymium nickelate.276
Static lattice and molecular dynamics simulations324 showed that although the incorporation of transition metal cations with the 3+ oxidation state (such as Co3+ or Fe3+) into the nickel sublattice increases the concentration of ionic charge carriers, these dopants simultaneously tend to reduce the ionic mobility. This generally agrees with the reported experimental results. Kilner and Shaw160 performed IEDP/SIMS studies of La2Ni1−yCoyO4+δ ceramics and found that within the solid solution formation range under oxidizing conditions (y = 0–0.2), cobalt doping has a rather minor impact on the oxygen diffusivity with similar values of D* for all compositions (despite the increase in δ with doping). Simultaneously, the substitution of Ni by Co decreases Ea for the surface exchange coefficient, k*, and enhances oxygen exchange, especially at lower temperatures.160 Similarly, the studies of co-substituted La1.5Sr0.5Ni1−yCoyO4+δ (y = 0–0.4) nickelates by oxygen permeation and Hebb–Wagner polarization methods at 800–1000 °C revealed that although doping by cobalt increases the interstitial oxygen content and improves the surface oxygen exchange, it also deteriorates the oxygen diffusivity, and to a lesser extent, the ionic conductivity.280 Berger et al.118 reported based on the ECR studies at pO2 = 10−3 atm at 600–800 °C that doping with cobalt in Pr2Ni0.9Co0.1O4+δ decreases the activation energy for surface oxygen exchange and substantially improves kchem at temperatures below 800 °C, which is ca. one order of magnitude at 600 °C. Later, they confirmed316 by analysis of the EIS data for Pr2Ni1−yCoyO4+δ (y = 0 and 0.1) microelectrodes at 550–850 °C that the substitution by cobalt improves the oxygen exchange at T < 800 °C and p(O2) = 10−3–10−2 atm, while the effect was opposite at atmospheric oxygen pressure.
Substitution of 10 at% of nickel by iron has a comparatively minor effect on the oxygen transport, as revealed by IEDP/SIMS studies at 700–840 °C.298 Specifically, D* and k* of La2Ni0.9Fe0.1O4+δ are similar to that of undoped lanthanum nickelate at higher temperatures (despite the higher δ), but the oxygen diffusivity tends to decline to some extent upon cooling with respect to La2NiO4+δ, and the opposite effect was observed for the surface exchange. Analysis of the oxygen permeation data for La2Ni0.9Fe0.1O4+δ ceramic membranes60,161 showed that doping by iron results in a slightly higher ionic mobility compared to La2NiO4+δ at 900–950 °C, but deteriorates the oxygen transport at lower temperatures. Furthermore, Klande et al.163 reported that the oxygen permeability of La2NiO4+δ membranes exceeds that of La2Ni0.9Fe0.1O4+δ in the entire studied temperature range (750–950 °C). Gilev et al.281 studied the oxygen transport in the La2−xSrxNi1−yFeyO4+δ (x = 0.5 and 0.8, y = 0.1–0.4) system employing the oxygen permeation and Hebb–Wagner polarizations techniques and found that co-substitution by iron (up to 40 at% in the nickel sublattice) enhances the oxygen permeability, bulk ionic diffusion and oxygen surface exchange, while the oxygen self-diffusion coefficient DO is lower compared to that of Fe-free La1.5Sr0.5NiO4+δ.280 Miyoshi et al.340 reported that co-doping by iron improves the oxygen permeability of Pr2Ni0.8−yCu0.2FeyO4+δ (y = 0–0.20) ceramics at 600–1000 °C with the best results obtained for y = 0.05.
The positive effects of co-substitutions by transition metal cations on oxygen transport were also reported for other (La,Sr)2(Ni,M)O4+δ systems. Gómez et al.165 performed ECR measurements of La1.8Sr0.2Ni0.95Mo0.05O4+δ at 600–900 °C and found that Dchem is almost an order of magnitude higher than that of La1.8Sr0.2NiO4+δ and comparable to that of undoped La2NiO4+δ (although with a two times lower activation energy, leading to a higher oxygen diffusivity at T < 700 °C), while the surface exchange coefficient, kchem, exceeds that of the undoped nickelate by more than an order of magnitude. Li et al.169 performed an analysis of EIS data obtained for La2−2xSr2xNi1−xMnxO4+δ electrodes (x = 0–0.30) at 600–800 °C and demonstrated that co-substitution by manganese promotes the surface exchange kinetics: the surface exchange coefficient, k, reaches the maximum for x = 0.10, but declines upon further doping.
Comparing the available oxygen permeation data for RP-type nickelate membranes with different dopants, one may also find the following trends:
– The oxygen transport in La2Ni0.9M0.1O4+δ at temperatures below 850–900 °C decreases in the sequence M = Ni > Co > Fe;60,163
– In the La2Ni0.8M0.2O4+δ series, the oxygen transport at 600–1000 °C was reported to decrease in the sequence M = Cu > Co > Fe > Mn;162
– The oxygen permeability of La2Ni0.8Cu0.2O4+δ is slightly lower compared to that of La2Ni0.9Co0.1O4+δ at 850–950 °C and similar at 700–800 °C;214,341
– Oxygen permeability in the PrNi0.75Cu0.20M0.05O4+δ series at 600–1000 °C was found to decline in the sequence M = Fe > Cr > V.185
Klande et al.163 reported that partial substitution of nickel by aluminum or magnesium resulted in the lower oxygen permeability of La2Ni0.9M0.1O4+δ (M = Al or Mg) ceramic membranes compared to the parent La2NiO4+δ, although this may be partly attributed to the presence of phase impurities.
Ishihara et al.194,195,198 performed extensive oxygen permeability screening tests at 600–1000 °C and found that the introduction of gallium into the nickel sublattice of Ln2Ni0.75Cu0.25O4+δ (Ln = Nd or Pr) combined with the introduction of A-site vacancies is a suitable approach to improve the oxygen permeability of nickelate membranes. The optimum composition was claimed to be Ln2−2x(Ni0.75Cu0.25)1−xGaxO4+δ with x = 0.05 and with better transport properties in the case of Ln = Pr.194,195,198 However, it should be noted that it is hard to distinguish between the effects of cation deficiency and gallium doping without detailed studies. As mentioned above, the oxygen permeability of A-site-deficient (Pr0.9La0.1)1.90Ni0.74Cu0.21Ga0.05O4+δ membranes was found to be more than 2 times that of the cation-stoichiometric analog (Pr0.9La0.1)2Ni0.74Cu0.21Ga0.05O4+δ.285 Hyodo et al.276 performed IEDP/SIMS studies of Pr1.9(Ni0.75Cu0.25)1−yGayO4+δ (y = 0 and 0.05) nickelates and found that gallium doping results in a slight improvement in the oxygen tracer diffusion coefficient, D*, and ionic conductivity (∼1.5 times, Table 3), and also results in some enhancement in oxygen exchange. This composition exhibits the highest ionic conductivity among the Ln2NiO4+δ-based phases reported thus far.
Based on the oxygen permeation screening tests at 600–1000 °C, the following trends should also be mentioned:
– The oxygen transport in Pr2Ni0.9M0.1O4+δ was reported to decrease in the sequence M = Mg > Ga > Al.162 Besides, the oxygen permeability of Pr2Ni0.9Mg0.1O4+δ membranes was also higher compared to that of Pr2Ni0.8M0.2O4+δ (M = Cu or Zn);162
– The oxygen permeability of PrNi0.75Cu0.20M0.05O4+δ membranes decreases in the sequence Al > In > Zr, in all cases being lower compared to M = Fe;185
– The oxygen transport in Pr1.90(Ni0.75Cu0.25)0.95M0.05O4+δ decreases in the sequence M = Ga > Al > In.195
5. Ln2NiO4+δ-based materials as electrodes for proton-conducting electrochemical cells
In this section, we discuss the results of research regarding the utilisation of Ln2NiO4+δ-based materials as electrodes of protonic ceramic electrochemical cells. The success of this application depends on many factors (Fig. 10), where the inherent properties of the RP phases (considered in detail in the previous sections) and their behaviour upon contact with proton-conducting electrolytes, including chemical reactivity, thermal compatibility and electrochemical activity.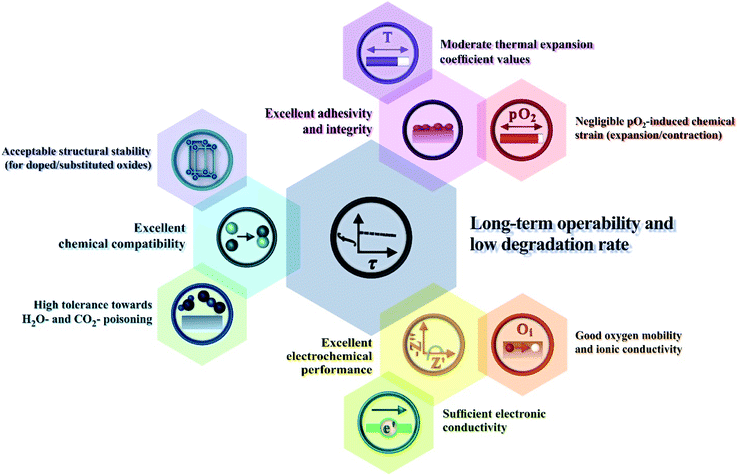 | ||
| Fig. 10 Main correlations between the performance of Ln2NiO4+δ electrode materials and their functional properties. | ||
5.1. Chemical compatibility with proton-conducting electrolytes
In terms of their thermodynamic stability, Ln2NiO4+δ-based phases exhibit considerable chemical tolerance towards interaction with state-of-the-art proton-conducting materials. This may be due to two main factors, i.e. their wide structural flexibility upon cationic interdiffusion, and the low number of impurity phases capable of being formed at interfaces upon long-term treatment.Lyagaeva et al.349 studied the chemical interaction features of 13 cathode materials with BaCe0.9Y0.1O3−δ (BCY) and BaZr0.8Y0.2O3−δ (BZY) electrolytes using 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 wt% mixtures calcined at 1100 °C for 10 h. The Co-containing cathodes and manganites, comprising simple cobaltites (Ba0.5Sr0.5CoO3−δ), layered cobaltites (GdBaCo2O5+δ, NdBaCo2O5+δ, and Y0.8Ca0.2BaCo4O7+δ), simple cobaltite-ferrites (Ba0.5Sr0.5Co0.2Fe0.8O3−δ, Ba0.5Sr0.5Co0.8Fe0.2O3−δ, and La0.6Sr0.4Co0.2Fe0.8O3−δ), layered cobaltite-ferrites (GdBaCoFeO5+δ and NdBa0.5Sr0.5Co1.5Fe0.5O5+δ) and manganites (La0.75Sr0.2MnO3−δ), are chemically incompatible either with one of the BCY and BZY phases or with both of them. However, the studied ferrites (Ba0.5Sr0.5FeO3−δ) and nickelates (LaNi0.6Fe0.4O3−δ and La2NiO4+δ) showed no interaction with both the BCY and BZY phases.
50 wt% mixtures calcined at 1100 °C for 10 h. The Co-containing cathodes and manganites, comprising simple cobaltites (Ba0.5Sr0.5CoO3−δ), layered cobaltites (GdBaCo2O5+δ, NdBaCo2O5+δ, and Y0.8Ca0.2BaCo4O7+δ), simple cobaltite-ferrites (Ba0.5Sr0.5Co0.2Fe0.8O3−δ, Ba0.5Sr0.5Co0.8Fe0.2O3−δ, and La0.6Sr0.4Co0.2Fe0.8O3−δ), layered cobaltite-ferrites (GdBaCoFeO5+δ and NdBa0.5Sr0.5Co1.5Fe0.5O5+δ) and manganites (La0.75Sr0.2MnO3−δ), are chemically incompatible either with one of the BCY and BZY phases or with both of them. However, the studied ferrites (Ba0.5Sr0.5FeO3−δ) and nickelates (LaNi0.6Fe0.4O3−δ and La2NiO4+δ) showed no interaction with both the BCY and BZY phases.
Tolchard and Grande350 applied more stringent conditions (1100 °C for 72 h) to reveal the interaction abilities of LaMnO3, LaFeO3, LaCoO3, and La2NiO4 phases with BaZrO3. Using XRD and SEM and EDX analyses, they found that LaMnO3 is the most unsuitable oxide, which results in the formation of 12.2 wt% of an La2Zr2O7 impurity phase according to the simplified reaction:
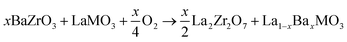 | (12) |
For the couples of LaFeO3/BaZrO3 and La2NiO4/BaZrO3, this impurity phase was also detected in amounts of 0.7 and 2.2 wt%, respectively. The highest chemical tolerance was reported for LaCoO3/BaZrO3, where no La2Zr2O7 was formed after prolonged high-temperature calcination. However, this does not lead to the conclusion that LaCoO3 is the most suitable for BaZrO3 since cationic interdiffusion (without decomposition of the original phases or appearance of new ones) can also occur. For example, cobalt-based solutions in a wide concentration range, i.e. BaZr1−xCoxO3−δ (0 ≤ x ≤ 0.4), can be formed,27,351 leading to significant disruption of the chemical compositions for both the basic LaCoO3 and BaZrO3 phases without the formation of any impurities. A similar situation has been described in other works,352,353 where Ba-enriched Ba0.5Sr0.5Co0.8Fe0.2O3−δ/Ba-deficient BaCe0.9Y0.1O3−δ and Co-enriched BaCe0.7Zr0.1Y0.2O3−δ/Y-enriched PrBaCo2O5+δ compositions were observed after prolonged high-temperature calcination.
Considering the model BaCeO3/Ln2NiO4+δ pair as an example, Ni-dissolution in BaCeO3 is limited to ∼1 mol%;354 Ln-dissolution may be also minimised if BaCeO3 is doped by acceptor dopants; Ba-dissolution in Ln2NiO4+δ is possible,355 but this improves the catalytic activity of the modified electrodes356 and is limited in the case of already Ba-doped nickelates (i.e. (Ln,Ba)2NiO4+δ); and finally, Ce-dissolution in the Ln2NiO4+δ parent phase is negligible. These features constitute quite encouraging results regarding the chemical compatibility of nickelates with state-of-the-art proton-conducting oxides, as shown in Table 4.
| Electrolyte | Electrode | Weight ratio | Calcination condition, T, °C/τ, h | Impurity phases (from XRD data) | Ref. |
|---|---|---|---|---|---|
| BaZrO3 | La2NiO4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1100/72 | La2Zr2O7 (trace) | 350 |
| La28−xW4+xO54+3x/2 | Pr2NiO4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
800/2 | Pr6O11 (trace) | 357 |
| La5.5WO11.25−δ | La2NiO4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1150/5 | La6W2O15 (trace) | 265 |
| BaCe0.9Y0.1O3−δ | Pr2NiO4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1200/1 | (Ce,Pr)O2 and NiO | 231 |
| BaCe0.7Zr0.1Y0.1Yb0.1O3−δ | Nd2NiO4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1200/3 | No interaction | 358 |
| BaCe0.89Gd0.1Cu0.01O3−δ | La1.7Ba0.3NiO4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
700/1000 | BaO (trace) | 359 |
| BaCe0.8Y0.2O3−δ | La2NiO4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1100/10 | No interaction | 349 |
| BaZr0.8Y0.2O3−δ | La2NiO4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1100/10 | No interaction | 349 |
| BaZr0.1Ce0.7Y0.2O3−δ | Pr1.8La0.2Ni0.74Cu0.21Nb0.05O4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
950/3 | No interaction | 360 |
| BaCe0.5Zr0.3Dy0.2O3−δ | Nd1.95Ba0.05NiO4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1100/10 | No interaction | 361 |
| BaCe0.55Zr0.3Y0.15O3−δ | Pr2NiO4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
800, 900 | (Ce,Pr)O2 (at T ≥ 900![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C) °C) |
362 |
| 1000, 1100 | |||||
| 1200/2 | |||||
| BaZr0.1Ce0.7Y0.2O3−δ | La1.2Sr0.8Ni0.6Fe0.4O4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
900/5 | No interaction | 363 |
| BaCe0.5Zr0.3Dy0.2O3−δ | Pr1.9Ba0.1NiO4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1350/5 | NiO | 364 |
| La2Ce2O7−δ | Pr2NiO4+δ | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1150 | Pr6O11 and La2NiO4+δ | 365 |
5.2. Mechanical compatibility with proton-conducting electrolytes
Components of solid oxide electrochemical systems are typically subjected to severe conditions under both fabrication of the cells (very high co-sintering temperatures) and their operation (reduced temperatures, but high gradients of electrochemically active components). Thus, to achieve excellent integrity of multi-layered structures with no further unacceptable consequences (electrode delamination, cracking and other failures), materials should be selected based on their thermo- (chemico-) mechanical properties. Generally, this issue has been thoroughly described by Løken et al.,366 who reviewed the thermal and chemical expansion features of proton-conducting electrolytes together with the compatibility aspects of their use with different electrode materials. To briefly summarise their main conclusions, suitable electrodes should exhibit TEC values close to that of the widely studied protonic conductors ((8–12) × 10−6 K−1), featuring a low contribution from chemical expansion.| αcomposite = (1 − x)αelectrode + xαelectrolyte |
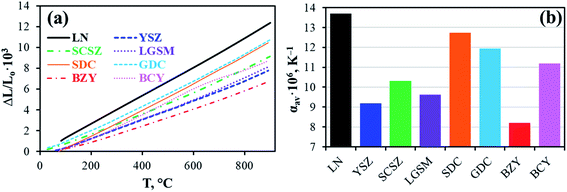 | ||
| Fig. 11 Thermal expansion behaviour (a) and average TEC values (b) of some oxygen-ionic and proton-conducting electrolytes compared with LN. These data were taken from ref. 157 for LN, ref. 367 for YSZ and LGSM, ref. 368 for SDC, ref. 369 for GDC and SCSZ, and ref. 370 for BZY and BCY. Abbreviations: LN = La2NiO4+δ, YSZ = Zr0.9Y0.1O2−δ, LGSM = La0.9Sr0.1Ga0.8Mg0.2O3−δ, SDC = Ce0.8Sm0.2O2−δ, GDC = Ce0.9Gd0.1O2−δ, SCSZ = (Sc2O3)0.1(CeO2)0.01(ZrO2)0.89, BZY = BaZr0.8Y0.2O3−δ, and BCY = BaCe0.8Y0.2O3−δ. | ||
Together with composite materials, the TEC levels of Ln2NiO4+δ-based materials can be widely tuned via the doping approach. Table 5 lists some doped oxides and their average TECs determined within the entire studied temperature range.
| Composition | α av × 106, K−1 | Ref. |
|---|---|---|
| La2NiO4+δ | ||
| La2NiO4+δ | 12.6 | 114 |
| 13.0 | 53, 72 and 371 | |
| 13.1 | 340 | |
| 13.5 | 372 | |
| 13.8 | 218 | |
| La1.95Ba0.05NiO4+δ | 13.2 | 373 |
| La1.8Sr0.2NiO4+δ | 12.6 | 371 and 374 |
| La1.75Sr0.25NiO4+δ | 11.2 | 339 |
| La1.7Sr0.3NiO4+δ | 13.9 | 359 |
| La1.7Sr0.3Ni0.9Mn0.1O4+δ | 15.3 | 171 |
| La0.2Sr1.8NiO4+δ | 13.8 | 374 |
| La1.8Ca0.2NiO4+δ | 14.5 | 131 |
| La1.7Ca0.3NiO4+δ | 13.9 | 359 |
| 14.2 | 132 | |
| La1.6Ca0.4Ni0.9Fe0.1O4+δ | 14.6 | 131 |
| La1.6Ca0.4Ni0.9Cu0.1O4+δ | 14.9 | 131 |
| La1.7Ba0.3NiO4+δ | 15.2 | 359 |
| La2Ni0.6Cu0.4O4+δ | 13.0 | 375 |
| La2Ni0.9Co0.1O4+δ | 12.8 | 204 and 205 |
| La2Ni0.9Fe0.1O4+δ | 13.8 | 376 |
| 12.7 | 377 | |
| La2Ni0.8Cu0.2O4+δ | 14.2 | 376 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Pr2NiO4+δ | ||
| Pr2NiO4+δ | 13.2 | 378 |
| 13.3 | 372 | |
| 13.4 | 72 | |
| 13.6 | 53 | |
| 13.9 | 379 | |
| 15.5 | 101 | |
| Pr1.95Ba0.05NiO4+δ | 13.9 | 373 |
| PrLaNiO4+δ | 14.1 | 380 |
| Pr1.7Sr0.3NiO4+δ | 12.0 | 268 |
| 15.0 | 201 | |
| Pr1.2Sr0.8NiO4+δ | 12.9 | 268 |
| Pr1.5Sr0.5Ni0.5Co0.5O4+δ | 13.1 | 177 |
| Pr1.7Sr0.3Ni0.6Cu0.4O4+δ | 13.8 | 381 |
| Pr2Ni0.75Cu0.25Ga0.05 O4+δ | 12.7 | 382 |
| Pr1.7Ca0.3NiO4+δ | 14.5 | 132 |
| Pr1.6Ca0.4NiO4+δ | 13.7 | 101 |
| Pr2Ni0.9Co0.1O4+δ | 16.2 | 118 |
| Pr2Ni0.9Mo0.1O4+δ | 13.5 | 379 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Nd2NiO4+δ | ||
| Nd2NiO4+δ | 12.7 | 53 |
| 13.4 | 383 | |
| 14.5 | 384 | |
| 15.0 | 132 | |
| Nd1.95Ba0.05NiO4+δ | 13.4 | 373 |
| Nd1.8Sr0.2NiO4+δ | 12.9 | 91 |
| Nd1.6Sr0.4NiO4+δ | 13.0 | 385 |
| Nd1.2Sr0.8NiO4+δ | 14.4 | 385 |
| NdSrNiO4+δ | 12.3 | 108 |
| Nd1.9Ca0.1NiO4+δ | 15.1 | 132 |
| Nd1.8Ca0.2NiO4+δ | 14.3 | 132 |
| Nd1.7Ca0.3NiO4+δ | 13.5 | 132 |
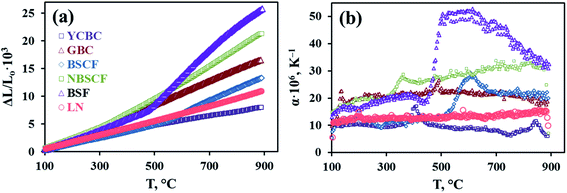 | ||
| Fig. 12 Thermal expansion (a) and TEC values (b) of some electrode materials as a function of temperature (ambient air atmosphere). Data is presented based on experiments. Abbreviations: LN = La2NiO4+δ, YCBC = Y0.8Ca0.2BaCo4O7+δ, GBC = GdBaCo2O5+δ, BSCF = Ba0.5Sr0.5Co0.8Fe0.2O3−δ, BSF = Ba0.5Sr0.5FeO3−δ, and NBSCF = NdBa0.5Sr0.5Co1.5Fe0.5O5+δ. Reproduced with permission.349 Copyright 2017, Elsevier. | ||
The Ni-based Ruddlesden–Popper phases are attractive from the viewpoint of chemical-induced strain effects (Fig. 13), showing an inappreciable response in dimensional changes towards oxygen deviation (δ) from the stoichiometric values or oxygen partial pressure variations. This unique pO2-tolerance strain originates from the structural features of nickelates.376 Oxygen desorption of Ln2NiO4+δ results in two opposite effects, i.e. contraction of the c-parameters owing to the release of interstitial oxygen from the rock-salt layers and expansion of the perovskite-like layers (a–b plane) due to charge compensation by the partial reduction of existing cations (Ni3+). The combination of these effects results in negligible overall expansion. Conversely, defect formation and interaction upon oxygen desorption occur within the sole structure of the conventional perovskite- and fluorite-related materials. For Co- and Fe-based oxides, oxygen vacancies are also formed (that should contract the cell), but cation reduction and cation–cation repulsion have a greater influence, leading to overall chemical expansion.
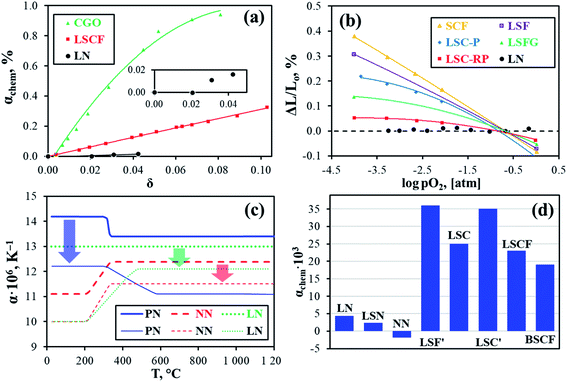 | ||
| Fig. 13 Chemical strain effects for some oxide materials: (a) chemical expansion coefficient as a function of the oxygen non- (over-) stoichiometry and (b) dimensional change as a function of oxygen partial pressure at 800 °C. These graphs presented in ref. 376 and 394 were prepared based on the data in ref. 395–400. (c) Temperature dependence of TECs for nickelates under oxidising (pO2 = 0.2 atm) and reducing (He, pO2 = 1 × 10−4 atm) atmospheres.72 (d) Chemical expansion coefficients for some oxygen electrodes at 800 °C in air.91,120,401 Abbreviations: LN = La2NiO4+δ, NN = Nd2NiO4+δ, PN = Pr2NiO4+δ, LSN = La1.8Sr0.2NiO4+δ, CGO = Ce0.9Gd0.1O1.95−δ, LSCF = La0.6Sr0.4Co0.2Fe0.8O3−δ, SCF = SrCo0.8Fe0.2O3−δ, LSF = La0.3Sr0.7FeO3−δ, LSF′ = La0.6Sr0.4FeO3−δ, LSC-P = La0.5Sr0.5CoO3−δ, LSC = La0.6Sr0.4CoO3−δ, LSC′ = La0.3Sr0.7CoO3−δ, LSFG = La0.3Sr0.7Fe0.6Ga0.4O3−δ, LSC-RP = LaSrCoO4+δ, and BSCF = Ba0.5Sr0.5Co0.2Fe0.8O3−δ. | ||
Interesting results were obtained by Flura et al.72 in their study on the structural parameters of basic nickelates (La2NiO4+δ, Nd2NiO4+δ, and Pr2NiO4+δ) utilising high-temperature XRD analysis, revealing the effects of temperature, measurement atmosphere and phase transitions on the thermo-chemical response of the corresponding ceramics (Fig. 13c). Based on this analysis, decreasing pO2 from the conventional value of air to ∼1 × 10−4 atm (helium atmosphere) resulted in an apparent decrease in TEC across the entire temperature range. Simultaneously, the TEC behaviour of Pr2NiO4+δ was distinct from that of other nickelates, where its phase transition (Bmab → I4/mmm) decreased the TECs, while the phase transitions for La2NiO4+δ and Nd2NiO4+δ (Fmmm → I4/mmm occurred around 150 and 500 °C, respectively) were found to increase the TECs with respect to the low-temperature range. The dilatometry data of Berger et al.118 confirm that the TECs decreased with a reduction in pO2 for a Pr-based nickelate (Pr2Ni0.9Co0.1O4+δ) within the low-temperature range of 12.2 × 10−6 K−1 at pO2 = 1 atm to 10.8 × 10−6 K−1 at pO2 = 1 × 10−2 atm. However, the TECs increased for the high-temperature range of 15.9 × 10−6 to 16.9 × 10−6 K−1 due to the oxygen desorption mechanism. The difference between these two works is the low-temperature structure of praseodymium nickelate (Bmab72 and Fmmm118), implying that this can also affect the achieved TECs and their relation relative to each other in different temperature regions.
5.3. Proton transportation
The RP phases of the first order, A2BO4+δ, are typically hyperstoichiometric compounds having an excess of interstitial oxygen in their structure. It is evident that the appearance of proton transport (if existing) in A2BO4+δ occurs with different mechanism(s) compared with the conventional acceptor-doped perovskites, where proton defects are formed under dissociative adsorption of water molecules by existing oxygen vacancies:402–404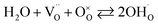 | (13) |
In contrast, the interstitial sites in the classical Ln2NiO4+δ compounds are important for proton transportation since H2O is more favourable for insertion at the interstitial sites, as shown in Fig. 14.
The protonation of oxides is generally achieved within a hydration process. The hydration equation for Ln2BO4+x can be written as:144
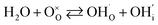 | (14) |
According to the equation, it seems that H2O is split into OH and H, while OH occupies the interstitial site and H attaches to the lattice oxygen. It should be noted that this is only an assumption since little research activity has been carried out to determine the exact mechanism for hydration and proton transportation in Ln2NiO4+δ materials. However, this assumption is reasonable if one considers the loss of the interstitial oxygen in the classical Ln2NiO4+δ (such as La2NiO4+x) at high temperatures,67 leaving the interstitial sites to be compensated by H2O. Although the loss of the interstitial oxygen was observed in La2NiO4+x, no observation of oxygen vacancy was reported in this study. Li et al.232 arrived at a similar conclusion. They studied the hydration ability of Pr2NiO4+x and found that the insertion of H2O at the interstitial sites is the most likely explanation for the protonation of this material. Although there are three possible ways for the formation of proton defects in Pr2NiO4+x, the very low H2 partial pressure at the cathode side eliminates the possibility of the direct combination of H2 with interstitial oxygen. They also revealed that the insertion of H2O at the oxygen vacancies through eqn (13) is not significant due to the very low oxygen vacancy content in the oxygen-rich environment for Pr2NiO4+x. Therefore, protonation can only occur with the insertion of H2O at the interstitial sites. However, differing from the opinion of Grimaud et al.144 that proton defects form at both interstitial sites and with lattice oxygen, Li et al. indicated that the H2O split reaction is only associated with the interstitial sites, with the reaction equation written as:
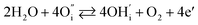 | (15) |
The difference in the opinion of researchers concerning the hydration process of Ln2NiO4+δ materials implies that this can be an interesting question for further study. Nevertheless, both studies agree that Ln2NiO4+δ has a different hydration mechanism in comparison with that for traditional ABO3−x perovskite oxides, while the interstitial sites play an important role in the protonation.
For the RP phases with pronounced basic properties (for example, BaLaInO4), the proton defects may be formed according to the following reactions:144,405–408
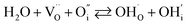 | (16) |
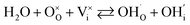 | (17) |
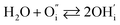 | (18) |
The first two reactions require vacancy (lattice or interstitial) defects. These defects occur to a considerable degree in nickelates, even those that are not doped by acceptors (eqn (19)). In detail, the heating of Ln2NiO4+δ leads to oxygen desorption, and correspondingly the appearance of the necessary vacancies (eqn (20)), which are theoretically capable of providing hydration. The third reaction does not require crystallographic or interstitial vacancies, allowing the formation of proton defects directly upon water interaction with interstitial oxygen. Tarasova et al.407 used IR spectroscopy to reveal the two energetically non-equivalent hydroxyl groups in BaLaInO4 and BaLaIn0.9Nb0.1O4+δ, confirming the possible realisation of eqn (14) and (15).
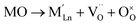 | (19) |
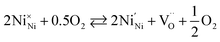 | (20) |
Grimaud et al.144 analysed the weight change of Pr2NiO4+δ in air with various pH2O levels (from 0.002 to 0.095 atm). This analysis revealed different weight changes depending on pH2O, but could not determine the actual proton concentration in praseodymium nickelate due to the difficulty associated with two simultaneous processes, hydration/dehydration and oxygen sorption/desorption.
Zhang et al.332 studied both oxygen migration and proton diffusivity in undoped and doped La2NiO4+δ using first-principle calculations, including analyses of relative energy, effective charge and electron density. They proposed a possible mechanism (Fig. 15) and found that proton transportation is unfavourable in a perfect La2NiO4+δ crystal; however, fast proton transport may occur for Co- and Cu-doped derivatives. It should be noted that unlike oxygen transport, proton migration is proposed to occur between the apical and equatorial oxygen ions with a resulting energy barrier of ∼1.1 eV, having five potential insertion sites on oxygen ions. This fact implies that the migration of protons between two rock-salt layers is unfavourable in nickelates in terms of a very large energy barrier, which is in accordance with the hydration of other RP phases.409,410 However, it is also noted that the calculated proton transport route, whether rotating or jumping, is associated with the lattice oxygen only, and no interstitial oxygen is considered. As discussed above, the interstitial oxygen can play an important role in the protonation for Ln2NiO4+δ, while the participation of interstitial oxygen may change the distance of proton migration, and thus alter the optimised migration routes. Therefore, it will be desirable to have a more comprehensive view concerning the first-principle calculations of proton transportation by also considering the interstitial oxygens. Although this aspect has yet to be considered in detail, it can be beneficial for an understanding of proton transportation in the Ln2NiO4+δ class of materials.
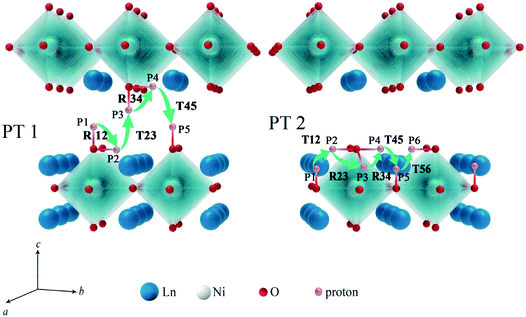 | ||
| Fig. 15 Schematic representations of two paths for proton transport (PT) between the inter-layer PT1 and inner-layer PT2. Pn (n = 1–6) are the possible proton locations and R and T refer to proton rotation and transfer, respectively.332 | ||
As can be seen above, the issue of the proton transportation in Ln2NiO4+δ phases remains open and should be evaluated in detail in future research.
5.4. Electrochemical activity towards oxygen- and proton-involving electrode processes
The electrochemical activity of electrodes depends on different parameters affecting the active zone where the electrochemical reactions occur. Among them, a number of parameters have a technology-related nature (particle size, tortuosity, and porosity), which regulates the triple phase boundary (TPB) length.411–415 Another set is related to the inherent properties of the phases, including oxygen and electron transport, which determine the activity of TPB. Although the complete separation of composition from technological parameters is a difficult task, some regularities can be revealed.Oxygen electrodes of SOFCs or PCFCs allow the realisation of the oxygen reduction reaction (ORR):
For SOFCs:
| O2(gas) + 4e−(electrode) ⇄ 2O2−(electrolyte) | (21) |
For PCFCs:
| O2(gas) + 4e−(electrode) + 4H+(electrolyte) ⇄ H2O(gas) | (22) |
This reaction occurs in the case of predominantly electronic conductors, such as Pt and LSM.416 When materials can also conduct oxygen-ions, they become mixed ionic-electronic conductors (MIECs).417–422 MIECs have a distinct advantage over electronic conductors since the ORR can occur at the surface of the ceramic electrode together with TPB:
 | (23) |
 | (24) |
Therefore, the TPB length is not limited by the contact of three phases, and this length can be extended due to additional pathways for oxygen molecules.
Despite having an ionic electrolyte type, the ORR comprises a combination of two consequent macroscopic processes, namely oxygen exchange at the surface of the electrodes and oxygen diffusion within the ceramic phase. On the one hand, these processes are characterised by kinetic parameters (oxygen exchange constant, k, and oxygen diffusion coefficient, D); on the other hand, they determine the polarisation resistance of the electrodes (Rp), as shown in particular by the ALS (Adler, Lane, Steele) model.423 Therefore, it is evident that there is a direct relation between Rp,k, and D. As can be seen from Fig. 16a, this correlation indeed exists, indicating that the lowest Rp values can be achieved for materials having the highest product of kD.
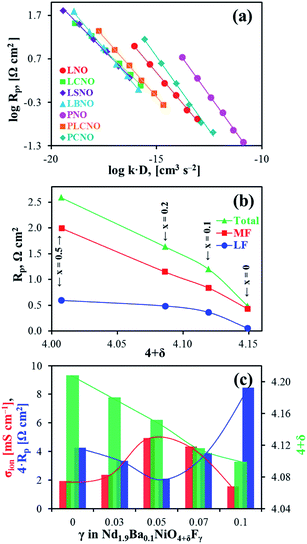 | ||
| Fig. 16 Correlation of polarisation resistances of Ln2NiO4+δ-based electrodes (Rp) measured on the symmetrical cells with proton-conducting electrolytes with kinetic parameters (kD), oxygen content (4 + δ) and ionic conductivity (σion) of nickelates. Panels (a), (b) and (c) were reproduced from works by Sadykov et al.,267 Grimaud et al.144 and Tarutin et al.,207 respectively. In panel (a) the following abbreviations are used: LNO = La2NiO4+δ, LCNO = La1.7Ca0.3NiO4+δ, LSNO = La1.7Sr0.3NiO4+δ, LBNO = La1.7Ba0.3NiO4+δ, PNO = Pr2NiO4+δ, PCNO = Pr1.7Ca0.3NiO4+δ, and PLCNO = Pr0.85La0.85Ba0.3NiO4+δ. Panel (b) highlights the results obtained for the PSN|BCY|PSN symmetrical cells at 600 °C and pH2O = 0.03 atm. Here, PSN = Pr2−xSrxNiO4+δ, and BCY = BaCe0.9Y0.1O3−δ. In panel (c), all the data are provided for 600 °C and the Rp values were obtained for symmetrical cells based on proton-conducting BaCe0.5Zr0.3Y0.1Y0.1O3−δ electrolyte. | ||
Grimaud et al. evaluated the electrochemical activity of Sr-doped Pr2NiO4+δ electrodes in the system with a BaCe0.9Y0.1O3−δ protonic conductor, and found that the optimal electrode performance was observed for the undoped Pr2NiO4+δ having a higher 4 + δ level.144 In detail, both partial (middle- and low-frequency) resistances, related with the charge transfer through the interface and the electrode reactions, respectively, decreased with 4 + δ growth (Fig. 16b). Most probably, the “Rp–(4 + δ)” relation is a special case that overlays with other tendencies. For example, no direct “Rp–(4 + δ)” correlation was revealed in the work of Tarutin et al.207 Instead, the electrochemical activity of the Nd2NiO4+δ-based electrodes was regulated by the oxygen-ionic conductivity (Fig. 16c) or oxygen diffusion coefficient, according to the Nernst–Einstein relationship.
Table 6 summarises the Ln2NiO4+δ-based electrodes obtained for symmetrical cells with proton-conducting electrolytes. Although the polarisation resistances vary across a wide range (∼3 orders of magnitude), the target values, after excluding the extreme examples, can be estimated to be ∼10, 3 and 0.5 Ω cm2 at 500, 600 and 700 °C, respectively, with a corresponding activation energy of ∼1 eV. Analysis of the activation energies shows that they drop in the range of ∼0.9–1.5 eV, implying that kinetic parameters (see Table 3) regulate the overall electrochemical activity of the electrodes.
| Electrode | Electrolyte | R p, Ω cm2 | E a, eV | Ref. | ||
|---|---|---|---|---|---|---|
| 500 °C | 600 °C | 700 °C | ||||
| La2NiO4+δ | BaCe0.9Y0.1O3−δ | 91.8 | 14.1 | — | 1.01 | 429 |
| La2NiO4+δ | BaCe0.9Y0.1O3−δ | 41.6 | 3.88 | — | 1.01 | 81 |
| La2NiO4+δ | La5.5WO11.25−δ | — | 35 | 11.5 | 1.36 | 265 |
| La2NiO4+δ | BaCe0.8Y0.2O3−δ | — | 20.8 | 4.94 | 1.01 | 349 |
| La2NiO4+δ | BaCe0.5Zr0.3Dy0.2O3−δ | 4.5 | 0.64 | 0.10 | 1.24 | 157 |
| La2Ni0.9Cu0.1O4+δ | BaCe0.5Zr0.3Dy0.2O3−δ | 4.7 | 0.92 | 0.21 | 0.96 | 157 |
| La2Ni0.8Cu0.2O4+δ | BaCe0.5Zr0.3Dy0.2O3−δ | 13.1 | 2.06 | 0.47 | 1.01 | 157 |
| La2Ni0.7Cu0.3O4+δ | BaCe0.5Zr0.3Dy0.2O3−δ | 42.3 | 7.90 | 1.20 | 1.08 | 157 |
| La1.5Pr0.5NiO4+δ | La5.5WO11.25−δ | — | 18.4 | 2.52 | 1.39 | 265 |
| 70%La2NiO4+δ –30%LaNi0.6Fe0.4O3−δ | BaZr0.1Ce0.7Y0.2O3−δ | — | 13.4 | 2.09 | 1.24 | 430 |
| 50%La2NiO4+δ –50%LaNi0.6Fe0.4O3−δ | BaZr0.1Ce0.7Y0.2O3−δ | — | 15.5 | 2.34 | 1.26 | 430 |
| 30%La2NiO4+δ –70%LaNi0.6Fe0.4O3−δ | BaZr0.1Ce0.7Y0.2O3−δ | — | 19.9 | 2.92 | 1.27 | 430 |
| 50%La2NiO4+δ –50%LaNi0.6Fe0.4O3−δ | BaZr0.1Ce0.7Y0.2O3−δ | — | 5.42 | 0.99 | 1.08 | 431 |
| La1.95Ba0.05NiO4+δ | BaCe0.5Zr0.3Dy0.2O3−δ | 37.9 | 5.56 | 1.11 | 1.08 | 432 |
| La1.7Ca0.3NiO4+δ | BaCe0.89Gd0.1Cu0.01O3−δ | — | 10.8 | 1.88 | 1.24 | 433 |
| La1.7Sr0.3NiO4+δ | BaCe0.89Gd0.1Cu0.01O3−δ | — | 5.99 | 0.74 | 1.47 | 433 |
| La1.7Ba0.3NiO4+δ | BaCe0.89Gd0.1Cu0.01O3−δ | — | 4.38 | 0.64 | 1.44 | 433 |
| La1.7Ba0.3NiO4+δ –BaCe0.89Gd0.1Cu0.01O3−δ | BaCe0.7Zr0.1Y0.2O3−δ | — | 1.52 | 0.21 | 1.35 | 433 |
| La1.7Ba0.3NiO4+δ –BaCe0.89Gd0.1Cu0.01O3−δ | BaCe0.89Gd0.1Cu0.01O3−δ | — | 4.64 | 0.62 | 1.35 | 359 |
| La1.7Ca0.3NiO4+δ –BaCe0.89Gd0.1Cu0.01O3−δ | BaCe0.89Gd0.1Cu0.01O3−δ | — | 6.14 | 1.14 | 1.21 | 359 |
| La1.7Sr0.3NiO4+δ –BaCe0.89Gd0.1Cu0.01O3−δ | BaCe0.89Gd0.1Cu0.01O3−δ | — | 9.59 | 0.82 | 1.34 | 359 |
| La1.7Ba0.3NiO4+δ –BaCe0.89Gd0.1Cu0.01O3−δ | CaZr0.95Sc0.05O3−δ | — | 278 | 45 | 1.14 | 434 |
| La1.7Ca0.3NiO4+δ –BaCe0.89Gd0.1Cu0.01O3−δ | CaZr0.95Sc0.05O3−δ | — | 666 | 128 | 1.20 | 434 |
| La1.7Sr0.3NiO4+δ –BaCe0.89Gd0.1Cu0.01O3−δ | CaZr0.95Sc0.05O3−δ | — | 213 | 30.0 | 1.24 | 434 |
| La1.2Sr0.8NiO4+δ | BaCe0.7Zr0.1Y0.2O3−δ | 1.58 | 0.29 | 0.07 | 0.93 | 435 |
| BaCe0.68Zr0.1Y0.1Yb0.1Cu0.02O3−δ infiltrated with 42.2 wt% La1.2Sr0.8NiO4−δ | BaCe0.68Zr0.1Y0.1Yb0.1Cu0.02O3−δ | 1.34 | 0.20 | 0.04 | 1.15 | 436 |
| LaSrNiO4+δ | BaCe0.9Y0.1O3−δ | — | 2.04 | 0.32 | 1.73 | 81 |
| Nd2NiO4+δ | BaCe0.9Y0.1O3−δ | 278 | 29.9 | 4.9 | 1.06 | 429 |
| Nd2NiO4+δ | BaCe0.9Y0.1O3−δ | 81.1 | 6.75 | 3.5 | 1.06 | 81 |
| Nd1.95Ba0.05NiO4+δ | BaCe0.5Zr0.3Dy0.2O3−δ | 24.6 | 3.42 | 0.45 | 1.25 | 432 |
| 60%Nd1.95NiO4+δ –40% BaZr0.1Ce0.7Y0.1Yb0.1O3−δ | BaZr0.1Ce0.7Y0.1Yb0.1O3−δ | — | 15.4 | 1.87 | 1.33 | 358 |
| 50%Nd1.95NiO4+δ –50% BaZr0.1Ce0.7Y0.1Yb0.1O3−δ | BaZr0.1Ce0.7Y0.1Yb0.1O3−δ | — | 9.55 | 1.47 | 1.24 | 358 |
| 50%Nd1.95NiO4+δ –50% BaZr0.1Ce0.7Y0.1Yb0.1O3−δ | BaZr0.1Ce0.7Y0.1Yb0.1O3−δ | — | 7.06 | 1.21 | 1.23 | 358 |
| Nd1.9Ba0.1NiO4+δ | BaZr0.3Ce0.5Y0.1Yb0.1O3−δ | 136 | 17.9 | 2.67 | 1.30 | 207 |
| Nd1.9Ba0.1NiO4+δ | BaCe0.5Zr0.3Dy0.2O3−δ | 115 | 15.9 | 1.8 | 1.40 | 437 |
| Nd1.9Ba0.2NiO4+δ | BaCe0.5Zr0.3Dy0.2O3−δ | 212 | 21.4 | 3.5 | 1.30 | 437 |
| Nd1.9Ba0.1NiO4+δF0.05 | BaZr0.3Ce0.5Y0.1Yb0.1O3−δ | 63.1 | 7.82 | 0.41 | 1.40 | 207 |
| Nd1.9Ba0.1NiO4+δF0.1 | BaZr0.3Ce0.5Y0.1Yb0.1O3−δ | 259 | 33.1 | 5.09 | 1.34 | 207 |
| NdSrNiO4+δ | BaCe0.9Y0.1O3−δ | 93.2 | 1.62 | 0.27 | 1.54 | 81 |
| Pr2NiO4+δ | BaCe0.9Y0.1O3−δ | 6.71 | 1.7 | 0.38 | 0.87 | 429 |
| Pr2NiO4+δ | BaCe0.9Y0.1O3−δ | 3.7 | 0.54 | 0.18 | 1.02 | 144 |
| Pr2NiO4+δ | BaCe0.9Y0.1O3−δ | 6.75 | 0.49 | 0.14 | 0.86 | 81 |
| Pr2NiO4+δ | BaCe0.9Y0.1O3−δ | 1.83 | 0.32 | 0.13 | 0.97 | 231 |
| Pr2NiO4+δ | BaCe0.9Y0.1O3−δ | 9.17 | 0.89 | 0.19 | 0.96 | 252 |
| (Pr0.9La0.1)2(Ni0.74Cu0.21Nb0.05)O4+δ | BaCe0.7Zr0.1Y0.2O3−δ | 5.07 | 0.77 | 0.17 | 1.03 | 360 |
| Pr1.9Ca0.1NiO4+δ | BaCe0.89Gd0.1Cu0.01O3−δ | — | 3.67 | 0.51 | 1.47 | 433 |
| Pr1.95Ba0.05NiO4+δ | BaCe0.5Zr0.3Dy0.2O3−δ | 10.0 | 0.62 | 0.19 | 1.19 | 434 |
| Pr1.9Sr0.1NiO4+δ | BaCe0.9Y0.1O3−δ | 9.92 | 1.16 | 0.21 | 1.22 | 144 |
| Pr1.8Sr0.2NiO4+δ | BaCe0.9Y0.1O3−δ | 14.5 | 1.92 | 0.39 | 1.18 | 144 |
| Pr1.5Sr0.5NiO4+δ | BaCe0.9Y0.1O3−δ | 30.1 | 2.7 | 0.45 | 1.26 | 144 |
| Pr1.2Sr0.8NiO4+δ | BaCe0.7Zr0.1Y0.2O3−δ | 3.47 | 0.57 | 0.13 | 0.98 | 435 |
The high noise of the listed Rp results is due to the technological features of the various materials. As can be seen, the compositions of the electrodes include basic nickelates and their doped or co-doped analogues and composites, which can be prepared by conventional means or utilising attractive techniques for the improvement of electroactivity (for example, infiltration). Moreover, depending on the compositions of the cells and external conditions, the Ln2NiO4+δ-based phases are reported to show proton transportation, thus constituting the class of triple-conducting materials.424–428,438 Thus, considering the above-mentioned factors, further elaboration will specify the important details affecting the electrochemical performance of the considered electrode materials.
Analysing the nature of ongoing electrode processes, it is rational to consider an algorithm for decoding the impedance spectra collected for symmetrical cells. According to Table 7, the corresponding spectra are described by two or three RQ-combinations (R is the partial resistance of Rp, while Q is the constant phase element). If the first of these combinations is mostly due to an ionic charge transfer between the electrolyte and electrode phases, the second (or third) combination(s) may be attributed to various processes, starting from the reduction of oxygen atoms and ending with molecular diffusion of gas components within a porous electrode. Again, this uncertainty in physical models occurs due to completely different electrochemical systems that have varying functional parameters.
| ET composition | ED composition | Conditions | Equivalent circuit | Description | Ref. |
|---|---|---|---|---|---|
| BaCe0.9Y0.1O3−δ | La2NiO4+δ | Wet air, pH2O = 0.03 atm | (RQ)MF–(RQ)LF | MF: ionic transfer reaction at the ED/ET interface | 81 |
| LF: oxygen dissociation and oxygen reduction reaction | |||||
| BaCe0.9Y0.1O3−δ | Pr2NiO4+δ | Wet air, pH2O = 0.03 atm | (RQ)MF–(RQ)LF | MF: H+ charge transfer at the ED/ET interface | 439 |
| LF: oxygen adsorption, oxygen dissociation and molecular diffusion | |||||
| BaCe0.9Y0.1O3−δ | Pr2NiO4+δ | Wet air, pH2O = 0.03–0.3 | (RQ)MF–(RQ)LF | MF: H+ charge transfer at the ED/ET interface | 144 |
| LF: water formation or water gas diffusion | |||||
| BaCe0.9Y0.1O3−δ | Pr2NiO4+δ | Wet air, pH2O = 0.2 | (RQ)MF–(RQ)LF | MF: H+ charge transfer at the ED/ET interface | 231 |
| LF: oxygen dissociative adsorption or oxygen reduction reaction | |||||
| BaZr0.7Ce0.2Y0.1O3−δ | La2NiO4+δ | Wet air, pH2O = 0.03 | (RQ)1–(RQ)2–(RQ)3 | 1: charge transfer at the ED/ET interface | 440 |
| 2: oxygen adsorption | |||||
| 3: molecular oxygen diffusion | |||||
| BaCe0.7Zr0.1Y0.2O3−δ (BCZY) | La2NiO4+δ and La2NiO4+δ –LaNi0.6Fe0.4O3−δ composites | — | (RQ)HF–(RQ)LF | HF: O2− charge transfer at the ED/ET interface | 430 |
| LF: oxygen adsorption, dissociation, charge transfer and molecular diffusion | |||||
| BCZY | BCZY–Ndr1.95NiO4+δ | Wet air, pH2O = 0.03 | (RQ)HF–(RQ)MF–(RQ)LF | HF: H+ charge transfer at the ED/ET interface | 358 |
| MF: oxygen reduction reaction | |||||
| LF: diffusion process of O− to TPB | |||||
| BCZY | La2NiO4+δ–LaNi0.6Fe0.4O3−δ | — | (RQ)HF–(RQ)LF | HF: O2− charge transfer at the ED/ET interface | 431 |
| LF: oxygen adsorption, dissociation, charge transfer and molecular diffusion | |||||
| BCZY | (Pr0.9La0.1)2Ni0.74Cu0.21Nb0.05O4+δ | — | (RQ)HF–(RQ)LF | HF: H+ charge transfer | 360 |
| LF: oxygen surface exchange | |||||
| BaCe0.5Zr0.3Dy0.2O3−δ | Nd1.95Ba0.05NiO4+δ | Dry air | (RQ)HF–(RQ)MF–(RQ)LF | HF: charge transfer across the electrode/electrolyte interface | 361 |
| MF: oxygen dissociation and surface diffusion | |||||
| LF: oxygen adsorption and gas-phase diffusion | |||||
| BCZY | Ln1.2Sr0.8NiO4+δ (Ln = La and Pr) | Ambient air | (RQ)HF–(RQ)LF | HF: bulk charge transfer process | 435 |
| LF: — | |||||
| BaCe0.6Zr0.2Y0.2O3−δ (BCZY′) | Pr2NiO4+δ–BCZY′ | Wet air, pH2O = 0.6 | (RQ)HF–(RQ)LF | HF: — | 232 |
| LF: — |
Among the numerous publications, there are a few works in which the authors tried to distinguish the factors associated with the inherent properties of nickelate phases and their microstructural parameters from each other.
For example, Grimaud et al.144 studied the simultaneous effects of pO2 and pH2O on the Rp of the Pr2NiO4+δ electrode at 600 °C. According to their results, Rp comprises the sum of two (medium- (MF) and low- (LF) frequency) processes. RMF is not affected by pH2O, but depends on the variation of pO2 according to the following relation: RMF ∼ (pO2)−1/4. On the contrary, the power function, n, for the RLF ∼ (pO2)−n relation changes from 0.44 for dry air (pH2O = 0.006 atm) to 0.61 for wet air (pH2O = 0.20 atm) due to the involved pH2O-associated processes.
In the next work of Grimaud et al.,441 special attention was paid to the electrode performance of Pr2NiO4+δ depending on the variation in pH2O and microstructural parameters. For a porous state of Pr2NiO4+δ, the following tendencies were observed: RMF ∼ (pH2O)−1/2 and RLF ∼ (pH2O)−1. Their study indicated that the H2O-assisted mechanism occurred for the considered system, namely proton charge transfer in the former case and water formation in the latter case. When the Pr2NiO4+δ electrode layer was prepared in a dense form, the first relation was again observed, confirming the ability of the nickelate to demonstrate proton transportation. However, no dependence (n = 0) was observed between RLF and pH2O that could be explained in terms of the limited diffusion of water molecules inside the electrodes.
Quarez et al.357 considered the effects of several parameters on the electrochemical activity of the same electrode, i.e. calcination temperature to fabricate the PN|LW|PN symmetrical cells, the thickness of the PN electrodes, and weight amount of LW phases in the PN–LW electrode composites (here PN = Pr2NiO4+δ and LW = La27.15W4.85O55+δ). Temperature- and thickness-related effects were predictable, where an improvement in electrochemical activity occurred for the highly porous electrodes (prepared at the lowest sintering temperature of 800 °C) and with the lowest thickness (12 μm against 24 and 36 μm for the other cases), implying that the determining role is played by molecular diffusion. However, no positive composition effect was observed upon the addition of the LW phase; therefore, composite materials do not always provide an incremental improvement in electrode functionality.
Technological effects were also evaluated by Solís et al.265 Here it was found that among three sintering temperatures (1050 °C, 1100 °C and 1150 °C), the best electrochemical activity for La1.5Pr0.5Ni0.8Co0.2O4+δ electrodes was achieved for the lowest temperature, confirming the crucial effect of electrode porosity.
From the provided examples, it is clear that the electrochemical activity of nickelates can be quite easily tuned by technological factors, especially sintering temperature, ensuring a certain electrode porosity. However, the performance of these electrodes can be also regulated by means of engineering techniques aimed at extending the surface of the electrochemically active zone.
Fig. 17 shows some of the main strategies associated with increasing the number of active parts in electrochemical reactions. These strategies aim at introducing an additional charge carrier together with the electron carrier, i.e. either oxygen-ions, protons or both.
A gradual complication of the provided scheme consists of substituting a pure electron conductor (Fig. 17a) with a mixed ionic-electronic conductor (MIEC) with O2−-transportation (Fig. 17b). Many complex oxides belong to these MIECs, including cobaltites,442–444 ferrites,434–448 nickelates52,234,379 having simple and layered structures, and solid solutions based on these classes.449–452 Utilisation of MIECs deposited on proton-conducting electrolytes allows the TPB to be extended by an MIEC phase perimeter limited by the electrolyte surface.
Another strategy for increasing the TPB involves the development of composite systems. Considering (O2−/h˙)-MIEC as an example, three different types of composites can be formed (Fig. 17c–e), consisting of an MIEC combined with an electronic, oxygen-ionic or protonic conductor. The last combination seems to represent the most promising variant since it allows transportation of three different types of charge carriers, some of which exist within one phase, while others exist within the second phase.
An increase in the TPB can be realised by means of nano-scaled sediments formed purposefully on the surface of the main porous phases (Fig. 17f and g). This method, which is known as infiltration, is widely used to achieve high performance electrodes.25,453–455 However, it should be noted that the number of active parts determining the TPB length may be lower than that for single-phase MIECs (see the comparison of Fig. 17b and g). Nevertheless, in most cases, this accelerates the electrochemical reactions, thus promoting the higher performance of electrodes and cells based thereupon.
The last example represents (Fig. 17h) a case when the electrochemically active zone for triple-conducting materials is dramatically increased, where a double phase boundary (DPB) replaces the TPB, which is limited by the contact of three phases. Specifically, the entire surface of the single-phase triple-conducting electrode becomes active towards the oxygen reduction and water evolution reactions. In this case, there are three types of charge carriers (as in the case of the composites presented in Fig. 17e), which simultaneously exist within the same phase.
The ability of these phases to show triple-conducting behaviour is presently under discussion. For example, there are reports confirming the hydration of the nickelate phases;144,441 however, no direct confirmation of the data has been presented. Moreover, the term “triple-conducting” should mean that all three partial (electronic, oxygen-ionic and protonic) conductivities are comparable. This has not been achieved for any state-of-the-art electrode system at 600–800 °C, where only temperatures as low as 200–400 °C allow the promotion of sufficient mobility/concentration of protons.456–458
To move from theoretical to experimental aspects, the research data corresponding to the above-mentioned examples of electrode systems is presented in Table 8. According to these observations, strategies related to infiltration and the design of triple-conducting materials are identified as the most reliable, resulting in the achievement of a polarisation resistance of less than 1 Ω cm2 at 600 °C. It is important to note that Section 5.4 reports data obtained for symmetrical cells, when the opposite electrode sides operate under the same conditions. In the real regimes of PCFCs or PCECs, only one electrode side operates under oxidising conditions, while the other is fed by reducing gases. Therefore, the performance of Ln2NiO4+δ-based electrodes also needs to be considered under real conditions.
| Case (see Fig. 17) | Example, EDa|ETb | Performance | Ref. | Remarks |
|---|---|---|---|---|
| R p, Ω cm2 | ||||
| a Electrode (ED) abbreviations: PSN = Pr1.4Sr0.6NiO4+δ, LN = La2NiO4+δ, NBN = Nd1.95Ba0.05NiO4+δ, LNF = LaNi0.6Fe0.4O3−δ, NN = Nd1.95NiO4+δ, LBN = La1.7Ba0.3NiO4+δ, PLNCN = (Pr0.9La0.1)2Ni0.74Cu0.21Nb0.05O4+δ, PN = Pr2NiO4+δ. b Electrolyte (ET) abbreviations: BCY = BaCe0.9Y0.1O3−δ, BCY20 = BaCe0.8Y0.2O3−δ, BCZD = BaCe0.5Zr0.3Dy0.2O3−δ, BCZY = BaCe0.7Zr0.1Y0.2O3−δ, SDC = Ce0.8Sm0.2O2−δ, BCGC = BaCe0.89Gd0.1Cu0.01O3−δ, BCZYYb = BaCe0.7Zr0.1Y0.2Yb0.1O3−δ, BZCY = BaZr0.7Ce0.2Y0.1O3−δ, inf is the infiltration, and bb is the backbone. | ||||
| Single-phase materials | ||||
| (b) | LN|BCY20 | 20.8 | 349 | |
| NBN|BCZD | 13.9 | 361 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Composite materials | ||||
| (c) | LN–LNF|BCZY | 13.4 | 430 | LN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LNF = 7 LNF = 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (wt ratio) 3 (wt ratio) |
| LN–LNF|BCZY | 19.9 | 430 | LN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LNF = 3 LNF = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (wt ratio) 7 (wt ratio) |
|
| LN–LNF|BCZY | 5.4 | 431 | LN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LNF = 1 LNF = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (wt ratio) 1 (wt ratio) |
|
| (d) | LNF–SDC|BCZY | 7.2 | 431 | LNF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SDC = 1 SDC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (wt ratio) 1 (wt ratio) |
| LBN–SDC|BCGC | 7.8 | 433 | LBN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SDC = 1 SDC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (wt ratio) + LNF current collector 1 (wt ratio) + LNF current collector |
|
| (e) | NN–BCZYYb|BCZYYb | 7.24 | 358 | NN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BCZYYb = 1 BCZYYb = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (wt ratio) 1 (wt ratio) |
| LBN–BCGC|BCGC | 4.6 | 359 | LBN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BCGC = 1 BCGC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (wt ratio) 1 (wt ratio) |
|
| LBN–BCGC|BCGC | 4.3 | 433 | LBN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BCGC = 1 BCGC = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (wt ratio) + LNF current collector 1 (wt ratio) + LNF current collector |
|
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Infiltration | ||||
| (f) | LNFinf–LNbb|BCZY | 0.31 | 459 | 31 wt% of infiltration component |
| (g) | LNinf–BZCYbb|BZCY | 29.3 | 440 | |
| PLNCNinf–BCZYbb|BCZY | 0.76 | 360 | 46.1 wt% of infiltration component | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Single-phase triple-conducting material | ||||
| (h) | PN|BCY | 0.89 | 144 | pH2O = 0.03 atm (0.31 Ω cm2 at pH2O = 0.30 atm) |
6. Applied peculiarities of Ln2NiO4+δ-based electrodes in proton-conducting electrochemical cells
This section highlights the features of applying Ln2NiO4-based electrodes in PCFCs or PCECs. Firstly, open-circuit voltage (OCV) conditions will be considered, and then the performance of the electrodes will be evaluated under electrochemical cell operating conditions.6.1. OCV conditions
The OCV conditions of any electrochemical cell represent important information since they allow conclusions to be formulated regarding cell integrity and electrolyte electron conductivity. Although OCV measurements (UOC = ∼1 V) are far from the conditions corresponding to the maximum power density (∼0.5 V) or thermoneutral voltage (∼1.3 V), the electrochemical characterisation of PCFCs/PCECs is almost always performed at OCV. In detail, the impedance spectra are measured at OCV applying a low acceleration voltage (20–50 mV). The spectra obtained in this way provide the corresponding information on ohmic resistance (RO) and polarisation resistance of the electrodes (Rp).Considering RO, the quality of the electrolytes used (in terms of composition and fabrication technique) can be estimated as follows:
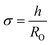 | (25) |
| Fuel electrode | Electrolytea (thickness) | Oxygen electrodeb | Electrochemical characteristics | Year | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|
| U OC, V | R O, Ω cm2 | R p, Ω cm2 | R t, Ω cm2 | σ, mS cm−1 | |||||
| a Electrolyte abbreviations: BCY = BaCe0.9Y0.1O3−δ, BCZY = BaCe0.7Zr0.1Y0.2O3−δ, BZY = BaZr0.85Y0.15O3−δ, BCZY44 = BaCe0.4Zr0.4Y0.2O3−δ, BCZY53 = BaCe0.5Zr0.3Y0.2O3−δ, BCZD = BaCe0.5Zr0.3Dy0.2O3−δ, BCZY15 = BaCe0.55Zr0.3Y0.15O3−δ, BCZY62 = BaCe0.6Zr0.2Y0.2O3−δ, BCGC = BaCe0.89Gd0.1Cu0.01O3−δ, BCZYYb = BaCe0.7Zr0.1Y0.2Yb0.1O3−δ, LC = La2Ce2O7, and BCZYYC = BaCe0.68Zr0.1Y0.1Yb0.1Cu0.02O3−δ. b Electrode abbreviations: PN = Pr2NiO4+δ, NN = Nd2NiO4+δ, LN = La2NiO4+δ, LCN = La1.9Ca0.1NiO4+δ, LNF = LaNi0.6Fe0.4O3−δ, PLNCN = (Pr0.9La0.1)2Ni0.74Cu0.21Nb0.05O4+δ, NBN = Nd1.95Ba0.05NiO4+δ, PS0.8N = Pr1.2Sr0.8NiO4+δ, LS0.8N = La1.2Sr0.8NiO4+δ, PCN = Pr1.7Ca0.3NiO4+δ, LSNF = La1.2Sr0.8Ni0.6Fe0.4O4+δ, PB10N = Pr1.9Ba0.1NiO4+δ, LNC = La2Ni0.8Cu0.2O4+δ, LCN = La1.9Ca0.1NiO4+δ, and PB5N = Pr1.85Ba0.05NiO4+δ. c Functional electrode (PCN–BCGC) is used together with the LNF collector layer. d Functional fuel electrode (reduced PB10N–BCZD) is used together with the supported fuel electrode layer (Ni–BCZD). | |||||||||
| Ni–BCY | BCY (40 μm) | PN | 1.15 | 1.84 | 2.76 | 4.60 | 2.2 | 2010 | 252 |
| Ni–BCY | BCY (27 μm) | NN | 1.06 | — | — | 4.8 | — | 2013 | 460 |
| Ni–BCY | BCY (50 μm) | PN | 1.09 | 0.81 | 0.8 | 1.61 | 6.2 | 2014 | 461 |
| Ni–BCZY | BCZY (20 μm) | LN | 1.04 | 0.64 | 0.96 | 1.60 | 3.1 | 2014 | 430 |
| Ni–BCZY | BCZY (20 μm) | 70%LN–30% LNF | 1.04 | 0.44 | 0.49 | 0.93 | 4.5 | 2014 | 430 |
| Ni–BCZY | BCZY (20 μm) | 50% LN–50% LNF | 1.05 | 0.50 | 0.51 | 1.01 | 4.0 | 2014 | 430 |
| Ni–BCZY | BCZY (20 μm) | 30% LN–70% LNF | 1.04 | 0.53 | 0.57 | 1.10 | 3.8 | 2014 | 430 |
| Ni–BCZY | BCZY (24 μm) | 50% LN–50% LNF | 1.04 | 0.54 | 0.59 | 1.13 | 4.4 | 2015 | 431 |
| Ni–BZY | BCZY44 (5 μm) | PN | 1.03 | 0.77 | 1.00 | 1.77 | 0.6 | 2015 | 462 |
| Ni–BCZY | BCZY (12 μm) | PLNCN | 1.01 | 0.33 | 0.32 | 0.65 | 3.6 | 2017 | 360 |
| Ni–BCZD | BCZD (15 μm) | NBN | 0.97 | 0.89 | 0.44 | 1.33 | 1.7 | 2018 | 361 |
| Ni–BCZY | BCZY (15 μm) | PS0.8N | 1.03 | 0.40 | 2.17 | 2.57 | 3.7 | 2018 | 435 |
| Ni–BCZY | BCZY (15 μm) | LS0.8N | 1.03 | 0.34 | 1.48 | 1.82 | 4.4 | 2018 | 435 |
| Ni–BCZY15 | BCZY15 (5 μm) | PN | 1.02 | 0.08 | 0.28 | 0.36 | 6.2 | 2018 | 362 |
| Ni–BCZY | BCZY (20 μm) | LN | 1.03 | 0.36 | 0.88 | 1.24 | 5.5 | 2018 | 459 |
| Ni–BCZY | BCZY (20 μm) | LN–13 wt% LNF | 1.03 | 0.37 | 0.36 | 0.73 | 5.4 | 2018 | 459 |
| Ni–BCZY | BCZY (20 μm) | LN–23 wt% LNF | 1.01 | 0.37 | 0.34 | 0.71 | 5.4 | 2018 | 459 |
| Ni–BCZY | BCZY (20 μm) | LN–31 wt% LNF | 0.99 | 0.29 | 0.31 | 0.60 | 6.8 | 2018 | 459 |
| Ni–BCZY | BCZY (20 μm) | LN–37 wt% LNF | 0.99 | 0.41 | 0.54 | 0.95 | 4.9 | 2018 | 459 |
| Ni–BCZY62 | BCZY62 (20 μm) | PN | 0.98 | 0.22 | 0.71 | 0.93 | 9.0 | 2018 | 232 |
| Ni–BCGC | BCGC (25 μm) | PCN–BCGC|LNF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
1.08 | — | — | 1.86 | — | 2018 | 463 |
| Ni–BCZY | BCZY (15 μm) | LSNF | 1.06 | 0.29 | 0.41 | 0.70 | 5.1 | 2019 | 363 |
| Ni–BCZD |PB10N–BCZDd | BCZD (25 μm) | PB10N–BCZD | 1.08 | 0.52 | 0.39 | 0.91 | 4.8 | 2019 | 364 |
| Ni–BCZYYb | BCZYYb (15 μm) | PN | 0.99 | 0.28 | 0.58 | 0.86 | 5.3 | 2019 | 365 |
| Ni–BCZYYb | LC|BCZYYb (20 μm) | PN | 0.95 | 0.49 | 1.11 | 1.60 | 4.0 | 2019 | 365 |
| Ni–BCZYYb | BCZYYb (35 μm) | LNC | 1.05 | 0.72 | 0.70 | 1.42 | 4.8 | 2019 | 157 |
| Ni–BCZD | BCZD (25 μm) | PB5N|LNF | 1.02 | 0.37 | 0.25 | 0.62 | 6.7 | 2020 | 464 |
| Ni–BCZYYC | BCZYYC (13 μm) | LS0.8N–BCZYYC | 1.01 | 0.19 | 0.36 | 0.55 | 6.8 | 2020 | 436 |
| Ni–BCZY53 | BCZY53 (—) | LCN | 1.02 | 0.18 | 0.28 | 0.46 | — | 220 | 465 |
| Ni–BCZD | BCZD (30 μm) | PB10N–BCZD | 1.03 | 0.43 | 0.18 | 0.61 | 8.3 | 2020 | 466 |
Considering Rp, the main strategies for improving the electrode performance were described in Section 5.4. As shown in Table 9, the polarisation resistances of Ln2NiO4-based electrodes are quite low, mostly reaching values below 1 Ω cm2 at 600 °C. The best results were achieved by An et al.362 utilising an undoped Pr2NiO4+δ electrode and Sun et al.436 utilising an infiltrated La1.2Sr0.8NiO4−δ–BaCe0.68Zr0.1Y0.1Yb0.1Cu0.02O3−δ electrode. Looking ahead, it can be noted that these cells also exhibit the highest performance in fuel cell (Table 10) and electrolysis cell (Table 11) operation modes. However, these correlations are not always observed since the electrode response may be considerably (and differently) altered with a variation in the bias. A vivid example of this conclusion was shown in the work by Danilov et al.,471 where the impedance data for a protonic ceramic electrochemical cell with a Pr1.95Ba0.05NiO4+δ (PBN) electrode was collected not only for OCV, but for the fuel cell (FC) and electrolysis cell (EC) regimes. As can be seen, the overall polarisation resistance of the electrodes monotonously decreased with an increase in bias at low measured temperatures, having a maximum OCV at higher temperatures. This peculiarity indicates that the impedance spectroscopy measurements should be performed under real voltage regimes instead of OCV.
| Fabrication details | Anode | Electrolyte a (thickness) | Cathodeb | P max, mW cm−2 | Year | Ref. | ||
|---|---|---|---|---|---|---|---|---|
500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C °C |
600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C °C |
700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C °C |
||||||
| a Electrolyte abbreviations: BCY = BaCe0.9Y0.1O3−δ, BCZY = BaCe0.7Zr0.1Y0.2O3−δ, BZY = BaZr0.85Y0.15O3−δ, BCZY44 = BaCe0.4Zr0.4Y0.2O3−δ, BCZD = BaCe0.5Zr0.3Dy0.2O3−δ, BCZY15 = BaCe0.55Zr0.3Y0.15O3−δ, BCZY62 = BaCe0.6Zr0.2Y0.2O3−δ, BCGC = BaCe0.89Gd0.1Cu0.01O3−δ, BCZYYb = BaCe0.7Zr0.1Y0.2Yb0.1O3−δ, LC = La2Ce2O7, and BCZYYC = BaCe0.68Zr0.1Y0.1Yb0.1Cu0.02O3−δ. b Electrode abbreviations: PN = Pr2NiO4+δ, NN = Nd2NiO4+δ, LN = La2NiO4+δ, LNF = LaNi0.6Fe0.4O3−δ, PLNCN = (Pr0.9La0.1)2Ni0.74Cu0.21Nb0.05O4+δ, NBN = Nd1.95Ba0.05NiO4+δ, PS0.8N = Pr1.2Sr0.8NiO4+δ, LS0.8N = La1.2Sr0.8NiO4+δ, PCN = Pr1.7Ca0.3NiO4+δ, LSNF = La1.2Sr0.8Ni0.6Fe0.4O4+δ, PB10N = Pr1.9Ba0.1NiO4+δ, LNC = La2Ni0.8Cu0.2O4+δ, and PB5N = Pr1.85Ba0.05NiO4+δ. c Functional cathode (PCN–BCGC) is used together with the LNF collector layer. d Functional anode (reduced PB10N–BCZD) is used together with the supported anode layer (Ni–BCZD). | ||||||||
| Co-pressing/screen-printing | Ni–BCY | BCY (40 μm) | PN | — | 96 | — | 2010 | 252 |
| Tape-casting/screen-printing | Ni–BCY | BCY (27 μm) | NN | — | 60 | — | 2013 | 460 |
| Co-pressing/screen-printing | Ni–BCY | BCY (50 μm) | PN | — | 184 | — | 2014 | 461 |
| Co-pressing/painting | Ni–BCZY | BCZY (20 μm) | LN | — | 196 | 398 | 2014 | 430 |
| Co-pressing/painting | Ni–BCZY | BCZY (20 μm) | 70% LN–30% LNF | — | 298 | 590 | 2014 | 430 |
| Co-pressing/painting | Ni–BCZY | BCZY (20 μm) | 50% LN–50% LNF | — | 273 | 532 | 2014 | 430 |
| Co-pressing/painting | Ni–BCZY | BCZY (20 μm) | 30% LN–70% LNF | — | 264 | 486 | 2014 | 430 |
| Co-pressing/painting | Ni–BCZY | BCZY (24 μm) | 50% LN–50% LNF | — | 266 | 490 | 2015 | 431 |
| Co-pressing/spin coating | Ni–BZY | BCZY44 (5 μm) | PN | — | 102 | 234 | 2015 | 462 |
| Tape-calendering/painting | Ni–BCZD | BCZD (30 μm) | LN | — | 130 | 215 | 2016 | 467 |
| Co-pressing/screen-printing | Ni–BCZY | BCZY (12 μm) | PLNCN | — | 420 | 770 | 2017 | 360 |
| Co-pressing/screen-printing | Ni–BCZY | BCZY (15 μm) | PS0.8N | — | 127 | 352 | 2018 | 435 |
| Co-pressing/screen-printing | Ni–BCZY | BCZY (15 μm) | LS0.8N | — | 223 | 461 | 2018 | 435 |
| Co-pressing/screen-printing | Ni–BCZY15 | BCZY15 (5 μm) | PN | 240 | 560 | — | 2018 | 362 |
| Co-pressing/painting | Ni–BCZY | BCZY (20 μm) | LN | — | 210 | 461 | 2018 | 459 |
| Co-pressing/painting | Ni–BCZY | BCZY (20 μm) | LN–13 wt% LNF | — | 361 | 623 | 2018 | 459 |
| Co-pressing/painting | Ni–BCZY | BCZY (20 μm) | LN–23 wt% LNF | — | 369 | 877 | 2018 | 459 |
| Co-pressing/painting | Ni–BCZY | BCZY (20 μm) | LN–31 wt% LNF | — | 369 | 969 | 2018 | 459 |
| Co-pressing/painting | Ni–BCZY | BCZY (20 μm) | LN–37 wt% LNF | — | 302 | 802 | 2018 | 459 |
| Dry-pressing/dip-coating/screen-printing | Ni–BCZY | BCZY (16 μm) | LS0.8N | — | 220 | 460 | 2018 | 468 |
| Dry-pressing/dip-coating/screen-printing | Ni–BCZYYC | BCZYYC (13 μm) | LS0.8N | — | 250 | 680 | 2018 | 469 |
| Tape-calendering/painting | Ni–BCGC | BCGC (25 μm) | PCN–BCGC|LNFc | — | 61 | 132 | 2018 | 463 |
| Co-pressing/painting | Ni–BCZY | BCZY (15 μm) | LSNF | 139 | 421 | 782 | 2019 | 363 |
| Tape-calendering | Ni–BCZD|PB10N –BCZDd | BCZD (25 μm) | PB10N–BCZD | — | 305 | 395 | 2019 | 364 |
| Tape-calendaring/spraying | Ni–BCZYYb | BCZYYb (35 μm) | LNC | — | 200 | 340 | 2019 | 157 |
| Co-pressing/screen-printing | Ni–BCZYYC | BCZYYC (13 μm) | LS0.8N–BCZYYC | — | 540 | 1220 | 2020 | 436 |
| Anodea | Electrolyteb (thickness) | Cathode | U OC, V | i @1.3 V, mA cm−2 | Year | Ref. | ||
|---|---|---|---|---|---|---|---|---|
| 600 °C | 700 °C | 600 °C | 700 °C | |||||
| a Anode abbreviations: LN = La2NiO4+δ, NBN = Nd1.95Ba0.05NiO4+δ, PS0.8N = Pr1.2Sr0.8NiO4+δ, LS0.8N = La1.2Sr0.8NiO4+δ, PN = Pr2NiO4+δ, PB10N = Pr1.9Ba0.1NiO4+δ, PB5N = Pr1.85Ba0.05NiO4+δ, LNF = LaNi0.6Fe0.4O3−δ, and NBNF = Nd1.9Ba0.1NiO4+δF0.05. b Electrolyte abbreviations: BCZD = BaCe0.5Zr0.3Dy0.2O3−δ, BCZY = BaCe0.7Zr0.1Y0.2O3−δ, BCZD35 = BaCe0.3Zr0.5Dy0.2O3−δ, BCZY62 = BaCe0.6Zr0.2Y0.2O3−δ, BCZYYC = BaCe0.68Zr0.1Y0.1Yb0.1Cu0.02O3−δ, BCZYYb = BaCe0.7Zr0.1Y0.2Yb0.1O3−δ, LC = La2Ce2O7, and BCZYYb53 = BaZr0.3Ce0.5Y0.1Yb0.1O3−δ. c Functional cathode (reduced PB10N–BCZD) is used together with the supported cathode layer (Ni–BCZD). d Functional anode (PCN–BCGC) is used together with the LNF collector layer. | ||||||||
| LN | BCZD (30 μm) | Ni–BCZD | 1.06 | 1.00 | 180 | 300 | 2016 | 467 |
| NBN | BCZD (15 μm) | Ni–BCZD | 0.97 | 0.94 | 155 | 400 | 2018 | 361 |
| PS0.8N | BCZY (15 μm) | Ni–BCZY | 1.03 | 0.97 | 350 | 1120 | 2018 | 435 |
| LS0.8N | BCZY (15 μm) | Ni–BCZY | 1.01 | 0.98 | 420 | 1410 | 2018 | 435 and 468 |
| NBN–BCZD35 | BCZD35 (50 μm) | Ni–BCZD35 | — | 0.9 | — | 542 | 2018 | 470 |
| PN | BCZY62 (20 μm) | Ni–BCZY62 | 0.98 | 0.93 | 345 | 950 | 2018 | 232 |
| LS0.8N | BCZYYC (13 μm) | Ni–BCZYYC | — | 1.01 | 590 | 1960 | 2018 | 469 |
| PB10N–BCZD | BCZD (25 μm) | Ni–BCZD| PB10N–BCZDc | 1.08 | 1.01 | 295 | 535 | 2019 | 364 |
| PN | BCZYYb (15 μm) | Ni–BCZYYb | 0.99 | 0.95 | 620 | 1643 | 2019 | 365 |
| PN | LC|BCZYYb (20 μm) | Ni–BCZYYb | 0.95 | 0.90 | 330 | 975 | 2019 | 365 |
| PB5N|LNFd | BCZD (25 μm) | Ni–BCZD | 1.02 | 0.94 | 610 | 855 | 2020 | 464 |
| NBNF | BCZYYb53 (25 μm) | BCZYYb53 | 0.99 | 0.93 | 360 | 1370 | 2020 | 207 |
| LS0.8N–BCZYYC | BCZYYC (13 μm) | Ni–BCZYYC | 1.01 | 0.99 | 1040 | 3020 | 2020 | 436 |
6.2. Fuel cell and electrolysis cell operation modes
Tables 10 and 11 list the evolution of existing results on the application of Ln2NiO4-based electrodes with proton-conducting electrolytes. According to the data, it can be seen that the intensive activity initiated in 2017 formed the basis for the work published in the following year. Although some research groups have demonstrated superior results for both PCFCs and PCECs, a significant number of works showed that the maximum power densities range between 200 and 400 mW cm−2 (fuel cell mode) at 600 °C, while the current densities range between 200 and 600 mA cm−2 (electrolysis mode) at 1.3 V and the same temperature.Principally, the literature data reports more promising performances, which can be associated with the utilisation of highly conductive electrode materials, such as simple and double cobaltites and their derivatives.472–476 Considering the current distribution, this indeed promotes the efficient supply or removal of electrons from the TPB regions to an external electrical circuit. However, as was mentioned in Section 5.2, even if excellent results are achieved for the first time, Co-based oxide-based electrodes suffer from thermo-mechanical incompatibility. Consequently, thermo-cycling and the long-term operation of cells featuring these electrodes may be unsuccessful.
The problem of the low conductivity of nickelates (below 100 S cm−1 for a gas-tight body) can be solved using additional current collector layers (for example, (La,Sr)MnO3, La(Ni,Fe)O3, Pt), which improve the current distribution characteristics by covering the surface of the origin electrode.
Generally, the achieved average levels are quite promising for the development of intermediate-temperature PCFCs and PCECs in terms of their up-scaling and durability.460,461 For example, Dailly and Marrony460 showed that a 3.5 × 3.5 cm2 PCFC with an Nd2NiO4+δ cathode exhibits no visible degradation at 600 °C for over 950 h.
7. Conclusion and future perspectives
The materials of the Ln2NiO4+δ-related class represent a promising alternative to the conventional ABO3 electrodes in terms of their application in solid oxide electrochemical cells, including protonic ceramic fuel cells (PCFCs) and protonic ceramic electrolysis cells (PCECs). Exhibiting high structural flexibility towards different types of doping, these layered nickelates enable purposeful tailoring of functional properties important for prospective application, including high phase stability, chemical and mechanical compatibility, and good mixed ionic-electronic conductivity and electrochemical performance.Numerous experimental results published over the last five years have shown that lanthanide nickelate-based electrodes demonstrate quite good performances, with polarisation resistance values as low as 0.3–1 Ω cm2 at 600 °C (open circuit voltage regime of PCFCs and PCFCs), which can remain stable over long term operation. These results constitute a possible basis for the scalable fabrication of durable PCFCs/PCECs.
However, although this review describes many advantages of layered nickelates in comparison with other possible oxygen electrodes, a number of pending issues still need to be solved/clarified:
(1) Degree of hydration/protonation of Ln2NiO4+δ-based materials. Revealing the effect of type and concentration of dopant(s) on the concentration of protons. Identification of mechanisms of proton transport in the layered phases. This information is needed for the design of triple-conducting materials having a high active electrode zone towards occurring (oxygen- and hydrogen-involved) electrochemical reactions. In addition, the mechanism studies for proton migration in layered nickelates are interesting and potentially important for proton transportation in oxides. Since oxygen vacancies are usually regarded as the prerequisite for hydration/protonation, the interstitial oxygens in layered nickelates may play a different role in the proton migration procedure in comparison with that in oxygen vacancy-containing oxides. This difference not only leads to a different strategy for designing materials, but also may inspire scientists to have a better understanding of the mechanism for proton migration since the whole landscape has not been revealed to date.
(2) Rational design of microstructural parameters. The provided analysis was carried out considering macroscopic parameters such as polarisation resistance. On the one hand, these parameters depend on internal solid phase properties; on the other hand, the performance is also affected by the electrode structure. Currently, no general information regarding the morphological properties of Ln2NiO4+δ-based electrodes exists in the literature. Although nano-structuring of electrodes is a widely employed approach for improving the electrode performance, the high calcination temperatures for achieving the desired Ln2NiO4+δ can be detrimental for the formation and/or maintenance of the nanostructure of the electrode. Thus, the use of advanced preparation techniques to lower the phase formation temperatures and shorten the dwell time can be beneficial for the formation of nanostructured electrodes with improved TPBs. Moreover, advanced electrode development techniques (three-dimensional ordered pore, finger-like, and nanowires-based structures),477–480 which deserve further studies, have not been used for Ln2NiO4+δ.
(3) New fabrication approaches to improve the electrochemical activity of Ln2NiO4+δ-based electrodes, in particular, adaptation of the plasma spraying technique, pulsed laser deposition, and exsolution, or optimisation of the impregnation method.481–484
(4) Further tailoring the functionality of Ln2NiO4+δ-based materials by introducing new dopants or their combination in appropriate concentrations at the Ln-, Ni- or O-sublattices (see, for example, the latest works485–489). The (co)doping strategy has great potential due to the previously-mentioned flexibility of the RP structures. The design of suitable composite materials also belongs to this direction.315,490,491
(5) Long-term features of Ln2NiO4+δ-based electrodes. To fabricate low-cost and performance-competitive PCFCs and PCECs, special attention should be devoted to the kinetic-related processes taking place over longer than 1000 h, including particle coarsening, porosity changes and chemical reactivity with CO2, high concentrations of H2O (in the case of electrolysis cells), and electrolyte components. All these factors affect the TPB length and its corresponding catalytic activity.
In summary, layered Ln2NiO4+δ oxides show potential suitability for application in protonic ceramic electrochemical cells as electrode materials due to their unique features. However, the application of layered Ln2NiO4+δ oxides has only emerged in recent years and many issues are still not clear, leaving great room for further exploration. The investigation of layered Ln2NiO4+δ oxides not only provides a solution for achieving high cell performance, which is the primary goal for practical applications, but also leads to an in-depth understanding of the scientific issues for the community, possibly opening a new door for the development of protonic ceramic electrochemical cells.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. Y. gratefully acknowledges financial support from the FCT, Portugal (project CICECO-Aveiro Institute of Materials, UIDB/50011/2020 & UIDP/50011/2020, financed by national funds through the FCT/MCTES and when appropriate co-financed by FEDER under the PT2020 Partnership Agreement). L. B. gratefully acknowledges the support from the National Natural Science Foundation of China (grant no. 51972183) and the Startup Funding for Talents at University of South China. A. T., J. L and D. M. are grateful to the national projects, supported by the Russian Science Foundation [grant no. 16-19-00104] and the Council of the President of the Russian Federation [scholarship no. CΠ-161.2018.1 and CΠ-1413.2019.1].References
- J. Speirs, P. Balcombe, P. Blomerus, M. Stettler, P. Achurra-Gonzalez, M. Woo, D. Ainalis, J. Cooper, A. Sharafian, W. Merida, D. Crow, S. Giarola, N. Shah, N. Brandon and A. Hawkes, Prog. Energy, 2020, 2, 012002 CrossRef.
- F. Dawood, M. Anda and G. M. Shafiullah, Int. J. Hydrogen Energy, 2020, 45, 3847–3869 CrossRef CAS.
- Z. Abdin, A. Zafaranloo, A. Rafiee, W. Mérida, W. Lipiński and K. R. Khalilpour, Renewable Sustainable Energy Rev., 2020, 120, 109620 CrossRef CAS.
- A. Martin, M.-F. Agnoletti and E. Brangier, Int. J. Hydrogen Energy, 2020, 45, 11889–11900 CrossRef CAS.
- G. Yang, C. Su, H. Shi, Y. Zhu, Y. Song, W. Zhou and Z. Shao, Energy Fuels, 2020 DOI:10.1021/acs.energyfuels.0c01887.
- V. Venkataraman, M. Pérez-Fortes, L. Wang, Y. S. Hajimolana, C. Boigues-Muñoz, A. Agostini, S. J. McPhail, F. Maréchal, J. V. Herle and P. V. Aravinda, J. Energy Storage, 2019, 24, 100782 CrossRef.
- A. M. Abdalla, S. Hossain, A. T. Azad, P. M. I. Petra, F. Begum, S. G. Eriksson and A. K. Azad, Renewable Sustainable Energy Rev., 2018, 82, 353–368 CrossRef CAS.
- Y. Meng, J. Gao, Z. Zhao, J. Amoroso, J. Tong and K. S. Brinkman, J. Mater. Sci., 2019, 54, 9291–9312 CrossRef CAS.
- J. Kim, S. Sengodan, S. Kim, O. Kwon, Y. Bu and G. Kim, Renewable Sustainable Energy Rev., 2019, 109, 606–618 CrossRef CAS.
- N. L. R. M. Rashid, A. A. Samat, A. A. Jais, M. R. Somalu, A. Muchtar, N. A. Baharuddin, W. N. Roslam and W. Isahak, Ceram. Int., 2019, 45, 6605–6615 CrossRef CAS.
- W. Wang, D. Medvedev and Z. Shao, Adv. Funct. Mater., 2019, 28, 1802592 CrossRef.
- D. Medvedev, Int. J. Hydrogen Energy, 2020, 44, 26711–26740 CrossRef.
- S. Hossain, A. M. Abdalla, S. N. BintiJamain, J. H. Zaini and A. K. Azad, Renewable Sustainable Energy Rev., 2017, 79, 750–764 CrossRef CAS.
- D. A. Medvedev, J. G. Lyagaeva, E. V. Gorbova, A. K. Demin and P. Tsiakaras, Prog. Mater. Sci., 2016, 75, 38–79 CrossRef CAS.
- C. Duan, R. J. Kee, H. Zhu, C. Karakaya, Y. Chen, S. Ricote, A. Jarry, E. J. Crumlin, D. Hook, R. Braun, N. P. Sullivan and R. O'Hayre, Nature, 2018, 557, 217–222 CrossRef CAS.
- C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Science, 2015, 349, 1321–1326 CrossRef CAS.
- S. Choi, C. J. Kucharczyk, Y. Liang, X. Zhang, I. Takeuchi, H.-I. Ji and S. M. Haile, Nat. Energy, 2018, 3, 202–210 CrossRef CAS.
- S. Choi, T. C. Davenport and S. M. Haile, Energy Environ. Sci., 2019, 12, 206–215 RSC.
- K. Bae, D. Y. Jang, H. J. Choi, D. Kim, J. Hong, B.-K. Kim, J.-H. Lee, J.-W. Son and J. H. Shim, Nat. Commun., 2017, 8, 14553 CrossRef CAS.
- H. An, H.-W. Lee, B.-K. Kim, J.-W. Son, K. J. Yoon, H. Kim, D. Shin, H.-I. Ji and J.-H. Lee, Nat. Energy, 2018, 3, 870–875 CrossRef CAS.
- Y. Wang, W. Li, L. Ma, W. Li and X. Liu, J. Mater. Sci. Technol., 2020, 55, 35–55 CrossRef.
- M. Reisert, A. Aphale and P. Singh, Materials, 2018, 11, 2169 CrossRef.
- B. Koo, K. Kim, J. K. Kim, H. Kwon, J. W. Han and W. Jung, Joule, 2018, 2, 1476–1499 CrossRef CAS.
- Z. Yang, M. Guo, N. Wang, C. Ma, J. Wang and M. Han, Int. J. Hydrogen Energy, 2017, 42, 24948–24959 CrossRef CAS.
- L. Fan, B. Zhu, P.-C. Su and C. He, Nano Energy, 2018, 45, 148–176 CrossRef CAS.
- W. Zhou, X. Wang, Y. Zhu, J. Dai, Y. Zhu and Z. Shao, Mater. Rev., 2018, 32, 337–356 Search PubMed.
- A. V. Kasyanova, L. R. Tarutina, A. O. Rudenko, J. G. Lyagaeva and D. A. Medvedev, Russ. Chem. Rev., 2020, 89, 667–692 CrossRef CAS.
- P. Kaur and K. Singh, Ceram. Int., 2020, 46, 5521–5535 CrossRef CAS.
- S. Afroze, A. Karim, Q. Cheok, S. Eriksson and A. K. Azad, Front. Energy, 2019, 13, 770–797 CrossRef.
- S. S. Hashim, F. Liang, W. Zhou and J. Sunarso, ChemElectroChem, 2019, 6, 3549–3569 CrossRef CAS.
- M. Rafique, H. Nawaz, M. S. Rafique, M. B. Tahir, G. Nabi and N. R. Khalid, Energy Res., 2019, 43, 2423–2446 CrossRef CAS.
- G. Nirala, D. Yadav and S. Upadhyay, J. Adv. Ceram., 2020, 9, 129–148 CrossRef CAS.
- D. Lee, Y.-L. Lee, A. Grimaud, W. T. Hong, M. D. Biegalski, D. Morgane and Y. Shao-Horn, J. Mater. Chem. A, 2014, 2, 6480–6487 RSC.
- S. Choi, S. Yoo, J.-Y. Shin and G. Kim, J. Electrochem. Soc., 2011, 158, B995–B999 CrossRef CAS.
- A. R. Gilev, E. A. Kiselev and V. A. Cherepanov, Solid State Ionics, 2019, 339, 115001 CrossRef CAS.
- M. Garali, M. Kahlaoui, B. Mohammed, A. Mater, C. B. Azouz and C. Chefi, Int. J. Hydrogen Energy, 2019, 44, 11020–11032 CrossRef CAS.
- B. Philippeau, F. Mauvy, C. Mazataud, S. Fourcade and J.-C. Grenier, Solid State Ionics, 2013, 249–250, 17–25 CrossRef CAS.
- X. Zhang, L. Zhang, J. Meng, W. Zhang, F. Meng, X. Liu and J. Meng, Int. J. Hydrogen Energy, 2017, 42, 29498–29510 CrossRef CAS.
- V. A. Sadykov, E. M. Sadovskaya, N. F. Eremeev, P. I. Skriabin, A. V. Krasnov, Y. N. Bespalko, S. N. Pavlova, Y. E. Fedorova, E. Y. Pikalova and A. V. Shlyakhtina, Russ. J. Electrochem., 2019, 55, 701–718 CrossRef CAS.
- S. N. Ruddlesden and P. Popper, Acta Crystallogr., 1958, 11, 54–55 CrossRef CAS.
- M. Greenblatt, Curr. Opin. Solid State Mater. Sci., 1997, 2, 174–183 CrossRef CAS.
- A. Demourgues, A. Wattiaux, J. C. Grenier, M. Pouchard, J. L. Soubeyroux, J. M. Dance and P. Hagenmuller, J. Solid State Chem., 1993, 105, 458–470 CrossRef CAS.
- A. Aguadero, J. A. Alonso, M. J. Martínez-Lope, M. T. Fernández-Díaz, M. J. Escudero and L. Daza, J. Mater. Chem., 2006, 16, 3402–3408 RSC.
- J. F. Ackerman, Mater. Res. Bull., 1979, 14, 487–491 CrossRef CAS.
- K. K. Singh, P. Ganguly and J. B. Goodenough, J. Solid State Chem., 1984, 52, 254–273 CrossRef CAS.
- P. Ganguly and C. N. R. Rao, J. Solid State Chem., 1984, 53, 193–216 CrossRef CAS.
- C. Frayret, A. Villesuzanne and M. Pouchard, Chem. Mater., 2005, 17, 6538–6544 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1996, A32, 751–767 Search PubMed.
- M. T. Fernández-Díaz, J. L. Martínez and J. Rodríguez-Carvajal, Solid State Ionics, 1993, 63–65, 902–906 CrossRef.
- C. Allançon, J. Rodríguez-Carvajal, M. T. Fernández-Díaz, P. Odier, J. M. Bassat, J. P. Loup and J. L. Martínez, Z. Phys. B: Condens. Matter, 1996, 100, 85–90 CrossRef.
- J. M. Bassat, P. Odier and J. P. Loup, J. Solid State Chem., 1994, 110, 124–135 CrossRef CAS.
- A. V. Kovalevsky, V. V. Kharton, A. A. Yaremchenko, Y. V. Pivak, E. V. Tsipis, S. O. Yakovlev, A. A. Markov, E. N. Naumovich and J. R. Frade, J. Electroceram., 2007, 18, 205–218 CrossRef CAS.
- E. Boehm, J.-M. Bassat, P. Dordor, F. Mauvy, J.-C. Grenier and P. Stevens, Solid State Ionics, 2005, 176, 2717–2725 CrossRef CAS.
- C. Allançon, A. Gonthier-Vassal, J. M. Bascat, J. P. Loup and P. Odier, Solid State Ionics, 1994, 74, 239–248 CrossRef.
- H. Tamura, A. Hayashi and Y. Ueda, Solid State Ionics, 1996, 258, 61–71 CAS.
- T. Nakamura, K. Yashiro, K. Sato and J. Mizusaki, Solid State Ionics, 2009, 180, 368–376 CrossRef CAS.
- V. Vashook, E. Girdauskaite, J. Zosel, T.-L. Wen, H. Ullmann and U. Guth, Solid State Ionics, 2006, 177, 1163–1171 CrossRef CAS.
- T. Nakamura, K. Yashiro, K. Sato and J. Mizusaki, J. Solid State Chem., 2009, 182, 1533–1537 CrossRef CAS.
- T. Nakamura, K. Yashiro, K. Sato and J. Mizusaki, Solid State Ionics, 2009, 180, 1406–1413 CrossRef CAS.
- V. V. Kharton, E. V. Tsipis, E. N. Naumovich, A. Thursfield, M. V. Patrakeev, V. A. Kolotygin, J. C. Waerenborgh and I. S. Metcalfe, J. Solid State Chem., 2008, 181, 1425–1433 CrossRef CAS.
- E. N. Naumovich, M. V. Patrakeev, V. V. Kharton, A. A. Yaremchenko, D. I. Logvinovich and F. M. B. Marques, Solid State Sci., 2005, 7, 1353–1362 CrossRef CAS.
- E. N. Naumovich, M. V. Patrakeev, V. V. Kharton, A. A. Yaremchenko, E. V. Tsipis, J. R. Frade, D. I. Logvinovich and F. M. B. Marques, Mater. Sci. Forum, 2006, 514–516, 397–401 CAS.
- H.-S. Kim and H. Yoo, Phys. Chem. Chem. Phys., 2010, 12, 4704–4713 RSC.
- S.-Y. Jeon, M.-B. Choi, J.-H. Hwang, E. D. Wachsman and S.-J. Song, J. Solid State Electrochem., 2012, 16, 785–793 CrossRef CAS.
- Y. Naumovich, Quantitative description of oxygen non-stoichiometry in mixed ionic and electronic conductors based on a non-ideal solution approach, Institute of Power Engineering, Warsaw, 2019 Search PubMed.
- H. Tamura, A. Hayashi and Y. Ueda, Phys. C, 1993, 216, 83–88 CrossRef CAS.
- S. J. Skinner, Solid State Sci., 2003, 5, 419–426 CrossRef CAS.
- J. D. Jorgensen, B. Dabrowski, S. Pei, D. R. Richards and D. G. Hinks, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 2187 CrossRef CAS.
- T. Broux, C. Prestipino, M. Bahout, S. Paofai, E. Elkaïm, V. Vibhu, J.-C. Grenier, A. Rougier, J.-M. Bassat and O. Hernandez, Dalton Trans., 2016, 45, 3024–3033 RSC.
- V. Vibhu, M. R. Suchomel, N. Penin, F. Weill, J.-C. Grenier, J.-M. Bassat and A. Rougier, Dalton Trans., 2019, 48, 266–277 RSC.
- S. M. Aspera, M. Sakaue, T. D. K. Wungu, M. Alaydrus, T. P. T. Linh, H. Kasai, M. Nakanishi and T. Ishihara, J. Phys.: Condens. Matter, 2012, 24, 405504 CrossRef CAS.
- A. Flura, S. Dru, C. Nicollet, V. Vibhu, S. Fourcade, E. Lebraud, A. Rougier, J.-M. Bassat and J.-C. Grenier, J. Solid State Chem., 2015, 228, 189–198 CrossRef CAS.
- R. K. Sharma, S.-K. Cheah, M. Burriel, L. Dessemond, J.-M. Bassat and E. Djurado, J. Mater. Chem. A, 2017, 5, 1120–1132 RSC.
- A. Montenegro-Hernández, J. Vega-Castillo, A. Caneirom and L. Mogni, J. Solid State Chem., 2019, 276, 210–216 CrossRef.
- D. Ning, A. Baki, T. Scherb, J. Song, A. Fantin, X. Liu, G. Schumacher, J. Banhart and H. J. M. Bouwmeester, Solid State Ionics, 2019, 342, 115056 CrossRef CAS.
- Y. Toyosumi, H. Ishikawa and K. Ishikawa, J. Alloys Compd., 2006, 408–412, 1200–1204 CrossRef CAS.
- M. Zaghrioui, F. Giovannelli, N. P. D. Brouri and I. Laffez, J. Solid State Chem., 2004, 177, 3351–3358 CrossRef CAS.
- S. M. Pikalov, L. B. Vedmid, E. A. Filonov, E. Y. Pikalova, J. G. Lyagaeva, N. A. Danilov and A. A. Murashkina, J. Alloys Compd., 2019, 801, 558–567 CrossRef CAS.
- Y. Takeda, M. Nishijima, N. Imanishi, R. Kanno, O. Yamamoto and M. Takano, J. Solid State Chem., 1992, 96, 72–83 CrossRef CAS.
- T. Ogier, C. Prestipino, S. Figueroa, F. Mauvy, J. Mougin, J. C. Grenier, A. Demourgues and J. M. Bassat, Chem. Phys. Lett., 2019, 727, 116–120 CrossRef CAS.
- J. Dailly, S. Fourcade, A. Largeteau, F. Mauvy, J. C. Grenier and M. Marrony, Electrochim. Acta, 2010, 55, 5847–5853 CrossRef CAS.
- E. Y. Pikalova, A. A. Kolchugin, V. A. Sadykov, E. M. Sadovskaya, E. A. Filonova, N. F. Eremeev and N. M. Bogdanovich, Int. J. Hydrogen Energy, 2018, 43, 17373–17386 CrossRef CAS.
- C. Allançon, P. Odier, J. M. Bassat and J. P. Loup, J. Solid State Chem., 1997, 131, 167–172 CrossRef.
- A. D. Rougier, A. Flura, C. Nicollet, V. Vibhu, S. Fourcade, E. Lebraud, J.-M. Bassat and J.-C. Grenier, ECS Trans., 2015, 68, 817–823 CrossRef CAS.
- H. Zhao, F. Mauvy, C. Lalanne, J.-M. Bassat, S. Fourcade and J.-C. Grenier, Solid State Ionics, 2008, 179, 2000–2005 CrossRef CAS.
- A. Egger, E. Bucher, W. Sitte, C. Lalanne and J.-M. Bassat, ECS Trans., 2009, 25, 2547–2556 CrossRef CAS.
- B. Gedziorowski, K. Cichy, A. Niemczyk, A. Olszewska, Z. Zhang, S. Kopec, K. Zheng, M. Marzec, M. Gajewska, Z. Du, H. Zhao and K. Swierczek, J. Eur. Ceram. Soc., 2020, 40, 4056–4066 CrossRef CAS.
- E. Niwa, T. Nakamura, J. Mizusaki and T. Hashimoto, Thermochim. Acta, 2011, 523, 46–50 CrossRef CAS.
- H. Ishikawa, Y. Toyosumi and K. Ishikawa, J. Alloys Compd., 2006, 406–412, 1196–1199 CrossRef.
- E. Niwa, K. Wakai, T. Hori, K. Yashiro, J. Mizusaki and T. Hashimoto, Thermochim. Acta, 2014, 575, 129–134 CrossRef CAS.
- T. Nakamura, K. Yashiro, K. Sato and J. Mizusaki, Solid State Ionics, 2010, 181, 402–411 CrossRef CAS.
- V. Sadykov, Y. Okhlupin, N. Yeremeev, Z. Vinokurov, A. Shmakov, V. Belyaev, N. Uvarov and J. Mertens, Solid State Ionics, 2014, 262, 918–922 CrossRef CAS.
- V. Vibhu, A. Rougier, C. Nicollet, A. Flura, J.-C. Grenier and J.-M. Bassat, Solid State Ionics, 2015, 278, 32–37 CrossRef CAS.
- A. Murata, C. Hai and M. Matsuda, Mater. Lett., 2014, 136, 292–294 CrossRef CAS.
- M. Sakai, C. Wang, T. Okiba, H. Soga and T. Hashimoto, J. Therm. Anal. Calorim., 2020, 142, 139–147 CrossRef CAS.
- E. Dogdibegovic, Q. Cai, N. S. Alabri, W. Guan and X.-D. Zhou, J. Electrochem. Soc., 2016, 164, F99–F106 CrossRef.
- G. Amow and S. J. Skinner, J. Solid State Electrochem., 2006, 10, 538–546 CrossRef CAS.
- J. P. Tang, R. I. Dass and A. Manthiram, Mater. Res. Bull., 2000, 35, 411–424 CrossRef CAS.
- K. Ruck, G. Krabbes and I. Vogel, Mater. Res. Bull., 1999, 34, 1689–1697 CrossRef CAS.
- Y. Shen, H. Zhao, X. Liua and N. Xu, Phys. Chem. Chem. Phys., 2010, 12, 15124–15131 RSC.
- E. Y. Pikalova, D. A. Medvedev and A. F. Khasanov, Phys. Solid State, 2010, 59, 694–702 CrossRef.
- V. A. Sadykov, E. Y. Pikalova, A. A. Kolchugin, E. A. Filonova, E. M. Sadovskaya, N. F. Eremeev, A. V. Ishchenko, A. V. Fetisov and S. M. Pikalov, Solid State Ionics, 2018, 317, 234–243 CrossRef CAS.
- S. W. Li and Y. F. Ren, Mater. Res. Bull., 1995, 30, 1505–1511 CrossRef.
- M. James and J. P. Attfield, J. Mater. Chem., 1996, 6, 57–62 RSC.
- Y. Takeda, R. Kanno, M. Sakano and O. Yamamoto, Mater. Res. Bull., 1990, 25, 293–306 CrossRef CAS.
- E. S. Kravchenko, K. V. Zakharchuk, V. V. Pankov and A. A. Yaremchenko, J. Belarus. State Univ. Chem., 2017, 1, 43–49 Search PubMed.
- A. Yaremchenko, E. Kravchenko, K. Zakharchuk, J. Grins, G. Svensson and V. Pankov, Oxygen-deficient Ruddlesden–Popper Pr1−xSr1+xNiO4−δ as prospective oxygen electrode materials for SOFC/SOEC, 21st International Conference on Solid State Ionics (SSI-21), Padua, Italy, 18–23 June 2017, Program Guide and Abstracts, abstract I-12_26/O, p. 365 Search PubMed.
- E. Kravchenko, D. Khalyavin, K. Zakharchuk, J. Grins, G. Svensson, V. Pankov and A. Yaremchenko, J. Mater. Chem. A, 2015, 3, 23852–23863 RSC.
- A. B. Austin, L. G. Carreiro and J. V. Marzik, Mater. Res. Bull., 1989, 24, 639–646 CrossRef CAS.
- Y. K. Chung, Y.-U. Kwon and S. H. Byeon, Bull. Korean Chem. Soc., 1995, 16, 120–125 CAS.
- H. Soga, C. Wang, T. Hayashi, T. Morise, E. Niwa and T. Hashimoto, ECS Trans., 2017, 78, 613–622 CrossRef CAS.
- K. K. Singh, P. Ganguly and C. N. R. Rao, Mater. Res. Bull., 1982, 17, 493–500 CrossRef CAS.
- E. Boehm, J.-M. Bassat, M. C. Steil, P. Dordor, F. Mauvy and J.-C. Grenier, Solid State Sci., 2003, 5, 973–981 CrossRef CAS.
- A. Aguadero, J. A. Alonso, M. J. Escudero and L. Daza, Solid State Ionics, 2008, 179, 393–400 CrossRef CAS.
- M. Sakai, C. Wang, T. Okiba, H. Soga, E. Niwa and T. Hashimoto, J. Therm. Anal. Calorim., 2019, 135, 2765–2774 CrossRef CAS.
- C. Wang, H. Soga, T. Okiba, E. Niwa and T. Hashimoto, Mater. Res. Bull., 2019, 111, 61–69 CrossRef CAS.
- G. Amow, P. S. Whitfield, I. J. Davidson, R. P. Hammond, C. N. Munnings and S. J. Skinner, Ceram. Int., 2004, 30, 1635–1639 CrossRef CAS.
- C. Berger, E. Bucher, A. Egger, A. T. Strasser, N. Schrödl, C. Gspan, J. Hofer and W. Sitte, Solid State Ionics, 2018, 316, 93–101 CrossRef CAS.
- S. Li, H. Tu, F. Li, M. T. Anwar and L. Yu, J. Alloys Compd., 2017, 694, 17–23 CrossRef CAS.
- T. Nakamura, Y. Ling and K. Amezawa, J. Mater. Chem. A, 2015, 3, 10471–10479 RSC.
- E. V. Tsipis, E. N. Naumovich, M. V. Patrakeev, J. C. Waerenborgh, Y. V. Pivak, P. Gaczyński and V. V. Kharton, J. Phys. Chem. Solids, 2007, 68, 1443–1455 CrossRef CAS.
- M.-L. Fontaine, C. Laberty-Robert, A. Barnabé, F. Ansart and P. Tailhades, Ceram. Int., 2004, 30, 2087–2098 CrossRef CAS.
- A. K. Ganguli, R. Nagarajan, G. R. Rao, N. Y. Vasanthacharya and C. N. R. Rao, Solid State Commun., 1989, 72, 195–197 CrossRef CAS.
- R. Benloucif, N. Nguyen, J. M. Greneche and B. Raveau, J. Phys. Chem. Solids, 1989, 50, 435–440 CrossRef CAS.
- C. Lalanne, G. Prosperi, J.-M. Bassat, F. Mauvy, S. Fourcade, P. Stevens, M. Zahid, S. Diethelm, J. Van herle and J.-C. Grenier, J. Power Sources, 2008, 185, 1218–1224 CrossRef CAS.
- F. Mauvy, C. Lalanne, J.-M. Bassat, J.-C. Grenier, A. Brisse, A.-L. Sauvet, C. Barthet and J. Fouletier, Solid State Ionics, 2009, 180, 1183–1189 CrossRef CAS.
- Y. Chen, B. Qian, G. Yang, D. Chen and Z. Shao, J. Mater. Chem. A, 2015, 3, 6501–6508 RSC.
- M. Ferkhi and H. A. Yahia, Mater. Res. Bull., 2016, 83, 268–274 CrossRef CAS.
- A. Usenka, V. Pankov, V. Vibhu, A. Flura, J.-C. Grenier and J.-M. Bassat, ECS Trans., 2019, 91, 1341–1353 CrossRef CAS.
- A. A. Kolchugin, E. Y. Pikalova, N. M. Bogdanovich, D. I. Bronin, S. M. Pikalov, S. V. Plaksin, M. V. Ananyev and V. A. Eremin, Solid State Ionics, 2016, 288, 48–53 CrossRef CAS.
- A. R. Gilev, E. A. Kiselev, D. M. Zakharov and V. A. Cherepanov, J. Alloys Compd., 2018, 753, 491–501 CrossRef CAS.
- E. Pikalova, A. Kolchugin, E. Filonova, N. Bogdanovich, S. Pikalov, M. Ananyev, N. Molchanova and A. Farlenkov, Solid State Ionics, 2018, 319, 130–140 CrossRef CAS.
- M. Khairy, P. Odier and J. Choisnet, J. Phys., Colloq., 1986, 47, C1-831–C1-835 CrossRef.
- I. Gopalakrishnan, G. Colsmann and B. Reuter, J. Solid State Chem., 1977, 22, 145–149 CrossRef.
- T. Nitadori, M. Muramatsu and M. Misono, Bull. Chem. Soc. Jpn., 1988, 61, 3831–3837 CrossRef CAS.
- K. Sreedhar and C. N. R. Rao, Mater. Res. Bull., 1990, 25, 1235–1242 CrossRef CAS.
- X. Granados, J. Fontcuberta, M. Vallet-Regi, M. J. Sayague and J. M. Gonza-Calbet, J. Solid State Chem., 1993, 102, 455–464 CrossRef CAS.
- L. V. Makhnach, V. V. Pankov and P. Strobel, Mater. Chem. Phys., 2008, 111, 125–130 CrossRef CAS.
- V. V. Vashook, S. P. Tolochko, I. I. Yushkevich, L. V. Makhnach, I. F. Kononyuk, H. Altenburg, J. Hauck and H. Ullmann, Solid State Ionics, 1998, 110, 245–253 CrossRef CAS.
- V. V. Vashook, I. I. Yushkevich, L. V. Kokhanovsky, L. V. Makhnach, S. P. Tolochko, I. F. Kononyuk, H. Ullmann and H. Altenburg, Solid State Ionics, 1999, 119, 23–30 CrossRef CAS.
- A. Aguadero, M. J. Escudero, M. Perez, J. A. Alonso, V. Pomjakushin and L. Daza, Dalton Trans., 2006, 4377–4383 RSC.
- T. Nakamura, K. Yashiro, K. Sato and J. Mizusaki, Phys. Chem. Chem. Phys., 2009, 11, 3055–3062 RSC.
- S. C. Chen, K. V. Ramanujachary and M. Greenblatt, J. Solid State Chem., 1993, 105, 444–457 CrossRef CAS.
- A. Grimaud, F. Mauvy, J. M. Bassat, S. Fourcade, M. Marrony and J. C. Grenier, J. Mater. Chem., 2012, 22, 16017–16025 RSC.
- E. Kravchenko, K. Zakharchuk, A. Viskup, J. Grins, G. Svensson, V. Pankov and A. Yaremchenko, ChemSusChem, 2017, 10, 600–611 CrossRef CAS.
- S. M. Doyle, M. P. S. Kumar and D. M. Paul, J. Phys.: Condens. Matter, 1992, 4, 3559–3568 CrossRef CAS.
- B. W. Arbuckle, K. V. Ramanujachary, Z. Zhang and M. Greenblatt, J. Solid State Chem., 1990, 88, 278–290 CrossRef CAS.
- T. Nakamura, K. Yashiro, K. Sato and J. Mizusaki, Mater. Chem. Phys., 2010, 122, 250–258 CrossRef CAS.
- J. Alonso, M. Vallet-Regi and J. M. Gonzalez-Calbet, Solid State Ionics, 1993, 66, 219–223 CrossRef CAS.
- M. Hücker, K. Chung, M. Chand, T. Vogt, J. M. Tranquada and D. J. Buttrey, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 064105 CrossRef.
- M. Jimenez-Ruiz, C. Prieto, J. L. Martinez and J. M. Alonso, J. Solid State Chem., 1998, 140, 278–284 CrossRef CAS.
- C. J. Liu, M. D. Mays, D. O. Cowan and M. G. Sanchez, Chem. Mater., 1991, 3, 495–500 CrossRef CAS.
- H.-S. Kim and H.-I. Yoo, Solid State Ionics, 2013, 232, 129–137 CrossRef CAS.
- Z. Li, R. Haugsrud, J. B. Smith and T. Norby, Solid State Ionics, 2009, 180, 1433–1441 CrossRef CAS.
- E. Kravchenko, A. Neagu, K. Zakharchuk, J. Grins, G. Svensson, V. Pankov and A. A. Yaremchenko, Eur. J. Inorg. Chem., 2018, 3320–3329 CrossRef CAS.
- A. Aguadero, M. Pereza, J. A. Alonso and L. Daza, J. Power Sources, 2005, 151, 52–56 CrossRef CAS.
- A. P. Tarutin, J. G. Lyagaeva, A. S. Farlenkov, A. I. Vylkov and D. M. Medvedev, Ceram. Int., 2019, 45, 16105–16112 CrossRef CAS.
- K. Zheng and K. Swierczek, Mater. Res. Bull., 2016, 84, 259–266 CrossRef CAS.
- Y. Wang, J. Cheng, Q. Jiang, J. Yang and J. Gao, J. Power Sources, 2011, 196, 3104–3108 CrossRef CAS.
- J. A. Kilner and C. K. M. Shaw, Solid State Ionics, 2002, 154–155, 523–527 CrossRef CAS.
- E. V. Tsipis, E. N. Naumovich, A. L. Shaula, M. V. Patrakeev, J. C. Waerenborgh and V. V. Kharton, Solid State Ionics, 2008, 179, 57–60 CrossRef CAS.
- S. Miyoshi, T. Furuno, O. Sangoanruang, H. Matsumoto and T. Ishihara, J. Electrochem. Soc., 2007, 154, B57–B62 CrossRef CAS.
- T. Klande, K. Efimov, S. Cusenza, K.-D. Becker and A. Feldhoff, J. Solid State Chem., 2011, 184, 3310–3318 CrossRef CAS.
- S. Crapanzano, I. V. Babich and L. Lefferts, Appl. Catal., A, 2010, 378, 144–150 CrossRef CAS.
- S. Y. Gómez, J. Gurauskis, V. Øygarden, D. Hotza, T. Grande and K. Wiik, Solid State Ionics, 2016, 292, 38–44 CrossRef.
- J. Zhu, D. Xiao, J. Li and X. Yang, Catal. Lett., 2009, 129, 240–246 CrossRef CAS.
- H. El Shinawi and C. Greaves, J. Mater. Chem., 2010, 20, 504–511 RSC.
- S. Yi, Y. Shen, H. Zhao, Z. Du, N. Chen and B. Huang, Electrochim. Acta, 2016, 219, 394–400 CrossRef CAS.
- W. Li, B. Guan, J. Yan, N. Zhang, X. Zhang and X. Liu, J. Power Sources, 2016, 318, 178–183 CrossRef CAS.
- L. Y. Gavrilova, T. V. Aksenova, L. A. Bannykh, Y. V. Teslenko and V. A. Cherepanov, J. Struct. Chem., 2003, 44, 248–251 CrossRef CAS.
- A. R. Gilev, E. A. Kiselev and V. A. Cherepanov, Solid State Ionics, 2015, 279, 53–59 CrossRef CAS.
- A. R. Gilev, E. A. Kiselev and V. A. Cherepanov, RSC Adv., 2016, 6, 72905–72917 RSC.
- R. Benloucif, N. Nguyen, J. M. Greneche and B. Raveau, J. Phys. Chem. Solids, 1991, 52, 381–387 CrossRef CAS.
- R. P. Forslund, W. G. Hardin, X. Rong, A. M. Abakumov, D. Filimonov, C. T. Alexander, J. T. Mefford, H. Iyer, A. M. Kolpak, K. P. Johnston and K. J. Stevenson, Nat. Commun., 2018, 9, 3150 CrossRef.
- H. Chaker, T. Roisnel, M. Potel and R. B. Hassen, J. Solid State Chem., 2004, 177, 4067–4072 CrossRef CAS.
- H. Chaker, I. Raies, A. Chouket, T. Roisnel and R. B. Hassen, Ionics, 2017, 23, 2229–2240 CrossRef CAS.
- S. Y. Istomin, O. M. Karakulina, M. G. Rozova, S. M. Kazakov, A. A. Gippius, E. V. Antipov, I. A. Bobrikov, A. M. Balagurov, A. A. Tsirlin, A. Michau, J. J. Biendicho and G. Svensson, RSC Adv., 2016, 6, 33951–33958 RSC.
- A. Chouket, O. Bidault, L. Combemale, O. Heintz, M. Khitouni and V. Optasanu, J. Alloys Compd., 2018, 732, 149–159 CrossRef CAS.
- J. E. Millburn and M. J. Rosseinsky, Chem. Mater., 1997, 9, 511–522 CrossRef CAS.
- F. Tonus, M. Bahout, P. D. Battle, T. Hansen, P. F. Henry and T. Roisnel, J. Mater. Chem., 2010, 20, 4103–4115 RSC.
- M. Jammali, R. B. Hassen and J. Rohlicek, Powder Diffr., 2012, 27, 184–188 CrossRef CAS.
- H. Chaker, T. Roisnel, M. Ceretti and R. B. Hassen, Powder Diffr., 2010, 25, 241–246 CrossRef CAS.
- M. Jammali, H. Chaker, K. Cherif and R. B. Hassen, J. Mater. Chem., 2010, 183, 1194–1199 CAS.
- S. E. Dutton, M. Bahout, P. D. Battle, F. Tonus and V. Demange, J. Solid State Chem., 2008, 181, 2217–2226 CrossRef CAS.
- T. Ishihara, S. Miyoshi, T. Furuno, O. Sanguanruang and H. Matsumoto, Solid State Ionics, 2006, 177, 3087–3091 CrossRef CAS.
- N. Ye and J. L. Hertz, Acta Mater., 2014, 63, 123–129 CrossRef CAS.
- K. Meeporn, N. Chanlek and P. Thongbai, RSC Adv., 2016, 6, 91377–91385 RSC.
- C. A. Silva, J. B. Silva, M. C. Silva-Santana, P. B. Silva and N. O. Moreno, Adv. Mater. Res., 2014, 975, 75–80 CAS.
- S. -Y. Jeon, B. Singh, Y. -S. Yoo, J. -H. Hwang and S. -J. Song, J. Am. Ceram. Soc., 2014, 97, 1489–1496 CrossRef CAS.
- S.-Y. Jeon, B. Singh, H.-N. Im, K.-P. Seong and S.-J. Song, J. Alloys Compd., 2014, 589, 572–578 CrossRef CAS.
- D. Reinen, U. Kesper and D. Belder, J. Solid State Chem., 1995, 116, 355–363 CrossRef CAS.
- V. F. Savchenko, L. V. Makhnach, I. I. Emelyanova and V. V. Pankov, Inorg. Mater., 2006, 42, 788–793 CrossRef CAS.
- Z. Zhang, Z. Du, A. Niemczyk, K. Li, H. Zhao and K. Swierczek, Solid State Ionics, 2018, 317, 26–31 CrossRef CAS.
- A. Kawahara and T. Ishihara, Electrochem. Solid-State Lett., 2010, 13, B76–B78 CrossRef CAS.
- T. Ishihara, N. Sirikanda, K. Nakashima, S. Miyoshi and H. Matsumoto, J. Electrochem. Soc., 2010, 157, B141–B146 CrossRef CAS.
- Q. Zhou, L. Qu, T. Zhang, Y. He, C. Zhao, M. Wang, T. Wei and Y. Zhang, J. Alloys Compd., 2020, 824, 153967 CrossRef CAS.
- M. Bansod, A. P. Khandale and S. S. Bhoga, Ionics, 2017, 23, 2561–2570 CrossRef CAS.
- T. Ishihara, K. Nakashima, S. Okada, M. Enoki and H. Matsumoto, Solid State Ionics, 2008, 179, 1367–1371 CrossRef CAS.
- J. Mao, S. Peng, C. Zhang, S. Qi, J. Cui, Y. Gong, S. Wang, C. Wu and Q. Zhou, J. Alloys Compd., 2019, 793, 519–525 CrossRef CAS.
- Q. Zheng, J. Xue, Q. Liao, Y. Wei, Z. Li and H. Wang, Chem. Eng. Sci., 2013, 101, 240–247 CrossRef CAS.
- H. W. Nie, T.-L. Wen, S. R. Wang, Y. S. Wang, U. Guth and V. Vashook, Solid State Ionics, 2006, 177, 1929–1932 CrossRef CAS.
- H. Lou, Y. Ge, P. Chen, M. Mei, F. Ma and G. Lü, J. Mater. Chem., 1997, 7, 2097–2101 RSC.
- Q. Li, Y. Fan, H. Zhao, L. P. Sun and L. H. Huo, J. Power Sources, 2007, 167, 64–68 CrossRef CAS.
- V. N. Chaudhari, A. P. Khandale and S. S. Bhoga, J. Power Sources, 2014, 248, 647–654 CrossRef CAS.
- V. Bhat, C. N. R. Rao and J. M. Honig, Solid State Commun., 1992, 81, 751–756 CrossRef CAS.
- B. W. Arbuckle, K. V. Ramanujachary, A. M. Buckley and M. Greenblatt, J. Mater. Chem., 1992, 97, 274–282 CAS.
- A. P. Tarutin, G. K. Vdovin, D. A. Medvedev and A. A. Yaremchenko, Electrochim. Acta, 2020, 337, 135808 CrossRef CAS.
- K. Wissel, J. Heldt, P. B. Groszewicz, S. Dasgupta, H. Breitzke, M. Donzelli, A. I. Waidha, A. D. Fortes, J. Rohrer, P. R. Slater, G. Buntkowsky and O. Clemens, Inorg. Chem., 2018, 57, 6549–6560 CrossRef CAS.
- M. Ali Nowroozi, K. Wissel, M. Donzelli, N. Hosseinpourkahvaz, S. Plana-Ruiz, U. Kolb, R. Schoch, M. Bauer, A. M. Malik, J. Rohrer, S. Ivlev, F. Kraus and O. Clemens, Commun. Mater., 2020, 1, 27 CrossRef.
- M. Zinkevich and F. Aldinger, J. Alloys Compd., 2004, 375, 147–161 CrossRef CAS.
- A. N. Petrov, V. A. Cherepanov, A. Y. Zuyev and V. M. Zhukovsky, J. Solid State Chem., 1988, 77, 1–14 CrossRef CAS.
- D. E. Rice and D. J. Buttrey, J. Solid State Chem., 1993, 105, 197–210 CrossRef CAS.
- A. A. Yaremchenko, V. V. Kharton, M. V. Patrakeev and J. R. Frade, J. Mater. Chem., 2003, 13, 1136–1144 RSC.
- V. V. Kharton, A. A. Yaremchenko, A. L. Shaula, M. V. Patrakeev, E. N. Naumovich, D. I. Logvinovich, J. R. Frade and F. M. BMarques, J. Solid State Chem., 2004, 177, 26–37 CrossRef CAS.
- P. Odier, Y. Nigara, J. Coutures and M. Sayer, J. Solid State Chem., 1985, 56, 32–40 CrossRef CAS.
- M. Zinkevich, N. Solak, H. Nitsche, M. Ahrens and F. Aldinger, J. Alloys Compd., 2007, 438, 92–99 CrossRef CAS.
- Y. Adachi, N. Hatada, K. Hirota, M. Kato and T. Uda, J. Am. Ceram. Soc., 2019, 102, 7077–7088 CrossRef CAS.
- G. Amow, I. J. Davidson and S. J. Skinner, Solid State Ionics, 2006, 177, 1205–1210 CrossRef CAS.
- N. Gauquelin, T. E. Weirich, M. Ceretti, W. Paulus and M. Schroeder, Monatsh. Chem., 2009, 140, 1095–1102 CrossRef CAS.
- A. Montenegro Hernández, L. Mogni and A. Caneiro, Int. J. Hydrogen Energy, 2010, 35, 6031–6036 CrossRef.
- R. Sayers and S. J. Skinner, J. Mater. Chem., 2011, 21, 414–419 RSC.
- J. D. Sullivan, D. J. Buttrey, D. E. Cox and J. Hriljac, J. Solid State Chem., 1991, 94, 337–351 CrossRef CAS.
- H. S. C. O'Neill and M. I. Pownceby, Contrib. Mineral. Petrol., 1993, 114, 296–314 CrossRef.
- P. Odier, C. Allançon and J. M. Bassat, J. Solid State Chem., 2000, 153, 381–385 CrossRef CAS.
- A. V. Kovalevsky, V. V. Kharton, A. A. Yaremchenko, Y. V. Pivak, E. N. Naumovich and J. R. Frade, J. Eur. Ceram. Soc., 2007, 27, 4269–4272 CrossRef CAS.
- A. Montenegro-Hernandez, J. Vega-Castillo, L. Mogni and A. Caneiro, Int. J. Hydrogen Energy, 2011, 36, 15704–15714 CrossRef CAS.
- S. Saher, J. Song, V. Vibhu, C. Nicollet, A. Flura, J.-M. Bassat and H. J. M. Bouwmeester, J. Mater. Chem. A, 2018, 6, 8331–8339 RSC.
- V. Vibhu, J.-M. Bassat, A. Flura, C. Nicollet, J.-C. Grenier and A. Rougier, ECS Trans., 2015, 68, 825–835 CrossRef CAS.
- V. Vibhu, A. Flura, A. Rougier, C. Nicollet, S. Fourcade, T. Hungria, J.-C. Grenier and J.-M. Bassat, J. Energy Chem., 2020, 46, 62–70 CrossRef.
- J. Xue, A. Schulz, H. Wang and A. Feldhoff, J. Membr. Sci., 2016, 497, 357–364 CrossRef CAS.
- P. Batocchi, F. Mauvy, S. Fourcade and M. Parco, Electrochim. Acta, 2014, 145, 1–10 CrossRef CAS.
- W. Li, B. Guan, L. Ma, S. Hu, N. Zhang and X. Liu, J. Mater. Chem. A, 2018, 6, 18057–18066 RSC.
- S. Upasen, P. Batocchi, F. Mauvy, A. Slodczyk and P. Colomban, J. Alloys Compd., 2015, 622, 1074–1085 CrossRef CAS.
- S. Engels, T. Markus, M. Modigell and L. Singheiser, J. Membr. Sci., 2011, 370, 58–69 CrossRef CAS.
- Q. Wei, S. Zhang, B. Meng, N. Han, Z. Zhu and S. Liu, Mater. Lett., 2018, 230, 161–165 CrossRef CAS.
- N. Han, Q. Wei, H. Tian, S. Zhang, Z. Zhu, J. Liu and S. Liu, Energy Technol., 2018, 7, 1800701 CrossRef.
- G. Chen, M. Widenmeyer, B. Tang, L. Kaeswurm, L. Wang, A. Feldhoff and A. Weidenkaff, Front. Chem. Sci. Eng., 2020, 14, 405–414 CrossRef CAS.
- K. S. Yun, J. H. Park, Y. Kwon, D. Y. Kim, C.-Y. Yoo, J. H. Yu and J. H. Joo, J. Mater. Chem. A, 2016, 4, 13549–13554 RSC.
- Y. Kwon, J. H. Park, S. M. Kang, G. D. Nam, J. W. Lee, J. H. Kim, D. Kim, S. M. Jeong, J. H. Yu and J. H. Joo, Energy Environ. Sci., 2019, 12, 1358–1368 RSC.
- S.-N. Lee, A. Atkinson and J. Kilner, ECS Trans., 2013, 57, 605–613 CrossRef.
- K. J. Lee, J. H. Chung, M. J. Lee and H. J. Hwang, J. Korean Ceram. Soc., 2019, 56, 160–166 CrossRef CAS.
- M. Yang, E. Bucher and W. Sitte, J. Power Sources, 2011, 196, 7313–7317 CrossRef CAS.
- Y. Gong, R. Wang, J. Banner, S. N. Basu, U. B. Pal and S. Gopalan, JOM, 2019, 71, 3848–3858 CrossRef CAS.
- A. Egger, N. Schrodl, C. Gspan and W. Sitte, Solid State Ionics, 2017, 299, 18–25 CrossRef CAS.
- N. Schrodl, E. Bucher, A. Egger, P. Kreiml, C. Teichert, T. Hoschen and W. Sitte, Solid State Ionics, 2015, 276, 62–71 CrossRef.
- N. Schrodl, A. Egger, C. Gspan, T. Hoschen, F. Horer and W. Sitte, Solid State Ionics, 2018, 322, 44–53 CrossRef.
- D.-P. Huang, Q. Xu, W. Chen, F. Zhang and H.-X. Liu, Ceram. Int., 2008, 34, 651–655 CrossRef CAS.
- M. Chen, B. H. Moon, S. H. Kim, B. H. Kim, Q. Xu and B. -G. Ahn, Fuel Cells, 2012, 12, 86–96 CrossRef CAS.
- D. Huang, Q. Xu, F. Zhang, W. Chen, H. Liu and J. Zhou, Mater. Lett., 2006, 60, 1892–1895 CrossRef CAS.
- S. Nishiyama, D. Sakaguchi and T. Hattori, Solid State Commun., 1995, 94, 279–282 CrossRef CAS.
- K. Ishikawa, W. Shibata, K. Watanabe, T. Isonaga, M. Hashimoto and Y. Suzuki, J. Solid State Chem., 1997, 131, 275–281 CrossRef CAS.
- G. Taillades, J. Dailly, M. Taillades-Jacquin, F. Mauvy, A. Essouhmi, M. Marrony, C. Lalanne, S. Fourcade, D. J. Jones, J. -C. Grenier and J. Roziere, Fuel Cells, 2010, 10, 166–173 CAS.
- A. A. Kolchugin, E. Y. Pikalova, N. M. Bogdanovich, D. I. Bronin and E. A. Filonova, Russ. J. Electrochem., 2017, 53, 826–833 CrossRef CAS.
- J. B. Goodenough, Mater. Res. Bull., 1973, 8, 423–431 CrossRef CAS.
- J. B. Goodenough and S. Ramasesha, Mater. Res. Bull., 1982, 17, 383–390 CrossRef CAS.
- J. B. Goodenough, J. Less-Common Met., 1986, 116, 83–93 CrossRef CAS.
- N. Poirot, P. Odier, P. Simon and F. Gervais, Solid State Sci., 2003, 5, 735–739 CrossRef CAS.
- S.-Y. Jeon, M.-B. Choi, J.-H. Hwang, E. D. Wachsman and S.-J. Song, J. Electrochem. Soc., 2011, 158, B476–B480 CrossRef CAS.
- C. N. R. Rao, D. J. Buttrey, N. Otsuka, P. Ganguly, H. R. Harrison, C. J. Sandberg and J. M. Honig, J. Solid State Chem., 1984, 51, 266–269 CrossRef CAS.
- J. M. Bassat, F. Gervais, P. Odier and J. P. Loup, Mater. Sci. Eng., B, 1989, 3, 507–514 CrossRef.
- K. Sugiyama, H. Nozaki, T. Takeuchi and H. Ikuta, J. Phys. Chem. Solids, 2002, 63, 979–982 CrossRef CAS.
- A. Murata, T. Uchikoshi and M. Matsuda, J. Power Sources, 2015, 293, 95–100 CrossRef CAS.
- A. L. Shaula, E. N. Naumovich, A. P. Viskup, V. V. Pankov, A. V. Kovalevsky and V. V. Kharton, Solid State Ionics, 2009, 180, 812–816 CrossRef CAS.
- J. M. Bassat, J. P. Loup and P. Odier, J. Phys.: Condens. Matter, 1994, 6, 8285–8293 CrossRef CAS.
- C. Solís, L. Navarrete and J. M. Serra, J. Power Sources, 2013, 240, 691–697 CrossRef.
- Y. Shen, H. Zhao, J. Xu, X. Zhang, K. Zheng and K. Swierczek, Int. J. Hydrogen Energy, 2014, 39, 1023–1029 CrossRef CAS.
- V. A. Sadykov, E. M. Sadovskaya, E. Y. Pikalova, A. A. Kolchugin, E. A. Filonova, S. M. Pikalov, N. F. Eremeev, A. V. Ishchenko, A. I. Lukashevich and J. M. Bassat, Ionics, 2018, 24, 1181–1193 CrossRef CAS.
- J. Yang, J. Cheng, Q. Jiang, Y. Wang, R. Wang and J. Gao, Int. J. Hydrogen Energy, 2012, 37, 1746–1751 CrossRef CAS.
- V. V. Vashook, N. E. Trofimenko, H. Ullmann and L. V. Makhnach, Solid State Ionics, 2000, 131, 329–336 CrossRef CAS.
- T. Klande, S. Cusenza, P. Gaczynski, K.-D. Becker, L. Dorrer, G. Borchardt and A. Feldhoff, Solid State Ionics, 2012, 222–223, 8–15 CrossRef CAS.
- M. V. Patrakeev, E. N. Naumovich, V. V. Kharton, A. A. Yaremchenko, E. V. Tsipis, P. Nunez and J. RFrade, Solid State Ionics, 2005, 176, 179–188 CrossRef CAS.
- V. V. Kharton, A. P. Viskup, E. N. Naumovich and F. M. B. Marques, J. Mater. Chem., 1999, 9, 2623–2629 RSC.
- V. V. Kharton, A. P. Viskup, A. V. Kovalevsky, E. N. Naumovich and F. M. B. Marques, Solid State Ionics, 2001, 143, 337–353 CrossRef CAS.
- B. I. Arias-Serrano, E. Kravchenko, K. Zakharchuk, J. Grins, G. Svensson, V. Pankov and A. Yaremchenko, ECS Trans., 2019, 91, 2387–2397 CrossRef CAS.
- Y. Shen, H. Zhao, K. Świerczek, Z. Du and Z. Xie, J. Power Sources, 2013, 240, 759–765 CrossRef CAS.
- J. Hyodo, K. Tominaga, Y.-W. Ju, S. Ida and T. Ishihara, Solid State Ionics, 2014, 256, 5–10 CrossRef CAS.
- J. M. Bassat, P. Odier, A. Villesuzanne, C. Marin and M. Pouchard, Solid State Ionics, 2004, 167, 341–347 CrossRef CAS.
- H.-S. Kim and H.-I. Yoo, Phys. Chem. Chem. Phys., 2011, 13, 4651–4658 RSC.
- H.-S. Kim and H.-I. Yoo, Phys. Chem. Chem. Phys., 2014, 16, 16595–16605 RSC.
- A. R. Gilev, E. A. Kiselev, D. S. Chezganov and V. A. Cherepanov, Ceram. Int., 2020, 46, 17553–17560 CrossRef CAS.
- A. R. Gilev, E. A. Kiselev and V. A. Cherepanov, J. Mater. Chem. A, 2018, 6, 5304–5312 RSC.
- V. A. Sadykov, E. Y. Pikalova, A. A. Kolchugin, A. V. Fetisov, E. M. Sadovskaya, E. A. Filonova, N. F. Eremeev, V. B. Goncharov, A. V. Krasnov, P. I. Skriabin, A. N. Shmakov, Z. S. Vinokurov, A. V. Ishchenko and S. M. Pikalov, Int. J. Hydrogen Energy, 2020, 45, 13625–13642 CrossRef CAS.
- F. Mauvy, E. Boehm, J. M. Bassat, J. C. Grenier and J. Fouletier, Solid State Ionics, 2007, 178, 1200–1204 CrossRef CAS.
- S.-Y. Jeon, Y.-S. Yoo, B. Singh, H.-N. Im and S.-J. Song, J. Electrochem. Soc., 2016, 163, F1302–F1307 CrossRef CAS.
- J. Xue, Q. Liao, W. Chen, H. J. M. Bouwmeester, H. Wang and A. Feldhoff, J. Mater. Chem. A, 2015, 3, 19107–19114 RSC.
- T. Ina, Y. Orikasa, T. Masese, T. Nakao, A. Mineshige, K. Amezawa, H. Tanida, T. Uruga and Y. Uchimoto, Electrochemistry, 2014, 82, 875–879 CrossRef CAS.
- A. Egger and W. Sitte, Solid State Ionics, 2014, 258, 30–37 CrossRef CAS.
- W. Li, B. Guan, X. Zhang, J. Yan, Y. Zhoua and X. Liu, Phys. Chem. Chem. Phys., 2016, 18, 8502–8511 RSC.
- Z. Li and R. Haugsrud, Solid State Ionics, 2012, 206, 67–71 CrossRef CAS.
- S. J. Skinner and J. A. Kilner, Solid State Ionics, 2000, 135, 709–712 CrossRef CAS.
- E. S. Tropin, M. V. Ananyev, A. S. Farlenkov, A. V. Khodimchuk, A. V. Berenov, A. V. Fetisov, V. A. Eremin and A. A. Kolchugin, J. Solid State Chem., 2018, 262, 199–213 CrossRef CAS.
- J. A. Kilner, S. J. Skinner and H. H. Brongersma, J. Solid State Electrochem., 2011, 15, 861–876 CrossRef CAS.
- T. Inprasit, S. Wongkasemjit, S. J. Skinner, M. Burriel and P. Limthongkul, RSC Adv., 2015, 5, 2486–2492 RSC.
- K. Develos-Bagarinao, J. D. Vero, H. Kishimoto, T. Ishiyama, K. Yamaji, T. Horita and H. Yokokawa, Phys. Chem. Chem. Phys., 2019, 21, 7183–7195 RSC.
- J. Railsback, G. Hughes, L. Mogni, A. Montenegro-Hernandez and S. Barnett, J. Electrochem. Soc., 2016, 163, F1433–F1439 CrossRef CAS.
- K. Yakal-Kremski, L. V. Mogni, A. Montenegro-Hernandez, A. Caneiro and S. A. Barnett, J. Electrochem. Soc., 2014, 161, F1366–F1374 CrossRef CAS.
- J. Hyodo, K. Tominaga, Y.-W. Ju, S. Ida and T. Ishihara, ECS Trans., 2014, 61, 123–129 CrossRef CAS.
- S. J. Skinner and J. A. Kilner, Ionics, 1999, 5, 171–174 CrossRef CAS.
- F. Mauvy, J. M. Bassat, E. Boehm, P. Dordor and J. P. Loup, Solid State Ionics, 2003, 158, 395–407 CrossRef CAS.
- R. Sayers, R. A. D. Souza, J. A. Kilner and S. J. Skinner, Solid State Ionics, 2010, 181, 386–391 CrossRef CAS.
- P.-M. Geffroy, L. Guironnet, H. J. M. Bouwmeester, T. Chartier, J.-C. Grenier and J.-M. Bassat, J. Eur. Ceram. Soc., 2019, 39, 59–65 CrossRef CAS.
- M. Burriel, H. Tellez, R. J. Chater, R. Castaing, P. Veber, M. Zaghrioui, T. Ishihara, J. A. Kilner and J.-M. Bassat, J. Phys. Chem. C, 2016, 120, 17927–17938 CrossRef CAS.
- J.-M. Bassat, M. Burriel, O. Wahyudi, R. Castaing, M. Ceretti, P. Veber, I. Weill, A. Villesuzanne, J.-C. Grenier, W. Paulus and J. A. Kilner, J. Phys. Chem. C, 2013, 117, 26466–26472 CrossRef CAS.
- M. Burriel, G. Garcia, J. Santiso, J. A. Kilner, R. J. Chater and S. J. Skinner, J. Mater. Chem., 2008, 18, 416–422 RSC.
- J. A. Lane and J. A. Kilner, Solid State Ionics, 2000, 136–137, 997–1001 CrossRef CAS.
- Z. Li, T. Norby and R. Haugsrud, J. Am. Ceram. Soc., 2012, 95, 2065–2073 CrossRef CAS.
- A. Egger, E. Bucher and W. Sitte, J. Electrochem. Soc., 2011, 158, B573–B579 CrossRef CAS.
- G. Kim, S. Wang, A. J. Jacobson and C. L. Chen, Solid State Ionics, 2006, 177, 1461–1467 CrossRef CAS.
- G. Garcia, M. Burriel, N. Bonanos and J. Santiso, J. Electrochem. Soc., 2008, 155, P28–P32 CrossRef CAS.
- J. B. Smith and T. Norby, J. Electrochem. Soc., 2006, 153, A233–A238 CrossRef CAS.
- S.-Y. Jeon, M.-B. Choi, H.-N. Im, J.-H. Hwang and S.-J. Song, J. Phys. Chem. Solids, 2012, 73, 656–660 CrossRef CAS.
- S.-Y. Jeon, H.-N. Im, B. Singh, S.-K. Hong and S.-J. Song, Ceram. Int., 2014, 40, 16785–16790 CrossRef CAS.
- R. Moreno, J. Zapata, J. Roqueta, N. Bagues and J. Santiso, J. Electrochem. Soc., 2014, 161, F3046–F3051 CrossRef CAS.
- R. Moreno, P. Garcia, J. Zapata, J. Roqueta, J. Chaigneau and J. Santiso, Chem. Mater., 2013, 25, 3640–3647 CrossRef CAS.
- M. Ghamarinia, A. Babaei and C. Zamani, Electrochim. Acta, 2020, 353, 136520 CrossRef CAS.
- C. Berger, A. Egger, R. Merkle, E. Bucher, B. Stuhlhofer, N. Schrodl, J. Lammer, C. Gspan, G. Logvenov and J. Maier, J. Electrochem. Soc., 2019, 166, F1088–F1095 CrossRef CAS.
- V. A. Sadykov, N. F. Eremeev, V. V. Usoltsev, A. S. Bobin, G. M. Alikina, V. V. Pelipenko, E. M. Sadovskaya, V. S. Muzykantov, N. N. Bulgakov and N. F. Uvarov, Russ. J. Electrochem., 2013, 49, 645–651 CrossRef CAS.
- N. M. Porotnikova, A. V. Khodimchuk, M. V. Ananyev, V. A. Eremin, E. S. Tropin, A. S. Farlenkov, E. Y. Pikalova and A. V. Fetisov, J. Solid State Electrochem., 2018, 22, 2115–2126 CrossRef CAS.
- H. J. M. Bouwmeester, C. Song, J. Zhu, J. Yi, M. S. Annalanda and B. A. Boukamp, Phys. Chem. Chem. Phys., 2009, 11, 9640–9643 RSC.
- A. Boreave, H. Tan, V. Roche, P. Vernoux and J.-P. Deloume, Solid State Ionics, 2008, 179, 1071–1075 CrossRef CAS.
- L. Minervini, R. W. Grimes, J. A. Kilner and K. E. Sickafus, J. Mater. Chem., 2000, 10, 2349–2354 RSC.
- M. S. D. Read, M. S. Islam, F. King and F. E. Hancock, J. Phys. Chem. B, 1999, 103, 1558–1562 CrossRef CAS.
- A. R. Cleave, J. A. Kilner, S. J. Skinner, S. T. Murphy and R. W. Grimes, Solid State Ionics, 2008, 179, 823–826 CrossRef CAS.
- E. N. Naumovich and V. V. Kharton, J. Mol. Struct.: THEOCHEM, 2010, 946, 57–64 CrossRef CAS.
- A. Chroneos, D. Parfitt, J. A. Kilner and R. W. Grimes, J. Mater. Chem., 2010, 20, 266–270 RSC.
- A. Piovano, A. Perrichon, M. Boehm, M. R. Johnson and W. Paulus, Phys. Chem. Chem. Phys., 2016, 18, 17398–17403 RSC.
- D. Parfitt, A. Chroneos, J. A. Kilner and R. W. Grimes, Phys. Chem. Chem. Phys., 2010, 12, 6834–6836 RSC.
- M. Yashima, H. Yamada, S. Nuansaeng and T. Ishihara, Chem. Mater., 2012, 24, 4100–4113 CrossRef CAS.
- W. Xie, Y.-L. Lee, Y. Shao-Horn and D. Morgan, J. Phys. Chem. Lett., 2016, 7, 1939–1944 CrossRef CAS.
- V. Sadykov, E. Pikalova, N. Eremeev, A. Shubin, I. Zilberberg, I. Prosvirin, E. Sadovskaya and A. Bukhtiyarov, Solid State Ionics, 2020, 344, 115155 CrossRef CAS.
- S. Xu, R. Jacobs and D. Morgan, Chem. Mater., 2018, 30, 7166–7177 CrossRef CAS.
- L. Zhang, F. Yao, J. Meng, W. Zhang, H. Wang, X. Liu, J. Meng and H. Zhang, J. Mater. Chem. A, 2019, 7, 18558–18567 RSC.
- M. Yashima, M. Enoki, T. Wakita, R. Ali, Y. Matsushita, F. Izumi and T. Ishihara, J. Am. Chem. Soc., 2008, 130, 2762–2763 CrossRef CAS.
- M. Yashima, N. Sirikanda and T. Ishihara, J. Am. Chem. Soc., 2010, 132, 2385–2392 CrossRef CAS.
- M. Schroeder and M.-A. Dragan, J. Mater. Sci., 2007, 42, 1972–1983 CrossRef CAS.
- Q. Liao, L. Zhuang, Y. Wei, J. Xue and H. Wang, Ceram. Int., 2018, 44, 10852–10857 CrossRef CAS.
- Z. Li, R. Haugsrud and T. Norby, Solid State Ionics, 2011, 184, 42–46 CrossRef CAS.
- Z. Li, R. Haugsrud, J. B. Smith and T. Norby, J. Electrochem. Soc., 2009, 156, B1039–B1044 CrossRef CAS.
- Z. Zhu, M. Li, C. Xia and H. J. M. Bouwmeester, J. Mater. Chem. A, 2017, 5, 14012–14019 RSC.
- S. Miyoshi, T. Furuno, H. Matsumoto and T. Ishihara, Solid State Ionics, 2006, 177, 2269–2273 CrossRef CAS.
- V. V. Kharton, A. A. Yaremchenko, E. V. Tsipis and J. R. Frade, in Proceedings of Eighth International Symposium on Solid Oxide Fuel Cells (SOFC-VIII), ed. S. C. Singhal and M. Dokiya, The Electrochemical Society Inc., Pennington, NJ, 2003, PV 2003-07, pp. 561–570 Search PubMed.
- N. A. Tarasova, A. O. Galisheva and I. E. Animitsa, Russ. J. Electrochem., 2019, 55, 756–761 CrossRef CAS.
- N. Tarasova and I. Animitsa, C. R. Chim., 2019, 22, 363–368 CrossRef CAS.
- N. Tarasova and I. Animitsa, Solid State Sci., 2019, 87, 87–92 CrossRef CAS.
- M. I. Vlasov, N. A. Tarasova, A. O. Galisheva, I. E. Animitsa and M. V. Ananyev, Phys. Chem. Chem. Phys., 2019, 21, 23459–23465 RSC.
- N. Tarasova and I. Animitsa, J. Fluorine Chem., 2018, 216, 107–111 CrossRef CAS.
- N. Tarasova and I. Animitsa, Solid State Ionics, 2018, 317, 21–25 CrossRef CAS.
- N. Tarasova and I. Animitsa, J. Alloys Compd., 2018, 739, 353–359 CrossRef CAS.
- J. Lyagaeva, D. Medvedev, E. Pikalova, S. Plaksin, A. Brouzgou, A. Demin and P. Tsiakaras, Int. J. Hydrogen Energy, 2017, 42, 1715–1723 CrossRef CAS.
- J. R. Tolchard and T. Grande, Solid State Ionics, 2007, 178, 593–599 CrossRef CAS.
- Y. Rao, S. Zhong, F. He, Z. Wang, R. Peng and Y. Lu, Int. J. Hydrogen Energy, 2012, 37, 12522–12527 CrossRef CAS.
- Y. Lin, R. Ran, Y. Zheng, Z. Shao, W. Jin, N. Xu and J. Ahn, J. Power Sources, 2008, 180, 15–22 CrossRef CAS.
- Y. Lin, R. Ran, C. Zhang, R. Cai and Z. Shao, J. Phys. Chem. A, 2010, 114, 3764–3772 CrossRef CAS.
- D. Medvedev, A. Murashkina, E. Pikalova, A. Demin, A. Podias and P. Tsiakaras, Prog. Mater. Sci., 2014, 60, 72–129 CrossRef CAS.
- Y. K. Chung, Y.-U. Kwon and S. H. Byeon, Bull. Korean Chem. Soc., 1995, 16, 120–125 CAS.
- Y. Zhu, D. Wang, F. Yuan, G. Zhang and H. Fu, Appl. Catal., B, 2008, 82, 255–263 CrossRef CAS.
- E. Quarez, Y. Oumellal and O. Joubert, Fuel Cells, 2013, 13, 34–41 CrossRef CAS.
- C. Yang, X. Zhang, H. Zhao, Y. Shen, Z. Du and C. Zhanga, Int. J. Hydrogen Energy, 2015, 40, 2800–2807 CrossRef CAS.
- E. Y. Pikalova and A. A. Kolchugin, Eurasian Chem.-Technol. J., 2016, 18, 3–11 CrossRef CAS.
- G. Li, H. Jin, Y. Cui, L. Gui, B. He and L. Zhao, J. Power Sources, 2017, 341, 192–198 CrossRef CAS.
- N. Danilov, J. Lyagaeva, G. Vdovin, E. Pikalova and D. Medvedev, Energy Convers. Manage., 2018, 172, 129–137 CrossRef CAS.
- H. An, D. Shin and H.-I. Ji, J. Korean Ceram. Soc., 2018, 55, 358–363 CrossRef CAS.
- L. Miao, J. Hou, Z. Gong, Z. Jin and W. Liu, Int. J. Hydrogen Energy, 2019, 44, 7531–7537 CrossRef CAS.
- A. Tarutin, J. Lyagaeva, A. Farlenkov, S. Plaksin, G. Vdovin, A. Demin and D. Medvedev, Mater, 2019, 12, 118 CrossRef CAS.
- W. Li, B. Guan, L. Ma, H. Tian and X. Liu, ACS Appl. Mater. Interfaces, 2019, 11, 18323–18330 CrossRef CAS.
- A. Løken, S. Ricote and S. Wachowski, Crystals, 2018, 8, 365 CrossRef.
- R. Raghvendra, R. K. Singh and P. Singh, J. Mater. Sci., 2014, 49, 5571–5578 CrossRef CAS.
- D. Tsvetkov, N. Tsvetkova, I. Ivanov, D. Malyshkin, V. Sereda and A. Zuev, Energies, 2019, 12, 417 CrossRef CAS.
- P. Gao, A. Bolon, M. Taneja, Z. Xie, N. Orlovskaya and M. Radovic, Solid State Ionics, 2017, 300, 1–9 CrossRef CAS.
- Y. G. Lyagaeva, D. A. Medvedev, A. K. Demin, P. Tsiakaras and O. G. Reznitskikh, Phys. Solid State, 2015, 57, 285–289 CrossRef CAS.
- Y.-P. Wang, Q. Xu, D.-P. Huang, K. Zhao, M. Chen and B.-H. Kim, Int. J. Hydrogen Energy, 2016, 41, 6476–6485 CrossRef CAS.
- V. Vibhu, A. Rougier, J.-C. Grenier and J.-M. Bassat, ECS Trans., 2013, 57, 2093–2100 CrossRef.
- Y. G. Lyagaeva, N. A. Danilov, M. Y. Gorshkov, G. K. Vdovin, B. D. Antonov, A. K. Demin and D. A. Medvedev, Russ. J. Appl. Chem., 2018, 91, 583–590 CrossRef CAS.
- Y.-P. Wang, Q. Xu, D.-P. Huang, K. Zhao, M. Chen and B.-H. Kim, Int. J. Hydrogen Energy, 2017, 42, 6290–6302 CrossRef CAS.
- A. Aguadero, J. A. Alonso, M. T. Fernandez-Diaz, M. J. Escudero and L. Daza, J. Power Sources, 2007, 169, 17–24 CrossRef CAS.
- V. V. Kharton, A. V. Kovalevsky, M. Avdeev, E. V. Tsipis, M. V. Patrakeev, A. A. Yaremchenko, E. N. Naumovich and J. R. Frade, Chem. Mater., 2007, 19, 2027–2033 CrossRef CAS.
- J. Yeyongchaiwat, K. Nonthawissarut, S. Charojrochkul and N. Sukpirom, Adv. Appl. Ceram., 2014, 114, 1–8 Search PubMed.
- X.-D. Zhou, J. W. Templeton, Z. Nie, H. Chen, J. W. Stevenson and L. R. Pederson, Electrochim. Acta, 2012, 71, 44–49 CrossRef CAS.
- J. Cheng, S. Zhang, B. Meng, J. Ding and X. Tan, J. Alloys Compd., 2018, 742, 966–976 CrossRef CAS.
- T.-W. Chiu, M.-X. Lin, H.-Y. Shih, B. Hwang, H.-Y. Chang and Y.-M. Wang, Ceram. Int., 2017, 43, S700–S704 CrossRef CAS.
- M. Li, J. Cheng, Y. Gan, S. Li, B. He and W. Sun, J. Power Sources, 2015, 275, 151–158 CrossRef CAS.
- X. Meng, S. Lü, S. Liu, X. Liu, Y. Sui, X. Li, M. Pang, B. Wang, Y. Ji and M. Z. Hu, Ceram. Int., 2015, 41, 12107–12114 CrossRef CAS.
- T. Chen, Y. Zhou, C. Yuan, M. Liu, X. Meng, Z. Zhan, C. Xia and S. Wang, J. Power Sources, 2014, 269, 812–817 CrossRef CAS.
- M. Letilly, A. L. G. L. Salle, M. Caldes, M. Marrony and O. Joubert, Fuel Cells, 2009, 9, 622–629 CrossRef CAS.
- L.-P. Sun, Q. Li, H. Zhao, L.-H. Huo and J.-C. Grenier, J. Power Sources, 2008, 183, 43–48 CrossRef CAS.
- R. Pelosato, G. Cordaro, D. Stucchi, C. Cristiani and G. Dotelli, J. Power Sources, 2015, 298, 46–67 CrossRef CAS.
- L. Mogni, F. Prado, C. Jimenez and A. Caneiro, Solid State Ionics, 2013, 240, 19–28 CrossRef CAS.
- B. Sikder, A. Chanda, S. Goswami, D. Bhattacharya and S. Velaga, Mater. Chem. Phys., 2019, 236, 121770 CrossRef CAS.
- L.-S. Unger, C. Niedrig, S. F. Wagner, W. Menesklou, S. Baumann, W. A. Meulenberg and E. Ivers-Tiffee, J. Eur. Ceram. Soc., 2018, 38, 2378–2387 CrossRef CAS.
- F. Liang, Z. Yang, H. Deng, J. Sunarso, L. Yang and J. Mao, J. Mater. Sci. Technol., 2019, 35, 1184–1191 CrossRef.
- H. Hao, L. Zhao, J. Hu, X. Hu and H. Hou, J. Rare Earths, 2009, 27, 815–818 CrossRef.
- N. A. Danilov, A. P. Tarutin, J. G. Lyagaeva, E. Y. Pikalova, A. A. Murashkina, D. A. Medvedev, M. V. Patrakeev and A. K. Demin, Ceram. Int., 2017, 43, 15418–15423 CrossRef CAS.
- W. H. Kan, K.-Y. Lai, A. Huq and A. Manthiram, J. Power Sources, 2016, 307, 454–461 CrossRef CAS.
- S. R. Bishop, D. Marrocchelli, C. Chatzichristodoulou, N. H. Perry, M. B. Mogensen, H. L. Tuller and E. D. Wachsman, Annu. Rev. Mater. Res., 2014, 44, 205–239 CrossRef CAS.
- S. R. Bishop, K. L. Duncan and E. D. Wachsman, J. Am. Ceram. Soc., 2010, 93, 4115–4121 CrossRef CAS.
- S. R. Bishop, K. L. Duncan and E. D. Wachsman, Acta Mater., 2009, 57, 3596–3605 CrossRef CAS.
- T. Nakamura, K. Yashiro, K. Sato and J. Mizusaki, Solid State Ionics, 2010, 181, 292–299 CrossRef CAS.
- S. R. Bishop, D. Marrocchelli, W. Fang, K. Amezawa, K. Yashiro and G. W. Watson, Energy Environ. Sci., 2013, 6, 1142–1146 RSC.
- V. V. Kharton, A. A. Yaremchenko, M. V. Patrakeev, E. N. Naumovich and F. M. B. Marques, J. Eur. Ceram. Soc., 2003, 23, 1417–1426 CrossRef CAS.
- V. V. Vashook, DSc. thesis, Institute of General and Inorganic Chemistry, National Belarus Academy of Sciences, Minsk, Belarus, 2000.
- H. Ullmann, N. Trofimenko, F. Tietz, D. Stöver and A. Ahmad-Khanlou, Solid State Ionics, 2000, 138, 79–90 CrossRef CAS.
- L. P. Putilov, N. A. Shevyrev, A. M. Mineev, A. S. Farlenkov, D. A. Medvedev and V. I. Tsidilkovski, Acta Mater., 2020, 190, 70–80 CrossRef CAS.
- K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359 CrossRef CAS.
- E. Fabbri, Daniele Pergolesi and Enrico Traversa, Chem. Soc. Rev., 2010, 39, 4355–4369 RSC.
- N. Tarasova, A. Galisheva and I. Animitsa, Ionics, 2020, 26, 5075–5088 CrossRef CAS.
- N. Tarasova, I. Animitsa and A. Galisheva, J. Solid State Electrochem., 2020, 24, 1497–1508 CrossRef CAS.
- N. A. Tarasova, A. O. Galisheva, I. E. Animitsa and D. V. Korona, Russ. J. Phys. Chem. A, 2020, 94, 818–821 CrossRef CAS.
- N. Tarasova, I. Animitsa, A. Galisheva and V. Pryakhina, Solid State Sci., 2020, 101, 106121 CrossRef CAS.
- M. Chen, Y. Xuan, F. Zhang, L. He, X. Wang, H. Pan, J. Ren and Z. Lin, Int. J. Hydrogen Energy, 2020, 45, 14964–14971 CrossRef CAS.
- W. Tan, D. Huan, W. Yang, N. Shi, W. Wang, R. Peng, X. Wu and Y. Lu, RSC Adv., 2018, 8, 26448–26460 RSC.
- G. Rinaldi, A. Nakajo, P. Burdet, M. Cantoni, W. K. S. Chiu and J. Van herle, Acta Mater., 2019, 178, 194–206 CrossRef CAS.
- H. Moussaoui, R. K. Sharma, J. Debayle, Y. Gavet, G. Delette and J. Laurencin, J. Power Sources, 2019, 412, 736–748 CrossRef CAS.
- W. Kong, M. Zhang, Z. Han and Q. Zhang, Appl. Sci., 2019, 9, 493 CrossRef CAS.
- P. Vijay, M. O. Tadéa, Z. Shao and M. Ni, Int. J. Hydrogen Energy, 2017, 42, 28836–28851 CrossRef CAS.
- X. Lu, T. M. M. Heenan, J. J. Bailey, T. Li, K. Li, D. J. L. Brett and P. R. Shearing, J. Power Sources, 2017, 365, 210–219 CrossRef CAS.
- E. V. Tsipis and V. V. Kharton, J. Solid State Electrochem., 2008, 12, 1039–1060 CrossRef CAS.
- X.-Y. Wu and A. F. Ghoniem, Prog. Energy Combust. Sci., 2019, 74, 1–30 CrossRef.
- A. A. Plazaola, A. C. Labella, Y. Liu, N. B. Porras, D. A. P. Tanaka, M. V. S. Annaland and F. Gallucci, Processes, 2019, 7, 128 CrossRef CAS.
- M. Acosta, F. Baiutti, A. Tarancón and J. L. MacManus-Driscoll, Adv. Mater. Interfaces, 2019, 6, 1900462 CrossRef.
- C. Li, J. J. Chew, A. Mahmoud, S. Liu and J. Sunarso, J. Membr. Sci., 2018, 567, 228–260 CrossRef CAS.
- C. Zhang, J. Sunarso and S. Liu, Chem. Soc. Rev., 2017, 46, 2941–3005 RSC.
- V. L. Kozhevnikov, I. A. Leonidov and M. V. Patrakeev, Russ. Chem. Rev., 2013, 82, 772–782 CrossRef.
- S. B. Adler, J. A. Lane and B. C. H. Steele, J. Electrochem. Soc., 1996, 143, 3554 CrossRef CAS.
- Z. Zhao, J. Cui, M. Zou, S. Mu, H. Huang, Y. Meng, K. He, K. S. Brinkman and J. Tong, J. Power Sources, 2020, 450, 227609 CrossRef CAS.
- C. Xia, Y. Mi, B. Wang, B. Lin, G. Chen and B. Zhu, Nat. Commun., 2019, 10, 1707 CrossRef.
- Y. Song, Y. Chen, W. Wang, C. Zhou, Y. Zhong, G. Yang, W. Zhou, M. Liu and Z. Shao, Joule, 2019, 3, 2842–2853 CrossRef CAS.
- K. Wei, N. Li, Y. Wu, W. Song, X. Wang, L. Guo, M. Khan, S. Wang, F. Zho and Y. Ling, Ceram. Int., 2019, 45, 18583–18591 CrossRef CAS.
- R. Ren, Z. Wang, C. Xu, W. Sun, J. Qiao, D. W. Rooneyc and K. Sun, J. Mater. Chem. A, 2019, 7, 18365–18372 RSC.
- J. C. Grenier, F. Mauvy, C. Lalanne, J.-M. Bassat, F. Chauveau, J. Mougin, J. Dailly and M. Marrony, ECS Trans., 2009, 25, 2537–2546 CrossRef CAS.
- J. Hou, Z. Zhu, J. Qian and W. Liu, J. Power Sources, 2014, 264, 67–75 CrossRef CAS.
- J. Hou, J. Qian, L. Bi, Z. Gong, R. Penga and W. Liu, J. Mater. Chem. A, 2015, 3, 2207–2215 RSC.
- Y. G. Lyagaeva, N. A. Danilov, M. Y. Gorshkov, G. K. Vdovin, B. D. Antonov, A. K. Demin and D. A. Medvedev, Russ. J. Appl. Chem., 2018, 91, 583–590 CrossRef CAS.
- E. P. Antonova, A. A. Kolchugin, E. Y. Pikalova, D. A. Medvedev and N. M. Bogdanovich, Solid State Ionics, 2017, 306, 55–61 CrossRef CAS.
- E. Y. Pikalova, N. M. Bogdanovich and A. V. Kuzmin, Russ. J. Electrochem., 2017, 53, 752–760 CrossRef CAS.
- S. Yang, Y. Wen, J. Zhang, Y. Lu, X. Ye and Z. Wen, Electrochim. Acta, 2018, 267, 269–277 CrossRef CAS.
- C. Sun, S. Yang, Y. Lu, J. Wen, X. Ye and Z. Wen, J. Power Sources, 2020, 449, 227498 CrossRef CAS.
- A. P. Tarutin, M. Y. Gorshkov, I. N. Bainov, G. K. Vdovin, A. I. Vylkov, J. G. Lyagaeva and D. A. Medvedev, Ceram. Int., 2020, 46, 24355–24364 CrossRef CAS.
- T. Park, J. Korean Soc. Precis. Eng., 2018, 35, 1141–1146 CrossRef.
- J. Dailly, F. Mauvy, M. Marrony, M. Pouchard and J.-C. Grenier, J. Solid State Electrochem., 2011, 15, 245–251 CrossRef CAS.
- S. M. Babiniec, S. Ricote and N. P. Sullivan, J. Electrochem. Soc., 2014, 161, F717–F723 CrossRef CAS.
- A. Grimaud, F. Mauvy, J. M. Bassat, S. Fourcade, L. Rocheron, M. Marrony and J. C. Grenier, J. Electrochem. Soc., 2012, 159, B683–B694 CrossRef CAS.
- A. Y. Zuev, V. V. Sereda and D. S. Tsvetkov, J. Electrochem. Soc., 2012, 159, F594–F599 CrossRef CAS.
- N. E. Volkova, V. A. Kolotygin, L. Y. Gavrilova, V. V. Kharton and V. A. Cherepanov, Solid State Ionics, 2014, 260, 15–20 CrossRef CAS.
- E. V. Tsipis, E. N. Naumovich, M. V. Patrakeev, A. A. Yaremchenko, I. P. Marozau, A. V. Kovalevsky, J. C. Waerenborgh and V. V. Kharton, Solid State Ionics, 2011, 192, 42–48 CrossRef CAS.
- E. V. Tsipis, M. V. Patrakeev, P. V. Anikina, E. N. Naumovich and V. V. Kharton, Mater. Lett., 2020, 265, 127425 CrossRef CAS.
- A. A. Markov, O. V. Merkulov, M. V. Patrakeev and I. A. Leonidov, Int. J. Hydrogen Energy, 2019, 44, 26807–26815 CrossRef CAS.
- C. Li, W. Li, J. J. Chew, S. Liu, X. Zhu and J. Sunarso, Sep. Purif. Technol., 2020, 235, 116224 CrossRef CAS.
- L. R. Tarutina, G. K. Vdovin, J. G. Lyagaeva and D. A. Medvedev, J. Alloys Compd., 2020, 831, 154895 CrossRef CAS.
- W. Deibert, M. E. Ivanova, S. Baumann, O. Guillon and W. A. Meulenberg, J. Membr. Sci., 2017, 543, 79–97 CrossRef CAS.
- M. Li, H. Niu, J. Druce, H. Téllez, T. Ishihara, J. A. Kilner, H. Gasparyan, M. J. Pitcher, W. Xu, J. F. Shin, L. M. Daniels, L. A. H. Jones, V. R. Dhanak, D. Hu, M. Zanella, J. B. Claridge and M. J. Rosseinsky, Adv. Mater., 2020, 32, 1905200 CrossRef CAS.
- K. Ishii, C. Matsunaga, K. Kobayashi, A. J. Stevenson, C. Tardivat and T. Uchikoshi, J. Eur. Ceram. Soc., 2019, 39, 5292–5297 CrossRef CAS.
- E. V. Shubnikova, M. P. Popov, S. F. Bychkov, S. A. Chizhik and A. P. Nemudry, Chem. Eng. J., 2019, 372, 251–259 CrossRef CAS.
- D. Ding, X. Li, S. Y. Lai, K. Gerdes and M. Liu, Energy Environ. Sci., 2014, 7, 552–575 RSC.
- S. P. Jiang, Int. J. Hydrogen Energy, 2012, 37, 449–470 CrossRef CAS.
- C. Zhao, Y. Li, W. Zhang, Y. Zheng, X. Lou, B. Yu, J. Chen, Y. Chen, M. Liu and J. Wang, Energy Environ. Sci., 2020, 13, 53–85 RSC.
- R. Zohourian, R. Merkle, G. Raimondi and J. Maier, Adv. Funct. Mater., 2018, 28, 1801241 CrossRef.
- R. Zohourian, R. Merkle and J. Maier, Solid State Ionics, 2017, 299, 64–69 CrossRef CAS.
- H. T. Lozano, J. Druce, S. J. Cooper and J. A. Kilner, Sci. Technol. Adv. Mater., 2017, 18, 977–986 CrossRef CAS.
- H. Tang, Z. Gong, Y. Wu, Z. Jin and W. Liu, Int. J. Hydrogen Energy, 2018, 43, 19749–19756 CrossRef CAS.
- J. Dailly and M. Marrony, J. Power Sources, 2013, 240, 323–327 CrossRef CAS.
- J. Dailly, M. Marrony, G. Taillades, M. Taillades-Jacquin, A. Grimaud, F. Mauvy, E. Louradour and J. Salmi, J. Power Sources, 2014, 255, 302–307 CrossRef CAS.
- N. Nasani, D. Ramasamy, S. Mikhalev, A. V. Kovalevsky and D. P. Fagg, J. Power Sources, 2015, 278, 582–589 CrossRef CAS.
- E. Pikalova, A. Kolchugin, N. Bogdanovich, D. Medvedev, J. Lyagaeva, L. Vedmid, M. Ananyev, S. Plaksin and A. Farlenkov, Int. J. Hydrogen Energy, 2020, 45, 13612–13624 CrossRef CAS.
- A. Tarutin, A. Kasyanova, J. Lyagaeva, G. Vdovin and D. Medvedev, J. Energy Chem., 2020, 40, 65–74 CrossRef.
- X. Li, D. Huan, N. Shi, Y. Yang, Y. Wan, C. Xia, R. Peng and Y. Lu, Int. J. Hydrogen Energy, 2020, 45, 17736–17744 CrossRef CAS.
- A. Tarutin, N. Danilov, J. Lyagaeva and D. Medvedev, Appl. Sci., 2020, 10, 2481 CrossRef CAS.
- J. Lyagaeva, N. Danilov, G. Vdovin, J. Bu, D. Medvedev, A. Demin and P. Tsiakaras, J. Mater. Chem. A, 2016, 4, 15390–15399 RSC.
- S. Yang, Y. Lu, Q. Wang, C. Sun, X. Ye and Z. Wen, Int. J. Hydrogen Energy, 2018, 43, 20050–20058 CrossRef CAS.
- S. Yang, S. Zhang, C. Sun, X. Ye and Z. Wen, ACS Appl. Mater. Interfaces, 2018, 10, 42387–42396 CrossRef CAS.
- N. Danilov, A. Tarutin, J. Lyagaeva, G. Vdovin and D. Medvedev, J. Mater. Chem. A, 2018, 6, 16341–16346 RSC.
- N. Danilov, J. Lyagaeva, G. Vdovin and D. Medvedev, Appl. Energy, 2019, 237, 924–934 CrossRef CAS.
- J. Li, J. Hou, Y. Lu, Q. Wang, X. Xi, Y. Fan, X.-Z. Fu and J.-L. Luo, J. Power Sources, 2020, 453, 227909 CrossRef CAS.
- Y. Bu, S. Joo, Y. Zhang, Y. Wang, D. Meng, X. Ge and G. Kim, J. Power Sources, 2020, 451, 227812 CrossRef CAS.
- S. Sun and Z. Cheng, J. Electrochem. Soc., 2020, 167, 024514 CrossRef CAS.
- D. Xie, K. Li, J. Yang, D. Yan, L. Jia, B. Chi, J. Pu and J. Li, Int. J. Hydrogen Energy, 2020 DOI:10.1016/j.ijhydene.2020.01.014.
- K. Miyazaki, Y. Ding, H. Muroyama, T. Matsui and K. Eguchi, Elecrtochemistry, 2020, 88, 28–33 CrossRef CAS.
- C. Ren, Y. Zhang, Q. Xu, T. Tian and F. Chen, Int. J. Hydrogen Energy, 2020, 45, 6926–6933 CrossRef CAS.
- M. Ahn, S. Hwang, S. Han, M. Choi, D. Byun and W. Lee, Korean J. Chem. Eng., 2020, 37, 1371–1378 CrossRef CAS.
- H. Tang, Z. Jin, Y. Wu, W. Liu and L. Bi, Electrochem. Commun., 2019, 100, 108–112 CrossRef CAS.
- A. He, J. Onishi, J. Gong and N. Shikazono, J. Power Sources, 2020, 478, 228771 CrossRef CAS.
- N. A. Baharuddin, N. F. A. Rahman, H. A. Rahman, M. R. Somalu, M. A. Azmi and J. Raharjo, Int. J. Energy Res., 2020, 44, 8269–8313 CrossRef.
- J. H. Shim, G. D. Han, H. J. Choi, Y. Kim, S. Xu, J. An, Y. B. Kim, T. Graf, T. D. Schladt, T. M. Gür and F. B. Prinz, Int. J. Precis. Eng. Manuf.- Green Technol., 2019, 6, 629–646 CrossRef.
- E. G. Kalinina and E. Y. Pikalova, Russ. Chem. Rev., 2019, 88, 1179–1219 CrossRef CAS.
- P. A. Connor, X. Yue, C. D. Savaniu, R. Price, G. Triantafyllou, M. Cassidy, G. Kerherve, D. J. Payne, R. C. Maher, L. F. Cohen, R. I. Tomov, B. A. Glowacki, R. V. Kumar and J. T. S. Irvine, Adv. Energy Mater., 2018, 8, 1800120 CrossRef.
- V. A. Tsvinkinberg, A. S. Tolkacheva, E. A. Filonova, O. I. Gyrdasova, S. M. Pikalov, V. A. Vorotnikov, A. I. Vylkov, N. I. Moskalenko and E. Y. Pikalova, J. Alloys Compd., 2020, 853, 156728 CrossRef.
- V. A. Sadykov, E. M. Sadovskaya, E. A. Filonova, N. F. Eremeev, V. D. Belyaev, V. A. Tsvinkinberg and E. Y. Pikalova, Solid State Ionics, 2020, 357, 115432 CrossRef.
- Q. Zhou, T. Zhang, C. Zhao, L. Qu, Y. He, T. Wei and X. Tong, Mater. Res. Bull., 2020, 131, 110986 CrossRef CAS.
- Y. Sadia, Y. Gelbstein and S. J. Skinner, J. Solid State Chem., 2020, 290, 121556 CrossRef CAS.
- Е. А. Filonova, E. Yu Pikalova, T. Yu Maksimchuk, А. I. Vylkov, S. M. Pikalov and A. Maignan, Int. J. Hydrogen Energy, 2020 DOI:10.1016/j.ijhydene.2020.10.243.
- M. Khoshkalam, Đ. Tripković, X. Tong, M. A. Faghihi-Sani, M. Chen and P. V. Hendriksen, J. Power Sources, 2020, 457, 228035 CrossRef CAS.
- T. Wan, A. Zhu, Y. Guo, C. Wang, S. Huang, H. Chen, G. Yang, W. Wang and Z. Shao, J. Power Sources, 2017, 348, 9–15 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta08132a |
| This journal is © The Royal Society of Chemistry 2021 |