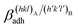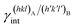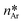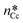Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Epitaxy: a methodological approach to the study of an old phenomenon
M.
Bruno
 *abc,
L.
Pastero
*abc,
L.
Pastero
 abc,
A.
Cotellucci
abc,
A.
Cotellucci
 a and
D.
Aquilano
a and
D.
Aquilano
 a
a
aDipartimento di Scienze della Terra, Università degli Studi di Torino, Via Valperga Caluso 35, 10125, Torino (TO), Italy. E-mail: marco.bruno@unito.it; Tel: +39 011 6705124
bSpectraLab s.r.l., Spin-off accademico dell'Università degli Studi di Torino, Via G. Quarello 15/a, 10135, Torino (TO), Italy
cNIS, Centre for Nanostructured Interfaces and Surfaces, Università degli Studi di Torino, Via G. Quarello 15/a, 10135, Torino (TO), Italy
First published on 5th May 2022
Abstract
Epitaxial growth is a long-standing crystallization phenomenon of great technological interest. Here, we present the use of a new methodology approach making full use of the concept of adhesion energy between two different crystal phases, A and B. This is achieved by using (i) the traditional crystal-chemical fit between A and B; (ii) the extensive use of Bollmann's approach to the 2D-lattice coincidences; (iii) the most accurate methods of calculation of the specific adhesion energy of A/B. We illustrate the approach with two case studies: (i) how epilayers of inorganic and monoclinic Li2CO3 (zabuyelite) can modify the crystal habit of the CaCO3 polymorphs, calcite (rhombohedral) and aragonite (orthorhombic); (ii) how a complex organic substance like sericin (silk fibroin like protein-SFLP) could stabilize aragonite and calcite, the most diffuse CaCO3 polymorphs, simply reproducing and mimicking in the laboratory what nature does.
1. Introduction
Epitaxy is a type of crystal growth in which a new crystalline phase is formed with one or more well-defined orientations coincident with respect to a crystalline substrate. It is possible to make the following distinction: (i) homoepitaxy, a crystalline substance grows on a crystalline substrate of the same material (e.g., twinned crystals), and (ii) heteroepitaxy, a crystalline substance grows on a crystalline substrate made with a different material (e.g., calcite above aragonite in mollusks' shells). To univocally define the orientation relationship (OR) of phases A and B that are epitaxially related, it is needed to specify: (i) the crystal faces that are in contact, (hkl)A/(h′k′l′)B; (ii) the 2D coincidence cell between (hkl)A and (h′k′l′)B. As regards point (ii), it is possible to identify many 2D coincidence cells1 by searching the 2D (m × n)-supercells that describe the (hkl)A and (h′k′l′)B surfaces and show their best parametric, angular and areal matches. According to the terminology universally accepted concerning epitaxy, when the lattice constants of phases A and B match, that is when (1 × 1)-A ≡ (1 × 1)-B, the interface is said to be coherent; when a relation such as (m × n)-A ≡ (k × s)-B exists, with m, n, k and s integers (and the supercell parameters are not too long on the lattice length scale), the interface is commensurate; otherwise it is incommensurate. Moreover, as widely discussed in some recent papers,2–9 crystal faces (hkl)A and (h′k′l′)B can show several surface terminations (e.g., different structures for the same surface). If the number of the surface terminations is p and r for (hkl)A and (h′k′l′)B, respectively, the number of possible interface configurations can be very high, p × r.Accordingly, epitaxy is strictly correlated with the formation of a crystalline interface. Then, the study of epitaxy cannot be separated by the investigations of the interfaces both at the observational and computational levels. Indeed, the formation of the interfaces fascinated mineralogists as Royer10 whose systematic observations established the crystallographic and crystal-chemical constraints of epitaxy. However, it was soon clear that macroscopic bi-crystals produced in laboratories are originated from more complex mechanisms than those described by Royer.11,12 It became then clear the need for powerful techniques for the analysis of the interfaces, e.g. see Kern,13 as well as theoretical and computational modeling.
At the computational level, to individuate the most probable epitaxial coincidence (i.e., the structure of the interface) one has to calculate the specific adhesion energy (or the corresponding specific interfacial energy, from Dupré–Young's equation) between the two phases for each 2D coincident cell identified:1 the lower the adhesion energy, the lower the probability to observe the corresponding epitaxial interface and, consequently, that particular crystallographic orientation. It is important to address that a good 2D lattice coincidence (2D-LC hereinafter) at the A/B interface is a “necessary but not sufficient condition” to establish the probability that epitaxy could occur. Indeed, the knowledge of the adhesion energy between phases A and B is the fundamental requirement to evaluate the probability of observing epitaxial relationships between two phases. Without this thermodynamic quantity, the only geometrical description of 2D-LCs does not allow the epitaxial phenomenon to be characterized in detail. Actually, a good 2D-LC at the A/B interface is nothing else than a geometrical implication of a physical property, i.e. a good adhesion between two epitaxial phases.
The specific adhesion energy, 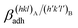 (J m−2), is the energy gained once the boundary interface is formed; the specific interfacial energy,
(J m−2), is the energy gained once the boundary interface is formed; the specific interfacial energy, 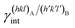 (J m−2), is the energy amount needed to increase the interface of a unit area.14 Adhesion energy is intimately related to the interfacial energy by Dupré's relation:13
(J m−2), is the energy amount needed to increase the interface of a unit area.14 Adhesion energy is intimately related to the interfacial energy by Dupré's relation:13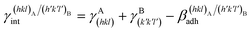 ; where γA(hkl) and
; where γA(hkl) and 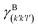 are the specific surface energies (J m−2) in the vacuum of the (hkl) and (h′k′l′) free faces of A and B, respectively. Calculations for determining
are the specific surface energies (J m−2) in the vacuum of the (hkl) and (h′k′l′) free faces of A and B, respectively. Calculations for determining 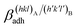 and
and 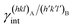 can be performed both at the empirical level,15 when force fields of the phases involved are known, and at the quantum-mechanical level.1,16–18
can be performed both at the empirical level,15 when force fields of the phases involved are known, and at the quantum-mechanical level.1,16–18
Crystalline interfaces determine both chemical and physical properties of devices for applications in mechanics, electronics, medicine, and in materials chemistry for designing and engineering of composite materials. To produce high quality materials with specific and controlled properties, it is needed to carry out research on surface and interface thermodynamics, as exposed in two well-documented and exhaustive books by Sutton and Baluffi19 and Bollmann,20 in a review on stress and strain in epitaxy21,22 and in the historical review by Kern.23 It is nowadays evident that an understanding of surface and interface properties is essential to deepen our knowledge in pure and applied research. Some examples are: (i) the selection of additives as crystal habit modifiers,24,25 (ii) the size dependent properties of associations of rock forming minerals in relation to the conditions of their formation,26,27 (iii) the kinetics of reactions at interfaces,28 (iv) the precipitation of minerals in natural aqueous environments as epilayers modifying the properties of the mineral–water interface, passivating significantly the surface of the underlying minerals and determining the composition of surface water,29,30 (v) the formation of human bones and bio-stones, (vi) the adsorption of DNA on mineral surfaces, (vii) the development of nacre platelets of mollusks, and (viii) the ordered crystallization of micro and nano-phases on substrates.31–33
In this contribution, we will describe only two phenomena related to crystal growth in which epitaxy plays a primary role: (i) selective ad/absorption of 2D-phase A on some faces of phase B (i.e., 2D adsorption-epitaxy);16 (ii) selection of the polymorph due to preferential adhesion on a (organic or inorganic) substrate.34 Point (i) will be elucidated by describing the ad/absorption of 2D crystals of zabuyelite (Li2CO3; S.G. C2/c; a0 = 8.3593 Å, b0 = 4.9725 Å, c0 = 6.1975 Å, β = 114.83°)35 above some forms of calcite (CaCO3; S.G. R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c; a0 = 4.988 Å, c0 = 17.061 Å)36 and aragonite (CaCO3; S.G. Pmcn; a0 = 4.9614 Å, b0 = 7.9671 Å, c0 = 5.7414 Å).37 2D epilayers of zabuyelite act as crystal habit modifiers, by slowing down the growth rate of some forms of calcite and aragonite. Instead, point (ii) will be faced by discussing how the use of a suitable substrate is able to trigger the formation of a metastable polymorph with respect to the stable one, under well-defined P and T conditions. We will discuss the formation of calcium carbonate polymorphs (calcite/aragonite) in the presence of sericin (SFPL, silk fibroin-like protein) that generate a sericin–aragonite–calcite self-assembled artificial composite with a hierarchical structure comparable to that of natural nacre.
c; a0 = 4.988 Å, c0 = 17.061 Å)36 and aragonite (CaCO3; S.G. Pmcn; a0 = 4.9614 Å, b0 = 7.9671 Å, c0 = 5.7414 Å).37 2D epilayers of zabuyelite act as crystal habit modifiers, by slowing down the growth rate of some forms of calcite and aragonite. Instead, point (ii) will be faced by discussing how the use of a suitable substrate is able to trigger the formation of a metastable polymorph with respect to the stable one, under well-defined P and T conditions. We will discuss the formation of calcium carbonate polymorphs (calcite/aragonite) in the presence of sericin (SFPL, silk fibroin-like protein) that generate a sericin–aragonite–calcite self-assembled artificial composite with a hierarchical structure comparable to that of natural nacre.
Point (i) will be discussed in light of a new approach, in which laboratory experiments and quantum-mechanical calculations were combined together, in order to provide an exhaustive picture of the phenomenon. In fact, to understand the intimate nature of this kind of epitaxy, a careful observation of the experiments, a geometric description of the interface at the reticular level and the determination of the adhesion energy of the phases involved are essential.
Quantum-mechanical calculations were not performed for point (ii), due to the extreme complexity of the system. But, a detailed geometrical analysis of the possible 2D-CLs between (00.1)Cc and (001)SFLP (sericin: SFLP, silk fibroin like protein), and (001)Ar and (001)SFLP was performed, along with several growth experiments to detail the effect of sericin on stabilization of CaCO3 polymorphs and crystal morphology.
In this short review, we decided to not describe the application of transmission electron microscopy (TEM) to the study of epitaxial growth. We are aware that its use is fundamental for complete characterization of the phenomenon, but we preferred to omit this technique for the following reasons: (i) we are not the best experts in its use, (ii) the examples described in this work were not observed with TEM, and (iii) we have deliberately chosen to propose an energetic and reticular description of epitaxy.
2. How to perform energy calculations
As detailed in the paper by Bruno et al.,1 adhesion energy calculation can be performed both at the empirical and quantum-mechanical levels at 0 K (i.e., static calculations). To investigate the interface structure between two phases in epitaxial relationship, a 2D periodic slab model38 must be adopted. Then, we need to construct a composed slab (A/B/A; Fig. 1a) to be optimized, for finding the equilibrium geometry of the interface at the minimum of its energy. The composed slab, made with phases A and B (slabs A and B in the following), is generated in the following way: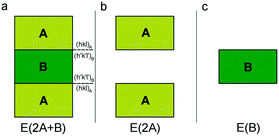 | ||
| Fig. 1 Schematic of the three systems to be optimized for calculating the adhesion energy: (a) composed slab A/B/A, (b) slab A/vacuum/A and (c) slab B. Redrawn from Bruno et al.1 | ||
(i) slabs A and B of a given thickness are made by cutting their respective bulk structures parallel to the hkl planes of interest and using the same 2D-LCs describing the epitaxy;
(ii) slab B is placed in between two slabs A;
(iii) the composed slab geometry (2D-CLs and atomic coordinates) is optimized by considering all the atoms free to move. The composed slab A/B/A is generated preserving the center of inversion or a mirror plane parallel to the face, to avoid the dipole moment component perpendicular to the slab. Indeed, the existence of an infinite 2D array of iso-oriented surface dipole moment-vectors would make the value of the electrical field in the surface sites infinite.39,40 Therefore, for the polar faces, surface energy would tend to infinity when increasing the thickness of the slab, which should be a physically inadmissible condition.
The calculations are done by considering the composed slabs with a thickness sufficient to obtain an accurate description of the interfaces. The slab thickness is considered appropriate when the bulk-like properties are reproduced at the centre of slabs A and B.
The adhesion energy is thus calculated as follows:
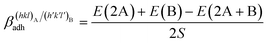 | (1) |
To take into account the T and P effects on the adhesion energy, very demanding calculations should be done, which cannot be performed with the computational resources at our disposal. Moreover, to the best of our knowledge, no studies on the effect of T and P on the energetics of the epitaxial interfaces are discussed. This lack of information prevents us from knowing the behaviour of the adhesion energies when both T and P increase. To have a realistic estimate of the temperature effect for the different interfaces, it is necessary to determine (at the ab initio level) the frequencies of the vibrational modes of the composed slabs, which are essential for calculating the vibrational contribution (i.e., vibrational energy and vibrational entropy) to the interface energy of an epitaxial system.
3. 2D epitaxy as a habit modifier
The influence of lithium on the growth morphology of calcite was discussed, for the first time, by Rajam and Mann41 who found the appearance of the structurally unstable kinked (K) {00.1} pinacoid, in addition to the classic cleavage {10.4} rhombohedron, in calcite crystals growing from aqueous solution in the presence of Li+ ions. The occurrence of the {00.1} form in calcite was explained in terms of random absorption of Li+ into the growing 00.1 lattice planes that slows down the growth rate of the corresponding surfaces.Successive studies on calcite growth from aqueous solutions in the presence of variable Li+ concentrations showed that the character of both the {00.1} and {01.8} forms of calcite changes from kinked (K) and stepped (S) to flat (F), respectively.42–45 When increasing the Li+ concentration, the morphology of calcite turns from the sole {10.4} form to a flat pseudo-hexagonal shape dominated by the {00.1} pinacoid. This behavior was attributed to the epitaxy between calcite and zabuyelite (Za). Further experiments16 showed that high Li+ concentrations into the mother solution (a Li+/Ca2+ molar ratio higher than 15, and a very high supersaturation value with respect to both aragonite, 0.57, and calcite, 0.71) determine not only the character modification of several forms of calcite, but also the formation of aragonite, a second CaCO3 phase, with a pseudo-hexagonal prismatic morphology accompanied by a repeated twinning on the 110 plane (Fig. 2). All these experiments have highlighted that the transition “calcite → morphologically modified calcite → morphologically modified aragonite” occurs in solution and depends on the Li+/Ca2+ ratio. Summing up, the 2D-epitaxies calcite/zabuyelite and aragonite/zabuyelite could play a determining role in two distinct and in-sequence growth processes.
 | ||
| Fig. 2 Calcium carbonate polymorph grown in the presence of lithium in solution: (a) calcite cleavage rhombohedron with initial rounding of corners and apexes (modified from Aquilano et al.46); (b) prismatic aragonite crystals associated with flat, pseudo-hexagonal calcite crystals (modified from Aquilano et al.16). | ||
(i) Habit modification of calcite
When the lithium concentration in the mother phase is moderate, 5 < Li+/Ca2+ < 15, the {00.1}-K, {01.8}-S and {10.4}-F forms of calcite are progressively affected by the 2D epitaxy of zabuyelite, with the increasing morphological importance of the {00.1} pinacoid. Accordingly, the crystal habit becomes more and more {00.1} platy.(ii) Polymorphic transition: calcite → aragonite
As much as lithium concentration increases, Li+/Ca2+ > 15, aragonite crystals start appearing in the growth solution as single and twinned individuals, accompanied by large and {00.1} platy pseudo-hexagonal calcite. Their habit is squat-prismatic, with a large {001} pinacoid and equant {110} and {100} prisms. This polymorphic transition proves that the epi-adsorption of the 2D island of zabuyelite overcomes the critical activation energy for the 3D nucleation of aragonite, owing to the lowering of its weighted surface energy.To explain the peculiar morphology of the calcite and aragonite crystals grown in the presence of Li+, Aquilano et al.16,46 determined both the structure and energetics of the (10.4)Cc/(001)Za, (00.1)Cc/(001)Za, (001)Ar/(001)Za, (001)Ar/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)Za and (001)Ar/(
01)Za and (001)Ar/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02)Za interfaces, through quantum-mechanical calculations at the DFT (density functional theory) level. They used the computational strategy previously described and the 2D near-coincidence meshes reported in Table 1. Computational details and description of the possible (00.1)Cc and (001)Ar terminations are reported by Aquilano et al.,16,46 and will not be further discussed. Here, we only take into account the epitaxial interfaces showing the lowest interfacial and the highest adhesion energy, whose values are listed in Table 1.
02)Za interfaces, through quantum-mechanical calculations at the DFT (density functional theory) level. They used the computational strategy previously described and the 2D near-coincidence meshes reported in Table 1. Computational details and description of the possible (00.1)Cc and (001)Ar terminations are reported by Aquilano et al.,16,46 and will not be further discussed. Here, we only take into account the epitaxial interfaces showing the lowest interfacial and the highest adhesion energy, whose values are listed in Table 1.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)Za and (001)Ar/(
01)Za and (001)Ar/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02)Za interfaces
02)Za interfaces
| Interface | 2D cell | ||
|---|---|---|---|
| (10.4)Cc/(001)Za | [010]Cc ≡ [010]Za | 0.380 | 0.307 |
1/3 × [42![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ]Cc ≡ [100]Za ]Cc ≡ [100]Za |
|||
| (00.1)Cc/(001)Za | [100]Cc ≡ [010]Za | 1.264 | 0.220 |
| [120]Cc ≡ [100]Za | |||
| (001)Ar/(001)Za | [100]Ar ≡ [010]Za | 0.283 | 0.509 |
| [010]Ar ≡ [100]Za | |||
(001)Ar/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)Za 01)Za |
[100]Ar ≡ [010]Za | 0.595 | 0.297 |
| [010]Ar ≡ [101]Za | |||
(001)Ar/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02)Za 02)Za |
[100]Ar ≡ [010]Za | 0.440 | 0.502 |
| 2 × [010]Ar ≡ [201]Za |
By examining Table 1, it is possible to highlight that:
(i) 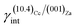 = 0.307 J m−2 is lower2 than the surface energy of (10.4)Cc, γ(10.4)Cc being 0.507 J m−2;2
= 0.307 J m−2 is lower2 than the surface energy of (10.4)Cc, γ(10.4)Cc being 0.507 J m−2;2
(ii) 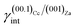 = 0.220 J m−2 is noteworthily lower7 than the surface energy of (00.1)Cc, where γ(00.1)Cc = 0.711 J m−2;7
= 0.220 J m−2 is noteworthily lower7 than the surface energy of (00.1)Cc, where γ(00.1)Cc = 0.711 J m−2;7
(iii) (001)Ar shows a strong affinity with (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)Za; indeed, the (001)Ar/(
01)Za; indeed, the (001)Ar/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)Za interface has an interfacial energy of
01)Za interface has an interfacial energy of 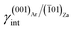 = 0.297 J m−2, lower than those of the (001)Ar/(001)Za and (001)Ar/(
= 0.297 J m−2, lower than those of the (001)Ar/(001)Za and (001)Ar/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02)Za interfaces.16 Moreover,
02)Za interfaces.16 Moreover, 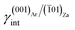 is lower with respect to the surface energy of (001)Ar, being γ(001)Ar = 0.612 J m−2.16
is lower with respect to the surface energy of (001)Ar, being γ(001)Ar = 0.612 J m−2.16
From these results, it follows that the 2D epitaxial adhesion of zabuyelite above the (00.1)Cc, (10.4)Cc and (001)Ar faces can strongly modify the equilibrium shape (ES) of calcite and aragonite. Aquilano et al.46 compared the equilibrium morphologies of calcite and aragonite determined without and with 2D adhesion of zabuyelite (Fig. 3); the ES was drawn by using the Gibbs–Wulff theorem14 and the calculated values of the surface (interface) energies for calcite and aragonite.
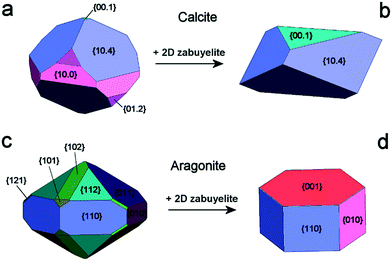 | ||
| Fig. 3 Equilibrium shapes of calcite and aragonite at 0 K. Calcite (a) and aragonite (c) in the vacuum; calcite (b) and aragonite (d), after the 2D-epitaxial adsorption of zabuyelite above (00.1)Cc, (10.4)Cc and (001)Ar. Redrawn from Aquilano et al.46 | ||
The ES of calcite in the absence of lithium is mainly composed of the following forms (Fig. 3a): the {10.4}-cleavage rhombohedron, {01.2}-steep rhombohedron, and {10.0}-prism; also {00.1} enters the ES, but from an area point of view its importance is negligible. When the 2D epitaxy of zabuyelite occurs, the ES changes dramatically (Fig. 3b): {10.0} and {01.2} disappear, whereas the area occupied by the form {00.1} increases. This strong ES modification is due to the contemporary lowering of the interfacial energy values, 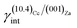 and
and 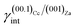 , with respect to the pure surface energies, γ(10.4)Cc and γ(00.1)Cc.
, with respect to the pure surface energies, γ(10.4)Cc and γ(00.1)Cc.
The aragonite ES, in the absence of lithium, is rich in crystallographic forms (Fig. 3c): {102}, {101}, {121}, {112}, {011}, {110} and {010}, whereas interestingly, {001} does not enter the ES. When lithium is present in the system, {001} is stabilized by the 2D epitaxy of zabuyelite, allowing this form to enter the ES (Fig. 3d) and, simultaneously, to obtain some crystallographic forms. The resulting pseudo-hexagonal ES is only composed of {001}, {110} and {010}. As for calcite, its modification is due to the 2D adsorption of zabuyelite that generates an interfacial energy, 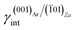 , lower than the surface energy, γ(001)Ar.
, lower than the surface energy, γ(001)Ar.
The equilibrium shapes, determined at the computational level (Fig. 3b and d), are very similar to the morphologies of the calcite and aragonite crystals obtained in the laboratory (Fig. 2), suggesting a correct interpretation of the phenomenon.
4. Epitaxy for the selection of the polymorph
One outstanding example of epitaxy, as the driving mechanism for polymorph selection, can be observed in biominerals. Crystals in biological mineralization are quite different from their abiotic counterparts because of their morphological behavior, uniform crystal size and crystallographic orientation. Biological crystals form under well-controlled conditions associated to an organic framework, or scaffold, called an “organic matrix”, built with extracellular macromolecules (β-chitin, silk-like proteins and glycoproteins containing aspartic acid-rich domains and covalently bound sulfated polysaccharides, synthesized by cells to fulfill functional purposes). While sulfate polysaccharides are believed to act as “calcium concentrators”, affecting mainly the local supersaturation (the “ionotropic effect” proposed by Chen),47 the aspartic acid-rich macromolecules are directly involved in the crystallization process, regulating nucleation, growth rates, morphologies and polymorph selection.48–52 Authors agree on the β-sheet conformation of the molecules in the organic matrix.53 The content in aspartic acid is usually pretty high; for instance, in scleractinian corals, it ranges between 40 and 50% molar of the protein assemblage, in mollusks it is 30% molar in the aragonite layers and more than 50% molar in the calcite layers.54 Higher acidic/basic ratios of amino acids have been generally recognized in the calcite-rich layers of mollusks' shells compared to aragonite layers,55 while glutamic acid or glutamine is usually associated with the presence of amorphous calcium carbonate in tissues, rather than the crystalline forms. The specificity of the organic matrix for the formation of calcium carbonate polymorphs has been considered in many papers, even if there is no complete agreement about its composition. However, the role of acidic proteins is the subject of many studies, even if there are a few in vivo pieces of evidence about their function as nucleators or mineral growth modulators, but a lot of in vitro data about their role.It is generally accepted that a stereochemical approach is essential to unravel the interactions between organic molecules and crystal surfaces: once adsorbed on crystal surfaces, aspartic acid-rich macromolecules are believed to act as nucleators of biominerals on some specific nucleation sites belonging to certain crystal forms with a suitable stereochemical configuration. Along with this effect, the adsorption of the same impurities results in modification of the growth rate of the faces affected by the interaction, leading to an overall effect on the crystal morphology.
In 1963, Hare55 suggested that proteins in the organic matrix are responsible for the polymorph selection in mollusk shells. Some successful in vitro experiments about the nucleation of different polymorphs have been done, even if the main crystal component is calcite, irrespective of the nature of the matrix components.56–58 Others53 demonstrated that macromolecules from natural aragonite or calcite layers in mollusks' shells can specifically induce aragonite or calcite to form in vitro, and that no other cations like magnesium, for instance, are required to select the polymorph. The authors considered the 3D structure of the nucleation site (macromolecular conformation and local microenvironment) which is responsible for the control exerted on nucleation, considering that the same macromolecules adsorbed on polystyrene spheres (with or without β-silk sheets) induced only calcite formation while aragonite was missing.50,53 On the other hand, vaterite precipitates in the chitin matrix in the presence of the aragonite-associated macromolecules when β-silk is missing. The authors proposed an association between the presence of silk fibroin with the ion diffusion or accessibility to the chitin surface.
Addadi and Weiner51 discussed the effect of acidic macromolecules in a β-sheet configuration on calcium salts of dicarboxylic acids and calcite, stressing the point that the morphological effect of silk proteins is exerted on the crystal forms exposing carboxylic groups in the proper orientation in relation to the surface, pointing out the attention on the stereochemical configuration required to trigger the morphological effect. Then again, in calcite, the stereochemical effect of the array of aspartic acid-rich macromolecules on the crystals is acted during nucleation, stabilizing the {00.1} form with respect to the layer of acidic molecules adsorbed on the vessel walls and driving the crystal growth with a precise orientation of the [001]-c axis, as generally occurs in biological crystallization.
Yet, X-ray electron diffraction made it possible to formulate the hypothesis of a model structure for the organic matrix, with a layer of β-chitin at the core of the organic scaffold, housed between two layers of silk fibroin-like proteins (SFLP hereinafter) and acidic macromolecules coating the chitin surfaces, as reported in Fig. 4.59,60 Acidic molecules belonging to the former silk fibroin gel phase have been found in the mineralized volume too.59,61
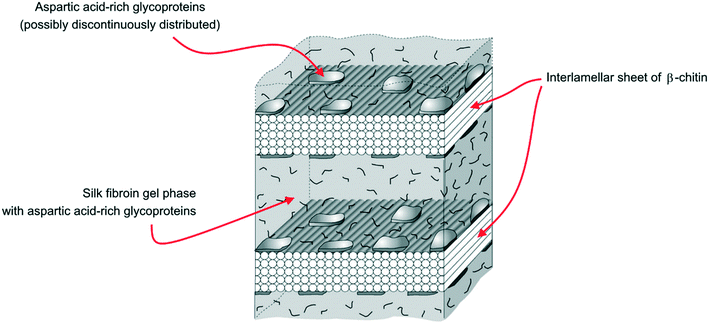 | ||
| Fig. 4 The demineralized layer of the organic scaffold in the Atrina shell, showing the interlamellar sheet of β-chitin pinched between two layers of silk fibroin gel (modified from Levi-Kalisman et al.59). | ||
Matrix molecules have been found to show repeating motifs62,63 and well-defined mutual crystallographic orientations with respect to the mineral fraction, suggesting epitaxial relationships60 between the two.
Starting from the works of the Bath's school,64 who have initiated the beginning on the new way to “biomineralization”, we realized that a trifle had been committed to the fundamentals of epitaxy. In the basic paper by Mann,65 one can clearly understand that the “epitaxial hypothesis” is grounded on the direct comparison between the (001) unit cell parameters (in Å) of SFLP, a0 = 4.7 and b0 = 6.9, and those of the (001) aragonite, a0 = 4.96 and b0 = 7.9; concerning height “c”, as the third dimension of the SFLP (a, b) lattice, one has to recollect that this is not a problem. In fact, thickness “c” depends solely on the composite section of a mollusc shell where the organic matrix (β-chitin, SFLP and acidic macromolecules) bounded by minerals, aragonite, varies; a simple and complete shell reconstruction has been made by Mann.65 Nothing could be more misleading than this reductive view of epitaxy which does not correspond to the general principle according to which the minimum of the potential energy is obtained whenever a new complex system is defined in nature, as is the shell of a bivalve. In a case like this, the living being produces an organic substance (substrate) which, in turn, protects the being from the external world with the formation (deposit) of two polymorphs (aragonite and calcite) synthesized from the surrounding seawater where calcium and carbon dioxide are abound. Triple epitaxy (001)SFLP → platy (001)Ar → columnar [001]Cc is the result of such a phenomenon: the crystallographic selection is made by the 2D-LCs arising at the two new interfaces and the adhesion energy chooses, among these found in the 2D-LCs, the ones that allow the minimum potential energy to be realized. Only in this way can we obtain the frightening stiffness that the shell we are talking about possesses.
In the legacy of studies about biomineralization, in 2018 we addressed the attention on the effect of a typical SFLP, sericin34 (from Bombyx moori), on calcium carbonate precipitation, stressing its double effect as a polymorph picker and morphology directing agent.
In the experiments, we obtained spherulitic aggregates of aragonite and calcite nucleating around CO2 bubbles at the air/solution interface, only in the presence of sericin. For the experimental details, please refer34 to the original paper.
Spherulites showed a narrow size distribution curve depending on i) the local supersaturation and ii) the gas partial pressure into the vessel that, in turn, along with the surface tension dependent on the concentration of sericin in solution, controls the size of the bubbles working as nucleation centers. Spherulitic structures like these were reported by Falini et al.53 and Cheng et al.66 who related the presence of sericin to the precipitation of aragonite.
We found the spherulites grown by an inner layer of fine platelets of aragonite arranged at a tangent of the core bubble and tightly associated with sericin, whose intense Raman fingerprint is detectable in the whole aragonite layer. The platelet size distribution is related to the concentration of sericin in solution. The external layer of the spherulites is made with calcite crystals grown with their three-fold axes oriented perpendicular to the aragonite substrate. The sericin signal decreases with the distance from the core. The structure of the spherulite is reported in Fig. 5.
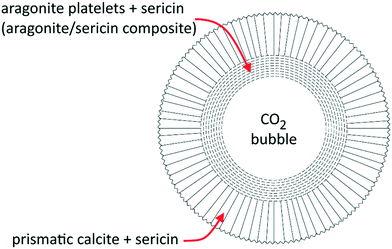 | ||
| Fig. 5 Structure of the spherulite grown in the presence of sericin. Around the core cavity (a CO2 bubble) aragonite and calcite grow in concentric shells. Modified from Pastero and Aquilano.34 | ||
The formation of these structures is spontaneous and isothermal and occurs in quasi-stagnant, sericin-enriched calcium carbonate solutions, which were supersaturated by CO2 bubbling. Their behavior resembles the mussel shell's design, with the aragonite floor made of platelets intimately blended with the organic matrix and a calcite external shield of crystals oriented perpendicularly with respect to the former.
We studied the epitaxial growth mechanism to explain both the stabilization of aragonite by the action of sericin, ordered in β-sheets because of the lower local pH in close proximity of the CO2 bubble, and the growth of a prismatic layer of calcite, with a well-defined orientation of calcite crystals with respect to the aragonite substrate.
Starting from the morphologies experimentally obtained, we checked the 2D-CLs (geometric conditions for the epitaxial agreement) at the (001)Ar/(001)SFLP and (00.1)Cc/(001)SFLP interfaces to evaluate the chance of a polymorph stabilization by the action of the impurity and finally at the (00.1)Cc/(001)Ar interface, to evaluate the transition from a calcium carbonate polymorph to another one.
Table 2 reports some of the best 2D-CLs for each interface considered, irrespective of cell multiplicity. The complete list can be found in the original paper.34 It is worth noting that the epitaxial conditions in the case of calcite/sericin are not as good as those in the case of aragonite/sericin, even if the epitaxial growth is geometrically suitable. This emphasizes the role of epitaxy in polymorph stabilization as well. In the case of calcite/aragonite, the epitaxial conditions for the crystal forms experimentally obtained are remarkably good, supporting the hypothesis of a crystallographic control over the mutual orientation of the calcium carbonate polymorphs.
| Interface | 2D cell | Linear misfit (%) | 2D-LC area misfit (%) |
|---|---|---|---|
| (001)Ar/(001)SFLP | [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00]Ar ≡ [ 00]Ar ≡ [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]SFLP 0]SFLP |
−1.22 | +0.5 |
1/2 × [1![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) 0]Ar ≡ [4 0]Ar ≡ [4![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]SFLP 0]SFLP |
+0.69 | ||
[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0]Ar ≡ [ 0]Ar ≡ [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0]SFLP 0]SFLP |
−0.39 | +0.5 | |
1/2 × [3![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) 0]Ar ≡ 2×[2 0]Ar ≡ 2×[2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]SFLP 0]SFLP |
+1.27 | ||
| (00.1)Cc/(001)SFLP | 1/2 × [120]Cc ≡ [120]SFLP | +3.18 | −1.34 |
| [100]Cc ≡ [210]SFLP | −9.92 | ||
[1![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 0]Cc ≡ [140]SFLP 0]Cc ≡ [140]SFLP |
+0.39 | +9.64 | |
| 1/2 × [100]Cc ≡ [110]SFLP | +5.04 | ||
| (00.1)Cc/(001)Ar | [1![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 0]Cc ≡ [0 0]Cc ≡ [0![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 0]Ar 0]Ar |
+4.53 | +0.04 |
[![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 0]Cc ≡ [ 0]Cc ≡ [![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]Ar 0]Ar |
−3.74 | ||
[320]Cc ≡ [2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]Ar 0]Ar |
−3.74 | −2.28 | |
| 5 × [010]Cc ≡ 2 × [210]Ar | +2.01 |
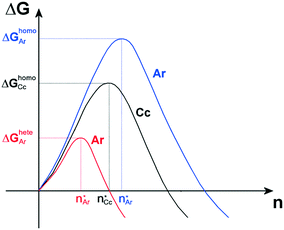
From a thermodynamic point of view, the nucleation of aragonite is favorable with respect to calcite as the adhesion energy between aragonite and the organic substrate is higher than that between calcite and the same organic substrate. Indeed, according to classical nucleation theory (CNT),14 in the absence of a substrate and for moderate supersaturation in aqueous solution, homogeneous nucleation of calcite is always preferred than that of aragonite, being ΔGhomoCc < ΔGhomoAr, which are the homogeneous activation energies for calcite and aragonite (Fig. 6). When an organic substrate is able to set up a good adhesion with aragonite but not with calcite, then the adhesion energy of the aragonite/substrate interface strongly reduces the activation energy for heterogeneous nucleation of aragonite, ΔGheteAr, which becomes lower than that for homogeneous nucleation of calcite ΔGheteAr < ΔGhomoCc, favoring in this way the formation of aragonite.
5. Conclusions
In this paper, several fundamental concepts concerning epitaxy have been reviewed. In particular, we stressed that a good 2D-LC at the A/B interface is a necessary but not a sufficient condition to establish the probability to observe epitaxy. Indeed, the knowledge of the adhesion energy between phases A and B is the fundamental requirement to evaluate the probability to observe epitaxial relationships between the two phases. Epitaxy is discussed in light of a methodological approach, in which laboratory experiments and quantum-mechanical calculations (if any) were combined together, for providing an exhaustive description of the phenomenon. In fact, to deepen the understanding of the intimate nature of epitaxy, a careful observation of the experiments, a geometric description of the interface and the determination of the adhesion energy of the phases involved are strictly required.We believe that it is necessary, in the final phase, to reiterate the reasons why we used directly the 2D-lattice coincidences, instead of adopting CSL (coincidence site lattice) and/or DSCL (displacement shift complete) relationships. We have carefully studied the basic studies of Bollmann and his followers,67 from the time the 0-lattice theory appeared; their refined treatment on the reticular and physical levels is essentially directed towards the grain boundaries and to dislocations, especially in high-symmetry systems. For our purposes, we are much cruder and have to do with homoepitaxies and heteroepitaxies of superposed lattices; we have also proved the validity of our 2D-LC choice since we predicted and calculated68–70 the periodic polysynthetic twins (PPTs) occurring in normal alkane (n-C28H58 and n-C34H70) crystals, since the 70s.
Two phenomena related to crystal growth in which epitaxy plays a primary role were described: (i) selective ad/absorption of two-dimensional zabuyelite on some faces of the calcite and aragonite (i.e., 2D epitaxy) as crystal habit modifiers; (ii) selection of the CaCO3 polymorph (calcite or aragonite) due to preferential adhesion on an organic substrate. We showed as well that the 2D epitaxial adhesion of zabuyelite above the {00.1}Cc, {10.4}Cc and {001}Ar forms can strongly modify the equilibrium shape of both calcite and aragonite. Moreover, we showed that the epitaxial growth mechanism is able to explain the stabilization of aragonite by the action of an organic substrate, i.e.: ordered sericin in β-sheets.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The present study has been partly funded by the project PRIN 2017 (2017L83S77) of the Italian Ministry for Education, University and Research (MIUR).References
- M. Bruno, M. Rubbo, L. Pastero, F. R. Massaro, F. Nestola and D. Aquilano, Cryst. Growth Des., 2015, 15, 2979–2987 CrossRef CAS
.
- M. Bruno and E. Bittarello, Minerals, 2018, 8, 323 CrossRef
.
- M. Rubbo, M. Bruno and M. Prencipe, Surf. Sci., 2015, 632, 180–184 CrossRef CAS
.
- F. R. Massaro, M. Bruno and F. Nestola, CrystEngComm, 2014, 16, 9224–9235 RSC
.
- F. R. Massaro, M. Bruno and F. Nestola, Cryst. Growth Des., 2014, 14, 2357–2365 CrossRef CAS
.
- F. R. Massaro, M. Bruno and M. Rubbo, CrystEngComm, 2014, 16, 627–635 RSC
.
- M. Bruno, F. R. Massaro, M. Prencipe and D. Aquilano, CrystEngComm, 2010, 12, 3626–3633 RSC
.
- M. Bruno, D. Aquilano and M. Prencipe, Cryst. Growth Des., 2009, 9, 1912–1916 CrossRef CAS
.
- M. Bruno, F. R. Massaro and M. Prencipe, Surf. Sci., 2008, 602, 2774–2782 CrossRef CAS
.
- M. L. Royer, Bull. Soc. Fr. Mineral., 1928, 51, 7–159 Search PubMed
.
- J. H. van der Merwe, Discuss. Faraday Soc., 1949, 5, 201–214 RSC
.
- O. G. Engel, J. Res. Natl. Inst. Stand. Technol., 1953, 50, 249 CAS
.
- R. Kern, Bull. Mineral., 1978, 101, 202–233 CAS
.
-
B. Mutaftschiev, The Atomistic Nature in Crystal Growth, Springer-Verlag, Berlin, 2001 Search PubMed
.
- M. Bruno, F. R. Massaro and M. Rubbo, CrystEngComm, 2017, 19, 3939–3946 RSC
.
- D. Aquilano, L. Pastero and M. Bruno, Cryst. Growth Des., 2019, 19, 3969–3978 CrossRef CAS
.
- E. Bittarello, M. Bruno and D. Aquilano, CrystEngComm, 2019, 21, 2920–2928 RSC
.
- M. Bruno, M. Rubbo, D. Aquilano, F. R. Massaro and F. Nestola, Earth Planet. Sci. Lett., 2016, 435, 31–35 CrossRef CAS
.
-
A. P. Sutton and R. W. Baluffi, Interfaces in Crystalline Materials, Clarendon Press, Oxford, 1996 Search PubMed
.
-
W. Bollmann, Crystal defects and crystalline interfaces, Springer, Berlin, 1970 Search PubMed
.
-
M. Hanbücken and J. P. Deville, Stress and Strain in Epitaxy: theoretical concepts, measurements and applications, Elsevier, 2001 Search PubMed
.
- P. Müller and A. Saúl, Surf. Sci. Rep., 2004, 54, 157–258 CrossRef
.
- R. Kern, Cryst. Res. Technol., 2013, 48, 727–782 CrossRef CAS
.
-
Advances in crystal growth inhibition technologies, ed. Z. Amjad, Plenum Press, New York, 2000 Search PubMed
.
-
Mineral scale formation and inhibition, ed. Z. Amjad, Plenum Press, New York, 1995 Search PubMed
.
- C. Ma and A. Navrotsky, Chem. Mater., 2012, 24, 2311–2315 CrossRef CAS
.
- N. Birkner and A. Navrotsky, Am. Mineral., 2012, 97, 1291–1298 CrossRef CAS
.
- H. Schmalzried, Pure Appl. Chem., 2000, 72, 2137–2147 CrossRef CAS
.
-
Mineral–Water Interface Geochemistry, Reviews in Mineralogy and Geochemistry, ed. M. F. Hochella and A. F. White, Mineralogical Society of America, 1990, vol. 23 Search PubMed
.
-
Thermodynamics and kinetics of water rocks interaction, Reviews in Mineralogy and Geochemistry, ed. E. H. Oelkers and J. Schott, Mineralogical Society of America, 2009, vol. 70 Search PubMed
.
-
G. H. Nancollas, Biological Mineralization and Demineralization, Springer-Verlag, New York, 1982 Search PubMed
.
-
S. Mann, Biomineralization, Principles and Concepts in Bioinorganic Materials Chemistry, Oxford University press, New York, 2002 Search PubMed
.
-
Biomineralization, Reviews in Mineralogy and Geochemistry, ed. P. M. Dove, J. J. De Yoreo and S. Weiner, Mineralogical Society of America, 2003, vol. 54 Search PubMed
.
- L. Pastero and D. Aquilano, Crystals, 2018, 8, 263 CrossRef
.
- H. Effenberger and J. Zemann, Z. Kristallogr. Krist., 1979, 150, 133–138 CrossRef CAS
.
- S. A. Markgraf and R. J. Reeder, Am. Mineral., 1985, 70, 590–600 CAS
.
- J. P. R. de Villiers, Am. Mineral., 1971, 56, 758–767 CAS
.
-
R. Dovesi, B. Civalleri, R. Orlando, C. Roetti and V. R. Saunders, in Reviews in Computational Chemistry, ed. B. K. Lipkowitz, R. Larter and T. R. Cundari, John Wiley & Sons, Inc., New York, 2005, vol. 1, pp. 1–125 Search PubMed
.
- M. Bruno and S. Ghignone, CrystEngComm, 2021, 23, 4791–4798 RSC
.
- M. Bruno, Cryst. Res. Technol., 2013, 48, 811–818 CrossRef CAS
.
- S. Rajam and S. Mann, J. Chem. Soc., Chem. Commun., 1990, 1789–1791 RSC
.
- D. Aquilano and L. Pastero, Cryst. Res. Technol., 2013, 48, 819–839 CrossRef CAS
.
- L. Pastero and D. Aquilano, Cryst. Growth Des., 2008, 8, 3451–3460 CrossRef CAS
.
- L. Pastero, D. Aquilano, E. Costa and M. Rubbo, J. Cryst. Growth, 2005, 275, e1625–e1630 CrossRef CAS
.
- L. Pastero, E. Costa, M. Bruno, M. Rubbo, G. Sgualdino and D. Aquilano, Cryst. Growth Des., 2004, 4, 485–490 CrossRef CAS
.
- D. Aquilano, M. Bruno and L. Pastero, Cryst. Growth Des., 2020, 20, 2497–2507 CrossRef CAS
.
- C. C. Chen and A. L. Boskey, Calcif. Tissue Int., 1985, 37, 395–400 CrossRef CAS PubMed
.
- S. Weiner and L. Addadi, J. Mater. Chem., 1997, 7, 689–702 RSC
.
-
S. Mann, J. Webb and R. J. P. Williams, Biomineralization: chemical and biochemical perspectives, Elsevier, New York, 1989 Search PubMed
.
- L. Addadi, J. Moradian, E. Shay, N. G. Maroudas and S. Weiner, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 2732–2736 CrossRef CAS PubMed
.
- L. Addadi and S. Weiner, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 4110–4114 CrossRef CAS PubMed
.
- S. Weiner, Calcif. Tissue Int., 1979, 29, 163–167 CrossRef CAS PubMed
.
- G. Falini, S. Albeck, S. Weiner and L. Addadi, Science, 1996, 271, 67–69 CrossRef
.
- B. A. Gotliv, L. Addadi and S. Weiner, ChemBioChem, 2003, 4, 522–529 CrossRef CAS PubMed
.
- P. E. Hare, Science, 1963, 139, 216–217 CrossRef CAS PubMed
.
- A. M. Bernhardt, D. M. Manyak and K. M. Wilbur, J. Molluscan Stud., 1985, 51, 284–289 Search PubMed
.
- E. M. Greenfield, D. C. Wilson and M. A. Crenshaw, Integr. Comp. Biol., 1984, 24, 925–932 CAS
.
- K. M. Wilbur and N. Watabe, Ann. N. Y. Acad. Sci., 1963, 109, 82–112 CrossRef CAS PubMed
.
- Y. Levi-Kalisman, G. Falini, L. Addadi and S. Weiner, J. Struct. Biol., 2001, 135, 8–17 CrossRef CAS PubMed
.
- S. Weiner and W. Traub, FEBS Lett., 1980, 111, 311–316 CrossRef CAS
.
-
L. Addadi, A. Berman and S. Weiner, in Mechanisms and Phylogeny of Mineralization in Biological Systems, ed. S. Suga and H. Nakahara, Springer-Verlag, Berlin, 1991, pp. 29–33 Search PubMed
.
- I. Sarashina and K. Endo, Am. Mineral., 1998, 83, 1510–1515 CrossRef CAS
.
- S. Miyamoto, R. Koyanagi, Y. Nakazawa, A. Nagano, Y. Abiko, M. Inada, C. Miyaura and T. Asakura, J. Biosci. Bioeng., 2013, 115, 575–578 CrossRef CAS PubMed
.
-
S. Mann, N. H. C. Sparks and V. J. Wade, in Iron Biominerals, ed. R. B. Frenkel and R. P. Blakemore, Plenum Press, New York, 1990, pp. 21–49 Search PubMed
.
- S. Mann, Nature, 1988, 332, 119–124 CrossRef CAS
.
- C. Cheng, Z. Shao and F. Vollrath, Adv. Funct. Mater., 2008, 18, 2172–2179 CrossRef CAS
.
- W. Bollmann, M. H. Yoo, B. T. M. Loh and S. Mendelson, in National Bureau of Standards Special Publication, ed. J. A. Simmons, R. de Wit and R. Bullough, US Dept. of Commerce, 1970, pp. 547–562 Search PubMed.
- D. Aquilano, J. Cryst. Growth, 1977, 37, 215–218 CrossRef CAS
.
- R. Boistelle and D. Aquilano, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1977, 33, 642–648 CrossRef
.
- R. Boistelle and D. Aquilano, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 406–413 CrossRef
.
| This journal is © The Royal Society of Chemistry 2022 |