Open Access Article
Open Access ArticleMolecular hydrogen isotope separation by a graphdiyne membrane: a quantum-mechanical study
Esther
García-Arroyo
 ab,
José
Campos-Martínez
ab,
José
Campos-Martínez
 a,
Massimiliano
Bartolomei
a,
Massimiliano
Bartolomei
 *a,
Fernando
Pirani
*a,
Fernando
Pirani
 c and
Marta I.
Hernández
c and
Marta I.
Hernández
 *a
*a
aInstituto de Física Fundamental, Consejo Superior de Investigaciones Científicas (IFF-CSIC), Serrano 123, 28006 Madrid, Spain. E-mail: maxbart@iff.csic.es; marta@iff.csic.es
bDoctoral Programme in Condensed Matter Physics, Nanoscience and Biophysics, Doctoral School Universidad Autónoma de Madrid, Spain
cDipartimento di Chimica, Biologia e Biotecnologie, Università di Perugia, Perugia, Italy
First published on 13th June 2022
Abstract
Graphdiyne (GDY) has emerged as a very promising two-dimensional (2D) membrane for gas separation technologies. One of the most challenging goals is the separation of deuterium (D2) and tritium (T2) from a mixture with the most abundant hydrogen isotope, H2, an achievement that would be of great value for a number of industrial and scientific applications. In this work we study the separation of hydrogen isotopes in their transport through a GDY membrane due to mass-dependent quantum effects that are enhanced by the confinement provided by its intrinsic sub-nanometric pores. A reliable improved Lennard-Jones force field, optimized on accurate ab initio calculations, has been built to describe the molecule–membrane interaction, where the molecule is treated as a pseudoatom. The quantum dynamics of the molecules impacting on the membrane along a complete set of incidence directions have been rigorously addressed by means of wave packet calculations in the 3D space, which have allowed us to obtain transmission probabilities and, in turn, permeances, as the thermal average of the molecular flux per unit pressure. The effect of the different incidence directions on the probabilities is analyzed in detail and it is concluded that restricting the simulations to a perpendicular incidence leads to reasonable results. Moreover, it is found that a simple 1D model—using a zero-point energy-corrected interaction potential—provides an excellent agreement with the 3D probailities for perpendicular incidence conditions. Finally, D2/H2 and T2/H2 selectivities are found to reach maximum values of about 6 and 21 at ≈50 and 45 K, respectively, a feature due to a balance between zero-point energy and tunneling effects in the transport dynamics. Permeances at these temperatures are below recommended values for practical applications, however, at slightly higher temperatures (77 K) they become acceptable while the selectivities preserve promising values, particularly for the separation of tritium.
1 Introduction
Deuterium (D2) is an essential substance for several applications in industry, scientific research and medicine. In addition, there is a great interest in the efficient production of D2 and tritium (T2) for their use in the emerging nuclear fusion industry. Separation of these scarce isotopes from a mixture with H2 is a tremendous challenge because standard technologies for gas separation are not efficient for isotope separation, as they rely on physicochemical properties that are nearly identical for these species. A very interesting alternative is quantum sieving, first proposed by Beenakker et al.,1 where the mass-dependent quantum-mechanical behavior of the isotopes is enhanced by confinement in sub-nanometric spaces. Based on these ideas, there has been an impressive progress in the use of nanoporous materials for isotope separation.2–4 An issue—also occurring in the separation of gases in general—is that large selectivities for separation are often accompanied by low permeances (thermal molecular flux per unit pressure) and vice versa.5 As permeance is usually inversely proportional to the membrane thickness, new one-atomic-thick, two-dimensional (2D) nanoporous membranes offer great prospect for large selectivities without compromising the permeability.6–10One promising 2D membrane for the separation of hydrogen isotopes is graphdiyne (GDY). Since the first report on its synthesis in 2010,11 there has been a tremendous increase of experimental and theoretical studies on GDY, where several properties have been studied for applications in catalysis, electronics, batteries, solar cells, etc.12–14 In particular, GDY appears to be an ideal membrane for gas separation applications15,16 due to its mechanical stability, chemical inertness and, specially, its porous structure, which is characterized by benzene-like rings linked by diacetylene chains giving rise to a uniform mesh of subnanometric triangular pores.17 Interestingly enough, hydrogen purification has been one of the first applications proposed for this material. Based on Density Functional Theory calculations, Jiao et al.18 predicted that GDY could be very efficient for the separation of H2 from a mixture with CH4 and CO. Several other computational studies have appeared19–26 proposing, for instance, an improvement of the H2 permeability/selectivity by means of nitrogen23 or positive charge24,26 doping of the GDY pores. As far as we are aware, hydrogen isotope separation by GDY has not been addressed yet.
We believe that it is important to study the isotope separation by 2D membranes as accurately as possible, with the aim to provide reliable references for simpler models which are often employed in the literature. These processes commonly involve an energy barrier, at the center of the pore, in the molecule–membrane interaction. For light species (within the quantum-mechanical description of the motion of the nuclei), there are two features that are quite important: the tunneling through the barrier and the quantization of the energy levels of the transition state (TS) at the pore center, generally called zero-point energy (ZPE) effects. While tunneling favors the transmission of the lighter isotope, ZPE effects enhance the transport of the heavier species.27,28 The selectivity for isotope separation is the result of a delicate balance between these effects, a balance that sometimes simple methods fail to describe correctly. As an example, some of us applied the three-dimensional time-dependent wave-packet (3D-TDWP) propagation method (first designed for atom-surface scattering29) to study the transport and separation of He isotopes through 2D membranes.30 The results were compared with predictions based on tunneling-corrected TS theory (tunn-TST).28 A good agreement was found for the dependence of the 4He/3He selectivity with temperature when the separation membrane is GDY. However, for a holey graphene model, tunn-TST overestimates considerably the 4He/3He selectivity because it is unable to account for the extent of tunneling as well as other quantum features (resonances) found in the accurate treatment.30 Helium isotopes quantum sieving through a graphtriyne membrane was also studied by means of the 3D-TDWP calculations,31 which have served as benchmarks for ring polymer molecular dynamics calculations.32
In this work, the transport and separation of hydrogen isotopes by GDY are studied by means of 3D-TDWP calculations. A reliable force field describing the interaction potential energy between H2, treated as a pseudoatom, and GDY is built and optimized on previously reported accurate first principles calculations.33 For the first time, all relevant directions of incidence of the particles are taken into account in the computations and the results are compared with more commonly employed treatments that only consider a perpendicular approach to the membrane. In addition, we test a simpler model-recently employed in related studies34,35 – which involves one-dimensional wave packet (1D-TDWP) calculations of transmission probabilities along a ZPE-corrected potential energy curve36,37 in the perpendicular approach. Permeances of H2 and D2 are reported as functions of temperature as well as their D2/H2 selectivity ratio. Separation of tritium is also addressed within the more approximated treatments.
The paper is arranged as follows. In Section 2, the interaction potential is described and the methods for the calculation of quantum-mechanical probabilities and permeances are summarized. Results are reported and discussed in Section 3, concerning transmission probabilities, permeances, selectivities as well as a comparison with more approximate models. Finally, conclusions are outlined in Section 4. An Appendix is dedicated to provide some computational details.
2 Theoretical approach
We consider the transport of an H2 molecule or its isotopes through a periodic and rigid GDY membrane. In the present approach, the molecules are treated as point-like particles (pseudoatoms), an approximation usually adequate to describe the molecules in their ground rotational state (para-H2, ortho-D2, para-T2). The ab initio study of ref. 33 indicates that this is a reasonable approach, as the computed interaction energies do not differ too much for different orientations of the molecule around the pore region, where the corresponding anisotropy is expected to be the largest. Indeed, it was found that parallel and perpendicular orientations of H2 with respect to the GDY plane involve similar permeation barriers (a difference of 2 meV for barrier heights of about 50 meV).33 On the other hand, in the present model there is no need to invoke other processes such as the H2 dissociation and subsequent formation of C–H bonds in the membrane, since they involve energy barriers much larger than the H2 translational energies considered here (about 2.1 eV for the hydrogenation of acethylenic carbon atoms38 and larger values for benzenic ones39,40).In what follows and within the Born-Oppenheimer scheme of separation of the electronic and nuclei motion, we will firstly present the force field employed (representing the solution of the electronic Schrödinger equation), then, the 3D-TDWP method (within the Schrödinger equation for the motion of the nuclei) to compute the transmission probabilities and finally, the calculation of permeances and selectivities and some approximate models for the perpendicular incidence.
2.1 Interaction potential
The total H2–GDY interaction potential is described as a sum of H2–C pairwise contributions (H2 as a point-like particle), each one represented by a potential term Vi: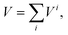 | (1) |
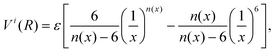 | (2) |
The ILJ parameters that have been used are reported in Table 1. Zeroth-order values of ε and Rm were obtained from data of the polarizabilities of the interacting partners,42 following expressions reported in ref. 43. In this way, these parameters maintain a physical meaning and, in turn, are transferable to other systems involving H2 interacting with graphene derivatives. These values, together with the remaining β parameter, were subsequently optimized on the basis of comparisons of the ILJ energies with reference ab initio energies for a set of selected positions of the center of mass of H2 with respect to the GDY pore (shown in Fig. 1). Within the adopted pseudoatom approximation, the ILJ force field represents the interaction for an average over all possible orientations of the molecule. The reference ab initio energies adequate to this purpose were obtained by averaging the ab initio interaction potential profiles of ref. 33 corresponding to two parallel and one perpendicular orientations of the molecule with respect to the GDY plane. In addition, it is noted that those ab initio estimations were obtained for the interaction between H2 and a specific (rigid) GDY molecular precursor, shown in the upper panel of Fig. 1. This molecular prototype represents the smallest approximation of a GDY pore and it has been previously used to assess the features of the interaction between GDY and different atomic and molecular species.33,44,45 It is worth pointing out that this precursor includes H atoms which saturate some C atoms of the benzenic rings, so it was necessary to determine ILJ parameters also for the H2–H interaction (included in Table 1). However, these H2–H parameters are not needed to compute the interaction with the extended GDY membrane, which is only formed by carbon atoms.
| Pair | R m | ε | β |
|---|---|---|---|
| H2–C | 3.503 | 4.569 | 6.5 |
| H2–H | 3.279 | 2.301 | 9.0 |
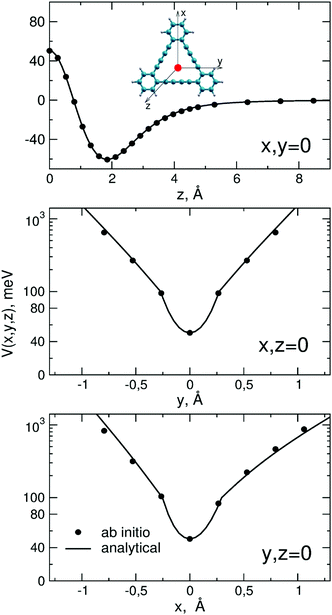 | ||
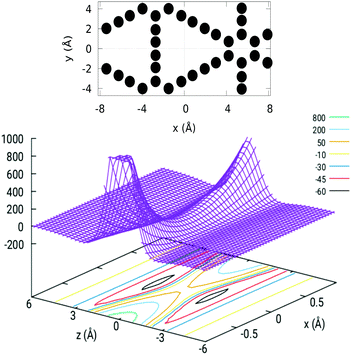
| Fig. 1 Potential energy for the interaction between H2 (described as a pseudoatom) and the smallest precursor of the GDY pore. Upper panel: Planar molecular prototype used to represent the GDY pore; interaction profile for the H2 out-of-plane perpendicular approach towards the pore center (z axis). Intermediate and lower panels: interaction profile for the H2 in-plane displacements with respect to the pore center along x and y, respectively. Full circles have been obtained by averaging the ab initio energies for two parallel and one perpendicular orientations of H2 onto the GDY plane.33 The analytic ILJ force field is shown with solid lines. | ||
In Fig. 1 a comparison between the ILJ force field and the reference ab initio calculations is presented for different interaction profiles, corresponding to out-of-plane (z axis) and in-plane (x and y axes) displacements of the center of mass of the H2 molecule with respect to the center of the pore. A quite good agreement can be observed for both out-of-plane and in-plane interaction potential features, which validate the reliability of the current force field. Notice that the final optimized ε and Rm parameters reported in Table 1 differ from their zeroth-order estimates by just about 1%. In the upper panel, a low barrier (of about 50 meV) for H2 permeation through the pore can be noticed, which is in agreement with the previous theoretical prediction reported in ref. 33 (50 meV). From the intermediate and lower panels a quite large interaction anisotropy is also evidenced when the H2 molecule is out of the pore geometric center: even for displacements as short as 0.25–0.30 Å in both directions the potential is more than twice and then it increases rapidly reaching very repulsive values of about 1 eV at distances of around 1 Å from the pore center.
The GDY unit cell used in this work, set on the z = 0 plane, is illustrated in the upper panel of Fig. 2. The interaction potential between H2 and GDY has been obtained by applying eqn (1) to as many carbon atoms in the membrane until the desired convergence is reached (including up to ten “shells” of unit cells around the central one). Dependence of V with x and z, for y = 0, is depicted in the lower panel of Fig. 2. The center of the pore coincides with the origin of the coordinate system and at this point, V = 47.75 meV; this value equals the barrier height since the zero of energy is set for an infinite separation of the molecule from the membrane. At this point, the potential exhibits a saddle-point topography while for larger distances from the membrane (about 2 Å) there is a well (63 meV) formed by van der Waals attractive forces (physical adsorption well).
2.2 Three-dimensional time-dependent wave packet (3D-TDWP) propagation
The 3D-TDWP method applied to the transmission of atoms through a 2D membrane has been described in ref. 30, therefore here we will just present a brief summary and discuss some aspects that are specific of the present study. A comprehensive exposition of the time-dependent approach of quantum mechanics can be found elsewhere.46,47The Hamiltonian for the interaction of a point-like H2 isotope of mass m with a GDY membrane can be written as
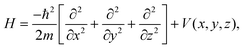 | (3) |
A wave packet representing the molecule is discretized in a grid of evenly spaced (x, y, z) points. Following the work of Yinnon and Kosloff,29 the periodicity of the system is exploited by limiting the ranges of coordinates x and y to those of a unit cell (Fig. 2). The range in the perpendicular coordinate, z, should be large enough to describe the evolution of the wave packet from the initial approach to the membrane up to the final distancing from it after the interaction. The initial wave packet is given by
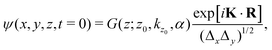 | (4) |
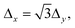 Δy = 9.45 Å). The values of K must be chosen such that the plane wave is periodic with the lattice,29 a condition achieved when
Δy = 9.45 Å). The values of K must be chosen such that the plane wave is periodic with the lattice,29 a condition achieved when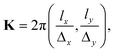 | (5) |
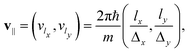 | (6) |
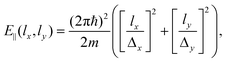 | (7) |
The solution of the time-dependent Schrödinger equation, ψ(t) = exp(−iHt/ħ)ψ(0), will allow us to extract the probability of transmission through the membrane, 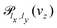 . The propagation of the wavepacket is carried out employing the Split-Operator method49 where the evolution operator, exp(−iHt/ħ), is approximately splitted as a product of potential and kinetic evolution operators, which are successively applied to the wavepacket. Propagation with the potential and kinetic terms is performed in the space and momentum representations, respectively. The fast Fourier transform is used to transform the wavepacket between both representations. The error associated to the Split-Operator method is
. The propagation of the wavepacket is carried out employing the Split-Operator method49 where the evolution operator, exp(−iHt/ħ), is approximately splitted as a product of potential and kinetic evolution operators, which are successively applied to the wavepacket. Propagation with the potential and kinetic terms is performed in the space and momentum representations, respectively. The fast Fourier transform is used to transform the wavepacket between both representations. The error associated to the Split-Operator method is 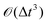 .47
.47
The stationary wave function, Ψ+E(x, y, z), can be obtained from ψ(x, y, z, t) using the Fourier transform from the time to the energy space.46,50 Finally, the transmission probability is obtained from the flux of Ψ+E(x, y, z) through a surface z = zf separating transmitted from incident and reflected waves,30,51
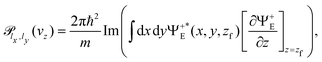 | (8) |
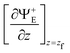 indicates the derivative of Ψ+E(x, y, z) with respect to z, computed at z = zf.
indicates the derivative of Ψ+E(x, y, z) with respect to z, computed at z = zf.
Details of these calculations are given in the Appendix.
2.3 Calculation of permeances and selectivities
The flux of molecules with a certain velocity v = (vx,vy,vz) crossing a membrane placed in the (x, y) plane can be defined as the product of the flux of molecules hitting the membrane, Z, and the probability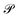 that these molecules actually cross the membrane
that these molecules actually cross the membrane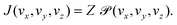 | (9) |
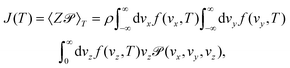 | (10) |
The permeance S of the membrane for the molecular transmission is defined as the thermal flux J(T) divided by ΔP, the pressure difference across the membrane.9 The gas is assumed to be sufficiently diluted in the feed side of the membrane at a pressure P and temperature T. Despite existing a molecular flow through the membrane pores, the gas-membrane system can be considered in equilibrium if the pores are sufficiently small compared to the mean free path of the gas,52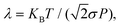 where σ is the molecular cross sectional area. Taking σH2 = 27 Å2 and for T = 40 K and P = 10 bar, λ = 15 Å, much larger than the pore size, of less than 1 Å. Therefore the system can be safely regarded as in equilibrium for pressures below 10 bar. In these conditions, the ideal gas law is valid and it is used to substitute ρ in eqn (10) by P/KBT. In this way, the permeance writes
where σ is the molecular cross sectional area. Taking σH2 = 27 Å2 and for T = 40 K and P = 10 bar, λ = 15 Å, much larger than the pore size, of less than 1 Å. Therefore the system can be safely regarded as in equilibrium for pressures below 10 bar. In these conditions, the ideal gas law is valid and it is used to substitute ρ in eqn (10) by P/KBT. In this way, the permeance writes
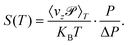 | (11) |
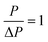 and the permeance becomes independent of pressure (a very weak dependence of the permeance on pressure has been confirmed by different molecular dynamics calculations53–55). Some other specific values of P/ΔP could be set, as done in ref. 20 and 56.
and the permeance becomes independent of pressure (a very weak dependence of the permeance on pressure has been confirmed by different molecular dynamics calculations53–55). Some other specific values of P/ΔP could be set, as done in ref. 20 and 56.
Finally, when two different molecular species A and B are hitting the membrane, the A/B selectivity or separation factor is given by the ratio of the permeances of A and B,
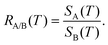 | (12) |
In this work we have run 3D-TDWP calculations for a set of incident conditions (lx,ly), where lx,y varies from −lmaxx,y to lmaxx,y with Δlx,y increments. In this way, the permeance is actually computed using a trapezoidal rule for the integration in vx and vy,
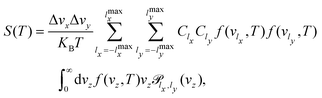 | (13) |
It should be noted that a different (less exact) definition of permeance has been used in the literature,20,31,32,35,56,57 where the molecular flux Z and the transmission probability are separately averaged over the Maxwell-Boltzmann distribution:
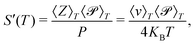 | (14) |
2.4 The case of perpendicular incidence: 3D and 1D calculations
We aim to study the effect on the permeances of just computing the 3D transmission probability (Section 2.2) along the perpendicular incidence, an approach employed in some previous works30,31 and that considerably reduces the computational cost. For this approximation, the permeances are computed by setting the equation above that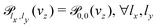 , leading to
, leading to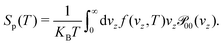 | (15) |
In addition, we have considered a low-cost 1D model for the transmission probability at perpendicular incidence, which has recently been employed in related works.34,35 This model, related to reaction path theories,36,37 involves an adiabatic separation between the coordinates parallel to the membrane (x, y) and the perpendicular one (z). In a first step, the Schrödinger equation is solved for the parallel degrees of freedom at various fixed distances z,
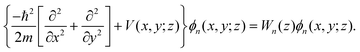 | (16) |
The eigenvalues Wn(z) are the so-called adiabatic potential energies. The ground state energies, W0(z), correspond to the ZPE-corrected potential along the perpendicular direction. In other words, the ZPE along the perpendicular incidence, associated to the ground-state vibrations of the center of mass of the molecule along the x and y directions, is the difference W0(z) − V(0,0,z). This correction will differ for the various isotopes studied due to their different mass m. Next, the transmission probability is obtained by solving a 1D Schrödinger equation along z, using W0(z) as effective potentials. This task has been carried out by adapting the 3D-TDWP approach described above to a 1D problem. Then, these probabilities are scaled using a factor γ that takes into account the fraction of the membrane that is effective for the transmission,30,58
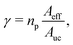 | (17) |
Eqn (16) is also used to compute a set of energies and wave functions at z = 0, a task that helps to understand—within the ideas of the TS theory—various features of the transmission probabilities, as shown below.
The bound-state problem of eqn (16) has been solved following the procedures described in ref. 28.
3 Results
In Fig. 3 we present the quantum-mechanical probabilities (eqn (8)) for the transmission of H2 and D2 through GDY, obtained for different incidences (lx,ly) of the initial wave packets. First of all, we discuss the “staircase” structure of these probabilities aided by some concepts of the TS theory.59 In this scheme, the different energy levels and functions of the TS are obtained by diagonalizing the Hamiltonian of eqn (16) for z = 0, where the bottleneck for the transmission is. These energy levels Wn(0) are given in Table 2 for H2 and D2 and the corresponding wave functions for D2 are depicted in Fig. 4. It can be seen that the thresholds of the different “steps” of the probabilities (see vertical arrows in Fig. 3) occur at energies very close to the TS energies of Table 2. In this way, these energies can be considered as the effective (and successive) energy barriers for permeation. It can be seen that the transmission probabilities for the perpendicular incidence (lx,ly) = (0,0) (black lines in Fig. 3) lack the “second” threshold (the rise of probability at the energy of the n = 2, 3 states). This is due to the relationship between the symmetries of the initial wave packet and those of the TS wave functions: an initial wave packet with (lx,ly) = (0,0) does not populate states antisymmetric with respect to the y or x axis, as the n = 2, 3 states (Fig. 4). Apart from that, it is worth noting the large difference between the first energy thresholds (100.63 for H2 and 84.85 and D2) and the potential energy barrier (47.75 meV), in other words, the large ZPEs involved (52.88 and 37.1 meV for H2 and D2, respectively). This is due to the light masses of the molecules as well as the confinement imposed by the interaction potential along the x and y directions (Fig. 1). Moreover, the lower energy threshold of D2 with respect to that of H2 will cause a preferred permeation of the heavier isotope over a wide range of temperatures, as will be seen below. Note that this ZPE appears in an intrinsic manner when solving the 3D time-dependent Schrödinger equation, producing an effective permeation barrier, whereas it can be clearly identified as the difference W0(z = 0) − V(0,0,0) in the solution of eqn (16) within the TS theory.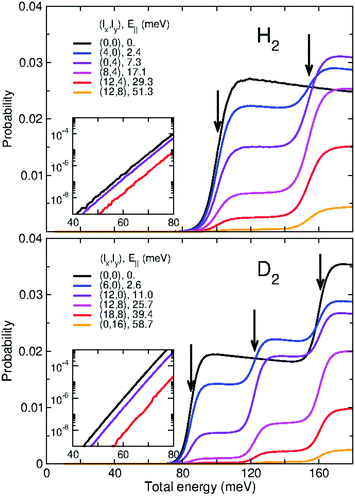 | ||
| Fig. 3 3D-TDWP transmission probabilities for H2–GDY (upper panel) and D2–GDY (lower panel) as functions of the total translational energy (meV) for different incidences (lx,ly). The corresponding parallel energies E‖ (lx,ly) (eqn (7)) are indicated in the legends. Arrows show the energy levels of the transition state (Table 2). Insets depict the behavior of some of the probabilities in the low energy range. See text for discussion. | ||
| n | Energy (meV) | |
|---|---|---|
| H2 | D2 | |
| 0 | 100.63 | 84.85 |
| 1 | 154.35 | 122.36 |
| 2 | 154.35 | 122.36 |
| 3 | 208.57 | 160.11 |
| 4 | 210.16 | 160.95 |
| 5 | 210.16 | 160.95 |
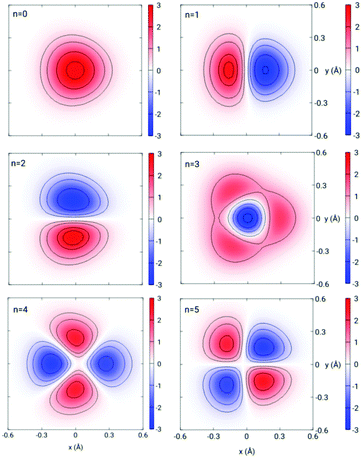 | ||
| Fig. 4 Contour plots of the wave functions ϕn(x, y; z = 0) (in arbitrary units) of the D2–GDY transition state for levels n = 0–5. | ||
In the insets of Fig. 3 we present the low-energy behavior of some of the transmission probabilities, specifically, the probabilities for (lx,ly) = (0,0), (0,4) and (12,4), for H2, and (0,0), (12,0) and (18,8), for D2. For these energies, tunneling effects play an important role in the behavior of the probabilities. It can be clearly seen that the probabilities decrease exponentially as energy decreases. This decay occurs at a smaller rate in the case of H2, because tunneling is much easier for this light molecule than for the heavier D2. Indeed, at the lowest translational energies (40 meV), the transmission probabilities for H2 become larger than those for D2. This behavior is at the origin of the maximum value found for the D2/H2 selectivity as a function of the temperature, as described below.
It is worth discussing in more detail the dependence of the transmission probabilities with the different incidence conditions (lx,ly) of the wave packet. In Fig. 3 it is seen that all the probabilities rise at the same energy thresholds, however the height of the “plateau” that they reach rapidly decreases with the parallel energy, E‖(lx,ly). Interestingly, we have found that for the various combinations of lx, ly that lead to the same E‖(lx,ly), the transmission probabilities are equal. For instance, (lx,ly) = (12,4) and (0,8) have identical E‖ (because 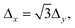 see eqn (7)) and the associated probabilities are found to be identical too. This property allows us to plot the H2 and D2 probabilities as functions of E‖ for various fixed values of E, as shown in Fig. 5. For total energies below the second permeation threshold (E < 154 and <122 meV for H2 and D2, respectively), it is quite clear that the probabilities decrease exponentially with E‖. This behavior is modified for higher energies due to the rise of the probabilities with (lx,ly) ≠ (0,0) at the second threshold, discussed above. A decrease of the probabilities with E‖ was reasonably expected since the wave packets that approach the membrane in directions distant from the perpendicular one do not access too directly to the pore region. However, it is difficult to foresee the specific dependence (as it is determined by intricate details of the dynamics), so it is noteworthy to have found a simple exponential decay. Notice also that the decay rate is stronger for the D2 probabilities than for the H2 ones.
see eqn (7)) and the associated probabilities are found to be identical too. This property allows us to plot the H2 and D2 probabilities as functions of E‖ for various fixed values of E, as shown in Fig. 5. For total energies below the second permeation threshold (E < 154 and <122 meV for H2 and D2, respectively), it is quite clear that the probabilities decrease exponentially with E‖. This behavior is modified for higher energies due to the rise of the probabilities with (lx,ly) ≠ (0,0) at the second threshold, discussed above. A decrease of the probabilities with E‖ was reasonably expected since the wave packets that approach the membrane in directions distant from the perpendicular one do not access too directly to the pore region. However, it is difficult to foresee the specific dependence (as it is determined by intricate details of the dynamics), so it is noteworthy to have found a simple exponential decay. Notice also that the decay rate is stronger for the D2 probabilities than for the H2 ones.
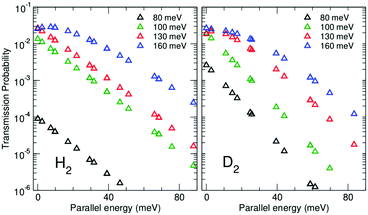 | ||
| Fig. 5 3D-TDWP transmission probabilities for H2–GDY (left panel) and D2–GDY (right panel) as functions of parallel energy E‖ (meV) for total translational energies equal to 80, 100, 130 and 160 meV. | ||
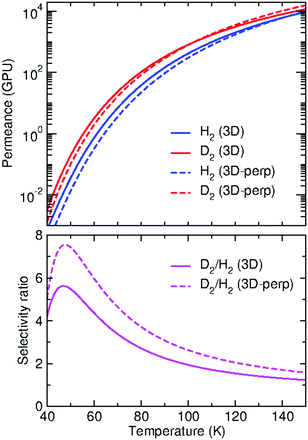
Permeances of GDY for the transport of H2 and D2, in gas permeance units (GPU), are reported in Fig. 6 (upper panel) for temperatures between 40 and 150 K. D2/H2 selectivities are presented in the lower panel of the same Figure. We first discuss the permeances obtained from the calculations that include all the incidence conditions (lx,ly) considered (eqn (13), solid lines in the Figure). It can be seen that the permeances increase by several orders of magnitude as temperature increases and that the D2 permeances are clearly larger than the H2 ones at all temperatures. Hence, the resulting D2/H2 selectivity is always larger than one. This behavior is mainly due to the ZPE effects, discussed above, which make the D2 probability threshold to be at a lower energy than the H2 one (Fig. 3), with a consequent increase of the integral of eqn (13). However, the D2/H2 selectivity does not monotonously increase as temperature decreases, as it would be expected if ZPE effects were prevalent,28 but reaches a maximum value of 5.6 at 47 K. This maximum is due to the increasing role of tunneling effects:28 as temperature decreases, the H2 permeances do not decrease as fast as the D2 ones because H2 tunnels more effectively than D2 (see insets of Fig. 3), so at some temperature the D2/H2 selectivity eventually decreases. The maximum selectivity reached is close to the acceptable reference value of 6 for separation applications.60 However, the D2 permeance at 47 K is ≈0.1 GPU, rather small compared to the minimum accepted value for industrial applications, of 20 GPU.60 It would probably be more convenient to design applications at higher temperatures, where permeances are higher and operations are easier. For instance, at the temperature of liquid nitrogen (77 K), deuterium permeance rises to ≈70 GPU and the selectivity still has a reasonable value of about 3.
Permeances obtained by restricting the calculations to the perpendicular incidence (eqn (15)) are also shown in Fig. 6. This approximation, here named as “3D-perp”, has been the approach followed in some of our previous works.30,31 It is interesting to explore its range of validity since it involves a considerable saving of computational time. It can be seen that the approximation provides a reasonable estimation of the permeances. The approximation works slightly worse for H2, for which we find a larger underestimation of the permeances at most of the considered temperatures. As a result, the corresponding selectivity ratio predicts a more favorable separation of D2, with a maximum value of 7.6 at 47.5 K (lower panel of Fig. 6). Still, the 3D-perp approximation gives a good estimation of the overall temperature dependence of the selectivity.
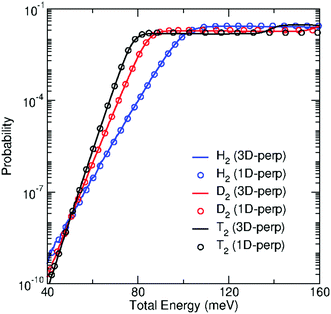
In addition, we have performed 1D-TDWP calculations of the transmission probabilities for the perpendicular incidence within the approach described in Section 2.4. The transmission of T2 molecules has been additionally studied within this model, and the 3D-TDWP probability for the perpendicular incidence has been also computed for the sake of comparison. As mentioned above, the 1D model probabilities are scaled using the factor given by eqn (17), which requires the estimation of the effective size of the pore, Aeff. As in a previous work,30 this quantity has been obtained by computing the area where the squared modulus of the TS wavefunction, |ϕ0(x, y;0)|2 is larger than a cutoff set to 10−4. This has led to Aeff = 1.08, 0.78 and 0.65 Å2 for H2, D2 and T2, respectively. Such probabilities, named as “1D-perp”, are compared with the 3D-perp probabilities in Fig. 7. It can be seen that the agreement between both calculations is outstanding for all energies up to the first energy threshold, which shows the importance of correcting the interaction potential along the perpendicular direction with the ZPE of the parallel degrees of freedom. It is specially noticeable how the 1D-perp probabilities perfectly replicate the 3D ones all along the tunneling region. The following “steps” in the probabilities at higher energies are not reproduced since higher adiabatic potential energies (Wn(z), n > 0) were not taken into account in the model. Nevertheless, we have checked that probabilities at these higher energies do not play a significant role in the calculation of the permeances, so 3D-perp and 1D-perp permeances are almost identical in the studied temperature range.
As a summary, the selectivities for D2/H2, T2/D2, and T2/H2 separation, obtained from 3D-perp calculations, are presented in Fig. 8. As expected from the relative extent of quantum effects in the three isotopes, the T2/D2 ratio is rather small at all temperatures whereas the T2/H2 selectivity becomes the largest, reaching a maximum of 21 at 45 K. Similarly to the case of the D2/H2 separation, the T2 permeance is quite small at this temperature (≈0.05 GPU) but it rapidly increases reaching acceptable values at temperatures where the selectivity is still very promising (e.g. at 77 K, the permeance is about 90 GPU and the selectivity ratio, 7).
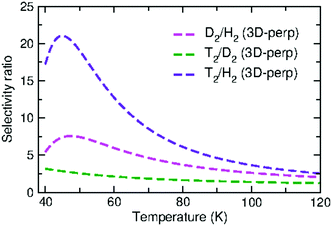 | ||
| Fig. 8 Selectivity ratios for D2/H2, T2/D2, and T2/H2 as functions of temperature (K), as estimated from the 1D model. | ||
4 Concluding remarks
In this work we have carried out a quantum-mechanical study of the transport of hydrogen molecules through graphdiyne and the capacity of this 2D carbon membrane to separate their isotopes. A wave packet propagation method has been applied where the motion of the molecules, within the pseudoatom approximation, is simulated in the 3D space. The calculations were performed using a realistic Improved Lennard-Jones force field, which has been built on the basis of previous accurate electronic structure calculations. For the first time, transmission probabilities have been computed for a complete set of different incidence directions of the wave packets, which in turn are used to adequately estimate permeances. In this way, these calculations have served to test the reliability of less expensive computations. Firstly, it has been found that restricting the simulations to the perpendicular incidence direction gives, despite some quantitative differences, a reasonable estimation of the temperature dependence of the permeances and selectivities. Secondly, an even simpler model, using 1D effective potential energy curves, gives an excellent agreement with the 3D probabilities for the perpendicular approach, regarding both tunneling and zero-point energy effects. It would be very interesting to further explore the validity of this 1D model for other 2D nanoporous materials and molecules.It has been found that the D2/H2 and T2/H2 selectivities reach rather high values at low temperatures (about 6 at T ≈ 50 K and 21 at 45 K, respectively). However, at these temperatures the corresponding permeances are too small for practical experiments. It would rather be interesting to design applications at somewhat higher temperatures where the permeances values become acceptable and the selectivities are still favorable for separation of deuterium or tritium from hydrogen.
An important improvement of the present approach would be to explicitly incorporate the dependence of the interaction potentials on the relative orientation of H2 and its rotational degrees of freedom in the wave packet dynamics (including rotationally excited states, e.g. ortho-H2), a project planned for the near future. Another relevant aspect regards the impact of the motion of the carbon atoms of GDY on the permeances of the studied isotopes. This effect could be estimated by calculations where the positions of the C atoms are relaxed at each relative position of H2; in such a case, a reduction of the permeation barrier is expected due to a pore deformation during molecular penetration, as found for He-/Ne-GDY by means of DFT periodic calculations.44 An explicit account of the vibrations of the membrane as well as other interesting aspects (such as the role of different mixture ratios, thermodynamic conditions, physical adsorption, etc.) could be studied by classical molecular dynamics simulations.53–55
This study can be extended along various interesting directions. For example, the present procedure for obtaining realistic force fields can be used to study the transport of hydrogen and other gases through other graphynes, especially graphtetrayne, which has been recently synthesized.61 Also, in relation with recent proposals of coherent diffraction in the transmission of atoms through graphene,62 it could be worth exploring the diffraction pattern of atoms transmitted through graphynes, estimated by the projection of the transmitted wave packet onto well-defined wave vector states.63 Work in some of these directions is in progress.
Conflicts of interest
There are no conflicts to declare.Appendix
Here we present the computational details of the 3D-TDWP calculations outlined in Section 2.2. All calculations were carried out using an in-house code developed in our group.The Gaussian wavepacket of eqn (4) can be written as
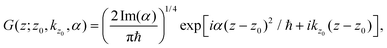 | (18) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/Im
2/Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)1/2. Typically used values are z0 = 17–25 Å (a sufficiently large initial separation from the membrane) and σ = 1–2 Å. For each incidence condition we have run calculations for various kz0 values to adequately represent the transmission probabilities in the chosen energy range (E = 5–180 meV). The wave packets were represented in the 3D space where the parallel coordinates x and y range along the unit cell and z ∈ [−30:45) Å. The number of points in the discretization of the wave packet vary depending on the molecule: for H2, (nx,ny,nz) they are typically (96,64,512) whereas for D2 and T2, (128,96,768) and (192,128,1024), respectively. A time step δt = 0.04 fs was used in the application of the Split-Operator algorithm.49 The wave packets were propagated up to a total of 3–5 ps. Larger total times were considered when the wave packet involved very low energy components of the wave packet, particularly for H2 (up to 25 ps). To obtain the transmission probability (eqn (8)), the flux surface was placed at zf = −3 Å. To prevent unphysical behavior of the wave packets at the edges of the z interval (the non-periodic coordinate) and following the method of ref. 64 and 65 they were splitted every 0.5 fs into “interaction” and “product” wave packets using the damping function f± (z) = exp[−β (z − z±)2], were f+ and f− are defined in the asymptotic regions z < z− = −10 Å and z > z+ = 25 Å, respectively, and β = 3 × 10−3 Å−2. After splitting, propagation is resumed using the interaction portion of the wave packet.
α)1/2. Typically used values are z0 = 17–25 Å (a sufficiently large initial separation from the membrane) and σ = 1–2 Å. For each incidence condition we have run calculations for various kz0 values to adequately represent the transmission probabilities in the chosen energy range (E = 5–180 meV). The wave packets were represented in the 3D space where the parallel coordinates x and y range along the unit cell and z ∈ [−30:45) Å. The number of points in the discretization of the wave packet vary depending on the molecule: for H2, (nx,ny,nz) they are typically (96,64,512) whereas for D2 and T2, (128,96,768) and (192,128,1024), respectively. A time step δt = 0.04 fs was used in the application of the Split-Operator algorithm.49 The wave packets were propagated up to a total of 3–5 ps. Larger total times were considered when the wave packet involved very low energy components of the wave packet, particularly for H2 (up to 25 ps). To obtain the transmission probability (eqn (8)), the flux surface was placed at zf = −3 Å. To prevent unphysical behavior of the wave packets at the edges of the z interval (the non-periodic coordinate) and following the method of ref. 64 and 65 they were splitted every 0.5 fs into “interaction” and “product” wave packets using the damping function f± (z) = exp[−β (z − z±)2], were f+ and f− are defined in the asymptotic regions z < z− = −10 Å and z > z+ = 25 Å, respectively, and β = 3 × 10−3 Å−2. After splitting, propagation is resumed using the interaction portion of the wave packet.
Many convergence checks were carried out by varying the time step, the number of grid points, the grid size along coordinate z, the absorption regions, etc. The computed transmission probabilities barely changed upon these modifications. In particular, it was checked in most of the calculations that halving the time step did not produce any appreciable change in the probabilities. Slightly different probabilities (differences of about 1%) where found when enlarging the number of grid points (from (96,64,512) to (144,96,768), for instance) in the range of the largest translational energies.
Acknowledgements
The work has been funded by Spanish Agencia Estatal de Investigación PID2020-114957GB-I00/AEI/10.13039/501100011033 and PID2020-114654GB-I00/AEI/10.13039/501100011033. E. G.-A. thanks financial support from Comunidad de Madrid (Spain), under the “Garantía Juvenil” Program (PEJ-2019-AI/IND-14267). Allocation of computing time by CESGA (Spain) is also acknowledged.Notes and references
- J. J. M. Beenakker, V. D. Borman and S. Y. Krylov, Chem. Phys. Lett., 1995, 232, 379–382 CrossRef CAS.
- J. Cai, Y. Xing and X. Zhao, RSC Adv., 2012, 2, 8579–8586 RSC.
- J. Y. Kim, H. Oh and H. R. Moon, Adv. Mater., 2019, 31, 1805293 CrossRef PubMed.
- L. G. Gao, R. M. Zhang, X. Xu and D. G. Truhlar, J. Am. Chem. Soc., 2019, 141, 13635–13642 CrossRef CAS PubMed.
- L. M. Robeson, J. Membr. Sci., 2008, 320, 390–400 CrossRef CAS.
- D.-e Jiang, V. R. Cooper and S. Dai, Nano Lett., 2009, 9, 4019–4024 CrossRef CAS PubMed.
- S. P. Koenig, L. Wang, J. Pellegrino and J. S. Bunch, Nat. Nanotechnol., 2012, 7, 728–732 CrossRef CAS PubMed.
- Y. Jiao, A. Du, M. Hankel and S. C. Smith, Phys. Chem. Chem. Phys., 2013, 15, 4832–4843 RSC.
- L. Wang, M. S. H. Boutilier, P. R. Kidambi, D. Jang, N. G. Hadjiconstantinou and R. Karnik, Nat. Nanotechnol., 2017, 12, 509–522 CrossRef CAS PubMed.
- C. Owais, A. James, C. John, R. Dhali and R. S. Swathi, J. Phys. Chem. B, 2018, 122, 5127–5146 CrossRef CAS PubMed.
- G. Li, Y. Li, H. Liu, Y. Guo, Y. Li and D. Zhu, Chem. Commun., 2010, 46, 3256–3258 RSC.
- C. Huang, Y. Li, N. Wang, Y. Xue, Z. Zuo, H. Liu and Y. Li, Chem. Rev., 2018, 118, 7744–7803 CrossRef CAS PubMed.
- A. James, C. John, C. Owais, S. N. Myakala, S. Chandra Shekar, J. R. Choudhuri and R. S. Swathi, RSC Adv., 2018, 8, 22998–23018 RSC.
- R. Sakamoto, N. Fukui, H. Maeda, R. Matsuoka, R. Toyoda and H. Nishihara, Adv. Mater., 2019, 31, 1804211 CrossRef CAS PubMed.
- H. Qiu, M. Xue, C. Shen, Z. Zhang and W. Guo, Adv. Mater., 2019, 31, 1803772 CrossRef CAS PubMed.
- J. Xu and S. Meng, J. Phys. D: Appl. Phys., 2020, 53, 493003 CrossRef CAS.
- R. H. Baughman, H. Eckhardt and M. Kerte, J. Chem. Phys., 1987, 87, 6687–6699 CrossRef CAS.
- Y. Jiao, A. Du, M. Hankel, Z. Zhu, V. Rudolph and S. C. Smith, Chem. Commun., 2011, 47, 11843–11845 RSC.
- S. W. Cranford and M. J. Buehler, Carbon, 2011, 49, 4111–4121 CrossRef CAS.
- H. Zhang, X. He, M. Zhao, M. Zhang, L. Zhao, X. Feng and Y. Luo, J. Phys. Chem. C, 2012, 116, 16634–16638 CrossRef CAS.
- W.-h Zhao, L.-f Yuan and J.-l Yang, Chin. J. Chem. Phys., 2012, 25, 434–440 CrossRef CAS.
- H. Zhang, X. Zhao, M. Zhang, Y. Luo, G. Li and M. Zhao, J. Phys. D: Appl. Phys., 2013, 46, 495307 CrossRef.
- Y. Jiao, A. Du, S. C. Smith, Z. Zhu and S. Z. Qiao, J. Mater. Chem. A, 2015, 3, 6767–6771 RSC.
- X. Tan, L. Kou, H. A. Tahini and S. C. Smith, Mol. Simul., 2016, 42, 573–579 CrossRef CAS.
- P. Sang, L. Zhao, J. Xu, Z. Shi, S. Guo, Y. Yu, H. Zhu, Z. Yan and W. Guo, Int. J. Hydrogen Energy, 2017, 42, 5168–5176 CrossRef CAS.
- Q. Liu, L. Cheng and G. Liu, Membranes, 2020, 10, 286 CrossRef CAS PubMed.
- J. Schrier and J. McClain, Chem. Phys. Lett., 2012, 521, 118–124 CrossRef CAS.
- M. I. Hernández, M. Bartolomei and J. Campos-Martínez, J. Phys. Chem. A, 2015, 119, 10743–10749 CrossRef PubMed.
- A. T. Yinnon and R. Kosloff, Chem. Phys. Lett., 1983, 102, 216–223 CrossRef CAS.
- A. Gijón, J. Campos-Martínez and M. I. Hernández, J. Phys. Chem. C, 2017, 121, 19751–19757 CrossRef.
- M. I. Hernández, M. Bartolomei and J. Campos-Martínez, Nanomaterials, 2021, 11, 73 CrossRef PubMed.
- S. Bhowmick, M. I. Hernández, J. Campos-Martínez and Y. V. Suleimanov, Phys. Chem. Chem. Phys., 2021, 23, 18547–18557 RSC.
- M. Bartolomei, E. Carmona-Novillo and G. Giorgi, Carbon, 2015, 95, 1076–1081 CrossRef CAS.
- Y. Qu, F. Li and M. Zhao, Sci. Rep., 2017, 7, 1483 CrossRef PubMed.
- M. Li, L. Wang, H. Lei, Y. Yang, Y.-Q. Li, M. Zhao, J. Guan, W. Li and Y. Qu, Adv. Theory Simul., 2021, n/a, 2100327 Search PubMed.
- W. H. Miller, N. C. Handy and J. E. Adams, J. Chem. Phys., 1980, 72, 99–112 CrossRef CAS.
- J. L. Bao and D. G. Truhlar, Chem. Soc. Rev., 2017, 46, 7548–7596 RSC.
- G. M. Psofogiannakis and G. E. Froudakis, J. Phys. Chem. C, 2012, 116, 19211–19214 CrossRef CAS.
- F. Costanzo, P. L. Silvestrelli and F. Ancilotto, J. Chem. Theory Comput., 2012, 8, 1288–1294 CrossRef CAS PubMed.
- M. Bartolomei, M. I. Hernández, J. Campos-Martínez, R. Hernández-Lamoneda and G. Giorgi, Carbon, 2021, 178, 718–727 CrossRef CAS.
- F. Pirani, S. Brizi, L. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Phys. Chem. Chem. Phys., 2008, 10, 5489–5503 RSC.
- A. Gavezzotti, J. Phys. Chem. B, 2003, 107, 2344–2353 CrossRef CAS.
- R. Cambi, D. Cappelletti, G. Liuti and F. Pirani, J. Chem. Phys., 1991, 95, 1852–1861 CrossRef CAS.
- M. Bartolomei, E. Carmona-Novillo, M. I. Hernández, J. Campos-Martínez, F. Pirani and G. Giorgi, J. Phys. Chem. C, 2014, 118, 29966–29972 CrossRef CAS.
- M. Bartolomei, E. Carmona-Novillo, M. I. Hernández, J. Campos-Martínez, F. Pirani, G. Giorgi and K. Yamashita, J. Phys. Chem. Lett., 2014, 5, 751–755 CrossRef CAS PubMed.
- J. Z. H. Zhang, Theory and Application of Quantum Molecular Dynamics, World Scientific, Singapore, 1999 Search PubMed.
- R. Gerber, R. Kosloff and M. Berman, Comput. Phys. Rep., 1986, 5, 61–113 CrossRef.
- E. J. Heller, J. Chem. Phys., 1975, 62, 1544–1555 CrossRef CAS.
- M. D. Feit, J. A. Fleck and A. Steiger, J. Comput. Phys., 1982, 47, 412–433 CrossRef CAS.
- D. Zhang and J. Z. H. Zhang, J. Chem. Phys., 1991, 101, 1146–1156 CrossRef.
- W. H. Miller, J. Chem. Phys., 1974, 61, 1823–1834 CrossRef CAS.
- S. Blundell and K. M. Blundell, Concepts in Thermal Physics, Oxford University Press, 2006 Search PubMed.
- C. Sun, M. S. H. Boutilier, H. Au, P. Poesio, B. Bai, R. Karnik and N. G. Hadjiconstantinou, Langmuir, 2014, 30, 675–682 CrossRef CAS PubMed.
- H. Liu, S. Dai and D.-E. Jiang, Nanoscale, 2013, 5, 9984–9987 RSC.
- Y. B. Apriliyanto, N. Faginas Lago, A. Lombardi, S. Evangelisti, M. Bartolomei, T. Leininger and F. Pirani, J. Phys. Chem. C, 2018, 122, 16195–16208 CrossRef CAS.
- S. Blankenburg, M. Bieri, R. Fasel, K. Müllen, C. A. Pignedoli and D. Passerone, Small, 2010, 6, 2266–2271 CrossRef CAS PubMed.
- A. W. Hauser, J. Schrier and P. Schwerdtfeger, J. Phys. Chem. C, 2012, 116, 10819–10827 CrossRef CAS.
- Y. Wang, J. Li, Q. Yang and C. Zhong, ACS Appl. Mater. Interfaces, 2016, 8, 8694–8701 CrossRef CAS PubMed.
- M. Hankel, H. Zhang, T. X. Nguyen, S. K. Bhatia, S. K. Gray and S. C. Smith, Phys. Chem. Chem. Phys., 2011, 13, 7834–7844 RSC.
- Z. Zhou, J. Membr. Sci., 2006, 281, 754–756 CrossRef.
- Q. Pan, S. Chen, F. Wu, C. Shao, J. Sun, L. Sun, Z. Zhang, Y. Man, Z. Li, Y. He and L. Zhao, CCS Chem., 2020, 2, 1368 Search PubMed.
- C. Brand, M. Debiossac, T. Susi, F. Aguillon, J. Kotakoski, P. Roncin and M. Arndt, New J. Phys., 2019, 21, 033004 CrossRef CAS.
- M. I. Hernández, J. Campos-Martínez, S. Miret-Artés and R. D. Coalson, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 8300–8309 CrossRef PubMed.
- R. Heather and H. Metiu, J. Chem. Phys., 1987, 86, 5009–5017 CrossRef CAS.
- P. Pernot and W. A. Lester, Int. J. Quantum Chem., 1991, 40, 577–588 CrossRef CAS.
| This journal is © the Owner Societies 2022 |