DOI:
10.1039/D2CP01144A
(Perspective)
Phys. Chem. Chem. Phys., 2022,
24, 16942-16972
Atom–surface scattering in the classical multiphonon regime
Received
8th March 2022
, Accepted 22nd June 2022
First published on 29th June 2022
Abstract
Many experiments that utilize beams of incident atoms colliding with surfaces as a probe of surface properties are carried out at large energies, high temperatures and with large mass atoms. Under these conditions the scattering process does not exhibit quantum mechanical properties such as diffraction or single-phonon excitation, but rather can be treated with classical physics. This is a review of work carried out by the authors over a span of several years to develop theoretical frameworks using classical physics for describing the scattering interactions of atom with surfaces.
1 Introduction
There is a long history of using well defined beams of atoms or small molecules as probes for determining properties of surfaces. The earliest successful such experiments were carried out by Otto Stern and his collaborators1,2 in which they demonstrated, with thermal energy beams of H2 and He, two-dimensional diffraction patterns from LiF(001). These experiments came shortly after similar results by Davisson and Germer, using electron beams scattered from metal surfaces, demonstrated the existence of the de Broglie wavelength of the electron.3 Not only did the experiments of Stern and coworkers measure the structure of the LiF(001) surface, but their experiments were the first demonstration that the concept of a de Broglie wavelength applied to composite particles such as He atoms or hydrogen molecules.2
Since the later decades of the last century, there has been a resurgence of experimental work using atomic and molecular beams as probes of surface properties.4–9 This renewed interest came at the heels of big advances in vacuum technology and the development of molecular jet beams, which have a much greater energy and angular resolution than the thermal beams with which Stern and his collaborators worked.
The greatest detail of the atom–surface interaction is obtained in experiments carried out in the quantum mechanical regime, which roughly means low projectile energies, low surface temperatures and small projectile mass. A slightly better definition of the quantum regime is when the de Broglie wavelength is comparable to the surface core atom spacing and the incident energy is comparable to phonon energies in the target surface, e.g., implying energies less than 100 meV for He atoms. Under favorable conditions such experiments can reveal in great detail features of the gas–surface interaction potential, surface order and structure via measurements of diffraction peaks. Surface phonons can be investigated in the single quantum excitation limit, and even defects on the surface are revealed in the diffuse scattering between diffraction peaks.
However, many experiments have been carried out in the classical (or multiphonon) regime, so named because the theories of classical physics can be used to describe these measurements. This implies larger incident energies, higher surface temperatures often combined with larger mass projectiles such as the rare gases heavier than He. Under these conditions all quantum features such as diffraction peaks or single phonon features are suppressed, or more precisely as explained below in Section 2, the Debye–Waller factor becomes vanishingly small and individual quantum features become unmeasurable. What this leaves behind are rather broad single and sometimes multiple peaks characteristic of classical scattering.
The transition from quantum to classical atom–surface scattering is illustrated in Fig. 1, which in the front of the schematic shows a typical angular scan taken at low energy. The angular scan, in which total scattered intensity is plotted against the incident angle θi primarily shows sharp diffraction peaks, and in this case the specular (00) peak is dominant. Above, in the first inset is an energy-resolved measurement (typically measured with time-of-flight (TOF) methods) taken at a single point on the angular scan, in this case marked TOF1. The energy-resolved spectrum, which is a plot of intensity versus TOF, shows several peaks. The peak marked el. is the diffuse elastic peak caused by diffuse scattering at all angles by defects. The other peaks are typical of single surface phonon excitations, the two additional peaks indicated both occur at shorter TOF times than elastic which indicates that the projectile atom has gained energy. Now, in the direction of this 2D plot marked as increasing incident wave vector (increasing energy) the diffraction peaks become smaller and closer together, until at large incident energies they disappear altogether and merge into a broad feature, which in fact is the envelope of the underlying, but invisible quantum features. The second insert is a TOF energy-resolved spectrum taken at the place marked TOF2 and it also exhibits only a broad single-peaked feature. The TOF marked el. in the insert TOF2 is the approximate position where the projectile has neither energy gain nor energy loss.
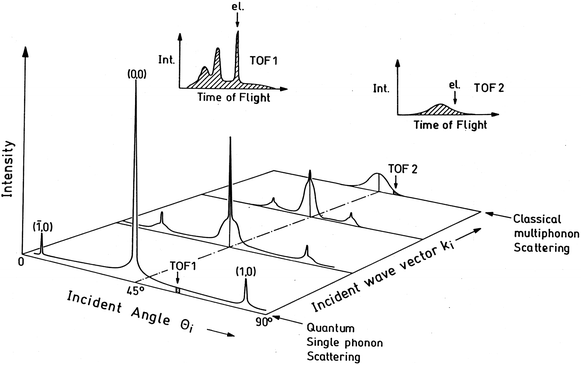 |
| | Fig. 1 A depiction of the transition from quantum mechanical scattering (in the front) to classical scattering (in the rear) as a function of increasing incident particle wave vector (increasing energy). At low incident energies, sharp quantum features are observed in both the angular distributions and the energy-resolved TOF1 and TOF2 plots (insets), while at large energy only broad classical features appear. Courtesy of J. R. Manson and J. P. Toennies. | |
Even though it would appear that having only rather broad features in the classical regime should lead to more limited information than could be obtained from observations of the scattered spectra in the quantum mechanical regime, nevertheless there is still a great deal of physical information that can be extracted. Perhaps foremost are measurements of energy and momentum transfer in gas–surface interactions, i.e., accommodation coefficients and friction coefficients. Basic surface structure is revealed in rainbow peaks arising from surface corrugation, and these can be due to both direct scattering and inelastic scattering. Measurements of the temperature dependence of classical peak features can give information on the nature of the surface corrugation and its average height. Other aspects of the interaction potential such as the attractive physisorption well can be probed by comparing direct scattering to trapping-desorption events, and the latter can often lead to scattered distributions that approach the Knudsen flux, i.e., the scattered distribution expected from a surface which is desorbing particles in equilibrium at its temperature. An important factor in a gas–surface collision is the number of atoms belonging to the surface that become involved and this can be determined by measuring the effective mass with which the incoming projectile interacts. Scattering is very sensitive to this effective mass and experiments of rare gases interacting with molten metals have shown that this can be an effective way of measuring alloy concentrations in the surface region. Such experiments, in fact can be isotope sensitive, both with respect to the projectiles and atoms in the target.10–12 An interesting observation is that in special cases a classical inelastic peak can be misinterpreted as a broadened single-phonon peak in an energy-resolved spectrum. Classical theory can be used to identify such situations.
As mentioned above, surface rainbows are a very important aspect of this type of scattering. These rainbows were first observed experimentally by Oman13 and Lorenzen and Raff14 but were not recognized as such until McClure15–17 using a classical trajectory analysis realized the similarity with the atmospheric rainbow. Two lobes at opposite sides of the specular scattering angle were indicative of the surface rainbow effect. Smith et al.18,19 identified the surface rainbow experimentally by measuring the scattering of rare gas atoms (in particular, Ne atoms) in thermal beams from a LiF(001) surface. With higher resolution apparatus (not an effusive molecular beam source) and a lower surface temperature to avoid a stronger Debye–Waller (DW) attenuation, Boato's group20 observed sharper lobes than Smith et al. Subsequently, Garibaldi et al.21 developed a simple theory for atom diffraction and classical and quantum rainbow scattering by assuming that the surface behaves as a hard corrugated wall. The number of experimental studies in which the rainbow effect was observed increased rapidly. The hard wall model was extended by Garibaldi et al. to diatom–surface scattering.22 Kleyn et al.23 measured the final rotational energy distribution of NO scattered from an Ag(111) surface. They suggested that features in the rotational distribution may be attributed to rotational rainbows which was later on confirmed by Schinke.24
Classical trajectory calculations are routine nowadays where the gas–surface interaction is substituted by a more realistic interaction potential such as Lennard-Jones or Morse potentials and corrugated Morse potentials25 with the correct long range behavior. The classical analysis of elastic scattering with realistic interactions as well as periodic corrugated surfaces has also led to an exhaustive and detailed study of two aspects very much related to the rainbow effect: catastrophes and chaotic behavior. This extensive work has been reviewed by Kleyn and Horn26 and Guantes et al.27–29 Interestingly enough, when one of the rainbow angles reaches π/2 one finds the onset of a multiple scattering regime or chaos appearing from the so-called skipping singularity.
On the other hand, Brako and Newns30–32 developed a classical model for atom scattering from metals in which the motion of the incident particle is coupled linearly to the phonon bath of the surface. They derived an analytical expression for the angular distribution as well as for the energy and momentum transfer. However, surface corrugation was not included in their theory so they could not account for rainbows. Thermal effects in the presence of corrugation were first treated by Tully using his so-called washboard model.33,34 Pollak and Miret-Artés focused on stochastic approaches based on a generalized Langevin equation of motion of the particles scattered from the surface which is modelled as a thermal bath of phonons.35–41 In particular, it is also convenient to see if the fitted model parameters (the well depth and stiffness parameter of the vertical potential) are reliable by carrying out some ab initio computations of the potential energy between the incoming atom and the surface. The accurate calculation of these potentials is not a routine task because correlated methods with large basis sets are mandatory for a reliable account of the van der Waals interaction. The potential energy curves were calculated by means of the approximate coupled cluster doubles model RICC2.38
A first order perturbation theory leads to analytical formulae for the angular distributions and energy loss spectra in the presence of surface corrugation and thermal fluctuations. This work was later extended to second order perturbation theory.42–44 The introduction of friction coefficients to atom–surface scattering is helpful in interpreting these experimental data and providing insight into the scattering process. Furthermore, it would be also very interesting to analyze the experimental results issued from the well-known technique called grazing incidence fast atom diffraction (GIFAD) and the theoretical ones by this methodology.45
The above list of useful features that can be extracted under classical conditions is only partial, and they and other features will be discussed in the following sections. The objective of this review is to present several variants of classical physics theories that can be used to explain and interpret experimental observations. The theories discussed here result in analytical mathematical formulas which are relatively straightforward to use and calculate. There are other ways of carrying out calculations of gas–surface scattering in the classical regime and these are primarily variants of molecular dynamics simulations which, in the simplest terms attempt to recreate the experiment in a computer simulation using an interaction potential for the surface. Many such molecular dynamics simulations have been carried out, but we will not discuss those here.46–49
In the following Section 2 we present a very brief introduction into the basic elements of the quantum theory of surface scattering, including diffraction and single phonon features. This enables us to describe how the classical regime develops as the average number of phonons in a given collision increases. In Section 3 a classical mechanical theory of atom–surface scattering is presented starting from a generalization of the classic problem of a two-body collision. This problem was generalized by Brako and Newns31,32 to account for the broken symmetry inherent in a surface collision, i.e., the surface itself presents 2D symmetry, but symmetry is broken in the direction perpendicular to the surface. This is further developed to include the effects of an interaction potential and corrugation of the surface. Section 4 presents a different approach to the theory in which the vibrations of the surface are treated as an equilibrium Langevin bath together with friction coefficients, which could be called classical stochastic scattering theory. Sections 5 and 6, respectively, give a few examples to illustrate how the theories of Sections 3 and 4 have proved to be useful. Finally, in Section 7 we present a few concluding remarks and some perspectives.
2 Brief description of single and multiple phonon excitation
In order to more clearly understand how multiple excitation of phonons in an atom–surface collision can result in a classical scattering distribution it is of interest to consider how, with increasing incident energy, the scattering pattern gradually evolves from being quantum mechanical to classical multiphonon excitation. For this, one needs to begin with a purely quantum starting point, and for describing scattering an exact expression to start from is the generalized golden rule of Fermi which gives the transition rate wfi in terms of the transition matrix Tfi as50,51| | 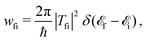 | (1) |
where the energies ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) i and
i and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) f are the initial and final total energies of the entire system of interest, consisting of surface and projectile atom described by the Hamiltonianwhere Hph is the Hamiltonian of the surface including phonon vibrations and Hatom is the Hamiltonian of the incoming projectile atom, and these are connected by the interaction potential V. The labels i and f denote the good quantum numbers of the initial and final states of the system when the atom and surface are widely separated and not coupled by the interaction potential V.
f are the initial and final total energies of the entire system of interest, consisting of surface and projectile atom described by the Hamiltonianwhere Hph is the Hamiltonian of the surface including phonon vibrations and Hatom is the Hamiltonian of the incoming projectile atom, and these are connected by the interaction potential V. The labels i and f denote the good quantum numbers of the initial and final states of the system when the atom and surface are widely separated and not coupled by the interaction potential V.
An important aspect is that in scattering from a many-body object the initial and final states of that object are far too complicated to be measurable, hence one must average over initial states of the surface and sum over all possible final surface states. This averaging over initial states and summing over final surface states leads to a transition rate that depends only on the initial ki and final kf wave vectors of the projectile atom
| | 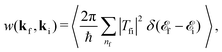 | (3) |
where the large brackets 〈⋯〉 signify the average over an equilibrium distribution of initial surface states and the summation is over final surface states.
In an actual surface scattering experiment, the most detailed quantity that is measured is the differential reflection coefficient d3R/dΩf![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dEf which is the fraction of the incident beam intensity scattered into the small final energy interval dEf and the small solid angle dΩf. This is related to the transition rate of eqn (3) by
dEf which is the fraction of the incident beam intensity scattered into the small final energy interval dEf and the small solid angle dΩf. This is related to the transition rate of eqn (3) by
| | 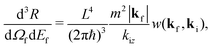 | (4) |
where
kiz, which is proportional to the incident flux, is the component of
ki normal to the surface and
L is a quantization length.
One other nuance that must be considered is the type of detector used in the experiments. Most atom beam detectors are so-called density detectors and the probability of detection is proportional to the time the atom spends passing through the detector. This means that faster atoms have a proportionately less chance of being detected. To account for this situation the differential reflection coefficient of eqn (4) above should be divided by the final speed, which is proportional to |kf|.
The interaction potential V is usually written as a pairwise sum over all unit cells of the surface 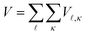 where the discrete variable
where the discrete variable ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) counts surface unit cells and κ counts elements within the unit cell. For simplicity we will assume Bravais unit cells containing only one surface atom and neglect the summation over κ. Then the simplest realistic form for the interaction potential is
counts surface unit cells and κ counts elements within the unit cell. For simplicity we will assume Bravais unit cells containing only one surface atom and neglect the summation over κ. Then the simplest realistic form for the interaction potential is
| | 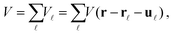 | (5) |
where
r![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
is the position of the
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
-th unit cell and
u![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
is its vibrational displacement. When the potential is a pairwise summation such as
eqn (5) then the transition operator, from which the transition matrix elements
Tfi are formed, is also a pairwise summation
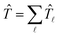
.
With a potential of the form of eqn (5) the transition rate of eqn (3) can be evaluated exactly for elastic scattering. Without going into details, which can be found elsewhere,52–54 the result for purely elastic diffraction for an ordered surface with no defects is
| | 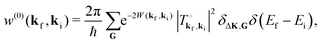 | (6) |
where Δ
K =
Kf −
Ki is the difference between final and initial wave vectors parallel to the surface and
G a reciprocal lattice vector of the surface. This is an exact result, within the kinematic approximations of a rigidly vibrating Bravais surface unit cell and assuming vibrations within the harmonic approximation. The two
δ-functions show that the only observable scattering intensities are diffraction peaks occurring with
Kf =
Ki ±
G and the final wave vector perpendicular to the surface is given by energy conservation
| | 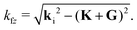 | (7) |
Each of the diffraction peaks has an intensity proportional to the squared transition matrix
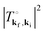
. Each peak is also multiplied by a Debye–Waller factor exp{−2
W(
kf,
ki)} whose argument is given by
| | 2W(kf, ki) = 〈(Δk·u![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (0))2〉, (0))2〉, | (8) |
where Δ
k =
kf −
ki is the scattering vector; in other words, the argument of the Debye–Waller factor involves the mean square vibrational displacement and is independent of the unit cell number
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
.
An approximate evaluation of 2W which has proven useful in explaining many experiments is to use the result valid for neutron or X-ray scattering from a Debye distribution of phonons at temperatures T as large or larger than the Debye temperature ΘD. This gives the result 2W = 3ħ2Δk2T/[kBMΘD2] where kB is the Boltzmann constant and M is the effective mass of the surface. An even clearer view of the behavior of the Debye–Waller factor comes from its evaluation for the specular diffraction beam which is
| | 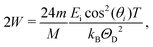 | (9) |
where
m is the mass of the projectile atom,
Ei is the incident energy and
θi is the incident angle measured relative to the normal to the surface. The appearance of the Debye–Waller factor in the elastic diffraction intensity of
eqn (6) provides an opportunity to discuss the relationship of quantum mechanical scattering and classical multiphonon scattering. It can be shown that a good estimate of the total number of phonons excited in a collision is given by the value of the exponent 2
W. Thus, when 2
W is comparable to or less than unity the predominant scattering features will be elastic diffraction and the inelastic scattering will be dominated by single phonon processes. In this case, a quantum mechanical theory is necessary to describe the scattering process. On the other hand, when 2
W ≫ 1,
i.e., when large numbers of phonons are excited, the Debye–Waller factor exp{−2
W} becomes vanishingly small implying that all quantum features are suppressed; this is when classical physics becomes appropriate to describe the scattering. It is clear from
eqn (9) that 2
W becomes large when the product of mass ratio, incident energy and temperature get large, and this is perhaps the most precise definition of conditions under which classical theory is valid for describing the surface scattering process.
Single phonon excitation can also be evaluated with a treatment similar to that which produces the elastic scattering intensity of eqn (6) and the resulting transition rate for the creation or annihilation of a phonon with frequency ω(ΔK, ν) (where ν is the branch index of the phonon mode) is
| | 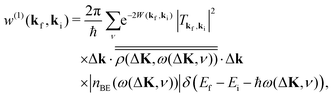 | (10) |
where the Bose–Einstein function is given by
nBE(
ω) = [exp(
ħω/
kBT) − 1]
−1. We have used the fact that −
nBE(−
ω(Δ
K,
ν)) =
nBE(
ω(Δ
K,
ν)) + 1. The term proportional to
nBE describes single phonon annihilation in which the incoming atom gains energy, while the term proportional to
nBE + 1 is for phonon creation processes. The dyadic
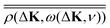
is essentially the surface projection of the phonon density of states.
52 Just as in the case of elastic diffraction of
eqn (6), it is seen that the strength of a single phonon creation or annihilation peak is governed by the Debye–Waller factor. When the Debye–Waller factor becomes vanishingly small, which is when many phonons are excited, then the intensity of single phonon peaks becomes unmeasurable and once again this is the signal that the scattering can be described by classical theory.
There is yet another case of real relevance to the question of excitations of multiple phonons and this is when the surface can be imagined to have only a single phonon mode, the so-called Einstein mode vibrational model. Such a situation is actually physically realized rather well for two classes of systems involving surfaces. The first is adsorbed layers of the heavy rare gases on ordered metal surfaces, where the dispersionless vertical vibrational mode of the rare gas layer (the ZA mode) can have energies in the range of 2–10 meV. The other is adsorbed small molecules such as CO on metal substrates, where the frustrated translational vibrational mode can have energies in the range of 4–10 meV and is also dispersionless. In both cases, scattering with He atom beams can excite as many as 10–20 resolvable peaks corresponding to multiple excitations of the single Einstein-like mode.
In the case in which the interaction potential contains only a single phonon mode of frequency ω the transition rate of eqn (3) can be solved leading to the following result55,56
| | 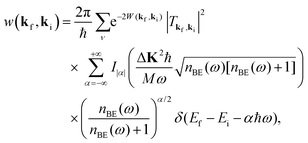 | (11) |
where
Iα(
z) is the modified Bessel function of order
α.
Eqn (11) is a series of discrete intensity peaks in which positive values of
α correspond to multiple phonon annihilation with the atom projectile gaining the energy supplied by the phonons, and negative
α denotes phonon creation and energy loss from the incident atom. In the extreme low temperature limit, where the occupation number
nBE(
ω) approaches zero,
eqn (11) becomes the well known Poisson distribution. Just as in the other quantum expressions above for elastic and single phonon processes, this Einstein mode model intensity is governed by a Debye–Waller factor. As the argument of the Debye–Waller factor becomes larger and larger (
e.g., with increasing incident energy or temperature) the peaks are suppressed and shifted away from the elastic point denoted by
α = 0. In the extreme multiphonon limit what is left is basically the envelope of all the quantum peaks, and this region is where classical theory can be used to describe the process.
An example demonstrating the usefulness of this equation for describing surface Einstein modes appears in Fig. 2 which shows several results of calculations using eqn (11) compared to measurements of He scattering from a 0.028 coverage of CO molecules adsorbed on a Cu(001) surface with the scattering plane aligned with the100 azimuthal direction. There is a fixed source-detector angle of 105° between the incident beam and the detector direction. The experimental measurements are shown as open circles and the calculations are the solid curve. The sharp delta-function peaks produced by eqn (11) have been broadened to match the widths of the measured phonon peaks. The number N shown in each panel is a relative normalization factor used to match the calculated curve to the measured intensities. The adsorbate mode that is being excited multiple times in Fig. 2 is the frustrated translation of the CO molecule (T). The molecule sits at an on-top position over a Cu atom with the carbon atom next to the Cu. The frustrated translational mode is a wagging motion with an energy of about 4 meV. Because of the translational nature of this mode it is more readily excited with larger parallel wave vectors K of the incident He atoms. Thus in Fig. 2 when the incident angle is small and closer to normal the number of phonon excitations is small, but as the incident angle is increased to a near-glancing configuration at θi = 76° more than ten excitations are visible. Peaks appear at both energy gain (phonon annihilation) and energy loss, and in this case when there are large numbers of excitations the envelope of the quantum peaks is shifted strongly to the energy loss side.
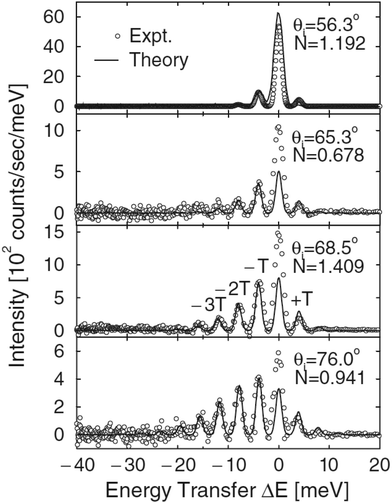 |
| | Fig. 2 Four different energy resolved helium atom scattering spectra on Cu(001) taken along the100 azimuth with a CO coverage of 0.028. The incident energy is 66.6 meV and the incident angles range from 56.3° to 76° as marked. Experimental points are marked as open circles while the solid curves are the results of theory. In these plots, T means the frustrated translational mode of the CO molecule and N a relative normalization factor used to match the calculated curve to the measured intensities. (Reprinted with permission from ref. 55, Copyright [1988] American Physical Society.) | |
Fig. 2 once again provides an illustration of the evolution from the quantum mechanical regime towards the classical regime. As the number of excitations becomes larger, as in the bottom panel, there is a clear envelope of the purely quantum peaks. The classical regime is that in which the number of phonons excited is so large that they can no longer be distinguished and what remains observable is this classical envelope.
3 Classical scattering theory
The history of a neutral particle colliding with a target under conditions in which many vibrational quanta are excited goes back to the early days of neutron scattering from solids. A review dating from the middle of the last century57 gives the following equation for the transition rate| | 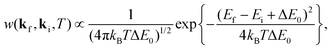 | (12) |
where Ef and Ei are the final and intial energies of the neutron after making a collision with a target nucleus, Ef = ħ2kf2/2m and similarly for Ei, with m the mass of the neutron. The recoil energy is ΔE0 = (ħkf − ħki)2/2M where M is the mass of a nucleus of the solid, under the assumption that all of the atoms in the solid are the same.
A similar expression to eqn (12) has proved to be useful in describing low energy ion scattering from metal surfaces, so it is an interesting exercise to see how it can be derived as a generalization of the well known problem of the collision of two hard spheres. Consider a projectile particle of mass m whose incident energy is Ei = pi2/2m and a moving target particle of mass M whose initial energy is εi = Pi2/2M. Both energy and momentum must be conserved in the collision so the transition rate is of the form
| | w(pf, pi) ∝ Fδ(Ef − Ei + εf − εi)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(pf − pi + Pf − Pi), δ(pf − pi + Pf − Pi), | (13) |
where
F is a form factor describing the shape of the particles, and for hard spheres
F is simply a constant that can be taken to be unity. If this system is to be compared to a surface scattering experiment, then one must do the equivalent of summing over all final states of the target and averaging over all its initial states. The corresponding process here is to sum
eqn (13) over all final target momenta
Pf and average over all initial momenta
Pi. If the distribution function of initial momenta
Pi is a Maxwell–Boltzmann distribution, for example as is the case for the distribution of momenta in a gas at equilibrium at temperature
T or the similar distribution function of momenta of an atom in a harmonic solid crystal, then the sum and averaging result in precisely the same result as
eqn (12) multiplied by the factor
F. Below, we will discuss more general approaches that lead to
eqn (12) and also identify the factor
F with the squared transition matrix |
Tfi|
2. In Section 5 we will show an application of
eqn (12) in which it nicely describes the scattering spectra of low energy ions scattering from a metal surface.
Brako and Newns developed a significant improvement to eqn (12) in which the target particle was replaced by the surface of a semi-infinite slab. Beginning with a purely quantum mechanical starting point, similar to eqn (3) above they included the correct conditions of conservation of momentum. A large planar surface, due to its symmetry, imposes a conservation condition on the parallel momentum of the projectile. For example, an ordered, periodic surface conserves parallel momentum modulo a surface reciprocal lattice vector, Kf = Ki + G, which is the diffraction condition, whereas the projectile momentum parallel to the axis perpendicular to the surface is not conserved due to the broken symmetry in that direction. By ignoring the interaction potential between the atomic projectile and the surface Brako and Newns were able to evaluate the scattering transition rate in the classical limit of excitation of large numbers of phonons to obtain the following expression31,32
| | 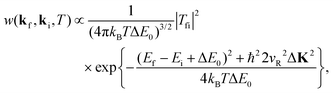 | (14) |
where
vR is a weighted average of phonon velocities parallel to the surface, and Δ
K is the surface-parallel component of the scattering vector
kf −
ki. As stated above, Brako and Newns treated only the excitation of multiple phonon quanta and did not include the interaction potential between the projectile and surface, thus their form factor was simply a constant, |
Tfi|
2 = 1.
Much later the Brako–Newns solution was re-examined, beginning with the quantum mechanical Fermi golden rule transition rate of eqn (3), but including an interaction potential between the projectile and the surface.52,58 This treatment was based on only two approximations, the assumption of a rapid collision compared to a typical phonon vibration period and assuming decoupling of the phonon field from the interaction potential. This approach led again to eqn (14), but with the form factor clearly identified. The transition matrix Tfi was shown to be the transition matrix of the elastic part of the interaction potential taken with respect to its own eigenstate wavefunctions extended off the energy shell, i.e., the quantum mechanical wavefunctions are those of the elastic part of the potential, but for incident and final energies that include the energy gains and losses transferred to the target surface via the multiple phonon excitations. Such transition matrices have been used since the very early days of quantum mechanics, e.g., for a purely one-dimensional repulsive exponential potential between the projectile and surface these are known as the Mott–Jackson matrix elements59 or for a 1-D Morse potential they are known as the Morse matrix elements.60
An important condition that any many-body scattering theory should obey is detailed balancing. Detailed balancing is a special relationship between a transition from state ki to state kf and its inverse, a transition in which the two momenta are reversed. It is a manifestation of quantum mechanics that remains present in the classical limit. In a quantum mechanical excitation of a single phonon of frequency ω the probability of phonon creation is proportional to n(ω) + 1 while the probability of annihilation of the same phonon is proportional to n(ω). Thus the probability of phonon creation between the same two momentum states is larger than that for annihilation by a factor of exp{ħω/kBT}. For the simultaneous excitation of two or more phonons a similar relation holds. This implies that for the classical regime of multiphonon excitation the transition rate w(kf, ki, T) is related to its inverse w(ki, kf, T) by the following relation
| | 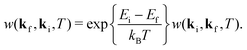 | (15) |
It can be readily shown that the transition rates of both
eqn (12) and (14) obey the above condition of detailed balancing.
A fundamental aspect of surface morphology that has been investigated with atom–surface scattering under classical conditions is the surface corrugation. Effects of corrugation are detected in the temperature dependence of the scattered spectra, and for ordered surfaces with large corrugations the spectra can exhibit rainbow patterns. Both of these aspects are discussed in connection with examples below in Sections 5 and 6. Corrugation is usually expressed through a corrugation function ξ(R) where R is the 2-D position vector parallel to the surface. The corrugation function defines the classical turning point of the incoming atom's motion and is given by the following equation
where
z is the component of the position vector perpendicular to the surface. A very useful potential model in atom–surface theory is the hard wall potential in which the surface is represented by a strong repulsive wall with a corrugation given by
eqn (16). Obviously, the corrugation in the case of a disordered surface will be rough, while the corrugation will be an ordered periodic function for a crystalline surface.
The theory, from which the transition rate of eqn (14) was developed, has been expanded to include surface corrugation, both for the corrugation of an ordered crystalline surface or for a rough corrugated surface.61,62 Starting from the fully quantum mechanical transition rate of eqn (3), applying the eikonal approximation to a potential with corrugation ξ(R) and then taking the limit of large numbers of phonons excited leads to the following expression
| | 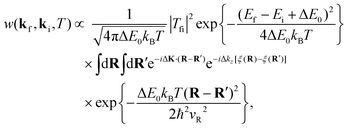 | (17) |
where the perpendicular component of the scattering vector is Δ
kz =
kfz −
kiz = |
kfz| + |
kiz|.
Eqn (17) is actually a semiclassical expression in the sense that the double integral over the surface accounts for quantum mechanical interference between parts of the incident wavefunction scattering from different positions on the surface. However, for large projectile energies, the coherence length for quantum interference becomes negligibly small, and for an ordered surface the double integral can be replaced by integrals over a single unit cell, multiplied by the number of unit cells which is simply a large constant. In the special limiting case where the corrugation function
ξ(
R) is taken to be a constant, in other words, for a smooth flat surface,
eqn (17) reduces to the result of
eqn (14) for the smooth surface model.
4 Classical stochastic scattering theory
In this section, this scattering is going to be considered theoretically from a different perspective. The dynamics is entirely described by classical mechanics from the very beginning by considering an interaction potential as well as a corrugation function. The scattering will be studied within the first order perturbation theory in the corrugation amplitude. Only in-plane scattering and first order theory will be discussed here in order to simplify the discussion and avoid cumbersome final analytical expressions. Even at this level of the theory, the physics is quite eloquent and provides the main ingredients of the corresponding dynamics. The corresponding 3D theory40,41 and the second order perturbation theory have also been developed.42–44
4.1 Elastic scattering
Let us consider the scattering of a particle with mass m and momentum pz in the direction which is vertical to the surface and momenta px and py in the directions parallel to the surface. The corresponding Hamiltonian underlying the dynamics of the particle can be written in general as| | 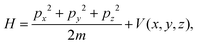 | (18) |
where a perfectly ordered crystal surface is assumed with the interaction potential given by V(x, y, z) displaying a periodic structure in the x, y plane. When the particle is sufficiently distant from the surface, this interaction potential will vanish.
The momenta of the incident particle are denoted by pxi, pyi, pzi and the initial vertical momentum is assumed to be negative whereas the initial horizontal momenta are positive. The angle of incidence θi relative to the direction vertical to the surface is then
| | 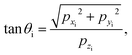 | (19) |
which is by definition negative, −π/2 ≤
θi ≤ 0. The azimuthal angle of incidence, in the
x −
y plane is
| | 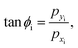 | (20) |
and by definition 0 ≤
ϕi ≤ π/2. The scattered particle is characterized by the final momenta
pxf,
pyf,
pzf. The scattering angle
θf relative to the vertical to the surface (0 ≤
θf ≤ π/2) is given by
| | 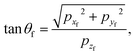 | (21) |
and the final azimuthal angle by
| | 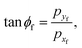 | (22) |
such that 0 ≤
ϕf ≤ 2π.
If a rectangular surface unit cell with lx and ly for the horizontal directions is assumed, then one has that the final momentum distribution can be written as
| | 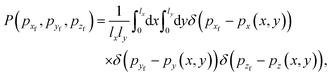 | (23) |
where
pj(
x,
y), with
j =
x,
y,
z, denote the momenta of the particle when the collision with the surface is over. Similarly, the angular distribution of the scattered particle is given by
| | 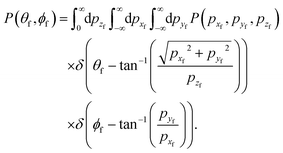 | (24) |
In order to simplify further the general theory, only in-plane scattering will be presented here. Remember that in most experimental setups only in-plane scattering events are measured. In-plane measurements are such that the initial and final azimuthal angles are the same, and may be set equal to zero and the initial and final momentum in the horizontal y direction is by definition zero. The in-plane momentum distribution is then given by
| | 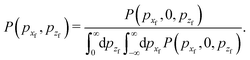 | (25) |
Trajectories initiated in the plane remain in the plane and one must only consider a two dimensional momentum distribution
P(
pxf,
pzf) as in
eqn (23) except for the
y coordinate. Analogously, the angular distribution
P(
θf) with −π/2 ≤
θf ≤ π/2 is obtained as in
eqn (24), except for azimuthal. However, one should keep in mind that the experimental measurement in the plane includes contributions from the full three dimensional dynamics.
The simplest model of in-plane scattering for a frozen surface can be obtained by Taylor expanding the interaction potential V(x, z) around the equilibrium points of the surface leading typically to two components, a potential of interaction in the vertical direction ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (z) and a corrugation function ξ(x) in the parallel direction
(z) and a corrugation function ξ(x) in the parallel direction
| | ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (z + h(x)) ≃ (z + h(x)) ≃ ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (z) + (z) + ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ′(z)ξ(x), ′(z)ξ(x), | (26) |
by assuming that the corrugation amplitude is smaller than the unit cell length. Initially the particle distance from the surface is sufficiently large, such that the potential of interaction with the surface vanishes. The particle is assumed to be initiated at the time −
t0 with initial vertical (negative) momentum
pzi and (positive) horizontal momentum
pxi. The zero-th order motion is decoupled, the vertical motion is governed by the vertical Hamiltonian
| | 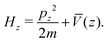 | (27) |
The horizontal motion is that of a free particle with constant velocity
vxi =
pxi/
m. The particle impacts the surface at time
t = 0 and then leaves the interaction region by the time
t0 which is taken to be sufficiently large to assure that the scattering event is over. Classical trajectories must be integrated over a time (2
t0) which is sufficiently long such that all scattered particles will have exited the interaction region, say
t0 → ∞.
One must estimate the final momenta after the scattering process to obtain the final angular distribution. This is easily achieved by first-order perturbation theory for which the small parameter of the theory is the corrugation height. From Hamilton's equations for the horizontal motion one readily finds that
| | 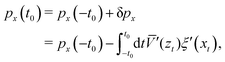 | (28) |
where
zt gives the
z-component of the classical trajectory. In the horizontal direction the motion is to zero-th order that of a free particle (parallel momentum conservation)
| | 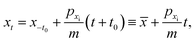 | (29) |
where
pxi =
px(−
t0) is used. Within this perturbation theory, the Jacobian of the transformation between the initial value of the horizontal coordinate
x−t0 to its value upon the impact point
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
is unity.
The corrugation function ξ(x) is assumed to be periodic with period l reflecting the periodicity of the surface. This function in general can be Fourier expanded as
| | 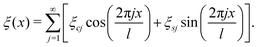 | (30) |
By using the symmetry of the zero-th order motion along the vertical direction, one thus finds that
| | 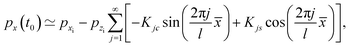 | (31) |
with the following notation
| | 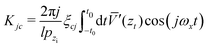 | (32) |
| | 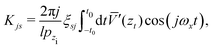 | (33) |
and the impact corrugation function
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
(
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
) responsible for the momentum shift can be written as
| | 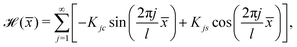 | (34) |
which is formed by the points of impact,
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
. Furthermore, the horizontal frequency is defined as
| | 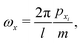 | (35) |
and
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif)
′(
zt) is symmetric with respect to time.
Under these conditions, there is no energy transfer between the particle and the surface, so that one can use energy conservation to determine to leading order also the change in the vertical momentum
| | 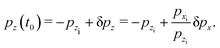 | (36) |
The momentum shifts determine directly the final momentum and angular distribution. Thus, one finds
| | 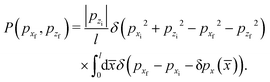 | (37) |
The corresponding angular distribution is
| | 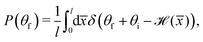 | (38) |
and the so-called classic deflection function is given by the argument of the Dirac
δ-function. For further insight, let us consider the simple case of a single Fourier component, so that
ξ1c =
ξ and
K1c =
K and all other coefficients vanish. One readily obtains that the angular distribution is formally given by
| | 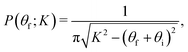 | (39) |
for the hard wall model where
K = 4π
ξ/
l is the rainbow angle shift. In this limit, the angular distribution is symmetric about the specular scattering angle. This distribution is independent of the energy or the mass of the scattered particle. The same observation is found for a pure repulsive potential.
41
As commented above, the rainbow shift parameter is in general determined not only by the corrugation amplitude but also by the dynamics of the scattered particle, as may be inferred through eqn (32) and (33). As an illustration, let us consider a Morse interaction potential written as
| | ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (z) = V0[(exp(−αz) − 1)2 − 1], (z) = V0[(exp(−αz) − 1)2 − 1], | (40) |
with a well depth given by
V0 and
α the stiffness parameter. The unperturbed trajectory of the Morse oscillator is known analytically to be
| | 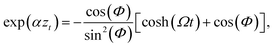 | (41) |
with
| | 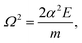 | (42) |
and
| | 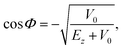 | (43) |
where
Ez =
pzi2/(2
m) is the energy in the vertical direction. Then, the rainbow shift parameter becomes
| | 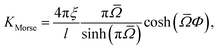 | (44) |
with
| | 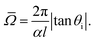 | (45) |
Keeping the angle of incidence fixed, the angle
Φ decreases from π to π/2 as the energy is increased, causing the rainbow shift parameter to decrease accordingly. It is the presence of an attractive well that causes the distance between the rainbow angles to decrease with increasing energy. Although qualitatively, and shown later on, this effect may be found also in the hard wall model, the change estimated by perturbation theory is stronger. The well also introduces a further dependence on the angle of incidence. Keeping the energy fixed but changing the angle of incidence from vertical to grazing causes a reduction of the vertical energy, such that
Φ increases as the deviation of the angle of incidence from the vertical increases. This leads to an increase in the rainbow shift parameter and maybe to its non-monotonic dependence on the angle of incidence.
4.2 Inelastic scattering
Energy exchange between the particle and the surface in this type of scattering is going to be described here by the well-known Caldeira–Leggett Hamiltonian.63,64 In this context, it is assumed that the interaction with phonons may be modelled by linear coupling terms to the bath surface modes for both the vertical and horizontal coordinates. Both interactions are modulated by a function of the vertical coordinate, which vanishes when the vertical distance is sufficiently large. An additional condition is translational invariance of the Hamiltonian, that is, since the surface is periodic along the horizontal coordinate, the Hamiltonian must reflect this periodicity. Thus, the 3D Hamiltonian governing the scattering event is| | 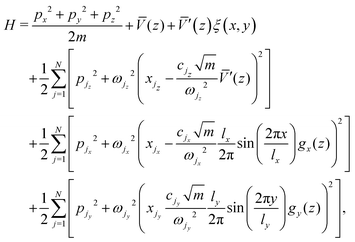 | (46) |
where N is the number of oscillators, the horizontal and vertical surface modes being characterized by the mass weighted momenta and coordinates pji, xji, j = 1,…,N; and i = x, y, z for the three components in the three cartesian directions. Translational invariance of the model is assured since the term coupling the horizontal motions to the respective phonon baths is periodic in the horizontal coordinate. When the particle is far from the surface it does not interact with the phonons, so that the surface Hamiltonian (in mass weighted coordinates and momenta) is| | 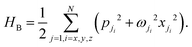 | (47) |
The classical equations of motion for linearly coupled harmonic oscillators are generalized Langevin equations. Introducing the spectral densities| | 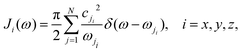 | (48) |
and associated friction functions| | 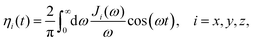 | (49) |
the corresponding equations for the horizontal motions take the form| | 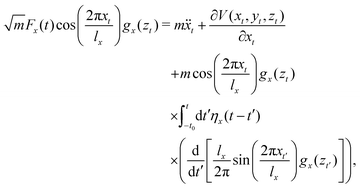 | (50) |
and| | 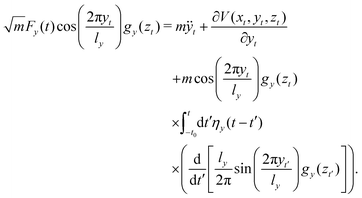 | (51) |
The generalized equation for the vertical motion is more complicated, but is not needed explicitly. In the absence of dissipation, the unperturbed vertical motion is taken to be an even function of time such that the particle reaches the vertical turning point at time t = 0. Trajectories are again initiated at the time −t0. The projectile is initially sufficiently distant from the surface, such that at the vicinity of z0 all the coupling functions vanish and the motion is that of a free particle. The noise functions| | 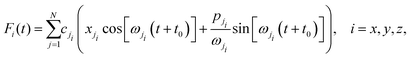 | (52) |
depend only on the initial conditions of the bath in the absence of particle surface interaction. They obey the fluctuation–dissipation relations| | 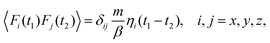 | (53) |
where the averaging is over the thermal distribution associated with the classical bath Hamiltonian as given in eqn (47). When considering the motion of a rare gas projectile whose interaction with the surface and the phonons does not include any strong chemical interactions, it is reasonable to assume that the system bath couplings are weak and Ohmic, that is,| | | ηi(t) = 2ηiδ(t), i = x, y, z, | (54) |
and the dynamics is in the Markovian regime (no memory), leading to standard Langevin equations. The assumption of Ohmic friction (as in eqn (54)) implies that at low frequencies, the spectral density J(ω) ∼ ω. One may justify this choice when considering phonon friction and the interaction of the scattered particle with the atoms of the surface.
It is well known that when considering surface diffusion,65 the surface may be described in terms of purely harmonic interactions, then the autocorrelation function of the force of the surface atoms on the diffusing particle may be considered to be Ohmic (that is, eqn (53) applies for constant friction). This is especially so if the atomic frequencies of motion are lower than the Debye frequency of the crystal.66 In principle, there is some difference between the friction felt by a particle diffusing on the surface and a particle scattered from it. The distance of the particle from the surface changes in time. The frictional forces are themselves functions of the vertical distance. In this model, it is assumed that the friction may be factorized as a product of a distance dependent function gi(z) and a friction function γ(t). This assumption allows one to relate the friction coefficients used to describe the scattering event to the friction coefficient used to describe surface diffusion. It is typically small when compared to the frequency of motion of the adsorbed particle, corroborating the rather small friction coefficients needed to fit the experimental data for broadening of rainbow scattering features due to surface temperature. The frictional forces felt by both scattered and diffusing particles are not necessarily limited to phonon friction. Especially for metals one should also consider electronic interactions such as electron–hole pair production. This process also leads to exchange of energy of the scattered particle with the surface. Fortunately, this energy loss mechanism may also be considered roughly in terms of an Ohmic frictional force.64,67,68 The friction coefficients used in this Hamiltonian model may thus be considered as coming from the additive sum of all sources of particle surface interactions which lead to energy loss of the particle.
In order to better illustrate the theory, one is restricted again to in-plane inelastic scattering. The zero-th order motion for the surface modes is that of uncoupled harmonic oscillators
| | 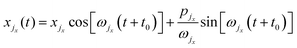 | (55) |
| | pjx(t) = −xjxωjx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin[ωjx(t + t0)] + pjx sin[ωjx(t + t0)] + pjx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos[ωjx(t + t0)]. cos[ωjx(t + t0)]. | (56) |
One then uses first order perturbation theory with respect to the corrugation as well as the coupling between the particle and the surface modes, to find from
eqn (50) three contributions to the shift in the horizontal momentum
| | δpx ≡ px(t0) − px(−t0) ≃ −pzi![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ( (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) + Δpx,1 + Δpx,2. ) + Δpx,1 + Δpx,2. | (57) |
The first term on the right hand side is the shift induced by the corrugation and takes the same form as in the absence of surface friction. The second term Δ
px,1 is a frictional momentum shift which, after an integration by parts, may be expressed in terms of the friction coefficient and the vertical motion coupling function as
| | 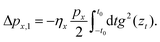 | (58) |
The third term on the right hand side is a noise induced momentum shift Δ
px,2| | 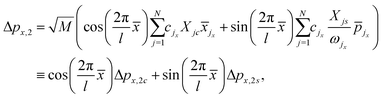 | (59) |
with
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) jx
jx =
xjx(
t = 0),
![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) jx
jx =
pjx(
t = 0) and
| | 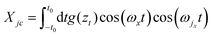 | (60) |
| | 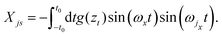 | (61) |
The energy loss to the bath may be divided into two parts, an average energy loss and a fluctuational energy loss
| | 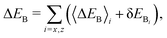 | (62) |
which are further subdivided into separate average and fluctuational energy losses in the horizontal and vertical directions. One may also use perturbation theory to obtain an estimate for the average energy loss to the bath due to the motion in the
x direction. The equation of motion for the
j-th bath mode is that of a forced harmonic oscillator, which can be solved implicitly in terms of the motion of the particle and the zero-th order solution for the particle equations of motion is inserted. Then, one considers the final energy of all of the bath modes after the collision and compares it with the energy prior to the collision to find that the average energy loss is
| | 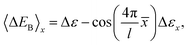 | (63) |
where
| | 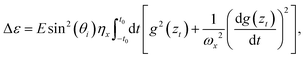 | (64) |
and
| | 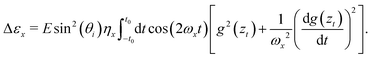 | (65) |
The fluctuational energy loss in the horizontal direction is
| | 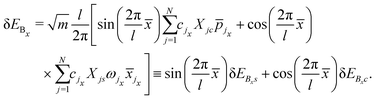 | (66) |
Eqn (63) expresses the fact that the energy loss for the horizontal motion may depend significantly on the point of impact of the scattered particle with the surface. As discussed in Section 6, the periodic dependence of the energy loss on the point of impact (
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
) implies the existence of what is known as energy loss rainbows. Energy loss rainbows will appear at least in principle whenever the derivative of the energy loss with respect to the impact parameter vanishes.
The average energy loss to the bath due to the vertical motion is found in similar fashion, by considering the surface modes coupled to the vertical motion (note that the dimension of ηx is time−1 while that of ηz is time3/mass2)
| | 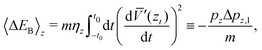 | (67) |
and the associated fluctuational energy loss is
| | 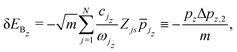 | (68) |
with
| | 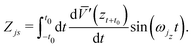 | (69) |
The second moments of the fluctuational energy losses are obtained by averaging over the initial conditions of the unperturbed bath. One finds that they are proportional to the average energy losses
| | 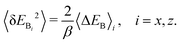 | (70) |
The shift in the final momentum in the vertical direction is obtained
via energy conservation as in the uncoupled case, except that here one has to take into consideration the energy losses to the phonon baths
| | | pzδpz = mΔEB + pxδpx. | (71) |
Finally, the expression for the angular distribution has the same form as in the absence of dissipation, except that now one has to include the averaging over the phonon baths. For this purpose, one notes that
| | 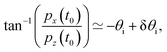 | (72) |
where to lowest order in the momentum shifts
| | 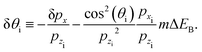 | (73) |
The averaging over the bath variables involves a few Gaussian integrations and one finds that the angular distribution is given by the expression
| | 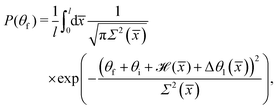 | (74) |
where the angular shift is
| | 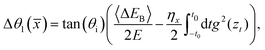 | (75) |
and the variance
| |  | (76) |
The coupling to the phonon bath smooths the distribution. If the coupling is strong, the phonon coupling will dominate and the distribution will be a single bell shaped Gaussian-like peak. However, for sufficiently weak coupling, one will observe a Gaussian-like broadening of the multiple rainbow peaks.
The angular shift Δθ1(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) is of special interest. It implies that even in the absence of corrugation, one may observe rainbows in the angular distribution which are induced by friction. These have been referred to as friction induced rainbows,41 not observed or reported yet in the literature. They result from the fact that the energy transfer to the surface may depend on the impact parameter. Such surface induced rainbows will be observable only at very low surface temperature. From eqn (70), one notes that as the temperature increases, the fluctuations increase and they will mask the rainbow structure induced by the energy loss.
) is of special interest. It implies that even in the absence of corrugation, one may observe rainbows in the angular distribution which are induced by friction. These have been referred to as friction induced rainbows,41 not observed or reported yet in the literature. They result from the fact that the energy transfer to the surface may depend on the impact parameter. Such surface induced rainbows will be observable only at very low surface temperature. From eqn (70), one notes that as the temperature increases, the fluctuations increase and they will mask the rainbow structure induced by the energy loss.
Several limits are interesting to discuss. First, if there is no coupling to the bath then the angular shift vanishes and one regains the angular distribution in the absence of dissipation
| | 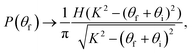 | (77) |
where
H(
x) is the Heaviside function. Second, in the absence of corrugation, there is no energy loss in the horizontal direction and the lattice length diverges. The shifted Gaussian angular distribution (shifted to angles larger than specular due to the energy loss in the vertical direction) is given by
| | 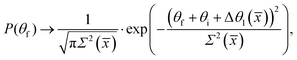 | (78) |
where the angular shift is always negative and the angular distribution is centered about an angle that is greater than the specular position (since the momentum in the horizontal direction is conserved while in the vertical direction has become smaller in magnitude). Third, in the limit of zero temperature (the so-called static limit), the variance vanishes and the angular shift is not zero but the broadening due to the phonon bath also vanishes
| | 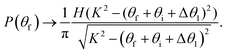 | (79) |
And fourth, the next step is to calculate the final energy distribution, or the so-called energy-loss distribution from the joint probability distribution for finding the scattered atom at the final scattering angle and final energy
E. After a few Gaussian integrations for the bath coordinates, one readily finds
| | 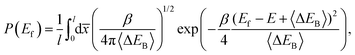 | (80) |
and this is a generalization of Brako's result.
36 Due to the coupling of the horizontal mode to the phonon bath, the energy loss does depend on the horizontal coordinate. One has to average over the energy loss distribution found for each value of the horizontal coordinate. The energy deflection function depends linearly on the friction coefficient (in the weak damping limit) but it is temperature independent since it gives the average change in the energy loss. This function is expected to have extrema which show up as divergences in the final energy distribution. These peaks have been assigned to be energy-loss rainbows. This means that the energy loss is a periodic function due to the periodicity of the surface. The effect of the fluctuations, and thus the temperature, is then to broaden the energy-loss distribution. In the high horizontal frequency limit, this dependence vanishes and one recovers Brako's result.
5 Applications of classical theory
5.1 Low-energy ion scattering
As stated above, eqn (12) with the form factor |Tfi|2 taken to be a constant was originally used to explain multiple phonon excitation in experiments of neutron scattering from solids. An application to surface scattering was to analyze low energy alkali ion scattering from metal surfaces.12,69
An extensive study of the scattering of Na+ ions from a clean and ordered Cu(001) surface over a range of energies from 100 to 400 eV was published in 1994 by Cooper and coworkers.70 They identified three distinct peaks in their energy-resolved scattered spectra and all three peaks showed significant energy loss to the surface. The peak with the largest energy loss was clearly identified as due to single scattering with one Cu atom, and this energy loss could be more than half of the incident energy depending on incident and final scattering angles. The two other peaks were at somewhat smaller energy loss and were identified as due to successive multiple collisions, in which after the first collision the Na+ ion continued on moving in the surface to collide with a second atom or with two successive atoms.
Extensive measurements of the width of the single-collision peak were made over a large range of the experimentally controllable parameters, which were temperature T and incident energy Ei. These experiments showed that the peak width behaved in a manner that did not agree with previous calculations based on the trajectory approximation. However, their results agreed well with a more detailed evaluation of the width developed by Burke, Jensen and Kohn.71 Cooper et al. attributed the disagreement to the fact that the trajectory approximation does not include recoil of the target atom. The trajectory approximation, which is widely used in high energy ion scattering, assumes that the speed of the projectile does not change during the collision, hence it does not include the energy losses due to the recoiling target atoms. This is clearly a poor approximation when the projectile is shown to lose half or more of its initial energy upon colliding with the surface. Thus the trajectory approximation misses an important fundamental effect. The theory of Burke et al., although limited to an evaluation of the width of the single scattering peak, correctly includes recoil and shows that there is a large and qualitative difference when compared to the trajectory approximation.
Shortly after the publication of the work of Cooper et al. it was shown that the hard sphere collision expression of eqn (12) gives the same results for the width of the single scattering peak as that of Burke et al., but in addition it is a more complete theory since it predicts the entire scattering spectrum. When compared to the data of Cooper et al. quite reasonable results were obtained for the complete description of the intensity and positions of single scattering peaks. It is also worthwhile noting that this single scattering peak is sensitive to small changes in mass of either the target or projectile atom. A change of the mass of either Cu or Na by 1 amu results in, respectively, a 1% or 3% shift in the calculated peak position, showing that atom–surface scattering could be of interest to questions of isotope separation. In fact, initial calculations using the tabulated mass of 64 amu for Cu were significantly improved after taking into account the natural isotope abundance of Cu (69% mass 63 and 31% mass 65).
Fig. 3 shows a more recently measured series of energy-resolved spectra using, instead of Na ions, K+ ions colliding with a Cu(001) surface at incident and final polar angles of 45° with respect to the normal and an incident energy of 154 eV.72 Shown are seven different spectra taken at surface temperatures ranging from 330 to 923 K. Here also three distinct energy loss peaks are visible, with the peak at smallest final energy due to single collisions and the other peaks due to successive double and triple collisions with individual Cu atoms. The experimental points are shown together with solid curves which are calculations determined from eqn (12). The single collision peak is calculated directly from eqn (12), while the multiple collision peaks are calculated by adding convolutions of two and three collisions. The paths of these multiple collision trajectories were chosen to match similar collisions predicted by a molecular dynamics simulation of the scattering. It is clear that the single collision peak, and its temperature dependence, is well explained by eqn (12) and the multiple collision peaks are also reasonably predicted. In this work further measurements were made for the temperature T dependence of the intensity and widths of all the peaks. The intensity of the single scattering peak (most probable intensity) varied very nearly as 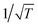 and its full width at half maximum (FWHM) was very closely linearly dependent on
and its full width at half maximum (FWHM) was very closely linearly dependent on 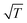 as predicted by eqn (12). For the multiple scattering peaks, the dependence of intensity and FWHM is not simply predicted by eqn (12), but calculations with the multiple collision convolutions of eqn (12) gave reasonably good agreement with the measured behavior.
as predicted by eqn (12). For the multiple scattering peaks, the dependence of intensity and FWHM is not simply predicted by eqn (12), but calculations with the multiple collision convolutions of eqn (12) gave reasonably good agreement with the measured behavior.
 |
| | Fig. 3 Energy-resolved intensity spectra for K+ ions incident on a Cu(001) target plotted as a function of relative final energy. The incident energy is Ei = 154 eV and the incident and final angles were both 45°. The temperature ranges from 330 to 923 K as marked. Experimental points are shown as open circles and the solid curves are calculations. The peak at the smallest final energy (greatest energy loss) is for single scattering, and the other two peaks are due to double and triple successive collisions. (Reprinted with permission from ref. 72, Copyright [2004] American Physical Society.) | |
5.2 Scattering from metal surfaces
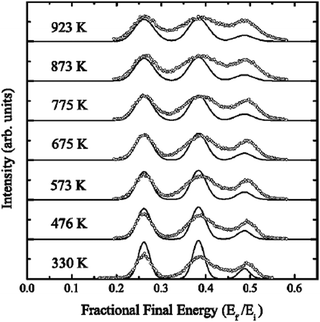
Fig. 4 gives an example of measurements of energy resolved spectra, scattered intensity versus final energy, in this case for 0.08 eV Ar atoms scattering from a Ru(0001) surface.73 The detector angle is 20°, the incident polar angle is 40° and five different surface temperatures are shown ranging from 140 to 850 K. Rare gas scattering from a number of different metal surfaces such as Ni, Ir and Ru has been analyzed using the smooth surface model of eqn (14). Here we would like to use the case of Ar/Ru(0001) as an example to show what sort of physical information can be extracted from such experiments. Shown as solid curves are calculations of the smooth surface model of eqn (14) and they match the data reasonably at all temperatures.74,75 The experimental data were normalized to have approximately the same maximum peak value for the single observed broad peak at each temperature, so the intensities are in arbitrary units. The dashed curves are the calculations normalized only to a single point at 140 K in order to indicate the calculated temperature dependence of the absolute intensities.
 |
| | Fig. 4 Energy-resolved spectra, scattered intensity versus final energy, of Ar scattered from Ru(0001) with an incident energy of 0.08 eV and temperatures ranging from 140 to 850 K as marked. The incident and final polar angles are θi = 40° and θf = 20°. Theoretical calculations are shown as solid curves and the dashed curves indicate the calculated intensities relative to that at T = 140 K. (Reprinted with permission from ref. 73, Copyright [2002] Royal Chemistry Society.) | |
The phonon speed parameter was chosen to be vR = 3200 m s−1, which compares closely to standard measured values for the Rayleigh velocity which is 3608 m s−1 for the Ru(0001) [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] direction and 3494 m s−1 for the [1
0] direction and 3494 m s−1 for the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] azimuth. The effective mass, chosen to give the best fit to the data, is rather large. Here, M = 2.3 times the mass of a single Ru atom, or 232.5 amu. This value is larger than the values used in the analysis of rare gases scattering from molten metal surfaces, to be discussed below, where the effective mass turned out to be very close to the mass of a single atom of the liquid metals.
00] azimuth. The effective mass, chosen to give the best fit to the data, is rather large. Here, M = 2.3 times the mass of a single Ru atom, or 232.5 amu. This value is larger than the values used in the analysis of rare gases scattering from molten metal surfaces, to be discussed below, where the effective mass turned out to be very close to the mass of a single atom of the liquid metals.
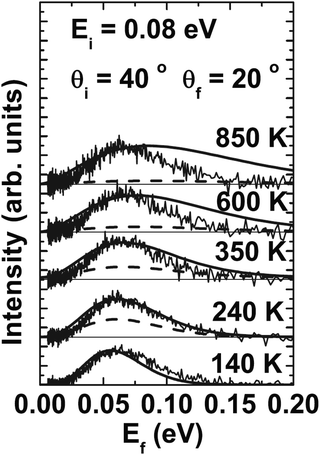
Angular distributions for Ar scattering from a hydrogen covered Ru surface were also measured. Fig. 5 shows angular distributions taken at four different incident angles from 40° to 70° as marked for Ar/Ru(0001)–(1 × 1)H in the [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] direction. The incident energy is Ei = 0.065 eV and T = 140 K. The solid curves are the calculations using the same parameters as for Fig. 4, which seems to indicate that the adsorbed layer of the light mass hydrogen atoms has little effect on the scattering of Ar atoms at this energy.
0] direction. The incident energy is Ei = 0.065 eV and T = 140 K. The solid curves are the calculations using the same parameters as for Fig. 4, which seems to indicate that the adsorbed layer of the light mass hydrogen atoms has little effect on the scattering of Ar atoms at this energy.
 |
| | Fig. 5 Ar scattering from Ru(0001)–(1 × 1)H in the [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] direction for incident energy Ei = 0.065 eV and T = 140 K. Angular distributions for four different incident angles ranging from 40° to 70° are shown as marked. The solid curves are calculations. (Reprinted with permission from ref. 73, Copyright [2002] Royal Chemistry Society.) 0] direction for incident energy Ei = 0.065 eV and T = 140 K. Angular distributions for four different incident angles ranging from 40° to 70° are shown as marked. The solid curves are calculations. (Reprinted with permission from ref. 73, Copyright [2002] Royal Chemistry Society.) | |
The agreement between experiment and theory shown in Fig. 4 and 5 makes it clear that the smooth surface model provides the essential physics necessary to explain the measured data, but indicates that the effective mass is considerably larger than that of a single Ru atom. This large mass of approximately 2.3 Ru atoms is interpreted as indicating that the incoming Ar atoms do not collide with a single Ru atom, but instead simultaneously interact with several surface atoms. In a different and independent experiment a similarly large effective mass for Ru(0001) has been reported for the scattering of nitrogen molecules from Ru(0001) which indicates that the size of the effective mass is a property of the target and not of the projectile.76 Such a large effective mass has interesting consequences, because it predicts that all rare gas scattering at low energies, particularly for small masses such as He and Ne, should be strongly reflective in the specular direction and exhibit more quantum mechanical features than might otherwise be expected. This prediction has, in fact, been verified by subsequent measurements of He and Ne scattering from Ru(0001).77
In order to understand the above statement it is of interest to recall from Section 2 above that all quantum mechanical features, such as diffraction, single phonon excitation and diffuse elastic scattering, are associated with the Debye–Waller factor of eqn (8), of which the most used approximation is eqn (9). For neutron scattering from a target the mass M is precisely defined as the mass of a single target nucleus. However, in the case of atom–surface scattering M cannot be precisely defined and must be regarded as an effective mass. This poses a vexing problem, for example when an attempt is made to extract the surface Debye temperature ΘD from a measurement of the temperature dependence of the Debye–Waller factor. Since ΘD appears in eqn (9) as the product MΘD2, if the value of the effective mass is not known, then ΘD cannot be precisely determined. Thus both the mass M and the Debye temperature ΘD must be regarded as effective values if measured only in a quantum mechanical experiment.
However, this problem is resolved by making measurements on the same system, but at energies and temperatures large enough to drive the system into the classical regime where 2W is large and the Debye–Waller factor is small. Then all quantum features are suppressed. This is because the theoretical treatment that leads to predictions of quantum intensities such as the diffraction of eqn (6) show that the effective mass M is identical with that which appears in the smooth surface model of eqn (14) in the recoil energy ΔE0 = ħ2(kf − ki)2/2M. Thus the measurement in the classical regime can produce a value of M which is independent of the Debye temperature and then can be used in connection with eqn (9) to obtain a precise value of ΘD from the temperature dependence of the Debye–Waller factor.
The discussion above now makes it clear why the rather large effective mass of Ru as measured in the Ar scattering experiments is important. A large effective mass M leads to a smaller overall value for 2W, and consequently a larger Debye–Waller factor, as seen from eqn (9) and consequently increases the intensity of all quantum features. Since it is expected that this large effective mass is not a property of the projectile atom, but a property of the Ru(0001) target surface, it is reasonable to expect that the other common rare gas projectiles, namely Xe, Kr, Ne and He, would also scatter with a large effective mass. So, especially for He and Ne, enhanced quantum features would be expected in low energy scattering. To put it in even simpler terms, one would anticipate that for He and Ne scattering the elastic (quantum) reflectivity would be enhanced as compared to other metal targets at similar energies and temperatures. As mentioned above, this special property of Ru(0001) has indeed been verified.77 This enhanced reflectivity could be of importance to the question of building a scanning atomic projectile microscope that uses a reflective mirror to concentrate the projectile beam.
Why Ru(0001) exhibits such a large effective mass in atom surface scattering is not totally clear, but is probably related to the hcp structure of the Ru crystal. The hcp(0001) surface exhibits ab–ab stacking meaning that directly underneath each surface Ru atom there is another Ru atom as a nearest neighbor. This contrasts with the abc–abc stacking of an fcc metal, where directly beneath a surface atom the next atom is two layers below. Assuming that the special nature of hcp stacking is indeed a factor in the large effective mass, then one would expect that other hcp metals should be investigated. First on the list would be osmium which not only has nearly twice the mass of Ru but is also directly below Ru in the periodic table of the elements.
5.3 Rare gas scattering from liquid metal surfaces
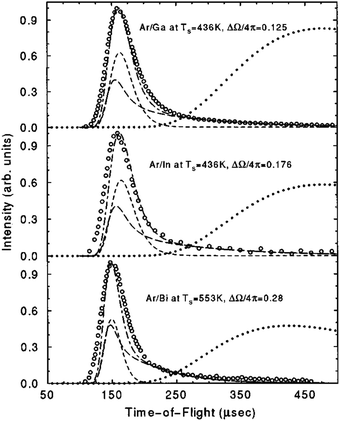
Experiments using rare gas atoms as probes of liquid metal surfaces are a subject of great interest, not only for investigating the structure and dynamics, but also as a sensitive measure of alloying of mixtures of molten metals and how it differs at the surface relative to bulk alloy content. Nathanson and coworkers perfected the experimental methods for keeping the surfaces clean for low melting point molten metals, and they carried out a long series of experiments in which rare gases, primarily Ar, were scattered off of molten Ga, In and Bi.78 They measured energy resolved spectra as well as angular distributions, both in the scattering plane and out of plane.
The energy-resolved spectra, measured with time of flight detectors, exhibited a broad single peak structure with a most probable final intensity located somewhere around 60% of the incident energy, and examples are shown in Fig. 6. The measured energy-resolved peaks did not resemble the equilibrium Knudsen flux, sometimes known as the cosine law. The Knudsen flux arises from a gas desorbing in equilibrium with the surface temperature and is proportional to an equilibrium Maxwell–Boltzmann distribution multiplied by the flux normal to a flat surface, which is proportional to the normal component of the velocity |v|f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θf. Correctly normalized and written as a differential reflection coefficient it is given by
θf. Correctly normalized and written as a differential reflection coefficient it is given by
| | 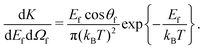 | (81) |
The Knudsen flux associated with all temperatures measured (for example, for Ga from 300 K up to 700 K) has a peak intensity at a much lower energy and is much broader. This indicates that the scattering was primarily due to direct collisions, with perhaps only a small fraction of double collisions.
 |
| | Fig. 6 Energy-resolved time-of-flight spectra for a 0.95 eV incident Ar beam on the three molten metals Ga, In and Bi. The temperature is 436 K for Ga and In and 553 K for Bi. The incident and final polar angles are 55°. The experimental points from ref. 78 are shown as open circles. The theoretical curves are as follows: (i) short-dashed is single collisions only, (ii) long dashed is the double collision contribution only, and (iii) the dash-dotted curve is the sum of single plus double collisions. For comparison the corresponding equilibrium desorption (Knudsen flux) is shown as a dotted curve. (Reprinted with permission from ref. 79, Copyright [1997] American Institute of Physics.) | |
The in-plane angular distributions, such as those examples shown in the left panels of Fig. 7, were measured with a fixed incident angle and variable final polar angle. They consist of a lobe, or a single broad peak with a FWHM of the order of 20° and a most probable final intensity at a polar angle somewhat larger than the incident angle; i.e., the angular distributions were somewhat supraspecular. The out-of-plane angular distributions were also single broad peaks of about the same FWHM, indicating that the probability of atoms scattered out-of-plane was approximately the same as the in-plane probability. In other words the scattered lobe is symmetric about the scattering plane and slightly supraspecular.
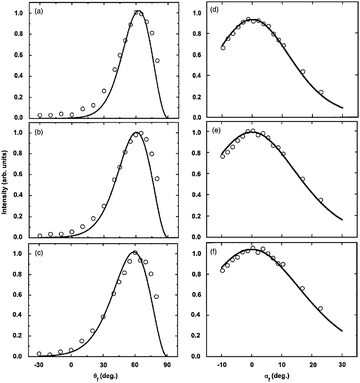 |
| | Fig. 7 In plane angular distributions (left panels) and out-of-plane angular distributions (right panels) for Ar scattering from molten Ga with an incident angle of 55° and incident energy of 0.95 eV for three different values of temperature: (a) and (d) 308 K, (b) and (e) 436 K, and (c) and (f) 586 K. Data from ref. 78 are open circles and calculations are the solid curves. (Reprinted with permission from ref. 79, Copyright [1997] American Institute of Physics.) | |
Three examples of energy resolved spectra are shown in Fig. 6. The in plane scattered intensity is plotted versus TOF for Ar scattering from the three different molten metals at three different temperatures as marked.79 The incident energy is 0.95 eV and the incident and final polar angles are fixed at 55°, i.e., the detector is in the specular position. The experimental data are shown as open circles. The single scattering calculated from the smooth surface model of eqn (14) is shown as a short-dashed curve. The single scattering curve is almost sufficient to describe the data, having roughly the same FWHM and peak position, although it does not have sufficient intensity to describe the long low-energy (large TOF) tail of the data. By adding a small fraction of double scattering, shown as a long-dashed curve, the sum of single plus double scattering (dash-dotted curve) matches the experimentally measured spectra quite well. This double scattering is calculated as a convolution of all possible double collisions with nearest metal atom neighbors on the surface, with each collision calculated by eqn (14). The Knudsen flux is also shown in Fig. 6 as a dotted curve expected from the equilibrium Maxwell–Boltzmann distribution of a gas at the same temperature as the metal. The Knudsen distribution is significantly broader with a peak at a much lower final energy. The large deviation of the experimentally measured scattered lobe from a Knudsen flux definitely rules out the possibility of a significant amount of trapping-desorption (the process in which the incoming gas atom gets trapped in the physisorption well and then is subsequently desorbed in equilibrium with the surface) in these experiments.
Fig. 7 shows three examples of typical angular distributions, both in plane and perpendicularly out of plane keeping the final polar angle fixed as explained below. These are for Ar scattering from molten Ga at three different temperatures as marked. The incident energy is 0.95 eV and the incident angle is 55°. The left panels show the in plane angular distributions and the out of plane scattering is in the right panels. They are clearly broad single peak features and it is seen that the peak position (most probable final angle) is about 5° larger than the specular position at θf = 55°, making the scattering slightly supraspecular, but with a significant intensity scattered at angles near to the surface normal direction and even non-zero intensity scattered back into the quadrant of the incident beam. The peak position does not vary much with surface temperature, but there is a detectable increase in FWHM with increasing T as would be expected from the differential reflection coefficient of eqn (14). The calculations shown as solid curves are carried out with the smooth surface model of eqn (14) and good agreement with the experimental points is obtained using only single collisions with the surface.80 The calculations were carried out with the velocity parameter vR = 650 m s−1 and, for the case of molten Ga, the effective surface mass was taken to be 1.65 times that of a Ga atom. For all spectra for Ar scattering from In and Bi the effective mass was that of a single In or Bi atom. The need for a slightly larger mass for Ga was dictated by the calculated position of the most probable energy of the energy-resolved spectra which is quite sensitive to M. Physically, this slightly increased effective mass is probably due to the fact that Ga is known to retain some layered structure at temperatures even above the melting point, implying stronger bonding in the liquid state. Molten In and Bi do not exhibit such layering behavior.
A little extra explanation is required for the out-of-plane angular distributions, shown in the right panels of Fig. 7. They are taken with a special geometry; the final polar angle was fixed at the most probable final angle and then the detector was moved in a linear direction perpendicular to the scattering plane. This makes for a scattering angle between the detector and the scattering plane denoted by αf in the figures. Measurements were made for αf on both sides of the scattering plane, and for more than 20° on one side. The measurements are symmetric with respect to the scattering plane and exhibit a FWHM that is approximately the same as that measured in-plane. The calculations using the single-collision differential reflection coefficient of eqn (14) describe the data quite well.
Mentioned above was the question of using rare gas scattering to measure alloys of molten metals and surface segregation of such alloys. In the course of their work on molten metals Nathanson et al. investigated alloy mixtures of bismuth and gallium.49,81 They examined the scattering of Ar and Xe beams from Ga–Bi alloys containing small fractions of Bi (Ga with 0.02 and 0.2 atomic percent of Bi) with measurements carried out at surface temperatures ranging from just above the melting point of Ga to nearly 900 K. The measurements were then compared with the results at similar temperatures for pure Ga and Bi. These experiments are of interest because liquid metals exhibit selective surface segregation of the alloy components and this segregation behavior can vary strongly with temperature. They also have distinct wetting properties, including wetting transitions.82–86 The surface segregation was monitored using Auger electron spectroscopy, and it was confirmed that at low temperatures the alloy surfaces were almost entirely Bi while at the highest temperatures the surface was dominated by Ga atoms.
Rare gas scattering is quite sensitive to the surface mass and this suggests that such experiments could be used to measure the atomic composition of the outermost layers of the molten alloys. This was confirmed with calculations using the smooth surface model of eqn (14) together with contributions due to double collisions which were calculated with convolution products of eqn (14).11 The TOF energy-resolved measurements were shown to be very sensitive to the ratio of Bi to Ga at the surface, and these measurements combined with the calculation were at least equally good at predicting the degree of surface segregation as the Auger measurements.
5.4 Rainbows and large corrugations
In Section 3 above a theory was developed for describing semiclassical and classical scattering from surfaces that have corrugation. If the surface is ordered and has a large corrugation amplitude then the phenomenon of rainbow scattering can become apparent in the scattered angular distribution spectra. Rainbows are most easily visualized by considering a beam of light reflecting from a mirror surface which is periodically corrugated. Strong reflection in the specular direction is expected from the areas that are nearly flat, i.e., the tops of the peaks and the bottoms of the troughs. However, reflection is also strong from the areas of the corrugation where there are inflection points, and in the directions “specular” to the locally nearly planar inflection regions there is also strong reflection, and this is the rainbow scattering. In fact, the simple description above applies to simple rainbows, and the situation can be much more complicated under circumstances where the light can make multiple reflections from the surface.26
For atom–surface scattering under classical conditions purely elastic reflection does not exist, as energy is transferred to and from the surface with every collision. Thus, the “classic” description of a simple rainbow reflection of the above paragraph is modified by the energy transfer. There are two principle modifications: first the sharp mirror beam reflection in the specular and rainbow directions is broadened by the energy transfer, and second, both are shifted in angular position. By the latter, it is meant that the peak position of the specular or rainbow may be at a greater or smaller angle than the corresponding simple mirror reflection. This shift may be to larger angles or to smaller angles depending upon whether net energy is transferred to or from the surface by the incoming atomic beam.
An example of rainbow scattering appears in Fig. 8 for the case of Ar scattering from LiF(001). Shown is a series of three angular distributions for Ar, with an energy of 525 meV, scattering from LiF(001) in the [100] direction.87 These angular distributions were taken with a fixed angle of 90° between the incident beam and detector direction, thus θi changes simultaneously with θf. Observed in Fig. 8 is a clear double-peaked structure in the angular distribution spectra, which is particularly evident at the lowest temperature of 300 K. This is a typical manifestation of surface rainbow scattering in which, for purely elastic scattering, a strong peak is seen in roughly the direction specular to the surface plane, and then a secondary rainbow peak is seen close to the direction specular to the inflection points (or points of maximum slope) of the surface corrugation function. In Fig. 8, the largest peak appears at approximately θf = 40°, which is at a smaller angle than the specular position of 45°, and this shift in position is due to the effects of inelastic energy losses to the phonons. The surface corrugation of LiF(001) in the [100] direction resembles a 1-D “corn row” pattern with a small but much reduced corrugation along the rows. Thus one expects a single rainbow and that is the peak observed at approximately θf = 55°. As the temperature is increased the double-peaked structure becomes less distinct, due to excitations of even greater numbers of phonons, approaching a very broad and asymmetric single peak at the largest temperature of 573 K.
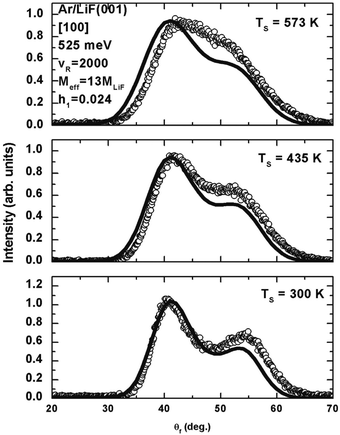 |
| | Fig. 8 Angular distributions for Ar scattering from LiF(001) in the [100] direction at three different temperatures from 300 to 573 K as marked. The incident energy is 0.525 eV. There is a fixed angle of 90° between the incident beam and detector direction. The experimental data are shown as open circles and the solid curves are calculations using eqn (17) with a corrugation parameter h = 0.024. (Reprinted with permission from ref. 88, Copyright [2015] Elsevier.) | |
The calculations shown as solid curves in Fig. 8 were carried out using eqn (17) with a 1-D corrugation function of eqn (16) given by88
| | 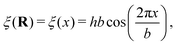 | (82) |
where the dimension
x is in the direction perpendicular to the rows of corrugation. The lattice parameter of bulk LiF is
a = 4.02 Å, which makes
b =
a/2 in the [100] direction, thus calculations based on
eqn (17) depend on three parameters. These are the dimensionless corrugation parameter
h, the effective mass
M, and the velocity parameter
vR. Although the corrugation of
eqn (82) is assumed to be one-dimensional, the scattering theory of
eqn (17) is fully three-dimensional and energy exchange and scattering involves all three directions, but only the in plane intensity is shown in
Fig. 8. The velocity parameter was taken to be 2000 m s
−1 which is roughly comparable to the Rayleigh phonon speed, the effective mass of the LiF is chosen to be the mass of 13 LiF molecules, and the corrugation parameter is
h = 0.024. The calculations are most sensitive to the corrugation parameter
h and the value 0.024 was fitted to best match the data at the lowest temperature. The calculations explain how the two peaks seem to merge towards a single broad and asymmetric peak as the temperature increases. This example demonstrates that the corrugated surface model of
eqn (17) is useful for explaining rainbow scattering and in the process provides important quantitative information about the corrugation function and its height
h.
5.5 Determining average surface corrugation
The energy landscape of atom–surface scattering is usually defined as the interaction potential energy evaluated at the classical turning point plotted as a function of coordinate directions parallel to the surface. Knowledge of the energy landscape is essential in determining the interactions of atoms or molecules with a surface and is an important first step in predicting results of scattering spectra, predicting chemical reactions and in studying catalysis. In the classical multiphonon excitation regime, atom scattering can provide important physical information on the energy landscape, even in the case of rough surfaces.61,89
In Section 5.4 above the analysis of rainbow scattering of Ar from LiF(001) shown in Fig. 8 indicates how information about the energy landscape is obtained from ordered surfaces, namely it revealed the corrugation function. However, even for rough surfaces such as molten metals relatively simple measurements analyzed by the corrugated surface model of eqn (17) can provide important information about the landscape. As an example, Fig. 9 shows a set of experimental measurements of the temperature dependence of the most probable intensity (peak intensity) in the energy-resolved scattering spectra of an incident Ar beam scattering from molten In. The incident energy is 0.43 eV and the incident and detector angles are at the specular position with θi = θf = 55°.78 The temperatures range from just above the melting temperature of In up to well over 500 K and the peak intensity exhibits a monotonic decrease with increasing T as shown by the experimental points. Such a straightforward measurement produces an accurate estimate of the average corrugation height of the energy landscape of the In surface.
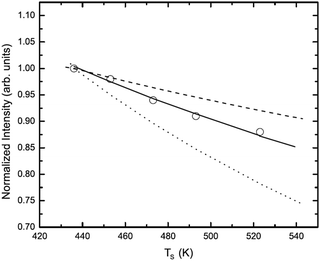 |
| | Fig. 9 Peak maximum temperature dependence of a 0.43 eV beam of Ar incident on a molten In surface with incident and final polar angles of 55°. The dashed curve is the expected result for a highly corrugated surface from eqn (12) and the dotted curve is the result for a smooth, uncorrugated surface from eqn (14). The calculation for a corrugated surface using eqn (17) is shown as a solid curve. The data points, shown as open circles, are from Nathanson et al.78 (Reprinted with permission from ref. 61, Copyright [2012] American Physical Society.) | |
For an understanding of the way in which such a simple measurement can extract information about the corrugation it is useful to compare eqn (12) and (14). The smooth surface model of eqn (14), which has been shown above to give reasonable predictions of experimental scattering spectra, has a peak intensity dependence that decreases as 1/T3/2 as is made clear from the prefactor multiplying the exponential. This is to be contrasted with eqn (12) which can be thought of as representing scattering from a highly corrugated surface, since it describes scattering from isolated surface atoms. Its multiplicative prefactor shows that the peak intensity of eqn (12) decreases more slowly as 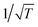 . These two temperature behaviors are plotted in Fig. 9 as dotted and dashed curves, respectively, and they represent the extreme behaviors expected. In other words, a surface with corrugation intermediate between that of a perfectly smooth surface or a highly rough surface essentially consisting of isolated atoms would exhibit a peak intensity decrease that is intermediate between these two extreme behaviors. It is clear from Fig. 9 that the experimental points exhibit this intermediate behavior.
. These two temperature behaviors are plotted in Fig. 9 as dotted and dashed curves, respectively, and they represent the extreme behaviors expected. In other words, a surface with corrugation intermediate between that of a perfectly smooth surface or a highly rough surface essentially consisting of isolated atoms would exhibit a peak intensity decrease that is intermediate between these two extreme behaviors. It is clear from Fig. 9 that the experimental points exhibit this intermediate behavior.
The calculations using eqn (17) are shown as a solid curve passing through the experimental points. Under the classical conditions of this experiment the quantum coherence width is small and there is negligible quantum interference arising from waves reflected from different parts of the surface. Consequently, the integrals in eqn (17) can be limited to a single typical scattering cell of the surface. This cell does not necessarily need to correspond to a unit cell of an ordered surface, nor does it need to have a particular shape, but rather needs to be a calculational cell large enough to accommodate the roughness expected. For the calculations shown in Fig. 9 describing the interaction of an incoming Ar atom with liquid In a 2-D sinusoidal function is chosen
| | 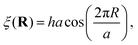 | (83) |
where
a is the average interatomic spacing in the bulk liquid,
R is the two-dimensional displacement parallel to the surface and
R is its magnitude which ranges from zero to
a/2. This corresponds to a corrugation profile for a typical surface atom with a trough-to-crest height of 2
ha, or a root mean square elevation of
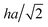
.
With the corrugation function of eqn (83) and parameters vR = 450 m s−1 and mass M equal to that of a single In atom the solid curve passing through the data in Fig. 9 is the result of the calculation.61 A least-squares fit of the calculations to the data points gives h = 0.29, which for the In interatomic distance of a = 3.14 Å gives a corrugation amplitude ha = 0.91 Å for a typical In atom at the liquid surface. The rms deviation of the fit is 0.0047, which corresponds to a standard deviation uncertainty in the amplitude h of less than 3%.
Further calculations have determined that the value of the average landscape corrugation is not strongly dependent on the specific nature of the corrugation function. Almost the same results for the corrugation amplitude are obtained if the 2-D sinusoidal corrugation function of eqn (83) is replaced by a 2-D Gaussian or some similar “bump” on the surface. The differential reflection coefficient of eqn (17) with the corrugation of eqn (83) explains not only the peak intensity experimental data shown in Fig. 9, but it also gives good agreement with all the scattering spectra measured for the Ar/In molten metal system discussed above in Section 5.3. These consist of the energy-resolved TOF spectra, in-plane angular distributions, and out-of-plane angular distributions. The corrugated surface model of eqn (17) is clearly capable of describing the complete scattering spectra and extracting important information such as the average corrugation height from experimental measurements.
5.6 Trapping-desorption versus direct scattering
A very old empirical concept that has been used in the field of gas–surface interactions is the assumption that when a beam of atoms is directed toward a target surface a fraction is directly scattered after a single collision while the remainder is trapped at the surface and comes approximately into equilibrium and eventually desorbes with the equilibrium distribution at the temperature of the surface. This equilibrium distribution is the Knudsen flux, or the cosine scattering law. Such an assumption was used by J. C. Maxwell in 1879 because it enabled a solution to a big problem, namely that an isolated gas of elastic scatterers will not by itself come to equilibrium.90
Modern experiments carried out under high vacuum and clean conditions have demonstrated that scattering of beams of rare gas atoms from metal surfaces can exhibit a strong peak of direct scattering and a broader low-energy peak that looks like the tail of the equilibrium Knudsen distribution.91 The direct scattering is assumed to consist of mostly single collision events with some additional contributions coming from double, triple and other small numbers of multiple collisions and interactions in the physisorption well. Good explanations of this behavior have been provided with molecular dynamics calculations using realistic interaction potentials.92 Recently, a model has been developed that contains the basic physics of the scattering process, with a rather straightforward interaction potential, and is also simple enough that it clearly demonstrates both direct scattering effects, the trapping-desorption component as well as illustrating the necessary conditions for the approach to equilibrium.
Fig. 10 shows an example of experimental data exhibiting direct scattering in combination with a trapping-desorption component. This is for Ar atom with an incident energy of 0.365 eV scattering from Au(111) covered with a single layer of 1-decanethiol at a temperature of 135 K.93 Three different data sets are shown as TOF plots for three different combinations of incident and final angles. In each case there is a distinct peak at high energy or small TOF and then a much broader shoulder and long tail at low energy or large TOF. The high energy peak is the direct scattering and the broad low-energy feature is the trapping-desorption component. The theoretical calculations using an iterative approach as explained below in connection with eqn (84) are the solid and dashed-dotted curves. The dashed curve is a Knudsen distribution at the corresponding temperature and it agrees well only with the long low-energy tail of the data.
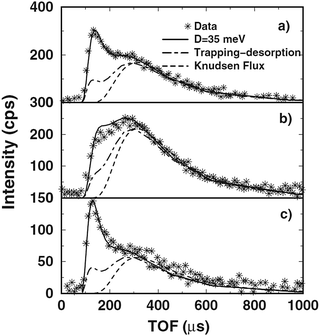 |
| | Fig. 10 Intensity versus TOF for 365 meV Ar scattering from a 1-decanethiol monolayer on Au(111) with a temperature of 135 K. The incident and detector polar angles are (a) θi = 45° and θf = 50°, (b) θi = 30° and θf = 50°, and (c) θi = 30° and θf = 80°. The solid curves are calculations with mass ratio μ = 0.56 and well depth D = 35. The trapping-desorption fraction of the calculations are shown as dash-dotted curves and the dashed curves are the Knudsen distribution. (Reprinted with permission from ref. 94, Copyright [2008] American Physical Society). | |
As an introduction to the process of building a theoretical model that can describe trapping-desorption, it is of interest to describe the essential features that such a model should contain. When a beam of incoming atoms interacts with a surface that is not too corrugated, a fraction will be directly scattered after a single collision, while the remainder will be trapped in the physisorption potential well. Large corrugations would lead also to the process of multiple collisions with different parts of the corrugation, but as will be shown such processes are not essential to describe the approach to equilibrium. Of the trapped fraction, some will lose sufficient energy to be actually trapped in the well with negative total energy, while others, even though they have positive total energy, will scatter at angles sufficiently close to grazing, so that they will have negative energy associated with motion normal to the surface and will be deflected back towards the surface by the attractive van der Waals part of the well. In the past this positive energy part of the trapped particles has sometimes been called the chattering fraction. For the case of quantum mechanical scattering, such events are called resonant scattering into the physisorption well, and also sometimes called selective adsorption. The trapped portion of the incident beam particles will continue to have interactions with the surface, and with each subsequent collision some will receive enough energy and will be projected sufficiently close to the surface normal that they escape, while the rest will remain trapped. Eventually, in a closed system, all initially trapped particles will ultimately leave the surface. However, at low temperatures and with deep potential wells this can require a substantial amount of time.
Perhaps the simplest model that contains all three components of the scattering, i.e., direct, positive energy chattering-trapping and negative energy trapping, is an interaction potential that consists of a hard repulsive wall with an attractive square well in front. Let the hard respulsive wall have the scattering properties of the differential reflection coefficient of eqn (12), while the square well representing the physisorption potential remains rigid.94,95 The square well at first glance may appear very rudimentary. However, for the classical scattering regime it correctly includes the two main features produced by any attractive physisorption well, and these are an increase in the energy associated with normal motion in the well and the associated refraction of the incident beam towards more normal directions to the surface. It should also be noted that the leading term in a van der Waals potential has a rigid attractive part that does not contribute to inelastic scattering. The leading van der Waals term in front of a semi-infinite surface varies as −C3/z3 and this behavior is the result of a pairwise sum over all atomic cores in the semi-infinite solid. Even though each of these cores vibrates, this sum averages the vibrational displacements over all cores so that the leading term does not vibrate. Only the parts of the potential that vibrate can contribute to energy transfer in a collision. Thus, the use of a square well with a rigid attractive part is a reasonable choice, at least for classical atom–surface scattering. Additionally, the width of the square well does not enter.
An iterative method, based on the qualitative description in the above paragraph has been developed in which the incoming gas atom enters the square well, gains energy and is refracted towards the surface, then collides with the wall where it exchanges energy. This initial energy transfer is given by the differential reflection labeled as dR0(pf, pi)/dEfdΩf which is taken to be that of eqn (12). At this initial collision, a portion of the incoming particles is scattered back into the continuum, and these constitute a part of the direct scattering, often the biggest part, while the remaining particles are trapped in the physisorption well. Those trapped particles are followed as they bounce off the attractive square well and continue to have collisions with the surface, and at each iteration the negative energy fraction, the chattering fraction, and the additional fraction which is desorbed are recalculated. In this way, the distribution of the slowly diminishing trapped fraction as well as the energy and angular distribution of the desorbed particles are followed and added to the distribution of particles already having left the surface. It is also clear that using this iterative differential reflection coefficient an average trapping time can be calculated. By following the initial direct scattering and the sum of all of the subsequently desorbed particles, the approach to the final distribution of the trapping-desorption fraction is monitored.
The multiple scattering events occuring with the trapped particles are taken to be convolutions of single scattering collisions with the repulsive wall, and the total differential reflection coefficient after n such collision iterations is written as
| | 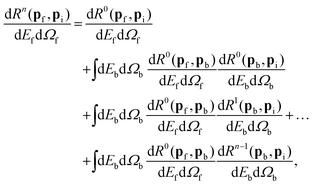 | (84) |
where the intermediate integrations in the higher order terms are carried out only over those energies and angles belonging to particles that remain trapped in the bound states. The iterations are carried out to a large enough number
n for which there is a very small fraction of the incident beam remaining trapped.
The solid curves in Fig. 10 show the results of calculations using the scheme of eqn (84). The total iteration number was typically more than n = 500, until less than 1% of the initially captured particles remained trapped in the potential well. The upper panel with θi = 45° and θf = 50° and the lower panel with θi = 30° and θf = 80° give a clear distinction between the rather sharp peak at a short time of flight (high energy) and a broader shoulder at larger times. The appearance of such a distinct direct scattering peak is due to the fact that the incident energy is significantly larger than the depth of the potential well. The solid curves in Fig. 10 are calculations carried out with an effective mass ratio μ = m/M = 0.56 obtained by fitting mainly to the high-energy direct scattering peak. The well depth of D = 35 meV was obtained by fitting largely to the low-energy tail. The dash-dotted curve shows the total contribution from all higher order multiple collisions in eqn (84), i.e., all except for the initial zero-th order direct collision. The behavior of the data is predicted by the calculations rather well, and the dashed-dotted curves show clearly the separation between the direct and trapping-desorption fractions. The value of D = 35 meV is in agreement with that of the potential energy function for this system developed in ref. 93 in which the physisorption well depth was determined to vary from 33 to 67 meV depending on the relative position within the surface unit cell over the self-assembled layer. The effective mass ratio corresponds to a surface mass of M = 71 amu, somewhat smaller than the 174.3 amu mass of the 1-decanethiol molecule, and is slightly smaller than the value μ = 0.62 obtained in ref. 93 by a fitting based on the Baule equations for hard sphere scattering. The results are sensitive to the effective mass. For example calculations with μ = 0.62 give a direct scattering peak positioned at a TOF time nearly 10 μs shorter which is equivalent to 15 meV larger in energy.
The remaining calculation shown in Fig. 10 as a dashed curve is the Knudsen flux which agrees well with the long low-energy tail of the distribution at large TOF. It is clear from the agreement at larger TOF times with the Knudsen curve that the biggest part of the trapping-desorption fraction emerges very nearly at thermal energies. However, the dash-dotted curve showing the trapping-desorption fraction itself has a multiple-peaked structure with a small sub-peak appearing at nearly the same final energy as the direct single-scattering contribution. This small, high-energy sub-peak arises from the first few collisions as the initially adsorbed particles continue to travel in the potential well. These first few collisions have a high probability of ejecting particles back into the continuum with relatively little loss of energy, i.e., energy comparable to that of the direct scattering fraction. This demonstrates that the direct scattering peak is composed not entirely of the results of the initial collision, but that some particles that are initially weakly trapped will also contribute to the direct scattering peak.
5.7 Approach to an equilibrium Knudsen distribution
In this section we wish to discuss and determine conditions in which an equilibrium Knudsen flux is to be expected in gas surface interactions. The treatment will be based on the scattering model of Section 5.6 and its eqn (84) above. Thus it becomes important to recognize that the model of eqn (84) applied to a repulsive wall with a square attractive potential well is realistic enough to explain real measured systems, such as the Ar scattering spectra of Fig. 10. Here we give examples of situations in which an incident beam gives rise to a scattered (or desorbed) distribution that approaches an equilibrium distribution. This treatment also gives an indication of the applicability of the Maxwell assumption.90
An example calculation of the evolution of the energy distribution as a function of the number n of iterations in eqn (84) surface is shown in Fig. 11. In this case Ar atoms with a translational energy of 1 meV are directed towards the surface at an incident angle of 45°. The square well depth is 80 meV and the surface temperature is 303 K. The lowest, dotted curve shows the scattered energy distribution after the first iteration, which is the second collision with the surface. The corresponding trapping fraction is P1 = 0.954, indicating that 95.4% of the incident particles remain trapped in the potential well. The other curves, as marked on Fig. 11, show the evolution of the continuum scattered distribution after the number of iterations is increased to 5, 50, and 500. After 500 iterations there is still roughly one-third of the incident particles remaining trapped. After 2124 iterations the trapped fraction drops below an arbitrary threshold of 1% of the incident particles and the energy distribution at all final scattered angles becomes very nearly the expected equilibrium Knudsen flux, which is shown as a curve of open circles.
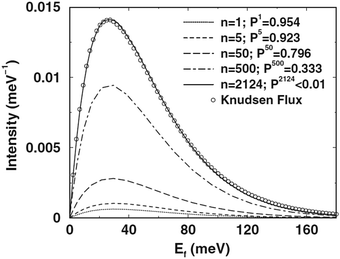 |
| | Fig. 11 Scattered intensity versus final energy for low incident energy Ar scattering from a tungsten surface with physisorption well depth 80 meV and temperature 303 K. The approach to an equilibrium Knudsen distribution is shown as a function of number of collisions n after becoming initially trapped in the well. Five curves of the intensity scattered away from the surface after the iteration numbers n = 1, 5, 50, 500 and 2124 are shown. The quantity Pn is the fraction of Ar particles remaining in the physisorption well after n collisions with the surface. A Knudsen equilibrium flux is shown as open circles. (Reprinted with permission from ref. 94, Copyright [2008] American Physical Society.) | |
Fig. 12 shows the development of the angular distribution for the same conditions as in Fig. 11. As a function of iteration number the progression towards the equilibrium cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θf distribution is evident although the expected behavior is achieved more slowly than that of the energy distribution exhibited in Fig. 11. The Knudsen flux is, of course, independent of azimuthal angle ϕ and the calculations of Fig. 11 and 12 very quickly become independent of ϕ with increasing iteration number n.
θf distribution is evident although the expected behavior is achieved more slowly than that of the energy distribution exhibited in Fig. 11. The Knudsen flux is, of course, independent of azimuthal angle ϕ and the calculations of Fig. 11 and 12 very quickly become independent of ϕ with increasing iteration number n.
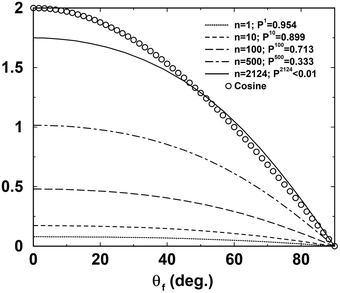 |
| | Fig. 12 The evolution of the final distribution in polar angle θf for the same Ar/W system as in Fig. 11. The Knudsen cosine distribution is shown as open circles. (Reprinted with permission from ref. 94, Copyright [2008] American Physical Society.) | |
Typical average desorption times were also calculated, and the method used here was to use the distribution fraction for the trapped fraction to calculate root mean square speeds. For the conditions of Fig. 11 and 12 it is found that the root mean square desorption time (or time trapped in the physisorption well) is about 2.5 × 10−9 s.
This work on the approach of surface scattering to equilibrium conditions is interesting for a number of reasons. Not the least important is that it shows that a relatively simple model of the interaction potential can lead to equilibrium under the right types of incident beam conditions. Namely, it shows that the interaction potential model must contain two essential ingredients, a physisorption well depth and allowance for transfer of mechanical energy between the projectile and the surface atoms. The most important part of the theory is to use a mechanism for energy transfer that is based on reasonably correct statistical mechanics. In this case we used the transition rate for thermalized two-body collisions of eqn (12) which is known to obey the law of detailed balancing of eqn (15). The Maxwell assumption is confirmed, i.e., the assumption that part of the beam is directly scattered and the remainder resembles an equilibrium distribution, but that assumption is obeyed well only when the adsorption well depth is large and the incident gas energies are comparable to or smaller than the well depth.94,95
6 Applications of classical stochastic scattering theory
In this section, it will be shown how the classical stochastic theory works for some selected scattering systems by considering only in-plane scattering and first order perturbation theory.
The first scattering system to analyze is the scattering of Ar on LiF(100). In principle, it would be seemingly unjustified to use an asymmetric corrugation of the surface. However as noted by Tully33 when considering the washboard model, “the probability P2(x) of striking the surface at position x is not uniform. There is a larger probability of striking a region where the surface slopes toward the incoming beam than where the surface slopes away”. If the corrugation function is ξ(x) then the probability is33
| | 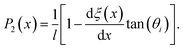 | (85) |
If one considers the simple sinusoidal corrugation function
| | 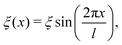 | (86) |
then the effective corrugation
ξeff(
x) “seen” by the incident particle is a product of the probability of arriving at the point
x and the actual corrugation at that point
| | 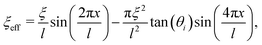 | (87) |
showing explicitly how the asymmetry may be modelled in terms of an added higher order sinusoidal term in the corrugation. One also notes that the second order term goes as
ξ2 while the perturbation theory is correct only to order
ξ. Thus, the vertical potential encountered by the particle depends on the impact parameter. Within the first order perturbation of this theory, the vertical potential felt by the particle is independent of the impact parameter, hence the asymmetry does not appear naturally within it. However, it may be modelled according to
eqn (87). This then creates an effective classical deflection function which is asymmetric leading to an asymmetry in the angular distribution.
Kondo et al.96 reported the experimental angular distributions of Ar atoms scattered from an LiF(001) surface (in the [100] direction) as a function of incident energy. Their experimental setup is such that the width of the incident beam is typically around 1°. As mentioned above, in these experiments the angle between the incident beam and the detector is fixed at 90° and the angle of incidence is varied. At the measured energies they find an asymmetric double peaked angular distribution, typical of rainbow scattering. They also find that the rainbow angles decrease with increasing incident energy. They fit their experimental results to the washboard model, albeit by using a different rainbow angle for each energy separately. Their rainbow angle parameter decreases with increasing energy from a value of 10.4° at 315 meV to 7.0° at 705 meV incident energy. They consider this to be a counterintuitive lessening of corrugation with increasing energy.
In Fig. 13 a good fit to the experimental data is plotted when the corrugation function is assumed to be
| | 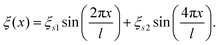 | (88) |
The parameters used are the atomic mass of Ar
m = 39.948 amu, the well depth
V0 = 88 meV as reported elsewhere
97 and the lattice length
l = 4 Å as measured by Ekinci and Toennies.
98 The Morse stiffness parameter was set as
αl = 3, the corrugation heights were
ξs1 = 0.20125 a.u. and
ξs2 = 0.054 a.u. The reduced friction coefficients were
![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) z
z =
![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) x
x = 0.00338 where
| | ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) x = ηx/ω0, x = ηx/ω0, | (89) |
and
| | ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) z = m2ω03ηz, z = m2ω03ηz, | (90) |
and
is the harmonic frequency of the Morse potential. The magnitude of the reduced friction parameters shows that the friction is weak. Five parameters are used to fit the experimental data, as all other parameters were obtained from experimental knowledge, and the surface temperature was taken to be 300 K. The fits by using this theory are slightly better than those reported by Kondo
et al. using the washboard model. The fitting procedure is not carried out for each distribution separately and the theory seems to account correctly for the energy dependence of the rainbow angles. The distributions are not symmetric and therefore the second order corrugation term was added. The decrease of the rainbow angles with energy is a result of the dynamics and does not imply that the corrugation becomes smaller with increasing energy, as suggested by Kondo
et al.
 |
| | Fig. 13 Experimental and theoretical angular distributions for the in plane scattering of Ar on a LiF(100) surface at T = 300 K. The scattered intensity is shown as a function of the final scattering angle, keeping a fixed 90° angle between the incident and scattered beam. The solid circles are the experimental results of Kondo et al.96 The theoretical plots are based on the classical perturbation theory, using a Morse oscillator potential for the vertical motion with well depth of 88 meV and stiffness parameter αl = 3, where the lattice length is l = 4 Å. The reduced friction parameters eqn (89) and (90) used are ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) z = z = ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) x = 0.00338, the corrugation heights are ξs1 = 0.20125 a.u. and ξs2 = 0.054 a.u. The plots from bottom to top show the distributions for the energies 315, 435, 525, 620 and 705 meV, respectively. (Reprinted with permission from ref. 37, Copyright [2009] American Physical Society.). x = 0.00338, the corrugation heights are ξs1 = 0.20125 a.u. and ξs2 = 0.054 a.u. The plots from bottom to top show the distributions for the energies 315, 435, 525, 620 and 705 meV, respectively. (Reprinted with permission from ref. 37, Copyright [2009] American Physical Society.). | |
Amirav et al.99 showed that the angular distribution for the scattering of Ar on Ag(100) evolves from a slightly asymmetric angular distribution at an angle of incidence of −30°, to a symmetric double peaked distribution at −45° and to a single bell shaped distribution at 60°. If one assumes that these results were obtained at room temperature (the surface temperature is not reported in that work), the 2D calculations were carried out for l = 2.8 Å,100V0 = 70 meV,101α = 1.0714 Å−1, M = 39.948 amu, ξs1 = −0.1057 Å, ξs2 = 0.0106 Å, ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) x = 0.00139 and
x = 0.00139 and ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) z = 0.000908, and incident energy of 2500 meV. The width of the incident beam was reported as going from 5% to 8% and therefore should be accounted for in the theoretical results.102 One simple way to do this is by adding a constant width of 0.085 radians. On the (a) panel of Fig. 14 the theoretical results (broadened with a fixed width of 0.085 radians) are compared with the measured results of Amirav et al.99 displaying a quantitative agreement. The asymmetry here is smaller than the asymmetry found in the Ar–LiF(100) system but the trend is similar. The rainbow scattering appears at low incident scattering angle and disappears as the scattering angle is increased as observed more clearly on the (b) panel of Fig. 14 where it is plotted the normalized angular distributions without the added broadening. At the incidence angle of −45°, one still sees the rainbow scattering, however, the asymmetry is almost gone. Increasing the angle of incidence to −60° wipes out the rainbows and one remains with a single peaked distribution.
z = 0.000908, and incident energy of 2500 meV. The width of the incident beam was reported as going from 5% to 8% and therefore should be accounted for in the theoretical results.102 One simple way to do this is by adding a constant width of 0.085 radians. On the (a) panel of Fig. 14 the theoretical results (broadened with a fixed width of 0.085 radians) are compared with the measured results of Amirav et al.99 displaying a quantitative agreement. The asymmetry here is smaller than the asymmetry found in the Ar–LiF(100) system but the trend is similar. The rainbow scattering appears at low incident scattering angle and disappears as the scattering angle is increased as observed more clearly on the (b) panel of Fig. 14 where it is plotted the normalized angular distributions without the added broadening. At the incidence angle of −45°, one still sees the rainbow scattering, however, the asymmetry is almost gone. Increasing the angle of incidence to −60° wipes out the rainbows and one remains with a single peaked distribution.
 |
| | Fig. 14 Angular distributions for the scattering of Ar on an Ag(100) surface seen in panel (a). The solid lines correspond to angular distributions obtained from the Morse potential model at an angle of incidence of −30, −45 and −60 degrees, respectively. The normalized distributions were multiplied by a constant factor of 1.54, 1.02 and 0.92 respectively to facilitate the comparison with the unnormalized experimental data. Solid circles are the respective experimental angular distributions adapted from Amirav et al. Normalized theoretical distributions for the scattering of Ar on Ag(100) without the added broadening shown in panel (b). (Reprinted with permission from ref. 37, Copyright [2009] American Physical Society.) | |
A nice illustration where the asymmetry is more pronounced is the scattering of Kr from Ag(100). For this system the following parameters are used, namely, V0 = 100 meV,101l = 2.8 Å,100α = 2.143 Å−1, M = 83.8 amu, ξs1 = −0.0450 Å, ξs2 = 0.0476 Å, ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) x = 0.000603 and
x = 0.000603 and ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) z = 0.000431 and incident energy of 6600 meV with T = 297 K. The resulting angular distributions are broadened by a constant factor of 0.09 radians. On the (a) panel of Fig. 15, a comparison between experimental and theoretical results are plotted. The fit is not as good as in the previous case, especially at the −45° angle of incidence. The normalized theoretical distributions without an extra broadening are shown on the (b) panel of Fig. 15. It is observed that the asymmetry is so strong that a three peaked distribution is predicted when the incident angle is −30° and that the rainbow scattering may still be observed when the incident angle is −60°. The distance between the two central rainbows decreases with increasing scattering angle, as does the asymmetry.
z = 0.000431 and incident energy of 6600 meV with T = 297 K. The resulting angular distributions are broadened by a constant factor of 0.09 radians. On the (a) panel of Fig. 15, a comparison between experimental and theoretical results are plotted. The fit is not as good as in the previous case, especially at the −45° angle of incidence. The normalized theoretical distributions without an extra broadening are shown on the (b) panel of Fig. 15. It is observed that the asymmetry is so strong that a three peaked distribution is predicted when the incident angle is −30° and that the rainbow scattering may still be observed when the incident angle is −60°. The distance between the two central rainbows decreases with increasing scattering angle, as does the asymmetry.
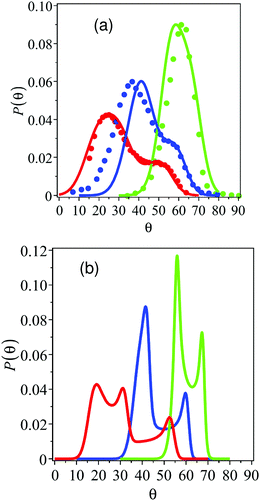 |
| | Fig. 15 Angular distributions for the scattering of Kr on an Ag(100) surface seen in panel (a). Solid lines correspond to the theoretical distributions based on the Morse potential model at the incidence angles of −30, −45 and −60 degrees and, solid circles, the corresponding experimental ones. The normalized distributions were multiplied as before by a constant factor of 1.3, 1.35 and 1.78, respectively. Normalized theoretical distributions for the scattering of Kr on Ag(100) but without the added broadening used for the comparison to the experimental results shown in panel (b). (Reprinted with permission from ref. 37, Copyright [2009] American Physical Society.) | |
On the other hand, the scattering of Ar atoms from a hydrogen saturated tungsten W(100) surface was measured by Schweizer et al.103 The wealth of experimental data allows one to follow the fitting of the theoretical parameters step by step, demonstrating that the fits are not accidental and should provide a reasonable description of the scattering dynamics. There are six free parameters in the corrugated Morse model, namely the well depth V0, the stiffness parameter α, the corrugation parameters ξs1 and ξs2 and the Ohmic friction coefficients ηx and ηz. The lattice length l = 4.6 Å is taken from ref. 103 and the mass of Ar is m = 39 amu. The observed asymmetry in the angular distributions is not very strong. This implies that the second order corrugation height will be small as compared with the first order corrugation height which is ξ2/ξ1 ≪ 1. To zero-th order one should then consider the incident energy and angle dependence of the first order rainbow shift function. Experimentally, at the angle of incidence of −30° and a surface temperature of T = 90 K, the distance between the rainbow angles decreases from a value of ∼23° at the incident energy E = 65 meV to ∼11° at E = 220 meV. At the same time, the decay of the rainbow shift function increases exponentially with the magnitude of the reduced frequency, ![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) , so that it cannot be too large. There is though a third piece of information. Schweizer et al. reported that at the −60° angle of incidence, the rainbow structure disappears, implying that the value of the rainbow shift function at this angle must be smaller than its value at −30°. Since the magnitude of
, so that it cannot be too large. There is though a third piece of information. Schweizer et al. reported that at the −60° angle of incidence, the rainbow structure disappears, implying that the value of the rainbow shift function at this angle must be smaller than its value at −30°. Since the magnitude of ![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) is determined by the product αl (where α is the Morse potential stiffness parameter) these observations lead to the conclusion that the product αl ≃ 2. With some fine tuning one can then determine that αl = 2 is optimal.
is determined by the product αl (where α is the Morse potential stiffness parameter) these observations lead to the conclusion that the product αl ≃ 2. With some fine tuning one can then determine that αl = 2 is optimal.
The same information helps in determining the Morse potential well depth V0. As mentioned, the experiment shows that the rainbow function decreases rather quickly with energy. This implies that the angle Φ must change rather rapidly with energy, as it is Φ which determines the energy dependence of the rainbow shift function. The well depth must thus be of the same order of magnitude as the energy at which the rainbow function changes rapidly, which in turn sets the value of V0 ≃ 50 meV. In practice, it was found that the best fit to the data was obtained using V0 = 60 meV. This is somewhat smaller than the value of 100 meV employed by Schweizer et al. in their theoretical analysis. The actual measured magnitude of the distance between the rainbow peaks sets the magnitude of the primary corrugation parameter around ξs1 = 0.1 a.u., which is approximately double the corrugation height used by Schweizer et al. in their analysis. In practice, the value ξs1 = 0.099 a.u.38 was employed.
Three fitting parameters are varied, namely, the friction coefficients and the second order corrugation height ξs2. It is also noted from ref. 103 that the experimentally measured average energy lost to the surface is ∼7 meV at the −30° angle of incidence and surface temperature T = 90 K. This sets the limits for the sum of the two friction coefficients. Their ratio is obtained by noting that under all conditions, the center of the measured angular distribution is approximately specular. This implies that the friction induced shift function must be small at all incidence energies. This then led to the reduced values of the friction coefficients ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) x = 0.00267 and
x = 0.00267 and ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) z = 0.00228. The second order corrugation parameter is responsible for the asymmetry of the angular distribution and may be determined by the asymmetry of the measured angular distribution at the −30° angle of incidence. The optimized value was ξs2 = −0.007 a.u. which is indeed much smaller than the first order corrugation height.
z = 0.00228. The second order corrugation parameter is responsible for the asymmetry of the angular distribution and may be determined by the asymmetry of the measured angular distribution at the −30° angle of incidence. The optimized value was ξs2 = −0.007 a.u. which is indeed much smaller than the first order corrugation height.
Results for the angular distributions for θi = −30° and the different incidence energies are presented in Fig. 16. The solid circles are the experimental results,103 the solid lines are the theoretical fits as obtained with the parameter set described above. The incident energies are from bottom to top 65 meV, 130 meV and 220 meV respectively (the distributions are displaced by 0.06 for the sake of clarity). Note that for the 65 meV case plotted in the figure are two different experimental distributions, the asterisks are adapted from the experiment.103 The two experimental distributions are not identical, one has a larger rainbow peak for sub-specular angles, while the second one has the larger rainbow peak at super-specular angles. This provides a rough indication of the experimental error in the angular distributions. In all fits the differences between them and the experimental results are not substantially larger than the differences between the two experimental distributions, implying that given uncertainty in the published data these are satisfactory fits.
 |
| | Fig. 16 Energy dependence of the angular distribution of Ar scattered on a hydrogen covered W(100) surface for a −30° angle of incidence and surface temperature of 90 K. Solid circles and asterisks are the experimental results adapted from Fig. 8 of ref. 103. The plots from bottom to top are for the incidence energies of 65, 130 and 220 meV, respectively. They have been shifted by a factor of 0.06 for the sake of clarity. From bottom to top, the normalized theoretical distributions have been multiplied by the constant factors of 1, 1.1 and 1.25 so as to compare with the (un-normalized) experimental results. (Reprinted with permission from ref. 38, Copyright [2010] American Physical Society.) | |
Schweizer et al. also reported the surface temperature dependence of the angular distributions measured at θi = −30°, E = 65 meV and T = 90, 140, 190 and 250 K. The classical stochastic theory is compared with the experimental results in Fig. 17. The central feature of the four distributions (displaced from each other by 0.03) is that the rainbow peaks are broadened as the temperature is increased. This is predicted from this theory since the variance of the distribution (Σ2) increases linearly with the temperature. This broadening smears out the rainbows and their asymmetry, the rainbow peaks become less significant as the temperature is increased.
 |
| | Fig. 17 Temperature dependence of the angular distribution of Ar scattered on a 2H–W(100) surface for a −30° angle of incidence and 65 meV incidence energy. Solid circles are the experimental results adapted from Fig. 10 of ref. 103. The plots from bottom to top are for the surface temperatures of 90, 140, 190 and 250 K, respectively. They have been shifted by a factor of 0.03 for the sake of clarity. From bottom to top, the normalized theoretical distributions have been multiplied by the constant factors of 1, 1.1, 1.14 and 1.25, respectively, so as to compare with the (un-normalized) experimental results. (Reprinted with permission from ref. 38, Copyright [2010] American Physical Society.) | |
Perhaps the most puzzling aspect of the Ar–2H–W(100) system was the drastic change of the angular distribution with the angle of incidence. It was shown that when the angle of incidence is increased to −60° the rainbow feature seems to disappear. One is left with a rather broad bell shaped distribution which is quasi-specular. This decrease in the distance between the rainbow angles then leads to the single lobe peaks shown in Fig. 18 where calculations are compared with the experimental distributions. Note especially that when E = 65 meV, the theoretical angular distribution is quite flat about the maximum, the width is due to the two rainbow angles which are smeared by the coupling to the phonons. If one would lower the surface temperature, it is predicted that the angular distribution even at this large angle of incidence would again become bimodal, reflecting the rainbow scattering. The theoretical full widths at half maximum of the theoretical angular distributions shown in this figure are 34° and 21° for the low and high energies respectively, these should be compared with the respective experimental values reported of 36° ± 3° and 25° ± 2°, respectively.
 |
| | Fig. 18 Energy dependence of the angular distribution of Ar scattered on a 2H–W(100) surface for a −60° angle of incidence and surface temperature of 90 K. Solid circles are the experimental results adapted from Fig. 14 of ref. 103. The plots are for the incidence energies of 65 and 110 meV, the broader plot is at the lower energy. The normalized theoretical distributions at 65 and 110 meV have been multiplied by the respective constant factors of 0.93 and 1.35 so as to compare with the (un-normalized) experimental results. (Reprinted with permission from ref. 38, Copyright [2010] American Physical Society.) | |
It should be mentioned that ab initio quantum chemistry computations verified that the fitted Morse potential parameters are in qualitative agreement with a computed Ar–W interaction potential.38
Finally, another interesting aspect of the 1D scattering is that the final energy of a scattered particle will typically depend on the impact parameter according to the so-called energy deflection function, 〈Ef(x)〉. This function, in analogy with the classical deflection function, displays extrema as a function of the impact parameter leading to peaks in the final energy distribution. These peaks are due to friction and this function reflects somehow the corrugation dependent energy loss to the surface, which comes about from the interactions with the surface which have been called energy loss rainbows.41 The same is expected for 2D scattering.
The final average energy may be rewritten as a sum of two terms, the initial incident energy and the average energy lost to the surface 〈ΔE(x)〉. Using the Hamiltonian model as given in eqn (46) one has that the final energy distribution may be written as
| | 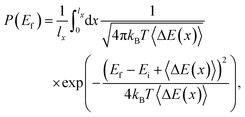 | (91) |
and the average energy loss function 〈Δ
E(
x)〉 may also be termed as the energy loss deflection function; it is the average energy lost to the surface at impact parameters
x.
If this analysis is carried out for the scattering of Ar from the LiF surface with the same parameters previously used, one finds numerically (by computing the numerically exact trajectories) the energy deflection functions (for an incident Ar energy of 3000 meV) shown in Fig. 19. From the extrema one would expect four peaks at an angle of incidence of −15°, but only two rainbows energies are anticipated at −60°. The resulting energy loss distributions are shown in Fig. 20. They were computed using both direct numerical simulation (symbols in Fig. 20) and the analytical expression for the energy distribution of eqn (91) (solid curves). The energy loss distributions are calculated at the incidence angles of 0°, −15°, −45°, and −60° and at three different surface temperatures of 0.5, 30, and 90 K. From this figure one notices that as the temperature and incident angle increase, the rainbow structure is broadened and eventually disappears.
 |
| | Fig. 19 Energy loss to the bath displayed as a function of the impact parameter calculated at a temperature of 0 K for a model of Ar scattered from a LiF surface. The solid (black) line, dashed (red) line, dotted (green) line and dot-dashed (blue) line correspond to incident angles of 0°, −15°, −45°, and −60°, respectively. Note the multiple extrema of the energy loss deflection functions. (Reprinted with permission from ref. 39, Copyright [2010] American Physical Society.) | |
 |
| | Fig. 20 Theoretical final energy distributions for the scattering of Ar on LiF at incidence angles of 0°, −15°, −45°, and −60° displayed in panels a–d. The (green) dots, (red) circles, and (blue) squares correspond to the numerical distributions calculated at temperatures of 0.5, 30, and 90 K, respectively. The associated solid curves represent the analytic distributions calculated from eqn (91). (Reprinted with permission from ref. 39, Copyright [2010] American Physical Society.) | |
Interestingly enough, energy loss rainbows are different from angular rainbows. Energy loss rainbows are caused by friction whereas angular rainbows are destroyed by friction. Energy loss rainbows may result from different parts of the corrugation potential, so that they may complement information on the corrugation potential obtained from angular rainbows. The observation of energy loss rainbows should be possible if the distance between the peaks is larger than the variance of the energy distribution 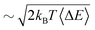 (where 〈ΔE〉 is the overall average energy loss). Thus, lowering the surface temperature, changing the angle of incidence towards the vertical and increasing the incidence energy will enhance the probability of observing the energy loss rainbows. The latter condition is based on the observation that the distance between the energy loss rainbows increases linearly with increasing incidence energy while the width increases only as the square root of the energy loss.
(where 〈ΔE〉 is the overall average energy loss). Thus, lowering the surface temperature, changing the angle of incidence towards the vertical and increasing the incidence energy will enhance the probability of observing the energy loss rainbows. The latter condition is based on the observation that the distance between the energy loss rainbows increases linearly with increasing incidence energy while the width increases only as the square root of the energy loss.
It is not yet clear whether energy loss rainbows have been observed experimentally or have not been recognized as such. The energy loss distribution of Ne scattered from a Self Assembled Monolayer (SAM) of 1-decanethiol on Au(111) has been measured by Sibener and coworkers48,104 as discussed above and shown in Fig. 10. For a 45° angle of incidence and Ne incident energies of 250 and 550 meV, they observed a bimodal energy distribution which disappeared when the angle of incidence was increased to 60° and the energy lowered to 65.3 meV. Bimodal energy distributions have also been observed in scattering from liquids, however, typically, the low energy peak is considered to be a thermal trapping-desorption peak and has nothing to do with energy loss rainbows. However, Isa et al.48 attributed the bimodal peak observed in the Ne scattering from SAMs to Ne colliding with different parts of the adsorbed molecule at different lateral distances. The different lateral distances may give rise to energy loss rainbows and one may obtain a good fit of the experimental energy loss data based on the energy loss rainbow analysis.39
7 Conclusions
Reviewed in this Perspective are two different approaches to treating atom–surface scattering interactions in the limit where classical physics is applicable. For atomic projectiles with incident energies of a few eV or less the predominant means of energy exchange with a surface is via multiple excitations of phonons. A brief description of the transition from the quantum mechanical regime of elastic (zero energy transfer) and single-phonon excitations to the classical domain of large numbers of phonon excitations is discussed. The somewhat ill-defined transition to the regime where classical physics is applicable is most readily expressed in terms of the Debye–Waller factor, appearing in eqn (6) and (10), which governs the attenuation of all quantum features in the scattered spectra, and these include diffraction peaks, diffuse elastic peaks, resonance signals, and single phonon peaks. The dimensionless exponent of the Debye–Waller factor 2W(kf, ki), which appears in eqn (8), is recognized as being a reasonable estimate of the total number of phonons created and annihilated in a given atom–surface collision. Thus, when the number of phonons excited becomes large all quantum peaks and features in the scattered spectra are suppressed and what remains are broader features. The condition for 2W(kf, ki) to become large is that the product of mass ratio (ratio of projectile mass to effective mass of the surface), incident energy and surface temperature becomes large.
In spite of the loss of more detailed information contained in features that can be observed under quantum mechanical conditions, there is nevertheless much information concerning the projectile–surface interaction that can be gleaned from measurements made in the classical multiphonon regime. This includes determination of the number of target atomic cores that are involved in the collision, the surface corrugation amplitude, and rainbow features arising from a corrugated surface. Discussions of rainbow features figure prominently in both theoretical approaches presented here.
The first approach discussed here is based on theory developed in the 1980s by Brako and Newns.30–32 They, in turn, had extended work developed several decades prior for describing multiple phonon excitations in neutron scattering, and their advance was to include the law of conservation of momentum. In a collision with a large, flat surface it is best to express momentum conservation in quantum mechanical terms; momentum is not conserved in the direction perpendicular to the surface (because the surface breaks the symmetry in that direction), but parallel momentum is conserved modulo a reciprocal lattice vector. The Brako–Newns theory did not include an interaction potential between the projectile atom and the surface, thus it could not describe surface corrugation or roughness, and hence cannot explain rainbow scattering features. The extensions reviewed here involve inclusion of an atom–surface potential and surface corrugation.
Several representative examples are presented in which comparisons of classical theory with experimental measurements reveal the size of the surface mass involved in the collision, give estimates of surface corrugation amplitudes and explain rainbow features. In addition the theory can explain trapping and desorption features observed in the experimental spectra and can explain how a gas interacting with a surface makes its approach to equilibrium at the surface temperature.
The second approach termed here as classical stochastic theory starts from a detailed description of the classical dynamics of elastic and inelastic scattering. For the inelastic case, this analysis is carried out within the Langevin formalism (stochastic approach) by beginning with the well-known Caldeira–Leggett Hamiltoninan. Although this theory has been developed for 2D and 3D scattering as well as within first and second order perturbation approximations in terms of the corrugation amplitude (it is supposed that the unit cell length is greater than the corrugation amplitude in each horizontal direction), only in-plane scattering and first order perturbation theory have been presented here. In order to further develop the corresponding theory an interaction potential together with a static corrugation are important ingredients that must be taken into account. The energy loss or energy dissipation is due to friction (Ohmic friction is assumed) and also depends on the surface temperature by means of a noise term (white noise). A new fitting parameter in this theory is the friction coefficient which is related to the spectral density of the thermal bath which is expressed in terms of harmonic oscillators simulating the phonon modes. In order to provide final analytical expressions for angular and energy loss distributions, a corrugated Morse potential (where the corrugation is placed in the repulsive part of the Morse potential) has been widely considered in its applications. Obviously, this theory is general enough to allow any interaction potential. Even more, a van der Waals tail could also be implemented for a better characterization of the scattering. Whereas at first order of perturbation the theoretical results can be solved analytically, the second order results require numerical calculations. Furthermore, this theory is a good starting point for any semiclassical and hybrid classical-quantum method in order to reach the classical-quantum transition. Some preliminary work in this direction can be found elsewhere.35,43,44 This more general approach led to a classical stochastic theory of surface sticking which has been applied thus far to only one set of experimental data.44
In this work, some selected applications have been presented in order to illustrate how each theory works and what type of results and discussion arise for each system analyzed. Clearly, in both cases, information about the surface structure and/or the gas–surface interaction is extracted. For example, both theories agree that the distance between the rainbow angles depends on the corrugation height of the surface as well as the incident energy. For the second approach, the energy dependence of the rainbow angles was partially accounted for by introduction of a shallow well preceding the hard wall so that the energy dependence could be used to provide an estimate of the physisorption well depth. The surface temperature broadens but does not necessarily destroy the rainbow features in the final angular distribution. This implies that the interaction of the particle with the surface is weak. The friction coefficients are weak, hence one may again employ classical perturbation theory to describe the dynamics of the particle surface interaction. The measured temperature dependence of the angular distribution with its rainbow peaks, together with energy loss measurements could thus be inverted in order to obtain an estimate of the particle surface interaction in terms of friction coefficients for the motion in the vertical and horizontal directions. One of the interesting outcomes is a deeper understanding of the intertwining between energy loss and the angular dependence of the scattering. There is a direct relationship between the location of the maximum (or maxima) of the angular distribution and the extent of energy loss to the horizontal and vertical directions. The first order perturbation theory does have its limitations; it cannot be applied to multiple scattering (multiple bounces of the incoming particle along the surface) and is invalid at grazing angles of incidence.
An important common feature of both theories presented here is that, under appropriate limiting conditions, they both lead to forms of the Brako–Newns expressions. This analysis also predicts an interesting type of rainbows called energy loss rainbows and friction induced rainbows although it remains somewhat unclear if such features have yet been identified experimentally.
Another topic of interest is the scattering of particles from liquid surfaces. Nathanson and coworkers have probed energy transfer, sticking, reactivity and more.105–107 Sibener and coworkers have analyzed the properties of clean, adsorbate decorated and thin-film covered interfaces.108–113 Although as a first guess one might expect that the disorder of a liquid surface would lead to a smearing out of rainbow features, as perhaps seen in a number of studies105–107,114 this may not be always the case. Even in liquids, one may expect ordered patterns on a length scale which is considerably larger than a single lattice length of a crystal and these might induce rainbow scattering features. Similarly, randomly distributed adsorbates would tend to destroy rainbow scattering features, but at least in the presence of low coverage, one might expect rainbow features to survive. Their broadening at low surface temperature could reflect features of the dilute surface coverage. There is a need for more theoretical work on scattering from these more complex surfaces.
Although the stochastic approach seems to be satisfactory, there remains room for improvements and extensions. The leading order perturbation theory is insufficient for describing asymmetry in final angular distributions of atom surface scattering. Perhaps one of the most important issues is to carry out ab initio and DFT calculations of the atom–surface interaction potential and combine them with on-the-fly classical molecular dynamics simulations. Rainbow features, energy loss rainbows and other qualitative features of rainbow scattering should be verified through such computations. At present they emanate from model potentials whose validity is not well established in terms of the true potential of interaction of the particle with the surface. On-the-fly computations would justify the characterization of the scattering dynamics in terms of only a few relevant physical parameters, as obtained from the present Morse potential Langevin dynamics based models.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
SMA would like to express his gratitude to Eli Pollak for a very long, close and fruitful collaboration; in particular, in the development of the classical stochastic theory. SMA also acknowledges support from Ministerio de Ciencia e Innovación through a grant with reference FIS2021-125735NB-I00 and from Fundación Humanismo y Ciencia.
References
- F. Knauer and O. Stern, Z. Phys., 1929, 53, 779 CrossRef CAS
 ; O. Stern, Naturwissenschaften, 1929, 17, 391 CrossRef
; O. Stern, Naturwissenschaften, 1929, 17, 391 CrossRef  .
.
- I. Estermann and O. Stern, Z. Phys., 1930, 61, 95 CrossRef
 ; I. Estermann, R. Frisch and O. Stern, Z. Phys., 1932, 73, 348 CrossRef
; I. Estermann, R. Frisch and O. Stern, Z. Phys., 1932, 73, 348 CrossRef  ;
O. R. Frisch, What Little I Remember, Cambridge University Press, Cambridge, 1979 Search PubMed
;
O. R. Frisch, What Little I Remember, Cambridge University Press, Cambridge, 1979 Search PubMed  .
.
- C. J. Davisson and L. H. Germer, Nature, 1927, 119, 558 CrossRef CAS
 .
.
-
G. Benedek and J. P. Toennies, Atomic Scale Dynamics at Surfaces, Springer Series in Surface Sciences, Springer Press, Berlin, 2019 Search PubMed
 .
.
- D. Farías and K.-H. Rieder, Rep. Prog. Phys., 1998, 61, 1575 CrossRef
 .
.
- V. Bortolani and A. C. Levi, Rev. Nuov. Cim., 1986, 9, 1 CrossRef
 .
.
- J. A. Barker and D. J. Auerbach, Faraday Discuss., 1985, 80, 277 RSC
 .
.
-
Springer Series in Surface Sciences, ed. E. Hulpke, Springer Press, Heidelberg, 1992, vol. 27 Search PubMed
 .
.
- B. Gumhalter, Phys. Rep., 2001, 351, 1 CrossRef CAS
 .
.
- K. J. Nihill, J. D. Graham and S. J. Sibener, Phys. Rev. Lett., 2017, 119, 176001 CrossRef PubMed
 .
.
- J. Dai and J. R. Manson, J. Chem. Phys., 2003, 119, 9842 CrossRef CAS
 .
.
- A. Muis and J. R. Manson, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 2205 CrossRef CAS PubMed
 .
.
- R. A. Oman, J. Chem. Phys., 1968, 48, 3919 CrossRef CAS
 .
.
- J. Lorenzen and L. M. Raff, J. Chem. Phys., 1968, 49, 1165 CrossRef CAS
 .
.
- J. D. McClure, J. Chem. Phys., 1969, 51, 1687 CrossRef CAS
 .
.
- J. D. McClure, J. Chem. Phys., 1970, 52, 2712 CrossRef CAS
 .
.
- J. D. McClure, J. Chem. Phys., 1972, 57, 2810–2823 CrossRef CAS
 .
.
- J. N. Smith, D. R. O'Keefe, H. Saltsburg and R. L. Palmer, J. Chem. Phys., 1969, 50, 4667 CrossRef CAS
 .
.
- J. N. Smith, D. R. O'Keefe and R. L. Palmer, J. Chem. Phys., 1970, 52, 315 CrossRef CAS
 .
.
- G. Boato, P. Cantini, U. Garibaldi, A. C. Levi, L. Mattera, R. Spadacini and G. E. Tommei, J. Phys. C, 1973, 6, L394 CrossRef CAS
 .
.
- U. Garibaldi, A. C. Levi, R. Spadacini and G. E. Tommei, Surf. Sci., 1975, 48, 649 CrossRef CAS
 .
.
- U. Garibaldi, A. C. Levi, R. Spadacini and G. E. Tommei, Surf. Sci., 1976, 55, 40 CrossRef CAS
 .
.
- A. W. Kleyn, A. C. Luntz and D. J. Auerbach, Phys. Rev. Lett., 1981, 47, 1169 CrossRef CAS
 .
.
- R. Schinke, J. Phys. Chem., 1982, 76, 2352 CrossRef CAS
 .
.
- G. Armand and J. R. Manson, Surf. Sci., 1982, 119, L299 CrossRef CAS
 .
.
- A. W. Kleyn and T. C. M. Horn, Phys. Rep., 1991, 199, 191 CrossRef CAS
 .
.
- S. Miret-Artés, J. Margalef-Roig, R. Guantes, F. Borondo and C. Jaffé, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 10397 CrossRef PubMed
 .
.
- R. Guantes, F. Borondo, J. Margalef-Roig, S. Miret-Artés and J. R. Manson, Surf. Sci., 1997, 375, L379 CrossRef CAS
 .
.
- R. Guantes, A. S. Sanz, J. Margalef-Roig and S. Miret-Artés, Surf. Sci. Rep., 2004, 53, 199 CrossRef CAS
 .
.
- R. Brako, Surf. Sci., 1982, 123, 439 CrossRef CAS
 .
.
- R. Brako and D. M. Newns, Surf. Sci., 1982, 117, 42 CrossRef CAS
 .
.
- R. Brako and D. M. Newns, Phys. Rev. Lett., 1982, 48, 1859 CrossRef CAS
 .
.
- J. C. Tully, J. Chem. Phys., 1990, 92, 680 CrossRef CAS
 .
.
- T. Yan, W. L. Hase and J. C. Tully, J. Chem. Phys., 2004, 120, 1031 CrossRef CAS PubMed
 .
.
- E. Pollak, S. Sengupta and S. Miret-Artés, J. Chem. Phys., 2008, 129, 054107 CrossRef PubMed
 .
.
- E. Pollak and S. Miret-Artés, J. Chem. Phys., 2009, 130, 194710 CrossRef PubMed
 ; E. Pollak and S. Miret-Artés, J. Chem. Phys., 2010, 132, 049901 CrossRef
; E. Pollak and S. Miret-Artés, J. Chem. Phys., 2010, 132, 049901 CrossRef  .
.
- E. Pollak, J. M. Moix and S. Miret-Artés, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 165420 CrossRef
 ; E. Pollak, J. M. Moix and S. Miret-Artés, Phys. Rev. B: Condens. Matter Mater. Phys., 2010,(81), 039902 CrossRef
; E. Pollak, J. M. Moix and S. Miret-Artés, Phys. Rev. B: Condens. Matter Mater. Phys., 2010,(81), 039902 CrossRef  .
.
- E. Pollak and J. Tatchen, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115404 CrossRef
 ; E. Pollak and J. Tatchen, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 049903 CrossRef
; E. Pollak and J. Tatchen, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 049903 CrossRef  .
.
- J. Moix, E. Pollak and S. Miret-Artés, Phys. Rev. Lett., 2010, 104, 116103 CrossRef PubMed
 .
.
- E. Pollak and S. Miret-Artés, Chem. Phys., 2010, 375, 337 CrossRef CAS
 .
.
- S. Miret-Artés and E. Pollak, Surf. Sci. Rep., 2012, 67, 161 CrossRef
 .
.
- Y. Zhou, E. Pollak and S. Miret-Artés, J. Chem. Phys., 2014, 140, 024709 CrossRef PubMed
 .
.
- E. Pollak and S. Miret-Artés, J. Phys. Chem. C, 2015, 119, 14532 CrossRef CAS
 .
.
- T. Sahoo and E. Pollak, J. Chem. Phys., 2015, 143, 064706 CrossRef PubMed
 .
.
- M. Debiossac, P. Pang and P. Roncin, Phys. Chem. Chem. Phys., 2021, 23, 7615 RSC
 .
.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061 CrossRef CAS
 .
.
- M. Head-Gordon and J. C. Tully, J. Chem. Phys., 1995, 103, 10137 CrossRef CAS
 .
.
- N. Isa, K. D. Gibson, T. Yan, W. Hase and S. J. Sibener, Chem. Phys., 2004, 120, 2417 CAS
 .
.
- D. Chase, M. Manning, J. Morgan, G. Nathanson and B. Gerber, J. Chem. Phys., 2000, 133, 9279 CrossRef
 .
.
-
L. S. Rodberg and R. M. Thaler, Introduction to the Quantum Theory of Scattering, Academic Press, New York, 1967 Search PubMed
 .
.
-
R. G. Newton, Scattering theory of waves and particles, Springer Verlag, New York, 1982 Search PubMed
 .
.
- J. R. Manson, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 6924 CrossRef PubMed
 .
.
- J. R. Manson, Comput. Phys. Commun., 1994, 80, 145 CrossRef CAS
 .
.
-
Handbook of Surface Science, ed. J. R. Manson, E. Hasselbrink and B. I. Lundqvist, 2008, vol. 3, p. 53 Search PubMed
 .
.
- J. R. Manson, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 6750 CrossRef PubMed
 .
.
-
G. D. Mahan, Many Particle Physics, Plenum Press, New York and London, 1990 Search PubMed
 .
.
- A. Sjolander, Ark. Fys., 1959, 14, 314 Search PubMed
 .
.
- J. R. Manson, V. Celli and D. Himes, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 2782 CrossRef CAS PubMed
 .
.
- J. M. Jackson and N. F. Mott, Proc. R. Soc. A, 1932, 137, 703 CAS
 .
.
- P. M. Morse, Phys. Rev., 1929, 34, 57 CrossRef CAS
 .
.
- W. W. Hayes and J. R. Manson, Phys. Rev. Lett., 2012, 109, 063203 CrossRef CAS PubMed
 .
.
- H. Shichibe, Y. Satake, K. Watanabe, A. Kinjyo, A. Kunihara, Y. Yamada, M. Sasaki, W. W. Hayes and J. R. Manson, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155403 CrossRef
 .
.
- A. O. Caldeira and A. J. Leggett, Ann. Phys., 1983, 149, 374 Search PubMed
 .
.
-
U. Weiss, Quantum Dissipative Systems, World Scientific, 1999 Search PubMed
 .
.
- S. Miret-Artés and E. Pollak, J. Phys.: Condens. Matter, 2005, 17, S4133 CrossRef
 .
.
- Y. Georgievskii, M. A. Kozhushner and E. Pollak, J. Chem. Phys., 1995, 102, 6908 CrossRef CAS
 .
.
- J. I. Juristi, M. Alducin, R. Diez-Muiño, H. F. Busnengo and A. Salin, Phys. Rev. Lett., 2008, 100, 116102 CrossRef PubMed
 .
.
- A. C. Luntz, I. Makkonen, M. Persson and S. Holloway, Phys. Rev. Lett., 2009, 102, 109601 CrossRef CAS PubMed
 .
.
- J. R. Manson and R. H. Ritchie, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 4881 CrossRef CAS PubMed
 .
.
- C. A. DiRubio, D. M. Goodstein, B. H. Cooper and K. Burke, Phys. Rev. Lett., 1994, 73, 2768 CrossRef CAS PubMed
 .
.
- K. Burke, J. H. Jensen and W. Kohn, Surf. Sci., 1991, 241, 211 CrossRef CAS
 .
.
- J. Powers, J. R. Manson, C. E. Sosolik, J. R. Hampton, A. C. Lavery and B. H. Cooper, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 115413 CrossRef
 .
.
- B. Berenbak, S. Zboray, B. Riedmuller, D. C. Papageorgopoulos, S. Stolte and A. W. Kleyn, Phys. Chem. Chem. Phys., 2002, 4, 68 RSC
 .
.
- W. W. Hayes and J. R. Manson, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 1134 CrossRef
 .
.
- W. W. Hayes and J. R. Manson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 089904(E) CrossRef
 .
.
- H. Ambaye and J. R. Manson, J. Chem. Phys., 2006, 125, 176101 CrossRef PubMed
 .
.
- M. Minniti, C. Diaz, J. L. F. Cunado, A. Politano, D. Maccariello, F. Martin, D. Farías and R. Miranda, J. Phys.: Condens. Matter, 2012, 24, 354002 CrossRef CAS PubMed
 .
.
- W. R. Ronk, D. V. Kowalski, M. Manning and G. Nathanson, J. Chem. Phys., 1996, 104, 4842 CrossRef CAS
 .
.
- A. Muis and J. R. Manson, J. Chem. Phys., 1997, 107, 1655 CrossRef CAS
 .
.
- W. W. Hayes and J. R. Manson, J. Chem. Phys., 2007, 127, 164714 CrossRef CAS PubMed
 .
.
- J. Morgan and G. M. Nathanson, J. Chem. Phys., 2001, 114, 1958 CrossRef CAS
 .
.
- D. Nattland, P. D. Poh, S. C. Muller and W. Freyland, J. Non-Cryst. Solids, 1996, 772, 205 Search PubMed
 .
.
- M. Zhao, D. Chekmarev and S. A. Rice, J. Chem. Phys., 1998, 108, 5055 CrossRef CAS
 .
.
- E. B. Flom, M. Li, A. Acero, N. Maskil and S. A. Rice, Science, 1993, 260, 332 CrossRef CAS PubMed
 .
.
- H. Tostmann, E. DiMasi, O. G. Shpyrko, P. S. Pershan, B. M. Ocko and M. Deutsch, Phys. Rev. Lett., 2000, 84, 4385 CrossRef CAS PubMed
 .
.
- E. DiMasi, H. Tostmann, O. G. Shpyrko, P. Huber, B. M. Ocko, P. S. Pershan, M. Deutsch and L. E. Berman, Phys. Rev. Lett., 2001, 86, 1538 CrossRef CAS PubMed
 .
.
- T. Kondo, H. S. Kato, T. Yamada, S. Yamamoto and M. Kawai, J. Chem. Phys., 2005, 122, 244713 CrossRef PubMed
 .
.
- W. W. Hayes and J. R. Manson, Surf. Sci., 2015, 641, 72 CrossRef CAS
 .
.
- E. Pollak and J. R. Manson, J. Phys.: Condens. Matt., 2012, 24, 104001 CrossRef PubMed
 .
.
- J. C. Maxwell, Philos. Trans. R. Soc. London, 1879, 170, 251 Search PubMed
 .
.
- J. E. Hurst, C. A. Becker, J. P. Cowin, K. C. Janda, L. Wharton and D. J. Auerbach, Phys. Rev. Lett., 1979, 43, 1175 CrossRef CAS
 .
.
- J. C. Tully, Faraday Discuss., Chem. Soc., 1985, 80, 291 RSC
 .
.
- K. D. Gibson, N. Isa and S. J. Sibener, J. Chem. Phys., 2003, 119, 13083 CrossRef CAS
 .
.
- G. Fan and J. R. Manson, Phys. Rev. Lett., 2008, 101, 063202 CrossRef PubMed
 .
.
- G. Fan and J. R. Manson, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 045424 CrossRef
 .
.
- T. Kondo, H. S. Kato, T. Yamada, S. Yamamoto and M. Kawai, Eur. Phys. J. D, 2006, 38, 129 CrossRef CAS
 .
.
- J. R. Klein and M. W. Cole, Surf. Sci., 1979, 79, 269 CrossRef CAS
 .
.
- Y. Ekinci and J. P. Toennies, Surf. Sci., 2004, 563, 127 CrossRef CAS
 .
.
- A. Amirav, M. J. Cardillo, P. L. Trevor, C. Lim and J. C. Tully, J. Chem. Phys., 1987, 87, 1796 CrossRef CAS
 .
.
- A. Raukema, R. J. Dirksen and A. W. Kleyn, J. Chem. Phys., 1995, 103, 6217 CrossRef CAS
 .
.
- G. Vidali, G. Ihm, H.-Y. Kim and M. W. Cole, Surf. Sci. Rep., 1991, 12, 135 CrossRef
 .
.
- P. S. Weiss, A. Amirav, P. L. Trevor and M. J. Cardillo, J. Vac. Sci. Technol., A, 1988, 6, 889 CrossRef CAS
 .
.
- E. K. Schweizer, C. T. Rettner and S. Holloway, Surf. Sci., 1991, 249, 335 CrossRef CAS
 .
.
- T. Yan, N. Isa, K. D. Gibson, S. J. Sibener and W. L. Hase, J. Phys. Chem. A, 2004, 107, 10600 CrossRef
 .
.
- M. E. Saecker, S. T. Govoni, D. V. KowalsuI, M. E. King and G. M. Nathanson, Science, 1991, 252, 1421 CrossRef CAS PubMed
 .
.
- G. M. Nathanson, Ann. Rev. Phys. Chem., 2004, 55, 231 CrossRef CAS PubMed
 .
.
- T. Krebs and G. M. Nathanson, J. Phys. Chem. A, 2011, 115, 482 CrossRef CAS PubMed
 .
.
- M. A. Freedman, A. W. Rosenbaum and S. J. Sibener, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 113410 CrossRef
 .
.
- K. D. Gibson, S. J. Sibener, H. P. Upadhyaya, A. L. Brunsvold, J. Zhang, T. K. Minton and D. Troya, J. Phys. Chem. A, 2008, 128, 224708 CrossRef CAS PubMed
 .
.
- M. A. Freedman, J. S. Becker, A. W. Rosenbaum and S. J. Sibener, J. Chem. Phys., 2008, 129, 44906 CrossRef PubMed
 .
.
- K.
D. Gibson and S. J. Sibener, J. Phys. Chem. C, 2009, 113, 13325 CrossRef CAS
 .
.
- J. S. Becker, R. D. Brown, E. Johansson, N. S. Lewis and S. J. Sibener, J. Chem. Phys., 2010, 133, 104705 CrossRef PubMed
 .
.
- K. D. Gibson, D. R. Killelea, H. Yuan, J. S. Becker and S. J. Sibener, J. Chem. Phys., 2011, 134, 034703 CrossRef CAS PubMed
 .
.
- D. Chase, M. Manning, J. A. Morgan, G. M. Nathanson and R. B. Gerber, J. Chem. Phys., 2000, 113, 9279 CrossRef CAS
 .
.
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab and
S.
Miret-Artés
ab and
S.
Miret-Artés
 *ac
*ac
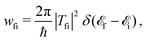
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) i and
i and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) f are the initial and final total energies of the entire system of interest, consisting of surface and projectile atom described by the Hamiltonian
f are the initial and final total energies of the entire system of interest, consisting of surface and projectile atom described by the Hamiltonian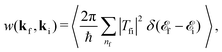
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dEf which is the fraction of the incident beam intensity scattered into the small final energy interval dEf and the small solid angle dΩf. This is related to the transition rate of eqn (3) by
dEf which is the fraction of the incident beam intensity scattered into the small final energy interval dEf and the small solid angle dΩf. This is related to the transition rate of eqn (3) by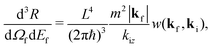
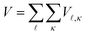 where the discrete variable
where the discrete variable ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) counts surface unit cells and κ counts elements within the unit cell. For simplicity we will assume Bravais unit cells containing only one surface atom and neglect the summation over κ. Then the simplest realistic form for the interaction potential is
counts surface unit cells and κ counts elements within the unit cell. For simplicity we will assume Bravais unit cells containing only one surface atom and neglect the summation over κ. Then the simplest realistic form for the interaction potential is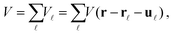
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the position of the
is the position of the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) -th unit cell and u
-th unit cell and u![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is its vibrational displacement. When the potential is a pairwise summation such as eqn (5) then the transition operator, from which the transition matrix elements Tfi are formed, is also a pairwise summation
is its vibrational displacement. When the potential is a pairwise summation such as eqn (5) then the transition operator, from which the transition matrix elements Tfi are formed, is also a pairwise summation 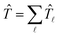 .
.
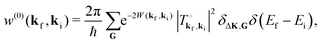
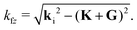
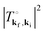 . Each peak is also multiplied by a Debye–Waller factor exp{−2W(kf, ki)} whose argument is given by
. Each peak is also multiplied by a Debye–Waller factor exp{−2W(kf, ki)} whose argument is given by![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (0))2〉,
(0))2〉,![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) .
.
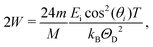
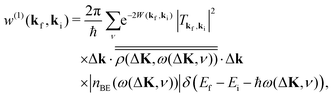
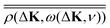 is essentially the surface projection of the phonon density of states.52 Just as in the case of elastic diffraction of eqn (6), it is seen that the strength of a single phonon creation or annihilation peak is governed by the Debye–Waller factor. When the Debye–Waller factor becomes vanishingly small, which is when many phonons are excited, then the intensity of single phonon peaks becomes unmeasurable and once again this is the signal that the scattering can be described by classical theory.
is essentially the surface projection of the phonon density of states.52 Just as in the case of elastic diffraction of eqn (6), it is seen that the strength of a single phonon creation or annihilation peak is governed by the Debye–Waller factor. When the Debye–Waller factor becomes vanishingly small, which is when many phonons are excited, then the intensity of single phonon peaks becomes unmeasurable and once again this is the signal that the scattering can be described by classical theory.
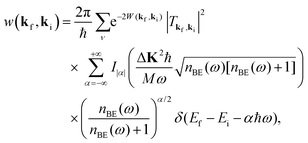

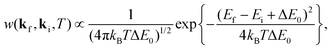
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(pf − pi + Pf − Pi),
δ(pf − pi + Pf − Pi),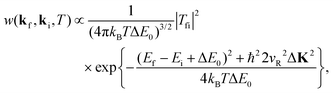
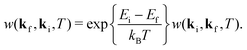
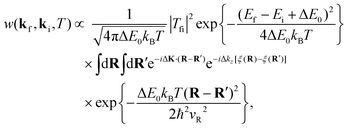
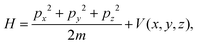
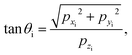
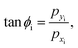
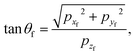
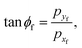
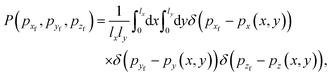
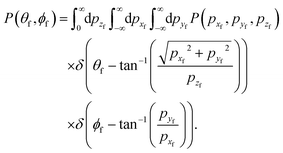
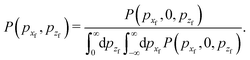
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (z) and a corrugation function ξ(x) in the parallel direction
(z) and a corrugation function ξ(x) in the parallel direction![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (z + h(x)) ≃
(z + h(x)) ≃ ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (z) +
(z) + ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ′(z)ξ(x),
′(z)ξ(x),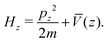
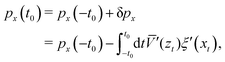
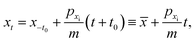
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) is unity.
is unity.
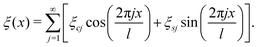
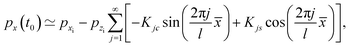
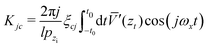
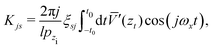
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (
(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) responsible for the momentum shift can be written as
) responsible for the momentum shift can be written as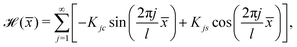
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) . Furthermore, the horizontal frequency is defined as
. Furthermore, the horizontal frequency is defined as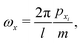
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ′(zt) is symmetric with respect to time.
′(zt) is symmetric with respect to time.
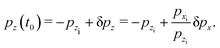
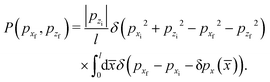
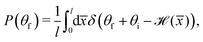
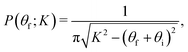
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (z) = V0[(exp(−αz) − 1)2 − 1],
(z) = V0[(exp(−αz) − 1)2 − 1],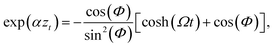
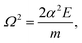
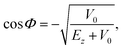
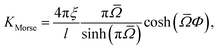
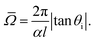
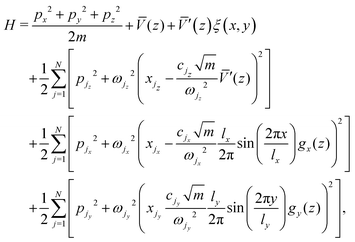
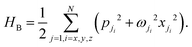
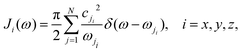
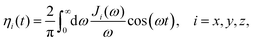
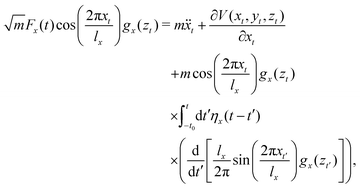
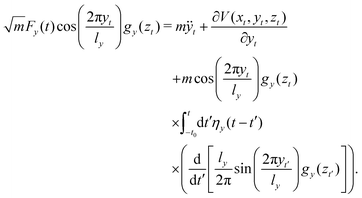
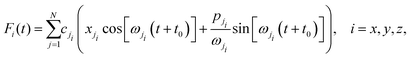
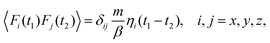
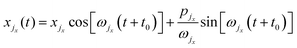
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin[ωjx(t + t0)] + pjx
sin[ωjx(t + t0)] + pjx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos[ωjx(t + t0)].
cos[ωjx(t + t0)].![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (
(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) + Δpx,1 + Δpx,2.
) + Δpx,1 + Δpx,2.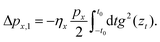
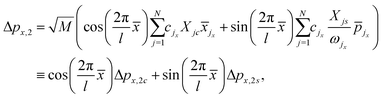
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) jx = xjx(t = 0),
jx = xjx(t = 0), ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) jx = pjx(t = 0) and
jx = pjx(t = 0) and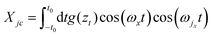
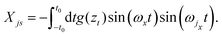
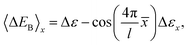
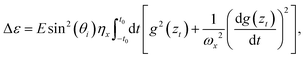
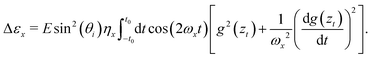
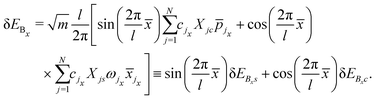
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) implies the existence of what is known as energy loss rainbows. Energy loss rainbows will appear at least in principle whenever the derivative of the energy loss with respect to the impact parameter vanishes.
) implies the existence of what is known as energy loss rainbows. Energy loss rainbows will appear at least in principle whenever the derivative of the energy loss with respect to the impact parameter vanishes.
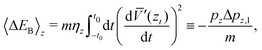
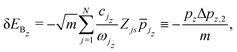
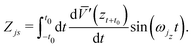
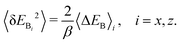
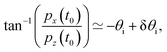
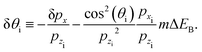
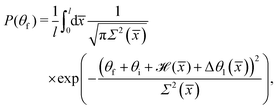
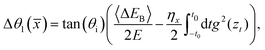

![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) is of special interest. It implies that even in the absence of corrugation, one may observe rainbows in the angular distribution which are induced by friction. These have been referred to as friction induced rainbows,41 not observed or reported yet in the literature. They result from the fact that the energy transfer to the surface may depend on the impact parameter. Such surface induced rainbows will be observable only at very low surface temperature. From eqn (70), one notes that as the temperature increases, the fluctuations increase and they will mask the rainbow structure induced by the energy loss.
) is of special interest. It implies that even in the absence of corrugation, one may observe rainbows in the angular distribution which are induced by friction. These have been referred to as friction induced rainbows,41 not observed or reported yet in the literature. They result from the fact that the energy transfer to the surface may depend on the impact parameter. Such surface induced rainbows will be observable only at very low surface temperature. From eqn (70), one notes that as the temperature increases, the fluctuations increase and they will mask the rainbow structure induced by the energy loss.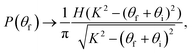
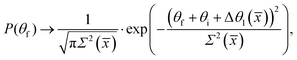
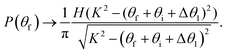
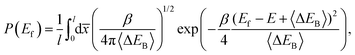
 and its full width at half maximum (FWHM) was very closely linearly dependent on
and its full width at half maximum (FWHM) was very closely linearly dependent on  as predicted by eqn (12). For the multiple scattering peaks, the dependence of intensity and FWHM is not simply predicted by eqn (12), but calculations with the multiple collision convolutions of eqn (12) gave reasonably good agreement with the measured behavior.
as predicted by eqn (12). For the multiple scattering peaks, the dependence of intensity and FWHM is not simply predicted by eqn (12), but calculations with the multiple collision convolutions of eqn (12) gave reasonably good agreement with the measured behavior.

![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] direction and 3494 m s−1 for the [1
0] direction and 3494 m s−1 for the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] azimuth. The effective mass, chosen to give the best fit to the data, is rather large. Here, M = 2.3 times the mass of a single Ru atom, or 232.5 amu. This value is larger than the values used in the analysis of rare gases scattering from molten metal surfaces, to be discussed below, where the effective mass turned out to be very close to the mass of a single atom of the liquid metals.
00] azimuth. The effective mass, chosen to give the best fit to the data, is rather large. Here, M = 2.3 times the mass of a single Ru atom, or 232.5 amu. This value is larger than the values used in the analysis of rare gases scattering from molten metal surfaces, to be discussed below, where the effective mass turned out to be very close to the mass of a single atom of the liquid metals.![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] direction. The incident energy is Ei = 0.065 eV and T = 140 K. The solid curves are the calculations using the same parameters as for Fig. 4, which seems to indicate that the adsorbed layer of the light mass hydrogen atoms has little effect on the scattering of Ar atoms at this energy.
0] direction. The incident energy is Ei = 0.065 eV and T = 140 K. The solid curves are the calculations using the same parameters as for Fig. 4, which seems to indicate that the adsorbed layer of the light mass hydrogen atoms has little effect on the scattering of Ar atoms at this energy.
![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] direction for incident energy Ei = 0.065 eV and T = 140 K. Angular distributions for four different incident angles ranging from 40° to 70° are shown as marked. The solid curves are calculations. (Reprinted with permission from ref. 73, Copyright [2002] Royal Chemistry Society.)
0] direction for incident energy Ei = 0.065 eV and T = 140 K. Angular distributions for four different incident angles ranging from 40° to 70° are shown as marked. The solid curves are calculations. (Reprinted with permission from ref. 73, Copyright [2002] Royal Chemistry Society.)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θf. Correctly normalized and written as a differential reflection coefficient it is given by
θf. Correctly normalized and written as a differential reflection coefficient it is given by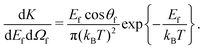



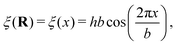

 . These two temperature behaviors are plotted in Fig. 9 as dotted and dashed curves, respectively, and they represent the extreme behaviors expected. In other words, a surface with corrugation intermediate between that of a perfectly smooth surface or a highly rough surface essentially consisting of isolated atoms would exhibit a peak intensity decrease that is intermediate between these two extreme behaviors. It is clear from Fig. 9 that the experimental points exhibit this intermediate behavior.
. These two temperature behaviors are plotted in Fig. 9 as dotted and dashed curves, respectively, and they represent the extreme behaviors expected. In other words, a surface with corrugation intermediate between that of a perfectly smooth surface or a highly rough surface essentially consisting of isolated atoms would exhibit a peak intensity decrease that is intermediate between these two extreme behaviors. It is clear from Fig. 9 that the experimental points exhibit this intermediate behavior.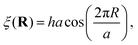
 .
.

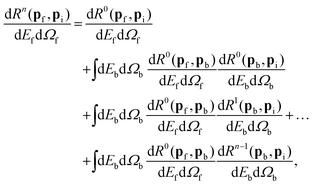

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θf distribution is evident although the expected behavior is achieved more slowly than that of the energy distribution exhibited in Fig. 11. The Knudsen flux is, of course, independent of azimuthal angle ϕ and the calculations of Fig. 11 and 12 very quickly become independent of ϕ with increasing iteration number n.
θf distribution is evident although the expected behavior is achieved more slowly than that of the energy distribution exhibited in Fig. 11. The Knudsen flux is, of course, independent of azimuthal angle ϕ and the calculations of Fig. 11 and 12 very quickly become independent of ϕ with increasing iteration number n.
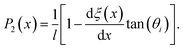
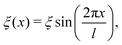
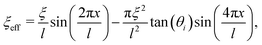
![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) z =
z = ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) x = 0.00338 where
x = 0.00338 where![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) x = ηx/ω0,
x = ηx/ω0,![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) z = m2ω03ηz,
z = m2ω03ηz,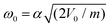 is the harmonic frequency of the Morse potential. The magnitude of the reduced friction parameters shows that the friction is weak. Five parameters are used to fit the experimental data, as all other parameters were obtained from experimental knowledge, and the surface temperature was taken to be 300 K. The fits by using this theory are slightly better than those reported by Kondo et al. using the washboard model. The fitting procedure is not carried out for each distribution separately and the theory seems to account correctly for the energy dependence of the rainbow angles. The distributions are not symmetric and therefore the second order corrugation term was added. The decrease of the rainbow angles with energy is a result of the dynamics and does not imply that the corrugation becomes smaller with increasing energy, as suggested by Kondo et al.
is the harmonic frequency of the Morse potential. The magnitude of the reduced friction parameters shows that the friction is weak. Five parameters are used to fit the experimental data, as all other parameters were obtained from experimental knowledge, and the surface temperature was taken to be 300 K. The fits by using this theory are slightly better than those reported by Kondo et al. using the washboard model. The fitting procedure is not carried out for each distribution separately and the theory seems to account correctly for the energy dependence of the rainbow angles. The distributions are not symmetric and therefore the second order corrugation term was added. The decrease of the rainbow angles with energy is a result of the dynamics and does not imply that the corrugation becomes smaller with increasing energy, as suggested by Kondo et al.

![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) z =
z = ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) x = 0.00338, the corrugation heights are ξs1 = 0.20125 a.u. and ξs2 = 0.054 a.u. The plots from bottom to top show the distributions for the energies 315, 435, 525, 620 and 705 meV, respectively. (Reprinted with permission from ref. 37, Copyright [2009] American Physical Society.).
x = 0.00338, the corrugation heights are ξs1 = 0.20125 a.u. and ξs2 = 0.054 a.u. The plots from bottom to top show the distributions for the energies 315, 435, 525, 620 and 705 meV, respectively. (Reprinted with permission from ref. 37, Copyright [2009] American Physical Society.).![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) x = 0.00139 and
x = 0.00139 and ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) z = 0.000908, and incident energy of 2500 meV. The width of the incident beam was reported as going from 5% to 8% and therefore should be accounted for in the theoretical results.102 One simple way to do this is by adding a constant width of 0.085 radians. On the (a) panel of Fig. 14 the theoretical results (broadened with a fixed width of 0.085 radians) are compared with the measured results of Amirav et al.99 displaying a quantitative agreement. The asymmetry here is smaller than the asymmetry found in the Ar–LiF(100) system but the trend is similar. The rainbow scattering appears at low incident scattering angle and disappears as the scattering angle is increased as observed more clearly on the (b) panel of Fig. 14 where it is plotted the normalized angular distributions without the added broadening. At the incidence angle of −45°, one still sees the rainbow scattering, however, the asymmetry is almost gone. Increasing the angle of incidence to −60° wipes out the rainbows and one remains with a single peaked distribution.
z = 0.000908, and incident energy of 2500 meV. The width of the incident beam was reported as going from 5% to 8% and therefore should be accounted for in the theoretical results.102 One simple way to do this is by adding a constant width of 0.085 radians. On the (a) panel of Fig. 14 the theoretical results (broadened with a fixed width of 0.085 radians) are compared with the measured results of Amirav et al.99 displaying a quantitative agreement. The asymmetry here is smaller than the asymmetry found in the Ar–LiF(100) system but the trend is similar. The rainbow scattering appears at low incident scattering angle and disappears as the scattering angle is increased as observed more clearly on the (b) panel of Fig. 14 where it is plotted the normalized angular distributions without the added broadening. At the incidence angle of −45°, one still sees the rainbow scattering, however, the asymmetry is almost gone. Increasing the angle of incidence to −60° wipes out the rainbows and one remains with a single peaked distribution.
![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) x = 0.000603 and
x = 0.000603 and ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) z = 0.000431 and incident energy of 6600 meV with T = 297 K. The resulting angular distributions are broadened by a constant factor of 0.09 radians. On the (a) panel of Fig. 15, a comparison between experimental and theoretical results are plotted. The fit is not as good as in the previous case, especially at the −45° angle of incidence. The normalized theoretical distributions without an extra broadening are shown on the (b) panel of Fig. 15. It is observed that the asymmetry is so strong that a three peaked distribution is predicted when the incident angle is −30° and that the rainbow scattering may still be observed when the incident angle is −60°. The distance between the two central rainbows decreases with increasing scattering angle, as does the asymmetry.
z = 0.000431 and incident energy of 6600 meV with T = 297 K. The resulting angular distributions are broadened by a constant factor of 0.09 radians. On the (a) panel of Fig. 15, a comparison between experimental and theoretical results are plotted. The fit is not as good as in the previous case, especially at the −45° angle of incidence. The normalized theoretical distributions without an extra broadening are shown on the (b) panel of Fig. 15. It is observed that the asymmetry is so strong that a three peaked distribution is predicted when the incident angle is −30° and that the rainbow scattering may still be observed when the incident angle is −60°. The distance between the two central rainbows decreases with increasing scattering angle, as does the asymmetry.
![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) , so that it cannot be too large. There is though a third piece of information. Schweizer et al. reported that at the −60° angle of incidence, the rainbow structure disappears, implying that the value of the rainbow shift function at this angle must be smaller than its value at −30°. Since the magnitude of
, so that it cannot be too large. There is though a third piece of information. Schweizer et al. reported that at the −60° angle of incidence, the rainbow structure disappears, implying that the value of the rainbow shift function at this angle must be smaller than its value at −30°. Since the magnitude of ![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) is determined by the product αl (where α is the Morse potential stiffness parameter) these observations lead to the conclusion that the product αl ≃ 2. With some fine tuning one can then determine that αl = 2 is optimal.
is determined by the product αl (where α is the Morse potential stiffness parameter) these observations lead to the conclusion that the product αl ≃ 2. With some fine tuning one can then determine that αl = 2 is optimal.![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) x = 0.00267 and
x = 0.00267 and ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) z = 0.00228. The second order corrugation parameter is responsible for the asymmetry of the angular distribution and may be determined by the asymmetry of the measured angular distribution at the −30° angle of incidence. The optimized value was ξs2 = −0.007 a.u. which is indeed much smaller than the first order corrugation height.
z = 0.00228. The second order corrugation parameter is responsible for the asymmetry of the angular distribution and may be determined by the asymmetry of the measured angular distribution at the −30° angle of incidence. The optimized value was ξs2 = −0.007 a.u. which is indeed much smaller than the first order corrugation height.


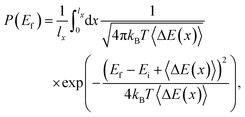


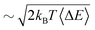 (where 〈ΔE〉 is the overall average energy loss). Thus, lowering the surface temperature, changing the angle of incidence towards the vertical and increasing the incidence energy will enhance the probability of observing the energy loss rainbows. The latter condition is based on the observation that the distance between the energy loss rainbows increases linearly with increasing incidence energy while the width increases only as the square root of the energy loss.
(where 〈ΔE〉 is the overall average energy loss). Thus, lowering the surface temperature, changing the angle of incidence towards the vertical and increasing the incidence energy will enhance the probability of observing the energy loss rainbows. The latter condition is based on the observation that the distance between the energy loss rainbows increases linearly with increasing incidence energy while the width increases only as the square root of the energy loss.; O. Stern, Naturwissenschaften, 1929, 17, 391 CrossRef
.
; I. Estermann, R. Frisch and O. Stern, Z. Phys., 1932, 73, 348 CrossRef
; O. R. Frisch, What Little I Remember, Cambridge University Press, Cambridge, 1979 Search PubMed
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
; E. Pollak and S. Miret-Artés, J. Chem. Phys., 2010, 132, 049901 CrossRef
.
; E. Pollak, J. M. Moix and S. Miret-Artés, Phys. Rev. B: Condens. Matter Mater. Phys., 2010,(81), 039902 CrossRef
.
; E. Pollak and J. Tatchen, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 049903 CrossRef
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

