Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Role of natural organic matter and hardness on lead release from galvanic corrosion†
Patrick W.
King‡
 *a,
Sigrid
Peldszus
*a,
Sigrid
Peldszus
 a,
Anushka
Mishrra
a,
Anushka
Mishrra
 b,
Benjamin F.
Trueman
b,
Benjamin F.
Trueman
 c,
Kimia
Aghasadeghi
a,
Graham A.
Gagnon
c,
Kimia
Aghasadeghi
a,
Graham A.
Gagnon
 c,
Daniel E.
Giammar
c,
Daniel E.
Giammar
 b and
Peter M.
Huck
a
b and
Peter M.
Huck
a
aDepartment of Civil and Environmental Engineering, University of Waterloo, Waterloo, ON N2L 3G1, Canada. E-mail: pwking@uwaterloo.ca; Tel: +1 519 878 2093
bDepartment of Energy, Environmental & Chemical Engineering, Washington University in St. Louis, St. Louis, MO 63130, USA
cDepartment of Civil & Resource Engineering, Dalhousie University, Halifax, NS B3H 4R2, Canada
First published on 20th June 2022
Abstract
Lead release into drinking water from lead service lines, lead containing solder and plumbing fixtures continues to challenge many utilities. Corrosion inhibitors such as orthophosphate are often added to water to mitigate lead release, but their use may not be feasible for many utilities and may not be sufficient to meet regulatory limits. Thus, there is a need to identify other treatment strategies to minimize lead release. Two possible means that have not been thoroughly studied include natural organic matter (NOM) removal and hardness adjustment (e.g., water softening). Accordingly, this study employed a two-level fractional factorial design to investigate the role of NOM and hardness in conjunction with dissolved inorganic carbon (DIC), and pH, on the galvanic corrosion of lead. This study followed a “dump and fill” protocol and employed test pieces consisting of new lead and copper pipes with an external galvanic connection. Suwannee River NOM (SRNOM) increased the release of dissolved lead by an order of magnitude in collected water samples. To be precise, average dissolved lead release in the synthetic waters with and without SRNOM was 140 and 2460 μg L−1 respectively (potentially significant [i.e., 0.05 < p < 0.1]; p = 0.060). Using fluorescence excitation emission matrices, it was found that the release of dissolved lead was correlated to decreases in the NOM humic-like peaks A (R2 = 0.85; p = 4.4 × 10−8) and C (R2 = 0.87; p = 1.3 × 10−8). It is plausible that the decrease in fluorescence was due to the quenching effect of lead–NOM complexation, providing evidence that complexation mobilized dissolved lead. Hardness and DIC did not have a significant effect on lead release, however the galvanic current between the lead and copper pipes was 28.5 μA higher when the DIC concentration was 80 mg L−1 compared to 10 mg L−1 (potentially significant; p = 0.051). Finally, average total lead release at a pH of 7 was 7190 μg L−1 compared to only 2800 μg L−1 at a pH of 8.5 (potentially significant; p = 0.089), and there was some indication that the impact of SRNOM was lower at a higher pH.
Water impactThis study determined that untreated natural organic matter (NOM) can greatly increase dissolved lead release from lead service lines, although its role on total lead release remains unclear. Furthermore, hardness was not found to have an impact on lead release. Therefore, these results suggest that utilities should focus on controlling NOM in addition to other established corrosion control practices. |
Introduction
Lead is a regulated contaminant in drinking water as it can cause elevated blood lead levels, which are linked to neurological and neurodevelopmental disorders.1,2 For example, Health Canada3 has set a maximum acceptable concentration guideline of 5 μg L−1, which was recently lowered from 10 μg L−1. The most common sources of lead in drinking water include lead service lines, lead-containing solder and plumbing fixtures, and galvanized iron pipes.4 Corrosion and the subsequent lead release are often accelerated if there is a galvanic connection between lead and another metal such as copper. This is due to the nobility of the metals, since lead is less noble than copper it corrodes preferentially in a galvanic couple.5 Lead release can further be increased from galvanic corrosion due to a local drop in pH near the lead surface, thus increasing its solubility.5,6 Galvanic connections in the distribution system can occur following partial lead service line replacements5,7,8 which are practiced in some systems even though full lead service line replacements are advised (e.g., ref. 9).Corrosion inhibitors, mainly orthophosphate, are often added in the water treatment process to mitigate lead release.10 However, their use may not be appropriate for all utilities, for example if there are stringent phosphorus discharge limits for wastewater.11 In such cases, other adjustments to water chemistry may be required to meet regulatory lead limits. It is well known that lead solubility is highly dependent on the pH and dissolved inorganic carbon (DIC) concentration. Based on solubility modelling, in a lead(II) carbonate system the minimum solubility of lead occurs at a pH of about 9.8 and a total inorganic carbon (TIC) concentration of about 40 mg CaCO3 per L.12–14 In practice, the target value for pH adjustment can be lower than 9,10 as in many cases it is not feasible to adjust to higher pH values, especially in hard waters with high alkalinity. As well, particulate lead generated through galvanic corrosion can make total lead release highly variable, even at pH values that minimize lead solubility.5,15
The impact of DIC on galvanic corrosion is complex, as it can buffer against pH changes near the lead surface which can decrease lead solubility but can also increase the corrosion rate and the production of oxidized lead.5,8,16,17 An optimal alkalinity, which is related to DIC concentration, is approximately 30–75 mg CaCO3 per L based on lead solubility and practical guidance.10,13,18–20 However, it is unclear if raising the alkalinity over 75 mg CaCO3 per L will increase or decrease lead release, and this is likely case specific and pH dependent.5,16,20–22 In fact, based on solubility modelling for a lead(II) carbonate system, Schock and Gardels14 showed that the DIC has little impact at pH values around 8 which is common for waters used in corrosion studies and may explain the variable results. However, it is largely unknown what role, if any, that DIC may have on a system with high levels of NOM, indicating a need to evaluate potential interaction effects between these factors with regards to lead release.
Hardness adjustment could also potentially mitigate lead release. In the past, it was thought that water with high hardness would form protective calcium carbonate scales on lead pipes to mitigate lead release.23 However, more recent literature has advised against the use of calcium carbonate oversaturation as a corrosion control method, as it has been suggested that corrosion has little to do with calcium carbonate precipitation and notable quantities of calcium carbonate are seldom found on lead pipes.12,24–27 However, further research is still required as some studies have found that hardness can influence scale formation19,28–30 and that calcium can decrease the concentration of colloidal lead by altering the zeta potential of the colloids.31 As well, divalent cations such as magnesium and calcium can adsorb to lead phosphate particles promoting their aggregation and lead immobilization.32 To the authors' knowledge there have been no previous studies that have investigated hardness independently from DIC under parallel experimental systems.
Natural organic matter (NOM) removal could also be beneficial for utilities aiming to reduce lead release. In laboratory-based studies, NOM greatly increased the release of dissolved lead (<0.45 μm) in a variety of waters, most likely by forming complexes with lead.33 Additionally, NOM has been found to alter the structure of corrosion scales33,34 and alter the zeta potential of colloidal particles33–35 leading to colloidal dispersion of lead-rich colloids (0.001–1 μm).33–35 Both the formation of lead–NOM complexes and colloidal dispersion have been identified in soft waters using size exclusion chromatography combined with inductively coupled plasma mass spectrometry (ICP-MS) and ultraviolet absorption at 254 nm (UV254) detection,36–38 as well as with field flow fractionation coupled with ICP-MS and UV254 detection.39 However, which NOM components are responsible for complexing with lead and causing colloidal dispersion is unclear. There is also a need to evaluate the impact of NOM in a variety of hard waters with different background chemistry.
This research consisted of a bench scale study conducted to address knowledge gaps pertaining to NOM and hardness control on lead release from galvanic corrosion. This study employed a two-level fractional factorial design with two mid-point replicates, in order to (1) systematically investigate the impact of pH, DIC, hardness and NOM on galvanic corrosion, lead release and scale formation; (2) explore changes in NOM fractions upon stagnation in lead and copper test pieces using liquid chromatography with organic carbon detection (LC-OCD) and fluorescence excitation emission matrix (FEEM), and (3) compare measured dissolved lead concentrations to the theoretical solubility. Synthetic waters without a disinfectant or corrosion inhibitors were utilized to focus on the water quality factors of interest without additional complexity. This prevented the NOM from reacting with a disinfectant, thus providing a worst-case scenario for NOM induced lead release that is representative of utilities that use groundwater without a disinfectant. The hardness was controlled separately from DIC to better study the impact of hardness on corrosion.
Materials and methods
Test pieces
The test pieces were based on a design in Parks et al.40 (Fig. S1†). New lead pipes (length: 50 cm, outer diameter: 1.0 in. [2.54 cm], inner diameter: 0.75 in. [1.91 cm]) were connected to new type M copper pipes (length: 50 cm, nominal diameter: 0.75 in. [1.91 cm], outer diameter: 0.875 in. [2.22 cm], inner diameter: 0.81 in. [2.06 cm]) with flexible polyvinylchloride tubing and were separated using a 0.125 in. [0.32 cm] thick rubber washer. The pipes were galvanically connected with bronze ground clamps and copper wire 10 cm from the junction and were plugged using rubber stoppers and plumber's tape. New lead pipes instead of harvested lead pipes were utilized to decrease variability from pre-existing corrosion scales. New pipes with a galvanic connection provided a worst-case scenario to assess corrosion and metal release. Although lead release is different in new lead pipes compared to harvested lead pipes, the same general trends are expected in many cases.5,28,41–44 The cleaning and pretesting of the test pieces are outlined in the ESI.†Experimental design
The impact of four water quality factors (pH, DIC, hardness and NOM) on lead release was investigated using a 24−1 fractional factorial design with eight factorial points and two mid-point replicates, set at the halfway point between the low and high levels of all four factors. A factorial design is an efficient experimental design for analyzing the main and interaction effects of multiple factors45 with a minimal number of conditions (test pieces), and it has been used in previous corrosion research.46 Each of the test pieces were sampled three times over a period of 20 weeks, providing good replication of measurements. This study was intended to identify the effects of the factors, if any, and not to develop a model as it is expected that the relationships are non-linear.The water quality factors had low, mid-point, and high levels of 7.0[pH−], 7.75[pH0] and 8.5[pH+] for pH, 10[DIC−], 45[DIC0] and 80[DIC+] mg C per L for DIC, 50[Hard−], 250[Hard0] and 450[Hard+] mg CaCO3 per L for hardness and 0[NOM−], 3.5[NOM0] and 7[NOM+] mg C per L for NOM using Suwannee River NOM (SRNOM) (Table 1). Reference SRNOM from the International Humic Substances Society was selected as it is from a natural source, is more representative of real NOM than humic or fulvic acid standards and has been used in previous corrosion research.46,47 A high level for NOM of 7 mg C per L was selected as it was used in a previous corrosion study that followed a factorial design46 and it resulted in a mid-point level (3.5 mg C per L) that is characteristic of treated drinking water from several sources in Southern Ontario. Each effect was estimated from the eight factorial points and the two mid-point replicates were used to provide an estimate of the error and make the design more robust against outliers.45 The synthetic water preparation is outlined in the ESI† and Table S1.
| Test piece | pH | DIC | Hardness | NOM |
|---|---|---|---|---|
| TP1[pH−/DIC−/Hard−/NOM−] | − | − | − | − |
| TP2[pH+/DIC−/Hard−/NOM+] | + | − | − | + |
| TP3[pH−/DIC+/Hard−/NOM+] | − | + | − | + |
| TP4[pH+/DIC+/Hard−/NOM−] | + | + | − | − |
| TP5[pH−/DIC−/Hard+/NOM+] | − | − | + | + |
| TP6[pH+/DIC−/Hard+/NOM−] | + | − | + | − |
| TP7[pH−/DIC+/Hard+/NOM−] | − | + | + | − |
| TP8[pH+/DIC+/Hard+/NOM+] | + | + | + | + |
| TP9[pH0/DIC0/Hard0/NOM0] | 0 | 0 | 0 | 0 |
| TP10[pH0/DIC0/Hard0/NOM0] | 0 | 0 | 0 | 0 |
| Level | pH | DIC | Hardness | NOM |
|---|---|---|---|---|
| mg C per L | mg CaCO3 per L | mg DOC per L | ||
| − | 7 | 10 | 50 | 0 |
| 0 | 7.75 | 45 | 250 | 3.5 |
| + | 8.5 | 80 | 450 | 7 |
Sample collection
The experiment followed a “dump and fill” protocol5 over a period of 20 weeks at room temperature (approximately 20 °C). Each Tuesday, a new batch of water was prepared for Wednesday (48 hour stagnation), Friday (72 hour stagnation) and Monday (48 hour stagnation) water replacements. Water quality parameters were routinely analyzed in the freshly prepared synthetic waters (Table S2†) and were close to the target values (Table S3†). The galvanic current was measured prior to sample collection on Wednesdays (Table S2†).The samples were collected in accordance with the method outlined in the ESI.† The total lead and copper concentrations were measured from weekly composite samples, while the reported dissolved and particulate lead (total – dissolved) concentrations were from select individual 48 hour stagnation events (Monday–Wednesday) (Table S2†). Additionally, several other water quality parameters (e.g., pH, DIC, hardness, dissolved organic carbon (DOC), specific conductance, and turbidity) were measured from the water collected after the final 48 hour stagnation event of the week (Tables S2 and S3†). Except for NOM, changes to the water quality following stagnation in the test pieces are discussed in the ESI.† All the effects were calculated based on the target value of the water quality factors (pH, DIC, hardness, and NOM).
Analytical methods
The galvanic current between the lead and copper pipes was measured using a multimeter (400 Ω resistance; Klein Tools® MM400). Lead and copper samples were analyzed by ICP-MS (Thermofisher X series II; Standard Method 3125) at Dalhousie University.48 The detection limits for lead and copper were 0.4 and 0.7 μg L−1 respectively.NOM characterization using FEEM and LC-OCD analyses were conducted on filtered samples (0.45 μm, polyethersulfone, Pall Corporation Supor®) and were stored in prebaked glass vials (450 °C, ≥1 hour) at 4 °C prior to analysis. Samples for FEEM were analyzed within 48 hours of collection on a Cary Eclipse Fluorescence Spectrophotometer (Agilent Technologies) in a 1 cm quartz cuvette. Excitation (Ex) wavelengths ranged from 250 to 380 nm with 10 nm increments and emission (Em) wavelengths were monitored from 300 to 600 nm at 1 nm increments. FEEMs were evaluated using peak picking49 and the NOM humic-like peak A maximum was at Ex/Em = 250 nm/461 nm, while the NOM humic-like peak C maximum was at Ex/Em = 340 nm/457 nm (Fig. S2†).50 Samples for LC-OCD were normally analyzed within one week of collection and ChromCALC software was used to integrate the chromatograms (Fig. S3†).51
The pH (Thermo Scientific Orion 9106BNWP, Standard Method 4500-H+ B), alkalinity (Standard Method 2320B), specific conductance (YSI Professional Plus, Standard Method 2510B), turbidity (HACH® 2100Q Portable Turbidimeter, Standard Method 2130B), and chloride and sulfate concentrations (Thermo Scientific DionexTM ICS-1100, Standard Method 4110C) were measured according to standard methods.48 The DIC concentration was estimated using chemical equilibrium relationships based on pH and alkalinity. Several metals including calcium, magnesium, and sodium were measured using collision reaction cell ICP-MS (measured by ALS Limited, Waterloo, Ontario, modified from EPA 6020B).52 The hardness was estimated based on the calcium and magnesium concentrations (Standard Method 2340B).48
The scale analysis was completed at Washington University in St. Louis at the end of the 20 week long experiment in accordance with methods described in previous work.53,54 In short, imaging using a scanning electron microscope (SEM) (Thermofisher Quattro S E-SEM), energy dispersive X-ray spectroscopy (EDS) (Oxford AzTec energy dispersive X-ray spectrometer), X-ray powder diffraction (XRD) (Bruker d8 Advance C-ray diffractometer with Cu Kα radiation) and ICP-MS (PerkinElmer Elan DRCII) analyses were completed. More details on the scale analysis are included in the ESI.†
Data analysis
The main effects of each factor for galvanic current, lead release, and copper release were calculated as the difference in the average response at the high level and the low level. The two factor interaction effects were calculated as the difference in the average response when both the factors were at the same level and when they were at different levels. The weekly measurements were treated as repeat measurements and analysis of variance (ANOVA) analysis was completed with MATLAB® using average values. To improve normality, the copper data was transformed using the Box Cox method with a λ = 0.5.45 Meanwhile, the galvanic current and lead data were not transformed (λ = 1). The statistical analysis is discussed in detail in the ESI.† Lead solubility in the synthetic waters was modeled using tidyphreeqc,55 an R interface for the USGS' PHREEQC,56 and pbcusol,57 an extension of tidyphreeqc for lead and copper solubility modeling. The modeling methodology is discussed in the ESI† and a list of reactions and constants is provided in Table S4.†Results and discussion
Impact of water quality factors on galvanic corrosion
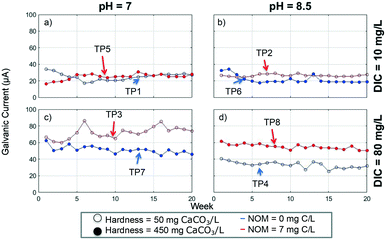
There were large differences among the test pieces for various parameters (Table S5†), suggesting that different conditions had substantial effects on these parameters. Yet, there were challenges associated with demonstrating, with statistical significance, the effects of the different experimental variables on observed results. Effects with significance less than 5% (p < 0.05) were considered to be significant, while effects between 5% and 10% (0.05 < p < 0.1) were designated potentially significant (Tables 2 and S6†). Significance at 10% (p < 0.1) has been reported in previous corrosion research studies (e.g. ref. 18 and 22).| Parameter | pH (P) | DIC (D) | Hardness (H) | NOM (N) | |
|---|---|---|---|---|---|
| a Low (n = 4), mid-point (n = 2), and high (n = 4) indicate the average value when the water quality factor was at that level. b Effects were calculated from untransformed data while significance was calculated from untransformed data for galvanic current and lead release and Box Cox transformed data with λ = 0.5 for copper. c Bolded values were found to be significant at 10% and bolded and italicized values were found to be significant at 5%. d The effects for particulate lead release could not be statistically determined as the ANOVA model had a potentially significant lack of fit error (p = 0.089). | |||||
| Galvanic current (μA) | Low (−)a | 43.3 | 24.5 | 39.2 | 32.8 |
| Mid-point (0)a | 43.6 | 43.6 | 43.6 | 43.6 | |
| High (+)a | 34.1 | 52.9 | 38.3 | 44.6 | |
| Effectb | −9.2 | 28.4 | −0.9 | 11.8 | |
| p-Value | 0.15 | 0.051 | 0.76 | 0.12 | |
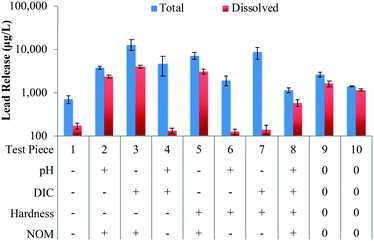
| Total lead (μg L−1) | Low (−) | 7190 | 3350 | 5360 | 3870 |
| Mid-point (0) | 2000 | 2000 | 2000 | 2000 | |
| High (+) | 2800 | 6640 | 4630 | 6130 | |
| Effect | −4390 | 3290 | −730 | 2260 | |
| p-Value | 0.089 | 0.12 | 0.45 | 0.17 | |
| Dissolved lead (μg L−1) | Low (−) | 1810 | 1410 | 1630 | 140 |
| Mid-point (0) | 1360 | 1360 | 1360 | 1360 | |
| High (+) | 785 | 1190 | 970 | 2460 | |
| Effect | −1030 | −230 | −650 | 2320 | |
| p-Value | 0.13 | 0.49 | 0.21 | 0.060 | |
| Particulate lead (μg L−1)d | Low (−) | 8140 | 2050 | 6030 | 3780 |
| Mid-point (0) | 790 | 790 | 790 | 790 | |
| High (+) | 1820 | 7920 | 3930 | 6180 | |
| Effect | −6320 | 5870 | −2100 | 2400 | |
| p-Value | 0.053 | 0.057 | 0.16 | 0.14 | |
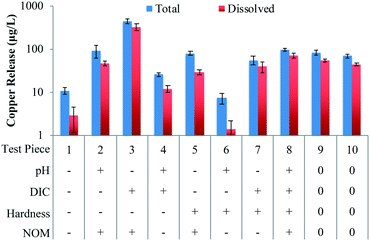
| Total copper (μg L−1) | Low (−) | 146 | 47.6 | 141 | 24.8 |
| Mid-point (0) | 77.1 | 77.1 | 77.1 | 77.1 | |
| High (+) | 55.8 | 154 | 60.4 | 177 | |
| Effect | −90 | 107 | −81 | 152 | |
| p-Value | 0.076 | 0.054 | 0.11 | 0.034 | |
| Dissolved copper (μg L−1) | Low (−) | 99.5 | 20.2 | 97.0 | 14.0 |
| Mid-point (0) | 50.1 | 50.1 | 50.1 | 50.1 | |
| High (+) | 33.1 | 112 | 35.6 | 119 | |
| Effect | −66.4 | 92 | −61.4 | 105 | |
| p-Value | 0.083 | 0.045 | 0.11 | 0.036 | |
| Particulate copper (μg L−1) | Low (−) | 37.8 | 22.9 | 28.2 | 14.2 |
| Mid-point (0) | 19.1 | 19.1 | 19.1 | 19.1 | |
| High (+) | 17.4 | 32.3 | 27.0 | 41.0 | |
| Effect | −20.4 | 9.3 | −1.3 | 26.7 | |
| p-Value | 0.056 | 0.096 | 0.35 | 0.042 | |
The SRNOM was found to have a potentially significant effect (p = 0.060) on dissolved lead release; with the addition of 7 mg C per L of SRNOM increasing dissolved lead release by 2320 μg L−1 (Table 2). Average dissolved lead release in the test pieces exposed to water with 7 mg C per L of SRNOM was extremely high and ranged from 578 (TP8[pH+/DIC+/Hard+/NOM+]) to 3890 μg L−1 (TP3[pH−/DIC+/Hard−/NOM+]). The two test pieces with the highest dissolved lead release both had 7 mg C/L of SRNOM and a low pH of 7.0 (i.e. TP3[pH−/DIC+/Hard−/NOM+]: 3890 μg L−1 and TP5[pH−/DIC−/Hard+/NOM+]: 3050 μg L−1). This is in accordance with previous studies where waters with a low pH were more susceptible to the negative impacts of NOM.33,58 However, there was still a notable increase in dissolved lead at high pH values when SRNOM was present suggesting that the effect of NOM is not negligible in these waters. These results suggest that improvements to NOM removal can reduce dissolved lead release in a variety of waters.
The order of magnitude increase in dissolved lead release from adding SRNOM is consistent with the literature.46,47 However, the dissolved lead concentrations in the present study were an order of magnitude higher than in previous work (average of 2460 vs. 273 μg L−1).46 Possible explanations for this difference include, in the present study, a lack of disinfectant, more aggressive water, and the use of new instead of harvested lead pipes. In previous studies, complexation or colloidal dispersion were thought to be primarily responsible for the drastic increase in dissolved lead release in the presence of NOM (e.g. ref. 33, 35 and 39).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 μg L−1 (TP3[pH−/DIC+/Hard−/NOM+]) (Table S5†). Total lead release was highly variable with no apparent temporal trends and coefficients of variation ranging from 9.1% (TP10[pH0/DIC0/Hard0/NOM0]) to 122.6% (TP4[pH+/DIC+/Hard−/NOM−]). The pure error was relatively high and although a high variability is commonly reported, trapping of particulate lead at the junction between the lead and copper pipes may have been a contributing factor.15
600 μg L−1 (TP3[pH−/DIC+/Hard−/NOM+]) (Table S5†). Total lead release was highly variable with no apparent temporal trends and coefficients of variation ranging from 9.1% (TP10[pH0/DIC0/Hard0/NOM0]) to 122.6% (TP4[pH+/DIC+/Hard−/NOM−]). The pure error was relatively high and although a high variability is commonly reported, trapping of particulate lead at the junction between the lead and copper pipes may have been a contributing factor.15
The pH had a potentially significant effect on total lead release with an increase in pH from 7.0 to 8.5 decreasing lead release by an average of 4390 μg L−1 (Table 2), as was expected based on previous research.14,21,27,43 Similar to the dissolved lead results, the DIC did not have a significant effect on total lead release (Table 2), which is in accordance with previous studies.5,17,46 As well, NOM did not have a significant effect on total lead release (Table 2), due to large amounts of particulate lead in many of the test pieces. However, as determined from the samples from the individual 48 hour stagnation events, NOM generally increased the percentage of total lead that was dissolved. When 3.5 or 7 mg C per L of SRNOM was present, dissolved lead comprised between 17.7% (TP3[pH−/DIC+/Hard−/NOM+]) and 81.4% (TP10[pH0/DIC0/Hard0/NOM0]) of total lead compared to between only 1.5% (TP7[pH−/DIC+/Hard+/NOM−]) and 29.9% (TP1[pH−/DIC−/Hard−/NOM−]) in the test pieces without SRNOM (Table S5†). In addition, for waters with low pH and low DIC, it appeared that NOM may have increased total lead release, as lead release was consistently much higher in TP5[pH−/DIC−/Hard+/NOM+] than in TP1[pH−/DIC−/Hard−/NOM−] (Table S6 and Fig. S8†). Under similar water quality (e.g. low pH and DIC), other studies have reported the negative impacts of NOM.33,58
Furthermore, the hardness had a negligible impact on total lead release (Table 2) indicating that hardness adjustment is not likely to be an effective corrosion control strategy. This finding is in accordance with some previous studies,12,18,25–27 but is in contrast to other studies that have suggested that hardness and calcium can have an impact on lead release (e.g. ref. 28, 29 and 31). Colling et al.28 found that waters with a hardness to alkalinity ratio greater than 1.7 released more lead than waters with a ratio less than 1.7. In that study, waters with higher lead release formed more rigid scales on lead pipes than waters with lower lead release, although it is not clear if the hardness-to-alkalinity ratio was responsible for this difference in scale structure.28 This relationship was not found in the current study, most likely due to different background water quality, although the large range of hardness to alkalinity ratios in the synthetic waters may also have played a role. Bisogni et al.31 found that at a concentration of 5 mg L−1, calcium destabilized colloidal lead particles by altering the zeta potential. However, increasing the calcium concentration from 5 to 40 mg L−1 did not provide any additional benefit,31 which may explain why this was not observed in the present study.
Faraday's law was used to predict the amount of oxidized lead produced from galvanic corrosion using the galvanic current, as described in the ESI.†7 Over the entire experiment, between 2.9% (TP8[pH+/DIC+/Hard+/NOM+]) and 40.7% (TP5[pH−/DIC−/Hard+/NOM+]) of the oxidized lead predicted by Faraday's law was released into the water (Table S7†). This is a relatively high amount of lead release compared to other studies; Cartier et al.7 found that between about 13–18% of oxidized lead was released while Wang et al.59 reported even lower percentages. Nonetheless, it is presumed that the majority of the oxidized lead accumulated in the corrosion scales (59.3–97.1%). It is likely that some of the corrosion scales that formed were dislodged on a sporadic basis, which would explain why total lead release was high and variable.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 μg L−1) (Table S5†). The release of particulate lead was sporadic and highly variable, with coefficients of variation ranging from 39% (TP10[pH0/DIC0/Hard0/NOM0]) to 123% (TP3[pH−/DIC+/Hard−/NOM+]). The lack of fit error from ANOVA was found to be potentially significant (p = 0.089) for particulate lead release and therefore the statistical significance of the effects could not be determined.
100 μg L−1) (Table S5†). The release of particulate lead was sporadic and highly variable, with coefficients of variation ranging from 39% (TP10[pH0/DIC0/Hard0/NOM0]) to 123% (TP3[pH−/DIC+/Hard−/NOM+]). The lack of fit error from ANOVA was found to be potentially significant (p = 0.089) for particulate lead release and therefore the statistical significance of the effects could not be determined.
In the samples from the individual 48 hour stagnation events, particulate lead comprised between 18.6% (TP10[pH0/DIC0/Hard0/NOM0]) and 82.3% (TP3[pH−/DIC+/Hard−/NOM+]) of total lead in the test pieces with SRNOM (3.5 or 7 mg C per L) and between 70.6% (TP1[pH−/DIC−/Hard−/NOM−]) and 98.5% (TP7[pH–/DIC+/Hard+/NOM–]) of total lead in the test pieces without NOM. This difference could be related to the higher dissolved lead in the test pieces with SRNOM, which is most likely due to NOM complexation and/or colloidal dispersion. In the absence of NOM, these mechanisms are not at play and particulate lead dominates the total lead content. There is some evidence in waters with low pH and low DIC that SRNOM may increase particulate lead as TP5(pH−/DIC−/Hard+/NOM+) had notably higher particulate lead release than TP1(pH−/DIC−/Hard−/NOM−) and this is a potential finding that warrants further investigation (Table S6 and Fig. S8†).
An increase in the pH from 7.0 to 8.5 potentially significantly decreased the release of total copper by 90 μg L−1, dissolved copper by 66.4 μg L−1, and particulate copper by 20.4 μg L−1 (Table 2). An increase in the DIC concentration from 10 to 80 mg L−1 significantly increased the release of dissolved copper by 92 μg L−1, and potentially significantly increased the release of total copper by 107 μg L−1 and particulate copper by 9.3 μg L−1 (Table 2). The sum of the pH/DIC interaction and the hardness/NOM interaction was found to have a potentially significant effect on both total and dissolved copper release (Table S6†) and it is more likely that the pH/DIC interaction was the potentially significant effect. This is in accordance with previous studies and is likely due to the solubility of copper hydroxides and copper carbonate species.18,60,61
SRNOM at a concentration of 7 mg C per L significantly increased total copper release by 152 μg L−1, dissolved copper release by 105 μg L−1, and particulate copper release by 26.7 μg L−1 (Table 2). An increase in dissolved copper release due to NOM has been noted previously for other water types, and the proposed mechanisms include the formation of soluble copper–NOM complexes, colloidal dispersion, inhibition of the natural aging process, and alteration of corrosion scales.62–64 Hence, NOM removal has the potential to reduce copper release in addition to dissolved lead release.
Solubility modelling
Theoretical lead solubility in the presence of lead binding to NOM was modeled for the different waters using PHREEQC, via the R package pbcusol as outlined in the ESI.† A key assumption of the model was that lead carbonate solids would control solubility. More specifically, the model predicted that hydrocerussite (Pb3(CO3)2(OH)2) would control solubility in TP2[pH+/DIC−/Hard−/NOM+] and TP6[pH+/DIC−/Hard+/NOM−], while cerussite (PbCO3) would control solubility in all the other test pieces. The dissolved lead concentrations predicted by the model ranged from 148 (TP6[pH+/DIC−/Hard+/NOM−]) to 2221 μg L−1 (TP5[pH−/DIC−/Hard+/NOM+]) (Fig. S9 and Table S8†). The model overestimated dissolved lead in the synthetic waters without NOM and this may have been because the corrosion scales that formed were more complex than either cerussite or hydrocerussite, the system may not have reached equilibrium after 48–72 hours and a stable scale had not formed on the pipe surface as discussed later. Meanwhile, in most cases the model underestimated dissolved lead in the presence of SRNOM. A possible factor for this discrepancy is that the model did not explicitly account for colloidal dispersion of lead due to NOM, while dissolved lead measurements may have included Pb-NOM colloids. An exception to this was TP8[pH+/DIC+/Hard+/NOM+], which despite having 7 mg C per L of SRNOM had less dissolved lead release than was predicted by the model. One potential explanation is that the combination of high DIC and hardness protected against colloidal dispersion.32Changes to NOM following stagnation
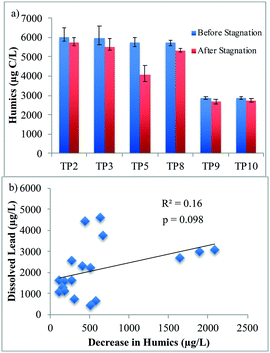
The decrease in humics concentration did not correlate with dissolved lead release (R2 = 0.16; p = 0.098; Fig. 4b). Furthermore, the aromaticity (specific ultraviolet absorption of the humics fraction, i.e. ratio of ultraviolet (UV) absorption to organic carbon concentration of the humics fraction) did not change significantly upon stagnation, except for TP5[pH−/DIC−/Hard+/NOM+], thus indicating no change in the humics composition.
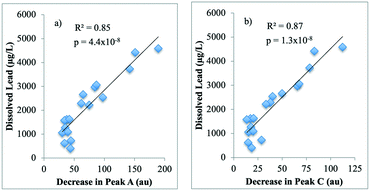
Strong correlations between the decrease in humic-like peak A (R2 = 0.85; p = 4.4 × 10−8; Fig. 5a) and peak C (R2 = 0.87; p = 1.3 × 10−8; Fig. 5b), and dissolved lead release were observed in the synthetic waters with SRNOM. This contrasts with the LC-OCD results, where no correlation was observed between a decrease in the concentration of the humics fraction and dissolved lead release. This difference may possibly be attributed to differences in analytical techniques; FEEM detects fluorophores and is presumably more sensitive to functional groups involved in complexation with lead, while LC-OCD separates fractions by apparent molecular weight and measures their carbon concentrations.
To the authors' knowledge, this is the first study to identify a correlation between a decrease in FEEM peak intensities and dissolved lead release. This result indicates that the humic-like peaks decreased proportionally to the amount of dissolved lead that was released. A possible explanation for the decrease in fluorescence intensities may be the formation of complexes between these humic-like fractions and dissolved lead. Indeed, NOM-metal binding has been found to have a quenching effect on the FEEM intensities of humic-like substances (e.g. ref. 65). This quenching effect is most likely due to the alteration of functional groups in the NOM that are responsible for fluorescence, as shown by studies on heavy metal binding and changes to NOM fluorescence (e.g. ref. 65 and 66). The incorporation of humic substances in the corrosion scales may also have contributed to this decrease.
Scale analysis
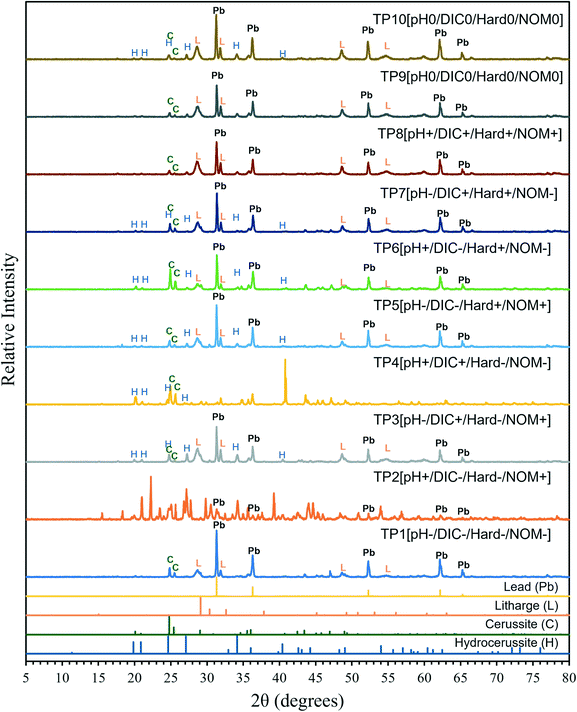
XRD results for the lead pipes of the test pieces are shown in Fig. 6 and Table S9† and the ICP-MS results for the scales are summarized in Table S10.† SEM-EDS analysis results for lead (Table S11†) and copper scale analysis results can be found in the ESI.† The XRD results indicate that cerussite was present on almost all the lead pipes (TP1, TP3–10). Several other lead solids were also detected on some of the lead pipes including hydrocerussite (TP3–7, TP10), litharge (PbO) (TP1, TP3, TP5–10), and elemental lead (TP1–3, TP5–10). The scales that formed were more complex than either cerussite (TP1, TP3–5, TP7–10) or hydrocerussite (TP2, TP6) assumed by the tidyphreeqc model. Elemental lead was probably present because the process of removing the scale from the inner surface of the lead pipes can also remove some of the unaltered lead. Although not predicted by the tidyphreeqc model, litharge was seen in the scales. Litharge is a more soluble solid than cerussite or hydrocerussite, which is why it was not predicted to have formed, and it may be present as a layer below the lead carbonates.30,67 Its presence may explain the measured dissolved lead concentrations that exceeded the expected solubility of cerussite and hydrocerussite. Calcium carbonate precipitation was not detected on the lead pipes even though several of the synthetic waters were estimated to have a positive Langelier saturation index (LSI). In contrast, some of the copper pipes did have magnesian calcite (TP4, TP6–8, TP10) detected by XRD together with substantial amounts of calcium as determined from elemental analysis of the scale composition.The SRNOM appeared to alter the colour of the lead corrosion scales, as the lead pipes not in contact with NOM formed white corrosion scales, while many of the lead pipes in contact with SRNOM formed corrosion scales that were shades of green, yellow, or brown (see example photographs in Fig. S13 and S14†). This coloration may be due to humic substances being incorporated into the lead corrosion scales,33,34,37 which would be supported by the decrease in LC-OCD humics concentrations and fluorescence. In the current study, the structure of the corrosion scales appeared to be similar in the test pieces exposed to water with and without SRNOM. This is in contrast with previous research, which found that in the presence of NOM, cerussite and hydrocerussite were less crystalline and contained an amorphous layer at the surface.33,34 This may be due to the high DIC concentration and hardness in the waters in the current study and its short duration (20 weeks). In Korshin et al.,34 NOM prevented the formation of cerussite and hindered the growth of hydrocerussite crystals. This is also in contrast to the current study, where cerussite (TP1, TP3–10) and hydrocerussite (TP3–7, TP10) were detected on many of the pipes with SRNOM. This may be because the lead coupons in Korshin et al.34 were exposed to water with a lower DIC concentration of approximately 4.3 mg L−1 (calculated from alkalinity = 15 mg CaCO3 per L) compared to 10 mg L−1 or higher in the current study.
Implications for the water treatment industry
Although lead concentrations in this study were far higher than in real-world sampling and represent a worst-case scenario, it is of note that SRNOM increased dissolved lead concentrations (<0.45 μg L−1) by approximately an order of magnitude. This is consistent with Locsin et al.68 and it is possible that some of the dissolved lead may in fact be colloidal in nature. Furthermore, the results of this study suggest that even in hard waters, NOM can greatly increase dissolved lead release. Follow-up experiments are required to confirm if NOM at lower concentrations (<3.5 mg C per L) in a variety of real waters and under different flow conditions, can have a similar effect. However, as Trueman et al.39 identified lead–NOM binding in treated drinking water, it is plausible that in some real waters similar findings could be observed. Despite this, the results of this study are not conclusive with regards to NOM and the release of particulate lead (i.e., particles greater than 0.45 μm). For waters without NOM, total lead was comprised primarily of particulate lead, while in waters with NOM dissolved lead was typically higher than particulate lead. It seems that NOM can facilitate a phase transition to dissolved lead most likely through complexation and colloidal dispersion. This also implies that the removal of NOM will likely reduce dissolved lead concentrations, but it does not necessarily follow that total lead concentrations will be reduced substantially. Thus, it is unclear whether NOM removal will impact total lead concentrations in consumers' taps. However, it is possible that in a system with more stable corrosion scales the benefits of reducing dissolved lead release may cause more notable decreases in total lead.In this study, an increase in DIC concentration from 10 to 80 mg L−1 did not reduce the release of lead resulting from galvanic corrosion. This contrasts with some studies such as Ma et al.,6 that have found DIC can decrease lead release by buffering against pH changes. This may not have been observed in the current study due to the influence of SRNOM and extremely high particulate lead release. Hardness did not have a significant effect on the galvanic current or lead release, however, it is possible that it could offer some degree of protection against highly dispersed lead colloids.32 Overall, the results from the present study suggest that hard water can still be aggressive towards lead in certain situations and that hardness adjustment is unlikely to have a large impact on lead release.
Conclusions
This study had the goal of determining the role of NOM on the galvanic corrosion of lead in hard drinking water. This was accomplished by employing a 24−1 fractional factorial design to examine the impact of pH, DIC, hardness, and NOM on the galvanic corrosion of lead. Overall, the following conclusions were made based on the results of the 20 week long “dump and fill” experiment using test pieces with new lead and copper pipes.• SRNOM had a potentially significant impact (p = 0.060) on the release of dissolved lead, with the addition of SRNOM at a concentration of 7 mg C per L increasing the release of dissolved lead by an average of 2320 μg L−1. This suggests that NOM removal or treatment can decrease dissolved lead concentrations, but it does not necessarily follow that total lead concentrations will be reduced. Without NOM dissolved lead may transition to particulate lead. However, based on previous research there is reason to be believe that NOM removal can reduce total lead in at least some situations.29,46,69
• Hardness did not have a significant impact on the galvanic current or lead release. Thus, hardness adjustment, such as water softening, is unlikely to have a noticeable impact on lead release.
• As expected, the pH and DIC concentration had potentially significant effects on total lead release (p = 0.089) and galvanic current (p = 0.051) respectively. An increase in the pH from 7 to 8.5 decreased total lead release by 4390 μg L−1. An increase in the DIC from 10 to 80 mg L−1 increased the galvanic current by an average of 28.4 μA.
• Strong correlations were identified between the release of dissolved lead and a decrease in the humic acid-like peak A (R2 = 0.85; p = 4.4 × 10−8) and peak C (R2 = 0.87; p = 1.3 × 10−8) intensities measured by FEEM. This result provides indirect evidence of complexation of dissolved lead by humic acid-like substances.
• Unlike previous reports, SRNOM did not seem to hinder scale formation (mainly cerussite and hydrocerussite) on the lead pipes. The synthetic waters with SRNOM formed corrosion scales that were shades of green, yellow, or brown on the lead pipes, while the synthetic waters without NOM formed white corrosion scales. This suggested that SRNOM was incorporated in the lead corrosion scales, although the scales were too thin to identify any structural differences.
• Scale analysis indicated that passivating scales such as calcium carbonate did not form on the lead pipes even in waters with a positive LSI. Furthermore, increasing the hardness and/or DIC concentration did not have a beneficial effect on lead release, suggesting that lead release could still be an issue for some utilities using hard waters.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The funding for this project was provided primarily by the Natural Sciences and Engineering Research Council of Canada (NSERC) in the form of an Industrial Research Chair in Water Treatment (Grant No. IRCPJ#147477-17) at the University of Waterloo. The authors acknowledge the technical support of Heather Daurie, Patrick Beaulieu, Yolanda Fang, Nancy Zhou, Lin Shen, Mark Merlau, and Mark Sobon. Lead author Patrick King was the recipient of an NSERC Alexander Graham Bell Canada Graduate Scholarship and a Queen Elizabeth II Graduate Scholarship in Science and Technology (QEII-GSST). Additional funding was provided to Benjamin Trueman through the Mitacs Accelerate Program (IT23352) and by NSERC through the Industrial Research Chair program (IRCPJ: 349838-16) at Dalhousie University.References
- A. P. Evens, D. M. Hryhorczuk, B. A. Lanphear, K. Rankin, D. Lewis, L. Forst and D. Rosenberg, The Impact of Low-Level Lead Toxicity on School Performance Among Children in the Chicago Public Schools: A Population-Based Retrospective Cohort Study, Environ. Health, 2015, 14, 21, DOI:10.1186/s12940-015-0008-9.
- M. C. Hanna-Attisha, J. C. LaChance, R. Sadler and A. Schnepp, Elevated Blood Lead Levels in Children Associated With the Flint Drinking Water Crisis: A Spatial Analysis of Risk and Public Health Response, Am. J. Public Health, 2016, 106(2), 283–290, DOI:10.2105/ajph.2015.30300.
- Health Canada, Guidelines for Canadian Drinking Water Quality: Guideline Technical Document – Lead, Water and Air Quality Bureau, Healthy Environments and Consumer Safety Branch, Ottawa, ON, 2019 Search PubMed.
- A. Sandvig, P. Kwan, G. Kirmeyer, B. Maynard, D. Mast, R. R. Trussell, S. Trussell, A. Cantor and A. Prescott, Contribution of Service Line and Plumbing Fixtures to Lead and Copper Rule Compliance Issues, Am. Water Works Assoc. Res. Foundation, Denver, CO, 2008 Search PubMed.
- S. Triantafyllidou and M. Edwards, Contribution of Galvanic Corrosion to Lead in Water After Partial Lead Service Line Replacements, Project 4088B, Am. Water Works Assoc. Res. Foundation, Denver, CO, 2010 Search PubMed.
- X. Ma, W. H. Lee and D. A. Lytle, In Situ 2D Maps of pH Shifts Across Brass–Lead Galvanic Joints Using Microelectrodes, Meas. Sci. Technol., 2016, 28(2), 025101, DOI:10.1088/1361-65.
- C. Cartier, R. B. Arnold, S. Triantafyllidou, M. Prévost and M. Edwards, Effect of Flow Rate and Lead/Copper Pipe Sequence on Lead Release from Service Lines, Water Res., 2012, 46(13), 4142–4152, DOI:10.1016/j.watres.2012.05.010.
- X. Ma, D. A. Lytle and W. H. Lee, Microelectrode Investigation on the Corrosion Initiation at Lead-Brass Galvanic Interfaces in Chlorinated Drinking Water, Langmuir, 2019, 35(40), 12947–12954, DOI:10.1021/acs.langmuir.9b02168.
- United States Environmental Protection Agency, SAB Evaluation of the Effectiveness of Partial Lead Service Line Replacements, 2011, Retrieved on October 24, 2021, from https://www.epa.gov/sites/default/files/2015-09/documents/sab_evaluation_partial_lead_service_lines_epa-sab-11-015.pdf Search PubMed.
- Health Canada, Guidance on Controlling Corrosion in Drinking Water Distribution Systems, Federal-Provincial-Territorial Committee on Drinking Water, Ottawa, ON, June 2009 Search PubMed.
- A. Cantor, Optimization of Phosphorus-Based Corrosion Control Chemicals Using a Comprehensive Perspective of Water Quality, Project 4586, Am. Water Works Assoc. Res. Foundation, Denver, CO, 2017 Search PubMed.
- American Water Works Association Research Foundation, Lead Control Strategies, Am. Water Works Assoc., Denver, CO, 1990 Search PubMed.
- M. R. Schock, Response of Lead Solubility to Dissolved Carbonate in Drinking Water, J. - Am. Water Works Assoc., 1980, 72(12), 695–704, DOI:10.1002/j.1551-8833.1980.tb04616.x.
- M. R. Schock and M. C. Gardels, Plumbosolvency Reduction by High pH and Low Carbonate-Solubility Relationships, J. - Am. Water Works Assoc., 1983, 75(2), 87–91, DOI:10.1002/j.1551-8833.1983.tb05072.x.
- B. Clark, C. Cartier, J. S. Clair, S. Triantafyllidou, M. Prévost and M. Edwards, Effect of Connection Type on Galvanic Corrosion Between Lead and Copper Pipes, J. - Am. Water Works Assoc., 2013, 105(7), E337–E351, DOI:10.5942/jawwa.2013.105.0088.
- R. B. Arnold, Master's thesis, New Insights into Lead and Copper Corrosion: Impacts of Galvanic Corrosion, Flow Pattern, Potential Reversal, and Natural Organic Matter, Virginia Polytechnic Institute and State University, 2011, Retrieved May 22, 2019, from https://vtechworks.lib.vt.edu/handle/10919/5534 Search PubMed.
- C. K. Nguyen, B. N. Clark, K. R. Stone and M. A. Edwards, Role of Chloride, Sulfate, and Alkalinity on Galvanic Lead Corrosion, Corrosion, 2011, 67(6), 065005, DOI:10.5006/1.3600449.
- D. M. Dodrill and M. Edwards, Corrosion Control on the Basis of Utility Experience, J. - Am. Water Works Assoc., 1995, 87(7), 74–85, DOI:10.1002/j.1551-8833.1995.tb06395.x.
- M. Edwards, L. S. McNeill, T. R. Holm and M. S. Lawrence, Role of Phosphate Inhibitors in Mitigating Lead and Copper Corrosion, Am. Water Works Assoc. Res. Foundation, Denver, CO, 2001 Search PubMed.
- M. Edwards and L. S. McNeill, Effect of Phosphate Inhibitors on Lead Release from Pipes, J. - Am. Water Works Assoc., 2002, 94(1), 79–90, DOI:10.1002/j.1551-8833.2002.tb09383.x.
- J. D. Noel, Y. Wang and D. E. Giammar, Effect of Water Chemistry on the Dissolution Rate of the Lead Corrosion Product Hydrocerussite, Water Res., 2014, 54, 237–246, DOI:10.1016/j.watres.2014.02.004.
- Y. S. Tam and P. Elefsiniotis, Corrosion Control in Water Supply Systems: Effect of pH, Alkalinity, and Orthophosphate on Lead and Copper Leaching from Brass Plumbing, J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng., 2009, 44(12), 1251–1260, DOI:10.1080/10934520903140009.
- D. T. Merrill and R. L. Sanks, Corrosion Control by Deposition of CaCO3 Films: Part 2, A Practical Approach for Operators, J. - Am. Water Works Assoc., 1977, 69(12), 634–640, DOI:10.1002/j.1551-8833.1977.tb06840.x.
- P. Leroy, Lead in Drinking Water-Origins, Solubility, Treatment, Aqua, 1993, 42(4), 233–238 CAS.
- C. S. Richards, F. Wang, W. C. Becker and M. A. Edwards, A 21st-Century Perspective on Calcium Carbonate Formation in Potable Water Systems, Environ. Eng. Sci., 2018, 35(3), 143–158, DOI:10.1089/ees.2017.0115.
- M. R. Schock, Understanding Corrosion Control Strategies for Lead, J. - Am. Water Works Assoc., 1989, 81(7), 88–100, DOI:10.1002/j.1551-8833.1989.tb03244.x.
- A. Wilczak, D. R. Hokanson, R. R. Trussell, M. Boozarpour and A. F. Degraca, Water Conditioning for LCR Compliance and Control of Metals Release in San Francisco's Water System, J. - Am. Water Works Assoc., 2010, 102(3), 52–64, DOI:10.1002/j.1551-8833.2010.tb10072.x.
- J. H. Colling, P. A. Whincup and C. R. Hayes, The Measurement of Plumbosolvency Propensity to Guide the Control of Lead in Tapwaters, J. Inst. Water Environ. Manage., 1987, 1(3), 263–269, DOI:10.1111/j.1747-6593.1987.tb01224.x.
- J. H. Colling, B. T. Croll, P. A. E. Whincup and C. Harward, Plumbosolvency Effects and Control in Hard Waters, J. Inst. Water Environ. Manage., 1992, 6(4), 259–268, DOI:10.1111/j.1747-6593.1992.tb00750.x.
- L. W. Wasserstrom, S. A. Miller, S. Triantafyllidou, M. K. DeSantis and M. R. Schock, Scale Formation Under Blended Phosphate Treatment for a Utility with Lead Pipes, J. - Am. Water Works Assoc., 2017, 109(11), E464–E478, DOI:10.5942/jawwa.2017.109.0121.
- J. J. Bisogni, I. S. Nassar and A. M. Menegaux, Effect of Calcium on Lead in Soft-Water Distribution Systems, J. Environ. Eng., 2000, 126(5), 475–478, DOI:10.1061/(asce)0733-9372(2000)126:5(475).
- J. Zhao, D. E. Giammar, J. D. Pasteris, C. Dai, Y. Bae and Y. Hu, Formation and Aggregation of Lead Phosphate Particles: Implications for Lead Immobilization in Water Supply Systems, Environ. Sci. Technol., 2018, 52(21), 12612–12623, DOI:10.1021/acs.est.8b02788.
- G. V. Korshin, J. F. Ferguson, A. N. Lancaster and H. Wu, Corrosion and Metal Release for Lead-Containing Materials: Influence of NOM, Am. Water Works Assoc. Res. Foundation, Denver, CO, 1999 Search PubMed.
- G. V. Korshin, J. F. Ferguson and A. N. Lancaster, Influence of Natural Organic Matter on the Morphology of Corroding Lead Surfaces and Behaviour(our of Lead-Containing Particles, Water Res., 2005, 39(5), 811–818, DOI:10.1016/j.watres.2004.12.009.
- G. V. Korshin and H. Liu, Preventing the Colloidal Dispersion of Pb(IV) Corrosion Scales and Lead Release in Drinking Water Distribution Systems, Environ. Sci.: Water Res. Technol., 2019, 5(7), 1262–1269, 10.1039/c9ew00231f.
- B. F. Trueman and G. A. Gagnon, A New Analytical Approach to Understanding Nanoscale Lead-Iron Interactions in Drinking Water Distribution Systems, J. Hazard. Mater., 2016, 311, 151–157, DOI:10.1016/j.jhazmat.2016.03.001.
- B. F. Trueman, G. A. Sweet, M. D. Harding, H. Estabrook, D. P. Bishop and G. A. Gagnon, Galvanic Corrosion of Lead by Iron (Oxyhydr)Oxides: Potential Impacts on Drinking Water Quality, Environ. Sci. Technol., 2017, 51(12), 6812–6820, DOI:10.1021/acs.est.7b01671.
- B. F. Trueman, W. H. Krkošek and G. A. Gagnon, Effects of Ortho- and Polyphosphates on Lead Speciation in Drinking Water, Environ. Sci.: Water Res. Technol., 2018, 4(4), 505–512, 10.1039/c7ew00521k.
- B. F. Trueman, T. Anaviapik-Soucie, V. L'Hérault and G. A. Gagnon, Characterizing Colloidal Metals in Drinking Water by Field Flow Fractionation, Environ. Sci.: Water Res. Technol., 2019, 5(12), 2202–2209, 10.1039/c9ew00560a.
- J. Parks, M. Edwards and A. Atassi, Non-Intrusive Methodology for Assessing Lead and Copper Corrosion, Am. Water Works Assoc. Res. Foundation, Denver, CO, 2014 Search PubMed.
- R. B. Arnold and M. Edwards, Potential Reversal and the Effects of Flow Pattern on Galvanic Corrosion of Lead, Environ. Sci. Technol., 2012, 46(20), 10941–10947, DOI:10.1021/es3017396.
- Y. Bae, J. D. Pasteris and D. E. Giammar, The Ability of Phosphate to Prevent Lead Release from Pipe Scale When Switching from Free Chlorine to Monochloramine, Environ. Sci. Technol., 2020, 54(2), 879–888, DOI:10.1021/acs.est.9b06019.
- D. E. Giammar, K. S. Nelson, J. D. Noel and Y. Xie, Water Chemistry Effects on Dissolution Rates of Lead Corrosion Products, Am. Water Works Assoc. Res. Foundation, Denver, CO, 2010 Search PubMed.
- B. Li, B. F. Trueman, S. Munoz, J. M. Locsin and G. A. Gagnon, Impact of Sodium Silicate on Lead Release and Colloid Size Distributions in Drinking Water, Water Res., 2021, 190, 116709, DOI:10.1016/j.watres.2020.116709.
- D. C. Montgomery, Design and Analysis of Experiments, John Wiley & Sons, Inc., Hoboken, NJ, 2013 Search PubMed.
- E. O. Zhou, S. J. O. Payne, R. O. Hofmann and R. C. Andrews, Factors Affecting Lead Release in Sodium Silicate-Treated Partial Lead Service Line Replacements, J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng., 2015, 50(9), 922–930, DOI:10.1080/10934529.2015.1030283.
- H. Willison and T. H. Boyer, Secondary Effects of Anion Exchange on Chloride, Sulfate, and Lead Release: Systems Approach to Corrosion Control, Water Res., 2012, 46(7), 2385–2394, DOI:10.1016/j.watres.2012.02.010.
- American Public Health Association, Standard Methods for the Examination of Water and Wastewater (21st ed.), American Water Works Association, & Water Environment Federation, Washington, DC, 2005 Search PubMed.
- J. A. Korak, A. D. Dotson, R. S. Summers and F. L. Rosario-Ortiz, Critical Analysis of Commonly Used Fluorescence Metrics to Characterize Dissolved Organic Matter, Water Res., 2014, 49, 327–338 CrossRef CAS PubMed.
- P. J. Coble, Characterization of Marine and Terrestrial DOM in Seawater Using Excitation-Emission Matrix Spectroscopy, Mar. Chem., 1996, 51(4), 325–346, DOI:10.1016/0304-4203(95)00062-3.
- S. A. Huber, A. Balz, M. Abert and W. Pronk, Characterisation of Aquatic Humic and Non-Humic Matter with Size-Exclusion Chromatography – Organic Carbon Detection – Organic Nitrogen Detection (LC-OCD-OND), Water Res., 2011, 45(2), 879–885, DOI:10.1016/j.watres.2010.09.023.
- United States Environmental Protection Agency, Method 6020B Inductively Coupled Plasma-Mass Spectrometry, 2014, Retrieved on February 5, 2019, from https://www.epa.gov/sites/production/files/2015-12/documents/6020b.pdf Search PubMed.
- K. Aghasadeghi, S. Peldszus, B. F. Trueman, A. Mishrra, M. G. Cooke, R. M. Slawson, D. E. Giammar, G. A. Gagnon and P. M. Huck, Pilot-Scale Comparison of Sodium Silicates, Orthophosphate, and pH Adjustment to Reduce Lead Release from Lead Service Lines, Water Res., 2021, 195, 116955, DOI:10.1016/j.watres.2021.116955.
- A. Mishrra, Z. Wang, V. Sidorkiewicz and D. E. Giammar, Effect of Sodium Silicate on Lead Release from Lead Service Lines, Water Res., 2021, 188, 116485, DOI:10.1016/j.watres.2020.116485.
- D. Dunnington, Tidyphreeqc: Tidy Geochemical Modeling Using Phreeqc, 2019, retrieved on February 13, 2020, from https://github.com/paleolimbot/tidyphreeqc Search PubMed.
- D. L. Parkhurst and C. A. J. Appelo, Description of input and examples for PHREEQC version 3--A computer program for speciation, batch- reaction, one-dimensional transport, and inverse geochemical calculations, U.S. Geological Survey Techniques and Methods, book 6, 2013, chaA43, p. p. 497, Retrieved on October 22, 2021 from https://pubs.usgs.gov/tm/06/a43 Search PubMed.
- B. F. Trueman, pbcusol: Predict Lead and Copper, 2021, Solubility. R package version 0.0.0.9000. Retrieved on October 22, 2021, from https://github.com/bentrueman/pbcusol Search PubMed.
- Y. Lin and R. L. Valentine, The Release of Lead from the Reduction of Lead Oxide (PbO2) by Natural Organic Matter, Environ. Sci. Technol., 2008, 42(3), 760–765, DOI:10.1021/es071984w2016.
- Y. Wang, V. Mehta, G. J. Welter and D. E. Giammar, Effect of Connection Methods on Lead Release from Galvanic Corrosion, J. - Am. Water Works Assoc., 2013, 105(7), E337–E351, DOI:10.5942/jawwa.2013.105.0088.
- M. Edwards, M. R. Schock and T. E. Meyer, Alkalinity, pH, and Copper Corrosion By-Product Release, J. - Am. Water Works Assoc., 1996, 88(3), 81–94, DOI:10.1002/j.1551-8833.1996.tb06521.x.
- W. Xiao, S. Hong, Z. Tang and J. S. Taylor, Effects of Blending on Total Copper Release in Distribution Systems, J. - Am. Water Works Assoc., 2007, 99(1), 78–88, DOI:10.1002/j.1551-8833.2007.tb07848.x.
- R. B. Arnold, A. Griffin and M. Edwards, Controlling Copper Corrosion in New Construction by Organic Matter Removal, J. - Am. Water Works Assoc., 2012, 104(5), E310–E317, DOI:10.5942/jawwa.2012.104.0072.
- M. Edwards and N. Sprague, Organic Matter and Copper Corrosion By-Product Release: A Mechanistic Study, Corros. Sci., 2001, 43(1), 1–18, DOI:10.1016/s0010-938x(00)00071-8.
- G. V. Korshin, S. A. Perry and J. F. Ferguson, Influence of NOM on Copper Corrosion, J. - Am. Water Works Assoc., 1996, 88(7), 36–47, DOI:10.1002/j.1551-8833.1996.tb06583.x.
- J. Wu, H. Zhang, P.-J. He and L.-M. Shao, Insight into the Heavy Metal Binding Potential of Dissolved Organic Matter in MSW Leachate using EEM Quenching Combined with PARAFAC Analysis, Water Res., 2011, 45(4), 1711–1719, DOI:10.1016/j.watres.2010.11.022.
- J. Wu, H. Zhang, L.-M. Shao and P.-J. He, Fluorescent Characteristics and Metal Binding Properties of Individual Molecular Weight Fractions in Municipal Solid Waste Leachate, Environ. Pollut., 2012, 162, 63–71, DOI:10.1016/j.envpol.2011.10.017.
- M. R. Schock, I. Wagner and R. J. Oliphant, Corrosion and Solubility of Lead in Drinking Water, In Internal Corrosion of Water Distribution SystemZs, Am. Water Works Assoc. Res. Foundation, Denver, CO, 1996, 2nd edn, pp. 131–230 Search PubMed.
- J. A. Locsin, K. M. Hood, E. Doré, B. F. Trueman and G. A. Gagnon, Colloidal Lead in Drinking Water: Formation, Occurance, and Characterization, Crit. Rev. Environ. Sci. Technol., 2022 DOI:10.1080/10643389.2022.2039549 , ahead of print, published on-line Feb. 27, 2022.
- S. J. de Mora, R. M. Harrison and S. J. Wilson, The Effect of Water Treatment on the Speciation and Concentration of Lead in Domestic Tap Water Derived from a Soft Upland Source, Water Res., 1987, 21(1), 83–94, DOI:10.1016/0043-1354(87)90102-3.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d1ew00903f |
| ‡ Present address: Jacobs Engineering Group Ltd., Winnipeg, MB, R3P 2P2, Canada. |
| This journal is © The Royal Society of Chemistry 2022 |