Emerging dynamic memristors for neuromorphic reservoir computing
Jie
Cao
ab,
Xumeng
Zhang
acb,
Hongfei
Cheng
d,
Jie
Qiu
a,
Xusheng
Liu
ab,
Ming
Wang
 *ac and
Qi
Liu
acb
*ac and
Qi
Liu
acb
aFrontier Institute of Chip and System, Zhangjiang Fudan International Innovation Center, Fudan University, Shanghai 200433, China. E-mail: wang_ming@fudan.edu.cn
bState Key Laboratory of ASIC and System, School of Microelectronics, Fudan University, Shanghai 200433, China
cShanghai Qi Zhi Institute, 41th Floor, AI Tower, No. 701 Yunjin Road, Xuhui District, Shanghai 200232, China
dInstitute of Materials Research and Engineering (A*STAR), 2 Fusionopolis Way, 138634, Singapore
First published on 2nd December 2021
Abstract
Reservoir computing (RC), as a brain-inspired neuromorphic computing algorithm, is capable of fast and energy-efficient temporal data analysis and prediction. Hardware implementation of RC systems can significantly reduce the computing time and energy, but it is hindered by current physical devices. Recently, dynamic memristors have proved to be promising for hardware implementation of such systems, benefiting from their fast and low-energy switching, nonlinear dynamics, and short-term memory behavior. In this work, we review striking results that leverage dynamic memristors to enhance the data processing abilities of RC systems based on resistive switching devices and magnetoresistive devices. The critical characteristic parameters of memristors affecting the performance of RC systems, such as reservoir size and decay time, are identified and discussed. Finally, we summarize the challenges this field faces in reliable and accurate task processing, and forecast the future directions of RC systems.
1. Introduction
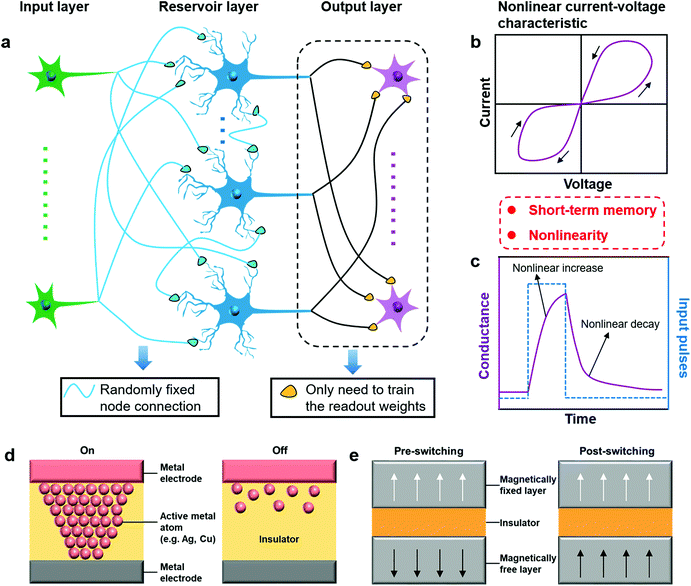
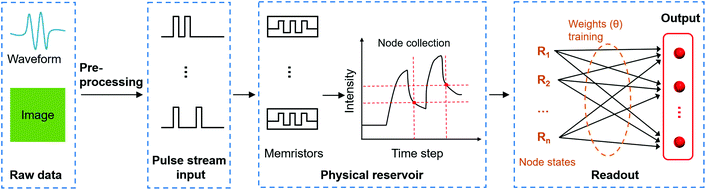
Artificial neural networks (ANNs) inspired by the biological brain have been proved to be a highly efficient computing paradigm for complex information processing, such as pattern recognition, object detection, and natural language processing.1–3 An ANN is composed of highly interconnected processing units or nodes called artificial neurons, where the junction between two neurons is referred to as an artificial synapse. According to the information flowing direction of the network, ANNs are classified into feedforward neural networks (FNNs) and recurrent neural networks (RNNs).4,5 FNNs allow signals to travel one way only from the input to the output, while RNNs have one or more cyclic (feedback) connections where the outputs of the network can be fed back into itself. As a result, sequential inputs can be encoded into the nonlinear dynamics of the network in RNNs, enabling RNNs to be good at dealing with temporal or sequential information.6 However, RNNs are usually difficult to be trained, which struggles with complex long-timescale nonlinear dynamics because of exploding gradient and vanishing gradient problems in cyclic connections.For addressing this deficiency, a variation framework of RNNs called reservoir computing (RC) is proposed to tackle complex temporal or sequential tasks.7 A typical RC system (Fig. 1a) is comprised of three main parts: the input, the reservoir, and the output. The input layer acts as the interface between the real-world information and the reservoir network. In the input layer, a preprocessing procedure is usually required to convert external information from the real world, such as images and speech signals, into temporal input signals. These input signals are then fed into the reservoir layer via fixed weight connections. The reservoir layer comprises a network of randomly interconnected nodes, enabling the input signals to be nonlinearly projected into a high-dimensional state space. In the high-dimensional space, the input signals that are hard to be separated in the low-dimensional space would become linearly separable due to the increased differentiation of features.8 In the reservoir network, only the node states connecting the reservoir layer and the output layer are required to be read out through linear weighted sums for recognition. As a result, the reservoir itself does not need to be trained and only the output connections with linear weights does, which makes the training process simple, fast, and energy-efficient, compared with other RNNs.2
Software-based RC systems have been used to solve temporal information analysis and prediction tasks, such as handwritten digit recognitions, speech recognitions, waveform classification, and chaotic system forecasting.9,10 Despite the advances in software-based RC systems, hardware implementation in RC algorithms is much more attractive due to its advantages in computing speed and energy consumption. Several materials and physical devices, such as atomic switch devices,11–13 self-organized nanostructured networks,14–17 dynamic memristors,18,19 spintronic oscillators,20–22 photonics,23–25 or field-programmable gate arrays,8,26,27 have been used for the physical implementation of RC systems. Among them, the memristor-based approach has made extensive progress in recent years, benefiting from inherent nonlinear resistive switching behaviors of memristors and ease of integration capabilities.14,28 However, the key requirements of physical memristors for the fast and highly efficient RC and main challenges of memristor-based RC systems are still unaddressed. Therefore, it is highly urgent to review the state-of-the-art memristor-based RC systems.
In this mini-review, we summarized recent progress in dynamic memristor-based RC systems in the last three years, including electrically resistive switching memory (RSM) type- and magnetoresistive switching memory (MSM) type-RC systems. The operation principles, characteristics, requirements, and challenges for each class are discussed in detail. Finally, the article is concluded with our perspectives on memristor-based RC systems.
2. Memristor-based RC systems
2.1 Operational principle of memristor-based RC systems
A physical device that could serve for the hardware implementation of RC systems requires two essential properties: short-term memory and nonlinear dynamics. The short-term memory behavior of the device under electrical stimuli allows the nonlinear increase and decay of electrical characteristics within short timescales from nanoseconds to milliseconds. The fast nonlinear and fading dynamics of the device can nonlinearly transform a time-series signal into a new, random high-dimensional feature space.Dynamic physical memristors can exhibit both short-term memory and nonlinear characteristics that are highly desired for the implementation of physical reservoir networks (Fig. 1b and c). A memristor is a nonlinear two-terminal electrically resistive switching device, whose conductance can be programmed (resistor function) by external electrical bias and subsequently remains stored (memory function).29,30 Although the stored information is expected to be non-volatile for ideal memristors, researchers have found that more and more physical memristors exhibit short-term memory behaviors since the programmed conductance state of these memristors has a limited retention time ranging from nanoseconds to several hours.31,32 The short-term memory behavior allows memristors to perform critical computational functions of the reservoir layer.33 Specifically, when a sequential stimulus is an input, the dynamic memristor exhibits a transient response by temporary conductance changes and then rapidly and nonlinearly decays to its initial state based on spontaneous physical effects (Fig. 2). These response states are read out by linear output weights which are trained using traditional machine-learning algorithms for predictions. Broadly, all recognizable physical variables of dynamic memristors, such as ions and magnetic domain wall motion, can be regarded as the node response states in the reservoirs. The physical variables with short-term memory and nonlinear decay characteristics can be used to implement the specific nonlinear transformations of the input information for computation.
Meanwhile, memristors can be fabricated using standard microelectronic processes and materials, allowing a high-density nanoscale integration. Such memristor arrays show potential to be dramatically smaller than comparable complementary metal oxide–semiconductor (CMOS) or other integrated devices with the same functionality.34,35 Therefore, these advantages make them ideal candidates for the physical implementation of RC systems.
So far, hardware implementation of RC systems with RSM and MSM has been reported. The RSM device has short-term memory and nonlinear properties due to the spontaneous diffusion process of cations and anions (Fig. 1d), while the MSM device possesses short-term memory and nonlinear characteristics originating from magnetoresistive effects (Fig. 1e).36 In the following chapters, we review recent progress on physical RC systems based on RSM and MSM devices. Several parameters that play key roles in the performance of RC systems, such as the reservoir size and time constant, are discussed in detail.
2.2 RSM-based RC systems
Biomimetic synaptic short-term plasticity (STP) behavior is pivotal for RSM devices to be used in RC systems.37,38 The state of an RSM device depends on not only the currently applied stimuli, but also its previous state. Specifically, when an electrical pulse is applied, the conductance state of the RSM will be increased due to the formation of nanoscale conductive filaments containing oxygen vacancies or metallic particles (such as Ag and Cu). When the electrical bias is removed, these oxygen vacancies or metallic particles would gradually redistribute to the initial steady state due to the effect of spontaneous recombination/diffusion, resulting in a nonlinear dynamic conductance decay.29,33,39,40 As a result, if several successive pulses with short intervals are applied, the conductance state will gradually increase, whereas if there are long time intervals between consecutive pulses, the conductance will decay to its initial state (Fig. 3b).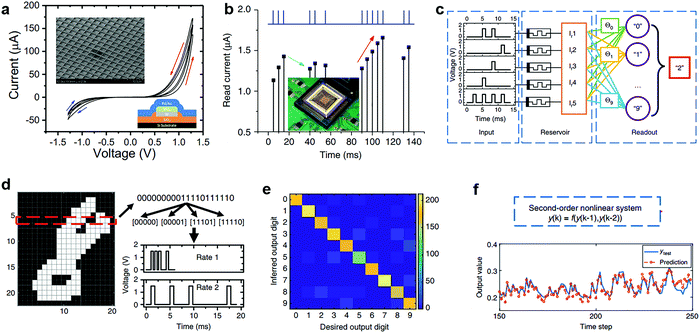 | ||
| Fig. 3 A physical RC system with a RSM-based reservoir network. (a) DC voltage sweeps of a WOx-based RSM. Upper inset: SEM image of a 32 × 32 RSM array. Bottom inset: schematic of the WOx-based RSM structure. (b) Response of a typical WOx RSM to a pulse stream with different time intervals between pulses. Inset: image of the RSM array wired-bonded to a chip. (c) Schematic of the RC system consisting of 5 RSM devices. (d) The process flow of a handwritten digit recognition using a RSM-based RC system. (e) False color confusion matrix showing the experimentally obtained classification results from the RC system vs. the desired outputs. (f) Solving a second-order nonlinear dynamic task by using a RSM-based RC system. Reproduced with permission from ref. 19. Copyright 2017, Nature Publishing Group. | ||
A RC system has been built by using a 32 × 32 WOx-based RSM array incorporating oxygen vacancy drift, and diffusion effects (Fig. 3a).19 The WOx-based RC system was experimentally implemented for image and handwritten classification tasks with a recognition accuracy of 88.1% (Fig. 3c–e). In addition to the classification tasks, the hardware RC system can perform complex system forecasting. A second-order nonlinear dynamic task with an implicit and hidden functional relationship was solved by this RC system, achieving a small normalized mean squared error of 3.61 × 10−3 (Fig. 3f).
The reservoir size is critical to RC systems. However, the number of effective reservoir node states for current RSM-based RC systems is usually limited due to the irrational device parameter sets, which restricts the dimensionality of the reservoir space, resulting in low prediction accuracy. For example, for a spoken-digit recognition task, continuous sound waveforms are firstly required to be transformed into input streams with 40 time steps (Fig. 4a).41 However, the temporal information of the early part of the input stream is not conveyed in the final responses due to the lack of effective nodes in the long time interval. As a consequence, the loss of information will lead to poor classification results.
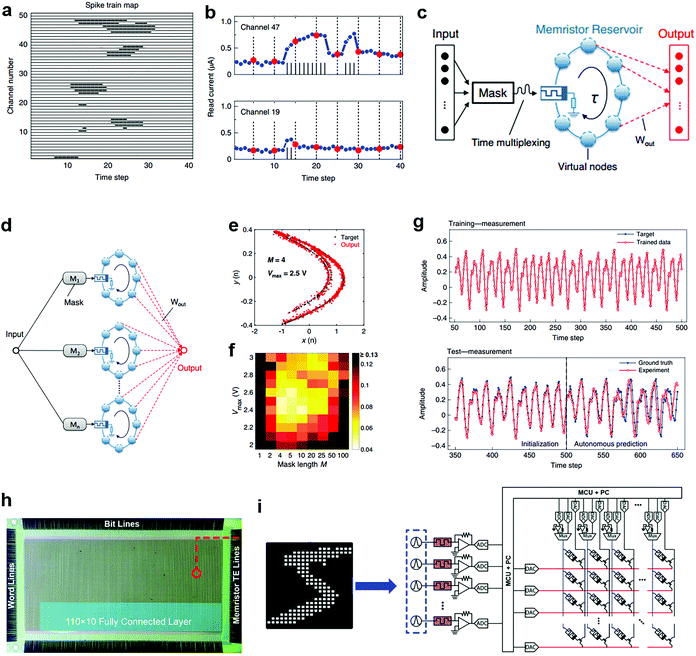 | ||
| Fig. 4 The virtual node approaches to expand the reservoir size of RSM-based RC systems. (a) Spoken-digit recognition task implementation. Digitized spike trains converted from the cochleagram. (b) Virtual nodes collected at the end of each equal interval. Reproduced with permission from ref. 41. Copyright 2019, Nature Publishing Group. (c) Schematic of the dynamic RSM-based RC system by the delayed-feedback virtual node approach. (d) Schematic of a dynamic RSM-based parallel RC system, where the mask sequences are different for every single RSM RC unit. (e) 2D display of the predicted results where the M and Vmax are 4 and 2.5 V, respectively. (f) The prediction error varies with the two test parameters M (1–100) and Vmax (2.0–3.0 V). Reproduced with permission from ref. 43. Copyright 2021, Nature Publishing Group. (g) Training and forecasting results obtained experimentally from the RSM-based RC system. Reproduced with permission from ref. 41. Copyright 2019, Nature Publishing Group. (h) Optical micrograph of the 128 × 64 1T1R crossbar with the probe card landed. (i) Schematic of the diffusive RSM-based dynamic reservoir for classifying MNIST-based temporal sequences. Reproduced with permission from ref. 18. Copyright 2019, Wiley-VCH Verlag GmbH & Co. KGaA. | ||
A general virtual node approach is proposed to solve this problem, which aims to increase the effective reservoir size for better mapping of the input features.26 Specifically, the whole input sequence is divided into n equal intervals, and the virtual node state at the end of each interval is recorded (Fig. 4b). This method effectively creates n virtual nodes from a single device, resulting in a higher recognition accuracy of 99.2% than the previous 88.1%.19 The same equal-time-step recording strategy was also adopted in another RSM-based RC system to increase the number of virtual nodes and efficiently analyze neural activity signals in real time.42
Another widely used virtual node method is to utilize a dynamical system comprising a nonlinear node subjected to delayed feedback (Fig. 4c).8,26 In contrast to the direct connection between the input and the reservoir layer of the conventional reservoir networks, the input information in a delayed feedback approach goes through the nonlinear nodes that perform the transformation and then propagates through a delayed-feedback line to the corresponding virtual nodes. A mask process with time multiplexing is applied to generate virtual nodes in the time domain.43 Specifically, the input signal is multiplied by a mask matrix and then converted into a strain of voltage pulses through a signal generation system. Every frame of the input signal can generate a pulse stream with total pulse length and width. To further improve the system performance, several single RSM-based reservoirs were connected in parallel to build a large parallel RC system to increase the reservoir size (Fig. 4d). Typical tasks, including waveform classification, spoken-digit recognition and Hénon map prediction, were used to verify the temporal signal processing capability of the RC system with virtual nodes, showing higher recognition accuracies and lower error rates than their previous scenarios (Fig. 4e and f).
Meanwhile, another credible alternative to increase the reservoir node states is to fully take advantage of the device-to-device variations, where the reservoir state can be represented by the collected states of all devices.44 As an example, the prediction of a chaotic system is challenging due to the positive Lyapunov exponent in chaotic systems, which leads to an exponential growth of separation of close trajectories. As a result, even small errors in prediction can quickly lead to divergence of the prediction from the ground truth.41 To address this problem, 20 RSM devices with relatively large variations were used to expand the effective reservoir size of the RC system through a nonlinear coupling of collective device states. Meanwhile, 50 virtual nodes were obtained from each memristor device with the same time step. After training, the autonomously generated output of the RC system matches well with the ground truth, revealing stable and accurate forecasting of the chaotic system (Fig. 4g).
In general, time constant τ, representing the decay behavior of conductance states over time, is also an important parameter to evaluate the performance of RC systems. A small time constant can reduce the time interval of the node state acquisition between adjacent patterns, thus speeding up the computing speed. However, most RSM devices have long decay time constants of tens or even hundreds of milliseconds (Table 1). For example, the time constant τ values of the WOx- and CsPbI3-based devices are about 50 ms and 39.1 ms, respectively.19,42 To improve the computing efficiency, volatile RSM devices have been developed by varying material compositions.45–47 For instance, Ag particles were doped into a SiO2 functional layer to fabricate a diffusive RSM device, which exhibits a small time constant (τ < 5 ms).18 Furthermore, a MNIST handwritten digit classification was achieved by employing diffusive RSM devices as reservoirs and a drift RSM-based 1T1R (one transistor and one memristor) array as the output layer, enabling the in situ learning of an RC system (Fig. 4h and i).
| Devices | Number of memristors for RC systems (unit) | Time constant τ | Tasks | Recognition ratio |
|---|---|---|---|---|
| (Pd/Au)/WOx/W (ref. 19) | 88 RSM | 50 ms | Handwritten digit recognition | 88.1% |
| (Pd/Au)/WOx/W (ref. 41) | 50 RSM | 50 ms | Spoken-digit recognition | 99.2% |
| Ti/(TiOx/TaOy)/Pt (ref. 43) | Single RSM | 400 μs | Spoken-digit recognition | 99.6% |
| Ag/CsPbI3/Ag (ref. 42) | Single RSM | 39.1 ± 24.8 ms | Neural activity analysis | — |
| Pd/(SiO2/Ag)/(Pt/Ti); Pd/Ta2O5/Ta (ref. 18) | 110 diffusive RSM; 110 × 10 1T1R array | <5 ms | Handwritten digit recognition | 83% |
| FTO/n-type crystalline molecular semiconductor/Cu (ref. 48) | Single RSM | <400 ms | Neuromorphic applications | — |
| Pt/Co bilayer system (ref. 21) | Single skyrmion MSM | <5 ns | Handwritten digit recognition | 87.6% |
| FeB/MgO/CoFeB (ref. 22) | Single STNO | 500 ns | Spoken-digit recognition | 95.7%–99.8% |
| (Cr/Au)/SnS/(Cr/Au) (ref. 49) | 5 paralleled RSM | Electrical stimuli: >10 ms | Korean sentence recognition | 91% |
| Optical stimuli: >3 s |
Notably, self-organized resistive switching networks of nanomaterials have been developed for physical RC systems, which show great merit of easy fabrication.14,15 For example, a self-organized polymer-coated silver nanowire network was recently constructed as the physical reservoir network for achieving image classification and time-series prediction tasks.14 Unlike the CMOS-based memristor crossbar arrays, the response of this physical reservoir network is represented by the conductivity map consisting of ionic motion at each junction of self-assembled nanowire networks. Benefitting from the intrinsic disorder of self-organized nanomaterials, the physical RC system demonstrates a high-density of devices with a low cost of device fabrication. This work provides a good example of using the short-term and nonlinear dynamics of nanomaterials for advanced brain-inspired computing.
2.3 MSM-based RC systems
MSM can also possess both short-term memory and nonlinear characteristics, which serve as another promising candidate for physical reservoir networks.21,36,50 These magnetic memristors with nonlinear resistance responses have been achieved by using magnetic skyrmion materials. The magnetic skyrmion is a topologically nontrivial spin texture with a quantized topological number, which is promising for spintronic applications because of its mobility driven by ultralow currents and room temperature stability.51 Benefitting from the nonlinear characteristics that originate from magnetization-dependent magnetoresistive effects, a magnetic skyrmion can accurately feature the reservoir node states.A Pt/Co bilayer system has been proposed to create current-driven skyrmion motion dynamics for reservoir networks.21 This skyrmion-based MSM device encodes the temporal information through spin-torque driven skyrmion motion. Skyrmions can be stabilized by interfacial Dzyaloshinskii–Moriya interactions and further nucleated and manipulated by current-induced spin torques in heavy metal/ferromagnetic systems (Fig. 5a).52–55 Here, a skyrmion is firstly created which then moves nonuniformly with a strong dependence on its current position, which is due to the nonlinear repulsive force on the skyrmion from the nonuniform dipole field and current-induced spin torques (Fig. 5b and c).21 In addition, MSM devices possess high-speed information processing ability due to the nanosecond-scale response (<10 ns). A handwritten recognition task was used to illustrate the performance of the MSM-based RC system (Fig. 5d). After the training using a gradient descent method, an optimized recognition accuracy of 87.6% is achieved (Fig. 5e).
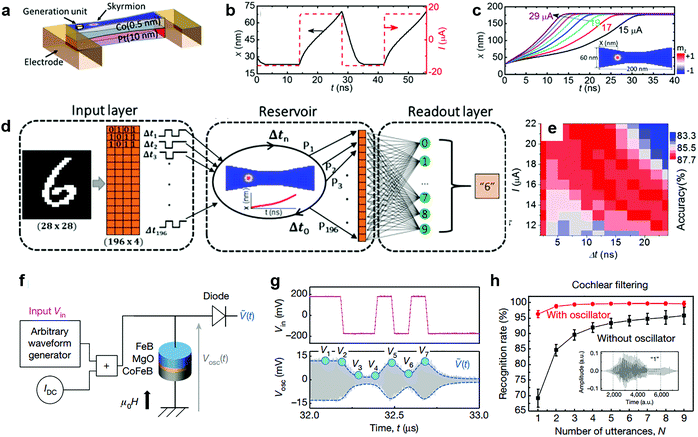 | ||
| Fig. 5 Demonstration of MSM-based RC systems, including the magnetic skyrmion memristor-based RC system and the STNO-based RC system. (a) Schematic of the structure of an MSM consisting of the dumbbell shape ferromagnetic Pt/Co bilayer. (b) The position x (left axis) of the skyrmion under the square current pulse stimulation (right axis). (c) Time dependent position x at current I varying between 15 μA and 29 μA in 2 μA steps. (d) Process flow diagram of handwritten digit recognition using an MSM-based RC system. (e) Pseudocolor mapping of the recognition accuracy rates. (f) Schematic of the STNO experimental set-up for the RC system. Reproduced with permission from ref. 21. Copyright 2019, AIP Publishing LLC. (g) Input Vin and measured microwave voltage Vosc emitted by the oscillator as a function of time. (h) Spoken-digit recognition process and the recognition rates. Reproduced with permission from ref. 22. Copyright 2017, Nature Publishing Group. | ||
Overall, MSM devices have several advantages for the physical implementation of RC systems. Firstly, the size of skyrmions is quite small with an average skyrmion diameter of about 10 nm, enabling a high-density reservoir network. Secondly, the power consumption of skyrmion devices is relatively low because of the efficient coupling between currents and skyrmions. Thirdly, skyrmion systems affected by electric and magnetic fields have complex diversity to enrich the reservoir nodal states.36 Despite obvious advantages, several aspects of MSM devices still need to be improved. The necessity of a high signal-to-noise ratio for efficient reservoir computing is a general guideline, which is also applied to magnetic spintronics. Since spintronic devices can be as small as a few nanometers, nanoscale devices tend to be noisy and lack the stability for data processing. Hence, it is necessary to investigate the stability of devices by tuning the material properties, electric and magnetic field parameters, etc. Meanwhile, since the skyrmion needs to relax back to its initial state to work properly upon switching off the voltage inputs, more complex dynamic characteristics such as STP behavior have not been developed in skyrmion systems. Moreover, although the current skyrmion memristors have been achieved by software simulation, the physical implementation of magnetoresistive memristor-based RC systems still remains a challenge.
Noteworthily, another class of spintronic devices, called spin-torque nano-oscillators (STNOs), also exhibit good potential for RC systems,20,22,56–58 and are different from magnetoresistive memristors. The STNO devices based on spin-transfer torques associated with a net spin current can generate a steady-state microwave oscillation in response to a DC electrical current (Fig. 5f and g). The complex nonlinear dynamics and short-term memory of STNOs are attributed to the synchronization effect of neighbouring oscillators caused by magnetic precession.59 STNO-based RC systems have also demonstrated good performance in dealing with time-series tasks, such as second-order nonlinear systems and spoken-digit recognition (Fig. 5h).20,22
3. Perspectives
RC systems have shown their superior strength in tackling temporal classification, regression, and forecasting tasks with low computational training costs and the fading gradient problem. Physical reservoirs have been demonstrated by using different dynamic memristors including RSM, MSM, and derived STNO. Nevertheless, current memristor-based RC systems are still in their infancy, particularly for the reservoir layer determined by the dynamic nonlinear behavior of memristors. The challenges and perspectives in the aspect of the constituent parts of RC systems are further discussed as follows.3.1. The input layer
The input layer serves as a bridge between the real-world information and the reservoir network. However, current memristor-based RC systems only involve processing relatively simple computing tasks because of diversity-deficient temporal inputs, which are far away from complex task requirements. The tight integration of sensing, computing, and other functions that biological systems exhibit to adapt to dynamic environments has served as an inspiration for intelligent systems.60–63 Inspired by the multifunctionality of biological systems, the fusion of multimodal sensing and emerging computing paradigm can significantly expand the RC system's interpretation and learning of various surrounding temporal sequence information.64,65 Several studies have revealed that the fusion of information from several modalities can significantly improve the RC performance compared to a single modality.49,66–68 In the future, we expect a tight integration of materials science, microelectronics, computer science, and other relevant disciplines to make critical advances in multimodal response sensors, memristors, or other emerging devices to widen the application fields of RC systems.The preprocessing of raw input signals is an essential prerequisite for memristor-based RC systems. The raw inputs are encoded into sequential voltage or current inputs to trigger the nonlinear transient responses of memristor-based physical reservoirs. There are two common approaches for preprocessing the raw inputs, namely binary matrix conversion and time-multiplexing.8,26 The purpose of these two methods is to maximize the network dimensionality of the reservoir network so that the reservoir can collect more information to distinguish the input feature effectively. In the future, researchers might devote much effort to realizing the goal of sufficient reservoir size for the high accuracy of RC systems.
3.2. Reservoir networks
The size of the reservoirs plays an important role in the data processing of the RC system. In essence, most existing research works are aimed at enriching the reservoir node states to increase the reservoir size, including the aspects of both device design and system architecture.As for the device design, a straightforward approach is to build up large-scale memristor arrays to expand the size of the reservoir that can work independently and in parallel to process the spatiotemporal data. Although the fabrication of a large-scale memristor array is not a big issue due to its easy processing, the device variability prevents us from simultaneously utilizing all memristor devices in the array for RC implementation. An exciting lead is to implement large-scale arrays, in which the device-to-device variability is regarded as a merit.41 However, cycle-to-cycle variations of individual devices are detrimental to RC systems due to the error source caused by cyclic variations during temporal data processing. The cycle-to-cycle variations of a memristor device will be a long-standing issue. Reducing the stochastic variation of a single device by advanced materials, structures and mechanisms will hold the primary status to improve the robustness of RC systems in the future. In addition, using interconnected devices to construct complex nonlinear interactions can further expand the width and depth of the reservoirs. However, the efficient interconnection of nanodevices is a substantial difficulty in the large-scale integrated array.
As for the system architecture, the virtual node method based on the delayed feedback approach has been proved to be valid to spatially map temporal information, because it can efficiently simplify the network architectures and achieve good computing performance.8,26 In addition to time-multiplexing, new preprocessing approaches corresponding to the virtual nodes should be developed in the future. Developing deep RC systems with deep layered architectures is also an effective method to increase the richness of the dynamic reservoirs at multiple time-scales.69 Such an approach shows the advantages of increasing the short-term memory capacity of RC models.
3.3. The output layer
The output layer conducts the interpretation of high-dimensional mapping and final classification. In this layer, the readout function is mainly trained to adjust the connection weights by the existing machine learning algorithms, such as linear regression. Developing new adaptive algorithms for the training of the output layer will be necessary to expand the application scope of RC systems.4. Conclusion
The past few years have witnessed tremendous efforts in physical RC systems due to their advantage in processing temporal information tasks. This mini-review discussed the state-of-art progress in the physical implementation of RC systems based on dynamic memristors, including RSM and MSM devices. Representative research results were reviewed and discussed, including material compositions, device structures, data processing, and applications. Meanwhile, several critical parameters of memristor-based RC systems, such as nonlinearity, short-term memory, reservoir size, and decay time, were also discussed. Finally, the challenges and directions of future research were outlined. We firmly believe that the interdisciplinary collaborative effort from the areas of materials, microelectronics, biology, and computer science would open new avenues for the application of hardware RC systems.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (62104042) and the Start-up Funding from Fudan University (JIH2321005).References
- D. Marković, A. Mizrahi, D. Querlioz and J. Grollier, Nat. Rev. Phys., 2020, 2, 499–510 CrossRef
.
- C. Kaspar, B. J. Ravoo, W. G. van der Wiel, S. V. Wegner and W. H. P. Pernice, Nature, 2021, 594, 345–355 CrossRef CAS PubMed
.
- C. Mead, Proc. IEEE, 1990, 78, 1629–1636 CrossRef
.
- W. Zaremba, I. Sutskever and O. Vinyals, 2014, arXiv preprint arXiv:1409.2329.
- M. Hibat-Allah, M. Ganahl, L. E. Hayward, R. G. Melko and J. Carrasquilla, Phys. Rev. Res., 2020, 2, 023358 CrossRef CAS
.
-
R. Pascanu, T. Mikolov and Y. Bengio, On the difficulty of training recurrent neural networks, International conference on machine learning, PMLR, 2013, pp. 1310–1318 Search PubMed
.
-
B. Schrauwen, D. Verstraeten and J. Van Campenhout, An overview of reservoir computing: theory, applications and implementations, Proceedings of the 15th European Symposium on Artificial Neural Networks, 2007, pp. 471–482 Search PubMed
.
- L. Appeltant, G. Van der Sande, J. Danckaert and I. Fischer, Sci. Rep., 2014, 4, 3629–3633 CrossRef CAS PubMed
.
- W. Maass, T. Natschläger and H. Markram, Neural Comput., 2002, 14, 2531–2560 CrossRef PubMed
.
-
H. Jaeger, Bonn, Germany: German National Research Center for Information Technology GMD Technical Report, 2001, vol. 148, p. 13 Search PubMed
.
- A. Z. Stieg, A. V. Avizienis, H. O. Sillin, C. Martin-Olmos, M. Aono and J. K. Gimzewski, Adv. Mater., 2012, 24, 286–293 CrossRef CAS PubMed
.
- H. O. Sillin, R. Aguilera, H.-H. Shieh, A. V. Avizienis, M. Aono, A. Z. Stieg and J. K. Gimzewski, Nanotechnology, 2013, 24, 384004 CrossRef PubMed
.
- H. Tanaka, M. Akai-Kasaya, A. TermehYousefi, L. Hong, L. Fu, H. Tamukoh, D. Tanaka, T. Asai and T. Ogawa, Nat. Commun., 2018, 9, 1–7 CrossRef CAS PubMed
.
- G. Milano, G. Pedretti, K. Montano, S. Ricci, S. Hashemkhani, L. Boarino, D. Ielmini and C. Ricciardi, Nat. Mater., 2021 DOI:10.1038/s41563-021-01099-9
.
- G. Milano, G. Pedretti, M. Fretto, L. Boarino, F. Benfenati, D. Ielmini, I. Valov and C. Ricciardi, Adv. Intell. Syst., 2020, 2, 2000096 CrossRef
.
- Y. Usami, B. van de Ven, D. G. Mathew, T. Chen, T. Kotooka, Y. Kawashima, Y. Tanaka, Y. Otsuka, H. Ohoyama, H. Tamukoh, H. Tanaka, W. G. van der Wiel and T. Matsumoto, Adv. Mater., 2021, 2102688, DOI:10.1002/adma.202102688
.
- M. D. Pike, S. K. Bose, J. B. Mallinson, S. K. Acharya, S. Shirai, E. Galli, S. J. Weddell, P. J. Bones, M. D. Arnold and S. A. Brown, Nano Lett., 2020, 20, 3935–3942 CrossRef CAS PubMed
.
- R. Midya, Z. Wang, S. Asapu, X. Zhang, M. Rao, W. Song, Y. Zhuo, N. Upadhyay, Q. Xia and J. J. Yang, Adv. Intell. Syst., 2019, 1, 1900084 CrossRef
.
- C. Du, F. Cai, M. A. Zidan, W. Ma, S. H. Lee and W. D. Lu, Nat. Commun., 2017, 8, 2204 CrossRef PubMed
.
- W. A. Borders, A. Z. Pervaiz, S. Fukami, K. Y. Camsari, H. Ohno and S. Datta, Nature, 2019, 573, 390–393 CrossRef CAS PubMed
.
- W. Jiang, L. Chen, K. Zhou, L. Li, Q. Fu, Y. Du and R. H. Liu, Appl. Phys. Lett., 2019, 115, 192403 CrossRef
.
- J. Torrejon, M. Riou, F. A. Araujo, S. Tsunegi, G. Khalsa, D. Querlioz, P. Bortolotti, V. Cros, K. Yakushiji, A. Fukushima, H. Kubota, S. Yuasa, M. D. Stiles and J. Grollier, Nature, 2017, 547, 428–431 CrossRef CAS PubMed
.
- Y. Paquot, F. Duport, A. Smerieri, J. Dambre, B. Schrauwen, M. Haelterman and S. Massar, Sci. Rep., 2012, 2, 1–6 Search PubMed
.
- L. Larger, M. C. Soriano, D. Brunner, L. Appeltant, J. M. Gutiérrez, L. Pesquera, C. R. Mirasso and I. Fischer, Opt. Express, 2012, 20, 3241–3249 CrossRef CAS PubMed
.
- L. Larger, A. Baylón-Fuentes, R. Martinenghi, V. S. Udaltsov, Y. K. Chembo and M. Jacquot, Phys. Rev. X, 2017, 7(1), 011015 Search PubMed
.
- L. Appeltant, M. C. Soriano, G. Van der Sande, J. Danckaert, S. Massar, J. Dambre, B. Schrauwen, C. R. Mirasso and I. Fischer, Nat. Commun., 2011, 2, 468–473 CrossRef CAS PubMed
.
- M. L. Alomar, V. Canals, N. Perez-Mora, V. Martínez-Moll and J. L. Rosselló, Comput. Intel. Neurosc., 2016, 2, 3917892 Search PubMed
.
- T. Shi, R. Wang, Z. Wu, Y. Sun, J. An and Q. Liu, Small Struct., 2021, 2, 2000109 CrossRef
.
- Z. Wang, H. Wu, G. W. Burr, C. S. Hwang, K. L. Wang, Q. Xia and J. J. Yang, Nat. Rev. Mater., 2020, 5, 173–195 CrossRef CAS
.
- Q. Xia and J. J. Yang, Nat. Mater., 2019, 18, 309–323 CrossRef CAS PubMed
.
- X. Zhang, J. Lu, Z. Wang, R. Wang, J. Wei, T. Shi, C. Dou, Z. Wu, J. Zhu, D. Shang, G. Xing, M. Chan, Q. Liu and M. Liu, Sci. Bull., 2021, 66, 1624–1633 CrossRef
.
- X. Zhang, Y. Zhuo, Q. Luo, Z. Wu, R. Midya, Z. Wang, W. Song, R. Wang, N. K. Upadhyay, Y. Fang, F. Kiani, M. Rao, Y. Yang, Q. Xia, Q. Liu, M. Liu and J. J. Yang, Nat. Commun., 2020, 11, 51 CrossRef CAS PubMed
.
- L. F. Abbott and W. G. Regehr, Nature, 2004, 431, 796–803 CrossRef CAS PubMed
.
- D. B. Strukov, G. S. Snider, D. R. Stewart and R. S. Williams, Nature, 2008, 453, 80–83 CrossRef CAS PubMed
.
- C. Yakopcic, T. M. Taha, G. Subramanyam, R. E. Pino and S. Rogers, IEEE Electron Device Lett., 2011, 32, 1436–1438 Search PubMed
.
- D. Prychynenko, M. Sitte, K. Litzius, B. Krüger, G. Bourianoff, M. Kläui, J. Sinova and K. Everschor-Sitte, Phys. Rev. Appl., 2018, 9(1), 014034 CrossRef CAS
.
- T. Ohno, T. Hasegawa, T. Tsuruoka, K. Terabe, J. K. Gimzewski and M. Aono, Nat. Mater., 2011, 10, 591–595 CrossRef CAS PubMed
.
- S. H. Jo, T. Chang, I. Ebong, B. B. Bhadviya, P. Mazumder and W. Lu, Nano Lett., 2010, 10, 1297–1301 CrossRef CAS PubMed
.
- T. Chang, S.-H. Jo and W. Lu, ACS Nano, 2011, 5, 7669–7676 CrossRef CAS PubMed
.
- T. Chang, S.-H. Jo, K.-H. Kim, P. Sheridan, S. Gaba and W. Lu, Appl. Phys. A: Mater. Sci. Process., 2011, 102, 857–863 CrossRef CAS
.
- J. Moon, W. Ma, J. H. Shin, F. Cai, C. Du, S. H. Lee and W. D. Lu, Nat. Electron., 2019, 2, 480–487 CrossRef
.
- X. Zhu, Q. Wang and W. D. Lu, Nat. Commun., 2020, 11, 2439 CrossRef CAS PubMed
.
- Y. Zhong, J. Tang, X. Li, B. Gao, H. Qian and H. Wu, Nat. Commun., 2021, 12, 408 CrossRef CAS PubMed
.
- H. An, M. S. Al-Mamun, M. K. Orlowski, L. Liu and Y. Yi, IEEE T. Comput. Aid. D., 2021, 40, 574–583 Search PubMed
.
- J. H. Yoon, Z. Wang, K. M. Kim, H. Wu, V. Ravichandran, Q. Xia, C. S. Hwang and J. J. Yang, Nat. Commun., 2018, 9, 1–9 CrossRef PubMed
.
- Y. Sun, C. Song, S. Yin, L. Qiao, Q. Wan, R. Wang, F. Zeng and F. Pan, Adv. Electron. Mater., 2020, 6, 2000695 CrossRef CAS
.
- H. Jiang, D. Belkin, S. E. Savel'ev, S. Lin, Z. Wang, Y. Li, S. Joshi, R. Midya, C. Li and M. Rao, Nat. Commun., 2017, 8, 1–9 CrossRef CAS PubMed
.
- E. Wlaźlak, P. Zawal and K. Szaciłowski, ACS Appl. Electron. Mater., 2020, 2, 329–338 CrossRef
.
- L. Sun, Z. Wang, J. Jiang, Y. Kim, B. Joo, S. Zheng, S. Lee, W. J. Yu, B.-S. Kong and H. Yang, Sci. Adv., 2021, 7, eabg1455 CrossRef CAS PubMed
.
- G. Bourianoff, D. Pinna, M. Sitte and K. Everschor-Sitte, AIP Adv., 2018, 8, 055602 CrossRef
.
- A. N. Bogdanov and D. A. Yablonskii, Zh. Eksp. Teor. Fiz., 1989, 95, 178 Search PubMed
.
- J. Sampaio, V. Cros, S. Rohart, A. Thiaville and A. Fert, Nat. Nanotechnol., 2013, 8, 839–844 CrossRef CAS PubMed
.
- R. Liu, W. Lim and S. Urazhdin, Phys. Rev. Lett., 2015, 114, 137201 CrossRef CAS PubMed
.
- W. Jiang, P. Upadhyaya, W. Zhang, G. Yu, M. B. Jungfleisch, F. Y. Fradin, J. E. Pearson, Y. Tserkovnyak, K. L. Wang and O. Heinonen, Science, 2015, 349, 283–286 CrossRef CAS PubMed
.
- L. Liu, O. Lee, T. Gudmundsen, D. Ralph and R. Buhrman, Phys. Rev. Lett., 2012, 109, 096602 CrossRef PubMed
.
- S. Tsunegi, T. Taniguchi, K. Nakajima, S. Miwa, K. Yakushiji, A. Fukushima, S. Yuasa and H. Kubota, Appl. Phys. Lett., 2019, 114, 164101 CrossRef
.
- T. Kanao, H. Suto, K. Mizushima, H. Goto, T. Tanamoto and T. Nagasawa, Phys. Rev. Appl., 2019, 12, 024052 CrossRef CAS
.
- M. Riou, J. Torrejon, B. Garitaine, F. A. Araujo, P. Bortolotti, V. Cros, S. Tsunegi, K. Yakushiji, A. Fukushima and H. Kubota, Phys. Rev. Appl., 2019, 12, 024049 CrossRef CAS PubMed
.
- S. Kaka, M. R. Pufall, W. H. Rippard, T. J. Silva, S. E. Russek and J. A. Katine, Nature, 2005, 437, 389–392 CrossRef CAS PubMed
.
- J. Cao, C. Zhou, G. Su, X. Zhang, T. Zhou, Z. Zhou and Y. Yang, Adv. Mater., 2019, 31, 1900042 CrossRef PubMed
.
- J. Cao, Z. Zhou, Q. Song, K. Chen, G. Su, T. Zhou, Z. Zheng, C. Lu and X. Zhang, ACS Nano, 2020, 14, 7055–7065 CrossRef CAS PubMed
.
- M. Wang, Y. Luo, T. Wang, C. Wan, L. Pan, S. Pan, K. He, A. Neo and X. Chen, Adv. Mater., 2021, 33, 2003014 CrossRef CAS PubMed
.
- M. Wang, W. Wang, W. R. Leow, C. Wan, G. Chen, Y. Zeng, J. Yu, Y. Liu, P. Cai, H. Wang, D. Ielmini and X. Chen, Adv. Mater., 2018, 30, 1802516 CrossRef PubMed
.
- J. Cao, C. Lu, J. Zhuang, M. Liu, X. Zhang, Y. Yu and Q. Tao, Angew. Chem., 2017, 129, 8921–8926 CrossRef
.
- J. Cao and X. Zhang, J. Appl. Phys., 2020, 128, 220901 CrossRef CAS
.
- M. Wang, Z. Yan, T. Wang, P. Cai, S. Gao, Y. Zeng, C. Wan, H. Wang, L. Pan and J. Yu, Nat. Electron., 2020, 3, 563–570 CrossRef
.
- T. Ohyama, C. M. Schneider-Mizell, R. D. Fetter, J. V. Aleman, R. Franconville, M. Rivera-Alba, B. D. Mensh, K. M. Branson, J. H. Simpson and J. W. Truman, Nature, 2015, 520, 633–639 CrossRef CAS PubMed
.
- M. Ehatisham-Ul-Haq, A. Javed, M. A. Azam, H. M. Malik, A. Irtaza, I. H. Lee and M. T. Mahmood, IEEE Access, 2019, 7, 60736–60751 Search PubMed
.
- C. Gallicchio, A. Micheli and L. Pedrelli, Neurocomputing, 2017, 268, 87–99 CrossRef
.
| This journal is © The Royal Society of Chemistry 2022 |