Open Access Article
Open Access ArticleThe effect of size, shape, coating and functionalization on nuclear relaxation properties in iron oxide core–shell nanoparticles: a brief review of the situation
Paolo
Arosio
 *a,
Francesco
Orsini
*a,
Francesco
Orsini
 a,
Francesca
Brero
a,
Francesca
Brero
 b,
Manuel
Mariani
b,
Claudia
Innocenti
b,
Manuel
Mariani
b,
Claudia
Innocenti
 cd,
Claudio
Sangregorio
cd,
Claudio
Sangregorio
 cd and
Alessandro
Lascialfari
cd and
Alessandro
Lascialfari
 b
b
aDipartimento di Fisica, INFN and INSTM RU, Università degli Studi di Milano, 20133 Milano, Italy. E-mail: paolo.arosio@unimi.it
bDipartimento di Fisica, INFN and INSTM RU, Università degli Studi di Pavia, 27100 Pavia, Italy
cDipartimento di Chimica, Università di Firenze and INSTM, 50019 Sesto Fiorentino (FI), Italy
dICCOM-CNR, 50019 Sesto Fiorentino (FI), Italy
First published on 20th February 2023
Abstract
In this perspective article, we present a short selection of some of the most significant case studies on magnetic nanoparticles for potential applications in nanomedicine, mainly magnetic resonance. For almost 10 years, our research activity focused on the comprehension of the physical mechanisms on the basis of the nuclear relaxation of magnetic nanoparticles in the presence of magnetic fields; taking advantage of the insights gathered over this time span, we report on the dependence of the relaxation behaviour on the chemico-physical properties of magnetic nanoparticles and discuss them in full detail. In particular, a critical review is carried out on the correlations between their efficiency as contrast agents in magnetic resonance imaging and the magnetic core of magnetic nanoparticles (mainly iron oxides), their size and shape, and the coating and solvent used for making them biocompatible and well dispersible in physiological media. Finally, the heuristic model proposed by Roch and coworkers is presented, as it was extensively adopted to describe most of the experimental data sets. The large amount of data analyzed allowed us to highlight both the advantages and limitations of the model.
1. Introduction
In the last few decades, the interest of several multidisciplinary research groups has been focused on magnetic nanoparticles (MNPs) for the unique properties arising from their size scale. Among the various areas in which they are employed, MNPs have been found to be promising systems for several biomedical applications.1–4 Besides their traditional use as contrast agents in magnetic resonance imaging (MRI)5–11 and in other multimodal techniques,12–18 their implementation as therapeutic agents in magnetic fluid hyperthermia (MFH),19–24 as nanovectors for local drug delivery,6,25–30 and in cell separation and biosensing applications31–36 has been extensively studied.MNPs proposed for biomedical use typically consist of a magnetic core of transition metal oxides (iron, cobalt, nickel, manganese, etc.) coated with a shell of organic moieties like polymers, sugars, and acids, and are dispersed in water or physiological media. For biomedical applications, engineering of the surface appears to be a crucial step in order to obtain colloidal stability, biocompatibility and biodegradability4,22,27,28,37,38 as well as to mitigate their nonspecific uptake by the reticuloendothelial system.39 Thanks to the “intrinsic” biocompatibility of iron, the most widely investigated MNPs are composed of a magnetite (Fe3O4) or maghemite (γ-Fe2O3) core, i.e. ferrimagnetic materials that behave as a single domain at the nanoscale (below about 150 nm), with superparamagnetic behaviour and consequently zero remanent magnetization due to thermal fluctuation. Magnetite and/or maghemite MNPs are preferred over other iron oxides for their high magnetic moment and their strongly reduced possibility to agglomerate once the applied magnetic field is removed.
For medical applications it is also fundamental to focus on and study the possible adverse effects of nanoparticles on human health. The charge and surface coating of iron oxide MNPs definitely influence their interaction with the human body.40 In the past, it was demonstrated that bare and coated (with –NH2 and –COOH) small iron oxide MNPs induced different responses depending on the specific cell lines of the brain, heart and kidneys.41 On the other hand, also the routinely used coatings, such as dextran, polyethylene oxide, citric acid, etc., must be tested accurately for every new MNP proposed, to ensure that no toxic moieties overcome the coating layer. Also nanoparticles coated with polyethylene glycol (PEG), that is known to reduce the immunological response, could be more toxic than the same MNPs covered with other coatings.42 Different kinds of toxicities should also be taken into account. Recently, we studied the effect of iron oxide MNPs coated with meso-2,3-dimercaptosuccinic acid on the cell proliferation of pancreatic cancer cells showing how the commonly used Trypan Blue assay reveals a poor toxicity of MNPs, while the clonogenic survival studies quantified a toxicity of around 50–60%.43
The above quoted papers are examples of toxicology studies on iron oxide-based MNPs that show how the lack of knowledge about the mechanisms involved in their possible toxicity implies a big work of specific characterization whenever a new product is proposed for MNP implementation in nanomedicine.
Although a considerable number of different MNPs have been developed for biomedical applications, a full understanding of the physical mechanisms that occur in the presence of biological media and their relationship with the characteristics of the MNPs – such as the core composition, size, shape, coating, dispersant, and functionalization – has not been achieved yet.
To date, gadolinium-based molecules are the most common contrast agents used for MRI. The main reasons are: (i) the possible use of extravascular44,45 and intravascular gadolinium chelates,46 (ii) the higher accuracy of Gd-based-enhanced MR angiography compared with that of conventional contrast angiography, and (iii) the ability to cross the blood–brain barrier.
As concerns the MNPs, the complex parameters influencing contrast enhancement make their development as non-specific CAs unsuitable. Nevertheless, their unique features, related for instance to the surface functionalization, may address the research efforts toward the realization of target-specific CAs.
Superparamagnetic iron oxide MNPs could be used as MRI contrast agents (CAs), as already done in the past for some approved materials (e.g. Endorem®) and later withdrawn from the market for commercial reasons, because they increase the nuclear relaxation rates (mainly the transverse one47,48) of the 1H nuclei contained in the human body. The nuclear relaxivities are defined as
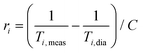 | (1) |
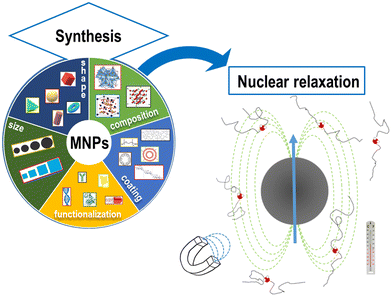
The physical mechanisms involved in the change of nuclear relaxation rates induced by MNPs are the subject of many current research studies aiming at developing new models to direct the design of optimal MNPs.31,49–53 The spin dynamics and the MNP nuclear relaxation behavior critically depend on the intrinsic properties of the MNPs (size, core type, etc.) as well as on the intensity of the external applied magnetic field, the temperature of application and the solvent used to disperse MNPs, as reported in Fig. 1.
In the case of functionalized MNPs, the coating plays a crucial role. The ideal one should consist of organic compounds which would be able to both affect the water molecule diffusion, causing a variation of nuclear relaxivity, and allow fast exchange to allocate the maximum number of water molecules near CAs. Nowadays, there is an extensive use of PEG chains which increase transverse relaxivity, due to the slowing down of the diffusion, while hydrophobic polymers decrease r2 values.54
Moreover, other different functionalizations can affect the correlation times (mainly the exchange of protons between the particle surface and bulk water, and the translation, diffusion, and rotation of free water molecules with respect to the MNPs) which then lead to nuclear relaxation.
For single domain MNPs, where all the atoms coherently respond to the external magnetic field,55–57 a magnetic moment, given by the sum of the spins inside the particle (as the orbital part is generally quenched for 3d metals), is associated with the particle. A uniaxial magnetic anisotropy energy, characterized by two minima,4,58,59 is invoked to model the magnetization reversal, the typical time scale of which is the Néel relaxation time (τN). Other characteristic correlation times are the Brownian time (τB) and the diffusion time (τD), both related to the motion of MNPs, and, wherever present, the so-called chemical exchange time (τex), related to the exchange process between a water molecule coordinated to the MNP surface and a water molecule of the medium.
In this perspective article, we present the results obtained by studying a quite large number of superparamagnetic MNPs which differ in the core size, core composition, shape, surface coating material and solvents used to obtain colloidal solutions. This roundup of studies offers the opportunity: (1) to discuss the obtained experimental evidence, (2) to test the efficacy of the Roch heuristic model on many different materials for describing the relaxation of superparamagnetic MNPs, and (3) to present some possible future perspectives in this research field.
It should be noted that the well-known model developed by Roch et al.60 was commonly used to fit the NMR dispersion (NMR-D) profiles. Indeed, an evaluation of important parameters such as the relaxation times, the distance of minimum approach of water molecules to MNPs, rd, the saturation magnetization, Ms, and the magnetic anisotropy energy barrier, EA, can be obtained by fitting the longitudinal NMR dispersion curves.
After the first section dedicated to the synthesis and characterization methods, we present the theoretical background useful to describe the influence of the magnetic core intrinsic properties (composition, size and shape) on the relaxation properties. In the next section, we discuss the impact of changing the solvent of the colloidal solutions and the role of the surface coating and its functionalization. In the last section, some general comments on the whole set of results obtained in these 10 years of research and some perspectives are proposed.
2. Synthetic procedures and characterization methods
For a detailed description of the synthetic procedures and experimental characterization of the different MNPs, the readers are suggested to refer to the corresponding articles. In this section, only the most relevant hints on the synthesis methods and the principal chemico-physical characteristics are reported.In ref. 61 four series of ferrite-based MNPs with a core size between 4 and 20 nm were obtained by the thermal decomposition method starting from different metal–organic precursors. The studied MNPs were: rhamnose-coated magnetite MNPs (S-Mag), oleate coated magnetite particles (P-Mag), oleic acid-coated manganese ferrite nanocrystals (MnFe) and non-stoichiometric oleic acid-coated cobalt ferrite MNPs (CoFe). In the case of the two series of magnetite MNPs, once properly coated, the samples were dispersed in water solutions.
In ref. 62, γ-Fe2O3 MNPs coated with oleic acid were again synthesized by thermal decomposition and transferred in water after the substitution of oleic acid with polyacrylic acid. Three samples of MNPs of magnetic core sizes of 10, 14 and 19 nm were studied.
A systematic investigation of CoxZnyFe3−(x+y)O4 MNPs synthesized by thermal decomposition with, on average, 8–9 nm size was reported in ref. 63, where the amount of cobalt was kept constant at ca. x = 0.6, while the Zn amount was varied in the range 0 < y < 0.4.
According to surfactant mediated colloidal routes in high boiling organic solvents under a nitrogen atmosphere, iron oxide based MNPs were prepared in ref. 64 with different core sizes, morphologies and dispersing media. In details, three core sizes (mean diameter d = 3, 8 and 17 nm) of spherical samples dispersed in an organic non-polar solvent (hexane) were prepared. In addition, an 8 nm spherical sample suspended in water (without removing the ligand directly attached at the surface of the inorganic core) and a cubic shaped sample dispersed in hexane with the same volume as the 8 nm spherical MNP were also prepared.
Aqueous dispersions of two series of maghemite MNPs of different mean diameters (d = 17 and 8 nm) coated with four different types of biocompatible negative polyelectrolytes, synthesized by adding each polyelectrolyte to an acidic solution of MNPs and, after dialysis against water, alkalinizing the solutions with hydroxide ammonium, were studied in ref. 65.
Finally, functionalized coating MNPs were investigated in ref. 66 and 67; ref. 66 regarded magnetite MNPs coated with random multiblock poly(ester-ether-urethane) copolymers (PEEU) of PCL and PEG decorated with folate and loaded with paclitaxel (PTX), designed to target the human breast MDA-MB-231 tumor. Ref. 67 was focused on the use of synthetic polyamide mimics of natural DNA and RNA, the peptide nucleic acid (PNA) oligomers, for the functionalization of iron oxide nanoparticles with a magnetic core dimension of 17 nm, in order to obtain a water soluble hybrid nanomaterial.
The chemical–physical characterization of all the studied MNPs was based on elemental analysis, X-ray diffraction, transmission electron microscopy, dynamic light scattering and, where possible, atomic force microscopy.
For the measurements of magnetic properties, DC magnetization and AC magnetic susceptibility were recorded on dry powder samples or concentrated colloidal solutions using superconducting quantum interference device (SQUID) magnetometers. The hysteresis curves were collected as a function of magnetic field (up to ±5 T) at different temperatures (300 K and 5 K). Zero-field-cooled (ZFC) and field-cooled (FC) magnetization curves were recorded as a function of temperature (5–300 K) at different static magnetic fields (ranging from 0.005 to 0.3 T) after cooling the samples in the absence (ZFC) or presence (FC) of the measuring field. AC magnetic susceptibility data were collected as a function of temperature (5–300 K) in the frequency range 1–1000 Hz.
The local spin dynamics and the MRI contrast efficiency were assessed by means of 1H nuclear magnetic resonance (NMR) relaxometric characterization. The NMR-dispersion profiles were collected at room temperature by measuring the longitudinal (T1) and the transverse (T2) nuclear relaxation varying the Larmor frequency of the investigated nuclei (2πνL = γB0, where γ = 2.67513 × 108 rad s−1 T−1 is the gyromagnetic factor of 1H) from 10 kHz up to 60 MHz and only for one case up to 120 MHz.56 For low-frequency relaxation measurements (from 0.01 MHz to 5.0 MHz), the fast-field-cycling technique was performed using a Smartracer Stelar NMR relaxometer. Higher-frequency (νL > 5.0 MHz) relaxation measurements were performed using Stelar Spinmaster and Apollo – Tecmag Fourier transform nuclear magnetic resonance (FT-NMR) spectrometers. For νL < 5.0 MHz, pre-polarized saturation recovery (for T1) and spin-echo (for T2) sequences were adopted. For frequencies νL > 5.0 MHz, non-pre-polarized saturation recovery (SR) and Carr Purcell Meiboom Gill (CPMG) pulse sequences were used for T1 and T2 measurements, respectively.
3. Results
3.1 Theoretical background
In order to understand the nuclear magnetic relaxation behaviour of superparamagnetic MNPs and therefore predict their efficiency as CAs in MRI, many models have been proposed in the literature.58,60,68–70 Many of these models assume that the dipolar magnetic field of the superparamagnetic MNPs produces local magnetic inhomogeneity which in turn modifies the nuclear relaxation processes of the dispersant protons with respect to the ones in the pure solvent. Essentially, the nuclear relaxation depends on the fluctuating hyperfine interaction between the high magnetic moment of the superparamagnetic MNPs and the nuclear magnetic moment of the hydrogen nuclei of the solvent. Indeed each proton experiences magnetic fluctuations because of its free diffusion in the magnetic inhomogeneity and the relaxation of the magnetization of superparamagnetic MNP due to the Néel and Brownian processes.The importance of the role played by the superparamagnetic MNP size and composition can be highlighted by considering the simplest case of uniaxial anisotropy, where the anisotropy energy per nanoparticle, EA, is correlated to its volume, V, and its anisotropy constant, K, which depends on the MNP composition, according to:
EA = K·V·sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (2) |
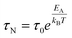 | (3) |
In eqn (3) the Néel relaxation time depends exponentially on the ratio between anisotropy (EA) and thermal energy (kBT) and, linearly, by a prefactor, τ0, that is of the order of 10−9 s for non-interacting MNPs.
When MNPs interact with each other, eqn (3) must be modified to correctly describe the experimental results. According to the Vogel–Fulcher model,72 a phenomenological parameter, T0, whose value is proportional to the inter-particle interaction, is introduced and eqn (3) becomes
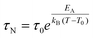 | (4) |
For biomedical applications, MNPs are normally dispersed in liquid, where they can randomly rotate and collide with solvent molecules (Brownian motion), thus inducing magnetization relaxation with the characteristic Brown relaxation time:
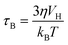 | (5) |
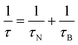 | (6) |
In order to deeply investigate the physical mechanisms on the basis of the nuclear relaxation of superparamagnetic MNPs, 1H-NMRD profiles, i.e. the nuclear relaxivities r1 and r2vs. the frequency for constant T, must be collected in the widest possible frequency range (or, equivalently, the widest applied magnetic field range), possibly including the frequencies associated with the fields used in clinical practice.
As already stated in the Introduction, the analysis of the 1H-NMRD profiles allows the estimation of some fundamental physical quantities of the MNPs, such as the Néel correlation time τN, by NMR, the distance of minimum approach rd of water molecules to MNPs and the magnetic anisotropy. To this aim the experimental 1H-NMRD profiles, obtained measuring the MNP samples here reported, were interpreted using the heuristic model of Roch et al.,60 where the expressions for the relaxivities, r1 (eqn (7)) and r2 (eqn (8)), employed in our work to perform the fitting procedure, are obtained by a linear combination of two contributions describing the high and low magnetic anisotropy cases, respectively:
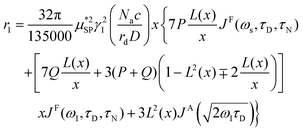 | (7) |
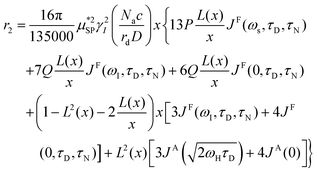 | (8) |
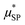 is the effective magnetic moment locally felt by the protons, γI is the proton gyromagnetic ratio, Na is Avogadro's number, c is the molar concentration of the magnetic part of the nanoparticles, rd is the minimum approach distance between protons and superparamagnetic MNPs, D is the self-diffusion coefficient of the medium, L(x) is the Langevin's function (where
is the effective magnetic moment locally felt by the protons, γI is the proton gyromagnetic ratio, Na is Avogadro's number, c is the molar concentration of the magnetic part of the nanoparticles, rd is the minimum approach distance between protons and superparamagnetic MNPs, D is the self-diffusion coefficient of the medium, L(x) is the Langevin's function (where  ), τD = (rd)2/D is the diffusion time that characterizes the fluctuation of the hyperfine interaction among the nuclear magnetic moments of the solvent 1H nuclei and the magnetic moment of superparamagnetic MNPs, τN is the Néel relaxation time at room temperature, and ωS and ωI are the electron and proton Larmor frequencies, respectively. The parameters P and Q are related to the degree of magnetic anisotropy of the system, being the weight of the spectral density functions JA and JF, respectively (P = 0 and Q = 1 for highly anisotropic systems, i.e. EA → ∞, while P = 1 and Q = 0 for low anisotropic systems, i.e. EA → 0, and P + Q ≤ 1). Consequently, for materials with increasing magnetic anisotropy energy and/or upon increasing the size of the magnetic cores, Q would progressively increase toward 1.
), τD = (rd)2/D is the diffusion time that characterizes the fluctuation of the hyperfine interaction among the nuclear magnetic moments of the solvent 1H nuclei and the magnetic moment of superparamagnetic MNPs, τN is the Néel relaxation time at room temperature, and ωS and ωI are the electron and proton Larmor frequencies, respectively. The parameters P and Q are related to the degree of magnetic anisotropy of the system, being the weight of the spectral density functions JA and JF, respectively (P = 0 and Q = 1 for highly anisotropic systems, i.e. EA → ∞, while P = 1 and Q = 0 for low anisotropic systems, i.e. EA → 0, and P + Q ≤ 1). Consequently, for materials with increasing magnetic anisotropy energy and/or upon increasing the size of the magnetic cores, Q would progressively increase toward 1.
In order to reduce the number of free parameters of the model, wherever possible, some quantities, independently evaluated with other experimental techniques, were used. For instance, the effective magnetic moment  can be estimated by the saturation magnetization value, Ms, obtained through magnetometry techniques, and by the average volume of the particles. In addition, TEM and AFM data can be used to establish reasonable constraints for the distance of minimum approach, rd, as it is expected to vary between the core diameter (TEM estimate) and the whole size of superparamagnetic MNPs, which includes the coating layer (AFM estimate).
can be estimated by the saturation magnetization value, Ms, obtained through magnetometry techniques, and by the average volume of the particles. In addition, TEM and AFM data can be used to establish reasonable constraints for the distance of minimum approach, rd, as it is expected to vary between the core diameter (TEM estimate) and the whole size of superparamagnetic MNPs, which includes the coating layer (AFM estimate).
3.2 The role of the magnetic core
The first example of the modus operandi explained at the end of the previous paragraph was proposed in ref. 61, where longitudinal relaxivity r1 curves were acquired experimentally on four different sets of MNPs dispersed in toluene or ultrapure water. The use of the fitting model allowed us to investigate the dependence of Néel and Curie contributions to nuclear relaxation on the magnetic core diameter and ion species and consequently the correlated dependence on the magnetic anisotropy energy density. In this study the obtained distances of minimum approach of the solvent molecules to the magnetic centres suggested the impossibility of the solvent to completely penetrate the organic coating. A notable comparison between the Néel relaxation time for all the samples obtained by the fitting of NMRD profiles and by the AC susceptibility data was performed (see Table 1). All the MNPs were superparamagnetic at room temperature and the estimation of τN from AC data using the phenomenological Vogel–Fulcher eqn (4), reported in Table 1, showed good agreement with the corresponding NMR data. This correspondence of values obtained from a sample-averaged technique, namely AC susceptibility, and a strongly local technique, namely NMR, is worth noting. The above-mentioned dependence of the fitting parameters P and Q on magnetic anisotropy and particle size is largely confirmed by the trend of the P/Q ratio as a function of the size and composition of the magnetic core, as can be seen in Table 1.| Sample | τ N (s rad−1) AC | τ N (s rad−1) NMR | d (nm) TEM | P/Q |
|---|---|---|---|---|
| From left to right: Estimation of the Néel relaxation time by AC and NMR data, nanoparticle size by TEM measurements and P/Q ratios. Reported AC τN values are estimated by fitting the AC susceptibility data to the Vogel–Fulcher eqn (4). NMR τN and P/Q are obtained by the analysis of 1H-NMRD profiles employing Roch's model. The studied nanoparticles were: rhamnose-coated magnetite NPs (S-Mag), oleate coated magnetite particles (P-Mag), oleic acid-coated manganese ferrite nanocrystals (MnFe) and non-stoichiometric oleic acid-coated cobalt ferrite (CoxFe3−xO4) NPs (CoFe). Label T denotes samples dispersed in toluene and label W denotes samples dispersed in water solutions. | ||||
| S-Mag/W-1 | 5.34 ± 1.00 × 10−9 | 9.73 ± 5.51 × 10−10 | 4.1 ± 0.6 | 0.45 ± 0.19 |
| S-Mag/W-2 | 2.80 ± 0.67 × 10−10 | 2.82 ± 1.66 × 10−9 | 6.7 ± 0.8 | 0.00 |
| S-Mag/W-3 | 4.40 ± 0.52 × 10−7 | 9.58 ± 2.80 × 10−8 | 18.2 ± 1.1 | 0.06 ± 0.02 |
| P-Mag/W-1 | — | 2.71 ± 2.94 × 10−9 | 5.5 ± 0.6 | 0.46 ± 0.29 |
| P-Mag/W-2 | — | 2.17 ± 1.81 × 10−9 | 8.0 ± 0.8 | 0.00 ± 0.11 |
| P-Mag/W-3 | 1.19 ± 0.22 × 10−8 | 3.36 ± 1.36 × 10−9 | 12.0 ± 0.7 | 0.06 ± 0.11 |
| P-Mag/T-1 | 3.44 ± 0.45 × 10−14 | 1.39 ± 1.12 × 10−9 | 5.5 ± 0.6 | 0.32 ± 0.26 |
| P-Mag/T-2 | 3.78 ± 0.12 × 10−9 | 3.30 ± 1.68 × 10−9 | 8.0 ± 0.8 | 0.06 ± 0.06 |
| P-Mag/T-3 | 4.29 ± 0.52 × 10−9 | 2.02 ± 2.07 × 10−9 | 12.0 ± 0.7 | 0.00 |
| MnFe/T-1 | 1.34 ± 0.10 × 10−12 | 3.33 ± 1.01 × 10−10 | 3.0 ± 0.2 | 1.06 ± 0.31 |
| MnFe/T-2 | — | 7.13 ± 3.81 × 10−10 | 4.8 ± 0.1 | 0.49 ± 0.12 |
| MnFe/T-3 | 1.36 ± 0.17 × 10−9 | 1.63 ± 3.03 × 10−10 | 6.0 ± 0.2 | 0.80 ± 0.30 |
| CoFe/T-1 | — | 2.89 ± 2.33 × 10−7 | 8.6 ± 1.1 | 0.08 ± 0.09 |
| CoFe/T-2 | 4.32 ± 0.31 × 10−5 | 5.21 ± 3.38 × 10−6 | 8.6 ± 1.1 | 0.06 ± 0.13 |
| CoFe/T-3 | 3.11 ± 0.31 × 10−9 | 6.24 ± 2.54 × 10−9 | 6.0 ± 1.4 | 0.05 ± 0.09 |
| CoFe/T-4 | 3.31 ± 0.53 × 10−9 | 2.05 ± 1.85 × 10−9 | 5.0 ± 1.2 | 0.05 ± 0.15 |
In ref. 62 we studied maghemite superparamagnetic MNPs coated with polyacrylic acid (PAA) and with different core sizes by means of longitudinal nuclear r1 profiles and transverse nuclear r2 profiles. This was one of the few cases53,64,65,67,73 where it was possible to measure r2 values at ν less than a few MHz, paying attention to the experimental parameters of the measurements, given the peculiarities of fast field cycling (FFC) technology necessary to reach low frequencies: the instability of the acquisition field and the need for refocusing pulses during the FFC relaxation period. MNPs studied in ref. 62 were specifically designed with the same PAA coating and three different sizes of the magnetic core (d = 10, 14 and 19 nm) in order to tailor their physical properties. The experimental longitudinal relaxivity profiles (see Fig. 2) for MNPs of 10 and 14 nm showed a flattening of r1 at low ν and a maximum at ν of a few MHz with a subsequent drop for ν ≥ 10–20 MHz. The sample with a 19 nm magnetic core showed a strongly enhanced r1 and this relatively high core size causes the flattening of the maximum at intermediate frequencies. On the other hand, the r1 profile of 19 nm MNPs showed a higher contrast efficiency compared to the other two samples, which behaved substantially in the same way.
 | ||
| Fig. 2 Longitudinal r1 (upper) and transverse r2 (bottom) NMRD profiles of the MNPs in ref. 54 collected at room temperature in the frequency range 0.01 < ν < 60 MHz and the best-fit curves obtained by applying Roch's model (solid lines). r1 and r2 profiles of the (dismissed) commercial compound Endorem® are reported as green symbols in all graphs.62 Reprinted with permission from ref. [“Tailoring the magnetic core of organic-coated iron oxides nanoparticles to influence their contrast efficiency for magnetic resonance imaging”, M. Basini, A. Guerrini, M. Cobianchi, F. Orsini, D. Bettega, M. Avolio, C. Innocenti, C. Sangregorio, A. Lascialfari and P. Arosio, J. Alloys Compd., 2019, 770, 58, doi: https://doi.org/10.1016/j.jallcom.2018.08.120]. Copyright 2019, Elsevier. | ||
The fitting procedure by the Roch's model well reproduced r1 experimental curves providing τN in accordance with the core size: upon increasing the particle size, the spin dynamics slowed down until spin freezing at low frequencies for 19 nm MNPs (NP_19). At the same time, the extrapolated values of P and Q parameters were perfectly correlated to the obtained τN; as the core size increases from 10 nm to 19 nm, Q increases indicating a progressively higher magnetic anisotropy barrier of the system. Finally, the rd values evaluated by NMR fitting were compared with TEM and AFM data and suggested an impermeability of the coating. The measured r2 profiles were compared with the predicted r2 NMRD profiles calculated with the parameters obtained from the r1 fitting. In Fig. 2, it is evident that the theoretical curve predicted for r2 disagreed with the experimental data all over the frequency range measured.
The same conclusion was attained in ref. 64 where the effect of size, shape and dispersant on the dynamical magnetic properties of colloidal suspensions of MNPs was investigated. In this study, spherical nanoparticles with an average diameter of 3.5, 8.5 and 17.5 nm dispersed in hexane were measured with 1H-NMR relaxometry and compared (see Fig. 3(a)).
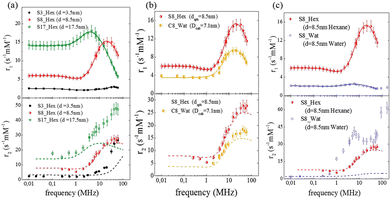 | ||
| Fig. 3 Longitudinal (r1) and transverse (r2) relaxivities (NMRD profiles) at room temperature measured on samples with different sizes (a), shapes (b), and dispersants (c) in ref. 64. The solid lines represent the best-fit curves of r1 obtained from Roch's model and the dashed lines are the r2 curves calculated using Roch's model and the best fit parameters obtained for r1. Reproduced from ref. [“Local spin dynamics of iron oxide magnetic nanoparticles dispersed in different solvents with variable size and shape: A 1H NMR study”, M. Basini, T. Orlando, P. Arosio, M. F. Casula, D. Espa, S. Murgia, C. Sangregorio, C. Innocenti, A. Lascialfari, J. Chem. Phys., 2017, (146), 034703; doi: https://doi.org/10.1063/1.4973979], with the permission of AIP Publishing. | ||
Also, in this study, the r1 NMRD profiles showed the typical behaviour of superparamagnetic MNPs and the NMR Néel relaxation time τN at room temperature (τN = 10−10–10−7 s), obtained using the Roch's model, confirming the results of DC and AC magnetic measurements. Again the trend followed by P and Q parameters was well correlated to the anisotropy energy barrier estimated by magnetic measurements, and to the slowing down of τN by increasing the size of superparamagnetic MNPs, except for the 3.5 nm sample that exhibited quite long times for both NMR and magnetic measurement techniques. Unfortunately, also in ref. 64 the r2 curves calculated using r1 fitting parameters did not reproduce the experimental profiles especially in the high field region. The results of the transverse nuclear relaxivity of the superparamagnetic MNPs were discussed using the universal scaling law proposed by Vuong et al.48 for nanoparticles in the motional averaging regime (MAR),74 where the Redfield condition ΔωτD < 1 is fulfilled (τD being the diffusion time and Δω being the angular frequency shift experienced by a proton at the equator of the particle). Vuong et al. showed that for an external magnetic field >1 T, r2 depends on the particle hydrodynamic diameter according to
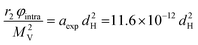 | (9) |
The influence of the chemical composition of the magnetic core in MNPs on the relaxometric properties was studied in ref. 63, where CoxZnyFe3−(x+y)O4 nanoparticles were investigated. In this study, the Co content was kept constant (x = 0.6), while a gradual substitution of iron with Zn2+ (0 ≤ y ≤ 0.4) allowed the study of the effect of zinc inclusion on the magnetic properties of MNPs. The longitudinal nuclear relaxivity profiles confirmed a clear decrease of the magnetic anisotropy with increasing Zn content, as pointed out by the magnetic measurements. In the absence of Zn, r1 showed the typical shape of a high magnetic anisotropy system, namely a plateau at low frequencies followed by a drop for ν ≳ few MHz, whereas r1 for particle with the highest content of Zn (y = 0.4) presented a maximum at intermediate frequencies (at ν ∼ 1.5 MHz), preceded by a plateau at low frequencies and followed by a decrease at high frequencies, denoting a lower degree of magnetic anisotropy (see Fig. 4). The fitting of r1 NMRD profiles with the Roch's model allowed again the estimation of the values of τN, rd and Ms. Here below the ranges of values found in ref. 55: 2.4 × 10−8 s < τN < 3.2 × 10−7 s, 5.6 nm < rd < 9.4 nm, and 76 Am2 kg−1 < Ms < 80 Am2 kg−1. Transverse r2 relaxivities were measured only for three magnetic fields, as reported in Fig. 4(b), and showed a marked dependence on the Zn content reaching 4–5 times higher values compared to Endorem® in the case of Zn content y = 0.4.
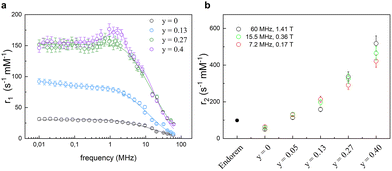 | ||
| Fig. 4 (a) Longitudinal r1 relaxivity profiles and the best-fit curves. (b) Transverse r2 relaxivity values measured at 7.2, 15.5, and 60 MHz as a function of the Zn amount compared with the dismissed commercial compound (Endorem®) (data acquired at 1.41 T) in ref. 63. Reprinted with permission from ref. [“Role of Zn2+ substitution on the magnetic, hyperthermic and relaxometric properties of cobalt ferrite nanoparticles”, M. Albino, E. Fantechi, C. Innocenti, A. López-Ortega, V. Bonanni, G. Campo, F. Pineider, M. Gurioli, P. Arosio, T. Orlando, G. Bertoni, C. de Julián Fernández, A. Lascialfari and C. Sangregorio, J. Phys. Chem. C, 2019, 123, 6148; doi: https://doi.org/10.1021/acs.jpcc.8b10998]. Copyright 2019, ACS Publications. | ||
3.3 The role of the shape
The effect of the shape of MNPs was studied in ref. 64, where the 8.5 nm spherical sample of superparamagnetic MNPs was compared with an analogous cubic-shaped sample with a square edge size of 7.1 nm and a diagonal size of 8.1 nm, in order to have nanoparticles with comparable volume. The longitudinal relaxivity reported in Fig. 3(b) shows lower values for the cubic-shaped sample over the whole frequency range. Both samples present similar superparamagnetic behaviour with small differences: the maximum of r1 of the cubic sample is slightly shifted at a lower frequency (ν = 15–20 MHz) with respect to the maximum of the spherical sample (ν = 20–25 MHz), and the dispersion at a low field is less pronounced.The fitting procedure of the cubic sample r1 NMRD profile provided values of P/Q, τN and rd parameters slightly different from the spherical sample and this discrepancy can be easily justified by considering the results obtained by other techniques (magnetic measurements, TEM, etc.). The r2 theoretical profile of samples obtained using the best-fitting parameters evaluated for the corresponding r1 does not reproduce adequately all the experimental curves, showing larger discrepancies at high fields for both samples and some failures around 1 MHz for the spherical one.
3.4 The influence of solvent
Another factor that can influence the superparamagnetic relaxation is the kind of solvent in which the MNPs are dispersed and the correlated MNP surface engineering necessary to allow their dispersion in water or in physiological solutions, a crucial condition for their potential application in biomedicine. In ref. 61 and 64 we partially investigated the effect of different surface engineering on the spin dynamics. In ref. 61, oleate coated magnetite particles dispersed in toluene (P-Mag/T series) and water (P-Mag/W series) were compared. It was not easy to single out a clear picture of the consequences of using different dispersion solvents, also because the recorded effects are simultaneously related to the coating needed to effectively carry out the dispersion (see the next section). As can be seen in Fig. 5, the r1 – maxima of P-Mag/W-1 and P-Mag/W-2 and the “corresponding” samples P-Mag/T-1 and P-Mag/T-2 were shifted in frequency, while the maximum of P-Mag/W-3 and P-Mag/T-3 was un-shifted. Moreover, r1 values differed slightly for the couples P-Mag/W-1||P-Mag/T-1 and P-Mag/W-3||P-Mag/T-3; in contrast, they decreased passing from P-Mag/T-2 to P-Mag/W-2. At the same time, the P/Q results obtained from the fitting suggested that the contribution from the Curie relaxation mechanism was enhanced from toluene to water. The hypothesis proposed was that the surface coating of P-Mag/W-series, modified using a poly(maleicanhydride) polymer shell intercalated with oleate molecules, produced an effect on the nuclear relaxometric properties by changing the distance of minimum approach of the solvent molecules.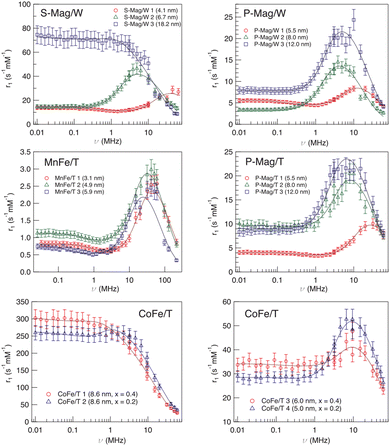 | ||
| Fig. 5 Longitudinal r1 relaxivity profiles at room temperature and the best-fit curves obtained with Roch's model (solid lines) for sample series S-Mag/W, P-Mag/T, P-Mag/W, MnFe/T and CoFe/T in ref. 61. Reproduced with permission from ref. [“NMR-D study of the local spin dynamics and magnetic anisotropy in different nearly monodispersed ferrite nanoparticles”, L. Bordonali, T. Kalaivani, K. P. V. Sabareesh, C. Innocenti, E. Fantechi, C. Sangregorio, M. F. Casula, L. Lartigue, J. Larionova, Y. Guari, M. Corti, P. Arosio and A. Lascialfari, J. Phys.: Condens. Matter, 2013, 25, 066008, doi: https://doi.org/10.1088/0953-8984/25/6/066008] © IOP Publishing. All rights reserved. | ||
In ref. 64 MNPs of 8.5 nm were dispersed in an aqueous based dispersant, adding a ternary system made of monoolein, lauroylcholin, and water to compare the nuclear relaxivity performances with a sample with the same magnetic core dispersed in hexane. The first evidence was a drastic lowering of r1 in the whole frequency range and the shift of the maximum position to lower magnetic fields for the sample dispersed in water in comparison with the one in hexane (see Fig. 3(c)). At the same time, for the water dispersed sample the value of τN obtained by fitting of NMR profiles was one order of magnitude higher than the τN of the sample in hexane, reflecting an enhancement of the magnetic anisotropy energy barrier as seen from AC measurements. In addition, the distance of minimum approach between the protons of the solution and the superparamagnetic MNP centre clearly increased when they were dispersed in water. The influence of the solvent on the nuclear relaxation time T2 became dramatically evident since the transfer into a water-based dispersant increased the r2 values of the superparamagnetic MNPs in all the range of investigated fields, the reproducibility of which had completely failed when the r2 curves calculated with the fitting parameters of r1 are used. A partial explanation of this behaviour could be ascribed to the particle aggregation due to the dispersant effect for the water-based sample, as explained in ref. 64, that prevents the diffusion of solvent near the magnetic centre (T1 effect), but, at the same time, makes nuclear spin–spin hyperfine interactions more efficient (T2 effect).
3.5 The effect of coating
In order to study the effect of coating on the relaxometric properties of MNPs, we recently65 investigated two series of nanoparticles composed of a maghemite core with mean diameters d = 17 and 8 nm coated with four different negative polyelectrolytes. The magnetic measurements indicated that both MNPs can be considered superparamagnetic at room temperature, because, even for the larger sample, the average blocking temperature is lower than 300 K. The experimental longitudinal relaxivity profiles of 17 nm superparamagnetic MNPs showed a constant increase of r1 with lowering the external magnetic fields, without the expected plateau at low fields, while a typical superparamagnetic trend of r1 profiles for the 8 nm samples, i.e. the presence of a maximum of the relaxivities and a slight dispersion at low fields, was found. The transverse relaxivity profiles of the 8 nm samples were similar to the one of the commercial Endorem® both as concerns the values and frequency behaviour, whereas in the case of the 17 nm sample, the r2 curves demonstrated a markedly increased relaxation efficiency. It is worth noting that the 17 nm sample coated with a copolymer of poly(methacrylic acid) (PMAA) with polyethylene glycol (PEG) displayed r2 values smaller than those of all the other samples at high Larmor frequencies. This result can be tentatively justified by a different surface spin disorder and/or particle aggregation effects induced by the PMAA-PEG copolymer. For what concerns the fitting of the 17 nm sample curves, we were not able to apply the Roch model probably because of the quite broad size distribution that didn't comply with the limit of validity of the model (i.e. MNP diameter <20 nm). In contrast, we were able to fit the r1 profiles of the 8 nm superparamagnetic MNPs obtaining the Néel relaxation time values typical of superparamagnetic nanoparticles of this size (3.5 × 10−9 s < τN < 3.9 × 10−9 s) and a distance of minimum approach of 1 ÷ 2 nm greater than the estimated core radius, thus proving the inability of water molecules to diffuse completely inside the coating.3.6 The effect of functionalization
As a further factor that could influence the nuclear relaxation mechanisms, we briefly investigated the effects of MNP functionalization on the relaxivity. In detail, with the purpose of designing a theranostic agent, in ref. 66 a biocompatible nanocarrier was decorated with folate for targeting human breast MDA-MB-231 tumor and loaded with magnetite nanoparticles and the antitumoral drug paclitaxel (PTX). The functionalization effect was particularly evident on the transverse relaxivity. Indeed, the r2 values doubled in the Larmor frequency range investigated (7 < ν < 60 MHz) when the organic carrier + magnetite core was functionalized with folate or with folate plus PTX, reaching r2 values up to 8 times higher with respect to Endorem®. These surprising results were confirmed by in vivo MRI experiments on nude mice which showed how the developed nanocarrier acted as a negative CA with better performances than Endorem® and how it was able to target MDA-MB-321 cells residing in the tumor area for a long time, up to some days.In ref. 67 we exploited the conjugation between peptide nucleic acid (PNA) oligomers and superparamagnetic MNPs in order to improve the PNA solubility and their cell permeability, with these oligomers being interesting for gene therapy applications. As is shown by the 1H-NMR results reported in ref. 67, the MNPs shortened the longitudinal and transverse nuclear relaxation times, enhancing the correlated relaxivities. This effect was less marked in the case of functionalized nanoparticles compared to the un-functionalized ones for r1, while in the case of r2 a lower efficiency at shortening the transverse relaxation time was registered for functionalized MNPs for a Larmor frequency below 0.2 MHz. The differences in relaxivity values, between the MNPs with or without PNA functionalization, could be justified by the increased size of particles once functionalized, as shown by AFM measurements and by the poor solubility of PNA. After MNP functionalization, the water molecules encountered more obstacles to approach the magnetic cores of nanoparticles, thus decreasing the efficacy at shortening the nuclear relaxation times.
4. Discussion
The aforementioned studies ref. 61–67 allowed us to discuss the results according to the microscopic characteristics of each kind of iron-oxide nanoparticle investigated. The strong dependence of nuclear relaxation properties on the size and composition of the magnetic core was confirmed by the experimental NMRD profiles. Indeed, the crystallinity, the magnetic anisotropy and the volume of the superparamagnetic MNPs influence directly their saturation magnetization and some correlation times, e.g. the rotational (τB), electronic relaxation (τN) and diffusion (τD) times. On the other hand, the shape of superparamagnetic MNPs seems to be less effective at perturbing the nuclear relaxation time of protons of the host media, see ref. 64.The influence of the solvent on the relaxometric properties of MNPs deserves a separate discussion. In fact, this effect cannot be separated by the coating procedure implemented in the synthetic protocols and a generalization of the influence of such a synthetic process on the r1 and/or r2 behaviour is still difficult to be evinced. The role of the solvent depends not only on which coating is used to cover the magnetic core but also on the synthetic path used to pass from hydrophobic conditions (normally the MNPs are first synthesized in organic solvents) to the hydrophilic ones (e.g. exchange of organic capping agents with polymers, acids, etc. or using an amphiphilic coating that intercalates with aliphatic domains, or other choices). For such a complex situation, although effects on the relaxation properties of MNPs are thoroughly expected, the possible causes are really difficult to be evinced, as seen in the example reported in ref. 61, where similar systems differing only in size (P-Mag/series) behaved in a different manner.
Another noteworthy aspect is the impact of the type of coating on relaxivity. Indeed, it should be important to understand if the coating is only an inert “spacer” between the magnetic core and the protons of the solvent or it is involved in the nuclear spin dynamics. In this perspective article, we reported our results in ref. 65 showing how different coatings on superparamagnetic MNPs similar in size didn't influence the relaxivity profiles. At the same time, some of us recently demonstrated by means of low-field muon spin relaxation measurements75 on full or hollow core maghemite superparamagnetic MNPs that how it is crucial to study high surface/volume ratio MNPs to unravel the influence of surface spin effects on the spin dynamics. Indeed, since the coating can modify the magnetic order of the surface spins for chemical–physical reasons, we think that it could be important to systematically study small MNPs (at a fixed core size below 4–6 nm) with different coatings using NMR with the purpose to single out their role in nuclear relaxation mechanisms and related spin surface effects.
Finally, for the effect of coating functionalization, as in the case of solvent effects, a large number of cases of MNPs with the same core but different coatings/functionalizations are needed. Once again, the functionalization influences both r1 and r2 and its effect strongly depends on which type of chemical moiety (molecules, oligomers, antigen, antibody, etc. …) is used.
As a last observation, it is worth reminding that the possibility of using theoretical models to interpret the longitudinal relaxivity experimental curves (Roch model in our papers) allowed us to extrapolate important quantitative information on the physical properties of the investigated superparamagnetic MNPs, like the distance of minimum approach of solvent protons to nanoparticles or the Néel relaxation time. In all the studied superparamagnetic MNPs, the r1 experimental data are well fitted by the heuristic theoretical model, and the parameters obtained clarify the nuclear spin mechanisms involved in the spin–lattice relaxation for all the nanoparticles that fulfilled the MAR. On the other hand, if the parameters obtained by the r1 fitting procedure are used also for predicting r2 profiles, the model does not properly describe all the experimental data. This point strongly suggests that physical mechanisms, not included in Roch's model, can contribute to the nuclear spin–spin relaxation. Currently, there is no clear indication on which mechanisms can be invoked to improve the model, with the possible ones being the electronic dipole–dipole interactions between the single MNPs, magnetic anisotropy other than uniaxial, the Brownian spin dynamics, the contribution from the water chemical exchange (if any) and the surface spin dynamics.
In order to summarize the effect of different intrinsic parameters of MNPs on their relaxometric properties, we reported in Table 2 a level of influence of each parameter on relaxivities that could be used as a recommendation guide by researchers.
| Intrinsic parameters | Influence on relaxivities | Comments |
|---|---|---|
| From left to right: List of the intrinsic parameters of MNP, level of influence on relaxivities (✹ low, ✹✹ medium-low, ✹✹✹ medium-high, ✹✹✹✹ high) and general comments. | ||
| Core dimension | ✹✹✹✹✹ | Optimal range 11–20 nm |
| Core composition | ✹✹✹✹ | Limited by toxicity |
| Solvent type | ✹✹✹ | Correlated to the type of coating |
| Shape | ✹/✹✹ | — |
| Coating | ✹✹ | More evident for small MNPs (below 4–5 nm) |
| Coating functionalization | ✹✹/✹✹✹ | Strongly dependent on the chemical moiety used |
5. Conclusions
In this perspective article, we presented and discussed our research activity of the last 10 years focused on the comprehension of the physical mechanisms on the basis of the nuclear relaxation of superparamagnetic nanoparticles as a function of their chemical–physical properties.Summarizing, the overall results showed a clear dependence of nuclear relaxivities r1 and r2 on the composition and size of the magnetic core of superparamagnetic MNPs and the solvent used to disperse superparamagnetic MNPs. In the case of maghemite/magnetite MNPs, which remain the most used MNPs to date for their low toxicity, the diameter of the magnetic core should be preferably bigger than 11–12 nm for obtaining a sizeable effect on the relaxometric efficiency, at least comparable to Endorem®. Doping iron oxide MNPs with Co, Mn, Zn, etc. strongly influences the nuclear relaxivities and their dependence on the field intensity, often leading to better results when compared with undoped MNPs. At the same time, these kinds of ions, if released in the cells, have an impact on the biocompatibility of the MNPs due to their toxicity and thus imply extensive studies on their cytotoxicity.
The effects of shape, coating and functionalization of the superparamagnetic MNPs need to be further investigated and interpreted also in view of developing effective models to predict their efficiency as MRI contrast agents.
Nevertheless, we recommend the research community involved in MNP synthesis and characterization to put an effort in the direction of investigating new systems where microscopic characteristics, like shape and coating, are changed in a systematic way. No clear and undisputed recommendation about the best features of shape and coating can be provided to date, mainly because of the absence of the above-mentioned systematic investigation. In fact, we observe that only by studying the magnetic behaviour as a function of one MNP parameter fixing the others (e.g. varying the shape and fixing the coating, composition, size, solvent, etc.), the obtained experimental results could be rationalized. For example, the great variability of type of functionalization from one group to another makes the interpretation of the results very complex and not unique. In order to reach this goal, a large number of MNPs should be available to the researchers.
As concerns the data interpretation, we adopted the heuristic model of Roch et al. to interpret our experimental NMR-D profiles and describe the spin dynamics involved in the relaxation processes quantifying its effects. The application of the model to a large number of cases pointed out a clear difference between its ability to describe longitudinal and transverse relaxivity. In the first case, indeed, the model was able to satisfactorily fit the r1 profiles of many different superparamagnetic MNPs providing information on some of their physical quantities such as, for instance, the Néel correlation time τN, by NMR, and the distance of minimum approach rd of solvent molecules near the superparamagnetic MNPs. As the r2 profiles are not well reproduced, we wish that this perspective article could be a stimulus for the future development of theoretical models capable of describing more extensively the nuclear magnetic relaxation of this type of nanoparticle.
Author contributions
The manuscript was written, reviewed and edited through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
EU COST project Eurelax (CA15209) is gratefully acknowledged. P. A. thanks Dipartimento di Fisica, Università degli Studi di Milano (Italy), for its support. C.I. gratefully acknowledges MUR and EU-FSE for the financial support of the Fix-term Researcher fellowship - PON Research and Innovation 2014–2020 (D.M 1062/2021). INFN (National Institute for Nuclear Physics) is also acknowledged for the support provided via PROTHYP and NAMASSTE projects.References
- L.-M. Lacroix, D. Ho and S. Sun, Curr. Top. Med. Chem., 2010, 10, 1184–1197 CrossRef CAS PubMed
.
-
A. K. A. Silva, A. Espinosa, J. Kolosnjaj-Tabi, C. Wilhelm and F. Gazeau, in Iron Oxides: From Nature to Applications, ed. D. Faivre, Wiley VCH, 2016, pp. 425–471 Search PubMed
.
- L. Yang, Z. Zhou, J. Song and X. Chen, Chem. Soc. Rev., 2019, 48, 5140–5176 RSC
.
- S. Laurent, D. Forge, M. Port, A. Roch, C. Robic, L. Vander Elst and R. N. Muller, Chem. Rev., 2008, 108, 2064–2110 CrossRef CAS PubMed
.
- S. Bajpai, S. Kr Tiwary, M. Sonker, A. Joshi, V. Gupta, Y. Kumar, N. Shreyash and S. Biswas, ACS Appl. Nano Mater., 2021, 4, 6441–6470 CrossRef CAS
.
- F. Yan, Y. Wang, S. He, S. Ku, W. Gu and L. Ye, J. Mater. Sci. Mater. Med., 2013, 24, 2371–2379 CrossRef CAS PubMed
.
- T. Sun, Y. Liu, C. Zhou, L. Zhang, X. Kang, S. Xiao, M. Du, Z. Xu, Y. Liu, G. Liu, M. Gong and D. Zhang, Nanoscale, 2021, 13, 7638 RSC
.
- J. Song, L. Lin, Z. Yang, R. Zhu, Z. Zhou, Z. W. Li, F. Wang, J. Chen, H. Yang and X. Chen, J. Am. Chem. Soc., 2019, 141, 8158–8170 CrossRef CAS PubMed
.
- Z. Shen, W. Fan, Z. Yang, Y. Liu, V. I. Bregadze, S. K. Mandal, B. C. Yung, L. Lin, T. Liu, W. Tang, L. Shan, Y. Liu, S. Zhu, S. Wang, W. Yang, L. H. Bryant, D. T. Nguyen, A. Wu and X. Chen, Small, 2019, 15, 1903422 CrossRef CAS PubMed
.
- X. R. Song, S. H. Li, J. Dai, L. Song, G. Huang, R. Lin, J. Li, G. Liu and H. H. Yang, Small, 2017, 13, 1603997 CrossRef PubMed
.
- L.-S. Lin, X. Yang, Z. Zhou, Z. Yang, O. Jacobson, Y. Liu, A. Yang, G. Niu, J. Song, H.-H. Yang and X. Chen, Adv. Mater., 2017, 29, 1606681 CrossRef PubMed
.
- D.-E. Lee, H. Koo, I.-C. Sun, J. H. Ryu, K. Kim and I. C. Kwon, Chem. Soc. Rev., 2012, 41, 2656–2672 RSC
.
- R. Di Corato, F. Gazeau, C. Le Visage, D. Fayol, P. Levitz, F. Lux, D. Letourneur, N. Luciani, O. Tillement and C. Wilhelm, ACS Nano, 2013, 7, 7500–7512 CrossRef CAS PubMed
.
- J. L. Bridot, A. C. Faure, S. Laurent, C. Rivière, C. Billotey, B. Hiba, M. Janier, V. Josserand, J. L. Coll, L. Vander Elst, R. Muller, S. Roux, P. Perriat and O. Tillement, J. Am. Chem. Soc., 2007, 129, 5076–5084 CrossRef CAS PubMed
.
- C. Tassa, S. Y. Shaw and R. Weissleder, Acc. Chem. Res., 2011, 44, 842–852 CrossRef CAS PubMed
.
- Z. Qin, B. Chen, Y. Mao, C. Shi, Y. Li, X. Huang, F. Yang and N. Gu, ACS Appl. Mater. Interfaces, 2020, 12, 57382–57390 CrossRef CAS PubMed
.
- X. Guan, J. Li, J. Cai, S. Huang, H. Liu, S. Wang, X. Zhang, Y. Sun, H. Liu, G. Xie and Z. Wang, Chem. Eng. J., 2021, 425, 130579 CrossRef CAS
.
- Q. Liu, L. Liu, C. Mo, X. Zhou, D. Chen, Y. He, H. He, W. Kang, Y. Zhao and G. Jin, J. Nanobiotechnol., 2021, 19, 171 CrossRef CAS PubMed
.
- R. Hergt, S. Dutz, R. Müller and M. Zeisberger, J. Phys.: Condens. Matter, 2006, 18, S2919 CrossRef CAS
.
- S. Dutz and R. Hergt, Nanotechnology, 2014, 25, 452001 CrossRef PubMed
.
- S. Dutz, N. Buske, J. Landers, C. Gräfe, H. Wende and J. H. Clement, Nanomaterials, 2020, 10, 1019 CrossRef CAS PubMed
.
- P. Pradhan, J. Giri, G. Samanta, H. D. Sarma, K. P. Mishra, J. Bellare, R. Banerjee and D. Bahadur, J. Biomed. Mater. Res., Part B, 2006, 81, 12–22 Search PubMed
.
- D. Cabrera, J. Camarero, D. Ortega and F. J. Teran, J. Nanopart. Res., 2015, 17, 121 CrossRef
.
- W. Wang, F. Li, S. Li, Y. Hu, M. Xu, Y. Zhang, M. I. Khan, S. Wang, M. Wu, W. Ding and B. Qiu, J. Mater. Sci. Technol., 2021, 81, 77–87 CrossRef CAS
.
- N. Shreyash, M. Sonker, S. Bajpai and S. Kr Tiwary, ACS Appl. Bio Mater., 2021, 4, 2307–2334 CrossRef CAS PubMed
.
- M. Arruebo, R. Fernández-Pacheco, M. R. Ibarra and J. Santamaría, Nano Today, 2007, 2, 22–32 CrossRef
.
- A. P. Douvalis, R. Zboril, A. B. Bourlinos, J. Tucek, S. Spyridi and T. Bakas, J. Nanopart. Res., 2012, 14, 1130 CrossRef
.
- B. Chertok, B. A. Moffat, A. E. David, F. Yu, C. Bergemann, B. D. Ross and V. C. Yang, Biomaterials, 2008, 29, 487–496 CrossRef CAS PubMed
.
- C. S. S. R. Kumar and F. Mohammad, Adv. Drug Delivery Rev., 2011, 63, 789–808 CrossRef CAS PubMed
.
- S. W. Lee, S. H. Lee and S. Biswal, Theranostics, 2012, 2, 403–412 CrossRef CAS PubMed
.
- K. Wu, D. Su, J. Liu, R. Saha and J.-P. Wang, Nanotechnology, 2019, 30, 502003 CrossRef CAS PubMed
.
-
G. Schmid, Nanoparticles: From Theory to Application, Wiley-VCH, Weinheim, 2004 Search PubMed
.
-
K. J. Klabunde, Nanoscale Materials in Chemistry, Wiley-Intersc., New York, 2001 Search PubMed
.
- A. P. Alivisatos, Science, 1996, 271, 933 CrossRef CAS
.
- M. P. Pileni, Nat. Mater., 2003, 2, 145 CrossRef CAS PubMed
.
-
V. K. Varadan, L. F. Chen and J. Xie, Nanomedicine: Design and Applications of Magnetic Nanomaterials, Nanosensors and Nanosystems, Wiley, 2008 Search PubMed
.
- H. Rui, R. Xing, Z. Xu, Y. Hou, S. Goo and S. Sun, Adv. Mater., 2010, 22, 2729–2742 CrossRef PubMed
.
- A. Plan Sangnier, A. B. Van de Walle, A. Curcio, R. Le Borgne, L. Motte, Y. Lalatonne and C. Wilhelm, Nanoscale, 2019, 11, 16488–16498 RSC
.
- E. Blanco, H. Shen and M. Ferrari, Nat. Biotechnol., 2015, 33, 941–951 CrossRef CAS PubMed
.
- H. Shagholani, S. M. Ghoreishi and S. H. Sharifi, J. Drug Delivery Sci. Technol., 2018, 45, 373–377 CrossRef CAS
.
- M. Mahmoudi, S. Laurent, M. A. Shokrgozar and M. Hosseinkhani, ACS Nano, 2011, 5, 7263–7276 CrossRef CAS PubMed
.
- P. M. L. Mojica Jr., E. Lima, M. M. Vasquez, V. E. Tognoli, H. E. Troiani, A. A. Pasa, T. B. Creczynski-Pasa, A. H. Silva, P. Gurman, L. Colombo and G. F. Goya, J. Biomed. Mater., 2014, 102, 860–868 CrossRef PubMed
.
- F. Brero, M. Albino, A. Antoccia, P. Arosio, M. Avolio, F. Berardinelli, D. Bettega, P. Calzolari, M. Ciocca, M. Corti, A. Facoetti, S. Gallo, F. Groppi, A. Guerrini, C. Innocenti, C. Lenardi, S. Locarno, S. Manenti, R. Marchesini, M. Mariani, F. Orsini, E. Pignoli, C. Sangregorio, I. Veronese and A. Lascialfari, Nanomaterials, 2020, 10, 1919 CrossRef CAS PubMed
.
- R. S. Pereira, F. S. Prato, G. Wisenberg and J. Sykes, Magn. Reson. Med., 1996, 36, 684–693 CrossRef CAS PubMed
.
- M. Saeed, M. F. Wendland, Y. Takehara, T. Masui and C. B. Higgins, Radiology, 1992, 182, 675–683 CrossRef CAS PubMed
.
- C. L. Wolfe, M. E. Moseley, M. G. Wikstrom, R. E. Sievers, M. F. Wendland, J. W. Dupon, W. E. Finkbeiner, M. J. Lipton, W. W. Parmley and R. C. Brasch, Circulation, 1989, 80, 969–982 CrossRef CAS PubMed
.
- D. Kruk, A. Korpała, S. Mehdizadeh Taheri, A. Kozłowski, S. Förster and E. A. Rössler, J. Chem. Phys., 2014, 140, 174504 CrossRef CAS PubMed
.
- Q. L. Vuong, J. F. Berret, J. Fresnais, Y. Gossuin and O. Sandre, Adv. Healthcare Mater., 2012, 1, 502–512 CrossRef CAS PubMed
.
- M. Jeon, M. V. Halbert, Z. R. Stephen and M. Zhang, Adv. Mater., 2020, 33, 1906539 CrossRef PubMed
.
- L. Yang, Z. Wang, L. Ma, A. Li, J. Xin, R. Wei, H. Lin, R. Wang, Z. Chen and J. Gao, ACS Nano, 2018, 12, 4605–4614 CrossRef CAS PubMed
.
- D. Bonvin, D. T. L. Alexander, A. Millán, R. Piñol, B. Sanz, G. F. Goya, A. Martínez, J. A. M. Bastiaansen, M. Stuber, K. J. Schenk, H. Hofmann and M. M. Ebersold, Nanomaterials, 2017, 7, 225 CrossRef PubMed
.
- T. Vangijzegem, D. Stanicki, A. Panepinto, V. Socoliuc, L. Vekas, R. N. Muller and S. Laurent, Nanomaterials, 2020, 10, 757 CrossRef CAS PubMed
.
- Y. Gossuin, T. Orlando, M. Basini, D. Henrard, A. Lascialfari, C. Mattea, S. Stapf and Q. L. Vuong, Nanotechnology, 2016, 27, 155706 CrossRef CAS PubMed
.
- C. Blanco-Andujar, A. Walter, G. Cotin, C. Bordeianu, D. Mertz, D. Felder-Flesch and S. Begin-Colin, Nanomedicine, 2016, 11, 1889–1910 CrossRef CAS PubMed
.
- K. E. Kellar, D. K. Fujii, W. H. H. Gunther, K. Briley-Sabø, A. Bjornerod, M. Spiller and S. H. Koenig, Acad. Radiol., 2002, 9, S34–S37 CrossRef PubMed
.
- S. Laurent, C. Nicotra, Y. Gossuin, A. Roch, L. Vander Elst, M. Cornant, P. Soleil and R. N. Muller, Phys. Status Solidi C, 2004, 1, 3644–3650 CrossRef CAS
.
- S. L. C. Pinho, S. Laurent, J. Rocha, A. Roch, M.-H. Delville, S. Mornet, L. D. Carlos, L. Vander Elst, R. N. Muller and C. F. G. C. Geraldes, J. Phys. Chem. C, 2012, 116, 2285–2291 CrossRef CAS
.
- M. Levy, F. Gazeau, C. Wilhelm, S. Neveu, M. Devaud and P. Levitz, J. Phys. Chem. C, 2013, 117, 15369–15374 CrossRef CAS
.
- Q. L. Vuong, P. Gillis, A. Roch and Y. Gossuin, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2017, 9, e1468 Search PubMed
.
- A. Roch, R. N. Muller and P. Gillis, J. Chem. Phys., 1999, 110, 5403 CrossRef CAS
.
- L. Bordonali, T. Kalaivani, K. P. V. Sabareesh, C. Innocenti, E. Fantechi, C. Sangregorio, M. F. Casula, L. Lartigue, J. Larionova, Y. Guari, M. Corti, P. Arosio and A. Lascialfari, J. Phys.: Condens. Matter, 2013, 25, 066008 CrossRef CAS PubMed
.
- M. Basini, A. Guerrini, M. Cobianchi, F. Orsini, D. Bettega, M. Avolio, C. Innocenti, C. Sangregorio, A. Lascialfari and P. Arosio, J. Alloys Compd., 2019, 770, 58–66 CrossRef CAS
.
- M. Albino, E. Fantechi, C. Innocenti, A. Lopez-Ortega, V. Bonanni, G. Campo, F. Pineider, M. Gurioli, P. Arosio, T. Orlando, G. Bertoni, C. de Julian Fernandez, A. Lascialfari and C. Sangregorio, J. Phys. Chem. C, 2019, 123, 6148–6157 CrossRef CAS
.
- M. Basini, T. Orlando, P. Arosio, M. F. Casula, D. Espa, S. Murgia, C. Sangregorio, C. Innocenti and A. Lascialfari, J. Chem. Phys., 2017, 146, 034703 CrossRef CAS PubMed
.
- F. Brero, M. Basini, M. Avolio, F. Orsini, P. Arosio, C. Sangregorio, C. Innocenti, A. Guerrini, J. Boucard, E. Ishow, M. Lecouvey, J. Fresnais, L. Lartigue and A. Lascialfari, Nanomaterials, 2020, 10, 1660 CrossRef CAS PubMed
.
- P. Arosio, F. Orsini, A. M. Piras, S. Sandreschi, F. Chiellini, M. Corti, M. Masa, M. Múčková, Ĺ. Schmidtová, C. Ravagli, G. Baldi, E. Nicolato, G. Conti, P. Marzola and A. Lascialfari, RSC Adv., 2015, 5, 39760 RSC
.
- M. Galli, A. Guerrini, S. Cauteruccio, P. Thakare, D. Dova, F. Orsini, P. Arosio, C. Carrara, C. Sangregorio, A. Lascialfari, D. Maggioni and E. Licandro, RSC Adv., 2017, 7, 15500 RSC
.
- A. Roch and R. N. Muller, Longitudinal relaxation of water protons in colloidal suspensions of superparamagnetic crystal. Proceedings of the 11th Annual Meeting of the Society of Magnetic Resonance in Medicine, Works in Progress, 1992, 1447.
- S. H. Koenig and K. E. Kellar, Magn. Reson. Med., 1995, 34, 227 CrossRef CAS PubMed
.
- A. Roch, R. N. Muller and P. Gillis, J. Magn. Reson. Imaging, 2001, 14, 94 CrossRef CAS PubMed
.
- L. Néel, Ann. Geophys., 1949, 5, 99 Search PubMed
.
- H. Vogel, Phys. Z., 1921, 22, 645 Search PubMed
; G. S. Fulcher, J. Am. Ceram. Soc., 1925, 8, 339 CrossRef CAS
.
- P. Arosio, J. Thévenot, T. Orlando, F. Orsini, M. Corti, M. Mariani, L. Bordonali, C. Innocenti, C. Sangregorio, H. Oliveira, S. Lecommandoux, A. Lascialfari and O. Sandre, J. Mater. Chem. B, 2013, 1, 5317 RSC
.
- R. A. Brooks, F. Moiny and P. Gills, Magn. Reson. Med., 2001, 45, 1014–1020 CrossRef CAS PubMed
.
- M. Basini, S. Sanna, T. Orlando, L. Bordonali, M. Cobianchi, P. Arosio, M. Mariani, D. Peddis, V. Bonanni, R. Mathieu, T. Kalaivani, G. Singh, J. Larionova, Y. Guari, L. Lartigue and A. Lascialfari, Phys. Rev. B, 2020, 102, 195424 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2023 |