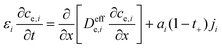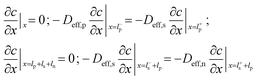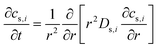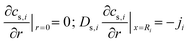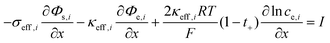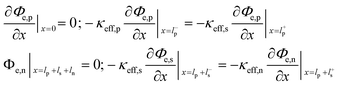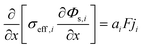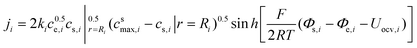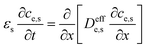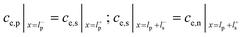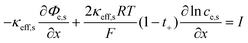Open Access Article
Open Access ArticleHealth prognostics for lithium-ion batteries: mechanisms, methods, and prospects
Yunhong
Che
 a,
Xiaosong
Hu
a,
Xiaosong
Hu
 *b,
Xianke
Lin
*b,
Xianke
Lin
 c,
Jia
Guo
c,
Jia
Guo
 a and
Remus
Teodorescu
a
a and
Remus
Teodorescu
a
aDepartment of Energy, Aalborg University, 9220, Aalborg, Denmark
bCollege of Mechanical and Vehicle Engineering, Chongqing University, 400044, Chongqing, China. E-mail: xiaosonghu@ieee.org
cDepartment of Automotive and Mechatronics Engineering, Ontario Tech University, L1G 0C5, Oshawa, Canada
First published on 4th January 2023
Abstract
Lithium-ion battery aging mechanism analysis and health prognostics are of great significance for a smart battery management system to ensure safe and optimal use of the battery system. This paper provides a comprehensive review of aging mechanisms and the state-of-the-art health prognostic methods and summarizes the main challenges and research prospects for battery health prognostics. First, the complex relationships among aging mechanisms, aging modes, influencing factors, and aging types are reviewed and summarized. Then, the battery health prognostic methods are divided according to different time scales and objectives, which include the short-term state of health estimation, long-term end-of-life prediction, and degradation trajectory prediction, followed by a detailed review of each prognostic task and method. For consistency, we first provide a clear and concise description of each method, showing the similarities and peculiarities of these methods, and then review several representative works. After that, comparative evaluations are conducted. The main advantages and disadvantages of each prognostic task and prognostic method are analyzed in detail. Next, key challenges are presented by considering the specific characteristics of each prognostic task. Moreover, for each challenge, potential solutions are presented and discussed. These proposed potential solutions to the main challenges are beneficial and can be considered by researchers in their further studies. Finally, the future trends of battery health prognostics are discussed, and several new ideas for battery health prognostics are proposed.
1. Introduction
Transportation electrification plays a significant role in reducing exhaust emissions, alleviating the excessive dependence on fossil fuels, and solving the current energy shortage and environmental pollution problems to a certain extent.1,2 Lithium-ion batteries, as one of the main energy storage devices, have been a limiting factor in the development of electric vehicles, electric ships, electric aircraft, etc.3,4 In addition, lithium-ion batteries are widely used in other fields, such as satellites, laptops, and smart grids.5–7 However, the internal electrochemical mechanism of lithium-ion batteries is very complex due to their dynamic, time-varying, and nonlinear characteristics.8,9 Besides the main reactions, aging-related side reactions occur at the same time. The capacity of lithium-ion batteries will gradually degrade, and the internal resistance will increase with storage and usage, which can be regarded as calendar aging and cyclic aging, respectively.10,11 The limited service life of batteries is one of the key factors restricting the commercial popularization of lithium-ion batteries in the above applications.12 However, the optimal use of batteries can help delay failures or end of life (EoL).13 Therefore, battery management systems (BMSs) are designed for more accurate and robust state estimation and lifetime prediction, as well as optimizing strategies that extend the service time.14,15Several policies have been established all over the world to promote the health management of batteries. The newest Advanced Clean Cars II Regulations proposed by the California air resources board have pointed out that sharing battery health information to drivers is essential, requiring a standardized state of health (SoH) indicator to be displayed on the dashboard in 2026 and thereafter.16 The advanced development of battery gigafactories and electric vehicle industries in Europe also promotes the establishment of related policies.17,18 For example, a new EU regulatory framework for batteries declares that safety and EoL management should be included.19 For health management-based policies, some research programs have been established to promote the development of battery health prognostics. For example, the “battery health” in Apple devices is an implementation of health estimation algorithms in portable devices. EU government has supported a big research program called “Battery 2030” with EUR 40.5 million, where battery health management and prognostic algorithms are important components.20 In addition, battery reuse and recycling policies pronounced by governments from Europe and China also indicate the importance of battery health prognostics,19,21 which promotes the research on this topic where health evaluations are significant steps to point out the health status of batteries.22,23
Aging and damage of lithium-ion batteries can lead to battery system failure, even property damage and personal injury.24,25 Batteries undergo degradation because complex and coupled side reactions occur along with the main electrochemical reactions during charging and discharging.26 These side reactions cause the degradation phenomenon. Understanding the main degradation mechanisms and the associated influencing factors can guide the optimal use of the battery, which helps delay the EoL. Different external environments and use conditions have different effects on these side reactions.27 However, lithium-ion batteries are still regarded as a “black box” whose internal aging states are difficult to measure directly by sensors. Therefore, the internal states need to be estimated using manually designed algorithms based on the measured parameters. Prognostics and health management (PHM) algorithms have been designed for BMSs to ensure the safe and reliable operation of batteries,28,29 which requires timely fault diagnostics and health prognostics. Fault diagnosis is one significant function of PHM to identify and prevent/mitigate potential failures. For example, early warning of internal short circuit faults in batteries is crucial for timely maintenance to prevent safety issues. For example, a thermal runaway caused by an internal short circuit could cause serious personal and property damage.30 Battery health prognostics are mainly needed for SoH estimation and lifetime (or remaining useful life (RUL)) prediction. To make it clear, the definition of battery SoH is the ratio of current capacity to nominal capacity.31 Battery lifetime or RUL is defined as the remaining available operating cycles before reaching the EoL, which typically refers to the cycle when the current capacity reaches 80% or 70% of the nominal capacity.32,33 Accurate and reliable battery SoH estimation and RUL prediction are of great significance and have attracted increasing research and industrial interest in recent years. Studying the degradation characteristics of lithium-ion batteries, extracting key aging factors, and developing non-destructive and real-time prognostics of SoH and the remaining lifetime of lithium-ion batteries can effectively help evaluate the health status of the batteries and establish a timely maintenance strategy to ensure safe operation.34 Health prognostics also support many other health management strategies in BMSs. Health information provided by the prognostics is one of the most important inputs for battery fault diagnosis in the early stages. Aging and lifetime prediction models are important for the optimal design of charging protocols and the energy management strategies of vehicle-to-grid interactions.35–37 Health prognostics also benefit the optimal second life utilization, where the health status is provided as a key indicator for the remaining service lifetime evaluation, sorting, and regrouping.38,39
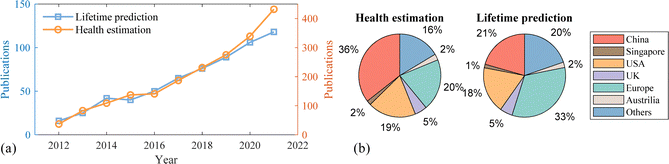
Due to the rapid development of electrified transportation and smart grid etc., research on battery PHM has also exploded. A statistical analysis of research on battery health estimation and lifetime prediction based on data collected from the Web of Science database is shown in Fig. 1, where the number of publications in the past ten years (2012–2021) is shown in Fig. 1(a), and the percentages in publications of different regions are shown in Fig. 1(b). It shows that the research interest in battery PHM has increased rapidly in the past few years, with a steady increase in publications of battery health estimation and lifetime prediction. Among several different main regions where the electric vehicle industries developed rapidly, the percentage of publications in this field also occupies a large amount. China, USA, and Europe have 75% of the publications in battery health estimation and 72% in battery lifetime prediction, and are the most three regions that publish research in this field. UK produced 5% of the whole publication. Therefore, battery health prognostic is one of the main trends in efficient and smart battery health management.40 It is important to review the main degradation mechanisms and the state-of-the-art methods of prognostics in this field since there are many different types of strategies and algorithms proposed for battery SoH estimation and lifetime prediction. A detailed review helps researchers understand the state-of-the-art methods and in the selection of appropriate methods.
The battery health prognostic methods proposed in publications generally include model-based, data-driven, and hybrid methods. Each of them in battery lifetime prognostics is introduced and evaluated in ref. 41. According to the prediction results, health prognostics can also be divided into probabilistic and non-probabilistic.47 The uncertainty expressions are given in the probabilistic method to illustrate the reliability of the predictions.48 Some review papers on this topic in recent years are listed in Table 1, where the main contents, advantages, and deficiencies are summarized. It can be seen from the table that the published reviews generally concentrate on either aging mechanisms or prognostic methods. The different battery health prognostic objectives under different applications are not described before introducing the specific prediction methods. However, the objectives are important and need to be decided since different methods may suit different practical needs. For example, EoL prediction and future degradation prediction in battery lifetime prediction are two different objectives, which require different methods. However, the existing review paper failed to distinguish them clearly. Besides, comprehensive evaluations based on multi-dimensional indices are also important to help researchers select the proper method. Finally, suggestions to address current challenges should be provided and discussed, and future trends need to be updated based on the state of art.
| Publication | Main content | Highlights | Drawbacks |
|---|---|---|---|
| Ref. 7 | ■ Main aging mechanisms and external affecting factors | ■ Comprehensive review of battery aging mechanisms | ■ Lack of battery health prognostic methods |
| ■ Aging diagnosis methods. | ■ Main physics-based methods for aging diagnosis | ■ No evaluations of different methods | |
| Ref. 25 | ■ Introduction of main aging mechanisms and aging origins | ■ Both calendar and cyclic aging under different mechanisms | ■ Data-driven methods are little |
| ■ Review of aging estimation methods | ■ Comprehensive review of different model-based methods | ■ Lack of comparisons among different methods | |
| Ref. 29 | ■ Summary of main health prognostic methods | ■ Both prognostic and management methods are included | ■ Battery SoH estimation and lifetime prognostic are not separated |
| ■ Introduction of battery health management strategies | ■ PHM on real engineered influence is discussed | ■ Lack of evaluations | |
| Ref. 33 | ■ Main ML-based methods for battery SoH estimation and lifetime prediction | ■ Quantity comparisons for each kind of ML methods | ■ Comparisons for SoH and lifetime are mixed up |
| ■ Collection of main research results for each type of method | ■ Comprehensive introduction of each ML method in battery health prognostics | ■ Other types of methods and aging mechanisms are missing | |
| Ref. 41 | ■ Methods for battery lifetime prediction and comparisons | ■ Critical comparisons and plentiful prospects | ■ Current methods with data-driven method are lacking |
| ■ Key challenges and main research trends | ■ Detailed introduction for all kinds of methods | ■ Aging mechanisms are simply included | |
| Ref. 42 | ■ Data-driven SoH estimation and lifetime prediction methods | ■ Comprehensive overview of the main data-driven methods | ■ Other types of methods are not included |
| ■ Aging mechanisms and influencing factors | ■ Evaluation of different data-driven methods | ■ Lack of EoL point prediction methods | |
| Ref. 43 | ■ Deep learning methods in battery PHM algorithms | ■ Summary of datasets for research of battery management | ■ Only focus on deep learning methods |
| ■ Evaluation of different deep learning algorithms | ■ Comprehensive overview of deep learning-based prediction | ■ Aging mechanisms are missing | |
| Ref. 44 | ■ Overview of SoH estimation and lifetime prediction methods | ■ Comprehensive review of SoH estimation methods | ■ Little cover of lifetime prediction methods |
| ■ Challenges with possible solutions and recommendations | ■ Both internal and external challenges are summarized | ■ Classification method is not comprehensive | |
| Ref. 45 | ■ Introduction of popular battery data sets | ■ Summary of battery aging data set acquisition | ■ Lack of comprehensive comparisons |
| ■ Review of key methods for battery states estimation and lifetime prediction | ■ Comprehensive review of battery states estimation and lifetime prediction | ■ Lack of aging mechanisms introduction | |
| Ref. 46 | ■ Introduction of ML-based lifetime prediction methods | ■ Containing main ML-based methods for lifetime prediction | ■ Data-driven methods are not fully contained |
| ■ Comparisons among different ML methods | ■ Comparison of method recommendations | ■ Lack of other prediction methods and aging mechanisms |
Therefore, this paper provides an overview of the main aging mechanisms, state-of-the-art techniques in battery health prognostics, comparative evaluations of different objectives and the corresponding methods, as well as main research challenges, potential solutions, and research prospects. The main contributions are summarized in the following four aspects. (1) Main aging mechanisms of lithium-ion batteries are briefly introduced, and the external influencing factors for aging are summarized. The correlation among aging mechanisms, aging modes, external factors, and aging types is illustrated. A summary of available public data sets for research of battery health prognostics is provided. (2) Objective-based method classification is proposed, followed by a detailed description of the state-of-the-art methods. A unified framework is adopted for the illustration of each method for a clearer and more comprehensive description and clear presentation of the differences among different methods. (3) Comprehensive evaluations of different prognostic tasks and methods are conducted, where different evaluations are considered, including accuracy, computational burden, data requirement, model generalization and robustness, implementation complexity, and publication trend. (4) The main challenges for battery health prognostics using each type of method in each prognostic task are summarized and discussed with potential solution suggestions. The research prospect of more accurate and reliable battery health prognostic methods in this field is presented, which helps researchers to focus on the main research problems and bottlenecks.
The overall content of this review article is shown in Fig. 2. It starts from the introduction and analysis of the main aging mechanisms and influencing factors to the detailed discussion of different time-scale prognostic tasks. The key research challenges follow the discussion of the state-of-the-art methods, some potential solutions are proposed, and the research prospects are presented at the end. The remainder of this review paper is arranged as follows. The main aging mechanisms and influencing factors are analyzed in Section 2. Then, popular battery aging datasets and methods for battery lifetime prediction are classified and reviewed in Section 3, followed by a comprehensive comparison of different methods in Section 4. Then, the key challenges with suggested solutions and future research prospects are provided in Section 5. Finally, a brief conclusion is presented in Section 6.
2. Aging mechanisms and influencing factor analysis
Lithium-ion batteries undergo inevitable aging during operation. Some cell manufacturing characteristics or external conditions can have an impact on the aging patterns. Typically, commercial lithium-ion batteries include coin cells, cylindrical, ellipsoidal, prismatic, and pouch cell types. Different battery packages create different internal mechanical stresses. In addition, battery aging is also affected by external factors such as ambient temperature, charge and discharge current magnitude, depth of discharge (DoD), and ambient humidity. What's more, the diversity of positive electrodes and negative electrodes, as well as internal component materials, also has huge impacts on the aging patterns. It is important to understand the common aging mechanisms and main influencing factors, which can help in the appropriate selection of prognostic methods and in developing more suitable and accurate models for battery health prognostics. In this section, key aging mechanisms on both cathodes and anodes are introduced in Section 2.1. The main influencing factors on the calendar and cyclic aging rates are then summarized in Section 2.2.2.1. Aging mechanisms
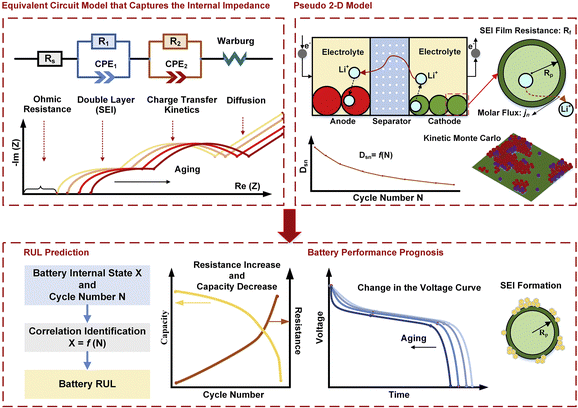
Some mechanistic models can model the aging process of lithium-ion batteries. The Pseudo-two-Dimensional (P2D), molecular dynamics (MD), and SEI growth models enable the simulation of the battery aging process. In these models, the internal side reactions of the battery based on detailed battery manufacturing parameters and operating condition parameters can be modeled. Besides, the equivalent circuit model (ECM) does not model the internal side reactions. However, it can be enhanced and used to predict aging by fitting the model parameters to aging data.49To model the aging mechanism, an electrochemical model usually serves as the basis. The P2D model, which was built on the porous electrode theory and concentrated solution theory, is most popular for high-fidelity modeling of batteries.50 The governing equations of the P2D model are listed in Table 2. However, the full analytical solution of the governing P2D model is unavailable. One way is to use numerical methods such as Finite-Element Method (FEM), finite-difference method, finite-volume method, etc.51 Another way is the simplification of the government equations, such as using mathematical approximation or physics simplification.52 Single particle models (SPMs), which use two spherical particles to represent the negative and positive electrodes and neglect the electrolyte concentration and potentials, keep the most important physics while significantly reducing the computational complexity which makes them popular for online real-time algorithms in battery health prognostics.53 In addition, the MD simulation is also one popular tool for the mechanistic analysis of chemical reactions inside the batteries. Several methods, including classical, ab initio, and machine learning-based MD, can be used.54 The classical potential energy functions are used to describe the atomic interactions in classic MD. The ab initio method is used by the ab initio MD to calculate the interaction forces, while the machine learning (ML) method is integrated into the MD for fast calculation and better transferability with high accuracy.54,55 Besides the modeling method, advanced sensors are also important for complete information acquisition inside batteries. These sensors can be implemented inside the batteries during design and manufacturing.56 For example, the internal temperature affects the aging mechanisms. This important information can be measured by the advanced sensors, which are very useful for the prognostics of battery health.57
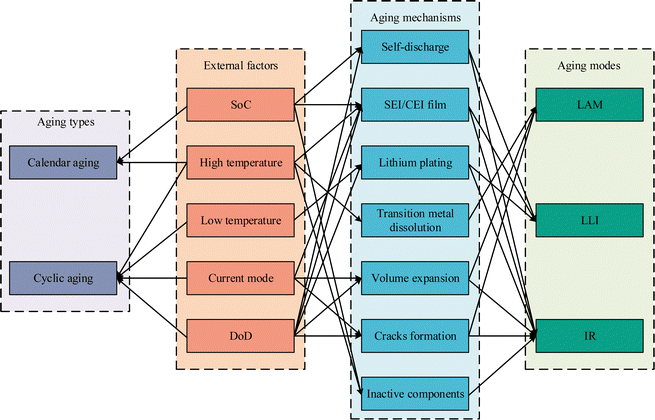
LAM is mainly caused by active particle loss due to current collector corrosion or binder decomposition, transition metal dissolution, and electrode particle cracking. LLI is mainly caused by the rupture and reformation of solid electrolyte interphase (SEI) films, electrolyte decomposition, and lithium plating.7 Besides, the formation of the SEI film and cracks in particles will lead to an increase in IR. A summary of the side reactions related to battery aging is shown in Fig. 3.41 The above primary degradation modes have different influences on the capacity decrease and internal resistance increase. In addition, different external conditions such as temperature and current rates have different effects on battery calendar and cyclic aging. Aging occurs in each part of the battery, and the external influencing factors will be introduced in detail below.
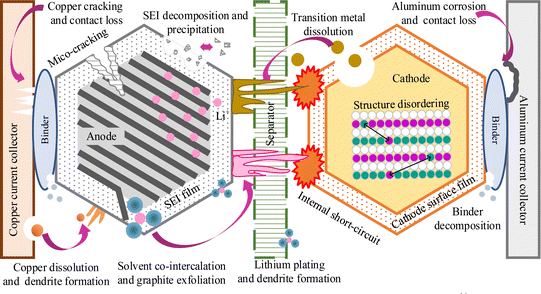 | ||
| Fig. 3 Main aging mechanisms for lithium-ion batteries, adapted from ref. 41 with permission. | ||
In short, the negative electrodes in the market are mainly graphite and graphite–silicon composite electrodes (C/Si and C/SiO2). Graphite–silicon composite electrodes show more volume expansion than pure graphite. Besides, they all suffer from some common aging modes, such as SEI film formation, transition metal deposition, and graphite exfoliation.
The main aging mechanism for graphite-based electrodes is the continuous formation of the SEI film on the electrolyte/electrode interface over time. Many types of chemical compounds have been found in the SEI, including lithium fluoride (LiF), lithium carbonate (Li2CO3), lithium oxide (Li2O), lithium methyl carbonate (LiOCO2CH3), lithium ethylene decarbonate ((LiOCO2CH2)2), etc.72,73 It is widely accepted that the reduction of a solvent molecule (for example, [EC]-) is a one-electron reaction occurring at the surface of graphite. First, the solvent molecule is reduced to form an intermediate radical anion (C3H4O3). Then, this radical anion undergoes further decomposition according to eqn. (8), forming the solid lithium ethylene decarbonate ((CH2OCO2Li)2).74,75 Therefore the reaction between C3H4O3 and electrons is widely used for SEI modeling.
| 2C3H4O3(l) + 2e− + 2Li+ ⇆ (CH2OCO2Li)2(s) + C2H4(g) | (8) |
The SEI film is naturally formed during the first charge after manufacturing, whose function is to protect the negative electrode from possible corrosion in the process of electrolyte reduction.76 However, the SEI film is not perfectly stable, which ruptures and reforms during cycling, resulting in continuous Li-ion loss and electrolyte decomposition.77 MD simulation is a great tool for understanding chemical reactions inside the battery and the SEI formation mechanism.78,79 Two reasons lead to SEI rupture. On the one hand, the solvent diffuses through the SEI and interacts with Li in the graphite, which can exfoliate the graphite, generate gas, and expands and ruptures the SEI film. On the other hand, the volume of graphite increases in the lithiation process, which causes SEI to rupture.80 Therefore, SEI film is continuously reformed and thickened, which causes the Li-ions to be continuously consumed.
The growth rate of the SEI layer can be modeled by a linear relationship with side reaction current density, which is expressed as follows:74
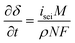 | (9) |
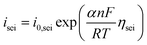 | (10) |
| ηsei = Vneg + ηneg − Vsei + rseiδI | (11) |
Metal (Li and transition metal) precipitation on the anode surface is another common side reaction that accelerates battery aging. Usually, lithium plating occurs under either high-rate charging, overcharging, or low-temperature conditions.81 The precipitated lithium metal can react with electrolyte, producing Li compounds that cover the anode surface, resulting in a considerable loss of Li inventory and an increased interface resistance, eventually leading to capacity degradation.82,83 The mathematic modeling of lithium plating is similar to the reaction of SEI side reaction since it also builds up a layer and clogs the anode pores.74 In addition, the plated Li can evolve into Li dendrites, which can penetrate the separator, causing an internal short-circuit and resulting in a possible safety problem.84 Moreover, the dissolution of transition metal from the cathode diffuses with the Li-ions, and deposits on the graphite surface or gets inserted into the graphite layer, which accelerates the exfoliation of graphite.
Besides, the decay of active materials (including mechanical damage of graphite particles and changes in the layer structure) is also an important factor in battery aging.85 The mechanical stress for lithium insertion and delithiation may cause mechanical failure, which can expand the graphite layer space and destroy the layer structure, resulting in accelerated graphite exfoliation.86 These phenomena would cause LAM and cause the SEI film to rupture, which leads to irreversible capacity loss.
In general, these positive electrodes are subject to some common aging-related reactions mainly including mainly including transition metal dissolution, phase transition, and crack formation.88 Transition metals are prone to react with species (such as HF) from electrolyte decomposition, and then dissolve, diffuse and deposit on the anode surface, as discussed above.89 Like the anode, the cathode also forms a passivation surface film during the first few cycles, which is commonly referred to as the catholyte electrolyte interface (CEI) film. The CEI film generally consists of lithium alkyl carbonates, lithium alkoxides, Li2CO3, etc.,90 These compounds are mainly produced from the side reactions between the cathode and the electrolyte. Note that the CEI film is generally thinner than the SEI film and does not cover the entire cathode surface. But it grows over cycling, which is the main reason for LLI and IR on the cathode.91
Cation mixing and lithium vacancies are the two most common structural failures in cathode materials. Cation mixing usually occurs at metal oxide cathodes due to the similar radius between some transition metal ions (Ni2+, Mn3+, Fe2+) and Li-ions.7 It leads to the distortion of the cathode structure, resulting in a reduced battery capacity. Besides, the inserted Li-ions in transition metal sites expand the interlayer spacing of the cathode, which hinders the transfer of electrons and increases the polarization of the battery.88 In addition, the cathode material may undergo irreversible phase transitions along with the battery aging process. Some phase transitions generate large mechanical stress, leading to crack formation as well as irreversible capacity degradation.92 Besides, the cathode cracks are also caused by the mechanical stress from the repeated processes of Li-ion intercalation and deintercalation.93
2.2. Influencing factors on battery aging
There are generally two types of aging, including calendar aging and cyclic aging.95 Battery calendar aging refers to the phenomenon that the available capacity decreases with time during battery storage. Cyclic aging refers to the irreversible capacity loss caused by repeated charge–discharge cycles. Different external conditions have different effects on the aging rate. Therefore, it is of great importance to fully understand the impact of various external factors on the battery aging rate, which helps build an accurate prognostic model for BMSs to extend the battery service life. The main factors leading to battery calendar aging and cyclic aging, the aging mechanisms accelerated by external factors, and the aging modes caused by the aging mechanisms are summarized and illustrated in Fig. 4.3. Battery health prognostics
In this section, a summary of the available data sets for research of battery health prognostics is first given in Section 3.1. Then the classification method for battery health prognostics will be provided and discussed in Section 3.2. After that, each type of method will be introduced, and their applications will be briefly summarized. The SoH estimation, EoL point prediction, and degradation trajectory prediction are reviewed in Sections 3.3, 3.4, and 3.5, respectively.3.1. Acquisition of battery aging data sets
Battery aging data are very important for battery health prognostics research. However, it is time and labor-consuming to obtain a large amount of data. Besides, the data quality is also affected by the operation and equipment. Therefore, some popular and recent datasets are summarized in this section. It is very helpful to make the data and code open access so that researchers can easily follow the research and develop their own studies based on the shared data and code. A common way to share the data and code related to the work is to provide the access link in the supplementary information of the published paper,111–114 which makes it easy to find for the readers. To share the data, a public data-sharing platform can be chosen, such as Zenodo,111,113,114 Mendeley,115 and OSF,116 or the personal website is also popular to share the data from the research group.35,117–119 For code sharing, it is convenient for readers to access when it is shared together with the related datasets,35,118,119 or a public code sharing platform can be chosen, such as Github.111,115 The detailed information of each data set is summarized in Table 2, where the battery chemistry and type, the aging cycling profiles, the degradation trends, and the publication year are included. Here the degradation trends mean the overall shape of the degradation curve, which includes sub-linear, linear, and super-linear.120Most public data are obtained from the aging experiment of the cylindric batteries, which are easy to experiment with due to their good stability and generally low nominal capacity. Only one data set from CALCE contains prismatic batteries, which were collected in 2014. However, due to their wide usage in EVs, more aging experiment on the prismatic cells are valuable for researchers developing and proving their advanced algorithms. Various types of battery cathode chemistries are included in these public data sets. For the profiles used for aging, most data sets used CC-CV charging and CC discharging procedures. Two data sets from MIT and Stanford were aged under multi-step fast charging followed by CC discharging. One data set from Oxford University and another from Stanford University contain dynamic discharging profiles, which are more relevant to practical applications. Two data sets from Cambridge University conducted aging on the coin batteries with EIS test. Most of the batteries show super-linear shapes and some of them are nearly linear and sub-linear. Overall, various scenarios and combinations of different batteries, aging profiles, and degradation curve shapes are included in these public data sets listed in Table 3. It is recommended that researchers choose several different data sets for their study of prognostic approaches, which enhances the validation.
| Data source | Chemistry of cathode | Battery types | Aging profiles (charging/discharging) | Degradation trends | Data and code link | Year |
|---|---|---|---|---|---|---|
| NASA121 | NCA | Cylindric | CC-CV/CC | Linear | https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/ | 2008 |
| CALCE122 | LCO | Pouch/prismatic | CC-CV/CC | Sub/super-linear | https://web.calce.umd.edu/batteries/data.htm | 2014 |
| Oxford123 | NCA | Pouch | CC-CV/dynamic + CC-CV/CC | Linear | https://ora.ox.ac.uk/objects/uuid:03ba4b01-cfed-46d3-9b1a-7d4a7bdf6fac | 2017 |
| Ref. 124 | LFP/NCA/NMC | Cylindric | CC-CV/CC | Linear | https://iopscience.iop.org/article/10.1149/2.1701712jes#s2 | 2017 |
| Ref. 119 | LFP | Cylindric | Multi-step CC − CC-CV/CC | Super-linear | https://data.matr.io/1/projects/5c48dd2bc625d700019f3204 | 2019 |
| Ref. 35 | LFP | Cylindric | Multi-step CC − CV/CC | Super-linear | https://data.matr.io/1/projects/5d80e633f405260001c0b60a | 2019 |
| Ref. 114 | LCO | Coin | CC-CV/CC | Sub-linear/linear | https://zenodo.org/record/3633835#.Y3YOLXbMJEY | 2020 |
| Ref. 117 | NCA | Cylindric | Calendar aging + CC-CV/CC | Linear | https://ora.ox.ac.uk/objects/uuid:de62b5d2-6154-426d-bcbb-30253ddb7d1e | 2020 |
| Ref. 125 | NMC | Cylindric | CC-CV/CC | Super-linear | https://git.rwth-aachen.de/isea/battery-degradation-trajectory-prediction | 2021 |
| Ref. 112 | — | Cylindric | CC-CV/CC | Super-linear | https://www.sciencedirect.com/science/article/pii/S2666389921001458?via%3Dihub#appsec2 | 2021 |
| Ref. 116 | NCM | Cylindric | CC-CV/CC-UDDS | Super-linear | https://osf.io/qsabn/?view_only=2a03b6c78ef14922a3e244f3d549de78 | 2022 |
| Ref. 113 | — | Coin | Random CC/CC | — | https://zenodo.org/record/6645536#.Y3YOd3bMJEY | 2022 |
| Ref. 126 | NCM/NCA | Cylindric | CC-CV/CC | Sub/super-linear | https://zenodo.org/record/6405084#.Y3YQ_3bMJEY/https://github.com/Yixiu-Wang/data-driven-capacity-estimation-from-voltage-relaxation | 2022 |
3.2. Classification of methods for battery health prognostics
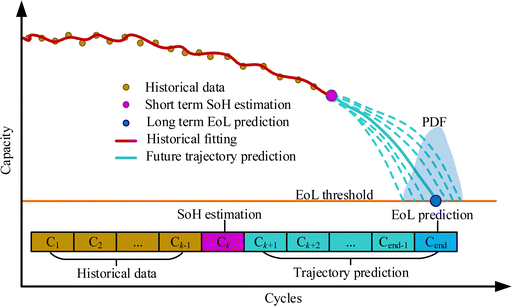
There are many types of methods for battery health prognostics, which are commonly divided into model-based, data-driven, and hybrid methods.41 This is a general classification for battery health prognostics despite different objectives. Unlike the classification above, for the first time, the prognostic objectives are used to divide the prognostic tasks into SoH estimation, EoL point prediction, and degradation trajectory prediction, respectively. Objective-based classification is used because different applications require different prediction objectives.The different objectives of the three tasks presented on the capacity degradation curve is illustrated in Fig. 5. At the current kth cycle, SoH focuses on capacity estimation at the current time, which is a short-term prognostic objective. The EoL prediction, on the other hand, concerns the end time when the battery reaches the EoL, indicating a long-term prediction objective. In contrast, the degradation trajectory prediction focuses more on the future degradation curve prediction until EoL.
The detailed classifications of battery health prediction are shown in Fig. 6. The objectives of the battery health prognostics are divided into three categories discussed above. Then, two types of methods are included in SoH estimation, which are model parameter optimization-based and machine learning based. For EoL prediction, data-driven methods are generally used which are further divided into feature-based methods and deep learning methods. The main difference is whether to extract the features manually or not. Finally, the degradation trajectory prediction contains three methods, which are curve fitting methods, model generation methods, and sequence prediction methods. They differ from each other in the way they predict future degradation curves. In this classification method, readers can consider their prediction task first, and then refer to the specific methods corresponding to this objective. The detailed concept, general implementation process, and representative works of the state of the art for each method are discussed in the following sub-sections.
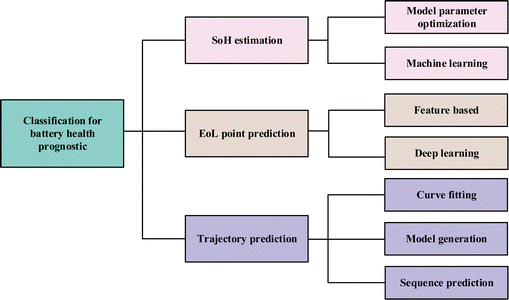 | ||
| Fig. 6 Classification of objectives and the corresponding methodologies for battery health prognostics. | ||
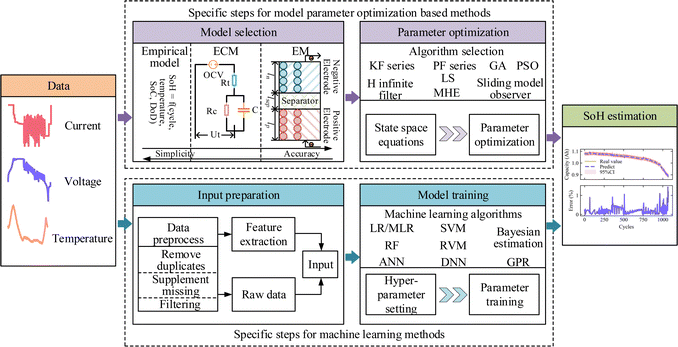
3.3. SoH estimation
Battery SoH estimation focuses on short-term capacity or resistance prognostics. Accurate estimation provides the health status of the battery at the current time, updates key parameters for other short-term state estimates such as SoC, guides optimal management strategy design, etc. The methods for battery SoH estimation contain model parameter optimization-based and machine learning methods, which will be reviewed in detail in the following subsections. The general process for the two types of methods for battery SoH estimation is illustrated in Fig. 7.SoH estimation via an empirical model is a simple yet mature method that maps the relationship between the influencing factors and battery SoH. For example, Chen et al.129 established a model that quantifies the relationship between the battery SoH and the diffusion capacity and temperature. The GA is used to identify the parameters to estimate the battery SoH online. Similarly, Zhang et al.130 considered the empirical model that captures the relationship between battery SoH and the charge transfer resistance, temperature, and SoC, where sequential quadratic programming was used for parameter optimization. A fused model containing capacity fade and internal resistance growth was built by Guha et al.131 PF was then used to optimize the model parameters for final SoH estimation. In addition, the empirical model that described the relationship between battery SoH and health indicators (HIs), which generally refers to some features extracted from measured data or calculated data, was built as the one state-space model, and the unscented PF was then applied for parameter optimization by Liu et al.132 However, poor physics interpretation and generalization become the main drawbacks of empirical models.
On the other hand, the ECM shows a satisfactory tradeoff between accuracy and complexity, which also has better physical interpretation compared to empirical models.133 1 resistor–capacitor (RC) and 2 RC models are the two most popular ECMs. Fleischer et al.134 used the weighted recursive least quadratic squares parameter estimator for the parameter estimation of a reduced 1 RC model, whose charge transfer resistance was used to quantify the SoH. Since different time-scales exist between different battery states, multi-scale estimation methods are widely used. For example, the adaptive sliding mode observer was used by Ning et al.,135 and the dual EKF was adopted by Yang et al.136 and Song et al.137 for the parameter optimization of the 1 RC model to estimate the SoH. Besides, the multi-scale modified MHE was proposed by Hu et al.138 for multi-state estimation based on the optimization of the parameters for the 1 RC ECM. The framework of the estimation process is shown in Fig. 8. The short-term SoC and SoP (state of power) estimations are combined with the long-term SoH estimation. Specifically, the real-time parameters of current and voltage are used for SoC estimation. The estimated SoC is further used for SoP (state of power) and SoH estimation. SoH is estimated during a long-time scale based on the ratio of the capacity variation to the SoC variation range. The estimated SoH is used to update the current capacity which helps the accurate estimation of SoC and SoP. The results showed the estimation accuracy superiority of mMHE compared to EKF. The 2 RC model with the above-mentioned sliding mode observer139,140 and DEKF141 was also widely used for battery SoH estimation. In addition, the genetic resampling PF was used to solve the multi-source noise to improve the accuracy of the SoH estimation for the battery pack by Bi et al.142 Zhu et al.143 integrated the unscented KF and improved the unscented PF for better accuracy and reducing the calculation time of SoH estimation. Finally, the fractional-order model (FOM), another type of ECM, is also becoming popular for battery state estimation. The FOM was combined with DEKF by Hu et al.144 to ensure that the estimated error was less than 1% for both SoC and SoH estimation. Yang et al.145 adopted GA for parameter optimization of the FOM to estimate SoH with absolute error less than 1.5%. However, the limited information obtained using current external sensors makes it hard for accurate and robust estimation under different scenarios. On the other hand, the internal sensing technology promotes smart battery development with highly efficient detection and management, such as thin film strain gauge and fiber sensing methods.146,147 For example, Wei et al.148 proposed a joint estimation framework with an embedded and distributed fiber optical sensor for internal and surface temperature measurement. After understanding the internal structure of the cylindrical battery by computerized tomography scanning, a 0.9 mm hole is drilled into the center of the negative terminal. Then, the positive terminal is isolated using the Kapton tape, and the sensor is inserted from the negative terminal. By combining it with a low-order observer, the estimated capacity reaches a maximum mean absolute error of less than 0.12 A h, and the comparisons between the conventional electrical model-based method indicate better accuracy and robustness of the proposed new sensor information integrated method.
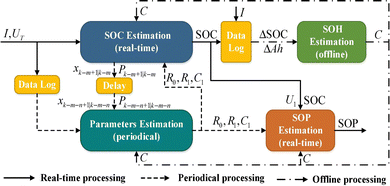 | ||
| Fig. 8 Typical framework of multi-state estimation, adapted from ref. 138 with permission. | ||
The last type of model for battery SoH estimation is EM, which uses partial differential equations to describe the internal electrochemical reactions. Therefore, the physical meaning and accuracy are the most significant advantages of EM. However, the complexity of the full P2D model is very high, which makes it difficult to solve. Therefore, two ways are generally used for the implementation of EM for battery SoH estimation. The first is to simplify the model. The most popular simplified EM is the single particle model, which assumes the electrode can be idealized as a single spherical solid particle.149 Zheng et al.150 proposed proportional-integral observers to estimate the SoC, capacity, and resistance with the SPM. Moura et al.151 used Padé approximation for parameter identification of the SPM and adaptive observer for SoH estimation. The SPM was also used by Hu et al.152 to construct a multi-scale MHE optimizer for battery SoC and SoH estimation. Another way is to simplify the partial differential equation via approximation methods to solve the P2D model. Gao et al.153 simplified the full P2D model using Padé approximation to obtain the state-space expression while ensuring the model's precision and observability. Then the dual extended Kalman filter (DEKF) was used for the co-estimation of battery SoC and SoH with RMSE less than 0.5%. Besides, the P2D model was simplified via parabolic profile approximation by Liu et al.154 The PF was then used for online state estimation and the SoH was estimated based on the average lithium concentrations predicted at the cut-off voltages.
In feature-based methods manually extracted features are needed to prepare the inputs, which is also known as HI extraction.155 These HIs refer to some indices extracted from measured or estimated parameters to reflect the aging status. General HI extraction can be divided into direct extraction from measured data such as current, voltage, and temperature, and indirect extraction from some calculated data such as incremental capacity (IC) curve and differential temperature (DT) curve. One common way to evaluate the effectiveness of the extracted HIs is to calculate the correlation coefficients between the HIs and battery capacity. The correlation coefficient analysis is also the most popular way to select the final inputs for machine learning, which is known as the filter-based method. However, it was pointed out in ref. 156 that the HIs simply selected based on the correlation coefficients may have high redundancy, and that some of them need also be removed from the subset. Another method is to use an optimal search method for HI selection, such as the wrapper method. The next step after input preparation is data-driven model training. Since the extracted HIs generally have high linear correlations with battery capacity, linear regression (LR) and multi-linear regression (MLR) can meet the requirement. Other nonlinear mapping algorithms also show satisfactory performance, such as support vector regression (SVR), random forest (RF), and artificial neural networks (ANN). To provide probabilistic estimation, Bayesian estimation, relevant vector regression (RVR), and Gaussian process regression (GPR) are popular. After the model is trained by the training data set, the model can be used for SoH estimation in the testing data set to evaluate the accuracy and reliability.
Extracting features from measured data is the direct way to implement feature-based SoH estimation. Meng et al.157 figured out that the voltage response to the pulse current varied with battery aging and selected four representative voltage values as features. The integration of several weak learners was proposed to boost the overall performance of the final SoH estimation.158 Sui et al.159 extracted the fuzzy entropy of the voltage response to the pulse current as a feature and used SVR to estimate the SoH. The method was verified at different aging temperatures. The information on the charging process was extracted to be the features by Roman et al.,160 such as voltage slope, mean voltage, energy, entropy, skewness, and time difference of the voltage curve. Then the pipeline was proposed to select features automatically for SoH estimation. Zhu et al.126 extracted similar features from the relaxation process after fully charging to estimate the SoH with different machine learning algorithms. Transfer learning was adopted to improve the accuracy of the estimation for different batteries.161 Transfer learning is one advanced learning method that uses knowledge from one domain and applies such knowledge to different but the related domains. It aims to reuse or transfer information from previously learned tasks to improve convergence efficiency and model accuracy in new tasks. Che et al.162 extracted features from partial discharging data and integrated the degradation pattern recognition and SoH estimation. Specifically, the detailed framework is shown in Fig. 9. First, standard deviation, Shannon entropy, and the first principal component are extracted as features from the partial capacity-voltage curve and partial differential capacity-voltage curve. These features are used for both pattern recognition that helps find the most relevant reference batteries as source batteries and SoH estimation modeling. Transfer learning with a probabilistic neural network was used for health prognostics. Only several checkpoints with real labels are used for the retraining process that achieves high accuracy and reliability of the estimations with errors of less than 2%. Features extracted from the EIS data also showed high correlations with battery capacity and were used for battery SoH estimation by Fu et al.163 and Zhang et al.114 Vilsen et al.164 extracted and selected features from the voltage curve using field data based on two stages of principal component analysis, and achieved the SoH estimation for practical use with MLR. Extracting features from transformed curves is also popular and effective for feature-based battery SoH estimation. For insistence, Wei et al.165 extracted both the morphological IC feature and entropy information of voltage from partial charging data to estimate battery SoH via ANN. She et al.166 extended the IC-based method for the SoH estimation of real-world EVs. The cell inconsistency was taken into consideration to illustrate the inconsistency variation during aging. DT voltammetry was used for the feature extraction by Wang et al.167 and Li et al.168 to estimate the battery SoH. The extraction method of DT is similar to that of IC. In addition to extracting features from measured data and transformed data for SoH estimation, the feature extraction from model parameters mentioned in the above subsection can be treated as a typical model-data fusion method. For example, the internal resistance and polarization resistance of the 1 RC ECM were extracted as features by Lyu et al.169 to estimate the battery SoH based on GPR. Representative features extracted from the SPM170 and electrochemical-thermal models171 also show satisfactory performance for battery SoH estimation. More physical explanations are contained by the features extracted from EM.
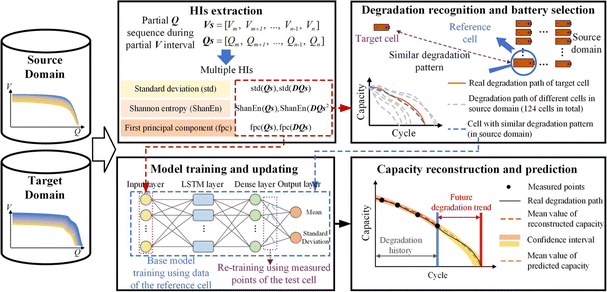 | ||
| Fig. 9 Typical framework for feature-based SoH estimation with transfer learning, adapted from ref. 162 with permission. | ||
Feature-free methods refer to machine learning-based battery SoH estimations without manual HIs extraction and selection process. Since the manually extracted HIs require specific data of the parameters and the HIs vary from one testing condition to other conditions, HIs usually have poor generalization. In addition, it is hard to find perfect HIs. Therefore, researchers use the raw measured data for the machine learning algorithm, in which the data-driven model is expected to extract the hidden features themselves. The automatic feature extraction by a data-driven model requires strong nonlinear ability, which makes the deep learning method the preferred choice. The auto-encoder and decoder with multi-layers are popular for automatic feature extraction. The convolutional neural network (CNN) and recurrent neural network (RNN) show satisfactory performance in this regard.115 Therefore, the model is trained directly by the processed raw data and then applied to SoH estimation.
Tagade et al.172 used the deep GPR framework for battery SoH estimation using raw data from the discharging process without feature engineering. The time series data of voltage and temperature were used directly as inputs. Jones et al.113 integrate the loading profile and the EIS measurement to achieve SoH estimation under random charging/discharging conditions, where historical information is not required. Gong et al.173 adopted the encoder–decoder model-based deep learning method for battery SoH estimation using the charging curves. For the encoder process, two-dimensional convolution modules were adopted, while the BP neural network was used in the decoder process for the final SoH estimation. Different types of batteries were used for the verification of the proposed method with errors of less than 2%. Zhou et al.174 proposed a temporal convolutional neural network (TCN) based deep learning method for battery SoH estimation using the raw data of partial voltage and temperature. Fan et al.175 fused the gated recurrent unit neural network (GRU) and CNN to improve the accuracy of SoH estimation using raw data of current, voltage, and temperature. A general method for battery health prognostics using CNN-based deep learning was proposed by Ruan et al.,176 where the internal electrochemical parameter degradation can also be diagnosed. The domain adaptation method was used by Han et al.177 and Ma et al.178 to improve the estimation accuracy under different battery applications using long-short-term memory (LSTM) and CNN bottleneck, respectively. The main idea was to reduce the domain discrepancy between the hidden layers which represent the information vector for the source domain and target domain.
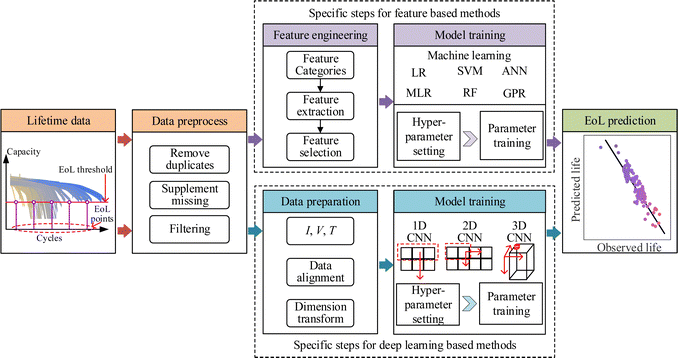
3.4. EoL point prediction
For long-term lifetime prediction, the first type of method is called EoL prediction, where the lifetime or RUL is directly regarded as a target to obtain feature-based machine learning or feature-free deep learning method. The flowcharts of these two methods are shown in Fig. 10. Since the EoL prediction is generally conducted by using multiple batteries, almost all the methods belong to data-driven methods. The main difference is whether specific feature engineering is needed and the selection of machine learning algorithms.Although in implementation we only need one feature data from one battery for lifetime prediction, in training, many batteries are needed to fit the regression relationship, which is time and labor-consuming. Therefore, few people had studied this type of method for battery lifetime prediction before Severson et al.119 generated a dataset consisting of 124 cells. They provided a feature that was calculated by the variance of capacity change between the 100th and 10th cycle, that is ΔQ100–10(V), which showed high correlation with battery EoL. Then, researchers from the same group proposed the capacity matrix concept along with a series feature representation. They also developed and compared various machine learning methods, which can be regarded as the benchmark of more advanced related studies.179,180 Some other researchers have conducted methods to improve the lifetime prediction accuracy based on the work of Severson et al.119 whether using more manually extracted features with the optimal feature selection method181–183 or improved hybrid machine learning algorithms.184,185
In addition to the feature-based lifetime prediction reviewed above, Paulson186 evaluated the feature-based lifetime prediction on their own data set, which includes 300 pouch batteries with six different cathode chemistries. Yan et al.187 extracted features from the IC curve to estimate the capacity first and then predicted the lifetime by fusing the empirical model and SVR-based predictions. Weng et al.188 extracted resistance at a low SoC as a feature, which realized very early stage lifetime prediction after manufacturing for NMC batteries. Stock et al.189 also managed to predict the lifetime of NMC batteries at an early stage with features extracted from electrochemical impedance spectroscopy (EIS) and cycling data. These two works show prospects for EoL point prediction with the resistance-based feature extraction method.
Due to the availability of a large amount of data, this type of method has also developed rapidly recently. The CNN-based method is the main method, because of its strong feature extraction ability. Due to the different input dimensions and feature extraction requirements, the 1D CNN, 2D CNN, and 3D CNN are adopted. For example, Hong et al.190 developed an end-to-end battery EoL prediction method based on a dilated CNN with uncertainty expression. The results showed better prediction accuracy compared to the feature-based prediction method proposed in ref. 119, with data containing only 4 cycles for inputs. The hybrid parallel residual CNN was proposed in ref. 191 to predict the lifetime of batteries. The voltage, current, and temperature were constructed as 3-dimensional inputs for CNN. Two attention algorithms were designed to highlight the prediction. The prediction results showed only a 1.1% error with only the first 60 cycles. Zhang et al.192 also predicted the EoL of batteries based on a similar deep-learning framework using partial charging curves that included only 20% of the capacity range. Hsu et al.193 adopted CNN for battery EoL prediction using only one cycle. The advantages of the deep learning extracted features compared to human-picked features for battery lifetime prediction were evaluated in this paper. These papers showed that the deep learning method has better accuracy and generalization than the feature-based EoL prediction, which would help deep learning-based prediction to become one main trend in this field. Recently, Ma et al.115 generated a dataset of aging batteries under different protocols to be used in their deep learning method for battery EoL prediction with unknown usages. As shown in Fig. 11, different usages cause different degradation patterns and capacity distributions. The authors used the partial voltage and charged capacity, differential partial voltage and charged capacity curves for the deep learning model training to map the relationship between the battery capacity and EoL. With the latest 30 cycles for the model's fine-tuning, the deep learning method achieved mean testing errors of less than 8.27% for battery EoL predictions without more historical information starting from fresh batteries. Cloud computing, big data platforms, etc., will promote the development of this type of method for online implementation.
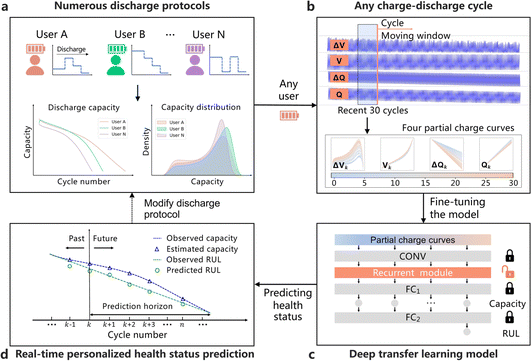 | ||
| Fig. 11 Typical framework for battery EoL prediction using deep learning, adapted from ref. 115 with permission. | ||
3.5. Degradation trajectory prediction
Although EoL prediction shows satisfactory results for both feature-based methods and deep learning methods with data at a very early aging stage, the obtained information is still lacking. For example, the specific degradations at different aging stages cannot be known. Therefore, degradation predictions try to predict the future trajectory curve of the degradations to provide more information for battery PHM. The main methods can be divided into three categories which include curve fitting, model generation, and sequence prediction methods. The general processes for these three types of methods and their specific steps are illustrated in Fig. 12. The detailed method description and the corresponding state of art are presented below.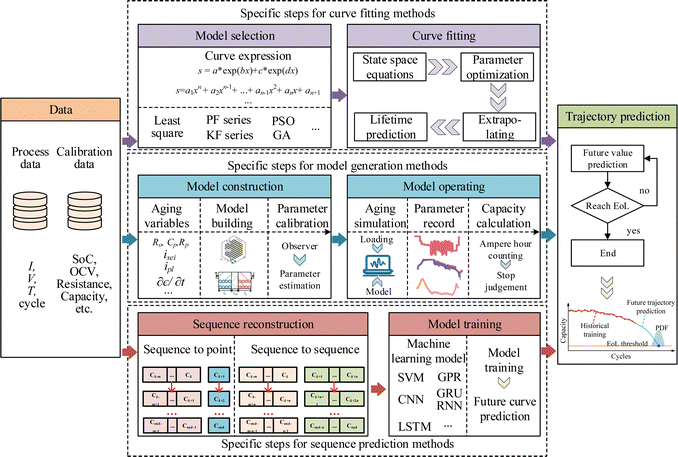 | ||
| Fig. 12 Methods for battery degradation trajectory prediction and the corresponding general framework. | ||
The curve fitting method is simple to implement in the PHM system and is mature in this field. Some representative works are reviewed to illustrate the usage and performance of this method. He et al.196 initialized the exponential model parameters based on the Dempster-Shafer theory using three training batteries, then Bayesian Monte Carlo was used to update the model parameters while acquiring new data to predict SoH and RUL. A semi-empirical model was proposed to model battery degradation and used together with a severity factor map within the hybrid vehicle simulator to minimize fuel consumption and battery degradation.197 The SEI layer growth and LAM can also be considered in the semi-empirical model to fit the aging curves for capacity estimation and RUL prediction.198 The calendar and cycle aging were combined in the semi-empirical model to fit the degradation, where the influence of DoD, C-rate, SoC, and rest periods were considered to improve the accuracy.199 The above stress factors on capacity degradation were evaluated in ref. 200, and the temperature was found to be the most significant factor in battery aging. Liu et al.201 combined the curve fitting process with GPR to provide the probabilistic prediction for the future capacity curve. The curve fitting method was used to quantify the mean function of GPR and transferred to the testing batteries with early updating. The sequential capacity estimation method was proposed in ref. 202 to update the parameter of the model for capacity degradation fitting. In addition to the model expression to map the relationship, machine learning can also be used to fit the curve that represents the relationship between the number of cycles and capacity or power fade for future degradation trajectory prediction.203 The main idea is the same as model-based fitting. Therefore, we put them in the same category as the curve fitting method. A typical fused method that combines the machine learning method and filtering-based curve fitting is shown in Fig. 13.204 The historical capacity degradation data are used to fit the exponential function and an LSTM model. Then, in the extrapolation-based prediction process, the predicted value of the LSTM served as the measurement to update the parameter of the empirical function by PF. The EoL is predefined to stop the prediction that calculates the RUL.
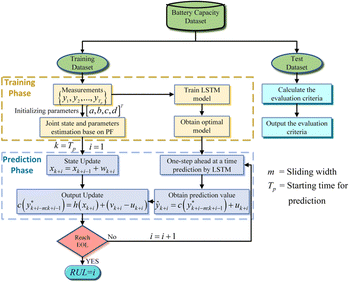 | ||
| Fig. 13 A typical framework for the fusion of filtering method and machine learning for degradation curve fitting-based trajectory prediction, adapted from ref. 204 with permission. | ||
 | ||
| Fig. 14 The general framework for model generation-based trajectory prediction and future voltage variation prediction, adapted from ref. 41 with permission. | ||
There are many works on this kind of generation. For example, Ecker et al.206 conducted an accelerated aging test to fit a semi-empirical aging model and then integrated the impedance-based electro-thermal model to simulate the aging of a high-power NMC/graphite lithium-ion battery. Atalay et al.207 developed a 1D–P2D battery model which considered multi-layered SEI, lithium-plating, and reduction of anode porosity kinetics. Then the model was used for both capacity estimation and lifetime prediction. Pinson et al.208 developed an SPM that considered the change of the SEI layer as the main aging phenomenon to predict the capacity fade and lifetime of batteries. Sulzer et al.209 used the adaptive inter-cycle extrapolation algorithm to accelerate the simulation of the SPM during aging for lifetime prediction. Li et al.210 proposed a comprehensive SPM with aging mechanisms for battery cycling capacity prediction, which achieved less than 2% prediction error over the entire lifetime. The volumetric fraction change on the cathode and lithium loss on the anode was considered as the mechanisms affecting battery aging. The main degradation mechanism at different aging stages has been illustrated. Kupper et al.211 integrated three aging mechanisms, including the formation and growth of SEI film, and dry-out of the electrode in the pseudo-3D model to simulate the aging process of LFP/C batteries. The aging model was successful in both calendric and cyclic aging simulations. Lui et al.212 proposed a physics-based model for battery lifetime prediction with the estimation for key parameter degradation. Reniers et al.74 also integrated different aging mechanisms into the SPM for the aging simulation of batteries, and a toolbox was provided to support simulation with different aging mechanism considerations.
Due to the high sequential relationship of the capacity variation and the ease of implementation, sequence prediction for battery trajectory prediction has been developed rapidly in recent years. The iterative method for sequence-to-point prediction was combined with the Gray model to predict the future capacity, and PF was added for the uncertainty expression of the predicted lifetime by Chen et al.169,214 A similar idea was also shown in ref. 215, where the LS-SVM was used to predict the capacity of the next cycle while PF is used to update the parameter. Since the degradation curves are impossible to be smooth in actual measurements, the degradation curve was first decomposed by empirical mode decomposition, and then two different models were used to fit the sequence model of the first two intrinsic mode functions to predict the future degradation curve.216,217 A cell-to-pack method was proposed in ref. 218 based on the sequence-to-point prediction of future HIs for each connected battery cell. Then the future capacities of both battery pack and each connected battery cell were predicted through GPR. The transfer learning strategy was adopted to adapt the varying properties of each connected cell by using the information from the separated aged battery cells. A fusion method was proposed in ref. 215, where the one-step capacity is predicted by the time-series model first, and then the dual filters were proposed to update the final predicted capacity.
Although the sequence-to-point method is easy to implement and only the historical degradation data are required for model construction, the method may encounter fast degradation or slope vanish problems. Therefore, the sequence-to-sequence method predicts future degradation curves via less interactive steps, which avoids the above problem. Sequence-to-sequence model uses the capacity sequence before the current cycle to predict the future capacity sequence until the EoL which reduces the iterative steps. A typical work using sequence-to-sequence-based prediction is shown in Fig. 15.219 Similar to the works shown in ref. 161, the authors extracted both data features and physics-based features to group the batteries into three groups that have long lifetimes, medium lifetimes, and short lifetimes. Two LSTM layers are used for the encoder and decoder that predict the capacity curve degradations. The results show that only 20% of the historical data of the encoder can produce the future trajectory curve with errors of less than 2.5%. Tong et al.220 used adaptive dropout-based LSTM and Monte Carlo simulation to predict the future capacity degradation curve for battery lifetime prediction via a many-to-many structure. With the first 25% of the degradation data, the prediction errors were less than 4%. Li et al.125 proposed the one-shot prediction method to predict the future capacity via a sequence-to-sequence method based on LSTM with autoencoder and decoder methods. The EoL point and knee point were predicted together with the future degradation sequence. The robustness of the proposed method was verified by adding noise to the original capacity, and the prediction errors remained less than 1.3%. They further proposed a multi-task method to predict the variation of capacity degradation and resistance increment in the future aging process.118
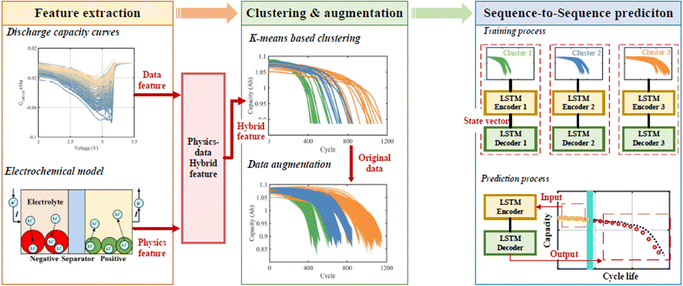 | ||
| Fig. 15 The typical framework for the sequence-to-sequence-based trajectory prediction, adapted from ref. 219 with permission. | ||
4. Comparative evaluations
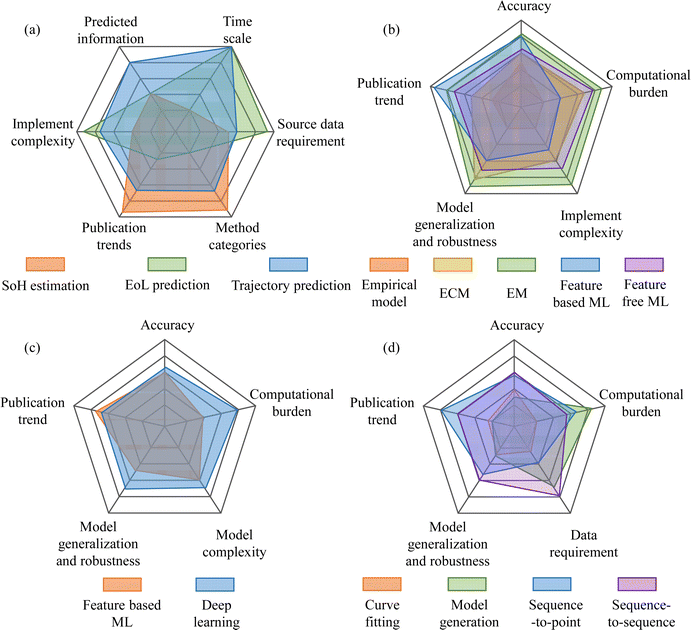
The objects for different types of health prognostic tasks are different, as mentioned before. In each prognostic task, various methods are used. In this section, the overall comparative evaluation for the SoH estimation, EoL prediction, and degradation trajectory prediction is first carried out. Then, the evaluations of different methods for each task are presented and discussed. These comparative evaluations are shown in Fig. 16, which are discussed in detail below.4.1. Evaluation for the prognostic tasks
The predicted information, timescales, source data requirements, method categories for each prognostic task, publication trend, and implementation are evaluated and compared. It is shown in Fig. 5 that SoH estimation and EoL prediction only focus on the prediction of one specific point, either for short-term or long-term. In contrast, all degradation values of the future SoH until the EoL point are needed to predict in the degradation trajectory prediction task, which provides more health information than SoH estimation and EoL prediction. For the data requirements, SoH estimation needs historical information or data from a few other batteries for the modeling, which is similar to the requirement of degradation trajectory prediction. While for the EoL prediction, since one battery has only one EoL point, a large number of batteries aged to EoL are needed to build the prediction model. It can be seen from the stat-of-the-art review in the above sections that the way SoH is estimated varies. Many methods can be used for SoH estimation; most of them are mature, and some have been used in real-world EVs. There are many methods for degradation trajectory prediction, but still a little less than SoH estimation. However, due to the limitation of data, EoL prediction has been developed slowly and has much fewer methods than SoH estimation and degradation trajectory prediction. Therefore, the publication trends for SoH estimation, degradation trajectory prediction, and EoL prediction also show a similar pattern. Batteries generally degrade in different ways due to random usage scenarios, which makes them have different degradation patterns and lifetimes. Therefore, the implementation of degradation trajectory prediction and EoL prediction is generally more difficult than SoH estimation. The EoL prediction in existing works is based on the aging of many batteries under similar conditions, which makes them difficult to implement in actual applications under various external conditions. The above evaluation is illustrated in Fig. 16(a).4.2. Evaluation of the prognostic methods
Comparative evaluations for methods of each specific task are presented in this section, where the methods for SoH estimation are firstly evaluated. Different aspects are considered to compare the different methods for battery SoH estimation, including accuracy, computational burden, implementation complexity, model generalization and robustness, and publication trends. Specific implementation methods are compared, which are empirical model-based, ECM model-based, EM model-based, feature-based ML, and feature-free ML. As mentioned before, the EM contains the most physical information while the empirical model contains the least, and the ECM is in the middle. The accuracy shows a similar trend while the computational burden shows the opposite trend. Feature-based machine learning is generally more accurate than feature-free machine learning and requires less computation. The accuracy of the ML learning-based method is similar to that of the ECM and EM model-based methods and is better than the empirical model-based method. However, the implementation complexity is higher because a strict feature engineering process is needed. Similarly, EM is the most difficult one for implementation, while the empirical model is easy to use in real-world applications. On the other hand, the empirical model has the worst model generalization and robustness, while the EM has the best. The ML-based method has similar performance to the ECM model-based method, while the feature-based method is worse than the feature free based method. Finally, for the publication trend, ML-based methods showed a higher growth rate than the model-based methods. The feature-based method has a bit higher growth rate than the feature free method. The EM-based method is more popular than the ECM, which has more research interest than the empirical model-based method. The main advantages and disadvantages of the different methods for battery SoH estimation are listed in Table 4.| Objective | Methodology | Advantages | Disadvantages |
|---|---|---|---|
| SoH estimation | Empirical model parameter optimization | □ Easy to implement in real world | □ Enough experiment to map the empirical model |
| □ Fast calculation | □ Poor generalization | ||
| □ Mature | □ Low accuracy | ||
| ECM parameter optimization | □ Better physical interpretability | □ Poor performance in low temperatures | |
| □ A few parameters | □ Poor performance with high current | ||
| □ Low computational burden | □ Difficult to implement in real world | ||
| EM parameter optimization | □ High physical interpretability | □ Difficult to implement in real world | |
| □ High accuracy | □ High computational burden | ||
| □ Robustness under extreme conditions | □ Difficult to calibrate parameters | ||
| Feature based ML | □ High accuracy | □ Poor generalization | |
| □ Low computational burden | □ Sensitive to work conditions | ||
| □ Easy to understand | □ Depending highly on the features | ||
| Feature free ML | □ Raw data only | □ High computational burden | |
| □ High accuracy | □ Sensitive to the processed raw data | ||
| □ Good generalization | □ Poor interpretability | ||
| EoL prediction | Feature based | □ Early prediction | □ Large requirement of experiments |
| □ Low computational burden | □ Difficult to find suitable features | ||
| □ High accuracy with one certain battery chemistry | □ Sensitive to battery chemistries and aging profiles | ||
| Deep learning | □ High accuracy in early prediction | □ High computational burden | |
| □ Good generalization | □ Difficult to implement in real world | ||
| □ Raw data only | □ Poor interpretability | ||
| Future trajectory prediction | Curve fitting | □ Clear correlation with indicators | □ Poor performance in early prediction |
| □ Fast calculation | □ Plenty of experiments are required | ||
| □ Support onboard application | □ Poor generalization and low accuracy | ||
| Model generation | □ Future process data are obtained | □ Difficult to calibrate parameters | |
| □ Better physical interpretability | □ Low accuracy | ||
| □ Support fast aging simulation | □ Difficult to implement onboard | ||
| Sequence to point prediction | □ Both historical data and data from other batteries support the modelling | □ Difficult for early prediction | |
| □ Accurate short-term prediction | □ Easy to diverge during iteration | ||
| □ Lower data requirement | □ Sensitive to window length | ||
| Sequence to sequence prediction | □ High accuracy | □ Require different degradation data | |
| □ Support early prediction | □ Poor generalization | ||
| □ Fast prediction in one shot | □ Data need to be in the same length |
To compare feature-based EoL prediction and deep learning-based EoL prediction, indices including the accuracy, computational burden, model complexity, generalization and robustness, and publication trend are considered. According to the published studies, the accuracy of deep learning-based EoL prediction is better than that of feature-based methods, while the computational burden and model complexity are much higher. The generalization and robustness for feature-based methods are poor since the specific feature for specific batteries and working conditions are needed, while those for the deep learning-based method are better since raw data are directly used. The publication trends for feature-based and deep learning methods are similar since all of them have become hot research topics recently. The main advantages and disadvantages of the feature based and deep learning methods for battery EoL point prediction are listed in Table 4.
Finally, a comparative evaluation among the curve fitting based, model generation based, sequence to point-based, and sequence to sequence-based degradation trajectory prediction is conducted and discussed. Similarly, prediction accuracy, computational burden, data requirement, model generalization and robustness, and publication trends are considered as comparative indices. First, the accuracy of curve fitting and sequence prediction is generally better than those of the model generation method since the parameters in the aging model are difficult to calibrate and vary. The sequence-to-sequence prediction method shows a little better accuracy than the sequence-to-point method because the integral error from the iterative process can be alleviated. However, the data required for the training of the sequence-to-sequence method are larger than that for the sequence-to-point method. The data required in the curve fitting method are small because only historical data are required or with degradation data from a few other batteries, which is like the sequence-to-point method. The model generation method needs the whole aging test to calibrate the model, and several different working conditions are needed, which are larger than the above two methods while less than the sequence-to-sequence method. The training burden for the sequence-to-sequence method is higher than for the sequence-to-point method, but fewer steps are required in the prediction process. The curve fitting method requires the least computation, while the model generation requires the most calculation time. Transfer learning is proposed as a data-driven method that improves model generalization. The curve fitting and model generation methods have a relatively poorer generation because the parameters are just suitable for the specific battery aging under specific conditions. Due to the advanced machine learning and availability of a large amount of data, the data-driven method shows a fast publication rate, especially the sequence-to-point prediction. The model generation is hard to implement and there are few studies. While the curve fitting method is the earliest and most mature, this also results in fewer publications than data-driven methods. The main advantages and disadvantages of the different methods for battery future trajectory prediction are listed in Table 4.
Therefore, when studying battery health prognostics, it is recommended to consider the specific task first, then select proper methods according to the main indices in the specific applications. However, from the comparative evaluations above, the model-based methods are mainly focused on the coupled EM modeling and the collaboration with data-driven methods is a promising approach to the complex problem. On the other hand, as the computation of the battery management system is approaching the limit, the advanced data-driven methods combined with cloud edge is a potential research direction. Therefore, in the next section, some practical challenges are listed with potential solutions, as well as research prospects considering the advanced methods and algorithms.
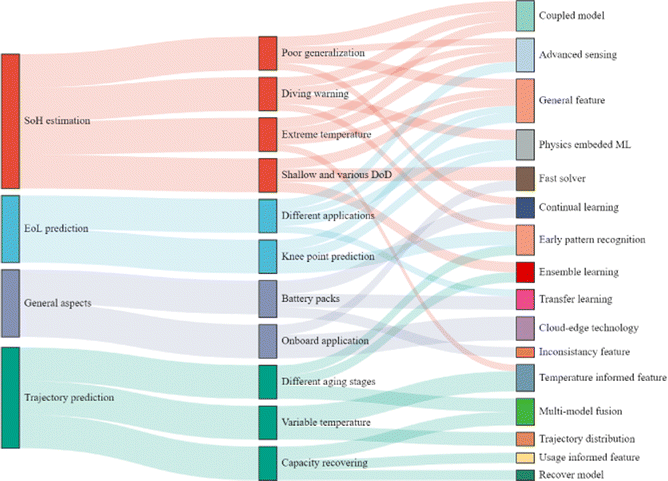
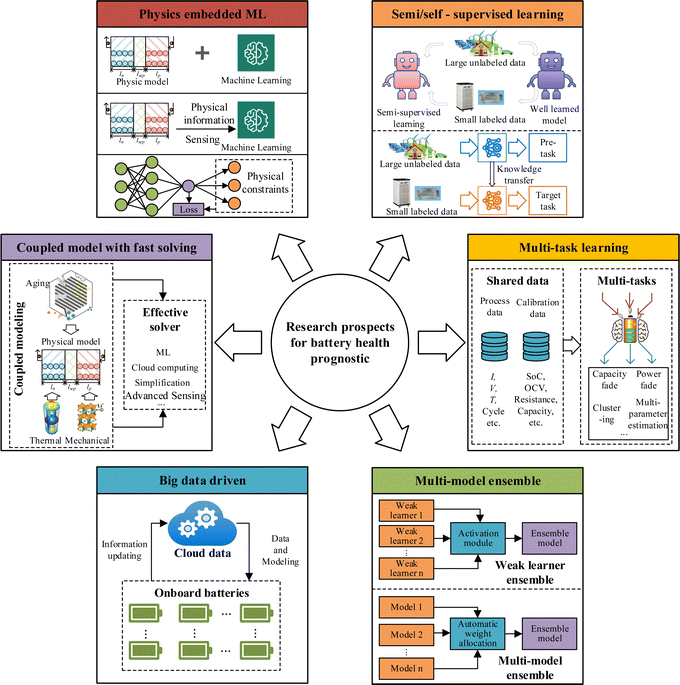
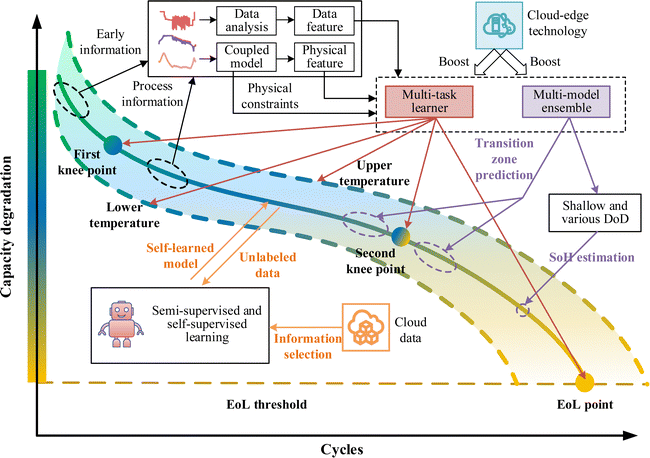
5. Key challenges and research prospects
Battery health prognostics is one significant and hot research topic in battery management. Various methods that consider different application requirements have been proposed in this field. It is important to know the key challenges and the main research focus. In this section, the main challenges and some potential solutions, as well as future research prospects, are presented and discussed.5.1. Main challenges and potential solutions
Many useful methods have been proposed in recent years for battery health prognostics and significant progress has been made in this field. However, there are still several major challenges in the following aspects, which are summarized according to the actual use. Some potential solutions for these challenges are presented and discussed. The evaluations of the potential solutions are also presented, considering the accuracy, robustness, and complexity. The overall illustration is shown in Fig. 17.A. Model transfer for different chemistries with different load profiles. The SoH estimation method is generally difficult to satisfy the accuracy requirement when the model is applied to batteries with different chemistries and different loading profiles. For the models built based on the model-parameter optimization-based method, the parameters are generally not suitable for other chemistries, and the model response can be different under different loading profiles. Therefore, it is challenging to build a model that can be used widely for different battery chemistries. For machine-learning-based SoH estimation, the trained model cannot cover different aging patterns either. For different battery chemistries and load conditions, the feature extracted either manually or automatically may have different correlation relationships between battery SoH and working conditions. Therefore, the highly coupled physics-based models are better for meeting the SoH estimation requirement under different scenarios. However, as the model become highly coupled, the computation and estimation of model parameters become the major challenges. Solving the coupled model may be achieved by designing a fast solver combining ML to establish the physics-informed machine learning framework. For example, the governing equations of P2D models can be solved by developing a physics-informed ML to accelerate the calculation. The accuracy and robustness remain high while reducing the computational complexity. Additionally, the low sampling frequency of the collected data in the real world is still challenging for the parameter calibration of mechanistic models. The advanced sensing technology is also a promising way to reduce the complex parameter identification process of the coupled electrochemical model by detecting the internal variations and key parameters related to battery aging such as the electrolyte density. For ML methods, labeled data from the source domain and unlabeled and insufficient labeled data from the target domain need to be used to estimate testing batteries. General features should be extracted to cover scenarios of different aging modes, which makes the data-driven model more robust and accurate under different aging scenarios. Continual learning is also a good way to learn the aging characteristics from different scenarios to make the trained model suitable for broad applications. The continual learning strategy can maintain the accuracy and robustness of the estimations under different new aging scenarios. However, the continuous online storage of huge amounts of data needs to be solved.
B. Estimation at extreme temperatures. Generally, research on battery health estimation only focuses on the verification at normal ambient temperatures. However, the battery electrochemical reactions at low temperatures differ considerably from those at normal temperatures, which makes the aging mechanisms and degradation patterns significantly different. The models also have poor performance under low temperatures, which makes it difficult to estimate the parameters accurately. This difficulty compromises the accuracy of the model-parameter optimization-based SoH estimation. On the other hand, the voltage and temperature responses varied under low temperatures, which makes it difficult to extract effective features. Therefore, the data-driven methods for SoH estimation also lose performance at low temperatures. Regarding the high-temperature conditions, battery aging accelerates and more potential failures such as fast growth of the SEI film and the degradation of the cathode material could happen. The high temperature changes the degradation patterns which causes the model developed at normal temperatures to perform poorly at high temperatures. For potential solutions, the temperature information needs to be added to the modeling of the model-parameter-based SoH estimation framework to ensure effective estimation at extreme temperatures. However, modeling at extreme temperatures is challenging since the internal electrochemical reactions have different representations from those at normal temperatures. Investigating highly coupled modeling is valuable to cover the estimation at extreme temperatures. The coupled model captures the aging and temperature information which makes the model accurate and robust under different temperature and aging scenarios. For the machine learning-based method, the effective feature extraction method suitable for large temperature ranges is one of the important research directions to ensure accurate estimation at extreme temperatures. Temperature-informed features should be extracted to represent characteristics under variable temperatures. These features can be extracted from the physics model such as the calculated SEI thickness parameter, lithium plating side reaction potential, etc. to accurately describe the aging mechanisms at extreme temperatures. However, the general features and temperature-dependent features, which have high robustness under different aging scenarios, are hard to extract and require a large number of experiments for investigations. In addition, the internal temperature sensing technology helps obtain accurate temperatures inside the battery, which will also improve the accuracy and robustness of the estimations in future smart batteries.
C. Estimation with the shallow and varying DoD. Generally, both parameter optimization-based and data-driven methods for battery SoH estimation require sufficient data covering stable and relatively wide DoD. However, in actual applications, shallow or varying DoDs are more common, which makes it difficult to use the built model for accurate battery SoH estimation. For example, different DoDs make the estimated parameters of the models inaccurate under the current conditions, which brings large errors to the final SoH estimation. In data-driven methods, the shallow DoD brings big challenges for effective manual or automatic feature extraction, which causes big errors to the SoH estimations. Therefore, the different and shallow DoDs in practical applications are one of the major challenges in battery SoH estimation. The parameter estimated by the model can be correlated to those at different DoD and SoC stages that support the model transfer at different stages for the final SoH estimation. For the data-driven methods, the correlation between the extracted feature at different DoDs also needs to be studied. Ensemble learning is also a good tool for improving estimation accuracy and robustness by integrating the features extracted from different stages. For practical applications, suitable sub-learners can be activated according to the real DoD.
D. Diving warning. In existing works, the SoH estimation and health warning cannot figure out the capacity diving phenomenon in advance. It is difficult to detect the diving before occurring. It is meaningful if the capacity diving can be predicted in advance, which helps implement proper maintenance to avoid further damage. However, it is still a big challenge for such early warning prediction since it is difficult to capture the changes inside the batteries during operation using the model. The precise physics-based model that captures the changes inside the batteries helps predict the potential capacity diving. A highly coupled and accurate model needs to be built and reliable parameter optimization algorithms are needed to provide an accurate detection of those small changes inside the batteries. The variation of key parameters related to capacity diving needs to be carefully monitored with high accuracy and robustness. Similarly, complexity is the main challenge for this kind of method. Machine learning can be used to map the relationship between these key parameters and the possibility and time of diving occurrence. However, the development of diving warnings is still unseen. Research in this field is challenging but significant. The early degradation pattern recognition algorithm helps predict the probability of fast degradation that is more prone to diving. The accuracy and robustness of these solutions are not as good as that of the physics-based method. However, they are more useful in online applications due to their simplicity compared with the physics-based method.
A. Prediction for different applications. Existing methods for battery EoL prediction, either feature-based or deep learning methods, only cover the prediction scenarios that the testing batteries and training batteries have the same battery types with similar aging conditions, which means they have similar degradation and lifetime distributions. However, it is difficult to obtain sufficient data for each battery type under similar external stresses to train the model for one specific prediction task. Even the same battery type can be used under various external stresses in practical applications. However, the different external stresses and battery types will have different degradation modes leading to different aging patterns and large discrepancies in lifetime distribution. Therefore, the EoL predictions for batteries that have different aging trajectories from the source batteries are still unsolved challenges. The features used for EoL prediction play significant roles in the accuracy and robustness of the prediction framework. The methods for either manual or automatic feature extraction should cover the different practical scenarios, which ensure the effectiveness of the model under different applications. Therefore, the features which are not sensitive to the specific operating conditions can improve the accuracy and robustness of the EoL prediction of batteries with different aging patterns. For example, these features can be obtained using advanced sensors that detect the mechanisms inside the batteries. In addition, the transfer learning strategy can also be considered to improve the prediction accuracy under different scenarios with fewer data for training under a new scenario.
B. Knee point prediction. Knee point is generally defined as the time after which the degradation accelerates.120 The degradation pattern for a specific battery is determined by many complex factors. The chemistry, environmental temperatures, and loading profiles can all change the shape of the degradation curves. Therefore, whether there is an obvious knee point and when it will appear are difficult to know before it appears. However, the degradation curve before and after the knee point shows significant differences. The difference in the degradation rate before and after the knee point also affects the accuracy of the life prediction model. Therefore, capturing the knee point has a huge effect on the accuracy of the final lifetime prediction. There are several knee point prediction methods proposed in recent years, but their effectiveness has not been proved under different application scenarios. The existing prediction framework generally predicts the whole degradation curve first and then calculates the knee point reversely. The knee point prediction at early stages is more significant for early maintenance and more accurate degradation trajectory prediction. Pattern recognition is supposed to figure out the curve shape and whether the degradation curve has a knee point. Then, both the feature-based and deep learning methods for EoL prediction at early stages can be explored to the early knee point prediction. For example, the mapping between the features extracted at early aging stages and the knee point can be studied to provide early predictions. Nevertheless, the accuracy and robustness are hard to ensure since the knee points are quite random at different stages due to the specific user applications. The probabilistic prediction can be adopted to provide a risk warning of knee points, which helps users for early maintenance.
A. Degradation prediction at variable temperatures. The existing method mainly focuses on the degradation trajectory prediction at a specific temperature. However, the temperature in actual applications varies. The model built using data at one temperature generally has poor accuracy at other temperatures. The main degradation mechanism under different temperatures has some differences, and the available capacity is also different, which causes the prediction model to lose accuracy. Therefore, degradation trajectory prediction of batteries at variable temperatures is challenging in practical applications. Therefore, the external environment temperatures should be considered in the prediction framework. The information on temperature change can be predicted based on the historical temperatures in one specific region. Then, temperature variations can be integrated into the prediction framework to provide prediction at variable temperatures. In addition, the degradation trajectory distributions between the lowest and highest temperature can be predicted to provide the potential lifetime distribution in the future considering the variable temperatures. When the trajectory distributions are predicted, the reliability of the prediction is improved, which provides more information for the users to help the decision of maintenance.
B. Detecting capacity recovery. The capacity recovering phenomenon is common during the degradation process, which generally occurs after rest. It is difficult to predict the future degradation curve since the time and extent of capacity recovery are hard to detect before it happens. The capacity recovery changes the degradation patterns which can change the time to reach EoL. However, the occurrence is completely random according to the user's habits. Therefore, detecting capacity recovery and considering it in the prediction have been challenging until now. A potential solution is to integrate the usage habit into the prediction framework. The extent of capacity recovery needs to be mapped to the stopping time, the shut-off current rate, environmental temperatures, etc. Then, the usage habit must be considered in the prediction, which helps detect when the capacity recovery may happen. Then, the extent of the recovery can be predicted based on the recovery prediction models. Finally, the degradation curve with capacity recovery prediction can be obtained. Although this is a proper way for the predictions of a capacity recovery, the capacity recovery is mainly affected by the use case, which makes the capacity recovery quite random. Therefore, the accuracy and robustness of this prediction are challenging.
C. Accurate prediction at different aging stages. The aging mechanisms do not remain the same during the entire degradation process. The variable external conditions also change the main internal aging mechanisms of batteries, which causes the batteries to have different degradation patterns at different aging stages. However, only a single model was built in the existing works, which is hard to cover the different aging patterns under different main aging mechanisms at the different aging stages. Therefore, accurate trajectory prediction for the whole life is still challenging considering the different aging characteristics at the different aging stages. The multi-stage prediction and model fusion strategy can be a proper solution to this challenge. Multiple sub-models can be built to represent the main degradation patterns at different stages. Then, degradation pattern recognition should detect which degradation stage is now to help in selecting the most suitable degradation models. At stage transitions, the fusion of two adjacent models can be considered to ensure a smooth transition. In addition, the multi-model fusion helps improve the accuracy and robustness of the prediction. However, the computational cost will increase, and the pattern recognition and model fusion methods still require substantial research.
A. Prognostics for battery packs. The published works mostly focus on health prognostics for battery cells. However, the batteries are connected in series and/or parallel to meet the energy and power requirements in practical applications. The inconsistency among the connected battery cells causes different degradation rates and influences the available capacity of the battery pack. The inconsistency increases with the usage, which brings extra degradation to the connected battery cells and the battery pack, and leads to different degradations for the connected battery cells. Moreover, the actual capacity for the connected batteries is not measurable in real applications, which makes it difficult to build the model based on the actual values. Therefore, the health prognostics for battery packs are closer to the actual demand while facing more challenges. Proper and accurate models for battery packs with acceptable computational burdens are required. The mechanistic models have high accuracy, but simplification of the model for battery packs is needed and inconsistency should be considered. For example, the mean difference modeling idea can be adopted since the overall characteristics of the batteries in a battery pack are similar while some differences exist. Therefore, a reference model containing the coupled mechanisms (like an electrochemical-thermal-aging coupled model) for the pack can be built for the overall representation of the battery pack while the difference among the batteries can be built via more simple models such as the ECM. The main internal reactions can be presented by the highly coupled mechanistic model while the differences are detected more quickly via the difference models. In addition, the battery digital twin can be built on the cloud with updated parameters of the mechanistic model, which makes the calculation faster. The data-driven methods that consider the inconsistency feature for battery pack health prognostics are also promising. The transfer learning using domain adaptation can be used for the health prognostics of connected battery cells in the battery pack since only unlabeled data of connected cells can be obtained. Besides, continuous learning is recommended to learn the various degradations of connected cells to make models have better accuracy and generalization.
B. Onboard application. The onboard application for the health prognostics for the real batteries suffers from the coupling challenges from the above and other factors, such as insufficient actual data, low sampling frequency, and so on. Insufficient data and low measurement accuracy make it difficult to build an online model, and using an offline model generally has poor accuracy since the onboard batteries degrade in various ways. Therefore, the actual applications of the most reviewed methods for onboard prediction still have many problems before reliable implementation. The model parameter estimation with optimization algorithms or model training using sparse data with relatively large noise is a promising way to promote onboard applications. In addition, the limited computational ability of the BMS makes it difficult to implement most of the advanced algorithms in practical applications despite the model parameter optimization methods or data-driven methods. The cloud-edge technology is a promising and feasible way to collaborate with the onboard BMS for the onboard applications of advanced prognostic methods. Specifically, the complex calculation for the mechanistic model can be processed on the cloud via the vehicle to internet technology. Some simplified models with parameter optimization can be processed onboard at the same time. For data-driven methods, the model trained in the lab can be adopted as the base model for online prognostics. Then, using the obtained data during usage, the model can be retrained to adapt to the specific aging scenarios to improve the model accuracy and robustness. This method can accelerate the convergency process with a much lower training computational burden. Cloud technology is also beneficial for fast calculation and for the storage of historical data which can be used for continual training of the model. The model estimation results and the estimated results of the data-driven methods can be references for each other to reduce unreliable results to improve the robustness of the final estimations.
5.2. Prospects of future research trends
Battery health prognostics is a hot topic in the battery management field. Some research prospects are presented in this section in the following five aspects. A graphical illustration of these five research prospects is shown in Fig. 18, which are discussed in detail in the following subsections.Another interesting topic is the self-supervised learning approach for battery health prognostics. It has been mentioned above that labeled data are insufficient in practical applications and sufficient unlabeled information can be obtained. Therefore, the advanced self-supervised method can be adopted properly to train a basic model by the unlabeled data, which helps the training convergence of the subsequent usage of the model for battery health prognostics. Since the unlabeled data are plentiful, the development of self-supervised-based methods plays a significant role in this field.
The parameters of the physical model varied with battery aging. The estimation of multiple aging-related parameters can be integrated into the multi-task learning framework to take advantage of artificial intelligence and reduce the computation time to promote online applications. The shared hidden relationship between the external measured parameters and internal states can be learned using the sharing layers, and the specific electrochemical parameters are then estimated using different task-specific blocks.
The potential implementations of the previously presented prospects (from 5.2.2 to 5.2.5), which are advanced machine learning-based methodologies, on battery health prognostic are demonstrated in Fig. 19. The potential research directions lie in the following aspects. In the early stages, the data analysis and coupled model are needed for the feature extraction to support the early prognostic of EoL and keen prediction (which support early pattern recognition). The coupled model also plays a significant role in the advanced machine learning algorithms to impose physical constraints to form physics-informed machine learning. The prediction of the knee points and the EoL points are supposed to be provided by the multi-task learning block. The degradation distribution between the temperature range can also be predicted by the multi-task by predicting the degradation curve at the higher temperatures and lower temperatures. When the pattern recognition tells that the degradation is passing through the transition zone, the multi-model ensemble methods should provide the fused prediction results of different degradation models to improve the accuracy. The process data during each cycle may have shallow and varying DoDs, where the multi-model ensemble framework helps support the estimation of current SoH. The computational burden of the multi-task and multi-model ensemble with physics information extraction will be greater than the computing power of the BMS. Then, the cloud-edge technology helps boost the online prognostic. The model can be learned on the cloud by updating the information from the usage edge. The predicted results can be sent back to the edge for control. Finally, in the usage process, generally, very few or no labeled data but unlabeled data can be obtained. Therefore, the semi-supervised method can be used, which can generate pseudo labels by using the learned model before to support the self-learning for final prediction. Another proper way is to use a self-supervised method to learn a general representative model. The limited labeled data can be used to fine-tune the semi-supervised learned model or for the downstream usage of the self-supervised learned model. The semi-supervised and self-supervised methods are promising frameworks to deal with the prediction requirements under practical applications. Here, the data collected from the big data platform can be selected to support the learning of the basic and general characteristics. Big-data driven is another promising research direction in the battery health prognostics. Some details are presented and discussed in the next subsection.
6. Conclusions
Battery health prognostics is essential for smart battery management and has become one of the hottest topics in this field. This review article provides a summary of the main aging mechanisms inside the batteries and the influencing factors; state-of-the-art methods in battery health prognostics, including SoH estimation, EoL point prediction, and degradation trajectory prediction; as well as the key challenges and research prospects. The aging mechanisms in both the anode and cathode are summarized, and the influencing factors for both calendar and cyclic aging are presented. To illustrate the coupled relationship among the aging mechanisms, aging modes, aging types, and external factors more clearly, a network figure is given.For battery health prognostics, the classification is presented based on the prognostic objectives and prediction time scales. The specific solutions for each prognostic task are introduced by the general flowchart, followed by the review of representative works. The unified framework provides a clear demonstration of the key steps for each prognostic method. After the detailed review of each prognostic method, comprehensive evaluations are provided and discussed. The overall evaluation among the three prognostic tasks is first discussed, followed by the comparisons for the specific solutions in each task. For a more comprehensive evaluation, multiple indices are included, such as accuracy, computational burden, robustness and generalization, predicted information, etc. The evaluation illustrates that the advanced data-driven methods and coupled physics models are the main research trends and have better application prospects.
Then, based on the comparative evaluations, some key challenges regarding each specific prognostic task and general aspects are summarized. Moreover, for each challenge, specific potential solutions are provided and discussed. Finally, the research prospects are provided and discussed. Several new ideas and methodologies are presented in detail. The roles and the collaborations of the advanced methods are demonstrated by a graphic framework to show the potential implementations. These insight challenges and prospects help guide efficient research direction in the field of battery health prognostics.
Abbreviations
| EoL | End of life |
| BMSs | Battery management systems |
| PHM | Prognostics and health management |
| SoH | State of health |
| RUL | Remaining useful life |
| P2D | Pseudo-two-dimensional |
| SPM | Single particle model |
| FEM | Finite-Element Method |
| MD | Molecular dynamics |
| LLI | Loss of lithium inventory |
| LAM | Loss of active material |
| IR | Increase of internal resistance |
| SEI | Solid electrolyte interphase |
| CEI | Catholyte electrolyte interface |
| SoC | State of charge |
| DoD | Depth of discharge |
| CC | Constant current |
| CV | Constant voltage |
| ECM | Equivalent circuit model |
| EM | Electrochemical model |
| KF | Kalman filter |
| PF | Particle filter |
| MHE | Moving horizon estimation |
| GA | Genetic algorithm |
| PSO | Particle swarm optimization |
| LS | Least square |
| HIs | Health indicators |
| RC | Resistor–capacitor |
| SoP | State of power |
| DEKF | Dual extended Kalman filter |
| IC | Incremental capacity |
| DT | Differential temperature |
| LR/MRL | Linear/multi-linear regression |
| SVR | Support vector regression |
| RF | Random forest |
| ANN | Artificial neural network |
| RVM | Relevant vector regression |
| GPR | Gaussian process regression |
| CNN | Conventional neural network |
| RNN | Recurrent neural network |
| TCN | Temporal convolutional neural network |
| GRU | Gated recurrent unit |
| LSTM | Long short-term memory |
| EIS | Electrochemical impedance spectroscopy |
| ML | Machine learning |
| DL | Deep learning |
Nomenclature
| c e,i | Electrolyte concentration (mol m−3) |
| c s,i | Solid phase concentration (mol m−3) |
| D e,i | Electrolyte diffusivity (m2 s−1) |
| D s,i | Solid-phase diffusivity (m2 s−1) |
| a i | Electrode specific interfacial area (m−1) |
| j i | Pore wall flux (mol m−2 s−1) |
| t + | Transference number |
| R | Gas constant |
| T | Battery temperature |
| F | Faraday's constant |
| U ocv | Open circuit potential |
| I | Applied current (A m−2) |
Greek symbols
| ε i | Porosity |
| Φ s | Solid phase potential (V) |
| Φ e | Liquid phase potential (V) |
| σ i | Solid phase conductivity (S m−1) |
| κ e,i | Liquid phase conductivity (S m−1) |
| i sei | SEI side current |
| δ | SEI layer thickness |
| α | Transfer coefficient |
Subscripts
| eff | Effective value |
| p | Positive electrode |
| s | Separator |
| n | Negative electrode |
Author contributions
Conceptualization: Y. C., X. H. and R. T.; investigation and methodology: Y. C. and X. H.; writing – original draft: Y. C., X. L. and J. G.; writing – review & editing: Y. C., X. H., X. L., J. G. and R. T.; visualization: Y. C.; validation: Y. C., X. L. and J. G.; funding acquisition, supervision, and project administration: X. H. and R. T.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the the Villum Foundation for Smart Battery project (No. 222860), the National Key Research and Development Program (No. 2022YFE0102700), and the National Natural Science Foundation of China (Grant No. 52111530194).References
- M. M. Thackeray, C. Wolverton and E. D. Isaacs, Energy Environ. Sci., 2012, 5, 7854–7863 RSC
.
- M. A. Hannan, M. S. H. Lipu, A. Hussain and A. Mohamed, Renewable Sustainable Energy Rev., 2017, 78, 834–854 CrossRef
.
- J. Cho, S. Jeong and Y. Kim, Prog. Energy Combust. Sci., 2015, 48, 84–101 CrossRef
.
- X. Hu, Z. Deng, X. Lin, Y. Xie and R. Teodorescu, Renewable Sustainable Energy Rev., 2021, 152, 111695 CrossRef
.
- T. M. Gür, Energy Environ. Sci., 2018, 11, 2696–2767 RSC
.
- Y. Wang, J. Tian, Z. Sun, L. Wang, R. Xu, M. Li and Z. Chen, Renewable Sustainable Energy Rev., 2020, 131, 110015 CrossRef
.
- R. Xiong, Y. Pan, W. Shen, H. Li and F. Sun, Renewable Sustainable Energy Rev., 2020, 131, 110048 CrossRef
.
- X. Hu, Y. Che, X. Lin and Z. Deng, IEEE/ASME Trans. Mechatronics, 2020, 25, 2622–2632 Search PubMed
.
- Y. Che, A. Foley, M. El-Gindy, X. Lin, X. Hu and M. Pecht, Automot. Innov., 2021, 4, 103–116 CrossRef
.
- X. Han, L. Lu, Y. Zheng, X. Feng, Z. Li, J. Li and M. Ouyang, eTransportation, 2019, 1, 100005 CrossRef
.
- K. Liu, Q. Peng, H. Sun, M. Fei, H. Ma and T. Hu, IEEE Trans. Ind. Informatics, 2022, 18, 8172–8181 Search PubMed
.
- H. Rahimi-Eichi, U. Ojha, F. Baronti and M. Y. Chow, IEEE Ind. Electron. Mag., 2013, 7, 4–16 Search PubMed
.
- S. T. Hung, D. C. Hopkins and C. R. Mosling, IEEE Trans. Ind. Electron., 1993, 40, 96–104 CrossRef
.
- X. Huang, W. Liu, J. Meng, Y. Li, S. Jin, R. Teodorescu and D. I. Stroe, IEEE J. Emerg. Sel. Top. Power Electron., 2021 DOI:10.1109/JESTPE.2021.3130424
.
- K. Liu, K. Li, Q. Peng and C. Zhang, Front. Mech. Eng., 2019, 14, 47–64 CrossRef
.
-
Staff Report: Initial Statement of Reasons, Public Hearing To Consider the Proposed Advanced Clean Cars Regulation, California Air Resources Board, 2022 Search PubMed
.
- M. Beuse, T. S. Schmidt and V. Wood, Science, 2018, 361, 1075–1077 CrossRef
.
- S. Haustein, A. F. Jensen and E. Cherchi, Energy Policy, 2021, 149, 112096 CrossRef
.
- European Parliament, Plenary – March I 2022, 2022.
- K. Edström, E. Ayerbe, I. E. Castelli, I. Cekic-Laskovic, R. Dominko, A. Grimaud, T. Vegge and W. Wentzel, Adv. Energy Mater., 2022, 12, 2200644 CrossRef
.
- M. of I. and I. T. of China, The Ministry of Industry and Information Technology will speed up the research and formulation of the management measures for the recycling and utilization of new energy vehicle power batteries, http://www.gov.cn/xinwen/2022-09/16/content_5710290.htm.
- J. Neumann, M. Petranikova, M. Meeus, J. D. Gamarra, R. Younesi, M. Winter and S. Nowak, Adv. Energy Mater., 2022, 12, 2102917 CrossRef
.
- A. Ran, Z. Liang, S. Chen, M. Cheng, C. Sun, F. Ma, K. Wang, B. Li, G. Zhou, X. Zhang, F. Kang and G. Wei, ACS Energy Lett., 2022, 3817–3825 CrossRef
.
- D. Ren, H. Hsu, R. Li, X. Feng, D. Guo, X. Han, L. Lu, X. He, S. Gao, J. Hou, Y. Li, Y. Wang and M. Ouyang, eTransportation, 2019, 2, 100034 CrossRef
.
- A. Barré, B. Deguilhem, S. Grolleau, M. Gérard, F. Suard and D. Riu, J. Power Sources, 2013, 241, 680–689 CrossRef
.
- M. Broussely, P. Biensan, F. Bonhomme, P. Blanchard, S. Herreyre, K. Nechev and R. J. Staniewicz, J. Power Sources, 2005, 146, 90–96 CrossRef
.
- C. Hendricks, N. Williard, S. Mathew and M. Pecht, J. Power Sources, 2015, 297, 113–120 CrossRef
.
- M. Rezvani, M. Abuali, S. Lee, J. Lee and J. Ni, SAE Tech. Pap. Ser., 2011, 191, 1–9 Search PubMed
.
- H. Meng and Y. F. Li, Renewable Sustainable Energy Rev., 2019, 116, 109405 CrossRef
.
- X. Hu, K. Zhang, K. Liu, X. Lin, S. Dey and S. Onori, IEEE Ind. Electron. Mag., 2020, 14, 65–91 Search PubMed
.
- S. Yang, C. Zhang, J. Jiang, W. Zhang, L. Zhang and Y. Wang, J. Cleaner Prod., 2021, 314, 128015 CrossRef
.
- V. Sulzer, P. Mohtat, A. Aitio, S. Lee, Y. T. Yeh, F. Steinbacher, M. U. Khan, J. W. Lee, J. B. Siegel, A. G. Stefanopoulou and D. A. Howey, Joule, 2021, 5, 1934–1955 CrossRef
.
- H. Rauf, M. Khalid and N. Arshad, Renewable Sustainable Energy Rev., 2022, 156, 111903 CrossRef
.
- Q. Wang, B. Mao, S. I. Stoliarov and J. Sun, Prog. Energy Combust. Sci., 2019, 73, 95–131 CrossRef
.
- P. M. Attia, A. Grover, N. Jin, K. A. Severson, T. M. Markov, Y. H. Liao, M. H. Chen, B. Cheong, N. Perkins, Z. Yang, P. K. Herring, M. Aykol, S. J. Harris, R. D. Braatz, S. Ermon and W. C. Chueh, Nature, 2020, 578, 397–402 CrossRef
.
- I. J. Fernández, C. F. Calvillo, A. Sánchez-Miralles and J. Boal, Energy, 2013, 60, 35–43 CrossRef
.
- X. Hu, X. Deng, F. Wang, Z. Deng, X. Lin, R. Teodorescu and M. G. Pecht, Proc. IEEE, 2022, 110, 735–753 Search PubMed
.
- M. Zheng, H. Salim, T. Liu, R. A. Stewart, J. Lu and S. Zhang, Energy Environ. Sci., 2021, 14, 5801–5815 RSC
.
- M. Lucu, E. Martinez-Laserna, I. Gandiaga and H. Camblong, J. Power Sources, 2018, 401, 85–101 CrossRef
.
- K. Liu, Z. Wei, C. Zhang, Y. Shang, R. Teodorescu and Q.-L. Han, IEEE/CAA J. Autom. Sin., 2022, 1–27 Search PubMed
.
- X. Hu, L. Xu, X. Lin and M. Pecht, Joule, 2020, 4, 310–346 CrossRef
.
- Y. Li, K. Liu, A. M. Foley, A. Zülke, M. Berecibar, E. Nanini-Maury, J. Van Mierlo and H. E. Hoster, Renewable Sustainable Energy Rev., 2019, 113, 109254 CrossRef
.
- Y. Zhang and Y. F. Li, Renewable Sustainable Energy Rev., 2022, 161, 112282 CrossRef
.
- M. S. H. Lipu, M. A. Hannan, A. Hussain, M. M. Hoque, P. J. Ker, M. H. M. Saad and A. Ayob, J. Cleaner Prod., 2018, 205, 115–133 CrossRef
.
- S. A. Hasib, S. Islam, R. K. Chakrabortty, M. J. Ryan, D. K. Saha, M. H. Ahamed, S. I. Moyeen, S. K. Das, M. F. Ali, M. R. Islam, Z. Tasneem and F. R. Badal, IEEE Access, 2021, 9, 86166–86193 Search PubMed
.
- S. Jin, X. Sui, X. Huang, S. Wang, R. Teodorescu and D. I. Stroe, Electronics, 2021, 10, 1–18 CrossRef CAS
.
- X. Sui, S. He, S. B. Vilsen, J. Meng, R. Teodorescu and D. I. Stroe, Appl. Energy, 2021, 300, 117346 CrossRef
.
- Y. Zhang, R. Xiong, H. He and M. G. Pecht, IEEE Trans. Ind. Electron., 2019, 66, 1585–1597 Search PubMed
.
- W. Guo, Z. Sun, S. B. Vilsen, J. Meng and D. I. Stroe, J. Energy Storage, 2022, 56, 105992 CrossRef
.
- J. Newman and W. Tiedemann, AIChE J., 1975, 21, 25–41 CrossRef CAS
.
- S. Santhanagopalan, Q. Guo, P. Ramadass and R. E. White, J. Power Sources, 2006, 156, 620–628 CrossRef CAS
.
- W. Luo, C. Lyu, L. Wang and L. Zhang, J. Power Sources, 2013, 241, 295–310 CrossRef CAS
.
- K. Liu, Y. Gao, C. Zhu, K. Li, M. Fei, C. Peng, X. Zhang and Q. L. Han, Control Eng. Pract., 2022, 124, 105176 CrossRef
.
- N. Yao, X. Chen, Z. H. Fu and Q. Zhang, Chem. Rev., 2022, 122, 10970–11021 CrossRef CAS
.
-
A. Kendall, M. Slattery and J. Dunn, Calif. EPA
.
- Z. Wei, J. Zhao, H. He, G. Ding, H. Cui and L. Liu, J. Power Sources, 2021, 489, 229462 CrossRef CAS
.
- G. Han, J. Yan, Z. Guo, D. Greenwood, J. Marco and Y. Yu, Renewable Sustainable Energy Rev., 2021, 150, 111514 CrossRef CAS
.
- L. Xu, X. Lin, Y. Xie and X. Hu, Energy Storage Mater., 2022, 45, 952–968 CrossRef
.
- C. M. Costa, E. Lizundia and S. Lanceros-Méndez, Prog. Energy Combust. Sci., 2020, 79, 100846 CrossRef
.
- B. Scrosati and J. Garche, J. Power Sources, 2010, 195, 2419–2430 CrossRef CAS
.
- M. Yousaf, U. Naseer, Y. Li, Z. Ali, N. Mahmood, L. Wang, P. Gao and S. Guo, Energy Environ. Sci., 2021, 14, 2670–2707 RSC
.
- J. S. Edge, S. O’Kane, R. Prosser, N. D. Kirkaldy, A. N. Patel, A. Hales, A. Ghosh, W. Ai, J. Chen, J. Yang, S. Li, M. C. Pang, L. Bravo Diaz, A. Tomaszewska, M. W. Marzook, K. N. Radhakrishnan, H. Wang, Y. Patel, B. Wu and G. J. Offer, Phys. Chem. Chem. Phys., 2021, 23, 8200–8221 RSC
.
- Y. P. Wu, E. Rahm and R. Holze, J. Power Sources, 2003, 114, 228–236 CrossRef CAS
.
- R. Kumar, S. Sahoo, E. Joanni, R. K. Singh, W. K. Tan, K. K. Kar and A. Matsuda, Prog. Energy Combust. Sci., 2019, 75, 100786 CrossRef
.
- L. Zhang, C. Zhu, S. Yu, D. Ge and H. Zhou, J. Energy Chem., 2022, 66, 260–294 CrossRef CAS
.
- S. Chae, M. Ko, K. Kim, K. Ahn and J. Cho, Joule, 2017, 1, 47–60 CrossRef CAS
.
- R. Dash and S. Pannala, Sci. Rep., 2016, 6, 6–13 CrossRef
.
- M. Salah, P. Murphy, C. Hall, C. Francis, R. Kerr and M. Fabretto, J. Power Sources, 2019, 414, 48–67 CrossRef CAS
.
- P. Li, H. Kim, S. T. Myung and Y. K. Sun, Energy Storage Mater., 2021, 35, 550–576 CrossRef
.
- P. Li, H. Kim, S. T. Myung and Y. K. Sun, Energy Storage Mater., 2021, 35, 550–576 CrossRef
.
- H. Li, H. Li, Y. Lai, Z. Yang, Q. Yang, Y. Liu, Z. Zheng, Y. Liu, Y. Sun, B. Zhong, Z. Wu and X. Guo, Adv. Energy Mater., 2022, 12, 1–25 Search PubMed
.
- J. S. Edge, S. O’Kane, R. Prosser, N. D. Kirkaldy, A. N. Patel, A. Hales, A. Ghosh, W. Ai, J. Chen, J. Yang, S. Li, M. C. Pang, L. Bravo Diaz, A. Tomaszewska, M. W. Marzook, K. N. Radhakrishnan, H. Wang, Y. Patel, B. Wu and G. J. Offer, Phys. Chem. Chem. Phys., 2021, 23, 8200–8221 RSC
.
- L. Wang, A. Menakath, F. Han, Y. Wang, P. Y. Zavalij, K. J. Gaskell, O. Borodin, D. Iuga, S. P. Brown, C. Wang, K. Xu and B. W. Eichhorn, Nat. Chem., 2019, 11, 789–796 CrossRef CAS PubMed
.
- J. M. Reniers, G. Mulder and D. A. Howey, J. Electrochem. Soc., 2019, 166, A3189–A3200 CrossRef
.
- C. Kupper and W. G. Bessler, J. Electrochem. Soc., 2017, 164, A304–A320 CrossRef CAS
.
- J. Guo, Y. Li, K. Pedersen and D. Stroe, Energies, 2021, 14, 1–22 CAS
.
- A. Sarkar, I. C. Nlebedim and P. Shrotriya, J. Power Sources, 2021, 502, 229145 CrossRef CAS
.
- N. Kumar and J. M. Seminario, J. Phys. Chem. C, 2016, 120, 16322–16332 CrossRef CAS
.
- P. Ganesh, D. E. Jiang and P. R. C. Kent, J. Phys. Chem. B, 2011, 115, 3085–3090 CrossRef CAS PubMed
.
- V. A. Agubra and J. W. Fergus, J. Power Sources, 2014, 268, 153–162 CrossRef CAS
.
- V. Agubra and J. Fergus, Materials, 2013, 6, 1310–1325 CrossRef CAS PubMed
.
- F. Li, J. He, J. Liu, M. Wu, Y. Hou, H. Wang, S. Qi, Q. Liu, J. Hu and J. Ma, Angew. Chem., Int. Ed., 2021, 60, 6600–6608 CrossRef CAS PubMed
.
- J. Guo, S. Jin, X. Sui, X. Huang, Y. Xu, Y. Li, D. W. Peter Kjær Kristensen and D.-I. Stroe, J. Mater. Chem. A, 2023, 11, 41–52 RSC
.
- R. Khurana, J. L. Schaefer, L. A. Archer and G. W. Coates, J. Am. Chem. Soc., 2014, 136, 7395–7402 CrossRef CAS PubMed
.
- H. Luo, Y. Xia and Q. Zhou, J. Power Sources, 2017, 357, 61–70 CrossRef CAS
.
- J. Guo, Y. Li, J. Meng, K. Pedersen, L. Gurevich and D. Stroe, J. Energy Chem., 2022, 74, 34–44 CrossRef CAS
.
- Y. Lyu, X. Wu, K. Wang, Z. Feng, T. Cheng, Y. Liu, M. Wang, R. Chen, L. Xu, J. Zhou, Y. Lu and B. Guo, Adv. Energy Mater., 2021, 11, 2000982 CrossRef CAS
.
- J. Vetter, P. Novák, M. R. Wagner, C. Veit, K. C. Möller, J. O. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler and A. Hammouche, J. Power Sources, 2005, 147, 269–281 CrossRef CAS
.
- D. R. Gallus, R. Schmitz, R. Wagner, B. Hoffmann, S. Nowak, I. Cekic-Laskovic, R. W. Schmitz and M. Winter, Electrochim. Acta, 2014, 134, 393–398 CrossRef CAS
.
- L. Castro, R. Dedryvère, J.-B. Ledeuil, J. Bréger, C. Tessier and D. Gonbeau, J. Electrochem. Soc., 2012, 159, A357–A363 CrossRef CAS
.
- K. Edström, T. Gustafsson and J. O. Thomas, Electrochim. Acta, 2004, 50, 397–403 CrossRef
.
- V. Pop, H. J. Bergveld, P. P. L. Regtien, J. H. G. Ophet Veld, D. Danilov and P. H. L. Notten, J. Electrochem. Soc., 2007, 154, A744 CrossRef CAS
.
- J. Guo and W. Li, ACS Appl. Energy Mater., 2022, 5, 397–406 CrossRef CAS
.
- X. Zhang, B. Winget, M. Doeff, J. W. Evans and T. M. Devine, J. Electrochem. Soc., 2005, 152, B448 CrossRef
.
- K. Liu, T. R. Ashwin, X. Hu, M. Lucu and W. D. Widanage, Renewable Sustainable Energy Rev., 2020, 131, 110017 CrossRef CAS
.
- R. Yazami and Y. F. Reynier, Electrochim. Acta, 2002, 47, 1217–1223 CrossRef CAS
.
- E. Redondo-Iglesias, P. Venet and S. Pelissier, IEEE Trans. Veh. Technol., 2018, 67, 104–113 Search PubMed
.
- M. R. Palacín and A. De Guibert, Science, 2016, 351, 1253292 CrossRef PubMed
.
- M. Ecker, N. Nieto, S. Käbitz, J. Schmalstieg, H. Blanke, A. Warnecke and D. U. Sauer, J. Power Sources, 2014, 248, 839–851 CrossRef CAS
.
- P. Keil, S. F. Schuster, J. Wilhelm, J. Travi, A. Hauser, R. C. Karl and A. Jossen, J. Electrochem. Soc., 2016, 163, A1872–A1880 CrossRef CAS
.
- K. Jalkanen, J. Karppinen, L. Skogström, T. Laurila, M. Nisula and K. Vuorilehto, Appl. Energy, 2015, 154, 160–172 CrossRef CAS
.
- S. Zhu, C. Hu, Y. Xu, Y. Jin and J. Shui, J. Energy Chem., 2020, 46, 208–214 CrossRef
.
- X. Hu, Y. Zheng, X. Lin and Y. Xie, IEEE Trans. Transp. Electrif., 2020, 6, 427–438 Search PubMed
.
- Y. Feng, L. Zhou, H. Ma, Z. Wu, Q. Zhao, H. Li, K. Zhang and J. Chen, Energy Environ. Sci., 2022, 15, 1711–1759 RSC
.
- T. Guan, S. Sun, Y. Gao, C. Du, P. Zuo, Y. Cui, L. Zhang and G. Yin, Appl. Energy, 2016, 177, 1–10 CrossRef CAS
.
- M. Fleischhammer, T. Waldmann, G. Bisle, B. I. Hogg and M. Wohlfahrt-Mehrens, J. Power Sources, 2015, 274, 432–439 CrossRef CAS
.
- T. Waldmann, M. Wilka, M. Kasper, M. Fleischhammer and M. Wohlfahrt-Mehrens, J. Power Sources, 2014, 262, 129–135 CrossRef CAS
.
- X. Lin, K. Khosravinia, X. Hu, J. Li and W. Lu, Prog. Energy Combust. Sci., 2021, 87, 100953 CrossRef
.
- M. Petzl, M. Kasper and M. A. Danzer, J. Power Sources, 2015, 275, 799–807 CrossRef CAS
.
- Y. Gao, J. Jiang, C. Zhang, W. Zhang and Y. Jiang, J. Power Sources, 2018, 400, 641–651 CrossRef CAS
.
- J. Zhu, Y. Wang, Y. Huang, R. Bhushan Gopaluni, Y. Cao, M. Heere, M. J. Mühlbauer, L. Mereacre, H. Dai, X. Liu, A. Senyshyn, X. Wei, M. Knapp and H. Ehrenberg, Nat. Commun., 2022, 13, 1–10 CAS
.
- X. Tang, K. Liu, K. Li, W. D. Widanage, E. Kendrick and F. Gao, Patterns, 2021, 2, 100302 CrossRef PubMed
.
- P. Jones, U. Stimming and A. A. Lee, Nat. Commun., 2022, 13, 4806 CrossRef CAS PubMed
.
- Y. Zhang, Q. Tang, Y. Zhang, J. Wang, U. Stimming and A. A. Lee, Nat. Commun., 2020, 11, 6–11 CrossRef PubMed
.
- G. Ma, S. Xu, B. Jiang, C. Cheng, X. Yang, Y. Shen, T. Yang, Y. Huang, H. Ding and Y. Yuan, Energy Environ. Sci., 2022, 15, 4083–4094 RSC
.
- G. Pozzato, A. Allam and S. Onori, Data Brief, 2022, 41, 107995 CrossRef CAS PubMed
.
- T. Raj, A. A. Wang, C. W. Monroe and D. A. Howey, Batteries Supercaps, 2020, 3, 1377–1385 CrossRef CAS
.
- W. Li, H. Zhang, B. van Vlijmen, P. Dechent and D. U. Sauer, Energy Storage Mater., 2022, 53, 453–466 CrossRef
.
- K. A. Severson, P. M. Attia, N. Jin, N. Perkins, B. Jiang, Z. Yang, M. H. Chen, M. Aykol, P. K. Herring, D. Fraggedakis, M. Z. Bazant, S. J. Harris, W. C. Chueh and R. D. Braatz, Nat. Energy, 2019, 4, 383–391 CrossRef
.
- P. M. Attia, A. A. Bills, F. B. Planella, P. Dechent, G. dos Reis, M. Dubarry, P. Gasper, R. Gilchrist, S. Greenbank, D. Howey, O. Liu, E. Khoo, Y. Preger, A. Soni, S. Sripad, A. Stefanopoulou and V. Sulzer, J. Electrochem. Soc., 2022, 169, 060517 CrossRef
.
- PCoE Battery Aging Dataset, https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/.
- CALCE Battery Dataset, https://web.calce.umd.edu/batteries/data.htm.
- Oxford Battery Degradation Dataset 1, https://ora.ox.ac.uk/objects/uuid:03ba4b01-cfed-46d3-9b1a-7d4a7bdf6fac.
- H. M. Barkholtz, A. Fresquez, B. R. Chalamala and S. R. Ferreira, J. Electrochem. Soc., 2017, 164, A2697–A2706 CrossRef CAS
.
- W. Li, N. Sengupta, P. Dechent, D. Howey, A. Annaswamy and D. U. Sauer, J. Power Sources, 2021, 506, 230024 CrossRef CAS
.
- J. Zhu, Y. Wang, Y. Huang, R. B. Gopaluni, Y. Cao, M. Heere, M. J. Mühlbauer, L. Mereacre, H. Dai, X. Liu, A. Senyshyn, X. Wei, M. Knapp and H. Ehrenberg, Nat. Commun., 2022, 13, 1–10 CAS
.
- X. Hu, F. Feng, K. Liu, L. Zhang, J. Xie and B. Liu, Renewable Sustainable Energy Rev., 2019, 114, 109334 CrossRef
.
- H. Shi, S. Wang, L. Wang, W. Xu, C. Fernandez, B. E. Dablu and Y. Zhang, J. Power Sources, 2022, 517, 230725 CrossRef CAS
.
- Z. Chen, C. C. Mi, Y. Fu, J. Xu and X. Gong, J. Power Sources, 2013, 240, 184–192 CrossRef CAS
.
- Q. Zhang, C. G. Huang, H. Li, G. Feng and W. Peng, IEEE Trans. Transp. Electrif., 2022, 8, 4633–4645 Search PubMed
.
- A. Guha and A. Patra, IEEE Trans. Transp. Electrif., 2017, 4, 135–146 Search PubMed
.
- D. Liu, X. Yin, Y. Song, W. Liu and Y. Peng, IEEE Access, 2018, 6, 40990–41001 Search PubMed
.
- X. Hu, S. Li and H. Peng, J. Power Sources, 2012, 198, 359–367 CrossRef CAS
.
- C. Fleischer, W. Waag, H. M. Heyn and D. U. Sauer, J. Power Sources, 2014, 262, 457–482 CrossRef CAS
.
- B. Ning, B. Cao, B. Wang and Z. Zou, Energy, 2018, 153, 732–742 CrossRef
.
- K. Yang, Z. Chen, Z. He, Y. Wang and Z. Zhou, Soft Comput., 2020, 24, 18661–18670 CrossRef
.
- Z. Song, J. Hou, X. Li, X. Wu, X. Hu, H. Hofmann and J. Sun, Energy, 2020, 193, 116732 CrossRef
.
- X. Hu, H. Jiang, F. Feng and B. Liu, Appl. Energy, 2020, 257, 114019 CrossRef
.
- J. Du, Z. Liu, Y. Wang and C. Wen, Control Eng. Pract., 2016, 54, 81–90 CrossRef
.
- S. R. Hashemi, A. M. Mahajan and S. Farhad, Energy, 2021, 229, 120699 CrossRef
.
- N. Wassiliadis, J. Adermann, A. Frericks, M. Pak, C. Reiter, B. Lohmann and M. Lienkamp, J. Energy Storage, 2018, 19, 73–87 CrossRef
.
- J. Bi, T. Zhang, H. Yu and Y. Kang, Appl. Energy, 2016, 182, 558–568 CrossRef CAS
.
- F. Zhu and J. Fu, IEEE Sens. J., 2021, 21, 25449–25456 CAS
.
- X. Hu, H. Yuan, C. Zou, Z. Li and L. Zhang, IEEE Trans. Veh. Technol., 2018, 67, 10319–10329 Search PubMed
.
- Q. Yang, J. Xu, X. Li, D. Xu and B. Cao, Int. J. Electr. Power Energy Syst., 2020, 119, 105883 CrossRef
.
- S. Zhu, L. Yang, J. Wen, X. Feng, P. Zhou, F. Xie, J. Zhou and Y. N. Wang, J. Power Sources, 2021, 516, 230669 CrossRef CAS
.
- Y. Yu, T. Vincent, J. Sansom, D. Greenwood and J. Marco, J. Energy Storage, 2022, 50, 104291 CrossRef
.
- Z. Wei, J. Hu, H. He, Y. Yu and J. Marco, IEEE Trans. Ind. Electron., 2023, 70, 555–565 Search PubMed
.
- X. Han, M. Ouyang, L. Lu and J. Li, J. Power Sources, 2015, 278, 814–825 CrossRef CAS
.
- L. Zheng, L. Zhang, J. Zhu, G. Wang and J. Jiang, Appl. Energy, 2016, 180, 424–434 CrossRef CAS
.
- S. J. Moura, N. A. Chaturvedi and M. Krstić, J. Dyn. Syst., Meas., Control, 2014, 136, 1–11 CrossRef
.
- X. Hu, D. Cao and B. Egardt, IEEE/ASME Trans. Mechatronics, 2018, 23, 167–178 Search PubMed
.
- Y. Gao, K. Liu, C. Zhu, X. Zhang and D. Zhang, IEEE Trans. Ind. Electron., 2022, 69, 2684–2696 Search PubMed
.
- B. Liu, X. Tang and F. Gao, Electrochim. Acta, 2020, 344, 136098 CrossRef CAS
.
- Z. Deng, X. Hu, S. Member, X. Lin, L. Xu, Y. Che and L. Hu, IEEE/ASME Trans. Mechatronics, 2021, 26, 1295–1306 Search PubMed
.
- X. Hu, Y. Che, X. Lin and S. Onori, IEEE Trans. Transp. Electrif., 2021, 7, 382–398 Search PubMed
.
- L. Cai, J. Meng, D. I. Stroe, G. Luo and R. Teodorescu, J. Power Sources, 2019, 412, 615–622 CrossRef CAS
.
- J. Meng, L. Cai, D. I. Stroe, X. Huang, J. Peng, T. Liu and R. Teodorescu, IEEE Trans. Ind. Electron., 2022, 69, 2659–2668 Search PubMed
.
- X. Sui, S. He, J. Meng, R. Teodorescu and D. I. Stroe, IEEE J. Emerg. Sel. Top. Power Electron., 2021, 9, 5125–5137 Search PubMed
.
- D. Roman, S. Saxena, V. Robu, M. Pecht and D. Flynn, Nat. Mach. Intell., 2021, 3, 447–456 CrossRef
.
- Z. Deng, X. Lin, J. Cai and X. Hu, J. Power Sources, 2022, 525, 231027 CrossRef CAS
.
- Y. Che, Y. Zheng, Y. Wu, X. Sui, P. Bharadwaj, D. Stroe, Y. Yang, X. Hu and R. Teodorescu, Appl. Energy, 2022, 323, 119663 CrossRef
.
- Y. Fu, J. Xu, M. Shi and X. Mei, IEEE Trans. Ind. Electron., 2022, 69, 7019–7028 Search PubMed
.
- S. B. Vilsen and D. I. Stroe, J. Cleaner Prod., 2021, 290, 125700 CrossRef
.
- Z. Wei, H. Ruan, Y. Li, J. Li, C. Zhang and H. He, IEEE Trans. Power Electron., 2022, 37, 7432–7442 Search PubMed
.
-
C. She, L. Zhang, Z. Wang, F. Sun, P. Liu and C. Song, IEEE J. Emerg. Sel. Top. Power Electron., 2021, pp. 1 Search PubMed
.
- Z. Wang, C. Yuan and X. Li, IEEE Trans. Transp. Electrif., 2021, 7, 16–25 Search PubMed
.
- X. Li, C. Yuan, Z. Wang and J. Xie, Energy, 2022, 239, 122206 CrossRef
.
- Z. Lyu, R. Gao and L. Chen, IEEE Trans. Power Electron., 2021, 36, 6228–6240 Search PubMed
.
- S. Kohtz, Y. Xu, Z. Zheng and P. Wang, Mech. Syst. Signal Process., 2022, 172, 109002 CrossRef
.
- D. Wang, Q. Zhang, H. Huang, B. Yang, H. Dong and J. Zhang, J. Energy Storage, 2022, 47, 103528 CrossRef
.
- P. Tagade, K. S. Hariharan, S. Ramachandran, A. Khandelwal, A. Naha, S. M. Kolake and S. H. Han, J. Power Sources, 2020, 445, 227281 CrossRef CAS
.
- Q. Gong, P. Wang and Z. Cheng, J. Energy Storage, 2022, 46, 103804 CrossRef
.
- D. Zhou and B. Wang, J. Energy Storage, 2022, 51, 104480 CrossRef
.
- Y. Fan, F. Xiao, C. Li, G. Yang and X. Tang, J. Energy Storage, 2020, 32, 101741 CrossRef
.
- H. Ruan, J. Chen, W. Ai and B. Wu, Energy AI, 2022, 9, 100158 CrossRef
.
- T. Han, Z. Wang and H. Meng, J. Power Sources, 2022, 520, 230823 CrossRef CAS
.
-
G. Ma, S. Xu, T. Yang, Z. Du, L. Zhu, H. Ding and Y. Yuan, IEEE Trans. Neural Networks Learn. Syst., 2022, pp. 1–11 Search PubMed
.
- P. Attia, M. E. Deetjen and J. Witmer, Elastic, 2018, 2, 2300 Search PubMed
.
- P. M. Attia, K. A. Severson and J. D. Witmer, J. Electrochem. Soc., 2021, 168, 090547 CrossRef CAS
.
- D. Gong, Y. Gao, Y. Kou and Y. Wang, J. Energy Storage, 2022, 51, 104376 CrossRef
.
- Z. Fei, F. Yang, K. L. Tsui, L. Li and Z. Zhang, Energy, 2021, 225, 120205 CrossRef
.
- S. Greenbank and D. Howey, IEEE Trans. Ind. Informatics, 2022, 18, 2965–2973 Search PubMed
.
- Y. Zhang, Z. Peng, Y. Guan and L. Wu, Energy, 2021, 221, 119901 CrossRef
.
-
S. Shen, V. Nemani, J. Liu, C. Hu and Z. Wang, 2020 IEEE Transp. Electrif. Conf. Expo, ITEC 2020, 2020, 181–184 Search PubMed
.
- N. H. Paulson, J. Kubal, L. Ward, S. Saxena, W. Lu and S. J. Babinec, J. Power Sources, 2022, 527, 231127 CrossRef CAS
.
- L. Yan, J. Peng, D. Gao, Y. Wu, Y. Liu, H. Li, W. Liu and Z. Huang, Energy, 2022, 243, 123038 CrossRef
.
- A. Weng, P. Mohtat, P. M. Attia, V. Sulzer, S. Lee, G. Less and A. Stefanopoulou, Joule, 2021, 5, 2971–2992 CrossRef CAS
.
- S. Stock, S. Pohlmann, F. J. Günter, L. Hille, J. Hagemeister and G. Reinhart, J. Energy Storage, 2022, 50, 104144 CrossRef
.
- J. Hong, D. Lee, E. R. Jeong and Y. Yi, Appl. Energy, 2020, 278, 115646 CrossRef
.
- Y. Yang, Appl. Energy, 2021, 292, 116897 CrossRef
.
- Q. Zhang, L. Yang, W. Guo, J. Qiang, C. Peng, Q. Li and Z. Deng, Energy, 2022, 241, 122716 CrossRef
.
- C. W. Hsu, R. Xiong, N. Y. Chen, J. Li and N. T. Tsou, Appl. Energy, 2022, 306, 118134 CrossRef CAS
.
- P. G. Anselma, P. Kollmeyer, J. Lempert, Z. Zhao, G. Belingardi and A. Emadi, Appl. Energy, 2021, 285, 116440 CrossRef
.
- N. Omar, M. A. Monem, Y. Firouz, J. Salminen, J. Smekens, O. Hegazy, H. Gaulous, G. Mulder, P. Van den Bossche, T. Coosemans and J. Van Mierlo, Appl. Energy, 2014, 113, 1575–1585 CrossRef CAS
.
- W. He, N. Williard, M. Osterman and M. Pecht, J. Power Sources, 2011, 196, 10314–10321 CrossRef CAS
.
- G. Suri and S. Onori, Energy, 2016, 96, 644–653 CrossRef
.
- Y. Zhang, R. Xiong, H. He, X. Qu and M. Pecht, Appl. Energy, 2019, 255, 113818 CrossRef CAS
.
- E. Sarasketa-Zabala, E. Martinez-Laserna, M. Berecibar, I. Gandiaga, L. M. Rodriguez-Martinez and I. Villarreal, Appl. Energy, 2016, 162, 839–852 CrossRef CAS
.
- Y. Cui, C. Du, G. Yin, Y. Gao, L. Zhang, T. Guan, L. Yang and F. Wang, J. Power Sources, 2015, 279, 123–132 CrossRef CAS
.
- K. Liu, X. Tang, R. Teodorescu, F. Gao and J. Meng, IEEE Trans. Energy Convers., 2021, 8969, 1–10 Search PubMed
.
- T. Sun, B. Xu, Y. Cui, X. Feng, X. Han and Y. Zheng, J. Power Sources, 2021, 484, 229248 CrossRef CAS
.
- M. A. Patil, P. Tagade, K. S. Hariharan, S. M. Kolake, T. Song, T. Yeo and S. Doo, Appl. Energy, 2015, 159, 285–297 CrossRef CAS
.
-
X. Hu, X. Yang, F. Feng, K. Liu and X. Lin, J. Dyn. Syst., Meas., Control, 2021, 143, 1–13 Search PubMed
.
- W. Gu, Z. Sun, X. Wei and H. Dai, Electrochim. Acta, 2014, 133, 107–116 CrossRef CAS
.
- M. Ecker, J. B. Gerschler, J. Vogel, S. Käbitz, F. Hust, P. Dechent and D. U. Sauer, J. Power Sources, 2012, 215, 248–257 CrossRef CAS
.
- S. Atalay, M. Sheikh, A. Mariani, Y. Merla, E. Bower and W. D. Widanage, J. Power Sources, 2020, 478, 229026 CrossRef CAS
.
- M. B. Pinson and M. Z. Bazant, J. Electrochem. Soc., 2013, 160, A243–A250 CrossRef CAS
.
- V. Sulzer, P. Mohtat, S. Pannala, J. B. Siegel and A. G. Stefanopoulou, J. Electrochem. Soc., 2021, 168, 120531 CrossRef CAS
.
- J. Li, R. G. Landers and J. Park, J. Power Sources, 2020, 456, 227950 CrossRef CAS
.
- C. Kupper, B. Weißhar, S. Rißmann and W. G. Bessler, J. Electrochem. Soc., 2018, 165, A3468–A3480 CrossRef CAS
.
- Y. H. Lui, M. Li, A. Downey, S. Shen, V. P. Nemani, H. Ye, C. VanElzen, G. Jain, S. Hu, S. Laflamme and C. Hu, J. Power Sources, 2021, 485, 229327 CrossRef CAS
.
- Y. Che, D. Stroe, X. Hu and R. Teodorescu, IEEE Trans. Ind. Informatics, 2022, 1–10 Search PubMed
.
- L. Chen, J. Chen, H. Wang, Y. Wang, J. An, Y. Yang and H. Pan, IEEE Trans. Power Electron., 2020, 35, 5850–5859 Search PubMed
.
- X. Li, Y. Ma and J. Zhu, Meas. J. Int. Meas. Confed., 2021, 184, 109935 CrossRef
.
- Z. Chen, L. Chen, W. Shen and K. Xu, IEEE Trans. Veh. Technol., 2022, 71, 1466–1479 Search PubMed
.
- K. Liu, Y. Shang, Q. Ouyang and W. D. Widanage, IEEE Trans. Ind. Electron., 2021, 68, 3170–3180 Search PubMed
.
- Y. Che, Z. Deng, X. Lin and L. Hu, IEEE Trans. Veh. Technol., 2021, 70, 1269–1277 Search PubMed
.
- L. Xu, Z. Deng, Y. Xie and X. Lin, IEEE Trans. Transp. Electrification, 2022 DOI:10.1109/TTE.2022.3212024
.
- Z. Tong, J. Miao, S. Tong and Y. Lu, J. Cleaner Prod., 2021, 317, 128265 CrossRef CAS
.
- R. G. Nascimento, M. Corbetta, C. S. Kulkarni and F. A. C. Viana, J. Power Sources, 2021, 513, 230526 CrossRef CAS
.
- M. Aykol, C. B. Gopal, A. Anapolsky, P. K. Herring, B. van Vlijmen, M. D. Berliner, M. Z. Bazant, R. D. Braatz, W. C. Chueh and B. D. Storey, J. Electrochem. Soc., 2021, 168, 030525 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2023 |