A hierarchical integrated 3D carbon electrode derived from gingko leaves via hydrothermal carbonization of H₃PO₄ for high-performance supercapacitors

Abstract

Electrochemical ultracapacitors derived from green and sustainable materials could demonstrate superior energy output and an ultra-long cycle life owing to large accessible surface area and obviously shortened ion diffusion pathways. Herein, we have established an efficient strategy to fabricate porous carbon (GLAC) from sustainable gingko leaf precursors by a facile hydrothermal activation of H₃PO₄ and low-cost pyrolysis. In this way, GLAC with a hierarchically porous structure exhibits extraordinary adaptability toward a high energy/power supercapacitor (∼709 F g⁻¹ at 1 A g⁻¹) in an aqueous electrolyte (1 M KOH). Notably, the GLAC-2-based supercapacitor displays an ultra-high stability of ∼98.24% even after 10 000 cycles (10 A g⁻¹) and an impressive energy density as large as ∼71 W h kg⁻¹ at a power density of 1.2 kW kg⁻¹. The results provide new insights that the facile synthetic procedure coupled with the excellent performance contributes to great potential for future application in the electrochemical energy storage field.

---

1. Introduction

With the development of the economy, the important goals of carbon peaking and carbon neutrality have been put forward to meet the demand for energy.^1–3 It is an essential strategy to prompt a new challenge in the development of clean, green, and highly efficient energy storage technologies to replace traditional energy (coal, oil, and natural gas).^4,5 Many clean and efficient energy storage and conversion devices have been exploited to alleviate environmental pollution and energy demand issues, such as fuel cells, metal–air batteries, electrochemical water splitting, and supercapacitors.^6–9 Supercapacitors (SCs) are considered as a potential candidate for electrochemical energy storage (EES) owing to their high-power density, fast charge/discharge rate, long cycling lifetime, low cost, and most importantly environment-friendly features.^10–12 Supercapacitors are classified as electrical double-layer capacitors (EDLCs) and pseudocapacitors (PCs) based on the energy storage mechanism.¹³ Carbon-based materials with a high porous surface area are mainly used in commercial EDLCs, which is ascribed to their large specific surface area, tunable pore size, high electrical conductivity, abundant precursors, and strong mechanical properties.¹⁴ Nevertheless, their practical applications have been restricted by virtue of high cost, low yield, complicated equipment, and harsh synthetic conditions.¹⁵ For example, the traditional preparation procedure of activated carbon materials is apt to cause material hardening and pore blockage, which greatly result in the decrease of the ion/electron transport capacity, electrical conductivity, and material utilization.¹⁶ Currently, various novel carbon materials such as graphene, carbon nanotubes, and fullerenes, have been explored through non-renewable fossil resources, accompanied by low yield and high cost.^17–20 Therefore, designing excellent electrode materials is desirable to achieve superior electrochemical capability of SCs.

Biomass is a kind of natural, abundant, and renewable resource.²¹ However, thousands of tons of agricultural waste are mainly incinerated, which usually pollutes the environment and increases carbon emissions, as well as costs money.²² With agricultural wastes as biomass raw materials, the strategy to fabricate carbon materials could not only reduce carbon emissions and environmental pollution but also advances energy conversion.²³ Biomass-derived carbon materials could be employed in many fields, which could be ascribed to their high electrical conductivity, large specific surface area, good chemical stability, and so on.²⁴ In addition, the elements of C, S, N and P from biomass generally could be self-doped in the carbon materials during the synthetic procedure.²⁵ Moreover, biomass derivatives with a natural hierarchical structure and special surface chemical properties could contribute to good compatibility with electrolytes and multiphase interfacial interaction for ion transfer and diffusion.^26–28

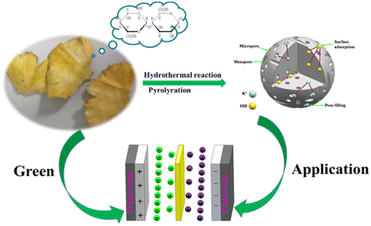
Gingko as a rare species of the Mesozoic relic belongs to the gingko plants of the ginkgo family, which is a Chinese specialty and is widely distributed in many regions of the world. Except for clinical applications such as coronary, angina pectoris, and hyperlipidemia, a large amount of gingko leaves are discarded as biomass waste. In addition, the various components of gingko leaves are rich in carbon, such as sugar, vitamin C, vitamin E, carotenes, carotenoids, and anthocyanins.^29,30 Based on this, our aim is to fabricate activated carbon materials with gingko leaves as a precursor for supercapacitors, which could not only enrich the selection of electrode material precursors but also realize the economic value maximization of waste gingko leaves.

Herein, we introduce a simple synthesis strategy to fabricate a porous activated carbon material derived from gingko leaves via hydrothermal carbonization of H₃PO₄ (Scheme 1). And then, the kinetics and the specific capacitance of the electrode material have been systematically explored. The reported strategy proposes a novel idea for integrating P-doped carbon materials with satisfactory properties in supercapacitors and provides a prospective strategy to rationally design a hierarchical architecture with multiple composites for electrochemical systems.

Scheme 1 Synthetic procedure of porous carbon from gingko leaves.

2. Experimental section

2.1 Materials and methods

2.1.1 Materials and reagent. Gingko leaves were collected from the campus garden at Southwest University, Chongqing, China, and dried by freezing. Nafion solution, poly(tetrafluoroethylene) (PTFE), and acetylene black were purchased from Sigma-Aldrich. Potassium hydroxide (KOH) and all other reagents were obtained from Adamas-beta®. All chemicals were used without further purification.

2.1.2 Preparation of gingko leaf-derived activated carbon (GLAC). Gingko leaves were cut into pieces and placed in a Teflon-lined stainless steel autoclave with H₃PO₄ (16 M) solution as an activating agent to carry out the hydrothermal reaction. And then, the autoclave was sealed and placed in an electric oven at a temperature of 120 °C for 3 h. After cooling down to room temperature naturally, the samples were centrifuged and freeze-dried. Next, the products were calcined at 700 °C under an Ar flow for 3 h. Finally, the black carbon material was washed with hot water several times and dried in an oven at 80 °C for 12 hours to afford GLAC-2. For comparison, GLAC-1, GLAC-3, and GLAC-4 were prepared at 600, 800, and 900 °C in accordance with the similar procedure to GLAC-2. In addition, freeze-dried gingko leaves treated with deionized water were obtained according to a similar procedure and the obtained porous carbon was denoted as GLC.

2.2 Characterization

The XRD patterns of all samples were recorded using powder X-ray diffraction (Shimadzu XRD-7000). The surface morphology and structure of samples were observed using scanning electron microscopy (FESEM, JSM-7800F) and transmission electron microscopy (TEM, JEOL 2100). Nitrogen sorption isotherms were obtained using an Autosorb-1 (Quantachrome Instruments). The specific surface area was calculated by the modified Brunauer–Emmett–Teller (BET) method. The pore size distributions and the pore volume were analyzed from the adsorption branch isotherms by the density functional theory (DFT) method. Moreover, the total pore volume (V_t) was estimated from the amount adsorbed at a relative pressure P/P₀ of 0.990. The micropore volume (V_mic) and micropore surface area (S_mic) were determined using the t-plot theory. Raman spectra were acquired with a Jobin-Yvon HR 800 spectrometer. X-ray photoelectron spectroscopy (XPS) measurements were performed on an Escalab 250xi (Thermo Fisher Scientific, USA). Fourier transform infrared (FT-IR) spectra were recorded on a Thermo Scientific Nicolet iS 50 spectrometer.

2.3 Electrochemical measurements

For the two-electrode system, a homogeneous slurry of the electroactive material, polytetrafluoroethylene (PTFE), and acetylene black with a weight ratio of 80:10:10 in ethanol was formed and coated on the nickel foam current collector (1 cm × 1 cm), then vacuum dried at 80 °C for 12 h. The loading of the active material for each working electrode was measured to be ∼3 mg cm⁻². And then, a glass-fiber filter paper (Waterman, GF/B) as a separator and 1 M KOH aqueous solution as the electrolyte were used to assemble a test cell. For the three-electrode system, the working electrode was manufactured via the dispersion of active carbon in a mixture of Nafion and ethanol (1 : 20) and dropping on a glassy carbon electrode, accompanied by platinum foil and Hg/HgO as the counter and reference electrodes, respectively. Electrochemical characterization was carried out on an electrochemical workstation (Shanghai Chenhua Instrument Co. Ltd, China).

For the two-electrode system, the gravimetric specific capacitance of a single electrode is calculated from the equation:

C_sp = 2I × Δt/m × ΔV (1)

where C_sp (F g⁻¹) is the specific capacitance based on the mass of the active carbons, I is the discharge current (A), Δt is the discharge time (s), ΔV is the voltage difference (except the ohm drop) within Δt (V), and m is the loading of the active material in each working electrode (g).

For the three-electrode system, the gravimetric specific capacitance can be calculated using the following equation:

C_sp = I × Δt/m × ΔV (2)

where I is the discharge current (A), Δt is the discharge time (s), ΔV is the voltage (V), and m is the mass of the active material (g).

The energy density E (W h kg⁻¹) and the power density P (W kg⁻¹) are calculated using equations:

E = C_spV²/(2 × 3.6) (3)

P = 3600E/Δt (4)

where t is the discharge time (s).

3. Results and discussion

3.1 Material characterization

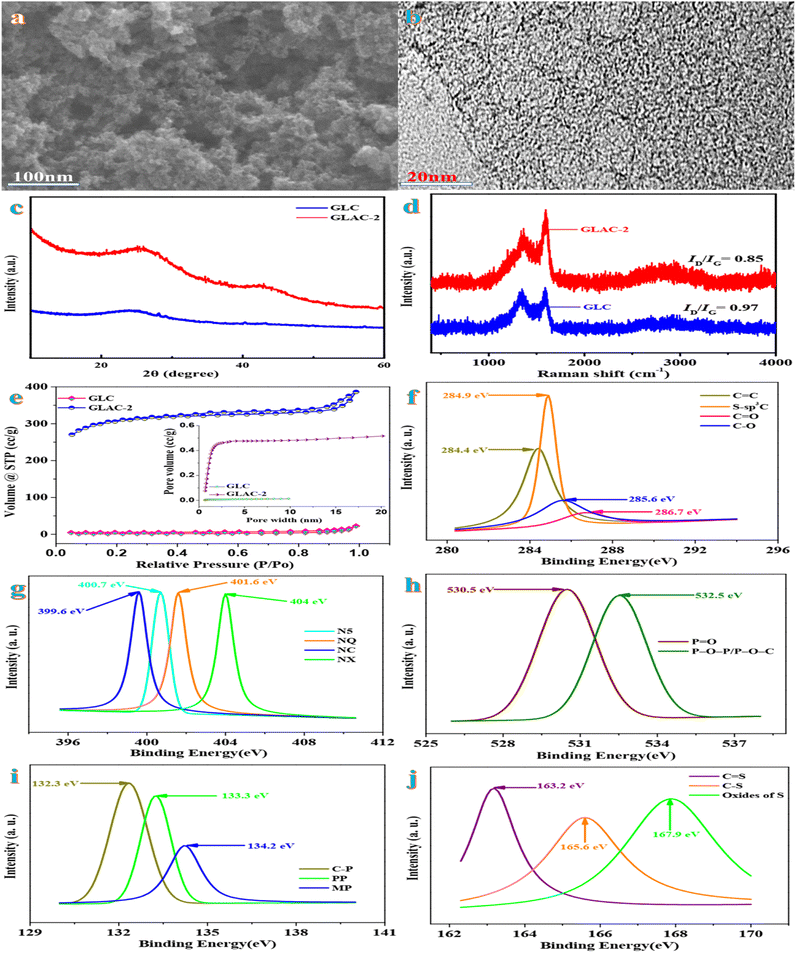
On account of an economic prospective, renewable natural gingko leaves indicate impressive sustainability as the precursor in the field of carbonaceous electrode materials. The scanning electron microscopy (SEM) image of GLAC-2 (Fig. 1a) reveals abundant interconnected pores, which supply numerous ion migration channels, short migration paths, and low diffusion resistance, thereby contributing to the electrochemical performance of the electrode.³¹ Compared with GLAC-2, the SEM image of GLC (Fig. S1†) exhibits a monolithic morphology, implying that the activation of H₃PO₄ could help to form thin sheets of carbon and to create a porous structure. The high-resolution TEM image of GLAC-2 (Fig. 1b) demonstrates that GLAC-2 consists of a crumpled, transparent nanostructure, which contributes to a super high surface area. In addition, there are abundant micro- and mesopores distributed in the whole carbon material, which are conducive to facilitating the diffusion of electrolyte ions and further a high-rate performance supercapacitor.³²

Fig. 1 (a) FESEM image of GLAC-2; (b) TEM image of GLAC-2; (c) XRD patterns of GLC and GLAC-2; (d) Raman spectrum of GLC and GLAC-2; (e) N₂ adsorption/desorption isotherms and the pore size distribution of GLC and GLAC-2; (f) high-resolution C 1s of GLAC-2; (g) high-resolution N 1s of GLAC-2; (h) high-resolution O 2p of GLAC-2; (i) high-resolution P 2p of GLAC-2; (j) high-resolution S 2p of GLAC-2.

These elemental composition results are in accordance with the FTIR spectra. According to the FTIR spectra in Fig. S2,† the characteristic peaks at around 3700, 1700, 1430, 1240, and 750 cm⁻¹ are ascribed to the vibrations of O–H, C=O, P=O/P–O–C, C–O–C, and the phenyl group, respectively.³³

Fig. 1c demonstrates the typical XRD patterns of GLAC-2 and GLC. Two characteristic peaks are located at 2θ = 24.8° (graphitized carbon layer) and 41.6° (disordered carbon layer), assigned to the (002) and (100) reflections of graphitic-like carbon.³⁴ The broadening of the (002) diffraction peak indicates a relatively low crystallinity, which confirms abundant amorphous defect sites in the samples.³⁵ This result is further verified using Raman spectra. Fig. 1d exhibits two intensive absorbance regions at nearly 1320 cm⁻¹ (D band) and 1590 cm⁻¹ (G band). Typically, the D band refers to defects and disorder in carbon materials, while the G band is related to the ordered graphitic layers in a 2D hexagonal lattice.³⁶ Generally, the peak intensity ratio I_D/I_G is employed as an indicator of graphitization degree in carbon materials. By means of the carbonization-activation process, the I_D/I_G ratio obviously decreases from 0.96 for GLC to 0.74 for GLAC-2, which confirms that the activation of H₃PO₄ could result in the increase of graphitization degree and further could contribute to the enhancement of electrochemical performance.³⁷

BET nitrogen adsorption–desorption analysis is conducted to investigate the porous nature of the samples for GLAC-2 and GLC (Fig. 1e). Based on the international union of pure and applied chemistry (IUPAC) classification, the isotherms of GLAC-2 indicate type IV isotherms with H₄ hysteresis, which confirms the presence of abundant pores varying from micro-to mesopores. Meanwhile, the hysteresis loop at high relative pressures (P/P₀ > 0.4) demonstrates the existence of a large amount of mesopores in the structure.³⁸ However for GLC, typical type I isotherms with a hysteresis of H₄ type are observed. Obviously, GLAC-2 indicates a hierarchical porous structure with a mixture of micropores and meso-/macropores, which contribute to easy electrolyte access and transport and rapid electron transfer.³⁹ Owing to the activation of H₃PO₄ and pyrolysis, the pore size distribution of GLAC-2 broadens, and the SSA and pore volume of GLAC-2 also increase. The detailed textural parameters of GLACs are summarized in Table 1. The BET specific surface areas (S_BET) of GLAC-2 (1133.66 m² g⁻¹) are higher than those of GLC (6.65 m² g⁻¹), owing to the etching and intercalation effects of H₃PO₄, which could generate plenty of pores within the sample. The gas molecules generated in the process of pyrolysis, such as H₂O, CO, CO₂, and NH₃, could be released and further open up closed pores, which contribute to the development of pores to form meso-/macropores. The hierarchical pore structure could provide a high electrochemically active surface area and plenty of ion-buffering reservoirs simultaneously, which contribute to high-performance energy storage.⁴⁰ On account of the DFT pore size distribution curve, the average pore size of GLAC-2 and GLC is primarily centered at 8.45 nm and 3.41 nm, respectively (Table 1), which demonstrates that a large amount of gas (CO and CO₂) could be generated during the procedure of the activation of H₃PO₄ and further lead to the increase of textural properties and ion adsorption sites. In view of the effect of reaction temperation on textural parameters, the BET surface area (S_BET) of GLAC-1 (600 °C) and GLAC-4 (900 °C) is 635.72 and 862.47 m² g⁻¹ and their corresponding total pore volumes (V_t) are 0.15 and 0.29 cm⁻³ g⁻¹ as well as the average pore size is 0.15 and 5.36 nm, respectively. When the activation temperature ranges from 600 °C to 700 °C, the textural properties similarly increase (635.72 m² g⁻¹, 0.15 cm⁻³ g⁻¹vs. 1133.66 m² g⁻¹, 0.42 cm⁻³ g⁻¹; GLAC-1 vs. GLAC-2). When the activation temperature is further increased to 900 °C, the textural properties reduce drastically due to the destruction of the structure (from 1133.66 m² g⁻¹ to 862.47 m² g⁻¹; from 0.42 cm⁻³ g⁻¹ to 0.29 cm⁻³ g⁻¹; GLAC-2 vs. GLAC-3 vs. GLAC-4). More importantly, this unique structure has a large SSA and plenty of hierarchical pores, which makes it applicable as an electrode material for supercapacitor applications.⁴¹

Table 1 Summary of BET characteristics of activated carbons

Sample	S BET	V tot	S mic	S me	S ma	V mic	V me	V ma
a S BET: BET surface area. b V tot: total volume. c S mic: micropore surface area. d S me: mesopore surface area. e S ma: macropore surface area. f V mic: micropore volume. g V me: mesopore volume. h V ma: macropore volume.
GLC	6.65	0.01	1.32	3.57	1.76	0.002	0.005	0.003
GLAC-1	635.72	0.15	123.53	416.28	95.91	0.03	0.0.08	0.004
GLAC-2	1133.66	0.42	241.35	763.62	128.69	0.105	0.276	0.039
GLAC-3	1021.35	0.36	264.37	573.54	183.44	0.09	0.215	0.055
GLAC-4	862.47	0.29	198.65	527.64	136.18	0.07	0.16	0.06

---

X-ray photoelectron spectroscopy (XPS) is carried out to investigate the composition and surface electronic states of GLAC-2. As shown in Fig. S3,† the survey XPS spectra of GLAC-2 confirm the existence of C, N, O, P, and S elements. The deconvoluted high-resolution C 1s spectrum displays the presence of four peaks (Fig. 1f) at 284.4, 284.9, 285.6, and 286.7 eV that could be assigned to C=C, S–sp³C, C–O, and C=O, respectively.⁴² The N 1s spectrum (Fig. 1g) reveals four component peaks at binding energies of 399.6, 400.7, 401.6, and 404 eV, which are attributed to NC, N-5, N-Q, and N-X, respectively.⁴³ The O 1s spectrum (Fig. 1h) could be split into the two peaks at 530.5 and 532.5 eV, corresponding to P=O and P–O–P/P–O–C.⁴⁴ The deconvoluted P 2p spectrum displays the presence of three peaks located at 132.3, 133.3, and 134.2 eV, which are ascribed to C–P, PP, and MP, respectively.⁴⁵ In addition, three distinguishable peaks in the spectrum of S 2p (Fig. 1j) at 163.2 eV, 165.6 eV, and 167.9 eV correspond to –C=S–, –C–S–C– and –C–SO_x–C–, respectively.⁴⁶ The presence of functional groups could provide pseudocapacitive reactive sites and further contribute to energy storage performance. Simultaneously, these functional groups also could participate in electrochemical redox reactions and further result in pseudo-capacitance. In general, the synergistic effect of N, O, P and S self-doped heteroatoms could contribute to electrochemical capacitance by means of the reversibility of the redox reactions and the surface wettability and compatibility.⁴⁷ On account of the aforementioned characterization, the activation mechanism of H₃PO₄ could be proposed to demonstrate the formation of the porous carbon structure. During the process, H₃PO₄ vibrates violently in water to refrain the adjacent cell walls from agglomerating, and then the atoms decomposed from the molecules of polysaccharides connect together in situ to produce hierarchical pores. In the process of the subsequent carbonization, the polymeric cellulose is hydrolyzed to oligosaccharides due to gas evolution, which could result in forming a porous structure.

3.2 Electrochemical behaviors of the electrode

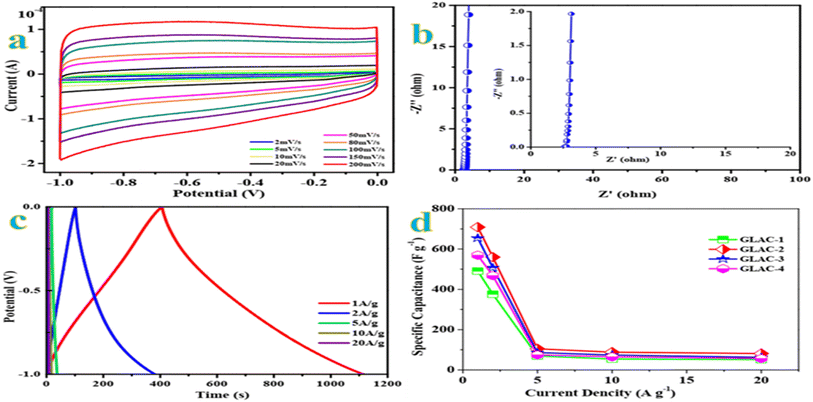
The cyclic voltammetry (CV) curves are recorded first at a standard scan rate of 100 mV s⁻¹ to get a glance of the electrochemical behavior of all materials. According to the CV curves in Fig. S5,† GLAC-2 encloses the largest area among the sample materials, which confirms the highest capacitance.⁴⁸ Moreover, the GLAC-2 electrode has a much faster current response than those of GLAC-1-, GLAC-3-, GLAC-4- and GLC-based electrodes, confirming the smallest diffusion resistance at the scan rate of 100 mV s⁻¹. Additionally, the CV curves of GLAC-2 exhibit an ideal rectangular shape at 100 mV s⁻¹, revealing a desired electric double-layer capacitor (EDLC) behavior.⁴⁹ As observed from the CV curves of GLAC-2 at various scan rates from 2 to 200 mV s⁻¹ (Fig. 2a), they still maintain a good rectangular-like shape even at a large scan rate of 200 mV s⁻¹, which displays a rapid ion transport process from the electrode/electrolyte interface into the inner active surface and superior capacitive performance of the electrode in quick scan rate operations.⁵⁰

Fig. 2 (a) CV curves of GLAC-2 at different scan rates. (b) Nyquist plots of GLAC-2. (c) Galvanostatic charge/discharge curves of GLAC-2 at different current densities. (d) Capacitances of GLAC samples prepared at different temperatures and current densities.

Electrochemical impedance spectroscopy (EIS) is carried out to further investigate the charge transport and accessibility of ions within the hierarchical architectures. In view of the Nyquist plots in Fig. 2b, the straight lines approximately vertical to the Z′ axis in the low-frequency region demonstrate the fast diffusion kinetics of electrolyte ions.⁵¹ In the medium frequency domains, the Warburg line with a slope of almost 45° refers to the Warburg diffusion resistance, and the semicircle in the mid-high frequency region is generally correlated to the charge transfer resistance, owing to Faraday reactions resulting from the surface functional groups.⁵² Obviously, the GLAC-2 electrode possesses a low ESR value of 1.7 Ω (15.71 kHz), which contributes to fast access of electrolyte ions and electron transfer in the procedure of the charge–discharge. Moreover, the phase angle of the GLAC-2 electrode is almost close to 90° for ideal capacitive behavior.⁵³

Galvanostatic charge–discharge (GCD) tests are further performed to investigate the electrochemical performances of the prepared samples utilizing the same voltage windows as for the CV test. As shown in Fig. 2c, the GCD profiles of GLAC-2 at various current densities manifest a triangular shape with nearly linear symmetry, which demonstrates the excellent electrochemical reversibility and a tiny inner resistance.⁵⁴ In addition, no obvious IR drop could be observed in the GLAC-2 electrode at 1 A g⁻¹, confirming the low internal resistance. Fig. 2d plots the relationship between the specific capacitances of resulting GLAC-based electrodes and the current densities. The GLAC-2 electrode exhibits specific capacitances of ∼709, ∼560, ∼105, ∼88, and ∼81 F g⁻¹ at 1, 2, 5, 10, and 20 A g⁻¹, respectively. The decrease of capacitance at higher current is generally attributed to increased ohmic resistance due to the ion “traffic jam” within the particles' micropores or due to the interaction of electrolyte with carbon functional groups or dangling bonds.⁵⁵ The results are also superior to those of many other carbonaceous capacitive materials derived from biomass,^56–58 which agrees well with the results obtained from CV tests. In addition, the specific capacitance of GLAC-2 (∼709 F g⁻¹ at 1 A g⁻¹) is much higher than that of GLC (∼264 F g⁻¹), which confirms the effect of activation of H₃PO₄ and pyrolysis. According to the effect of temperature on the performance, the specific capacitance of GLAC-2 at 700 °C (Fig. 2e) obviously exceeds that of GLAC-1 (600 °C) and GLAC-3 (800 °C) as well as (700 vs. 600 vs. 800 vs. 900 °C, 709 vs. 193.00 vs. 333.70 F g⁻¹ at 1 A g⁻¹; GLAC-2 vs. GLAC-1 vs. GLAC-3 vs. GLAC-4), owing to the higher surface area and large pore size of the former, which contribute to the kinetics of the ion adsorption process.⁵⁹

As shown in Fig. S4,† even after 10 000 continuous charge–discharge cycles at a constant current density of 10 A g⁻¹, the specific capacitance retention is still about 98.9% retention of its initial value. The excellent electrochemical capacitive performance of the GLAC-2 electrode could be rationally attributed to the feature of a loosely stacked nanostructure, abundant meso-/macropores, and broad interlayer spacing, which are conducive to alleviating the volume change in the process of ion intercalation.⁶⁰

3.3 Electrochemical behavior of the supercapacitor

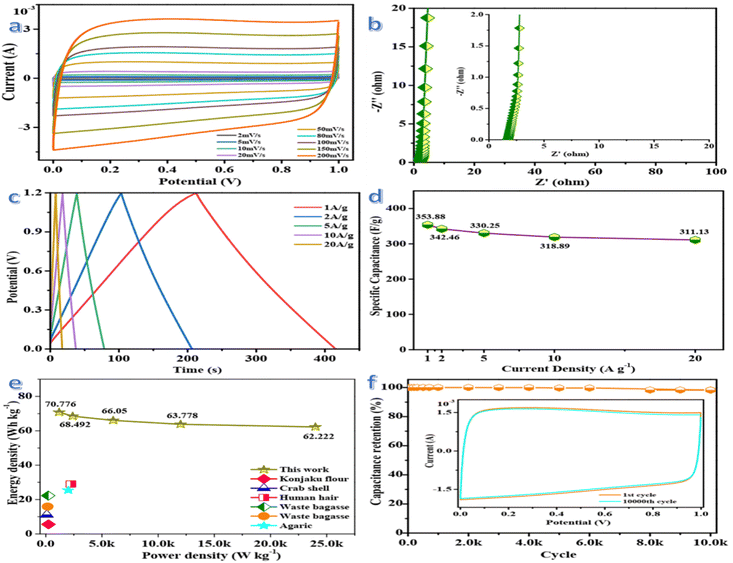
The electrochemical performance of GLAC-2-based supercapacitors is evaluated in a fully assembled two-electrode cell with 1 M KOH electrolyte. As shown in Fig. 3a, the CV curves in a symmetrical two-electrode configuration at different scan rates ranging from 2 to 200 mV s⁻¹ exhibit a typical quasi-rectangular shape with slight faradaic humps, indicating outstanding capacitive behavior of the supercapacitor.⁶¹ Even at a high scan rate of 200 mV s⁻¹, the CV profiles still exhibit excellent shape preservation, demonstrating rapid charge transport at the electrode/electrolyte interface.⁶² The high specific capacitance of the supercapacitor is correlated with the 3D carbon nano-architecture, hierarchical pores, and heteroatom-containing groups. The 3D carbon nano-architecture could shorten the ion diffusion length, the sufficient meso-/macropores could offer ion-transport pathways, and the abundant micropores could be applied as ion-storage sites for high charge-storage capacity, as well as the doping of heteroatoms could provide faradaic pseudocapacitance via redox reactions, which synergistically contribute to excellent electrochemical performance.⁶³

Fig. 3 (a) CV curves of the GLAC//GLAC symmetrical supercapacitor at different scan rates in the voltage window of 0–1.2 V. (b) Nyquist plots of the GLAC//GLAC symmetrical supercapacitor. (c) Galvanostatic charge/discharge curves of the GLAC//GLAC symmetrical supercapacitor at different current densities. (d) Specific capacitances of the as-assembled GLAC symmetrical supercapacitor based on the total mass of the active materials of the two electrodes at different current densities. (e) Ragone plots of the GLAC symmetrical supercapacitor and other previously reported carbon-based symmetric supercapacitors. (f) Cycle performance of the GLAC symmetrical supercapacitor at a current density of 10 A g⁻¹ (inset shows the photograph of CV curves for recycling).

Electrochemical impedance spectroscopy (EIS) measurements are carried out to gain more insights into the charge kinetics and the Nyquist plot is shown in Fig. 3b. The pattern of the plot indicates mainly a vertical line in the low-frequency region, which represents the diffusion resistance. Warburg impedance could be indicated in the region of medium frequencies, where the electrolyte ion penetrated into the depth of the micro/mesoporous network of the GLAC-2 electrode.⁶⁴ The inconspicuous semicircle in the high-frequency region of the plot displays a negligible charge-transfer resistance and a fast faradaic response in the electrode material, owing to the porous structures and functional groups of the electrode material. However, the capacitance is slowly developed at high frequencies, due to the abundant charge transfer complexes migrating with the rapid variety of the potential by overcoming the activation energy.⁶⁵ From the Nyquist plots, a small impedance of 2.12 Ω (106.338 kHz) could be deduced, which confirms the fast and efficient ionic transport in the KOH electrolyte.⁶⁶ As shown in Fig. 3c, the approximate symmetry and the linear GCD curves are indicated at different current densities from 1 to 20 A g⁻¹, confirming no obvious distortions due to pseudocapacitance and excellent capacitor behavior of the supercapacitor. And then, a slight IR drop emerges at the beginning of the discharge stage, demonstrating weak energy dissipation owing to the internal resistance of the GLAC-2 electrodes.⁶⁷ Based on the GCD curves, the specific capacitance of the supercapacitor gradually decreases with the increase in current densities from 1 to 20 A g⁻¹ but the specific capacitance could reach ∼354 F g⁻¹ at 1 A g⁻¹. Generally, the excellent rate capacity of the device is closely associated with the optimized pore structure and enlarged interlayer spacing, which enhance the transport, adsorption or intercalation of ions.⁶⁸Fig. 3d compares the capacitance of the device in a range of current densities from 1 to 20 A g⁻¹, which brings about the change of capacitance from ∼354 to ∼311 F g⁻¹. The specific capacitance is still as high as ∼311 F g⁻¹ with a retention of 87.9% at a high current density of 20 A g⁻¹. The superior rate capability of the device could be attributed to the optimized pore structure and enlarged interlayer spacing, which could enhance the transport, adsorption, or intercalation of ions, as demonstrated by the good diffusion performance in the low-frequency range of the Nyquist plot (Fig. 3b). The specific capacitance is decreased with an increase of the current density, which may be attributed to the slow diffusion and the migration of protons through the electrodes.⁶⁹ The lowered capacitance at higher current densities is also attributed to the insufficient electrolyte ion diffusion kinetics across the micropores owing to the narrow pore size at higher operating current densities; the reduced accumulation amount of electrolyte ions onto porous electrode interface results in the decrement in specific capacitance. Additionally, the presence of heteroatoms greatly reduces such resistance and increases the pore utilization to achieve a high capacitance.⁷⁰

The Ragone plots of GLAC-2 calculated at different current densities are presented in Fig. 3e. The energy density decreases slightly with the increase of the power density, confirming a large energy output at high power density. The maximum energy density can reach up to 70.78 W h kg⁻¹ at a power density of 1.2 kW kg⁻¹, and a high energy density of 62.22 W h kg⁻¹ can still be reached even at an ultrahigh output power density of 24 kW kg⁻¹, which is considerably higher than those of commercially activated carbon-based supercapacitors (3–5 W h kg⁻¹) and other previously reported biomass-derived heteroatom-doped carbonaceous symmetric supercapacitors.^71–73 It is well known that the energy density is suppressed with the increase of current density since the limited pores on the surface are accessed by electrolyte ions for fast discharging at high current density, whereas almost all pores could be utilized at a low current density. Such superior energy/power characteristics can be ascribed to the optimized stacked architecture and tunable pore configuration of electrode materials as well as the enhancement of the transmission of K⁺ and OH⁻ ions inside the material.⁷⁴ These results also indicate that the highly open network structure could promote ion diffusion at the electrolyte/electrode interface and further contribute to the electrolyte solution fully contacting the electroactive reaction sites. Moreover, the nanoporous carbon-based SC can accelerate the ion diffusion and enhance the accessibility of the electrolyte into the interior parts of the electrode and offer a larger number of active sites through its massive surface area (Fig. 4).⁷⁵

Fig. 4 Schematic illustration of the formation of a supercapacitor.

The cycling stability of the supercapacitor is evaluated at a current density of 10 A g⁻¹ within the potential window from 0 to 1.2 V. Notably, the specific capacitance grows a little initially, owing to the further infiltration and activation of the electrode material in the first few cycles from the as-prepared state. And then, 98.24% of its initial specific capacitance could be maintained after 10 000 cycles (Fig. 3f), demonstrating excellent reversibility and structural stability. The long-term cycling stability of the supercapacitor could be attributed to the high surface area and hierarchical structure of the carbon electrode, which facilitates the diffusion of OH⁻ ions and offers enough space for buffering the expansions in the processes of the charge and discharge.⁷⁶ Meanwhile, CV curves for 10 000th cycle is nearly overlapping with the first cycle, which demonstrates the excellent reversibility of the supercapacitor. The superior SC performance could be attributed to the 3D framework structure consisting of cross-linked carbon and a favorable pore network as well as the doping of heteroatoms, which could enhance the transport of electrolyte ions and effectively facilitate the intercalation/extraction of electrolyte ions as well as prolong the cycle lifespan.⁷⁷ Based on these results, the promising electrode material could fulfill the requirements of a supercapacitor with high power density and rate capability.

4 Conclusions

In summary, a facile and efficient H₃PO₄ activation strategy has been developed for the synthesis of porous carbon derived from sustainable gingko leaf precursors. Specifically, the as-obtained GLAC-2 exhibits a large specific surface area of 1133.66 m² g⁻¹, and a hierarchically porous structure, which contributes to a high specific capacitance of ∼709 F g⁻¹ at 1 A g⁻¹. The supercapacitor based on GLAC-2 demonstrates remarkable capacitive performance (∼354 F g⁻¹ at 1 A g⁻¹), superior rate capability (87.9% at 20 A g⁻¹), and long cycle life (only 1.76% capacitance loss over 10 000 cycles), and high energy density (70.78 W h kg⁻¹) at 1.2 kW kg⁻¹ in 1 M KOH aqueous electrolyte. The strategy in the present work provides a promising pathway to fabricate advanced nanocarbons from sustainable biomass for broad applications such as supercapacitors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the financial support from Faculty of Materials and Energy and Institute for Clean Energy & Advanced Materials, Southwest University and Chongqing Key Laboratory for Advanced Materials and Technologies of Clean Electrical Power Sources and the sponsor by the Natural Science Foundation of Chongqing, China (cstc2020jcyj-msxmX0019) and College Student Innovation and Entrepreneurship Training Program, Southwest University (S202210635259).

References

1. S. S. Bengtsen, L. Hamelin, L. Bregnbæk, L. L. Zou and M. Münster, Energy Environ. Sci., 2022, 15, 1950.
2. S. K. Karan and L. Hamelin, Resour., Conserv. Recycl., 2021, 164, 105211.
3. S. K. Karan and L. Hamelin, Renewable Sustainable Energy Rev., 2020, 134, 110350.
4. D. Tonini, L. Hamelin and T. F. Astrup, GCB Bioenergy, 2016, 8, 690.
5. W. Steffen, K. Richardson, J. RockstrÖm, S. E. Cornell, I. Fetzer, E. M. Bennett, R. Biggs, S. R. Carpenter, W. D. Vries, C. A. D. Wit, C. Folke, D. Gerten, J. Heinke, G. M. Mace, L. M. Persson, V. Ramanathan, B. Reyers and S. Sörlin, Science, 2015, 347, 6223.
6. X. T. Ren, N. Meng, L. Ventura, S. Goutianos, E. Barbieri, H. Zhang, H. X. Yan, M. J. Reece and E. Bilotti, J. Mater. Chem. A, 2022, 10, 10171.
7. J. J. Zhu, Y. Sun, J. Gao, Z. B. Qin, Y. N. Zhou, R. Tian and Y. Gao, Chem. Commun., 2022, 58, 5861.
8. B. Dunn, H. Kamath and J. M. Tarascon, Science, 2011, 334, 928.
9. Z. Yang, J. Zhang, M. C. K. Meyer, X. Lu, D. Choi, J. P. Lemmon and J. Liu, Chem. Rev., 2011, 111, 3577.
10. Y. Yue, Y. L. Huang and S. W. Bian, ACS Appl. Electron. Mater., 2021, 3, 2178.
11. Y. N. Liu, J. N. Zhang, H. T. Wang, X. H. Kang and S. W. Bian, Mater. Chem. Front., 2019, 3, 25.
12. Y. N. Liu, H. T. Wang, X. H. Kang, Y. F. Wang, S. Y. Yang and S. W. Bian, J. Power Sources, 2018, 402, 413.
13. E. Zhang, N. Fulik, G. P. Hao, H. Y. Zhang, K. Kaneko, L. Borchardt, E. Brunner and S. Kaskel, Angew. Chem., Int. Ed., 2019, 58, 13060.
14. M. Sandhiya, Vivekanand, S. S. Balaji and M. Sathish, ACS Appl. Energy Mater., 2020, 3, 11368.
15. Y. Shao, M. F. El-Kady, J. Sun, Y. Li, Q. Zhang, M. Zhu, H. Wang, B. Dunn and R. B. Kaner, Chem. Rev., 2018, 118, 9233.
16. S. Q. Zhu, J. C. Shu and M. S. Cao, Nanoscale, 2022, 14, 7322.
17. C. P. Han, J. Tong, X. Tang, D. Zhou, H. Duan, B. H. Li and G. X. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 10479.
18. R. Y. Shi, C. P. Han, H. F. Li, L. Xu, T. F. Zhang, J. Q. Li, Z. Q. Lin, C. P. Wong, F. Y. Kang and B. H. Li, J. Mater. Chem. A, 2018, 6, 17057.
19. C. C. Zhang, Q. Li, T. D. Wang, Y. D. Miao, J. Q. Qi, Y. W. Sui, Q. K. Meng, F. X. Wei, L. Zhu, W. Zhang and P. Cao, Nanoscale, 2022, 14, 6339.
20. P. B. Balakrishnan, N. Silvestri, T. F. Cabada, F. Marinaro, S. Fernandes, S. Fiorito, M. Miscuglio, D. Serantes, S. Ruta, K. Livesey, O. Hovorka, R. Chantrell and T. Pellegrino, Adv. Mater., 2020, 32, 11.
21. G. Y. Zhang, X. Liu, L. Wang and H. G. Fu, J. Mater. Chem. A, 2022, 10, 9277.
22. Y. E. Zhu, L. Yang, J. Sheng, Y. Chen, H. Gu, J. Wei and Z. Zhou, Adv. Energy Mater., 2017, 7, 1701222.
23. G. Wang, M. Yu and X. Feng, Chem. Soc. Rev., 2021, 50, 2388.
24. L. N. Song, W. Zhang, Y. Wang, X. Ge, L. C. Zou, H. F. Wang, X. X. Wang, Q. C. Liu, F. Li and J. J. Xu, Nat. Commun., 2020, 11, 2191.
25. Y. Wei, B. Wang, Y. Zhang, M. Zhang, Q. Wang, Y. Zhang and H. Wu, Adv. Funct. Mater., 2021, 31, 2006033.
26. Y. Wang, M. Qiao and X. Mamat, Chem. Eng. J., 2020, 402, 126214.
27. H. Luo, Y. V. Kaneti, Y. Ai, Y. Wu, F. Wei, J. Fu, J. Cheng, C. Jing, B. Yuliarto, M. Eguchi, J. Na, Y. Yamauchi and S. Liu, Adv. Mater., 2021, 33, 2007318.
28. J. Zhang, T. Zhu, Y. Wang, J. Cui, J. Sun, J. Yan, Y. Qin, X. Shu, Y. Zhang, J. Wu, C. S. Tiwary, P. M. Ajayan and Y. Wu, Mater. Today, 2020, 36, 83.
29. J. C. Xie, L. L. Zhu, H. P. Luo, L. Zhou, C. X. Li and X. J. Xu, J. Chromatogr. A, 2001, 934, 1.
30. C. L. Liang, Z. Y. Zhang, H. D. Zhang, L. F. Ye, J. F. He, J. M. Ou and Q. Z. Wu, Food Chem., 2020, 309, 125680.
31. D. W. Wang, J. W. Nai, L. Xu and T. Sun, ACS Sustainable Chem. Eng., 2019, 7, 18901.
32. Y. F. He, X. D. Zhuang, C. J. Lei, L. C. Lei, Y. Hou, Y. Y. Mai and X. L. Feng, Nano Today, 2019, 24, 103.
33. X. G. Liu, Y. L. Wen, X. C. Chen, A. Dymerska, R. Wrobel, J. Y. Zhu, X. Wen, Z. F. Liu and E. Mijowska, ACS Appl. Energy Mater., 2020, 3, 8562.
34. B. Q. Liu, Q. Zhang, Z. Wang, L. Li, Z. S. Jin, C. G. Wang, L. Y. Zhang, L. H. Chen and Z. M. Su, ACS Appl. Energy Mater., 2020, 12, 8225.
35. Z. Wang, J. H. Huang, Z. W. Guo, X. L. Dong, Y. Liu, Y. G. Wang and Y. Y. Xia, Joule, 2019, 3, 1289.
36. C. H. Lu, J. Meng, J. Zhang, X. Y. Chen, M. Z. Du, Y. P. Chen, C. Y. Hou, J. L. Wang, A. Q. Ju, X. H. Wang, Y. P. Qiu, S. R. Wang and K. Zhang, ACS Appl. Mater. Interfaces, 2019, 11(28), 25205.
37. W. Wei, Z. J. Chen, Y. Zhang, J. Chen, L. Wan, C. Du, M. J. Xie and X. F. Guo, J. Energy Chem., 2020, 48, 277.
38. X. Q. Zhu, F. J. Guo, C. C. Ji, H. Y. Mi, C. Z. Liu and J. S. Qiu, J. Mater. Chem. A, 2022, 10, 12856.
39. X. Qiu, N. Wang, Z. Wang, F. Wang and Y. G. Wang, Angew. Chem., Int. Ed., 2021, 60, 9610.
40. Z. Y. Song, L. Miao, L. Ruhlmann, Y. K. Lv, D. Z. Zhu, L. C. Li, L. H. Gan and M. X. Liu, Adv. Mater., 2021, 33, 2104148.
41. X. Wang, S. Y. Chen, C. Liu, Y. Yu, M. J. Xie and X. F. Guo, J. Energy Chem., 2022, 71, 521.
42. S. H. Yang, Y. Lin, X. F. Song, P. Zhang and L. Gao, ACS Appl. Mater. Interfaces, 2015, 7(32), 17884.
43. J. Y. Zhu, A. S. Childress, M. Karakaya, S. Dandeliya, A. Srivastava, Y. Lin, A. M. Rao and R. Podila, Adv. Mater., 2016, 28, 7185.
44. H. R. Peng, B. Yao, X. J. Wei, T. Y. Liu, T. Y. Kou, P. Xiao, Y. H. Zhang and Y. Li, Adv. Energy Mater., 2019, 9, 1803665.
45. J. H. Hou, C. B. Bao Cao, F. Idrees and X. L. Ma, ACS Nano, 2015, 9, 2556.
46. G. Y. Zhao, C. Chen, D. F. Yu, L. Sun, C. H. Yang, H. Zhang, Y. Sun, F. Besenbacher and M. Yu, Nano Energy, 2018, 47, 547.
47. G. Yuan, Y. R. Liang, H. Hu, H. M. Li, Y. Xiao, H. W. Dong, Y. L. Liu and M. T. Zheng, ACS Appl. Energy Mater., 2019, 11, 26946.
48. C. Chen, D. F. Yu, G. Y. Zhao, B. S. Du, W. Tang, L. Sun, Y. Sun, F. Besenbacher and M. Yu, Nano Energy, 2016, 27, 377.
49. F. Y. Liu, Z. X. Wang, H. T. Zhang, L. Jin, X. Chu, B. N. Gu, H. C. Huang and W. Q. Yang, Carbon, 2019, 149, 105.
50. X. G. Liu, C. D. Ma, J. X. Li, B. Zielinska, R. J. Kalenczuk, X. C. Chen, P. K. Chu, T. Tang and E. Mijowska, J. Power Sources, 2019, 412, 1.
51. M. Sevilla, G. A. Ferrero and A. B. Fuertes, Chem. Mater., 2017, 29, 6900.
52. J. Gong, J. Liu, X. C. Chen, Z. W. Jiang, X. Wen, E. Mijowska and T. Tang, J. Mater. Chem. A, 2015, 3, 341.
53. S. Y. Lu, M. Jin, Y. Zhang, Y. B. Niu, J. C. Gao and C. M. Li, Adv. Energy Mater., 2018, 8, 1702545.
54. J. Y. Zhu, A. S. Childress, M. Karakaya, S. Dandeliya, A. Srivastava, Y. Lin, A. M. Rao and R. Podila, Adv. Mater., 2016, 28, 7185.
55. M. Yang and Z. Zhou, Adv. Sci, 2017, 4, 1600408.
56. H. B. Feng, H. Hu, H. W. Dong, Y. Xiao, Y. J. Cai, B. F. Lei, Y. L. Liu and M. T. Zheng, J. Power Sources, 2016, 302, 164.
57. R. Thangavel, K. Kaliyappan, H. V. Ramasamy, X. L. Sun and Y. S. Lee, ChemSusChem, 2017, 10, 2805.
58. J. H. Yu, C. Yu, W. Guo, Z. Wang, S. F. Li, J. W. Chang, X. Y. Tan, Y. W. Ding, M. D. Zhang, L. Yang, Y. Y. Xie, R. Fu and J. S. Qiu, Nano Energy, 2019, 64, 103921.
59. Y. Song, T. Y. Liu, M. Y. Li, B. Yao, T. Y. Kou, D. Y. Feng, F. X. Wang, Y. X. Tong, X. X. Liu and Y. Li, Adv. Energy Mater., 2018, 8, 1801784.
60. L. Yao, Q. Wu, P. X. Zhang, J. M. Zhang, D. R. Wang, Y. liang Li, X. Z. Ren, H. W. Mi, L. B. Deng and Z. J. Zheng, Adv. Mater., 2018, 30, 1706054.
61. T. Y. Liu, F. Zhang, Y. Song and Y. Li, J. Mater. Chem. A, 2017, 5, 17705.
62. B. J. Yang, J. T. Chen, L. Y. Liu, P. J. Ma, B. Liu, J. W. Lang, Y. Tang and X. B. Yan, Energy Storage Mater., 2019, 23, 522.
63. Z. N. Li, S. Gadipelli, H. C. Li, C. A. Howard, D. J. L. Brett, P. R. Shearing, Z. X. Guo, I. P. Parkin and F. Li, Nat. Energy, 2020, 5, 160.
64. J. Choi, J. Lim, D. Kim, S. Park, B. Y. Yan, D. J. Ko, Y. Cho, L. Y. S. Lee and Y. Z. Piao, J. Mater. Chem. A, 2022, 10, 14501.
65. M. G. Park, J. W. Choi, I. W. Ock, G. H. Kim and J. K. Kang, Adv. Energy Mater., 2021, 11, 2003563.
66. N. Jayababu and D. Kim, Small, 2021, 7, 2102369.
67. W. Jiang, T. Wang, H. Chen, X. Suo, J. Y. Liang, W. S. Zhu, H. M. Li and S. Dai, Nano Energy, 2021, 79, 105464.
68. P. T. Xiao, S. Li, C. B. Yu, Y. Wang and Y. X. Xu, ACS Nano, 2020, 14, 10210.
69. Y. Xu, M. Y. Ou, Y. Liu, J. Xu, X. P. Sun, C. Fang, Q. Li, J. T. Han and Y. H. Huang, Nano Energy, 2020, 67, 104250.
70. Y. Liu, Z. H. Sun, X. Sun, Y. Lin, K. Tan, J. F. Sun, L. W. Liang, L. R. Hou and C. Z. Yuan, Angew. Chem., Int. Ed., 2020, 59, 2473.
71. J. Huang, J. Chen, Z. Y. Yin and J. G. Wu, Nanoscale Adv., 2020, 2, 3284.
72. A. Nordenström, N. Boulanger, A. Iakunkov, G. Li, R. Mysyk, G. Bracciale, P. Bondavalli and A. V. Talyzin, Nanoscale Adv, 2022, 4, 4689.
73. H. Zheng, Q. Cao, M. Zhu, D. Xu, H. Guo, Y. Li and J. Zhou, J. Mater. Chem. A, 2021, 9, 10120.
74. S. Sahoo, R. Kumar, E. Joanni, R. K. Siingh and J. J. Shim, J. Mater. Chem. A, 2022, 10, 13190.
75. J. J. Zhu, Y. Sun, J. Gao, Z. B. Qin, Y. N. Zhou, R. Tian and Y. Gao, Chem. Commun., 2022, 58, 5861.
76. X. T. Ren, N. Meng, L. Ventura, S. Goutianos, E. Barbieri, H. Zhang, H. X. Yan, M. J. Reece and E. Bilotti, J. Mater. Chem. A, 2022, 10, 10171.
77. S. Q. Zhu, J. C. Shu and M. S. Cao, Nanoscale, 2022, 14, 7322.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2na00758d

‡ Equal contribution to this work.

---