Impact of peripheral alkyl chain length on mesocrystal assemblies of G2 dendrons

Abstract

Unique sphere-packing mesophases such as Frank–Kasper (FK) phases have emerged from the viable design of intermolecular interactions in supramolecular assemblies. Herein, a series of C_n-G2-CONH₂ dendrons possessing an identical core wedge are investigated to elucidate the impact of peripheral alkyl chain lengths (C_n) on the formation of the close-packed structures. The C₁₈ and C₁₄ dendrons, of which the contour lengths of the periphery L_p are longer than the wedge length L_w, assemble into a uniform sphere-packing phase such as body-centred cubic (BCC), whereas the C₈ dendron with short (L_p < L_w) corona environment forms the FK A15 phase. Particularly in the intermediate C₁₂ and C₁₀ dendrons (L_p ≈ L_w), cooling the samples from an isotropic state leads to cooling-rate-dependent phase behaviours. The C₁₂ dendron produces two structures of hexagonal columnar and sphere-packing phases (BCC and A15), while the C₁₀ dendron generates the A15 and σ phases by the fast- and slow-cooling processes, respectively. Our results show the impact of peripheral alkyl chain lengths on the formation of mesocrystal phases, where the energy landscape of the dendrons at L_p/L_w ≈ 1 must be more complex and delicate than those with either longer or shorter peripheral alkyl chains.

---

Introduction

Supramolecular assemblies due to intermolecular interactions are a promising platform for creating mesoscopic lattices or scaffolds, where physicochemical properties such as solubility, catalytic reactivity, and optics vary with their morphologies.^1–4 One of the most studied supramolecular assemblies is the sphere-forming structure, where the molecules organize into spherical particles and further form close-packed arrangements.^5–7 The observed packing structures of these soft mesospheres are analogous to the intricate atomic configuration in metallic alloys coordinated with large and small atoms.^8–10 A class of materials forming metallic alloy-like structures includes dendrons,^11–13 surfactants,^10,14 block copolymers,^15,16 and other soft matters.^5,17–20 Recent explorations of these mesoscale assemblies have shown that the architectural design in molecular building components plays a significant role in determining their packing structures.^21–23

In this regard, the liquid crystal (LC) from dendron assembly has been of interest as it has a simple and versatile framework that offers a wide range of three-dimensional (3D) sphere-packing mesophases including 2D columnar analogs.^24,25 These alloy-like structures encompass the Frank–Kasper (FK) phases and quasicrystal approximants, which consist of spherical particles with different sizes, shapes, and coordination numbers.^26,27 The thermodynamic origin that determines such a packing structure is a delicate balance between intermolecular interactions to minimize the surface contact area with neighbouring particles and entropic chain stretching associated with filling the interparticle space uniformly.²⁸ In the close-packed structures, a particle with a long corona generates a high curvature between its core and corona, whereas for the limit of a very short corona, its curvature is presumed to be flatter as a result of short-range interactions.^29,30 Earlier theoretical investigations have suggested that a chain length ratio (L_p/L_w) between the outer corona (L_p) and wedges (L_w) is a parameter to modulate mesocrystal assemblies.^31–33

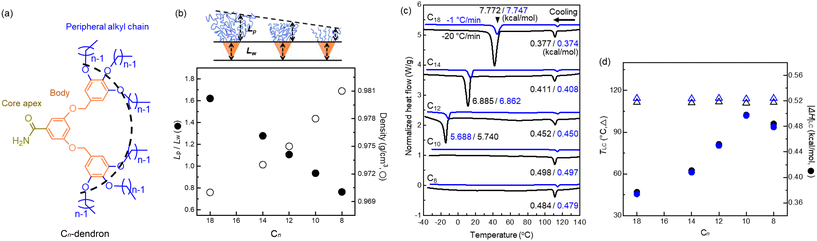
In this study, we fixed the core interaction and L_w of the dendrons and varied the length of peripheral alkyl chains that form the corona. The dendrons (Fig. S1 and S2†) were synthesized by a convergent method using different 1-bromoalkanes and characterised by ¹H nuclear magnetic resonance (NMR) and matrix-assisted laser desorption/ionization time-of-flight (MALDI-TOF). The effect of corona length in mesocrystal assemblies employing a model system C_n-G2-CONH₂ (hereafter; C_n dendron) was investigated (Fig. 1a). They all have the same wedge of a benzyl-ether body (orange) terminated with strong hydrogen-bonding CONH₂ apex (yellow), but various peripheral alkyl chains (blue) according to the C_n of n = 18, 14, 12, 10, and 8. A contour length ratio of L_p/L_w decreases from 1.62 to 0.76 as the C_n decreases (Fig. 1b), where C–C and C–N bond lengths are 1.21 and 1.13 Å, respectively, considering the bond angle restriction. This trend is inversely proprotional to the density variation of the dendrons, indicating that the C_n dendrons are well-designed to control over the fraction of periphery L_p.

Fig. 1 (a) Architecturally asymmetric C_n dendrons consisting of various peripheral alkyl chains (blue) and a benzyl-ether body (orange) terminated with an identical apex functionality of CONH₂ (yellow). (b) Contour length ratio (L_p/L_w) and density of the C_n dendrons. The top schemes represent the changes in the L_p with respect to a fixed L_w. (c) DSC thermograms of the C_n dendrons, measured at the cooling rates of −20 and −1 °C min⁻¹ (black and blue colours, respectively) from 140 to −40 °C. The numbers on the peaks denote the magnitude of enthalpic change (|ΔH|) at transitions as a unit of kcal mol⁻¹. (d) T_LC (open triangles) and |ΔH|_LC (closed circles) as a function of C_n, obtained from the DSC cooling scans.

Experimental

A series of C_n-G2-CONH₂s were synthesized by a convergent method reported in a previous study using different 1-bromoalkanes with carbon numbers of n = 18, 14, 12, 10, and 8.³⁴ The detailed processes and conditions are provided in the ESI.† Each C_n-G2-CONH₂ was characterized by ¹H NMR and MALDI-TOF. The densities of the dendrons were evaluated from a density gradient method using water/ethanol solutions. The thermal properties of the samples were examined by a PerkinElmer Diamond differential scanning calorimetry (DSC) with loading amounts of approximately 10–15 mg under nitrogen flow.

Small-angle X-ray scattering (SAXS) experiments were conducted at the 4C and 9A beamlines of the Pohang Accelerator Laboratory, Korea, and the 12-ID-B beamline of Advanced Photon Source, U.S. The operating conditions for the 4C and 9A beamlines were set to a wavelength of λ = 0.733–1.127 Å, a sample-to-detector distance (SDD) of 1.0–2.5 m, and an exposure time of 1–15 s; these conditions were similarly set at the 12-ID-B beamline with λ = 0.954 Å, SDD = 2 m, and an exposure time of 1–10 s. The scattered intensities were collected on a 2D detector of Rayonix SX165 and Pilatus2M at the target temperatures ranging from 30 to 130 °C.

Electron density (ED) maps of each morphology were reconstructed with the collected SAXS intensity profiles of dendron assemblies by a similar method to a previous study.³⁴ The peak positions and structure-factor intensities across q = 0.1–5.0 nm⁻¹ were assigned in accordance with the corresponding space-group symmetry and lattice parameter,^35,36 then recorded as the input values for SUPERFLIP software.³⁷ The converged results were averaged and visualized using MATLAB software (in 90% contour levels) to construct Voronoi cells for the experimental polyhedrons.

Results and discussion

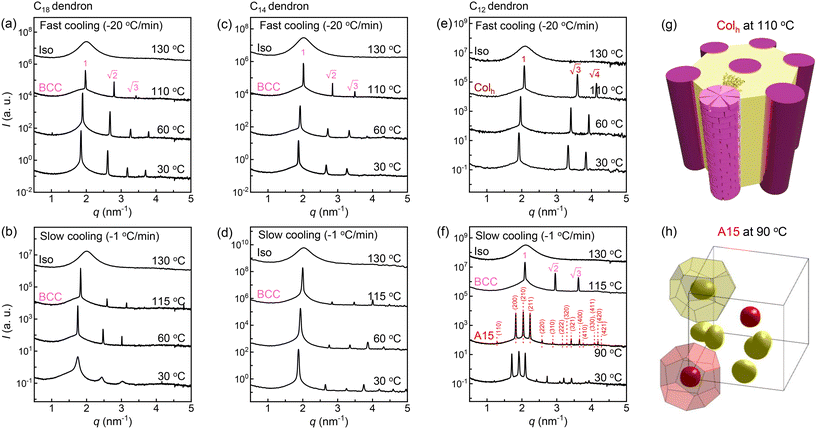
DSC thermograms of the C_n dendrons (Fig. 1c) were measured at cooling rates of −20 and −1 °C min⁻¹ (black and blue colours, respectively) from 140 to −40 °C. The thermograms with two different cooling rates appear to have no difference except for some slight shift of the transition temperatures. While the DSC signals from the slow-cooling (−1 °C min⁻¹) appear weaker, the enthalpic changes (|ΔH|s) of the two cooling rates are nearly identical because the heat flows during each transition are integrated as a function of transitional time. The exotherms at about 110 °C upon cooling represent the liquid crystallization from an isotropic state. The liquid-crystallization temperatures (T_LC) are consistent with the isotropization temperatures (T_iso) upon heating (Fig. S3†). The |ΔH|_LC slightly increases with decreasing C_n. Large exotherms at lower temperatures, observed in the C₁₈ to C₁₂ dendrons, correspond to the crystallization of peripheral alkyl chains. Both the crystallization temperature T_c and |ΔH|_c decrease with decreasing C_n and disappear below −30 °C for the C₁₀ and C₈ dendrons. The T_LC obtained upon cooling remains consistent at a high temperature of 126 °C for all the C_n dendrons (Fig. 1c and d) because of the identical cohesive interactions from CONH₂ apex. Since |ΔH|_LC should be proportional to the total number of hydrogen bonding involved in the mesocrystal assemblies, its overall increase with decreasing C_n may be related with an increase in crystallinity on the formation of LC.

SAXS intensity profiles of all dendron assemblies were recorded during cooling from the isotropic state (Iso), shown as a function of the scattering vector q = (4π/λ)sin θ, where 2θ and λ are the scattering angle and wavelength of X-ray beam, respectively. The samples were first heated to 130 °C (Fig. S4†) and additionally annealed for 10 min to erase the thermal history, then subjected to a cooling process. We performed crystallization experiments with two different rates of −20 and −1 °C min⁻¹ to 30 °C, which are hereafter denoted as the fast- and slow-cooling processes, respectively. The fast cooling of the C₁₈ dendron (Fig. 2a) exhibits a primary peak (q*) and higher-order peaks below 110 °C, and the peak intensities increase as the temperature decreases. A set of peaks with the position ratio of 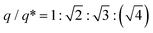corresponds to a BCC structure composed of single-type particles with equal size. The slow cooling of the C₁₈ dendron (Fig. 2b) generates the same BCC structure from 115 to 60 °C; consistent with the DSC result, this T_LC observed in the slow-cooling process is slightly higher than that in the fast-cooling process due to a kinetic effect. Similarly, the C₁₄ dendron presents the same phase behaviour of Iso-BCC (Fig. 2c and d) regardless of the cooling rate.

Fig. 2 SAXS intensity profiles of (a and b) C₁₈, (c and d) C₁₄, and (e and f) C₁₂ dendrons with two different cooling rates of −20 and −1 °C min⁻¹ from 130 to 30 °C. 3D morphologies reproduced from the ED maps of (g) the stacked Col_h and (h) A15 phases, which are obtained from the fast and slow cooling of the C₁₂ dendrons, respectively.

In the case of the fast cooling of the C₁₂ dendron, the position ratio of 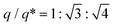is observed, indicating a hexagonal columnar (Col_h) structure (Fig. 2e). A 3D morphology of the stacked Col_h (Fig. 2g), of which the 2D ED map was reconstructed from the data at 110 °C, displays the columnar packing assemblies of the flat discotic-shaped dendrons. In contrast, the slow-cooling process causes a completely different phase transition; this C₁₂ dendron forms a BCC structure at 115 °C, which then transforms to the FK A15 structure at 90 °C (Fig. 2f). The A15 phase reconstructed from the data at 90 °C (Fig. 2h) displays two types of polyhedrons with the coordination number (CN) = 14 and 12. With further decreasing temperature, it retains the same A15 phase and no further transition to Col_h is observed even for an extended annealing period of 4 months at 30 °C. Interestingly to note, when the Col_h phase is heated back, it transitions to A15 and then BCC phases, indicating that the Col_h is a low-temperature structure but it cannot be generated once the dendrons are assembled into spherical particles.

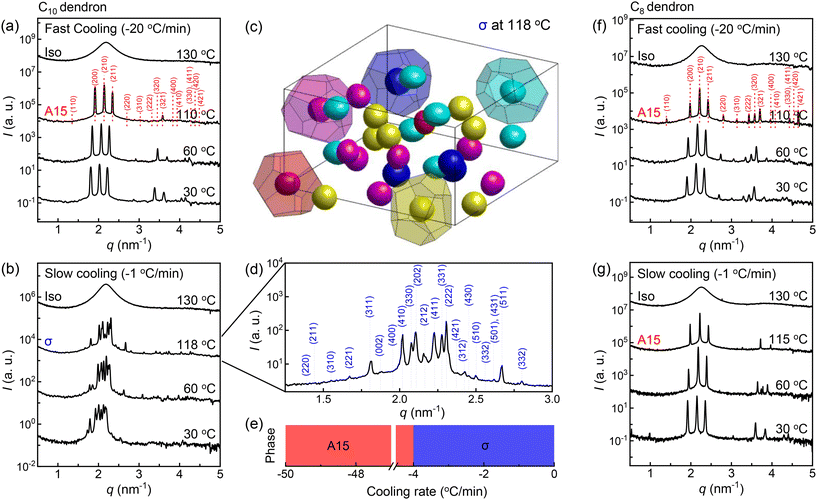
The C₁₀ dendron, in the fast-cooling process (Fig. 3a), forms the A15 structure and no further transition down to 30 °C. In contrast, the slow cooling of the C₁₀ dendron (Fig. 3b) produces new complex peaks of the FK σ structure (Fig. 3d). The ED map (Fig. 3c), which is reconstructed from the data at 118 °C, shows five different types of polyhedrons with CN = 15, 14, 14, 12, and 12, as delineated by red, yellow, magenta, cyan, and blue colours, respectively. We performed the cooling experiments with various cooling rates (Fig. 3e) and found that only two phases of A15 and σ emerge at faster and slower cooling rates than −4 °C min⁻¹, respectively. The C₈ dendron (Fig. 3f and g) shows the consistent formation of the A15 structure regardless of the cooling rates we studied. As seen in C₁₈ and C₁₄ samples, the slow-cooling process promotes the structure formation earlier or at higher temperature.

Fig. 3 SAXS intensity profiles of (a and b) C₁₀ dendron with two different cooling rates of −20 and −1 °C min⁻¹ from 130 to 30 °C. (c) 3D morphology of FK σ phase prepared by the slow cooling of the C₁₀ dendron. (d) Close-up intensity profile of the σ phase and Miller indices. (e) Cooling-rate-dependent phases of the C₁₀ dendron with two phases of A15 and σ determined by faster and slower cooling rates than −4 °C min⁻¹, respectively. SAXS intensity profiles of (f and g) C₈ dendron with two different cooling rates of −20 and −1 °C min⁻¹ from 130 to 30 °C, resulting in an identical phase behaviour of Iso-A15.

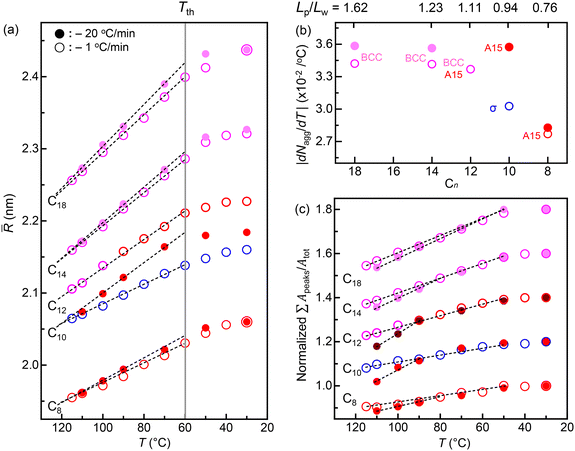
Considering a homologous peripheral region, the phase behaviours are intimately associated with the outer corona environment (or as a function of L_p/L_w). We analyzed the mean radii (R̄_s) of all the spherical particles as a function of temperature for the fast- and slow-cooling processes (Fig. 4a). As the temperature decreases, all the C_n dendrons reveal the linear increases in R until each threshold temperature (T_th) around 60 °C, followed by a relative plateau value of R. According to our prior study,³⁸ the temperature dependence of R showed that T_th decreases by alleviating the core (or cohesive) interactions from the functional apexes. Hence, the consistent T_ths of the C_n dendrons indicate the identical cohesive interactions from CONH₂ apex. Note that a curve of the C₁₂ dendron represents only an A15 phase obtained from the slow-cooling process for comparison, not a Col_h phase. Upon cooling from the isotropic states, a couple of initial R̄ for each C_n dendron are nearly identical at higher temperatures regardless of cooling rates. Except for the C₁₀ dendron, the early-stage slopes gradually decrease as the C_n decreases, and the fast-cooling slopes are somehow greater than the slow-cooling ones. The aggregation number (N_agg) was calculated by N_agg = R̄³N_Aρ/3M_w and plotted as a function of temperature for the fast- and slow-cooling processes (Fig. S5†), where N_A and M_w denote Avogadro's number (6.022 × 10²³ mol⁻¹) and the molecular weight, respectively. The density ρ was measured at 30 °C, assuming that its change with temperature is negligible compared to the change of R̄. During cooling from the Iso, the overall values of |dN_agg/dT| gently decrease with decreasing C_n (Fig. 4b), and in each C_n dendron, the fast-cooling values run higher than the slow-cooling ones.

Fig. 4 (a) Mean particle radii (R̄_s) of all the C_n dendron assemblies during the fast- and slow-cooling processes. The closed and open symbols denote R̄_s from the fast- and slow-cooling processes, respectively, and the dotted lines guide the temperature-dependent increasing rate in R̄ from each initial packing structure. A grey line denotes the threshold temperature (T_th). (b) |dN_agg/dT| during the fast- and slow-cooling processes. (c) ∑A_peaks/A_tot normalized by the value measured at 30 °C, where the integrated intensities of the LC scattering peaks were calculated with respect to total scattering intensities (∑A_peaks/A_tot). The intensity profiles are vertically shifted by a factor of 0.2 to avoid overlapping.

The SAXS data of all the C_n dendrons upon cooling show sharp but weak peaks at higher temperatures, and the peaks become broader while intensities increase (Fig. 2 and 3), corresponding to the nucleation and growth of the LC structures. At T_LC, the mesocrystal domains nucleate and grow fast. As the temperature decreases, new nuclei form in the interstitial region and thus grow into smaller domains. We, however, cannot neglect the possibility that initial larger domains may break into smaller ones as the domains encounter their neighbours. Integrated intensities of the LC scattering peaks were calculated with respect to total scattering intensities (∑A_peaks/A_tot), since it should be proportional to crystallinity on the formation of LC.^39,40

Assuming each dendron assembly reaches the maximum crystallinity at a low temperature of 30 °C, the temperature-dependent ∑A_peaks/A_tot was normalized by the value measured at 30 °C to correlate with the relative crystallinity (Fig. 4c). Even the same BCC phases obtained from C₁₈ and C₁₄ dendrons lead to different crystallinities at lower temperatures, as shown by ∑A_peaks/A_tot. A decrease in the slope near T_LC with decreasing C_n implies that the crystallinity on the formation of LC is higher for shorter C_n dendrons, agreeing with the DSC result displayed in Fig. 1d, where |ΔH|_LC increases with decreasing C_n. Accordingly, the overall decrease in |dN_agg/dT| with decreasing C_n (Fig. 4b) presumably attributed to an increase in crystallinity for shorter C_n dendrons, leaving fewer free dendrons available for the particle assemblies as the temperature decreases. In addition, the fast-cooling |dN_agg/dT| is greater than the slow-cooling one, indicating lower crystallinity on the formation of LC for the fast-cooling dendrons where more isolated or free dendrons are available to aggregate into the particles. Consistently, in the C₁₀ dendron, a remarkable difference in |dN_agg/dT| between the A15 and σ phases from the fast- and slow-cooling processes, respectively, matches a large difference in ∑A_peaks/A_tot at higher temperatures near T_LC.

Unlike the dendrons with either L_p/L_w > 1 or L_p/L_w < 1, unexpected phases were observed for the C₁₂ and C₁₀ dendrons that have the intermediate corona length of L_p/L_w ≈ 1. Similar phase behaviour has also been observed in the nanoparticle assembly systems by varying the alkane-thiol chain length.⁴¹ Particularly, forming σ phase means that the dendrons do not experience a significant energy barrier to generate spherical particles with different sizes, where the formation energies of larger and smaller particles are more advantageous with the intermediate corona length than with either long or short coronas. For the long C_n dendrons, the conformational entropy of peripheral alkyl chains is less likely to allow the formation of spherical particles with different sizes, whereas the short C_n dendron cannot afford to stretch differently. Intriguingly, these C₁₂ and C₁₀ dendrons show cooling-rate-dependent phase behaviours that have been similarly observed in other supramolecular systems^42–45 including block copolymers.¹⁶ The C₁₂ dendron undergoes structural transitions only between the epitaxially related structures such as the BCC and A15 due to a slight distortion of the lattice without massive interdiffusion of dendrons.⁴⁶ Once those structures were formed, they didn't transform into the 2D hexagonal Col_h or σ structures presumably because it requires a significant rearrangement of dendrons.

Conclusion

In summary, the T_LC's (or T_iso's) of all the C_n dendrons remain unchanged, indicating that the phase stability is not associated with the C_n but the cohesive interactions from the core apex. However, the sphere-packing phases achieved from the C_n dendrons turn out to be sensitive to the value of L_p/L_w. Especially at the intermediate corona length of L_p/L_w ≈ 1, the fast-cooling process enables the C₁₂ and C₁₀ dendrons to form low-temperature structures of Col_h and A15, respectively, (while the slow-cooling process allows high-temperature structures of BCC-A15 and σ, respectively); these are otherwise inaccessible each other due to the energy barriers. Our results on the crystallization kinetics with the C_n dendrons indicate that the energy landscape of the dendrons at L_p/L_w ≈ 1 must be more complex and delicate than those with either longer or shorter peripheral alkyl chains.

Author contributions

Under the instruction of DYR, BL, and WJ constructed the idea of characteristic dendron structures and performed SAXS analysis. TJ evaluated the structural information of sphere-packing phases from dendron assemblies as well as ED map reconstructions. HP synthesized and characterized dendron samples using NMR spectroscopy and MALDI-TOF mass spectrometry. JK assisted with reviewing experimental results. WL and HA provided an assistance with SAXS measurements as well as data analysis advice. DYR, WJ, and BL discussed the results together before writing up their manuscript in collaboration.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We acknowledge the Ministry of Science, ICT & Future Planning in Korea for funding the NRF Grants (2020R1A2C3004520, 2021R1A2C2006588, and 2022R1A4A1020543). SAXS experiments were conducted at the Pohang Accelerator Laboratory in Korea (4C and 9A beamlines) as well as at Advanced Photon Source (APS) within the Argonne National Laboratory in U.S. (12-ID-B beamline). The operation of the APS was supported by the U.S. Department of Energy, Office of Basic Energy Sciences through contract no. DE-AC0206CH11357.

References

1. M. Schmittel and V. Kalsani, in Functional Molecular Nanostructures, ed. A. D. Schlüter, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, pp. 1–53,  DOI:10.1007/b98165.
2. R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111, 6810–6918.
3. E. R. T. Tiekink, Coord. Chem. Rev., 2017, 345, 209–228.
4. Q. Song, Z. Cheng, M. Kariuki, S. C. L. Hall, S. K. Hill, J. Y. Rho and S. Perrier, Chem. Rev., 2021, 121, 13936–13995.
5. M. Huang, C.-H. Hsu, J. Wang, S. Mei, X. Dong, Y. Li, M. Li, H. Liu, W. Zhang, T. Aida, W.-B. Zhang, K. Yue and S. Z. D. Cheng, Science, 2015, 348, 424–428.
6. C. Tschierske, Angew. Chem., Int. Ed., 2013, 52, 8828–8878.
7. S. A. Kim, K.-J. Jeong, A. Yethiraj and M. K. Mahanthappa, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 4072–4077.
8. S. Lee, C. Leighton and F. S. Bates, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17723–17731.
9. K. Yue, M. Huang, R. L. Marson, J. He, J. Huang, Z. Zhou, J. Wang, C. Liu, X. Yan, K. Wu, Z. Guo, H. Liu, W. Zhang, P. Ni, C. Wesdemiotis, W.-B. Zhang, S. C. Glotzer and S. Z. D. Cheng, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14195–14200.
10. G. C. Shearman, A. I. I. Tyler, N. J. Brooks, R. H. Templer, O. Ces, R. V. Law and J. M. Seddon, Liq. Cryst., 2010, 37, 679–694.
11. V. S. K. Balagurusamy, G. Ungar, V. Percec and G. Johansson, J. Am. Chem. Soc., 1997, 119, 1539–1555.
12. G. Ungar, Y. Liu, X. Zeng, V. Percec and W.-D. Cho, Science, 2003, 299, 1208–1211.
13. X. Zeng, G. Ungar, Y. Liu, V. Percec, A. E. Dulcey and J. K. Hobbs, Nature, 2004, 428, 157–160.
14. S. A. Kim, K. J. Jeong, A. Yethiraj and M. K. Mahanthappa, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 4072–4077.
15. S. Lee, M. J. Bluemle and F. S. Bates, Science, 2010, 330, 349–353.
16. K. Kim, M. W. Schulze, A. Arora, R. M. Lewis, M. A. Hillmyer, K. D. Dorfman and F. S. Bates, Science, 2017, 356, 520–523.
17. S. Jeon, T. Jun, S. Jo, H. Ahn, S. Lee, B. Lee and D. Y. Ryu, Macromol. Rapid Commun., 2019, 40, 1900259.
18. K. K. Lachmayr, C. M. Wentz and L. R. Sita, Angew. Chem., Int. Ed., 2020, 59, 1521–1526.
19. J. H. Huang, Z. B. Su, M. J. Huang, R. C. Zhang, J. Wang, X. Y. Feng, R. Zhang, R. M. Zhang, W. P. Shan, X. Y. Yan, Q. Y. Guo, T. Liu, Y. C. Liu, Y. P. Cui, X. P. Li, A. C. Shi and S. Z. D. Cheng, Angew. Chem., Int. Ed., 2020, 59, 18563–18571.
20. X. Y. Feng, G. X. Liu, D. Guo, K. N. Lang, R. M. Zhang, J. H. Huang, Z. B. Su, Y. W. Li, M. J. Huang, T. Li and S. Z. D. Cheng, ACS Macro Lett., 2019, 8, 875–881.
21. T. Kato, N. Mizoshita and K. Kishimoto, Angew. Chem., Int. Ed., 2006, 45, 38–68.
22. P. Rajamalli and E. Prasad, Langmuir, 2013, 29, 1609–1617.
23. R. Fenyves, M. Schmutz, I. J. Horner, F. V. Bright and J. Rzayev, J. Am. Chem. Soc., 2014, 136, 7762–7770.
24. H.-J. Sun, S. Zhang and V. Percec, Chem. Soc. Rev., 2015, 44, 3900–3923.
25. G. Ungar, V. Percec, X. B. Zeng and P. Leowanawat, Isr. J. Chem., 2011, 51, 1206–1215.
26. J. Roth and F. Gähler, Eur. Phys. J. B, 1998, 6, 425–445.
27. G. Ungar and X. B. Zeng, Soft Matter, 2005, 1, 95–106.
28. C. R. Iacovella, A. S. Keys and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20935–20940.
29. G. A. McConnell, A. P. Gast, J. S. Huang and S. D. Smith, Phys. Rev. Lett., 1993, 71, 2102–2105.
30. J. Bang and T. P. Lodge, Macromol. Res., 2008, 16, 51–56.
31. M. Daoud and J. P. Cotton, J. Phys., 1982, 43, 531–538.
32. Y. Lauw, F. A. M. Leermakers, M. A. Cohen Stuart, O. V. Borisov and E. B. Zhulina, Macromolecules, 2006, 39, 3628–3641.
33. A. E. Marras, T. R. Campagna, J. R. Vieregg and M. V. Tirrell, Macromolecules, 2021, 54, 6585–6594.
34. T. Jun, H. Park, S. Jeon, S. Jo, H. Ahn, W.-D. Jang, B. Lee and D. Y. Ryu, J. Am. Chem. Soc., 2021, 143, 17548–17556.
35. T. Li, A. J. Senesi and B. Lee, Chem. Rev., 2016, 116, 11128–11180.
36. B. Lee, I. Park, H. Park, C.-T. Lo, T. Chang and R. E. Winans, J. Appl. Crystallogr., 2007, 40, 496–504.
37. L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786–790.
38. T. Jun, H. Park, S. Jeon, H. Ahn, W.-D. Jang, B. Lee and D. Y. Ryu, Nanoscale, 2022, 14, 16936–16943.
39. C. Vonk, J. Appl. Crystallogr., 1973, 6, 148–152.
40. D. J. Wilson, C. G. Vonk and A. H. Windle, Polymer, 1993, 34, 227–237.
41. B. Pansu, C. Goldmann, D. Constantin, M. Impéror-Clerc and J.-F. Sadoc, Soft Matter, 2021, 17, 6461–6469.
42. B. Moulton and M. J. Zaworotko, Chem. Rev., 2001, 101, 1629–1658.
43. F. Tantakitti, J. Boekhoven, X. Wang, R. V. Kazantsev, T. Yu, J. Li, E. Zhuang, R. Zandi, J. H. Ortony, C. J. Newcomb, L. C. Palmer, G. S. Shekhawat, M. O. de la Cruz, G. C. Schatz and S. I. Stupp, Nat. Mater., 2016, 15, 469–476.
44. N. M. Matsumoto, R. P. M. Lafleur, X. Lou, K.-C. Shih, S. P. W. Wijnands, C. Guibert, J. W. A. M. van Rosendaal, I. K. Voets, A. R. A. Palmans, Y. Lin and E. W. Meijer, J. Am. Chem. Soc., 2018, 140, 13308–13316.
45. J. Matern, Y. Dorca, L. Sánchez and G. Fernández, Angew. Chem., Int. Ed., 2019, 58, 16730–16740.
46. P. Xiao, D. Sheppard, J. Rogal and G. Henkelman, J. Chem. Phys., 2014, 140, 174104.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr01243c

‡ These authors contributed equally to this work.

---