Open Access Article
Open Access ArticleFirst principles reaction discovery: from the Schrodinger equation to experimental prediction for methane pyrolysis†
Rui
Xu
 ab,
Jan
Meisner‡
ab,
Jan
Meisner‡
 ab,
Alexander M.
Chang
ab,
Alexander M.
Chang
 ab,
Keiran C.
Thompson
ab,
Keiran C.
Thompson
 ab and
Todd J.
Martínez
ab and
Todd J.
Martínez
 *ab
*ab
aDepartment of Chemistry, The PULSE Institute, Stanford University, Stanford, CA 94305, USA. E-mail: toddjmartinez@gmail.com
bSLAC National Accelerator Laboratory, 2575 Sand Hill Road, Menlo Park, CA 94025, USA
First published on 9th June 2023
Abstract
Our recent success in exploiting graphical processing units (GPUs) to accelerate quantum chemistry computations led to the development of the ab initio nanoreactor, a computational framework for automatic reaction discovery and kinetic model construction. In this work, we apply the ab initio nanoreactor to methane pyrolysis, from automatic reaction discovery to path refinement and kinetic modeling. Elementary reactions occurring during methane pyrolysis are revealed using GPU-accelerated ab initio molecular dynamics simulations. Subsequently, these reaction paths are refined at a higher level of theory with optimized reactant, product, and transition state geometries. Reaction rate coefficients are calculated by transition state theory based on the optimized reaction paths. The discovered reactions lead to a kinetic model with 53 species and 134 reactions, which is validated against experimental data and simulations using literature kinetic models. We highlight the advantage of leveraging local brute force and Monte Carlo sensitivity analysis approaches for efficient identification of important reactions. Both sensitivity approaches can further improve the accuracy of the methane pyrolysis kinetic model. The results in this work demonstrate the power of the ab initio nanoreactor framework for computationally affordable systematic reaction discovery and accurate kinetic modeling.
1. Introduction
Reaction discovery in complex chemical systems has recently developed into a thriving research topic. A complex reaction network typically contains reactants, products, and all relevant intermediate species, connected by elementary reactions. Fundamental understanding of these reactions involves quantitative analysis of the potential energy surface (PES), estimation of the rates of reaction, and modeling of the evolution of the chemical system over time. The rapid growth in computational capabilities in the past decades opens the possibility for systematic exploration of complex chemical mechanisms.1–4 Many of these approaches are knowledge-based, as they assume chemical rules that guide the reaction discovery. Examples include methods using tabulated reaction templates (Netgen,5–7 EXGAS,8 RMG,9,10 and RING11,12), connectivity graphs (Zstruct13–15 and others16,17), and heuristics-rule-based reaction discovery (HAQC18–20 and Chemoton21–23). Some studies also applied machine learning tools,24–29 taking advantage of modern computational capabilities to generate large training datasets from selected chemical reaction rules24–26 or first principles.27,28Besides the knowledge-based reaction discovery approach, another systematic method for unraveling complex chemical mechanisms is reactive molecular dynamics (MD) simulations of freely reacting molecules.30–40 Perhaps the best way to allow for arbitrary bond rearrangements in the reactive MD is by using ab initio molecular dynamics,41,42 where the electronic Schrodinger equation is solved as needed to compute interatomic forces. The reactive MD approach bypasses the need for human heuristics by allowing chemical reactions to occur freely without predefined reaction rules. However, direct MD simulations under realistic chemical time scales and conditions are challenging, since the computationally accessible time scale is still too short compared to that of a realistic chemical reaction.43 A few studies have attempted to estimate rates of reaction events from the occurrence frequency over the simulation period,34,37–39,44 but it becomes very difficult to do this accurately because of the rarity of chemical events compared to molecular collisions.
A solution to the above issue is to decouple reaction rates from reaction discovery. In this strategy, it does not matter how reactions are discovered because the reaction rate is determined independently (e.g., with transition state theory). One is therefore free to use any of the existing accelerated dynamics and enhanced sampling approaches,45–54 or even new ones which might not provide a direct connection to reaction rates. Our recently developed ab initio nanoreactor30,31 introduces new acceleration techniques during ab initio molecular dynamics (AIMD), including ones inspired by high-pressure55 and shock-wave56,57 simulations. A virtual piston periodically pushes the molecules towards the reactor center, increasing the frequency of reactive events. Electronic structure calculations used to determine the interatomic forces in the nanoreactor are accelerated by graphical processing units (GPU),58–61 enabling on-the-fly AIMD simulations with density functional theory (DFT) in small to medium-sized basis sets. In a step that we call “refinement,” the reactions discovered from AIMD simulations are used to find minimum energy paths (MEPs), which include the minimum-energy geometries of both the reactant and product along with a transition state structure. From these refined paths, a kinetic model including reaction rate information can be constructed. Overall, the ab initio nanoreactor combines reaction discovery, path refinement, and kinetic modeling in a computationally affordable manner. We have previously demonstrated the capability of the ab initio nanoreactor for uncovering chemical pathways in the Urey–Miller experiment,30 acetylene polymerization,30 nitromethane decomposition,62 and multistep chemistry of a Donor–Acceptor Stenhouse Adduct (DASA) photoswitch.63 We have also developed a photochemical version which explores reaction dynamics on excited electronic states.64 Other workers have applied nanoreactor-like approaches to prebiotic formation of RNA precursors,65 terpene formation in nanocapsules,66 soot formation,67 and high-temperature graphene formation,68 highlighting its potential for reaction discovery across a broad range of chemistry.43,69 These previous studies demonstrate the nanoreactor's advantage for systematic and efficient exploration of complex chemical systems. Most of the earlier studies focused on reaction discovery and path refinement, and only limited attempts were made to build kinetic models.62 In the present contribution, we build a reaction network entirely from nanoreactor discovery and refinement and then validate this against experimental data and other literature kinetic models.
In this work, we apply the ab initio nanoreactor framework to methane combustion, specifically focusing on constructing and validating a chemical kinetic model for methane pyrolysis. Methane is the simplest hydrocarbon fuel for combustion. It is also an important practical fuel as it is the primary component (>85 molar%) in natural gas.70 Experimental and theoretical studies on methane combustion have been evolving for about half a century.71–78 One of the milestones is the development of GRI-Mech, a chemical kinetic model for methane79 (and later versions for natural gas80) combustion. Recently, there has been a revival of interest in methane and liquified natural gas (LNG) as potential aerospace propellants due to their higher specific-impulse and less-concerning environmental effects compared to some of the conventional kerosene-based fuels.81,82 New research studies have emerged for experimenting with methane combustion at a higher-pressure, and/or under engine-relevant conditions.83–86 As a subset of methane combustion chemistry, the pyrolytic reaction process is critical to predicting methane's combustion behavior and sooting propensity at fuel-rich conditions. Due to its importance, methane pyrolysis has also been extensively studied for many decades. Most of the studies are experimental efforts87–95 while theoretical studies in the literature are rare.96,97 Beyond the above reasons, we choose methane pyrolysis chemistry for its simplicity to test the validity of the nanoreactor methodology. This paper aims to achieve two major objectives. First, the accuracy of the nanoreactor-constructed kinetic model is validated against experimental data and modeling results from literature kinetic models. Second, we explore the suitability of sensitivity analysis and its potential for efficient identification of key reactions from a complex reaction network.
The paper is constructed as follows. Section 2 describes the nanoreactor framework and the methodology for reaction discovery, path refinement, rate coefficient calculation, kinetic modeling, and sensitivity analysis. Section 3 presents the results of the kinetic model validation and explores the applicability of the sensitivity analysis. Section 4 draws conclusions.
2. Methodology
The methane reaction network is automatically constructed by the ab initio nanoreactor through a streamlined workflow, which is illustrated in Fig. 1. Briefly, the reaction events are discovered and extracted from accelerated ab initio molecular dynamics simulations. The reaction paths detected during the discovery phase are further refined towards their corresponding minimum energy paths, including geometry optimization of reactants, products, and transition state configurations. Furthermore, the reaction rate parameters are calculated using transition state theory.98–101 The reaction kinetic model, consisting of all species and reactions discovered during the discovery/refinement phases (53 species and 134 reactions for the methane pyrolysis case studied here), is validated against experimental data and literature kinetic models. During the kinetic model validation, sensitivity analysis is performed to evaluate the relative importance of each reaction rate parameter. We describe the workflow in detail below.2.1. Reaction discovery
Reaction discovery in the nanoreactor was explored in ab initio molecular dynamics (AIMD) simulations using the unrestricted B3LYP density functional102,103 and a 3-21G basis set. All AIMD simulations are performed with GPU-accelerated energy and gradient calculations in the TeraChem electronic structure package.58–61 The simulations employed level shifting104 for open-shell states. Thermal smearing with fractional occupation number (FON) is enabled to accelerate self-consistent field (SCF) convergence.105 The electronic temperature for FON thermal smearing was set to 3160 K. The AIMD simulations started with 8 methane (CH4) molecules and 3 hydrogen (H) atoms as initial reactants with a spherical configuration (r = 4.2 Å) set by the Packmol program.106 Addition of the 3 H atoms can speed up reaction discovery, since hydrogen atoms are highly reactive free radicals and also the product of the initiation step of CH4 decomposition. The reasoning for the initial system size choice (i.e., 8 CH4 molecules with 3 H atoms) is provided later. The equations of motion were integrated using Langevin dynamics with a friction coefficient of 41 ps−1 and the velocity Verlet integrator at thermostat (equilibrium) temperatures (Teq) of 1500, 2000, 2500, 3000, and 3500 K, respectively (see Section S3 and Table S3† for details of all discovery runs). For each thermostat temperature condition, 10 discovery simulations covering 20 ps (with a 1 fs time step) were performed. This corresponds to a total of 1 ns discovery simulation time. In each simulation, a periodic piston compression potential was added to the ab initio potential energy surface in order to accelerate the reaction discovery: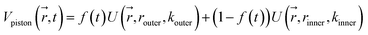 | (1) |
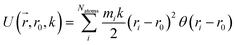 | (2) |
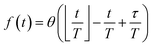 | (3) |
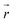 collects the distance of each atom from the simulation origin (center of the spherical piston), and the parameters are kouter = 4.5 kcal mol−1 Å−2 amu−1, router = 5.0 Å, kinner = 11.2 kcal mol−1 Å−2 amu−1, rinner = 3.4 Å, τ = 300 fs, T = 450 fs. The choice of these parameters and the initial system size (e.g., number of reactant molecules) are jointly determined by computational experiments in trial AIMD runs where two requirements should be fulfilled. First, the system should contain enough reactant molecules (yet not too many because of computational cost considerations) along with a sufficiently aggressive piston compression potential to ensure that chemical reactions occur during the lowest thermostat temperature simulations (i.e., 1500 K). Second, the piston potential must not be so aggressive that it hastens improbable processes such as spontaneous C–H bond rupture. As long as these parameters are reasonably determined from these two requirements, the discovery results should not be ultrasensitive to the parameters chosen. Furthermore, the function θ is the Heaviside step function, and ⌊⌋ is the floor function. The function f(t) acts as a rectangular wave oscillating between value one with duration τ and value zero with duration (T – τ). The function
collects the distance of each atom from the simulation origin (center of the spherical piston), and the parameters are kouter = 4.5 kcal mol−1 Å−2 amu−1, router = 5.0 Å, kinner = 11.2 kcal mol−1 Å−2 amu−1, rinner = 3.4 Å, τ = 300 fs, T = 450 fs. The choice of these parameters and the initial system size (e.g., number of reactant molecules) are jointly determined by computational experiments in trial AIMD runs where two requirements should be fulfilled. First, the system should contain enough reactant molecules (yet not too many because of computational cost considerations) along with a sufficiently aggressive piston compression potential to ensure that chemical reactions occur during the lowest thermostat temperature simulations (i.e., 1500 K). Second, the piston potential must not be so aggressive that it hastens improbable processes such as spontaneous C–H bond rupture. As long as these parameters are reasonably determined from these two requirements, the discovery results should not be ultrasensitive to the parameters chosen. Furthermore, the function θ is the Heaviside step function, and ⌊⌋ is the floor function. The function f(t) acts as a rectangular wave oscillating between value one with duration τ and value zero with duration (T – τ). The function 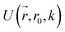 describes a radial half-harmonic potential which vanishes for atoms inside the spherical boundary defined by r0, and the force constant k is multiplied by the atomic mass to ensure equal acceleration on atoms with the same distance from the origin. In eqn (1), the harmonic potentials are switched between U(r, router, kouter) with duration τ and U(r, rinner, kinner) with duration (T – τ). The atoms within a radial position rinner < r < router experience a compression force towards the center of the reactor, leading to an increase in collision events. During each compression, the instantaneous temperature of the system can be much higher than the equilibrium temperature Teq. After the compression, the system is quenched to the target Teq, and the molecules quickly diffuse back to fill the larger reactor volume. An example temperature plot can be found in Section S3 (Fig. S1)† for further demonstration.
describes a radial half-harmonic potential which vanishes for atoms inside the spherical boundary defined by r0, and the force constant k is multiplied by the atomic mass to ensure equal acceleration on atoms with the same distance from the origin. In eqn (1), the harmonic potentials are switched between U(r, router, kouter) with duration τ and U(r, rinner, kinner) with duration (T – τ). The atoms within a radial position rinner < r < router experience a compression force towards the center of the reactor, leading to an increase in collision events. During each compression, the instantaneous temperature of the system can be much higher than the equilibrium temperature Teq. After the compression, the system is quenched to the target Teq, and the molecules quickly diffuse back to fill the larger reactor volume. An example temperature plot can be found in Section S3 (Fig. S1)† for further demonstration.
The simulated AIMD trajectories were analyzed to parse out reaction events. Detailed procedures can be found in our earlier work.30,31,62 Briefly, molecules in the AIMD trajectories were represented as a connectivity graph data structure where nodes correspond to atoms and edges correspond to covalent bonds. Reaction events were detected by changes in the connectivity graph as a function of time. Bond formation between atoms occurs when the bond order is greater than 0.7 and bond length is shorter than 1.2 covalent radii, while bond breaking happens when the bond order is below 0.1 and bond length exceeds 2.5 covalent radii. The raw signals of the time-dependent changes of the connectivity graph can be complicated by the large-amplitude vibrations within a molecule that introduce significant noise. To address this issue, we apply a two-state hidden Markov model (HMM).30,31 The noise is removed by estimating the most likely sequence of the hidden states, which should only contain the chemical reaction. The resulting reaction event consists of 40 frames of coordinates of reactants, products, and other geometry frames across the reaction event time interval. The initial reaction path is extracted from the AIMD trajectory and saved in a database for subsequent path refinement purposes. Charge and spin multiplicity values for the reaction path and its reactant and product species are computed and saved to the database. Details of the charge and spin multiplicity assignment is included in Section S4 in the ESI.†
2.2. Path refinement
The discovered reaction paths are refined using the same unrestricted B3LYP density functional102,103 and a larger 6-31G** basis set. Although using DFT may lead to inaccuracies in the optimized reaction path (e.g., reaction barrier height and reaction enthalpy) compared to a higher level of theory such as CCSD(T), we choose B3LYP/6-31G** based on two reasons. First, considering hundreds of reaction paths to be refined, DFT is computationally much cheaper than coupled-cluster theory. Second, we want to assess the accuracy of the later constructed kinetic model from a consistent method in both reaction discovery and path refinement. Nevertheless, we will see later that with kinetic modeling and appropriate sensitivity analysis, only a few reaction paths need to be refined with higher level of theory in the future work.The path refinement follows a three-step procedure. First, the endpoints (i.e. reactants and products) are optimized using the L-BFGS107 algorithm with delocalized internal coordinates (DLC).108 Cartesian coordinates are used as a back-up option when the optimization does not converge within 50 iterations. Second, after the endpoints of each reaction path have been minimized, a geodesic smoothing algorithm109 is employed to produce an initial guess path for future minimum energy path (MEP) search. Specifically, for each discovered reaction path, geodesic smoothing finds the local minimum of the total path length by updating one geometry frame (i.e., its coordinates) at a time. The smoothing procedure is performed iteratively until it converges when the change of path length is smaller than the convergence threshold. Overall, geodesic smoothing is trying to preserve the information from a discovered path, and at the same time, the smoothed geodesic paths have been shown as good starting guesses for minimum energy path search.109 The smoothed path is saved in our database, labeled as a “relaxed path”.
In the third step, we take the relaxed path as an initial guess and carry out MEP optimizations using the growing string method.110–112 During the MEP search, each reaction path is optimized with the translation–rotation-internal coordinate (TRIC) system which explicitly includes the translations and rotations of molecules.113 Since the reactions detected from discovery are not necessarily all elementary reactions, a reaction splitting algorithm is employed during the path optimization. A converged path will be split if it is found to contain an intermediate minimum node that is at least 3 kcal mol−1 lower in energy than the adjacent nodes. The newly split reactions are registered as relaxed paths and will be refined again. In each refined path, the highest energy point is used as the input for a transition state search, where the L-BFGS107 algorithm is used with DLC,108 and the norm of the energy gradient is minimized towards a saddle point. This approach may not guarantee a first-order saddle point on a reaction path, although this is most frequently the case for an elementary reaction that contains a transition state. In principle, one could carry out normal mode analysis at each putative transition state to ensure that all are first-order saddle points (and subject them to further optimization if they are not). Additional information about the transition state optimization is included in Section S5.3 of the ESI† (with distributions of imaginary frequency amplitudes in the transition state configurations in Fig. S2,† and the refined path for 10 most important reactions for CH4 destruction in Table S4†). The ESI† provides validation for the current transition state optimization workflow in the ab initio nanoreactor. As we will see later, the current transition state optimization framework may introduce some inaccuracy in rate constant estimations, but the overall impact on the kinetic modeling is not too significant. As an improvement, work is underway to incorporate some other transition state optimization algorithms, for example, the partitioned rational function optimization (P-RFO)114 approach which keeps track of the Hessian information during optimization and follows the eigenvector pointing towards the desired transition state configuration.
2.3. Thermodynamic and reaction rate parameter calculation
After all paths are refined, the macroscopic thermochemical properties (i.e., heat capacities Cp, entropies S, enthalpies H, and free energies G) of molecular species and transition state geometries are further computed. The entire computation procedure is detailed in Section S5 of the ESI.† We briefly describe the major points here. The thermochemical properties are derived from the expression for molecular partition function, which is assumed to be a product of translational, rotational, vibrational, and electronic partition functions.115| Q = QtransQrotQvibQelec | (4) |
In eqn (4), Qtrans is the translational partition function, whereas Qrot, Qvib, and Qelec are the rotational, vibrational, and electronic partition function, respectively. The contribution of Qtrans to the thermochemical properties is derived using the ideal gas law. The calculation of Qrot is based on the rigid rotor model. Qvib is computed as a classical vibrational partition function for polyatomic molecules, assuming each vibrational mode is a harmonic oscillator. For transition state geometries, we treat any small imaginary vibrational modes (which are lower than 30i cm−1 and usually correspond to hindered rotations) as real modes with the same amplitude. For both the endpoints and transition state geometries, low frequencies are treated as rotational modes rather than vibrational modes through Grimme's quasi-rigid rotor harmonic oscillator (RRHO) approach116 combined with a damping function117 to switch between the two alternate descriptions. The Qelec contribution to enthalpy includes electronic energy and the Yamaguchi spin projection118,119 for correcting spin contamination in unrestricted DFT calculations (see Section S5.4† for details). The electronic contribution to entropy includes the electronic degeneracy which is based on the spin multiplicity of each species. The calculated thermochemical properties of molecular species are tabulated as a function of temperature in the form of NASA9 polynomial coefficients.120 The fitting is performed using least squares within the 250–3000 K temperature range and at 1 bar reference pressure.
The rate of each reaction in the kinetic model is calculated using transition state theory (TST),98–101 in which the forward rate of a reaction is given by
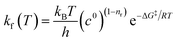 | (5) |
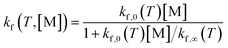 | (6) |
The final kinetic model is assembled with the reaction equations and their forward rate coefficients based on the modified Arrhenius equation (eqn (S40)†). Details of the rate coefficient calculation procedure can be found in Section S6.† The reaction kinetic model file in Cantera122 format (.cti) is also included in ESI.†
Lastly, we note that all the reaction rate parameters calculated and used in this work are referred to as phenomenological rate constants/coefficients, which are explicitly expressed to be dependent on macroscopic thermodynamic properties (e.g., temperature, and probably pressure), but independent of the time evolution of the reaction system. As Widom123 pointed out in 1965, a phenomenological rate constant should not be directly interpreted as the probability per unit time that reactants form products; rather, it encapsulates all the microscopic intermolecular and intramolecular transitions modes, regardless of whether the chemical system has reached a steady state energy distribution (SED). There has been some recent debate124–126 about whether it is appropriate to apply the phenomenological rate constants for modeling the gas-phase chemical reactions under high-temperature conditions. A practical solution to this problem is the master equation (ME) approach,127–130 which bypasses the use of phenomenological rate constants and directly simulates the species time-evolution in an energy-resolved chemical reaction system. A case study by Miller et al.125 suggests that the error induced by phenomenological rate constants seems to be small compared to the ME solutions, so long as they are estimated based on methods128,131–133 obeying detailed balance and taking into account both the internal energy relaxation eigenmodes (IERE) and chemically significant eigenmodes (CSE). Nevertheless, in this work, we simulate the kinetic evolution of the methane pyrolysis system using the phenomenological rate parameters.
2.4. Kinetic modeling and sensitivity analysis
Kinetic modeling is performed in Cantera,122 an open-source chemical kinetic numerical solver. The time evolution of species mole fractions (e.g., methane CH4, hydrogen H2, ethylene C2H4, and acetylene C2H2) are simulated as initial value problems in a zero-dimensional (0D) homogeneous reactor assuming ideal gas mixtures. The simulated species mole fractions are validated against experimental data collected from two shock tube facilities95 and a flow reactor facility,94 respectively. For shock tube experiments, the 0D reactor was assumed to be adiabatic and constant volume; for the flow reactor experiment, constant-pressure and constant-temperature assumptions were used for the simulation. Additional details of the experimental conditions and simulation approach is documented in Section S7 in ESI.† Because of the widespread interest in combustion reaction kinetics, numerous kinetic combustion models have been developed, based on a combination of experimental and theoretical information. We compare the simulation results from the ab initio nanoreactor kinetic model with four of these semiempirical models: (1) GRI Mech 3.0,80 an optimized reaction model designed for natural gas combustion, (2) the Appel, Bockhorn, Frenklach (ABF)134 model, which predicts well the fuel rich combustion behavior of small hydrocarbons (e.g. ethane, ethylene, and acetylene), (3) USC Mech II,135 a kinetic model that captures the combustion behaviors of H2/CO/C1–C4 hydrocarbons, and (4) AramcoMech 3.0,136 a recently developed kinetic model for H2/CO/C1–C4 hydrocarbon combustion. Additional information regarding these four kinetic models is included in Section S2.†Sensitivity analyses presented in this work are performed with two approaches. The first approach is to explore the impact of each rate coefficient following a local sensitivity analysis method.137,138 Briefly, it estimates the change of kinetic output with respect to the change of parameters in a kinetic model. For instance, the partial derivative ∂ci/∂kj represents the first-order local sensitivity coefficient for the concentration of species i with respect to rate coefficient kj. In practice, the rate parameters and the output quantities of a kinetic model may carry different units and orders, and a more practical approach is to calculate the normalized sensitivity coefficient, which represents the fractional change in concentration ci with respect to a fractional change of rate parameter kj.
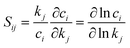 | (7) |
Practically, a coarse-grained estimation of Sij can be accessed through a finite difference brute-force method, where Sij is expressed as
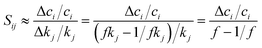 | (8) |
To estimate Sij using eqn (8), kinetic simulations need to be performed with each rate parameter kj up-scaled by a given factor f (where f > 1.0) and down-scaled by 1/f. The change of concentration ci, Δci = ci,fkj − ci,1/fkj represents the change evaluated at perturbed rate constant fkj and (1/f)kj. Therefore, given a chemical kinetic model consisting of n reactions, 2n simulations of species concentration ci are required to evaluate Sij. In this work, we choose f = 2, which is reasonably effective yet small for most of the chemical reactions.75,139 Finally, the impact of each rate parameter kj with respect to species concentration ci are ranked according to the absolute value of Sij. Details of this analysis will be discussed in the Results section.
The second sensitivity analysis approach is based on Monte Carlo (MC) sampling. While the brute-force sensitivity approach perturbs only one rate parameter at a time in a simulation, the MC-based sensitivity analysis allows all rate parameters to vary in one simulation. Specifically, for a particular set of MC sensitivity analysis, we perform 500 MC kinetic modeling calculations. In each MC kinetic modeling sample, the same target property is simulated (e.g., methane mole fraction at a given initial temperature, pressure, and simulation time), but all the rate parameters are randomly perturbed in their respective natural log space (i.e., ln(kj)) uniformly within a predefined upper-limit range (i.e., factor of 2, 10, and 100 in this work). In the MC-based sensitivity analysis, the modeling results are usually presented as an uncertainty band or a scatter of simulation points.140,141 The advantage of the MC-based sensitivity analysis will be shown and discussed later, as it takes into account the kinetic coupling among rate coefficients.
3. Results and discussions
3.1. Reaction network
After the reaction discovery and path refinement, the chemical kinetic model for methane pyrolysis is constructed. It consists of 53 species and 134 reactions. Fig. 2 shows a qualitative representation of the reaction network as a connectivity graph. In the graph, each node represents a unique species in the reaction network. Several common hydrocarbon species with less than four carbon atoms (C<4Hx) are highlighted with larger node sizes. The nodes are labeled with species chemical formula, and if necessary, some minimal information about molecular structure and spin multiplicity (e.g., in Fig. 2, c-C3H6 for cyclopropane, CH2(S) for singlet methylene, and C2H4(T) for triplet ethylene). Section S1 in ESI† lists all the 53 species with their labels in Fig. 2, modified SMILES string in the Cantera model, and their minimum-energy structures. In Fig. 2, each edge connecting two nodes indicates a reaction that involves these two species, one in reactant set and the other in product set. Reactions involving common (C<4Hx) species are also highlighted with heavier weights (displayed as thicker line widths). Note that one reaction may lead to multiple edges. For instance, dissociation of methane (CH4) into methyl radical (CH3) and hydrogen radical (H) results in an edge between nodes CH4 and CH3, and another edge between CH4 and H. Furthermore, there can be more than one reaction that involves two species connected by an edge. Taking the undirected edge between CH4 and CH3 as an example again, it represents any reaction that involves CH4 and CH3 as reactant and product or vice versa. Examples of these reactions are CH4 (+M) ⇔ CH3 + H (+M), CH4 + H ⇔ CH3 + H2, C2H6 + CH3 ⇔ C2H5 + CH4, and C2H4 + CH3 ⇔ C2H3 + CH4.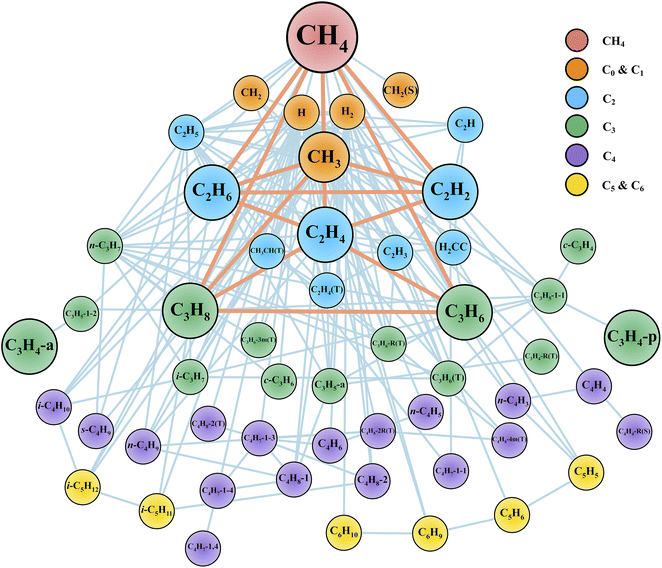 | ||
| Fig. 2 Reaction network displayed as a graph. Each node represents a unique species. Each edge connecting two nodes indicates a reaction that involves these two species, one in the reactant set and the other in the product set. Node labels are the species molecular formula and if necessary, some minimal information about molecular structures and spin multiplicity values (See Section S1 in ESI† for details). Common C<4 species (i.e., CH4, CH3, C2H6, C2H4, C2H2, C3H8, C3H6, C3H4-p, C3H4-a) are highlighted with larger node sizes. Reactions connecting key species are highlighted with thicker edge widths. We note that H2 molecule and H atom are important species as well, but they are not highlighted for better visualization since they are involved in most of the reactions in this network. | ||
The graph in Fig. 2 provides qualitative evidence of the ab initio nanoreactor's ability to identify not only important species and reactions, but also secondary reactions in an automated, hypothesis-free manner. Some common hydrocarbons are highlighted with larger node sizes, and they are methane (CH4), methyl (CH3), ethane (C2H6), ethylene (C2H4), acetylene (C2H2), propane (C3H8), propene (C3H6), propyne (C3H4-p) and allene (C3H4-a). Aromatic species, including single ring (e.g., benzene), and polycyclic aromatic hydrocarbons (PAHs) are not found in the present work because longer discovery trajectories are needed for these products to be found. The influence of the aromatic species on the kinetic evolution of the methane pyrolysis system is discussed later in the text. Furthermore, the nanoreactor not only captures almost all the important reactions impacting the global methane decomposition rates, as we will show later, but it also uncovers chemical reactions which are not considered by any literature kinetic models used in this work. We include two examples in ESI Section S8.† Path refinement and transition state optimization suggest their transition state structures both exist (with one imaginary frequency each). Due to the high reaction barriers, neither reaction shows up in the sensitivity analysis as shown later, but this nevertheless highlights the nanoreactor's potential for uncovering rare events.
3.2. Kinetic model validations for methane dissociation
The nanoreactor (NR) kinetic model is validated against experimental data collected from two recent methane pyrolysis experiments. The results are summarized in Fig. 3. Briefly, the top panels (Fig. 3a and b) show the comparison of simulated and experimental CH4 mole fractions in two shock tube facilities.95 One series of simulations is performed at initial temperatures T0 ranging from 1300 to 2400 K and initial pressure P0 of 1.4 bar, and the other is carried out at T0 ranging from 1100 to 2000 K and P0 = 30 bar.95 The bottom panels (Fig. 3c and d) show the comparison of simulated and experimental CH4 and H2 mole fractions in a flow reactor experiment. Simulations are performed at atmospheric pressure and 1050–1500 K temperature range.94 All kinetic modeling simulations are carried out as initial value problems in the 0D homogeneous reactor module in Cantera.122 Simulated species mole fractions are taken at the end of the simulation, which corresponds to the total reaction time trec. Details of the simulation procedure and some discussions of initial conditions are included in Section S7.† Overall, the simulated CH4 and H2 mole fractions by the nanoreactor model are in reasonable agreement with the experimental data, though discrepancies are observed. For instance, the nanoreactor model suggests faster methane decay kinetics compared to experiment in the lower pressure 1.4 atm case (Fig. 3a), and slower dissociation kinetics in the higher pressure (30 bar) case (Fig. 3b). The nanoreactor model also underpredicts H2 mole fractions as temperature rises. Here in this work, we do not wish to overemphasize the practice of kinetic model optimization towards experimental data as targets. Instead, we introduce (vide infra) two systematic sensitivity analysis approaches that can efficiently identify sets of rate parameters contributing to these discrepancies.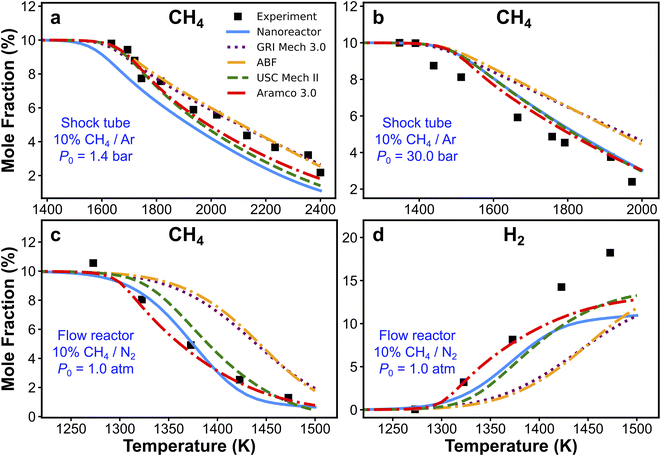 | ||
| Fig. 3 Experimental and simulated CH4 (a–c) and H2 (d) mole fractions. The experimental/simulation conditions are (a) 10% CH4/Ar, P0 = 1.4 bar, and trec = 2.87 ms; (b) 10% CH4/Ar, P0 = 30 bar, and trec = 14.8 ms; (c) and (d) 10% CH4/N2, P0 = 1.0 atm, and trec is reported in the experimental paper94 as a function of the initial temperature, as trec = 4.55 × 106/T0 (K) ms. | ||
Simulations from the nanoreactor (NR) kinetic model are compared with results from four pre-existing literature models: GRI Mech 3.0,80 Appel, Bockhorn, Frenklach (ABF)134 model, USC Mech II,135 and AramcoMech 3.0.136 As seen in Fig. 3, the difference of predictions among four literature kinetic models is noticeable. This might be somewhat surprising, since some of these models share similar or even identical rate parameters (see Section S6† for detailed comparison of selected reaction rates across these models). The predictions from the NR kinetic model, obtained automatically and without empirical input, largely fall within the range of predictions from the four literature models. Fig. 3d suggests that none of the models tested herein (including the nanoreactor) can capture the H2 production at the higher end of the test temperature range (i.e., ∼1480 K). Two possible reasons for this discrepancy were suggested in the original experimental work.94 First, the underprediction of H2 could be due to the inaccuracy of key H-abstraction reactions leading to H2 formation (e.g. CH4 + H ⇔ CH3 + H2, C2H6 + H ⇔ C2H5 + H2, C2H4 + H ⇔ C2H3 + H2).94 Secondly, there might be missing pathways related to formation and growth of large polycyclic aromatic hydrocarbons (PAHs).142 These PAH pathways are not discovered in the current nanoreactor reaction network because longer discovery trajectories are needed for such pathways to occur, and they are also missing in all the literature models except for the ABF model which includes only formation of PAHs up to four aromatic rings (i.e. pyrene). Monte Carlo sensitivity analyses (i.e., Sections 3.5 and S10†) can shed light on this issue.
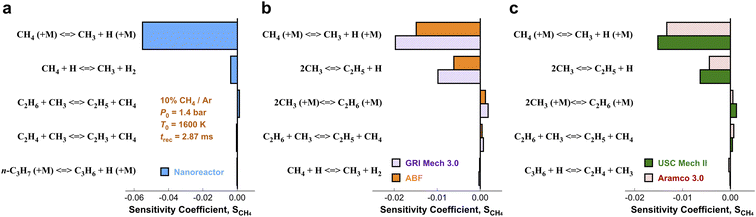
3.3. Local brute-force sensitivity analysis
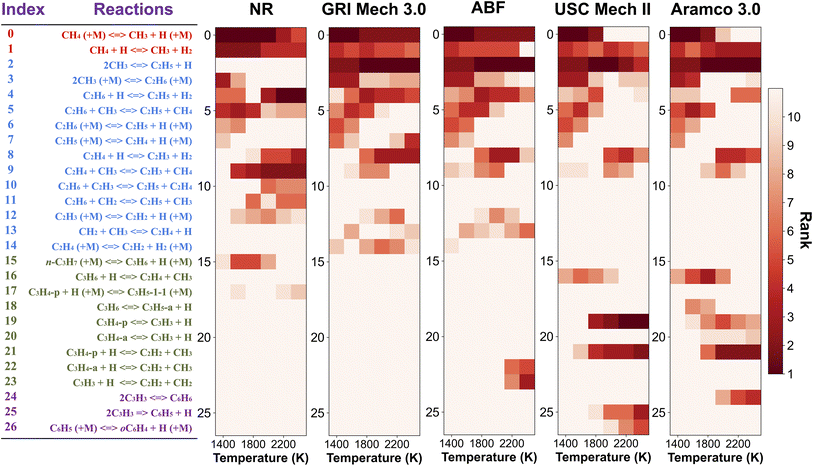
In order to pinpoint the origin of the differences observed in Fig. 3, we need to determine (1) how different rate parameters contribute to a particular kinetic modeling outcome, and (2) the weights and rankings of rate parameter contributions in a kinetic model. One example is to understand the difference of rate parameter contributions to CH4 predictions in Fig. 3a. A systematic approach to address these questions is the brute force local sensitivity analysis method.137,138 The calculation procedure for sensitivity coefficients was described above. All the brute-force local sensitivity analyses are performed with rate parameters up/down-scaled by a factor of 2 under the initial condition of experiments in Fig. 3a. We present results in Fig. 4 depicting the normalized CH4 sensitivity coefficients (eqn (8)) for the top five most important rate coefficients at 1600 K initial temperature, where the nanoreactor (NR) model predicts lower methane concentration (i.e., faster methane decay) compared to the other four kinetic models. Results from a broader assessment will be shown later in Fig. 5. Among all the five kinetic models analyzed, Fig. 4 shows that only one or two distinct reactions dominate the ranked sensitivity charts. At the condition tested, the rate of methane dissociation reaction CH4 (+M) ⇔ CH3 + H (+M) appears to be the most influential factor for methane decay among all five kinetic models. Its significance is much more pronounced in the NR model, as its sensitivity coefficient value in the NR bar chart (−0.055) is about three times its values in others (−0.020 in GRI, −0.015 in ABF, −0.015 in USC Mech II, and −0.013 in AramcoMech 3.0). In addition, the rate of 2CH3 ⇔ C2H5 + H is the second critical rate parameter in the four literature models. The results in Fig. 4 highlight an example of how local brute-force sensitivity works. At the condition tested, the difference in sensitivity spectra indicates that methane dissociation is mostly impacted by the rates of CH4 (+M) ⇔ CH3 + H (+M) and 2CH3 ⇔ C2H5 + H in the four literature models, while being solely affected by the former reaction in the nanoreactor model. The rate coefficient of CH4 (+M) ⇔ CH3 + H (+M) in the NR model is much higher than any other kinetic model (Section S6 and Fig. S4†), and this could possibly explain the faster methane decomposition kinetics predicted by the NR model. This result suggests further refining the reaction path of CH4 (+M) ⇔ CH3 + H (+M) at a higher level of theory (e.g., CCSD(T)) could be necessary. Moreover, the use of Hinshelwood theory121 for the low-pressure limit rate and transition state theory98–100 for the high-pressure limit rate constant could result in inaccurate estimation of rate constants. Work is underway to exploit improved theories for pressure dependent reactions, such as RRKM.143–145 Lastly, note that the rate of 2CH3 ⇔ C2H5 + H does not show up in the NR sensitivity analysis, and we focus on this below.The local sensitivity analysis is extended to more initial temperatures (1400, 1800, 2000, 2200, 2400 K) and the corresponding ranked bar charts are included in Section S10 in ESI.† Here we summarize the rankings of reaction rate in Fig. 5, as a two-dimensional (2D) sensitivity map of CH4 mole fractions calculated by the nanoreactor, GRI Mech 3.0, ABF, USC Mech II, and AramcoMech 3.0 reaction models. Each column in the 2D map represents an initial simulation temperature ranging from 1400 K to 2400 K, increasing in 200 K increments. Each row shows the sensitivity coefficient ranking of the corresponding reaction listed on the left side. The color map represents the rank of each reaction in the sensitivity map at a given initial temperature. Note that the darkest color in the 2D map indicates the highest ranked reaction, while the lightest color means that the reaction either ranks below the tenth rank or does not exist in the reaction model. We present the rankings of the sensitivity coefficients instead of their values for two reasons. First, the values of sensitivity coefficient may vary among different kinetic models. Second, the ranking map provides qualitative yet straightforward evidence of the relative importance of rate parameters in a kinetic model.
The 2D sensitivity ranking map reveals a few interesting facts. The overall sensitivity landscapes vary among five kinetic models, and the variation itself increases with higher initial temperature. At initial temperatures below 1800 K, four literature models display a similar ranking map albeit with a few minor differences. The reaction (R0) CH4 (+M) ⇔ CH3 + H (+M) is the most impactful for CH4 concentration prediction. The dominance of (R0) appears in all five kinetic models at 1400 and 1600 K, and starts to shift to the dominance of (R2) 2CH3 ⇔ C2H5 + H at 1800 K in all four literature models. The NR kinetic model highlights the importance of (R1) CH4 + H ⇔ CH3 + H2, as it ranks no. 2 in the NR sensitivity ranking while being a bit less critical in the other four models.
For initial temperatures exceeding 1800 K, the sensitivity ranking maps of CH4 start to diversify within the five models (Fig. 5). The divergence of the ranking maps beyond T0 = 1800 K also explains the enlarged variation of model predictions in Fig. 3a. Specifically, the top rank of reaction (R0) CH4 (+M) ⇔ CH3 + H (+M) is gradually taken over by (R2) 2CH3 ⇔ C2H5 + H in GRI, ABF, and Aramco, while (R4) C2H6 + H ⇔ C2H5 + H2 in the NR kinetic model and (R19) C3H4-p ⇔ C3H3 + H in USC Mech II. We again notice that reaction (R2) 2CH3 ⇔ C2H5 + H is not present in the NR sensitivity map over the entire range of temperatures tested. Discussion on this reaction is included in the ESI (Section S9).† This reaction (R2) has historically been considered as a chemically activated reaction.146–148 Under high-temperature reaction conditions, the recombination of two methyl (CH3) radicals forms a vibrationally activated adduct 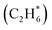 which is so energetic that it can skip over the potential energy well of ethane (C2H6) and directly form the product of ethyl (C2H5) and hydrogen (H) radicals. This well-skipping phenomenon can also happen in the reverse reaction direction. Reaction (R2) is discovered during the AIMD simulations and is identified as a triplet-spin-multiplicity reaction. Therefore, the resulting path refinement and transition state optimizations found a structure with triplet spin multiplicity close to a first-order saddle point (Section S9†). The rate coefficient of (R2) in the NR model appears to be much lower than the rates in all four literature models (Fig. S8†), where the theoretical RRKM rate parameters from Stewart et al.149 are adopted. A small sensitivity test is also conducted by replacing the rate of (R2) in the nanoreactor by the rate from Stewart et al.,149 and the result is illustrated in Section S9 and Fig. S9.† The sensitivity of this rate coefficient replacement is small for CH4, H2, and C2H2 yet noticeable for C2H4. We infer this small sensitivity may not truly reflect the inaccuracy of the NR (R2) rate coefficient, because the rate of methane dissociation, (R0) CH4 (+M) ⇔ CH3 + H (+M) in the nanoreactor kinetic model is much higher than other literature models. The H radical generation rate, which partially reflects the global reactivity of the methane pyrolysis system, is overly affected by the faster rate of CH4 (+M) ⇔ CH3 + H (+M). Therefore, the impact of 2CH3 ⇔ C2H5 + H could be further underestimated. Nevertheless, future work should involve accurate calculations of well-skipping/chemically activated reaction rates.
which is so energetic that it can skip over the potential energy well of ethane (C2H6) and directly form the product of ethyl (C2H5) and hydrogen (H) radicals. This well-skipping phenomenon can also happen in the reverse reaction direction. Reaction (R2) is discovered during the AIMD simulations and is identified as a triplet-spin-multiplicity reaction. Therefore, the resulting path refinement and transition state optimizations found a structure with triplet spin multiplicity close to a first-order saddle point (Section S9†). The rate coefficient of (R2) in the NR model appears to be much lower than the rates in all four literature models (Fig. S8†), where the theoretical RRKM rate parameters from Stewart et al.149 are adopted. A small sensitivity test is also conducted by replacing the rate of (R2) in the nanoreactor by the rate from Stewart et al.,149 and the result is illustrated in Section S9 and Fig. S9.† The sensitivity of this rate coefficient replacement is small for CH4, H2, and C2H2 yet noticeable for C2H4. We infer this small sensitivity may not truly reflect the inaccuracy of the NR (R2) rate coefficient, because the rate of methane dissociation, (R0) CH4 (+M) ⇔ CH3 + H (+M) in the nanoreactor kinetic model is much higher than other literature models. The H radical generation rate, which partially reflects the global reactivity of the methane pyrolysis system, is overly affected by the faster rate of CH4 (+M) ⇔ CH3 + H (+M). Therefore, the impact of 2CH3 ⇔ C2H5 + H could be further underestimated. Nevertheless, future work should involve accurate calculations of well-skipping/chemically activated reaction rates.
Despite the observations above, the NR model also qualitatively captures the importance of some additional C2 reactions, although their quantitative rankings and Sij values may vary. For instance, (R3) 2CH3 (+M) ⇔ C2H6, (R4) C2H6 + H ⇔ C2H5 + H2, (R5) C2H6 + CH3 ⇔ C2H5 + CH4, (R6) C2H6 (+M) ⇔ C2H5 + H (+M), (R8) C2H4 + H ⇔ C2H3 + H2, and (R9) C2H4 + CH3 ⇔ C2H3 + CH4. Compared to the literature kinetic models, the NR also tends to noticeably overemphasize the rates of (R4) C2H6 + H ⇔ C2H5 + H2 and (R9) C2H4 + CH3 ⇔ C2H3 + CH4. Such overemphasis is also observed in (R5), (R10), (R11), (R15), and (R17) but less pronounced. Another minor observation from USC Mech II and AramcoMech 3.0 is the significance of reaction rates (R19–26) leading to formation of aromatic species benzene (C6H6) and phenyl (C6H5), which also involves propyne (C3H4-p), allene (C3H4-a), propargyl (C3H3). This further explains their predictions of lower methane concentrations than GRI and ABF at higher temperatures in Fig. 3a–c, since a considerable amount of carbon is converted into benzene. Efforts to extend the reaction network to include benzene, propargyl, and propyne would be a good topic for future work.
Two major conclusions can be drawn from the results in Fig. 4 and 5. First, the rate of CH4 (+M) ⇔ CH3 + H (+M) is critical to accounting for CH4 mole fraction prediction. The current approach in the nanoreactor tends to overestimate its rate. Second, the chemically activated reaction 2CH3 ⇔ C2H5 + H has been discovered in the nanoreactor workflow, but the rate was extremely underestimated in the NR kinetic model. Future work should focus on improved theory (e.g., RRKM and/or master equations127–130) for estimating the rates of pressure-dependent unimolecular reactions and chemically activated reactions.146–148
3.4. Kinetic model validation for minor intermediates
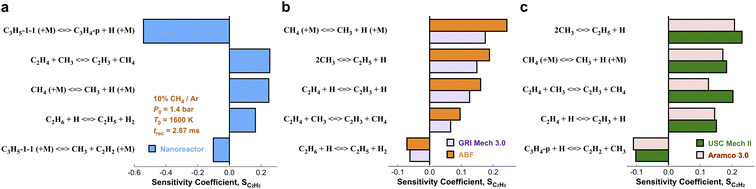
We have presented the prediction accuracy of our nanoreactor methane pyrolysis model for methane and hydrogen. The model has been subsequently tested for secondary species as well. Fig. 6 shows the comparison of experimentally measured and simulated ethylene (C2H4, Fig. 6a) and acetylene (C2H2, Fig. 6b) mole fractions. The experimental data are collected from the same shock tube facility in Fig. 3a at initial temperatures between 1600 to 2400 K and pressures of 1.4 bar.95 Simulations are conducted again, using the nanoreactor model along with four literature kinetic models. The nanoreactor model overpredicts the ethylene concentration by a factor of 2.5 at its maximum experimental value, similar to USC Mech II and AramcoMech 3.0. GRI and ABF models yield somewhat better agreement with the experimental C2H4 mole fractions. Fig. 6b suggests that the current nanoreactor model poorly predicts the C2H2 mole fractions over the temperature tested. The four literature models all agree reasonably well with the experimental C2H2 concentrations. Fig. 7 shows the ranked C2H2 sensitivity coefficient bar chart calculated at 1800 K initial temperature and 1.4 bar pressure. Clearly, the NR kinetic model shows a dominance of reaction C3H5-1-1 (+M) ⇔ C3H4-p + H (+M) (see Section S1† for the structure of C3H5-1-1 and C3H4-p), as its S value (−0.54) is more than two times that of the no. 2 ranking reaction in the NR model (C2H4 + CH3 ⇔ C2H3 + CH4, S = 0.25). We attribute this dominance primarily to an insufficient discovery of C>3 reactions, particularly reactions related to propyne (C3H4-p) and probably its isomer allene (C3H4-a). As depicted in Fig. 2, propyne (C3H4-p) appears to be a terminal node in the graph, and it has only one parent node C3H5-1-1, one of whose parent nodes is C2H2. The kinetic outcome of such subtree structure would make C3H4-p a kinetic sink for C2H2 destruction. Without additional reaction pathways discovered, concentration of C3H4-p will accumulate during the kinetic modeling of the NR model due to its relative stability compared to radicals in the reaction system. The sinking flux from C2H2 to C3H4-p is realized by two sequential reactions, CH3 + C2H2 (+M) ⇔ C3H5-1-1 (+M) (written in the reverse direction opposed to Fig. 7a) and C3H5-1-1 (+M) ⇔ C3H4-p + H (+M). Therefore, additional reaction discovery for C3H4-p (and its isomer C3H4-a) is necessary for more reasonable prediction of C2H2, and a more complete reaction network.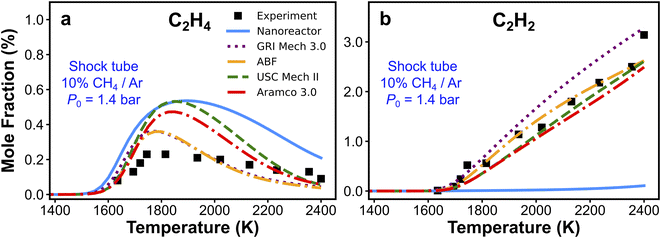 | ||
| Fig. 6 Experimental and simulated (a) C2H4 and (b) C2H2 mole fractions. The experimental/simulation condition is 10% CH4/Ar, P0 = 1.4 bar, and trec = 2.87 ms. | ||
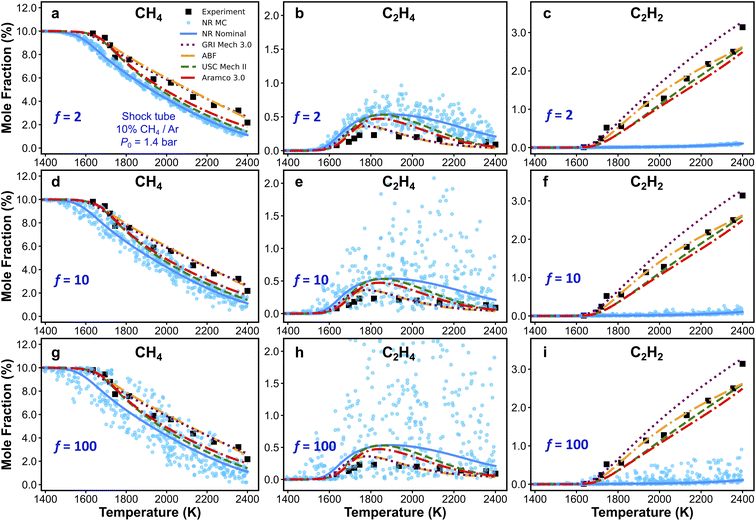
3.5. The Monte Carlo method
As discussed in the previous text, local brute-force sensitivity analysis is useful for quick sorting of rate parameters according to their influence on a particular kinetic output property. However, in a reaction kinetic model, rate coefficients can be strongly coupled within this high-dimensional parameter space. In this case, local brute-force sensitivity analysis may not be able to capture the kinetic couplings among reaction rates, as it only allows perturbation of one rate parameter at a time. Furthermore, it cannot map such degrees of coupling to the kinetic modeling outcomes (e.g., species concentration predictions). In this subsection, we further address the effect of reaction rate couplings on model predictions. Monte Carlo (MC) sensitivity analysis is used for this purpose and its description is included in the methods section. Fig. 8 shows scatter plots of CH4 (Fig. 8a, d and g), C2H4 (Fig. 8b, e and h), and C2H2 (Fig. 8c, f and i) concentrations simulated by the nanoreactor model with MC sensitivity approach. Each filled circle represents a MC kinetic simulation in which all the rate parameters in NR model are randomly perturbed within their natural log space (i.e., ln(kj)) uniformly. All the rate parameters are perturbed under an upper-limit factor of 2 (Fig. 8a–c), 10 (Fig. 8d–f), and 100 (Fig. 8g–i), respectively from the nominal values. The sensitivity analyses are performed under the condition of Fig. 3a (10% CH4/Ar, P0 = 1.4 bar, and trec = 2.87 ms).95 The choice of rate perturbation factors are roughly chosen according to the scale of inaccuracies in the reaction barrier and rate coefficient estimations. Taking the reaction barrier as an example, based on the Arrhenius law, a 1 kcal mol−1 inaccuracy in the barrier corresponds to a factor of ∼1.5 perturbation of the reaction rate at the temperature range of 1000–1100 K, which is the initiation of the flame preheat zone during combustion. Moreover, a 5 kcal mol−1 inaccuracy in reaction barrier leads to about a factor of 10 rate uncertainty, and a 10 kcal mol−1 corresponds to a factor of 100 rate uncertainty, both at 1000–1100 K. In summary, the goal of this MC sensitivity test is to explore the parameter space in a kinetic model and assess the outcome of uncertainty and inaccuracy of rate coefficients.As should be expected, the spread of predictions increases as the range of perturbations is increased in Fig. 8. For the CH4 and C2H4 mole fractions, one can see that small changes in key reaction rates could easily lead to better agreement with experiment. However, regardless of how much the rate parameters are perturbed, the simulated C2H2 mole fractions will not reproduce the experimental results. This suggests that the NR rate parameters are not the origin for the observed inaccurate prediction of C2H2. This bolsters our suggestion in Section 3.4, namely that the current reaction network requires additional expansion towards more reactions related to C2H2, and furthermore, propyne (C3H4-p), allene (C3H4-a), propargyl (C3H3), and probably higher carbon species. Additional MC results obtained at two other experimental conditions are included in Section S10 of the ESI.† Similar to the findings with respect to C2H2 in Fig. 8, the MC results for H2 in Fig. S15† suggest that no modification of the NR rate parameters will lead to agreement of H2 production within the NR kinetic model (see Fig. 3d). This suggests again that there are missing species and/or reactions (e.g., pathways for PAHs formation and growth as discussed above). Further discovery runs in the NR could expand the reaction network and would likely improve the agreement with experiment for C2H2 and H2 production. However, the number of species and reactions will grow very quickly. Therefore, it would be important to couple further growth with some form of coarse-graining for the kinetic model.150–152 Lastly, we emphasize that the MC sensitivity analyses are generally beneficial for exploring rate parameter space in a large chemical reaction network. In the realm of the ab initio nanoreactor reaction discovery, we envision that both brute-force and MC sensitivity analyses can be essential components in the nanoreactor workflow, and instructive for next round of reaction discovery and path refinement.
4. Conclusions
In the present work, a methane pyrolysis kinetic model is automatically constructed from first principles by the ab initio nanoreactor. The reactions during methane pyrolysis are discovered using GPU-accelerated ab initio molecular dynamics simulation, without human hypothesis or intervention. The reactions are subsequently refined towards their minimum energy paths using the growing string method. Reactants, products, and transition state geometries are optimized, and their thermochemical properties are computed. Reaction rate parameters are estimated using transition state theory. The kinetic model is validated against experimentally measured key species concentrations during methane pyrolysis over a wide range of thermodynamic conditions. The simulated results from the nanoreactor model are compared with the results from four literature combustion kinetic models. Overall, the nanoreactor model predicts major species (i.e., methane and hydrogen) with reasonable accuracy. We pointed out and discussed discrepancies between the predictions of the nanoreactor model and experiments, as well as among predictions of the nanoreactor model with four literature kinetic models.We introduce the method of local sensitivity analysis which efficiently identifies the importance of rate coefficients in a kinetic model with respect to a prediction outcome. The local sensitivity analysis suggests that future work should focus on improving the theoretical approach for pressure-dependent reactions and chemically activated reaction rate constant calculations. Another sensitivity analysis, the Monte Carlo method is used to explore the rate parameter space of the kinetic models. In addition to the local sensitivity analysis, the Monte Carlo sensitivity analysis suggests the current reaction network may be incomplete for prediction of C2 intermediate species such as acetylene. This leads to the future necessity of extending the subnetwork of acetylene into C3 and C4 species using ab initio molecular dynamics simulations. In the future, we envision the nanoreactor-based reaction discovery can be performed iteratively, leveraging kinetic modeling and sensitivity analysis as tools for efficient identification of critical reactions and rate parameters, and guidance for the next iteration of reaction discovery.
Data availability
The data supporing this article have been included as part of the ESI,† including, in particular the kinetic model in Cantera format.Author contributions
RX contributed to the conceptualization, data curation, formal analysis, investigation, methodology, software, visualization and writing (original draft) of the presented work. JM contributed to the data curation and formal analysis. AMC contributed to the formal analysis and software. KCT contributed to the methodology and project administration. TJM contributed to the conceptualization, funding acquisition, methodology, project administration, resources, and supervision. All the authors contributed to the review and editing phases of the draft.Conflicts of interest
TJM is co-founder of PetaChem, LLC.Acknowledgements
This work was supported by the Office of Naval Research (N00014-21-1-2151 and N00014-18-1-2659). RX and JM thank Dr Xiaolei Zhu for helpful discussions. JM thanks the Dr Leni-Schöninger Foundation and the Deutsche Forschungsgemeinschaft (project number 419817859) for financial support. AMC acknowledges support from National Science Foundation Graduate Research Fellowship and the Stanford Graduate Fellowship.References
- G. N. Simm, A. C. Vaucher and M. Reiher, Exploration of reaction pathways and chemical transformation networks, J. Phys. Chem. A, 2018, 123, 385–399 CrossRef.
- A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, Methods for exploring reaction space in molecular systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1354 Search PubMed.
- C. W. Coley, N. S. Eyke and K. F. Jensen, Autonomous discovery in the chemical sciences part I: Progress, Angew. Chem., Int. Ed., 2020, 59, 22858–22893 CrossRef CAS PubMed.
- C. W. Coley, N. S. Eyke and K. F. Jensen, Autonomous discovery in the chemical sciences part II: Outlook, Angew. Chem., Int. Ed., 2020, 59, 23414–23436 CrossRef CAS PubMed.
- L. J. Broadbelt, S. M. Stark and M. T. Klein, Computer generated pyrolysis modeling: on-the-fly generation of species, reactions, and rates, Ind. Eng. Chem. Res., 1994, 33, 790–799 CrossRef CAS.
- L. J. Broadbelt, S. Stark and M. Klein, Computer generated reaction modelling: decomposition and encoding algorithms for determining species uniqueness, Comput. Chem. Eng., 1996, 20, 113–129 CrossRef CAS.
- L. J. Broadbelt and J. Pfaendtner, Lexicography of kinetic modeling of complex reaction networks, AIChE J., 2005, 51, 2112–2121 CrossRef CAS.
- V. Warth, F. Battin-Leclerc, R. Fournet, P.-A. Glaude, G.-M. Côme and G. Scacchi, Computer based generation of reaction mechanisms for gas-phase oxidation, Comput. Chem., 2000, 24, 541–560 CrossRef CAS PubMed.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Reaction Mechanism Generator: Automatic construction of chemical kinetic mechanisms, Comput. Phys. Commun., 2016, 203, 212–225 CrossRef CAS.
- M. Liu, A. G. Dana, M. S. Johnson, M. J. Goldman, A. Jocher, A. M. Payne, C. A. Grambow, K. Han, N. W. Yee and E. J. Mazeau, Reaction mechanism generator v3.0: advances in automatic mechanism generation, J. Chem. Inf. Model., 2021, 61, 2686–2696 CrossRef CAS.
- S. Rangarajan, A. Bhan and P. Daoutidis, Rule-based generation of thermochemical routes to biomass conversion, Ind. Eng. Chem. Res., 2010, 49, 10459–10470 CrossRef CAS.
- S. Rangarajan, A. Bhan and P. Daoutidis, Language-oriented rule-based reaction network generation and analysis: description of RING, Comput. Chem. Eng., 2012, 45, 114–123 CrossRef CAS.
- P. M. Zimmerman, Automated discovery of chemically reasonable elementary reaction steps, J. Comput. Chem., 2013, 34, 1385–1392 CrossRef CAS.
- P. M. Zimmerman, Navigating molecular space for reaction mechanisms: an efficient, automated procedure, Mol. Simul., 2015, 41, 43–54 CrossRef CAS.
- A. L. Dewyer and P. M. Zimmerman, Finding reaction mechanisms, intuitive or otherwise, Org. Biomol. Chem., 2017, 15, 501–504 RSC.
- S. Habershon, Sampling reactive pathways with random walks in chemical space: applications to molecular dissociation and catalysis, J. Chem. Phys., 2015, 143, 094106 CrossRef PubMed.
- S. Habershon, Automated prediction of catalytic mechanism and rate law using graph-based reaction path sampling, J. Chem. Theory Comput., 2016, 12, 1786–1798 CrossRef CAS.
- D. Rappoport, C. J. Galvin, D. Y. Zubarev and A. Aspuru-Guzik, Complex chemical reaction networks from heuristics-aided quantum chemistry, J. Chem. Theory Comput., 2014, 10, 897–907 CrossRef CAS PubMed.
- D. Y. Zubarev, D. Rappoport and A. Aspuru-Guzik, Uncertainty of prebiotic scenarios: the case of the non-enzymatic reverse tricarboxylic acid cycle, Sci. Rep., 2015, 5, 1–7 Search PubMed.
- D. Rappoport and A. Aspuru-Guzik, Predicting feasible organic reaction pathways using heuristically aided quantum chemistry, J. Chem. Theory Comput., 2019, 15, 4099–4112 CrossRef CAS.
- M. Bergeler, G. N. Simm, J. Proppe and M. Reiher, Heuristics-guided exploration of reaction mechanisms, J. Chem. Theory Comput., 2015, 11, 5712–5722 CrossRef CAS.
- G. N. Simm and M. Reiher, Context-driven exploration of complex chemical reaction networks, J. Chem. Theory Comput., 2017, 13, 6108–6119 CrossRef CAS PubMed.
- J. P. Unsleber, S. A. Grimmel and M. Reiher, Chemoton 2.0: autonomous exploration of chemical reaction networks, J. Chem. Theory Comput., 2022, 18, 5393–5409 CrossRef CAS PubMed.
- J. N. Wei, D. Duvenaud and A. Aspuru-Guzik, Neural networks for the prediction of organic chemistry reactions, ACS Cent. Sci., 2016, 2, 725–732 CrossRef CAS.
- M. A. Kayala, C.-A. Azencott, J. H. Chen and P. Baldi, Learning to predict chemical reactions, J. Chem. Inf. Model., 2011, 51, 2209–2222 CrossRef CAS.
- M. A. Kayala and P. Baldi, ReactionPredictor: prediction of complex chemical reactions at the mechanistic level using machine learning, J. Chem. Inf. Model., 2012, 52, 2526–2540 CrossRef CAS.
- J. Kang, S. H. Noh, J. Hwang, H. Chun, H. Kim and B. Han, First-principles database driven computational neural network approach to the discovery of active ternary nanocatalysts for oxygen reduction reaction, Phys. Chem. Chem. Phys., 2018, 20, 24539–24544 RSC.
- C. A. Grambow, L. Pattanaik and W. H. Green, Deep learning of activation energies, J. Phys. Chem. Lett., 2020, 11, 2992–2997 CrossRef CAS PubMed.
- W. Ji and S. Deng, Autonomous discovery of unknown reaction pathways from data by chemical reaction neural network, J. Phys. Chem. A, 2021, 125, 1082–1092 CrossRef CAS PubMed.
- L.-P. Wang, A. Titov, R. McGibbon, F. Liu, V. S. Pande and T. J. Martínez, Discovering chemistry with an ab initio nanoreactor, Nat. Chem., 2014, 6, 1044–1048 CrossRef CAS.
- L.-P. Wang, R. T. McGibbon, V. S. Pande and T. J. Martínez, Automated discovery and refinement of reactive molecular dynamics pathways, J. Chem. Theory Comput., 2016, 12, 638–649 CrossRef CAS.
- K. Chenoweth, A. C. Van Duin and W. A. Goddard, ReaxFF reactive force field for molecular dynamics simulations of hydrocarbon oxidation, J. Phys. Chem. A, 2008, 112, 1040–1053 CrossRef CAS PubMed.
- T. Cheng, A. Jaramillo-Botero, W. A. Goddard III and H. Sun, Adaptive accelerated ReaxFF reactive dynamics with validation from simulating hydrogen combustion, J. Am. Chem. Soc., 2014, 136, 9434–9442 CrossRef CAS PubMed.
- M. Döntgen, M.-D. Przybylski-Freund, L. C. Kröger, W. A. Kopp, A. E. Ismail and K. Leonhard, Automated discovery of reaction pathways, rate constants, and transition states using reactive molecular dynamics simulations, J. Chem. Theory Comput., 2015, 11, 2517–2524 CrossRef PubMed.
- M. Döntgen, F. Schmalz, W. A. Kopp, L. C. Kröger and K. Leonhard, Automated chemical kinetic modeling via hybrid reactive molecular dynamics and quantum chemistry simulations, J. Chem. Inf. Model., 2018, 58, 1343–1355 CrossRef.
- K. L. Fleming, P. Tiwary and J. Pfaendtner, New approach for investigating reaction dynamics and rates with ab initio calculations, J. Phys. Chem. A, 2016, 120, 299–305 CrossRef CAS PubMed.
- Q. Yang, C. A. Sing-Long and E. J. Reed, Learning reduced kinetic Monte Carlo models of complex chemistry from molecular dynamics, Chem. Sci., 2017, 8, 5781–5796 RSC.
- E. Chen, Q. Yang, V. Dufour-Décieux, C. A. Sing-Long, R. Freitas and E. J. Reed, Transferable kinetic Monte Carlo models with thousands of reactions learned from molecular dynamics simulations, J. Phys. Chem. A, 2019, 123, 1874–1881 CrossRef CAS PubMed.
- V. Dufour-Décieux, R. Freitas and E. J. Reed, Atomic-Level Features for Kinetic Monte Carlo Models of Complex Chemistry from Molecular Dynamics Simulations, J. Phys. Chem. A, 2021, 125, 4233–4244 CrossRef PubMed.
- E. Martínez-Núñez, G. L. Barnes, D. R. Glowacki, S. Kopec, D. Peláez, A. Rodríguez, R. Rodríguez-Fernández, R. J. Shannon, J. J. Stewart and P. G. Tahoces, AutoMeKin2021: an open-source program for automated reaction discovery, J. Comput. Chem., 2021, 42, 2036–2048 CrossRef PubMed.
- R. Iftimie, P. Minary and M. E. Tuckerman, Ab initio molecular dynamics: concepts, recent developments, and future trends, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6654–6659 CrossRef CAS PubMed.
- H. B. Schlegel, Ab initio direct dynamics, Acc. Chem. Res., 2021, 54, 3749–3759 CrossRef CAS PubMed.
- T. J. Martínez, Ab initio reactive computer aided molecular design, Acc. Chem. Res., 2017, 50, 652–656 CrossRef PubMed.
- D. V. Ilyin, W. A. Goddard, J. J. Oppenheim and T. Cheng, First-principles–based reaction kinetics from reactive molecular dynamics simulations: application to hydrogen peroxide decomposition, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 18202–18208 CrossRef CAS.
- A. Laio and M. Parrinello, Escaping free-energy minima, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- G. Bussi and A. Laio, Using metadynamics to explore complex free-energy landscapes, Nat. Rev. Phys., 2020, 2, 200–212 CrossRef.
- A. F. Voter, Hyperdynamics: accelerated molecular dynamics of infrequent events, Phys. Rev. Lett., 1997, 78, 3908 CrossRef CAS.
- E. Carter, G. Ciccotti, J. T. Hynes and R. Kapral, Constrained reaction coordinate dynamics for the simulation of rare events, Chem. Phys. Lett., 1989, 156, 472–477 CrossRef CAS.
- M. Iannuzzi, A. Laio and M. Parrinello, Efficient exploration of reactive potential energy surfaces using Car-Parrinello molecular dynamics, Phys. Rev. Lett., 2003, 90, 238302 CrossRef PubMed.
- M. Invernizzi and M. Parrinello, Rethinking metadynamics: from bias potentials to probability distributions, J. Phys. Chem. Lett., 2020, 11, 2731–2736 CrossRef CAS.
- M. Invernizzi, P. M. Piaggi and M. Parrinello, Unified approach to enhanced sampling, Phys. Rev. X, 2020, 10, 041034 CAS.
- M. Deighan, M. Bonomi and J. Pfaendtner, Efficient simulation of explicitly solvated proteins in the well-tempered ensemble, J. Chem. Theory Comput., 2012, 8, 2189–2192 CrossRef CAS.
- M. Deighan and J. Pfaendtner, Exhaustively sampling peptide adsorption with metadynamics, Langmuir, 2013, 29, 7999–8009 CrossRef CAS PubMed.
- J. Pfaendtner and M. Bonomi, Efficient sampling of high-dimensional free-energy landscapes with parallel bias metadynamics, J. Chem. Theory Comput., 2015, 11, 5062–5067 CrossRef CAS PubMed.
- M. Bernasconi, G. L. Chiarotti, P. Focher, M. Parrinello and E. Tosatti, Solid-state polymerization of acetylene under pressure: ab initio simulation, Phys. Rev. Lett., 1997, 78, 2008 CrossRef CAS.
- N. Goldman, E. J. Reed, I.-F. W. Kuo, L. E. Fried, C. J. Mundy and A. Curioni, Ab initio simulation of the equation of state and kinetics of shocked water, J. Chem. Phys., 2009, 130, 124517 CrossRef PubMed.
- N. Goldman, E. J. Reed, L. E. Fried, I.-F. W. Kuo and A. Maiti, Synthesis of glycine-containing complexes in impacts of comets on early Earth, Nat. Chem., 2010, 2, 949–954 CrossRef CAS PubMed.
- S. Seritan, C. Bannwarth, B. S. Fales, E. G. Hohenstein, C. M. Isborn, S. I. Kokkila-Schumacher, X. Li, F. Liu, N. Luehr, J. W. Snyder Jr, C. Song, A. Titov, I. S. Ufimtsev, L.-P. Wang and T. J. Martínez, TeraChem: a graphical processing unit-accelerated electronic structure package for large-scale ab initio molecular dynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1494 CAS.
- I. S. Ufimtsev and T. J. Martínez, Quantum chemistry on graphical processing units. 1. Strategies for two-electron integral evaluation, J. Chem. Theory Comput., 2008, 4, 222–231 CrossRef CAS PubMed.
- I. S. Ufimtsev and T. J. Martínez, Quantum chemistry on graphical processing units. 2. Direct self-consistent-field implementation, J. Chem. Theory Comput., 2009, 5, 1004–1015 CrossRef CAS PubMed.
- I. S. Ufimtsev and T. J. Martínez, Quantum chemistry on graphical processing units. 3. Analytical energy gradients, geometry optimization, and first principles molecular dynamics, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed.
- J. Ford, S. Seritan, X. Zhu, M. N. Sakano, M. M. Islam, A. Strachan and T. J. Martínez, Nitromethane Decomposition via Automated Reaction Discovery and an Ab Initio Corrected Kinetic Model, J. Phys. Chem. A, 2021, 125, 1447–1460 CrossRef CAS PubMed.
- U. Raucci, D. M. Sanchez, T. J. Martínez and M. Parrinello, Enhanced Sampling Aided Design of Molecular Photoswitches, J. Am. Chem. Soc., 2022, 144, 19265–19271 CrossRef CAS PubMed.
- E. Pieri, D. Lahana, A. M. Chang, C. R. Aldaz, K. C. Thompson and T. J. Martínez, The non-adiabatic nanoreactor: towards the automated discovery of photochemistry, Chem. Sci., 2021, 12, 7294–7307 RSC.
- T. Das, S. Ghule and K. Vanka, Insights into the origin of life: did it begin from HCN and H2O?, ACS Cent. Sci., 2019, 5, 1532–1540 CrossRef CAS PubMed.
- E. Pahima, Q. Zhang, K. Tiefenbacher and D. T. Major, Discovering monoterpene catalysis inside nanocapsules with multiscale modeling and experiments, J. Am. Chem. Soc., 2019, 141, 6234–6246 CrossRef CAS PubMed.
- Q. Chu, C. Wang and D. Chen, Toward full ab initio modeling of soot formation in a nanoreactor, Carbon, 2022, 199, 87–95 CrossRef CAS.
- T. Lei, W. Guo, Q. Liu, H. Jiao, D.-B. Cao, B. Teng, Y.-W. Li, X. Liu and X.-D. Wen, Mechanism of graphene formation via detonation synthesis: a DFTB nanoreactor approach, J. Chem. Theory Comput., 2019, 15, 3654–3665 CrossRef CAS PubMed.
- J. Meisner, X. Zhu and T. J. Martínez, Computational discovery of the origins of life, ACS Cent. Sci., 2019, 5, 1493–1495 CrossRef CAS PubMed.
- Natural Gas Specs Sheet, Technical Report, North American Energy Standards Board, Houston, Texas, accessed, March 2022 Search PubMed.
- D. J. Seery and C. T. Bowman, An experimental and analytical study of methane oxidation behind shock waves, Combust. Flame, 1970, 14, 37–47 CrossRef CAS.
- G. B. Skinner, A. Lifshitz, K. Scheller and A. Burcat, Kinetics of methane oxidation, J. Chem. Phys., 1972, 56, 3853–3861 CrossRef CAS.
- L. D. Smoot, W. C. Hecker and G. A. Williams, Prediction of propagating methane-air flames, Combust. Flame, 1976, 26, 323–342 CrossRef CAS.
- C. K. Westbrook and F. L. Dryer, Chemical kinetic modeling of hydrocarbon combustion, Prog. Energy Combust. Sci., 1984, 10, 1–57 CrossRef CAS.
- W. Tsang and R. Hampson, Chemical kinetic data base for combustion chemistry. Part I. Methane and related compounds, J. Phys. Chem. Ref. Data, 1986, 15, 1087–1279 CrossRef CAS.
- F. N. Egolfopoulos, P. Cho and C. K. Law, Laminar flame speeds of methane-air mixtures under reduced and elevated pressures, Combust. Flame, 1989, 76, 375–391 CrossRef CAS.
- M. Frenklach, H. Wang and M. J. Rabinowitz, Optimization and analysis of large chemical kinetic mechanisms using the solution mapping method—combustion of methane, Prog. Energy Combust. Sci., 1992, 18, 47–73 CrossRef.
- E. L. Petersen, M. Röhrig, D. F. Davidson, R. K. Hanson and C. T. Bowman, High-pressure methane oxidation behind reflected shock waves, Symp. (Int.) Combust., 1996, 26, 799–806 CrossRef.
- M. Frenklach, H. Wang, C.-L. Yu, M. Goldenberg, C. T. Bowman, R. K. Hanson, D. F. Davidson, E. J. Chang, G. P. Smith, D. M. Golden, W. C. Gardiner and V. Lissianski, http://combustion.berkeley.edu/gri-mech/new21/version12/text12.html, accessed, March 1, 2023.
- G. P. Smith, D. M. Golden, M. Frenklach, N. W. Moriatry, E. Boris, G. Mikhail, C. T. Bowman, R. K. Hanson, S. Song, W. C. Gardiner, V. V. Lissianski and Z. Qin, GRI-Mech 3.0, https://combustion.berkeley.edu/gri-mech/version30/text30.html, accessed, March 1, 2023 Search PubMed.
- S. Frolov, V. Aksenov, V. Ivanov, S. Medvedev, I. Shamshin, N. Yakovlev and I. Kostenko, Rocket engine with continuous detonation combustion of the natural gas–oxygen propellant system, Dokl. Phys. Chem., 2018, 478, 31–34 CrossRef CAS.
- Y. Boué, P. Vinet, S. Magniant, T. Motomura, R. Blasi and J.-P. Dutheil, LOX/methane reusable rocket propulsion at reach with large scale demonstrators tested, Acta Astronaut., 2018, 152, 542–556 CrossRef.
- C. L. Journell, R. M. Gejji, I. V. Walters, A. I. Lemcherfi, C. D. Slabaugh and J. B. Stout, High-speed diagnostics in a natural gas–air rotating detonation engine, J. Propul. Power, 2020, 36, 498–507 CrossRef.
- Y. Wang, A. Movaghar, Z. Wang, Z. Liu, W. Sun, F. N. Egolfopoulos and Z. Chen, Laminar flame speeds of methane/air mixtures at engine conditions: performance of different kinetic models and power-law correlations, Combust. Flame, 2020, 218, 101–108 CrossRef CAS.
- J. Shao, A. M. Ferris, R. Choudhary, S. J. Cassady, D. F. Davidson and R. K. Hanson, Shock-induced ignition and pyrolysis of high-pressure methane and natural gas mixtures, Combust. Flame, 2020, 221, 364–370 CrossRef CAS.
- J. Crane, X. Shi, R. Xu and H. Wang, Natural gas versus methane: ignition kinetics and detonation limit behavior in small tubes, Combust. Flame, 2022, 237, 111719 CrossRef CAS.
- R. Hartig, J. Troe and H. Wagner, Thermal decomposition of methane behind reflected shock waves, Symp. (Int.) Combust., 1971, 13, 147–154 CrossRef.
- W. Gardiner Jr, J. Owen, T. Clark, J. Dove, S. Bauer, J. Miller and W. McLean, Rate and mechanism of methane pyrolysis from 2000o to 2700oK, Symp. (Int.) Combust., 1975, 15, 857–868 CrossRef.
- K. Tabayashi and S. Bauer, The early stages of pyrolysis and oxidation of methane, Combust. Flame, 1979, 34, 63–83 CrossRef CAS.
- Y. Hidaka, T. Nakamura, H. Tanaka, K. Inami and H. Kawano, High temperature pyrolysis of methane in shock waves. Rates for dissociative recombination reactions of methyl radicals and for propyne formation reaction, Int. J. Chem. Kinet., 1990, 22, 701–709 CrossRef CAS.
- D. Davidson, M. Di Rosa, A. Chang, R. Hanson and C. Bowman, A shock tube study of methane decomposition using laser absorption by CH3, Symp. (Int.) Combust., 1992, 24, 589–596 CrossRef.
- J. Kiefer and S. Kumaran, Rate of methane dissociation over 2800-4300 K: the low-pressure-limit rate constant, J. Phys. Chem., 1993, 97, 414–420 CrossRef CAS.
- Y. Hidaka, K. Sato, Y. Henmi, H. Tanaka and K. Inami, Shock-tube and modeling study of methane pyrolysis and oxidation, Combust. Flame, 1999, 118, 340–358 CrossRef CAS.
- C. Keramiotis, G. Vourliotakis, G. Skevis, M. Founti, C. Esarte, N. Sanchez, A. Millera, R. Bilbao and M. Alzueta, Experimental and computational study of methane mixtures pyrolysis in a flow reactor under atmospheric pressure, Energy, 2012, 43, 103–110 CrossRef CAS.
- D. Nativel, B. Shu, J. Herzler, M. Fikri and C. Schulz, Shock-tube study of methane pyrolysis in the context of energy-storage processes, Proc. Combust. Inst., 2019, 37, 197–204 CrossRef CAS.
- A. M. Dean, Detailed kinetic modeling of autocatalysis in methane pyrolysis, J. Phys. Chem., 1990, 94, 1432–1439 CrossRef CAS.
- D. M. Matheu, A. M. Dean, J. M. Grenda and W. H. Green, Mechanism generation with integrated pressure dependence: a new model for methane pyrolysis, J. Phys. Chem. A, 2003, 107, 8552–8565 CrossRef CAS.
- E. Wigner, The transition state method, Trans. Faraday Soc., 1938, 34, 29–41 RSC.
- H. Eyring, The activated complex in chemical reactions, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- M. G. Evans and M. Polanyi, Some applications of the transition state method to the calculation of reaction velocities, especially in solution, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, Current status of transition-state theory, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- A. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- V. Saunders and I. Hillier, A “Level–Shifting” method for converging closed shell Hartree–Fock wave functions, Int. J. Quantum Chem., 1973, 7, 699–705 CrossRef.
- A. D. Rabuck and G. E. Scuseria, Improving self-consistent field convergence by varying occupation numbers, J. Chem. Phys., 1999, 110, 695–700 CrossRef CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: a package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef.
- D. C. Liu and J. Nocedal, On the limited memory BFGS method for large scale optimization, Math. Program., 1989, 45, 503–528 CrossRef.
- J. Baker, A. Kessi and B. Delley, The generation and use of delocalized internal coordinates in geometry optimization, J. Chem. Phys., 1996, 105, 192–212 CrossRef CAS.
- X. Zhu, K. C. Thompson and T. J. Martínez, Geodesic interpolation for reaction pathways, J. Chem. Phys., 2019, 150, 164103 CrossRef PubMed.
- P. M. Zimmerman, Growing string method with interpolation and optimization in internal coordinates: Method and examples, J. Chem. Phys., 2013, 138, 184102 CrossRef.
- P. Zimmerman, Reliable transition state searches integrated with the growing string method, J. Chem. Theory Comput., 2013, 9, 3043–3050 CrossRef CAS PubMed.
- C. Aldaz, J. A. Kammeraad and P. M. Zimmerman, Discovery of conical intersection mediated photochemistry with growing string methods, Phys. Chem. Chem. Phys., 2018, 20, 27394–27405 RSC.
- L.-P. Wang and C. Song, Geometry optimization made simple with translation and rotation coordinates, J. Chem. Phys., 2016, 144, 214108 CrossRef PubMed.
- J. Baker, An algorithm for the location of transition states, J. Comput. Chem., 1986, 7, 385–395 CrossRef CAS.
- D. A. Mcquarrie, Statistical Mechanics, Harper & Row, New York, 1976 Search PubMed.
- S. Grimme, Supramolecular binding thermodynamics by dispersion-corrected density functional theory, Chem.–Eur. J., 2012, 18, 9955–9964 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- K. Yamaguchi, F. Jensen, A. Dorigo and K. Houk, A spin correction procedure for unrestricted Hartree-Fock and Møller-Plesset wavefunctions for singlet diradicals and polyradicals, Chem. Phys. Lett., 1988, 149, 537–542 CrossRef CAS.
- Y. Kitagawa, T. Saito and K. Yamaguchi, Approximate spin projection for broken-symmetry method and its application, in Symmetry (Group Theory) and Mathematical Treatment in Chemistry, ed. T. Akitsu, IntechOpen, London, 2018, pp. 121–139 Search PubMed.
- B. J. McBride, NASA Glenn coefficients for calculating thermodynamic properties of individual species, National Aeronautics and Space Administration, John H. Glenn Research Center, 2002 Search PubMed.
- C. N. Hinshelwood, On the theory of unimolecular reactions, Proc. R. Soc. London, Ser. A, 1926, 113, 230–233 CAS.
- D. G. Goodwin, H. K. Moffat, I. Schoegl, R. L. Speth and B. W. Weber, Cantera: An object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes, Version 2.6.0, 2022, DOI:10.5281/zenodo.6387882, https://www.cantera.org.
- B. Widom, Molecular Transitions and Chemical Reaction Rates: the stochastic model relates the rate of a chemical reaction to the underlying transition probabilities, Science, 1965, 148, 1555–1560 CrossRef CAS PubMed.
- J. R. Barker, M. Frenklach and D. M. Golden, When rate constants are not enough, J. Phys. Chem. A, 2015, 119, 7451–7461 CrossRef CAS.
- J. A. Miller, S. J. Klippenstein, S. H. Robertson, M. J. Pilling, R. Shannon, J. Zádor, A. W. Jasper, C. F. Goldsmith and M. P. Burke, Comment on “when rate constants are not enough”, J. Phys. Chem. A, 2016, 120, 306–312 CrossRef CAS PubMed.
- J. R. Barker, M. Frenklach and D. M. Golden, Reply to “Comment on ‘When rate constants are not enough’”, J. Phys. Chem. A, 2016, 120, 313–317 CrossRef CAS PubMed.
- I. Oppenheim, K. E. Shuler and G. H. Weiss, Stochastic processes in chemical physics: the master equation, MIT Press, Cambridge, MA, 1977 Search PubMed.
- J. A. Miller and S. J. Klippenstein, Master equation methods in gas phase chemical kinetics, J. Phys. Chem. A, 2006, 110, 10528–10544 CrossRef CAS PubMed.
- W. Tsang, V. Bedanov and M. Zachariah, Master equation analysis of thermal activation reactions: energy-transfer constraints on falloff behavior in the decomposition of reactive intermediates with low thresholds, J. Phys. Chem., 1996, 100, 4011–4018 CrossRef CAS.
- D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, MESMER: an open-source master equation solver for multi-energy well reactions, J. Phys. Chem. A, 2012, 116, 9545–9560 CrossRef CAS PubMed.
- J. T. Bartis and B. Widom, Stochastic models of the interconversion of three or more chemical species, J. Chem. Phys., 1974, 60, 3474–3482 CrossRef CAS.
- S. J. Klippenstein and J. A. Miller, From the time-dependent, multiple-well master equation to phenomenological rate coefficients, J. Phys. Chem. A, 2002, 106, 9267–9277 CrossRef CAS.
- J. A. Miller and S. J. Klippenstein, From the multiple-well master equation to phenomenological rate coefficients: reactions on a C3H4 potential energy surface, J. Phys. Chem. A, 2003, 107, 2680–2692 CrossRef CAS.
- J. Appel, H. Bockhorn and M. Frenklach, Kinetic modeling of soot formation with detailed chemistry and physics: laminar premixed flames of C2 hydrocarbons, Combust. Flame, 2000, 121, 122–136 CrossRef CAS.
- H. Wang, X. You, A. V. Joshi, S. G. Davis, A. Laskin, F. Egolfopoulos and C. K. Law, USC Mech Version II. High-temperature combustion reaction model of H2/CO/C1-C4 compounds, https://ignis.usc.edu:80/Mechanisms/USC-Mech%20II/USC_Mech%20II.htm, accessed, July 1 2022.
- C.-W. Zhou, Y. Li, U. Burke, C. Banyon, K. P. Somers, S. Ding, S. Khan, J. W. Hargis, T. Sikes, O. Mathieu, E. L. Peterson, M. AlAbbad, A. Farooq, Y. Pan, Y. Zhang, Z. Huang, J. Lopez, Z. Loparo, S. S. Vasu and H. J. Curran, An experimental and chemical kinetic modeling study of 1, 3-butadiene combustion: ignition delay time and laminar flame speed measurements, Combust. Flame, 2018, 197, 423–438 CrossRef CAS.
- T. Turányi, Applications of sensitivity analysis to combustion chemistry, Reliab. Eng. Syst. Saf., 1997, 57, 41–48 CrossRef.
- F. vom Lehn, L. Cai and H. Pitsch, Sensitivity analysis, uncertainty quantification, and optimization for thermochemical properties in chemical kinetic combustion models, Proc. Combust. Inst., 2019, 37, 771–779 CrossRef CAS.
- D. A. Sheen, X. You, H. Wang and T. Løvås, Spectral uncertainty quantification, propagation and optimization of a detailed kinetic model for ethylene combustion, Proc. Combust. Inst., 2009, 32, 535–542 CrossRef CAS.
- H. Wang and D. A. Sheen, Combustion kinetic model uncertainty quantification, propagation and minimization, Prog. Energy Combust. Sci., 2015, 47, 1–31 CrossRef.
- R. Xu and H. Wang, A physics-based approach to modeling real-fuel combustion chemistry–VII. Relationship between speciation measurement and reaction model accuracy, Combust. Flame, 2021, 224, 126–135 CrossRef CAS.
- H. Wang, Formation of nascent soot and other condensed-phase materials in flames, Proc. Combust. Inst., 2011, 33, 41–67 CrossRef CAS.
- O. K. Rice and H. C. Ramsperger, Theories of unimolecular gas reactions at low pressures, J. Am. Chem. Soc., 1927, 49, 1617–1629 CrossRef CAS.
- L. S. Kassel, Studies in homogeneous gas reactions. I, J. Phys. Chem., 1928, 32, 225–242 CrossRef CAS.
- R. A. Marcus, Unimolecular dissociations and free radical recombination reactions, J. Chem. Phys., 1952, 20, 359–364 CrossRef CAS.
- B. K. Carpenter, Nonstatistical dynamics in thermal reactions of polyatomic molecules, Annu. Rev. Phys. Chem., 2005, 56, 57–89 CrossRef CAS.
- L. M. Goldman, D. R. Glowacki and B. K. Carpenter, Nonstatistical dynamics in unlikely places: [1,5] hydrogen migration in chemically activated cyclopentadiene, J. Am. Chem. Soc., 2011, 133, 5312–5318 CrossRef CAS.
- B. K. Carpenter, Energy disposition in reactive intermediates, Chem. Rev., 2013, 113, 7265–7286 CrossRef CAS PubMed.
- P. Stewart, C. Larson and D. Golden, Pressure and temperature dependence of reactions proceeding via a bound complex. 2. Application to 2CH3 → C2H5+ H, Combust. Flame, 1989, 75, 25–31 CrossRef CAS.
- E. Ranzi, M. Dente, A. Goldaniga, G. Bozzano and T. Faravelli, Lumping procedures in detailed kinetic modeling of gasification, pyrolysis, partial oxidation and combustion of hydrocarbon mixtures, Prog. Energy Combust. Sci., 2001, 27, 99–139 CrossRef CAS.
- H. Wang, R. Xu, K. Wang, C. T. Bowman, R. K. Hanson, D. F. Davidson, K. Brezinsky and F. N. Egolfopoulos, A physics-based approach to modeling real-fuel combustion chemistry-I. Evidence from experiments, and thermodynamic, chemical kinetic and statistical considerations, Combust. Flame, 2018, 193, 502–519 CrossRef.
- R. Xu, K. Wang, S. Banerjee, J. Shao, T. Parise, Y. Zhu, S. Wang, A. Movaghar, D. J. Lee, R. Zhao, X. Han, Y. Gao, T. Lu, K. Brezinsky, F. Egolfopoulos, D. F. Davidson, R. Hanson, C. T. Bowman and H. Wang, A physics-based approach to modeling real-fuel combustion chemistry–II. Reaction kinetic models of jet and rocket fuels, Combust. Flame, 2018, 193, 520–537 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc01202f |
| ‡ Present address: Institute for Physical Chemistry, Heinrich Heine University, Düsseldorf, 40225, Germany. |
| This journal is © The Royal Society of Chemistry 2023 |