Machine learning-based q-RASPR modeling of power conversion efficiency of organic dyes in dye-sensitized solar cells†
Souvik
Pore
,
Arkaprava
Banerjee
 and
Kunal
Roy
and
Kunal
Roy
 *
*
Drug Theoretics and Chemoinformatics Laboratory, Department of Pharmaceutical Technology, Jadavpur University, 188 Raja S C Mullick Road, 700032, Kolkata, India. E-mail: kunalroy_in@yahoo.com; kunal.roy@jadavpuruniversity.in; Fax: +91-33-2837-1078; Tel: +91 9831594140
First published on 21st June 2023
Abstract
Different computational tools are now popularly used as an alternative to experiments for predicting several property endpoints of industrial importance. Recently, read-across and quantitative structure–property relationship (QSPR) have been merged to develop a new modeling technique read-across structure–property relationship (RASPR) which appears to have much potential in predictive modeling. This approach is also promising for modeling relatively smaller data sets as the similarity-based RASPR descriptors are computed from multiple structural and physicochemical features. To understand the potential of RASPR in data gap filling, we have undertaken a case study of modeling Power Conversion Efficiency (PCE) of different classes of organic dyes used in Dye-Sensitized Solar Cells (DSSCs) for renewable energy generation. We have used a large dataset of 429 compounds covering 4 classes of organic dyes. We initially performed read-across analysis using different similarity measures with structural analogues for query compounds and calculated the weighted average predictions. Based on the read-across optimized settings, RASPR descriptors were calculated, and these were then merged with the chemical descriptors, and finally, a single partial least squares (PLS) model was developed for each of the dye classes after feature selection, followed by additional Machine Learning (ML) models. The external prediction quality of the final RASPR models superseded those of the previously developed QSPR models using the same level of chemical information. The important structural features and similarity measures contributing to the PCE have been extracted using the RASPR method which can be used to enhance the PCE values in the newly designed dyes. The RASPR method may also be efficiently applied in modeling other properties of interest in a similar manner.
Introduction
Population growth has resulted in a significant rise in energy demand. To address this issue, alternative sources of energy in the form of renewable resources like solar energy, wind energy, geothermal energy, etc. should be increasingly used.1 Solar energy has been one of the most significant forms of renewable energy where the energy coming from the sun in the form of heat, and the radiation is converted into electrical energy by photovoltaic (PV) solar cells.2 The benefits of assimilating solar energy lie in its free availability, environmental friendliness, and sustainability.3 PV solar cells have undergone significant changes in their structures and composition since their development. PV solar cells can be classified into four generations based on their structural composition; 1st generation (Silicon Wafer based), 2nd generation (thin film based), 3rd generation (organic material-based), and 4th generation (perovskite-based solar cells).4 Dye-Sensitized Solar Cells (DSSCs) represent one of the important types of 3rd generation PV solar cells in which different types of organic dyes are used as photosensitizers.5The basic architecture of DSSCs is shown in Fig. 1a. It consists of 7 layers, namely a transparent substance (mainly glass or polymer), a transparent conductive oxide (TCO) layer (mainly Fluorine doped tin oxide (FTO), and Indium doped tin oxide (ITO) are used), a blocking layer (ZnO, In2O3, MgO, etc.), a semi-conductive oxide (SCO) layer (mainly TiO2) coated with photoactive dye, electrolyte solution and a counter electrode (Pt). In DSSCs, transparent substance – TCO layer – blocking layer – SCO layer – dye together form a photoanode (PA), and counter electrode – TCO layer – transparent substance is united to form the cathode. Electrolytes like iodide/triiodide (I−/I3−) solution is used for the preparation of DSSCs, where the electrolytes play an important role in the regeneration of dye by redox reaction.6 In DSSCs, the electrons are generated when the dye undergoes photoexcitation by absorbing radiation coming from the sun. The electrons are excited to the lowest unoccupied molecular orbital (LUMO) from the highest occupied molecular orbital (HOMO), and subsequently, electrons are transported to the TCO layer by the conduction band of the nanostructured SCO layer. From the TCO layer, the electrons flow through the external circuit and get collected at the platinum counter electrode site. The electrons are then transferred to the HOMO of dyes for their regeneration by the redox reaction of electrolytes which is catalyzed by a platinum counter electrode.6,7 The whole process for the generation of electrons is shown in Fig. 1b.
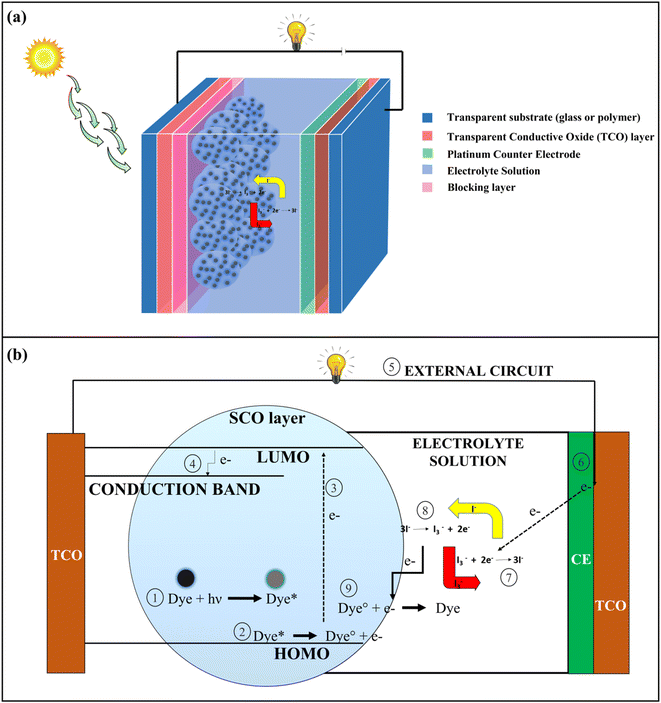 | ||
| Fig. 1 (a) Basic structure of a Dye-Sensitized Solar Cells (DSSCs) (b) Mechanism of electricity generation in DSSCs. | ||
In DSSCs, the dye is the key element for the generation of solar power, because it controls photon harvesting and electron generation.7 The dyes used in DSSCs can be classified into two groups namely metal-based inorganic dyes and metal-free organic dyes. The latter types are preferred due to having a low production cost, synthetically feasible, environment friendly, and easy to modify structure.8 Most of the metal-free organic dyes have donor–π–acceptor (D–π–A) type structural configuration in which conjugated π-systems like polyenes and oligothiophenes act as π spacers and have a rod-like configuration for the effective intramolecular charge transfer (ICT) by photoexcitation. The donor units are composed of different aromatic moieties like coumarins, triphenylamines, and porphyrins while the acceptor end contains structures like carboxylic acids and cyanoacrylic acids.7,8 The organic dyes have lower solar power conversion efficiency (PCE) as compared to the metal-based inorganic dyes due to the poor absorption at red and near-infrared spectrum of solar radiation, charge recombination at semi-conductive oxide layer surface and aggregation of dyes.8 In the recent past, different types of structural modifications have been performed to increase the absorption of solar radiation and PCE, like increasing the electron-donating ability of the donor and π-spacer by introducing an electron-donating group or increasing the electron-accepting ability of the acceptor by introducing the electron withdrawing group or increasing the length of π-spacer.9 Therefore, by altering the structures, it is possible to generate new dyes with higher PCE values while maintaining the same properties for all other performance-controlling factors. For designing a new dye molecule, a well-known scheme should be developed and checked before the synthesis of the molecule.
In the last few years, due to the low cost in computational methods and faster generation of results, in silico approaches have been extensively used to explore molecules to determine their properties. In silico approaches help to identify the active structural moieties responsible for the desired property and thus reduce synthetic complexities.10–12 Different types of in silico approaches like Quantitative Structure–Property Relationship (QSPR),13,14 Read-Across (RA)15,16 and various Machine learning (ML)17–20 methods are being used in the field of materials science. QSPR is a method that represents a mathematical relationship between the chemical structure and the property, and are developed based on the Organization for Economic Co-operation and Development (OECD) principles.13,14 Read-across (RA) is a similarity-based algorithm that predicts the response value of the query compounds by utilizing the similarity values of its close congeners, and this method is a potential alternative to the QSPR approach where lower number of data points are available.15,16 ML is a subset of Artificial Intelligence (AI) that enables machines to learn from previous data and improve their performance.17–20
In the recent past, various in silico studies have been conducted to explore the different classes of organic dyes.21–31 A cascaded QSPR model was developed by Li et al.29 using quantum chemical molecular descriptors in which combined quantum chemical calculation and machine learning methods were used to establish a relationship between PCE and molecular structures of different organic dyes. The PCE of phenothiazine-containing DSSCs was modeled by Kumar and Kumar24 using the CORAL software employing hybrid descriptors resulting from the combination of SMILES and hydrogen-suppressed graph (HSG). Combined QSPR modeling and quantum chemical analysis were performed by Kar et al.21 for 273 arylamine organic dyes to understand the electron transfer mechanism and photo-physical properties of dye. Venkatraman et al.31 developed a QSPR model for different phenothiazine derivatives using different structural descriptors and eigen-value (EVA) descriptors obtained from vibrational frequencies. Krishna et al.26 developed multiple Partial Least Squares (PLS) QSPR models for 1200 organic dyes of 7 classes, in order to know the important structural features contributing to higher PCE values. In the study, they have also designed 10 coumarin dyes using important structural feature obtained from the coumarin model with % PCE ranging from 8.93 to 10.62. Venkatraman et al.30 designed 5 novel phenothiazine dyes by the de novo design method using QSPR analysis and all new dyes show PCE over 9%. Kar et al.28 developed a QSPR model to establish the relationship between PCE and quantum chemical descriptors calculated from density functional theory (DFT) and time-dependent DFT (TD-DFT) methods to understand the basic electron transfer mechanism for arylamine-organic dye sensitizers. Seven indoline-based dyes with D–A–π–A molecular configuration designed using QSPR analysis were explored by Roy et al.27 using density functional theory (DFT) and time-dependent DFT (TD-DFT) methods to understand the different optoelectrical properties of dyes used in DSSCs. A QSPR model was proposed by Wen et al.22 which was obtained by combining the machine-learning approaches and computational quantum chemistry method and was used for virtual screening and to check the synthetic accessibility of the different organic dyes. In silico methods are thus important not only for the prediction of PCE values but also to explore the important structural and physicochemical properties of dyes that control the performance of DSSCs before synthesis of the dyes to save time, money, and resources.
In the present work, we have adopted a novel Quantitative Read-Across Structure–Property Relationship (q-RASPR) approach, which is analogous to the Quantitative Read-Across Structure Activity Relationship (q-RASAR) first reported by Banerjee and Roy,32,33 to generate different predictive models for the PCE using a wide array of compounds from 4 different classes. The q-RASPR is a supervised machine learning (ML) approach and is a combination of Read-Across and QSPR. Compound specific similarity and error-based measures were used as RASPR descriptors and combined with the initial descriptors to generate different predictive models.15,16,32 Different ML approaches in the form of Random Forest (RF), Gradient Boosting (GB), Extreme Gradient Boosting (or XGBoosting), Support Vector Machine (SVM), Linear Support Vector Machine (Linear SVM), Ridge Regression (RR) and Partial Least Squares (PLS) models were adopted to predict the PCEs of organic dye-based DSSCs.
Materials and methods
Data collection
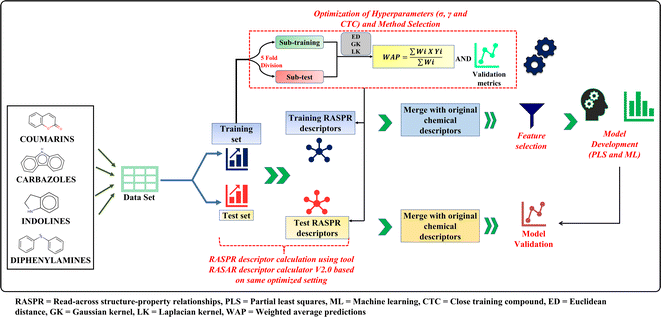
The current work deals with q-RASPR modeling of different organic dyes used in DSSCs for which experimental PCE and descriptor values are collected from the previous literature.26 To demonstrate the performance of the q-RASPR approach, in comparison to the previous QSPR models using the same combination of original descriptors and similarity descriptors computed from them (same level of chemical information), we have collected a total of 429 compounds distributed across 4 representative datasets, i.e. coumarins, carbazoles, indolines, and diphenylamines. One of the primary objectives of the current work is to evaluate the novel q-RASPR approach for the enhancement of the quality of predictions of the power conversion efficiency of DSSCs. As shown by Banerjee et al. (2023),34 q-RASPR models might be very useful even when the data set size is small as the similarity-based descriptors derived from the original structural and physicochemical variables act like latent variables thus allowing the usage of a greater amount of chemical information while using a lower number of regressing variables thus maintaining a more favorable degree of freedom. This is why we have taken here into consideration specifically the dye families with a relatively smaller number of data points. The original training and test sets were retained for the q-RASPR modeling analysis aiming at comparing with the previously developed QSPR model by Krishna et al.26 We used the same combination of structural and physicochemical descriptors as used in the original analysis. The dataset in each case was prepared by combining the descriptors of five individual models of the previous work and removing the common descriptors of these models. The logarithmic conversion of the endpoint parameter PCE was not required as it represents the performance of the solar cell. The datasets contain 56 coumarin dyes (42 training and 14 test compounds), 35 diphenylamine dyes (25 training and 10 test compounds), 179 carbazole dyes (125 training and 54 test compounds), and 159 indoline dyes (121 training and 38 test compounds). These datasets were used as input files for the calculation of the RASPR descriptors. The list of original structural and physicochemical descriptors used for read-across similarity computations (Table S1†) and the list of similarity descriptors used in q-RASPR model development (Table S2) are given in ESI SI-1.†Read-across hyperparameter optimization
Read-across is a data-gap filling method in which information of one or more chemicals is/are used to predict the endpoint of a target chemical. In read-across, structural similarity between a source compound (or a training compound) and a target compound (or a test compound) is used for the calculation of the endpoint value.15,16,35 A java-based tool Read-Across-v4.1 (available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home) was used for the computation of read-across-based predictions. This tool utilizes 3 different similarity-based methods, i.e., Euclidean distance (ED)-based similarity, Gaussian kernel (GK)-based similarity and the Laplacian kernel (LK)-based similarity methods for the computation of the predictions for the query compound(s).16 In compliance with the theory associated with Machine Learning, there is a need for the optimization of the hyperparameters associated with the three different similarity-based approaches. The Euclidean distance-based predictions require the optimum number of close source compounds, the Gaussian kernel-based predictions require the optimum value of σ and the number of close source compounds while the Laplacian kernel-based predictions require the optimum value of γ and the number of close source compounds.To select the optimum values for σ, and γ, the training set is randomly divided into 5 sub-training and sub-test sets by the sorted response-based division algorithm.36 Read-across-based predictions and validation metrics were calculated using these 5 sub-training and sub-test sets for each value of σ, γ, and CTC; and the average of external validation metrics for the subtest sets of 5 divisions was taken. The selection of the optimum σ and γ depends on whether the QF12 value (subtest set) is maximum for the GK and LK methods, respectively, and then the same values of σ and γ were applied for the original training and test sets at each value of close source compounds (CTC) between 2 to 10. The CTC value which corresponds to the maximum QF12 value (subtest set) in the ED approach is selected. These optimized settings of the σ, γ and CTC values were used for the computation of the RASPR descriptors. Note that the subtest sets are derived from the training set itself and different from the actual test set.
RASPR descriptor calculation
As defined by Todeschini and Consonni, a descriptor is “the final result of a logic and mathematical procedure which transforms chemical information encoded within a symbolic representation of a molecule into a useful number or the result of some standardized experiments”.37 In the present work, we have used different structural and physicochemical descriptors along with RASPR descriptors to develop predictive models. Different similarity and error-based measures obtained from the read-across-based predictions were used as RASPR descriptors.38 We have used RASAR-Desc-Calc-v2.0 (available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home) for RASPR descriptor calculation for both training and test sets. The calculation of the RASPR descriptors for the training set involves the Leave-same-out (LSO) algorithm38 which does not take the identical compound among the list of close source compounds. The optimized similarity-based method and the associated optimized hyperparameters were used for the computation of the RASPR descriptors. These RASPR descriptors were then combined with the initial structural and physicochemical descriptors and after subsequent feature selection based on cross-validation, q-RASPR models were generated. The optimized hyperparameter settings along with the similarity-based approach used for the calculation of the RASPR descriptors are shown in Table 1.| Datasets | Method | σ | γ | CTC |
|---|---|---|---|---|
| a GK = Gaussian kernel, LK = Laplacian kernel, CTC = Close training compound. | ||||
| Coumarins | GK | 1.75 | — | 8 |
| Carbazoles | GK | 2 | — | 5 |
| Indolines | LK | — | 0.5 | 5 |
| Diphenylamine | LK | — | 0.5 | 2 |
Feature selection and PLS model development
In the present work, we have used the Best Subset Selection (BSS) method to identify the significant descriptors or features that can influence the performance of DSSCs. Feature selection is important to reduce model noise and identify the significant descriptors for PCE in order to lower the risk of overtraining or overfitting.39,40 Significant descriptors for the models were identified by using the tool Best Subset Selection v2.1 (available from https://dtclab.webs.com/software-tools) using the cross-validation statistics.Best Subset Selection (BSS) is an algorithm that helps to identify the best descriptor combinations by developing models using a specific number of descriptor subset of input descriptors. This algorithm generates models using every possible combination of the descriptors, and the best combination is selected based on different internal validation metrics. Best Subset Selection is actually a grid search that identifies all possible combination of models from a given number of descriptors but the filters in the form of inter-correlation cut-off (<0.6) and R2 cut-off (>0.5) makes it an “intelligent grid search” which shows only the significant models. The number of descriptors in the models was selected based on the cross-validation QLOO2 score, and after that, we have developed several individual models for each data set, and the best models showing acceptable internal and external validation statistics are reported. For the present work, we have used the final models with 8 descriptors for coumarins, 5 descriptors for diphenylamines, 6 descriptors for indolines and 8 descriptors for carbazoles.
Partial Least Squares (PLS) is a generalized form of the multiple linear regression (MLR) that can be applied for collinear, correlated and noisy data containing multiple X variables (or descriptors) and one or more Y variable(s) (or endpoint(s)). The main idea behind PLS is to derive latent variables (LVs) T (or X-scores) and U (or Y-scores) from descriptors and response variables, respectively. These X-scores are then used to predict Y-scores which in turn are used to calculate the response.36 Here, we have used PLS_SingleY_1.0_14May2020 tool (available from https://dtclab.webs.com/software-tools) for the development of PLS models of selected descriptors. We have also compared the derived PLS models with other machine-learning models obtained using the same feature combinations.
For the purpose of interpretation and explanation of individual descriptors, different PLS plots were generated using SIMCA-P v10.0 software (https://www.sartorius.com/). We have generated the score plots (individual compounds are defined in the LV space and show their distribution and similarity among compounds), the loading plots (loading of all descriptors among the plotted first two LVs, and distance from the origin denote the importance of these descriptors), the Y-randomization plot (plot developed by plotting R2 and Q2 value of random models (Y axis) vs. correlation coefficient between observed PCE and permuted PCE), scatter plots (plots of predicted PCE (Y axis) vs. observed PCE (X axis)) and the variable importance plots (in the form of bubble plots).
Machine-learning (ML) models
Machine learning (ML) is a part of artificial intelligence which enables machines to learn from its past data and improve performance based on past experiences for the future aspect.41 In ML, machines are trained with a large amount of data and a suitable algorithm to accomplish a job. This trained algorithm is then applied to a query data set for reliable and accurate predictions. ML can be classified into 3 main groups: supervised (the labeled data is used to train the machine), unsupervised (the training data is not labeled) and reinforcement (feedback-based method, where the learning agents get a reward or penalty based on its action).42,43 In the present study, we have performed regression analysis using different supervised learning methods namely ridge regression (RR),44,45 linear support vector machine (LSVM),46 support vector machine (SVM),47 random forest (RF),47 gradient boosting (GB),44 and extreme gradient boost or XGBoost (XGB).48 Some details of these methods are given in ESI SI-1.†All the above-mentioned machine-learning models were developed using Anaconda Navigator software (version 2022.05) in Jupyter Notebook IDE (version 6.4.8)49 with python 3.10.4 64-bit. Different python-based modules were used such as numpy (version 1.23.5), pandas (version 1.5.2), Scikit-learn (version 1.2.0), matplotlib (version 3.5.1) and xgboost (version 1.7.1) for model development. For all the machine-learning models, we have used the same inputs as used for the PLS model development and optimized all the hyper-parameters by the cross-validation method using GridSearchCV function of Scikit-learn. For ML modeling, we standardized the descriptors and endpoints values based on the training set mean and standard deviation which were then used as the input.
In this work, we developed machine learning models using moderate sized data sets and a sufficient number of compounds for the validation of the models. Here, we optimized the hyper-parameters using the GridSearchCV method which is basically a cross-validation method in which the training set is divided into five-folds, and four folds are used to build the models each time when the remaining fold is used to validate the model. After building machine learning models, we calculated various cross-validation metrics to check that the models are not overfitted. The hyperparameter setting was chosen based on the best cross-validation statistics from the five-fold CV data. Again, a small difference between Mean Absolute Error (MAE) values for the training and test sets also indicates that the generated models are not overfitted.
Statistical quality and validation metrics
Validation of a model is important to justify the model quality and to determine its further application.36 There are different statistical metrics available to check the model quality, goodness-of-fit, robustness, reliability and predictivity. The model quality is checked by the determination coefficient (R2) and the explained variance (R2(adj)). The model quality is increased when its value become closer to 1. Model validation metrics can be classified into two groups – the internal validation metrics and the external validation metrics. Internal validation is performed only on the training set to check the goodness-of-fit and robustness of the model while the predictivity of a model is checked by an external validation performed on the test set. The robustness and goodness-of-fit of a model are checked by the internal validation metrics QLOO2 (leave-one-out correlation coefficient) performed on the training set. The original dataset is divided into a training set and a test set; the test set is used to check the predictivity of a model by calculating external validation metrics like QF12, QF22 and MAEtest.36 The validation metrics which demonstrated the quality of our PLS and ML models are shown in eqn (1)–(5).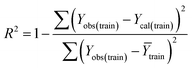 | (1) |
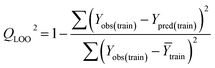 | (2) |
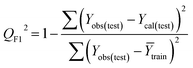 | (3) |
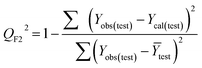 | (4) |
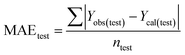 | (5) |
A model is considered to be well predictive if the values of Q2F1 and Q2F2 cross the threshold limit of 0.5 and MAEtest attains a minimum value.36
SHAP (SHapley additive exPlanation) analysis
The SHAP analysis is performed to identify the global and local contributions of each feature or descriptor for the predictions. By using SHAP, we can determine the feature's contribution in case of complex machine-learning models. SHAP uses the Shapley values to determine the feature contributions, the concept coming from the fair distribution in a cooperative game based on the player's importance.50 The Shapley values determine the contributions of different features (by the magnitude of the Shapley values) and direction (sign). The positive sign indicates a positive contribution to the predictions and the negative sign indicates a negative contribution to the predictions. The Shapley value for each feature is calculated using the following formula: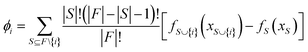 | (6) |
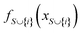 is the model output for a subset of features including a particular feature, fS(xS) is the model output for the subset of features without that feature, F is the number of input features and S is the number of features in a subset.50–52
is the model output for a subset of features including a particular feature, fS(xS) is the model output for the subset of features without that feature, F is the number of input features and S is the number of features in a subset.50–52
The complete workflow for the current work is shown in the Fig. 2.
Result and discussion
We have initially developed PLS models for each of the considered data sets and then compared the quality of these models to ML-derived model predictions.Partial least squares (PLS) models and interpretation of modeled descriptors
Most significant and statistically robust PLS models for different categories of dyes along with their quality in terms of different internal and external validation metrics are shown in Table 2. These models were developed with 8, 8, 6 and 5 descriptors for coumarins, carbazoles, indolines and diphenylamines, respectively, and all these models consist of both RASPR and 2D structural descriptors. The models were developed using 7, 3, 3 and 3 latent variables (LVs), respectively based on the leave-one-out Q2 values. All the developed models satisfy the threshold limit required to become robust, reliable and good predictivity.53| Types of organic dyes | PLS models | Training set metrics | Test set metrics | |||
|---|---|---|---|---|---|---|
| R 2 | Q LOO 2 | Q F1 2 | Q F2 2 | MAEtest (95%) (non-standardized) | ||
| a LV = Latent variables. | ||||||
| Coumarins (LV = 7) | PCE = −1.71195 + 0.60957 × SD Activity(GK) + 0.94835 × MaxPos(GK) − 0.75671 × nRCN + 1.07215 × nThiophenes − 1.01363 × nR#C + 1.18272 × nR = Ct − 0.12347 × T(S⋯S) + 0.76919 × C − 040 | 0.75 | 0.63 | 0.72 | 0.70 | 0.75 |
| Carbazoles (LV = 3) | PCE = −0.23418 + 1.26064 × Avg.Sim(GK) − 1.51529 × F06[N–N] + 0.92434 × nR10 + 0.19841 × F04[C–N] + 2.12686 × B04[N–O] − 0.4133 × N% + 2.35133 × F06[N–O] + 1.42348 × B02[C–S] | 0.71 | 0.66 | 0.77 | 0.76 | 0.61 |
| Indolines (LV = 3) | PCE = 1.52408 + 0.88535 × RA function(LK) − 0.89273 × CV sim(LK) − 0.92139 × Neg. Avg. Sim + 0.01956 × F04[C–N] + 0.70912 × B09[O–S] − 0.05307 × nCconj | 0.63 | 0.59 | 0.81 | 0.81 | 0.55 |
| Diphenylamines (LV = 3) | PCE = 1.28039 + 0.8856 × RA function(LK) + 1.53133 × SD similarity(LK) − 0.14367 × F01[C–N] − 0.15417 × StsC + 0.35804 × F04[N–S] | 0.83 | 0.73 | 0.90 | 0.90 | 0.62 |
The performance of the q-RASPR models toward the training set is in general inferior compared to the test set due to the algorithm of the RASPR descriptor calculation (Tables 2 and 3). For the calculation of RASPR descriptors for the training set, the algorithm works based on the “Leave Same Out (LSO) method”3,4 where identical compounds are not considered during the finding of close source compounds to avoid overfitting. In the case of any QSAR modeling study, chemical or physicochemical descriptors of a training compound are computed based on the structure or property of that particular compound. However, RASPR descriptors of a particular training compound are computed not from that particular compound, but from its close congeners based on the similarity features. Thus, the prediction aspect is in-built in the case of RASPR descriptor computation. A QSAR model is fitted based on the training set descriptor data while a RASPR model is fitted based on the leave-same-out “predicted” training set descriptor data. Again, during PLS model development, the number of components (LVs) of a PLS model is selected based on the cross-validation (Leave-One-Out (LOO) method). Due to the combined effect of leave-same-out descriptor computation followed by LOO cross-validation, q-RASPR models show inferior performance on the training data than on the test set data. Further details on this aspect are given while discussing other machine learning models (vide infra).
| Datasets | Methods | Training set metrics | Test set metrics | Optimized hyperparameters | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model statistics | Cross-validation statistics | Prediction statistics | ||||||||
| R 2 | MAELOO | MAE ± SEM (20 times 5-fold CV) | r2 ± SEM (20 times 5-fold CV) | MAE ± SEM (1000 times ShuffleSplit CV) | r2 ± SEM (1000 times ShuffleSplit CV) | MAEtest | Q F1 2 | |||
| Coumarins | PLS | 0.75 | 0.49 | 0.54 ± 0.015 | 0.41 ± 0.053 | 0.56 ± 0.004 | 0.44 ± 0.011 | 0.45 | 0.72 | n_components:7 |
| RR | 0.74 | 0.51 | 0.54 ± 0.011 | 0.46 ± 0.036 | 0.57 ± 0.003 | 0.48 ± 0.007 | 0.44 | 0.73 | ‘Alpha’: 1.0 | |
| LSVM | 0.72 | 0.52 | 0.60 ± 0.017 | 0.27 ± 0.077 | 0.62 ± 0.005 | 0.32 ± 0.015 | 0.49 | 0.67 | ‘C’: 1.0, ‘max_iter’: 1000 | |
| SVM | 0.74 | 0.66 | 0.67 ± 0.013 | 0.17 ± 0.053 | 0.67 ± 0.004 | 0.27 ± 0.009 | 0.5 | 0.68 | ‘C’: 1.0, ‘degree’: 2, ‘gamma’: ‘auto’ | |
| RF | 0.7 | 0.58 | 0.61 ± 0.013 | 0.23 ± 0.062 | 0.61 ± 0.004 | 0.35 ± 0.009 | 0.47 | 0.68 | ‘max_depth’:2, ‘min_samples_leaf’:2, ‘min_samples_split’:2, ‘n_estimators’:200 | |
| GB | 0.85 | 0.57 | 0.62 ± 0.014 | 0.18 ± 0.065 | 0.62 ± 0.003 | 0.32 ± 0.009 | 0.55 | 0.58 | ‘max_depth’:2, ‘min_samples_leaf’:3, ‘min_samples_split’:3, ‘n_estimators’:50 | |
| XGB | 0.75 | 0.49 | 0.54 ± 0.014 | 0.42 ± 0.050 | 0.56 ± 0.004 | 0.44 ± 0.011 | 0.45 | 0.72 | ‘booster’:’gblinear’, ‘learning_rate’:1.0, ‘max_depth’: none, ‘n_estimators’:90 | |
| Carbazoles | PLS | 0.71 | 0.47 | 0.47 ± 0.006 | 0.62 ± 0.012 | 0.48 ± 0.002 | 0.62 ± 0.004 | 0.31 | 0.77 | n_components:3 |
| RR | 0.71 | 0.47 | 0.47 ± 0.006 | 0.62 ± 0.011 | 0.48 ± 0.002 | 0.62 ± 0.003 | 0.32 | 0.77 | ‘Alpha’: 0.5 | |
| LSVM | 0.6 | 0.53 | 0.51 ± 0.008 | 0.53 ± 0.016 | 0.51 ± 0.002 | 0.54 ± 0.005 | 0.43 | 0.64 | ‘C’: 5.0, ‘max_iter’: 100 | |
| SVM | 0.84 | 0.53 | 0.51 ± 0.009 | 0.50 ± 0.014 | 0.52 ± 0.002 | 0.48 ± 0.004 | 0.41 | 0.63 | ‘C’: 25.0, ‘degree’: 2, ‘gamma’: ‘auto’ | |
| RF | 0.81 | 0.56 | 0.55 ± 0.009 | 0.44 ± 0.015 | 0.56 ± 0.002 | 0.41 ± 0.005 | 0.45 | 0.49 | ‘max_depth’:6, ‘min_samples_leaf’:1, ‘min_samples_split’:4, ‘n_estimators’:70 | |
| GB | 0.82 | 0.51 | 0.55 ± 0.009 | 0.44 ± 0.017 | 0.56 ± 0.002 | 0.42 ± 0.005 | 0.41 | 0.53 | ‘max_depth’:2, ‘min_samples_leaf’:5, ‘min_samples_split’:2, ‘n_estimators’:90 | |
| XGB | 0.71 | 0.47 | 0.47 ± 0.006 | 0.62 ± 0.012 | 0.48 ± 0.002 | 0.62 ± 0.003 | 0.32 | 0.77 | ‘Booster’: ‘Gblinear’, ‘learning_rate’:0.1, ‘max_depth’: none, ‘n_estimators’:90 | |
| Indolines | PLS | 0.63 | 0.48 | 0.49 ± 0.008 | 0.55 ± 0.017 | 0.49 ± 0.002 | 0.56 ± 0.004 | 0.3 | 0.81 | n_components:3 |
| RR | 0.63 | 0.49 | 0.49 ± 0.007 | 0.55 ± 0.016 | 0.49 ± 0.002 | 0.56 ± 0.004 | 0.3 | 0.82 | ‘Alpha’: 1.0 | |
| LSVM | 0.58 | 0.47 | 0.51 ± 0.008 | 0.51 ± 0.021 | 0.51 ± 0.002 | 0.53 ± 0.004 | 0.36 | 0.73 | ‘C’: 5.0, ‘max_iter’: 100 | |
| SVM | 0.71 | 0.5 | 0.51 ± 0.008 | 0.51 ± 0.018 | 0.52 ± 0.002 | 0.51 ± 0.004 | 0.34 | 0.76 | ‘C’: 1.0, ‘degree’: 2, ‘gamma’: ‘Scale’ | |
| RF | 0.83 | 0.45 | 0.48 ± 0.007 | 0.54 ± 0.016 | 0.49 ± 0.002 | 0.55 ± 0.004 | 0.42 | 0.65 | ‘max_depth’:5, ‘min_samples_leaf’:3, ‘min_samples_split’:2, ‘n_estimators’:80 | |
| GB | 0.81 | 0.49 | 0.51 ± 0.007 | 0.48 ± 0.017 | 0.51 ± 0.002 | 0.5 ± 0.004 | 0.36 | 0.73 | ‘max_depth’:2, ‘min_samples_leaf’:1, ‘min_samples_split’:5, ‘n_estimators’:50 | |
| XGB | 0.63 | 0.48 | 0.49 ± 0.008 | 0.55 ± 0.017 | 0.49 ± 0.002 | 0.56 ± 0.004 | 0.3 | 0.81 | ‘Booster’: ‘Gblinear’, ‘learning_rate’:1.0, ‘max_depth’: none, ‘n_estimators’:120 | |
| Diphenylamines | PLS | 0.83 | 0.44 | 0.47 ± 0.013 | 0.39 ± 0.072 | 0.48 ± 0.005 | 0.49 ± 0.031 | 0.31 | 0.9 | n_components:3 |
| RR | 0.83 | 0.44 | 0.49 ± 0.012 | 0.37 ± 0.071 | 0.5 ± 0.004 | 0.53 ± 0.013 | 0.31 | 0.91 | ‘Alpha’: 0.5 | |
| LSVM | 0.77 | 0.47 | 0.51 ± 0.016 | 0.18 ± 0.133 | 0.54 ± 0.005 | 0.38 ± 0.018 | 0.34 | 0.87 | ‘C’: 15.0, ‘max_iter’: 100 | |
| SVM | 0.87 | 0.48 | 0.55 ± 0.019 | 0.32 ± 0.066 | 0.57 ± 0.005 | 0.42 ± 0.014 | 0.64 | 0.61 | ‘C’: 1.0, ‘degree’: 2, ‘Gamma’: ‘auto’ | |
| RF | 0.88 | 0.48 | 0.51 ± 0.01 | 0.41 ± 0.059 | 0.51 ± 0.004 | 0.55 ± 0.01 | 0.4 | 0.8 | ‘max_depth’:2, ‘min_samples_leaf’:1, ‘min_samples_split’:3, ‘n_estimators’:120 | |
| GB | 1 | 0.56 | 0.56 ± 0.014 | 0.13 ± 0.109 | 0.54 ± 0.004 | 0.43 ± 0.013 | 0.43 | 0.78 | ‘max_depth’:3, ‘min_samples_leaf’:1, ‘min_samples_split’:5, ‘n_estimators’:60 | |
| XGB | 0.84 | 0.44 | 0.47 ± 0.014 | 0.37 ± 0.08 | 0.49 ± 0.005 | 0.5 ± 0.02 | 0.3 | 0.91 | ‘Booster’: ‘Gblinear’, ‘learning_rate’:0.1, ‘max_depth’: none, ‘n_estimators’:90 | |
The importance of the features toward the PCE is represented in the form of the bubble plot (Fig. S1 in ESI SI-1†), in which variable importance scores and coefficient scores are calculated by using SIMCA-P v10.0 software (https://www.sartorius.com/). The importance of these descriptors is represented by the diameter of the bubbles and their relative position along the y-axis whereas color difference denotes positive and negative contribution. The information related to all the datasets are provided in the ESI SI-2.†
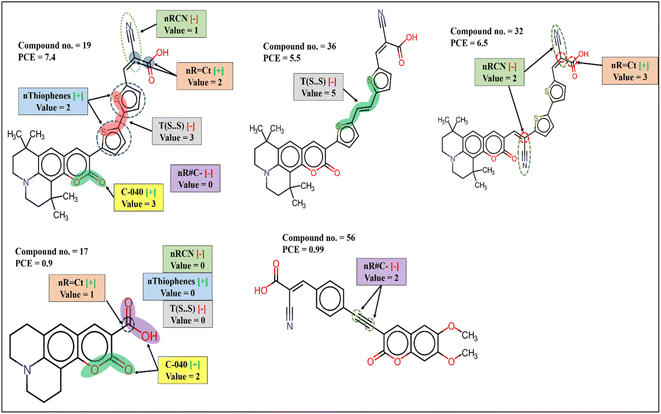
MaxPos(GK) is a RASPR descriptor that represents the similarity value to the nearest positive close source compound based on training set mean, obtained by Gaussian kernel similarity-based method.32 From the bubble plot, it was found that this descriptor has the highest contribution to the PCE, as shown in Fig. S1a.† MaxPos(GK) shows a positive contribution as reflected in following example: 19 (MaxPos(GK) = 1, PCE = 7.4), 20 (MaxPos(GK) = 1, PCE = 6.4) and vice versa for the dyes 56 (MaxPos(GK) = 0.014, PCE = 0.99), 22 (MaxPos(GK) = 0.004, PCE = 0.33). Any QSPR-derived predictions are based on the similarity assumptions; i.e., structurally similar compounds will have similar property or activity values. Thus, it is obvious that a data point showing structural similarity (MaxPos) to compounds having high response values will also have high response value and vice versa.
The functional group count descriptor nThiophene denoting the number of thiophene rings in the coumarin dyes contributes positively to the PCE. Therefore, presence of such functional group in the dye increases the performance of DSSCs as represented by the following examples: 19 (nThiophene = 2, PCE = 7.4), 32 (nThiophene = 2, PCE = 6.5). The PCE value may reduce for the compounds where no such functional group is present as shown in the following examples: 56 (nThiophene = 0, PCE = 0.99), 17 (nThiophene = 0, PCE = 0.9). Thiophene groups are the part of the π-spacer which not only improves light absorption and dipole moment but also decreases the dihedral angle between donor/acceptor and π-spacer plane for better orbital overlap which in turn improve electron injection to TiO2.54
Two other functional group count descriptors nR = Ct (number of an aliphatic tertiary carbon atom with the ‘sp2’ hybridization) and nR#C– (number of a non-terminal carbon atom with the ‘sp’ hybridization) have positive and negative contributions to the PCE, respectively. The presence of aliphatic tertiary ‘sp2’ hybridized C atom and the absence of non-terminal ‘sp’ hybridized C atom frequency of ‘s’ is responsible for the enhancement of absorption.55 The contribution of the descriptor nR = Ct is represented by the following examples: 35 (nR = Ct = 4, PCE = 6.2), 32 (nR = Ct = 3, PCE = 6.5), 17 (nR = Ct = 0, PCE = 0.9), 22 (nR = Ct = 0, PCE = 0.33); and the following examples represent the contribution of nR#C– 44 (nR#C– = 2, PCE = 1.35), 56 (nR#C– = 2, PCE = 0.99), 19 (nR#C– = 0, PCE = 7.4), 32 (nR#C– = 0, PCE = 6.5).
nRCN is a functional group count descriptor denoting the number of aliphatic nitriles in the dye which contributes negatively to the PCE of coumarin dyes. Therefore, with the increasing number of nitrile groups, the performance of DSSCs is reduced as indicated by the following examples: 44 (nRCN = 1, PCE = 1.35), 56 (nRCN = 1, PCE = 0.99) and vice versa for the dyes 10 (nRCN = 0, PCE = 3.7), 54 (nRCN = 0, PCE = 3.5) where no nitrile group is present. Anchoring groups are a part of the dye which involves adsorption on TiO2 surface that determines electron injection ability and optoelectrical property of the dye. Nitrile groups are generally a part of this anchoring group which may increase adsorption stability when CN group itself is involved in the binding. On the other hand, nitrile groups may reduce the photovoltaic property when it is not involved in binding.56
T(S⋯S) is a 2D atom pair descriptor that indicates the sum of the topological distance between two sulfur atoms where they are part of two thiophene rings. The negative contribution of this descriptor signifies that with the increasing distance between sulfur atoms, the performance of the DSSCs may decrease as represented by the following examples: 22 (T(S⋯S) = 31, PCE = 0.33), 3 (T(S⋯S) = 28, PCE = 1.77), 44 (T(S⋯S) = 21, PCE = 1.35) and vice versa for the dyes 19 (T(S⋯S) = 3, PCE = 7.4), 32 (T(S⋯S) = 3, PCE = 6.5), 29 (T(S⋯S) = 3, PCE = 6.07). The possible reason for this may be due to the disruption of the planar structure of the π-spacer and increase of dihedral angle between adjacent donor/acceptor and π-spacer. Another reason is that a hole is created in the π-spacer after injection of an electron to the TiO2; this hole is transferred to the donor part and prevents charge recombination. Therefore, with the increasing length of π-spacer, the possibility of this hole transfer is reduced, and this may cause back transfer of electron and reduce DSSC performances.54
C-040 is an atom-centered fragment descriptor that represents fragments like R–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X)–X/R–C#X/X
X)–X/R–C#X/X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X (R: any group linked through carbon; X: any electronegative atom like N, S, P, O, halogen; #: triple bond) in the dye which contributes positively to the PCE. The positive contribution of this descriptor signifies that the presence of such fragments in the dye may increase the performance of the dye as shown in the following examples: 19 (C-040 = 3, PCE = 7.4), 20 (C-040 = 3, PCE = 6.4), 35 (C-040 = 3, PCE = 6.2) and vice versa for the dyes 24 (C-040 = 2, PCE = 1.04), 17 (C-040 = 2, PCE = 0.9). These fragments are generally parts of the anchoring group containing carboxylic acid or cyanoacrylic acid as a binder which increases the stability of adsorption on TiO2 surface and helps in efficient electron transfer.56
X (R: any group linked through carbon; X: any electronegative atom like N, S, P, O, halogen; #: triple bond) in the dye which contributes positively to the PCE. The positive contribution of this descriptor signifies that the presence of such fragments in the dye may increase the performance of the dye as shown in the following examples: 19 (C-040 = 3, PCE = 7.4), 20 (C-040 = 3, PCE = 6.4), 35 (C-040 = 3, PCE = 6.2) and vice versa for the dyes 24 (C-040 = 2, PCE = 1.04), 17 (C-040 = 2, PCE = 0.9). These fragments are generally parts of the anchoring group containing carboxylic acid or cyanoacrylic acid as a binder which increases the stability of adsorption on TiO2 surface and helps in efficient electron transfer.56
SD Activity(GK) is a RASPR descriptor that denotes the weighted standard deviation of the response value of the selected close source compound for each query compound. The positive contribution of this descriptor32 is represented by the following examples: 29 (SD Activity(GK) = 1.53777, PCE = 6.07), 36 (SD Activity(GK) = 1.40648, PCE = 5.5), 7 (SD Activity(GK) = 1.04559, PCE = 1.1), 17 (SD Activity(GK) = 0.9868, PCE = 0.9).
The mechanistic interpretation of the 2D structural descriptor of the q-RASPR PLS model for the coumarin dyes is schematically represented in Fig. 3.
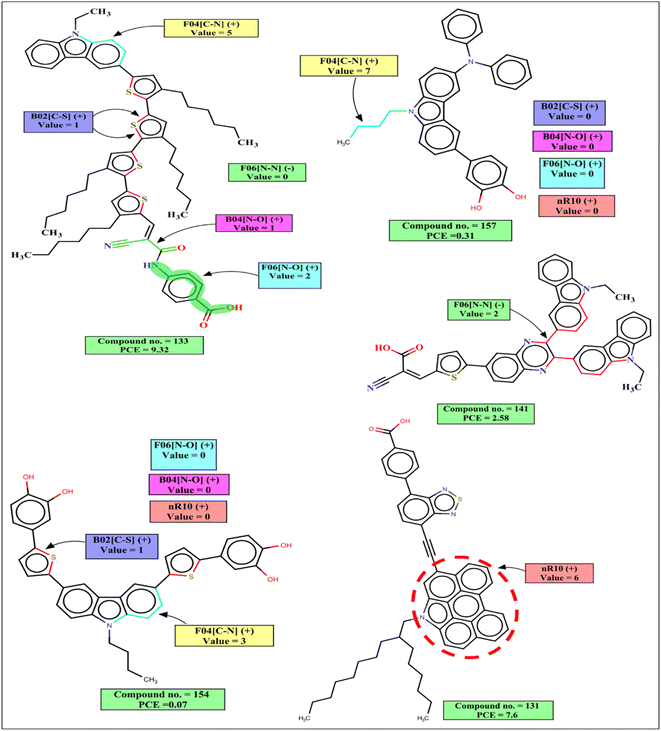
The 2D atom pair descriptor B04[N–O] indicates the presence or absence of nitrogen and oxygen atoms at the topological distance 4, and this descriptor contributes positively to the PCE. This fragment is part of an anchoring group cyanoacrylic acid. Cyanoacrylic acid is one of the most common anchoring groups for metal oxide (TiO2) surfaces because of its dual character of a strong adsorber and a good acceptor. Its strong binding with TiO2 provides stability to the adsorbed dyes which in turn helps in the efficient transfer of an electron to TiO2. This cyanoacrylic acid also has a strong electron-withdrawing ability which helps in intramolecular charge transfer from donor to metal oxide.55 Therefore, when such fragments are present in the dye, the performance of DSSCs will increase as represented by the following examples: 132 (B04[N–O] = 1, PCE = 12.5), 133 (B04[N–O] = 1, PCE = 9.32), 101 (B04[N–O] = 1, PCE = 8.09) and vice versa for the dyes 160 (B04[N–O] = 0, PCE = 0.34), 157 B04[N–O] = 0, (PCE = 0.31), 159 (B04[N–O] = 0, PCE = 0.21).
B02[C–S] is a 2D atom pair descriptor that indicates the presence or absence of carbon and sulfur at the topological distance 2. The positive contribution of this descriptor indicates that the presence of such fragment increases the performance of DSSCs. This fragment is a part of the thiophene group that acts as a π-spacer present between donor and acceptor moieties. This electron rich π-spacer is responsible for the enhancement absorption of photon which in turn increases PCE of carbazole dye.52 The positive contribution of this descriptor is represented by the following examples: 132 (B02[C–S] = 1, PCE = 12.5), 133 (B02[C–S] = 1, PCE = 9.32), 101 (B02[C–S] = 1, PCE = 8.09) and vice versa for the dyes 160 (B02[C–S] = 0, PCE = 0.34), 157 (B02[C–S] = 0, PCE = 0.31).
F06[N–O] is another 2D atom pair descriptor that indicates the frequency of nitrogen and oxygen atoms at the topological distance 6, and it contributes positively toward the PCE. This fragment is present in the dye either as a part of the phenyl moiety between acceptor (cyanoacrylic acid) and adsorber or as a part of the linker between the donor and π-spacer (furan or enedioxythiophene). A dye containing this fragment between acceptor and adsorber will have an improved performance by its diode like effect (which prevents the back transfer of electrons from TiO2 to the dye).57 It helps in an efficient intramolecular charge transfer for the dyes containing this fragment as a linker between the donor moiety and π-spacer.58 The positive contribution of this descriptor is represented by the following examples: 132 (F06[N–O] = 3, PCE = 12.5), 133 (F06[N–O] = 2, PCE = 9.32) and vice versa for the dyes where no such fragment is present, 160 (F06[N–O] = 0, PCE = 0.34), 157 (F06[N–O] = 0, PCE = 0.31).
F04[C–N] is a 2D atom pair descriptor that denotes the frequency of carbon and nitrogen atoms at the topological distance 4, and this descriptor contributes positively to the PCE. This fragment is present mainly as a part of the main scaffold (carbazole moiety) of the dye, and also in some dyes it is present adjacent to the carbazole moiety as a part of π-spacer. This fragment helps in the generation of electrons by a donor group and helps in the efficient transfer of electrons toward the acceptor part which in turn increases the performance of the DSSCs.59–61 The PCE value increases in the presence of such fragments in the dyes as indicated by the following examples: 50 (F04[C–N] = 22, PCE = 7.52), 101 (F04[C–N] = 17, PCE = 8.09), 130 (F04[C–N] = 15, PCE = 9.8) and vice versa for the dyes 97 (F04[C–N] = 0, PCE = 0.0538), 98 (F04[C–N] = 0, PCE = 0.0387) where no such fragment is present.
nR10 is a ring descriptor that indicates the number of 10 membered rings in a dye which contributes positively to the PCE. In this case, 6-membered or 5-membered aromatic rings are fused with the main carbazole scaffold of the dye and form a planar structure. These electron-rich centers help in the generation of electrons and due to their planar structure, the molar absorption coefficient and photon harvesting ability of the dye is increased which improve the performance of DSSCs.62,63 In some dyes, this fragment is also present as a part of the π-spacer which helps in the efficient transfer of electrons from a donor part to the acceptor part. Therefore, performances of DSSCs should increase when such ring system is present in the structures, which is indicated by the following examples: 130 (nR10 = 6, PCE = 9.8), 131 (nR10 = 6, PCE = 7.6) and vice versa for the dyes 159 (nR10 = 0, PCE = 0.21), 91 (nR10 = 0, PCE = 0.19), 154 (nR10 = 0, PCE = 0.07) where no 10 membered rings are present.
The negative contribution of the constitutional descriptor N% (percentage of the nitrogen atoms in the dye) and 2D atom pair descriptor F06[N–N] (frequency of two nitrogen atoms at the topological distance 6) indicates that the presence of such fragments hinders the performance of DSSCs. Higher numerical values of these descriptors of a dye may decrease the PCE value which is represented by the following examples: 91 (N% = 6.25, PCE = 0.19), 118 (N% = 5.6338, PCE = 0.89), 53 (N% = 4.83871, PCE = 0.99), 112 (N% = 4.83871, PCE = 0.96) for the descriptor N%; 141 (F06[N–N] = 2, PCE = 2.58), 138 (F06[N–N] = 2, PCE = 2.17) for F06[N–N]. On the other hand, dyes with lower numerical value of this descriptor may have higher PCE values as shown in following examples: 99 (N% = 1.81818, PCE = 7.58), 103 (N% = 1.50376, PCE = 7.54), 130 (N% = 1.34529, PCE = 9.8) for N%, 132 (F06[N–N] = 0, PCE = 12.5), 130 (F06[N–N] = 0, PCE = 9.8), 133 (F06[N–N] = 0, PCE = 8.09) for the F06[N–N].
Avg. Sim(GK) is a RASPR descriptor that denotes the mean similarity value of the selected close source compounds for each query compound based on the Gaussian kernel similarity-based method. The positive contribution of this descriptor indicates a molecule having a higher Avg. Sim value may have a higher PCE value as represented by the following examples: 94 (Avg. Sim(GK) = 0.92848, PCE = 7.33), 56 (Avg. Sim(GK) = 0.89553, PCE = 6.04), 99 (Avg. Sim(GK) = 0.75399, PCE = 7.58) and vice versa for the dyes 156 (Avg. Sim(GK) = 0.24768, PCE = 0.06), 154 (Avg. Sim(GK) = 0.04227, PCE = 0.07).
The interpretation of 2D structural descriptors for the carbazole dyes is represented schematically in Fig. 4.
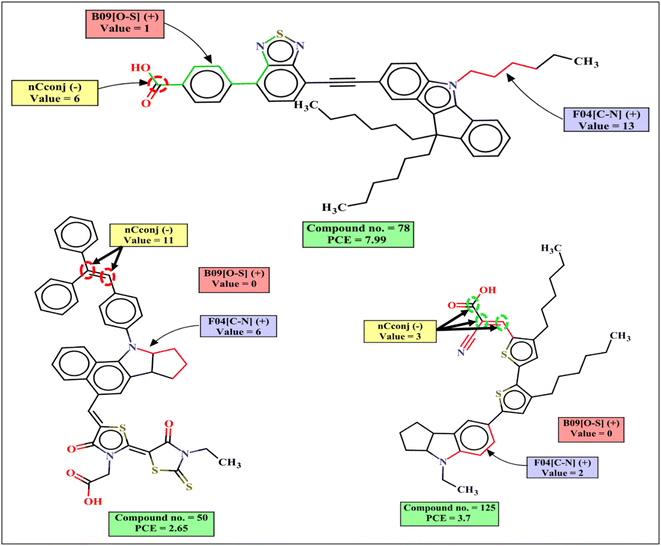
RA function is a Read-Across-derived RASPR descriptor which encodes information of all the selected structural and physicochemical descriptors.33 It contributes positively to the PCE as indicated by the following examples: 141 (RA function = 8.1741, PCE = 8.38), 8 (RA function = 7.9697, PCE = 7.12), 24 (RA function = 7.88, PCE = 9.2) and vice versa for the dye 129 (RA function = 1.8131, PCE = 1.48), 32 (RA function = 1.5372, PCE = 0.63), 30 (RA function = 1.4248, PCE = 0.77).
Both RASPR descriptors Neg.Avg.Sim (denoting the mean of the similarity values of the negative close source compounds for a particular query compound) and CVsim(LK) (coefficient of variation of the similarity values of the selected close source compound for each query compound) contribute negatively to the PCE. This is represented by the following examples: 93 (Neg.Avg.Similarity = 0.2883, PCE = 0.35), 108 (Neg.Avg.Similarity = 0.2883, PCE = 0.046) for Neg.Avg.Similarity; 93 (CVsim(LK) = 1.404, PCE = 0.35), 108 (CVsim(LK) = 1.404, PCE = 0.046) for CVsim(LK); and vice versa for the dye 144 (Neg.Avg.Similarity = 0, PCE = 8.78), 24 (Neg.Avg.Similarity = 0, PCE = 9.2), 135 (Neg.Avg.Similarity = 0, PCE = 8.61) for Neg.Avg.Similarity; 135 (CVsim(LK) = 0.4427, PCE = 8.61), 78 (CVsim(LK) = 0.3868, PCE = 7.99) for CVsim(LK).
The functional group count descriptor nCconj denotes the number of non-aromatic conjugated sp2 hybridized carbon atoms that contributes negatively to the PCE. The negative contribution of this descriptor signifies that the PCE value may decrease when the number of non-aromatic conjugated sp2 carbon increases as represented by the following examples: 11 (nCconj = 11, PCE = 2.65), 10 (nCconj = 10, PCE = 2.7) and vice versa for the dyes with a low numerical value of nCconj like 155 (nCconj = 1, PCE = 5.61) and 152 (nCconj = 1, PCE = 5.5).
F04[C–N] is a 2D atom pair descriptor that indicates the frequency of carbon and nitrogen atoms at the topological distance 4 in the dye, and this descriptor contributes positively to the PCE. It was found that if the donor group is present with a non-planar orientation with other groups, it may increase the PCE value. Although this fragment is present as a part of the dye in a non-planar structure, it may increase the performance of the DSSCs as indicated by its positive contribution to the PCE.64,65 Therefore, the presence of such fragment increases the performance of DSSCs as shown by the following examples: 21 (F04[C–N] = 21, PCE = 8.43), 8 (F04[C–N] = 20, PCE = 7.12), 24 (F04[C–N] = 18, PCE = 9.2) and vice versa for the dyes 105 (F04[C–N] = 3, PCE = 2.53), 164 (F04[C–N] = 3, PCE = 2.08).
Another 2D atom pair descriptor B09[O–S] indicates the presence or absence of oxygen and sulfur atoms at the topological distance 9, and this descriptor contributes positively to the PCE. This is a part of the anchoring group for the dye which contains this fragment. It helps to transfer electrons from the dye to the TiO2 surface through π-bond conjugation. Oxygen and sulfur atoms control electron density delocalization which helps in π bond conjugation. As a result, the molar extinction coefficient of the dye increases which may lead to shifting of the absorption maxima.65 If the topological distance between O and S is reduced or increased, the conformation of the dye will change which may decrease the anchoring stability of the dye and the performance of the DSSCs will be reduced.66,67 Dyes containing this type of fragment may increase PCE values as represented by the following examples: 78 (B09[O–S] = 1, PCE = 7.99), 21 (B09[O–S] = 1, PCE = 6.12), 131 (B09[O–S] = 1, PCE = 6.11) and vice versa for the dyes 30 (B09[O–S] = 0, PCE = 0.77), 32 (B09[O–S] = 0, PCE = 0.63), 93 (B09[O–S] = 0, PCE = 0.35).The mechanistic interpretation of the relevant descriptors for the indoline dataset is schematically represented in Fig. 5.
F01[C–N] is a 2D atom pair descriptor that indicates the frequency of carbon and nitrogen atoms at the topological distance of 1, and this descriptor contributes negatively to the PCE. In the presence of these fragments, the overall polarity of the dye will change which may lead to an increased intermolecular interaction in terms of different weak forces like hydrogen bonding, aromatic ring stacking, van der Waals force, etc. These weak forces may cause aggregation of dyes on the surface of the TiO2, and the performance of the DSSCs is reduced.68 Therefore, the presence of such fragment reduces the performance of the DSSCs as represented by the following examples: 35 (F01[C–N] = 11, PCE = 0.4), 34 (F01[C–N] = 10, PCE = 1) and vice versa for the dyes 3 (F01[C–N] = 4, PCE = 5.4), 22 (F01[C–N] = 4, PCE = 5.22), where no such fragment is present.
Another 2D atom pair descriptor F04[N–S] denotes the frequency of nitrogen and sulfur atoms at the topological distance 4, and this descriptor contributes positively to the PCE. This can be represented by the following examples: 27 (F04[N–S] = 2, PCE = 8), 26 (F04[N–S] = 2, PCE = 7.1), 17 (F04[N–S] = 2, PCE = 6.19) and vice versa for the dyes 34 (F04[N–S] = 0, PCE = 1), 33 (F04[N–S] = 0, PCE = 0.44), 35 (F04[N–S] = 0, PCE = 0.4) where no such fragment is present.
SD_similarity is a RASPR descriptor that denotes the standard deviation of the similarity values of close source compounds for each query compound. A high numerical value of the descriptor may increase PCE value as shown in the following examples: 7 (SD similarity = 0.33695, PCE = 7.05), 8 (SD similarity = 0.33274, PCE = 7.64) and vice versa for the dyes 35 (SD similarity = 0.177502, PCE = 0.4), 33 (SD similarity = 0.016381, PCE = 0.44).
StsC is an atom type E-state descriptor that indicates the sum of tsC E-states (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–), which contributes negatively to the PCE property of the DSSCs, as observed for the dyes 10 (StsC = 8.292574, PCE = 1.99), 13 (StsC = 7.76829, PCE = 3.16) and vice versa for the dyes 8 (StsC = 1.671126, PCE = 7.64), 7 (StsC = 1.644351, PCE = 7.05).
C–), which contributes negatively to the PCE property of the DSSCs, as observed for the dyes 10 (StsC = 8.292574, PCE = 1.99), 13 (StsC = 7.76829, PCE = 3.16) and vice versa for the dyes 8 (StsC = 1.671126, PCE = 7.64), 7 (StsC = 1.644351, PCE = 7.05).
The mechanistic interpretation of the significant 2D-structural descriptors for the diphenylamine dataset is schematically represented in Fig. 6.
 | ||
| Fig. 6 Mechanistic interpretation of the 2D structural descriptors of q-RASPR PLS model for the diphenylamine dataset. | ||
For all 4 datasets, different PLS plots like randomization plots, loading plots, and score plots were developed which are shown in the ESI SI-1.† For all the datasets, the PLS Scatter plots (Fig. S2†) show that there is not so much difference between observed and predicted PCE indicating the good quality of the test set predictions. The Y-randomization plots (Fig. S3†) show that all the models have R2 and Q2 intercept values within their threshold limits (0.3 for R2 and 0.05 for Q2), indicating that our models are not obtained by chance. The loading plots (Fig. S4†) show that the descriptors MaxPos(GK) (for coumarins), BO4[N–O] (for carbazoles) and RA function (for both indoline and diphenylamines) have the highest contributions to the PCE because they are present closest to the response variable (PCE). The score plots (Fig. S5†) show that there are 2 coumarin (3, 54), 5 carbazole (132, 138, 139, 140, 141) and 1 indoline (18) molecules which are present outside the applicability domain of the corresponding models (located outside the ellipse drawn on based on Hotelling t2 test).69
Machine-learning (ML) models
The qualities of the Machine-Learning (ML) models and the different validation metrics for all 4 datasets are shown in Table 3 along with their different optimized hyperparameter settings. To determine the models' quality and predictability, we calculated various quality and validation metrics on the training and test sets. For the purpose of comparison, we have also included PLS q-RASAR models for which the same method was used for calculation of the internal, external and cross-validation metrics. For all 4 datasets, ridge regression, XGBoost and PLS models show almost similar QF12, MAEtest and R2 score (of training set) values. There are two different aspects here regarding the quality of predictions from the q-RASPR models for the test sets. The first is the enhancement of prediction quality for the test set in case of a q-RASPR model in comparison to the corresponding QSPR model (vide infra the comparison section) while the second is the comparison of the prediction quality of the q-RASPR models for the test set in comparison to its fitting quality in case of the corresponding training set. The test set prediction quality may better be compared with the training set fitting ability by considering MAETest for the test set and MAELOO for the training set. In our opinion, QF12 for the test set should not be directly compared with R2 or Q2 values of the training set as these metrics depend on the distribution of the observed response values of the training and test set compounds around the training set mean, and usually these patterns may be different in the training and test sets.70 In our examples, MAETest values for the test sets in different models are lower than the corresponding MAELOO values for the training sets (Table 3). This also happened in the case of machine learning models like the random forest, Gradient Boost, and Extreme Gradient Boost for different data sets in Table 3. Thus, in terms of MAE as a metric (MAELOO for the training sets and MAETest for the test sets), the quality of the test set predictions is comparatively better in these examples.Now, as per the q-RASPR algorithm, the RASPR descriptors of both the training and test sets are computed from the structural congeners in the training set. It is natural that a data set may contain a few activity cliffs, which are similar to other compounds in structural features but have quite different response values from their structural congeners. The fitting ability of such compounds in the training set and the prediction ability of such compounds in the test set will naturally be poor, especially when we use similarity-based descriptors like RASPR descriptors. In our present examples, the training set size is much bigger than the corresponding test set size in order to maximize the learning ability of the models (as usual in conventional QSPR studies). Thus, the probability of the occurrence of such activity cliffs in the training sets is more than that in the corresponding test sets, which may explain (at least partially) the lower MAETest values in comparison to the corresponding MAELOO values of the training sets. The activity cliff aspect in q-RASPR modeling has been extensively discussed in our recent work.71
We have checked the number of activity cliffs in the training and test sets of the four different data sets based on novel Banerjee–Roy similarity coefficients as per ref. 71. A compound is considered an activity cliff when both of the two similarity coefficients do not show values as per the expected category (positive/negative, considering the training set response mean as the threshold). From Table 4, it is evident that in the case of each data set, the number of activity cliffs in a training set is much higher than the number of activity cliffs in the corresponding test sets. In the case of QSAR analysis, descriptors are computed directly from the structures of the compounds in question; however, RASAR descriptors are computed from close congeners of the compounds under consideration. In the case of activity cliffs, the similarity principle is not obeyed and thus the similarity descriptors computed from the close congeners cannot capture the structure–response relationship properly. In the case of QSAR analysis, the model fitting is done based on the whole training set in which activity cliffs may penalize a model but not to the extent to a RASAR model as in the latter case the similarity descriptors of the activity cliffs (not obeying the similarity principle) heavily penalize the model. This is more evident in the case of regression-based predictions, as precise quantitative predictions are considered here as also seen in ref. 38. Due to the lower number of activity cliffs in the test sets, the quality of predictions is less impacted. Such observations are not common in case of QSAR analysis including ML methods as in the latter case descriptors are not computed from close congeners of the compounds under consideration, rather computed from the same compounds. In fact, one of the objectives of RASAR modeling is to enhance the quality of predictions for the test set which may be at the expense of lowering the prediction quality for the training set. Further, the novel similarity coefficients71 may be used to identify activity cliffs and enhance the modelability of a data set.
| Dataset | Number of training set compounds | Number of test set compounds | Number of activity cliffs in the training seta | activity cliff in the training set (%) | Number of activity cliffs in the test seta | activity cliff in the test set (%) |
|---|---|---|---|---|---|---|
| a Computed based on similarity coefficients described in ref. 71. | ||||||
| Carbazoles | 124 | 54 | 37 | 29.84 | 14 | 25.93 |
| Coumarins | 42 | 14 | 7 | 16.66 | 2 | 14.29 |
| Diphenylamines | 25 | 10 | 6 | 24 | 1 | 10 |
| Indolines | 121 | 38 | 20 | 16.53 | 7 | 18.42 |
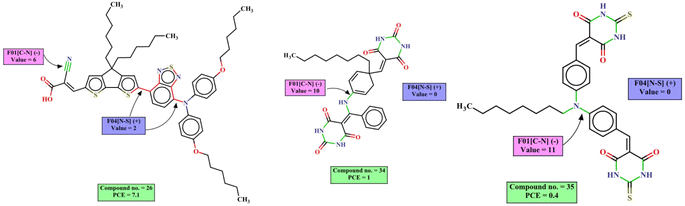
To further evaluate the quality of developed models, we have also performed 20 times 5-fold repetitive cross-validation, and 1000 times shuffle-split cross-validation with 30% data holding in the validation set. The result of cross-validation for the coumarin dataset is shown in the Fig. 7 and that for the carbazole, indoline and diphenylamine datasets are shown in Fig. S6–S8 in ESI SI-1.† For the coumarin dataset, the mean R2 value for both the repetitive CV and Shuffle-split CV indicates that the Ridge regression method is the best model among all models while the PLS and XGBoost models show comparable results. For the carbazole and indoline datasets, the ridge regression, PLS and XGBoost models show comparable results, as shown in Fig. S6 and S7.† For the diphenylamine dataset, the random forest model shows the highest mean R2 value in both repetitive cross-validation and shuffle-split cross-validation method but ridge regression, XGBoost and PLS models show comparable results, as shown in Fig. S8.†
 | ||
| Fig. 7 Cross-validation statistics based on 20 times 5-fold repetitive CV and 1000 shuffle split CV method (mean ± SEM) for the coumarin dataset. | ||
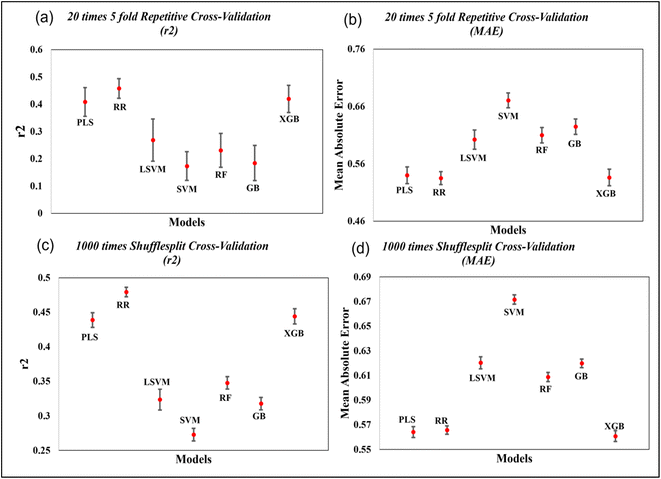
To evaluate the importance of descriptors in the machine-learning models, we have performed SHAP analysis on the training set data. We have represented the importance of descriptors in the form of heatmap plots of SHAP as shown in Fig. 8. The PLS, ridge regression and XGBoost models are considered here, and the plots of the remaining models are shown in the Fig. S9–S12 of ESI SI-1.† On the Y-axis of the heatmap plot, the features are arranged based on their mean absolute SHAP values, which in turn denotes their importance to the predictions. From the heatmap plot, we can also obtain how the model's prediction changes over every instance which is denoted by the wavy line above the plot. The colour difference in the plot indicates how the SHAP value of the features changes over every instance and how it affects the model's output.
 | ||
| Fig. 8 Heatmap plots for the PLS, Ridge regression and XGBoost models for all datasets, indicating relative importance of descriptors. | ||
A partial dependence plot shows the marginal effect of a feature (or two features) on the predicted outcome of a machine learning model. This plot can suggest the dependence interaction between two features. In case of an interaction with the other feature, a distinct vertical pattern of coloring will be seen. The partial dependence plots of selected ML models are shown in ESI SI-3.†
Design of new dyes with improved PCEs
We can design new dyes with improved power conversion efficiency (PCE) by incorporating structural fragments that have positive contributions to the PCE of solar cells or by removing fragments that contribute negatively to the PCE of solar cells. The favorable fragments improve PCE either by increasing intramolecular charge transfer or by increasing the anchoring stability of the dye on the TiO2 semiconductor oxide surface. The descriptors which encode the structural information help to identify the necessary modifications that must be made to improve the PCE. In this work, we use the PLS variable importance plot to identify the relative importance of the positive and negatively contributing descriptors. Based on this, we have designed new dyes with improved predicted PCE values as shown in ESI SI-3.† We have also checked the synthetic accessibility of the designed dyes.72For carbazole dyes, the incorporation of a cyano acrylic acid group increases the value of B04[N–O] (presence or absence of nitrogen and oxygen atoms at the topological distance 4) while a para-aminobenzoic acid group increases the value of F06[N–O] (count of nitrogen and oxygen at the topological distance 6). For example, the F06[N–O] value increases when one incorporates 4-(2-cyanoprop-2-enamido)benzoic acid (as shown in NCA1, NCA2 and NCA3) and 2-cyano-N-[4-(trimethoxysilyl)phenyl]prop-2-enamide (as shown in NCA4 and NCA5) moieties in the carbazole structure. These fragments are generally a part of the anchoring group which increases the stability of the binding of the dye with the TiO2 surface. We can increase the value of B02[C–S] (presence or absence of carbon and sulfur atoms at the topological distance of 2) by incorporating a thiophene group, increase the value of F04[C–N] (frequency of carbon and nitrogen atoms at the topological distance of 4) by attaching a long aliphatic chain to the nitrogen atoms and increase the value of nR10 (the number of 10-member rings) by incorporating 10 membered rings in the structure. All these fragments are responsible for the generation of electrons which are transferred to the TiO2 surface.
For coumarin dyes, one can increase the value of positively contributing descriptors like nThiophene (number of thiophene group), nR = Ct (number of aliphatic tertiary C atom with sp2 hybridization) and C-040 (R–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X)–X/R–C#X/X
X)–X/R–C#X/X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X). These descriptors are generally responsible for electron generation and intramolecular charge transfer. One can also try removing the negatively contributing descriptor nRCN (number of aliphatic nitrile groups). The nitrile group is a part of the anchoring group cyanoacrylic acid; therefore, one can try using other anchoring groups like carboxylic acid, pyridine, etc.
X). These descriptors are generally responsible for electron generation and intramolecular charge transfer. One can also try removing the negatively contributing descriptor nRCN (number of aliphatic nitrile groups). The nitrile group is a part of the anchoring group cyanoacrylic acid; therefore, one can try using other anchoring groups like carboxylic acid, pyridine, etc.
For diphenylamine dyes, one can increase the value of positively contributing descriptor F04[N–S] (frequency of nitrogen and sulfur atoms at the topological distance 4) by incorporating groups like a pyrimidine ring adjacent to a thiophene ring (as shown below in NDI1), 2,1,3-benzothiadiazole and 1,2,3-benzodithiazole groups adjacent to the thiophene and pyrimidine rings respectively (as shown below in NDI5 and NDI3). These fragments are generally a part of the linker between the donor part and the acceptor part which helps to improve performance by increasing intramolecular charge transfer.
For indoline dyes, one can increase the value of positively contributing descriptors like F04[C–N] (frequency of carbon and nitrogen atoms at the topological distance of 4) by attaching different aliphatic and aromatic groups to the nitrogen atoms, and B09[O–S] (presence of oxygen and sulfur atoms at the topological distance 9) by increasing the length of the π-spacer (for example, compound NIN1 is formed by incorporating a butylene group between the thiophene ring and the cyanoacrylic acid). These fragments help in the generation of electrons and improve intramolecular charge transfer.
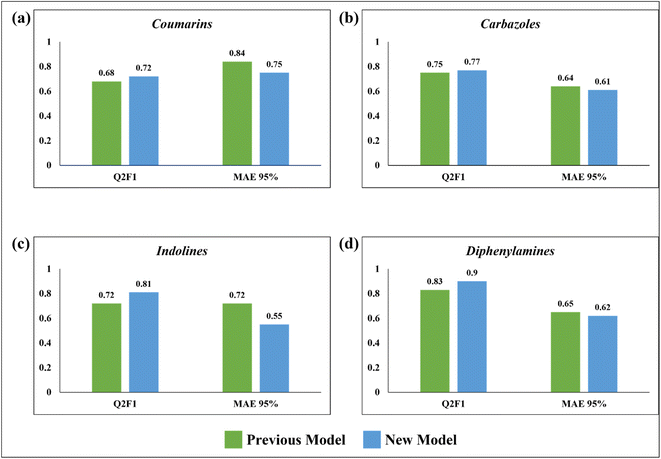
Comparison with the previous work
In 2020, Krishna et al. worked on the prediction of PCE value of metal free organic DSSCs by PLS regression using 2D structural descriptors.26 The models reported by them were statistically sound with good quality validation metrics. However, our q-RASPR PLS models outperformed them with better prediction quality with the same level of chemical information used, also explaining the importance of RASPR descriptor. The advantage of RASPR descriptors is that they are simple, easy to calculate and transferable. In comparison to the previous models, the present models have higher QF12 scores and lower MAEtest values. The comparison between the previous PLS QSPR models and the present q-RASPR PLS models is shown in the form of column plots in Fig. 9. The previous study developed five individual models and consensus models of datasets, but here we have considered only the best individual models for comparison. It is clear from the column plots that our newly developed models are much more predictive. This study shows that the inclusion of RASPR descriptors along with structural and physicochemical descriptors enhances the predictivity of the models.Conclusion
Solar energy is one of most important forms of renewable energy that meets the increasing demand of electrical energy. Various in silico approaches have been used to predict the power conversion efficiency (PCE) of DSSCs using structural and physicochemical features of dyes. In the present study, we have used RASPR descriptors along with 2D structural descriptors for the development of Partial Least Squares (PLS) and machine learning models of coumarin, carbazole, indoline and diphenylamine dyes. The developed q-RASPR models are statistically robust, and all the models show acceptable results for the internal validation and enhanced values of external validation metrics which indicate the importance of RASPR descriptors. The analysis of internal and external validation metrics of the developed q-RASPR models shows a surprising trend of better quality of predictions (in terms of MAE) for the test sets in comparison to the corresponding training sets which is contrary to the usual observations of better training set statistics than the corresponding test set statistics in case of QSAR models. This may happen due to a strange distribution of activity cliffs that for some reason affects the training set predictions more than the test set ones. This is indeed one of those strange (and rare) cases where the performances on the test set are better than on the training set. We have performed different cross-validation statistics to determine the quality of the developed model. We have also performed SHAP analysis on the training sets for all four datasets to determine the feature importance toward the endpoints. Using the developed and validated models, the PCE of a newly designed molecule can be determined before its synthesis, and it can save a lot of time, money, and resources. The software tools used for our work are easy to operate and most of them are freely accessible which make the modeling exercise simple and inexpensive. Hence, our developed models can give a direction for scientists and researchers present in different research areas or industrial organizations to design and synthesize new dyes. In this way, time, resources, and cost involved in the synthesis and experimentation can be reduced which may help to develop more efficient molecules.Data availability
The DTC Lab software tools are available from http://teqip.jdvu.ac.in/QSAR_Tools/(MLR BestSubsetSelection and MLR plus Validation), https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home (Quantitative Read-Across v4.1 and RASAR Descriptor Calculator v2.0), and https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home/machine-learning-model-development-guis (Machine Learning Model Development GUIs). The raw data files used to develop the models are provided in ESI.†Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. SP: computation, validation, software tool development, initial draft; AB: validation, editing, software tool development; KR: conceptualization, supervision, and editing.Conflicts of interest
There are no conflicts to delare.Acknowledgements
SP thanks the All India Council for Technical Education (AICTE), New Delhi for financial assistance. AB thanks Life Science Research Board, DRDO, New Delhi for a fellowship.References
- W. H. Chen and F. You, Sustainable building climate control with renewable energy sources using nonlinear model predictive control, Renewable Sustainable Energy Rev., 2022, 168, 112830 CrossRef.
- T. Z. Ang, M. Salem, M. Kamarol, H. S. Das, M. A. Nazari and N. Prabaharan, A comprehensive study of renewable energy sources: Classifications, challenges and suggestions, Energy Strategy Rev., 2022, 43, 100939 CrossRef.
- R. Venkateswari and S. Sreejith, Factors influencing the efficiency of photovoltaic system, Renewable Sustainable Energy Rev., 2019, 101, 376–394 CrossRef.
- P. Tonui, S. O. Oseni, G. Sharma, Q. Yan and G. Tessema Mola, Perovskites photovoltaic solar cells: An overview of current status, Renewable Sustainable Energy Rev., 2018, 91, 1025–1044 CrossRef CAS.
- S. Sharma, K. K. Jain and A. Sharma, Solar cells: In research and applications—A review, Mater. Sci. Appl., 2015, 06, 1145–1155 CAS.
- G. Nandan Arka, S. Bhushan Prasad and S. Singh, Comprehensive study on dye sensitized solar cell in subsystem level to excel performance potential: A review, Sol. Energy., 2021, 226, 192–213 CrossRef CAS.
- K. Sharma, V. Sharma and S. S. Sharma, Dye-sensitized solar cells: Fundamentals and current status, Nanoscale Res. Lett., 2018, 131, 1–46 Search PubMed.
- A. Baheti, K. R. Justin Thomas, C. T. Li, C. P. Lee and K. C. Ho, Fluorene-based sensitizers with a phenothiazine donor: Effect of mode of donor tethering on the performance of dye-sensitized solar cells, ACS Appl. Mater. Interfaces, 2015, 7, 2249–2262 CrossRef CAS PubMed.
- W. Zhang, Y. Wu, H. Zhu, Q. Chai, J. Liu, H. Li, X. Song and W. H. Zhu, Rational molecular engineering of indoline-based d–a–π–a organic sensitizers for long-wavelength-responsive dye-sensitized solar cells, ACS Appl. Mater. Interfaces, 2015, 7, 26802–26810 CrossRef CAS PubMed.
- S. Ekins, J. Mestres and B. Testa, In silico pharmacology for drug discovery: applications to targets and beyond, Br. J. Pharmacol., 2007, 152, 21–37 CrossRef CAS PubMed.
- S. Brogi, T. C. Ramalho, K. Kuca, J. L. Medina-Franco and M. Valko, Editorial: In silico methods for drug design and discovery, Front. Chem., 2020, 8, 612 CrossRef PubMed.
- B. Shaker, S. Ahmad, J. Lee, C. Jung and D. Na, In silico methods and tools for drug discovery, Comput. Biol. Med., 2021, 137, 104851 CrossRef PubMed.
- R. A. Lewis and D. Wood, Modern 2D QSAR for drug discovery, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 505–522 CAS.
- M. A. Lill, Multi-dimensional QSAR in drug discovery, Drug Discovery Today, 2007, 12, 1013–1017 CrossRef CAS PubMed.
- A. Banerjee, M. Chatterjee, P. De and K. Roy, Quantitative predictions from chemical read-across and their confidence measures, Chemom. Intell. Lab. Syst., 2022, 227, 104613 CrossRef CAS.
- M. Chatterjee, A. Banerjee, P. De, A. Gajewicz-Skretna and K. Roy, A novel quantitative read-across tool designed purposefully to fill the existing gaps in nanosafety data, Environ. Sci.: Nano, 2022, 9, 189–203 RSC.
- S. Dara, S. Dhamercherla, S. S. Jadav, C. M. Babu and M. J. Ahsan, Machine learning in drug discovery: A review, Artif. Intell. Rev., 2022, 55, 1947–1999 CrossRef PubMed.
- B. B. Goldman and W. P. Walters, Chapter 8. Machine learning in computational chemistry, Annu. Rep. Comput. Chem., 2006, 2, 127–140 CAS.
- L. Patel, T. Shukla, X. Huang, D. W. Ussery and S. Wang, Machine learning methods in drug discovery, Molecules, 2020, 25, 5277 CrossRef CAS PubMed.
- A. Lavecchia, Machine-learning approaches in drug discovery: methods and applications, Drug Discovery Today, 2015, 20, 318–331 CrossRef PubMed.
- S. Kar, J. K. Roy and J. Leszczynski, In silico designing of power conversion efficient organic lead dyes for solar cells using todays innovative approaches to assure renewable energy for future, npj Comput. Mater., 2017, 31, 1–12 Search PubMed.
- Y. Wen, L. Fu, G. Li, J. Ma and H. Ma, Accelerated discovery of potential organic dyes for dye-sensitized solar cells by interpretable machine learning models and virtual screening, Sol. RRL, 2020, 4, 2000110 CrossRef CAS.
- J. K. Roy, S. Kar and J. Leszczynski, Optoelectronic properties of c60 and c70 fullerene derivatives: designing and evaluating novel candidates for efficient P3HT polymer solar cells, Mater, 2019, 12, 2282 CrossRef CAS PubMed.
- A. Kumar and P. Kumar, Prediction of power conversion efficiency of phenothiazine-based dye-sensitized solar cells using Monte Carlo method with index of ideality of correlation, SAR QSAR Environ. Res., 2021, 32, 817–834 CrossRef CAS PubMed.
- H. Li, Y. Cui, Y. Liu, W. Li, Y. Shi, C. Fang, H. Li, T. Gao, L. Hu and Y. Lu, Ensemble learning for overall power conversion efficiency of the all-organic dye-sensitized solar cells, IEEE Access, 2018, 6, 34118–34126 Search PubMed.
- J. G. Krishna, P. K. Ojha, S. Kar, K. Roy and J. Leszczynski, Chemometric modeling of power conversion efficiency of organic dyes in dye sensitized solar cells for the future renewable energy, Nano Energy, 2020, 70, 104537 CrossRef CAS.
- J. K. Roy, S. Kar and J. Leszczynski, Electronic structure and optical properties of designed photo-efficient indoline-based dye-sensitizers with D–A–π–A framework, J. Phys. Chem. C, 2019, 123, 3309–3320 CrossRef CAS.
- S. Kar, J. K. Roy, D. Leszczynska and J. Leszczynski, Power conversion efficiency of arylamine organic dyes for dye-sensitized solar cells (DSSCs) explicit to cobalt electrolyte: understanding the structural attributes using a direct qspr approach, Computation, 2017, 5, 2 CrossRef.
- H. Li, Z. Zhong, L. Li, R. Gao, J. Cui, T. Gao, L. H. Hu, Y. Lu, Z. M. Su and H. Li, A cascaded QSAR model for efficient prediction of overall power conversion efficiency of all-organic dye-sensitized solar cells, J. Comput. Chem., 2015, 36, 1036–1046 CrossRef CAS PubMed.
- V. Venkatraman, M. Foscato, V. R. Jensen and B. K. Alsberg, Evolutionary de novo design of phenothiazine derivatives for dye-sensitized solar cells, J. Mater. Chem. A, 2015, 3, 9851–9860 RSC.
- V. Venkatraman and B. K. Alsberg, A quantitative structure-property relationship study of the photovoltaic performance of phenothiazine dyes, Dyes Pigm., 2015, 114, 69–77 CrossRef CAS.
- A. Banerjee and K. Roy, First report of q-RASAR modeling toward an approach of easy interpretability and efficient transferability, Mol. Diversity, 2022, 26, 2847–2862 CrossRef CAS PubMed.
- A. Banerjee, A. Gajewicz-Skretna and K. Roy, A machine learning q-RASPR approach for efficient predictions of the specific surface area of perovskites, Mol. Inf., 2023, 42, 2200261 CrossRef CAS PubMed.
- A. Banerjee, S. Kar, S. Pore and K. Roy, Efficient predictions of cytotoxicity of TiO2-based multi-component nanoparticles using a machine learning-based q-RASAR approach, Nanotoxicology, 2023, 17, 78–93 CrossRef CAS PubMed.
- S. Manganelli and E. Benfenati, Use of read-across tools, In Silico Methods for Predicting Drug Toxicity, ed. Benfenati E., Springer, Milan, Italy, 2016, pp. 305–322 Search PubMed.
- K. Roy, S. Kar and R. N. Das, Understanding the Basics of QSAR for Applications in Pharmaceutical Sciences and Risk Assessment, Academic Press, NY, 2015 Search PubMed.
- R. Todeschini and V. Consonni, Handbook of Molecular Descriptors, John Wiley & Sons, Germany, 2008 Search PubMed.
- A. Banerjee and K. Roy, Machine-learning-based similarity meets traditional QSAR:“q-RASAR” for the enhancement of the external predictivity and detection of prediction confidence outliers in an hERG toxicity dataset, Chemom. Intell. Lab. Syst., 2023, 237, 104829 CrossRef CAS.
- M. Goodarzi, B. Dejaegher and Y. V. Heyden, Feature selection methods in QSAR studies, J. AOAC Int., 2012, 95, 636–651 CrossRef CAS PubMed.
- M. Shahlaei, Descriptor selection methods in quantitative structure–activity relationship studies: a review study, Chem. Rev., 2013, 113, 8093–8103 CrossRef CAS PubMed.
- J. Vamathevan, D. Clark, P. Czodrowski, I. Dunham, E. Ferran, G. Lee, B. Li, A. Madabhushi, P. Shah, M. Spitzer and S. Zhao, Applications of machine learning in drug discovery and development, Nat. Rev. Drug Discovery, 2019, 18, 463–477 CrossRef CAS PubMed.
- M. I. Jordan and T. M. Mitchell, Machine learning: Trends, perspectives, and prospects, Science, 2015, 349, 255–260 CrossRef CAS PubMed.
- I. H. Sarker, Machine learning: Algorithms, real-world applications and research directions, SN Comput. Sci., 2021, 2, 160 CrossRef PubMed.
- A. Géron, Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow, O'Reilly Media, Inc., USA., 2022 Search PubMed.
- G. C. McDonald, Ridge regression, Wiley Interdiscip. Rev. Comput. Stat., 2009, 1, 93–100 CrossRef.
- R. Burbidge, M. Trotter, B. Buxton and S. Holden, Drug design by machine learning: support vector machines for pharmaceutical data analysis, Comput. Chem., 2001, 26, 5–14 CrossRef CAS PubMed.
- R. J. Chase, D. R. Harrison, A. Burke, G. M. Lackmann and A. McGovern, A machine learning tutorial for operational meteorology. Part I: Traditional machine learning, Weather Forecast., 2022, 37, 1509–1529 Search PubMed.
- T. Chen and C. Guestrin, Xgboost: A scalable tree boosting system, Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, 2016, pp. 785–794 Search PubMed.
- T. Kluyver, B. Ragan-Kelley, F. Pérez, B. E. Granger, M. Bussonnier, J. Frederic, K. Kelley, J. B. Hamrick, J. Grout, S. Corlay and P. Ivanov, Jupyter Notebooks-a Publishing Format for Reproducible Computational Workflows, 2016 Search PubMed.
- S. M. Lundberg and S. I. Lee, A unified approach to interpreting model predictions, Adv. Neural Inf. Process. Syst., 2017, 30, 4765–4774 Search PubMed.
- R. Rodríguez-Pérez and J. Bajorath, Interpretation of machine learning models using shapley values: application to compound potency and multi-target activity predictions, J. Comput.-Aided Mol. Des., 2020, 34, 1013–1026 CrossRef PubMed.
- A. Moncada-Torres, M. C. van Maaren, M. P. Hendriks, S. Siesling and G. Geleijnse, Explainable machine learning can outperform Cox regression predictions and provide insights in breast cancer survival, Sci. Rep., 2021, 11, 6968 CrossRef CAS PubMed.
- K. Roy and I. Mitra, On various metrics used for validation of predictive QSAR models with applications in virtual screening and focused library design, Comb. Chem. High Throughput Screening, 2011, 14, 450–474 CrossRef CAS PubMed.
- P. S. Gangadhar, A. Jagadeesh, M. N. Rajesh, A. S. George, S. Prasanthkumar, S. Soman and L. Giribabu, Role of π-spacer in regulating the photovoltaic performance of copper electrolyte dye-sensitized solar cells using triphenylimidazole dyes, Mater. Adv., 2022, 3, 1231–1239 RSC.
- P. S. Kalsi, Spectroscopy of Organic Compounds, New age international, New York, 2007 Search PubMed.
- W. C. Chen, S. Nachimuthu and J. C. Jiang, Revealing the influence of cyano in anchoring groups of organic dyes on adsorption stability and photovoltaic properties for dye-sensitized solar cells, Sci. Rep., 2017, 7, 1–13 CrossRef PubMed.
- L. Zhang and J. M. Cole, Anchoring groups for dye-sensitized solar cells, ACS Appl. Mater. Interfaces, 2015, 7, 3427–3455 CrossRef CAS PubMed.
- Y. Li, J. Liu, D. Liu, X. Li and Y. Xu, D–A–π–A based organic dyes for efficient DSSCs: A theoretical study on the role of π-spacer, Comput. Mater. Sci., 2019, 161, 163–176 CrossRef CAS.
- V. V. Divya and C. H. Suresh, Density functional theory study on the donating strength of donor systems in dye-sensitized solar cells, New J. Chem., 2020, 44, 7200–7209 RSC.
- B. G. Kim, K. Chung and J. Kim, Molecular design principle of all-organic dyes for dye-sensitized solar cells, Chem. - Eur. J., 2013, 19, 5220–5230 CrossRef CAS PubMed.
- O. Britel, A. Fitri, A. T. Benjelloun, A. Slimi, M. Benzakour and M. Mcharfi, Theoretical investigation of the influence of π-spacer on photovoltaic performances in carbazole-based dyes for dye-sensitized solar cells applications, J. Photochem. Photobiol., A, 2022, 428, 113870 CrossRef CAS.
- Z. Yao, M. Zhang, H. Wu, L. Yang, R. Li and P. Wang, Donor/acceptor indenoperylene dye for highly efficient organic dye-sensitized solar cells, J. Am. Chem. Soc., 2015, 137, 3799–3802 CrossRef CAS PubMed.
- Z. Yang, C. Shao and D. Cao, Screening donor groups of organic dyes for dye-sensitized solar cells, RSC Adv., 2015, 5, 22892–22898 RSC.
- A. Mahmood, Triphenylamine based dyes for dye sensitized solar cells: A review, Sol. Energy., 2016, 123, 127–144 CrossRef CAS.
- M. K. Hossain, M. F. Pervez, M. N. Mia, A. A. Mortuza, M. S. Rahaman, M. R. Karim, J. M. Islam, F. Ahmed and M. A. Khan, Effect of dye extracting solvents and sensitization time on photovoltaic performance of natural dye sensitized solar cells, Results Phys., 2017, 7, 1516–1523 CrossRef.
- L. Zhang and J. M. Cole, Anchoring groups for dye-sensitized solar cells, ACS Appl. Mater. Interfaces, 2015, 7, 3427–3455 CrossRef CAS PubMed.
- F. Ambrosio, N. Martsinovich and A. Troisi, What is the best anchoring group for a dye in a dye-sensitized solar cell?, J. Phys. Chem. Lett., 2012, 3, 1531–1535 CrossRef CAS PubMed.
- F. Xu, T. T. Testoff, L. Wang and X. Zhou, Cause, regulation and utilization of dye aggregation in dye-sensitized solar cells, Molecules, 2020, 25, 4478 CrossRef CAS PubMed.
- S. Wold, M. Sjöström and L. Eriksson, PLS-Regression: A basic tool of chemometrics, Chemom. Intell. Lab. Syst., 2001, 58, 109–130 CrossRef CAS.
- K. Roy, R. N. Das, P. Ambure and R. B. Aher, Be aware of error measures. Further studies on validation of predictive QSAR models, Chemom. Intell. Lab. Syst., 2016, 152, 18–33 CrossRef CAS.
- A. Banerjee and K. Roy, Prediction-inspired intelligent training for the development of c-RASAR models for organic skin sensitizers: Assessment of classification error rate from novel similarity coefficients, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-20v0k.
- P. Ertl and A. Schuffenhauer, Estimation of synthetic accessibility score of drug-like molecules based on molecular complexity and fragment contributions, J. Cheminf., 2009, 1, 8 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: SI-1 contains some details of different ML methods, different PLS model plots, cross-validation plots and SHAP plots. SI-2 contains raw data files in the Excel format. SI-3 contains SHAP partial dependence plots and a list of new designed dyes. See DOI: https://doi.org/10.1039/d3se00457k |
| This journal is © The Royal Society of Chemistry 2023 |