Emulsifying properties of plant-derived polypeptide and their conjugates: a self-consistent-field calculation study of the impact of hydrolysis

Abstract

By considering the hydrolysates of soy protein produced by trypsin as an example, the emulsion stabilizing properties of plant-based protein fragments have been investigated theoretically. We apply Self-Consistent-Field (SCF) calculations to determine the colloidal interactions induced between a pair of droplets stabilized by adsorbed layers of various soy protein fragments. The study is extended to conjugates of such polypeptides, formed by covalent bonding with a suitable hydrophilic sidechain (e.g. a polysaccharide). Our results show that the relatively longer fragments, with a greater number of hydrophobic amino acids, will display a stronger degree of adsorption affinity compared to the smaller hydrolysates, even where the latter may have a higher overall ratio of hydrophobic residues. This suggested that the degree of protein hydrolysis should be carefully controlled and limited to modest values to avoid the generation of a large number of short polypeptides, while still sufficient to improve solubility. While the emulsion stabilizing performance of a protein fragment type is strongly dependent on the conformation it adopts on the interface, we find this to be less critical for the conjugated polypeptides. However, we argue that with increasing degree of hydrolysis, many small fragments will not have the chance to form bonds with polysaccharides. It is demonstrated that the abundance of these unreacted polypeptides in the system severely reduces the efficiency of the conjugated longer protein fragments, preventing their presence on the surface of the droplets through competitive adsorption process.

---

1. Introduction

Oil-in-water (O/W) emulsion systems have applications in a wide variety of industrial fields. Formulations ranging from food products, pharmaceuticals, agrochemicals, cleaning consumables, cosmetics and personal care rely heavily on the use of O/W emulsions to deliver their desired functionality. This may involve encapsulating different active ingredients (e.g. vitamins, essential oils, drugs, flavors, pesticides) to improve their chemical and oxidative stability, their bioavailability, modulating their controlled release profile,^1–3 or simply to alter their rheological behavior (e.g. mouthfeel in foods).⁴

In addition to more conventional O/W emulsions, where dispersed oil droplets are stabilized by a molecularly adsorbed protective layer, a number of more novel designs for delivery of the required active substances include microemulsions, multiple emulsions, multilayer stabilized emulsions, high internal phase emulsions (i.e. HIPE), Pickering emulsions and emulsion gels. All of these have also received much attention in recent years.^3,5–8 Each of these systems displays its own distinct characteristics, advantages and disadvantages.

Animal proteins derived from milk, egg, and to a lesser extent meat, have proved to be very suitable biopolymeric emulsifiers, providing good emulsifying and emulsion stabilizing functionalities through a combination of steric and electrostatic mechanisms.^6,7,9 These emulsifiers are particularly relevant to food systems where the choice of using edible synthetic alternatives is very limited. Nonetheless, despite being renewable, the fact that such proteins are derived from animals has raised questions over their “green” credentials, and their continued sustainable use in food and a few other related industries. This has inspired a great number of researchers in recent years to consider the possibility of replacing these animal-derived proteins with plant-based ones, especially those that also offer a good source and balance of amino acids, such as soy and pea proteins.^10–14 These plant proteins have already been shown to act as a good candidate for formulating Pickering-type emulsion systems, where the highly aggregated nature of plant storage proteins lends itself well to creating protein particles for this purpose.^15–18 An alternative strategy, sometimes referred to as “Mickering emulsions”, sets to deliberately produce small soft solid particles that are basically protein gel networks formed by cross-linked biopolymer matrices via “bottom-up” or “top-down” routes.^8,14,19,20 Once again, the so formed microgel particles adsorb at the surface of oil droplets and aid their colloidal stability. This Pickering-type approach to using plant-based proteins as emulsifiers has seen a significant level of interest in the past few years. It has been the subject of many studies involving novel delivering vehicle. This is, at least in parts, due to the extraordinary stability that Pickering emulsions offer against coalescence, as well as their potential for tailoring lipid digestion in human gastrointestinal tract.^21,22

When viewed in the context of non-Pickering type emulsions, where fine well-dispersed submicron-sized droplets and a low viscosity liquid emulsion is desired, plant-sourced storage proteins exhibit rather low emulsifying capacity, as compared to the animal-derived ones such as casein and milk whey protein. This is mainly attributed to the limited solubility and complex aggregated properties of plant proteins, which in turn places a major obstacle to successful use of these proteins as effective molecularly adsorbed emulsifiers.^9,14,20 In order to overcome this issue, hydrolysis of plant proteins by enzymes has been suggested. This is proven to be a safe, economical and effective strategy to produce protein fragments with significantly improved solubility, and thus also often superior emulsifying abilities than the original intact proteins.^6,20,23 Moreover, compared to native proteins from which they are derived, fragmented plant proteins also seem to be more suitable for synthesizing conjugates with polysaccharides via Maillard reactions. Such conjugates are produced when covalent bonds are formed between protein fragments and the polysaccharides. This approach has been widely investigated in the literature. It has been demonstrated as a successful strategy in strengthening steric stabilization properties of the resulting molecules. The advantages of such conjugates are particularly noticeable in maintaining emulsion stability under harsh environmental processing conditions such as acidic pH, high ionic concentrations, or freeze–thaw cycles.^{10,12,24–27}

A large body of work has shown that the hydrolysis conditions, mainly the degree of hydrolysis (DH) and the type of enzymes with different levels of selectivity towards peptide bonds are the governing factors in determining the emulsification-related functionalities of generated polypeptides.^23,28 For example, a relatively low degree of hydrolysis at 4% was found to produce polypeptides that were best at maintaining the stability of O/W emulsions, superior to intact native Fava bean protein isolate or those that had undergone extensive hydrolysis with higher DH values of 9% and 15%.²⁹ Similarly, our own previous study¹³ involving polypeptides derived from soy protein and conjugated with maltodextrin, also provided evidence that a moderate hydrolysis with DH = 8% was desirable for improving the emulsifying capacities of soy proteins. Nonetheless, those beneficial effects become less prominent if soy protein is hydrolyzed further (DH > 8.0%). More evidence in support of this view have also been presented for hydrolysis of barley malt protein,³⁰ soy protein³¹ and even fish and other animal-based proteins.^32,33 With regards to the nature of enzyme, the study of Tamm et al.³⁴ and our previous work¹³ both highlighted that highly selective enzyme trypsin produced protein fragments with much superior emulsifying properties, in comparison to a less selective enzyme such as alcalase.

The above results have led to a more or less accepted view this days that limited hydrolysis can improve the emulsifying characteristics of proteins (particularly the less soluble storage plant-proteins), whereas too high a DH is usually not conducive for this purpose.²⁸ The plausible reason for this is that hydrolysis improves solubility of the proteins, a key consideration for possessing good emulsifying properties.^13,35 However, extensive fragmentation leads to relatively short polypeptide chains. These are not capable of providing the necessary steric repulsion needed for keeping the emulsion droplets well dispersed, even if they were extensively adsorbed at oil–water interfaces.³⁶ Despite the consensus, it must also be mentioned that there are several notable exceptions to the above studies. Some researchers have reported that increasing DH can continue to improve emulsifying characteristics of the hydrolysates even for very short polypeptide chains (although DH was still maintained down at quite low values in these studies),³⁷ whereas others observed that from the very onset hydrolysis proved detrimental.³⁸ The impacts of enzyme selectivity and the level of hydrolysis on the emulsifying behavior are closely related to the structural characteristics of the polypeptides generated, such as their molecular size and the degree of hydrophobicity.^13,28,29 However, due to the large number of cleavable sites on plant proteins vulnerable to attack by enzymes, experimental investigations tend to be based on a highly heterogeneous system where a large diversity of protein fragments are simultaneously present. The number of potentially different fragments arising from possible cleavage of m susceptible bonds during partial hydrolysis scales as ∼m². For examples, Ettelaie and Zengin have calculated that partial hydrolysis of α_s1-casein by trypsin, involving only 14 possible cleavable sites, can generate up to 253 distinct polypeptide types.³⁹ For less selective enzymes acting on larger plant-proteins, the number can be much higher. The abundance of these fragments in the final distribution rapidly alters with degree of hydrolysis (DH). The sensitivity and the difficulty of maintaining DH to a very high level of precision, coupled with the large multitude of polypeptides present in the distribution of hydrolysates, make the interpretations obtained from these experiments and any definitive conclusions rather hard to ascertain. One possible approach is to examine experimentally suggested hypothesis against theoretical and computer simulation studies. Such work can greatly simplify the situation and leads to a more unique insight by providing a better control over the distribution of hydrolysates, as for example one can achieve by focusing attention directly on the behavior of a few more prominent polypeptide fragments in the distribution.

In the current paper, we take soy protein as a well-known and widely used architype example of plant-based proteins. We use the numerical self-consistent-field (SCF) approach, and in particular the well-known Scheutjens–Fleer Scheme^40–42 for its implementation, to theoretically investigate surface adsorption behavior of polypeptides. We do so for fragments both prior and after they are conjugated with maltodextrin. A brief introduction to SCF calculations, including its advantages and limitations, and a more detailed account of the model for these polymeric systems are given in the next section, as well as in the ESI,† Section S1. In Section 3, we discuss two aspects of the interfacial and colloidal performances of these natural polymers. The first of these concerns an analysis of the influences of the structural attributes (e.g., size and degree of hydrophobicity) on the emulsifying and emulsion stabilizing behaviors of hydrolyzed proteins. This allows one to examine the role that the degree of hydrolysis (DH) plays in producing polypeptide fragments that are suitable molecular emulsifying agents. In the next stage, we consider the situation where fragments are assumed to be covalently bonded with maltodextrin (as can be obtained via Maillard reactions in practice and discussed in our previous work¹³). In a distribution involving a large number of small polypeptides, one may expect that many fragments will remain unconjugated. Just by the law of averages, a short polypeptide fragment is less likely to contain lysine residues (which are the reactive sites for bonding with maltodextrin) than one of its longer counterparts. The presence of such small, unbonded polypeptides in the system can serve to displace the larger, more desirable, conjugated chains away from oil–water interfaces. This in turn leads to the destabilization of the droplets. This scenario can be tested theoretically by considering a mixture of conjugated larger polypeptides and unbonded shorter ones, with both set of fragments being plausible derivatives from hydrolysis of soy β-conglycinin. The current work aims to offer useful understanding on the role of DH in producing conjugated protein fragments with optimal colloidal stabilizing performances.

Finally, it must be stressed that our attention here is solely on molecularly adsorbed layers. However, experimentally it is also possible to use both the intact plant-based proteins, as well as their hydrolysates, to form aggregated (or alternatively microgel) particles. A theoretical study of the surface behavior of these particulate types of Pickering emulsifiers will require different numerical or computer simulation techniques than SCF calculations, and therefore remains beyond the scope of this study. Nonetheless, a comparative study of the current work with such future research, performed for the same plant protein material, remains an interesting proposition to explore in future.

2. Methodology

2.1 SCF calculations applied to adsorbed interfacial layers

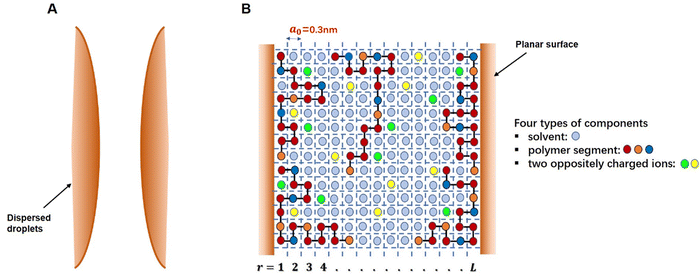
The self-consistent field (SCF) calculations in this project are performed by implementing the well-known Scheutjens–Fleer scheme.^40,41 The adaptation and the application of this method to problems involving models of coil-like disordered proteins was first introduced by Leermakers et al.⁴³ and Dickinson et al.^44,45 The predicted results in terms of the structures of interfacial layers formed by α_s1-casein and β-casein in these early studies were shown to be in good qualitative agreement with the data from neutron reflectometry experiments.^46–48 The theoretical results also provided a clear explanation for the observed differences in the colloidal stabilizing behavior of the two studied milk proteins.^44,45 The SCF calculations have also been successfully extended to a variety of other colloidally related interfacial materials, such as surface layers consisting of mixed biopolymers,^49,50 proteins + surfactants layers,⁵¹ protein–polysaccharide conjugates⁵² and to the study of fragmented proteins.³⁹

As with any numerically implemented method, the Scheutjens–Fleer scheme for performing the SCF calculations begins by discretizing the region of interest into a 3D grid (here taken to be a regular lattice). Fig. 1 provides a schematic 2D illustration of the model. Two interfaces, representing parts of the surfaces of two approaching droplets, are modelled as two parallel planar planes. The space in the gap between the planes is divided into layers parallel to the surfaces (r = 1, 2, 3, … L), each with a thickness equal to the size of a monomer, a₀. The layers are further subdivided into equal-sized cubic cells. For simplicity, all monomers (i.e. amino acid or glucose residues) making up the protein conjugated chains, as well as any ions or solvent molecules, are assumed to have the same nominal size. This size is chosen as the length of a peptide bond a₀ ∼ 0.3 nm.^39–41,50 Each monomer occupies a single lattice site, and all the sites are required to be occupied by either a polymer segment, an ion or a solvent molecule. The excluded volume (i.e. the fact that one monomer cannot reside on a lattice site already occupied by another monomer) is accounted for within SCF theory by imposing a constraint in the calculations where the sum of the average volume fractions of all monomer species at each lattice site has to add up to exactly 1. In particular, the presence of excluded volume constraints gives rise to increased exclusion of solvent from regions of higher polymer concentration, and the presence of more solvent where the polymer is depleted. When this is predicted to occur in the gap between the droplets, it immediately leads to induced repulsive or attractive interactions between the pair. The forces arise from the resulting osmotic pressure difference between the regions inside the gap and those in the rest of bulk solution.^53,54

Fig. 1 (A) A Schematic illustration of two approaching interfaces and the gap between them. (B) Magnified two-dimensional lattice model representation of the space between the surfaces and the modelling of different species occupying the gap, as used in SCF calculations.

An important initial step in performing the SCF calculations is the derivation of a coarse-grained free energy functional, F({ϕ^α(r)}),expressing the free energy change in the system in terms of variation of the concentrations of different species (polymer chains, solvent and ions), {ϕ^α(r)}, across the gap between the two surfaces. This requires a mathematically involved statistical mechanics averaging over all the position of various species that lead to ({ϕ^α(r)}).^55–57 The essential aim of self-consistent field (SCF) calculations from this point onward is to determine the most probable macrostates (i.e. set of density profiles for polymers, solvent and ions, in the gap between the pair of planar surfaces). Such states will be the ones that minimize the free energy F({ϕ^α(r)}) of the system. Note that because in our lattice model the grid size was chosen as the size of a monomer, the concentration or density for a certain type of monomer at any point is actually the same as its volume fraction there. Furthermore, given that the environment of all the lattice sites within a layer (i.e. all sites at the same perpendicular distance in the gap, away from the surfaces) is the same (see Fig. 1), the density of the monomers of a certain group α would be uniform within the layer. The density profile will only vary in a direction perpendicular to the two interfaces and not parallel to them.^39,50,58 Thus, the variations in the concentration of any type of monomers can be expressed as a function of the perpendicular distance r away from one or the other planar surface, ϕ^α(r), as already indicated.

Each possible set of concentration profile variation in the gap has a certain free energy associated with it. This determines the likelihood for the occurance of that profile. Therefore, strictly speaking, the thermodynamic quantities of interest need to be averaged over all possible variations in the density profiles, each weighted in accordance to their own probability of occurrence as determined by the appropriate Boltzmann factor ∼exp(−F({ϕ^α(r)})/k_BT). Unfortunately, the task of conducting this averaging over all sets of density profile variations is not feasible, and resort to suitable approximations needs to be made. SCF calculations, in line with other mean-field type theories, adopts the approximation that the average value of any quantity of interest is dominated by the most probable set of concentration profiles in the system, with the fluctuations around this set sufficiently small to be ignored.^39,57,59 The assumption becomes increasingly more valid for systems where adsorbed polymers form denser interfacial layers on the surfaces, as is the case in this study.^39,50,60

The concentration profiles of different monomer species are influenced by a variety of interactions between monomers in the system, including the short-ranged hydrophobic interactions, hydrogen bonds and longer-ranged electrostatic (coulombic) interactions. In SCF calculations, the net result of these interactions, as experienced by a monomer positioned at a given location, is represented by an “effective field” acting on it at that point. This field will of course vary from layer to layer. It will depend on the local environment and abundance of other species at the same and in the neighboring layers. As these fields are themselves related to how various molecules are distributed in the space between the two planar surfaces, they are not available or determined in advance. In other words, neither the distributions of different species nor the interacting fields resulting from them are known a priori. In order to overcome this issue, an iterative process is performed. Briefly, the iteration begins by choosing a rough trial set of interacting fields. Then the concentration profiles of various species are calculated under the influence of these fields. From the resulting computed concentration profiles, an improved set of fields are then obtained and employed to work out an updated set of concentration profiles. The procedure is repeated and is only terminated when the concentration profiles and the fields no longer change substantially with any further iterations. At this point, the calculations have converged, and the density profiles thus obtained can be shown to represent the desired most probable profiles, i.e. the ones that minimize the functional F({ϕ^α(r)}), subject to the solution incompressibility condition. The calculations can be performed for a series of separation distances between the two surfaces, to obtain the variations of free energy as a function of separation distance. This also provides the interactions between the two plates induced by the presence of adsorbed polymer layers. When further combined with the more direct attractive van der Waals interactions, the total colloidal interaction potential between two dispersed droplets, coated with polymers, is obtained. The graphs of the total colloidal interaction potentials (induced by adsorbed polymers on the surface of droplets), allow for a theoretical examination of the colloidal emulsion stabilizing ability of a particular polymer/protein to be made. The procedure for performing the above calculations and the iteration process is discussed in many excellent books, reviews and papers,^42,61,62 and in some of our own work.^52,63 As such, only a brief overview is provided here in the ESI,† Section S.1.

An important final point to make is that the SCF calculations only predict the equilibrium properties of a dispersed system, without considering any kinetic factors. Kinetics of adsorption can be important in a number of circumstances and especially during the formation of the emulsion droplets. This must be studied through more detailed but also time-consuming techniques such as those involving molecular dynamics simulations, if required.

2.2 Models

This section describes how the protein, polysaccharide and the covalent conjugates formed from them are modeled and represented in our SCF calculations. All the protein fragments appearing in our theoretical study are derived from soybean β-conglycinin α′ subunit. The primary structure of this protein chain, referred to as GLCAP-SOYBN (P11827), can be found in the database UniProt.⁶⁴ GLCAP-SOYBN (P11827) consists of 621 amino acid residues. To ensure that any fragment considered is a viable one with a realistic chance of appearing in a real hydrolyzed system, we apply ExPASy PeptideCutter Tool⁶⁵ to GLCAP-SOYBN (P11827), using trypsin as the enzyme, to predict the possible polypeptide fragments arising from the action of this enzyme. Trypsin is chosen here because our previous experimental work showed that soy-derived protein fragments, obtained under the influence of the selective enzyme trypsin, exhibited much better emulsifying and stabilizing properties than other more indiscriminate enzymes.¹³ Furthermore, the high selectivity of this enzyme towards the breakage of only a small subset of polypeptide bonds somewhat limits the variety of possible polypeptides that can be produced. This is helpful when we come to choose some of these as examples to consider in the current theoretical study.

In line with convention, the generated polypeptides will be referred to by stating the amino acid residues at both ends of a fragmented chain, starting with the one closest to the N-terminus side of the intact protein. In a practical situation, enzyme hydrolysis would produce many different types of polypeptides with a wide distribution of molecular sizes, as well as varying degrees of hydrophobicity, even for a relatively selective enzyme such as trypsin. A full theoretical representation will need to reflect all such chains, and furthermore, each in the correct fraction appropriate at any given degree of hydrolysis. However, to gain an insight into the effect of the simultaneous presence of small and large polypeptides on the emulsification ability of hydrolyzed protein, it suffices to only take a few typical pieces or sets of protein fragments in the study. We assume that these fragments, once generated, can be separated from the rest of the hydrolysates. The separation, at least in parts, can be achieved using filtration processes based on the molecular weight and/or hydrophobicity of chains, thus narrowing the subset of generated fragments under study. However, a discussion of the non-trivial practical issues associated with such separation are beyond the scope of the present work and will be addressed elsewhere.

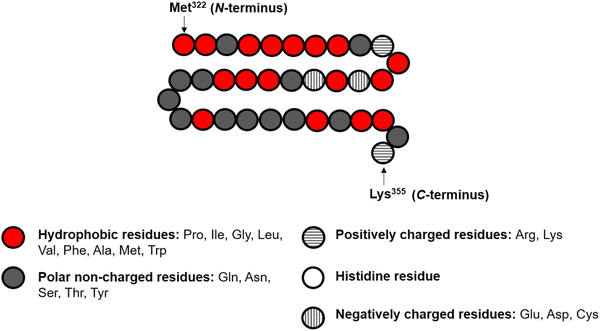
In the theoretical model system, in its simplest form (Fig. 1), there are four types of components present: solvent, polymers and two oppositely charged ions. An amino acid residue of a protein fragment, a glucose segment of maltodextrin, an ion or a solvent molecule are all taken to have a nominal size a₀ (i.e. the size of a lattice site in our calculations). Following Leermakers et al.,⁴³ the amino acid residues of the protein chains are grouped into five sets based on their degree of hydrophobicity, the nature of charge and the value of their pK_a. These are (1) hydrophobic, (2) polar but non-charged, (3) positively charged (under neutral pH), (4) histidine and (5) negatively charged (under neutral pH). Histidine is placed in a group of its own due to its rather different pK_a value compared to all the other positively charged amino acid residues. This classification of amino acids and the primary structure of a polypeptide containing 34 amino acid residues (i.e. Met³²²–Lys³⁵⁵), derived from soy β-conglycinin α′ subunit (P11827), are illustrated in Fig. 2 as an example.

Fig. 2 Representation of the primary structure of soy protein derived fragment Met³²²–Lys³⁵⁵ in our SCF calculations, with its various amino acid monomers assigned to one of the five designated groups.

The non-charged linear polysaccharide maltodextrin DE16.5–19.5 (M_w = 8.7 kDa), used in our previous experimental work,¹³ is considered to be made up of monomers belonging to a sixth separate category of their own. These sugar moieties are modeled as uncharged hydrophilic monomers. In accordance with its molecular weight, the maltodextrin DE16.5–19.5 (M_w = 8.7 kDa) consists of roughly 50 monomers. For modelling a protein–polysaccharide conjugate, the primary structure of the protein moiety is kept the same. The only difference is that now this is taken to be covalently bonded to polysaccharide chain, along the same lines as the model used in SCF calculations of Akinshina et al.⁵² The attachment to maltodextrin is either at a lysine site, or the residue at the N-terminus end of the polypeptide. These are sites where a covalent bond between protein and polysaccharide can form in practice during Maillard reactions.^66–68 Of course, a protein chain can in principle have many lysine sites and therefore can form bonds with more than one maltodextrin molecule. While it is possible to include this possibility in our model, in the presence of many small, fragmented chains, it is expected that there will be an excess of polypeptide chains relative to maltodextrin (in terms of molar ratio). Therefore, many fragments will not have the chance to form a covalent bond, and those that do are unlikely to have bonds with more than one maltodextrin chain. Hence, the probability of simultaneous attachment to several maltodextrin molecules can safely be neglected under these circumstances.

Finally, there are also positive and negative ions present in the theoretical model system. These constitute the last two categories, different from the other six groups mentioned so far.^50,52 The electrolyte here is taken to be of a simple monovalent type, e.g. NaCl. The presence of ions in the model, gives one the flexibility to adjust the background ionic strength in the study, where this is required.

The chemical nature of monomers in each group in our model is dictated by their interactions with monomers from other groups, as well as those with the solvent molecules and with the hydrophobic surfaces. The short-ranged parts of such interactions are reflected in a set of Flory–Huggins χ parameters. The values of these χ parameters are adopted from previously published work,^43,50,52 and are listed in Table 1. A positive value of χ indicates an unfavorable interaction between two different monomer sets, while a negative value signifies a favorable one, whenever the monomers are in proximity of each other, i.e. in the same or in adjacent layers. A χ parameter of −2k_BT between a hydrophobic residue (group 1 in the classification) and the surface is a typical value for the adsorption energy of a hydrophobic monomer onto such an O/W interface.⁵⁰ With no specific affinity for adsorption to the surface, monomers from all the other groups (including the ions and solvent molecules) have their interaction χ parameter with the surface set to be 0k_BT for simplicity.^50,52 The tendency of ions for hydration by solvent molecules (assumed to be water), is accounted for by the interaction parameter χ = −1k_BT, favoring a contact between the two, up and above that of solvent molecules with themselves.^39,52 Furthermore, the longer-ranged electrostatic interactions between various charged monomer groups, as determined by Coulomb's law, are explicitly taken into account in the model (see ESI,† Section S.1).

Table 1 The list of the Flory–Huggins interaction parameters (in units of k_BT) assigned between different types of monomers, as well as the value of pK_a for the charged amino acid groups. The numbers (0 to 8) in this table indicate the nine types of monomer sets in the model system: solvents (0), five groups of amino acid residues (1 to 5), glucose residues of maltodextrin (6) and positive and negative salt ions (7 and 8)

Monomer type	0	1	2	3	4	5	6	7	8
0-Solvent	0	1.0	0	0	0	0	0	−1.0	−1.0
1-Hydrophobic	1.0	0	2.0	2.5	2.5	2.5	2.5	2.5	2.5
2-Polar non-charged	0	2.0	0	0	0	0	0	0	0
3-Positively charged	0	2.5	0	0	0	0	0	0	0
4-Histidine	0	2.5	0	0	0	0	0	0	0
5-Negatively charged	0	2.5	0	0	0	0	0	0	0
6-Glucose residues	0	2.5	0	0	0	0	0	0	0
7-Positive ions	−1.0	2.5	0	0	0	0	0	0	0
8-Negative ions	−1.0	2.5	0	0	0	0	0	0	0
Surface	0	−2.0	0	0	0	0	0	0	0
pKa values				10	6.75	4.5

---

It is well known that the affinity of amphiphilic polymeric molecules including proteins, for adsorption to hydrophobic interfaces tends to be very high, as characterized by their very large effective Henry's adsorption constants.⁶⁹ Therefore, in a well-formulated protein stabilized emulsion, where excessive amount of emulsifier is undesirable, most of the protein will tend to adsorb onto the surface of emulsion droplets. The amount remaining in the bulk solution is often a very small fraction of the total protein in the entire system.³⁹ The densely adsorbed protein layers are in equilibrium with this very dilute solution. To reflect this, unless stated otherwise, the volume fraction of polymers in bulk solution is set to a low value of Φ_p = 1.0 × 10⁻¹⁰ for all the cases studied. We find that even at these low levels the protein coverage of the hydrophobic surface has already attained its saturation value. Any further increase in bulk concentration does not substantially alter the adsorbed amount. To emphasis then, a small value of Φ_p does not necessarily indicate a low emulsifier content in the whole system. The electrolyte volume fraction is maintained throughout this study at Φ_s = 0.01 (roughly corresponding to a concentration of 100 mM for NaCl). The environmental pH is fixed at a value close to the isoelectric point (IEP) of each protein fragment under investigation. This minimizes the electrostatic forces and allows one to explore the repulsion arising purely from the steric component. The situation considered then represents the worst-case scenario for each of our studied emulsifier protein fragments. As one may expect, the performance of each fragment improves further, once pH is altered away from its IEP.

3. Results and discussions

This study, from a theoretical viewpoint, looked at the real situation where Maillard conjugates are prepared from soy protein and maltodextrin and are used to stabilize a conventional O/W emulsion. All results are therefore generated for droplets of typical size 1 μm.

We follow the common practice in the literature that protein is hydrolyzed first before conjugation with polysaccharide is performed.^13,25,70 During hydrolysis by enzymes, multitudes of polypeptides with various structural attributes are generated and will co-exists in the system. We first explore the role of the size, degree of hydrophobicity and the conformation adopted by a fragment at the interface, in determining the type of interactions that the chain would induce between droplets. If the hydrolysis proceeds to a high level, there will be an increasing number of small polypeptides generated. Many of these relatively small polypeptides will not contain any lysine residues on their primary structures. This provides them with less of an opportunity to form covalent bonds with maltodextrin. Therefore, in the next part of our theoretical examination, we consider how the presence of these unconjugated small polypeptides would alter the colloidal stability of the emulsion. We will focus on the competitive adsorption between these small unbonded protein chains and large conjugated fragments, when they are both simultaneously present in the system.

In order to achieve the above objectives, five different polypeptides were carefully chosen from the selection of fragments that can realistically arise in partial hydrolysis of soy protein by trypsin. The characteristic properties of these selected polypeptides, including their size, degree of hydrophobicity and isoelectric point, are given in Table 2. This selection of polypeptides shows a reduced proportion of hydrophobic residues as their size grows. This is due to the fact that naturally derived proteins have hydrophobic and hydrophilic amino acid residues that are more or less evenly distributed along their backbone. Therefore, there is less of a chance for a long fragment to comprise of a large proportion of either hydrophobic or hydrophilic residues than a smaller one. In such a case, we deliberately selected one short and very hydrophobic fragment (Met³²²–Arg³³⁴) as a representative of small polypeptides, given that more hydrophilic short chains have a tendency not to adsorb to hydrophobic interfaces. Despite the limited choice of just five fragments, this still serves our goal of evaluating the importance of different structural attributes of the derived polypeptides on their emulsion stabilizing properties. In other respects, this selection of fragments is also a very good representation of produced chains, exhibiting various sizes, ratios of hydrophobic to hydrophilic amino acids and arrangements of different residues leading to different levels of “blockiness” (in terms of hydrophobic blocks). Furthermore, for the ease of demonstration, these fragments were chosen as they also have similar isoelectric points (between pH 5.0–6.0). Nonetheless, our data (not shown here) also indicate that the following discussion and resulting conclusions are largely applicable to situations where the protein fragments have different IEP values. Some additional data on a number of other fragments have also been included in the ESI,† Fig. S.1.

Table 2 The characteristic properties of the selected trypsin induced soy protein fragments, chosen for investigation in our study

Characteristics	Met^322–Arg^334	Met^322–Lys^355	Asn^356–Arg^425	His^160–Arg^290	Glu^93–Arg^302
Total number of amino acids	13	34	70	131	210
Number of hydrophobic residues	9	18	25	38	58
Hydrophobicity
(% of hydrophobic residues)	69.2%	52.9%	35.7%	29.0%	27.6%
Isoelectric point (pI)	5.5	6.0	5.0	6.0	5.5

---

3.1 Emulsion stabilizing capacity of protein fragments with different structural properties

3.1.1 Examination of the induced interaction potentials. One way to gain a theoretical insight into the colloidal stabilizing ability of a polymer is to examine the variation of the interaction potential induced by the adsorbed layers of the polymer between a pair of emulsion droplets. An increasing value of the interaction potential, with growing separation distance between droplets, indicates an overall attractive force. The converse implies the existence of a repulsive force at that separation. Consequently, droplets tend to remain around positions where no force is acting on them, i.e. at distances corresponding to the minimum in potential energy. This state is reflected by the depth of an energy well in the graph of the induced interaction potential, when plotted as a function of separation distance.^71,72 The absence of an energy well, or a sufficiently shallow (compared to say 10k_BT) well, indicates emulsifiers with a reasonable ability to ensure colloidal stability against aggregation.

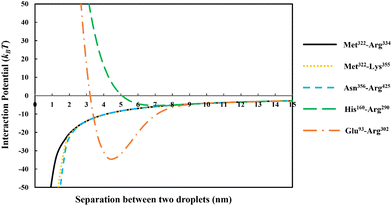
In Fig. 3 we have compared the total interaction potential induced between two oil droplets, when stabilized by each of our five selected soy protein fragments. The bulk pH value is set to 5.5, which is close to the IEP of all the polypeptides (see Table 2). The induced interaction potentials mediated by absorbed layers of the three relatively short fragments (i.e., Met³²²–Arg³³⁴, Met³²²–Lys³⁵⁵ and Asn³⁵⁶–Arg⁴²⁵) all look similar. In particular, no energy barrier is seen in any of these interaction potential curves to prevent the close approach of two droplets. This type of profile indicates the dominant role of attractive forces and a lack of the ability of the emulsifier to provide sufficient repulsion. As will be discussed in the following sections, the attraction is only in parts due to the direct van der Waals forces, but also has a component arising from the bridging effect of adsorbed fragments. With nothing hindering their eventual contact with each other in these cases, the prediction is that there will be severe flocculation of emulsion droplets (followed by their likely coalescence).

Fig. 3 The interaction potentials, plotted against the inter-droplet separation distance, resulting from the overlap of adsorbed layers of five different soy-derived polypeptides (i.e. Met³²²–Arg³³⁴, Met³²²–Lys³⁵⁵, Asn³⁵⁶–Arg⁴²⁵, His¹⁶⁰–Arg²⁹⁰ and Glu⁹³–Arg³⁰²) respectively. The diameter of oil droplets was taken as 1 μm. The results are produced at a background electrolyte volume fraction of 0.01 (roughly equals to 100 mM NaCl) and at pH = 5.5. The more direct van der Waals attraction between the droplets have also been included in these calculations.

For the inter-droplet potential that is generated by the adsorbed fragment Glu⁹³–Arg³⁰² (see Fig. 3), it is also seen that the attraction dominates as droplets approach each other. Only at very close inter-droplet separations, the induced repulsive force manages to overcome the attraction. The net result is the presence of a deep energy minimum well (∼−33k_BT) at a droplet–droplet separation distance of around 4.2 nm. Given the depth of this well, it is unlikely that the Brownian motion of droplets, or even agitation through simple shear, can disperse the droplets once trapped in this energy minimum. Once again, in this system, the droplets are predicted to undergo severe flocculation.^35,39 Flocculated droplets, involving molecularly adsorbed emulsifier films, have in turn a greatly enhanced chance of coalescing, with the emulsion system eventually breaking up as a result.

In contrast to the above predictions, there is barely a detectable energy well (depth less than 5k_BT) in the interaction potential of emulsion droplets when stabilized by soy fragment His¹⁶⁰–Arg²⁹⁰ (see Fig. 3). The droplets are seen to experience a progressively stronger repulsion with decreasing separation, at all distances of less than 6 nm. Therefore, unlike the other polypeptides discussed so far, this fragment is expected to impart sufficient colloidal stability to the droplets.

3.1.2 Typical conformation of fragments adsorbed at interfaces. The interaction potential profile between two approaching droplets coated by an amphiphilic polymer is the result of the overlap of the layers. Therefore, examining possible conformations taken by the polymer, when adsorbed on an interface, can be useful in understanding the nature of mediated forces. In Fig. 4 we present the average distance away from the interface for each of the monomer residue of our five chosen protein fragments, when they are adsorbed on a single isolated surface. Monomers of each fragment are assigned a sequence number along its backbone, counting from its N-terminus side. It is observed that all our three relatively short soy protein derived polypeptides, i.e. Met³²²–Arg³³⁴, Met³²²–Lys³⁵⁵ and Asn³⁵⁶–Arg⁴²⁵, lie almost flat at the interface when adsorbed. This is due to their primary sequence being comprised of multiple short hydrophobic and hydrophilic blocks. The presence of these short blocks prevents the chains from extending too far away from the surface,^63,73 leading to thin interfacial films. Indeed, the average position for any of the residues of these fragments are found not to exceed much beyond one monomer size a₀ away from the surface. This clearly demonstrates exactly how flat these fragments are lying on the surface. On the other hand, it is seen that the protein fragment His¹⁶⁰–Arg²⁹⁰ adopts a di-block-like configuration, with its N-terminus end extending away from the surface by ∼4.5a₀. This is the origin of the strong, and more importantly longer-ranged, steric repulsion as previously seen in Fig. 3. This repulsive force arises when interfacial layers on neighboring emulsion droplets overlap. Finally, the largest of our chosen protein fragments, i.e. Glu⁹³–Arg³⁰², behaves much more like a triblock-like polymer when adsorbed at the interface. This polypeptide has a central block consisting mostly of hydrophilic amino acids, in a fashion reminiscent of milk protein α_s1-casein. This central part tends to form a loop protruding away from the surface of the droplet, thus helping to form a more extended interfacial layer. The fragment Glu⁹³–Arg³⁰² is also able to adopt a bridging conformation, at certain ranges of inter-droplet separation distances. In such a configuration, the two hydrophobic ends of the protein fragment are adsorbed onto two separate but adjacent droplets. This results in an attractive force between the droplets over those separations. The net result is not desirable for the stability of the droplets against flocculation.^50,52,63,73 As mentioned, this situation is quite similar to the behavior of α_s1-casein, which is also known to be capable of inducing bridging flocculation of droplets.^44,45

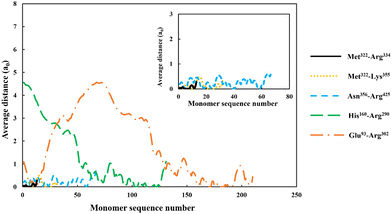Fig. 4 The average distance of each monomer residue, making up the adsorbed soy-derived fragments shown in Table 2, measured perpendicularly away from a hydrophobic surface. The distance (in units of monomer size), is plotted against the sequence number of monomers, starting with the first monomer at N-terminus end of a protein fragment. The inset shows a magnified version of data for the three shorter polypeptides, Met³²²–Arg³³⁴, Met³²²–Lys³⁵⁵ and Asn³⁵⁶–Arg⁴²⁵. All the results were obtained at a background electrolyte volume fraction of 0.01 (roughly equals to 100 mM NaCl) and at a solution pH = 5.5.

3.1.3 Interfacial structure and surface affinity. The conformations adopted by polymers at the interface are closely related to the film thickness and interfacial structure that is formed by the adsorbed layers of those polymers. In Fig. 5, the calculated density profiles for each protein fragment, when adsorbed on an isolated interface, have been presented. The variation of the volume fraction of the fragment is plotted as a function of distance perpendicular to the droplet surface. Let us first consider the three shortest chains. The flat conformations adopted by two of these, Met³²²–Lys³⁵⁵ and Asn³⁵⁶–Arg⁴²⁵ (as already seen in Fig. 4), also lead them to form rather thin surface layers with thicknesses of ∼1 nm (Fig. 5). In the absence of electrostatic interactions at pH = 5.5, close to IEP of the fragments, any remaining repulsion resulting from overlap of these thin layers are simply too short ranged to provide sufficient colloidal stability. Additionally, at the point of overlap, the presence of multiple hydrophobic blocks in the primary sequence of the polypeptides can result in the formation of bridges between a pair of neighbouring droplets. The bridges result from the possible simultaneous adsorption of a chain onto two nearby interfaces. The bridging attraction that results in such systems further adds to the already existing van der Waals forces, leading to flocculation of droplets.^63,73

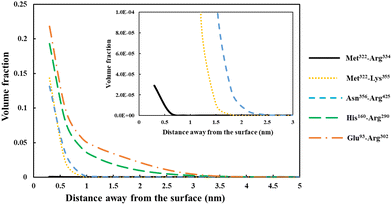Fig. 5 Density profile variation for our five different soy-protein derived polypeptides in Table 2, shown as a function of distance away from a hydrophobic surface. The inset graphs are magnified versions of the same results to more clearly present the data for the smallest fragment Met³²²–Arg³³⁴ (black line). All the calculations were performed at a background electrolyte volume fraction of 0.01 (roughly equals to 100 mM NaCl) and at a solution pH = 5.5.

For the shortest of our three small fragments, namely Met³²²–Arg³³⁴, we find a slightly different situation compared to the other two discussed above. This polypeptide has the highest proportion of the hydrophobic amino acids (69.2%, see Table 2) amongst all our five studied fragments. Despite this, it is seen from the inset graph in Fig. 5 that Met³²²–Arg³³⁴ displays a relatively poor degree of affinity for adsorption onto the surface of droplets, with only 3.23 × 10⁻⁴ adsorbed amino acid residues per unit area (a₀²) (see Table 3). This translates to only 0.75 μg m⁻² of adsorbed protein, taking the average molecular weight of an amino acid group as 125 Da. In contrast, the two slightly larger polypeptides (i.e. Met³²²–Lys³⁵⁵ and Asn³⁵⁶–Arg⁴²⁵) both adsorb at substantially higher levels onto a hydrophobic surface (2.57 × 10⁻¹ and 2.95 × 10⁻¹ monomers per unit area, respectively). Again, these equate to 0.594 mg m⁻² for Met³²²–Lys³⁵⁵ and 0.681 mg m⁻² for Asn³⁵⁶–Arg⁴²⁵. For the two longest polypeptides (His¹⁶⁰–Arg²⁹⁰ and Glu⁹³–Arg³⁰²), the adsorbed amount was even greater, although only 29.0% and 27.6% of the total residues (in comparison to 69.2% for Met³²²–Arg³³⁴, see Table 2) were hydrophobic. Not surprisingly then, Met³²²–Arg³³⁴ forms an interfacial film that is substantially thinner than all the other four fragments, as demonstrated by the graph in the inset of Fig. 5.

Table 3 The SCF calculated total adsorbed amount (in the unit of number of amino acid residues per monomer area, a₀²) for different polypeptides at the droplet surface. The results are produced at a background electrolyte volume fraction of 0.01 (roughly equals to 100 mM NaCl) and at pH = 5.5. The data is also converted and presented in the unit of mg m⁻², assuming an average molecular weight of 125 Da per amino acid reside

	Met^322–Arg^334	Met^322–Lys^355	Asn^356–Arg^425	His^160–Arg^290	Glu^93–Arg^302
Total adsorbed amount (monomers/a0^2)	0.323 × 10^−3	0.257	0.295	0.467	0.633
Total adsorbed amount (mg m^−2)	0.745 × 10^−3	0.594	0.681	1.08	1.46

---

The above observation emphasizes a somewhat obvious but rather important point. It is the actual number of the anchoring groups that is of a greater importance concerning the adsorption of chains, rather than their relative proportion. Long fragments with relatively small fraction of hydrophobic residues will still have many such anchoring monomers, whereas smaller chains, even with a high proportion of hydrophobic amino acids, may not. The lower adsorption of our small polypeptide Met³²²–Arg³³⁴ is mainly related to its smaller total binding energy, which in turn relates to the total number of hydrophobic anchoring residues. In the case of Met³²²–Arg³³⁴, with 9 out of its 13 amino acid monomers as hydrophobic, the total binding energy per chain is still substantially less than a larger fragment like Glu⁹³–Arg³⁰². The latter only has 27.6% of such residues (Table 2), which amounts to 58 hydrophobic residues. However, this is still considerably larger than 9 for Met³²²–Arg³³⁴. Though here we are mainly interested in coverages at or close to saturation, the differences in adsorbed amounts happen to be even starker at low surface adsorptions, below maximum coverage. The impact of the variation in the binding energies manifest itself more clearly when the coverage is not restricted by excluded volume and lateral interactions,⁶⁹ as is the case far from surface saturation for longer chains. This is similar to the situation observed for a small-molecular-weight surfactant. The bulk concentration for such molecules has to be much higher than for a large amphiphilic polymeric molecule, in order for the surface to attain sufficient coverage. For naturally occurring plant proteins, and polypeptides derived from them, the hydrophobic and hydrophilic amino acids are roughly distributed evenly along the backbone of the chains. As a result, a protein fragment with a larger size will normally also have a greater number of hydrophobic binding groups than a smaller one, and consequently can saturate the interface at much lower bulk concentrations.

So far, our focus has been on the total binding energy and its effect for adsorption of shorter versus longer fragments. However, a second important consideration for the poorer adsorption of small polymers is associated with the entropy of mixing when they are dissolved in a solvent. Whether a polymer will prefer to mix with the solvent and stay in the bulk, or for it to separate out from the solution phase, depends essentially on the balance between two factors: the enthalpic interactions with solvent and the entropy of mixing.^53,74 Provided that the enthalpic contribution to free energy of mixing is roughly the same for a certain amount (based on weight) of polypeptides dissolved in the solvent, then it is the entropy of mixing that largely determines the differences in the solubility of polypeptide species. However, the contribution of the polymer to the entropy of mixing decreases with a reduction in its molar concentration, and hence with increase in its molecular weight. This contribution becomes negligible for very large polymers. Consequently, smaller chains tend to have higher solubilities than large polymers.⁷⁴ The improvement of the solubility of proteins with increasing hydrolysis is indeed a well-established experimental fact.^13,75,76 In our case, the smaller polypeptide Met³²²–Arg³³⁴ will have a higher tendency to dissolve and remain in the aqueous phase, compared to the other larger fragments. This reflects in lower level of adsorption for Met³²²–Arg³³⁴.

The above results and discussions demonstrated a crucial criterion that the degree of hydrolysis (DH), which strongly governs the content of the bigger polypeptide chains present in the mixture, cannot be made too high. In choosing the correct DH, one must make a careful compromise between the presence of adequately longer fragments on one hand, and the required better solubility of the emulsifier on the other.

Before leaving our discussion of the fragments prior to forming conjugates, let us also consider the graphs in Fig. 5 for our two longest soy protein derived polypeptides (His¹⁶⁰–Arg²⁹⁰ and Glu⁹³–Arg³⁰²). Both fragments form substantially more extended interfacial layers. There is still an appreciable amount of polymer, up and above that in bulk solution, predicted at a distance as far as 3.0 nm from the surface. Given the much larger size of these fragments relative to the three shorter polypeptides, this may be expected. However, the extended nature of the adsorbed films is not purely the result of the size differences. It also comes about because both His¹⁶⁰–Arg²⁹⁰ and Glu⁹³–Arg³⁰² have reasonably large segments that consist predominantly of hydrophilic amino acids. As we have already seen in Fig. 4, these more hydrophilic blocks tend to protrude away from the interface, thus forming more desirable, thicker surface films.

3.2 Emulsion stabilizing properties of covalently bonded polypeptide–polysaccharide conjugates, and their competitive adsorption with small, unreacted protein fragments

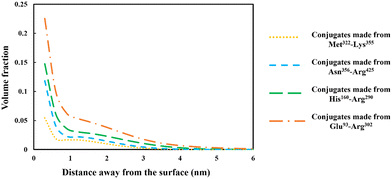
The discussion in the previous section clearly demonstrates that the large variety of polypeptides obtained during partial hydrolysis of a protein by an enzyme exhibit vastly differing colloidal and interfacial behaviors. What is desired are reasonably sized fragments that possess primary structures roughly resembling di-block polymers. However, the great majority of generated polypeptides will not have this feature and therefore unable to display a good emulsion stabilizing capacity, particularly in the absence of any electrostatic net charge close to their IEP. This situation is significantly altered following the covalent bonding of hydrophilic chains (such as polysaccharide or maltodextrin) to the protein fragments. The covalent bonding occurs through the commonly encountered heat induced or enzymatic Maillard reactions.^67,77,78

3.2.1 Structure of interfacial layers. In Fig. 6 we present the calculated density profiles of the conjugated polymers adsorbed onto an isolated single hydrophobic–hydrophilic interface. The variation of the protein volume fractions is displayed as a function of the distance perpendicular to the surface. The results were obtained for four of the five polypeptides in the previous section, exhibiting a sufficient degree of affinity for adsorption onto the surface. These are Met³²²–Lys³⁵⁵, Asn³⁵⁶–Arg⁴²⁵, His¹⁶⁰–Arg²⁹⁰ and Glu⁹³–Arg³⁰². Each polypeptide is now assumed to have been modified by attaching a hydrophilic chain, with a size of 50 monomer units, to the lysine residue closest to the N-terminus end of the fragment. This choice is to minimize the influence of the position of hydrophilic attachment on the colloidal stabilizing performance of the polymer, previously reported by Akinshina et al.,⁵² while still retaining a realistic site for the formation of the covalent bond.

Fig. 6 Density profiles of the conjugated polymers formed from each of the four soy-derived protein fragments (i.e. Met³²²–Lys³⁵⁵, Asn³⁵⁶–Arg⁴²⁵, His¹⁶⁰–Arg²⁹⁰ and Glu⁹³–Arg³⁰²), when bonded with a hydrophilic chain. The hydrophilic chain (representing maltodextrin) consisted of 50 monomers. The volume fraction variation of the fragments is plotted against the distance away from the hydrophobic surface. The results are produced for each conjugate as if it was present by itself only, and at a background electrolyte volume fraction of 0.01 (equals to 100 mM NaCl) with solution pH = 5.5.

From graphs in Fig. 6, the interfacial structure of the adsorbed conjugated protein fragments can be examined. These should be compared to those formed by the unreacted chains presented in Fig. 5. The modification to the structure of the interfacial layer, as formed by the adsorbed conjugated polypeptides, is most pronounced for the two shorter polypeptides Met³²²–Lys³⁵⁵ and Asn³⁵⁶–Arg⁴²⁵. There was a fourfold increase in thickness of the interfacial film from ∼1 nm when unbonded, to roughly 3.5 nm for the conjugated chains. For larger fragments, His¹⁶⁰–Arg²⁹⁰ and Glu⁹³–Arg³⁰², the increase is less modest but still significant, up from 3.5 nm when unmodified to 5 and 6 nm respectively, for the corresponding conjugates.

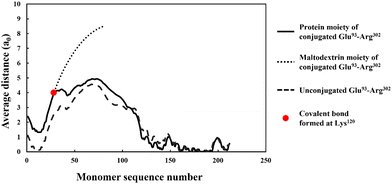
More importantly, the extended interfacial structure of the adsorbed layer as formed by conjugated polypeptides, displays a multilayer-layer-like feature. A distinct inner sub-layer, with a thickness of less than 1 nm, is followed by an outer more extended one of several nanometers (see Fig. 6). Our calculations reveal (results not shown here) that the inner part comprises mainly of amino acid residues, while the outer sub-layer consists mostly of monomers of the attached hydrophilic chain (i.e. maltodextrin). This feature is the result of the conformation adopted by conjugated polypeptides, as best illustrated in Fig. 7. The figure shows the calculated average distance of each amino acid of the conjugated protein fragment, as measured from the interface, plotted against the monomer sequence number (starting from the N-terminus side). Also included are the average positions of the monomers of the hydrophilic side chain, attached to a lysine residue of the polypeptide at position Lys¹²⁰ (monomer 28 on the fragment and indicated with a red dot on the graph). For comparison, the same data for the unconjugated Glu⁹³–Arg³⁰² is also included in Fig. 7, displayed as the dashed line. The protein part of the conjugate is seen to remain close to the surface, indicating that it forms the inner sub-layer and hence the anchoring section of the combined conjugated chain. The hydrophilic maltodextrin chain protrudes out away from the surface into the aqueous phase, forming the outer sub-layer. It is also observed that the covalent attachment of a hydrophilic chain to Glu⁹³–Arg³⁰² does not significantly alter how the C-terminus end of the fragment arranges itself on the interface. In contrast, the average position of the monomers on the N-terminus end of the fragment, being closer to the cross-link point, are found to reside slightly further away from the surface. One can observe that the bonding with the hydrophilic sidechain is starting to alter the conformation of the adsorbed chains, changing its behavior from what was closer to a tri-block chain towards the more advantageous di-block-like one.

Fig. 7 The average distance of each monomer residue (in the unit of monomer size), comprising the protein part of the conjugate formed from soy protein fragment Glu⁹³–Arg³⁰². The average distance is measured from the hydrophobic interface and is plotted against the monomer sequence number starting from the N-terminus side (black solid line). The dotted line shows a similar result for the hydrophilic attached sidechain, while the dashed line is for a Glu⁹³–Arg³⁰² fragment that does not have the sidechain (i.e. not reacted). The calculations were performed with a background electrolyte volume fraction of 0.01 (equals to 100 mM NaCl) and at a solution pH = 5.5.

3.2.2 Induced colloidal interactions by conjugates. The most crucial advantage of the thicker “two-layer like” interfacial structure, coupled with an adsorption behavior that approximately mimics a di-block polymer, is the ability to induce stronger and longer ranged steric repulsion between two approaching droplets covered with such layers. Indeed, this is clearly seen to be the case in the graphs of Fig. 8, displaying the mediated colloidal interaction between two droplets stabilized by each of our four different conjugates. Recall from Fig. 3 that it was predicted that the three unmodified polypeptides (Met³²²–Lys³⁵⁵, Asn³⁵⁶–Arg⁴²⁵ and Glu⁹³–Arg³⁰²) had not provided sufficient steric repulsion to prevent aggregation of droplets. In fact, in some cases they had led to an attraction between the emulsion droplets, contributing to their flocculation. The corresponding interfacial layers, formed from adsorption of conjugates containing each of these protein fragments, are observed to vastly improve this situation (Fig. 8). The minimum energy wells generated by all these polypeptide–maltodextrin complexes remained relatively shallow (−4 to −6k_BT), irrespective of whether the conjugate was formed from larger or smaller fragments. For example, for the conjugate consisting of the shorter Met³²²–Lys³⁵⁵ (made up of 34 residues) the depth of minimum is ∼6k_BT, whereas that formed form the larger fragment Glu⁹³–Arg³⁰² (consisting of 210 amino acid residues) is only slightly shallower at 4k_BT. Although such energy minima in the droplet–droplet interaction potentials still result in weak flocs, from a practical point of view these can easily be broken by the application of shear or even the Brownian motion of droplets themselves.^35,39 This situation can be improved further if one is willing to use larger hydrophilic chains, to within a limit. This is discussed further in the following, taking our soy protein fragment Asn³⁵⁶–Arg⁴²⁵ as an example.

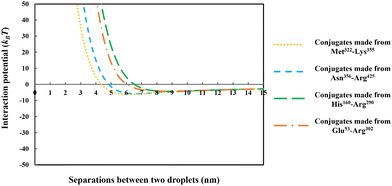Fig. 8 The interaction potential, plotted against the inter-droplet separation distance, mediated by the adsorbed layers of the conjugated chains. The conjugates are formed from each of the four soy-protein hydrolyzed polypeptides of Fig. 6, bonded with a hydrophilic chain (representing maltodextrin) consisting of 50 monomers. The size of the oil droplets in all the calculations was taken as 1 μm, with the bulk electrolyte volume fraction and pH as 0.01 (equals to 100 mM NaCl) and 5.5, respectively.

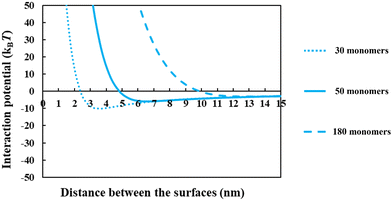
From the above discussions thus far, it is seen that for protein fragments possessing enough hydrophobic anchoring groups to ensure strong adsorption, the performance of the resulting conjugated emulsifier is not particularly sensitive on the size of the polypeptide part of the conjugate molecule. In contrast, the molecular size of the polysaccharide/maltodextrin attachment is found to have a far greater impact on the stabilizing ability of the conjugated polymers. This is not entirely surprising, since for conjugates the primary role of the protein fragment solely becomes one of ensuring that the complex is sufficiently amphiphilic, allowing it to possess a strong affinity for the surface. Once this is achieved, further increases in the size or the degree of hydrophobicity of the polypeptide have little impact on additional surface behavior of the complex. For conjugates, unlike unreacted fragments, the main responsibility for providing the strong, long-ranged steric repulsion has been delegated to the polysaccharide side chain. In Fig. 9, the inter-droplet potentials, induced by the conjugated emulsifiers consisting of our protein fragment Asn³⁵⁶–Arg⁴²⁵ attached to hydrophilic chains of various sizes (i.e. 30, 50 and 180 sugar residues), have been plotted against the separation distance. Recall from Fig. 3 that the droplets stabilized by non-bonded polypeptide Asn³⁵⁶–Arg⁴²⁵ are predicted to undergo severe flocculation as a result of the strong net attractive force. The same polypeptide, when modified by covalent bonding with a short hydrophilic chain of 30 sugar residues, is already found to form a more suitable emulsifier (see dotted line in Fig. 9). However, the potential well has a value ∼−11k_BT which is just deep enough to cause some droplet aggregation. If we increase the size of the hydrophilic attachment by six-fold to 180 sugar moieties (see dashed line in Fig. 9), this energy well almost disappears since the inter-droplet repulsion becomes operational at a longer separation distance of ∼11 nm.

Fig. 9 The interaction potential plotted against the separation distance between a pair of droplets, induced by the adsorbed protein + maltodextrin conjugates consisting of soy protein fragment Asn³⁵⁶–Arg⁴²⁵ with attached hydrophilic chains of various sizes (i.e. 30, 50 and 180 monomers). Droplets are assumed to be 1 μm in diameter. All the results were calculated with a background electrolyte volume fraction of 0.01 (roughly equating to 100 mM NaCl) and at a solution pH = 5.5.

The results in Fig. 8 and 9 indicated a crucial criterion in developing the desired emulsification properties of the conjugated polymers formed from protein fragments and polysaccharide. When a protein is covalently bonded to a polysaccharide or maltodextrin, the function of protein with regards to the provision of repulsive colloidal forces between droplets is altered. Protein part of the conjugate molecule is now only responsible for ensuring a reasonably strong anchoring of the composite molecule to the surface. The responsibility for forming a thick interfacial film and inducing sufficient steric repulsion is now all but delegated to the more hydrophilic polysaccharide part of the chain. Therefore, when a blend of different polypeptides with varying structural properties is generated by the enzymatic hydrolysis and conjugated with polysaccharides, a suitable emulsifier is formed so long as the protein moieties can achieve a sufficient level of adsorption for the Maillard complexes.

3.2.3 Competitive adsorption. The case considered above assumes that all produced protein fragments have fully reacted and bonded to at least one maltodextrin chain. However, this situation would be altered if extensive hydrolysis leads to generation of many small protein fragments. For in such a case the deviation from the stoichiometric ratio will be such that many polypeptides will not have a chance to react. Furthermore, as discussed previously, the small fragments are less likely to contain lysine residues and therefore have fewer potential sites for the formation of a covalent bond with maltodextrin. The presence of an overwhelming number of unconjugated small polypeptides would disturb the adsorption of large, conjugated polymers, as we hope to demonstrate using the results of our calculations below.

Let us consider the competitive adsorption behavior between small unconjugated Met³²²–Lys³⁵⁵ polypeptides and the larger conjugated Glu⁹³–Arg³⁰² fragments, with latter having formed bonds with maltodextrin chains of size 50 monomers at its position Lys¹²⁰. Of course, this is a much-simplified version of a real system in which many other different kinds of conjugated and unbonded protein fragments, apart from the two chosen polypeptides here, also coexist. Nonetheless, despite its simplicity, this bimodal mixture still allows one to demonstrate the important consequences of the competitive adsorption between the larger bonded and the smaller unreacted protein fragments, concerning the emulsifying properties in the mixed system.

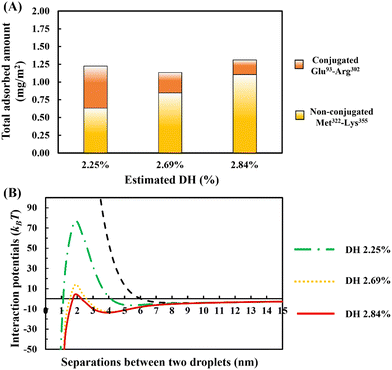
In Fig. 10A, the amount of adsorption is shown. This is obtained using our SCF calculations for different ratios of the bulk concentrations of our two chosen fragments. In each case, we have also estimated and given the degree of hydrolysis (see ESI,† Section S.2) that leads to the corresponding concentration ratio. We have defined DH to be the fraction of actual peptide bonds broken to all those that are susceptible to hydrolysis by trypsin. It is seen that the total amount of surface coverage stays roughly the same at ∼1.25 mg m⁻², showing little variation with DH. However, as hydrolysis by trypsin progresses further, the proportion of small polypeptides Met³²²–Lys³⁵⁵ in the adsorbed mixed interfacial film increases substantially. For instance, when DH increases from 2.25% to 2.84%, the amount of adsorbed Met³²²–Lys³⁵⁵ almost doubles and replaces around 80% of the conjugated Glu⁹³–Arg³⁰² on the surface. Such mixed films induce very differing interaction potentials between oil droplets, as the surface coverage ratio of unbonded Met³²²–Lys³⁵⁵ to conjugated Glu⁹³–Arg³⁰² protein fragments is altered (see Fig. 10B). With increasing displacement of the conjugated Glu⁹³–Arg³⁰², a secondary energy well appears in the mediated interaction potential. This becomes deeper and shifts to shorter droplet–droplet separation distances for hydrolysates produced at higher DH values. At the same time, it is seen that the energy barrier, resisting the close approach of droplets, also becomes smaller. When more than ∼70% of the conjugated Glu⁹³–Arg³⁰² fragment is displaced (i.e. when the DH exceeds ∼2.6%), the secondary energy well has a value ∼−13k_BT. This is sufficient to trap the droplets upon their collisions with each other, and thus leads to the onset of droplet aggregation. In addition, at a DH ∼2.6%, the height of the energy barrier is reduced to ∼12k_BT. This begins to be less than that normally needed (say 20k_BT)³⁵ to fully prevent the droplets from falling into the deep primary energy minimum, after long periods of storage. The presence of both primary and secondary minima, for cases involving significant displacement of Glu⁹³–Arg³⁰² by Met³²²–Lys³⁵⁵, can clearly be observed in the calculated interaction potential curves of Fig. 10B. Any further increase in the DH of the used protein hydrolysates, beyond 2.6%, would substantially worsen the situation and leads to inferior emulsifiers that are not capable of preventing strong aggregation, and thus also the likely coalescence of droplets.

Fig. 10 The competitive adsorption behavior showing the amount of the conjugated and the unreacted protein fragments adsorbed on the surface (A), and the interaction potential between a pair of droplets, induced by the presence of mixed adsorbed films on their surfaces, plotted against the inter-droplet separation distance (B). The mixed adsorbed layers consist of unbonded Met³²²–Lys³⁵⁵ and conjugated Glu⁹³–Arg³⁰² soy protein derived fragments. The conjugated protein fragment was formed by a link on one of its lysine sites with a hydrophilic chain comprising of 50 monomers. The relative abundance of the two polypeptides in bulk solution is chosen in each case (while keeping the total amount of polypeptides the same) to correspond roughly to that resulting from the given DH (%) values. The interaction potential generated by interfacial layers formed by pure conjugate, only involving Glu⁹³–Arg³⁰², is also presented (as dashed black line) in (B) for comparison. The diameter of oil droplets was taken as 1 μm. The results are produced at a background electrolyte volume fraction of 0.01 (roughly equal to 100 mM NaCl) and at a pH value of 5.5.

The above theoretical results have significant implications for the practical synthesis of emulsifiers based on Maillard complexes of plant protein hydrolysates + polysaccharides. It is found that the presence of a relatively small number of unbonded polypeptides, generated at low level of hydrolysis, would not significantly alter the colloidal stabilizing properties of the generated emulsifier. However, higher levels of protein hydrolysis will produce a substantial number of short polypeptides. These by themselves produce thin and not particularly useful interracial layers. They are also less likely to form the desired conjugated emulsifier with polysaccharide, as the chances of finding many lysine reaction sites on a short chain is not high. In the presence of many such unreacted short polypeptides, these chains compete for surface adsorption with the longer, and more useful, conjugated fragments in the system. At higher DH values, the number ratio becomes such that it simply masks any useful emulsion stabilizing properties that the latter conjugated protein fragments may be able to offer. It may be possible to filter out these shorter polypeptides to remedy the situation. However, this still means that a large fraction of protein material is wasted and not usefully utilized.

4. Conclusions

In this study, the colloidal stabilizing behaviors of protein fragments, both prior to and post conjugation with a hydrophilic sidechain such as maltodextrin were theoretically examined. We use hydrolysates of soy protein, produced by the action of trypsin, as realistic examples. The investigation is based on the use of theoretical self-consistent field (SCF) calculations.

For polypeptides to provide a satisfactory level of colloidal stabilization, they are required to adsorb sufficiently and ensure a good level of surface coverage of emulsion droplets. We found that small polypeptide fragments were not capable of meeting this criterion, despite many of them having a reasonable ratio of hydrophobic to total amino acid residues. It is seen that the total number of hydrophobic monomers, as opposed to their relative ratio, plays the prominent role in dictating the adsorbed number of chains. From the above results, we can also conclude that the process of enzymatic hydrolysis should not be overdone. For any given plant protein to be a satisfactory molecular (as opposed to Pickering type) emulsifier,³⁵ the degree of hydrolysis must be carefully optimized to achieve the best possible compromise between good solubility and emulsifying performance.

In a mixture of protein fragments obtained by partial hydrolysis, a broad distribution of various types of polypeptides is generated. We have demonstrated that sufficiently long polypeptides, with a primary sequence of amino acids roughly resembling a di-block-type structure, are the ones in the distribution that provide the best level of steric stabilization. The desirability of having this kind of structure in relation to emulsification properties is not surprising.^6,36 However, more interestingly, it is demonstrated that this requirement for a di-block-like structure can largely be relaxed through covalent grafting of a hydrophilic chain (e.g. a polysaccharide of sufficient length) to any protein fragment, so long as the polypeptide possesses a suitable level of affinity for adsorption. Our results show that all these conjugated molecules will have a comparably good emulsion stabilizing performance against droplet flocculation, regardless of the large differences in the molecular size, degree of hydrophobicity and the configurations on the interface of the polypeptide part of the conjugate.

Hydrolysis of a protein, followed by conjugation of produced fragments with polysaccharide, will in practice lead to various different species. In particular, the theoretical results indicate that in itself the coexistence of conjugated polymers, formed from small and large fragments, does not make a significant difference to the flocculation stability of the emulsion system stabilized by such mixtures. However, in situations where the enzymatic hydrolysis proceeds to such an extent where a large number of short chains are produced, an overwhelming number of these small polypeptides will not have the chance to react and form conjugates. The presence of these unbonded fragments is found to have a very detrimental impact on the emulsion stabilizing properties of the system. The good emulsifying properties of larger conjugated fragments in the system are largely rendered useless due to their competitive displacement from the interfaces by the far more abundant, but short unreacted polypeptides in the system.

The theoretical results in this study provide a considerably clearer understanding of the experimental trends already reported in the literature involving the study of food emulsifiers based on Maillard complexes of plant protein fragments with polysaccharides.^13,25,79 It is worth noting that while our study used trypsin hydrolyzed soy protein as an example, the analysis and general conclusions presented are not solely limited to this protein alone. They should equally apply to proteins from many other sources (including animal-derived proteins).

Author contributions

Yue Ding: conceptualization, visualization, methodology, software, investigation, formal analysis, interpretation of data, writing – original draft. Adem Zengin: software, methodology, interpretation of data, validation, writing – review & editing. Weiwei Cheng: validation, writing – review & editing. Libo Wang: validation, writing – review & editing. Rammile Ettelaie: conceptualization, methodology, software, investigation, validation, interpretation of data, supervision, writing – review & editing.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

One of us (RE), wishes to acknowledge M. Y. Janny and M. Akhtar for several useful discussions.

References

1. R. Dubey, T. C. Shami and K. U. Bhasker Rao, Def. Sci. J., 2009, 59, 82–95.
2. C. Burgos-Díaz, T. Wandersleben, A. M. Marqués and M. Rubilar, Curr. Opin. Colloid Interface Sci., 2016, 25, 51–57.
3. D. J. McClements, Ann. Rev. Food Sci. Technol., 2010, 1, 241–269.
4. J. Sirison, T. Ishii, K. Matsumiya, Y. Higashino, Y. Nambu, M. Samoto, M. Sugiyama and Y. Matsumura, Food Hydrocolloids, 2023, 141, 108745.
5. D. J. McClements, Curr. Opin. Colloid Interface Sci., 2012, 17, 235–245.
6. R. Ettelaie, A. Zengin and S. V. Lishchuk, Curr. Opin. Colloid Interface Sci., 2017, 28, 46–55.
7. E. Dickinson, Ann. Rev. Food Sci. Technol., 2015, 6, 211–233.
8. B. S. Murray, Curr. Opin. Food Sci., 2019, 27, 57–63.
9. E. Dickinson, Food Hydrocolloids, 2019, 96, 209–223.
10. F. Zha, Z. Yang, J. Rao and B. Chen, J. Agric. Food Chem., 2019, 67, 10195–10206.
11. Y.-H. Cheng, W.-J. Tang, Z. Xu, L. Wen and M.-L. Chen, Int. J. Food Sci. Technol., 2018, 53, 372–380.
12. R. R. Naik, Y. Wang and C. Selomulya, Crit. Rev. Food Sci. Nutr., 2022, 62, 7036–7061.
13. Y. Ding, L. Chen, Y. Shi, M. Akhtar, J. Chen and R. Ettelaie, Food Hydrocolloids, 2021, 113, 106519.
14. C. Berton-Carabin and K. Schroën, Curr. Opin. Food Sci., 2019, 27, 74–81.
15. S. Zhang, M. Holmes, R. Ettelaie and A. Sarkar, Food Hydrocolloids, 2020, 102, 105583.
16. X. Yan, C. Ma, F. Cui, D. J. McClements, X. Liu and F. Liu, Trends Food Sci. Technol., 2020, 103, 293–303.
17. F. Liu and C.-H. Tang, J. Agric. Food Chem., 2013, 61, 8888–8898.
18. X. Liu, Y.-Q. Huang, X.-W. Chen, Z.-Y. Deng and X.-Q. Yang, J. Cereal Sci., 2019, 87, 46–51.
19. E. Dickinson, Curr. Opin. Food Sci., 2020, 33, 52–60.
20. T. G. Burger and Y. Zhang, Trends Food Sci. Technol., 2019, 86, 25–33.
21. A. Sarkar, S. Zhang, M. Holmes and R. Ettelaie, Adv. Colloid Interface Sci., 2019, 263, 195–211.
22. A. Sarkar, V. Ademuyiwa, S. Stubley, N. H. Esa, F. M. Goycoolea, X. Qin, F. Gonzalez and C. Olvera, Food Hydrocolloids, 2018, 84, 282–291.
23. D. Lin, L.-C. Sun, Y.-L. Chen, G.-M. Liu, S. Miao and M.-J. Cao, Trends Food Sci. Technol., 2022, 129, 11–24.
24. Y. Li, F. Zhong, W. Ji, W. Yokoyama, C. F. Shoemaker, S. Zhu and W. S. Xia, Food Hydrocolloids, 2013, 30, 53–60.
25. J. Yu, G. Wang, X. Wang, Y. Xu, S. Chen, X. Wang and L. Jiang, LWT--Food Sci. Technol., 2018, 91, 63–69.
26. A. Kimura, M. R. G. Tandang-Silvas, T. Fukuda, C. Cabanos, Y. Takegawa, M. Amano, S.-I. Nishimura, Y. Matsumura, S. Utsumi and N. Maruyama, J. Agric. Food Chem., 2010, 58, 2923–2930.
27. K. Xu and P. Yao, Langmuir, 2009, 25, 9714–9720.
28. Y. Wang, Z. Li, H. Li and C. Selomulya, Curr. Opin. Food Sci., 2022, 48, 100949.
29. C. Liu, M. Bhattarai, K. S. Mikkonen and M. Heinonen, J. Agric. Food Chem., 2019, 67, 6625–6632.
30. I. Celus, K. Brijs and J. A. Delcour, J. Agric. Food Chem., 2007, 55, 8703–8710.
31. J. A. Lopes-da-Silva and S. R. Monteiro, Food Chem., 2019, 294, 216–223.
32. R. Intarasirisawat, S. Benjakul, W. Visessanguan and J. Wu, Food Chem., 2012, 135, 3039–3048.
33. S. Severin and W. S. Xia, J. Food Biochem., 2006, 30, 77–97.
34. F. Tamm, S. Herbst, A. Brodkorb and S. Drusch, Food Hydrocolloids, 2016, 58, 204–214.
35. E. Dickinson, An introduction to food colloids, Oxford University Press, Oxford, 1992.
36. B. S. Murray, R. Ettelaie, A. Sarkar, A. R. Mackie and E. Dickinson, Food Hydrocolloids, 2021, 117, 106696.
37. A. Nisov, D. Ercili-Cura and E. Nordlund, Food Chem., 2020, 302, 125274.
38. N. A. Avramenko, N. H. Low and M. T. Nickerson, Food Res. Int., 2013, 51, 162–169.
39. R. Ettelaie, A. Zengin and H. Lee, Biopolymers, 2014, 101, 945–958.
40. J. M. H. M. Scheutjens and G. J. Fleer, J. Phys. Chem., 1979, 83, 1619–1635.
41. J. M. H. M. Scheutjens and G. J. Fleer, J. Phys. Chem., 1980, 84, 178–190.
42. O. A. Evers, J. M. H. M. Scheutjens and G. J. Fleer, Macromolecules, 1990, 23, 5221–5233.
43. F. A. M. Leermakers, P. J. Atkinson, E. Dickinson and D. S. Horne, J. Colloid Interface Sci., 1996, 178, 681–693.
44. E. Dickinson, D. S. Horne, V. J. Pinfield and F. A. M. Leermakers, J. Chem. Soc., Faraday Trans., 1997, 93, 425–432.
45. E. Dickinson, V. J. Pinfield, D. S. Horne and F. A. M. Leermakers, J. Chem. Soc., Faraday Trans., 1997, 93, 1785–1790.
46. P. J. Atkinson, E. Dickinson, D. S. Horne and R. M. Richardson, J. Chem. Soc., Faraday Trans., 1995, 91, 2847–2854.
47. P. J. Atkinson, E. Dickinson, D. S. Horne, F. A. M. Leermakers and R. M. Richardson, Berichte der Bunsengesellschaft fur Physikalische Chemie, 1996, 100, 994–998.
48. E. Dickinson, D. S. Horne, J. S. Phipps and R. M. Richardson, Langmuir, 1993, 9, 242–248.
49. E. L. Parkinson, R. Ettelaie and E. Dickinson, Biomacromolecules, 2005, 6, 3018–3029.
50. R. Ettelaie, A. Akinshina and E. Dickinson, Faraday Discuss., 2008, 139, 161–178.
51. R. Ettelaie, E. Dickinson and L. Pugnaloni, J. Phys.: Condens. Matter, 2014, 26, 464109.
52. A. Akinshina, R. Ettelaie, E. Dickinson and G. Smyth, Biomacromolecules, 2008, 9, 3188–3200.
53. K. A. Dill and S. Bromberg, in Molecular driving forces: statistical thermodynamics in chemistry and biology, ed. K. A. Dill and S. Bromberg, Garland, New York, London, 2003, ch. 31, pp. 593–608.
54. K. A. Dill and S. Bromberg, in Molecular driving forces: statistical thermodynamics in chemistry and biology, ed. K. A. Dill and S. Bromberg, Garland, New York, London, 2003, ch. 34, pp. 685–698.
55. M. Doi and S. F. Edwards, The theory of polymer dynamics, Clarendon, Oxford, 1986.
56. A. I. U. Grosberg and A. R. Khokhlov, Statistical physics of macromolecules, AIP Press, New York, 1994.
57. G. J. Fleer, M. A. Cohen Stuart and J. M. H. M. Scheutjens, J. Am. Chem. Soc., 1996, 118, 10678.
58. R. Ettelaie, E. Dickinson and B. S. Murray, in Food Colloids - Interactions, Microstructure and Processing, ed. E. Dickinson, Royal Society of Chemistry, 2005, pp. 74–84.
59. I. M. Lifshits, A. Y. Grosberg and A. R. Khokhlov, Rev. Mod. Phys., 1978, 50, 683–713.
60. R. Ettelaie, A. Akinshina and S. Maurer, Soft Matter, 2012, 8, 7582–7597.
61. G. J. Fleer, M. A. Cohen Stuart, J. M. H. M. Scheutjens, T. Cosgrove and B. Vincent, Polymers at interfaces, Chapman & Hall, London, 1993.
62. G. J. Fleer, M. A. Cohen Stuart and F. A. M. Leermakers, in Fundamentals of Interface and Colloid Science, ed. J. Lyklema, Academic Press, San Diego, USA, 2005.
63. R. Ettelaie, B. S. Murray and E. L. James, Colloids Surf., B, 2003, 31, 195–206.
64. M. Magrane, M. J. Martin, C. O'Donovan and R. Apweiler, in The Proteomics Protocols Handbook, ed. J. M. Walker, Humana Press, Totowa, NJ, 2005, pp. 609–618.
65. E. Gasteiger, C. Hoogland, A. Gattiker, S. Duvaud, M. R. Wilkins, R. D. Appel and B. Amos, in The Proteomics Protocols Handbook, ed. J. M. Walker, Humana Press, Totowa, NJ, 2005, pp. 571–607.
66. T. J. Wooster and M. A. Augustin, J. Colloid Interface Sci., 2007, 313, 665–675.
67. M. Akhtar and R. Ding, Curr. Opin. Colloid Interface Sci., 2017, 28, 31–36.
68. C. M. Oliver, L. D. Melton and R. A. Stanley, Crit. Rev. Food Sci. Nutr., 2006, 46, 337–350.
69. M. Mu, F. A. M. Leermakers, J. Chen, M. Holmes and R. Ettelaie, J. Colloid Interface Sci., 2023, 644, 333–345.
70. A. Kato, K. Shimokawa and K. Kobayashi, J. Agric. Food Chem., 1991, 39, 1053–1056.
71. J. Coupland, in An introduction to the physical chemistry of food, ed. J. Coupland, Springer, Berlin, 2014, pp. 19–40.
72. D. J. McClements, in Food Emulsions: Principles, Practices, and Techniques, ed. D. J. McClements, CRC Press, Boca Raton, Third edn, 2015, pp. 29–53.
73. C. M. Wijmans, F. A. M. Leermakers and G. J. Fleer, J. Colloid Interface Sci., 1994, 167, 124–134.
74. J. Coupland, in An introduction to the physical chemistry of food, ed. J. Coupland, Springer, Berlin, 2014, pp. 107–129.
75. L. Chen, J. Chen, L. Yu and K. Wu, Food Sci. Technol., 2016, 69, 1–8.
76. V. Klompong, S. Benjakul, D. Kantachote and F. Shahidi, Food Chem., 2007, 102, 1317–1327.
77. E. Dickinson and M. G. Semenova, Colloids Surf., 1992, 64, 299–310.
78. Y. Liu, M. P. Yadav and L. Yin, Food Hydrocolloids, 2018, 77, 986–994.
79. J. Zhang, N. Wu, X. Yang, X. He and L. Wang, Food Hydrocolloids, 2012, 28, 301–312.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00855j

---