Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
N2 adsorption on high-entropy alloy surfaces: unveiling the role of local environments†
Rafael B.
Araujo
* and
Tomas
Edvinsson
 *
*
Department of Materials Science and Engineering, The Ångstrom Laboratory, Uppsala University, P.O. Box 35, SE-751 03 Uppsala, Sweden. E-mail: rafael.araujo@angstrom.uu.se; tomas.edvinsson@angstrom.uu.se
First published on 23rd March 2023
Abstract
Developing highly active catalysts to electrochemically reduce N2 to NH3 under ambient conditions is challenging but bears the promise of using ammonia as a potential energy vector in sustainable energy technology. One of the scientific challenges concerns the inertness of N2 emanating from the highly stable triple bonds and the lack of dipole moments, making N2 fixation on catalytic surfaces difficult. Another critical challenge is that electrons are more prone to reduce hydrogen than N2 at the surface, forming a scaling relationship where the reduction ability of the catalyst most often benefits hydrogen reduction instead of nitrogen reduction. Here we show that high-entropy alloys (HEA) – a new class of catalysts with vast compositional and structural possibilities, can enhance N2 fixation. More specifically, we investigate the role of the local environment in the first and second solvation shell of the adsorbing elements in the bond strength between the dinitrogen molecules and the HEA surfaces. Density functional theory using a Bayesian error estimation functional and vdW interactions is employed to clarify the properties dictating the local bonding. The results show that although the main property calibrating the N2 bond strength is the d-band centers of the adsorbing elements, the value of the d-band centers of the adsorbing elements is further regulated by their local environment, mainly from the elements in the first solvation shell due to electron donor–acceptor interactions. Therefore, there exists a first solvation shell effect of the adsorbing elements on the bond strength between N2 molecules and the surface of HEAs. The results show that apart from the direct active site, the indirect relation adds further modulation abilities where the local interactions with a breath of metallic elements could be used in HEAs to engineer specific surface environments. This is utilized here to form a strategy for delivering higher bond strength with the N2 molecules, mitigating the fixation issue. The analysis is corroborated by correlation analysis of the properties affecting the interaction, thus forming a solid framework of the model, easily extendable to other chemical reactions and surface interaction problems.
10th anniversary statementWe would like to extend our heartfelt congratulations to J. Materials Chemistry A on the occasion of the 10th anniversary, for its high quality editorial and peer-review work making it a key journal in the materials science community. We have been privileged to publish work within diverse disciplines that include optical quantum confinement, tuning of optoelectronic properties in mixed lead halide perovskites, fundamental properties of lanthanide perovskites, highlighting a new carbon allotrope, up-scaling of water splitting modules using earth-abundant catalysts, purely theoretical studies related to electronic structure, Rashba spin–orbit split in 2D perovskites, and machine learning approaches to materials science. These examples reflect the width and breadth of the editorial board and assigned expert peer-reviewing scientists associated with the journal. The ability to assess and critically judge both chemical and physical aspects of materials chemistry, experimentally and theoretically, are in our opinion important factors for the rise in achievements and high impact of the journal in the last 10 years. We are glad to have been a small part of the contributions to the journal output and believe that J. Materials Chemistry A will have many years of impactful publications for the coming next 10 years and beyond. |
Introduction
NH3 is essential to the global economy as a fertilizer and feedstock chemical for industry.1 Moreover, ammonia is a potential energy vector stemming from its high hydrogen content and simple liquefaction, where liquid ammonia is a route to store and transport hydrogen. Currently, ammonia is industrially produced via the Haber–Bosch process, where a large amount of energy is required to break the N2 triple bonds and the process releases CO2 into the atmosphere, thus, aggravating the greenhouse effect.2 One strategy to circumvent these issues and to produce more eco-friendly NH3, is to use sustainable electricity with an electrochemical process to reduce N2 into NH3. The main bottleneck for present-day electrolysis is the low faradaic efficiency at appreciable rates that do not reach industrial requirements.3 Amongst other things, this is caused by the competition between nitrogen reduction reaction (NRR) and hydrogen evolution reaction (HER)4 and also related to the N2 fixation issue that is somehow aggravated by the poor accessibility of N2 molecules to the catalytic surfaces due to, for instance, the poor N2 solubility.5,6We believe that a more detailed understanding of how interactions between N2 molecules and catalytic surfaces occur may provide progress in promoting an improved ammonia production rate with the possibility of mitigating the N2 fixation issue. As the solution would depend on a detailed balance between the improved fixation of an inert molecule with the simultaneous repulsion and surface state control, of another species, a surface system that contains many degrees of freedom would be beneficial. The repulsion of protons and proton control systems can be achieved by choice of solvent and/or surface hydrophobicity tuning, while a critical challenge in all situations is to adhere N2 on the surface. Here, we present a detailed mechanistic study of how the interactions between the N2 molecules depend on the local composition of the surfaces of a new class of catalysts named high-entropy alloys (HEAs).
The concept of HEAs with entropy stabilization came out around 2004 when two independent research groups showed that multiple-element materials containing at least five different species could be formed into a homogeneous phase.7,8 Since then, HEAs have emerged as a material to be used in harsh chemical conditions and an alternative to the currently used electrocatalysts in different applications.9,10 This class of materials offers the advantages of high physicochemical stability – of interest to industrial applications – and a compositional diversity that provides possibilities to deliver high activity and selectivity. The nature of these catalytic surfaces, formed by at least five different species, leads to a compositional and structural diversity that permits a continuous tuning for selectivity and activity of the electrochemical transformations. Moreover, the complexity of the adsorbate–surface interactions opens the possibility of breaking scaling relations, surpassing the Sabatier principle guideline for catalytic activity. Pedersen et al.11 have recently shown that species on threefold hollow sites of HEAs could partially circumvent scaling relations with the adsorption of species on top sites due to the different coordination of threefold sites compared to on top sites. In this context, HEA surfaces would offer the possibility of species/concentration optimization to achieve greater N2 coverages (N2 adsorbs on the top position in the distal pathway), while still maintaining the adsorption strength of other intermediates, like NH* that adsorbs in the threefold hollow sites, in the range where activity is effective.
We explore how N2 molecules in the on-top sites (distal N2 molecule) interact with the catalytic surface of high-entropy alloys (HEA). More specifically, we have investigated the role of the local environment quantified as the structure and elemental compositing of the solvation shells around the adsorbing elements, and how this affects the bond strength between the dinitrogen molecules and the HEA surfaces. Density functional theory (DFT) was employed using the framework of a Bayesian error estimation functional and vdW interaction to investigate the N2 adsorption on HEA's microstructures composed of five elements chosen among Mo–Cr–Mn–Fe–Co–Ni–Cu. We have also estimated the relations between the N2 adsorption energies and properties of the HEAs like d band centers (BCs) and Bader charges of adsorbing elements.
Several strategies have been reported in the literature to enhance nitrogen reduction reaction (NRR), where they all more or less are related to nitrogen fixating surfaces with either proton deficiency or electron starving (and thus low rate). For instance, Yang et al.12 have reviewed approaches related to the defect engineering strategies for NRR like vacancy, doping, single atoms, amorphization, and high-index facet since these can regulate the local coordination environment, hence, affecting the intrinsic activity with respect to hydrogen evolution reaction (HER) versus NRR. Amongst metallic catalysts, Ru, Pd, Mo, and Au have shown significant activity for ammonia production at low rates that, in most cases, are subscribed to stepped facets that enable N2 fixation and sluggish HER.13 Suppressing the highly competitive hydrogen evaluation reaction (HER) normally requires suppression of proton and electron accessibility, shifting the HER chemical equilibrium, designing catalysts, tuning electrolytes, and increasing N2 mass transport.12,14,15 The work of Kani et al.16 have, for instance, evaluated such modifications to induce higher activities and selectivity using a Cu catalyst. A strategy incorporating effects also from the electrolyte by using a bismuth nanocrystal catalyst and adding potassium cations in the electrolyte was recently employed by Hao et al.17 The reported high Faradaic efficiency (FE) of 66% was assigned to: (i) bismuth 6p band and the N 2p orbitals interact strongly, and with that a higher N2 fixation than to more commonly applied transition metals, and (ii) nitrogen-reduction intermediates that are stabilized by the addition of potassium in the electrolyte – increased selectivity. Zhang et al.18 was one of the first groups reporting that HEAs could be used to reduce nitrogen, where 38.5% FE was achieved using HEA RuFeCoNiCu nanoparticles with a small size of 16 nm and signifies the promises of the approach, although remaining challenge is to perform the reaction with NRR selectivity versus HER also at high rates.
Despite recent development in electrochemical ammonia production, the low selectivity at high rates has hampered its application on an industrial scale. In addition, traditional trial-error approaches to optimize catalysts can be very slow and expansive due to the number of experiments needed to be performed, especially if the catalyst has a complex and multi-component composition. Computational modeling based on quantum mechanics, however, can uncover reaction mechanisms and molecular interactions more effectively than the mostly applied experimental “trial-error” methods, therefore, offering a rational designing tool for novel catalysts. So far, most investigations applying HEAs as catalysts are experimental due to difficulties extending theoretically established models towards HEA's multi-component surfaces.19 This is primarily due to the intrinsic randomization of the lattice that needs to be taken into consideration in the calculations. Machine learning (ML) techniques are here attractive approaches that promise to substantially accelerate the screening for promising HEAs that can be experimentally tested and verified. Identifying key limiting steps and/or the governing principles of the reaction can substantially reduce computational time compared to standard approaches, like density functional theory (DFT).20–26 Thus, allowing the search and screening over larger compositional spaces. Examples of the synergy between DFT and key parameter ML to model and screen HEAs to catalyze reactions are the recent work of Batchelor et al.27 and Pedersen et al.28 They used DFT to train machines over hundreds of adsorption energies on HEAs microstates and, further, used these machines to screen for selective and active catalysts for oxygen, carbon dioxide, and carbon monoxide reduction reactions (ORR, CO2, and CO, respectively). Special attention with respect to NRR must be paid to the work of Saidi et al.,29 while the recent experimental work of Xie et al.30 confirmed the adsorption of N atoms on the HEA surfaces as a descriptor of the catalytic activity for NRR. The aforementioned work by Saidi et al.29 developed a machine learning approach based on a convolutional neural network that screened optimum HEA catalysts for ammonia oxidation and reduction, using scaling relations and the Brønsted–Evans–Polanyi (BEP) relationship. The results showed that the 25/45 Co/Mo ratio, identified experimentally, in Mo–Co–Fe–Ni–Cu increases the probability of finding sites with similar adsorption energy as the obtained for Ru, which is one of the most effective catalysts for ammonia oxidation up to date. Another work by W. A. Saidi has also recently investigated scaling relationships on HEA using DFT and ML.31
Although N2 is the most abundant molecule in the atmosphere (78.1%), its triple bond and the lack of dipole moments make it one of the most inert species and, hence, very hard to catalyze due to the lack of nitrogen fixation on catalytic surfaces.13 In this context, the development of efficient electrocatalysts for NRR should account for the well-known N2 fixation issue. The adsorption strength of N2 molecules in the distal position on transition metal surfaces correlates with d BCs positions with respect to the Fermi level of the transition metal due to the “push–pull” mechanism with σ-donation and π*-back donation.32 It is hence expected that transition metals earlier in the periodic system with a d BC closer to the Fermi level, like Mo, have stronger N2-surface interaction than species with d BC farther from the Fermi level. Although this forms the basis for one descriptor of the bond formation, further aspects are typically required for an understanding of the role of neighbouring elements and compositions in the design of multi-element catalysts. Though the d BC concept is well established for single or few-element transition metal alloys, electron donor–acceptor interactions and local mixing are expected to play an essential role in the molecular–surface interaction for complex alloys, and, therefore, in HEAs. Understanding this interaction would facilitate a more effective design of catalysts that can mitigate the N2 fixation issue.
Computational details
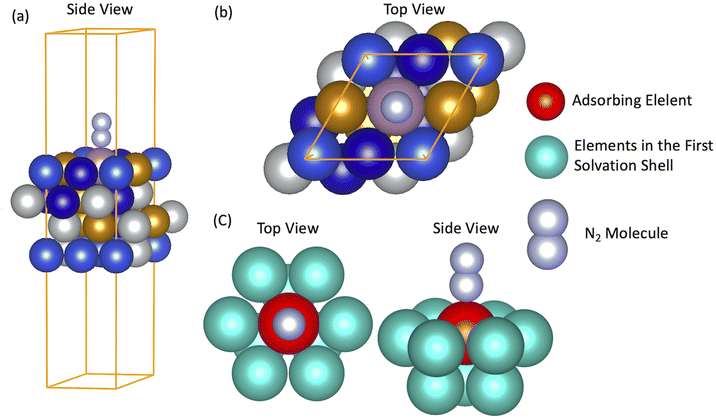
To approach the problem with nitrogen fixation, we first have to consider that bonds formed between small molecules and catalytic surfaces have a local character, hence, are determined by the microstructure of the local site of the HEAs. This means that formation and bond mechanisms between dinitrogen and the surface can be inferred by modeling microstructures of a specific HEA surface, where a random mixing needs to be considered to form a representative situation with respect to the experimental situation, with random mixing and atomic dispersion to mimic the experimental HEA.27–29 In our study, 556 microstructures are randomly created with five elements that are amongst the species Mo–Cr–Mn–Fe–Co–Ni–Cu. Fig. 1(a) and (b) display one example from the 556 cases of a HEA microstructure that, in this case, is formed by Mo–Fe–Co–Ni–Cu.N2 adsorption energies on the randomly created microstates were calculated as ΔE(N2) = EN2 − E* − Ngas-phase2. Here, N2 molecules sit vertically on the top of the active centers (N2 adsorbed in the distal position).
To achieve a deeper understanding of how the properties of the as-prepared catalyst would dictate the N2-surface bond strength and their relation with the HEA surface, d BCs and Bader charges of the active centers (adsorbing element + first solvation shell − elements in red and light blue in Fig. 1(c)) of the microstructures are calculated before the adsorption of the N2 molecule (pure slab).33,34 Band centers (BCs) are calculated as the centroid of projected density of states (PDOS) transition metal (TM) d orbitals relative to the Fermi level – shifted to 0 eV – as:
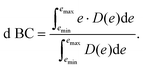 | (1) |
Here, e stands for the energy of the electronic bands, while D(e) is the density of states for such energy. Therefore, for the d BCs, D(e) refers to the projected density of states for d orbitals of TMs. The lower energy bound (emin in eq. (1)) is chosen to be −9 eV while emax is set to 9 eV.
The projected augmented wave method was used to solve the Kohn–Sham equations implemented in the Vienna ab initio Simulation Package (VASP).35,36 The wave functions were expanded using plane-waves with a cutoff energy of 450 eV while a (4 × 4 × 1) k-point mesh was used to sample over the Brillouin zone. Smearing of 0.1 eV was employed to obtain partial occupations using the Methfessel–Paxton scheme of second order. Spin-polarized orbitals were used in a FM state and the BEEF–vdW37 functional was used to describe Kohn–Sham Hamiltonian's exchange and correlation term. BEEF–vdW is one of the most accurate functionals to describe adsorption energies on transition metal surfaces.38,39 The structural models were built into a 2 × 2 × 4 face centered cubic (FCC) (111) slab with a vacuum of 20 Å, to avoid interaction amongst periodic images, and the two topmost layers were allowed to be geometry optimized. In contrast, the two bottom layers were fixed to the optimized bulk structure. Atoms were optimized until a maximum force of 0.05 eV Å−1 was obtained. Lattice parameters of the slabs are set on a weighted average basis and assume species have FCC bulk structures, similar to Batchelor et al.27 Bulk optimizations were performed with a k-point mesh of 15 × 15 × 15 in a FCC structures and the obtained lattice parameters are summarized in Table S1.† The charge state of the elements in the HEAs were investigated using Bader's quantum theory of atoms in molecules (QTAIM) as implemented in the Bader program.40–42 The Lobster package was employed to access the projected crystal orbital Hamiltonian population (-pCOHP).43,44 Aiming to compare the results with a different structural model (checking how surface coverage can change the results), a supercell containing 64 atoms (a 4 × 4 × 4 FCC (111) slab) was built using the special quasi-random approximation (SQS) to achieve ideal mixing of the elements.45 All parameters employed in this part of the investigation are similar to the case where the surface model is randomly built with the 2 × 2 × 4 FCC (111) slab. It is important to emphasize that valence electron concentration (VEC) has an important effect on the phase stability of HEAs and delimits their ground state phases, as, for instance, FCC, BCC or a mixture of these phases. The work of Guo et al.9 showed that HEAs with a VEC higher than 8 are more prone to form FCC lattices, meanwhile BCC phases are found to be more stable for cases where VEC is smaller than 6.87 – this is also confirmed in ref. 30,46 and 47. For HEAs with VEC between 6.87 and 8, a mixture of BCC + FCC phases are observed. Though the distinct ground state phases depend on the HEA's elements and their concentrations, in other words VEC, this work considers all HEAs in the FCC phase once most 556 HEAs microstructures have VEC higher than 7. That facilitates the rationalization of the obtained results.
Pearson correlation coefficients (R) were employed to estimate how well a set of data correlated linearly. This can be understood as a normalized measure of the covariance in which results vary between 1 and −1. Perfect correlation is obtained when R approaches 1 or −1, while no correlation is observed if R is close to zero.
Results
Building the structural model
The adsorption energy of N2 molecules on the catalytic surface of the 556 randomly created microstructures formed by five elements amongst Mo–Cr–Mn–Fe–Co–Ni–Cu are calculated using the framework of DFT. Fig. 1 displays one example of employed microstructure formed with Mo–Fe–Co–Ni–Cu. With the 556 investigated cases, a vast compositional ensemble of N2 adsorption energies is obtained and features of the adsorptions on distinct elements can be assessed. This approach to model HEAs is being used in different investigations, e.g., for CO and CO2 reduction where results are experimentally demonstrated, NH3 oxidation27–29 and HEAs for N2 reduction.48Comparing a specific case modeled with different slab structure
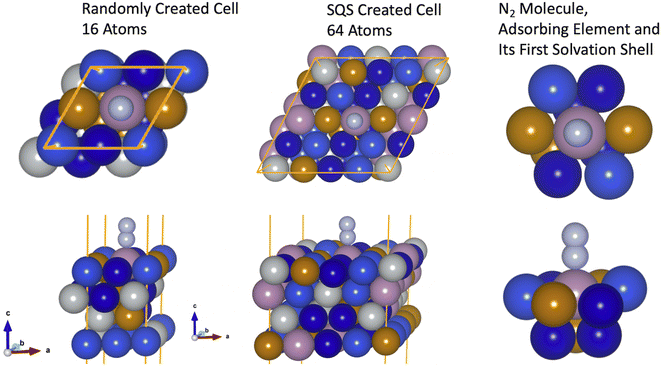
First, to check the hypothesis that the bond formation is a local process49 and also that the electronic properties on the first solvation shell around the adsorbing element are sufficient to explain the features behind the N2 bond formation mechanisms, we started by investigating two models formed by the elements Mo–Fe–Co–Ni–Cu. In the first case, the slab used to model the HEA was built with a supercell of 64 atoms and the inherent randomness of elements was accounted via the special quasirandom structure (SQS) approach.45 In the second case, a slab with 16 atoms is employed where atoms are randomly displaced (Fig. 2). Further, the solvation shell of the adsorbing element of the bigger model was modified such that it has the same elements as in the smaller model. This structure is formed by Mo as the adsorbing element plus 4 × CO, 2 × Cu, 3 × Fe in the first solvation shell of the adsorbing element (Fig. 2). The other elements of the structural models are maintained as built with the SQS approach. The difference in size between the two models will help us to confirm that small microstructures of the HEA are enough to capture the features of N2 adsorption on the HEA surface (assuming that coverage effects are small since in one case a coverage of 0.25 ML is used while for the other model a coverage of 0.06 ML). Moreover, it also indicates that the description of the bond mechanisms can be achieved by accounting only for the first solvation shell, since, out of the first solvation shell region, elements of the two models are different.N2 adsorption energy turned out to be −0.65 eV for the smaller model, while for the other case −0.63 eV (a difference of only 0.02 eV). This confirms that the bond strength between N2 and the catalytic surface depends mainly on the elements on the first solvation shell and microstructures with slabs containing 16 atoms can be used to access such property without loss of information.
Adsorption energies on the 556 microstructures
The calculated N2 adsorption energies were separated into groups regarding the element on which N2 molecules are sited on the top position (red element in Fig. 1(c)). A normal distribution was fitted for each group and the average value was calculated and highlighted in colors (Fig. 3). A significant variation of the adsorption energies is obtained, with values going from about −1.0 eV up to 0.4 eV. As expected, this variation endorses the variety of elements on the catalytic surface of the HEA that contains transition metals interacting with different bond strengths with N2 molecules. Average adsorption energies for each set of bonding elements considered here highlight the trend (Table S2†) where averaged energies grow following the series Mo < Cr < Co < Fe < Mn < Ni < Cu. Hence, one way to mitigate the N2 fixation issue found in the electrochemical nitrogen reduction reactions is to employ alloys containing Mo. This could rationalize why MoCo alloys show good activity towards NRR.50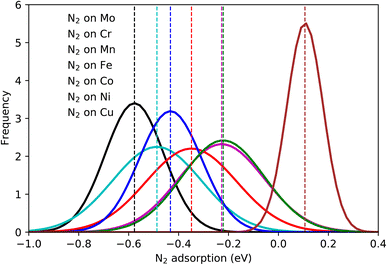 | ||
| Fig. 3 Normal distributions of the N2 adsorption energy on the atoms Mo–Cr–Mn–Fe–Co–Ni–Cu by considering 556 randomly created microstates. | ||
Although the element-wise analysis brings essential information, the variation of the N2 adsorption energy displayed for each element can still be significant. For instance, values of N2 adsorbed on Mo can vary from −0.3 eV up to −0.8 eV with an average of −0.58 eV and a standard deviation of 0.1 eV. Clearly, this shows that the bond strength between N2 and the HEA surface has a strong dependence on properties beyond single-element properties, with a direct or indirect relation with the shell around the bonding element. Here, the concept of direct or indirect relation means that: (i) direct relation should occur if dinitrogen molecules show reasonable interaction with atoms in the first solvation shell – direct relation with the first solvation shell. (ii) indirect relation refers to the case where the first solvation shell modifies the electronic structure of the adsorbing element (electron donor–acceptor interactions), affecting the bond strength between N2 and the referent element. A mixture of both considered relations could also exist.
Bond formation analysis for a specific case
In order to acquire insights into the bond formation between the HEA surface and N2 molecules estimating the interaction amongst pairs of elements, projected crystal orbital Hamiltonian population (-pCOHP) analysis was employed for the small model (Fig. 2). The -pCOHP method can provide partitioned band structure energy into bonding, non-bonding and anti-bonding energy regions of local pairs, hence, its integral delivers how strong the interaction of the pairs in question is. The integrated value of the summed-up -pCOHP between N2 – (first solvation shell elements) amounts to 0.56 eV while the integrated value of the -pCOHP between the pairs N2-(adsorbing element) is 3.53 eV (Fig. 4). The analysis shows that the bond strength between N2 molecules and the HEA substrate is almost exclusively due to the direct relation between N2 and the adsorbed atom with minor direct relation with the first solvation shell elements. Therefore, the influence of the first solvation shell elements in the N2 adsorption energies occurs via a change in the electronic structure of the adsorbing atom (electron donor–acceptor interactions) that, hence, interacts directly with the dinitrogen molecule.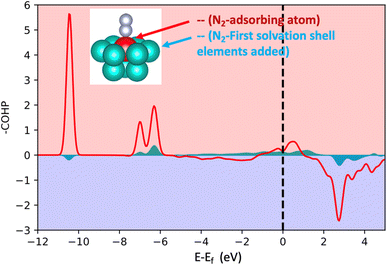 | ||
| Fig. 4 Projected crystal orbital Hamilton population (-pCOHP) analysis for the bonds between N2 and the adsorbing atoms and between N2 and the first solvation shell. The used model is shown in Fig. 2 (the case of 16 atoms). The red represents the summed-up interactions between N2 and the adsorbing element while light blue represents summed pairs of elements from the first solvation shell and N2. | ||
Bader charges and d BCs on the HEA surfaces
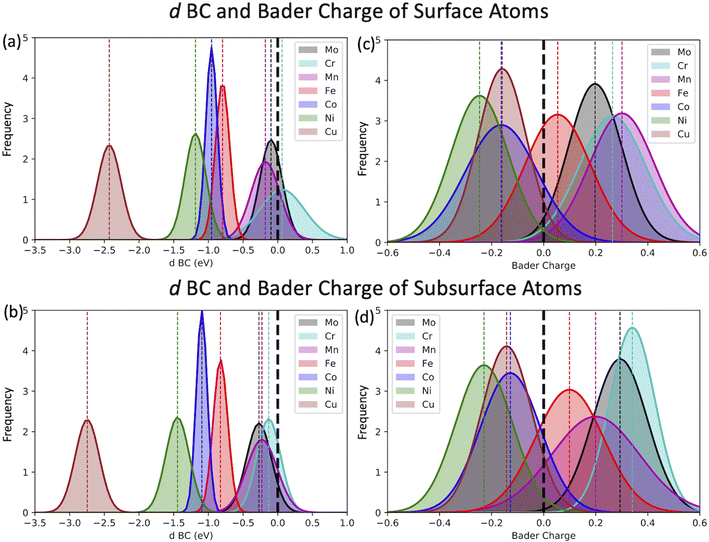
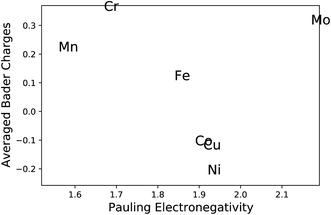
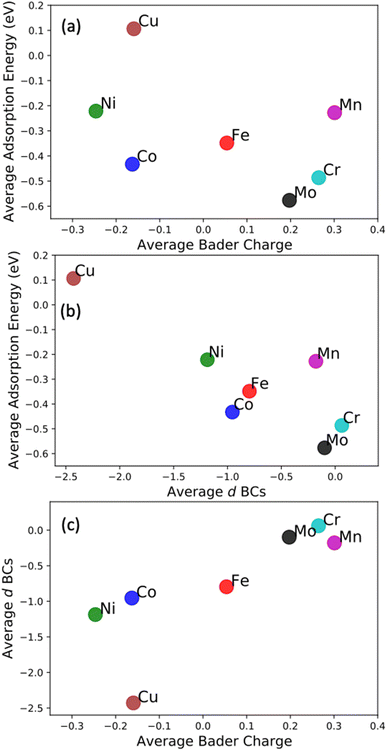
The most common approach to describe the dinitrogen bond mechanism on transition metal surfaces (on the vertical position and sited on the top site) is the “push–pull” mechanism with σ-donation and π*-back donation.32 This mechanism leads to a bond strength that correlates with the d BC position with respect to the Fermi level of the transition metals. The hypothesis here is that the local charge transference (electron donor–acceptor interactions) between the elements of the HEA microstructure shifts the d BSs of the adsorbing elements, hence, being the main responsible for the influence of the first solvation shell in the N2 adsorption energy. To better understand these relations and test this hypothesis, the d BCs of the N2 adsorbing elements and the Bader charges of the N2 adsorbing elements on the surfaces are plotted together with their respective averages (Fig. 5). The d BCs displayed significant variation with values ranging from −3.0 eV up to 1.0 eV due to the distinct number of d populated states amongst the investigated transition metals. Even when considering a specific element like Mo, i.e., there is a variance in the d BC center, similar to the case of N2 adsorption energies. There is also a shift in the d BCs of the elements when considering cases on the surface or in the subsurface of the structure. Fig. 5 also shows the Bader charges of elements in the first layer (direct contact with the N2 molecule) of the considered surface and the Bader charges of elements in the sublayer. Ni, Co and Cu, on average, receive electrons from the local environment, becoming negatively charged, while, on average, Mo, Cr, Fe and Mn become positively charged. Generally, the charge transferences correlate with the electronegativities of species in HEAs as defined by, e.g., Pauling. Fig. 6 shows the averaged Bader charges vs. the Pauling electronegativity of the referent elements and the results showed that the charge transference follows the trends of the species electronegativity, but with the exceptions of Mn and Mo. There is also a difference when extracting the Bader charge of a specific element on the surface or at the subsurface position. For instance, Mn is the more positively charged element, on average, when observed on the surface of the HEA, but at the subsurface position, there is a shift towards a more neutral state.We want to point out that a specific configuration can show more beneficial adsorption properties, but the averaged value among different local environments is here chosen as it more faithfully mimics the experimental condition where no specific control of the local environment around the adsorption site can be tailored in these entropically mixed systems. The analysis of the averaged properties can still bear significant information and be insightful regarding the average magnitude of charge transfer from the solvation shell elements toward the adsorbing element shifts the d BCs, hence, changing the N2 adsorption strength. Fig. 7 shows the averaged values of d BCs, Bader charges and N2 adsorption of the adsorbing elements Mo–Cr–Mn–Fe–Co–Ni–Cu and how they correlate. Firstly, a moderate correlation coefficient R is found between the averaged Bader charges of the adsorbing elements and the averaged N2 adsorption energies (Fig. 7(a)) where R reaches −0.47. On the other hand, the averaged d BCs and the averaged N2 adsorption energies show some level of correlation with R being −0.84. As already mentioned, this is the result of the “push–pull” adsorption mechanism that involves the d states of the transition metal and the p states of the N2 molecule.32 Moreover, the averaged d BCs also correlate with the averaged Bader charges with an R of 0.8. Elements with higher values of averaged d BC (meaning closer to the Fermi level) tend to donate electrons to the elements with averaged d BC far from the Fermi level, hence creating these relationships.
Importance of features for averaged properties
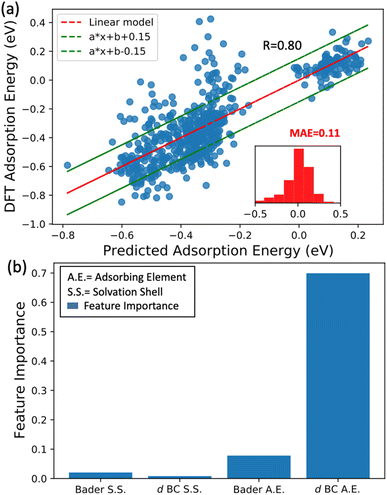
In the previous subsection, we showed that the averaged d BCs of the adsorbing elements correlate with the averaged N2 bond strength, where in turn, the averaged Bader charges of the adsorbing elements correlate with the averaged d BCs. In this section, we look into more detail at the relations between the Bader charges and d BCs of the adsorbing elements, and the Bader charges and d BCs of the elements in the first solvation shell with the N2 adsorption energies.We have established a multi-linear regression model fitted on the 556 adsorption energies of N2 molecules sited on the top position of the transition metals. The representation used in the multi-linear model involves the access of the d BCs and Bader Charges of elements at each specific region: (i) first solvation shell (light blue in Fig. 1(c)) and (ii) the adsorbing element (red in Fig. 1(c)). In other words, the model estimates the influence of the Bader charges and d BCs from the elements in the solvation shell and the elements directly binding with the N2 molecules (adsorbing element). A correlation coefficient of 0.8 is obtained between the built model data and the DFT data (Fig. 8(a)). This confirms the existent relation between these properties and the N2 adsorption energies. It is important to highlight that modeling the N2 adsorption energies within a linear relationship with the respective properties (Bader charges and d BCs) can be a too simplistic picture of the problem, due to issues like ground state energy magnetic solutions (low-high spin solutions) that varies case-by-case depending on the local environment, therefore breaking the linearity of the adsorption energy with the referent properties, d BCs depend on the magnetic solutions.51 Yet, the results still yielded an MAE of 0.11 eV between the results from DFT and the model. Moreover, most of the errors are in a range of −0.15 eV and 0.15 eV (inset of Fig. 8(a)).
Aiming to understand the impact of each feature on the model, a feature permutation algorithm is employed (Fig. 8(b)). The approach measures the changes in the model correlation after randomly permutating a specific feature, breaking the relationship between the true measure and the predicted data.52 For instance, a randomization of the Bader charges of all elements in the first solvation is performed and the difference in the correlation coefficients before and after the randomization is computed. This variation is named feature importance (FI). Here, values close to zero mean low importance while values closer to one implicate high importance for the N2 bond strength. The randomization of the values of d BCs and Bader Charges from elements in the first solvation shell leads to a very small variation of R, hence low importance for the N2 adsorption energy. On the other hand, shuffling the data related to the d BCs of the adsorbing element leads to a FI of 0.7, while shuffling the Bader charge of the adsorbing element leads to a FI of 0.07. This analysis clearly shows that d BCs of the adsorbing elements have much more importance than their Bader charges. At this point and in connection with the results found by the -pCOHP in the previews subsection for one specific case, we can confirm that indirect relations referring to the case where the first solvation shell modifies the electronic structure of the adsorbing element (electron donor–acceptor interactions) is the main factor affecting the bond strength between N2 and the referent element with a minor contribution from a direct relationship with the elements in the first solvation shell. Moreover, the shifts in the d BCs of the adsorbing elements due to the charge transference would explain the variation of the N2 adsorption energies and this is discussed next section.
d BCs of the adsorbing element and the Bader charge of the adsorbing element vs. the composition of the first solvation shell:
To generalize the above results, we have established a multi-linear regression model fitted on the 556 microstructures to correlate the d BCs and Bader Charges of the adsorbing elements with the species on the first solvation shell. Differently from the previous multi-linear model, the representation used here involves frequency counting the number of elements of each specific species on the first solvation shell (light blue in Fig. 1), instead of checking their respective d BCs and Bader charges, like in the previous section. This defines a regression problem as: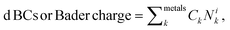 where Nik is the number of atoms of species k in the first solvation shell. The correlations (R values) between the Bader charges calculated with the multilinear model and the Bader charges of the adsorbing elements calculated via DFT displayed Rs higher than 0.96 for all cases but for Mn (Fig. 9(a) and S1†). There exist also a correlation between the d BCs and the first solvation shell composition in which Ni and Cu revealed Rs higher than 0.9 (Fig. 9(b) and S2†). However, R for the other elements varied between 0.8 and 0.5, thus, indicating an elementwise dependence of the solvation shell configuration on the d BC of the adsorbing element. These results reveal that the charge transfer from the solvation shell towards the adsorbing element is linearly related to the species concentration. Moreover, the transferred charge from the solvation shell to the adsorbing element will change the d BCs. However, the d BCs shifts depend on the magnetic states of the referent element51 and, hence, partially breaking the linear relation between the charge transference and the d BCs shift.
where Nik is the number of atoms of species k in the first solvation shell. The correlations (R values) between the Bader charges calculated with the multilinear model and the Bader charges of the adsorbing elements calculated via DFT displayed Rs higher than 0.96 for all cases but for Mn (Fig. 9(a) and S1†). There exist also a correlation between the d BCs and the first solvation shell composition in which Ni and Cu revealed Rs higher than 0.9 (Fig. 9(b) and S2†). However, R for the other elements varied between 0.8 and 0.5, thus, indicating an elementwise dependence of the solvation shell configuration on the d BC of the adsorbing element. These results reveal that the charge transfer from the solvation shell towards the adsorbing element is linearly related to the species concentration. Moreover, the transferred charge from the solvation shell to the adsorbing element will change the d BCs. However, the d BCs shifts depend on the magnetic states of the referent element51 and, hence, partially breaking the linear relation between the charge transference and the d BCs shift.
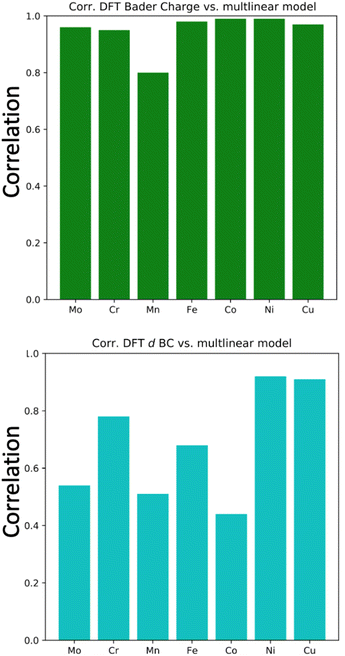 | ||
| Fig. 9 Correlation coefficients between the DFT computed d BC and DFT computed Bader charge vs. the d BCs and Bader charges calculated with the proposed linear models. | ||
Summary and conclusions
In this work, we have used the framework of DFT with vdW interaction to investigate the effects of the atomic solvation shell (the local environment) in the N2 adsorption energies of 556 randomly created HEA's microstructures. The computed adsorption energies depend on the adsorbing element, as expected, and the first solvation shell in the HEA. This indicates that the bond strength between N2 and the HEA surface has a direct and indirect relation with the first solvation shell of the bonding element. The results show that (i) a direct relationship should occur if dinitrogen molecules show reasonable interaction with atoms in the first solvation shell. (ii) indirect relation refers to the case where the first solvation shell modifies the electronic structure of the adsorbing element (electron donor–acceptor interactions), hence, affecting the bond strength between N2 and the referent element. A mixture of both considered relations could also exist.The N2 bond strengths on the HEA surfaces were investigated and the effects of surrounding elements were analysed in some detail. N2 Bond strengths between two different cells, one with 16 atoms and another with 64 atoms, were compared, and the similarity of these structures remained in the adsorbing element and their first solvation shell. The surrounding elements were randomly changed and adsorption energies differed by only 0.02 eV, showing that the N2 adsorption energies mainly depend on the adsorbing element and the first solvation shell. Subsequently, the results of the -pCOHP showed a minor direct interaction between the solvation shell elements and the N2 molecule, hence, reinforcing the idea that the solvation shell's role is to modify the adsorbing element electronic structure instead of a direct interaction with the N2 molecules. Further, the electronic structure of the adsorbing elements and their first solvation shell were analyzed based on their d BCs and Bader charges. These properties also displayed variations in similar elements that depend on the composition of their first solvation shell. This indicates that the variation of the N2 adsorption energies is a product of the variation of the adsorbing element's electronic structure. Moreover, the averaged values of Bader charges displayed some level of correlations with their d BCs and, as expected and due to the “push–pull” bond mechanism, the averaged d BCs also showed to follow the averaged N2 adsorption energies trends. Finally, this indicates a picture where the charge transference shifts the d BCs, which further modifies the N2 bond strength values. The results show that the N2 adsorption energy relies mainly on the d BCs of the adsorbing elements with a minor effect of their Bader charge. No correlation between the Bader charge and d BCs of the first solvation shell with the N2 adsorption energies was obtained. This confirms the corroborating results from the -pCOHP calculations that revealed a minor direct interaction between the N2 and the solvation shell. The results affirm that the shift in the d BCs due to the electron donor–acceptor interactions is the main factor behind the N2 bond strength variation on similar adsorbing elements. A multi-linear model is presented to identify if the charge transference from the solvation shell linearly affects the shift of the d BCs and how the shell composition plays a role in these effects. The representation here involves frequency counting the number of elements of each specific species on the first solvation shell. Their concentration linearly correlates with the Bader charge of the adsorbing elements. However, though some correlation was found, R values are smaller for d BCs, but for the case of Ni and Cu. This means that the charge transfer has a direct relation with the composition of the shell; however, the shift in the d BCs is also element-dependent and depends on their magnetic solutions. The results disclosed the mechanisms behind the obtained variation of N2 adsorption energies in HEAs (more specifically, here HEAs formed by Mo–Cr–Mn–Fe–Co–Ni–Cu) and the role of the first solvation shell on the bond strength. Though the reported results are for the adsorption of N2, the framework and analysis should be of general interest for other small molecules where the bond formation depends on the d BCs of the adsorbing elements and charge transfer from neighbouring shells.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the European Union's Horizon 2020 research and innovation programme under the call H2020-LC-SC3-2020-RES-RIA in the TELEGRAM project [grant agreement no. 101006941]. The computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) via the project SNIC 2021/5-282, partially funded by the Swedish Research Council through grant agreement no. 2019-05591.References
- G. Qing,
et al., Recent Advances and Challenges of Electrocatalytic N2 Reduction to Ammonia, Chem. Rev., 2020, 120, 5437–5516 CrossRef CAS PubMed
.
- S. L. Foster,
et al., Catalysts for nitrogen reduction to ammonia, Nat. Catal., 2018, 1, 490–500 CrossRef
.
- C. Tang and S. Z. Qiao, How to explore ambient electrocatalytic nitrogen reduction reliably and insightfully, Chem. Soc. Rev., 2019, 48, 3166–3180 RSC
.
- J. Deng, J. A. Iñiguez and C. Liu, Electrocatalytic Nitrogen Reduction at Low Temperature, Joule, 2018, 2, 846–856 CrossRef CAS
.
- M. Wang,
et al., Salting-out effect promoting highly efficient ambient ammonia synthesis, Nat. Commun., 2021, 12, 3198 CrossRef CAS
.
- M. A. Légaré,
et al., Nitrogen fixation and reduction at boron, Science, 2018, 359, 896–900 CrossRef
.
- J. W. Yeh,
et al., Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes, Adv. Eng. Mater., 2004, 6, 299–303 CrossRef CAS
.
- B. Cantor, I. T. H. Chang, P. Knight and A. J. B. Vincent, Microstructural development in equiatomic multicomponent alloys, Mater. Sci. Eng., A, 2004, 375–377, 213–218 CrossRef
.
- S. Guo,
et al., Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys, J. Appl. Phys., 2011, 109(10), 103505 CrossRef
.
- Y. Sun and S. Dai, High-entropy materials for catalysis: A new frontier, Sci. Adv., 2021, 7, 1–24 Search PubMed
.
- J. K. Pedersen, T. A. A. Batchelor, D. Yan, L. E. J. Skjegstad and J. Rossmeisl, Surface electrocatalysis on high-entropy alloys, Curr. Opin. Electrochem., 2021, 26, 100651 CrossRef CAS
.
- C. Yang,
et al., Defect engineering for electrochemical nitrogen reduction reaction to ammonia, Nano Energy, 2020, 77, 105126 CrossRef CAS
.
- N. Cao and G. Zheng, Aqueous electrocatalytic N2 reduction under ambient conditions, Nano Res., 2018, 11, 2992–3008 CrossRef CAS
.
- N. Furuya and H. Yoshiba, Electroreduction of nitrogen to ammonia on gas-diffusion electrodes loaded with inorganic catalyst, J. Electroanal. Chem., 1990, 291, 269–272 CrossRef CAS
.
- Y. Ren,
et al., Strategies to suppress hydrogen evolution for highly selective electrocatalytic nitrogen reduction: Challenges and perspectives, Energy Environ. Sci., 2021, 14, 1176–1193 RSC
.
- N. C. Kani, A. Prajapati, B. A. Collins, J. D. Goodpaster and M. R. Singh, Competing effects of pH, cation identity, H2O saturation, and N2 concentration on the activity and selectivity of electrochemical reduction of N2 to NH3 on electrodeposited Cu at ambient conditions, ACS Catal., 2020, 10, 14592–14603 CrossRef CAS
.
- Y. C. Hao,
et al., Promoting nitrogen electroreduction to ammonia with bismuth nanocrystals and potassium cations in water, Nat. Catal., 2019, 2, 448–456 CrossRef CAS
.
- D. Zhang,
et al., Multi-Site Electrocatalysts Boost pH-Universal Nitrogen Reduction by High-Entropy Alloys, Adv. Funct. Mater., 2021, 31, 1–8 Search PubMed
.
- T. Löffler, A. Ludwig, J. Rossmeisl and W. Schuhmann, What Makes High-Entropy Alloys Exceptional Electrocatalysts?, Angew. Chem., Int. Ed., 2021, 60, 26894–26903 CrossRef PubMed
.
- M. Kim,
et al., Artificial Intelligence to Accelerate the Discovery of N2 Electroreduction Catalysts, Chem. Mater., 2020, 32, 709–720 CrossRef CAS
.
- M. Zafari, D. Kumar, M. Umer and K. S. Kim, Machine learning-based high throughput screening for nitrogen fixation on boron-doped single atom catalysts, J. Mater. Chem. A, 2020, 8, 5209–5216 RSC
.
- A. Chen, X. Zhang, L. Chen, S. Yao and Z. Zhou, A Machine Learning Model on Simple Features for CO2 Reduction Electrocatalysts, J. Phys. Chem. C, 2020, 124, 22471–22478 CrossRef CAS
.
- Z. W. Chen,
et al., Machine-learning-accelerated discovery of single-atom catalysts based on bidirectional activation mechanism, Chem Catal., 2021, 1, 183–195 CrossRef CAS
.
- Z. Yang, W. Gao and Q. Jiang, A machine learning scheme for the catalytic activity of alloys with intrinsic descriptors, J. Mater. Chem. A, 2020, 8, 17507–17515 RSC
.
- N. Zhang,
et al., Machine Learning in Screening High Performance Electrocatalysts for CO2 Reduction, Small Methods, 2021, 5, 1–19 Search PubMed
.
- E. M. Y. Lee,
et al., Neural Network Sampling of the Free Energy Landscape for Nitrogen Dissociation on Ruthenium, J. Phys. Chem. Lett., 2021, 12, 2954–2962 CrossRef CAS PubMed
.
- T. A. A. Batchelor,
et al., High-Entropy Alloys as a Discovery Platform for Electrocatalysis, Joule, 2019, 3, 834–845 CrossRef CAS
.
- J. K. Pedersen, T. A. A. Batchelor, A. Bagger and J. Rossmeisl, High-Entropy Alloys as Catalysts for the CO2 and CO Reduction Reactions: Experimental Realization, ACS Catal., 2020, 10, 3658–3663 CrossRef
.
- W. A. Saidi, W. Shadid and G. Veser, Optimization of High-Entropy Alloy Catalyst for Ammonia Decomposition and Ammonia Synthesis, J. Phys. Chem. Lett., 2021, 12, 5185–5192 CrossRef CAS PubMed
.
- P. Xie,
et al., Highly efficient decomposition of ammonia using high-entropy alloy catalysts, Nat. Commun., 2019, 10, 1–12 CrossRef CAS
.
- W. A. Saidi, Emergence of local scaling relations in adsorption energies on high-entropy alloys, npj Comput. Mater., 2022, 8, 86 CrossRef CAS
.
- L. G. M. Pettersson and A. Nilsson, A molecular perspective on the d-band model: Synergy between experiment and theory, Top. Catal., 2014, 57, 2–13 CrossRef CAS
.
- B. Hammer and J. K. Nørskov, Electronic factors determining the reactivity of metal surfaces, Surf. Sci., 1995, 343, 211–220 CrossRef CAS
.
- P. J. Robinson and K. A. Holbrook, Why gold is the noblest of all the metals, Nature, 1995, 376, 238–240 CrossRef
.
- G. Kresse and J. Furthműller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS PubMed
.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B, 1999, 59, 1758 CrossRef CAS
.
- J. Wellendorff,
et al., Density functionals for surface science: Exchange-correlation model development with Bayesian error estimation, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 32–34 CrossRef
.
- S. Mallikarjun Sharada, R. K. B. Karlsson, Y. Maimaiti, J. Voss and T. Bligaard, Adsorption on transition metal surfaces: Transferability and accuracy of DFT using the ADS41 dataset, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 100, 035439 CrossRef
.
- J. Wellendorff,
et al., A benchmark database for adsorption bond energies to transition metal surfaces and comparison to selected DFT functionals, Surf. Sci., 2015, 640, 36–44 CrossRef CAS
.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef
.
- W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed
.
- A. Allouche, Software News and Updates Gabedit – A Graphical User Interface for Computational Chemistry Softwares, J. Comput. Chem., 2012, 32, 174–182 CrossRef PubMed
.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, Crystal orbital Hamilton population (COHP) analysis as projected from plane-wave basis sets, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed
.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, LOBSTER: A tool to extract chemical bonding from plane-wave based DFT, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed
.
- A. Zunger, S. H. Wei, L. G. Ferreira and J. E. Bernard, Special quasirandom structures, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS PubMed
.
- X. Yang and Y. Zhang, Prediction of high-entropy stabilized solid-solution in multi-component alloys, Mater. Chem. Phys., 2012, 132, 233–238 CrossRef CAS
.
- R. Chen,
et al., Composition design of high entropy alloys using the valence electron concentration to balance strength and ductility, Acta Mater., 2018, 144, 129–137 CrossRef CAS
.
- R. B. Araujo, I. B. Pehlivan and T. Edvinsson, High-entropy alloy catalysts: Fundamental aspects, promises towards electrochemical NH3 production, and lessons to learn from deep neural networks, Nano Energy, 2022, 105, 108027 CrossRef
.
- R. B. Araujo, G. L. S. Rodrigues, E. C. dos Santos and L. G. M. Pettersson, Adsorption energies on transition metal surfaces: towards an accurate and balanced description, Nat. Commun., 2022, 13, 1–14 Search PubMed
.
- C. J. H. Jacobsen,
et al., Catalyst design by interpolation in the periodic table: Bimetallic ammonia synthesis catalysts, J. Am. Chem. Soc., 2001, 123, 8404–8405 CrossRef CAS PubMed
.
- S. Bhattacharjee, U. V. Waghmare and S. C. Lee, An improved d-band model of the catalytic activity of magnetic transition metal surfaces, Sci. Rep., 2016, 6, 1–10 CrossRef PubMed
.
-
W. Deng, Z. Huang, J. Zhang and J. Xu, A data mining based system for transaction fraud detection, in 2021 IEEE Int. Conf. Consum. Electron. Comput. Eng. ICCECE, 2021, vol. 2021, pp. 542–545, DOI: DOI:10.1109/ICCECE51280.2021.9342376
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta09348k |
| This journal is © The Royal Society of Chemistry 2023 |