Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanism-based and data-driven modeling in cell-free synthetic biology
Angelina
Yurchenko
 abc,
Gökçe
Özkul
abc,
Natal A. W.
van Riel
def,
Jan C. M.
van Hest
abc,
Gökçe
Özkul
abc,
Natal A. W.
van Riel
def,
Jan C. M.
van Hest
 gh and
Tom F. A.
de Greef
gh and
Tom F. A.
de Greef
 *abcij
*abcij
aLaboratory of Chemical Biology, Department of Biomedical Engineering, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands. E-mail: t.f.a.d.greef@tue.nl
bInstitute for Complex Molecular Systems Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands
cSynthetic Biology Group, Department of Biomedical Engineering, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands
dComputational Biology Group, Department of Biomedical Engineering, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands
eEindhoven MedTech Innovation Center, 5612 AX Eindhoven, The Netherlands
fDepartment of Vascular Medicine, Amsterdam UMC, Amsterdam, The Netherlands
gBio-Organic Chemistry, Institute for Complex Molecular Systems, Eindhoven University of Technology, Eindhoven 5600 MB, The Netherlands
hBiomedical Engineering, Institute for Complex Molecular Systems, Eindhoven University of Technology, Eindhoven 5600 MB, The Netherlands
iInstitute for Molecules and Materials, Radboud University, 6525 AJ Nijmegen, The Netherlands
jCenter for Living Technologies, Eindhoven-Wageningen-Utrecht Alliance, 3584 CB Utrecht, The Netherlands
First published on 4th June 2024
Abstract
Cell-free systems have emerged as a versatile platform in synthetic biology, finding applications in various areas such as prototyping synthetic circuits, biosensor development, and biomanufacturing. To streamline the prototyping process, cell-free systems often incorporate a modeling step that predicts the outcomes of various experimental scenarios, providing a deeper insight into the underlying mechanisms and functions. There are two recognized approaches for modeling these systems: mechanism-based modeling, which models the underlying reaction mechanisms; and data-driven modeling, which makes predictions based on data without preconceived interactions between system components. In this highlight, we focus on the latest advancements in both modeling approaches for cell-free systems, exploring their potential for the design and optimization of synthetic genetic circuits.
1. Introduction
Synthetic biology has traditionally aimed to design novel biological systems by constructing and implementing genetic circuits into living cells.1 This approach is intended to regulate the behavior of an organism by installing desired functions.2 However, introduction of exogenous genes into a host cell burdens its metabolic processes, reduces cell growth, and hence limits the production of the target product.3 Moreover, the prototyping process of new genetic circuits in vivo is laborious and expensive.4,5 Therefore, to overcome these challenges, cell-free protein synthesis (CFPS) has emerged as a synthetic biology breadboard.6,7CFPS aims to reconstruct the transcription–translation (TXTL) mechanism of living cells (Fig. 1(a)), using either purified components8 or cell lysate that aims to provide the necessary components for the TXTL machinery.9 CFPS offers numerous advantages over cell-based systems which include the ability to synthesize toxic products,10 elimination of competition between synthetic and endogenous circuits,1 and alleviation of membrane transport limitations.6 Additionally, CFPS allows for more precise control over reaction conditions, which diversifies its application to prototyping genetic parts,6,7 biosensor development,10,11 biomanufacturing,5 educational purposes,12 and even constructing artificial cells.13 To facilitate and rationalize the prototyping process, CFPS often incorporates a modeling step that predicts the outcomes of different experimental scenarios and allows one to gain a deeper understanding of underlying mechanisms.4
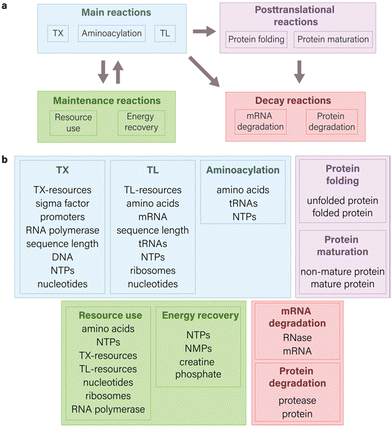 | ||
| Fig. 1 Components of an ODE model for CFPS system. (a) Scope of possible reactions for modeling cell-free gene expression. The main reactions aim to illustrate the fundamental principles of the central dogma and encompass transcription, translation, and aminoacylation processes. Maintenance reactions are centered on illustrating the kinetics of resource use and energy regeneration. When integrated with the main reactions,14 they contribute to intricate interactions within system components, thereby enhancing the capability to build predictive models. Decay reactions in the context of CFPS systems primarily focus on degradation processes related to mRNA and proteins, though they are not limited solely to these components. Posttranslational processes are directed towards the modification changes that proteins undergo after their synthesis. The directional arrows in a diagram indicate direction of interaction between various species of reactions. (b) Common molecular species involved in TXTL which are used in equations. The integration of various molecular species into a model relies on both the granularity of the model and the specific research outcomes sought. | ||
Mechanism-based modeling is a widely used modeling technique that describes TXTL dynamics by constructing a coupled system of rate equations of the underlying reactions.14 Usually, this modeling approach is represented by ordinary differential equational models (ODE) based on Michaelis–Menten, Hill, and mass-action kinetics.4 The main advantage of this modeling technique is the ability to transfer knowledge of molecular interactions into kinetics, which simplifies the interpretation of the model output.15 While ODE models provide a high level of explainability and the ability to construct a model based on predefined interactions, their major limitation lies in estimating kinetic parameters. The presence of covariance among parameters hinders accurate parameter estimation in this type of modeling.4,14,16,17
Another, more modern, modeling approach for CFPS systems is data-driven modeling, also known as machine learning. Unlike traditional ODE models, machine learning does not consider any predefined interaction between molecules but instead learns the relationship between input and output data.18 By training on multi-dimensional datasets, machine learning can reveal high-level interactions between reaction components, capturing the complexity of CFPS.19 In comparison to ODE models that study reaction components individually, therefore neglecting their explicit interactions with each other,17 machine learning is less biased when trying to understand the system's overall complexity. However, because this approach is data-dependent, its major limitations are size and variability of training datasets. These factors directly influence accuracy of a developed model and, hence, explainability of obtained predictions.20
In this highlight, we focus on the state-of-the-art mechanism-based modeling and machine-learning approaches in CFPS, along with their potential to design and optimize novel cell-free genetic circuits. We first introduce a mechanism-based modeling approach, focusing on the types of reactions used for the different cell-free systems, followed by a discussion on the parameter estimation process. Then we review the integration of machine learning into the optimization of CFPS systems.
2. Mechanism-based modeling
Mechanism-based modeling attempts to make models of biological systems through assumptions regarding their underlying mechanisms.21 Within the context of modeling CFPS systems, ordinary differential equation (ODE) models are the preferred choice due to their proficiency in capturing the dynamic behavior of genetic circuits over time while maintaining computational efficiency.22 ODE models encompass a system of differential equations that model the rate of change of various chemical species within CFPS systems.23 This framework facilitates predictions regarding system behavior under diverse conditions, including variations in DNA template and enzyme concentrations or external stimuli. Additionally, ODE models are instrumental in experimental design and offer valuable insights for optimizing cell-free systems.242.1 Reactions in cell-free protein synthesis
In the modeling of CFPS, the selection of reactions and the corresponding species significantly influence the simulated expression of the target gene (Fig. 1 and 2). Multiple types of reactions can be employed to model CFPS, falling into four primary categories: main reactions (TXTL, aminoacylation), posttranslational processes (protein folding and maturation), maintenance reactions (resource use, energy recovery), and decay reactions (mRNA and protein degradation) (Fig. 1(a)). The specific choice of reaction species, however, is contingent upon the modeling goals and may vary depending on the desired level of details (Fig. 1(b)).In this section, we focus on examining the impact of incorporating various types of reactions into ODE models for CFPS, by providing examples from literature, focusing on different modeling objectives, and emphasizing key insights found with the specific model structure.
To capture the dynamics of mRNA and protein synthesis in a cell-free system, Karzbrun et al. developed a coarse-grained model by considering reactions involving transcription, translation, and mRNA and protein degradation.26 The authors show that the rate of mRNA production depends on the binding kinetics of RNA polymerase to DNA and the length of synthesized mRNA. In contrast, the rate of protein synthesis depends on the binding of ribosomes to mRNA and the length of the protein. However, because the model does not account for resource depletion, simulated dynamics are only relevant for the first hour of the experiment, before the depletion of resources and buildup of metabolites (Fig. 2(a) and (b)).
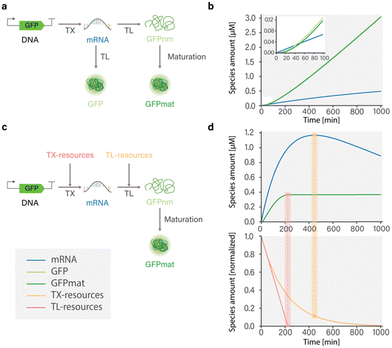 | ||
| Fig. 2 Influence of model composition on simulated dynamics of cell-free GFP expression in the PURE system; (a) structure of model developed by Karzbrun26 that includes TXTL reactions with and without protein maturation processes; (b) simulated dynamics of the model developed by Karzbrun.26 Simulation of GFP expression dynamics shows that incorporation of protein maturation processes results in delayed appearance of detectable GFP. Protein and mRNA synthesis do not reach a steady state due to the absence of resource use reactions that limit synthesis. (c) Structure of model developed by Stögbauer14 that includes TXTL, resource use, and protein maturation reactions; (d) simulated dynamics of the model developed by Stögbauer.14 Protein synthesis reaches a steady state coinciding with the depletion of translational resources (TL-resources), as indicated by the red rectangular highlight. Notably, overall mRNA concentration decreases over time, even in the presence of available transcriptional resources (TX-resources), as indicated by the yellow rectangular. This underscores the importance of providing a more comprehensive description of resource use. | ||
Mavelli et al. designed a kinetic model describing protein synthesis in the (protein synthesis using recombinant elements) PURE system8 that takes into account transcription, translation, aminoacylation, energy recovery, and transcription and translation degradation.28 The composition of the proposed model results in accurate prediction of mRNA kinetics, but with some lack of accuracy in predicting protein kinetics which is potentially stemming from an oversimplified representation of the translation process.28 Nevertheless, the model successfully captures the fundamental principles of cell-free TXTL and can be utilized to identify crucial components of the system. Consequently, ribosomes, translation factors, tRNAs, RNA polymerase, DNA, and NTPs are identified as the most influential species for achieving high productivity. Additionally, based on the simple energy recovery equation, it is evident that a significant portion of energy is consumed during transcription. To achieve more efficient energy utilization, it is recommended to reduce the concentration of DNA, while ensuring that there is no significant decline in protein production.28
Stögbauer et al. developed a kinetic model capturing the late phase of expression in the PURE system based on eight free parameters and considering transcription, translation, protein maturation, RNA degradation, and resource decay reactions.14 In their work, the resources involved in transcription and translation processes are represented as two distinct pools comprising various components such as polymerases, ribosomes, tRNAs, NTPs, and potentially other unknown factors. These resource pools are incorporated into TXTL reactions and are subject to degradation. The authors found that in the PURE system, ribosomes, rather than NTPs specifically, were responsible for synthesis degradation. Adding fresh ribosomes after 3 hours of the experiment successfully restored GFP expression. Importantly, this effect was not observed in an Escherichia coli lysate system, suggesting an important difference in protein expression between E. coli lysate and the PURE system. Furthermore, it was demonstrated that the transition from a linear response phase to a saturation phase in protein yield is a result of resource exhaustion. The timing of this transition is dependent on the concentration of the DNA template, as only a fraction of mRNA is successfully translated into protein.
By generalizing the model of Stögbauer,14 Chizzolini et al.29 designed a kinetic model that accounts for resource use and; therefore, enables the screening of genetic constructs to identify those with the desired activity. This advanced model incorporates parameters related to the activity of biological parts (the strength of transcriptional promoters and ribosome binding sites (RBSs)). Additionally, it includes two noise parameters specifically designed to account for batch-to-batch variations, which arise due to fluctuations in the concentrations of DNA templates and components of the PURE system. The model successfully predicted the expression levels of red (RFP), green (GFP), and blue (BFP) fluorescent protein encoding constructs with strong promoters and RBS. However, the same model lacked accuracy for constructs with moderate and weak strength promoters and RBSs, resulting in an average absolute difference between predictions and experimental data of 32% for RFP, 11% for GFP, and 17% for BFP. When the model was used to predict the behavior of a genetic cascade, the model correctly identified parts responsible for a high yield but was not able to predict the variability in protein synthesis. Lastly, the model was tested on a two-gene repressor circuit. The authors found that the predicted data for transcription and translation correlates well with the experimental data. However, the predicted absolute concentrations are overestimated, which was explained by the absence of factors that account for RNA folding.
Marshall and Noireaux30 developed a simple kinetic model that captures the basic mechanism, distinct regimes, and resource limitations associated with in vitro gene expression. Similar to the work by Stögbauer et al.,14 their model is based on three differential equations representing the intricate processes of transcription, translation, mRNA degradation, and protein maturation. However, their approach incorporates resource utilization through the inclusion of two conservation reactions (for RNA polymerase and ribosomes), which assumes the absence of resource degradation and maintain a constant total concentration of resources. The research demonstrates that protein production follows three distinct regimes: transient, steady state, and plateau, the latter signifying the cessation of gene expression. Furthermore, the study reveals that the maximum rate of protein production, which is influenced by plasmid concentration, exhibits two regimes: linear and saturation. In the linear regime, an increase in plasmid concentration results in a proportional increase in protein production. However, the transition to the saturation regime occurs when augmenting of the plasmid concentration no longer results in a higher rate of protein production. This shift is primarily attributed to the depletion of ribosomes associated with messenger RNAs. Building upon this key insight, the researchers utilize their findings to develop a load calculator capable of determining the optimal DNA concentration considering various factors such as promoter strengths, UTR strength, and gene length.
Moore et al. developed a detailed model that takes into account the shared use of resources such as NTPs and 3-PGA secondary energy sources needed for regeneration of NTPs, amino acids, RNA polymerase, and ribosomes.31 This model accurately predicts CFPS from previously non-modeled bacterial species and can be used as a tool for prototyping novel genetic constructs. The model describes transcription as a three-step process that includes the binding of RNA polymerase to the promoter, promoter escape, and transcription elongation. Similarly, translation is also modeled as a three-step process involving ribosome binding to the RBS, translation initiation, and translation elongation. Moreover, the model incorporates reactions for mRNA degradation, NTPs degradation and regeneration, and inactivation of ribosomes. Using this modeling framework researchers identified that overall protein yield can be increased by improving the metabolism of the secondary energy source. Additionally, the model suggests that transcriptional capacity could be a limiting factor in protein synthesis.
Singhal et al. proposed a comprehensive computational toolbox for generating deterministic mass action kinetics models of genetic circuits within a cell-free system.4 The toolbox includes reactions for transcription (modeled as a four-stage process), translation (modeled as a six-stage process), protein maturation, RNA degradation, consumption and regeneration of resources (amino acids, RNA polymerase, ribosomes, NTPs), and transcriptional regulation reactions. In addition, the toolbox incorporates a library of parts, including DNA, mRNA, protein, small molecules, and other miscellaneous species, that can be used to create a circuit model. The toolbox was employed to model an incoherent feed-forward loop (IFFL) circuit under different experimental conditions, demonstrating its applicability. However, while the generated model successfully predicted the qualitative behavior of the cell-free genetic circuit, it faced limitations in accurately capturing the quantitative aspects of the circuit's behavior. The authors hypothesized that these discrepancies may stem from the parameter estimation procedure, which involves splitting parameter inference into multiple stages. In this procedure, a subset of parameters is optimized in each stage while parameters from the previous stage are fixed.
To capture the dynamics of GFP cell-free expression in the PURE system, Carrara et al.32 advanced the model by Mavelli et al.8 by including posttranslational processes, protein folding and maturation, which were found to be limiting. Although the model successfully predicted the final protein concentration, the production rate slightly deviated from the true rate. This mismatch can be attributed to the inadequate consideration of cooperativity and nonlinearity that are present in the system.32
2.2 Parameter estimation
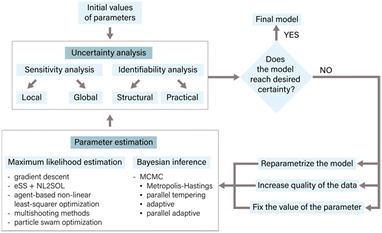
In the context of ODE models, parameters often represent fixed constants with respect to time33 and are proportional to the rates of the underlying reactions.34 Accurate parameter estimation is a keystone in correlating a model to experimental data, enabling reliable inferences and predictions. Parameter estimation involves determining the values of unknown parameters in a given model using available data.24,35The process of parameter estimation is iterative (Fig. 3) and involves several steps to refine and improve the parameter values of the model. The process starts with an initial estimate of parameter values derived from literature or expert knowledge. Following the initial estimate, an uncertainty analysis of the parameters is conducted to quantify the uncertainty within the current model structure and its subsequent impact on the predictions.36 Methods like sensitivity analysis, identifiability analysis, and bootstrapping are employed for determining parameter uncertainty.33,35,37 The results of the uncertainty analysis determine the next steps in the parameter estimation process. These findings may necessitate a refinement of the model through reparameterization, a process in which specific parameter values are either fixed or eliminated. Additionally, the uncertainty analysis can guide the generation of new experimental data with higher information density to improve the parameter estimates.17 Once the necessary model modifications have been made and/or new experimental data has been generated, initial parameter values are adjusted with the use of appropriate estimation methods. Commonly used estimation approaches include maximum likelihood estimation, which aims to find parameter values that minimize the discrepancy between model predictions and experimental data, and Bayesian inference, which combines prior knowledge about parameters with experimental data to estimate posterior distributions of parameters.24,33 After parameter estimation, it is crucial to conduct another round of uncertainty analysis to assess the uncertainty in the newly estimated parameters and evaluate the overall model certainty.35 This iterative process continues until the desired level of certainty is achieved, which could be related to specific performance metrics, prediction accuracy, or addressing particular research questions.24,33,37 By following this iterative process of parameter estimation, uncertainty analysis, and model refinement, the model can be continuously improved, resulting in more reliable and accurate predictions.17
In this section, we focus on methods for parameter estimation, followed by a discussion of the two most popular methods for the identification of parameter uncertainty, i.e., sensitivity and identifiability analysis. We end with a discussion of strategies to increase the certainty of predictions.
The goal of maximum likelihood estimation is to determine the optimal set of parameters for a dynamic model to achieve the closest match to the experimental data. This process entails maximizing a likelihood function, which quantifies the agreement between model predictions and actual observations.24 To achieve this maximization, various optimization algorithms are commonly employed. These algorithms encompass a wide range of techniques, including gradient descent, differential evolution methods,38 genetic algorithms,39 particle swarm optimization,40 simulated annealing,41,42 multiple shooting methods,43,44 enhanced scatter search,45 Kalman filtering,34 and agent-based non-linear least-squarer optimization.17
In contrast, Bayesian inference aims to determine the posterior distribution of parameter values. This posterior distribution represents updated beliefs about the parameters after incorporating both prior knowledge and observed data, which enables simultaneous assessment of parameter values with a determination of parameters’ uncertainty. Sampling methods such as Markov Chain Monte Carlo (MCMC) are commonly used to approximate the posterior distribution of parameters. There are many variations of MCMC algorithms, such as Metropolis–Hastings, adaptive, parallel tempering, and parallel adaptive. These variations offer different strategies and enhancements to improve the efficiency and effectiveness of MCMC estimation. To gain a comprehensive understanding and compare these methods, we refer the reader to the survey conducted by Valderrama–Bahamóndez and Fröhlich.46
For complex posterior distributions that are challenging to evaluate using sampling methods, the estimation process often relies on one of the optimization algorithms described above. These algorithms aim to minimize the Kullback–Leibler divergence between the approximate distribution and the true posterior distribution, enabling effective exploration and characterization of posterior distributions.47
Sensitivity analysis. Sensitivity analysis is a common practice used for determining parameter uncertainty.33 Sensitivity analysis determines how the model output varies in response to changes in the model's parameters. There are two major types of sensitivity analysis: local and global.48,49 Local sensitivity analysis involves assessing the impact of small changes around a default parameter value on the model output. This effect is quantified using sensitivity coefficients, which are calculated as the first-order partial derivatives of the system output concerning the input parameters. Methods for the calculation of the derivative include finite difference approximation, direct differential method, adjoint sensitivity analysis, and metabolic control analysis.49 Local sensitivity analysis is typically performed by perturbing one parameter at a time, and it does not provide insights into the interdependencies among parameters. In contrast, global sensitivity analysis quantifies the significance of model inputs and their interactions in relation to the model output. Methods of global sensitivity analysis include parameter space sampling (Latin hypercube sampling), multi-parametric sensitivity analysis, partial rank correlation coefficient analysis, Morris sensitivity analysis method, Weighted average of local sensitivities, Sobol sensitivity analysis, Fourier amplitude sensitivity test, and Random sampling high-dimensional model representation.49 For a deeper exploration of differences between local and global sensitivity analysis, along with recommendations on their implementations, we direct the reader to Zi's extensive review.49
Identifiability analysis. Parameter identifiability refers to the ability to determine the values of the model parameters without ambiguity and serves as a key approach for determining parameter uncertainty.37 There are two types of parameter identifiability: a priori (structural) and a posteriori (practical). Structural identifiability implies the possibility of finding unique values for parameters taking into consideration the structure of the model.50 Several approaches commonly employed for this purpose include sensitivity analysis, differential algebra, differential geometry, power series expansion, generating series, and seminumerical methods.37 However, the majority of these methods are only suitable for models with low-dimensional parameter space due to high computational costs. While structural identifiability implies the possibility of determining a unique set of parameters from noise-free data, practical identifiability refers to the precision with which parameters can be estimated from the present data.37 The lack of practical identifiability often arises from two primary factors: the parameter's negligible influence on the system,51 which can be assessed through sensitivity analysis, and potential interdependencies among parameters,51 which can be evaluated by examining the collinearity of parametric sensitivities51 using Fisher information matrix17,24 or by performing a Profile likelihood analysis.33,37
1. Reparametrization or simplification of the model via elimination of parameters.52
2. Inferring values of nonidentifiable parameters from other sources.52
3. Implementation of optimal experimental design in order to increase the quality of the data.17,24
The reparametrization approach is meant to reduce model complexity by eliminating redundant parameters, so the number of nonidentifiable parameters is reduced by the number of total correlated sets, leading to improved estimation outcomes. Joubert et al.52 highlighted that, while simplification of the parameter space can be an effective strategy in over-parametrized models, it cannot be implemented for parameters that are essential for a model.
In cases when nonidentifiable parameters are essential for a model and therefore cannot be eliminated, one possible solution is to infer parameter values from literature or biochemical databases. The concept behind this approach is that if the value of one unknown parameter within a correlated set is known, it disrupts the correlation between parameters. Joubert et al.52 emphasized that, even if parameter values are acquired from the existing literature, they might still necessitate recalibration using experimental data. Therefore, caution should always be exercised when undertaking such recalibration to ensure accuracy and reliability.
The final approach tackles the challenge of acquiring a sufficiently comprehensive dataset to enable precise parameter estimation.24 It entails employing optimal experimental design (OED),53 a methodology that formulates dynamic experiments strategically to yield experimental data with the highest attainable statistical quality for parameter estimation. OED focuses on devising experiments that optimize the precision, efficiency, and information content of the resulting data, leading to enhanced accuracy in parameter estimates.
The study conducted by van Sluijs et al.17 demonstrates the effectiveness of employing a microfluidic-based OED in disrupting covariation among parameters, consequently increasing the accuracy of parameter estimation in cell-free genetic networks. The central concept behind the proposed methodology is to leverage OED to identify optimal inflow patterns of inputs into a microfluidic device, resulting in higher information density in the experimental data. To determine the inflow pattern, researchers carefully analyzed parameter identifiability from a database of in silico experiments, focusing on the inflow patterns that have the most significant impact on the distribution of individual parameters (i.e., a pattern that minimizes the determinant of the Fisher information matrix). By controlling the inflow pattern of reporter, activator, and repressor DNA constructs into a microfluidic device, authors were able to increase the information density and disrupt covariance between parameters, leading to more accurate estimations of the parameters of the model of incoherent feed-forward loop. This advancement highlights the considerable potential of OED in the forward design of intricate cell-free genetic networks.
3. Data-driven modeling
In contrast to mechanism-based modeling, a data-driven approach known as machine learning departs from constructing models based on predefined reaction mechanisms. Instead, it leverages computational algorithms to discern patterns from available data.54 Machine learning is broadly classified into two types: supervised and unsupervised learning.55 In supervised learning (Fig. 4(a)), algorithms are trained using labeled datasets, known as training datasets, to infer the mapping between features (X) and corresponding labels (Y). During training, algorithms investigate the statistical relationships between features and labels, optimizing parameters through gradient descent and minimizing a chosen loss function to enhance predictive accuracy. Commonly used loss functions include root-mean-squared error (RMSE), mean-squared error (MSE), mean absolute error (MAE), and coefficient of determination (R2). This type of machine learning is versatile for predictive modeling across a range of outcomes, including binary responses (e.g., distinguishing good or bad riboregulators56) and categorical labels (e.g., determining the on, off, or on/off state of an RNA switch57) for classification problems, and continuous values (such as protein yield58) for regression problems.19 The most commonly used supervised algorithms include linear regression, Ridge regression, Lasso regression, logistic regression, support vector machines, decision trees, ensemble methods, K-nearest neighbors, artificial neural networks, and naïve Bayes.54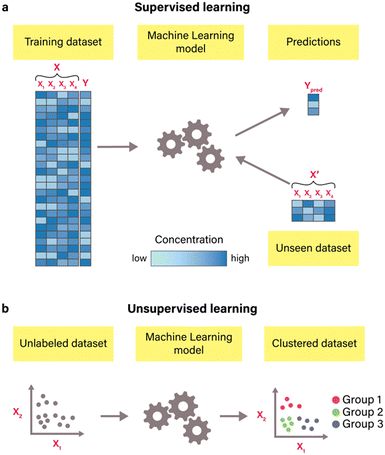 | ||
| Fig. 4 Common types of machine learning algorithms. (a) Supervised learning. In supervised learning machine learning, a model is trained on a labeled dataset consisting of features (X) and their corresponding labels (Y). Each column (X1, X2, X3, and X4) corresponds to a specific feature (e.g., specific buffer component), and each row is one observation (e.g., one buffer composition) with its corresponding output label (e.g., protein yield).20 The model's predictions (Ypred) are obtained from the unseen dataset. This dataset consists of the same features as the training dataset but with different data points (X′). Different colors of data points in datasets correspond to specific concentrations of compounds, with increased concentration levels manifesting as deeper, more intense colors. (b) – Unsupervised learning. In unsupervised learning, algorithms are trained on datasets that contain only features (e.g., X1 and X2) without any labeled output values. These algorithms identify patterns and structures within the data. For instance, clustering algorithms that are illustrated here group similar data points based on their feature values, which results in clustering data into three distinct groups. | ||
Unsupervised learning (Fig. 4(b)), on the other hand, operates without labeled datasets. Instead, it uncovers structures and patterns within unlabeled data (i.e., data that only contains features), enabling insights into the inherent organization of the data without explicit guidance.54 For instance, unsupervised methods such as clustering can be used for identifying distinct groups of data, such as protein sequences with similar properties59 and gene clusters,60 while dimension reduction methods such as principal component analysis and independent principal component analysis can be used for data visualization and exploratory data analysis.61
An important subset of machine learning that is useful for modeling cell-free systems is deep learning, also known as representation learning. This method enables the utilization of large, high-dimensional data sets for both supervised and unsupervised modeling purposes.20,55 By using artificial neural networks, deep learning extracts intricate patterns from the input data. For instance, it can discern secondary-structure motifs from RNA sequences, enabling accurate predictions of RNA function.56 The most commonly used neural network architectures include multilayer perceptrons (MLP), convolutional neural networks (CNN), recurrent neural networks, transformers, and graph neural networks. To gain a broader overview of the deep learning methods, we refer readers to surveys conducted by Beardall et al.20 and Greener et al.62
In the past decade, supervised, unsupervised, and especially deep learning machine learning models have shown to be incredibly versatile in the field of synthetic biology. They are useful in areas such as sequence design,56,57,63 protein structure prediction,64 and image recognition.65 Nevertheless, within the context of CFPS, their utilization has predominantly centered around system optimization and sequence design, which constitutes the primary focus of this section.
3.1 Optimal experimental design
System optimization is a crucial step within the context of CFPS to fully harness its inherent potential.66 To tackle the optimization challenge, various experimental methods have been devised. One commonly employed approach, known as One Factor at a Time (OFAT), involves fine-tuning the system's components one by one. However, OFAT often falls short of achieving optimal performance,67 primarily due to its vulnerability to the initial values assigned to individual variables.66 One promising solution to address these limitations involves adopting an optimal experimental design approach known as Bayesian optimization, also referred to as active learning, and widely recognized in the machine learning community.68–70 Bayesian optimization is a form of supervised learning that strategically selects the most informative data points for labeling, thereby reducing the necessary number of experiments to optimize the biological objective function that either does not have a defined functional form or is expensive to query. This function serves as a mathematical representation of a specific biological process, that maps input features X to corresponding labels Y.70–72Bayesian optimization is an iterative process (Fig. 5) that begins with the training of a machine-learning model using a training dataset. This model serves as a surrogate model that helps to approximate a biological objective function.72 After training, the model predicts labels and assesses uncertainty for unlabeled data points. These predictions and uncertainty values guide the acquisition function, which selects the most informative data points for further examination. These chosen data points are then labeled with the assistance of an oracle, often portrayed as a human domain expert, and merged into the initial labeled dataset. This iterative process continues until the desired outcome is reached.68–70
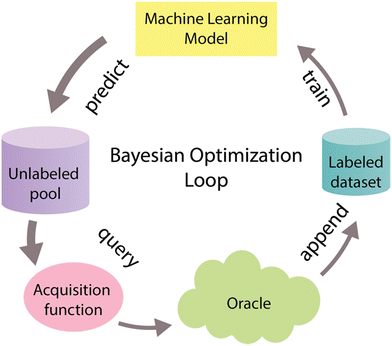 | ||
| Fig. 5 Bayesian optimization cycle. The Bayesian optimization cycle initiates with the training of a machine learning model using an initial labeled dataset. Following this training, the model predicts labels and assesses the associated uncertainty for data points within an unlabeled pool. These predictions and uncertainty scores serve as inputs for the acquisition function, which strategically chooses the most informative data points to include in the sample. Subsequently, these highly informative data points are labeled with the assistance of an oracle (i.e. an experimentalist) and then incorporated into the initial labeled dataset. This iterative process continues until the desired outcome is achieved.62–64 Different widths of arrows represent the amount of data that goes through the cycle. | ||
The common choice for the acquisition function in synthetic biology problems58,71 is the upper confidence bound (UCB), which assigns a higher priority to data points with larger uncertainty estimates, as these are deemed more likely to offer valuable information for refining the model. Other types of acquisition functions include the probability of improvement, expected model change, variance reduction, Fisher information ratio, and estimated error reduction.69
Borkowski et al.58 demonstrated that implementation of Bayesian Optimization for lysate-based buffer optimization increases GFP production by 34 times in comparison with initial buffer composition. Their investigation focused on 11 buffer components, including Mg-glutamate, K-glutamate, amino acid mix, tRNA, CoA, NAD, cAMP, folinic acid, spermidine, 3-PGA, and NTPs. Utilizing an ensemble of MLPs as a predictive model, they achieved an R2 value of 0.93. This model was further utilized for investigation of the dependence between the yield and the component concentration through a mutual information score, a method that quantifies mutual dependence between two variables. Their analysis revealed that Mg-glutamate, K-glutamate, amino acids, spermidine, 3-PGA, and NTPs exert a significant influence on protein synthesis.
In addition to Borkowski et al.,58 Pandi et al.71 extended this approach for a variety of cell-free systems by introducing METIS, a user-friendly and versatile machine-learning workflow. METIS facilitates data-driven optimization of a biological objective function, even with limited datasets, due to the utilization of the XGBoost regressor73 as a predictive model, which shows good performance even with small datasets. To showcase METIS's utility in optimizing different biological objective functions, the algorithm was applied to genetic circuits, transcriptional and translational units, and complex metabolic networks such as the CETCH cycle. Notably, when applied to CFPS GFP optimization using similar composition as Borkowski et al.,58 METIS identified tRNAs and Mg-glutamate as crucial components for GFP optimization, while cAMP and NAD were deemed less significant contributors, contrary to the findings of Borkowski et al.
These cases demonstrate the versatility of BO for optimizing various types of cell-free systems at different levels of complexity.
3.2 Sequence design
Recent advances in deep learning have enabled the utilization of high-dimensional biological data, such as DNA and protein sequences, for predictive modeling applications. One such application is the utilization of deep learning models for the design and optimization of synthetic genetic circuits.Pandi et al.74 demonstrated the accelerated de novo development of antimicrobial peptides (AMPs) in the CFPS pipeline through the application of deep learning techniques. Their approach involved a combination of unsupervised and supervised deep learning methods, enabling the exploration of 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 theoretical sequences and subsequent prioritization of 500 candidates for CFPS screening. Following screening experiments, 30 of these AMP candidates were identified as functional, with 6 showing potent antimicrobial activity against multidrug-resistant pathogens. Importantly, these peptides showed no emergence of resistance and minimal toxicity in human cells. For AMP sequence exploration, they utilized generative deep learning, an unsupervised method that uncovers design principles within specific sequences, such as proteins, and generates novel sequences based on these learned rules. They employed a variational autoencoder as the generative model, initially trained on protein datasets from Uniprot to learn design principles. Through transfer learning, this autoencoder was fine-tuned to adapt to AMP sequences. The generated AMPs were then prioritized based on minimum inhibitory concentration, predicted by a supervised model. For this supervised aspect, they employed a combination of Convolutional Neural Networks (CNN) and Recurrent Neural Networks (RNN).
000 theoretical sequences and subsequent prioritization of 500 candidates for CFPS screening. Following screening experiments, 30 of these AMP candidates were identified as functional, with 6 showing potent antimicrobial activity against multidrug-resistant pathogens. Importantly, these peptides showed no emergence of resistance and minimal toxicity in human cells. For AMP sequence exploration, they utilized generative deep learning, an unsupervised method that uncovers design principles within specific sequences, such as proteins, and generates novel sequences based on these learned rules. They employed a variational autoencoder as the generative model, initially trained on protein datasets from Uniprot to learn design principles. Through transfer learning, this autoencoder was fine-tuned to adapt to AMP sequences. The generated AMPs were then prioritized based on minimum inhibitory concentration, predicted by a supervised model. For this supervised aspect, they employed a combination of Convolutional Neural Networks (CNN) and Recurrent Neural Networks (RNN).
Overall, this work showcases a high potential for combining CFPS and deep learning methods for the high-throughput development of novel proteins.
4. Conclusions
The rapid growth of cell-free synthetic biology necessitates the incorporation of the modeling process into design and prototyping of genetic circuits, enabling alignment with the burgeoning interest in this field. Both mechanism-based and data-driven modeling approaches play a pivotal role in modeling CFPS systems, with each approach finding its specific niche of applicability.Mechanism-based models, due to their fundamental modeling principles, are invaluable for developing a comprehensive understanding of a system's behavior and effectively identifying bottlenecks in the CFPS process. This approach necessitates an in-depth understanding of the underlying mechanisms which leads to the need to select appropriate kinetic reactions. With regards to CFPS reactions, TXTL,26 resource use,4,14,29,30 and protein maturation14,29,30 are found to be essential for model structure. Depending on the research objectives, aforementioned reactions can be described on different levels of granularity, with additional integration of other types of reactions including aminoacylation,28 energy use,28 and protein folding.32 Another important factor for the development of a predictive model is an accurate parameter estimation. This process is iterative and includes an evaluation step often involving optimization or Bayesian methods, followed by determination of the parameters’ uncertainty using techniques such as sensitivity, identifiability analysis, and bootstrapping. Improving the certainty of estimated parameters can be achieved through reparametrization, inferring parameter values from external sources, and enhancing data quality using optimal experimental design techniques. Nonetheless, in the context of this modeling approach, individual system components are frequently examined in isolation, potentially introducing biases that hinder a comprehensive understanding of the overall system behavior.
Conversely, data-driven modeling relies on the statistical analysis of input and output data within the CFPS system, making it particularly advantageous for optimal experimental design.58 A fundamental prerequisite for the effective deployment of data-driven models is the availability of informative and diverse datasets for model training. This condition can be met through the utilization of Bayesian optimization techniques.3,71
Furthermore, the rapid advancements in deep learning techniques have opened a compelling avenue for the application of data-driven models in the domain of cell-free synthetic biology, particularly in the realm of sequence design. In this context, a machine learning model serves as a tool for designing, validating, and optimizing genetic sequences with desired outcomes. A noteworthy example is the utilization of deep learning methodologies to accelerate the de novo development of antimicrobial peptides.74
A notable challenge of data-driven models is the interpretability of obtained results, which could potentially be addressed with the use of explainable AI methods. For instance, in sequence design, examining motifs or partial motifs detected by convolutional filters and assessing the positional importance of nucleotides can provide valuable insights into sequence design rules.56,57
Overall, both modeling methods are of paramount importance in guiding the development of novel synthetic circuits. To address the limitations inherent in each approach, one promising solution is the adoption of a hybrid modeling strategy.75,76 This strategy involves amalgamating the interpretability of mechanism-based modeling with the ability to represent high-level interactions among reaction components provided by data-driven models.
Author contributions
A. Yurchenko – conceptualization, writing, original draft, review & edits; visualization. G. Özkul – writing, review & edits. N. A. W. van Riel – supervision. J. C. M. van Hest – supervision. T. F. A. de Greef – conceptualization, writing, review & edits, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funded by the European Union and supported by the UK Engineering and Physical Sciences Research Council (GA 101072980). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Executive Agency. Neither the European Union nor the granting authority can be held responsible for them.Notes and references
- C. E. Hodgman and M. C. Jewett, Metab. Eng., 2012, 14, 261–269 CrossRef CAS PubMed.
- M. El Karoui, M. Hoyos-Flight and L. Fletcher, Front. Bioeng. Biotechnol., 2019, 1–8 Search PubMed.
- O. Borkowski, C. Bricio, M. Murgiano, B. Rothschild-Mancinelli, G.-B. Stan and T. Ellis, Nat. Commun., 2018, 9, 1–11 CrossRef CAS PubMed.
- V. Singhal, Z. A. Tuza, Z. Z. Sun and R. M. Murray, Synth. Biol., 2021, 1–16 CAS.
- R. J. R. Kelwick, A. J. Webb and P. S. Freemont, Front. Bioeng. Biotechnol., 2020, 8, 1–15 CrossRef PubMed.
- D. Garenne, M. C. Haines, E. F. Romantseva, P. Freemont, E. A. Strychalski and V. Noireaux, Nat. Rev. Methods Primer, 2021, 1, 1–18 CrossRef.
- Cell-Free Gene Expression: Methods and Protocols, ed. A. S. Karim and M. C. Jewett, Springer, US, New York, NY, 2022 Search PubMed.
- Y. Shimizu, A. Inoue, Y. Tomari, T. Suzuki, T. Yokogawa, K. Nishikawa and T. Ueda, Nat. Biotechnol., 2001, 19, 751–755 CrossRef CAS PubMed.
- J. Shin and V. Noireaux, ACS Synth. Biol., 2012, 1, 29–41 CrossRef CAS PubMed.
- J. K. Jung, K. K. Alam, M. S. Verosloff, D. A. Capdevila, M. Desmau, P. R. Clauer, J. W. Lee, P. Q. Nguyen, P. A. Pastén, S. J. Matiasek, J.-F. Gaillard, D. P. Giedroc, J. J. Collins and J. B. Lucks, Nat. Biotechnol., 2020, 38, 1451–1459 CrossRef CAS PubMed.
- L. Zhang, W. Guo and Y. Lu, Biotechnol. J., 2020, 15, 1–14 Search PubMed.
- L. C. Williams, N. E. Gregorio, B. So, W. Y. Kao, A. L. Kiste, P. A. Patel, K. R. Watts and J. P. Oza, Front. Bioeng. Biotechnol., 2020, 8, 1–13 CrossRef PubMed.
- D. T. Gonzales, N. Yandrapalli, T. Robinson, C. Zechner and T.-Y. D. Tang, ACS Synth. Biol., 2022, 11, 205–215 CrossRef CAS PubMed.
- T. Stögbauer, L. Windhager, R. Zimmer and J. O. Rädler, Integr. Biol., 2012, 4, 494–501 CrossRef PubMed.
- C. Kreutz, Front. Phys., 2020, 8, 1–14 CrossRef.
- M. Koch, J.-L. Faulon and O. Borkowski, Front. Bioeng. Biotechnol., 2018, 6, 1–6 CrossRef PubMed.
- B. Van Sluijs, R. J. M. Maas, A. J. Van Der Linden, T. F. A. De Greef and W. T. S. Huck, Nat. Commun., 2022, 13, 1–11 Search PubMed.
- J.-L. Faulon and L. Faure, Curr. Opin. Chem. Biol., 2021, 65, 85–92 CrossRef CAS PubMed.
- D. M. Camacho, K. M. Collins, R. K. Powers, J. C. Costello and J. J. Collins, Cell, 2018, 173, 1581–1592 CrossRef CAS PubMed.
- W. A. V. Beardall, G.-B. Stan and M. J. Dunlop, GEN Biotechnol., 2022, 1, 360–371 CrossRef CAS PubMed.
- R. E. Baker, J.-M. Peña, J. Jayamohan and A. Jérusalem, Biol. Lett., 2018, 14, 1–4 Search PubMed.
- A. Ay and D. N. Arnosti, Crit. Rev. Biochem. Mol. Biol., 2011, 46, 137–151 CrossRef PubMed.
- Encyclopedia of Systems Biology, ed. W. Dubitzky, O. Wolkenhauer, K.-H. Cho and H. Yokota, Springer, New York, New York, NY, 2013 Search PubMed.
- J. R. Banga and E. Balsa-Canto, Essays Biochem., 2008, 45, 195–210 CrossRef CAS PubMed.
- Z. A. Tuza, V. Singhal, J. Kim and R. M. Murray, in 52nd IEEE Conference on Decision and Control, IEEE, Firenze, 2013, 1404–1410.
- E. Karzbrun, J. Shin, R. H. Bar-Ziv and V. Noireaux, Phys. Rev. Lett., 2011, 106, 048104 CrossRef PubMed.
- M. R. McFarland, C. D. Keller, B. M. Childers, S. A. Adeniyi, H. Corrigall, A. Raguin, M. C. Romano and I. Stansfield, Nucleic Acids Res., 2020, 48, 3071–3088 CrossRef CAS PubMed.
- F. Mavelli, R. Marangoni and P. Stano, Bull. Math. Biol., 2015, 77, 1185–1212 CrossRef CAS PubMed.
- F. Chizzolini, M. Forlin, N. Yeh Martín, G. Berloffa, D. Cecchi and S. S. Mansy, ACS Synth. Biol., 2017, 6, 638–647 CrossRef CAS PubMed.
- R. Marshall and V. Noireaux, Sci. Rep., 2019, 9, 1–12 CrossRef CAS PubMed.
- S. J. Moore, J. T. MacDonald, S. Wienecke, A. Ishwarbhai, A. Tsipa, R. Aw, N. Kylilis, D. J. Bell, D. W. McClymont, K. Jensen, K. M. Polizzi, R. Biedendieck and P. S. Freemont, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E4340–E4349 CrossRef CAS PubMed.
- P. Carrara, E. Altamura, F. D’Angelo, F. Mavelli and P. Stano, Data, 2018, 3, 41 CrossRef.
- J. Vanlier, C. A. Tiemann, P. A. J. Hilbers and N. A. W. Van Riel, Math. Biosci., 2013, 246, 305–314 CrossRef CAS PubMed.
- G. Lillacci and M. Khammash, PLoS Comput. Biol., 2010, 6, 1–17 CrossRef PubMed.
- K. Jaqaman and G. Danuser, Nat. Rev. Mol. Cell Biol., 2006, 7, 813–819 CrossRef CAS PubMed.
- M. R. Andalibi, P. Bowen, A. Carino and A. Testino, Comput. Chem. Eng., 2020, 140, 1–19 CrossRef.
- F.-G. Wieland, A. L. Hauber, M. Rosenblatt, C. Tönsing and J. Timmer, Curr. Opin. Syst. Biol., 2021, 25, 60–69 CrossRef CAS.
- H. Peng, Z. Guo, C. Deng and Z. Wu, J. Comput. Sci., 2018, 26, 501–511 CrossRef.
- M. Abdel-Basset, L. Abdel-Fatah and A. K. Sangaiah, Computational Intelligence for Multimedia Big Data on the Cloud with Engineering Applications, Elsevier, 2018, pp. 185–231 Search PubMed.
- D. Akman, O. Akman and E. Schaefer, J. Appl. Math., 2018, 2018, 1–9 CrossRef.
- F. Hussain, S. K. Jha, S. Jha and C. J. Langmead, Int. J. Bioinf. Res. Appl., 2014, 10, 1–27 CrossRef.
- N. Mamano and W. B. Hayes, Bioinformatics, 2017, 33, 2156–2164 CrossRef CAS PubMed.
- George Mason University and F. Hamilton, SIAM Undergrad. Res. Online, 2011, 4, 16–31 CrossRef.
- M. Peifer and J. Timmer, IET Syst. Biol., 2007, 1, 78–88 CrossRef CAS PubMed.
- J. A. Egea, E. Vazquez, J. R. Banga and R. Martí, J. Glob. Optim., 2009, 43, 175–190 CrossRef.
- G. I. Valderrama-Bahamóndez and H. Fröhlich, Front. Appl. Math. Stat., 2019, 5, 1–10 CrossRef.
- C. W. Fox and S. J. Roberts, Artif. Intell. Rev., 2012, 38, 85–95 CrossRef.
- G. Qian and A. Mahdi, Math. Biosci., 2020, 323, 1–19 CrossRef PubMed.
- Z. Zi, IET Syst. Biol., 2011, 5, 336–346 CrossRef CAS PubMed.
- F. Anstett-Collin, L. Denis-Vidal and G. Millérioux, Annu. Rev. Control, 2020, 50, 139–149 CrossRef.
- A. Gábor, A. F. Villaverde and J. R. Banga, BMC Syst. Biol., 2017, 11, 1–16 CrossRef PubMed.
- D. Joubert, J. D. Stigter and J. Molenaar, Math. Biosci., 2020, 323, 1–10 CrossRef PubMed.
- F. Pukelsheim, Optimal Design of Experiments, Society for Industrial and Applied Mathematics, 2006 Search PubMed.
- C. M. Bishop, Pattern recognition and machine learning, Springer, New York, 2006 Search PubMed.
- Y. LeCun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436–444 CrossRef CAS PubMed.
- J. A. Valeri, K. M. Collins, P. Ramesh, M. A. Alcantar, B. A. Lepe, T. K. Lu and D. M. Camacho, Nat. Commun., 2020, 11, 1–14 CrossRef PubMed.
- N. M. Angenent-Mari, A. S. Garruss, L. R. Soenksen, G. Church and J. J. Collins, Nat. Commun., 2020, 11, 1–12 CrossRef PubMed.
- O. Borkowski, M. Koch, A. Zettor, A. Pandi, A. C. Batista, P. Soudier and J.-L. Faulon, Nat. Commun., 2020, 11, 1–8 CrossRef PubMed.
- Y. Qiu, J. Hu and G.-W. Wei, Nat. Comput. Sci., 2021, 1, 809–818 CrossRef PubMed.
- J. Oyelade, I. Isewon, F. Oladipupo, O. Aromolaran, E. Uwoghiren, F. Ameh, M. Achas and E. Adebiyi, Bioinf. Biol. Insights, 2016, 10, 237–253 Search PubMed.
- C. A. Duran-Villalobos, O. Ogonah, B. Melinek, D. G. Bracewell, T. Hallam and B. Lennox, AIChE J., 2021, 67, 1–12 CrossRef.
- J. G. Greener, S. M. Kandathil, L. Moffat and D. T. Jones, Nat. Rev. Mol. Cell Biol., 2022, 23, 40–55 CrossRef CAS PubMed.
- K. M. Chen, E. M. Cofer, J. Zhou and O. G. Troyanskaya, Nat. Methods, 2019, 16, 315–318 CrossRef CAS PubMed.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- D. A. Van Valen, T. Kudo, K. M. Lane, D. N. Macklin, N. T. Quach, M. M. DeFelice, I. Maayan, Y. Tanouchi, E. A. Ashley and M. W. Covert, PLoS Comput. Biol., 2016, 12, 1–24 CrossRef PubMed.
- J. Gilman, L. Walls, L. Bandiera and F. Menolascina, ACS Synth. Biol., 2021, 10, 1–18 CrossRef CAS PubMed.
- A. Jain, P. Hurkat and S. K. Jain, Chem. Phys. Lipids, 2019, 224, 1–16 CrossRef PubMed.
- P. Ren, Y. Xiao, X. Chang, P.-Y. Huang, Z. Li, B. B. Gupta, X. Chen and X. Wang, ACM Comput. Surv., 2021, 54, 1–180 Search PubMed.
- B. Settles, Active Learning Literature Survey, University of Wisconsin-Madison Department of Computer Sciences, 2010 Search PubMed.
- E. Brochu, V. M. Cora and N. de Freitas, arXiv, 2010, preprint, arXiv:1012.2599 DOI:10.48550/arXiv.1012.2599.
- A. Pandi, C. Diehl, A. Yazdizadeh Kharrazi, S. A. Scholz, E. Bobkova, L. Faure, M. Nattermann, D. Adam, N. Chapin, Y. Foroughijabbari, C. Moritz, N. Paczia, N. S. Cortina, J.-L. Faulon and T. J. Erb, Nat. Commun., 2022, 13, 1–15 Search PubMed.
- B. Lei, T. Q. Kirk, A. Bhattacharya, D. Pati, X. Qian, R. Arroyave and B. K. Mallick, npj Comput. Mater., 2021, 7, 1–12 CrossRef.
- T. Chen and C. Guestrin, in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, San Francisco California USA, 2016, 785–794.
- A. Pandi, D. Adam, A. Zare, V. T. Trinh, S. L. Schaefer, M. Burt, B. Klabunde, E. Bobkova, M. Kushwaha, Y. Foroughijabbari, P. Braun, C. Spahn, C. Preußer, E. Pogge Von Strandmann, H. B. Bode, H. Von Buttlar, W. Bertrams, A. L. Jung, F. Abendroth, B. Schmeck, G. Hummer, O. Vázquez and T. J. Erb, Nat. Commun., 2023, 14, 1–14 Search PubMed.
- J. Pinto, J. R. C. Ramos, R. S. Costa and R. Oliveira, AI, 2023, 4, 303–318 Search PubMed.
- C. Rackauckas, Y. Ma, J. Martensen, C. Warner, K. Zubov, R. Supekar, D. Skinner, A. Ramadhan and A. Edelman, arXiv, 2021, preprint, arXiv:2001.04385 DOI:10.48550/arXiv.2001.04385.
| This journal is © The Royal Society of Chemistry 2024 |