Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tuning sorbent properties to reduce the cost of direct air capture†
Hannah E.
Holmes‡
 ,
Sayan
Banerjee‡
,
Anthony
Vallace
,
Ryan P.
Lively
,
Sayan
Banerjee‡
,
Anthony
Vallace
,
Ryan P.
Lively
 ,
Christopher W.
Jones
* and
Matthew J.
Realff
,
Christopher W.
Jones
* and
Matthew J.
Realff
 *
*
School of Chemical & Biomolecular Engineering, Georgia Institute of Technology, 311 Ferst Drive, Atlanta, Georgia 30332, USA. E-mail: christopher.jones@chbe.gatech.edu; matthew.realff@chbe.gatech.edu
First published on 4th June 2024
Abstract
The question has shifted from whether solid sorbents can work in direct air capture (DAC) technologies to which solid sorbents are more economically advantaged. Determining this is challenging due to the influence of many different yet interconnected sorbent properties on the cost of CO2 capture. Existing DAC economic models oversimplify sorbent stability by treating it as a simple replacement rate, neglecting crucial factors such as capacity loss rate and form. To address this challenge, we have developed an economic model that accounts for sorbent degradation in DAC processes. By factoring in capacity loss over time, our model provides a more accurate estimate of the cost associated with DAC and highlights the optimum time for sorbent replacement. We then identified sorbent characteristics and process features that minimize both the carbon footprint and the cost of captured CO2. To further investigate the interplay of sorbent properties and DAC cost, we constructed a series of alkyl- and epoxy-functionalized polyamine sorbents. The sorbents’ CO2 uptake, heat of adsorption and capacity fade were adjusted via a one-step modification, varying the proportions of primary, secondary, and tertiary amines. We then integrated the experimentally-measured parameters, including the form of degradation, into our economic model to probe which combination of sorbent properties results in the lowest cost of DAC for a fixed operating condition. The results provide guidelines and priorities for sorbent performance metrics that will yield the most cost-effective DAC technologies.
Broader contextDirect air capture (DAC) technologies are expected to play a critical role in addressing climate change. By removing carbon dioxide from the atmosphere, DAC offers a pathway to mitigate the long-term effects of existing atmospheric carbon dioxide and achieve net-zero emissions. A key component of DAC is the sorbent used to separate carbon dioxide from the air. As efforts are made to scale up DAC, it is essential to understand the complex relationships between sorbent properties and overall process cost. Current economic analyses simplify sorbent stability by assuming constant sorbent performance until replacement, but this shortcoming potentially leads to important errors in both the cost and environmental impact. In particular, failure to account for the loss in sorbent performance can result in turning the direct air capture plant into a net positive emitter if the sorbent is not replaced soon enough. We developed an economic model that accounts for sorbent degradation, including the rate and form of capacity loss over time. By coupling the capacity-fade model with experimental tuning of sorbents, we gain insight into how competing sorbent properties influence the overall cost. The findings offer priorities for sorbent properties that will facilitate scale-up of cost-effective DAC technologies. |
1 Introduction
Direct air capture (DAC) technologies are projected to play a crucial role in addressing climate change by removing carbon dioxide (CO2) from the atmosphere, allowing us to mitigate the long-term consequences of existing atmospheric carbon dioxide and achieve net-zero emissions.1,2 The key component in DAC technologies is the material used to capture and separate CO2 from the air. Solid adsorbents, in contrast to liquid absorbents, offer advantages such as lower energy requirements for regeneration, modularity, and mitigation of corrosion and evaporation challenges.3,4 Many promising adsorbents have been proposed for DAC to date, including metal–organic frameworks,5–7 zeolites,8,9 and supported amine materials.3,4,10,11The primary challenge for widescale DAC implementation is not whether sorbents can effectively remove CO2 from the air, as operational DAC plants currently exist.12,13 Instead, the most significant hurdle is the economic viability of DAC. In contrast to post-combustion CO2 capture processes, in which revenue for the CO2 emitter is still possible, DAC lacks an intrinsic revenue source. Post-combustion processes capture CO2 from flue gas that is emitted from electricity generation (i.e., combustion to produce steam for turbines also produces CO2-rich flue gas). Thus, post-combustion processes will contain a revenue stream from the produced electricity, which is intrinsic to the process. In contrast, direct air capture does not follow a production process and therefore does not have an associated revenue stream. This has driven an intense effort on advancing sorbent materials to reduce process costs, including increasing CO2 capacity,14,15 reducing regeneration energy requirements,16–18 and increasing sorbent stability.19,20
However, many of these sorbent properties are interconnected, often in inverse relationships. For example, increasing the CO2 affinity increases the CO2 uptake, but it also increases the CO2 heat of adsorption, thus increasing regeneration energy demands. Similarly, increasing the desorption temperature can improve the working capacity, but it may also accelerate the degradation rate and shorten the sorbent lifetime. Without the guidance of an economic model tailored to DAC, it is challenging to determine whether improving one property actually reduces overall process costs when considering other properties. While many promising adsorbents with varying capacity, heat of adsorption, and stability have been proposed for DAC, it is unclear which combination of properties provides the most economically viable option due to the complex relationships between sorbent properties and process cost. This complexity has left materials researchers without clear guidelines or priorities for performance metrics.
Furthermore, there is a shortcoming in current DAC economic models when accounting for a sorbent's stability. Existing models assume the sorbent (or in some cases solvent) has constant performance until replacement and thus incorporate stability as a simple replacement rate.21–29 However, this oversimplification fails to consider sorbent capacity fade over time, which is inevitable as a sorbent degrades (e.g., oxidation, amine loss, fouling, poisoning, urea formation). Our prior analysis of a bioenergy with carbon capture and storage (BECCS) process revealed that incorporating a sorbent's capacity fade into the economic model significantly increases the predicted process cost and alters the recommended sorbent replacement times.30 These findings indicate that the details of a sorbent's degradation, specifically the rate and form of capacity fade over time, are crucial to include when evaluating competing properties and comparing process costs for different sorbents.
These gaps lead to the first two questions addressed in this work: (1) how does sorbent degradation affect the DAC carbon footprint and cost of CO2 capture? (2) do the capacity fade (loss) rate and form (e.g., linear, exponential) affect the optimal replacement time? To answer these, we developed a capacity-fade economic model for DAC. The model can be used for any sorbent and contactor combination, but we focused our analysis on amines supported in structured contactors in a temperature vacuum swing adsorption process.
Amine-based sorbents are a common choice in DAC technologies due to their high affinity for CO2, even at low concentrations.31 Amines bind CO2 through chemical bonds to form carbamate, carbamic acid, hydronium carbamate, carbonate, or bicarbonate. The end-product depends on the amine surface coverage, presence of water, and amine–solid support interactions.18,32–35 This results in steep adsorption isotherms (strong type I) that lead to significant CO2 uptakes at low CO2 partial pressures – a critical feature for DAC applications.36–38 Implementing amines in structured contactors can enable a lower pressure drop, indirect heating, and thermal management (i.e., cooling) during adsorption.39 Temperature or temperature/vacuum swing adsorption are the process modes typically coupled with amine sorbents, as the high uptake at low partial pressures makes adsorption based on pressure swing alone a challenging option.40
Polymeric or oligomeric amines (polyamines) are a particularly promising form of amine due to their high density of amine sites and lower volatility compared to smaller amine molecules. Modification of polyamines with epoxide groups has been explored previously as a method for enhancing sorbent properties.41–47 Choi et al. demonstrated that functionalizing poly(ethyleneimine) with 1,2-epoxybutane reduces the heat of adsorption and increases the stability by altering the primary, secondary, and tertiary amine fractions.42,48 Increasing the extent of functionalization increasingly benefits the heat of adsorption and stability, but it also negatively impacts the sorbent's capacity.42
It remains unclear which functional group and extent of functionalization result in the most economically advantaged DAC process, but we hypothesized based on previous work from Min et al. that this functionalization could be used to systematically tune sorbent properties for optimal DAC performance.48 All previous optimization has been performed for post-combustion CO2 capture processes, but the optimum properties will depend on the concentration of CO2 in the feed. For example, Lively and Realff demonstrated that as the adsorbate mole fraction decreases, the adsorbate–adsorbent affinity resulting in the highest separation efficiency increases.49 When coupled with a capacity-fade economic model, the one-step modification of polyamines could be used to target a combination of sorbent properties that results in the lowest cost of CO2 capture. This led us to the final two questions addressed in this work: (3) can we modify polyamine sorbents with different functional groups to systematically tune performance in DAC (working capacity, heat of adsorption, degradation rate)? (4) which combination of properties results in the most economically advantaged sorbent for DAC?
To address all four questions, we first developed a capacity-fade economic model for DAC that includes sorbent degradation. We used the model to explore how various types and rates of sorbent degradation affect the viability of DAC, specifically through the carbon footprint and cost of captured CO2. The most critical sorbent characteristics and process features for minimizing the carbon footprint and cost were identified. We then experimentally synthesized a series of polyamines functionalized with various side chains (methyl, propyl, and 2-hydroxypropyl, with the latter made via 1,2-epoxypropane functionalization) in mesoporous silica SBA-15 supports. The functionalization is used to systematically alter the working capacity, energy requirement, and degradation rate, and the experimentally-measured parameters are integrated into the model to compare the economic feasibility. Combining a capacity-fade economic model with experimental tuning of sorbents provides insight into how competing sorbent properties balance and influence the overall cost of direct air capture. These findings provide guidelines and priorities for sorbent performance properties as scale-up of DAC processes is pursued.
2 Methodology
2.1 Analysis framework
A detailed description of the economic model is provided in Section S3 of the ESI.† The model framework aligns with our previous work focused on BECCS.30 The economic analysis methodology for chemical processes from Turton et al. was used.50 We also followed guidelines on CCS economic analysis methodology from Rubin et al., Danaci et al., van der Spek et al., Roussanaly et al., and the U.S. National Energy Technology Laboratory.51–56The cost of direct air capture is comprised of capital costs, operation and maintenance costs (O&M), and sorbent costs, and the total cost is expressed as the levelized cost of CO2 capture (LCOC), defined in eqn (1),
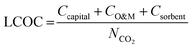 | (1) |
2.2 System design
The solid sorbent direct air capture plant is designed to capture 1 Mt-CO2 per year. The sorbent, which is polyamine supported on silica in this analysis, is assumed to be in polymeric structured contactors, and the contactors are installed in the process as modules (Fig. 1). The model is agnostic to the geometry of the contactor (i.e., fibers, monolith, laminate). Rather, the inputs are the sorbent loading inside the contactor (e.g., sorbent to polymer mass fraction), contactor density, module void fraction, module cross-sectional area, module length, and pressure drop. These parameters can be changed to account for various contactor geometries (e.g., cylindrical hollow fibers vs. square-channel monoliths). Representative values for a polyamine–silica/polymer structured contactor were chosen for this analysis, including a sorbent (amine + support) loading of 50%, contactor density of 730 kg m−3, module void fraction of 50%, module cross-sectional area of 1 m2, and pressure drop of 500 Pa.The module size is connected to the blower flow rate and CO2 recovery, and the model uses a solver system to couple these system properties (Section S3.C of ESI†). Direct steaming is used to regenerate the sorbent via condensation of saturated steam on the sorbent. Sorbent replacement refers to only the amine being replaced. This is done via a washing procedure.57,58 The silica and contactor lifetime is longer (5 years).
A temperature swing adsorption (TSA) process is utilized with the following steps: (1) adsorption, (2) vacuum to remove interstitial air from module, (3) heat to desorption temperature (95–100 °C),15 (4) desorption, and (5) cool to adsorption temperature (25–30 °C). The vacuum is only used momentarily to remove the interstitial air before heating. Removing interstitial air prior to desorption reduces oxidation and increases CO2 product purity.
Blower and vacuum pump scheduling is utilized in the model to reduce the capital cost while maintaining the system within physically reasonable bounds. In short, to minimize the capital cost of blowers and vacuum pumps, many modules can be centralized around one blower and vacuum pump. A group of modules that share blower(s) and vacuum pump(s) will be referred to as a cluster. However, the centralized design can lead to unintended downtime for modules without proper vacuum pump placement and scheduling, illustrated in Fig. S1 (ESI†). Module downtime reduces the plant utilization and therefore increases the total cost. To mitigate these problems, we designed a vacuum pump schedule for a cluster containing 20 modules, one blower, and two vacuum pumps (Fig. S2, ESI†). The central blower rotates between the outer 20 modules during the adsorption steps, and each vacuum pump can service four parallel modules at one time. A schedule for a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adsorption to desorption time (1200 s
1 adsorption to desorption time (1200 s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 s) is illustrated in Fig. S2b (ESI†).
600 s) is illustrated in Fig. S2b (ESI†).
2.3 Incorporating sorbent capacity fade
The primary difference in our capacity-fade model versus a model that does not consider sorbent degradation is the relationship between the cumulative amount of CO2 captured (NCO2) and time. If a sorbent maintains a constant capacity, it will capture a consistent amount of CO2 each cycle. However, when a sorbent degrades, the amount of CO2 captured varies from cycle to cycle, leading to a nonlinear NCO2 with respect to time. Tracking the captured CO2 each cycle for tens of thousands of cycles would be computationally expensive, so we instead employ integration to determine the cumulative amount of CO2 captured at specific time points based on the relationship between working capacity and time.Mathematically, a DAC module or cluster can be likened to a continuous stirred tank reactor (CSTR) with a reaction. The order of the reaction term depends on the type of sorbent degradation. As an example, if the sorbent has exponentially decaying capacity, the system is describable by the differential equation with a first order reaction in eqn (2),
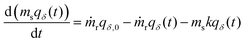 | (2) |
Integration of eqn (2) over time provides the cumulative amount of CO2 captured, as expressed in eqn (S23) (ESI†). When the sorbent is not replaced each cycle but is instead replaced en-masse (i.e., all at once), eqn (2) can be simplified accordingly (eqn (S22), ESI†). As the sorbent degrades, the necessary energy consumption changes in addition to the amount of CO2 captured. To account for this, the electrical and thermal energy are fitted separately to four-term polynomial expressions for convenience (eqn (S60) and (S65), ESI†). The polynomial expressions are then integrated over time to find the cumulative energy consumption (eqn (S61) and (S66), ESI†).
2.4 Carbon footprint of direct air capture
Multiple aspects of direct air capture processes have associated carbon emissions, including the (1) energy source, (2) sorbent materials (including their synthesis, manufacturing, and disposal), (3) equipment materials and manufacturing, (4) sorbent transport and storage, and (5) CO2 compression, purification, transport, utilization, and storage. In this analysis, we considered cradle-to-gate carbon emissions from energy, sorbent materials, and equipment materials and manufacturing. Cradle-to-gate analysis is sufficient for this comparative study.59 The amount of CO2 captured is a fixed parameter, and thus the downstream environmental impacts are identical across the scenarios. However, it is important to note that CO2 transportation and storage emissions can contribute significantly (accounting for over half of the total DAC greenhouse gas emissions in some cases).60 The downstream emissions will vary substantially depending on the plant and storage locations and end-use of the CO2 product (storage vs. utilization).60,61 Optimizing and assessing downstream emissions is the subject of ongoing research.62–64 The carbon footprint of the sorbent includes disposing both the polyamine and silica. However, the polyamine can be replaced via a simple washing procedure without replacing the silica in the polymeric contactors.57 Thus, the sorbent carbon footprint used here (4 kg CO2,eq. per MW h) is a conservative value.To determine the electrical energy carbon footprint, the cumulative electrical energy consumption is converted to a cumulative amount of CO2 emissions based on the energy source (Section S3.L of ESI†). A carbon footprint is also calculated for thermal energy based on its electricity equivalent. The electrical and thermal energy carbon footprints are combined with the carbon footprint of the sorbent and equipment materials and construction to determine the total carbon footprint.
Calculation methods for carbon footprint vary in literature.63 Here, we utilize two metrics to facilitate comparison with different literature sources, following the methods of Deutz et al., Qiu et al., and de Jonge et al.61,65,66 The first metric is carbon footprint (CF), which is the amount of CO2 captured subtracted from the amount of CO2 emitted, normalized to the amount of CO2 captured (eqn (3)). If more CO2 is emitted than captured, the carbon footprint is positive, whereas a negative carbon footprint indicates more CO2 is captured than emitted. An ideal CO2 capture process with no associated emissions or environmental impact will have a carbon footprint of −1 t-CO2e per t-CO2 captured.
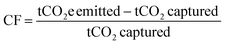 | (3) |
For calculating DAC carbon footprint, the amount of CO2 captured is subtracted from the sum of the carbon footprints of the energy, adsorbents, and equipment materials and manufacturing.
The second metric is carbon removal efficiency,61,65 which is typically multiplied by 100 and expressed as a percent (eqn (4)). The carbon removal efficiency is the negative of carbon footprint, or the amount of CO2 emitted subtracted from the amount captured, normalized to the amount captured A positive carbon removal efficiency indicates that more CO2 is captured than emitted, and a negative efficiency indicates more CO2 emitted than captured. A CO2 capture process with no environmental impacts has a carbon removal efficiency of 100%.
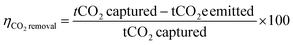 | (4) |
Since the carbon removal efficiency is simply the negative of carbon footprint multiplied by 100, the two metrics have an linear relationship. For example, a carbon footprint of −0.7 t-CO2 emitted per t-CO2 captured corresponds to a carbon efficiency of 70%, and carbon footprint of −0.5 t-CO2 emitted per t-CO2 captured corresponds to a 50% carbon removal efficiency. Increasing the carbon footprint (less negative) will decrease the carbon removal efficiency.
The fractional carbon removal efficiency is employed to convert the total process cost from $ per tonne of captured CO2 to $ per tonne of net CO2, where the “net CO2” refers to the captured CO2 minus the emitted CO2 (eqn (5)).
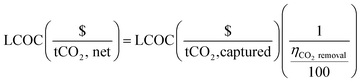 | (5) |
More details on calculating the carbon footprint are provided in Section S3.L of the ESI.†
2.5 Adsorbent preparation
Functionalization of PEI with hydrophobic groups (such as methyl, propyl) was carried out by a simple single-step addition reaction with alkyl halides under refluxing conditions. In comparison, the functionalization of PEI with 1,2 epoxypropane was carried out in ambient conditions. This ambient temperature is attributed to the high reactivity of epoxides with nucleophilic amines.48 (Scheme S1, ESI†).Controlled amounts of adducts were added dropwise to methanolic solutions of PEI (MW 800, nitrogen content: 18 mmol g−1) under stirring. The modified PEI sorbents are denoted as n-x-PEI, where “x” denotes the functional group such as methyl (M), propyl (P) and 2-hydroxypropyl (HP) and “n” denotes the molar ratio of the functional reagent (e.g., 1,2-epoxypropane) to total moles of nitrogen in PEI. Total moles of nitrogen includes the nitrogen in primary, secondary, and tertiary amines.
SBA-15 was impregnated with modified PEIs by wet impregnation. First, SBA-15 was dried overnight under vacuum (<20 mTorr) at 110 °C. The desired amount of PEI was dissolved in 15 mL methanol and added to the desired amount of SBA-15. The mixture was allowed to stir at room temperature for at least 6 h. Methanol was removed by rotary evaporation at room temperature. The resulting powder was dried overnight under vacuum (<20 mTorr) at room temperature. The resulting dried powder composites were stored in ambient lab conditions. The composites were characterized using quantitative 13C NMR spectroscopy, N2 physisorption, gravimetric CO2 adsorption, and differential scanning calorimetry. More details on the synthesis procedures and characterization procedures are provided in Section S6 in the ESI.†
3 Results and discussion
3.1 The role of sorbent degradation in carbon footprint
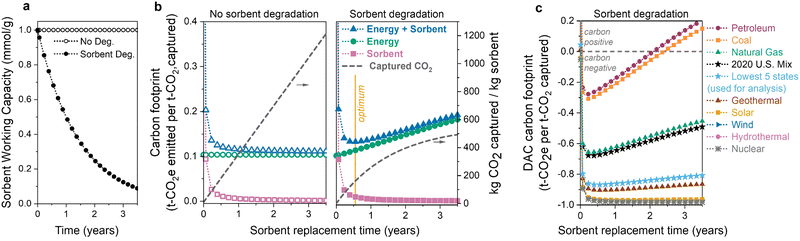
The first question is: how does sorbent degradation affect the DAC carbon footprint and cost of CO2 capture? Carbon capture cost is often reported as dollars per tonne of CO2 captured, but this metric overlooks the underlying carbon footprint, or associated carbon emissions, of the process. Including the carbon footprint in cost predictions is vital to accurately access the viability of various DAC technologies.60,61 In Fig. 2, we illustrate how sorbent degradation affects the carbon footprints of the sorbent, energy, and the combined total (sorbent + energy). Here, the sorbent is considered to be replaced all at once (en-masse), so the sorbent lifetime is equivalent to the replacement time. Specifically, a sorbent lifetime of 1 year indicates that all of the sorbent is replaced at 1-year intervals. Sorbent replacement refers to replacement of the polyamine only. The sorbent carbon footprint utilized in this analysis includes disposal of both the polyamine and silica, so the sorbent carbon footprint values are conservative estimates.The input parameters used for the economic analysis are provided in Table S1 (ESI†). The parameters were chosen as a representative set of sorbent and process parameters for a polyamine–silica contactor in a temperature-swing adsorption process (see Section 2.2 and Fig. 1). For example, the parameters include a working capacity of 1.0 mmol g−1, heat of adsorption of −70 kJ mol−1, 50 wt% loading of polyamine–silica in the contactor, pressure drop of 500 Pa, cycle time of 1800 seconds (1200 s adsorption, 600 s desorption), and CO2 recovery of 50%. The pressure drop is a fixed input that was chosen as a mid-range estimate based on both theoretical calculations and experimental measurements for structured contactors in literature.10,29,39,67 The adsorption time includes cooling, and the desorption time includes a brief vacuum step and heating. The productivity (1.0 mmol g−1 fiber per h) is consistent with that measured by Kong et al. for PEI-silica/cellulose acetate fibers.15
In Fig. 2(a) and (b), when sorbent degradation is not considered (left panel of Fig. 2(b)), the sorbent capacity remains constant, resulting in a constant rate of CO2 captured (i.e., there is a linear relationship between the amount of CO2 captured and sorbent lifetime). In contrast, when sorbent degradation is included (Fig. 2(b), right panel), there is a non-linear relationship between CO2 captured and sorbent lifetime as the sorbent's capacity decreases each cycle. Exponential capacity fade (first-order deactivation) is used here as an example. The model does not include a specific degradation mechanism but rather a generic capacity loss profile over time. To keep the model as general as possible, we only change the capacity and do not consider changes to other sorbent properties as the sorbent degrades, such as the heat of adsorption. We also do not consider changes to operating parameters (e.g., cycle time) as the sorbent degrades.
In both scenarios, the sorbent carbon footprint is highest at short lifetimes due to the relatively small amount of CO2 captured. The carbon emissions associated with sorbent manufacturing and disposal are not compensated by the limited CO2 captured when the sorbent lifetime is short. As the sorbent lifetime is extended, the carbon footprint decreases, regardless of whether or not the sorbent is degrading.
In contrast, the energy carbon footprint is influenced by sorbent degradation. In Fig. 2(b) (left panel) when there is no sorbent degradation, the energy carbon footprint remains constant because the amount of energy to capture one tonne of CO2 does not change. However, when there is sorbent degradation (Fig. 2(b), right panel), the energy carbon footprint increases as the sorbent is used for longer. There is a slight reduction in the total energy required as the sorbent degrades. The same amount of air is blown across the contactor (and thus the same blower energy), but the thermal energy will decrease slightly. The regeneration energy decreases as there will be less product to desorb as the contactor degrades. However, the reduction in CO2 captured is significantly more than the slight reduction in total energy, and thus the energy per tonne of CO2 (and energy climate change impact) increases.
Combining the energy and sorbent carbon footprints provides a total carbon footprint. When the sorbent degrades over time, there is a minimum carbon footprint when the decreasing sorbent carbon footprint and increasing energy carbon footprint balance each other, marked with a yellow line in the right panel of Fig. 2(b). The location of this minimum carbon footprint will influence the optimum sorbent replacement time.
The choice of energy source has a substantial impact on the climate change impact and carbon footprint of DAC.12,60,61,68–70 Non-renewable energy sources, such as petroleum and coal, emit high amounts of carbon dioxide per MW h of energy produced, while low-carbon sources like wind, hydropower, and nuclear emit much less CO2. The choice of energy source has a large influence on the total DAC carbon footprint, illustrated in Fig. 2(c). Carbon-intensive energy sources such as petroleum and coal have higher carbon footprints across all lifetimes. Although others have previously recognized the limited supply of large scale low-carbon electricity as an obstacle for DAC,70 we can see that this need becomes even more significant once we consider sorbent capacity fade. As the sorbent degrades, the carbon footprint of DAC processes using carbon-intensive energy increases significantly over time. Using a carbon-intensive energy source (such as petroleum or coal) with a degrading sorbent can lead to positive carbon footprints, at which point the DAC process is emitting more CO2 than it has captured. Without including sorbent degradation in our analysis, we would not be able to predict the shift to positive CO2 emissions.
To minimize the impact of the energy source, direct air capture processes are typically proposed to be located in regions with low-carbon-footprint grid mixes or powered directly by renewable electricity or waste heat. This makes the U.S. grid mix carbon footprint (461 kg CO2 per MW h in 2020) an inaccurate representation of the expected carbon footprint for DAC. Thus, we use an average of the five states with the lowest carbon footprints (171 kg CO2 per MW h) throughout the analysis here (Tables S25 and S26, ESI†), including the results in Sections 3.2–3.5. The average carbon footprint of the lowest five states is in light blue in Fig. 2(c). In our analysis, the thermal energy is assumed to come from power plant steam, but using other thermal energy sources such as waste heat or heat pumps could further reduce the energy consumption and thermal carbon footprint.61,71 Heat integration techniques, such as mechanical vapor compression or moving/rotating beds, should also be explored in future work.72,73
Two important conclusions can be made from these results. (1) Sorbent degradation can unintentionally lead to high carbon footprints (including positive emissions), especially when carbon-intensive energy sources are used. (2) Sorbent capacity fade must be included in DAC economic modelling to determine the replacement time that leads to the highest climate benefits.
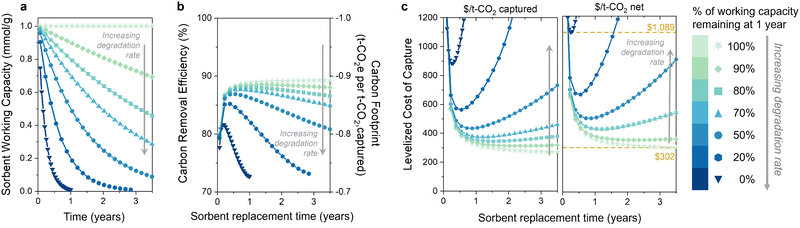
3.2 Increasing rates of sorbent degradation
The second question is: do the capacity fade (loss) rate and form (e.g., linear, exponential) affect the optimal replacement time? We first illustrate the influence of the sorbent degradation rate on carbon footprint and cost in Fig. 3 for seven rates of exponential capacity fade. Fig. 3(a) illustrates the sorbent working capacity as a function of time for the various degradation rates. The rates range from no degradation to none of the initial capacity remaining after 1 year. We again observe an optimum in carbon removal efficiency and carbon footprint when sorbent degradation is included (Fig. 3(b)). At higher degradation rates, there is a noteworthy reduction in the carbon removal efficiency due to the decreasing captured CO2. The increase in energy-related emissions drives the overall carbon removal efficiency down as the sorbent lifetime is extended, approaching a value of 70% (or −0.7 tonne CO2 eq. per t-CO2 captured) for the higher degradation rates. The carbon footprint and carbon removal efficiency have a negative linear relationship, so a decrease in the carbon removal efficiency corresponds to an increase in carbon footprint. The energy carbon footprint used here was an average of the five states with the lowest carbon footprints (171 kg CO2 per MW h).The levelized cost of capture (LCOC) is shown in Fig. 3(c), reported as $ per t-CO2 captured in the left panel (carbon footprint not included) and $ per t-CO2 net in the right panel (carbon footprint included). As expected, increasing the sorbent degradation rate increases the LCOC. Notably, incorporating degradation into the levelized cost of CO2 capture results in an optimum sorbent replacement time that minimizes the DAC process cost. This optimum has not been demonstrated previously for DAC, but it does align with our findings for the BECCS process previously studied. It arises in a slightly different manner than BECCS without an associated revenue from electricity sales.30
As the sorbent degrades, the rate of CO2 capture decreases, as less CO2 is captured every subsequent cycle. This leads to increasing capital and operation and maintenance costs per tonne of captured CO2. (It is important to note that the total capital does not change since the system is designed for no sorbent degradation – only the capital cost per tonne of captured CO2 changes.) However, using the sorbent for longer results in more CO2 captured with that sorbent, which reduces sorbent costs regardless of degradation. The increasing capital and O&M costs balance the decreasing sorbent cost at some sorbent lifetime, at which point the sorbent should be replaced.
It is evident from these results that the rate of degradation also plays a crucial role in determining the optimal sorbent replacement time. For instance, the sorbent with 50% capacity loss after one year should be replaced at one-year intervals to achieve the lowest cost of capture. In contrast, the sorbent exhibiting a 10% capacity loss after one year (90% remaining) should be replaced at three-year intervals. For sorbents with no degradation, the cost will continue decreasing with increasing replacement time. Therefore, there is no optimum replacement time for stable sorbents, but rather they should be used for as long as possible. The difference in DAC cost between the lowest and highest degradation rates at the optimum replacement time is approximately $700 per tonne of net CO2 captured (marked with yellow lines in Fig. 3(c)). This substantial difference in cost underscores the importance of incorporating degradation rate measurements when determining the most economically viable sorbent replacement times.
A capacity-fade model will also be critical when considering process improvements. For example, the working capacity of a sorbent can often be increased by increasing the desorption temperature. However, this may also lead to an increased degradation rate due to the higher temperature during desorption. These results indicate that the increase in productivity could be counteracted by the decrease in CO2 captured over the sorbent's lifetime. Using a cost metric with an integrated carbon footprint (Fig. 3(c), right panel) can be used to optimize the performance and cost of DAC systems while also minimizing their environmental impact.
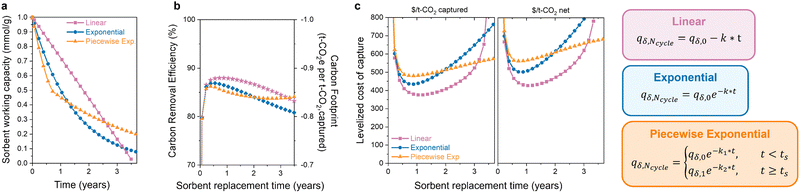
3.3 Different forms of degradation
The latter half of the previous question was how the degradation form affects the optimal replacement time. Sorbent degradation, specifically how the capacity fades over time, is dictated by the degradation mechanism. In Fig. 4(a), three functional forms of sorbent degradation are illustrated: (1) linear, (2) exponential, and (3) piecewise exponential. Linear degradation is characterized by a constant rate of capacity decline over time. This form of degradation is typically expected in scenarios where sorbent material physically exits the bed, when pores become obstructed with contaminants (fouling), or in cases of structural collapse, where the degradation does not depend on the remaining adsorption sites.74 Exponential degradation, in contrast to the linear form, depends on the concentration of available sites. This type of degradation is frequently observed in instances of poisoning of chemical adsorbents, where the rate of deactivation is proportional to the remaining sites. Piecewise exponential degradation, sometimes referred to as “hockey stick kinetics,” encompasses two or more exponential functions with distinct break points. The first exponential function exhibits a more rapid rate of degradation compared to later functions. This functional has been observed for amine-supported materials, where the initial rate of degradation is faster as primary amines are deactivated first, eventually leading to a seemingly stable or plateaued capacity.75 Volatilization of low molecular weight amines can also cause faster degradation,76 which results in a higher initial rate for polyamine sorbents with a molecular weight distribution.The functional form of degradation not only provides insight into the specific mechanism, but it also impacts the carbon footprint and process cost of DAC. The extent of this impact depends on the initial capacity and decay constant (denoted as “k”) associated with each functional form. In Fig. 4(b) and (c), the carbon footprint and DAC cost of the three functional forms are compared, all with the same initial capacity, to highlight how different degradation forms affect the economic viability. In the case of linear degradation, a rapid decline in capacity is observed. The decrease in capacity reduces the carbon removal efficiency as the sorbent captures less CO2 with a comparable energy consumption. This impacts the cost per net tonne of CO2 and emphasizes the necessity of considering carbon footprint, as it can significantly influence the economic viability of DAC systems. As mentioned before, the extent of this impact varies significantly with the choice of energy source. The observed increase in carbon footprint and cost will be less pronounced when energy sources with low carbon emissions are utilized. Here, the energy carbon footprint is an average of the five states with the lowest carbon footprints (171 kg CO2 per MW h).
The exponential and piecewise exponential functional forms exhibit similar carbon footprints due to the comparable working capacities. However, there is a difference in the DAC process cost. The initial steeper capacity decline in the piecewise exponential functional form leads to a slightly higher process cost initially compared to that of the exponential form. However, this is reversed at longer lifetimes due to lower degradation rate of the piecewise exponential function after its initial decline. In a scenario where we have to choose between these three sorbent options, the most economically favorable choice would be to use the sorbent displaying linear decay and replace it every year. However, the most economically favorable choice will depend on the sorbent parameters in the scenario. Different initial working capacities and degradation rates will lead to a different result. Without the capacity-fade economic model, the answer would be ambiguous.
3.4 Tuning polyamine properties via epoxy modification
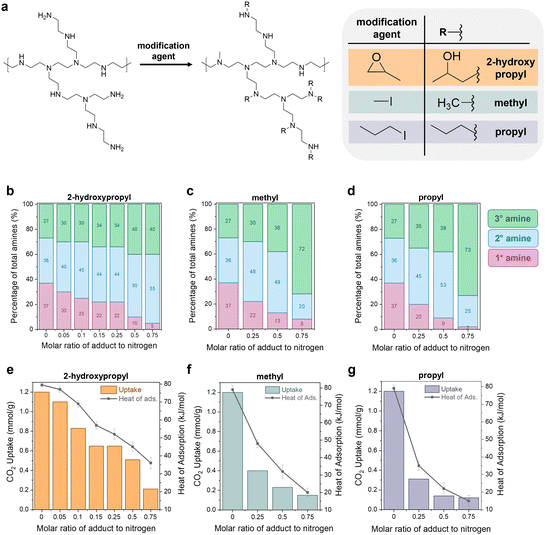
The previous sections illustrate how a sorbent's degradation rate and form affect the overall carbon footprint and cost of DAC, with guidelines provided for economic viability. The next question was: can we modify polyamine sorbents with different functional groups to systematically tune performance in DAC (working capacity, heat of adsorption, degradation rate)? Experimentally improving a sorbent's stability to lower the DAC cost is often not straightforward due to the interconnected nature of sorbent properties. This complexity has been observed in both crosslinking and epoxide functionalization of polyamines, where increasing the functionalization increases stability, but it also reduces the CO2 capacity and heat of adsorption.11,42,44,77,78To explore this further, we built a small library of modified polyamine sorbents to study with our newly developed capacity-fade model. We used a simple modification scheme to functionalize the polyamines in a mesoporous silica support (Fig. 5(a)). We hypothesized that we could use this one-step modification to tune the sorbent's heat of adsorption, working capacity, and stability through the choice of functional group and extent of functionalization. As the functional groups attach to the amine sites, the reacted primary amines will convert to secondary amines. The secondary amines will convert to tertiary amines, which are typically inactive for CO2 capture. Increasing the proportion of secondary and tertiary amines in the sample is expected to simultaneously reduce the capacity and heat of adsorption by decreasing the binding strength of CO2 with the material. Three functional groups were tested (reagent in parentheses): 2-hydroxypropyl (1,2-epoxypropane), methyl (methyl iodide), and propyl (propyl iodide).
The modified poly(ethyleneimine) (PEI) SBA-15 sorbents were prepared by impregnating a solution of n-x-PEI in methanol into SBA-15, where “x” denotes the functional group such as methyl (M), propyl (P) and 2-hydroxypropyl (HP) and “n” denotes the molar ratio of the functional reagent (e.g., 1,2-epoxypropane) to total moles of nitrogen in PEI. For example, 0.25HP-PEI was prepared with methanol, PEI, 1,2-epoxypropane solution that contained 0.25 moles of 1,2-epoxypropane per mole of nitrogen in PEI. Complete details of the synthesis and characterization of the sorbents are provided in Section S6 of the ESI.† As expected, increasing the loading of modified PEI in the sample reduces the pore volume (Table S33, ESI†). Excessive PEI loading can lead to reduced CO2 uptake.79–81 Several studies have previously concluded that there is a maximum adsorption capacity of PEI at around 40% organic loading in the SBA-15 framework.82,83 Thus, all studies in this work were performed at a fixed 40 wt% organic loading in the SBA-15.
The amount of adduct in the amine solution can be used to control the extent of functionalization and final properties of the sample, illustrated in Fig. 5(b)–(g). The CO2 uptakes in Fig. 5(e)–(g) were measured gravimetrically using a temperature swing adsorption process (adsorption: 30 °C, 400 ppm CO2 in He; regeneration: 110 °C, He), and the CO2 heats of adsorption were measured in a thermogravimetric analysis/differential scanning calorimetry (TGA/DSC) system under 400 ppm. As expected, unmodified PEI/SBA-15 (molar ratio of adduct to nitrogen = 0) exhibited the highest CO2 uptake (1.2 mmol g−1) and heat of sorption (−80 kJ mol−1); these measurements are consistent with previous literature.78,84,85
Characterization beyond measuring the CO2 uptake, heat of adsorption, and degradation rate is not critical for the economic model. However, we choose to include these details here to emphasize the connection that must be made between experimental sorbent design, process engineering, and economic analysis. In order to effectively tune sorbent properties to reduce the cost of direct air capture, we need to clearly understand how our tuning affects the performance, which requires knowledge of details such as the amine state distributions and steric hindrance of functional groups.
Quantitative liquid-phase 13C NMR (Fig. S11, ESI†) was used to characterize the amine state distributions in the unmodified and modified PEIs.86 According to the quantitative analysis, the unmodified PEI possesses a primary![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) secondary
secondary![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tertiary amine ratio of 36
tertiary amine ratio of 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26, respectively. As the amount of adduct in solution and subsequent functionalization with methyl, propyl, and 2-hydroxypropyl groups increases (from 0–0.75 in Fig. 5(b)–(d)), the proportion of primary amines in the sample (pink bars) gradually decreased. The secondary amines (blue bars) and tertiary amines (green bars) increased.
26, respectively. As the amount of adduct in solution and subsequent functionalization with methyl, propyl, and 2-hydroxypropyl groups increases (from 0–0.75 in Fig. 5(b)–(d)), the proportion of primary amines in the sample (pink bars) gradually decreased. The secondary amines (blue bars) and tertiary amines (green bars) increased.
Notably, the increase in the secondary amine portion (pink bars) was much faster than the increase in the tertiary amine portion (green bars). For example, for methyl modification in Fig. 5(c), the secondary amines increase from 36% to 48% in the 0.25Me-PEI/SBA-15 sample, but the tertiary amines only increase from 27% to 30%. This indicates that the functionalization is selective towards converting primary amines to secondary amines rather than the alkylation of secondary amines to tertiary amines. This effect is even more pronounced when the chain length of the adduct is increased. For instance, in the case of methyl-modified PEI, 70% of the methyl reagent (CH3I) reacted was attributed to the conversion of primary to secondary amines. In comparison, the other 30% was used for the conversion of secondary to tertiary amines. In the case of propyl-modified PEI, 90% of the adduct went towards converting primary amines to secondary.
We suggest that this selectivity is due to steric hindrance of the secondary amine sites, which provides less accessible reaction sites compared to the primary amines.44 In the case of reaction with 1,2-epoxypropane (Fig. 5(b)), a similar reaction trend in primary amine sites is observed. However, the conversion of primary to secondary amines was not as pronounced as propyl-modified PEIs. The selective alkylation of primary to secondary amines is desirable to limit reductions in CO2 adsorption capacities, as tertiary amines capture CO2 much less efficiently than primary and secondary amines.87,88
Similar degrees of functionalization were observed for the three different adducts. For example, with a 0.25 molar ratio of adduct to nitrogen in the solution, regardless of the adduct, the resulting samples have 20–22% primary amines (pink), 44–48% secondary amines (blue), and 30–35% tertiary amines (green). Despite the similar extent of functionalization, differences are observed in performance between the different functional groups. For the 0.25 molar ratio functionalization solutions, the CO2 capacity is more significantly reduced when the hydrophobic alkyl groups such as methyl and propyl were used for modification, and the reduction is even more pronounced for the larger propyl group (Fig. 5(f) and (g)). In contrast, the hydrophilic 2-hydroxypropyl modified PEI (Fig. 5(e)) retains approximately 0.6 mmol g−1 CO2 capacity, with a heat of adsorption of −45 kJ mol−1, while the methyl- and propyl-functionalized PEI materials have CO2 uptakes of less than 0.4 mmol g−1 and heats of adsorption between −45 and −35 kJ mol−1.
The trends in CO2 uptake are consistent with the heat of CO2 adsorption measured in a in a TGA/DSC system under 400 ppm (Fig. 5(e)–(g), right y-axis). Unmodified PEI showed the largest heat of adsorption for CO2 (−80 kJ mol−1). The methyl-modified-PEI samples (Fig. 5(f)) showed a substantially lower heat of CO2 adsorption (−20 to −50 kJ mol−1), which decreased gradually as the side chains became bulkier, or when more alkyl groups are added. This can be attributed to longer chains reducing the accessibility of amines due to steric hindrance, weakening carbamate species formation.42,89,90 In the case of 2-hydroxypropyl functionalized samples (Fig. 5(e)), the heat of adsorption is determined by steric factors as well as the electron-withdrawing nature of the adduct, which reduces the basicity of the amine sites and results in weaker amine–CO2 interactions.43,48 Notably, the heat of adsorption is higher in similarly titrated 2-hydroxypropyl modified PEI versus methyl modified PEI. This suggests more accessible amines and the formation of more enthalpically favored alkylammonium carbamate groups in 2-hydropxypropyl PEI. Because of its greater retention of capacity, the 2-hydroxypropyl-modified PEI materials (HP-PEIs) were identified as the best candidates for further study.
3.5 Cost predictions for modified sorbents
The final question is: which combination of properties results in the most economically advantaged sorbent for DAC? The significant impact of stability on the economic feasibility of sorbents is evident from the wide variation in cost observed with different degradation rates, as shown in Fig. 3. Using experimentally measured heats of adsorption and working capacities (Fig. 5), we estimated the DAC levelized cost of CO2 capture for each sorbent (Fig. 6(a)). Without considering stability differences, the LCOC of the HP-modified sorbents ($325–395 per t-CO2) surpasses that of the unmodified PEI ($315 per t-CO2). The cost difference is primarily attributed to the reduced working capacity of the functionalized samples, which necessitates more sorbent for capturing the same amount of CO2. The increased sorbent amount consequently increases the sensible heat (light blue bar). The lower heat of adsorption of the modified samples does reduce the latent heat (red bar), but it is not enough to overcome the consequences of the reduced working capacity.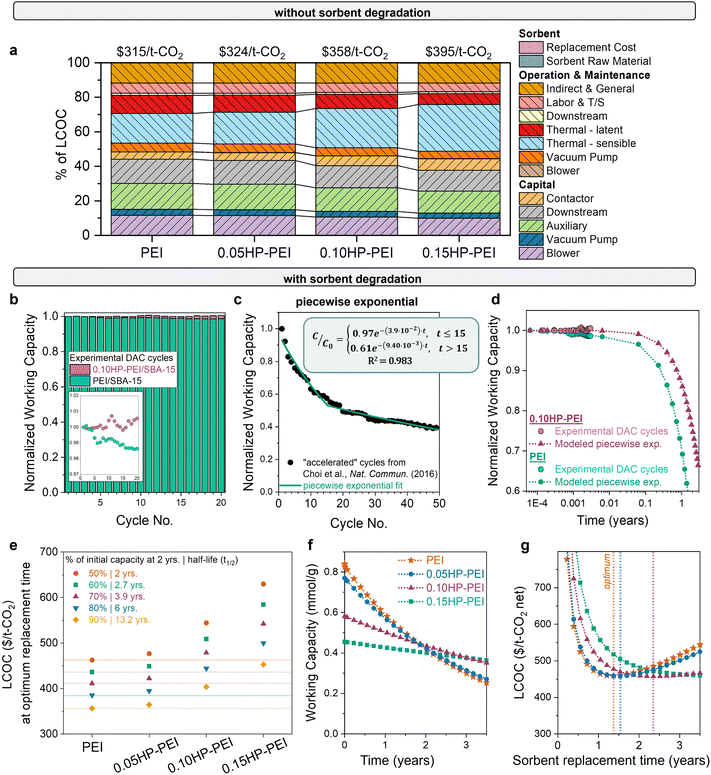 | ||
| Fig. 6 DAC cost with modified PEI sorbents. (a) DAC cost and cost components using unmodified and modified PEI samples, with no degradation included. Sorbent cost components are minor. (b) Capacity decrease over time for unmodified and modified PEI (0.15HP-PEI), measured gravimetrically. The inset displays the same data magnified. (c) Cyclic capacity data for unmodified PEI in accelerated conditions from Choi et al., fit to a piecewise exponential equation. (d) Comparison of experimental DAC cyclic capacity data with the piecewise exponential function used in the model. (e) Cost of unmodified and modified samples as a function of degradation rate. The points below each PEI horizontal line have a lower cost of CO2 capture. For example, if PEI degrades 50% in 2 years, then 0.05HP-PEI must degrade less than 60% in 2 years to achieve a lower cost of CO2 capture. (f) Illustration of the necessary stability of each sorbent for equivalent DAC cost. Capacity fade profiles of modified PEI that result in the same cost at the optimum replacement time. (g) LCOC for each of the sorbents with the capacity fade profile from (f). The dotted line indicates the optimum replacement time (minimum LCOC). The parameters used for each of the sorbents are listed in Table S2 (ESI†). | ||
However, this cost comparison in Fig. 6(a) overlooks stability differences. Previous studies have demonstrated that functionalization of polyamines with 2-hydoxybutyl improves the cyclic stability,41–47 and Goeppert et al. also established the stability of pentaethylenehexamine (PEHA) and tetraethylenepentamine (TEPA) functionalized with 2-hydroxypropyl (HP).11,91 Similar enhancement in stability is expected for HP-functionalized PEI. To confirm, we evaluated the working capacity of unmodified PEI and 0.10HP-PEI over 20 cycles (Fig. 6(b)). The cycles consisted of 60 minutes of adsorption (35 °C, 400 ppm CO2 in N2) followed by 10 minutes of desorption (90 °C, N2).
Even for only 20 cycles in mild conditions, the enhanced stability of the HP-PEI compared to unmodified PEI is evident. The unmodified PEI exhibited approximately 2% capacity loss, likely due to the formation of cyclic urea under repeated dry temperature swing cycles, as reported in past studies.92–94 However, after modification with 2-hydroxypropyl, this degradation is suppressed. The steric hindrance around the active primary amine sites provided by 2-hydroxypropyl groups can slow down the formation of intermediates.95 The hydroxyl group in the adduct provides additional hydrogen bonds that may stabilize the carbamic acid/carbamate species and prevent them from undergoing cyclization reactions.42 It has been demonstrated that higher extents of functionalization result in further stability enhancement.42
The gravimetric analysis instrument (TGA) is not air-tight (Fig. S9, ESI†), and we hypothesize that the presence of trace oxygen at high temperature desorption conditions is contributing to degradation as well. This is consistent with previous literature demonstrating the impact of oxygen on the degradation of amines.19,46,95 Oxidative cleavage of C–N bonds at the primary amines can lead to a significant loss of CO2 affinity.96 Guta et al. observed 80% sorbent deactivation after 8 days (17% deactivation in 3 hours) in 400 ppm CO2 per air at 70 °C, in contrast to 2% sorbent deactivation after 8 days in 400 ppm CO2 per N2 at the same temperature.19
To determine which degradation form best fits the deactivation data, we analyzed cyclic stability data from Choi et al. with harsher cycle conditions – higher-concentration, humid CO2 (15%) for adsorption and pure CO2 at a higher temperature (120 °C) for desorption. The harsher cycle conditions accelerate degradation, providing insight into the degradation profile at longer times. With the accelerated conditions, Choi et al. observed a 40% loss in the working capacity unmodified PEI over 50 cycles, in contrast to the 2% loss in Fig. 6(b) with adsorption in 400 ppm, dry CO2 and desorption in N2 at 90 °C. The accelerated degradation data were fit to linear, exponential, and piecewise exponential functions, and the piecewise exponential function was determined to be the best fit for the unmodified and modified polyamine sorbents (Fig. 6(c) and Fig. S7, ESI†).
The question remains: how much stability improvement is necessary to offset the reduced working capacity of the modified PEI sorbents? The answer is useful not only for the 2-hydroxypropyl functionalized polyamine series but also any sorbent modification that improves stability at the expense of productivity. To answer the question for one case, we evaluated the DAC cost of PEI, 0.05HP-PEI, 0.10HP-PEI, and 0.15HP-PEI with various degradation rates, using the experimentally measured properties and piecewise exponential form. The observed experimental capacity loss in Fig. 6(b) was used to define the deactivation in the first part of the piecewise form (Fig. 6(d)). The resulting costs for each of the sorbents with varying degradation rates are shown in Fig. 6(e). For the unmodified samples, the points below each PEI horizontal line have a lower cost of CO2 capture. For example, if PEI has a degradation rate of 2.2 × 10−5 cycle−1, then 0.05HP-PEI must have a degradation rate lower than 1.6 × 10−5 cycle−1 to achieve a lower cost of CO2 capture.
We then determined the degradation rate at which the modified samples yielded an equivalent DAC cost to unmodified PEI. The necessary capacity fade profile for each modified sorbent is depicted in Fig. 6(f), and the resulting LCOC for each is in Fig. 6(g). As the degree of functionalization increases and working capacity decreases, greater stability enhancement is necessary to achieve the same cost. For instance, 0.05HP-PEI requires only a slight stability improvement over unmodified PEI, whereas 0.15HP-PEI requires significantly higher stability (Fig. 6(f)). If the sorbents are only used for a short amount of time before replacement, the unmodified PEI results in a lower cost of CO2 capture due to its higher working capacity (Fig. 6(g)). However, as the sorbent usage time is extended, the umodified PEI will degrade more than the modified HP-PEIs.
The results presented in Fig. 6(f) and (g) reflect a scenario in which the unmodified PEI loses 50% of its capacity in two years, consistent with the deactivation timeline observed in Climeworks amine sorbents as described by Deutz et al.61 However, the PEI degradation rate will depend on the selected cycle parameters and environmental factors, such as humidity, temperature, and the concentration of other air contaminants. The results for several PEI degradation rates in Fig. 6(e) account for this variability, providing both a sensitivity analysis and guidance for processes with different observed degradation rates.
While experimental degradation data in literature could be fit to estimate decay constants, there are two limitations that reduce the merit of those decay constants. First, the small number of cycles limits the accuracy of the rates, as the limited number of cycles may be missing a lower degradation rate at longer sorbent lifetimes. For example, the rate of degradation of monoethanolamine (MEA) begins to slow after approx. 50 hours of oxygen exposure at high temperatures (120–160 °C),97 and Fan et al. observed a shift in the degradation rate of PEI after 80 cycles with dry flue gas containing 200 ppm SO2.75 Thus, there is uncertainty in the long time degradation behavior. The second limitation is that decay constants are specific to cycle conditions, so economic conclusions derived from one set of data may not extend to processes with different air humidity, air temperature, desorption temperature, cycle time, etc. In real operation, these factors change continuously. These limitations in measuring the degradation rate prevent us from predicting the cost of CO2 capture for each sorbent. Rather, we only provide necessary stability metrics to achieve cost reductions compared to an unmodified sample. Future work should consider employing verified accelerated aging testing to assess sorbent stability within more reasonable time frames.19,98,99 We used accelerated aging here as a tool for determining degradation form in Fig. 6(c) and (d), but the challenge of connecting accelerated degradation times to actual process times remains.
Fig. 7 compares the impact of degradation rate, working capacity, and cycle time (kinetics) on the total DAC cost. The top three figures illustrate five working capacities, and the bottom three illustrate five cycle times. The left, middle, and right panels are no degradation, 70% capacity remaining at 1 year (exponential decay), and 50% capacity remaining at 1 year (exponential decay), respectively. All figures are displayed as a function of sorbent replacement time. By comparing the three panels with varying degradation rates, we can see that the degradation rate has a substantial impact on the cost when the working capacity is low or when the cycle time is high, due to the large amount of sorbent required. It is important to note that the parameters used for these cost estimates are quite conservative. Thus, we also evaluated a “best case scenario” in which all of the model parameters are set at highly optimistic values, some of which may be beyond the current state-of-the-art (Table S1, ESI†). This includes an optimistic energy carbon footprint of 17 kg CO2,eq. per MW h, in contrast to the 171 kg CO2,eq. per MW h that was used in the rest of the analysis. These “best case scenario” parameters result in a cost of slightly above $135 per t-CO2.
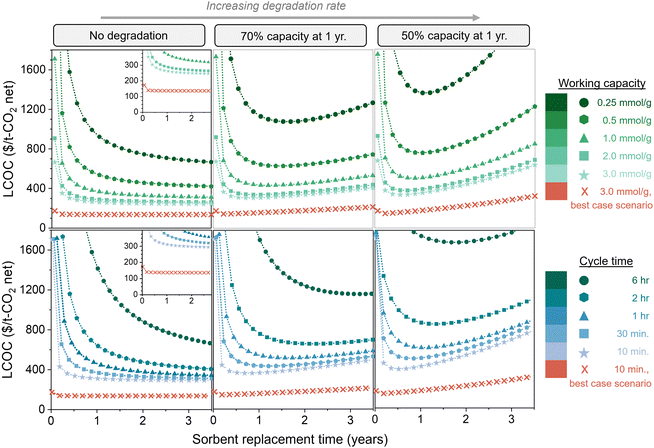 | ||
| Fig. 7 Impact of sorbent degradation rate on cost with varying productivity. Levelized cost of CO2 captured ($ per t-CO2 net, including carbon footprint) is shown as a function of degradation rate, working capacity, cycle time, and sorbent replacement time. The top three figures illustrate various working capacities, and the bottom three figures illustrate various cycle times. The left, middle, and right panels are no degradation, 70% capacity remaining at 1 year (exponential decay), and 50% capacity remaining at 1 year (exponential decay), respectively. The insets on the left panel display the same data magnified. The highly optimistic parameters used for the “best case scenario” are listed in Table S1 (ESI†). | ||
The difference between no degradation and fast degradation is less significant for sorbents with working capacities above 2.0 mmol g−1, but continuing to use degrading sorbents past the optimum replacement time will increase the cost. Additionally, it is clear that using a sorbent with a high capacity and high degradation rate can be less economically viable than a sorbent with a low capacity and low degradation rate. Similarly, sorbents with fast kinetics (i.e., short cycle times) and high degradation rates can be higher in cost than sorbents with longer cycle times and low degradation rates. Without an economic model, it would not be clear which combination of properties results in the most economically viable process due to the complex relationships between sorbent properties and process cost. A single sorbent property cannot be used as a predictor for economic viability of DAC.
4 Conclusions
An economic model with the capability to analyze sorbent degradation was developed for direct air capture. Sorbent degradation not only leads to higher costs than anticipated, but it can also result in high carbon footprints, especially when carbon-intensive energy sources are used. The capacity-fade model can be used to determine the sorbent replacement time that optimizes the performance and cost of DAC systems while also minimizing their environmental impact. The degradation form and rate both influence the carbon footprint, cost, and optimal sorbent replacement time.The working capacity, heat of adsorption, and stability of polyamine sorbents were experimentally tuned using a one-step modification with alkyl or epoxy reactants, producing alkyl or hydroxyalkyl functional groups on the polyamine. The stability of the functionalized sorbents can outweigh the lower working capacity in some cases, emphasizing the important role of sorbent stability in economic feasibility.47 Degradation information coupled with a capacity-fade economic model is vital for accurately predicting the cost of direct air capture.
There are some key limitations of this study. First, the potential for increased suppression of H2O sorption due to the addition of the hydrophobic functional groups was not explored. Water sorption can affect the adsorbent stability, capacity, and thermal energy requirements, and we previously demonstrated the significant impact of these effects on the economic viability of BECCS.30 Water management with effective heat integration will be critical for the success of DAC technologies.72,100,101 Additionally, the cost of functionalizing sorbents was also not considered. While this is thought to be minimal for polyamines, the cost of modifications could be substantial for other adsorbents such as MOFs, and thus modeling this cost is the focus of ongoing research.102 The reduced carbon footprint of polyamine replacement via the recommended washing procedure should also be explored further.57 Finally, diverse thermal energy sources, such as waste heat or heat pumps, and heat integration strategies should also be considered in future work.71–73
Author contributions
H. E. H. contributed to the technoeconomic model development, analysis, writing of the initial draft, and figure preparation. S. B. contributed to writing the initial draft of Section 3.4. S. B. and A. V. contributed to sample preparation and characterization. R. P. L, C. W. J., and M. J. R. contributed to conceptualization, supervision, and funding acquisition. All authors contributed to discussion, interpretation of data, and review and editing of the manuscript.Conflicts of interest
The authors declare the following competing financial interest(s): C. W. J. has a financial interest in several DAC companies that seek to commercialize CO2 capture from air. This work is not associated with any of these companies. C. W. J. has a conflict-of-interest management plan in place at Georgia Tech.Acknowledgements
This research was funded by the Advanced Research Projects Agency-Energy of the U.S. Department of Energy under award no. DE-AR0001414. H. E. Holmes thanks the National Science Foundation Graduate Research Fellowship Program and the ARCS Foundation for her financial support. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-2039655.References
- S. Solomon, G. K. Plattner, R. Knutti and P. Friedlingstein, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 1704–1709 CrossRef CAS PubMed.
- K. S. Lackner, S. Brennan, J. M. Matter, A. H. A. Park, A. Wright and B. van der Zwaan, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 13156–13162 CrossRef CAS PubMed.
- X. Y. Shi, H. Xiao, H. Azarabadi, J. Z. Song, X. L. Wu, X. Chen and K. S. Lackner, Angew. Chem., Int. Ed., 2020, 59, 6984–7006 CrossRef CAS PubMed.
- A. Goeppert, S. Meth, G. K. S. Prakash and G. A. Olah, Energy Environ. Sci., 2010, 3, 1949–1960 RSC.
- L. A. Darunte, A. D. Oetomo, K. S. Walton, D. S. Sholl and C. W. Jones, ACS Sustainable Chem. Eng., 2016, 4, 5761–5768 CrossRef CAS.
- T. M. McDonald, W. R. Lee, J. A. Mason, B. M. Wiers, C. S. Hong and J. R. Long, J. Am. Chem. Soc., 2012, 134, 7056–7065 CrossRef CAS PubMed.
- Y. H. Lee, Y. Kwon, C. Kim, Y. E. Hwang, M. Choi, Y. Park, A. Jamal and D. Y. Koh, JACS Au, 2021, 1, 1198–1207 CrossRef CAS PubMed.
- M. Y. Song, G. Rim, F. H. Kong, P. Priyadarshini, C. Rosu, R. P. Lively and C. W. Jones, Ind. Eng. Chem. Res., 2022, 36, 13624–13634 CrossRef.
- A. Kumar, D. G. Madden, M. Lusi, K. J. Chen, E. A. Daniels, T. Curtin, J. J. Perry and M. J. Zaworotko, Angew. Chem., Int. Ed., 2015, 54, 14372–14377 CrossRef CAS PubMed.
- A. R. Sujan, S. H. Pang, G. H. Zhu, C. W. Jones and R. P. Lively, ACS Sustainable Chem. Eng., 2019, 7, 5264–5273 CrossRef CAS.
- A. Goeppert, H. Zhang, R. Sen, H. Dang and G. K. S. Prakash, ChemSusChem, 2019, 12, 1712–1723 CrossRef CAS PubMed.
- M. Erans, E. S. Sanz-Pérez, D. P. Hanak, Z. Clulow, D. M. Reiner and G. A. Mutch, Energy Environ. Sci., 2022, 15, 1360–1405 RSC.
- M. Bui, C. S. Adjiman, A. Bardow, E. J. Anthony, A. Boston, S. Brown, P. S. Fennell, S. Fuss, A. Galindo, L. A. Hackett, J. P. Hallett, H. J. Herzog, G. Jackson, J. Kemper, S. Krevor, G. C. Maitland, M. Matuszewski, I. S. Metcalfe, C. Petit, G. Puxty, J. Reimer, D. M. Reiner, E. S. Rubin, S. A. Scott, N. Shah, B. Smit, J. P. M. Trusler, P. Webley, J. Wilcox and N. Mac Dowell, Energy Environ. Sci., 2018, 11, 1062–1176 RSC.
- Y. H. Miao, Y. Z. Wang, B. Y. Ge, Z. J. He, X. C. Zhu, J. Li, S. K. Liu and L. J. Yu, Adv. Sci., 2023, 10, 2207253 CrossRef CAS PubMed.
- F. H. Kong, G. Rim, P. Priyadarshini, M. Y. Song, M. J. Realff, R. P. Lively and C. W. Jones, Sustainable Energy Fuels, 2023, 7, 4461–4473 RSC.
- J. Elfving, J. Kauppinen, M. Jegoroff, V. Ruuskanen, L. Jarvinen and T. Sainio, Chem. Eng. J., 2021, 404, 126337 CrossRef CAS.
- R. Kumar, S. Ohtani and N. Tsunoji, Microporous Mesoporous Mater., 2023, 360, 112714 CrossRef CAS.
- G. Rim, F. H. Kong, M. Y. Song, C. Rosu, P. Priyadarshini, R. P. Lively and C. W. Jones, JACS Au, 2022, 2, 380–393 CrossRef CAS PubMed.
- J. C. Yoseph, A. Guta, S. Li, G. Innocenti, S. H. Pang, M. A. Sakwa-Novak, C. Sievers and C. W. Jones, ACS Appl. Mater. Interfaces, 2023, 15, 46790–46802 CrossRef PubMed.
- S. Bose, D. Sengupta, C. D. Malliakas, K. B. Idrees, H. Xie, X. Wang, M. L. Barsoum, N. M. Barker, V. P. Dravid, T. Islamoglu and O. K. Farha, Chem. Sci., 2023, 14, 9380–9388 RSC.
- H. Azarabadi and K. S. Lackner, Appl. Energy, 2019, 250, 959–975 CrossRef.
- J. Young, N. McQueen, C. Charalambous, S. Foteinis, O. Hawrot, M. Ojeda, H. Pilorge, J. Andresen, P. Psarras, P. Renforth, S. Garcia and M. van der Spek, One Earth, 2023, 6, 899–917 CrossRef.
- D. W. Keith, G. Holmes, D. S. Angelo and K. Heidel, Joule, 2018, 2, 1573–1594 CrossRef CAS.
- N. McQueen, P. Psarras, H. Pilorgé, S. Liguori, J. J. He, M. Y. Yuan, C. M. Woodall, K. Kian, L. Pierpoint, J. Jurewicz, J. M. Lucas, R. Jacobson, N. Deich and J. Wilcox, Environ. Sci. Technol., 2020, 54, 7542–7551 CrossRef CAS PubMed.
- N. McQueen, M. J. Desmond, R. H. Socolow, P. Psarras and J. Wilcox, Front. Clim., 2021, 2, 618644 CrossRef.
- F. Sabatino, A. Grimm, F. Gallucci, M. V. Annaland, G. J. Kramer and M. Gazzani, Joule, 2021, 5, 2047–2076 CrossRef CAS.
- M. Fasihi, O. Efimova and C. Breyer, J. Cleaner Prod., 2019, 224, 957–980 CrossRef CAS.
- J. Valentine, Z. Alexander, H. Sally, M. Hari, W. Mark, R. Naksha, K. Aaron, S. Mike, S. Mark and F. Timothy, Direct Air Capture Case Studies: Sorbent System, United States, Web, 2022 Search PubMed.
- E. Tegeler, Y. Cui, M. Masoudi, A. M. Bahmanpour, T. Colbert, J. Hensel and V. Balakotaiah, Chem. Eng. Sci., 2023, 281, 119107 CrossRef CAS.
- H. E. Holmes, R. P. Lively and M. J. Realff, JACS Au, 2021, 1, 795–806 CrossRef CAS PubMed.
- E. S. Sanz-Perez, C. R. Murdock, S. A. Didas and C. W. Jones, Chem. Rev., 2016, 116, 11840–11876 CrossRef CAS PubMed.
- G. Rim, P. Priyadarshini, M. Y. Song, Y. X. Wang, A. D. Bai, M. J. Realff, R. P. Lively and C. W. Jones, J. Am. Chem. Soc., 2023, 145, 7190–7204 CrossRef CAS PubMed.
- S. A. Didas, M. A. Salcwa-Novak, G. S. Foo, C. Sievers and C. W. Jones, J. Phys. Chem. Lett., 2014, 5, 4194–4200 CrossRef CAS PubMed.
- C. J. Yoo, L. C. Lee and C. W. Jones, Langmuir, 2015, 31, 13350–13360 CrossRef CAS PubMed.
- R. W. Faig, T. M. O. Popp, A. M. Fracaroli, E. A. Kapustin, M. J. Kalmutzki, R. M. Altamimi, F. Fathieh, J. A. Reimer and O. M. Yaghi, J. Am. Chem. Soc., 2017, 139, 12125–12128 CrossRef PubMed.
- Y. H. Miao, Z. J. He, X. C. Zhu, D. Izikowitz and J. Li, Chem. Eng. J., 2021, 426, 131875 CrossRef CAS.
- A. Cherevotan, J. Raj and S. C. Peter, J. Mater. Chem. A, 2021, 9, 27271–27303 RSC.
- S. A. Didas, S. Choi, W. Chaikittisilp and C. W. Jones, Acc. Chem. Res., 2015, 48, 2680–2687 CrossRef CAS PubMed.
- S. Dewitt, A. Sinha, J. Kalyanaraman, F. Zhang, M. J. Realff and R. P. Lively, Annu. Rev. Chem. Biomol. Eng., 2018, 9, 129–152 CrossRef PubMed.
- S. Choi, J. H. Drese and C. W. Jones, ChemSusChem, 2009, 2, 796–854 CrossRef CAS PubMed.
- J. M. Kolle and A. Sayari, Ind. Eng. Chem. Res., 2020, 59, 6944–6950 CrossRef CAS.
- W. Choi, K. Min, C. Kim, Y. S. Ko, J. Jeon, H. Seo, Y. K. Park and M. Choi, Nat. Commun., 2016, 7, 12640 CrossRef CAS PubMed.
- L. Tao, Q. Zhang, T. Li and S. Deng, J. Environ. Chem. Eng., 2022, 10, 108620 CrossRef CAS.
- S. Park, J. Kim, Y.-J. Won, C. Kim, M. Choi, W. Jung, K. S. Lee, J.-G. Na, S.-H. Cho, S. Y. Lee and J. S. Lee, Ind. Eng. Chem. Res., 2018, 57, 13923–13931 CrossRef CAS.
- S. Park, K. Choi, H. J. Yu, Y.-J. Won, C. Kim, M. Choi, S.-H. Cho, J.-H. Lee, S. Y. Lee and J. S. Lee, Ind. Eng. Chem. Res., 2018, 57, 4632–4639 CrossRef CAS.
- K. Min, W. Choi, C. Kim and M. Choi, Nat. Commun., 2018, 9, 726 CrossRef PubMed.
- W. Choi, J. Park, C. Kim and M. Choi, Chem. Eng. J., 2021, 408, 127289 CrossRef CAS.
- K. Min, W. Choi, C. Kim and M. Choi, ACS Appl. Mater. Interfaces, 2018, 10, 23825–23833 CrossRef CAS PubMed.
- R. P. Lively and M. J. Realff, AIChE J., 2016, 62, 3699–3705 CrossRef CAS.
- R. Turton; R. C. Bailie; W. B. Wallace; J. A. Shaeiwitze and D. Bhattacharyya, Analysis, Synthesis, and Design of Chemical Processes, Prentice Hall, 4th edn, 2012 Search PubMed.
- D. Danaci, P. A. Webley and C. Petit, Frontiers in Chemical Engineering, 2021, 2, 602430 CrossRef.
- E. S. Rubin, Int. J. Greenhouse Gas Control, 2012, 10, 181–190 CrossRef.
- E. S. Rubin, C. Short, G. Booras, J. Davison, C. Ekstrom, M. Matuszewski and S. McCoy, Int. J. Greenhouse Gas Control, 2013, 17, 488–503 CrossRef CAS.
- M. van der Spek, S. Roussanaly and E. S. Rubin, Int. J. Greenhouse Gas Control, 2019, 83, 91–104 CrossRef.
- S. Roussanaly, N. Berghout, T. Fout, M. Garcia, S. Gardarsdottir, S. M. Nazir, A. Ramirez and E. S. Rubin, Int. J. Greenhouse Gas Control, 2021, 106, 103263 CrossRef CAS.
- NETL, Quality Guidelines for Energy System Studies, Pittsburgh, PA, 2022 Search PubMed.
- Y. Labreche, R. P. Lively, F. Rezaei, G. Chen, C. W. Jones and W. J. Koros, Chem. Eng. J., 2013, 221, 166–175 CrossRef CAS.
- Y. F. Fan, Y. Labreche, R. P. Lively, C. W. Jones and W. J. Koros, AIChE J., 2014, 60, 3878–3887 CrossRef CAS.
- L. J. Müller, A. Kätelhön, M. Bachmann, A. Zimmermann, A. Sternberg and A. Bardow, Front. Energy Res., 2020, 8, 15 CrossRef.
- T. Terlouw, K. Treyer, C. Bauer and M. Mazzotti, Environ. Sci. Technol., 2021, 55, 11397–11411 CrossRef CAS PubMed.
- S. Deutz and A. Bardow, Nat. Energy, 2021, 6, 203–213 CrossRef CAS.
- P. Gabrielli, J. Campos, V. Becattini, M. Mazzotti and G. Sansavini, Int. J. Greenhouse Gas Control, 2022, 121, 103797 CrossRef CAS.
- L. J. Müller, A. Kätelhön, S. Bringezu, S. McCoy, S. Suh, R. Edwards, V. Sick, S. Kaiser, R. Cuéllar-Franca, A. El Khamlichi, J. H. Lee, N. von der Assen and A. Bardow, Energy Environ. Sci., 2020, 13, 2979–2992 RSC.
- N. Thonemann and M. Pizzol, Energy Environ. Sci., 2019, 12, 2253–2263 RSC.
- M. M. J. de Jonge, J. Daemen, J. M. Loriaux, Z. J. N. Steinmann and M. A. J. Huijbregts, Int. J. Greenhouse Gas Control, 2019, 80, 25–31 CrossRef CAS.
- Y. Qiu, P. Lamers, V. Daioglou, N. McQueen, H.-S. de Boer, M. Harmsen, J. Wilcox, A. Bardow and S. Suh, Nat. Commun., 2022, 13, 3635 CrossRef CAS PubMed.
- M. Song, G. Rim, Y. Wang, I. Borne, C. W. Jones and R. P. Lively, Chem. Eng. J., 2023, 477, 147135 CrossRef CAS.
- F. Creutzig, C. Breyer, J. Hilaire, J. Minx, G. P. Peters and R. Socolow, Energy Environ. Sci., 2019, 12, 1805–1817 RSC.
- S. Chiquier, P. Patrizio, M. Bui, N. Sunny and N. Mac Dowell, Energy Environ. Sci., 2022, 15, 4389–4403 RSC.
- L. K. Küng, S. Aeschlimann, C. Charalambous, F. McIlwaine, J. Young, N. Shannon, K. Strassel, C. N. Maesano, R. Kahsar, D. Pike, M. van der Spek and S. Garcia, Energy Environ. Sci., 2023, 16, 4280–4304 RSC.
- G. Leonzio and N. L. Shah, Ind. Eng. Chem. Res., 2022, 61, 13221–13230 CrossRef CAS.
- H. E. Holmes, M. J. Realff and R. P. Lively, Nat. Chem. Eng., 2024, 1, 208–215 CrossRef.
- X. W. Wu, R. Krishnamoorti and P. Bollini, Annu. Rev. Chem. Biomol. Eng., 2022, 13, 279–300 CrossRef CAS PubMed.
- H. E. Holmes, R. D. Schreck, P. Narayanan, S. Ghosh, W. Sun, M. J. Realff and R. P. Lively, Sustainable Energy Fuels, 2023, 7, 4602–4607 RSC.
- Y. F. Fan, F. Rezaei, Y. Labreche, R. P. Lively, W. J. Koros and C. W. Jones, Fuel, 2015, 160, 153–164 CrossRef CAS.
- G. G. Qi, L. L. Fu, B. H. Choi and E. P. Giannelis, Energy Environ. Sci., 2012, 5, 7368–7375 RSC.
- H. Jung, S. Jeon, D. H. Jo, J. Huh and S. H. Kim, Chem. Eng. J., 2017, 307, 836–844 CrossRef CAS.
- C. Kim, W. Choi and M. Choi, ACS Appl. Mater. Interfaces, 2019, 11, 16586–16593 CrossRef CAS PubMed.
- C. Choi, R. L. Kadam, S. Gaikwad, K. S. Hwang and S. Han, Microporous Mesoporous Mater., 2020, 296, 110006 CrossRef CAS.
- X. Z. Guo, L. Ding, K. Kanamori, K. Nakanishi and H. Yang, Microporous Mesoporous Mater., 2017, 245, 51–57 CrossRef CAS.
- G. G. Qi, Y. B. Wang, L. Estevez, X. N. Duan, N. Anako, A. H. A. Park, W. Li, C. W. Jones and E. P. Giannelis, Energy Environ. Sci., 2011, 4, 444–452 RSC.
- H. J. Moon, J. M. Carrillo, J. Leisen, B. G. Sumpter, N. C. Osti, M. Tyagi and C. W. Jones, J. Am. Chem. Soc., 2022, 144, 11664–11675 CrossRef CAS PubMed.
- K. Wang, H. Y. Shang, L. Li, X. L. Yan, Z. F. Yan, C. G. Liu and Q. F. Zha, J. Nat. Gas Chem., 2012, 21, 319–323 CrossRef CAS.
- W. Chaikittisilp, H.-J. Kim and C. W. Jones, Energy Fuels, 2011, 25, 5528–5537 CrossRef CAS.
- K. M. Li, J. G. Jiang, F. Yan, S. C. Tian and X. J. Chen, Appl. Energy, 2014, 136, 750–755 CrossRef CAS.
- J. H. Drese, S. Choi, R. P. Lively, W. J. Koros, D. J. Fauth, M. L. Gray and C. W. Jones, Adv. Funct. Mater., 2009, 19, 3821–3832 CrossRef CAS.
- D. M. D'Alessandro, B. Smit and J. R. Long, Angew. Chem., Int. Ed., 2010, 49, 6058–6082 CrossRef PubMed.
- J. J. Lee, C. H. Chen, D. Shimon, S. E. Hayes, C. Sievers and C. W. Jones, J. Phys. Chem. C, 2017, 121, 23480–23487 CrossRef CAS.
- P. D. Vaidya and E. Y. Kenig, Chem. Eng. Technol., 2007, 30, 1467–1474 CrossRef CAS.
- M. A. Alkhabbaz, P. Bollini, G. S. Foo, C. Sievers and C. W. Jones, J. Am. Chem. Soc., 2014, 136, 13170–13173 CrossRef CAS PubMed.
- A. Goeppert, H. Zhang, G. A. Olah and G. K. S. Prakash, US Pat., 10,751,689, 2020 Search PubMed.
- A. Sayari, A. Heydari-Gorji and Y. Yang, J. Am. Chem. Soc., 2012, 134, 13834–13842 CrossRef CAS PubMed.
- C. Y. Wu, H. Y. Cheng, R. X. Liu, Q. A. Wang, Y. F. Hao, Y. C. Yu and F. Y. Zhao, Green Chem., 2010, 12, 1811–1816 RSC.
- S. A. Didas, R. S. Zhu, N. A. Brunelli, D. S. Sholl and C. W. Jones, J. Phys. Chem. C, 2014, 118, 12302–12311 CrossRef CAS.
- H. Lepaumier, D. Picq and P. L. Carrette, Ind. Eng. Chem. Res., 2009, 48, 9061–9067 CrossRef CAS.
- J. S. A. Carneiro, G. Innocenti, H. J. Moon, Y. Guta, L. Proano, C. Sievers, M. A. Sakwa-Novak, E. W. Ping and C. W. Jones, Angew. Chem., Int. Ed., 2023, 62, e202302887 CrossRef CAS PubMed.
- T. Supap, R. Idem, A. Veawab, A. Aroonwilas, P. Tontiwachwuthikul, A. Chakma and B. D. Kybett, Ind. Eng. Chem. Res., 2001, 40, 3445–3450 CrossRef CAS.
- S. H. Pang, C. Han, D. S. Sholl, C. W. Jones and R. P. Lively, Chem. Mater., 2016, 28, 6960–6967 CrossRef CAS.
- C. Rosu, S. H. Pang, A. R. Sujan, M. A. Sakwa-Novak, E. W. Ping and C. W. Jones, ACS Appl. Mater. Interfaces, 2020, 12, 38085–38097 CrossRef CAS PubMed.
- M. N. Dods, S. C. Weston and J. R. Long, Adv. Mater., 2022, 34, 2204277 CrossRef CAS PubMed.
- D. Fu and M. E. Davis, Cell Rep. Phys. Sci., 2023, 4, 101389 CrossRef CAS.
- C. Zhang, X. Q. Zhang, T. Y. Su, Y. H. Zhang, L. W. Wang and X. C. Zhu, Renewable Sustainable Energy Rev., 2023, 184, 113473 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee00616j |
| ‡ Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |