Open Access Article
Open Access ArticleUncovering fast solid-acid proton conductors based on dynamics of polyanion groups and proton bonding strength†
Pjotrs
Žguns‡
 a,
Konstantin
Klyukin‡
a,
Konstantin
Klyukin‡
 ac,
Louis S.
Wang
ac,
Louis S.
Wang
 d,
Grace
Xiong
d,
Grace
Xiong
 d,
Ju
Li
d,
Ju
Li
 ab,
Sossina M.
Haile
ab,
Sossina M.
Haile
 d and
Bilge
Yildiz
d and
Bilge
Yildiz
 *ab
*ab
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA. E-mail: byildiz@mit.edu
bDepartment of Nuclear Science and Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA
cDepartment of Materials Engineering, Auburn University, Auburn, Alabama 36849, USA
dDepartment of Materials Science and Engineering, Northwestern University, Evanston, IL 60208, USA
First published on 19th June 2024
Abstract
Achieving high proton conductivity in inorganic solids is key for advancing many electrochemical technologies, including low-energy nano-electronics and energy-efficient fuel cells and electrolyzers. A quantitative understanding of the physical traits of a material that regulate proton diffusion is necessary for accelerating the discovery of fast proton conductors. In this work, we have mapped the structural, chemical and dynamic properties of solid acids to the elementary steps of the Grotthuss mechanism of proton diffusion. Our approach combines ab initio molecular dynamics simulations, analysis of phonon spectra and atomic structure calculations. We have identified the donor–hydrogen bond lengths and the acidity of polyanion groups as key descriptors of local proton transfer and the vibrational frequencies of the cation framework as the key descriptor of lattice flexibility. The latter facilitates rotations of polyanion groups and long-range proton migration in solid acid proton conductors. The calculated lattice flexibility also correlates with the experimentally reported superprotonic transition temperatures. Using these descriptors, we have screened the Materials Project database and identified potential solid acid proton conductors with monovalent, divalent and trivalent cations, including Ag+, Sr2+, Ba2+ and Er3+ cations, which go beyond the traditionally considered monovalent alkali cations (Cs+, Rb+, K+, and NH4+) in solid acids.
Broader contextDiscovery of fast proton conductors can significantly advance a wide range of technologies, including hydrogen fuel cells, electrolyzers, electrosynthesis of fuels, batteries and brain-inspired computing devices. Here, we identify promising fast proton conductors, focusing particularly on the class of solid acids, and go well beyond the traditionally considered chemistries. The key to this is having found physically based descriptors that map the structure and dynamics of the lattice to the atomistic mechanism of proton transport in solids, by leveraging computational tools, physical models, and extensive materials databases. These physical descriptors of proton conduction also provide paths for increasing the conductivity and decreasing the temperature of superprotonic transition. With the rapid growth of materials databases, our approach lays ground for the physically informed search of fast proton conductors and enlarges the chemical space of materials to power the green revolution. |
Introduction
Inorganic solid electrolyte materials with high proton conductivity are important for advancing electrochemical devices for energy conversion, energy storage and energy-efficient computing, such as ceramic fuel cells and electrolyzers,1–5 solid acid fuel cells,6–8 hydrogen generators,9 solid-state proton batteries,10,11 electrochromic devices,12 and magneto-ionic13,14 and analog neuromorphic15–18 computing hardware. Although high proton conductivities are reported for a range of material classes,19–22 most of them show slow proton conductivity at low temperatures (i.e., at room temperature), require special conditions such as a humid environment, or are not compatible with particular technological standards. For example, state-of-the-art perovskite oxide ceramic electrolytes demonstrate sizable proton conductivity (10−3 S cm−1) only above ∼300 °C.22 At lower temperatures, proton diffusion in the bulk of perovskites is slow, and the reported room temperature conductivities are attributed to accumulated water interlayers, e.g., along grain boundaries or nanopores, rather than diffusion in the bulk lattice.22 Metal–organic frameworks (MOFs)23 and polymers such as Nafion24 provide a conductivity of up to 10−2 S cm−1 at room temperature. These materials often require high humidity to conduct protons, and they are typically permeable to alcohols rendering them inapplicable for power generation using such fuels. Furthermore, they are incompatible with the processing of nanoelectronics using the complementary metal-oxide semiconductor (CMOS) technology. Novel solid-state proton conductors are sought after for near ambient-temperature applications. A quantitative understanding of the critical physical, structural, and chemical traits of a material that control proton conduction is necessary for developing the respective materials design strategies.Solid acids constitute a promising class of proton conductors.19,25 Solid acids are composed of metal cations and a network of polyanion groups (e.g., SeO4, SO4, and PO4) that normally do not share corners or edges and are linked solely by hydrogen bonds. At low temperatures, the rigid hydrogen bonding network in solid acids results in low proton conductivities (∼10−5 S cm−1).6,19 In the solid acids that exhibit high conductivities (>10−3 S cm−1), fast proton transport is achieved above the Tsp temperature of first-order, superprotonic transition (Tsp is typically within 100–300 °C).6,19,25 The characteristic features of the superprotonic phase are facile rotation of polyanion groups (which even leads to their rotational disorder) and the accompanying dynamical disorder of hydrogen bond networks.19,25 Both of these traits enable fast proton conduction via the Grotthuss mechanism19,26 above the Tsp in solid acids. The rich compositional space available for solid acids allows tuning the properties of these compounds and potentially achieving high proton conductivity at lower temperatures.
High-throughput computational screening of materials is a promising approach for identifying fast proton conductors. Recently, extensive efforts have been devoted to screening solid-state Li-ions27–34 and O-conductors,34–36 allowing one to identify and experimentally verify promising solid-state electrolytes for the advancement of solid-state batteries and fuel cell technologies. The undertaken screening approaches can be broadly classified into three groups that use: (1) interpretable physical descriptors that are based on the ion diffusion mechanism,29,33 (2) a data-driven approach to train machine learning models but not necessarily provide interpretable insights into the microscopic origin of why certain compounds are better ionic conductors than others,27,30,35–37 and (3) high-throughput molecular dynamics (MD) simulations28 to directly probe ionic diffusivities of screened compounds. Among the first two approaches, the first one that incorporates physical laws governing the microscopic diffusion mechanism into the screening makes models more robust and interpretable and thus may be deemed superior38 to the second one.
Computational screening for better proton conductors has been mostly limited to perovskites and related oxides.36,39–41 It was found that the energy barriers for the covalent O–H bond rotation and proton transfer between acceptors and donors correlate with the energy of the O–H bond.42 High-throughput studies of double-perovskites40 and ternary oxides41 revealed a correlation of the proton transfer barrier with the proton–acceptor distance, dH⋯O, as well as with the B-cation radius.40 Another study demonstrated that oxygen affinity in the vicinity of dopants correlates positively with experimentally measured proton conductivities.43 Recently developed machine learning models used experimental data to link extrinsic parameters such as temperature and chemical composition to proton concentrations in perovskite oxides,36,39 without providing microscopic insights into the meaning of these extrinsic parameters. To the best of our knowledge, a search for physical descriptors and high throughput screening of proton-conducting electrolytes other than perovskites and related ceramic oxides have not been previously reported.
In this work, we consider materials that have hydrogen in their chemical formula and particularly examine the class of solid acids. We impose this limitation (that H is part of the structure) to focus on proton migration and its rate-limiting factors, without the need to consider the thermodynamics of proton incorporation. We first identify the physical descriptors of fast proton conduction in solid acids by establishing correlations between candidate descriptors and proton conductivities computed by means of ab initio molecular dynamics (AIMD) simulations. Next, we screen compounds from the Materials Project44 database (that were also reported as existing under ambient conditions according to the ICSD45 database) to select promising materials and then calculate their proton conductivity using machine-learning accelerated AIMD.46–48 A detailed description of computational methods is available in Section S1 (ESI†). Through these methods we identify promising solid acid proton conductors containing cations outside of the traditionally considered monovalent alkali cation-based solid acids (Cs+, Rb+, K+, and NH4+). These include the monovalent cations Ag+ and Tl+ as well as the divalent and trivalent cations such as Ba2+, Sr2+ and Er3+. In addition, we show that the descriptors of high proton conductivity, in particular lattice flexibility, may also be useful for predicting the transition temperature in known superprotonic conductors. Our work demonstrates that understanding the physical descriptors of the governing proton conduction mechanism can allow identification of new material candidates with rationally targeted properties.
Descriptors of the Grotthuss mechanism
The Grotthuss mechanism19,25,26 is the underlying proton conduction mechanism in solid acids. It is broadly a two-step process (Fig. 1) involving: (i) proton transfer from donor to acceptor sites in which a covalent proton–donor bond is broken and a new covalent proton–acceptor bond is created and (ii) reorganization of the environment, specifically rotation of polyanion groups,19,25,49 bringing the proton close to a new acceptor site and preventing a backward transfer to the original donor site.19 For fast diffusion, the rates of both steps must be high. For example, slow or constrained rotation would confine protons to hopping mostly between the original donor and acceptor sites (Fig. 1). Below, we hypothesize descriptors of each step of the Grotthuss mechanism.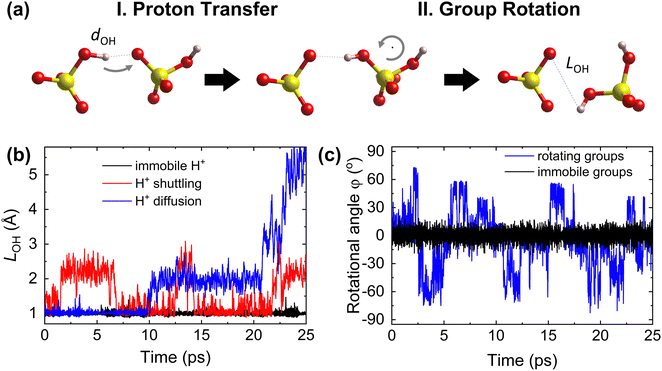 | ||
| Fig. 1 Steps of proton diffusion via the Grotthuss mechanism in a solid acid. (a) Donor and acceptor groups in a solid acid (yellow: S, red: O, and pink: H) Left: the proton is covalently bound to the initial donor (O on the left) and forms a hydrogen bond with the initial acceptor (O on the right). Middle: the proton has hopped and is covalently bound to the initial acceptor. Right: the acceptor group has rotated, taking the proton further away from the initial donor. (b) Time evolution of the proton–donor distance, LOH, calculated from AIMD trajectories, showing three cases of proton transfer kinetics: an immobile proton, proton “shuttling” (confinement to back-and-forth motion between the same donor and acceptor), and long-range proton diffusion. (c) Time evolution of the azimuthal angle, φ, characterizing group rotation, where φ is defined within the internal coordinate system for each group vector (see Section S1 in the ESI†), calculated from AIMD simulations, showing two cases: rotationally immobile groups (φ ≈ 0°) and rotationally mobile groups (displaying a large change of φ). | ||
Proton transfer descriptors
Proton bonding to donor (D) and acceptor (A) atoms shows universal features. When the covalent D–H bond, dDH, elongates, the hydrogen bond H⋯A, dH⋯A, shrinks, and vice versa.50 Moreover, the inverse relation between dDH and dH⋯A is universal and holds well in various compounds.19,50 This implies that the bond lengths dDH, dH⋯A and dDA are interdependent,51 such that any one of them can be used as a descriptor of hydrogen bonding strength or proton transfer ease. The energy barrier for proton transfer grows with increasing transfer distance between acceptor and donor sites.19 In molecular complexes, the proton transfer is nearly barrierless for dOO ≈ 2.4 Å and the barrier increases to about 1 eV for dOO ≈ 3 Å.19,52 Similar relations of the proton transfer barrier to the donor–acceptor distances, dDA, were shown for perovskite oxides,53,54 solid acids49 and ternary oxides.41 We expect that the proton barrier dependence on the bond lengths is general for different compounds with O–H⋯O bonds. Thus, we have assessed the covalent bond length, dDH, as a descriptor of proton transfer in solid acids.The energy barrier of proton transfer should similarly correlate with any other trait that reflects the D–H bond strength. For example, the acid dissociation constant, pKa,55–58 a common concept in liquid aqueous systems, reflects the extent of proton dissociation according to reaction: H3PO4 + H2O → (H2PO4)− + H3O+, and we have assessed its relation to proton transfer in solid acids. Other possible descriptors include the bond stretching frequency50 and bond order50 or metrics that quantify the covalency of the donor–proton bond. The O 2p band center characterizes the covalence of bonds involving oxygen in metal oxides and is shown to correlate with the oxygen ion migration barrier59 and hydrogen binding strength.60 The position of O 2p states on the absolute energy scale was also found to correlate with proton affinity in closed-shell oxides.61
Group rotation descriptors
Rotational and network flexibilities are needed to enable the facile rotation of polyanion groups19,25,49 to take the protons away from the vicinity of the original donor site. Superprotonic phase transition in solid acids is characterized by facile group rotations. This flexibility can be assessed from the lattice dynamics descriptors that reflect the rotational energy barrier. These include phonon band centers or phonon modes with a strong rotational character such as the so-called rigid unit modes.62 Indeed, if rotational phonon modes of polyanion groups have a low frequency, one may expect63 that the energy barrier to group rotation is small. However, the identification of rotational modes of polyanion groups in solid acids and particularly their contribution to the Grotthuss mechanism is not trivial, as many modes may contribute to a rotational event. For high-throughput screening, we sought to describe the ease of rotation with a simple descriptor representing the most relevant modes. Along these lines, the force constants corresponding to octahedral rotations of low-frequency phonon modes were shown to correlate with oxygen anion interstitial migration barrier in Ruddlesden–Popper oxides.64 Similarly, the average phonon band center of mobile Li-ion sites was found to correlate positively with their migration enthalpy.63 The importance of the local structure65 and lattice dynamics for proton66 and hydrogen67 conductivities was recently noted, and quantification of their role in proton conduction is desirable. For this purpose, as explained later, we have assessed the vibrational phonon modes of the framework cations as a proxy to the rotational flexibility of the polyanion groups.Descriptors of group rotations may also be deduced from the topology of the hydrogen bonds or bonding constraints that rotating groups are subject to. For example, Maxwell has shown that frames (e.g., made of struts and pins) are flexible if the number of degrees of freedom is larger than the number of constraints.62,68 For solid acids, such analysis may include consideration of the number of bonds between the rotating groups and the rest of the crystal framework (i.e., Cs–O in CsHSO4). Although in solid acids the number of bonds can be very high (yet these “bonds” may be weak), they still develop exceptional rotational flexibility. Similarly, one may have to consider the topology of the hydrogen bonding network as it influences the rotations of polyanion groups.19,25
Summary of candidate descriptors
The complete set of hypothesized descriptors is summarized in Table 1. For proton transfer, we explicitly and quantitatively consider hydrogen bond lengths (both the covalent dOH and the hydrogen bond dH⋯O), the acid dissociation constant, pKa, and the O 2p band center position. The O–H stretching frequency was not assessed due to a higher computational cost as compared to dOH. We did not find a generalizable correlation of the O 2p band center to the proton transport in our dataset (see Fig. S2 in the ESI†). While this could be due to various reasons, the relevant conclusion here is that the O 2p band center does not serve as a useful predictor of proton conductivity in solid acid materials. For rotational flexibility of the polyanion groups, we focused on the phonon modes of cations as a proxy, since the explicit assessment of the polyanion rotational modes and topological features was too complex to quantify across different structures and data sets.| Descriptor | Property |
|---|---|
| Proton transfer | |
| d OH (O–H bond length) (structural)* | O–H bond strength |
| d H⋯O (H⋯O distance) (structural)* | H-bonding network |
| pKa (acid dissociation constant) (chemical)* | Dissociation ease |
| ω OH (O–H stretching frequency) (dynamic) | O–H bond strength |
| O 2p band center (electronic)* | O–H bond strength |
| Rotational flexibility | |
| Phonon modes of polyanion groups (dynamic) | Lattice flexibility |
| Phonon modes of cations (dynamic)* | Lattice flexibility |
| Topological features, constraints (structural) | Structural reorganization |
Results and discussion
Descriptors of proton transfer
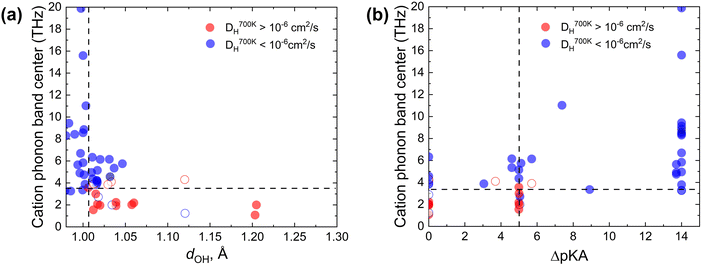
To test the proposed proton transfer descriptors (Table 1), we evaluated their correlation to the local metric of proton transfer, LOH,max (Fig. 1a and b) and the proton diffusivity, DH, both extracted from AIMD simulations of 25 ps length at 700 K (see Section S1 in the ESI† for the comprehensive description of methods). LOH ≈ 1.5 Å is a typical mid-point between a donor and an acceptor. Thus, if LOH,max ≲ 1.5 Å, it can be concluded that the protons are immobile. Conversely, if 1.5 Å ≲ LOH,max ≲ 2 Å, then proton transfer across the hydrogen bond occurred and if LOH,max ≳ 2 Å, then the proton underwent additional diffusion (likely via polyanion group reorientation). Selecting LOH,max ≈ 1.5 Å defines a threshold metric for proton transfer, where larger values include both local proton transfer events and long-range proton diffusion.The dOH descriptor (defined as the largest of the O–H bond lengths in the initial structure; see Fig. 2a) showed a significant correlation with both LOH,max and DH (Fig. 2b and c). All materials with a dOH of > 1.007 Å demonstrated some proton transfer/diffusion, whereas materials with shorter O–H bonds demonstrated negligible transfer/diffusion. The ΔpKa descriptor (the minimum absolute difference between the proton donor and acceptor group acidities) also showed a significant effect on both LOH,max and DH (Fig. 2d and e). Nearly all materials with a ΔpKa of < 5 demonstrated proton transfer/diffusion, whereas materials with larger ΔpKa demonstrated negligible transfer/diffusion. Indeed, a large ΔpKa value indicates that the energy difference between the acceptor and donor sites is large, which can increase the energy barrier.69,70 The inherently low differences between the first and second and the second and third dissociation constants in sulfuric, phosphoric, arsenic, and selenic acids 58 are in agreement with fast local transport in superprotonic CsH2PO4,71 CsH2AsO4,71 CsHSO472 and CsHSeO472 and essentially indicate that the number of protons per polyanion group varies without incurring a high energy penalty, in support of the long-range proton transport. Among the two correlated descriptors (dOH and ΔpKa, see Fig. S3 in the ESI†), we expect that dOH is more robust and accurate, encoding any structural/bonding variations in the solid that the tabulated pKa values may not reflect. Therefore, we used dOH in the final screening.
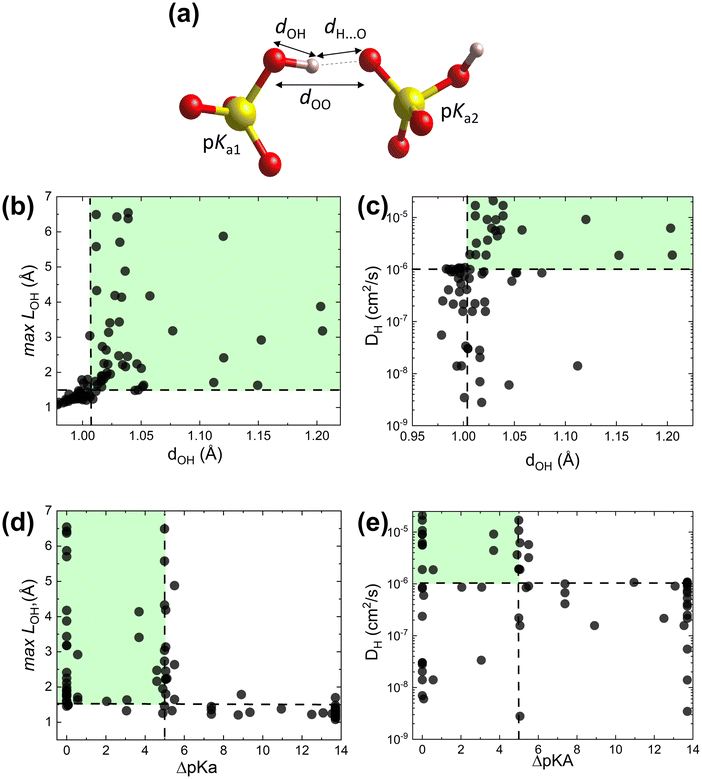 | ||
| Fig. 2 AIMD results from the initial dataset to extract proton transfer descriptors. (a) Schematic showing dOH, dH⋯O, dOO and pKa for donor and acceptor groups in a solid acid (color code: S is yellow, O is red, and H is pink). (b) Maximal distance travelled by the proton from its initial donor atom during the AIMD run, LOH,max, vs. the maximal initial O–H bond length, dOH. (c) Proton diffusivity, DHvs. dOH. (d) LOH,maxvs. ΔpKa. (e) DHvs. ΔpKa. All data at 700 K (the trajectory length is 25 ps). Dashed lines correspond to the selected cut-offs: DH cut-off is set to 10−6 cm2 s−1, which corresponds to about 0.02 S cm−1 conductivity at 700 K and is above the AIMD accuracy limits (for further details see Computational methods, Section S1 in the ESI†). | ||
The data further show that the suggested criterion (dOH > 1.007 Å) is necessary, but not sufficient, to identify fast conductors. Several examples of large dOH materials show moderate values of LOH,max (∼2 Å), Fig. 2b, and accordingly low diffusivities (DH < 10−6 cm2 s−1), Fig. 2c. Thus, by applying this criterion, we can filter out materials with a slow transfer rate (viz., poor conductors), but not every remaining material will be a fast proton conductor.
Descriptors of group rotation
As indicated in Table 1, we have hypothesized cation phonon modes to control the ease of rotational motion of polyanion groups. Accordingly, we analyzed the vibrational modes associated with group rotation and the flexibility of the lattice. We found that rotational modes of polyanion groups are often accompanied by pronounced displacements of the framework cations. This observation is consistent with arguments from the literature.19Fig. 3a shows the pattern of atomic displacements for a selected low-frequency phonon mode in CsHSO4. Cs cations execute pronounced excursions during the SO4 group rotation. The framework created by the cesium cations must be flexible to enable frequent and extensive rotations of polyanion tetrahedra. Remarkably, the cesium phonon spectrum in CsHSO4 has a peak only in the low-frequency range, as seen in Fig. 3b. This is because the cesium ions do not form strong covalent bonds and are largely “detached” from the stretching and bending modes of SO4 polyanions. This means that the cation phonon band center (ωcat) can serve as a proxy for all the low-frequency rotational modes in solid acids. Therefore, we use ωcat as a descriptor of the lattice dynamic flexibility and the ease of the polyanion group rotations.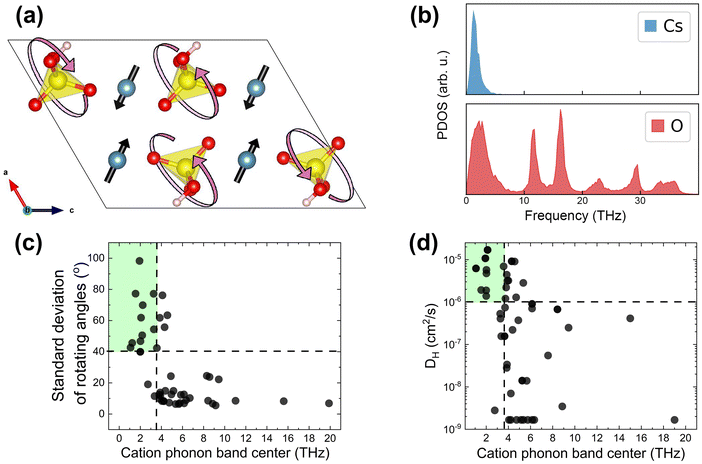 | ||
| Fig. 3 AIMD results from the initial dataset to extract group rotation descriptors. (a) Schematic of a low-frequency mode of SO4 rotations accompanied by large displacements of Cs cations in CsHSO4 (mp-1192419, P21/c;73 Cs is blue, S is yellow, O is red, and H is pink). The SO4 unit is largely intact, i.e., the S–O bonds are not stretched during this rotation. (b) Cation and oxygen phonon density of states of CsHSO4 (estimated as the power spectrum of the atomic velocities). (c) Rotational metric (the larger of the standard deviations of the polar and azimuthal angles, θ and φ, in spherical coordinates, characterizing group rotation, see Section S1 in the ESI†) vs. the cation phonon band center. (d) Proton diffusivity, DH, vs. the cation phonon band center. Compounds that do not possess mono-oxyanion groups were excluded from analysis (Table S1, ESI†). All data at 700 K. | ||
We define the rotational flexibility metric based on the standard deviations of the angles characterizing group rotations (i.e., the polar and azimuthal angles, θ and φ, in the internal spherical coordinate system for each group vector, see Section S1 in the ESI†). We take the larger of the standard deviations of these two angles of rotation and show its dependence on the cation phonon band centers of the considered materials in Fig. 3c. The correlation between the proton diffusivity and the cation phonon band centers is shown in Fig. 3d. The majority of compounds with a low cation phonon band center (below about 3.5 THz) show good rotational flexibility, i.e. a large standard deviation of θ or φ, along with high proton diffusivity. For these compounds, the standard deviation of rotational angles is generally ≥40°, indicating pronounced rotational excursions. This also means that 3 standard deviations correspond to about 120°, which is comparable to the 109.5° angle of the full tetrahedron rotation of the polyanion groups. Upon analyzing the maximal rotation angles observed during AIMD, a similar partition of compounds was found (Fig. S4, ESI†); i.e., compounds that show full rotation of the polyanion tetrahedral with maximal rotational angles above 109.5° mostly have cation phonon band centers below 3.5 THz. Conversely, the majority of compounds with a high cation phonon band center (above about 3.5 THz) show poor rotational flexibility, with a rotational metric of lower than 40° (in fact, mostly lower than 40° as seen in Fig. 3c), and low diffusivity, indicating that the polyanion group rotation is limited. This correlation holds for all the compounds that we screened, except for a few that we excluded from consideration because the framework cations were partially or fully coordinated with water molecules (e.g., Nd(H2O)2(H0.5SeO3)2 and Mg(H2O)6(SeO3)), which block correlated motion between the cation and the polyanion groups. Consequently, these compounds require a different metric to characterize the rotational motion of polyanion groups independent from the framework cations.62,74
Combining descriptors of proton transfer and group rotation
Since the Grotthuss mechanism is a two-step process, we considered separate descriptors for each step. One can see that individually each descriptor imposes a necessary but insufficient condition for achieving a high diffusion coefficient for protons in solid acids. For example, the proton–donor bond length needs to be longer than a certain cut-off dOH for proton transfer to take place (Fig. 2b and d), but this does not guarantee that diffusion will be long-range. Similarly, a low cation phonon band center favors good rotational flexibility, but it does not guarantee that proton transfer will be facile.Fig. 4 shows a grouping of the simulated proton diffusion coefficients as a function of descriptors of both the proton transfer and the group rotation steps. We see that most of the fast proton conductors (DH700K > 10−6 cm2 s−1, red data points in Fig. 4a) cluster in the region with a low cation phonon band center (≲3.5 THz) and a large initial O–H bond length (dOH ≳ 1.007 Å). We observe a similar clustering in the ΔpKavs. ωcat coordinates (Fig. 4b). The chosen cutoffs for ωcat and dOH allow us to separate proton conducting and non-conducting compounds with a low number of false-positive (3) and false-negative (4) cases. By using one descriptor each for proton transfer and for group rotation kinetics, we can predict which materials are expected to show both facile local proton hops and facile group rotation and therefore should be good proton conductors.
In summary, our results show that the length of the proton–donor covalent bond, dOH, and the difference between donor and acceptor acidities, ΔpKa, are good descriptors of the ease of proton transfer, and the cation phonon band center, ωcat, is a good descriptor of the rotational flexibility of polyanion groups. Therefore, we next use these physically based descriptors to identify novel proton conductors by means of high-throughput computational screening. Between dOH and ΔpKa, we use the former in the high-throughput screening, as a more facile and structurally sensitive descriptor that we extract directly from the simulated structure in our calculations.
High-throughput screening based on physical descriptors
The screening workflow introduced in Computational methods (Section S1 in the ESI†) is detailed in Fig. 5. After an initial screening of 5207 materials based on various properties (steps I–IV), the dataset contained 874 compounds that possess low electronic conductivity, have hydrogen bonds, and are considered synthesizable. We have applied screening based on the identified descriptors on this data set of 874 compounds. Specifically, we selected materials that possess polyanion groups with a donor–hydrogen bond length, dOH, longer than 1.007 Å (step V) and have a cation with the phonon band center, ωcat, below 3.5 THz (step VI). Application of these criteria eliminated about 84% of materials that were not expected to be fast proton conductors, thus leaving 143 candidates (of which, 112 had unique compositions). The final dataset includes these 143 candidates. For these materials, we performed Machine Learning Force Field accelerated AIMD (MLFF–AIMD)46–48 simulations to screen proton diffusivities at 650 K (step VII). We provide the complete list of materials, respective descriptors, and computed diffusivities in Table S2 (ESI†). Subsequently (step VIII), we selected the most promising compounds and explored their diffusivities in detail by MD (either AIMD or MLFF–AIMD) as a function of temperature below 650 K.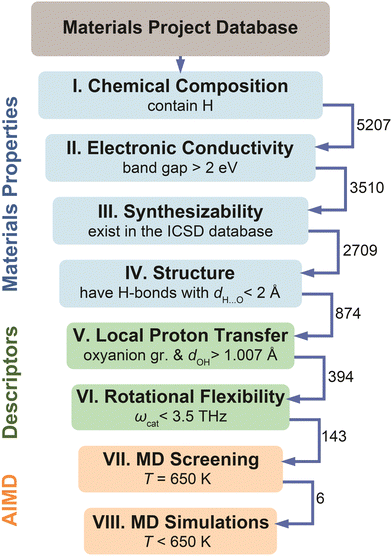 | ||
| Fig. 5 Flowchart of the high-throughput screening of the Materials Project44 database based on the materials properties (steps I–IV), the identified physical descriptors (steps V–VI), and MD diffusivities (steps VII–VIII). See Computational methods, Section S1 in the ESI,† for details regarding each step. The numbers near arrows show how many compounds reached the next step. | ||
Before presenting the results of the diffusivity calculations, it is of value to consider the material properties of the 143 candidate conductors (Table S2, ESI†) treated in the final dataset. The majority of solid acids that satisfy the used criteria dOH > 1.007 Å and ωcat < 3.5 THz are the Cs, Rb, and K-based ones (about 76%), and the rest are based on other cations including Ag+, Hg+, Tl+, Ba2+, Cd2+, Pb2+, Sr2+, Er3+, U6+ and Bix+ (Fig. 6a). As evident in the scatter plot of features of these compounds, Fig. 6a, the dOH values range from 1.007 Å to about 1.2 Å showing no preference across various elements or cation charges. In contrast, the ωcat value broadly depends on the chemical element itself, leading to the formation of clusters of ωcat values around each of Tl, Cs, Rb, Ag, Ba, and K-based compounds. The compound-averaged ωcat values decrease as the effective cation radii increase (see Fig. S5, ESI†). This corroborates earlier hypotheses that large cations generally provide an increased lattice flexibility.19,75 However, as can be seen in Fig. 6a, the cation size alone is not a sufficient condition for quantitatively relating to flexibility; i.e., there is a range of ωcat values for a group of compounds with the same cation. Different crystal structures with the same cation can have different flexibilities reflected with different cation phonon band centers. For example, Cs containing compounds have cation phonon band centers ranging from 1.2 THz to 2.7 THz. We also recognize that some compounds that passed the screening are toxic or radioactive, containing for example, Tl and U, and thus are not desirable for practical applications.
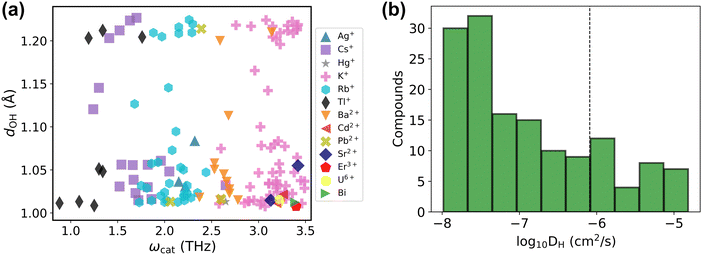 | ||
| Fig. 6 Final dataset analysis. (a) The final dataset presented as the scatter plot of the maximal dOHvs. cation phonon band center ωcat. Different cations are highlighted with different colors (for compounds with multiple cations, the lowest ωcat is plotted). The list of these compounds is provided in Table S2 (ESI†). (b) Histogram of diffusivities of the final dataset computed at 650 K using machine learning force field accelerated AIMD (MLFF–AIMD) simulations. The vertical dashed line marks DH ≈ 10−6 cm2 s−1. | ||
The computed diffusivities of the 143 compounds (from Fig. 6a and Table S2, ESI†) in the final dataset are presented as a histogram in Fig. 6b. About 30 compounds show high conductivity as evaluated at 650 K (DH ≳ 10−6 cm2 s−1; see discussion below regarding compounds with low conductivities). Importantly, our screening procedure finds most of the known Cs, Rb, and K-based compounds with superprotonic transitions, e.g., K3H(SeO4)2, Rb3H(SeO4)2, Cs3H(SeO4)2, CsHSO4, and CsHSeO4,6,76,77 which satisfy the proposed descriptor criteria and also demonstrate reasonable diffusivity in MD tests (see Table S2, ESI†). We also identify several less known Cs, Rb, and K-based compounds such as Cs(HF)(H2PO4), Rb(H2.5AsO4)2, and K4(H3AsO4)(HSO4)2(SO4) that might be promising proton conductors (Table S2, ESI†).
We were particularly intrigued to find fast proton conductors among solid acids based on “unconventional” cations such as Ag+, Ba2+, Sr2+, and Er3+. We explored several such compounds using MD simulations as shown in Fig. 7 and summarized in Table 2. Their conductivities reach 10−2 S cm−1 at 500 K (Table 2), ranging from 10−3 to 10−1 S cm−1 between 400 and 600 K (Fig. 7). For example, Er(HSO4)378 shows 10−2 S cm−1 at 500 K and Ag(H3O)(HSO4)279 shows 0.5 mS cm−1 at 400 K. The latter solid also supports vehicle diffusion, though it is a minor contribution to diffusion compared to the Grotthuss mechanism. Significantly, the calculated conductivities are higher than or comparable to that of CsHSO4 (mp-1192419, P21/c ref. 73) as shown in Fig. 7. To the best of our knowledge, the conductivities of these identified solid acids (Table 2 and Fig. 7) have not been experimentally reported in the literature.
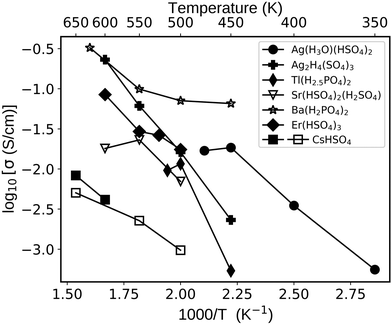 | ||
| Fig. 7 Proton conductivities of selected solid acids calculated with AIMD (full symbols) and MLFF–AIMD (open symbols). The cell sizes and shapes were constrained to the room temperature (or low temperature) phases as retrieved from the Materials Project database (see Table 2). The simulated CsHSO4 (mp-1192419) conductivity is shown as a baseline (MLFF–AIMD and AIMD demonstrate consistent results; see Section S1 in the ESI† for further details). | ||
| Compound | mp-ID | ICSD-ID | Ref. | σ H (500 K) (mS cm−1) |
|---|---|---|---|---|
| a Hygroscopic, requires an inert atmosphere (see corresponding ref.) b Meta-stable phase (triclinic) according to ref. 80. | ||||
| Ag(H3O)(HSO4)2a | mp-24072 | 408948 | 79 | 17 [@475 K] |
| Ag2H4(SO4)3a | mp-867593 | 408949 | 79 | 16 |
| Tl(H2.5PO4)2 | mp-696762 | 30509 | 81 | 12 |
| Sr(HSO4)2(H2SO4)a | mp-757723 | 404139 | 82 | 7 |
| Ba(H2PO4)2b | mp-706543 | 2420 | 83 | 70 |
| Er(HSO4)3a | mp-24640 | 408804 | 78 | 17 |
In light of the low number of false positives indicated in Fig. 4, we were surprised that a large number of compounds passed our screening (Fig. 6a) but does not show fast proton diffusion at 650 K (Fig. 6b, Table S2, ESI†). There can be two reasons for this. First is that our screening criteria may be incomplete, and the screening model could be improved to filter out more of the non-conducting compounds by considering other factors, e.g., the spatial arrangement of donor–acceptor sites and/or topology84 of the hydrogen bonding network. In addition, some compounds have more than one cation, and we have screened based on only the one cation that has the ωcat of <3.5 THz. For example, our dataset contained 40 solid acids that have more than one cation, such as Ba2Cd(H1.5PO4)4, Ba2CaH6(PO4)4, and Ni3AgH2(PO4)3, and the great majority of them showed negligible diffusion (Table S2, ESI†). All these compounds had another non-soft cation (ωcat > 3.5 THz), which can constrain the lattice flexibility. This is in agreement with our earlier experimental study that observed no superprotonic transition in Cs2Na(HSO4)3 and CsNa2(HSO4)3 and suggested that strong Na–O bonds hinder structural flexibility.75
A second reason for finding many of the screened compounds (from Fig. 6) with low proton diffusion at 650 K can be the use of the NVT ensemble in our MD simulations. By constraining the cell shape and volume, we do not allow explicit phase transitions (only rearrangements facilitated by temperature, see Fig. S6 and S7, ESI†). This constraint may suppress plausible superprotonic transitions and decrease diffusivity (e.g., the simulated diffusivity of CsHSO4 in Fig. 6 is by one order of magnitude lower than the experimental one,6 and not every CsHSO4 phase shows high diffusivity, see Table S2, ESI†). On the other hand, the predicted high conductivity does not guarantee that the phase will be stable at the simulated temperatures. For example, we predict triclinic83 Ba(H2PO4)2 to show exceptional conductivity (Fig. 7); however, this phase is hard to stabilize.80 The more stable orthorhombic phase does not show high proton conductivity either in experiments85 or in our simulations (see mp-706400 record in Table S2, ESI†). Likewise, we cannot predict whether melting precedes86,87 a superprotonic transition. Another limitation of the NVT ensemble is the assumption of a fixed stoichiometry and composition. However, in practice, proton conductivity in these compounds depends on the humidity and temperature, e.g., causing dehydration88–90 or disproportionation,91 both of which can affect conductivity. These examples of the behavior of Ba(H2PO4)2 show that our MD diffusivities are influenced by the NVT ensemble, and explicit modelling of phase transitions would be desirable, yet challenging at present. Nevertheless, the calculated MD diffusivities (Table 2 and Fig. 7) remain strong indicators of fast proton conductivity in these compounds.
Our screening was limited to the Materials Project44 database (about 154 thousand materials), yet more conductors may be identified by screening larger databases such as ICSD45 (about 281 thousand compounds), OQMD92 (about 1 million compounds), or GNoME (about 2.2 million compounds).93 Rapid development of databases93 and inverse materials design methods38,94–97 presents an opportunity for such descriptor-based search of fast proton conductors with desirable properties (low Tsp, high chemical and thermal stabilities, etc.). In this regard, it is promising that our screening, albeit limited to the MP database, could uncover solid acids with less explored chemistries, demonstrating potential for screening of larger datasets93 in future studies.
The established physical descriptors could be applied to other classes of proton conductors. However, such an expansion of the method requires considering the specifics of proton transfer and the Grotthuss reorganization of the environment, and the chemistry and structure in each class of material, resulting in different quantitative relations of the descriptors to the conductivity. Possible classes include but are not limited to perovskites and other ceramic oxides22 as well as polymer conductors.24 For example, in metal oxides, while we do not expect significant rotations of the metal–oxygen polyhedra (as opposed to the rotations of polyanion groups in solid acids), we can expect that the lattice flexibility can still play a role by dynamically bringing closer donor–acceptor pairs assisted by different phonon modes at finite temperatures. Similar design principles, such as searching for complex compounds with a continuous hydrogen bonding network as in the newly discovered ZrH5(PO4)3 solid acid,98 provide another promising route to find fast, solid-state proton conductors.
Superprotonic transition temperature and its correlation with cation phonon band centers
For superprotonic solid acids, it is imperative to know not only whether a high conductivity phase exists, but also the temperature above which the high conductivity phase is stable, i.e., the superprotonic transition temperature, Tsp. It is desirable to obtain materials with relatively low Tsp such that the superprotonic phase is encountered prior to melting or dehydration.99 To address this, we explored correlations between Tsp and the descriptor of group rotation flexibility. The rationale is that the polyanion sublattice “rotationally melts” in the superprotonic phase; therefore, Tsp should correlate with the rotational flexibility and descriptors thereof.We found that the experimentally measured Tsp in a comprehensive set of Cs-containing superprotonic solid acids correlates with the calculated cation phonon band center, Fig. 8. For compounds with multiple, inequivalent Cs sites, which display distinct band centers for each unique Cs (e.g., Cs2HSO4H2PO4 [1.43 THz and 1.60 THz] and Cs3(HSO4)2(H2PO4) [1.36 THz, 1.50 THz, 1.81 THz]), we used the average frequencies from different cation sites. The greater the flexibility of the cation framework under ambient conditions, the lower the temperature required for transitioning to the superprotonic phase. This observed correlation implies that the superprotonic transition in these materials is indeed related to the rotational flexibility of polyanion groups. However, the rotational flexibility may alternatively lead to a complete melting transition, as is the case for two of the nine compounds considered, and additional criteria will be required to distinguish between the type of transition that occurs. Significantly, two identified Rb superprotonic compounds fall along the same trend line with the Cs compounds, reflecting chemical similarity between these species. The representative K compound indicated in Fig. 8 deviates from the trend line. Because there are a very limited number of experimental reports of superprotonic phase transition in solid acids that do not include Cs, the possibilities for elucidating the specific role of the cation species are limited, though cation mass may directly play a role by affecting the force constants (Fig. S8, ESI†).
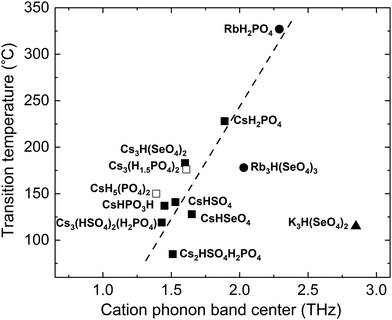 | ||
| Fig. 8 Experimental superprotonic transition temperature, Tsp, of solid acids from the literature vs. the average cation phonon band center, ωcat, which is calculated in this work for each of those compounds. Open squares represent the melting temperatures of compounds that do not show superprotonic transition (i.e., melt below an accessible Tsp). The trend line is the guide to the eye. Data points for Cs-based compounds77,87,90,100–106 are squares, Rb-based compounds77,103 are circles, and the K-based77 solid acid is shown as a triangle. | ||
Dependence of Tsp on the softness of the cation framework underscores the importance of lattice flexibility. A large cation size alone is not a sufficient quantitative indicator of increased lattice flexibility and the lowering of Tsp. As seen in Fig. 8, even for solid acids with the same framework cation, Cs, Tsp varies more than 100 °C and the ωcat varies by about 1 THz. Explicit quantification of lattice flexibility (i.e., through the cation phonon band center, as done here) appears to be a more useful predictor of Tsp. Since the correlation between ωcat and Tsp is not precise, consideration of other factors, for example, bonding network topology, inequivalence of cation sites and the role of multiple phonon band centers, and disparity of the cation masses, may provide further insights into the complete set of factors that control Tsp.
Conclusion
In this work, we have established quantitative conditions for physical descriptors that enable high proton conductivity in solid acids. The physical descriptors correspond to the two key steps of proton transport based on the Grotthuss mechanism. The ease of proton transfer between the donor and acceptor sites depends on the donor–proton (O–H) bond strength, inversely related to the bond length dOH; i.e., larger dOH leads to easier local proton transfer. Similarly, the smaller the difference in pKa of the donor and acceptor sites, the easier the local proton transfer. The rotational flexibility of the polyanion groups depends on the phonon band center of the framework cation sublattice, ωcat; i.e., lower ωcat leads to a softer cation framework, a more flexible lattice and easier group rotations. The cation phonon band center also correlates with the experimentally reported temperatures of superprotonic transition. This finding suggests that increasing the lattice flexibility to facilitate polyanion group rotations can decrease Tsp and help achieve high proton conductivity at lower temperatures. Our work provides guidance on how to quantify the rotational flexibility and Tsp based on the lattice dynamics features for arbitrary compositions. The model for descriptors of proton conductivity and Tsp can be further improved in the future to include other possible factors, such as the network topology of hydrogen bonds and structural constraints on the group rotations.Based on the identified descriptors, we screened the Materials Project44 database and revealed potential solid acid proton conductors. The well-known fast proton conductors with Cs+, Rb+, and K+ framework cations satisfy our descriptor criteria. We also found prospective fast proton conductors with “unconventional” cations for solid acid proton conductors. These include Ag+, Ba2+, Sr2+ and Er3+ framework cations. AIMD simulations indicate that these compounds can possess proton conductivities that are higher than that of CsHSO4. This finding of “unconventional” chemistries suggests that there is an opportunity to reveal more solid acid proton conductors by screening larger materials databases. We expect that the available compositional space of proton-conducting solid acids is broader than what has been used so far. We believe that our results will inspire further studies to investigate larger materials datasets and implement novel proton-conducting solid acids for different applications from energy conversion to electronic devices.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was primarily supported by the Hydrogen in Information and Energy Sciences (HEISs) Center, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award # DE-SC0023450. P.Ž. thanks the Knut and Alice Wallenberg Foundation scholarship program for supporting part of his postdoctoral studies at the Massachusetts Institute of Technology. L.W. was supported by a Graduate Research Fellowship from the US National Science Foundation (NSF). G. X. was supported by the NSF Grant No. OAC 2118201. The authors acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing the HPC resources on the Frontera supercomputer (allocation # DMR20012) that have contributed to the first principles simulations and MD results reported within this work.References
- C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O’Hayre, Science (1979), 2015, 349, 1321–1326 Search PubMed.
- S. Choi, C. J. Kucharczyk, Y. Liang, X. Zhang, I. Takeuchi, H.-I. Ji and S. M. Haile, Nat. Energy, 2018, 3, 202–210 Search PubMed.
- H. An, H. W. Lee, B. K. Kim, J. W. Son, K. J. Yoon, H. Kim, D. Shin, H. Il Ji and J. H. Lee, Nat. Energy, 2018, 3, 870–875 Search PubMed.
- H. Ding, W. Wu, C. Jiang, Y. Ding, W. Bian, B. Hu, P. Singh, C. J. Orme, L. Wang, Y. Zhang and D. Ding, Nat. Commun, 2020, 11, 1907 Search PubMed.
- F. Liu, H. Deng, H. Ding, P. Kazempoor, B. Liu and C. Duan, Joule, 2023, 7, 1308–1332 CrossRef CAS.
- S. M. Haile, D. A. Boysen, C. R. I. Chisholm and R. B. Merie, Nature, 2001, 410, 910–913 CrossRef CAS PubMed.
- D. A. Boysen, T. Uda, C. R. I. Chisholm and S. M. Haile, Science (1979), 2004, 303, 68–70 Search PubMed.
- T. Uda, D. A. Boysen, C. R. I. Chisholm and S. M. Haile, Electrochem. Solid-State Lett., 2006, 9, A261–A264 CrossRef CAS.
- D. K. Lim, A. B. Plymill, H. Paik, X. Qian, S. Zecevic, C. R. I. Chisholm and S. M. Haile, Joule, 2020, 4, 2338–2347 CrossRef CAS.
- X. Wu, J. J. Hong, W. Shin, L. Ma, T. Liu, X. Bi, Y. Yuan, Y. Qi, T. W. Surta, W. Huang, J. Neuefeind, T. Wu, P. A. Greaney, J. Lu and X. Ji, Nat. Energy, 2019, 4, 123–130 CrossRef CAS.
- L. Yan, J. Huang, Z. Guo, X. Dong, Z. Wang and Y. Wang, ACS Energy Lett., 2020, 685–691 CrossRef CAS.
- Z. Shao, A. Huang, C. Ming, J. Bell, P. Yu, Y.-Y. Sun, L. Jin, L. Ma, H. Luo, P. Jin and X. Cao, Nat. Electron., 2022, 5, 1–8 CrossRef.
- A. J. Tan, M. Huang, C. O. Avci, F. Büttner, M. Mann, W. Hu, C. Mazzoli, S. Wilkins, H. L. Tuller and G. S. D. Beach, Nat. Mater., 2019, 18, 35–41 CrossRef CAS PubMed.
- M. Huang, M. U. Hasan, K. Klyukin, D. Zhang, D. Lyu, P. Gargiani, M. Valvidares, S. Sheffels, A. Churikova, F. Büttner, J. Zehner, L. Caretta, K. Y. Lee, J. Chang, J. P. Wang, K. Leistner, B. Yildiz and G. S. D. Beach, Nat. Nanotechnol., 2021, 16, 981–988 CrossRef CAS PubMed.
- X. Yao, K. Klyukin, W. Lu, M. Onen, S. Ryu, D. Kim, N. Emond, I. Waluyo, A. Hunt, J. A. del Alamo, J. Li and B. Yildiz, Nat. Commun., 2020, 11, 3134 CrossRef CAS PubMed.
- M. Onen, N. Emond, J. Li, B. Yildiz and J. A. Del Alamo, Nano Lett., 2021, 21, 6111–6116 CrossRef CAS PubMed.
- M. Onen, N. Emond, B. Wang, D. Zhang, F. M. Ross, J. Li, B. Yildiz and J. A. del Alamo, Science (1979), 2022, 377, 539–543 CAS.
- M. Huang, M. Schwacke, M. Onen, J. del Alamo, J. Li and B. Yildiz, Adv. Mater., 2022, 2205169 Search PubMed.
- K.-D. Kreuer, Chem. Mater., 1996, 8, 610–641 Search PubMed.
- T. Norby, Solid State Ionics, 1999, 125, 1–11 CrossRef CAS.
- L. Malavasi, C. A. J. Fisher and M. S. Islam, Chem. Soc. Rev., 2010, 39, 4370–4387 RSC.
- Y. Meng, J. Gao, Z. Zhao, J. Amoroso, J. Tong and K. S. Brinkman, J. Mater. Sci., 2019, 54, 9291–9312 Search PubMed.
- K. Biradha, A. Goswami, R. Moi and S. Saha, Dalton Trans., 2021, 50, 10655–10673 Search PubMed.
- Y. Sone, P. Ekdunge and D. Simonsson, J. Electrochem. Soc., 1996, 143, 1254–1259 Search PubMed.
- A. I. Baranov, Crystallogr. Rep., 2003, 48, 1012–1037 CrossRef CAS.
- K. D. Kreuer, Solid State Ionics, 1997, 94, 55–62 CrossRef CAS.
- Y. Zhang, X. He, Z. Chen, Q. Bai, A. M. Nolan, C. A. Roberts, D. Banerjee, T. Matsunaga, Y. Mo and C. Ling, Nat. Commun., 2019, 10, 1–7 CrossRef PubMed.
- L. Kahle, A. Marcolongo and N. Marzari, Energy Environ. Sci., 2020, 13, 928–948 Search PubMed.
- S. Muy, J. Voss, R. Schlem, R. Koerver, S. J. Sedlmaier, F. Maglia, P. Lamp, W. G. Zeier and Y. Shao-Horn, iScience, 2019, 16, 270–282 Search PubMed.
- A. D. Sendek, E. D. Cubuk, E. R. Antoniuk, G. Cheon, Y. Cui and E. J. Reed, Chem. Mater., 2019, 31, 342–352 CrossRef CAS.
- B. He, P. Mi, A. Ye, S. Chi, Y. Jiao, L. Zhang, B. Pu, Z. Zou, W. Zhang, M. Avdeev, S. Adams, J. Zhao and S. Shi, Acta Mater, 2021, 203, 116490 CrossRef CAS.
- B. He, S. Chi, A. Ye, P. Mi, L. Zhang, B. Pu, Z. Zou, Y. Ran, Q. Zhao, D. Wang, W. Zhang, J. Zhao, S. Adams, M. Avdeev and S. Shi, Sci Data, 2020, 7, 1–14 CrossRef PubMed.
- K. J. Jun, Y. Sun, Y. Xiao, Y. Zeng, R. Kim, H. Kim, L. J. Miara, D. Im, Y. Wang and G. Ceder, Nat. Mater., 2022, 21, 924–931 CrossRef CAS PubMed.
- C. López, A. Emperador, E. Saucedo, R. Rurali and C. Cazorla, Mater. Horiz., 2023, 10, 1757–1768 RSC.
- M. Matsubara, A. Suzumura, N. Ohba and R. Asahi, Commun. Mater., 2020, 1, 1–6 CrossRef.
- P. Priya and N. R. Aluru, npj Comput. Mater., 2021, 7, 1–12 CrossRef.
- A. D. Sendek, Q. Yang, E. D. Cubuk, K. A. N. Duerloo, Y. Cui and E. J. Reed, Energy Environ. Sci., 2017, 10, 306–320 Search PubMed.
- K. E. Willcox, O. Ghattas and P. Heimbach, Nat. Comput. Sci., 2021, 1, 166–168 Search PubMed.
- J. Hyodo, K. Tsujikawa, M. Shiga, Y. Okuyama and Y. Yamazaki, ACS Energy Lett., 2021, 6, 2985–2992 CrossRef CAS.
- M. S. Islam, S. Wang, A. M. Nolan and Y. Mo, Chem. Mater., 2021, 33, 8278–8288 CrossRef CAS.
- M. S. Islam, S. Wang, A. T. Hall and Y. Mo, Chem. Mater., 2022, 34, 5938–5948 CrossRef CAS.
- N. Bork, N. Bonanos, J. Rossmeisl and T. Vegge, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 014103 CrossRef.
- Y. Yamazaki, A. Kuwabara, J. Hyodo, Y. Okuyama, C. A. J. Fisher and S. M. Haile, Chem. Mater., 2020, 32, 7292–7300 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- A. Belkly, M. Helderman, V. L. Karen and P. Ulkch, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 364–369 CrossRef PubMed.
- R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701 CrossRef CAS PubMed.
- R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 14105 CrossRef CAS.
- R. Jinnouchi, F. Karsai, C. Verdi, R. Asahi and G. Kresse, J. Chem. Phys., 2020, 152, 234102 CrossRef CAS PubMed.
- C. Dreßler and D. Sebastiani, Phys. Chem. Chem. Phys., 2020, 22, 10738–10752 RSC.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- M. Ichikawa, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 2074–2080 Search PubMed.
- D. Borgis, G. Tarjus and H. Azzouz, J. Chem. Phys., 1992, 97, 1390–1400 CrossRef CAS.
- W. Münch, G. Seifert, K. D. Kreuer and J. Maier, Solid State Ionics, 1997, 97, 39–44 CrossRef.
- M. F. Hoedl, A. Chesnokov, D. Gryaznov, R. Merkle, E. A. Kotomin and J. Maier, J. Mater. Chem. A, 2023, 11, 6336–6348 RSC.
- D. A. Evans and D. H. Ripin, “pKa's of Inorganic and Oxo-Acids,” can be found under https://www.wanglab.chem.pitt.edu/wp-content/uploads/2017/09/Evans-D.-A.-Ripin-D.-H.-The-Evans-pKa-Table-Harvard-2006.pdf.
- C. J. Peacock and G. Nickless, Z. Naturforsch., A: Phys. Sci., 1969, 24, 245–247 CAS.
- “Engineering ToolBox, ( 2017), Inorganic Acids and Bases – pKa Values.,” can be found under https://www.engineeringtoolbox.com/pKa-inorganic-acid-base-hydrated-metal-ion-monoprotic-diprotic-triprotic-tetraprotic-d_1950.html.
- W. M. Haynes, ed., CRC Handbook of Chemistry and Physics, Taylor & Francis, 2014 Search PubMed.
- T. T. Mayeshiba and D. D. Morgan, Solid State Ionics, 2016, 296, 71–77 CrossRef CAS.
- C. F. Dickens, J. H. Montoya, A. R. Kulkarni, M. Bajdich and J. K. Nørskov, Surf. Sci., 2019, 681, 122–129 CrossRef CAS.
- T. S. Bjørheim, M. F. Hoedl, R. Merkle, E. A. Kotomin and J. Maier, J. Phys. Chem. C, 2020, 124, 1277–1284 CrossRef.
- M. T. Dove, Philos. Trans. R. Soc., A, 2019, 377, DOI:10.1098/RSTA.2018.0222.
- S. Muy, J. C. Bachman, L. Giordano, H. H. Chang, D. L. Abernathy, D. Bansal, O. Delaire, S. Hori, R. Kanno, F. Maglia, S. Lupart, P. Lamp and Y. Shao-Horn, Energy Environ. Sci., 2018, 11, 850–859 RSC.
- X. Li and N. A. Benedek, Chem. Mater., 2015, 27, 2647–2652 CrossRef CAS.
- A. Torayev, L. Sperrin, M. A. Gomez, J. A. Kattirtzi, C. Merlet and C. P. Grey, J. Phys. Chem. C, 2020, 124, 16689–16701 CrossRef CAS PubMed.
- T. Itakura, H. Matsui, T. Tada, S. Kitagawa, A. Demessence and S. Horike, Chem. Sci., 2020, 11, 1538–1541 RSC.
- V. Korostelev, J. Wagner and K. Klyukin, J. Mater. Chem. A, 2023, 11, 23576–23588 RSC.
- J. C. Maxwell, London, Edinburgh Dublin Philos. Mag. J. Sci., 1864, 27, 294–299 CrossRef.
- R. P. Bell, Proc. R. Soc. London, 1936, 154, 414–429 Search PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1936, 32, 1333–1360 RSC.
- A. I. Baranov, V. P. Khiznichenko and L. A. Shuvalov, Ferroelectrics, 1989, 100, 135–141 CrossRef CAS.
- A. I. Baranov, L. A. Shuvalov and N. M. Shchagina, JETP Lett., 1982, 36, 459–462 Search PubMed.
- K. Itoh, T. Ukeda, T. Ozaki and E. Nakamura, IUCr, Acta Crystallogr., 1990, C46, 358–361 CAS.
- M. T. Dove, J. Du, Z. Wei, D. A. Keen, M. G. Tucker and A. E. Phillips, Phys. Rev. B, 2020, 102, 094105 CrossRef CAS.
- C. R. I. Chisholm, L. A. Cowan and S. M. Haile, Chem. Mater., 2001, 13, 2909–2912 CrossRef CAS.
- A. Goñi-Urtiaga, D. Presvytes and K. Scott, Int. J. Hydrogen Energy, 2012, 37, 3358–3372 CrossRef.
- D. Yi, S. Sanghvi, C. P. Kowalski and S. M. Haile, Chem. Mater., 2019, 31, 9807–9818 CrossRef CAS.
- M. S. Wickleder, Z. Anorg. Allg. Chem., 1998, 624, 1347–1354 CrossRef CAS.
- A. Stiewe, E. Kemnitz and S. Troyanov, Z. Anorg. Allg. Chem., 1999, 625, 329–335 CrossRef CAS.
- B. Prelesnik, R. Herak, M. Čurić and I. Krstanović, Acta Crystallogr., 1978, 34, 76–78 CrossRef.
- Y. Oddon, J.-R. Vignalou, A. Tranquard and G. Pèpe, Acta Crystallogr., 1978, 34, 3510–3514 CrossRef.
- C. Werner, E. Kemnitz, H. Worzala and S. Trojanov, Z. Naturforsch., B: J. Chem. Sci., 1996, 51, 952–958 CrossRef CAS.
- J. D. Gilbert and P. G. Lenhert, Acta Crystallogr., 1978, 34, 3309–3312 CrossRef.
- K. S. Gomez-Haibach and M. A. Gomez, J. Phys. Chem. B, 2023, 127, 9258–9266 CrossRef CAS PubMed.
- I. N. Bagryantseva and V. G. Ponomareva, Inorg. Mater., 2018, 54, 366–373 CrossRef CAS.
- S. Chandrasekhar, R. Shashidhar and N. Tara, Mol. Cryst. Liq. Cryst., 1970, 10, 337–358 CrossRef CAS.
- G. V. Lavrova, E. B. Burgina, A. A. Matvienko and V. G. Ponomareva, Solid State Ionics, 2006, 177, 1117–1122 CrossRef CAS.
- S. M. Haile, C. R. I. Chisholm, K. Sasaki, D. A. Boysen and T. Uda, Faraday Discuss., 2006, 134, 17–39 RSC.
- Y. K. Taninouchi, T. Uda, Y. Awakura, A. Ikeda and S. M. Haile, J. Mater. Chem., 2007, 17, 3182–3189 RSC.
- A. Ikeda and S. M. Haile, Solid State Ionics, 2012, 213, 63–71 CrossRef CAS.
- L. A. Cowan, R. M. Morcos, N. Hatada, A. Navrotsky and S. M. Haile, Solid State Ionics, 2008, 179, 305–313 CrossRef CAS.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, NPJ Comput Mater, 2015, 1, 15010 CrossRef CAS.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 624, 80–85 CrossRef CAS PubMed.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science (1979), 2018, 361, 360–365 CAS.
- V. Fung, J. Zhang, G. Hu, P. Ganesh and B. G. Sumpter, npj Comput. Mater., 2021, 7, 200 CrossRef.
- Z. Ren, S. I. P. Tian, J. Noh, F. Oviedo, G. Xing, J. Li, Q. Liang, R. Zhu, A. G. Aberle, S. Sun, X. Wang, Y. Liu, Q. Li, S. Jayavelu, K. Hippalgaonkar, Y. Jung and T. Buonassisi, Matter., 2022, 5, 314–335 CrossRef CAS.
- M. A. Q. Microsoft Research AI4Science, https://arxiv.org/abs/2311.07361, 2023.
- S. Fop, R. Vivani, S. Masci, M. Casciola and A. Donnadio, Angew. Chem.,– Int. Ed., 2023, 62, e2022184 CrossRef PubMed.
- S. Chandrasekhar, R. Shashidhar and N. Tara, Mol. Cryst. Liq. Cryst., 1970, 10, 337–358 CrossRef CAS.
- Z. Jiráak, M. Dlouhá, S. Vratislav, A. M. Balagurov, A. I. Beskrovnyi, V. I. Gordelii, I. D. Datt and L. A. Shwalov, Phys. Status Solidi A, 1987, 100, K117–K122 CrossRef.
- S. M. Haile, G. Lentz, K. D. Kreuer and J. Maier, Solid State Ionics, 1995, 77, 128–134 CrossRef CAS.
- M. A. Zakharov, S. I. Troyanov and E. Kemnitz, Z. Kristallogr., 2001, 216, 172–175 CAS.
- D. A. Boysen, S. M. Haile, H. Liu and R. A. Secco, Chem. Mater., 2003, 15, 727–736 CrossRef CAS.
- S. Sanghvi and S. M. Haile, Solid State Ionics, 2020, 349, 115291 CrossRef CAS.
- C. R. I. Chisholm, R. B. Merle, D. A. Boysen and S. M. Haile, Chem. Mater., 2002, 14, 3889–3893 CrossRef CAS.
- C. R. I. Chisholm and S. M. Haile, Solid State Ionics, 2000, 136–137, 229–241 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee01219d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |