Open Access Article
Open Access ArticleGreen chemistry: advancing planetary phosphorus sustainability through the synergy of graphene oxide modified with magnetic nanoparticles (M@GO) for extracting tertiary effluent phosphorus in sewage treatment plants
Andrea
Muñoz-Garcia†
a,
Pablo
Montoro-Leal†
a,
María del Mar
López Guerrero
 *a,
Carlos
Vereda-Alonso
*a,
Carlos
Vereda-Alonso
 b and
Elisa
Vereda Alonso
b and
Elisa
Vereda Alonso
 a
a
aDepartment of Analytical Chemistry, University of Malaga, 29071 Malaga, Spain. E-mail: mmlopez@uma.es
bDepartment of Chemical Engineering, University of Malaga, 29071 Malaga, Spain
First published on 12th April 2024
Abstract
Securing the enduring sustainability of global phosphorus (P) utilization has become a key societal priority. The application of green chemistry and green engineering presents an opportunity to mitigate these challenges and contribute to the sustainable closure of the global phosphorus cycle by addressing the extraction of phosphorus from waste and subsequent reuse. In this manuscript the feasibility of a novel magnetic graphene oxide for wastewater phosphorus recovery/removal is described. The primary technical benefit of this solid adsorbent lies in its easy separation from treated water through magnetic field application. The key factors affecting the sorption efficiency (contact time, pH, and adsorbent dosage) are studied. During the first 30 min, at pH 8 and with a dosage of 0.8 g L−1, 25% of the initial concentration is reduced. Among the 3 thermodynamic models proposed, the Langmuir isotherm provides the best fit to the experimental results, with a maximum adsorption capacity of 2.69 mg g−1. Four kinetic models are evaluated to describe the adsorption of phosphorus on this magnetic graphene oxide for different initial adsorbate concentrations and adsorbent dosages. Among them, Langmuir kinetics provide the best fit to the experimental data. The adsorption rate constant is 0.72 L mg−1 h−1, and the desorption rate is 0.58 h−1, in accordance with the identified Langmuir isotherm. Parameter values calculated from a mass transfer kinetic model indicate that the mass transfer of phosphorus between the bulk liquid and the solid surface is not the rate-limiting step of the adsorption process. Following the separation of this magnetic solid from the treated wastewater, an ammonia aqueous solution can recover the phosphorus from the solid adsorbent. Preliminary results show absorbed phosphorus recovery yields above 99% with a solid–liquid ratio up to 5 times higher than that used in the adsorption process.
Environmental significanceFrom a circular economy perspective, wastewater treatment plants (WWTPs) play a crucial role in the management of phosphorus. Therefore, the removal and recovery of phosphate is incredibly attractive, proposing itself as a sustainable approach to deal with the challenge of lack of renewable P deposits and reduce the environmental impact of P in water. |
Introduction
Phosphorus is an element of vital importance in the development of industry and agriculture. Phosphorus is used in detergents, toothpastes, fireworks, and in the heads of matches.1Phosphorus (P) together with nitrogen (N) and potassium (K) is a biolimiting nutrient for plants, being included as a chemical constituent of fertilizers.2 Phosphate is necessary for plant growth. Phosphorus is not found as a free element on earth due to its high reactivity. As a consequence of the high consumption of phosphorus, more and more reserves of phosphate minerals are being exploited (1 g kg−1),3,4 being found mainly as phosphate. Thus, P is a relatively restricted resource. Additionally, it is classified by the European Union as a strategically important material, as indicated in its list of critical raw materials (CRMs).5 The cost of phosphate rock (PR) utilized in fertilizer production impacts the expenses associated with food, particularly in the case of cereals, and subsequently, it contributes to global hunger. As a result, numerous countries are addressing this issue to tackle the challenges arising from the abrupt rise in the cost of phosphate rock.6 From a circular economy perspective, wastewater treatment plants (WWTPs) play a crucial role in the management of phosphorus. Therefore, the removal and recovery of phosphate is incredibly attractive, proposing itself as a sustainable approach to deal with the challenge of lack of renewable P deposits and reduce the environmental impact of P in water.7
On the other hand, anthropogenic phosphorus cycles are at the center of two major challenges, food safety and environmental protection. Phosphate compounds, such as orthophosphates and polyphosphates, are potential contributors to eutrophication. Therefore, their removal from industrial and domestic wastewater is imperative prior to discharge. Certainly, the extraction and recuperation of phosphorus from wastewater treatment plants (WWTPs) have the dual benefits of diminishing eutrophication and fulfilling the need for phosphorus-based fertilizers.6 However, wastewater treatment and phosphorus removal from wastewater is frequently an expensive process8 and so far, the results of phosphorus recovery from wastewater for the production of fertilizers fall within a range from 10–25% to 70–90% of phosphorus.
Effluent quality standards are under continuous update. Currently, in Europe, the allowable values for discharges from urban wastewater treatment plants (UWWTP) to sensitive areas that are prone to eutrophication are within the range of 1 to 2 mg L−1 for phosphorus.9 These values are even lower in the US, being within the range of 0.05 to 0.1 mg L−1 P.10
There are many methods available for the removal of phosphorus present in water. The most widely used methods for phosphate removal are chemical precipitation using iron coagulants11–13 and biological processes.14,15 However, these methods do not provide the removal rates required to gather the discharge regulations. Chemical precipitation typically achieves removal rates between 50% and 80%, while biological processes achieve removal rates ranging from 10% to 25%. Although chemical precipitation remains a well-established and highly effective method for phosphorus removal, widely used in numerous wastewater treatment plants (WWTPs), ongoing research is dedicated to significantly improving phosphorus removal to minimize the consumption of chemicals, reduce treatment costs and ensure a more sustainable overall process. As a result, the recovery of P from wastewater is evidently a trending topic.
Sorption is a simple, economical, and environmentally friendly method of removing phosphorus from water. Many studies have reported the use of different materials for phosphorus removal via sorption (limestone, shale, slag, iron-rich gravel, zeolite, marble dust, etc.).16,17 Recently, the development and application of nanoscale adsorbents have emerged as a promising methodology for remediating a diverse range of contaminants from wastewater.18–21 Among available sorbents graphene oxide (GO) stands out. This sorbent has a large surface area with a high density of polar oxygen, presenting different functional groups such as epoxy, carboxylic acid, carbonyl and hydroxyl groups. Additionally, it features a rich system of delocalized π–π electrons that strongly interacts with organic compounds.22 GO can be modified with magnetic nanoparticles (MNPs)23,24 for use in magnetic solid phase extraction (MSPE). In this work, a novel patented magnetic graphene oxide25 was synthesized through double coupling between iron oxide MNPs and GO, and was called M@GO. The double coupling confers greater stability and durability to the material. A notable advantage of this adsorbent lies in its straightforward recoverability from treated water through the application of a magnetic field.
To date, M@GO has been effectively employed for the chemical analysis of metals in aqueous media as an on-line adsorbent.26–28 However, its application on a larger scale in the field of environmental engineering remains unstudied. The objective of the current study was to assess the viability of M@GO as a phosphorus sorbent, for both its removal and recovery from real wastewater. This type of study requires an understanding of the thermodynamics and kinetics associated with the adsorption process. Therefore, the most important parameters affecting sorption performance (contact time, pH and adsorbent dosage) are optimized. In only 30 min, with a dosage of 0.8 g L−1, the initial concentration of phosphate (expressed as phosphorus) is reduced by 25%. These results are similar or better than those results reported in the bibliography. Also, to the best of our knowledge, the only one making the recovery/removal using green chemistry, avoiding the use of hazardous reagents and/or great volumes of those. In addition, M@GO can be reused, thus the decontamination is performed without generating contaminated sludges, which are difficult to manage.
Different thermodynamic and kinetic models are proposed to describe phosphorus adsorption on M@GO, indicating the rate-limiting step of the process. The surface morphology of M@GO, with and without adsorbed phosphorus, was studied by X-ray photoelectron spectroscopy (XPS) and energy dispersive X-ray spectroscopy-transmission electron microscopy (EDX-TEM). Additionally, this study explores beyond mere removal and delved into the field of phosphorus recovery from M@GO, aiming to convert waste into a valuable resource suitable for recycling as a fertilizer.
Materials and methods
Wastewater and M@GO
The wastewater stock was collected from the tertiary treatment outlet of the Peñón del Cuervo UWWTP (Málaga, Spain) managed by EMASA. The pH of the wastewater was 8.3 and the phosphate concentration was 2.8 mg L−1 PO4–P. Microbiological parameters indicate the absence of bacteria, and the turbidity was 7.7 NTU. This wastewater stock was stored in 2 L plastic bottles in a freezer at −20 °C until use. It should be noted that this UWWTP is not affected by the phosphorus levels required by the EU since it does not discharge into sensitive areas.The adsorbent nanomaterial, M@GO, was synthesized in the laboratory following the procedure indicated in the bibliography.25
Batch sorption experiments
The removal of phosphorus from the wastewater was studied by batch experiments. These experiments were carried out by mixing a known mass of M@GO with 25 mL of wastewater within a 50 mL polypropylene tube for different contact times. The temperature was maintained at 25 °C and mixing was carried out on an end-over-end shaker at 40 rpm. Afterward, the supernatant was decanted, while the particles were retained within the polypropylene tube using a neodymium magnet. This method obviated the need for a centrifugation step. All experiments were performed in triplicate.The concentrations of phosphorus in the supernatants were determined by the Watanabe and Olsen method,29 based on the ammonium molybdate spectrophotometric method. This method is based on the formation of phosphomolybdate ion complexes (PO43−·12MoO4) and it is used for estimation of PO43−. Therefore, this is the phosphorus species studied in this work, expressed as PO4–P.
The effect of the initial water pH on PO4–P removal was evaluated for a M@GO dosage of 0.8 g L−1. Sodium phosphate solutions in deionized water buffered at different pH values (2 to 12) were used for these experiments. The pH was set in each case using: diluted HCl (pH = 2), acetic acid–sodium acetate buffers (3 < pH < 5), boric acid–borax buffers (5 < pH < 10), and diluted NaOH (pH > 10). In these experiments, the contact time was 10 min and mixing was performed in an ultrasonic bath. The separation of M@GO and the determination of PO4–P in the supernatants were performed following the same procedure as described above.
The effect of M@GO dosage on the PO4–P removal was studied by varying the solid to liquid ratio (S/L) from 0.4 g L−1 to 1.6 g L−1 for the initial PO4–P concentration of the wastewater and under the optimized initial pH.
The kinetic experiments were carried out for 3 different initial PO4–P concentrations: the original concentration (2.8 mg L−1 PO4–P), a higher one (5.4 mg L−1 PO4–P) and a lower one (1.2 mg L−1 PO4–P). The highest concentration was achieved by spiking the necessary amount of sodium phosphate to the original wastewater. The lower concentration was obtained by diluting the original wastewater with distilled water. All those experiments were performed with a M@GO dosage of 0.8 g L−1. Additionally, kinetic experiments were also conducted for the original wastewater using M@GO dosages of 0.4 g L−1 and 1.6 g L−1. The contact times used were: 10 min, 20 min, 30 min, 1 h, 2 h, 3 h, and 5 h.
The adsorption isotherm at 25 °C was obtained from the batch experiment results obtained at a M@GO dosage of 0.8 g L−1 and at a contact time of 5 h. The PO4–P initial concentration was varied from 1.2 mg L−1 PO4–P to 5.4 mg L−1 PO4–P. Additionally, the adsorption equilibrium was also studied at M@GO dosages of 0.4 g L−1 and 1.8 g L−1 to assess the dosage effect on equilibrium.
The PO4–P sorption capacity of M@GO and the percentage of PO4–P removed from water were obtained, at a contact time t, as:
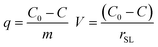 | (1) |
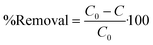 | (2) |
Adsorption models
The Freundlich isotherm equation can be expressed as:
| qe = KfCe(1/n) | (3) |
The Langmuir isotherm equation can be expressed as:
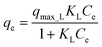 | (4) |
The Dubinin–Radushkevich (DR) isotherm model is based on the potential theory of adsorption in which the distribution of adsorption space is a function of adsorption potential.30 This model is used to describe the adsorption on a heterogeneous surface and allow the determination of the energy of adsorption.38
qe = qmax_DR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βε2) exp(−βε2) | (5) |
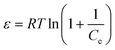 | (6) |
The value of the adsorption energy, E (J mol−1), is obtained from the following equation.
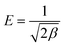 | (7) |
Pseudo-first order equation. The “empirical kinetic equation proposed by Lagergren in 1898”39 is “the most widely used rate equation for sorption of a solute from a liquid solution”.40 The integral form of this rate equation is:
| q = qe(1 − exp(−k1t)) | (8) |
Pseudo-second order equation. This model would be equivalent to the pseudo-first order but proposing that the adsorbate reacts with two adsorption sites. The integral form of this rate equation is:
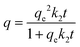 | (9) |
However, these empirical models can be derived from different theoretical approaches based on fundamental theories of sorption kinetics.34,39
Kinetic approach to Langmuir isotherm. A kinetic derivation of the Langmuir isotherm can be achieved by assuming an elementary adsorption and desorption mechanism whose rate is expressed by:
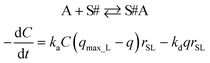 | (10) |
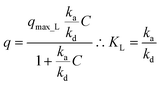 | (11) |
Solving the mass balance eqn (1) for (q·rSL) yields
| q·rSL = (C0 − C) | (12) |
Substituting q·rSL into eqn (10) and rearranging, the sorption rate is
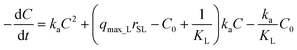 | (13) |
Separating variables and integrating with the limits C = C0 when t = 0:
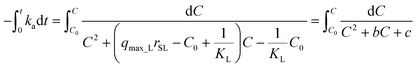 | (14) |
The integral form of this rate equation is:
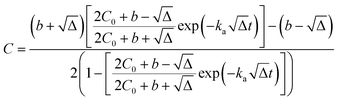 | (15) |
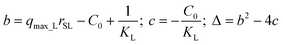 | (16) |
Mass transfer. This mechanistic approach is used when the overall rate of adsorption is limited by the rate of mass-transfer of adsorbate between the bulk liquid and the surface of the adsorbent. The rate of mass transfer across an interface that separates two phases may be expressed by:
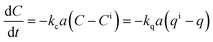 | (17) |
It is generally assumed that liquid and solid concentrations at the interface are in equilibrium. Thus, if equilibrium were described by a Langmuir isotherm, the concentrations at the interface could be obtained by simultaneously solving the following equations.
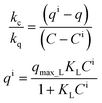 | (18) |
Solving the system eqn (18) for the solute concentration at the liquid interface yields:
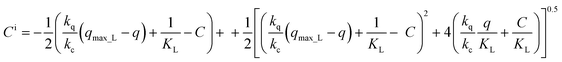 | (19) |
The sorption rate as a function of the concentration of the adsorbate in the liquid phase is obtained by elimination of q into eqn (19) using the mass balance eqn (1) and then substituting Ci into eqn (17):
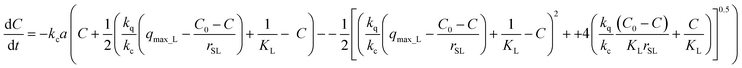 | (20) |
To the best of authors' knowledge, an integral form of eqn (20) cannot be obtained, so in this case, that integration is performed using the fourth-order Runge–Kutta integration method.41
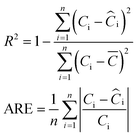 | (21) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) is the average of the experimental concentrations, and n is the number of experimental points obtained in the experiment.
is the average of the experimental concentrations, and n is the number of experimental points obtained in the experiment.
Although many of the proposed models can be expressed in a linearized form, the fits are performed by non-linear regression, as recommended by the literature.42–44 Linear modeling entails the transformation of data usually at different scales, which limits the comparison of the parameters chosen for model validation. Model assessment should be done at the original scale of the data.43
For the adsorption isotherm models, non-linear two-parameter fits were performed by minimizing the sum of square error (SSE):
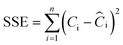 | (22) |
Once the adsorption isotherm model is chosen, non-linear one-parameter fits were performed for the proposed kinetic models since the values of isotherm parameters have been previously obtained (kinetics must be consistent with equilibrium). Thus, the only one unknown parameter is the corresponding rate constant. However, non-linear two-parameter fit had to be performed for the mass transfer model, since the two mass-transfer coefficients are unknowns. According to the proposed models, it is expected that the kinetic parameters are independent of the M@GO dosage (rSL) and of the initial concentration of PO4–P (C0). Thus, the fit of each model was performed simultaneously to all the experimental data obtained in the 5 kinetic experiments (3 dosages and 3 initial concentrations). The standard deviations in those experiments are not the same for all experimental points, so the fits were performed by minimizing the sum of the squares of the errors divided by their corresponding standard deviation (χ2):45
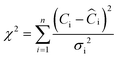 | (23) |
Results and discussion
Effect of pH and contact time
Results obtained from sodium phosphate buffered solutions indicate that the optimum pH range for phosphate adsorption on M@GO is between pH 3 and 9, with a maximum adsorption at pH 8. As can be seen in Fig. 1, phosphate adsorption decreases sharply at pH values above 9.5, suggesting that adsorption may be reversible.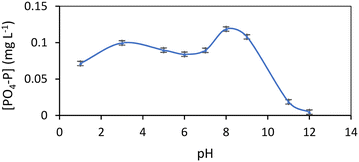 | ||
| Fig. 1 Effect of pH on aqueous PO4–P concentration for a M@GO dosage of 0.8 g L−1. The error bars represent 2 times the standard deviation of the aqueous concentrations of triplicate experiments. | ||
The pH value of wastewater (8.3) is close to the pH value at which the maximum phosphate adsorption was found for the sodium phosphate solutions. Thus, the initial pH was not modified in the adsorption experiments performed with the wastewater.
Regarding contact time, Fig. 2 shows the effect of contact time on PO4–P adsorption from wastewater on M@GO at a dosage of 0.8 g L−1. The error bars represent 2 times the standard deviation of the aqueous concentrations of triplicate experiments. As can be seen, the aqueous PO4–P concentration rapidly decreases within the first 3 hours, remaining constant for longer contact times. In the first 5 hours, M@GO removes from 40% of PO4–P, for its highest initial concentration, to 60% for its lowest one. These removals are practically identical to those obtained at a contact time of 24 h, therefore, for subsequent experiments, equilibrium is considered to be reached after 5 h.
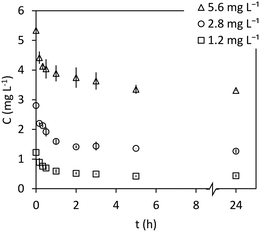 | ||
| Fig. 2 Effect of contact time on aqueous PO4–P concentration for a M@GO dosage of 0.8 g L−1 and at three different initial PO4–P concentrations. | ||
In addition, the PO4–P concentration of the original wastewater (2.8 mg L−1) is reduced in 30 min of treatment to levels below those required by the EU for discharges in sensitive areas from UWWTPs with an equivalent population (p.e.) of between 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–100
000–100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Although this is sufficient to comply with the EU criteria, which require adherence to either concentration values or percentage reduction, it should be noted that if the percentage reduction criterion is chosen, the minimum value of 80% reduction would not be achieved.
000. Although this is sufficient to comply with the EU criteria, which require adherence to either concentration values or percentage reduction, it should be noted that if the percentage reduction criterion is chosen, the minimum value of 80% reduction would not be achieved.
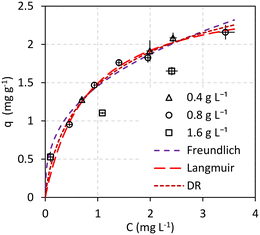
Adsorption isotherm
Fig. 3 shows the results of the adsorption experiments carried out until the equilibrium. The error bars represent 2 times the standard deviation of the concentrations, both in the liquid (the horizontal ones) and in the solid (the vertical ones), of triplicate experiments. This graph also differentiates the tests carried out at different dosages of M@GO, making the effect of dosage on equilibrium visible as well. As can be seen, there are no significant differences between the results obtained at dosages of 0.4 g L−1 and 0.8 g L−1. However, the points obtained for a dosage of 1.6 g L−1 clearly deviate from the trend followed by the results at lower dosages. This effect may be due to the agglomeration of the M@GO nanoparticles at high dosages, which would reduce the free surface area per unit mass available for PO4–P adsorption.Thus, the 3 isotherm models proposed (Freundlich, Langmuir and Dubinin–Radushkevich) were fitted to the experimental results obtained at M@GO dosages below 1.6 g L−1. The Solver tool of Microsoft Excel was used to perform a non-linear two-parameter fit for each model minimizing the SSE. The results of these fits are shown in Fig. 3 and in Table 1. As can be seen, the best fit corresponds to the Langmuir isotherm, based on both its higher R2 value and its lower ARE value. The second-best fit corresponds to the Dubinin–Radushkevich isotherm, whose graphical representation is almost indistinguishable from that of Langmuir. The interest of the DR model is the adsorption energy, whose value here is lower than 8 kJ mol−1. This could indicate that the process corresponds to a physical adsorption.46
| Isotherm model | Parameters | |
|---|---|---|
| Freundlich | K F (L1/n mg(1−1/n) g−1) = | 1.46 |
| n (—) = | 2.75 | |
| R 2 = | 0.9821 | |
| ARE (%) = | 5.44% | |
| Langmuir | K L (L mg−1) = | 1.25 |
| q max_L (mg g−1) = | 2.69 | |
| R 2 = | 0.9983 | |
| ARE (%) = | 2.23% | |
| Dubinin–Radushkevich | β (mol2 J−2) = | 1.06 × 10−8 |
| q max_DB (mg g−1) = | 3.21 | |
| E (kJ mol−1) = | 7.04 | |
| R 2 = | 0.9931 | |
| ARE (%) = | 3.56% | |
The value of qmax_L = 2.69 mg g−1 (Table 1) obtained for M@GO is similar or higher than others found in the literature for other forms and types of carbon in real wastewater samples.47
For comparative purposes, data of analogous methods reported in the literature are registered in Table 2. The direct comparison is difficult due to the different experimental conditions. Nonetheless, the removal for the target element using the developed method were similar or better than those results reported in the bibliography. Also, to the best of the authors' knowledge, the only one making the recovery/removal using green chemistry, avoiding the use of hazardous reagents and/or great volumes of those; as well as the appearance of contaminated sludge that must be disposed.
| Treatment process | Samples | P removed | Ref. |
|---|---|---|---|
| CPR Chemical phosphorus removal. EBPR Enhanced biological P removal. | |||
| CPR with FeSO4 addition | Digested sludge | 67% | 48 |
| Digested sludge | 60% | ||
| Dewatered sludge | 47% | ||
| CPR with FeClSO4 addition | Liquid sludge | 80% | 49 |
| Dried granules | |||
| EBPR | Activated sludge | 9–26% | 50 |
| AB technology with Fe addition | A-stage surplus sludge | 52–55% | 50 |
| B-stage surplus sludge | 37–43% | ||
| Digested sludge | 47–59% | ||
| Not mentioned | Excess and digested sludge | 70–90% | 51 |
| CPR activated carbon nitric-acid treatment, thermal modification treatment and nitric-acid thermal treatment | Groundwater and wastewater | 80% | 52 |
| CPR laterite soil thermal treatment and activated carbon thermal treatment | Synthetic wastewater | 59–63% | 53 |
| 68–69% | |||
| CPR with M@GO | Wastewater Malaga | 75% | This work |
Kinetic study
Once it has been proven that the Langmuir isotherm adequately describes the adsorption equilibrium, the next step is to find a kinetic model consistent with the equilibrium model. Thus, as indicated in section model validation, the parameters of the Langmuir isotherm calculated in the previous section will be included in all proposed kinetic models. Therefore, the only unknowns are the kinetic parameters involved in those models.For pseudo-first and pseudo-second order models, this entails obtaining an expression for qe by substituting the mass balance eqn (1) in the Langmuir isotherm equation eqn (4), which yields:
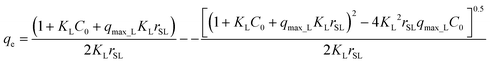 | (24) |
For the MT model, it should be considered that the M@GO dosage affects the values of the volumetric mass-transfer coefficients through the interfacial area per unit of liquid volume. Thus, if the two coefficients for a dosage of 0.8 g L−1 are used as fitting parameters, those for a dosage of 0.4 g L−1 should be half of those for a dosage of 0.8 g L−1. Analogously, the coefficients for 1.6 g L−1 should be twice those for 0.8 g L−1.
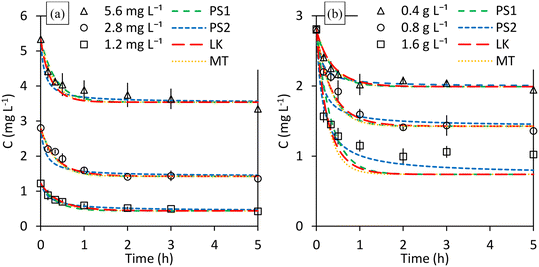
Furthermore, since it is expected that both initial PO4–P concentration and M@GO dosage do not affect those kinetic parameters, the fit of each kinetic model is performed simultaneously to all the experimental data obtained in 4 of the 5 kinetic experiments. The results obtained at a M@GO dosage of 1.6 g L−1 are excluded from these fits for the same reason that they were excluded in the adsorption isotherm fits: M@GO dosage does affect the equilibrium at values above 0.8 g L−1. However, once those fits are done, the results of those models for a dosage of 1.6 g L−1 are also presented in the following figures and tables. The Solver tool of Microsoft Excel was used to perform a non-linear one-parameter fit for each model (two-parameters fit for MT model) minimizing the chi-squared (χ2).
Fig. 4a shows the results of the kinetic experiments carried out with a M@GO dosage of 0.8 g L−1 for different initial PO4–P concentrations. The dashed lines represent the fit of the proposed models to the experimental data. At first glance, the pseudo first order (PS1), Langmuir kinetics (LK), and mass-transfer (MT) models are able to adequately reproduce the experimental results, and therefore, also the effect of the initial concentration on the adsorption process. The pseudo second order (PS2) model fails at the first 30 min of the experiment for an initial concentration of 2.8 mg L−1.
Similarly, Fig. 4b shows the results of the kinetic experiments carried out with an initial phosphorous concentration of 2.8 mg L−1 for different M@GO dosages. As can be seen, again the PS1, LK and MT models reproduce sufficiently well the effect of increasing the M@GO dosage from 0.4 g L−1 to 0.8 g L−1. However, none of those models adequately reproduce the results obtained at a M@GO dosage of 1.6 g L−1, whose results were excluded from these fits for the reasons already indicated above.
Table 3 shows the values of the parameters used to assess the goodness-of-fit of each model, as well as the calculated values of the kinetic parameters. The column labeled “All” contains the R2 and ARE values calculated with all results of the 4 kinetic experiments performed at M@GO dosages below 1.6 g L−1. The rest of the columns present the values of the same parameters calculated individually for each kinetic experiment, which comes from the same global fit.
| Model | Parameters | C 0 (mg L−1) | All | 2.8 | 5.4 | 1.2 | 2.8 | |
|---|---|---|---|---|---|---|---|---|
| r SL (g L−1) | 0.8 | 0.8 | 0.8 | 0.4 | ||||
| a Values of the volumetric mass-transfer coefficient for a M@GO dosage of 0.8 g L−1. | ||||||||
| PS1 | k 1 (h−1) = | 2.87 | R 2 | 0.993 | 0.957 | 0.916 | 0.940 | 0.959 |
| ARE | 5.1% | 4.7% | 4.2% | 9.3% | 2.3% | |||
| PS2 | k 2 (g mg−1 h−1) = | 5.17 | R 2 | 0.989 | 0.858 | 0.893 | 0.990 | 0.949 |
| ARE | 4.9% | 8.2% | 4.8% | 3.9% | 2.6% | |||
| LK | k a (L mg−1 h−1) = | 0.72 | R 2 | 0.993 | 0.968 | 0.897 | 0.959 | 0.944 |
| ARE | 4.8% | 4.1% | 4.5% | 7.6% | 2.9% | |||
| MT | k c a (h−1)a = | 1.96 | R 2 | 0.993 | 0.953 | 0.913 | 0.950 | 0.947 |
| k q a (g L−1 h−1)a = | 2.96 | ARE | 5.0% | 4.9% | 4.1% | 8.6% | 2.7% | |
As shown in Table 3, the best fit according to ARE corresponds to the LK model (4.8%), followed by PS2, MT and PS1 models in ARE increasing order. If R2 is selected as a validation criterion, no significant differences are observed between PS1, LK and MT, with PS2 presenting the worst value. Thus, the LK model is the best model to simulate the adsorption process. Additionally, its theoretical basis is an advantage over empirical models whose theoretical basis is not so clear.
Finally, the values of the volumetric mass-transfer coefficients obtained from the fit of the MT model can indicate if mass-transfer is limiting the overall rate of the adsorption process. If M@GO nanoparticles are assumed to be spheres about 100 nm in diameter (D), the mass-transfer surface area (interface) per unit liquid volume can be estimated as
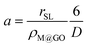 | (25) |
Characterization
Fig. 5 shows a TEM image of the morphology of the M@GO surface (a), in which it can be observed that the Fe3O4 nanoparticles, with a diameter between 12 and 20 nm, are randomly fixed between the graphene oxide sheets. The amplification of the phosphorus region in the XPS spectrum shows the corresponding peak (b). This figure also shows the EDX spectroscopy of M@GO before (c) and after (d) the phosphorus adsorption. As can be seen, the adsorbed phosphorus (green dots) is mainly distributed on the iron nanoparticles (pink color) and, to a lesser extent, also between the graphene sheets (blue color). | ||
| Fig. 5 TEM image of M@GO (a), XPS spectra P region (b), EDX images of M@GO before (c) and after (d) phosphorus adsorption. | ||
From the N2 adsorption–desorption experiment for M@GO without P, a type IV isotherm was obtained, which is typical of mesoporous materials. The nanomaterial presents a pore size and specific surface of 93 Å and 47.04 ± 0.16 m2 g−1.
Desorption study
The results of the 17 CCD experiments indicated that the parameter contact time was statistically significant at the 95% confidence level (p < 0.05), as can be seen in the Pareto chart, Fig. 6a. The response surface obtained is shown in Fig. 6b. Using the optimized parameters, 2 mL NH4OH 5% w/w, and a contact time of 130 min, the absorbed PO4–P recovery yields (95 ± 4)% with a solid–liquid ratio up to 5 greater than the ratio used in the adsorption process.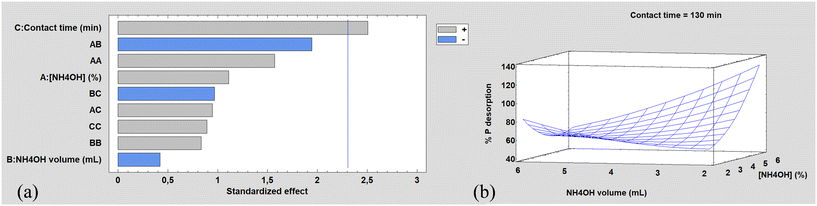 | ||
| Fig. 6 CCD results: (a) standardized Pareto chart. (b) Response surface. The P desorption percentage is referred to phosphate species. | ||
The standardized Pareto chart (Fig. 6a) illustrates that the only one significant factor affecting phosphate desorption is the contact time, with a p-value = 0.037 < 0.05. Ammonia concentration (A) has a positive influence on the response function (% P desorption) and ammonia volume (B) has a negative influence on the response function. The central composite factorial design results reveal a crossed interaction between the two factors under investigation (ammonia concentration and volume of ammonia solution) leading to the curvature of the response surface. As can be seen in Fig. 6b, the recovery of adsorbed PO4–P increases with ammonia concentration when the volume of ammonia solution is low. However, contrary to expectations, this behavior is not observed for higher volumes of ammonia solution. Similarly, the effect of ammonia solution volume follows the same pattern. Higher PO4–P recovery would be expected for lower solution volumes (resulting in a higher solid mass to solution volume ratio); however, this behavior is only evident for high ammonia concentrations.
This crossed interaction between ammonia concentration and volume of ammonia solution likely arises from the involvement of multiple equilibrium reactions in the overall recovery process. These preliminary results do not allow for further conclusions regarding the recovery mechanism.
Conclusion
The new sorbent material (M@GO) can be used for the recovery/removal of phosphate from a real tertiary effluent in a sewage treatment plant. The adsorption process makes it possible to reduce the PO4–P concentration to 75% of the least restrictive value allowed by European legislation for UWWTP discharges in sensitive areas.The Langmuir isotherm model adequately describes the adsorption equilibrium, resulting in a maximum adsorption capacity of 2.69 mg g−1. The adsorption energy value calculated by fitting the Dubinin–Radushkevich isotherm (7.04 kJ mol−1) indicates that the process corresponds to a physical adsorption. Among the four models studied, the Langmuir kinetic model best reproduces the PO4–P adsorption kinetics, yielding an adsorption rate constant of 0.72 L mg−1 h−1. The value of the liquid mass-transfer coefficient resulting from the fit of the mass transfer model (kc = 1.5 × 10−8 m s−1) indicates that the rate-limiting step is the adsorption step and not the mass transfer between the bulk liquid and the solid surface.
The desorption results indicate that the adsorption process is reversible. Desorption using ammonia solution yields PO4–P recoveries of (95 ± 4)% of that retained in M@GO with a much higher solid–liquid ratio than that used in the adsorption from the wastewater.
The results obtained after optimizing the most important parameters of the adsorption process (pH, contact time, M@GO dosage) suggest that a continuous stirred tank adsorption process is a promising application to investigate and for scaling up to an urban wastewater treatment plant. Thus, further research should focus on assessing the monetary benefits and environmental risks, including the potential effects of reusing the adsorbent for multiple adsorption/desorption cycles on phosphate removal and recovery efficiencies.
Author contributions
Andrea Muñoz-Garcia: investigation, methodology, data curation. Pablo Montoro-Leal: investigation, methodology, data curation. María del Mar López-Guerrero: investigation, methodology, supervision, writing – review & editing. Carlos Vereda-Alonso: software, writing – original draft, writing – review & editing, funding acquisition. Elisa Vereda Alonso: conceptualization, writing – review & editing, funding acquisition.Conflicts of interest
The authors have no relevant financial or non-financial interests to disclose.Acknowledgements
This work was supported by the Spanish Ministry of Science and Innovation [Research Project PID2021-126794OB-I00], the University of Málaga [Support for Prototypes E3/05/21], [II Plan Propio (B1-2022_20 and B4-2023-19)] and CEI MAR funds. Muñoz-Garcia and Montoro-Leal also acknowledge the collaboration grant and fellowship FPU18/05371, respectively, obtained from the Spanish Ministry of Science and Innovation. Funding for open access charge: Universidad de Malaga/CBUA. The authors acknowledge all the collaboration with EMASA.References
- S. Dey, A. Sreenivasulu, G. T. N. Veerendra, A. V. Phani Manoj and N. Haripavan, Synthesis and characterization of mango leaves biosorbents for removal of iron and phosphorous from contaminated water, Appl. Surf. Sci. Adv., 2022, 11, 100292 CrossRef
.
- F. W. Wellmer and R. W. Scholz, The Right to Know the Geopotential of Minerals for Ensuring Food Supply Security: The Case of Phosphorus, J. Ind. Ecol., 2015, 19, 3–6 CrossRef
.
- N. Boujelben, J. Bouzid, Z. Elouear, M. Feki, F. Jamoussi and A. Montiel, Phosphorus removal from aqueous solution using iron coated natural and engineered sorbents, J. Hazard. Mater., 2008, 151, 103–110 CrossRef CAS PubMed
.
- J. W. Choi, S.-Y. Lee, K.-Y. Park, K.-B. Lee, D.-J. Kim and S.-H. Lee, Investigation of phosphorous removal from wastewater through ion exchange of mesostructure based on inorganic material, Desalination, 2011, 266, 281–285 CrossRef CAS
.
- G. A. Blengini, C. EL Latunussa, U. Eynard, C. Torres de Matos, D. Wittmer, K. Georgitzikis, C. Pavel, S. Carrara, L. Mancini, M. Unguru, D. Blagoeva, F. Mathieux and D. Pennington, Study on the EU's list of Critical Raw Materials - Final Report, Directorate-General for Internal Market, Industry, Entrepreneurship and SMEs (European Commission), 2020 Search PubMed.
- F. Di Capua, S. de Sario, A. Ferraro, A. Petrella, M. Race, F. Pirozzi, U. Fratino and D. Spasiano, Phosphorous removal and recovery from urban wastewater: Current practices and new directions, Sci. Total Environ., 2022, 823, 153750 CrossRef CAS PubMed
.
- P. J. A. Withers, J. J. Elser, J. Hilton, H. Ohtake, W. J. Schipper and K. C. van Dijk, Greening the global phosphorus cycle: how green chemistry can help achieve planetary P sustainability, Green Chem., 2015, 17, 2087–2099 RSC
.
- A. Das Gupta, S. Sarkar, P. Ghosh, T. Saha and A. K. Sil, Phosphorous dynamics of the aquatic system constitutes an important axis for waste water purification in natural treatment pond(s) in East Kolkata Wetlands, Ecol. Eng., 2016, 90, 63–67 CrossRef
.
- The Council of the European communities, 2014.
- J. López, M. Reig, E. Licon, C. Valderrama, O. Gibert and J. L. Cortina, Evaluating the integration of nanofiltration membranes in advanced water reclamation schemes using synthetic solutions: From phosphorous removal to phosphorous circularity, Sep. Purif. Technol., 2022, 290, 120914 CrossRef
.
- M. I. Aguilar, J. Sáez, M. Lloréns, A. Soler and J. F. Ortuño, Nutrient removal and sludge production in the coagulation–flocculation process, Water Res., 2002, 36, 2910–2919 CrossRef CAS PubMed
.
- A. H. Caravelli, E. M. Contreras and N. E. Zaritzky, Phosphorous removal in batch systems using ferric chloride in the presence of activated sludges, J. Hazard. Mater., 2010, 177, 199–208 CrossRef CAS PubMed
.
- Y. Zhou, X. H. Xing, Z. Liu, L. Cui, A. Yu, Q. Feng and H. Yang, Enhanced coagulation of ferric chloride aided by tannic acid for phosphorus removal from wastewater, Chemosphere, 2008, 72, 290–298 CrossRef CAS PubMed
.
- T. Mino, M. C. M. van Loosdrecht and J. J. Heijnen, Microbiology and biochemistry of the enhanced biological phosphate removal process, Water Res., 1998, 32, 3193–3207 CrossRef CAS
.
- D. Mulkerrins, A. D. W. Dobson and E. Colleran, Parameters affecting biological phosphate removal from wastewaters, Environ. Int., 2004, 30, 249–259 CrossRef CAS PubMed
.
- E. Osama, O. Junya and H. Kazuaki, Removal of Phosphorus from Water Using Marble Dust as Sorbent Material, J. Environ. Prot., 2012, 3(8), 709–714 CrossRef
.
- C. A. Prochaska and A. I. Zouboulis, Removal of phosphates by pilot vertical-flow constructed
wetlands using a mixture of sand and dolomite as substrate, Ecol. Eng., 2006, 26, 293–303 CrossRef
.
- M. El-Kammah, E. Elkhatib, S. Gouveia, C. Cameselle and E. Aboukila, Enhanced removal of Thiamethoxam from wastewater using waste-derived nanoparticles: Adsorption performance and mechanisms, Environ. Technol. Innovation, 2022, 28, 102713 CrossRef CAS
.
- A. Gulyás, S. Genç, Z. S. Can and N. Semerci, Phosphate recovery from sewage sludge supernatants using magnetic nanoparticles, J. Water Process Eng., 2021, 40, 101843 CrossRef
.
- M. Kaur, M. Kaur, D. Singh, M. Feng and V. K. Sharma, Magnesium ferrite-nitrogen–doped graphene oxide nanocomposite: effective adsorptive removal of lead(II) and arsenic(III), Environ. Sci. Pollut. Res., 2022, 29, 48260–48275 CrossRef CAS PubMed
.
- M. Verma, R. Borah, A. Kumar, S.-H. Chae, S.-Y. Pan, V. Kumar, M. S. Vlaskin and H. Kim, Capturing of inorganic and organic pollutants simultaneously from complex wastewater using recyclable magnetically chitosan functionalized with EDTA adsorbent, Process Saf. Environ. Prot., 2022, 167, 56–66 CrossRef CAS
.
- D. R. Dreyer, A. D. Todd and C. W. Bielawski, Harnessing the chemistry of graphene oxide, Chem. Soc. Rev., 2014, 43, 5288–5301 RSC
.
- B. F. do Nascimento, C. M. B. de Araújo, D. del Carmen Pinto Osorio, L. F. O. Silva, G. L. Dotto, J. V. F. L. Cavalcanti and M. A. da Motta Sobrinho, Adsorption of chloroquine, propranolol, and metformin in aqueous solutions using magnetic graphene oxide nanocomposite, Environ. Sci. Pollut. Res., 2023, 30, 85344–85358 CrossRef CAS PubMed
.
- M. K. Goswami, A. Srivastava, R. K. Dohare, A. K. Tiwari and A. Srivastav, Recent advances in conducting polymer-based magnetic nanosorbents for dyes and heavy metal removal: fabrication, applications, and perspective, Environ. Sci. Pollut. Res., 2023, 30, 73031–73060 CrossRef CAS PubMed
.
-
P. Montoro-Leal, J. C. García-Mesa, M. M. López Guerrero and E. I. Vereda Alonso, Material compuesto adsorbente de metales basado en óxido de grafeno magnético y procedimiento de obtención, Oficina Española de Patentes y Marcas, ES 2844942, 2021, European patent application EP 4095097A1, 2022
.
- P. Montoro-Leal, J. C. García-Mesa, I. Morales-Benítez, L. Vázquez-Palomo, M. del M. López Guerrero and E. I. Vereda Alonso, Synthesis of a novel magnetic nanomaterial for the development of a multielemental speciation method of lead, mercury, and vanadium via HPLC-ICP MS, Microchim. Acta, 2023, 190, 296 CrossRef CAS PubMed
.
- P. Montoro-Leal, J. C. García-Mesa, I. Morales-Benítez, A. García de Torres and E. I. Vereda Alonso, Semiautomatic method for the ultra-trace arsenic speciation in environmental and biological samples via magnetic solid phase extraction prior to HPLC-ICP-MS determination, Talanta, 2021, 235, 122769 CrossRef CAS PubMed
.
- I. Morales-Benítez, P. Montoro-Leal, J. C. García-Mesa, M. M. López Guerrero and E. Vereda Alonso, New magnetic chelating sorbent for chromium speciation by magnetic solid phase extraction on-line with inductively coupled plasma optical emission spectrometry, Talanta, 2023, 256, 124262 CrossRef PubMed
.
- F. S. Watanabe and S. R. Olsen, Test of an Ascorbic Acid Method for Determining Phosphorus in Water and NaHCO3 Extracts from Soil, Soil Sci. Soc. Am. J., 1965, 29, 677–678 CrossRef CAS
.
- M. M. Dubinin, The Potential Theory of Adsorption of Gases and Vapors for Adsorbents with Energetically Nonuniform Surfaces, Chem. Rev., 1960, 60, 235–241 CrossRef CAS
.
- H. Freundlich, Über die Adsorption in Lösungen, Z. Phys. Chem., 1907, 57U, 385–470 CrossRef
.
- N. D. Hutson and R. T. Yang, Theoretical basis for the Dubinin-Radushkevitch (D-R) adsorption isotherm equation, Adsorption, 1997, 3, 189–195 CrossRef CAS
.
- I. Langmuir, The constitution and fundamental properties of solids and liquids. Part I. Solids, J. Am. Chem. Soc., 1916, 38, 2221–2295 CrossRef CAS
.
- Y. Liu and Y.-J. Liu, Biosorption isotherms, kinetics and thermodynamics, Sep. Purif. Technol., 2008, 61, 229–242 CrossRef CAS
.
- M. Villen-Guzman, D. Gutierrez-Pinilla, C. Gomez-Lahoz, C. Vereda-Alonso, J. M. Rodriguez-Maroto and B. Arhoun, Optimization of Ni (II) biosorption from aqueous solution on modified lemon peel, Environ. Res., 2019, 179, 108849 CrossRef CAS PubMed
.
- N. Boujelben, F. Bouhamed, Z. Elouear, J. Bouzid and M. Feki, Removal of phosphorus ions from aqueous solutions using manganese-oxide-coated sand and brick, Desalin. Water Treat., 2014, 52, 2282–2292 CrossRef CAS
.
- U. A. Edet and A. O. Ifelebuegu, Kinetics, Isotherms, and Thermodynamic Modeling of the Adsorption of Phosphates from Model Wastewater Using Recycled Brick Waste, Processes, 2020, 8, 665 CrossRef CAS
.
- M. A. Al-Anber, Thermodynamics Approach in the Adsorption of Heavy Metals, IntechOpen, 2011 Search PubMed.
- W. Rudzinski and W. Plazinski, Kinetics of Solute Adsorption at Solid/Solution Interfaces: A Theoretical Development of the Empirical Pseudo-First and Pseudo-Second Order Kinetic Rate Equations, Based on Applying the Statistical Rate Theory of Interfacial Transport, J. Phys. Chem. B, 2006, 110, 16514–16525 CrossRef CAS PubMed
.
- Y. S. Ho, J. C. Y. Ng and G. McKay, Kinetics of Pollutant Sorption by Biosorbents: Review, Sep. Purif. Methods, 2000, 29, 189–232 CrossRef CAS
.
-
S. Chapra and R. Canale, Numerical Methods for Engineers, McGraw-Hill Education, 2009 Search PubMed
.
- E. C. Lima, F. Sher, A. Guleria, M. R. Saeb, I. Anastopoulos, H. N. Tran and A. Hosseini-Bandegharaei, Is one performing the treatment data of adsorption kinetics correctly?, J. Environ. Chem. Eng., 2021, 9, 104813 CrossRef CAS
.
- E. D. Revellame, D. L. Fortela, W. Sharp, R. Hernandez and M. E. Zappi, Adsorption kinetic modeling using pseudo-first order and pseudo-second order rate laws: A review, Clean. Eng. Technol., 2020, 1, 100032 CrossRef
.
- J.-P. Simonin, On the comparison of pseudo-first order and pseudo-second order rate laws in the modeling of adsorption kinetics, Chem. Eng. J., 2016, 300, 254–263 CrossRef CAS
.
-
W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, in Numerical Recipes in C: The Art of Scientific Computing, Cambridge University Press, 2nd edn, 1992 Search PubMed
.
- M. Chabani, A. Amrane and A. Bensmaili, Kinetic modelling of the adsorption of nitrates by ion exchange resin, Chem. Eng. J., 2006, 125, 111–117 CrossRef CAS
.
- X. Xiao, S. Liu, X. Zhang and S. Zheng, Phosphorus removal and recovery from secondary effluent in sewage treatment plant by magnetite mineral microparticles, Powder Technol., 2017, 306, 68–73 CrossRef CAS
.
- E. Frossard, J. P. Bauer and F. Lothe, Evidence of vivianite in FeSO4-flocculated sludges, Water Res., 1997, 31, 2449–2454 CrossRef CAS
.
- M. S. Poffet, K. Käser and T. A. Jenny, Thermal Runaway of Dried Sewage Sludge Granules in Storage Tanks, Chimia, 2008, 62, 29 CrossRef CAS
.
- P. Wilfert, A. Mandalidis, A. I. Dugulan, K. Goubitz, L. Korving, H. Temmink, G. J. Witkamp and M. C. M. Van Loosdrecht, Vivianite as an important iron phosphate precipitate in sewage treatment plants, Water Res., 2016, 104, 449–460 CrossRef CAS PubMed
.
- P. Wilfert, A. I. Dugulan, K. Goubitz, L. Korving, G. J. Witkamp and M. C. M. Van Loosdrecht, Vivianite as the main phosphate mineral in digested sewage sludge and its role for phosphate recovery, Water Res., 2018, 144, 312–321 CrossRef CAS PubMed
.
- A. M. E. Khalil, O. Eljamal, T. W. M. Amen, Y. Sugihara and N. Matsunaga, Optimized nano-scale zero-valent iron supported on treated activated carbon for enhanced nitrate and phosphate removal from water, Chem. Eng. J., 2017, 309, 349–365 CrossRef CAS
.
- U. Sreekumar, A. K. Thalla and V. V. Nair, Comparative evaluation of phosphate abatement using laterite soil and activated carbon, Int. J. Environ. Sci. Technol., 2019, 16, 4493–4502 CrossRef CAS
.
- V. J. Inglezakis, M. Balsamo and F. Montagnaro, Liquid–Solid
Mass Transfer in Adsorption Systems—An Overlooked Resistance?, Ind. Eng. Chem. Res., 2020, 59, 22007–22016 CrossRef CAS
.
Footnote |
| † Equal contribution. |
| This journal is © The Royal Society of Chemistry 2024 |