Open Access Article
Open Access ArticleAdsorption and vibrational spectroscopy of CO on the surface of MgO from periodic local coupled-cluster theory†
Hong-Zhou
Ye
 *a and
Timothy C.
Berkelbach
*a and
Timothy C.
Berkelbach
 *ab
*ab
aDepartment of Chemistry, Columbia University, New York, NY 10027, USA. E-mail: hzyechem@gmail.com; t.berkelbach@columbia.edu
bInitiative for Computational Catalysis, Flatiron Institute, New York, NY 10010, USA
First published on 6th March 2024
Abstract
The adsorption of CO on the surface of MgO has long been a model problem in surface chemistry. Here, we report periodic Gaussian-based calculations for this problem using second-order perturbation theory (MP2) and coupled-cluster theory with single and double excitations (CCSD) and perturbative triple excitations [CCSD(T)], with the latter two performed using a recently developed extension of the local natural orbital approximation to problems with periodic boundary conditions. The low cost of periodic local correlation calculations allows us to calculate the full CCSD(T) binding curve of CO approaching the surface of MgO (and thus the adsorption energy) and the two-dimensional potential energy surface (PES) as a function of the distance from the surface and the CO stretching coordinate. From the PES, we obtain the fundamental vibrational frequency of CO on MgO, whose shift from the gas phase value is a common experimental probe of surface adsorption. We find that CCSD(T) correctly predicts a positive frequency shift upon adsorption of +14.7 cm−1, in excellent agreement with the experimental shift of +14.3 cm−1. We use our CCSD(T) results to assess the accuracy of MP2, CCSD, and several density functional theory (DFT) approximations, including exchange correlation functionals and dispersion corrections. We find that MP2 and CCSD yield reasonable binding energies and frequency shifts, whereas many DFT calculations overestimate the magnitude of the adsorption energy by 5–15 kJ mol−1 and predict a negative frequency shift of about −20 cm−1, which we attribute to self-interaction-induced delocalization errors that are mildly ameliorated with hybrid functionals. Our findings highlight the accuracy and computational efficiency of the periodic local correlation for the simulation of surface chemistry with accurate wavefunction methods.
I. Introduction
The adsorption of a molecule on to the surface of a substrate is the first step of many interfacial physicochemical processes such as heterogeneous catalysis1,2 and gas storage and separation.3–5 Accurate determination of the adsorption energy, and more generally the potential energy surface (PES), is thus vital for understanding the structure and dynamics of the adsorption process, which in turn facilitates the interpretation of relevant interfacial experiments (e.g., molecular beam,1,6,7 temperature-programmed desorption,8–11 and surface vibrational spectroscopies12,13). Nonetheless, this has been proven a challenging computational task over the past two decades.14,15 The major difficulty stems from the inherently weak yet correlated nature of surface–adsorbate interactions, which necessitates achieving sub-kJ mol−1 accuracy for reliable comparison with experiments14–17 and development of accurate force fields for molecular dynamics.18–21 The demanded high accuracy is typically out of reach by density functional theory22 (DFT) whose performance can depend sensitively on the choice of approximate exchange–correlation functionals (especially because of self-interaction errors) and dispersion correction methods.1,23–26In principle, correlated wavefunction theories that include the correct many-body physics hold promise for computational surface science. In practice, however, their applicability is often hindered by the high computational cost required to reach convergence with respect to the one-particle basis set size, the supercell and slab size, and the level of electron correlation treatment. In this work, we focus on CO adsorption on the MgO (001) surface, which is an extensively studied model system for high levels of theory.16,17,27,28 Recently, Shi and co-workers17 applied coupled-cluster theory with singles, doubles, and perturbative triples29 [CCSD(T)], commonly known as the “gold standard” of main-group quantum chemistry, within an embedded-cluster framework30 to produce their best estimate of the adsorption energy, −19.2 ± 1.0 kJ mol−1, which was in good agreement with that calculated by canonical periodic CCSD(T) and diffusion Monte Carlo, as well as the value estimated from temperature-programmed desorption experiments11 (about −20.0 kJ mol−1).
In a preprint version of the present manuscript,31 we applied our recently developed periodic local CCSD(T) method32,33 to calculate an adsorption energy in good agreement with the above values. Due to the use of local correlation theory and recent developments in periodic integral evaluation34–36 and correlation-consistent Gaussian basis sets,37 these calculations were relatively affordable: they were generated from scratch in a few days, requiring about 18k CPU hours. Because of this low cost, we now extend our work to calculate a smooth, two-dimensional PES for CO on MgO, from which we calculate the vibrational frequency shift of CO stretching upon adsorption to be +14.7 cm−1, which is in nearly quantitative agreement with the infrared experimental result38 of +14.3 cm−1. Using the CCSD(T) PES, we assess the accuracy of lower-level wavefunction theories and various DFT protocols that combine commonly used exchange–correlation functionals and dispersion corrections with respect to the calculated binding curve (Section III B) and vibrational frequency shift of CO stretching upon adsorption (Section III C). We find that none of the tested DFT protocols can achieve high accuracy in both the binding energy and the vibrational frequency. By contrast, MP2 reproduces the entire CCSD(T) PES within about 1 kJ mol−1 and the vibrational frequency shift within about 1 cm−1, while CCSD performs slightly worse with an error of about 4 kJ mol−1 and 3 cm−1, respectively. We conclude the work in Section IV with a discussion on potential future developments.
II. Computational details
The system being studied is shown in Fig. 1A. A CO molecule is adsorbed with its C end on a five-fold coordinated Mg site of the pristine MgO (001) surface. The physisorption results in only slight perturbations to the surface and negligible change of the CO bond length. We model the surface using a two-layer MgO slab, which is sufficient to converge the calculated adsorption energy to accuracy within 0.3 kJ mol−1 (Table S5†). The equilibrium geometries for CO, MgO, and MgO + CO are obtained using DFT with the Perdew–Burke–Ernzerhof (PBE) functional41 and the D3 dispersion correction42 using Quantum Espresso.43,44 Atoms in the bottom layer of the MgO slab are fixed during geometry optimization.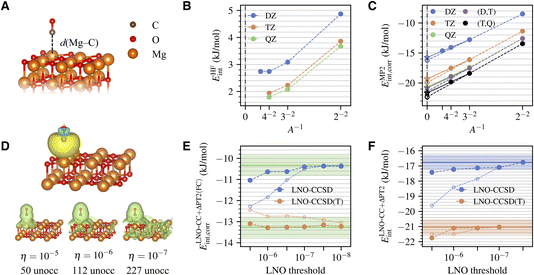 | ||
| Fig. 1 (A) Atomic structures of a CO molecule physically adsorbed on a MgO (001) surface. The Mg–C distance is highlighted. (B) Convergence of the HF interaction energy with surface and basis set sizes. (C) Convergence of the correlation part of the MP2 interaction energy with surface and basis set sizes. The TDL results estimated by extrapolating the surface size with A = 2 × 2 and 3 × 3 and with A = 3 × 3 and 4 × 4 are shown as dashed and solid lines, respectively. The CBS results from (DZ,TZ) and (TZ,QZ) extrapolation are also shown. (D) Isosurface plot of a representative localized occupied orbital on the CO molecule (obtained using the generalized Pipek–Mezey method39,40) and the density of the corresponding unoccupied LNOs with tightening truncation threshold η (generated for a 3 × 3 surface using the TZ basis set). The number of unoccupied LNOs are listed at the bottom, which is only a fraction of the total number of unoccupied orbitals, 1083. (E) Convergence of the correlation part of the frozen-core LNO-CCSD/CCSD(T) interaction energy with the LNO truncation threshold η for a 2 × 2 surface with (DZ,TZ)-extrapolated CBS limit. Both the regular LNO-CCSD/CCSD(T) results (hollow circles) and those corrected using eqn (7) (filled circles) are shown. The corrected LNO-CCSD/CCSD(T) interaction energies are seen to converge much faster to the canonical CCSD/CCSD(T) results, as indicated by the green horizontal line (the shaded area indicates an error of ±0.5 kJ mol−1). (F) Convergence of the correlation part of the final LNO-CCSD/CCSD(T) interaction energy with the LNO truncation threshold η. The (DZ,TZ) extrapolated CBS limit is employed. Results from two different schemes for the TDL extrapolation, A = 2 × 2 and 3 × 3 (filled circles) and A = 3 × 3 and 4 × 4 (hollow circles), agree well at convergence. The converged LNO-CCSD/CCSD(T) values are indicated by the solid horizontal line, with the shaded area indicating an error of ±0.5 kJ mol−1. | ||
We calculate the adsorption energy of CO on MgO as follows
| Eads = Eint + Δgeom | (1) |
All wavefunction calculations are performed with the PySCF code.45,46 The GTH-cc-pVXZ basis sets,37 augmented by diffuse functions for the CO molecule and nearby surface atoms, are employed with the GTH pseudopotential optimized for HF.47–49 All interaction energies are corrected for basis set superposition error. The two-electron integrals are treated by the range-separated density fitting algorithm,34,35 and the integrable divergence of the HF exchange is treated using a Madelung constant correction.50–52 The O(N6)/O(N7) cost scaling of canonical CCSD/CCSD(T) is avoided by a periodic extension of the local natural orbital (LNO) approximation, which we have recently applied to study the dissociation of water on the surface of Al2O3 and TiO2.32 Our periodic implementation, detailed in ref. 32, closely follows the molecular LNO-CCSD/CCSD(T) originally developed by Kállay and co-workers.53,54 We calculate the correlation energy of a supercell containing N electrons as a sum of contributions from all N localized occupied orbitals i,
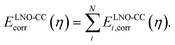 | (2) |
| ELNO-CC+ΔPT2corr(η) = EMP2corr + ΔELNO-CCcorr(η) | (3) |
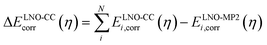 | (4) |
III. CO on MgO (001) surface
A. Equilibrium adsorption energy
We first validate our periodic LNO-CC methodology by calculating the equilibrium adsorption energy Eads for a single CO molecule adsorbed on the MgO (001) surface. Reference values of Eads can be derived from the desorption activation energy measured by temperature-programmed desorption experiments.9–11 This was done earlier by Boese and Sauer16 who obtained a reference value of −20.6 ± 2.4 kJ mol−1 based on the experimental work by Dohnálek et al.,11 and more recently by Shi and co-workers17 who derived a modified value of −19.2 ± 1.0 kJ mol−1 by averaging two experimental results.9,11 A correct theoretical prediction of Eads, however, necessitates the use of correlated wavefunction methods. Boese and Sauer16 employed cluster-based MP2-in-DFT embedding and found an Eads of −20.9 ± 0.7 kJ mol−1, and Shi and co-workers17 calculated Eads using embedded-cluster LNO-CCSD(T) to be −19.2 ± 1.0 kJ mol−1. Clearly, both values are in good agreement with experimental estimates.We revisit this problem to establish a protocol to achieve sub-kJ mol−1 accuracy for the CCSD(T) interaction energy. We use a fixed d(Mg–C) = 2.460 Å for this purpose, which also facilitates comparison with previous works.16,17,28,55 Using eqn (3), the CC interaction energy can be calculated as
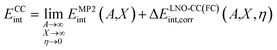 | (5) |
The MP2 interaction energy can be further decomposed as a sum of the HF part (EHFint) and the MP2 correlation part (EMP2int,corr). Fig. 1B shows the convergence of EHFint(A,X). We see that using a 4 × 4 surface and a QZ basis set essentially attains both the TDL and the CBS limit, giving EHFint(A∞,X∞) ≈ 1.8 ± 0.1 kJ mol−1, where half the difference between TZ and QZ results is taken as an estimate of the remaining basis set incompleteness error. Fig. 1C shows the convergence of EMP2int,corr(A,X), which is slower than that of EHFint(A,X) in both parameters. However, reliable extrapolations to both limits can be performed based on the asymptotic behaviors
| EMP2int,corr(A,X) ≈ EMP2int,corr(A∞,X) + c1A−1 | (6a) |
| EMP2int,corr(A,X) ≈ EMP2int,corr(A,X∞) + c2X−3 | (6b) |
Transitioning to CC, we first show in Fig. 1E the η-convergence of ELNO-CC+ΔPT2(FC)int,corr(A,X,η), extrapolated to the CBS limit based on DZ and TZ results for a 2 × 2 surface. The system is small enough (about 650 orbitals in the TZ basis set) to allow performing canonical CC calculations, whose results are also shown in Fig. 1E for comparison. We see that the error of LNO-CCSD(T) (orange hollow circles) drops fast to 0.5 kJ mol−1 with a modest threshold of 10−6, but achieving a similar accuracy in LNO-CCSD (blue hollow circles) requires a tighter threshold of 10−7. While LNO-CC calculations with a tight threshold of 10−7 are feasible for larger systems, a more efficient alternative is to correct the LNO-CC results by the difference from an inexpensive canonical CC calculation using DZ basis set and 2 × 2 surface, which we denoted as
| ΔCC(FC)(η) = ECC(FC)int,corr(2 × 2,DZ) − ELNO-CC(FC)int,corr(2 × 2,DZ,η) | (7) |
To obtain our final estimate of the CC interaction energy using eqn (5), we extrapolate ΔELNO-CC(FC)int,corr(A,X,η) to the TDL and the CBS limit using A = 2 × 2 and 3 × 3 and the DZ and TZ basis sets, and add this number to the converged EMP2int determined above. The resulting η-dependent LNO-CC interaction energy is then converged with respect to η (Fig. 1F). Our best estimate of the CCSD and CCSD(T) interaction energy, obtained with η = 10−7, is −16.8 ± 0.5 kJ mol−1 and −21.0 ± 0.5 kJ mol−1, where the error bar combines that of EMP2int (0.3 kJ mol−1), of ΔCC(FC) (0.2 kJ mol−1), and of the LNO truncation error which is estimated to be 0.3 kJ mol−1 using the difference between the two LNO-CCSD calculations with the tightest thresholds shown in Fig. 1F.
Our final numbers for the HF, MP2, CCSD, and CCSD(T) Eads are summarized in Table 1, where they are compared to both the experimental reference and other computational results from literature. Compared to ref. 17, our periodic Gaussian-based approach shows sub-kJ mol−1 agreement with the embedded-cluster approach for both the MP2 and CCSD(T) adsorption energy, and a slightly worse agreement of 2 kJ mol−1 with the periodic plane-wave CCSD and CCSD(T), likely due to the larger error bar associated with the latter. Given the use of slightly different geometries and different strategies to attain convergence along the necessary theoretical axes, the level of agreement achieved between our work and ref. 17 is remarkable. Our final CCSD(T) adsorption energy, −20.0 ± 0.5 kJ mol−1, also agrees well with corrected16,17 temperature-programmed desorption experimental results.9,11 By contrast, insufficient convergence along one or more of the theoretical axes can lead to significant errors in the calculated interaction energy,28,55 which has been discussed thoroughly in previous work.17
| Method | Comput. detailsa | E ads (kJ mol−1) | Reference |
|---|---|---|---|
| a Gaussian-type orbital (GTO), plane wave (PW), frozen natural orbital (FNO), diffusion Monte Carlo (DMC). b Based on TPD experiments in ref. 11. c Based on TPD experiments in ref. 9 and 11. | |||
| HF | Periodic/GTO | +2.9 ± 0.1 | This work |
| MP2 | Periodic/GTO | −18.8 ± 0.3 | |
| CCSD | Periodic/GTO/LNO | −15.7 ± 0.5 | |
| CCSD(T) | Periodic/GTO/LNO | −20.0 ± 0.5 | |
| MP2 | Cluster/GTO | −18.5 ± 0.5 | Ref. 17 |
| CCSD(T) | Cluster/GTO/LNO | −19.2 ± 0.6 | |
| CCSD | Periodic/PW/FNO | −14.0 ± 2.1 | |
| CCSD(T) | Periodic/PW/FNO | −18.6 ± 2.1 | |
| DMC | Periodic | −18.1 ± 2.3 | |
| Experiments | −20.6 ± 2.4b | Ref. 16 | |
| −19.2 ± 1.0c | Ref. 17 | ||
B. Full binding curve
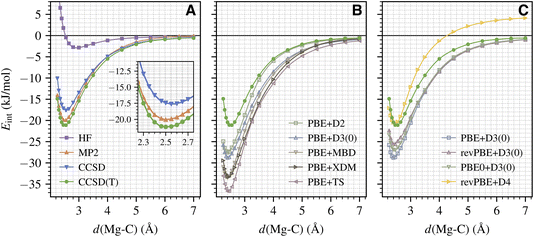
We now employ the established protocol to calculate the full binding curve for CO adsorption on the MgO (001) surface. An accurate binding curve is important for understanding the adsorption/desorption dynamics,56 which can be directly related to molecular beam experiments.1 Here, we focus on calculating the variation of Eint as a function of d(Mg–C) (with atoms in the surface kept frozen). The results from the wavefunction methods discussed in Section III A are shown in Fig. 2A. We see that our protocol generates smooth energy curves for all methods including CCSD(T). This is remarkable given the small energy scale involved here (about 2 kJ mol−1 near equilibrium; see the inset of Fig. 2A) and highlights the extremely high fidelity of our periodic LNO-CCSD(T) methodology. Performance-wise, CCSD and MP2 underestimate the CCSD(T) binding energy by about 4 and 1 kJ mol−1 for a wide range of d(Mg–C) near the equilibrium geometry, which is consistent with the trend discussed in Section III A for the equilibrium Eads. All three methods smoothly approach the correct dissociation limit. Interestingly, the HF binding curve does show a shallow well of about −3 kJ mol−1 at a large d(Mg–C) of nearly 3 Å.Armed with CCSD(T) results, we can now assess the performance of different DFT methods. Fig. 2B presents the binding curves obtained using the PBE functional with five popular dispersion correction models: the exchange-hole dipole moment (XDM) model,57 the Tkatchenko–Scheffler (TS) model,58 the many-body dispersion (MBD) model,59 and two different generations of Grimme's DFT-D model (D2 (ref. 60) and D3 (ref. 42)). We see that all five DFT protocols significantly overestimate the equilibrium binding energy by about 6 kJ mol−1 (D2) to 16 kJ mol−1 (TS) and predict the equilibrium Mg–C separation to be too small by 5–10 pm. To investigate the effect of different exchange–correlation functionals, in Fig. 2C we present binding curves calculated using PBE and its two extensions, revPBE61 and PBE0,62 all corrected by the D3 dispersion correction. It is evident that both revPBE and PBE0 ameliorate PBE's overbinding behavior, but the improvement is way too small. As seen in Fig. 2C, we find that revPBE+D4 (ref. 63) gives the best performance near the equilibrium geometry, in agreement with ref. 17, but the D4 dispersion energy does not decay properly to zero in the dissociation limit.
C. Frequency shift of CO stretching
We now employ the established protocol to calculate the vibrational frequency of CO on the MgO (001) surface. Experimentally, this has been measured by infrared spectroscopy38 to be νCO(ads) = 2157.5 cm−1. Compared to the gas-phase frequency of νCO(g) = 2143.2 cm−1, this corresponds to a positive vibrational frequency shift ΔνCO = νCO(ads) − νCO(g) = 14.3 cm−1. Such frequency shifts are commonly used for probing both the structural and electronic information of a surface.10,64 Accurately resolving such a small frequency shift serves as a stringent test for electronic structure theory.A minimal theoretical description necessitates calculating a two-dimensional potential energy surface for the CO bond length d(C–O) and the surface–CO distance, chosen here to be D(Mg–CO), the distance between the CO center of mass and the surface Mg atom (the surface is kept frozen at its equilibrium geometry following previous work65). We calculate this two-dimensional PES using various electronic structure methods by performing a series of single-point calculations over a total of 130 different geometries and fitting the resulting energy data using a sixth-order polynomial. The fitting error is found to be less than 0.5 kJ mol−1 for all electronic structure methods discussed below. We then extract νCO(ads) in the harmonic approximation from the second derivatives of the fitted PES. We calculate νCO(g) in a similar manner from a one-dimensional PES of d(C–O) for a free CO molecule. See the ESI for more details.†
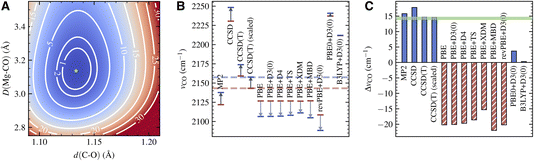
The PES for the surface adsorbed CO obtained using LNO-CCSD(T) is shown in Fig. 3A. The contour of the PES displays a characteristic elliptical shape for the coupling of a strong vibrational mode to a weak one. From the PES of the adsorbed CO and that of a free CO (not shown), we extract νCCSD(T)CO(ads) = 2173.9 cm−1 and νCCSD(T)CO(g) = 2159.2 cm−1, both of which are about 16 cm−1 higher than the experimentally observed frequencies. As a result, the frequency shift predicted by CCSD(T), ΔνCCSD(T)CO = 14.7 cm−1, is in quantitative agreement with experiment, with an error less than 0.5 cm−1. From a practical point of view, the harmonic CCSD(T) overestimation of vibrational frequencies of small molecules is well known and usually corrected by applying an empirical scaling factor.66,67 The nearly perfect agreement between the computational and experimental ΔνCO thus indicates a highly transferrable scaling factor for CO in gas and condensed phases. Indeed, applying the scaling factor 0.9926 determined by our gas-phase calculation and the experiment, we obtain a scaled vibrational frequency for adsorbed CO, νCCSD(T)-scaledCO(ads) = 2157.8 cm−1, which agrees nearly perfectly with the experimental frequency.
The CCSD(T) frequency and frequency shift discussed above are displayed in Fig. 3B and C. In the same plots, we also show the absolute frequency and frequency shift predicted by several different electronic structure methods. MP2 slightly underestimates νCO(ads) by about 20 cm−1, while CCSD overestimates it by about 90 cm−1. However, both methods also predict a similar trend for νCO(g), making their frequency shift, 15.8 cm−1 from MP2 and 17.8 cm−1 from CCSD, in reasonable agreement with the experiment.
In contrast, DFT with semilocal functionals, such as PBE and revPBE, predicts a large negative ΔνCO ranging from −15 to −20 cm−1, regardless of the dispersion correction being used (Fig. 3C). This qualitative error is caused by the imbalanced error in the adsorbed and gas-phase calculations: while both νCO(ads) and νCO(g) are underestimated, the former is underestimated to a much larger extent (Fig. 3B), likely due to a larger delocalization error in condensed-phase systems. Improvement is seen by using hybrid functionals such as PBE0 and B3LYP, which suffer less from the delocalization error due to partial inclusion of the HF exchange energy.68 However, the predicted ΔνCO, 3.7 cm−1 from PBE0+D3(0) and 0.3 cm−1 from B3LYP + D3(0), are still too small compared to the experiment. Despite having qualitatively correct shapes, the PESs obtained using these DFT methods exhibit clear quantitative deviations from the CCSD(T) PES (Fig. S5†). This highlights the challenge for achieving spectroscopic accuracy for vibrations of adsorbed molecules with commonly used DFT methods.
IV. Conclusion
To summarize, we computationally studied the adsorption of a single CO molecule on the MgO (001) surface using the “gold-standard” method of quantum chemistry, CCSD(T), made possible by our recently developed periodic LNO-CCSD(T) method. After validating our method using the equilibrium adsorption energy, we leverage the low computational cost and high fidelity of LNO-CCSD(T) to calculate a smooth, two-dimensional PES for CO on MgO, from which we extract the vibrational frequencies and frequency shift of CO stretching upon adsorption, finding quantitative agreement with infrared spectroscopy. Using the CCSD(T) PES, we assess the accuracy of lower-level wavefunction theories and various DFT protocols that combine commonly used exchange–correlation functionals and dispersion corrections. We find that none of the tested DFT protocols can achieve high accuracy in both the binding energy and the vibrational frequency. By contrast, MP2 reproduces the entire CCSD(T) PES quite accurately, while CCSD performs slightly worse but still qualitatively correctly.The ability to generate a smooth PES with high accuracy is a longstanding challenge in computational surface science for benchmarking and improving lower-level theories like DFT1,14,56,69,70 and more recently, for training high-quality machine learning potentials that enable accurate ab initio molecular dynamics study of surface reactions.18,20,21 For insulating and semiconducting surfaces with weak electron correlation, the smooth and accurate PESs attainable through our periodic local CCSD(T) method are thus very promising to fulfill both goals. But for chemistry on the surface of metals or strongly correlated solids, for which CCSD(T) is inapplicable,71–76 new methods are sorely needed.
Conflicts of interest
The authors declare no competing conflicts of interest.Acknowledgements
This work was supported by the National Science Foundation under Grant No. CHE-1848369 and by the Columbia Center for Computational Electrochemistry. We acknowledge computing resources from Columbia University's Shared Research Computing Facility project, which is supported by NIH Research Facility Improvement Grant 1G20RR030893-01, and associated funds from the New York State Empire State Development, Division of Science, Technology and Innovation (NYSTAR) Contract C090171, both awarded April 15, 2010.References
- G.-J. Kroes, Phys. Chem. Chem. Phys., 2021, 23, 8962 RSC
.
- T.-N. Ye, S.-W. Park, Y. Lu, J. Li, J. Wu, M. Sasase, M. Kitano and H. Hosono, J. Am. Chem. Soc., 2021, 143, 12857 CrossRef CAS PubMed
.
- K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T.-H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724 CrossRef CAS PubMed
.
- O. T. Qazvini, R. Babarao and S. G. Telfer, Nat. Commun., 2021, 12, 197 CrossRef CAS PubMed
.
- M. Chang, T. Yan, Y. Wei, J.-X. Wang, D. Liu and J.-F. Chen, Chem. Mater., 2022, 34, 9134 CrossRef CAS
.
- A. W. Kleyn, Chem. Soc. Rev., 2003, 32, 87 RSC
.
- Z.-T. Wang, Y.-G. Wang, R. Mu, Y. Yoon, A. Dahal, G. K. Schenter, V.-A. Glezakou, R. Rousseau, I. Lyubinetsky and Z. Dohnálek, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1801 CrossRef CAS PubMed
.
- J. L. Falconer and J. A. Schwarz, Catal. Rev. Sci. Eng., 1983, 25, 141 CrossRef CAS
.
- R. Wichtendahl, M. Rodriguez-Rodrigo, U. Härtel, H. Kuhlenbeck and H.-J. Freund, Phys. Status Solidi A, 1999, 173, 93 CrossRef CAS
.
- M. Sterrer, T. Risse and H.-J. Freund, Appl. Catal., A, 2006, 307, 58 CrossRef CAS
.
- Z. Dohnálek, G. A. Kimmel, S. A. Joyce, P. Ayotte, R. S. Smith and B. D. Kay, J. Phys. Chem. B, 2001, 105, 3747 CrossRef
.
- L. Zhang, C. Tian, G. A. Waychunas and Y. R. Shen, J. Am. Chem. Soc., 2008, 130, 7686 CrossRef CAS PubMed
.
- F. M. Geiger, Annu. Rev. Phys. Chem., 2009, 60, 61 CrossRef CAS PubMed
.
- L. Schimka, J. Harl, A. Stroppa, A. Grüneis, M. Marsman, F. Mittendorfer and G. Kresse, Nat. Mater., 2010, 9, 741 CrossRef CAS PubMed
.
- J. Sauer, Acc. Chem. Res., 2019, 52, 3502 CrossRef CAS PubMed
.
- A. D. Boese and J. Sauer, Phys. Chem. Chem. Phys., 2013, 15, 16481 RSC
.
- B. X. Shi, A. Zen, V. Kapil, P. R. Nagy, A. Grüneis and A. Michaelides, J. Am. Chem. Soc., 2023, 145, 25372 CrossRef CAS PubMed
.
- L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed
.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142 CrossRef CAS PubMed
.
- B. Wen, M. F. C. Andrade, L.-M. Liu and A. Selloni, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2212250120 CrossRef CAS PubMed
.
- Z. Zeng, F. Wodaczek, K. Liu, F. Stein, J. Hutter, J. Chen and B. Cheng, Nat. Commun., 2023, 14, 6131 CrossRef CAS PubMed
.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef
.
- A. J. R. Hensley, K. Ghale, C. Rieg, T. Dang, E. Anderst, F. Studt, C. T. Campbell, J.-S. McEwen and Y. Xu, J. Phys. Chem. C, 2017, 121, 4937 CrossRef CAS
.
- F. R. Rehak, G. Piccini, M. Alessio and J. Sauer, Phys. Chem. Chem. Phys., 2020, 22, 7577 RSC
.
- E. W. F. Smeets and G.-J. Kroes, J. Phys. Chem. C, 2021, 125, 8993 CrossRef CAS PubMed
.
- G. Meng, R. Yin, X. Zhou and B. Jiang, J. Phys. Chem. C, 2021, 125, 24958 CrossRef CAS
.
- M. Alessio, D. Usvyat and J. Sauer, J. Chem. Theory Comput., 2019, 15, 1329 CrossRef CAS PubMed
.
- A. Mitra, M. R. Hermes, M. Cho, V. Agarawal and L. Gagliardi, J. Phys. Chem. Lett., 2022, 13, 7483 CrossRef CAS PubMed
.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS
.
- B. X. Shi, V. Kapil, A. Zen, J. Chen, A. Alavi and A. Michaelides, J. Chem. Phys., 2022, 156, 124704 CrossRef CAS PubMed
.
- H.-Z. Ye and T. C. Berkelbach, arXiv, 2023, preprint, arXiv:2309.14651v2, DOI:10.48550/arXiv.2309.14651.
- H.-Z. Ye and T. C. Berkelbach, arXiv, 2023, preprint, arXiv:2309.14640, DOI:10.48550/arXiv.2309.14640.
- H.-Z. Ye and T. C. Berkelbach, arXiv, 2024, preprint, arXiv:2407.11258, DOI:10.48550/arXiv.2407.11258.
- H.-Z. Ye and T. C. Berkelbach, J. Chem. Phys., 2021, 154, 131104 CrossRef CAS PubMed
.
- H.-Z. Ye and T. C. Berkelbach, J. Chem. Phys., 2021, 155, 124106 CrossRef CAS PubMed
.
- S. J. Bintrim, T. C. Berkelbach and H.-Z. Ye, J. Chem. Theory Comput., 2022, 18, 5374 CrossRef CAS PubMed
.
- H.-Z. Ye and T. C. Berkelbach, J. Chem. Theory Comput., 2022, 18, 1595 CrossRef CAS PubMed
.
- G. Spoto, E. Gribov, A. Damin, G. Ricchiardi and A. Zecchina, Surf. Sci., 2003, 540, L605 CrossRef CAS
.
- J. Pipek and P. G. Mezey, J. Chem. Phys., 1989, 90, 4916 CrossRef CAS
.
- S. Lehtola and H. Jónsson, J. Chem. Theory Comput., 2014, 10, 642 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed
.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed
.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340 Search PubMed
.
- Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen, Z.-H. Cui, J. J. Eriksen, Y. Gao, S. Guo, J. Hermann, M. R. Hermes, K. Koh, P. Koval, S. Lehtola, Z. Li, J. Liu, N. Mardirossian, J. D. McClain, M. Motta, B. Mussard, H. Q. Pham, A. Pulkin, W. Purwanto, P. J. Robinson, E. Ronca, E. R. Sayfutyarova, M. Scheurer, H. F. Schurkus, J. E. T. Smith, C. Sun, S.-N. Sun, S. Upadhyay, L. K. Wagner, X. Wang, A. White, J. D. Whitfield, M. J. Williamson, S. Wouters, J. Yang, J. M. Yu, T. Zhu, T. C. Berkelbach, S. Sharma, A. Y. Sokolov and G. K.-L. Chan, J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed
.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS PubMed
.
- C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641 CrossRef CAS
.
-
J. Hutter, New optimization of GTH pseudopotentials for PBE, SCAN, PBE0 functionals. GTH pseudopotentials for Hartree-Fock. NLCC pseudopotentials for PBE, 2019, https://github.com/juerghutter/GTH Search PubMed
.
- J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, J. Chem. Phys., 2006, 124, 154709 CrossRef CAS PubMed
.
- P. Broqvist, A. Alkauskas and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 085114 CrossRef
.
- R. Sundararaman and T. A. Arias, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165122 CrossRef
.
- Z. Rolik and M. Kállay, J. Chem. Phys., 2011, 135, 104111 CrossRef PubMed
.
- Z. Rolik, L. Szegedy, I. Ladjánszki, B. Ladóczki and M. Kállay, J. Chem. Phys., 2013, 139, 094105 CrossRef PubMed
.
- A. Mazheika and S. V. Levchenko, J. Phys. Chem. C, 2016, 120, 26934 CrossRef CAS
.
- E. W. F. Smeets, J. Voss and G.-J. Kroes, J. Phys. Chem. A, 2019, 123, 5395 CrossRef CAS PubMed
.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 122, 154104 CrossRef PubMed
.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed
.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed
.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed
.
- Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS
.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS
.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed
.
- J. B. Benziger and L. Larson, J. Catal., 1982, 77, 550 CrossRef CAS
.
- N. He, M. Huang and F. A. Evangelista, J. Phys. Chem. A, 2023, 127, 1975 CrossRef CAS PubMed
.
- A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502 CrossRef CAS
.
- D. P. Tew, W. Klopper, M. Heckert and J. Gauss, J. Phys. Chem. A, 2007, 111, 11242 CrossRef CAS PubMed
.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315 CrossRef CAS
.
- J. M. Boereboom, M. Wijzenbroek, M. F. Somers and G. J. Kroes, J. Chem. Phys., 2013, 139, 244707 CrossRef CAS PubMed
.
- T. Tchakoua, E. W. F. Smeets, M. Somers and G.-J. Kroes, J. Phys. Chem. C, 2019, 123, 20420 CrossRef CAS
.
- M. Motta, C. Genovese, F. Ma, Z.-H. Cui, R. Sawaya, G. K.-L. Chan, N. Chepiga, P. Helms, C. Jiménez-Hoyos, A. J. Millis, U. Ray, E. Ronca, H. Shi, S. Sorella, E. M. Stoudenmire, S. R. White and S. Zhang, (Simons Collaboration on the Many-Electron Problem), Phys. Rev. X, 2020, 10, 031058 CAS
.
- M. S. Church and B. M. Rubenstein, J. Chem. Phys., 2021, 154, 184103 CrossRef CAS PubMed
.
- J. Lee, H. Q. Pham and D. R. Reichman, J. Chem. Theory Comput., 2022, 18, 7024 CrossRef CAS PubMed
.
- T. N. Mihm, T. Schäfer, S. K. Ramadugu, L. Weiler, A. Grüneis and J. J. Shepherd, Nat. Comput. Sci., 2021, 1, 801 CrossRef PubMed
.
- V. A. Neufeld and T. C. Berkelbach, Phys. Rev. Lett., 2023, 131, 186402 CrossRef CAS PubMed
.
- N. Masios, A. Irmler, T. Schäfer and A. Grüneis, Phys. Rev. Lett., 2023, 131, 186401 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00041b |
| This journal is © The Royal Society of Chemistry 2024 |