Open Access Article
Open Access ArticleA new concept for correction of instrumental isotopic fractionation in MC-ICP-MS using a pair of monoisotopic elements: a critical evaluation†
Andrii
Tupys
a,
Klaudia
Tetfejer
a,
Ludwik
Halicz
ab,
Ewa
Bulska
 a and
Jakub
Karasiński
a and
Jakub
Karasiński
 *a
*a
aFaculty of Chemistry, Biological and Chemical Research Centre, University of Warsaw, 101 Żwirki i Wigury St., 02-089 Warsaw, Poland. E-mail: jkarasinski@cnbc.uw.edu.pl
bGeological Survey of Israel, 32 Yeshayahu Leibowitz St., Jerusalem 9692100, Israel
First published on 30th October 2024
Abstract
In this research work, we investigated the possibility of using mixtures of monoisotopic elements (93Nb/89Y, 165Ho/159Tb and 209Bi/197Au) as calibrators for accurate determination of isotope ratios by multicollector mass spectrometry (MC-ICP-MS). The potential advantage of using monoisotopic elements for calibration lies in their significantly lower uncertainty in atomic masses. This would certainly affect the uncertainty of a measured isotope ratio after data processing, particularly if absolute isotope ratios are being evaluated. Model isotopic systems (87Sr/86Sr–93Nb/89Y, 92Zr/90Zr–93Nb/89Y, 208Pb/207Pb–209Bi/197Au and 167Er/166Er–165Ho/159Tb) were selected and the Internal Standard method (Russell's law) and optimized regression model (ORM) for isotope measurements, using the mentioned mixtures of monoisotopic elements as calibrators, were applied. The precision and trueness of the obtained results were assessed. For example, the 167Er/166Er isotope ratio in a certified reference material of erbium was measured using a gravimetric mixture of Ho and Tb as well as a 160Gd/158Gd pair (NRC GADS-1) as instrumental isotopic fractionation (IIF) calibrators in ORM. Although the average result for both approaches was in the range of instrumental error (0.68223 ± 0.00351 with 165Ho/159Tb and 0.68236 ± 0.00034 with 160Gd/158Gd), the precision was ten times lower when a mixture of monoisotopic elements was used for correction. Based on the results obtained, it was assessed that Russell's law does not provide a correct description for systems with a mixture of two monoisotopic elements, probably due to the assumption of equal IIF for the analyte and internal calibrator. In our opinion, such an assumption is not true in a system when the internal calibrator is a pair of two different elements. A new mathematical description of such a system could enable the introduction of a suitable correction. The ORM method is free from assumptions about the same IIF for individual chemical entities and for this reason it looks more encouraging and shows the potential to be useable even with a mixture of monoisotopic elements as calibrators. In this paper we present experimental results confirming this assumption, although the current challenge is to ensure a sufficiently high precision of calibrator ratio measurement and, consequently, better regression linearity and higher precision of the obtained results.
Introduction
Interest in the isotopes of elements and their abundances has been continuously growing in the last few centuries. Although isotope amount ratio measurements can be performed using techniques other than mass spectrometry, such as gravimetry, nuclear magnetic resonance (NMR) spectroscopy or infrared (IR) spectroscopy, the use of these methods is rare. Since the mid-twentieth century, in fact, mass spectrometry has become the de facto method for isotope amount ratio measurements and hence the need for calibration of isotope amount ratio measurements remains a state-of-the-art activity.Natural isotopic fractionation occurs with low intensity for non-traditional stable isotopes. For this reason, natural differences in isotopic composition are very slight, and thus it is necessary to maintain high precision of results to be able to distinguish the isotopic composition of the given element in the analyzed objects. The rapid development of technology has relatively recently enabled the construction of analytical instruments that allow measurement of natural isotope fractionation with satisfactory precision. That is why the analytical chemistry of isotope ratios is a relatively new area, but not a sufficiently explored branch of science. Fortunately, it has been developing very fast recently since the invention of multiple collector mass spectrometry with ionization in inductively coupled plasma (MC-ICP-MS) which is now accepted as a gold standard in providing reliable isotope fractionation data.1,2 This technique offers efficient ionization, high mass resolution and high-precision measurements with relatively low sample consumption and high throughput. On the other hand, MC-ICP-MS requires the application of a very complex instrument, which is sensitive to memory effects, sample matrix composition and suffers from spectral interferences.2 In fact, the most important limitation of the measurements performed with MC-ICP-MS is the necessity to correct the disturbance in instrumental fractionation which causes the measured isotope ratio to never equal the actual value.
For monoisotopic elements, the atomic mass is simply the mass of the single naturally occurring isotope. There is no need to account for the relative abundances and atomic masses of multiple isotopes, which simplifies the determination process. Moreover, in polyisotopic elements, variations in natural isotopic abundances due to isotopic fractionation can introduce uncertainty. Monoisotopic elements do not have this issue, reducing potential sources of error. IIF corrections used in accurate isotope ratio measurements often rely on reference standards whose isotopic compositions and atomic masses are well-characterized. Any uncertainty in the atomic mass of these standards propagates through to the measurements of samples calibrated against them. In addition correction for this bias requires knowledge of the accurate atomic masses. Uncertainty in atomic masses thus propagates into uncertainty in the corrected isotope ratios. It is also worth mentioning that statistical methods used to process and interpret isotopic data often depend on the precision of the input values, including atomic masses. Uncertainty in atomic masses can introduce additional variability in statistical analyses, thereby increasing the overall uncertainty in isotope ratio measurements.
Over the last few decades, various IIF correction methodologies have been used for the determination of isotope amount ratios.3–5 However, it should be noted that for some elements none of those methods can be applied, due to them not possessing at least 4 isotopes (double spike model) or having no neighboring element with a close atomic mass that could be used as a calibrator (Internal Standard or regression model). That is why for such elements, e.g., magnesium, there is no other possibility but to use the standard-sample bracketing (SSB) isotopic fractionation correction model.6 However, this model also has its advantages and limitations. Correctly performed calibration of this type allows results with high trueness and precision to be obtained. Additionally, since each isotope ratio is corrected separately, mass independent fractionation (MIF) has no effect on the accuracy of this model.5 The main limitation of SSB is the need to perfectly match the matrix between the standard and the sample, which is often difficult (due to the difficulty in isolating a sufficiently pure fraction of the analyzed element, e.g., Mg). Failure to meet this condition usually gives results subject to systematic error.
The second calibration strategy that is most frequently used is the inter-elemental internal calibration, also known as the Internal Standard (IS) model. It requires the addition of a foreign element to the sample.7–9 In some cases intra-elemental internal calibration (e.g., Sr) can be carried out, but the number of isotope pairs with a known and stable ratio is limited, so there is no other possibility but to check for neighboring elements as calibrators. This model is based on an assumption that both the analyte and calibrator undergo the same mass discrimination in the instrument,5 which in most cases is not exactly correct. This drawback is solved in the third and the most state-of-the-art method for IIF correction – the optimized regression model (ORM).10–13 It utilizes the significant temporal correlated drift of the IIF of both elements when using MC-ICP-MS and turns this adverse phenomenon into an advantage. The only shortcoming of this correction model is that it is time-consuming. The combination of IS or ORM models with SSB provides even better results of IIF correction, and was successfully used by our research group.14,15
Still in both combined correction strategies (IS-SSB and ORM-SSB) the application of the isotopic pair of known isotopic ratios is required. For some analytes it is not difficult to find an appropriate neighboring element (Tl for Pb;7 Br, Rb or Sr for Se,14etc.). However, there are some opposite elements in the periodic table, e.g., Mg or Ba, that do not have any options of calibrators with a close atomic mass. Consequently, for several elements there is no certified isotopic reference standard with established absolute isotope ratios approved by the IUPAC Commission on Isotopic Abundances and Atomic Weights (CIAAW).16 So no calibrated absolute isotope ratio measurements can be carried out for them on MC-ICP-MS using a second element as a calibrator. This is one of the key problems that limit the further development of analytical chemistry of isotope ratios. Although some efforts have been made recently to overcome this limitation, e.g., by the application of the triple-isotope calibration approach,17,18 this problem is still far from being solved.
In this work a completely new (according to our knowledge) strategy for accurate measurements of isotope ratios without referring to isotopic standards will be tested. Ultimately this will be achieved through the use of gravimetric mixtures of monoisotopic elements as IIF calibrators in MC-ICP-MS. The possible mixtures of monoisotopic elements that can be used as calibrators in isotope ratio measurements are summarized in Table 1. A possible big advantage of using monoisotopic elements for calibration is their much lower uncertainty on the atomic masses, which would certainly have an impact on the uncertainty of a measured isotope ratio after data processing, especially if absolute isotope ratios are being assessed. We used mixtures of monoisotopic elements with a composition determined by calibration to verify if it is possible to use such mixtures as calibrators in the ORM method and the Internal Standard method.
| Studied elements | Fe | Sr or Zr | Dy or Er | Hg, Tl or Pb |
| Proposed calibrators | Mn and Co | Y and Nb | Tb, Ho or Tm | Au and Bi |
| Calibrators' atomic mass estimates19 | Mn 54.938043 ± 0.000002 | Y 88.905838 ± 0.000002 | Tb 158.925354 ± 0.000007 | Au 196.966570 ± 0.000004 |
Co 58.933![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 194 ± 0.000003 194 ± 0.000003 |
Nb 92.90637 ± 0.00001 | Ho 164.930329 ± 0.000005 | Bi 208.98040 ± 0.00001 | |
| Tm 168.934219 ± 0.000005 | ||||
| Possible spectral interferences20 | For Mn: 40Ar14N1H+, 39K16O+, 37Cl18O+, 40Ar15N+, 38Ar17O+, 36Ar18O1H+, 38Ar16O1H+, 37Cl17O1H+, 23Na32S+, 36Ar19F+ | For Y: 51V38Ar+, 53Cr36Ar+, 49Ti40Ar+, 73Ge16O+; 72Ge17O+, 71Ga18O+ | For Tb: 143Nd16O+ | For Au: 181Ta16O+ |
| For Co: 43Ca16O+, 42Ca16O1H+, 24Mg35Cl+, 36Ar23Na+, 40Ar18O1H+, 40Ar19F+ | For Nb: 55Mn38Ar+, 57Fe36Ar+, 53Cr40Ar+, 77Se16O+, 75As18O+ | For Ho: 149Sm16O+ | For Bi: 193Ir16O+ | |
| For Tm: 153Eu16O+ | ||||
| Faraday cup configuration | Not studied yet | H8 – 93Nb; H6 – 92Zr; H4 – 91Zr; H2 – 90Zr; Ax – 89Y; L2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) – 88Sr; L4 – 87Sr; L5 – 86Sr – 88Sr; L4 – 87Sr; L5 – 86Sr |
H8 – 170Er; H7 – 169Tm; H6 – 168Er; H5 – 167Er; H4 – 166Er; H3 – 165Ho; H2 – 164Er; L3 – 159Tb | H6 – 209Bi; H5 – 208Pb; H4 – 207Pb; H3 – 206Pb; H2 – 205Tl, H1 – 204Pb; Ax – 203Tl; L5 – 197Au |
| Intensity (dry plasma), V/10 ppb | — | Y – 5.0 | Tb – 6.7 | Au – 3.8 |
| Nb – 5.0 | Ho – 6.7 | Bi – 19 | ||
| Tm – 6.7 |
Internal Standard (IS) and Optimized Regression Model (ORM) calibration protocols were both used in parallel to find out whether any of these calibration methods allow the use of a gravimetric mixture of two monoisotopic elements as an internal calibrator (ORM). These calibration methods are known for their robustness and ability to correct for matrix effects,5,21,22 but the ORM method in particular may be attractive for this purpose because it is free from the assumptions burdening Russell's law, especially the assumption of uniformity of IIF for the calibrator and analyte.
Experimental
Standards
The following isotopic standards were used: SRM 987 (strontium isotopic standard, National Institute of Standards and Technology (NIST), Maryland, USA); ZIRC-1 (zirconium solution at 1000 mg kg−1 in 2% HNO3 and 0.1% HF; National Research Council (NRC), Ottawa, Canada); GADS-1 (gadolinium solution at 1000 mg kg−1 in 2% HNO3; NRC); SRM 981 (lead isotopic standard, NIST); SRM 997 (thallium isotopic standard, NIST). Also, the following reference materials certified for concentrations were applied: yttrium in 2% HNO3 (1000 μg mL−1, High-Purity Standards (HPS), North Charleston, SC); niobium in 2% HNO3 + 0.5% HF (1000 μg mL−1, HPS); terbium in 2% HNO3 (1000 μg mL−1, HPS); holmium in 2% HNO3 (1000 μg mL−1, HPS); erbium in 2% HNO3 (1000 μg mL−1, HPS). Strontium carbonate (isotopic standard NIST SRM 987) was dissolved in 3 mol L−1 nitric acid (Merck Suprapur®); NIST SRM 981 was also dissolved in nitric acid and diluted to approximately 40 μg L−1 Pb with 2% HNO3. The rest of the standards were readily available as solutions.The mixtures of monoisotopic elements were usually prepared by gravimetric weighing of corresponding single element standards (0.5 g each) in one vessel (usually a 1.5 mL tube, Eppendorf, Hamburg, Germany).
Instrumental setup
| RF power | 1300 W |
| Coolant flow (Ar) | 13 L min−1 |
| Auxiliary flow (Ar) | 1.1 L min−1 |
| Nebulizer gas (Ar) | 36.0 psi |
| Interference cones | Nickel |
| Resolution mode | Low (∼300) |
| Number of measurement blocks | 1 |
| Number of measurements in a block | 20 |
| Magnet delay time, s | 3 |
| Integration time, s | |
| – Zero measurement | 30 |
| – Sample measurement | 10 |
IIF correction
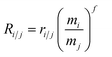 | (1) |
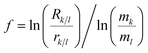 | (2) |
In all IS experiments, the entire measurement cycle consisted of 20 replicates with a constant integration time (t = 10 s per replicate) and blank correction by ESA (Electrostatic analyzer) deflection. All measurements for monoisotopic elements and the most abundant isotope of polyisotopic elements were taken at a signal intensity between 40 and 50 V. The blank signals for different isotopes were in the range of several millivolts, so the signal-to-blank ratio for studied elements was up to 5000.
The relationship of the natural logarithms of the measured isotope ratios at different RF power is linear and can be expressed by the equation:
| ln(ri/j) = a + b × ln(rk/l) | (3) |
The actual isotope ratio R is proportional to the measured ratio r, and further equations can be derived from the above equation to calculate isotope ratios free from instrumental fractionation (mass discrimination effect) and independent of the assumption that different isotope pairs undergo identical isotopic fractionation, as assumed in the traditional IS model:
| Ri/j = ea × Rk/lb | (4) |
In fact, the advantage of ORM over the Internal Standard method is the lack of assumption of atomic mass-dependent fractionation.5,25,26
The ORM measurements were carried out using the Time Resolved Analysis mode (TRA) and real zero blank correction.
Results
IS calibration using 93Nb/89Y
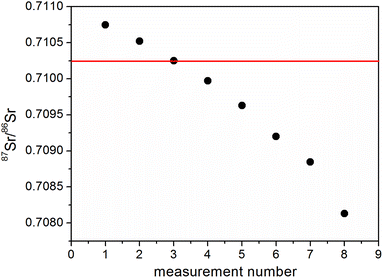
Firstly, an attempt was made to use a model mixture of niobium and yttrium as a calibrator. We hypothesized that this pair of monoisotopic elements could be used in isotope ratio measurements of several elements: Rb, Sr, Zr, Mo or Ru. In this experiment the pure solutions of strontium, niobium and yttrium were mixed and studied.The 93Nb/89Y ratio was initially determined by measurement using the Internal Standard method with the 88Sr/86Sr (NIST 987) pair as a calibrator. As a next step the 87Sr/86Sr isotope ratio was measured using the 93Nb/89Y mixture as an internal calibrator. The average result for the 87Sr/86Sr ratio obtained using the 93Nb/89Y mixture for IS correction was equal to 0.70966 (2SD 0.00179). The difference between this result and the literature value (0.71025 (ref. 27)) is considerable (δ = −0.83‰). However, the most important observation was that the stability of subsequent measurements of the same solution under optimized conditions was poor and a constant drift of the results was observed (Fig. 1).
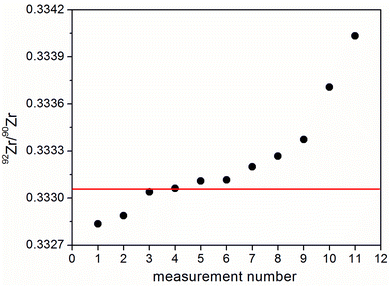
A similar phenomenon was observed when zirconium was measured instead of strontium using the same monoisotope mixture (Fig. 2). The average result (n = 8) for the 92Zr/90Zr ratio (0.33340; 2SD 0.0010) lies within the uncertainty range of the previously published result (0.33305 ± 0.00052 (ref. 28)) and the extended uncertainty range from the corresponding certified values of ZIRC-1 (0.33305 ± 0.00104). But the more results obtained, the further they deviate from these uncertainty ranges.
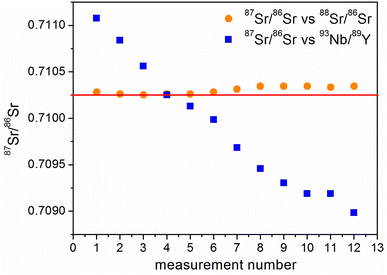
The size of these deviations during the application of a monoisotopic mixture is easier to visualize when compared with the results of intra-elemental calibration of strontium. The 87Sr/86Sr ratios were measured simultaneously from the same solution using different pairs of isotopes as calibrators: 93Nb/89Y and 88Sr/86Sr (Fig. 3). It is clear that the 93Nb/89Y pair cannot act as an internal calibrator as a significant drift is observed for the corresponding curve in Fig. 3 in comparison with the calibration using 88Sr/86Sr. Besides, 87Sr/86Sr vs.93Nb/89Y results are very sensitive to changes in measurement conditions (e.g., gas flows, plasma power).
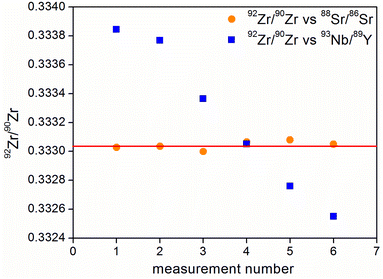
The same phenomenon was observed when zirconium isotope ratios were measured with an IIF correction using strontium isotopes and the 93Nb/89Y pair (Fig. 4). Beside a significant drift, the 92Zr/90Zr ratio measured versus93Nb/89Y was also sensitive to changes in measurement conditions.
It can be clearly observed that the measured 93Nb/89Y isotope ratio does not remain stable under the selected working conditions. This may be due to the difference in chemical properties of these two elements. The most important reason for the observations is the fact that different chemical elements are subjected to different drifts in the instrument, although they have similar atomic weight values. These slight, systematic changes in sensitivity are different for each element. As long as a pair of isotopes of the same element is measured, this drift has a minimal effect on the measured isotope ratio because both isotopes of the same element are affected in a very similar way. On the basis of all performed experiments we observed the phenomenon that when the calibrator is a pair of isotopes of two different elements, those small changes in sensitivity to individual elements (drift of the instrument) result in a continuous and significant change in the measured ratio between these two elements.
It can be seen that for isotopes of the same element the instrument behaves as a simultaneous one (signal changes are strongly correlated), while for two different elements (Nb and Y) signal changes are not correlated. Probably a different mathematical description is needed to deal with this type of drift.
IS calibration using 209Bi/197Au
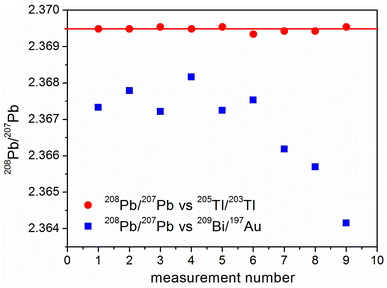
A similar experiment was carried out for a different pair of monoisotopic elements in order to check whether the observed phenomenon for the pair 93Nb/89Y is a unique one or could be considered as a general rule. For this purpose lead isotope ratios were measures using a mixture of gold and bismuth as a calibrator. In parallel Pb was also measured with an IIF correction using thallium. As can be seen from Fig. 5, the repeatability of the Pb isotope ratio measurements with 209Bi/197Au is strongly affected in comparison with the application of thallium as an internal calibrator. In addition, a constant drift of results also appears.IS calibration using 165Ho/159Tb
Finally, it was decided to perform an analogous experiment on monoisotopic elements, but with possibly similar physicochemical properties. From this point of view some rare earth elements could be selected, especially gadolinium, dysprosium, erbium, terbium, holmium and thulium, as besides similar chemical properties they also have close atomic masses. In theory, the 165Ho/159Tb pair could be useful in dysprosium isotope ratio measurements as most Dy isotopes have atomic masses which lie between the corresponding masses of Ho and Tb. Similarly the Tm/Ho system is promising for gadolinium and erbium isotope ratio analysis. The experiment with an internal calibrator performed for gadolinium as an analyte and the 165Ho/159Tb mixture as a calibrator gave analogous results as in the case of the isotope systems described above (88/87Sr–93Nb/89Y, 92/90Zr–93Nb/89Y, 208/207Pb–209Bi/197Au).As a next step we attempted to correct the observed drift and performed REE measurements by combining the Internal Standard and Standard Sample Bracketing methods (IS SSB). The solution of gadolinium standard GADS-1 (50 μg kg−1 Gd) was spiked with an appropriately prepared 165Ho/159Tb mixture (and served as a bracketing standard). Nine repeated measurements (brackets) of Gd isotope ratios were taken using 165Ho/159Tb as an internal calibrator. Four ratios of Gd isotopes were studied. The results and respective SD values are presented in Table 3. The results indicate that the use of the IS-SSB combination in the case of matrix samples allowed results with much better trueness and precision to be obtained compared to the results obtained with SSB only. The use of this combination made it possible to significantly reduce the impact of the drift of monoisotopic elements on the measurement result of the analyte isotopic ratio in model matrix samples.
| δ | δ 160Gd/158Gd | δ 160Gd/157Gd | δ 160Gd/156Gd | δ 160Gd/155Gd |
|---|---|---|---|---|
| IS SSB (Tb/Ho corrected) delta values | ||||
| Average (n = 9) | 0.099 | 0.148 | 0.201 | 0.199 |
| SD | 0.022 | 0.041 | 0.060 | 0.080 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| SSB delta values | ||||
| Average (n = 9) | −0.166 | −0.250 | −0.312 | −0.480 |
| SD | 0.280 | 0.413 | 0.567 | 0.687 |
Based on the results from Table 3, we summarize that the use of an internal calibrator in the form of a Tb/Ho mixture allowed for a significant improvement in both the precision and trueness of the results obtained for matrix samples in comparison to results not corrected by any internal calibrator. We emphasize that this observation is true when conducting measurements in the IS SSB regime. The results obtained in this way do not differ significantly in terms of precision and trueness from the results obtained for samples without a matrix (average delta +0.10 ± 0.12, n = 9). At the same time, the results obtained for matrix samples using the SSB method without correction with an internal calibrator show a significant systematic error, and the results of subsequent repeated measurements differ significantly, resulting in very low precision. We explain this observation by the occurrence of serious matrix effects, the impact of which the SSB method is unable to correct.
ORM measurements
The next important issue was to check whether ORM with a mixture of monoisotopic elements as a calibrator allows correct isotopic results to be obtained. Due to the significant physicochemical similarities, we chose rare earth elements as a model system. Our first observation was that by using a mixture of monoisotopic elements (165Ho/159Tb) as calibrators to measure both Gd and Er isotopic ratios, we obtained linear relationships between the natural logarithm of analyte isotopic ratio and natural logarithm of calibrator ratio. Compared to the “classic” ORM curve in which both the analyte and the calibrator are pairs of the same element, it can be seen that the intercept a and the slope b are very different from the theoretical ones when mass fractionation factors for two REEs are assumed to be the same.10 For example, for a system where 167Er/166Er is the analyte and 165Ho/159Tb is a calibrator the theoretical slope is 0.162 and the measured slope is 0.067, and the theoretical intercept is at around 0.98 (based on natural abundances) and the measured intercept is −0.376. This proves that changes in plasma power cause a much greater change in the measured Ho to Tb ratio than in the case of two isotopes of the same element.To further explore the capabilities of the ORM method a solution containing Gd (NRC GADS-1), Er, Ho and Tb was prepared. As the 167Er/166Er ratio was unknown, first ORM with 160Gd/158Gd (NRC GADS-1 isotopic standard) as a calibrator was used to estimate the 167Er/166Er ratio value. At the same time, we collected data enabling the calculation of the Er isotope ratio using Russell's law. The obtained results are presented in Table 4 and ESI 1.†
| ORM 167Er/166Er vs.160Gd/158Gd | IS 167Er/166Er vs.160Gd/158Gd | |
|---|---|---|
| Mean value | 0.68236 | 0.68287 |
| SD | 0.00034 | 0.00007 |
| N | 34 | 58 |
It should be noted that the results for the IS and ORM methods differ significantly. Since examining whether the Er–Gd system meets the assumptions made for Russell's law is beyond the scope of this work (and we do not discuss it here), in the rest of the work we adopted the result obtained by the ORM method. We also emphasize that the aim of this work is not to determine the true values for the studied isotopic systems, but to perform a critical evaluation of the applicability of the two discussed calibration methods.
Later in the experiment, we measured the 165Ho/159Tb ratio using the ORM method with 160Gd/158Gd (NRC GADS-1) as a calibrator. Examples of data processing according to the ORM method are presented in ESI 2.† In the following measurement session (different day, different conditions) we used the same solution, but this time we used the ORM method with 165Ho/159Tb as a calibrator to measure the 167Er/166Er isotope ratio. As the reference value of the 165Ho/159Tb ratio, we used the value determined by the ORM method in the measurement session preceding these measurements.
Based on the results summarized in Table 5, it can be found that the average value (0.68223) lies within a standard deviation of the value presented in Table 3. However, it should be stressed that the results obtained from individual sessions differ significantly and do not meet the conditions of high reproducibility imposed on isotopic measurements. Additionally, it was observed that the precision of determining the 165Ho/159Tb ratio (here we mean a single point in the logarithmic coordinates) is one order of magnitude worse than that of the gadolinium or erbium isotope ratio and further decreases as the plasma power value moves away from optimal plasma power value. Ultimately, the reproducibility of the ORM results obtained for the system with the 165Ho/159Tb mixture as the calibrator is worse than that of the ORM results obtained for the system with Gd as the calibrator and for the Gd/Er system with correction based on Russell's law. Despite many attempts, at this stage of the experiment, we were not able to find such compromise measurement conditions to ensure equally high precision of measurement of both the Er isotope pair and the 165Ho/159Tb pair. We emphasize, however, that the aim of our work was to investigate the possibility of using the Internal Standard method and the optimized regression model for measurements with a mixture of two monoisotopic elements as a calibrator. It is necessary to carry out selected parameters of validation of the ORM method used that way and to check in detail which of the factors is directly responsible for the worse reproducibility and general difficulties in obtaining ORM curves of satisfactory quality (e.g., with a high coefficient of determination).
| ORM 167Er/166Er vs.165Ho/159Tb as a calibrator | ||||
|---|---|---|---|---|
| Session number | 1 | 2 | 3 | 4 |
| 167Er/166Er mean | 0.68224 | 0.68257 | 0.68235 | 0.68174 |
| SD | 0.00035 | 0.00024 | 0.00028 | 0.00518 |
| N | 7 | 3 | 8 | 7 |
| δ vs. 0.68236 | −0.18 | 0.30 | −0.02 | −0.92 |
| Average value with SD: 0.68223 ± 0.00351 | ||||
Discussion and conclusions
We explored the suitability of mixtures of monoisotopic elements as an internal calibrator (Russell's law) for measuring isotopic ratios. Initially we hypothesized that such a system may be an attractive alternative to the calibration methods previously used. It seemed that the use of isotopes, although of different elements, but with close enough atomic masses, would ensure their similar behavior under measurement conditions.During the preparation of an in-house isotope standard, as done in this research, all possible factors contributing to the total measurement uncertainty must be considered.29 The primary source of uncertainty in preparing monoisotope mixtures likely originates from the weighing of the respective solutions of each element. Therefore, only relatively large amounts of solutions (>0.5 g) were weighed on scales with high precision (up to 0.01 mg).
Despite this, the significant discrepancy between the theoretical and experimental isotope ratios in the in-house standard that we observed could not be solely attributed to weighing uncertainty. In fact, even after accounting for differences in the first ionization potential between two monoisotopic elements, the results improved but were still not accurate enough. This suggests that factors such as second and consecutive ionization energies, mass discrimination effect, and other physicochemical properties of the studied atoms may need to be considered for a more accurate estimation of the true isotope ratio in the prepared mixtures.
Sufficient effects were not achieved, and in our opinion, the most important reasons for the observations are the fact that different chemical elements undergo instrumental drift differently. Consequently, the measured ratio of two isotopes of different elements changes significantly during the measurement session. This leads to results of unsatisfactory precision and potentially subject to systematic error (depending on at what point in the measurement session the measurement is performed).
Our main conclusion is that maybe only a possible revised mathematical description will allow the use of a monoisotopic element pair as an internal calibrator due to the significant drift of results and the inability to maintain adequate repeatability of the results. An important observation is also the fact that small changes in measurement parameters, such as plasma power or nebulizer gas flow rate, cause very large changes in the obtained result, and therefore do not make it possible to maintain the results independent of changes in measurement conditions, which is one of the main functions of the internal calibrator. However, the use of a pair of monoisotopic elements as internal calibrators, combined with the SSB method (IS SSB), makes it possible to reduce the impact of the discussed drift on the results of relative measurements. Additionally, we observe the fact that the internal calibrator in the form of a pair of monoisotopic elements makes it possible to correct the influence of matrix effects in the case of relative measurements carried out in the IS SSB regime. This observation can be summarized as follows: SSB is so sensitive to matrix influences that it is better to correct them even with an imperfect internal calibrator like a monoisotopic mixture than to apply no correction at all. So in isotopic systems where it is not possible to use a “classic” calibrator, monoisotope calibrators make it possible to improve precision, trueness and robustness to matrix influences.
ORM measurements revealed that changes in plasma power induce larger changes in the measured ratios of monoisotopic elements (165Ho/159Tb) compared to a pair of isotopes of the same element. The obtained ORM dependencies were linear, but their coefficients a and b were radically different from the theoretical ones (e.g., slope around 0.077 instead of 0.34, or 0.067 instead of 0.162). Additionally, the precision of measuring the 165Ho/159Tb ratio was an order of magnitude lower than that of Gd or Er, which results in the location of each regression point on the X axis being more random and, consequently, the obtained R coefficient was worse and the ORM result more aleatory. The lower precision and consequently lower reproducibility of measuring the ratios of monoisotopic elements compared to the precision of measuring Gd or Er may be explained by the drift during the integration time of each ORM point for each plasma power (200 seconds). At this stage of the experiment, we were unable to ensure equally high precision in measuring both the analyte (Gd or Er) and the calibrator (165Ho/159Tb). Secondly, the exact ratio between monoisotopic elements remains unknown, as there are described above problems with measuring it. Such a mixture can be prepared gravimetrically, but in this case there are also some limitations which are beyond the scope of this work. For these reasons, we are currently unable to decide with certainty whether the use of ORM with a 165Ho/159Tb mixture as a calibrator can give true and precise isotopic results and what is the potential of this calibration procedure to correct matrix influences. In the near future, we plan to continue our research on this topic.
Based on the described research, we currently believe that Russell's law does not provide a correct description for systems with a mixture of two monoisotopic elements, probably due to the assumption of equal IIF for the analyte and standard (which, in our opinion, does not occur in the case of two monoisotopic elements). The introduction of a suitable correction could be enabled by a new mathematical description of such a system, e.g., by applying the multivariate meta-regression approach30 or the GIMiCK algorithm.31 At this stage, ORM looks encouraging and shows the potential to be usable even with a mixture of monoisotopic elements as calibrators. The current challenge is to ensure a sufficiently high precision of calibrator ratio measurement and, consequently, better regression linearity and higher precision of the obtained results.
Data availability
During this investigation no new software nor original code was produced. The complete datasets and raw data generated during this project are combined in the ESI.†Author contributions
Andrii Tupys: methodology, investigations, data curation, writing – original draft, writing – review & editing. Klaudia Tetfejer: investigation, data curation, writing – review & editing. Ludwik Halicz: conceptualization and methodology, data curation, writing – original draft, writing – review & editing. Ewa Bulska: writing – review & editing, resources, supervision and project administration. Jakub Karasiński: conceptualization and methodology, investigation, resources, data curation, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by the National Science Centre, Poland, under research project “Application of the ORM for precise determination of the isotope ratios of elements” grant, contract number UMO-2021/41/B/ST4/04231.Notes and references
- J. Irrgeher and T. Prohaska, Application of non-traditional stable isotopes in analytical ecogeochemistry assessed by MC ICP-MS - A critical review, Anal. Bioanal. Chem., 2016, 408, 369–385 CrossRef CAS PubMed.
- D. Lu, T. Zhang, X. Yang, P. Su, Q. Liu and G. Jiang, Recent advances in the analysis of non-traditional stable isotopes by multi-collector inductively coupled plasma mass spectrometry, J. Anal. At. Spectrom., 2017, 32, 1848–1861 RSC.
- F. Albarède, P. Telouk, J. Blichert-Toft, M. Boyet, A. Agranier and B. Nelson, Precise and accurate isotopic measurements using multiple-collector ICPMS, Geochim. Cosmochim. Acta, 2004, 68, 2725–2744 CrossRef.
- J. Meija, L. Yang, Z. Mester and R. E. Sturgeon, Correction of Instrumental Mass Discrimination for Isotope Ratio Determination with Multi-Collector Inductively Coupled Plasma Mass Spectrometry, Isotopic Analysis: Fundamentals and Applications Using ICP-MS, 2012, pp. 113–137 Search PubMed.
- L. Yang, S. Tong, L. Zhou, Z. Hu, Z. Mester and J. Meija, A critical review on isotopic fractionation correction methods for accurate isotope amount ratio measurements by MC-ICP-MS, J. Anal. At. Spectrom., 2018, 33, 1849–1861 RSC.
- K. Wrobel, J. Karasiński, A. Tupys, M. A. Arroyo Negrete, L. Halicz, K. Wrobel and E. Bulska, Magnesium–Isotope Fractionation in Chlorophyll-a Extracted from Two Plants with Different Pathways of Carbon Fixation (C3, C4), Molecules, 2020, 25, 1644 CrossRef CAS PubMed.
- H. P. Longerich, B. J. Fryer and D. F. Strong, Determination of lead isotope ratios by inductively coupled plasma-mass spectrometry (ICP-MS), Spectrochim. Acta, Part B, 1987, 42, 39–48 CrossRef.
- J. D. Blum and B. A. Bergquist, Reporting of variations in the natural isotopic composition of mercury, Anal. Bioanal. Chem., 2007, 388, 353–359 CrossRef CAS PubMed.
- C. Gallon, J. Aggarwal and A. R. Flegal, Comparison of mass discrimination correction methods and sample introduction systems for the determination of lead isotopic composition using a multicollector inductively coupled plasma mass spectrometer, Anal. Chem., 2008, 80, 8355–8363 CrossRef CAS PubMed.
- C. N. Maréchal, P. Télouk and F. Albarède, Precise analysis of copper and zinc isotopic compositions by plasma-source mass spectrometry, Chem. Geol., 1999, 156, 251–273 CrossRef.
- W. M. White, F. Albarède and P. Télouk, High-precision analysis of Pb isotope ratios by multi-collector ICP-MS, Chem. Geol., 2000, 167, 257–270 CrossRef CAS.
- J. Woodhead, A simple method for obtaining highly accurate Pb isotope data by MC-ICP-MS, J. Anal. At. Spectrom., 2002, 17, 1381–1385 RSC.
- J. Meija, L. Yang, R. E. Sturgeon and Z. Mester, Certification of natural isotopic abundance inorganic mercury reference material NIMS-1 for absolute isotopic composition and atomic weight, J. Anal. At. Spectrom., 2010, 25, 384–389 RSC.
- J. Karasiński, A. Tupys, L. Yang, Z. Mester, L. Halicz and E. Bulska, Novel Approach for the Accurate Determination of Se Isotope Ratio by Multicollector ICP-MS, Anal. Chem., 2020, 92, 16097–16104 CrossRef PubMed.
- J. Karasiński, A. Tupys, L. Halicz and E. Bulska, A Novel Approach for the Determination of the Ge Isotope Ratio Using Liquid-Liquid Extraction and Hydride Generation by Multicollector Inductively Coupled Plasma Mass Spectrometry, Anal. Chem., 2021, 93, 13548–13554 CrossRef PubMed.
- W. A. Brand, T. B. Coplen, J. Vogl, M. Rosner and T. Prohaska, Assessment of international reference materials for isotope-ratio analysis (IUPAC technical report), Pure Appl. Chem., 2014, 86, 425–467 CAS.
- J. Vogl, The triple-isotope calibration approach: a universal and standard-free calibration approach for obtaining absolute isotope ratios of multi-isotopic elements, Anal. Bioanal. Chem., 2021, 413, 821–826 CrossRef CAS PubMed.
- M. Tatzel, J. Vogl, M. Rosner, M. J. Henehan and T. Tütken, Triple Isotope Fractionation Exponents of Elements Measured by MC-ICP-MS - An Example of Mg, Anal. Chem., 2019, 91(22), 14314–14322 CrossRef CAS PubMed.
- T. Prohaska, J. Irrgeher, J. Benefield, J. K. Böhlke, L. A. Chesson, T. B. Coplen, T. Ding, P. J. H. Dunn, M. Gröning, N. E. Holden, H. A. J. Meijer, H. Moossen, A. Possolo, Y. Takahashi, J. Vogl, T. Walczyk, J. Wang, M. E. Wieser, S. Yoneda, X. K. Zhu and J. Meija, Standard atomic weights of the elements 2021 (IUPAC Technical Report), Pure Appl. Chem., 2022, 94, 573–600 CrossRef CAS.
- T. W. May and R. H. Wiedmeyer, A Table of Polyatomic Interferences in ICP-MS Isotope Abundance Interference, At. Spectrosc., 1998, 19, 150–155 CAS.
- L. Yang, Accurate and precise determination of isotopic ratios by MC-ICP-MS: A review, Mass Spectrom. Rev., 2009, 28, 990–1011 CrossRef CAS PubMed.
- J. Karasiński, A. Tupys, L. Yang, Z. Mester, L. Halicz and E. Bulska, Novel Approach for the Accurate Determination of Se Isotope Ratio by Multicollector ICP-MS, Anal. Chem., 2020, 92, 16097–16104 CrossRef PubMed.
- S. Ehrlich, I. Gavrielia, L. B. Dorb and L. Halicz, Direct high-precision measurements of the 87Sr/86Sr isotope ratio in natural water, carbonates and related materials by multiple collector inductively coupled plasma mass spectrometry (MC-ICP-MS), J. Anal. At. Spectrom., 2001, 16, 1389–1392 RSC.
- D. Malinovsky, P. J. H. Dunn and H. Goenaga-Infante, Calibration of Mo isotope amount ratio measurements by MC-ICPMS using normalisation to an internal standard and improved experimental design, J. Anal. At. Spectrom., 2016, 31, 1978–1988 RSC.
- L. Yang and J. Meija, Resolving the germanium atomic weight disparity using multicollector ICPMS, Anal. Chem., 2010, 82, 4188–4193 CrossRef CAS PubMed.
- L. Yang, R. E. Sturgeon, Z. Mester and J. Meija, Metrological triangle for measurements of isotope amount ratios of silver, indium, and antimony using multicollector-inductively coupled plasma mass spectrometry: The 21st century Harvard method, Anal. Chem., 2010, 82, 8978–8982 CrossRef CAS PubMed.
- J. Karasinski, E. Bulska, M. Wojciechowski, A. A. Krata and L. Halicz, On-line separation of strontium from a matrix and determination of the 87Sr/86Sr ratio by Ion Chromatography/Multicollector-ICPMS, J. Anal. At. Spectrom., 2016, 31, 1459–1463 RSC.
- J. He, J. Meija and L. Yang, Determination of the Isotopic Composition of Zirconium Using MC-ICPMS and a Regression Model for Mass Bias Correction, Anal. Chem., 2021, 93, 5107–5113 CrossRef CAS PubMed.
- J. Vogl, O. Rienitz, A. Pramann and L. Flierl, Scale Conversion and Uncertainty Calculations in Isotope Delta Measurements, Geostand. Geoanal. Res., 2022, 46, 773–787 CrossRef.
- J. Meija and A. Possolo, Data reduction framework for standard atomic weights and isotopic compositions of the elements, Metrologia, 2017, 54, 229–238 CrossRef CAS.
- A. Stoll-Werian, L. Flierl, O. Rienitz, J. Noordmann, R. Kessel and A. Pramann, Absolute isotope ratios – Analytical solution for the determination of calibration factors for any number of isotopes and isotopologues, Spectrochim. Acta, Part B, 2019, 157, 76–83 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ja00117f |
| This journal is © The Royal Society of Chemistry 2024 |