Open Access Article
Open Access ArticleAre topological insulators promising thermoelectrics?†
Michael Y.
Toriyama
 * and
G. Jeffrey
Snyder
* and
G. Jeffrey
Snyder
 *
*
Department of Materials Science and Engineering, Northwestern University, Evanston, IL 60208, USA. E-mail: MichaelToriyama2024@u.northwestern.edu; jeff.snyder@northwestern.edu
First published on 3rd January 2024
Abstract
Some of the best thermoelectric (TE) materials to date are also topological insulators (TIs). While many studies have investigated the effects of topologically-protected TI surface states on TE properties, the conditions needed to realize such effects are quite different from typical operating conditions of TE devices for, e.g., power generation and room-temperature Peltier cooling. As a result, it is still unclear what properties of TIs, especially those related to the bulk band structure, are beneficial for TE performance, if any. Here, we perform high-throughput transport calculations using density functional theory to reveal that, within the same structure type, TIs tend to outperform normal insulators as TEs when properly optimized. The calculations also indicate that the TE performance is higher for TIs with strongly inverted bands. To explain these observations, we develop models based on Boltzmann transport theory which show that warping driven by band inversion, a key characteristic of TIs, is responsible for the high TE performance of TIs. We find that warping benefits the TE performance because of reduced transport mass and effectively higher valley degeneracy. Our results show that the band inversion strength is a critical property of a TI dictating the TE performance, and we suggest potential strategies to tune the inversion strength and enhance the TE performance in TIs, such as alloying and strain engineering. The study marks TIs as serious candidates for TE applications owing to band inversion-driven warping.
New conceptsThe ability to convert electricity to thermal energy and vice versa using thermoelectric devices can enable revolutionary technologies such as waste heat recovery and eco-friendly cooling. Despite their potential, thermoelectrics often suffer from low efficiency, prompting the need to discover and optimize materials for improving performance. It has been speculated that topological insulators possess characteristics that are favorable for thermoelectrics, but this remains an open question due to a lack of thermoelectric measurements on known topological insulators. Here, we combine first-principles calculations with electron transport modeling to identify trends and pinpoint features unique to topological insulators that give rise to high thermoelectric efficiency. Although topological insulators are best known for their unique surface properties, we look beneath the surface to reveal that their bulk properties offer exceptional advantages for thermoelectrics. Through a phenomenon that we call “band inversion-driven warping”, we find that topological insulators can possess high electrical conductivity and high thermopower – two properties that are often difficult to optimize simultaneously in thermoelectrics. By forging a dynamic synergy between two traditionally separate fields of materials science, our study unveils a new frontier for discovering and designing topological insulators for energy conversion applications. |
1 Introduction
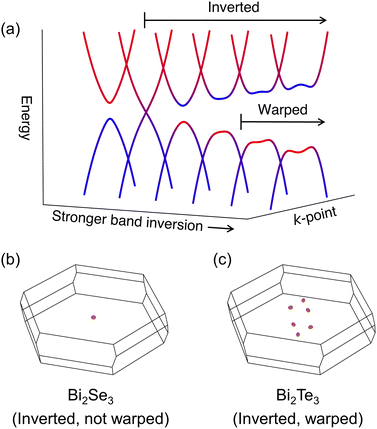
The impressive thermoelectric (TE) performance of Bi2Te3 is indisputable.1 Equipped with a valley degeneracy of NV = 6 or more,2 Bi2Te3-based materials have recorded some of the highest zTs near room temperature to date and have long been the material of choice for applications such as Peltier cooling of optoelectronics. The high valley degeneracy in particular has been attributed to topological properties of the material; namely, the bulk band structure becomes warped due to the strong band inversion, causing the band edges to be offset to low-symmetry k-points in the Brillouin zone.1,3,4 Here, “warped” bands are characterized as having a non-parabolic “M” shape for the valence band and “W” shape for the conduction band (Fig. 1a), as opposed to the conventional “U” shape of parabolic bands. Warped bands exhibit a valley degeneracy that is n-fold larger than a conventional parabolic band, where n is typically between 2 and 6 depending on higher order interactions.5,6Previous studies have shown that the band inversion strength is a key property that determines whether bulk bands in a TI are warped (a phenomenon known as band inversion-driven warping) and, as a result, exhibit high valley degeneracy. In particular, bulk bands in a TI are warped when the band inversion strength is sufficiently high, as described in ref. 5 and 6. The bands in the TI material Bi2Se3, for example, are not warped as evidenced by the single-valleyed electronic structure (NV = 1, Fig. 1b). In contrast, the bands are sufficiently inverted in Bi2Te3, giving rise to a comparatively higher valley degeneracy of NV = 6 (Fig. 1c). The distinction can be attributed to the spin–orbit interaction which, in Bi2Te3, is stronger and thus leads to higher band inversion strength.6
The band inversion strength can be understood from the energy separation between the valence and conduction band edges at the k-point where band inversion occurs, k0. We measure the energy separation using a quantitative parameter M0. Mathematically (see Section 3 for more details), it is convenient to define M0 so that M0 > 0 represents noninverted bands (i.e., normal insulators) and M0 < 0 represents inverted bands (i.e., TIs). The magnitude of M0 is the same for both types of bands:
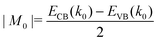 | (1) |
TIs are particularly known for unusual properties arising from topologically-protected surface states,7–9 and the influence of such surface states on TE properties have been studied quite thoroughly.10–13 Namely, it is known that the effects of surface states are dominant at low temperatures (typically below ∼150 K)14,15 and in samples with high surface-to-volume ratio (e.g., thin films16,17 and nanograined samples18,19). However, the same band inversion that gives rise to surface states in TIs is also closely tied to warping and valley degeneracy (i.e., features of the bulk band structure). As bulk effects related to topological character are relatively unknown, several key questions regarding TE properties in TIs remain to be answered. First, it has not been confirmed whether warped bulk bands of TIs are advantageous for TE performance, if at all. High valley degeneracy is beneficial for TEs when intervalley scattering is weak,20 but given that scattering may be enhanced when multiple bands exist at the same k-point,21 warping that results in valleys located at nearby points in k-space may also lead to high rates of scattering by, e.g., phonons. Second, material properties that fundamentally link TIs to TE performance are not well-known. Though it can be hypothesized that the band inversion strength is one such property due to its relation to valley degeneracy,6 this has not yet been confirmed through explicit analyses of TE properties. A detailed understanding may help guide material discovery efforts and band engineering strategies for high-performing TEs.
Here, we perform a detailed analysis of TE properties that result from band inversion-driven warping of bulk bands in TIs. We initially run density functional theory (DFT) calculations on the known TIs Bi2Te3 and Bi2Se3, as well as a large set of compounds crystallizing in the ZrBeSi-type structure to identify trends. We find from DFT calculations that TIs tend to exhibit higher zT than normal insulators in the same structure type; in fact, the TE performance is seemingly higher when the bands in a TI are more strongly inverted. To understand these trends, we build an appropriate model of the band structure using k•p theory and derive the resulting transport properties. The model indicates that band inversion-driven warping is the phenomenon responsible for benefiting TE performance. Despite scattering events, the reduced transport mass and effectively higher valley degeneracy with warping gives rise to high zT. Moreover, the band inversion strength is found to be a key property that dictates the TE performance of TIs. We suggest design rules to engineer band inversion in TIs for improving TE performance. Our assessment confirms that TIs are indeed promising for TE applications from the perspective of charge transport in the bulk.
2 Materials survey
We evaluate the TE performances of a large set of materials by running Boltzmann transport theory-based calculations using density functional theory (DFT) and the Ab initio scattering and transport (AMSET) software.22 The scattering rates are calculated by considering three mechanisms: acoustic deformation potential scattering, ionized impurity scattering, and polar optical phonon scattering. This is distinct from assuming a constant scattering time, which sometimes yields inaccurate predictions of transport properties.23–25 From the scattering rates, we calculate the electrical conductivity, Seebeck coefficient, and electronic thermal conductivity. The computational details can be found in the ESI.†The calculated transport properties of Bi2Te3 at 300 K are in close agreement with experimentally-measured values1 for both n- and p-type (Fig. S1, ESI†). Note that we obtain good agreement when the transport properties are calculated using the experimental band gap (Eg = 0.14 eV) and lattice thermal conductivity (κL = 1.37 W m−1 K−1) at 300 K. We calculate the maximum attainable zT at 300 K (denoted “max. zT300K” in Fig. 2) by appropriately shifting the Fermi level to the optimum doping amount. We find, in agreement with experimental observations, that Bi2Te3 outperforms Bi2Se3 as a TE material at 300 K when optimally doped. This can partly be attributed to the warped band structure of Bi2Te3, which yields a comparatively higher valley degeneracy (Fig. 1c) than the single-valleyed Bi2Se3 (Fig. 1b). Since warping is related to the band inversion strength, the comparison between Bi2Te3 and Bi2Se3 is the first indication that materials with strongly inverted bands can attain higher zT than those with weakly inverted bands.
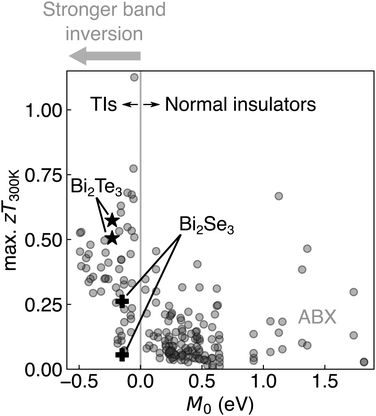 | ||
Fig. 2 The calculated maximum zT at 300 K (denoted “max. zT300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K”) for Bi2Te3 (star), Bi2Se3 (plus), and ZrBeSi-type ABX compounds (circles). The maximum zT is determined by shifting the Fermi level to the optimum doping amount. There are two points for each compound, representing n- and p-type. M0, described by eqn (1), is a measure of the energy separation of the band edges at the Γ-point for the present set of materials, where M0 > 0 represents noninverted bands (i.e., normal insulators) and M0 < 0 represents inverted bands (i.e., topological insulators, or TIs). More negative M0 values represent stronger band inversion. Topological insulators seem to exhibit higher zT than normal insulators, and the TE performance appears to trend upward with more inverted bands. K”) for Bi2Te3 (star), Bi2Se3 (plus), and ZrBeSi-type ABX compounds (circles). The maximum zT is determined by shifting the Fermi level to the optimum doping amount. There are two points for each compound, representing n- and p-type. M0, described by eqn (1), is a measure of the energy separation of the band edges at the Γ-point for the present set of materials, where M0 > 0 represents noninverted bands (i.e., normal insulators) and M0 < 0 represents inverted bands (i.e., topological insulators, or TIs). More negative M0 values represent stronger band inversion. Topological insulators seem to exhibit higher zT than normal insulators, and the TE performance appears to trend upward with more inverted bands. | ||
To perform a more meaningful comparison between TIs with varying band inversion strengths, as well as normal insulators which do not have inverted bands, a larger set of materials is needed. We therefore consider a set of A+1B+2X−3 compounds (A+1 = Li, Na, K, Rb, Cs, Cu, Ag, Au; B+2 = Be, Mg, Ca, Sr, Ba, Yb, Zn, Cd, Hg; X−3 = N, P, As, Sb, Bi) that crystallize in the ZrBeSi-type structure (space group: P63/mmc),26 which is known to host a variety of topological character including normal insulators and TIs.27 Calculating the properties of ABX compounds enables us to identify trends within the ZrBeSi structure type. Given the variety of chemistries and topological characters surveyed in the ABX family, we hypothesize that the general trends elucidated in this analysis can extend to other structure types as well. We later develop and discuss a generalized transport model that is agnostic of the crystal structure (Sections 3 and 4) which largely validates this hypothesis. The data reported in this study are available in a public repository.28
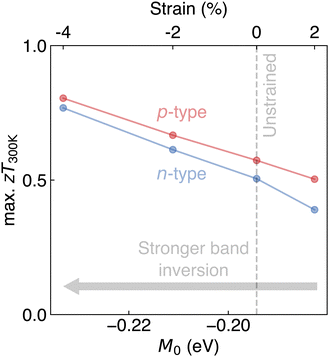
We plot the calculated maximum zT at 300 K against M0 in Fig. 2 (see the ESI† for computational details). From an initial survey across the diverse set of ABX compounds, we can arrive at two general observations: (i) TIs (M0 < 0) tend to exhibit higher zT than normal insulators (M0 > 0) within the same structure type, and (ii) the TE performance appears to be higher for TIs exhibiting stronger band inversion (i.e., more negative M0).
The variability in the data shown in Fig. 2, however, calls to question which specific attributes give rise to high TE performance in TIs within a given structure type. It is often reasoned that TIs are good candidates for TEs due to the heavy elements that are typically found in TIs (e.g., Bi), which tend to lower thermal conductivity.10,29 Our results support this conclusion, as a large number of TIs (red points in Fig. 3a) have an estimated κL<1 W m−1 K−1, partly explaining the high zT (Fig. 2). However, our calculations also strongly substantiates the value of inverted bands in TIs for electrical transport properties. The weighted mobility (μw) is often interpreted as a figure-of-merit for the electronic properties of TE materials.30 The estimated μw (see the ESI† for computational details) are quite high for TIs, with many exceeding 100 cm2 V−1 s−1 at 300 K (Fig. 3a). As a result, TIs tend to be clustered in the high μw – low κL quadrant (Fig. 3a), explaining why the quality factor B ∝ μw/κL tends to be quite high for TIs compared to normal insulators (Fig. S2a, ESI†). Since B provides a measure of the maximum attainable zT of a material,31 our results show that the high zT of TIs (Fig. 2) can be explained by high μw and low κL.
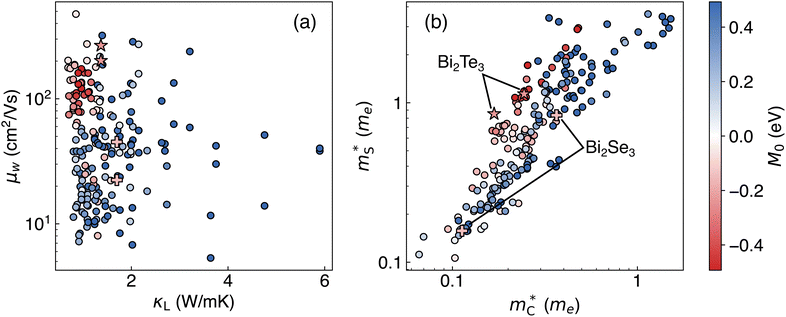 | ||
Fig. 3 Material properties of Bi2Te3 (star), Bi2Se3 (plus), and ZrBeSi-type ABX compounds (circles), showing (a) weighted mobility μw and lattice thermal conductivity κL, and (b) Seebeck mass 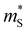 and conductivity mass and conductivity mass 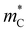 . All properties are evaluated at 300 K and at the band edges. The color represents M0, described by eqn (1), where normal insulators (M0 > 0) are blue and topological insulators (M0 < 0) are red. Topological insulators exhibit favorable thermal and electrical transport properties compared to normal insulators. . All properties are evaluated at 300 K and at the band edges. The color represents M0, described by eqn (1), where normal insulators (M0 > 0) are blue and topological insulators (M0 < 0) are red. Topological insulators exhibit favorable thermal and electrical transport properties compared to normal insulators. | ||
We inspect the electronic properties further to understand the origin of high μw in TIs. Namely, we compute the Seebeck effective mass (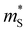 ) and the conductivity effective mass (
) and the conductivity effective mass (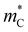 ) from DFT calculations of the Seebeck coefficient and electrical conductivity (see the ESI† for details). We can express
) from DFT calculations of the Seebeck coefficient and electrical conductivity (see the ESI† for details). We can express 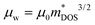 , where the density of states effective mass
, where the density of states effective mass 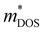 can be measured by
can be measured by 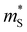 , and the intrinsic mobility
, and the intrinsic mobility 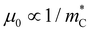 . In other words, there are two main ingredients for high μw: high
. In other words, there are two main ingredients for high μw: high 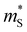 , and low
, and low 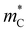 . Many TIs in the present study exhibit such characteristics, with
. Many TIs in the present study exhibit such characteristics, with 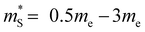 and
and 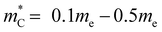 (Fig. 3b). We also evaluate the Fermi surface complexity factor
(Fig. 3b). We also evaluate the Fermi surface complexity factor 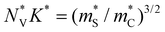 , which can be interpreted as a metric for the effective number of carrier pockets contributing to electrical transport.32 As expected, TIs tend to exhibit high
, which can be interpreted as a metric for the effective number of carrier pockets contributing to electrical transport.32 As expected, TIs tend to exhibit high 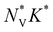 (Fig. S2b, ESI†), which explains the large μw values (Fig. 3a).
(Fig. S2b, ESI†), which explains the large μw values (Fig. 3a).
The DFT calculations show that the high TE performance in TIs, within the same structure type, originate from favorable thermal and electrical transport properties. The high μw of TIs in particular can be attributed to both high 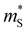 and low
and low 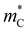 , properties that are related to the bulk band structure of the material. We show in the following sections that models based on Boltzmann transport theory, which are independent of the specific structure, are consistent with the results of the DFT calculations and elucidate key features of the TI bulk band structure that generally benefit TE performance.
, properties that are related to the bulk band structure of the material. We show in the following sections that models based on Boltzmann transport theory, which are independent of the specific structure, are consistent with the results of the DFT calculations and elucidate key features of the TI bulk band structure that generally benefit TE performance.
3 Band structure model
Charge transport properties in a material are often modeled using simplifying assumptions of the band structure and scattering mechanism of charge carriers. Commonly, the electronic structure is modeled using a parabolic band,31,33–36 and scattering by acoustic phonons via a deformation potential is considered.37 The drawback of the parabolic band model however is that it does not capture warping effects induced by band inversion in TIs. This is because the coupling between the valence and conduction band edges with secondary bands (i.e., bands that are not the band edges) is not taken into account.6Warped band structures can be modeled using k•p perturbation theory by expanding to second order in k. Here, we model the valence and conduction band edges explicitly and build an appropriate 2 × 2 Hamiltonian. The k•p Hamiltonian, assuming isotropic symmetry, takes the form
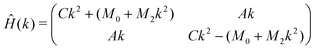 | (2) |
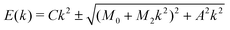 | (3) |
System-specific band structure models have been developed for TIs such as Bi2Se3 and Bi2Te3,38–40 SnTe,5 and NaCaBi.41 The Hamiltonian in eqn (2) is the base form of the Hamiltonians adopted in the cases listed above, where additional parameters are necessary to satisfy symmetry constraints in specific cases. In other words, the effective Hamiltonian in eqn (2) represents the lowest-order model needed to describe warped band structures in TIs. The main advantage of the simplified band structure model is that it permits a fully analytical derivation of the transport properties and reveals the essential physics that relates topological character to TE performance.
When the bands are inverted (M0 < 0), there is a critical band inversion strength (M0,c) that determines whether the bands are single-valleyed or warped. We define warping in terms of the curvature of the band at the k-point where band inversion occurs; the definition is therefore somewhat distinct from previous usage of the term.42 For example, the conduction band is single-valleyed if the band has a “U” shape and positive curvature, and warped if it has a “W” shape and negative curvature (Fig. 1a). From eqn (3), M0,c is determined by the expression6
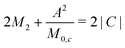 | (4) |
If M0 < M0,c, then the bands are warped. If M0 > M0,c on the other hand, the bands are single-valleyed. In other words, even if the bands are inverted (M0 < 0) in a TI, the bands must be sufficiently inverted (M0 < M0,c) for warping to occur.5,6 The concept is illustrated in Fig. 1a.
4 Transport model for band inversion-induced warped bands
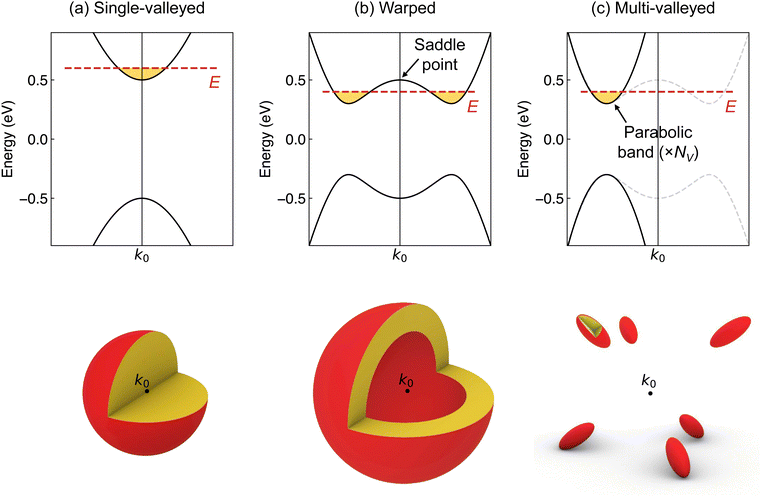
We model charge transport properties using the standard Boltzmann transport formalism under the relaxation time approximation.43–45 To understand the model, it is useful to recognize the Fermi surface geometry for a band described by eqn (3), which can be either single-valleyed or warped. For a single-valleyed band, the Fermi surface is spherical for all energies, and the states inside the sphere are filled (Fig. 4a). When the band is warped and the conduction band forms a “W” shape, there is a local saddle point at k0 that is |M0| eV above mid-gap (Fig. 4b). If the Fermi energy is above the saddle point, then the Fermi surface is spherical. If the Fermi energy is below the saddle point on the other hand, due to the isotropic nature of the band, the Fermi surface will consist of two concentric spheres (Fig. 4b). The filled states will then occupy the volume of a hollowed sphere, as opposed to the volume of a complete sphere as in a single-valleyed band.We refer to the transport properties derived from eqn (3) as the “warped band transport model” (see the ESI† for details). The maximum zT at 300 K, which is determined by adjusting the doping level appropriately, is shown in Fig. 5a as a function of M0. Note that a particular set of values, listed in the ESI,† are used for the C, A, and M2 parameters present in eqn (3); the qualitative results hold regardless of the specific values.
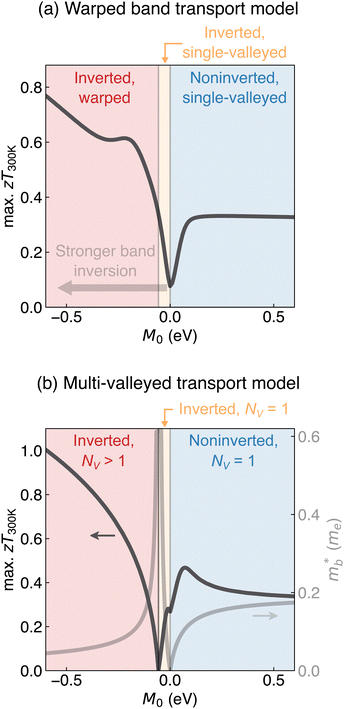 | ||
Fig. 5 Maximum attainable zT at 300 K (denoted “max. zT300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K”) calculated using (a) the warped band transport model and (b) the multi-valleyed transport model. M0, described by eqn (1), is such that M0 > 0 represents noninverted bands (i.e., normal insulators) and M0 < 0 represents inverted bands (i.e., topological insulators). Characteristics of the band structure, such as inversion and warping, are differentiated by the background shading. Parameters of the model are listed in the ESI.† The results are in qualitative agreement with the trend observed in DFT calculations in Fig. 2. The thermoelectric performance is higher for topological insulators exhibiting stronger band inversion (i.e., more negative M0). K”) calculated using (a) the warped band transport model and (b) the multi-valleyed transport model. M0, described by eqn (1), is such that M0 > 0 represents noninverted bands (i.e., normal insulators) and M0 < 0 represents inverted bands (i.e., topological insulators). Characteristics of the band structure, such as inversion and warping, are differentiated by the background shading. Parameters of the model are listed in the ESI.† The results are in qualitative agreement with the trend observed in DFT calculations in Fig. 2. The thermoelectric performance is higher for topological insulators exhibiting stronger band inversion (i.e., more negative M0). | ||
When the bands are not inverted (M0 > 0, blue region in Fig. 5a), the initial increase in zT with M0 is due to the increasing band gap and, as a result, weaker bipolar conduction effects. The TE performance then stagnates at large M0, because the TE performance at sufficiently large band gaps is limited by the properties of the majority carrier type. The overall behavior of zT when M0 > 0 (i.e., when the material is a normal insulator) is unsurprisingly reminiscent of a two-band transport model with parabolic valence and conduction bands.46
When the bands are inverted (M0 < 0, yellow and red regions in Fig. 5a), the TE performance increases with the band inversion strength (i.e., more negative M0). The bump in the maximum zT near M0 = −0.25 in the warped region originates from scattering between the inner and outer Fermi spheres, which results in a transition from a single-peaked zT profile to a two-peaked profile. A ring-like quartic (i.e., warped) band exhibits a similar two-peaked profile in the power factor.47 A higher zT is attainable with inverted warped bands (M0 < M0,c, red region) than with noninverted bands (M0 > 0, blue region). In fact, regardless of other details of the electronic structure, namely A and M2 in eqn (3), the maximum zT in most cases is higher for TIs with strongly inverted bands (Fig. S3, ESI†).
Together with DFT calculations (Section 2), our results provide compelling evidence that TIs are promising candidates for TEs. The utility of the warped band transport model is that it reveals how the maximum zT changes from modifications in the band structure only, since κL is kept constant. Notably, the model shows that M0 is a key property that strongly influences the TE performance of a material. When M0 < M0,c, the band inversion strength M0 can be interpreted as the degree to which inverted bands in a TI are warped. As a result, the model reveals that band warping, which is driven by band inversion, is responsible for the high zT in TIs.
5 What aspects of band warping are beneficial for thermoelectric performance?
The high zT of materials with inverted warped bands can be understood by initially examining the individual transport properties. For warped bands, the zT is higher than that of single-valleyed bands for a wide range of doping levels (Fig. S4a, ESI†). Since the lattice thermal conductivity is kept constant in the model, the high zT of a warped band can be attributed to the high power factor (Fig. S4b, ESI†). The power factor is enhanced by the electrical conductivity (Fig. S4c, ESI†) without compromising the Seebeck coefficient (Fig. S4d, ESI†).The transport properties suggest that warped bands possess characteristics of a multi-valleyed electronic structure. However, it is difficult to explicitly understand properties such as the effective mass and valley degeneracy from the warped band transport model, since the hollowed sphere-type Fermi surface of a warped band (Fig. 4b) is geometrically distinct from, e.g., an ellipsoidal Fermi surface. In a real material, when bands are warped due to band inversion, often the hollowed Fermi sphere breaks into a finite number of carrier pockets.5,6 Such multi-valleyed Fermi surfaces are evident in TIs such as Bi2Te3 (Fig. 1c) and rock-salt SnSe.5
In order to model a multi-valleyed band structure that still depends on band inversion in TIs, we fit a parabolic band 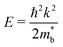 to the edge of the band structure described by eqn (3) as illustrated in Fig. 4c. Material-specific features such as M0 are embedded in the band effective mass
to the edge of the band structure described by eqn (3) as illustrated in Fig. 4c. Material-specific features such as M0 are embedded in the band effective mass 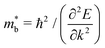 . We subsequently derive the TE properties as if we are considering parabolic bands with valley degeneracy NV, where NV > 1 only when M0 < M0,c (i.e., when the bands are inverted and warped). The “multi-valleyed transport model” (see the ESI† for details) therefore allows us to understand the effects of band inversion on TE properties through the familiar lexicon of parabolic band transport.
. We subsequently derive the TE properties as if we are considering parabolic bands with valley degeneracy NV, where NV > 1 only when M0 < M0,c (i.e., when the bands are inverted and warped). The “multi-valleyed transport model” (see the ESI† for details) therefore allows us to understand the effects of band inversion on TE properties through the familiar lexicon of parabolic band transport.
For a normal insulator (M0 > 0, blue region in Fig. 5b), the maximum zT initially rises with M0 because the band gap gets larger and bipolar conduction effects are suppressed. The drop in zT for larger M0 is due to the increasing 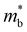 , which lowers the electrical conductivity. Similar to Kane band transport, the monotonic relationship between the band gap and
, which lowers the electrical conductivity. Similar to Kane band transport, the monotonic relationship between the band gap and 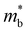 results in a so-called “optimum band gap” for maximizing zT.48,49 When the bands are inverted but still single-valleyed (M0,c < M0 < 0, yellow region in Fig. 5b), the zT decreases as M0 becomes more negative due to the increase in
results in a so-called “optimum band gap” for maximizing zT.48,49 When the bands are inverted but still single-valleyed (M0,c < M0 < 0, yellow region in Fig. 5b), the zT decreases as M0 becomes more negative due to the increase in 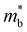 and, correspondingly, decrease in conductivity. If the bands are multi-valleyed (M0 < M0,c, red region in Fig. 5b), the TE performance enhances with stronger band inversion (i.e., more negative M0). The rising zT can be attributed to the lowering of
and, correspondingly, decrease in conductivity. If the bands are multi-valleyed (M0 < M0,c, red region in Fig. 5b), the TE performance enhances with stronger band inversion (i.e., more negative M0). The rising zT can be attributed to the lowering of 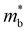 for the NV parabolic bands, which improves the conductivity (Fig. S5, ESI†).
for the NV parabolic bands, which improves the conductivity (Fig. S5, ESI†).
The maximum zT from a multi-valleyed band structure (Fig. 5b) follows a profile that is similar to that of warped bands (Fig. 5a), notably when the bands are sufficiently inverted (M0 ≪ M0,c). Both models show that the maximum zT of a TI rises as the band inversion strength increases (i.e., more negative M0). The fitted parabolic bands within the multi-valleyed model (Fig. 4c) are distinct from warped bands (Fig. 4b); however, the qualitative agreement between the two models suggests that the benefits of warped bands on TE performance (as shown in Fig. 5a) can be attributed to a quantity similar to 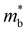 . In particular, effects similar to band sharpening (i.e., lower
. In particular, effects similar to band sharpening (i.e., lower 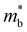 ) may be responsible for the increase in conductivity and zT with band inversion strength for warped bands (Fig. 5a and Fig. S4, ESI†).
) may be responsible for the increase in conductivity and zT with band inversion strength for warped bands (Fig. 5a and Fig. S4, ESI†).
We test this hypothesis by evaluating the conductivity mass (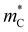 ) from the warped band transport model (see the ESI† for details).
) from the warped band transport model (see the ESI† for details). 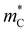 , in this way, can be interpreted as a proxy for
, in this way, can be interpreted as a proxy for 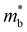 . Note that
. Note that 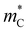 is ill-defined when bipolar conduction effects are significant, and we therefore calculate the quantity for |M0| > 0.15 eV. Indeed, we find that
is ill-defined when bipolar conduction effects are significant, and we therefore calculate the quantity for |M0| > 0.15 eV. Indeed, we find that 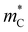 of warped bands decreases as M0 becomes more negative (Fig. 6a), indicating that band warping indeed leads to effectively sharper bands.
of warped bands decreases as M0 becomes more negative (Fig. 6a), indicating that band warping indeed leads to effectively sharper bands.
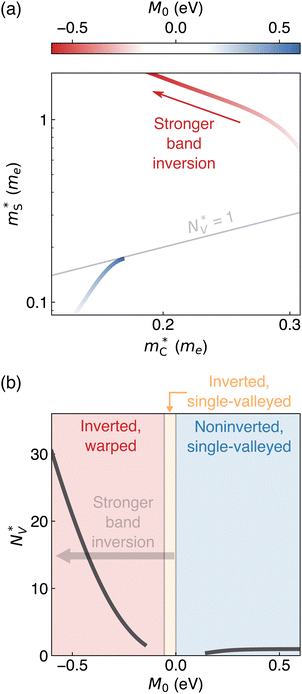 | ||
Fig. 6 (a) The Seebeck effective mass 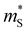 and conductivity mass and conductivity mass 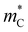 , calculated from transport properties within the warped band transport model. The color represents M0, where normal insulators (M0 > 0) are blue and topological insulators (M0 < 0) are red. (b) Effective valley degeneracy , calculated from transport properties within the warped band transport model. The color represents M0, where normal insulators (M0 > 0) are blue and topological insulators (M0 < 0) are red. (b) Effective valley degeneracy 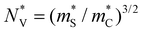 plotted against M0. The background shading indicates characteristics of the band structure, such as inversion and warping. Parameters of the model are listed in the ESI.† The high maximum zT of topological insulators can be explained by the effectively higher valley degeneracy of a warped band structure. plotted against M0. The background shading indicates characteristics of the band structure, such as inversion and warping. Parameters of the model are listed in the ESI.† The high maximum zT of topological insulators can be explained by the effectively higher valley degeneracy of a warped band structure. | ||
We also evaluate an effective mass from the Seebeck coefficient (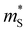 ) as an analogue to the density of states effective mass,50 allowing us to designate an “effective valley degeneracy”
) as an analogue to the density of states effective mass,50 allowing us to designate an “effective valley degeneracy” 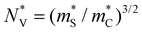 to a warped band (see the ESI† for details). Strictly speaking,
to a warped band (see the ESI† for details). Strictly speaking, 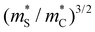 defines the Fermi surface complexity factor
defines the Fermi surface complexity factor 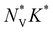 ;32 however, the anisotropy factor K* = 1 due to the isotropic nature of the model. For a normal insulator with noninverted bands, only a single band contributes to transport. Accordingly, we find
;32 however, the anisotropy factor K* = 1 due to the isotropic nature of the model. For a normal insulator with noninverted bands, only a single band contributes to transport. Accordingly, we find 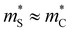 and
and 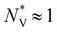 (Fig. 6). On the other hand, warped bands possess higher
(Fig. 6). On the other hand, warped bands possess higher 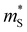 than noninverted bands, consistent with the idea of band inversion-driven high valley degeneracy.6 Perhaps more interestingly,
than noninverted bands, consistent with the idea of band inversion-driven high valley degeneracy.6 Perhaps more interestingly, 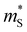 monotonically increases with the band inversion strength (Fig. 6a). Combined with the decreasing
monotonically increases with the band inversion strength (Fig. 6a). Combined with the decreasing 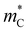 , we find that
, we find that 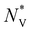 trends upward with stronger band inversion (Fig. 6b).
trends upward with stronger band inversion (Fig. 6b).
Transport modeling therefore indicates that band inversion-driven warping leads to a combination of lower conductivity mass and higher effective valley degeneracy, which explains the rise in maximum zT with the band inversion strength for warped bands (M0 < M0,c). The results are consistent with DFT calculations (Section 2); materials with strongly inverted bands tend to be characterized by high 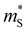 and low
and low 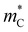 (Fig. 3b), explaining the high μw and, in part, high maximum zT. In summary, our model shows that
(Fig. 3b), explaining the high μw and, in part, high maximum zT. In summary, our model shows that
1. Band inversion-driven warping, which can be characterized by low conductivity mass and high effective valley degeneracy, is the critical phenomenon that leads to high TE performance in TIs, and
2. The band inversion strength is a key property that strongly influences the maximum attainable zT of TIs.
Our results so far have shown how and why the zT varies with the topological character of a material. The results can also allow us to envision design strategies to improve the TE performance by leveraging the electronic structure topology.
6 Design strategies
The results of the DFT calculations and transport modeling elucidate the critical nature of the band inversion strength in TIs for TE performance. This can be attributed to the lower conductivity mass and effectively higher valley degeneracy when the bands are warped due to band inversion. In other words, by strengthening band inversion in a TI and, as a result, warping the bands, the TE performance can be enhanced.The band inversion strength is related to the relative energy difference between the valence and conduction band edges at the k-point where band inversion occurs, as described by eqn (1). As a result, band inversion is affected by the interaction strength between atomic orbitals of neighboring atoms,51 such as sp-interactions between the cation and anion at the L-point in rock-salt systems.5,52,53 Additional interactions, such as spin–orbit coupling (SOC), can also contribute significantly to band inversion, as demonstrated in systems such as Bi2Te3, Bi2Se3, and Bi2Te2Se.1–3 By tuning the interaction strength, one should expect the band inversion strength and, correspondingly, TE performance, to vary.
As a proof of concept, we show using DFT transport calculations that increasing the band inversion strength in a TI material indeed leads to an increase in the TE performance. We demonstrate this effect by tuning the SOC strength in Bi2Se3, following the methodology described in ref. 6. Tuning the SOC strength relative to the normal amount (i.e., 100%) correspondingly changes the band inversion strength; in particular, if the SOC interaction is stronger, then the bands at the Γ-point are more inverted. By weakening the SOC interaction, we observe a transition between having inverted (M0 < 0) and noninverted (M0 > 0) bands (Fig. S6, ESI†). A similar topological transition has been observed in Bi2Te3 and Bi2Te2Se by varying the SOC strength.3 The wide range of SOC strengths tested in this study allows us to examine the TE performance across a wide range of M0. Note that the M0 values presented in this section are taken directly from DFT, as opposed to the value resulting from the necessary shift to the experimental band gap as done in Section 2 (see the ESI† for computational details).
When the bands are inverted, increasing the SOC strength and, correspondingly, the band inversion strength leads to an enhancement in the maximum attainable zT for both p-type Bi2Se3 (Fig. 7a) and n-type Bi2Se3 (Fig. 7d). The zT improvement is not monotonic in p-type Bi2Se3 (Fig. 7a), where a slight dip in zT between 110% and 120% SOC coincides with the transition between a single-valleyed and warped/multi-valleyed valence band structure (Fig. 7b and c). Within the regime where the bands are inverted but single-valleyed (i.e., the yellow regions in Fig. 7a and d), the maximum attainable zT rises monotonically. This behavior is accompanied by an elongation of the conduction band Fermi surface with increasing SOC strength (Fig. 7e and f). A different behavior is observed when the bands are not inverted (i.e., the blue regions in Fig. 7a and d). Namely, the maximum attainable zT initially rises with M0 due to avoiding bipolar conduction effects, before stagnating for larger M0. The trend in zT with the band inversion strength closely matches the results of the warped band transport model (Fig. 5a).
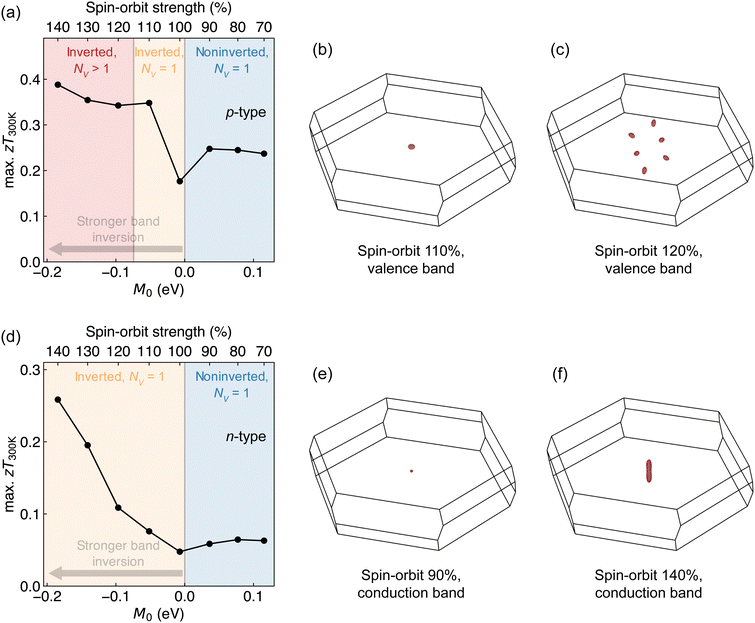 | ||
| Fig. 7 The calculated maximum zT at 300 K for (a) p-type and (d) n-type Bi2Se3 with different spin–orbit coupling (SOC) strengths. M0, described by eqn (1), modulates with the SOC strength, which is listed relative to the normal amount at 100%. Fermi surfaces for the valence band are shown at (b) 110% SOC and (c) 120% SOC, i.e., the boundary between single-valleyed and multi-valleyed bands despite being inverted in both cases. Fermi surfaces are also shown for the conduction band at (e) 90% SOC and (f) 140% SOC. All Fermi surfaces are calculated at 10 meV away from the band edge. These calculations show that strengthening band inversion can lead to an increase in the thermoelectric performance, thereby serving as a proof of concept for the results of transport modeling. | ||
A more direct method of modifying the band inversion strength is to strain the material. Orbital interactions are enhanced when atoms are closer together, leading to a lowering (raising) of bonding (antibonding) molecular orbitals upon compression and, as a result, stronger band inversion. We demonstrate this effect in Bi2Te3 by calculating the TE performance in a hydrostatically stressed state using DFT. We test strain values between −5% (compressed) and 2% (tensile-strained) to understand the trend when the atoms are both closer together and further apart relative to their equilibrium positions. There is a clear trend between the strain and optimized TE performance (Fig. 8). In the compressed state, the bands at the Γ-point in Bi2Te3 are more inverted and M0 is more negative than in the equilibrium state (Fig. S7, ESI†). The maximum zT at 300 K is correspondingly higher as M0 is more negative, consistent with the results of transport modeling (Fig. 5).
Of course, tuning the SOC strength and applying hydrostatic strain are idealized scenarios which neglect other effects such as the formation of defects and dislocations. The analysis nonetheless serves as a direct proof of concept for attaining higher TE performance by engineering the band inversion strength. Lattice strain is often a byproduct of doping and alloying, sometimes referred to as “chemical pressure”.54 Since Bi2Te3 is commonly alloyed with Bi2Se3 or Sb2Te3, both of which have smaller lattice constants than Bi2Te3, it is not unreasonable to speculate that the band inversion strength is modified in part due to the compressive strain when alloyed. SOC interactions may also be affected by doping and alloying. It has been shown that the nontrivial electronic structure of Bi2Te2Se is highly sensitive to the SOC strength.3 As a result, the increase in both electrical conductivity and Seebeck coefficient in Bi2Te2Se with sulfur doping has been attributed to variations in the SOC strength.55 It has also been shown that alloying SnTe with PbTe and GeTe leads to an increase in the Seebeck coefficient for similar carrier concentrations,56 which can be attributed to a composite effect from variations in both lattice strain and SOC strength on band inversion.
7 Conclusion
The band inversion strength is a key feature of topological insulators (TIs) that affects the thermoelectric (TE) performance. From DFT transport calculations and transport modeling, we show that TIs have the potential to perform well as TEs, and even outperform normal insulators within the same structure type. The favorable transport properties of TIs can be attributed to band inversion-driven warping, which leads to lower conductivity mass and effectively higher valley degeneracy. We predict that stronger band inversion is correlated with higher TE performance in TIs. We demonstrate this effect directly by tuning the SOC strength in Bi2Se3 and applying hydrostatic strain to Bi2Te3, both of which confirm the increase in zT with stronger band inversion. Our study not only reveals that band inversion-driven warping is the key phenomenon responsible for high TE performance in TIs, but also serves as motivation to pursue TIs as potential candidates for next-generation TE materials.Author contributions
Michael Y. Toriyama: conceptualization, investigation, data curation, formal analysis, methodology, writing (original draft), writing (editing). G. Jeffrey Snyder: conceptualization, investigation, methodology, writing (editing), supervision, project administration.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Prashun Gorai and Øven Andreas Grimenes for helpful discussions. We also thank Berhanu Snyder for helping to generate the 3D renderings of the Fermi surfaces. M. Y. T. is funded by the United States Department of Energy through the Computational Science Graduate Fellowship (DOE CSGF) under grant number DE-SC0020347. M. Y. T. also acknowledges support from the Johannes and Julia Randall Weertman Graduate Fellowship. This research was supported in part through the computational resources and staff contributions provided for the Quest high performance computing facility at Northwestern University which is jointly supported by the Office of the Provost, the Office for Research, and Northwestern University Information Technology.References
- I. T. Witting, T. C. Chasapis, F. Ricci, M. Peters, N. A. Heinz, G. Hautier and G. J. Snyder, Adv. Electron. Mater., 2019, 5, 1800904 CrossRef.
- I. T. Witting, F. Ricci, T. C. Chasapis, G. Hautier and G. J. Snyder, Research, 2020, 2020, 1 CrossRef PubMed.
- H. Shi, D. Parker, M.-H. Du and D. J. Singh, Phys. Rev. Appl., 2015, 3, 014004 CrossRef CAS.
- J. P. Heremans, R. J. Cava and N. Samarth, Nat. Rev. Mater., 2017, 2, 1 CrossRef.
- M. Toriyama, M. K. Brod, L. C. Gomes, F. A. Bipasha, B. Assaf, E. Ertekin and G. J. Snyder, J. Mater. Chem. A, 2022, 10, 1588 RSC.
- M. Y. Toriyama and G. J. Snyder, Cell Rep. Phys. Sci., 2023, 4, 101392 CrossRef.
- M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82, 3045 CrossRef CAS.
- D. Kong and Y. Cui, Nat. Chem., 2011, 3, 845 CrossRef CAS PubMed.
- T. V. Menshchikova, M. Otrokov, S. Tsirkin, D. Samorokov, V. Bebneva, A. Ernst, V. Kuznetsov and E. V. Chulkov, Nano Lett., 2013, 13, 6064 CrossRef CAS PubMed.
- N. Xu, Y. Xu and J. Zhu, npj Quant. Mater., 2017, 2, 51 CrossRef.
- J. Gooth, G. Schierning, C. Felser and K. Nielsch, MRS Bull., 2018, 43, 187 CrossRef CAS.
- Y. V. Ivanov, A. T. Burkov and D. A. Pshenay-Severin, Phys. Status Solidi B, 2018, 255, 1800020 CrossRef.
- C. Fu, Y. Sun and C. Felser, APL Mater., 2020, 8, 040913 CrossRef CAS.
- R. Takahashi and S. Murakami, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 161302 CrossRef.
- P. Ghaemi, R. S. Mong and J. E. Moore, Phys. Rev. Lett., 2010, 105, 166603 CrossRef PubMed.
- F. Rittweger, N. Hinsche, P. Zahn and I. Mertig, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035439 CrossRef.
- N. F. Hinsche, S. Zastrow, J. Gooth, L. Pudewill, R. Zierold, F. Rittweger, T. Rauch, J. Henk, K. Nielsch and I. Mertig, ACS Nano, 2015, 9, 4406 CrossRef CAS PubMed.
- G. Sun, L. Li, X. Qin, D. Li, T. Zou, H. Xin, B. Ren, J. Zhang, Y. Li and X. Li, Appl. Phys. Lett., 2015, 106, 053102 CrossRef.
- S. Izadi, A. Bhattacharya, S. Salloum, J. W. Han, L. Schnatmann, U. Wolff, N. Perez, G. Bendt, I. Ennen, A. Hütten, K. Nielsch, S. Schulz, M. Mittendorff and G. Shierning, Small, 2023, 19, 2204850 CrossRef CAS PubMed.
- P. Norouzzadeh and D. Vashaee, Sci. Rep., 2016, 6, 1 CrossRef PubMed.
- J. Park, M. Dylla, Y. Xia, M. Wood, G. J. Snyder and A. Jain, Nat. Commun., 2021, 12, 1 CrossRef PubMed.
- A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Nat. Commun., 2021, 12, 1 CrossRef PubMed.
- E. S. Toberer, A. F. May, C. J. Scanlon and G. J. Snyder, J. Appl. Phys., 2009, 105, 063701 CrossRef.
- W. Chen, J.-H. Pöhls, G. Hautier, D. Broberg, S. Bajaj, U. Aydemir, Z. M. Gibbs, H. Zhu, M. Asta, G. J. Snyder, B. Meredig, M. A. White, K. Persson and A. Jain, J. Mater. Chem. C, 2016, 4, 4414 RSC.
- Y. Katsura, M. Kumagai, T. Kodani, M. Kaneshige, Y. Ando, S. Gunji, Y. Imai, H. Ouchi, K. Tobita, K. Kimura and K. Tsuda, Sci. Technol. Adv. Mater., 2019, 20, 511 CrossRef CAS.
- X. Zhang, L. Yu, A. Zakutayev and A. Zunger, Adv. Funct. Mater., 2012, 22, 1425 CrossRef CAS.
- X. Zhang, Q. Liu, Q. Xu, X. Dai and A. Zunger, J. Am. Chem. Soc., 2018, 140, 13687 CrossRef CAS PubMed.
- https://github.com/mathtoriyama/Papers/tree/main/2023/TI_TE .
- L. Müchler, F. Casper, B. Yan, S. Chadov and C. Felser, Phys. Status Solidi, 2013, 7, 91 Search PubMed.
- G. J. Snyder, A. H. Snyder, M. Wood, R. Gurunathan, B. H. Snyder and C. Niu, Adv. Mater., 2020, 32, 2001537 CrossRef CAS PubMed.
- A. Zevalkink, D. M. Smiadak, J. L. Blackburn, A. J. Ferguson, M. L. Chabinyc, O. Delaire, J. Wang, K. Kovnir, J. Martin, L. T. Schelhas, T. D. Sparks, S. D. Kang, M. T. Dylla, G. J. Snyder, B. R. Ortiz and E. S. Toberer, Appl. Phys. Rev., 2018, 5, 021303 Search PubMed.
- Z. M. Gibbs, F. Ricci, G. Li, H. Zhu, K. Persson, G. Ceder, G. Hautier, A. Jain and G. J. Snyder, npj Comput. Mater, 2017, 3, 8 CrossRef.
- A. F. May and G. J. Snyder, Materials, preparation, and characterization in thermoelectrics, CRC press, 2017, p. 207 Search PubMed.
- H. Naithani and T. Dasgupta, ACS Appl. Energy Mater., 2019, 3, 2200 CrossRef.
- J. de Boor, J. Materiomics, 2021, 7, 603 CrossRef.
- H. Wang, R. Gurunathan, C. Fu, R. Cui, T. Zhu and G. J. Snyder, Mater. Adv., 2022, 3, 734 RSC.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72 CrossRef CAS.
- H. Zhang, C.-X. Liu, X.-L. Qi, X. Dai, Z. Fang and S.-C. Zhang, Nat. Phys., 2009, 5, 438 Search PubMed.
- L. Fu, Phys. Rev. Lett., 2009, 103, 266801 CrossRef PubMed.
- C.-X. Liu, X.-L. Qi, H. Zhang, X. Dai, Z. Fang and S.-C. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 045122 CrossRef.
- D. Shao, Z. Guo, X. Wu, S. Nie, J. Sun, H. Weng and Z. Wang, Phys. Rev. Res., 2021, 3, 013278 CrossRef CAS.
- N. A. Mecholsky, L. Resca, I. L. Pegg and M. Fornari, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 155131 CrossRef.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Cengage Learning, 1976, vol. 3 Search PubMed.
- B. M. Askerov, Electron transport phenomena in semiconductors, World scientific, 1994 Search PubMed.
- M. Lundstrom, Fundamentals of carrier transport, 2002.
- M. Y. Toriyama, A. N. Carranco, G. J. Snyder and P. Gorai, Mater. Horiz., 2023, 10, 4256 RSC.
- C. Rudderham and J. Maassen, J. Appl. Phys., 2020, 127, 065105 CrossRef CAS.
- J. O. Sofo and G. Mahan, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 4565 CrossRef CAS PubMed.
- E. H. Hasdeo, L. Krisna, M. Y. Hanna, B. E. Gunara, N. T. Hung and A. R. Nugraha, J. Appl. Phys., 2019, 126, 035109 CrossRef.
- G. J. Snyder, A. Pereyra and R. Gurunathan, Adv. Funct. Mater., 2022, 32, 2112772 CrossRef CAS.
- Z. Zhu, Y. Cheng and U. Schwingenschlögl, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235401 CrossRef.
- M. K. Brod, M. Y. Toriyama and G. J. Snyder, Chem. Mater., 2020, 32, 9771 CrossRef CAS.
- M. K. Brod and G. J. Snyder, J. Mater. Chem. A, 2021, 9, 12119 RSC.
- K. Lin, Q. Li, R. Yu, J. Chen, J. P. Attfield and X. Xing, Chem. Soc. Rev., 2022, 51, 5351 RSC.
- Devender, P. Gehring, A. Gaul, A. Hoyer, K. Vaklinova, R. J. Mehta, M. Burghard, T. Borca-Tasciuc, D. J. Singh, K. Kern and G. Ramanath, Adv. Mater., 2016, 28, 6436 CrossRef CAS PubMed.
- G. Xie, Z. Li, T. Luo, H. Bai, J. Sun, Y. Xiao, L.-D. Zhao, J. Wu, G. Tan and X. Tang, Nano Energy, 2020, 69, 104395 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh01930f |
| This journal is © The Royal Society of Chemistry 2024 |