Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hybrid quantum-classical polarizability model for single molecule biosensing†
Ekaterina
Zossimova
 *ab,
Johannes
Fiedler
*ab,
Johannes
Fiedler
 c,
Frank
Vollmer
a and
Michael
Walter
c,
Frank
Vollmer
a and
Michael
Walter
 bde
bde
aDepartment of Physics and Astronomy, Living Systems Institute, University of Exeter, EX4 4QD, Exeter, UK. E-mail: ez216@exeter.ac.uk
bFreiburg Center for Interactive Materials and Bioinspired Technologies (FIT), University of Freiburg, D-79110 Freiburg, Germany
cDepartment of Physics and Technology, University of Bergen, Allégaten 55, 5007 Bergen, Norway
dCluster of Excellence livMatS @ FIT, Freiburg, Germany
eFraunhofer IWM, MikroTribologie Centrum μTC, Freiburg, Germany
First published on 26th February 2024
Abstract
Optical whispering gallery mode biosensors are able to detect single molecules through effects of their polarizability. We address the factors that affect the polarizability of amino acids, which are the building blocks of life, via electronic structure theory. Amino acids are detected in aqueous environments, where their polarizability is different compared to the gasphase due to solvent effects. Solvent effects include structural changes, protonation and the local field enhancement through the solvent (water). We analyse the impact of these effects and find that all contribute to an increased effective polarizability in the solvent. We also address the excess polarizability relative to the displaced water cavity and develop a hybrid quantum-classical model that is in good agreement with self-consistent calculations. We apply our model to calculate the excess polarizability of 20 proteinogenic amino acids and determine the minimum resolution required to distinguish the different molecules and their ionised conformers based on their polarizability.
1 Introduction
In the pursuit of developing biosensors with high spatial and temporal resolution, many new techniques have been invented to detect things that would otherwise not be visible to the naked human eye. A subclass of these techniques do not rely on images at all – instead they exploit the resonant properties of optical whispering gallery modes (WGM) to detect single molecules1–3 down to 13-mer oligonucleotides4,5 and Ångström-sized amino acids.6 Molecules interacting with the biosensing field perturb the stable resonance of the WGM, and the magnitude of the perturbation is recorded as a signal, encoding information about the characteristic properties of target molecules.Amino acids are the building blocks for proteins that are central for living systems. It is essential to understand how to categorise and potentially differentiate amino acids7 using optical biosensors due to their diverse applications in healthcare, environmental monitoring, biotechnology, and scientific research.8,9 Amino acids are particularly sensitive to solvent effects due to their amphoteric behaviour. At low pH, the amino group (–NH2) acts as a base and accepts a proton from the solvent. At high pH, the carboxyl group (–COOH) donates a proton to the surrounding medium.
Within first-order perturbation theory, the shift of the WGM resonance is proportional to the dipole polarizability of the molecule in excess of the displaced solvent,10i.e. the excess polarizability of the molecule 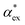 . Numerous methods exist to calculate the gasphase polarizability α of molecules, including additive atomistic models,11,12 electronic structure methods13,14 and machine learning algorithms15–17 as the polarizability is central for the understanding of e.g. weak van der Waals interactions.18–20 However, it is not so obvious how to transform
. Numerous methods exist to calculate the gasphase polarizability α of molecules, including additive atomistic models,11,12 electronic structure methods13,14 and machine learning algorithms15–17 as the polarizability is central for the understanding of e.g. weak van der Waals interactions.18–20 However, it is not so obvious how to transform 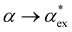 when the molecule is in a solvent21,22 due to several screening and field enhancement effects.23,24 Developing an accurate model for
when the molecule is in a solvent21,22 due to several screening and field enhancement effects.23,24 Developing an accurate model for 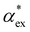 can help to decode the biosensor signals and improve the specificity of polarizability-based biosensing techniques.
can help to decode the biosensor signals and improve the specificity of polarizability-based biosensing techniques.
Density functional theory (DFT) is a quantum-mechanical method that is used to calculate molecular properties from their electronic density. DFT intrinsically accounts for molecular charge and can be conveniently combined with implicit solvent models to study solvated single molecules where the solvent is modelled as a continuum.25–27 The inclusion of solvent effects is essential as the protonation state of the amino acid can be expected to affect its polarizability. Previous studies have shown that implicit solvent models are able to describe the relative energetic stability of different conformers and protonation states of molecules in aqueous environments.28–31
Here, we model the solvation shell encompassing the molecule as a smooth cavity32 to obtain optimised solvated structures of 20 proteinogenic amino acids, including their different protonation states. The smooth cavity model does not distinguish between the externally applied field and the local field seen by the solute molecule. The local fields are required to calculate 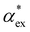 and can be included using the classical Onsager model.33 This leads to a self-consistent equation for the polarizability that must be solved numerically.24 Alternatively, we also propose a hybrid quantum-classical model for
and can be included using the classical Onsager model.33 This leads to a self-consistent equation for the polarizability that must be solved numerically.24 Alternatively, we also propose a hybrid quantum-classical model for 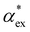 that combines DFT calculations for molecular polarizability (without local field corrections) and scattering effects through a 3-layer cavity model for finite-sized particles. We implement both approaches in GPAW DFT code34,35 and find that they give comparable results for
that combines DFT calculations for molecular polarizability (without local field corrections) and scattering effects through a 3-layer cavity model for finite-sized particles. We implement both approaches in GPAW DFT code34,35 and find that they give comparable results for 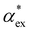 . However, the hybrid quantum-classical model outperforms the numerical model in terms of computational speed and efficiency.
. However, the hybrid quantum-classical model outperforms the numerical model in terms of computational speed and efficiency.
2 Effective polarizability model
The dipole polarizability α of a molecule describes the magnitude of the induced dipole moment due to an applied electric field F| μ = μ0 + αF, | (1) |
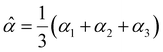 | (2) |
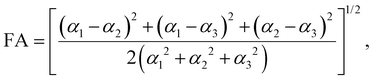 | (3) |
The WGM laser typically probes molecules using near-infrared to visible light to avoid radiation damage on the molecular level.2 The associated frequencies are well below the electronic excitations of amino acids,37 such that we can consider their real-valued response functions in the electrostatic limit,38i.e. α(ωWGM) ≈ Re[α(ω ↦ 0)] ≡ α. This defines the electronic static polarizability of the molecule, which should represent a good approximation at the frequency of the exciting light.22,39 We further assume that the molecules are very small compared to the wavelength of the WGM laser, such that the spatial variation of the biosensing field in the range of the molecule can be neglected.
Under these conditions, the linearity in the external field F allows us to calculate α as
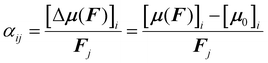 | (4) |
There are changes for molecules in a solvent,21,23,40,41 where the best model to describe these effects is not settled in the literature.42 The influence of the solvent can be separated conceptually into two main factors:22 first, the solvent affects the electron density of the molecules; second, it changes the local field FL acting at the position of the molecule.23,33 Generally, the effective polarizability within the solvent α* is defined analogously to eqn (1) as22
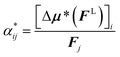 | (5) |
3 Results and discussion
3.1 Solvent vs. gasphase polarizability
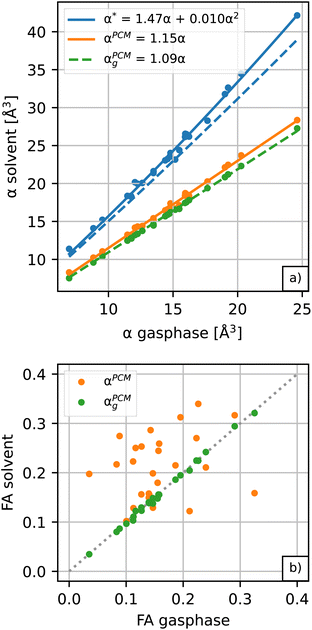
Amino acids are usually present in an aqueous environment. Therefore, this situation is most important. In order to understand the solvent effects on the polarizability of amino acids, it is nevertheless interesting to compare their gasphase polarizabilities to their corresponding polarizabilities within water using different approximations. Fig. 1 gives this comparison, where we observe first of all that α-gasphase occupies a range from 7.0 Å3 for glycine (G) to 24.6 Å3 for tryptophan (W). The gasphase FA is found in the range from 0.04 for lysine (K) to 0.33 for histidine (H+).Using α-gasphase as a reference, we can determine αPCMg,ij = [ΔμPCMg(FL)]i/FLj within the polarizable continuum model (PCM) using the gasphase nuclear structure to isolate the effect of the solvent on the electronic density. Fig. 1a shows that this merely scales the gasphase polarizability by 9% consistently. The increase in the PCM polarizability compared to the gasphase is commonly found in the literature,43,44 but was criticised by some authors.45 The FA of the gasphase structures is not changed within the PCM, as shown by the green data points in Fig. 1b. The FA is thus solely caused by structural asymmetries within the molecule.
We next consider conformational and structural changes of the amino acids in water. Amino acids have charge-neutral functional groups in the gasphase, whereas these become ionised in the solvent. Most of the proteinogenic amino acids are zwitterions at physiological pH and several are either anions (aspartic acid, glutamic acid) or cations (arginine, lysine). The unbalanced charge distribution across the ionised conformers is more sensitive to the external field, resulting in a larger polarizability for the solvated vs. gasphase structures in the PCM solvent (αPCMvs. αPCMg in Fig. 1a). The polarizability increase due to conformational change is approximately 5.5% on average, resulting in a total scaling factor of 1.15 relative to α-gasphase.
The conformational and structural changes also affect the FA, as shown by the orange data points in Fig. 1b. The solvated structures tend to have a higher polarizability anisotropy compared to the gasphase structures. Only histidine (H+), aspartic acid (D−, D) and leucine (L) show a lower fractional anisotropy for the solvated structures compared to the gasphase structures in the PCM solvent. These molecules correspond to the orange data points below the dashed identity line in Fig. 1b.
Finally, we have to consider changes in the local field due to the formation of a cavity around the solute molecule. This is not accounted for in our electronic structure calculations of αPCM. We turn to a classical cavity model, originally formulated by Onsager,33 to calculate the field enhancement within the cavity.
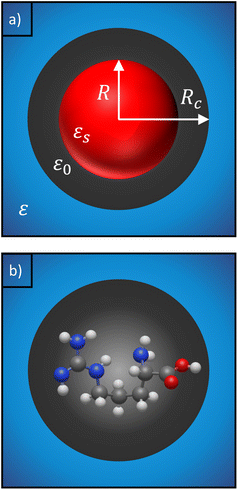
The solute molecule is described as a polarizable point dipole in the center of a spherical cavity with volume V. The solvent surrounding the cavity is described by the PCM with relative permittivity ε. The local field acting on the solute molecule can be represented as a superposition of a cavity field and reaction field, the latter of which depends recursively on the polarizability of the solute molecule. This leads to an equation for the local field enhancement, η = FL/F, which can be written as23,24,33
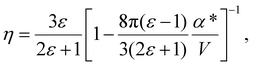 | (6) |
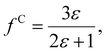 | (7) |
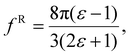 | (8) |
We solve eqn (5) and (6) self-consistently. In the first step of the self-consistent cycle, we start with an initial guess for α*
| α* ≈ αPCMηPCM | (9) |
3.2 Excess polarizability of amino acids
In experiments, the polarizability of target molecules is measured relative to the pure solvent. The pure solvent provides a baseline value for the polarizability measurement, and the molecule is detected by its polarizability in excess of the displaced solvent. In particular, in WGM experiments, the observed shift is caused by the change in polarizability when the resonator is in contact with the detected molecule instead of the omnipresent water.5,6,46 We formulate two different models to calculate the excess polarizability of amino acids; the first uses our numerical results for α*, and the second is a hybrid quantum-classical model inspired by a 3-layer cavity model in classical electromagnetism.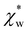 , respectively. We can express the excess polarizability
, respectively. We can express the excess polarizability 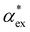 in terms of the polarizability densities as
in terms of the polarizability densities as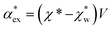 | (10) |
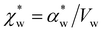 . Assuming that the solvent is water, we can calculate
. Assuming that the solvent is water, we can calculate 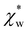 by simulating a single explicit water molecule in an otherwise implicit background of water, following the self-consistent approach described above. The cavity volume of the solute molecule V and single explicit water molecule Vw can be calculated in GPAW using the Kirkwood–Buff method.47 We find that
by simulating a single explicit water molecule in an otherwise implicit background of water, following the self-consistent approach described above. The cavity volume of the solute molecule V and single explicit water molecule Vw can be calculated in GPAW using the Kirkwood–Buff method.47 We find that 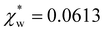 from numerical calculations.
from numerical calculations.
We note that 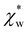 can also be calculated analytically using the polarizability density of water from the Lorentz–Lorenz equation,
can also be calculated analytically using the polarizability density of water from the Lorentz–Lorenz equation,
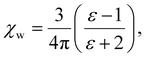 | (11) |
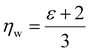 | (12) |
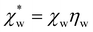 , which simplifies to
, which simplifies to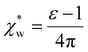 | (13) |
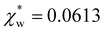 using the permittivity of water at optical frequencies, which is the same as our numerical result from the self-consistent calculation.
using the permittivity of water at optical frequencies, which is the same as our numerical result from the self-consistent calculation.
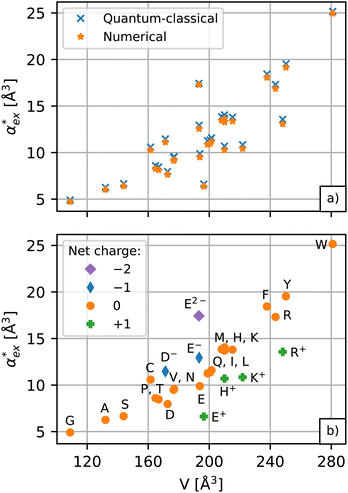
The results for the excess polarizability of amino acids using the self-consistent numerical model in eqn (10) are shown in Fig. 3a. Generally, the excess polarizability of the amino acids tends to be smaller than the gasphase polarizability, except for tryptophan, where the polarizability enhancement due to solvent effects overcompensates the negative contributions of the displaced water (see Fig. S2 in ESI†).
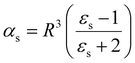 | (14) |
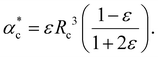 | (15) |
Note, that the polarizabilities defined in eqn (14) and (15) are scaled by a factor of (4πε0)−1 to get volumetric units.
The polarizability can be derived from the viewpoint of the field as a scattering process at the outer boundary of a multi-layer cavity using the scattering Green function for a spherically layered system.48,49 This leads to an equation for the excess polarizability, given by21
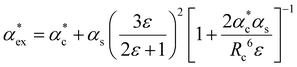 | (16) |
We can replace the hard sphere in the classical model with a real molecule as shown in Fig. 2b. In doing so, we substitute the polarizability of the molecule without local field corrections αPCM for αs in eqn (16) and show that
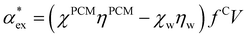 | (17) |
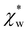 in eqn (13). We can use Rc3 = 3V/4π to convert between the cavity radius and volume.
in eqn (13). We can use Rc3 = 3V/4π to convert between the cavity radius and volume.
The numerical model in eqn (10) and the hybrid quantum-classical model in eqn (17) give very similar results for the excess polarizability, as shown in Fig. 3a. The benefit of using eqn (17) is that the excess polarizability is expressed in terms of χPCM, which is less computationally expensive to calculate than the self-consistent polarizability density χ* that appears in eqn (10). For the set of 20 amino acids considered here, it takes approximately 7 iterations of the self-consistent equation to converge the result for α*. Therefore, the calculation of χPCM is approximately 7 times faster than χ*, on average.
Returning to eqn (17), we can define the excess polarizability density as 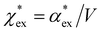 . We can express eqn (17) as a quadratic polynomial in terms of χPCM by using a Taylor series expansion for ηPCM in the limit of small fRχPCM as ηPCM ≈ fC(1 + fRχPCM). This lets us express
. We can express eqn (17) as a quadratic polynomial in terms of χPCM by using a Taylor series expansion for ηPCM in the limit of small fRχPCM as ηPCM ≈ fC(1 + fRχPCM). This lets us express 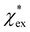 in powers of χPCM as
in powers of χPCM as
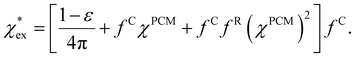 | (18) |
The quadratic equation for 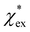 agrees very well with the amino acids data, as shown in Fig. 4.
agrees very well with the amino acids data, as shown in Fig. 4. 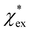 is generally smaller than χPCM in the range 0.00 < χPCM < 0.12, although the two quantities become comparable as χPCM increases due to the approximately quadratic scaling of the reaction field term. The excess polarizability density of water is zero since water is the background medium.
is generally smaller than χPCM in the range 0.00 < χPCM < 0.12, although the two quantities become comparable as χPCM increases due to the approximately quadratic scaling of the reaction field term. The excess polarizability density of water is zero since water is the background medium.
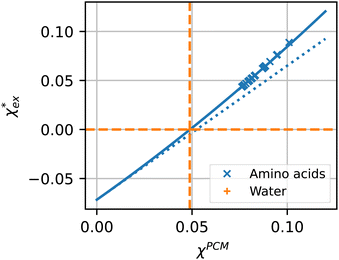 | ||
| Fig. 4 Solid blue line: quadratic approximation for the excess polarizability density, see eqn (18). Dotted blue line: linear approximation for the excess polarizability density (no reaction field, fR = 0). The reference values for water are shown as orange dashed lines for comparison [χw = 0.0488 from the Clausius–Mossotti relation in eqn (11)]. | ||
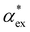 , assuming that the binding site of the molecule can be well controlled in experiments. The polarizability roughly correlates with the molecular volume, as shown in Fig. 3b. Glycine (G) is the smallest molecule studied and has the lowest excess polarizability; tryptophan (W) is the largest molecule studied and has the highest excess polarizability. Assuming that the biosensing field has the same intensity at the position of both molecules, we would expect glycine to produce the smallest shift in the biosensor signal and tryptophan the largest. The biosensor would need to resolve a polarizability difference of approximately 20 Å3 to distinguish the two molecules with extreme polarizabilities. Other molecules, such as cysteine (C) and lysine (K+) would be more difficult to resolve based on
, assuming that the binding site of the molecule can be well controlled in experiments. The polarizability roughly correlates with the molecular volume, as shown in Fig. 3b. Glycine (G) is the smallest molecule studied and has the lowest excess polarizability; tryptophan (W) is the largest molecule studied and has the highest excess polarizability. Assuming that the biosensing field has the same intensity at the position of both molecules, we would expect glycine to produce the smallest shift in the biosensor signal and tryptophan the largest. The biosensor would need to resolve a polarizability difference of approximately 20 Å3 to distinguish the two molecules with extreme polarizabilities. Other molecules, such as cysteine (C) and lysine (K+) would be more difficult to resolve based on 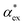 , despite the significant difference in cavity volume.
, despite the significant difference in cavity volume.
3.3 Effect of molecular charge
Biosensing experiments are often performed in a phosphate or a carbonate buffer, which stabilise different pH ranges. Amino acids have highly ionizable functional groups that can exchange protons with the surrounding water.31 The number of protons exchanged depends on the pKa values of the functional groups and on the availability of protons, i.e. the pH of the solution. It can be expected that the removal of a proton leads to an increase of the polarizability as the number of electrons responsible for the polarizability does not change, but they are less bound due to the lower nuclear charge. The hybrid quantum-classical model indeed predicts that negative charged molecules (anions) have a larger polarizability and that positively charged molecules (cations) have a lower polarizability compared to their charge neutral counterparts. This effect can be seen in Fig. 3b for aspartic acid (D), glutamic acid (E), histidine (H), lysine (K) and arginine (R).We use glutamic acid as an example to compare how other polarizability models consider the effect of charge. Glutamic acid plays an important role in neuroscience, the food industry (e.g. monosodium glutamate), and energy production in the body where glutamate is involved in various metabolic pathways. Glutamic acid has two carboxyl groups (pK1 = 2.13, pK2 = 4.31) and an amine group (pK3 = 9.67).50 The net charge of glutamic acid is q = −1 at physiological pH but can vary between q = +1 in a highly acidic environment (fully protonated) and q = −2 in a highly alkaline environment (fully deprotonated). The actual protonation state for a given pH can be evaluated using the Henderson–Hasselbalch equation51–53 as detailed in ESI†.
Optimised structures of solvated glutamic acid ions are used to compare different polarizability models in describing the effect of pH in Fig. 5. The direct DFT calculation through the hybrid quantum-classical model shows the expected behaviour of increasing polarizability with increasing charge. This effect cannot be captured with additive atomistic models, such as the Thole model,11 because there the molecular polarizability always scales with the number of atoms only. The AlphaML (B3LYP) machine learning algorithm also cannot capture this effect because it has been trained on a dataset of neutral molecules,54,55 where the effect of charge would not be evident. The polarizability difference between conjugate acid–base pairs in these atomistic (and machine learning) models is roughly equal to the polarizability of a hydrogen atom αH = 0.7 Å3, but no hydrogen atoms are removed from the amino acids in reality. The hybrid model thus finds a much larger polarizability difference between conjugate acid–base pairs (between 1.7–2.5 Å3) with the opposite charge dependence.
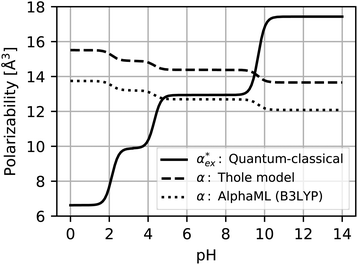 | ||
| Fig. 5 Polarizability of glutamic acid as a function of pH. The hybrid quantum-classical calculation includes solvent effects and is sensitive to the electronic density of the molecule. The Thole model11 is an additive atomistic model and can only capture the effect of adding or removing a hydrogen atom between conjugate acid–base pairs. The machine learning algorithm15,16 (AlphaML) has not been trained on charged molecules and captures the same effect as the Thole model. | ||
4 Conclusions
We have shown that amino acid polarizabilities in the solvent are enhanced as compared to gasphase counterparts, due to different structures, different charge, and most importantly local field enhancements. We have developed a self-consistent excess polarizability model based on finite field polarizabilities determined in a continuum solvent model. We furthermore showed that the computationally less demanding hybrid excess polarizability model proposed in eqn (17) leads to very similar results.Our results will help to decode the signals from single molecule biosensing experiments, where it is important to accurately quantify the excess polarizability of single molecules. The solute molecule can be identified through 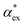 by measuring the magnitude of the biosensor signals. The fractional anisotropy can also be used to identify single molecules by measuring the shift ratio between transverse electric (TE) and transverse magnetic (TM) modes.56–58 Some of the molecules, such as cysteine (C), asparagine (N) and valine (V), may be hard to distinguish based on
by measuring the magnitude of the biosensor signals. The fractional anisotropy can also be used to identify single molecules by measuring the shift ratio between transverse electric (TE) and transverse magnetic (TM) modes.56–58 Some of the molecules, such as cysteine (C), asparagine (N) and valine (V), may be hard to distinguish based on 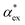 alone. However, the TE to TM shift ratio provides a second molecular fingerprint to help differentiate and categorise the biosensor signals. The shift ratio is expected to be larger for a molecule with high anisotropy and can be referenced against the fractional anisotropy data† to help identify the target molecules. The results presented here form a guide on the experimental sensitivity required to differentiate between different amino acids using WGM-based biosensors. The methods presented can also be applied to other molecules that are of physiological significance.
alone. However, the TE to TM shift ratio provides a second molecular fingerprint to help differentiate and categorise the biosensor signals. The shift ratio is expected to be larger for a molecule with high anisotropy and can be referenced against the fractional anisotropy data† to help identify the target molecules. The results presented here form a guide on the experimental sensitivity required to differentiate between different amino acids using WGM-based biosensors. The methods presented can also be applied to other molecules that are of physiological significance.
5 Computational details
We obtain the gasphase structures of amino acids from the NOMAD repository,59 where we use the structures published by Ropo et al.60 as a starting point to generate the corresponding solvated conformers. We start with the subset of 1694 calcium-coordinated structures provided there and remove the divalent calcium ion to generate a set of initial structures. We use the cation-coordinated structures, as opposed to the bare gasphase structures, to obtain a mix of initial structures that resemble zwitterionic and non-zwitterionic conformers. Sampling a range of initial structures is important because the relaxation algorithm converges to the nearest local minimum in the energy landscape, which may not be representative of the global energetic minimum.The electronic structure of the molecules is described with the GPAW DFT package.34,35,61 The electron density and Kohn–Sham states are described within the projector augmented wave (PAW) method, where the smooth parts are represented on real space grids. The grid spacing in the simulation is 0.2 Å for representing the smooth wavefunctions within the PAW description. The size of the simulation box ensures that each atom is at least 4 Å away from its boundary. We use the PBE exchange–correlation functional62 in the calculation of the DFT energy. The aqueous environment is described by the polarizable continuum model (PCM).32
The amino acid conformers are relaxed using the Broyden–Fletcher–Goldfarb–Shanno algorithm as implemented in the atomic simulation environment (ASE)63 until the maximal force on each atom is below 0.05 eV Å−1, corresponding to the structure of the molecule in the next local minimum of the energy landscape. Here, we use the static permittivity of water (εstat = 78.36)64 in the ground state DFT calculations. The resulting amino acid conformers are sorted according to their relative energies. We consider different protonation states separately, since the net charge can fluctuate depending on the pH of the buffer solution. We find that charge neutral amino acids prefer the zwitterionic form in an aqueous environment. We further consider different protonation states of arginine (R), lysine (K), histidine (H), glutamic acid (E) and aspartic acid (D), which exist predominantly in their ionised form at neutral pH. We use the lowest energy conformers in the polarizability calculations and note the minor variation due to different gasphase and solvated conformers, see Fig. S4 and S5 in ESI,† respectively.
The molecular polarizabilities are calculated from eqn (4) using the finite-field method with external field strength |F| = 0.01 V Å−1. This field strength is tested to be sufficiently small to avoid higher-order contributions and still large enough to avoid numerical difficulties.65 The calculation using finite fields does not have convergence issues in contrast to perturbation theory approaches (see ESI† for the comparison between linear response time-dependent DFT (TDDFT)66 and the finite field method). We apply the same approach to calculate the polarizability in an aqueous environment αPCM using eqn (5) and the local field strength, |FL| = η|F|. Here, we use the optical permittivity of water (εopt = 1.77)67 in the solvation model for the calculation of αPCM because the biosensor typically probes the molecules at optical to near-infrared frequencies, where the permittivity of water is equal to the squared refractive index.
Our description relies on the application of the PCM, which does not account for explicit water molecules that may interact with and stick to charged groups of the amino acids. Such situations can be modelled by including explicit water molecules within the solute region.68,69 However, including explicit water molecules raises the question of how to separate the polarizability of the amino acids from that of the attached water molecules. Wannier orbitals may be a solution,70,71 but this approach largely influences the calculated polarizabilities (see Table S3 in ESI†). Furthermore, we note that an implicit description of the solvent is consistent with the 3-layer cavity model that is used to describe the scattering of the fields (see Fig. 2), where the background medium is represented by its permittivity, ε. It is not immediately clear how this description has to be adjusted in the case of additional explicit water molecules. Answering these questions is beyond the scope of the presented work and has to be assigned to future investigations.
Author contributions
E. Z., M. W. and J. F. conceptualised the excess polarizability models. E. Z. and M. W. developed the code to calculate the excess polarizability and wrote the original draft of the manuscript. E. Z. collected and visualised the data. F. V. and M. W. acquired funding for the project and all authors contributed to review and edit the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. Z. and M. W. acknowledge support from the German Research Foundation (grant number: WA 1687/10-1); E. Z. and F. V. acknowledge support from the Engineering and Physical Sciences Research Council (grant numbers: EP/R031428/1 and EP/T002875/1). J. F. gratefully acknowledges support from the European Union (H2020-MSCA-IF-2020, grant number: 101031712). E. Z. and M. W. are thankful for the computing resources provided by the state of Baden-Württemberg through bwHPC and the German Research Foundation through grant number INST 40/575-1 FUGG (NEMO and JUSTUS 2 clusters). The authors thank Dr Charlie Wand for the helpful discussions and for proofreading the manuscript.Notes and references
- F. Vollmer and S. Arnold, Nat. Methods, 2008, 5, 591–596 CrossRef CAS PubMed.
- N. Toropov, G. Cabello, M. P. Serrano, R. R. Gutha, M. Rafti and F. Vollmer, Light: Sci. Appl., 2021, 10, 42 CrossRef CAS PubMed.
- D. Yu, M. Humar, K. Meserve, R. C. Bailey, S. N. Chormaic and F. Vollmer, Nat. Rev. Methods Primers, 2021, 1, 83 CrossRef CAS.
- M. D. Baaske, M. R. Foreman and F. Vollmer, Nat. Nanotechnol., 2014, 9, 933–939 CrossRef CAS PubMed.
- N. Eerqing, S. Subramanian, J. Rubio, T. Lutz, H.-Y. Wu, J. Anders, C. Soeller and F. Vollmer, ACS Photonics, 2021, 8, 2882–2888 CrossRef CAS.
- S. Vincent, S. Subramanian and F. Vollmer, Nat. Commun., 2020, 11, 2043 CrossRef CAS PubMed.
- H. Ouldali, K. Sarthak, T. Ensslen, F. Piguet, P. Manivet, J. Pelta, J. C. Behrends, A. Aksimentiev and A. Oukhaled, Nat. Biotechnol., 2020, 38, 176–181 CrossRef CAS PubMed.
- A. M. Pettiwala and P. K. Singh, Curr. Med. Chem., 2018, 25, 2272–2290 CrossRef CAS PubMed.
- H. Kosakamoto, N. Okamoto, H. Aikawa, Y. Sugiura, M. Suematsu, R. Niwa, M. Miura and F. Obata, Nat. Metab., 2022, 4, 944–959 CrossRef CAS PubMed.
- S. Arnold, M. Khoshsima, I. Teraoka, S. Holler and F. Vollmer, Opt. Lett., 2003, 28, 272 CrossRef CAS PubMed.
- B. T. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- L. S. Booth, E. V. Browne, N. P. Mauranyapin, L. S. Madsen, S. Barfoot, A. Mark and W. P. Bowen, Sci. Rep., 2022, 12, 1995 CrossRef CAS PubMed.
- S. Millefiori, A. Alparone, A. Millefiori and A. Vanella, Biophys. Chem., 2008, 132, 139–147 CrossRef CAS PubMed.
- L. H. R. D. Santos, A. Krawczuk and P. Macchi, J. Phys. Chem. A, 2015, 119, 3285–3298 CrossRef PubMed.
- D. M. Wilkins, A. Grisafi, Y. Yang, K. U. Lao, R. A. DiStasio and M. Ceriotti, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 3401–3406 CrossRef CAS PubMed.
- Y. Yang, K. U. Lao, D. M. Wilkins, A. Grisafi, M. Ceriotti and R. A. DiStasio, Sci. Data, 2019, 6, 152 CrossRef PubMed.
- C. Feng, J. Xi, Y. Zhang, B. Jiang and Y. Zhou, J. Chem. Theory Comput., 2023, 1207–1217 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- R. A. DiStasio, V. V. Gobre and A. Tkatchenko, J. Phys.: Condens. Matter, 2014, 26, 213202 CrossRef PubMed.
- S. Y. Buhmann, Dispersion Forces I – Macroscopic Quantum, Springer, 2012, vol. 247 Search PubMed.
- J. Fiedler, P. Thiyam, A. Kurumbail, F. A. Burger, M. Walter, C. Persson, I. Brevik, D. F. Parsons, M. Boström and S. Y. Buhmann, J. Phys. Chem. A, 2017, 121, 9742–9751 CrossRef CAS PubMed.
- J. Fiedler, M. Walter and S. Y. Buhmann, J. Chem. Phys., 2021, 154, 104102 CrossRef CAS PubMed.
- A. Aubret, M. Orrit and F. Kulzer, ChemPhysChem, 2019, 20, 345–355 CrossRef CAS PubMed.
- R. Wortmann and D. M. Bishop, J. Chem. Phys., 1998, 108, 1001–1007 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- G. Fisicaro, L. Genovese, O. Andreussi, S. Mandal, N. N. Nair, N. Marzari and S. Goedecker, J. Chem. Theory Comput., 2017, 13, 3829–3845 CrossRef CAS PubMed.
- S. Ringe, N. G. Hörmann, H. Oberhofer and K. Reuter, Chem. Rev., 2022, 122, 10777–10820 CrossRef CAS PubMed.
- D. L. Crittenden, M. Chebib and M. J. T. Jordan, J. Phys. Chem. A, 2004, 108, 203–211 CrossRef CAS.
- M. Targema, N. O. Obi-Egbedi and M. D. Adeoye, Comput. Theor. Chem., 2013, 1012, 47–53 CrossRef CAS.
- F. Comitani, K. Rossi, M. Ceriotti, M. E. Sanz and C. Molteni, J. Chem. Phys., 2017, 146, 145102 CrossRef PubMed.
- R. Ghassemizadeh, B. Moore, T. Momose and M. Walter, J. Phys. Chem. B, 2019, 123, 4392–4399 CrossRef CAS PubMed.
- A. Held and M. Walter, J. Chem. Phys., 2014, 141, 174108 CrossRef PubMed.
- L. Onsager, J. Am. Chem. Soc., 1936, 58, 1486–1493 CrossRef CAS.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Møller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. H. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens. Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- P. W. Atkins and R. S. Friedman, Molecular Quantum Mechanics, OUP, Oxford, 2011 Search PubMed.
- R. Maul, M. Preuss, F. Ortmann, K. Hannewald and F. Bechstedt, J. Phys. Chem. A, 2007, 111, 4370–4377 CrossRef CAS PubMed.
- J. Fiedler, K. Berland, J. W. Borchert, R. W. Corkery, A. Eisfeld, D. Gelbwaser-Klimovsky, M. M. Greve, B. Holst, K. Jacobs, M. Krüger, D. F. Parsons, C. Persson, M. Presselt, T. Reisinger, S. Scheel, F. Stienkemeier, M. Tømterud, M. Walter, R. T. Weitz and J. Zalieckas, Phys. Chem. Chem. Phys., 2023, 25, 2671–2705 RSC.
- M. Walter and M. Moseler, J. Chem. Theory Comput., 2020, 16, 576–586 CrossRef PubMed.
- S. Pipolo, S. Corni and R. Cammi, J. Chem. Phys., 2014, 140, 164114 CrossRef PubMed.
- R. Cammi, J. Comput. Chem., 2019, 40, 2309–2317 CrossRef CAS PubMed.
- J. Fiedler, D. F. Parsons, F. A. Burger, P. Thiyam, M. Walter, I. Brevik, C. Persson, S. Y. Buhmann and M. Boström, Phys. Chem. Chem. Phys., 2019, 21, 21296–21304 RSC.
- M. M. Alam, V. Kundi and P. P. Thankachan, Phys. Chem. Chem. Phys., 2016, 18, 21833–21842 RSC.
- W. Liang, X. Li, L. R. Dalton, B. H. Robinson and B. E. Eichinger, J. Phys. Chem. B, 2011, 115, 12566–12570 CrossRef CAS PubMed.
- M. Medved’, Š. Budzák, W. Bartkowiak and H. Reis, Handbook of Computational Chemistry, Springer International Publishing, Cham, 2017, pp. 741–794 Search PubMed.
- J. Topolancik and F. Vollmer, Biophys. J., 2007, 92, 2223–2229 CrossRef CAS PubMed.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1951, 19, 774–777 CrossRef CAS.
- L.-W. Li, P.-S. Kooi, M.-S. Leong and T.-S. Yee, IEEE Trans. Microwave Theory Tech., 1994, 42, 2302–2310 CrossRef.
- M. S. Tomaš, Phys. Rev. A, 2001, 63, 053811 CrossRef.
- CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, 2014 Search PubMed.
- L. J. Henderson, Am. J. Physiol., 1908, 173–179 CrossRef CAS.
- K. Hasselbalch, Die Berechnung der Wasserstoffzahl des Blutes aus der freien und gebundenen Kohlensäure desselben, und die Sauerstoffbindung des Blutes als Funktion der Wasserstoffzahl, Julius Springer, 1916 Search PubMed.
- P. A. Sims, J. Chem. Educ., 2010, 87, 803–808 CrossRef CAS.
- L. C. Blum and J.-L. Reymond, J. Am. Chem. Soc., 2009, 131, 8732 CrossRef CAS PubMed.
- G. Montavon, M. Rupp, V. Gobre, A. Vazquez-Mayagoitia, K. Hansen, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, New J. Phys., 2013, 15, 095003 CrossRef CAS.
- I. Teraoka, S. Arnold and F. Vollmer, J. Opt. Soc. Am. B, 2003, 20, 1937 CrossRef CAS.
- I. Teraoka and S. Arnold, J. Opt. Soc. Am. B, 2006, 23, 1381 CrossRef CAS.
- I. Teraoka and S. Arnold, J. Appl. Phys., 2007, 101, 023505 CrossRef.
- M. Ropo, C. Baldauf and V. Blum, NOMAD Repository Entry, 2015, https://nomad-lab.eu/prod/v1/gui/dataset/doi/10.17172/NOMAD/20150526220502.
- M. Ropo, M. Schneider, C. Baldauf and V. Blum, Sci. Data, 2016, 3, 160009 CrossRef CAS PubMed.
- J. J. Mortensen, A. H. Larsen, M. Kuisma, A. V. Ivanov, A. Taghizadeh, A. Peterson, A. Haldar, A. O. Dohn, C. Schäfer, E. O. Jónsson, E. D. Hermes, F. A. Nilsson, G. Kastlunger, G. Levi, H. Jónsson, H. Häkkinen, J. Fojt, J. Kangsabanik, J. Sødequist, J. Lehtomäki, J. Heske, J. Enkovaara, K. T. Winther, M. Dulak, M. M. Melander, M. Ovesen, M. Louhivuori, M. Walter, M. Gjerding, O. Lopez-Acevedo, P. Erhart, R. Warmbier, R. Würdemann, S. Kaappa, S. Latini, T. M. Boland, T. Bligaard, T. Skovhus, T. Susi, T. Maxson, T. Rossi, X. Chen, Y. L. A. Schmerwitz, J. Schiøtz, T. Olsen, K. W. Jacobsen and K. S. Thygesen, GPAW: open Python package for electronic-structure calculations, arXiv, 2023, preprint, arXiv:2310.14776 [cond-mat, physics:physics], DOI:10.48550/arXiv.2310.14776.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- M. Uematsu and E. U. Franck, J. Phys. Chem. Ref. Data, 1980, 9, 1291–1306 CrossRef CAS.
- D. Porezag and M. R. Pederson, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 7830–7836 CrossRef CAS PubMed.
- M. Walter, H. Häkkinen, L. Lehtovaara, M. Puska, J. Enkovaara, C. Rostgaard and J. J. Mortensen, J. Chem. Phys., 2008, 128, 244101 CrossRef PubMed.
- G. M. Hale and M. R. Querry, Appl. Opt., 1973, 12, 555 CrossRef CAS PubMed.
- D. Himmel, S. K. Goll, I. Leito and I. Krossing, Chem. – Eur. J., 2011, 17, 5808–5826 CrossRef CAS PubMed.
- O. Brügner, T. Reichenbach, M. Sommer and M. Walter, J. Phys. Chem. A, 2017, 121, 2683–2687 CrossRef PubMed.
- P. L. Silvestrelli and M. Parrinello, Phys. Rev. Lett., 1999, 82, 3308–3311 CrossRef CAS.
- J. J. Molina, S. Lectez, S. Tazi, M. Salanne, J.-F. Dufrêche, J. Roques, E. Simoni, P. A. Madden and P. Turq, J. Chem. Phys., 2011, 134, 014511 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Tabulated polarizabilities of amino acids; comparison of linear response TDDFT polarizabilities versus finite field polarizabilities; relative energetic stability of amino acid conformers in gasphase and solvent; polarizabilities determined from Wannier orbitals. See DOI: https://doi.org/10.1039/d3nr05396b |
| This journal is © The Royal Society of Chemistry 2024 |