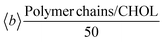Open Access Article
Open Access ArticleThe effect of polymer coating on nanoparticles’ interaction with lipid membranes studied by coarse-grained molecular dynamics simulations†
Edoardo
Donadoni
 ab,
Paulo
Siani
a,
Giulia
Frigerio
ab,
Paulo
Siani
a,
Giulia
Frigerio
 a,
Carolina
Milani
a,
Qiang
Cui
a,
Carolina
Milani
a,
Qiang
Cui
 b and
Cristiana
Di Valentin
b and
Cristiana
Di Valentin
 *ac
*ac
aDepartment of Materials Science, University of Milano-Bicocca, via R. Cozzi 55, 20125 Milan, Italy. E-mail: cristiana.divalentin@unimib.it
bDepartment of Chemistry, Boston University, 590 Commonwealth Ave, Boston, MA 02215, USA
cBioNanoMedicine Center NANOMIB, University of Milano-Bicocca, Italy
First published on 8th April 2024
Abstract
Nanoparticles’ (NPs) permeation through cell membranes, whether it happens via passive or active transport, is an essential initial step for their cellular internalization. The NPs’ surface coating impacts the way they translocate through the lipid bilayer and the spontaneity of the process. Understanding the molecular details of NPs’ interaction with cell membranes allows the design of nanosystems with optimal characteristics for crossing the lipid bilayer: computer simulations are a powerful tool for this purpose. In this work, we have performed coarse-grained molecular dynamics simulations and free energy calculations on spherical titanium dioxide NPs conjugated with polymer chains of different chemical compositions. We have demonstrated that the hydrophobic/hydrophilic character of the chains, more than the nature of their terminal group, plays a crucial role in determining the NPs’ interaction with the lipid bilayer and the thermodynamic spontaneity of NPs’ translocation from water to the membrane. We envision that this computational work will be helpful to the experimental community in terms of the rational design of NPs for efficient cell membrane permeation.
1. Introduction
Titanium dioxide (TiO2) nanoparticles (NPs) have been under the spotlight of nanomedicine as innovative theranostic platforms. Thanks to their excellent photocatalytic properties and ease of surface functionalization, they have found applications in photodynamic therapy,1–3 as drug delivery systems4 or targeting nanodevices in targeted cancer therapies,5–7 as well as in tumor diagnostics.8–10Nonetheless, a noteworthy disadvantage in the clinical use of TiO2 NPs and, in general, of inorganic NPs is their higher intrinsic toxicity,11,12 compared to organic NPs. Upon injection into the human bloodstream, they interact with the proteins of the serum, which adsorb on the NPs’ surface, producing a protein corona.13 Protein corona creation, also known as the opsonization process, is the beginning of the recognition and sequestration of NPs from the bloodstream by macrophages: depending on the NPs’ dimension, they are either expelled through renal filtration (<5 nm) or they accumulate in the spleen or the liver.14
One way to overcome protein corona formation and therefore prolong the NPs’ blood circulation lifetime is to cover their surface with biocompatibility enhancing agents, among which polyethylene glycol (PEG) polymer chains have proven to be efficient in shielding NPs from the interaction with serum proteins, due to a combination of steric hindrance and electrostatic forces, hence protecting the NPs from macrophage attack.15–17 These stealth NPs have superior efficacy for reaching tumor sites compared to unprotected NPs.
There are different ways for NPs to enter tumor cells. If they are functionalized with ligands that recognize specific protein receptors on tumor cells, they are internalized by receptor-mediated endocytosis: this strategy is called active targeting.18 However, even in the absence of selective ligand–receptor interactions, NPs have been shown to accumulate at tumor sites and passively diffuse into tumor cells. Such observation is due to the leaky vasculature of the tumor cell tissues, compared to those of healthy cells, which favors the collection and permeation of the NPs. This is referred to as the enhanced permeability and retention (EPR) effect and forms the basis of passive targeting.19
Thus, it is evident that after avoiding the immune system response, the next barrier for the NPs is represented by the tumor cell membrane, made of phospholipids and sterols and organized in bilayers.20 Understanding the molecular details of NPs’ translocation through the cell membrane is of utmost importance, since the NPs’ coating influences the rate or even the spontaneity of the membrane translocation.
Besides fluorescence microscopy21 and atomic force microscopy,22 super-resolution stimulated emission depletion (STED) microscopy23 is a powerful and widely used technique for visualizing the interactions and cellular uptake of nanosystems. Raman spectroscopy and infrared absorption spectroscopy are compelling methods for non-destructive and label-free imaging while retaining chemical selectivity.24 Moreover, when integrated with optical microscopy, these techniques offer robust approaches for non-invasive chemical imaging.25,26
However, many limitations still exist at the experimental level in characterizing the nano–bio interactions. On the one hand, electron microscopy and fluorescence microscopy allow for particle identification at the cellular level, but they are predominantly qualitative and exhibit low throughput. Moreover, they usually do not inherently enable the analysis of dynamic processes occurring during the interactions between nanoparticles and cells. On the other hand, the main limitation of Raman spectroscopy resides in its spatial resolution, which is determined by the wavelength of the incident light that is restricted to hundreds of nanometers. Therefore, an alternative approach is to conduct molecular simulations.
In this respect, several all-atom molecular dynamics (AAMD) studies have tackled the interaction of small drug molecules with lipid membranes,27–30 including a recent work by some of us,31 where we investigated the penetration of the anticancer agent doxorubicin (DOX) through non-standard lipid bilayers composed of sphingomyelin and sphingomyelin/cholesterol. The role of the membrane phase and composition was elucidated by both structural and thermodynamic analyses, revealing that DOX penetration is favored in less ordered lipid phases and that the presence of cholesterol defines additional hydrophilic regions where the DOX penetration is spontaneous.
There are fewer AAMD studies on inorganic NP interactions with lipid membranes. We note studies on fullerene C60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 or gold33 NPs interacting with di-myristoyl-phoshatidylcholine or dipalmitoylphosphatidylcholine/dipalmitoylphosphatidylglycerole (DPPC/DPPG) membranes, respectively. Moreover, Aranha et al.34 reported on the adhesion of a 3 nm × 2 nm truncated bipyramidal anatase TiO2 NP to lipid bilayers, considering both zwitterionic and negatively charged lipids: their results show that the TiO2 NP interacts mostly with the anionic lipid bilayers, leading to a greater membrane curvature compared to electroneutral ones.
32 or gold33 NPs interacting with di-myristoyl-phoshatidylcholine or dipalmitoylphosphatidylcholine/dipalmitoylphosphatidylglycerole (DPPC/DPPG) membranes, respectively. Moreover, Aranha et al.34 reported on the adhesion of a 3 nm × 2 nm truncated bipyramidal anatase TiO2 NP to lipid bilayers, considering both zwitterionic and negatively charged lipids: their results show that the TiO2 NP interacts mostly with the anionic lipid bilayers, leading to a greater membrane curvature compared to electroneutral ones.
Although providing atomic level insights, AAMD simulations have spatial and temporal limitations, which allow the observation of only the early stages of NPs’ interaction with membranes. For this reason, coarse-grained molecular dynamics (CGMD) simulations are typically exploited to study membrane penetration by NPs,35 where a longer simulation time (on the order of μs) is reached, and membrane models of more realistic size can be included at the expense of a less detailed and accurate description of the system.36–38
Along this line, we can find studies on inorganic nanosystems like zinc sulfide quantum dots,39 although most of the work has been done with gold NPs and the MARTINI40 force field (FF). Notably, studies on unbiased CGMD of bare41 or small alkyl ligand-functionalized42 Au NPs penetrating lipid membranes have been recently reported. Furthermore, free energy calculations coupled with CGMD have been employed to compute the potential of mean force (PMF) profiles of NP translocation across lipid bilayers. For instance, Lunnoo et al.43 described the roles played by the size, shape, surface charge and aggregation of bare gold NPs in determining their uptake by mammalian cells and found that aggregation reduces the permeability of the NPs. The same authors investigated how the surface charge of functionalized Au NPs (cationic, anionic or zwitterionic) impacts their translocation through lipid membranes and concluded that zwitterionic Au NPs have higher translocation free energy barriers than charged NPs.44,45 Also, Lin et al.46 examined the effect of the surface charge sign and density of Au NPs grafted with thiol chains containing different terminal groups, which either repel or adhere to or penetrate the lipid bilayers. Salassi et al.,47 instead, observed that the protonation of the carboxylic groups of thiol-conjugated gold NPs makes their interaction with the lipid membrane less disruptive.
Computational studies probing the interaction between NPs coated with long polymer chains and lipid bilayers are still scarce in the literature. To mention one, Li et al.48 found that the length of the PEG chains conjugated to hydrophobic or hydrophilic NPs, together with the dimension of the NPs itself, has a crucial impact on the shielding effect of grafted PEG molecules, i.e. on the suppression of the membrane bending caused by the NPs.
To fill this gap, in this work we use CGMD simulations to investigate how the different chemical nature of polymer chains affects their interaction with a phospholipid membrane, when they are either free or conjugated to a spherical NP. We consider several polymer types that differ in the hydrophobicity/hydrophilicity ratio of monomeric units and in the charge of the terminal groups. Moreover, by means of free energy calculations, we determine the free energy profiles associated with the translocation of the nanoconjugates from bulk water to the membrane center, depending on their different surface coating.
2. Computational methods
2.1. Systems and their nomenclature
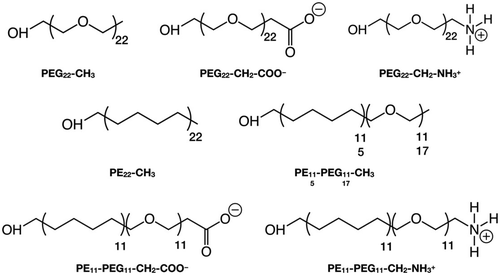
In this section, we introduce the various systems studied in this work and their corresponding nomenclature. The polymer chains we considered are (Scheme 1):1. Polyethylene glycol (PEG), HOCH2-[CH2OCH2]n-X, where n = 22 and X = CH3, CH2-COO−, CH2-NH3+
2. Polyethylene (PE), HOCH2-[CH2CH2CH2CH2]n-CH3, where n = 22
3. Mixed polyethylene–polyethylene glycol (PE–PEG), HOCH2-[CH2CH2CH2CH2]n-[CH2OCH2]m-X, where n = m = 11 or n = 5, m = 17 and X = CH3, CH2-COO−, CH2-NH3+, where the PE and PEG parts are linked by an ether bond (–CH2–O–CH2–), after removing one H from the –CH3 terminal group of the PEn-CH3 and the H atom of the –OH group of the PEGm−1-X, as shown in Scheme S1.†
The polymer chains are named after their chemical acronym, i.e. PEn, PEGn or PEn-PEGm, where n and m indicate the number of units and “-” indicates covalent bonding. To identify the specific termination, the chain name is followed by the terminal group, i.e. methyl (–CH3), deprotonated carboxyl (–CH2–COO−) or protonated amine (–CH2–NH3+), e.g. PE11-PEG11-CH3. When the terminal group is written as -X, we refer to chains that may terminate with any of these possible terminal groups, e.g. PEG22-X refers simultaneously to PEG22-CH3, PEG22-CH2-COO− and PEG22-CH2-NH3+.
The nanoparticle is referred to as NP and, when it is coated with polymer chains through undissociated –OH group attached to a surface Ti atom, the resulting nanoconjugates are named with the NP label followed by the number and name of the attached polymer chains, e.g. NP-50-PE11-PEG11-CH3.
The lipid membrane is abbreviated as MEMB. Systems where a single polymer chain or the coated NP is placed with the lipid bilayer are named with the MEMB label followed by the corresponding polymer or NP involved, e.g. MEMB/PE11-PEG11-CH3 or MEMB/NP-50-PE11-PEG11-CH3, where “/” stands for non-covalent interactions.
2.2. All-atom molecular dynamics (AAMD) simulations
The AAMD simulations of single polymer chains in solution were performed using the GROMACS49 (2021.3 version) package. The CHARMM36 FF50–53 parameters for PEG chains were assigned with the Ligand Reader and Modeler54 module on the CHARMM-GUI55 web-based interface. The Solution Builder56 module of CHARMM-GUI was used to solvate the PEG chains in cubic boxes with the dimension of 75 × 75 × 75 Å3 filled with CHARMM-modified TIP3P (mTIP3P)57–59 water molecules; Na+ and Cl− ions were added to reach the physiological salt concentration of 0.15 M. After energy minimization, the system was heated to 303 K and equilibrated for 1 ns, then an NPT MD simulation was run up to 100 ns. The Nosé–Hoover60,61 thermostat with a coupling constant of 1.0 ps and the Parrinello–Rahman62 barostat with a coupling constant of 5.0 ps were used to control the temperature (303 K) and pressure (1 bar). We employed the LINCS63 algorithm to constrain the bonds involving H atoms and Newton's equations of motion were integrated using the Velocity-Verlet64 algorithm with a timestep of 2.0 fs. Long-range electrostatic interactions were handled with the Particle Mesh Ewald65 method with a cutoff distance of 12 Å, while short-range repulsive and attractive interactions were treated by the Lennard-Jones (LJ) potential and the Lorentz–Berthelot combining rules with an energy switching function that ramped smoothly between an inner cutoff of 10 Å and an outer cutoff of 12 Å. Periodic boundary conditions were imposed.For the AAMD simulations involving the TiO2 nanoparticle, we used the LAMMPS66 (29 Sep 2021 version) package. The bare TiO2 NP model was designed by our group in previous works67,68 and consists of a spherical anatase nanoparticle, carved from the crystalline bulk anatase structure and fully relaxed, first at the Density Functional Tight-Binding (DFTB) level of theory with a simulated annealing procedure, followed by a Density Functional Theory (DFT) optimization using the B3LYP hybrid functional. The stoichiometry of the NP is (TiO2)223·10H2O and it is characterized by an approximate diameter of 2.2 nm. In previous studies,69,70 we grafted the surface of this TiO2 NP model with 50 methoxy-PEG polymer chains, corresponding to a grafting density of 2.25 chains nm−2, and then performed energy minimization followed by classical MD simulations at 300 K. This model has been modified to obtain the systems used for the current study. We extended the PEG chains by another 11 monomeric units and minimized at the classical level. Here, besides the methyl (–CH3), we considered other chain terminal groups, i.e. deprotonated carboxyl (–CH2–COO−) and protonated amine (–CH2–NH3+). The NP was described by an improved Matsui–Akaogi FF, reparametrized by Brandt and Lyubartsev,71 while the CHARMM36 FF50–53 was employed for the adsorbed PEG chains. The FF used for the functionalized NP has been tested and validated for a TiO2 NP tethered with small organic molecules72 and employed in our previous works.73–76 TiO2-PEG topologies were generated by means of the Moltemplate77 package for LAMMPS and the systems were immersed in a 220 × 220 × 220 Å3 mTIP3P57–59 water box, built with the PACKMOL78 software. During all the atomistic MD simulations, we held the geometry of the NP core and of the anchoring PEG -OH groups fixed at the DFTB geometry. We treated the nanoparticle as a rigid body, free to translate and rotate as a whole, with its internal degrees of freedom fixed at the DFTB-optimized geometry through the RIGID79 package in LAMMPS.72–75 This approach keeps the DFTB relative atomic positions within the TiO2 NP and avoids any misshaping of the core during the MD simulation. The remaining degrees of freedom were free to evolve in time, at 303 K (NVT ensemble), with a 2 fs timestep, and the SHAKE80 algorithm imposed holonomic constraints on all the covalent bonds involving hydrogen atoms. Periodic boundary conditions were used. Long-range electrostatic interactions were evaluated by the particle–particle–particle–mesh (PPPM)81 solver, using a real-space cutoff of 12 Å. Short-range Lennard-Jones (12-6) interactions were smoothly truncated with a 12 Å cutoff by means of a switching function applied between 10 and 12 Å. Several minimization steps ensured that no overlaps between the atoms occurred, then an NVT equilibration followed and finally, a production run of 30 ns.
2.3. Coarse-grained molecular dynamics (CGMD) simulations
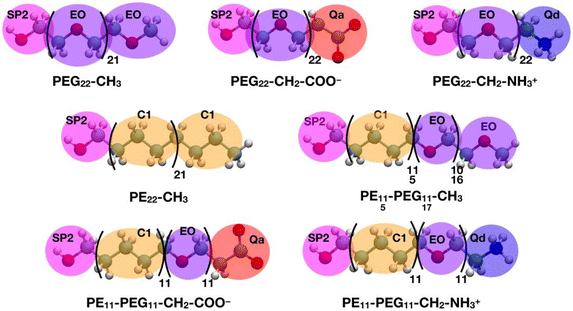
All the CGMD simulations were performed using the GROMACS49 (2021.3 version) package. The polymer chain topologies were generated with the polyply82 suite and the MARTINI 2 parameters set proposed by Grunewald et al.83 In Scheme 2, the all-atom representations of each polymer chain and the corresponding coarse-grained mapping are shown.The single polymer chains were solvated in cubic boxes with sides of 11 × 11 × 11 nm3 filled with MARTINI84 water and Na+ and Cl− were added to counterbalance the charge of the solute and mimic the physiological salt concentration of 0.15 M. After energy minimization, the systems were heated to 303 K and equilibrated for 100 ns, then an NPT MD simulation was run up to 30 μs. The velocity-rescale85 thermostat with a coupling constant of 1.0 ps and the Parrinello–Rahman62 barostat with a coupling constant of 5.0 ps were used to control the temperature (303 K) and pressure (1 bar). Newton's equations of motion were integrated in time using the Velocity-Verlet86 algorithm with a timestep of 20 fs. Van der Waals interactions were computed with the Lennard-Jones (12-6) potential. Long-range electrostatic interactions were handled with the reaction field electrostatics87–89 (dielectric constant of 15) with a coulombic cutoff of 1.1 nm. Periodic boundary conditions were imposed.
The membrane models were designed using the CHARMM GUI Membrane Builder90,91 plugin. We prepared two 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine/cholesterol (POPC/CHOL) bilayers, both with 10% M content of CHOL: a smaller one (1300 lipids, 19 × 19 nm2) and a larger one (3000 lipids, 29 × 29 nm2), solvated on both sides with MARTINI water. Then, the standard minimization and equilibration steps were performed under semi-isotropic pressure coupling, using the MARTINI 2 FF.84
Single polymer chains were inserted in the middle of the smaller POPC/CHOL bilayer (1300 lipids), then the systems were relaxed and equilibrated at 303 K for 100 ns in 19 × 19 × 25 nm3 MARTINI water boxes with 0.15 M NaCl, where the z-position (perpendicular to the bilayer) of the polymer chains’ center of mass was constrained with a force constant of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2. Then, the constraint was removed, and a 5 μs production followed.
000 kJ mol−1 nm−2. Then, the constraint was removed, and a 5 μs production followed.
The TiO2 NP was described as a single particle with σ = 2.2 nm and ε = 4.5 kJ mol−1,92 following a minimalist approach.93 The NP surface was decorated with 50 polymer chains using the PACKMOL78 program, reproducing the 2.25 chains nm−2 grafting density of the AA models. In the case of the PEG22-X chains, the terminal hydroxyl group bead (SP2 type in Scheme 2) was kept fixed at a distance of 1.3 nm from the NP center. As shown in Scheme 1, the label PE22-CH3 represents a polyethylene chain that has been functionalized with an anchoring –OH group (SP2 bead) to simulate the same type of interaction with the NP surface of PEG22-X chains. Finally, mixed PEn-PEGm-X chains were grafted to the NP from the PE side, in analogy to what was just described for PE22-CH3 chains.
Then, the PEGylated NP systems were solvated in 15 × 15 × 15 nm3 cubic boxes with MARTINI water and 0.15 M NaCl. After minimization, a 10 ns equilibration and 10 μs production at 303 K were performed, where the distance between the centers of mass of the polymer chains’ SP2 beads and the NP was constrained with a force constant of 1000 kJ mol−1 nm−2.
The functionalized NPs were introduced in the center of the larger POPC/CHOL membrane (3000 lipids) by means of the gmx insert-molecules utility in GROMACS,49 which removed the lipid molecules overlapping with the nanoconjugates. The systems were relaxed and equilibrated at 303 K in 29 × 29 × 45 nm3 MARTINI water boxes with 0.15 M NaCl, where the z-position of the NP center of mass was constrained with a force constant of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2; constraints were also applied to the positions of the polymer chains’ SP2 beads. Then, the constraint on the NP z-position was removed and a 5 μs production followed.
000 kJ mol−1 nm−2; constraints were also applied to the positions of the polymer chains’ SP2 beads. Then, the constraint on the NP z-position was removed and a 5 μs production followed.
2.4. Free energy calculations
The simulation protocol used in this work for the free energy calculations involves two steps: the first one is Steered Molecular Dynamics (SMD), which is followed by Umbrella Sampling (US) simulations. The SMD step was necessary to collect a series of configurations along the selected reaction coordinate (ξ) that represents the z-distance of the NP from the membrane center. During this procedure, the subunits were pushed away from one another by applying a biasing potential to their centers of mass (COM). The COM of the subunits were oriented along the z-direction. During the pulling simulations, a harmonic potential with a force constant of 1000 kJ mol−1 nm−2 was applied only along the z-direction with a pulling rate of 0.001 nm ps−1. Frames representing a COM spacing of 0.2 nm, referred to as configurations, were extracted from the pulling trajectories and used as starting points for the US simulations. The US simulations were performed at 303 K and 1 atm for 200 ns, where each configuration was restrained within a window corresponding to the chosen COM distance by applying a harmonic potential with a force constant of 1000 kJ mol−1 nm−2. All the SMD and the US simulations were carried out using the MARTINI 2 force field and the GROMACS code. The Potential of Mean Force (PMF) was calculated on the last 50 ns of the US simulations from the umbrella histograms using the Weighted Histogram Analysis Method (WHAM)94 implemented in GROMACS and error bars were calculated with the bootstrap method.From the PMF profiles, we extracted the nanoconjugates ΔGtranslocation, defined as:
| ΔGtranslocation = Gmembrane(ξ) − Gwater (ξ) | (1) |
2.5. Simulation analysis
The calculations of the non-bonded interaction energies (vdW and electrostatic) were performed through the gmx energy package, implemented in the GROMACS code.The radius of gyration calculations were performed with the gmx gyrate module, implemented in the GROMACS code.
All distances were computed through the interdist tool included in the open-source software LOOS 3.1.95 Number density profiles were obtained by the density-dist tool included in LOOS. We calculated the number density along the bilayer normal direction (z), subdividing the simulation box into several parallelepiped-shaped slots with a z-dimension of 0.1 Å, counting the number of particles for each bin and normalizing it by the volume of the slab.
2.6. Validation of CG parameters against AAMD simulations
In this section, we aim at validating the set of CG parameters proposed by Grunewald et al.83 that we used to describe three PEG22-X chains with different terminal groups, i.e. methyl (PEG22-CH3), deprotonated carboxyl (PEG22-CH2-COO−) and protonated amine (PEG22-CH2-NH3+), against atomistic MD simulations, where the PEG22-X chains are described by the CHARMM36 FF.53The first validation is based on the comparison between 30 μs CGMD and 100 ns AAMD simulations of single PEG22-X chains in a 0.15 M NaCl water solution at 303 K, from which last-frame snapshots are shown in Fig. S1 of the ESI.†
The CG parameters are assessed based on the radius of gyration (Rg) of PEG22-X chains, whose average values over the last 10 ns of AAMD and the last 10 μs of CGMD simulations are listed in Table 1, with associated standard deviations.
| System | R g (Å) | |
|---|---|---|
| AAMD | CGMD | |
| PEG22-CH3 | 10.4 (±2.0) | 10.6 (± 1.9) |
| PEG22-CH2-COO− | 10.5 (±2.0) | 11.1 (±1.9) |
| PEG22-CH2-NH3+ | 10.3 (±2.1) | 11.1 (±1.9) |
We observe good agreement of Rg data between AAMD and CGMD simulations: although the CG parameters set overestimates Rg, the difference lies within the error bar of the statistics.
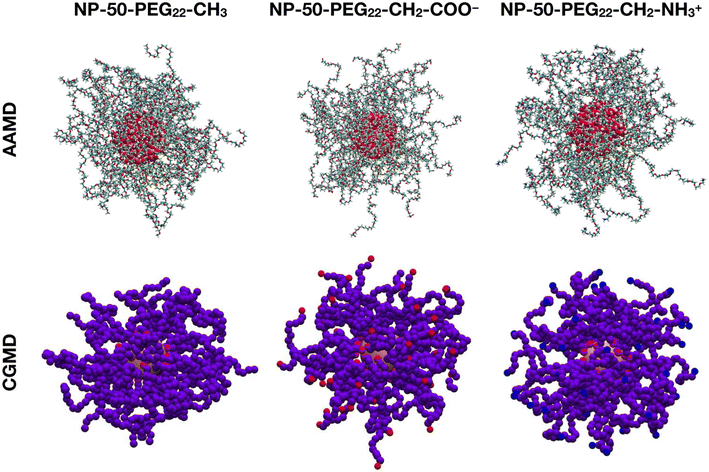
The second validation is conducted on 10 μs CGMD against 30 ns AAMD simulations of a spherical TiO2 NP with a diameter of 2.2 nm, functionalized with 50 PEG22-X chains with different terminal groups and immersed in a 0.15 M NaCl water solution at 303 K. The last-frame snapshots from the MD runs are shown in Fig. 1.
We observe that the PEG22-CH2-COO− and the PEG22-CH2-NH3+ chains have their charged terminal groups pointing towards the solution and thus are more stretched out than the PEG22-CH3 chains.
In Table 2 we report the average Rg values of the 50 PEG22-X chains attached to the NP, calculated for the last 10 ns of 30 ns AAMD and the last 1 μs of 10 μs CGMD simulations.
| System | R g (Å) | |
|---|---|---|
| AAMD | CGMD | |
| NP-50-PEG22-CH3 | 10.5 (±0.5) | 11.4 (±0.4) |
| NP-50-PEG22-CH2-COO− | 11.6 (±0.5) | 12.2 (±0.4) |
| NP-50-PEG22-CH2-NH3+ | 11.3 (±1.4) | 12.2 (±0.4) |
Once again, there is fair agreement between AAMD and CGMD simulations, with a slight overestimation of Rg by CG parameters. In addition, the Rg values of the charged PEG22-X chains (PEG22-CH2-COO− and PEG22-CH2-NH3+) are higher than those of NP-50-PEG22-CH3 in both AAMD and CGMD simulations, which reflects the behavior of PEG22-CH2-COO− and PEG22-CH2-NH3+ chains of having their charged ends pointing toward the bulk water phase, hence being less coiled than PEG22-CH3 chains.
As further validation, in Fig. S2† we have also computed the average radial distribution function (rdf) of the PEG chains with respect to the center of the NP, along the last 1 μs of 10 μs CGMD simulations of NP-50-PEG22-X systems in water at 303 K and 1 atm and compared it with that from the last 10 ns of 30 ns AAMD simulations of the corresponding systems. Given the agreement of the rdf peak positions between AA and CG simulations, we further confirm the validity of the CG parameters.
In conclusion, we have assessed the reliability of PEG22-X CG parameters by a comparative conformational analysis of PEG22-X chains with different terminal groups, free or attached to a spherical NP in water, in CGMD vs. AAMD simulations. This validation supports us to simulate, at a CG level, the interaction of these PEG22-X chains and other polymer chains containing a PEG portion, with a lipid bilayer.
3. Results and discussion
The results are organized as follows: in section 3.1 and section 3.2, respectively, we discuss the effects of the chemical nature of the polymer's terminal group and the hydrophobic/hydrophilic character of the chains on the interaction of both single chains and polymer-conjugated spherical NPs with a POPC/CHOL lipid membrane. In section 3.3, we analyze the nanoconjugate–membrane interaction from an energetic point of view. Finally, in section 3.4, we compute free energy profiles of the coated NPs penetration through the lipid membrane.3.1. Effect of the chemical nature of the polymer chains’ terminal group
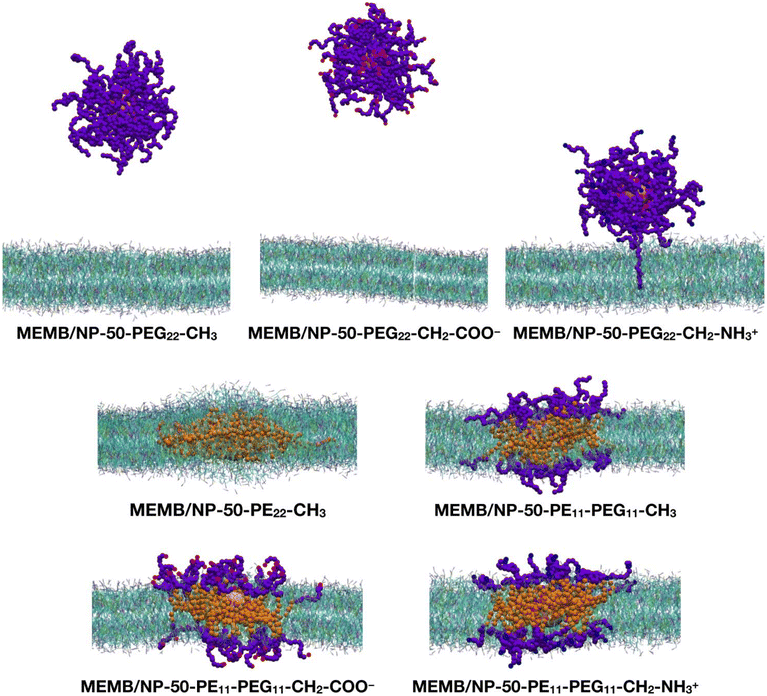
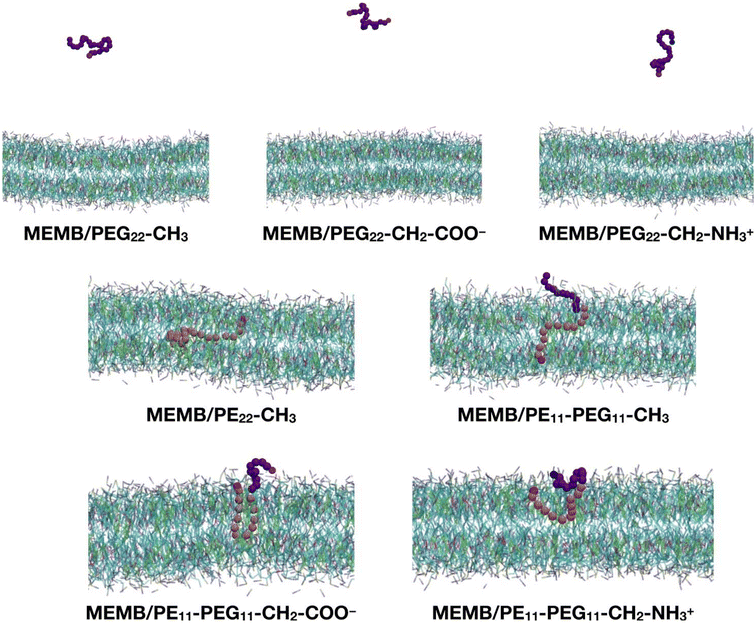
In this section, we study the effect of the chemical nature of the polymer's terminal group on the interaction of coated NPs with a lipid membrane. The polymer chains that we have considered are: PEG22-CH3, PEG22-CH2-COO−, PEG22-CH2-NH3+, PE22-CH3, PE11-PEG11-CH3, PE11-PEG11-CH2-COO− and PE11-PEG11-CH2-NH3+ (see Scheme 1).As a preliminary step, we considered a single chain of each type and inserted it in the center of a solvated POPC/CHOL lipid bilayer (1300 lipids, 10% M CHOL). The system was relaxed, equilibrated and let to evolve in time for 5 μs. In Fig. 2 we report the last-frame snapshots of the CGMD simulations for the seven systems.
We observe that by the end of the simulation, all the PEG22-X chains are completely expelled from the membrane. In contrast, the other polymers remain fully inside the bilayer: in the case of the PE22-CH3 chain, its hydrocarbon portion is found entirely in the lipid tail region and its –OH group (SP2 bead) in the POPC glycerol groups region. In the case of the mixed PE11-PEG11-X chains, while the PE part penetrates deeper inside the membrane, the PEG part stays in the headgroups region or at the water/headgroups interface. Moreover, the PE11-PEG11-CH3 chain is less coiled than the PE11-PEG11-CH2-COO− and PE11-PEG11-CH2-NH3+ ones, as the end groups are found at opposite membrane leaflets.
Next, we performed CGMD simulations of a spherical NP coated by 50 polymer chains of the same type as those just discussed above and placed in the middle of a POPC/CHOL bilayer. Given the larger size of the coated NP compared to the single polymer chain, in this case we used a larger membrane model, with the same membrane composition. Note that the lipid molecules in the region overlapping with the nanoconjugate had to be removed. The coated NP was constrained at the center of the membrane during the equilibration, then the constraints were removed, and a 5 μs production phase followed. In Fig. 3, the last-frame snapshots from the MD simulations are shown.
At the end of the 5 μs CGMD simulation, in the MEMB/NP-50-PEG22-CH3 and MEMB/NP-50-PEG22-CH2-COO− systems, the functionalized NP is found in the bulk water phase, whereas in the MEMB/NP-50-PEG22-CH2-NH3+ system, although the NP is outside the bilayer, some PEG22-NH3+ chains interact with the lipid's phosphate groups at the surface, and one chain is still located inside the bilayer.
For the latter system, in order to exclude that the coated NP is kinetically trapped in the configuration shown in Fig. 3, we have performed two replicas of the MEMB/NP-50-PEG22-CH2-NH3+ system: a 1 μs CGMD simulation, starting from the structure at 5 μs of the original simulation and assigning different initial velocities, and a 5 μs CGMD simulation starting from the equilibrated structure at 100 ns of the original simulation and assigning different initial velocities. In Fig. S3 and S4,† the last-frame snapshots of the two simulations are shown. In both cases, the configurations of the coated NP are similar to the one of the original simulation.
Based on these observations, we conclude that the PEG -CH2-NH3+ groups interact more favorably with the POPC phosphates than PEG -CH2-COO− with the POPC choline groups. We rationalize this different interaction, i.e. of Qa (PEG -CH2-COO− group) and Qd (PEG -CH2-NH3+ group) beads with choline (Q0) and phosphate (Qa) beads, respectively, due to the different Lennard-Jones (LJ) parameters, since electrostatic interactions are equivalent in the entity. To prove our hypothesis, in Fig. S5† we have plotted the Qd–Qa and Qa–Q0 LJ interaction profiles. Indeed, we observe that the LJ interaction for the Qd/Qa pair is more attractive than that for the Qa/Q0 pair.
In the MEMB/NP-50-PE22-CH3 system, the nanoconjugate is completely immersed in the membrane, and some lipid molecules are wrapped around it from above and below the plane of the membrane, to avoid the interaction of the hydrophobic PE chains with water. This observation is in line with the known poor solubility of PE in water. To further investigate the water stability of the PE-coated NPs, we have performed a 5 μs CGMD simulation of the NP grafted with 50 PE22-CH3 chains, whose first and last frame snapshots are shown in Fig. S6.† Moreover, in Table S1† the average PE-PE and PE-water non-bonded interaction energies on the last 1 μs are reported. Our results reveal that PE chains interact among themselves more favorably than with the solution, as the PE–PE interaction energy is about 6.5 times more negative than the PE–water energy.
Finally, in the systems with mixed PE11-PEG11-X chains, both the NP and the PE portion of the chains are entirely located inside the bilayer, while the PEG portion lies in the bilayer polar region, spanning from the glycerol group area to the headgroups, and to the water/headgroups interface.
To better understand the configuration of the coating polymer chains on the NP, we have also calculated their average rdf with respect to the center of the NP, on the last 1 μs of the 5 μs CGMD simulations. The rdf profiles are reported in Fig. S7.†
We must also specify that since our NP model is represented by a single bead and the coating polymer chains are attached to the NP by constraining their terminal SP2 bead, the chains can diffuse on the NP surface. To quantify the extent of chain displacement from the initial position, we have computed the average root-mean-square deviation (RMSD) of the chains’ SP2 bead position on the last 1 μs of 5 μs CGMD simulations of MEMB/NP-50-PEG22-X, MEMB/NP-50-PE22-CH3 and MEMB/NP-50-PE11-PEG11-X systems, as reported in Table S2.† The average RMSD values are rather small, if compared to the vdW diameter of the SP2 beads (0.48 nm). Moreover, the low standard deviations indicate that the average RMSD values are representative of each SP2 bead during the simulation. We have also observed from the MD runs that the SP2 anchoring beads of the chains homogeneously cover the surface of the spherical NP throughout the simulation, and that the chains do not detach from the NP surface. Therefore, we can deduce that the interaction with the membrane is not affected by polymer diffusion.
In Fig. S8,† the z-position of the NP center and that of the POPC phosphate groups is monitored along the 5 μs MD simulation of the seven nanoconjugates interacting with the POPC/CHOL bilayer. Among the PEGylated NP systems, the NP-50-PEG22-CH3 is the one that leaves the lipid bilayer first (after about 300 ns), followed by NP-50-PEG22-CH2-COO− (800 ns) and NP-50-PEG22-CH2-NH3+ (900 ns). In addition, while the first two are found in the bulk-water phase, the last one has the NP centered at about 60 Å from the membrane center, so that the –CH2–NH3+ groups can interact with the POPC phosphate groups, as shown in Fig. 3. In the systems with PE22-CH3 or mixed PE11-PEG11-X chains, the NP remains placed approximately at the same z-position (about 5 Å from the membrane center).
To visualize the dynamics of the PEGylated NPs, in Fig. S9† the evolution of their relative position to the bilayer at different times along the MD is shown. In particular, we see that after 1 μs the NP coated with the PEG22-CH3 chains has already left the membrane; however the other two PEGylated nanosystems still interact with the bilayer by the PEG22-X chains, even if the NP has gone outside the membrane. Moreover, the NP-50-PEG22-CH2-NH3+ system interacts with the membrane by a greater number of PEG22-X chains with respect to the NP-50-PEG22-CH2-COO− system, which at the end loses all the contacts with the lipid bilayer and moves away from it.
To conclude this section, we have found that the nature of the chain terminal group does not play a crucial role in determining the stability of the nanoconjugates inside the membrane, but only affects the interaction of the coating chains with the bilayer. In the case of PEGylated NPs we have observed that NPs covered with PEG chains with different terminal groups are expelled from the membrane more or less easily and that is determined by the nature of the chain/membrane interactions.
3.2. Effect of hydrophobic/hydrophilic character of the chains
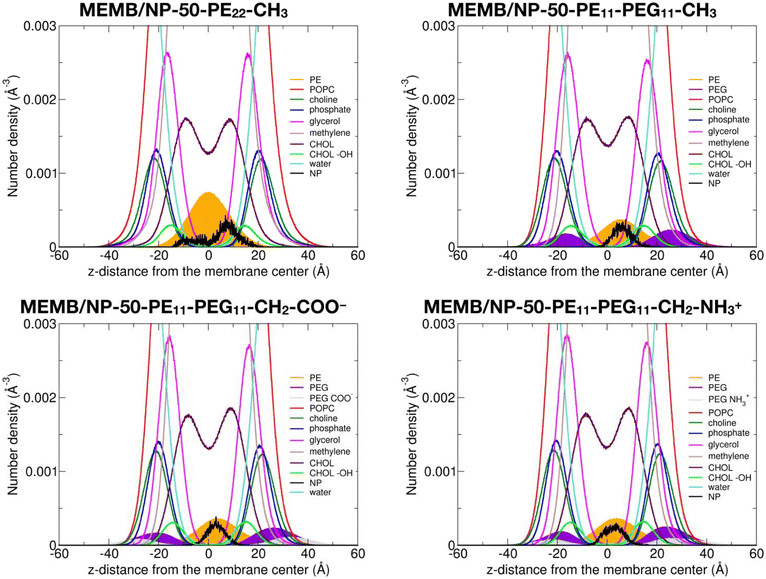
In this section, we discuss the impact of the hydrophobic/hydrophilic content of the polymer chains on the stability of the single chains or of the coated NPs inside the lipid membrane.To quantitatively determine the position of the different nanoconjugates with respect to the bilayer, in Fig. 4, we report the number density profiles, averaged on the last 1 μs of the MD production, along the membrane normal direction (z), for the systems where the NP is still inside the lipid bilayer.
First, we compare the density profiles of the polymer chains in Fig. 4 with those of the single polymer chains interacting with the POPC/CHOL membrane in Fig. S10.† At a first glance, the agreement is rather good. In particular, the PE profiles are positioned at the center of the bilayer and a little shifted toward the bulk water in the MEMB/NP-50-PE22-CH3 and MEMB/PE22-CH3 and in the MEMB/NP-50-PE11-PEG11-X and MEMB/PE11-PEG11-X systems, respectively, and that is true for all the terminal groups considered. This shift is likely driven by the PEG portion, which is stable in the membrane's polar regions.
The PEG profiles in all PEG-containing nanosystems in Fig. 4, when compared to isolated PEG chains in Fig. S10,† have their maximum centered more toward the headgroups region than toward the glycerol groups. Here, different terminal groups behave slightly differently: the –CH2–NH3+ profile maximum is deeper inside the membrane than that of –CH2–COO− because the former interacts with the POPC phosphates, while the latter with the POPC choline groups.
We notice that the PE profile is set at the center of the membrane for the PE22-CH3 chain, while it is slightly shifted to higher z values for the PE11-PEG11-X chains. The PE hydroxyl interacts with the POPC glycerol groups. The PEG profiles are centered between the POPC glycerol and POPC headgroups regions, whereas the terminal –CH2–COO− and –CH2–NH3+ groups are located in the choline and phosphate group regions, respectively.
Finally, the NP profile indicates that the NP center is a bit closer to the membrane center in the systems with PE22-CH3 chains than in those with mixed PE11-PEG11-X chains, since the latter more favorably interact with the hydrophilic portion of the membrane.
In Fig. S11 and Fig. S12,† we also report the density profiles for the isolated PEG22-X chains with different terminal groups and the corresponding PEGylated NPs. Based on Fig. S11,† we can clearly confirm that all three types of isolated PEG22-X chains prefer to be solvated in bulk water. In Fig. S12,† in the presence of the NP, some distinctions must be made: since no overlap between the PEG (violet) and POPC (red) profiles in the MEMB/NP-50-PEG22-CH3 and MEMB/NP-50-PEG22-CH2-COO− systems is observed, PEG22-X chains are more stable in the bulk water phase, whereas a little intersection in the MEMB/NP-50-PEG22-CH2-NH3+ system indicates that most of the PEG22-CH2-NH3+ chains interact with the POPC phosphate groups (except one of them which is buried inside the membrane as shown in Fig. 3).
Based on the analysis above, we conclude that the PEG portion of the coating chains tends to stabilize the NP in bulk water or to favor the interaction with phosphate groups, whereas the PE portion of the coating chains leads to the stabilization of the NP inside the bilayer. However, the PEG portion is important to improve biocompatibility of the NP; therefore we decided to test whether the NP can still be stable in the bilayer even at a lower PE/PEG ratio than that considered so far (PE11-PEG11). To this aim we investigated a NP coating by 50 PE5-PEG17-CH3 chains. Fig. S13a† clearly confirms the stability of this new nanosystem in the lipid bilayer.
In Fig. S13b,† the density profile averaged on the last 1 μs of the 5 μs MD simulation of the MEMB/NP-50-PE5-PEG17-CH3 system is shown. With respect to Fig. 4, we observe a broadening of the PE profile maximum peak between −10 and 10 Å on z, even though it is centered at the membrane center. In contrast, the PEG profile is more shifted towards the bulk water phase, due to the increase in the length of the PEG portion, which is stable in hydrophilic environments.
Therefore, based on the results reported in this section, we conclude that PEG22-X polymer chains are not stable inside the POPC/CHOL membrane, whereas the presence of an aliphatic component in the chain makes them interact with the bilayer, through both their PE and PEG portions. Conjugation with either PE22-CH3 or PE11-PEG11-X chains prevents the NP from escaping from the bilayer, as it happens with PEGylated NPs. Moreover, we have seen that the change in the PE/PEG ratio of the conjugated polymer chains (in particular, shortening the PE part and elongating the PEG part) does not hamper the NP from staying inside the membrane, but only affects the distribution of the coating chains.
3.3. Energy composition analysis
In order to quantify the interactions of the nanoconjugates with the membrane from an energetic point of view, in Table 3 we report the polymer chain/membrane non-bonded interaction energy, split over the POPC and CHOL contributions and normalized by the number of the polymer chains (50).| System | Non-bonded interaction energy (kcal mol−1) | ||
|---|---|---|---|
| Polymer chains/polymer chains | |||
| MEMB/NP-50-PEG22-CH3 | 0 | 0 | −1352 (±8) |
| MEMB/NP-50-PEG22-CH2-COO− | 0 | 0 | −1266 (±7) |
| MEMB/NP-50-PEG22-CH2-NH3+ | PEG: −2.9 (±0.1) | PEG: −0.05 (±0.01) | −1322 (±6) |
| CH2-NH3+: −0.91 (±0.01) | CH2-NH3+: −0.02 (±0.01) | ||
| TOT: −3.8 (±0.1) | TOT: −0.07 (±0.01) | ||
| MEMB/NP-50-PE22-CH3 | PE: −49.8 (±0.3) | PE: −12 (±1) | −3121 (±14) |
| CH3: −2.4 (±0.3) | CH3: −1 (±1) | ||
| TOT: −52.2 (±0.4) | TOT: −13 (±1) | ||
| MEMB/NP-50-PE11-PEG11-CH3 | PE: −43.7 (±0.3) | PE: −5.3 (±0.2) | PE/PE: −1133 (±6) |
| PEG: −32.1 (±0.4) | PEG: −0.4 (±0.1) | PEG/PEG: −404 (±7) | |
| CH3: −3.2 (±0.4) | CH3: −0.1 (±0.1) | PE/PEG: −96 (±3) | |
| TOT: −79.0 (± 0.6) | TOT: −5.8 (±0.2) | ||
| MEMB/NP-50-PE11-PEG11-CH2-COO− | PE: −43.5 (±0.2) | PE: −5.4 (±0.2) | PE/PE: −1140 (±6) |
| PEG: −31.0 (±0.4) | PEG: −0.43 (±0.02) | PEG/PEG: −337 (±5) | |
| CH2-COO−: −2.28 (±0.03) | CH2-COO−: −0.021 (±0.004) | PE/PEG: −86 (±2) | |
| TOT: −76.8 (±0.5) | TOT: −5.8 (±0.2) | ||
| MEMB/NP-50-PE11-PEG11-CH2-NH3+ | PE: −43.3 (±0.1) | PE: −5.8 (±0.4) | PE/PE: −1141 (±6) |
| PEG: −36.2 (±0.2) | PEG: −0.54 (±0.02) | PEG/PEG: −346 (±4) | |
| CH2-NH3+: −6.0 (±0.2) | CH2-NH3+: −0.123 (±0.004) | PE/PEG: −94 (±1) | |
| TOT: −85.5 (±0.3) | TOT: −6.5 (±0.4) | ||
We observe that among the nanoconjugates with the mixed PE11-PEG11-X chains, the NP-50-PE11-PEG11-CH2–NH3+ system shows the most favorable interaction with the POPC lipids, followed by, in descending order, NP-50-PE11-PEG11-CH3 and NP-50-PE11-PEG11-CH2-COO−. This trend is due to electrostatic forces, which are absent in MEMB/NP-50-PE11-PEG11-CH3 and repulsive for NP-50-PE11-PEG11-CH2-COO−.
Unlike what is reported in Table S3† for the single polymer chains interacting with the lipid bilayer, where none of the interaction of the three types of PEG22-X chains is null, here we register a small interaction of the PEG22-CH2-NH3+ chains with the POPC molecules (−3.8 kcal mol−1). Finally, compared to the results in Table S3,† the interaction per single polymer chain with the membrane is smaller, which is due to the interaction among the chains on the same NP.
Finally, in Table 3 we also report the average interchain PE–PE, PE–PEG and PEG–PEG interaction energies over the last 1 μs of the MD simulations for all systems under investigation. For the mixed chains we observe that while the PE–PE and PE–PEG interactions are practically constant regardless of the terminal group, the PEG–PEG interactions (in absolute value) follow the trend: –CH3 > –CH2–NH3+ > –CH2–COO−, which indicates that charged chains of the same sign repel each other more than neutral chains, and that the chain repulsion is greater for –CH2–COO− than –CH2–NH3+. This is true also for the PEGylated systems.
3.4. Thermodynamics of nanoconjugates’ permeation through the lipid membrane
In this last section, we provide thermodynamic data on the penetration process of selected nanoconjugates, i.e. NP-50-PEG22-CH3, NP-50-PE22-CH3, NP-50-PE11-PEG11-CH3 and NP-50-PE5-PEG17-CH3, through the POPC/CHOL lipid membrane by means of free energy calculations, with the aim of defining the spontaneity of membrane translocation by these nanosystems. Large positive variations in free energy values indicate a poor affinity of the nanoconjugate towards the membrane, and negative variations suggest that the nanoconjugate may enter the membrane. However, if the negative variation is too large it will hardly cross the membrane and enter the cell. Therefore, optimal free energy variations are expected to be small negative values.The simulation protocol we followed consists of two steps. The first one is a SMD simulation, where the NP, starting from the middle of the lipid double layer, was pulled out from the membrane along the bilayer normal direction (z) with a constant harmonic force for 20 ns (for further details, see section 2.4). In Fig. S14,† the intensity of the pulling force and the NP z-position along the SMD trajectory are shown. Moreover, in Fig. S15,† we also report some selected snapshots from the pulling trajectory of the MEMB/NP-50-PEG22-CH3 system.
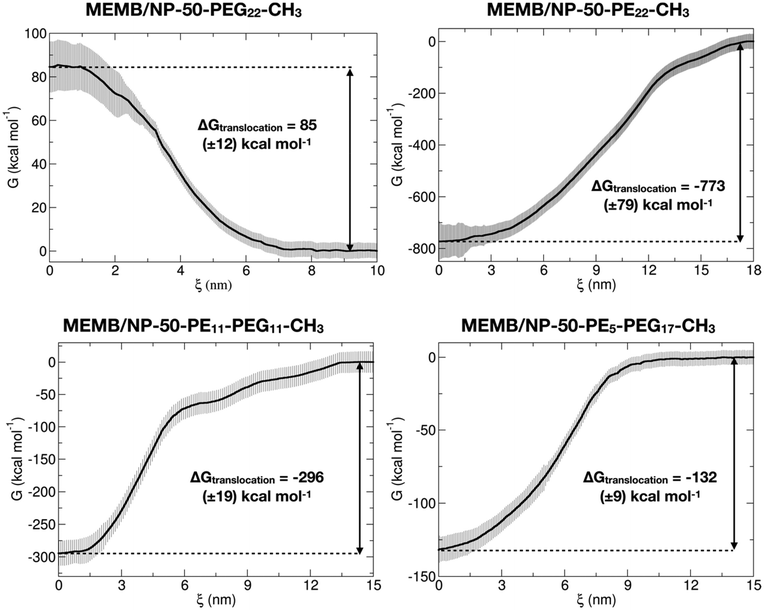
In the second step, configurations with a COM spacing of 0.2 nm were extracted from the pulling trajectories and used as the starting point for US simulations, conducted at 303 K and 1 atm for 200 ns, where the z-position of the NP center was restrained within a specific window corresponding to the chosen COM distance. The Potential of Mean Force (PMF) was computed using data from the last 50 ns of the US simulations. In Fig. 5, the PMF profiles of the considered systems are shown. Moreover, in Fig. S16† we report the corresponding umbrella histograms.
We observe that the PMF profile of the MEMB/NP-50-PEG22-CH3 system presents a positive free energy barrier (of 85 kcal mol−1) for the nanoconjugate translocation from the bulk water to the membrane, which is in agreement with the results of the unbiased CGMD simulations, where the PEGylated NP is found outside the membrane, in the water phase, at the end of the 5 μs MD simulation. In contrast, for the other three investigated systems, the PMF profile has its minimum inside the membrane, again in accordance with the unbiased simulations of the previous section. Moreover, the deepest free energy well is for the MEMB/NP-50-PE22-CH3 system (−773 kcal mol−1), which is also expected to exhibit poor biocompatibility. Indeed, it has been found that PE nanoparticles have cytotoxic effects on cells, which depend on nanoparticle dimension, number, shape, superficial hydrophobicity and oxidation.96 However, PE chains of similar length to the ones considered in this work have already been proposed as spacers between the NP and the PEG layer for gold NP functionalization. Alkyl-PEG coating resulted in a great decrease of protein adsorption and macrophage uptake.97
Coating with mixed chains, containing some PEG, not only improves stealth properties, but also leads to less negative values of ΔGtranslocation (eqn (1), see section 2.4) (about −296 kcal mol−1 for MEMB/NP-50-PE11-PEG11-CH3 and −132 kcal mol−1 for MEMB/NP-50-PE5-PEG17-CH3). The larger the PEG content, the less negative the ΔGtranslocation value. One could further vary the PE/PEG ratio to tune the ΔGtranslocation to an optimum value.
To conclude this section, free energy calculations confirm that PEGylated nanosystems are not thermodynamically stable inside the lipid bilayer, as observed in the unbiased CGMD simulations of the previous section. In contrast, based on these thermodynamic data, NPs covered with PE or mixed PE-PEG chains will spontaneously translocate from the bulk water to the membrane, as the variation of free energy associated with the process is negative. The latter systems, in particular, turn out to be the best candidates for clinical applications, as they combine biocompatibility and smaller ΔGtranslocation values that may allow membrane crossing and cell penetration.
4. Conclusions
In this work, we have studied the interaction of spherical TiO2 NPs coated with polymer chains of different chemical compositions with phospholipid membranes by coarse-grained MD simulations.In the first part of the work, we aimed at assessing the CG parameters of the PEG chains by systematic comparison with atomistic MD simulations, performed on both single PEG22-X chains in solution or attached to the NP. We found fair agreement on structural parameters between AA and CG data, which encouraged us to perform the second part of the study.
As a first investigation, we have performed unbiased CGMD simulations on single polymer chains inserted in the middle of a POPC/CHOL lipid membrane. Our results have shown that PEG22-X chains escape from the bilayer, whereas PE22-CH3 or mixed PE11-PEG11-X chains remain inside the membrane. Both these observations are independent of the nature of the polymer's terminal group.
The following step introduced the coated NP in the middle of the membrane. The unbiased CGMD simulations have mostly confirmed the results on single polymer chains. However, for PEGylated NPs, we have observed that the different terminal groups of the chains affect the escape time of the nanoconjugates from the membrane to the bulk water phase. Moreover, for mixed chains, the PE/PEG ratio does not impact significantly the position of the NP inside the membrane, but only the conformational arrangement of the chains.
Finally, in the last part of the work, we have conducted umbrella sampling calculations to determine Gibbs free energy variations as a measure of the thermodynamic spontaneity of these nanoconjugates to penetrate the lipid bilayer. In agreement with unbiased MD simulations, PEGylated nanosystems show a positive free energy barrier of translocation from water to the membrane, whereas the free energy variation is negative for NPs conjugated with PE or mixed chains, and it is lower for decreasing PE content, which could favor both the biocompatibility and cell penetration.
These findings offer a strong foundation for the rational design of nanosystems with optimal interaction with and diffusion capabilities through cell membranes. We have demonstrated that the mixed hydrophobic/hydrophilic character of the coating polymer chains plays a more pivotal role in influencing the stability of the NPs within the lipid membrane, compared to the nature of the chain terminal group, which only has a marginal impact.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The authors are grateful to Prof. Francesca Re and Prof. Roberto Fiammengo for fruitful discussion and to Lorenzo Ferraro for his technical support. The research leading to these results has received funding from the European Union – NextGenerationEU through the Italian Ministry of University and Research under PNRR – M4C2-I1.3 Project PE_00000019 “HEAL ITALIA” to Prof. Cristiana Di Valentin CUP H43C22000830006 of the University of Milano Bicocca.References
- E. A. Rozhkova, I. Ulasov, B. Lai, N. M. Dimitrijevic, M. S. Lesniak and T. Rajh, Nano Lett., 2009, 9, 3337–3342 CrossRef CAS PubMed
.
- N. Kotagiri, G. P. Sudlow, W. J. Akers and S. Achilefu, Nat. Nanotechnol., 2015, 10, 370–379 CrossRef CAS PubMed
.
- D. Duan, H. Liu, Y. Xu, Y. Han, M. Xu, Z. Zhang and Z. Liu, ACS Appl. Mater. Interfaces, 2018, 10, 5278–5286 CrossRef CAS
.
- N. K. Shrestha, J. M. Macak, F. Schmidt-Stein, R. Hahn, C. T. Mierke, B. Fabry and P. Schmuki, Angew. Chem., Int. Ed., 2009, 48, 969–972 CrossRef CAS PubMed
.
- A. Dayan, G. Fleminger and O. Ashur-Fabian, RSC Adv., 2018, 8, 9112–9119 RSC
.
- J. Ai, B. Liu and W. Liu, Mater. Sci. Eng., C, 2017, 76, 1181–1187 CrossRef CAS
.
- J.-S. Lan, L. Liu, R.-F. Zeng, Y.-H. Qin, J.-W. Hou, S.-S. Xie, S. Yue, J. Yang, R. J. Y. Ho, Y. Ding and T. Zhang, Chem. Eng. J., 2021, 407, 127212 CrossRef CAS
.
- K. T. Thurn, T. Paunesku, A. Wu, E. M. B. Brown, B. Lai, S. Vogt, J. Maser, M. Aslam, V. Dravid, R. Bergan and G. E. Woloschak, Small, 2009, 5, 1318–1325 CrossRef CAS PubMed
.
- P. J. Endres, T. Paunesku, S. Vogt, T. J. Meade and G. E. Woloschak, J. Am. Chem. Soc., 2007, 129, 15760–15761 CrossRef CAS
.
- K. Brown, T. Thurn, L. Xin, W. Liu, R. Bazak, S. Chen, B. Lai, S. Vogt, C. Jacobsen, T. Paunesku and G. E. Woloschak, Nano Res., 2018, 11, 464–476 CrossRef CAS
.
- M. Hamzeh and G. I. Sunahara, Toxicol. in Vitro, 2013, 27, 864–873 CrossRef CAS PubMed
.
- B. Trouiller, R. Reliene, A. Westbrook, P. Solaimani and R. H. Schiestl, Cancer Res., 2009, 69, 8784–8789 CrossRef CAS PubMed
.
- M. Lundqvist and T. Cedervall, Small, 2020, 16, 2000892 CrossRef CAS
.
- S. Chapman, M. Dobrovolskaia, K. Farahani, A. Goodwin, A. Joshi, H. Lee, T. Meade, M. Pomper, K. Ptak, J. Rao, R. Singh, S. Sridhar, S. Stern, A. Wang, J. B. Weaver, G. Woloschak and L. Yang, Nano Today, 2013, 8, 454–460 CrossRef CAS
.
- J. V. Jokerst, T. Lobovkina, R. N. Zare and S. S. Gambhir, Nanomedicine, 2011, 6, 715–728 CrossRef CAS PubMed
.
- S. Y. Fam, C. F. Chee, C. Y. Yong, K. L. Ho, A. R. Mariatulqabtiah and W. S. Tan, Nanomaterials, 2020, 10, 787 CrossRef CAS PubMed
.
- J. S. Suk, Q. Xu, N. Kim, J. Hanes and L. M. Ensign, Adv. Drug Delivery Rev., 2016, 99, 28–51 CrossRef CAS
.
- W. Chen, Z. Sun and L. Lu, Angew. Chem., Int. Ed., 2021, 60, 5626–5643 CrossRef CAS
.
- N. Bertrand, J. Wu, X. Xu, N. Kamaly and O. C. Farokhzad, Adv. Drug Delivery Rev., 2014, 66, 2–25 CrossRef CAS PubMed
.
- C. Tanford, Science, 1978, 200, 1012–1018 CrossRef CAS
.
- A. Chaudhury, K. Debnath, N. R. Jana and J. K. Basu, Nanoscale, 2024, 16, 856–867 RSC
.
- N. Biswas, R. Bhattacharya, A. Saha, N. R. Jana and J. K. Basu, Phys. Chem. Chem. Phys., 2015, 17, 24238–24247 RSC
.
- R. Chelladurai, K. Debnath, N. R. Jana and J. K. Basu, Langmuir, 2018, 34, 1691–1699 CrossRef CAS PubMed
.
- B. Kann, H. L. Offerhaus, M. Windbergs and C. Otto, Adv. Drug Delivery Rev., 2015, 89, 71–90 CrossRef CAS PubMed
.
- P. Lasch, A. Pacifico and M. Diem, Biopolymers, 2002, 67, 335–338 CrossRef PubMed
.
- M. Diem, M. Romeo, S. Boydston-White, M. Miljković and C. Matthäus, Analyst, 2004, 129, 880–885 RSC
.
- A. J. van Hell, M. N. Melo, W. J. van Blitterswijk, D. M. Gueth, T. M. Braumuller, L. R. C. Pedrosa, J.-Y. Song, S. J. Marrink, G. A. Koning, J. Jonkers and M. Verheij, Sci. Rep., 2013, 3, 1949 CrossRef
.
- D. Toroz and I. R. Gould, Sci. Rep., 2019, 9, 2155 CrossRef CAS
.
- A. C. Alves, A. Magarkar, M. Horta, J. L. F. C. Lima, A. Bunker, C. Nunes and S. Reis, Sci. Rep., 2017, 7, 6343 CrossRef PubMed
.
- J. M. Siegfried, T. G. Burke and T. R. Tritton, Biochem. Pharmacol., 1985, 34, 593–598 CrossRef CAS PubMed
.
- P. Siani, E. Donadoni, L. Ferraro, F. Re and C. Di Valentin, Biochim. Biophys. Acta, Biomembr., 2022, 1864, 183763 CrossRef CAS
.
- D. Bedrov, G. D. Smith, H. Davande and L. Li, J. Phys. Chem. B, 2008, 112, 2078–2084 CrossRef CAS
.
- H. Liu and Y. Pei, Langmuir, 2022, 38, 1653–1661 CrossRef CAS PubMed
.
- M. P. Aranha, D. Mukherjee, L. Petridis and B. Khomami, Langmuir, 2020, 36, 1043–1052 CrossRef CAS
.
- H. Ding, W. Tian and Y. Ma, ACS Nano, 2012, 6, 1230–1238 CrossRef CAS PubMed
.
- S. Franco-Ulloa, D. Guarnieri, L. Riccardi, P. P. Pompa and M. De Vivo, J. Chem. Theory Comput., 2021, 17, 4512–4523 CrossRef CAS PubMed
.
- F. Simonelli, D. Bochicchio, R. Ferrando and G. Rossi, J. Phys. Chem. Lett., 2015, 6, 3175–3179 CrossRef CAS
.
- S. Salassi, F. Simonelli, D. Bochicchio, R. Ferrando and G. Rossi, J. Phys. Chem. C, 2017, 121, 10927–10935 CrossRef CAS
.
- U. Kumar Basak, C. Roobala, J. K. Basu and P. K. Maiti, J. Phys.: Condens. Matter, 2020, 32, 104003 CrossRef
.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed
.
- S. I. Hossain, N. S. Gandhi, Z. E. Hughes and S. C. Saha, J. Phys. Chem. B, 2021, 125, 1392–1401 CrossRef CAS PubMed
.
- M. Das, U. Dahal, O. Mesele, D. Liang and Q. Cui, J. Phys. Chem. B, 2019, 123, 10547–10561 CrossRef CAS PubMed
.
- T. Lunnoo, J. Assawakhajornsak and T. Puangmali, J. Phys. Chem. C, 2019, 123, 3801–3810 CrossRef CAS
.
- T. Lunnoo, J. Assawakhajornsak, S. Ruangchai and T. Puangmali, J. Phys. Chem. B, 2020, 124, 1898–1908 CrossRef CAS PubMed
.
- E. Canepa, S. Salassi, F. Simonelli, R. Ferrando, R. Rolandi, C. Lambruschini, F. Canepa, S. Dante, A. Relini and G. Rossi, Sci. Rep., 2021, 11, 1256 CrossRef CAS PubMed
.
- J. Lin, H. Zhang, Z. Chen and Y. Zheng, ACS Nano, 2010, 4, 5421–5429 CrossRef CAS PubMed
.
- S. Salassi, E. Canepa, R. Ferrando and G. Rossi, RSC Adv., 2019, 9, 13992–13997 RSC
.
- Y. Li and Y. Hu, RSC Adv., 2014, 4, 51022–51031 RSC
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef
.
- R. B. Best, X. Zhu, J. Shim, P. E. M. Lopes, J. Mittal, M. Feig and A. D. MacKerell, J. Chem. Theory Comput., 2012, 8, 3257–3273 CrossRef CAS PubMed
.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. MacKerell, Nat. Methods, 2017, 14, 71–73 CrossRef CAS PubMed
.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed
.
- J. Huang and A. D. MacKerell, J. Comput. Chem., 2013, 34, 2135–2145 CrossRef CAS PubMed
.
- S. Kim, J. Lee, S. Jo, C. L. Brooks, H. S. Lee and W. Im, J. Comput. Chem., 2017, 38, 1879–1886 CrossRef CAS
.
- S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef CAS PubMed
.
- J. Lee, X. Cheng, J. M. Swails, M. S. Yeom, P. K. Eastman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong, Y. Qi, S. Jo, V. S. Pande, D. A. Case, C. L. Brooks, A. D. MacKerell, J. B. Klauda and W. Im, J. Chem. Theory Comput., 2016, 12, 405–413 CrossRef CAS PubMed
.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS
.
- S. R. Durell, B. R. Brooks and A. Ben-Naim, J. Phys. Chem., 1994, 98, 2198–2202 CrossRef CAS
.
- E. Neria, S. Fischer and M. Karplus, J. Chem. Phys., 1996, 105, 1902–1921 CrossRef CAS
.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef
.
- W. G. Hoover, Phys Rev APhys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed
.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS
.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS
.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef CAS
.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS
.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
- D. Selli, G. Fazio and C. Di Valentin, J. Chem. Phys., 2017, 147, 164701 CrossRef PubMed
.
- G. Fazio, L. Ferrighi and C. Di Valentin, J. Phys. Chem. C, 2015, 119, 20735–20746 CrossRef CAS
.
- D. Selli, S. Motta and C. Di Valentin, J. Colloid Interface Sci., 2019, 555, 519–531 CrossRef CAS PubMed
.
- D. Selli, M. Tawfilas, M. Mauri, R. Simonutti and C. Di Valentin, Chem. Mater., 2019, 31, 7531–7546 CrossRef CAS PubMed
.
- E. G. Brandt and A. P. Lyubartsev, J. Phys. Chem. C, 2015, 119, 18110–18125 CrossRef CAS
.
- P. Siani and C. Di Valentin, Nanoscale, 2022, 14, 5121–5137 RSC
.
- E. Donadoni, P. Siani, G. Frigerio and C. Di Valentin, Nanoscale, 2022, 14, 12099–12116 RSC
.
- P. Siani, G. Frigerio, E. Donadoni and C. Di Valentin, J. Colloid Interface Sci., 2022, 627, 126–141 CrossRef CAS PubMed
.
- E. Donadoni, G. Frigerio, P. Siani, S. Motta, J. Vertemara, L. De Gioia, L. Bonati and C. Di Valentin, ACS Biomater. Sci. Eng., 2023, 9, 6123–6137 CrossRef CAS PubMed
.
- G. Frigerio, E. Donadoni, P. Siani, J. Vertemara, S. Motta, L. Bonati, L. De Gioia and C. Di Valentin, Nanoscale, 2024, 16, 4063–4081 RSC
.
- A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J.-E. Shea, G. J. Jensen and D. S. Goodsell, J. Mol. Biol., 2021, 433, 166841 CrossRef CAS PubMed
.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed
.
- H. Kamberaj, R. J. Low and M. P. Neal, J. Chem. Phys., 2005, 122, 224114 CrossRef CAS PubMed
.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS
.
-
R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, CRC Press, 2021 Search PubMed
.
- F. Grünewald, R. Alessandri, P. C. Kroon, L. Monticelli, P. C. T. Souza and S. J. Marrink, Nat. Commun., 2022, 13, 68 CrossRef PubMed
.
- F. Grunewald, G. Rossi, A. H. de Vries, S. J. Marrink and L. Monticelli, J. Phys. Chem. B, 2018, 122, 7436–7449 CrossRef CAS PubMed
.
- D. H. de Jong, G. Singh, W. F. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schäfer, X. Periole, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2013, 9, 687–697 CrossRef CAS PubMed
.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed
.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637–649 CrossRef CAS
.
- J. A. Barker and R. O. Watts, Mol. Phys., 1973, 26, 789–792 CrossRef CAS
.
- I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451–5459 CrossRef CAS
.
- P. H. Hünenberger and W. F. van Gunsteren, J. Chem. Phys., 1998, 108, 6117–6134 CrossRef
.
- E. L. Wu, X. Cheng, S. Jo, H. Rui, K. C. Song, E. M. Dávila-Contreras, Y. Qi, J. Lee, V. Monje-Galvan, R. M. Venable, J. B. Klauda and W. Im, J. Comput. Chem., 2014, 35, 1997–2004 CrossRef CAS PubMed
.
- S. Jo, J. B. Lim, J. B. Klauda and W. Im, Biophys. J., 2009, 97, 50–58 CrossRef CAS PubMed
.
- Z. Rinkevicius, M. Kaminskas, P. Palevičius, M. Ragulskis, K. Bočkutė, M. Sriubas and G. Laukaitis, Phys. Chem. Chem. Phys., 2022, 24, 27731–27741 RSC
.
- G. Brancolini and V. Tozzini, Front. Mol. Biosci., 2019, 6, 50 CrossRef CAS PubMed
.
- B. Roux, Comput. Phys. Commun., 1995, 91, 275–282 CrossRef CAS
.
- T. D. Romo, N. Leioatts and A. Grossfield, J. Comput. Chem., 2014, 35, 2305–2318 CrossRef CAS PubMed
.
- E. Gazzano, P. Bracco, A. Bistolfi, E. Aldieri, D. Ghigo, M. Boffano, L. Costa and E. B. Del Prever, Int. J. Immunopathol. Pharmacol., 2011, 24, 61–67 CrossRef CAS PubMed
.
- T. A. Larson, P. P. Joshi and K. Sokolov, ACS Nano, 2012, 6, 9182–9190 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr00495g |
| This journal is © The Royal Society of Chemistry 2024 |

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bead in magenta. Water and ions are hidden for clarity.
C bead in magenta. Water and ions are hidden for clarity.