Fragmentation patterns of DNA-stabilized silver nanoclusters under mass spectrometry†
Rweetuparna
Guha
 a,
Sami
Malola
e,
Malak
Rafik
a,
Maya
Khatun
e,
Anna
Gonzàlez-Rosell
a,
Sami
Malola
e,
Malak
Rafik
a,
Maya
Khatun
e,
Anna
Gonzàlez-Rosell
 a,
Hannu
Häkkinen
a,
Hannu
Häkkinen
 e and
Stacy M.
Copp
e and
Stacy M.
Copp
 *abcd
*abcd
aDepartment of Materials Science and Engineering, University of California, Irvine, CA 92697, USA. E-mail: stacy.copp@uci.edu
bDepartment of Physics and Astronomy, University of California, Irvine, CA 92697, USA
cDepartment of Chemical and Biomolecular Engineering, University of California, Irvine, CA 92697, USA
dDepartment of Chemistry, University of California, Irvine, CA 92697, USA
eDepartments of Chemistry and Physics, Nanoscience Center, University of Jyväskylä, Jyväskylä 40014, Finland
First published on 10th October 2024
Abstract
DNA-stabilized silver nanoclusters (AgN-DNAs) are emitters with tuneable structures and photophysical properties. While understanding of the sequence–structure–property relationships of AgN-DNAs has advanced significantly, their chemical transformations and degradation pathways are far less understood. To advance understanding of these pathways, we analysed the fragmentation products of 21 different red and NIR AgN-DNAs using negative ion mode electrospray ionization mass spectrometry (ESI-MS). AgN-DNAs were found to lose Ag+ under ESI-MS conditions, and sufficient loss of silver atoms can lead to a transition to a lesser number of effective valence electrons, N0. Of more than 400 mass spectral peaks analysed, only even values of N0 were identified, suggesting that solution-phase AgN-DNAs with odd values of N0 are unlikely to be stable. AgN-DNAs stabilized by three DNA strands were found to fragment significantly more than AgN-DNAs stabilized by two DNA strands. Moreover, the fragmentation behaviour depends strongly on the DNA template sequence, with diverse fragmentation patterns even for AgN-DNAs with similar molecular formulae. Molecular dynamics simulations, with forces calculated from density functional theory, of the fragmentation of (DNA)2(Ag16Cl2)8+ with a known crystal structure show that the 6-electron Ag16Cl2 core fragments into a 4-electron Ag10 and a 2-electron Ag6, preserving electron-pairing rules even at early stages of the fragmentation process, in agreement with experimental observation. These findings provide new insights into the mechanisms by which AgN-DNAs degrade and transform, with relevance for their applications in sensing and biomedical applications.
Introduction
DNA-stabilized silver nanoclusters (AgN-DNAs) are emerging as promising emitters for biological sensing and imaging applications due to their uniquely tunable photophysical properties and biocompatible surface chemistries. These ultrasmall nanoparticles (1–3 nm) range in size from about 10 to 30 Ag atoms and are encapsulated by 1–3 single-stranded DNA oligomers. The DNA oligomer acts as a multidentate ligand for silver, stabilizing AgN-DNAs with exceptionally high atomic precision. The DNA sequence encodes the size and shape of the AgN-DNA, ultimately dictating its photophysical properties.1 The properties of AgN-DNAs can also be sensitive to changes in the local environment,2 which has been harnessed by strategies using probes such as NanoCluster Beacons to sense nucleic acids and other analytes.3,4 AgN-DNAs exhibit many favourable properties as emitters: a wide palette of emission wavelengths ranging from visible to near-infrared (NIR),1,5 as well as high Stokes shifts6 and quantum yields,7 especially as compared to those of commonly used NIR organic dyes. These properties have driven recent interest in NIR AgN-DNAs as candidates for bioimaging in the tissue transparency windows.The fundamental understanding of AgN-DNA sequence–structure–property relationships has been significantly advanced by studies of atomically precise AgN-DNAs purified by high-performance liquid chromatography (HPLC) and sized by high-resolution electrospray ionization mass spectrometry (ESI-MS).5 In contrast, chemical transformations involving AgN-DNAs remain poorly understood. The clearly demonstrated applications of AgN-DNAs in biosensing and imaging3,8–11 demand an in-depth understanding of such mechanisms, which may underlie colorimetry-based sensing and are important for understanding the possible decomposition routes of AgN-DNAs in vivo. Recent work by Petty and coauthors investigated the degradation of one Ag10-DNA under laser-driven photobleaching, providing some of the first insights into AgN-DNA decomposition.12 This type of investigation is lacking for nearly all other AgN-DNAs reported to date.
Mass spectrometry offers a sensitive way to investigate metal nanocluster stability and reactions in the gas phase. For example, collision-induced dissociation (CID) and time-dependent trapped ion mobility spectrometry (TIMS) have been used to elucidate the effects of ligands, ligand–metal core interactions, and structures of intermediates formed during the dissociation of monolayer-protected noble metal clusters.13–17 These experimental approaches have also improved understanding of inter-cluster reactions of reactive coinage metal clusters during solution-phase formation of alloy clusters.18,19 Mass spectrometry could also provide insights into how AgN-DNA species transform or degrade. However, unlike monolayer-protected metal nanoclusters, which are typically stabilized by small molecules such as thiols,20,21 phosphines,22 and carbenes,23 AgN-DNAs are stabilized by much bulkier DNA oligomer ligands, which makes it more challenging to use ESI-MS to determine nanocluster composition. AgN-DNA mass spectra can be acquired under native-like ESI-MS conditions, using techniques that were developed to preserve the solution-phase structure of noncovalent nucleic acid complexes.1,24–27 During ESI-induced desolvation, liquid is forced through a needle on which a voltage is applied in order to create an aerosol. As the resulting droplets evaporate, the negatively charged phosphate backbones are partially protonated due to proton transfer from ammonium ions to phosphate groups.28 Even under such conditions, mass spectra of AgN-DNAs also show the presence of multiple smaller-mass fragments with varying silver contents. These include nanoclusters with fewer valence electrons, which are known to have distinct fluorescence excitation and emission spectra.24,27,29–32 Because of the optical purity33 exhibited by the HPLC-purified AgN-DNAs that have been examined by ESI-MS, these smaller-mass products are attributed to fragmentation of AgN-DNAs during ESI-MS. We hypothesize that this fragmentation could be used to probe the chemical properties of AgN-DNAs without CID.
Based on this hypothesis, we investigated a large set of 21 different AgN-DNA species with diverse ligand compositions, nanocluster silver contents, NAg, and numbers of effective valence electrons, N0. We found that the patterns of fragmentation products formed during ESI-MS depend strongly on the DNA template sequence and ligand chemistry of the AgN-DNA species. In all cases, AgN-DNAs are observed to lose Ag+ in the gas phase while preserving N0. When NAg reaches a lower limit, which is unique to each AgN-DNA species, the fragments can transition to smaller values of N0. Even in these transient species, only even values of N0 are observed. Density functional theory (DFT) provides insights into the dissociation mechanism of (DNA)2(Ag16Cl2)8+ with a known X-ray crystal structure,34 whose N0 = 6 Ag16 core dissociates into two smaller Ag6 and Ag10 species with N0 values of 2 and 4, respectively. This analysis provides key insights into the lability of AgN-DNAs, including mechanisms that may underlie behaviour of relevance to AgN-DNA-based sensing mechanisms and to their degradation in biological settings, of relevance to properties such as cytotoxicity.
Results
21 AgN-DNAs were selected from a library designed using machine learning-aided high-throughput experiments.35–38 AgN-DNAs were purified using HPLC to obtain atomically precise AgN-DNAs with high purity, and optical spectra confirm the presence of a single emissive species in the HPLC-purified samples.30 These AgN-DNAs exhibit peak emission at the far red to near-infrared (NIR) spectral border and varying molecular formulae (Table 1). As in previous work, the molecular formula is assigned to the nanocluster product with the greatest number of silver atoms (NAg) resolved in the mass spectrum, using negative ion mode ESI-MS.30 (As noted previously, NAg may not represent the silver content of the nanocluster core because additional Ag+ could bind to the DNA ligand shell without being incorporated into the nanocluster core. Accurate assignment of the silver content of the AgN core requires comparing AgN-DNA mass spectra with X-ray crystal structures, which are presently available for very few AgN-DNAs.34,39,40) Negative ion mode ESI-MS is used for AgN-DNA characterization because this is a sensitive method for studying noncovalent nucleic acid complexes. At neutral pH, phosphate groups are deprotonated and nucleobases are typically neutral. For more details regarding the utility of negative ion mode ESI-MS for nucleic acids, readers are directed to a comprehensive review by Largy et al.28 Synthesis procedures, HPLC chromatograms, and mass spectra have been previously reported for all AgN-DNAs except for I.8, which is shown in Fig. S1 and S2.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,29,30 For clarity, the mass spectra of all other AgN-DNAs are shown in Fig. S3–S20.†
2,29,30 For clarity, the mass spectra of all other AgN-DNAs are shown in Fig. S3–S20.†
| Name | DNA sequence (5′ to 3′) | Chemical composition | Molecular formula |
|---|---|---|---|
| Group I: Ag N -DNAs containing n s = 2 and N 0 = 6 | |||
| I.1 | GTCCGGGCCA | C192H244N78O116P18Ag20 | (DNA)2(Ag20)14+ |
| I.2 | ACCAATGACC | C192H244N78O110P18Ag15 | (DNA)2(Ag15)9+ |
| I.3 | CCAGCCCGGA | C190H242N80O112P18Ag18 | (DNA)2(Ag18)12+ |
| I.4 | GTAGTCCCTA | C194H248N70O118P18Ag16 | (DNA)2(Ag16)10+ |
| I.5 | ATCCCCTGTC | C190H248N62O120P18Ag17 | (DNA)2(Ag17)11+ |
| I.6 | AGTCACGACA | C194H244N82O110P18Ag16 | (DNA)2(Ag16)10+ |
| I.7 | GCCCCCCCGC | C184H242N68O116P18Ag14 | (DNA)2(Ag14)8+ |
| I.8 | CCGGAATCCG | C192H244N78O114P18Ag20 | (DNA)2(Ag20)14+ |
| Group II: Ag N -DNAs containing n s = 3 and N 0 = 6 | |||
| II.1 | CCCGGCCGAA | C285H363N120O168P27Ag18 | (DNA)3(Ag18)12+ |
| II.2 | CCCGGAGAAG | C291H363N132O165P27Ag22 | (DNA)3(Ag22)16+ |
| II.3 | CCTGGGGAAA | C294H366N129O168P27Ag16 | (DNA)3(Ag16)10+ |
| Group III: Ag N -DNAs containing n s = 2, chlorido ligands, and N 0 = 6 | |||
| III.1 | AACCCCACGT | C190H244N74O112P18ClAg15 | (DNA)2(Ag15Cl)7+ |
| III.2 | CACCTAGCGA | C192H244N78O112P18Cl2Ag16 | (DNA)2(Ag16Cl2)8+ |
| III.3 | CACC![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) AGCGA AGCGA |
C192H242N84O108P18Cl2Ag16 | (DNA)2(Ag16Cl2)8+ |
| III.4 | CACC![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) AGCGA AGCGA |
C190H242N80O110P18Cl2Ag16 | (DNA)2(Ag16Cl2)8+ |
| III.5 | CACC![[G with combining low line]](https://www.rsc.org/images/entities/char_0047_0332.gif) AGCGA AGCGA |
C192H242N84O110P18Cl2Ag16 | (DNA)2(Ag16Cl2)8+ |
| III.6 | CACCTAGCG_ | C172H220N68O102P16Cl2Ag16 | (DNA)2(Ag16Cl2)8+ |
| Group IV: Ag N -DNAs containing n s = 2 and N 0 = 8 | |||
| IV.1 | GCGCAAGATG | C196H244N86O112P18Ag19 | (DNA)2(Ag19)11+ |
| IV.2 | GACGACGGAT | C196H244N86O112P18Ag17 | (DNA)2(Ag17)9+ |
| IV.3 | ATCTCCACAG | C129H246N72O114P18Ag16 | (DNA)2(Ag16)8+ |
| IV.4 | AGGCGATCAT | C196H246N80O114P18Ag20 | (DNA)2(Ag20)12+ |
The mass spectrum is used to determine the AgN-DNA molecular formula using previously established methods,26,41 which are detailed in ESI section 3.1.† The experimental isotopic distribution for a specific product is compared to calculated distributions to determine the total number of DNA strands (ns), the total silver content (N), and the overall charge of the nanocluster (Qc) of the AgN-DNA. (Note that if chlorido ligands are present, these will contribute to the calculation of Qc.) The molecular formula is denoted as (DNA)ns(AgN)Qc+, and N0 is calculated as N0 = N − Qc. For example, I.1 has the molecular formula, (DNA)2(Ag20)14+ and has N0 = 20–14 = 6 valence electrons (Table 1).
Mass spectra for all AgN-DNA species were acquired using identical ESI-MS conditions. Bethur et al. previously reported that parameters such as capillary voltage, desolvation temperature, desolvation gas flow, and injection flow rate influence the relative intensities of the mass spectral peaks of DNA-Ag+ complexes.42 Thus, uniform ESI-MS conditions must be used for all 21 AgN-DNAs studied here to allow direct comparison of fragmentation products resolved in their mass spectra. The selected ESI-MS conditions (Methods) were found to minimize the fragmentation of AgN-DNAs into smaller-mass products. We note that desolvation temperature affects the relative intensity of mass peaks at different charge states z (Fig. S22†) but does not affect the number of effective valence electrons of the AgN core, N0, for each identified mass product (Fig. S23 and Table S1†). This supports that the experimental methods used here have relevance to more general chemical transformations of AgN-DNAs. Moreover, we did not observe any evidence of DNA oligomer fragmentation in any of the analyzed mass spectra, supporting that only the nanocluster fragments, and not the DNA oligomer itself. This is in contrast to past work that used activated electron photodetachment to fragment the DNA backbone and thereby gain structural insights into AgN-DNAs.43
Table 1 groups AgN-DNAs by their ligand composition, i.e. the number of ssDNA oligomers (ns) and the presence or absence of chlorido ligands, and by N0.30Group I AgN-DNAs have N0 = 6 and ns = 2. Group II AgN-DNAs contain N0 = 6 and ns = 3; these emitters exhibit the shortest Stokes shift among all four groups.30Group III AgN-DNAs exhibit N0 = 6, ns = 2, and additional chlorido ligands. These AgN-DNAs exhibit higher Stokes shifts than AgN-DNAs without chloridos6 and are stable under physiologically relevant buffers. Group IV AgN-DNAs exhibit N0 = 8 and ns = 2, and two of these display microsecond-lived luminescence rather than the nanosecond-lived fluorescence of most AgN-DNAs.29 It has been hypothesized that N0 = 6 AgN-DNAs are rod-shaped, while Group IV AgN-DNAs have a quasi-spherical geometry due to their “magic number” of 8 valence electrons.30
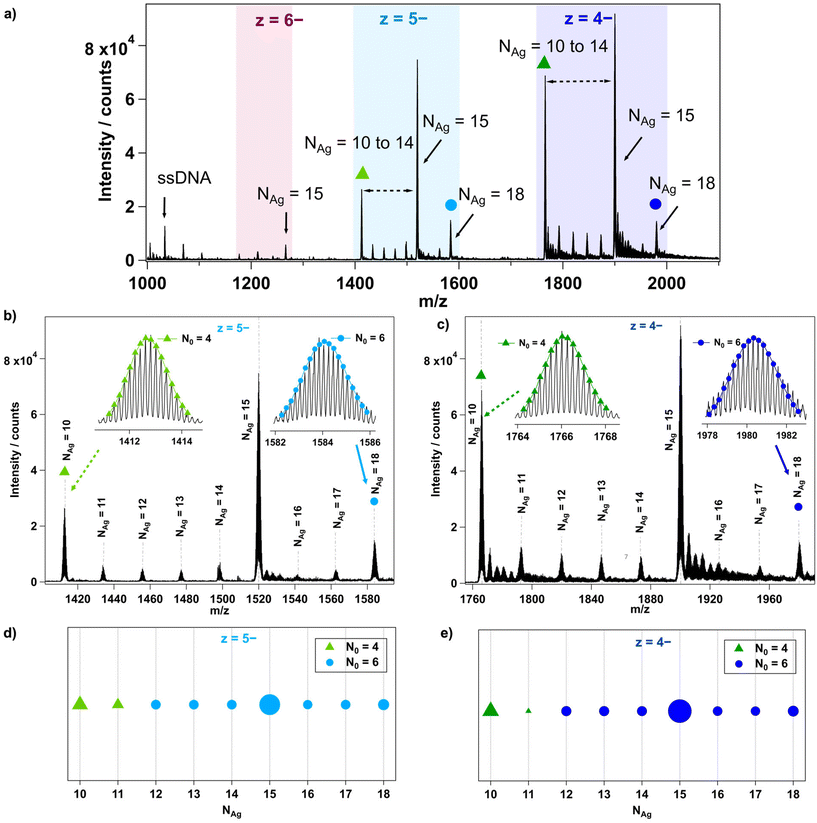
The mass spectrum of each AgN-DNA was analyzed in detail to determine the composition of each resolved peak, as illustrated in Fig. 1 for I.3. First, each peak's charge state, z, is determined from the isotope pattern, whose adjacent peaks are spaced by 1/z. For example, I.3 in Fig. 1 has three resolved charge states for products corresponding to nanoclusters: z = −4, −5, and −6 (Fig. 1a). Next, the number of stabilizing ssDNA oligomers, ns, and the total number of silver atoms, NAg, are determined for each resolved peak. For I.3, mass peaks containing ns = 2 and NAg = 10 to 18 were identified (Fig. 1a–c). Peaks at lower m/z correspond to single oligomers (ns = 1) with and without a few Ag+. The effective valence electron count, N0, is then determined for each peak by fitting the calculated isotopic distribution to the experimental isotopic distribution (insets, Fig. 1b and c). Readers can find details about this fitting in past works.24,27,29,30 Lastly, N0vs. NAg is plotted for all resolved products, using marker shape and color to denote the value of N0 and marker size to denote the intensity of the mass spectral peak (Fig. 1d and e). Further details are provided in ESI section 3.†
6-electron AgN-DNAs with two DNA strands
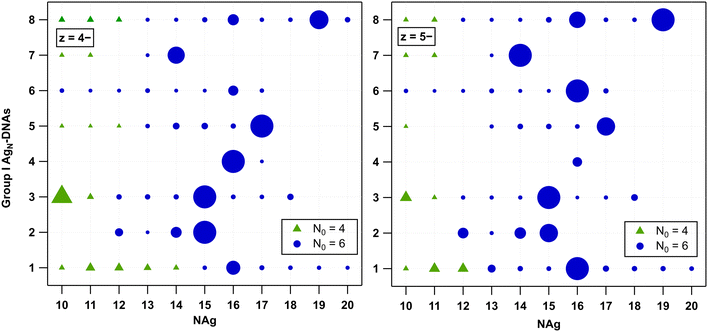
We first analysed the fragmentation patterns for Group I AgN-DNAs, which are the most abundant class of AgN-DNAs presented in Table 1 and whose molecular formulae correspond to ns = 2 and N0 = 6. Fig. 2 displays N0vs. NAg values for all detected products at z = −4 and −5 charge states; products at z = −3 and −6 charge states are significantly less intense and are shown in Fig. S24.† A range of fragments with ns = 2 and N0 = 6 are resolved, suggesting that the HPLC-purified AgN-DNAs can lose Ag+ during ESI-MS. Because no Group I AgN-DNA has a solved X-ray crystal structure, it is not possible to discern whether Ag+ is removed from the AgN core or from sites on the DNA template that are not incorporated into the AgN core, as has been resolved in AgN-DNA crystal structures.34,39,40,44Five Group I AgN-DNAs exhibit fragments that transition from N0 = 6 to N0 = 4 when NAg diminishes sufficiently. The exact value of NAg at this transition ranges from 10 to 14 and, in some cases, depends somewhat on the charge state z. Fragments of I.2, I.4, and I.6 are never observed to transition to N0 = 4. This diversity in the transition point from 6-electron to 4-electron clusters, as well as its dependence on the DNA template sequence and, in some cases, z, suggests that the fragmentation process of AgN-DNAs depends on the stability of the specific nanocluster. A similar decomposition of AgN-DNAs into smaller fragments under laser irradiation was investigated by Petty et al., where the laser-driven degradation of an AgN-DNA with Ag106+ (N0 = 4) species led to the formation of a series of fragments of Ag64+, Ag75+, Ag86+, and Ag97+ species with N0 = 2.12
No odd values of N0 were observed for any Group I AgN-DNA. Odd N0 values would indicate the presence of a valence electron with unpaired spin, which is expected to be energetically disfavoured. Moreover, no correlation is apparent between the previously reported circular dichroism (CD) signatures30 and the different fragmentation patterns of these AgN-DNAs.
6-electron AgN-DNAs with three DNA strands
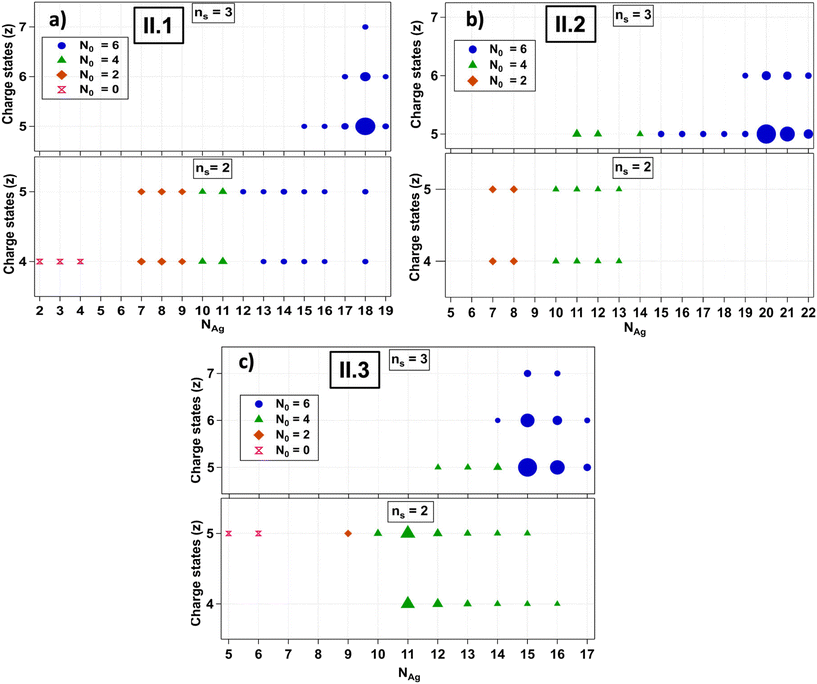
The fragmentation patterns of Group II AgN-DNAs are significantly more complex than those of Group I (Fig. S11–S13†). Past studies noted the increased fragmentation propensity of ns = 3 AgN-DNAs under ESI-MS.30II.2 has a higher hydrodynamic volume than typical ns = 2 AgN-DNAs,7 and the other Group II species are likely similar in volume. This increased size may promote fragmentation during ESI-MS.Group II AgN-DNAs were observed to fragment into smaller nanoclusters by the loss of silver and/or ssDNA oligomers, forming both ns = 3 and ns = 2 fragments that are resolved at different charge states. To facilitate the analysis of this more complex set of processes, Fig. 3 displays mass spectral compositions separately for each AgN-DNA species and separates ns = 3 and ns = 2 products into separate panels, with the charge state indicated on the vertical axes. We first discuss II.1. This emitter exhibits fragments due to the loss of Ag+ from the original ns = 3 AgN-DNA, as well as ns = 2 fragments due to the loss of one DNA oligomer and/or silver (Fig. 3a). ns = 3 fragments are most intense at the −5 charge state and retain N0 = 6 at all values of NAg and z, while ns = 2 fragments exhibit a wide range of NAg values at N0 = 6, 4, 2, and 0. Interestingly, N0 = 2 and 0 were not observed for Group I AgN-DNAs. This diversity of fragments supports that the loss of a DNA ligand produces highly reactive products that can transform into a wide range of daughter species. N0 = 0 fragments may correspond to two oligomers linked by silver-mediated base pairs.5
II.2 and II.3 also exhibit ns = 3 and ns = 2 fragments, but in contrast to II.1, their ns = 3 fragments do transition to N0 = 4 with sufficient loss of silver (Fig. 3b and c). Moreover, the loss of one ssDNA always coincides with a transition from N0 = 6 to N0 = 4 in II.2 and II.3. This may suggest that II.2 and II.3 have more “tightly” bound DNA templates whose removal more significantly destabilizes the AgN as compared to II.1. Notably, II.3 is the largest Group II species and loses up to 7 Ag+ before fragments transition to N0 = 4 products. The enhanced propensity of ns = 3 AgN-DNAs to fragment during ESI-MS may also be correlated with lower stability under biological conditions, which would offset benefits of their higher quantum yields. Future studies should assess the fitness of ns = 3 AgN-DNAs for biological imaging and sensing applications.
6-electron AgN-DNAs with two DNA strands and chlorido ligand(s)
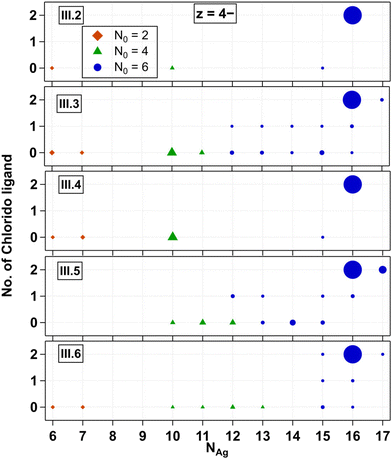
We next investigate Group III AgN-DNAs, which are protected by ns = 2 ssDNA and additional chlorido ligand(s). These recently discovered AgN-DNAs exhibit evidence for less chiral structures than AgN-DNAs without chloridos,30 as well as enhanced stability in chlorine-containing buffers.45III.2 through III.6 are (DNA)2(Ag16Cl2)8+ types stabilised by variations of a DNA template that differ by only one nucleobase, either in position 5 or removal of the adenine in position 10 (Table 1). These emitters have known X-ray crystal structures and very similar photophysical properties.34,39,40,45Fig. 4 shows all products detected for III.2 through III.6 at z = −4. z = −5 trends are similar and are shown in Fig. S25.† We observed that chlorido ligands are first removed as the mass of the fragmented products decreases, while preserving N0 = 6. As the mass continues to decrease after chlorido and Ag+ removal, N0 transitions from 6 to 4 at NAg = 11 to 13 occur. Species containing N0 = 2 are observed at NAg = 6 and 7, while those at NAg = 8 and 9 are notably absent from the mass spectra in all cases. The behaviour of III.1 is similar to that of III.2 and its variants as shown in Fig. S26.†Despite having identical molecular formulae, AgN-DNAs in Fig. 4 exhibit differences in their fragmentation patterns. This further supports that AgN-DNA fragmentation under negative ion mode ESI-MS is highly sensitive to the nucleobase sequence and not solely dependent on the molecular composition of the nanocluster core. We note that while III.4 exhibited only five resolvable products (Fig. 4), its mass spectrum also contained many ssDNA products with various contents (Fig. S16†). Thus, its lack of fragmentation products with ns = 2 should not be construed as a sign of enhanced stability as compared to those of other AgN-DNAs shown in Fig. 4.
Crystal structures have confirmed that III.2 through III.6 are composed of a Ag16 core stabilized by two DNA oligomers and two chlorido ligands.45 Thus, it is notable that a higher-mass product with NAg = 17 is resolved for III.3, III.5, and III.6 (Fig. 4), as was also evident previously.45 This additional silver is likely to be an Ag+ bound to the DNA ligand shell but not within the AgN core, perhaps attached to a nucleobase that is not directly ligated to the AgN. Such Ag+ is apparent in AgN-DNA crystal structures,44 and it is likely that Ag+ that is not within the AgN core is present in other AgN-DNAs as well, including those reported in Fig. 2 and 3.
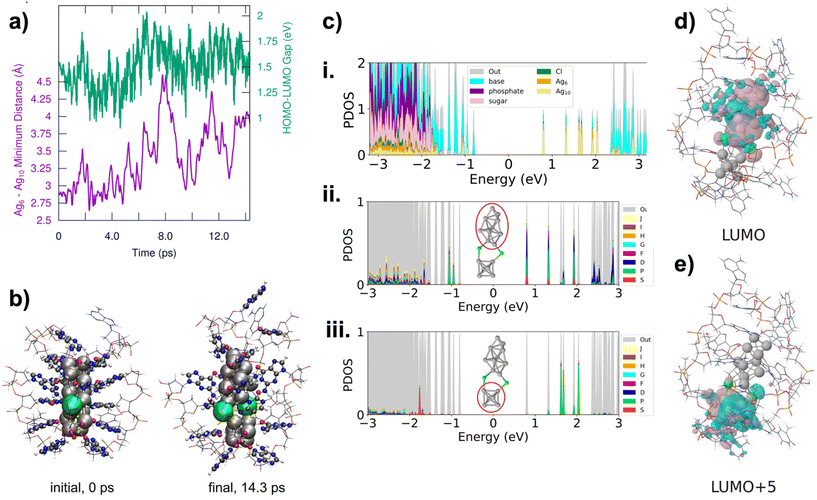
III.2 through III.6 are the only HPLC-purifiable AgN-DNAs with currently known X-ray crystal structures that include resolved DNA ligands.34,39,40 This provides the opportunity to use ab initio calculations to investigate the early stages of the fragmentation process of AgN-DNAs, including both structural and electronic changes during fragmentation. In particular, III.6 has been well-studied by the Häkkinen group recently.45–47 The fragmentation of III.6 under ESI-MS was modelled with DFT-based molecular dynamics simulations using an implicit water solvent model. This is a compromise of the true experimental conditions under ESI-MS, which presumably desolvates the water molecules from the AgN-DNA. The solvent conditions involved during ESI-MS at the very beginning of the fragmentation process, including effects of droplet charging and evaporation, are unclear, and it would be computationally demanding or even intractable to model all the effects realistically. Under the simulation conditions, the Ag16 core was observed to dissociate into Ag6 and Ag10 fragments, which separated at the point where the two chlorido ligands were attached to the Ag16 surface (Fig. 5a and b). The Ag6 fragment is compact and symmetric, and octahedral in shape, while the Ag10 is less symmetric and prolate in shape. Despite increasing separation of the two fragments, the HOMO–LUMO gap did not change substantially over the course of the simulation (Fig. 5a).
We next analysed the two Ag6 and Ag10 fragments to determine their effective valence electron count, N0. Fig. 5c shows the partial density of states (PDOS) for the entire system and for Ag6 and Ag10 fragments. All frontier molecular orbitals of III.6 are shown in Fig. S26,† with selected orbitals shown in Fig. 5d and e. These calculations show that the Ag6 fragment has an occupied S state and three unoccupied P states, consistent with a 2e− (1S2) system, i.e. N0 = 2. This would also be consistent with the spheroidal shape of Ag6. The Ag10 fragment shows electronic states that correspond to S and P, consistent with a 4e− (1S21P2) system. Symmetries of frontier molecular orbitals shown in Fig. 5d and e further support that the original Ag16Cl2 fragments into one N0 = 4 Ag10 and one N0 = 2 Ag6. The frontier molecular orbital of the LUMO (Fig. 5d) is primarily localized on Ag10 and shows two nodes, while the frontier molecular orbital of the LUMO+5 is localized on Ag6 and shows only a single node. This interpretation is consistent with our experimental observation that (DNA)2(Ag16Cl2)8+ fragments into N0 = 2 and N0 = 4 nanoclusters, with sizes in the range of Ag6 and Ag10. Thus, even at early stages in the fragmentation of AgN-DNAs, there is likely an electronic driving force towards fragmentation into nanoclusters with even valence electron counts, supporting our observation of only N0 = 0, 2, 4, and 6 products in the mass spectra analyzed in this study.
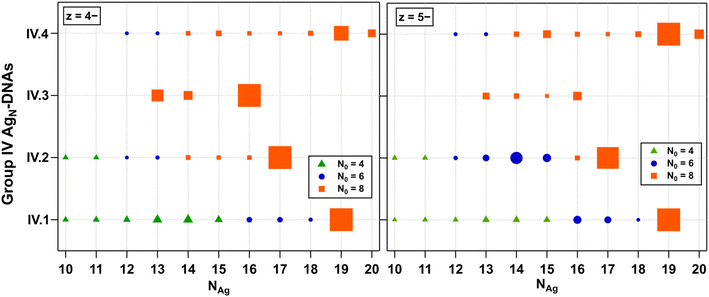
8-electron AgN-DNAs (Group IV)
Finally, we examined the fragmentation patterns of Group IV AgN-DNAs, which have been hypothesized to be spheroidal structures rather than the rod-like structures of 6-electron AgN-DNAs.29,30 Mass spectral peak intensities were the highest at z = −5 and −4, and these products are shown in Fig. 6. Fig. S27† shows z = −6 and −3 products. Just as for Groups I, II, and III, Group IV fragmentation products and the value of NAg at which N0 transitions from 8 to 6 to 4 are highly dependent on the DNA template sequence. IV.1 and IV.2 fragment into products with N0 = 8, 6, and 4. IV.3 fragments never transition to smaller N0; the stability of the N0 = 8 products down to NAg = 13 contrasts with those in Fig. 2–4, in which three AgN-DNAs have transitioned to N0 = 4 fragments at NAg = 13. IV.4 fragments into products with N0 = 8 and 6. IV.1 is the only Group 4 species with a defined absorbance peak >500 nm, which may suggest that the AgN core is more anisotropic than the other Group IV AgN-DNAs. Increased anisotropy could lead to a greater propensity to fragment into a variety of smaller products. X-ray crystal structures of Group IV AgN-DNAs would enable further interrogation of the fragmentation processes of these nanoclusters.Discussion
This study investigated how AgN-DNAs fragment during negative ion mode ESI-MS, driven by the hypothesis that this unintentional fragmentation can provide insights into the chemical properties of AgN-DNAs without CID. Unlike monolayer-protected metal nanoclusters, which require significantly higher energies to induce fragmentation,13 AgN-DNAs display multiple fragmentation products under native-like negative mode ESI-MS. This greater propensity to fragment may be due to several factors: the bulkier nature of DNA ligands compared to that of small molecule ligands, the polyelectrolyte nature of DNA and the process of partial protonation that occurs during negative ion mode ESI,28 and the weaker Ag–N or Ag–O bonds in AgN-DNAs as compared to Ag–S bonds in thiol-stabilized silver nanoclusters. In ammonium acetate solution, the phosphate backbone of nucleic acids partially protonates due to proton transfer from ammonium to phosphate. This process occurs during desolvation and may occur at the same time as fragmentation events; therefore, these two processes should not be considered sequential events but rather concurrent events. Due to the harsh nature of this process, desolvation by ESI may be viewed as a “stress test” of the stability of Ag-DNAs in the gas phase.Our analysis of 21 different AgN-DNAs consistently showed that the fragmentation of AgN-DNAs under ESI-MS strongly depends on the DNA sequence. We observed no single consistent value of total silver content NAg at which the effective valence electron count N0 transitions to lesser values, supporting that the specific DNA template sequence strongly determines the chemical stability of AgN-DNAs. Even small sequence alterations that preserve the overall AgN-DNA structure can cause variations in stability, as is evident in III.2 and its variants, where a single nucleobase alteration impacts fragmentation patterns.
All fragments detectable by ESI-MS in this study exhibited even valence electron counts: N0 = 0, 2, 4, 6, or 8. The spectral purity of the 21 HPLC-purified AgN-DNAs strongly supports that the smaller nanocluster products detected in mass spectra were not present in any appreciable quantity before ESI-MS and therefore formed due to fragmentation. Because such fragments may include species that are transiently stable in the gas phase but not stable in solution, the absence of odd valence electron counts is significant. Simulation of III.6 further supports the strong electronic driving force towards forming fragments that retain even values of N0, as electronic states begin to localize on fragments even in early stages. Thus, it is highly unlikely that AgN-DNAs with odd valence electron counts would be stable in solution. We suggest that reports of solution-stable AgN-DNAs with odd values of N0 may be affected by slight miscalibration of the mass spectrometer, as precision to a single proton is required for accurate N0 assignment, and this level of precision can be challenging to achieve at high m/z values where AgN-DNAs are detected by ESI-MS.
Our findings also support the presence of Ag+ ions that are coordinated to the DNA ligands yet not within the AgN core in HPLC-purified AgN-DNAs. We observed multiple examples of these products for (DNA)2(Ag16Cl2)8+ with a known X-ray crystal structure (Fig. 4), and possible products for other AgN-DNAs are evident (Fig. 2, 3 and 5). If easily removed by ESI-MS, such Ag+ may be weakly bound and could have implications for the cytotoxicity of those AgN-DNA species. Future efforts are needed to resolve AgN-DNA crystal structures and thereby assign nanocluster composition in conjunction with ESI-MS, as well as to investigate whether loosely bound Ag+ influences factors such as the cytotoxicity of AgN-DNAs, which will be essential for developing their biomedical applications. Moreover, our findings strongly suggest that cytotoxicity will depend on the DNA template sequence of a specific AgN-DNA, as has been previously reported.48
The information this study provides on the degree of lability of DNA and chlorido ligands for specific AgN-DNA species could inform novel strategies to tune solution-phase AgN-DNA chemical transformations and ligand protection. Ag+ shedding in solution may drive the transformation of AgN-DNAs into smaller AgN-DNAs, including those with lower N0 values that will display significantly shifted emission wavelengths.49 We propose that such a transformation, accompanied by the loss of Ag+, or movement of Ag+ away from or towards the AgN core, is the underlying mechanism of colorimetric AgN-DNA sensing schemes such as NanoCluster Beacons,4,50–52 which generally exhibit red-green transitions. Thus, an inherent degree of lability may be key to AgN-DNA sensing schemes. Moreover, the propensity to fragment under ESI-MS may correlate with emitter stability and degradation of AgN-DNAs in vivo. AgN-DNAs with chlorido ligands demonstrate exceptional stability in physiological buffers, and the presence of chloride ions in solution can dramatically enhance AgN-DNA emission intensity.2 Thus, investigating the lability of chlorido ligands in the gas phase could reveal mechanisms to more controllably protect AgN-DNAs with chlorides and improve their biocompatibility. Finally, similar methods may be useful for investigating the properties of noble metal nanoclusters stabilized by other biomolecular ligands.53–55
Conclusion
Detailed analysis of the fragmentation patterns of 21 HPLC-purified AgN-DNAs under negative ion mode ESI-MS shows that fragmentation is strongly dependent on the AgN-DNA template sequence. AgN-DNAs appear to lose silver including Ag+ during ESI-MS, and the fragmentation patterns of Ag16-DNAs of known X-ray crystal structures confirm that a fraction of these Ag+ may be bound to the DNA ligand shell but not a part of the initial AgN core. With sufficient loss of silver, the nanocluster's effective valence electron count, N0, can decrease. The detected nanocluster fragments only exhibit even values of N0, strongly supporting the likelihood that AgN-DNAs with odd valence electron counts are unlikely to be stable in solution. Molecular dynamics simulations, with forces calculated from density functional theory, of an Ag16-DNA with a known crystal structure support the dissociation of the nanocluster core into two smaller nanocluster species, each containing an even number of valence electrons, which is further supported by the symmetry of the frontier molecular orbitals of the fragment species. Together, these results provide new insights into the chemistry of AgN-DNAs in the gas phase and may have relevance to both chemical transformations of AgN-DNAs that enable colorometric sensing schemes and degradation of AgN-DNAs in vivo, where loss of Ag+ may contribute to cytotoxicity. Future mass spectral studies using tools such as CID and TIMS may shed further light on chemical reactions involving AgN-DNAs.Methods
Synthesis and purification of AgN-DNAs
AgN-DNAs were synthesized by the addition of stoichiometric amounts of AgNO3 to an aqueous solution of DNA oligomer (Integrated DNA Technologies, standard desalting) in 10 mM ammonium acetate (pH 7), followed by the partial reduction of silver content using a 0.5 molar ratio of a freshly prepared aqueous solution of NaBH4. The solution was kept at 4 °C (or stated otherwise) in the dark until concentration by spin filtering and then purification using reverse-phase HPLC. Following HPLC, the solvent was exchanged into 10 mM ammonium acetate, pH 7. Details on the synthesis and purification methods, HPLC chromatograms and mass spectra of the AgN-DNAs have been previously reported.2,29,30Mass spectrometry
Electrospray ionization mass spectrometry (ESI-MS) was performed using a Waters Xevo G2-XS QTof. Samples were directly injected at 0.1 mL min−1 in negative ion mode with a 2 kV capillary voltage, 30 V cone voltage and no collision energy. Spectra were collected from 1000 to 4000 m/z with an integration time of 1 s. Source and desolvation temperatures were 80 and 150 °C, respectively. Gas flows were 45 L h−1 for the cone and 450 L h−1 for the desolvation. Samples were injected with 50 mM NH4OAc – MeOH (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20) solution at pH 7. The mass spectra of AgN-DNAs are shown in Fig. S3 to S21.† Determination of nanocluster size (total number of silver N, ligand composition i.e., the number of DNA strands ns, and the presence of additional chlorido ligands) and the overall charge, Qc (and hence determining the number of effective valence electron count N0) was performed by fitting the calculated isotopic distribution of the AgN-DNA to the experimental spectra (details in the ESI†). Calculated isotopic distributions were obtained from MassLynx using the chemical formula and corrected for the overall positive charge (oxidation state, Qc) of the nanocluster core.
20) solution at pH 7. The mass spectra of AgN-DNAs are shown in Fig. S3 to S21.† Determination of nanocluster size (total number of silver N, ligand composition i.e., the number of DNA strands ns, and the presence of additional chlorido ligands) and the overall charge, Qc (and hence determining the number of effective valence electron count N0) was performed by fitting the calculated isotopic distribution of the AgN-DNA to the experimental spectra (details in the ESI†). Calculated isotopic distributions were obtained from MassLynx using the chemical formula and corrected for the overall positive charge (oxidation state, Qc) of the nanocluster core.
Molecular dynamics and density functional theory calculations
DFT was implemented in the software GPAW,56,57 with real space grids with a grid spacing of 0.2 and Perdew–Burke–Ernzerhof (PBE) functional.58 The nanocluster structure was created based on the experimentally solved crystal structure by Vosch, et al.34 which was later confirmed to include 2 Cl ligands on the Ag core surface and computationally analyzed as a corrected model structure.45,47 An implicit water solvent model was used in all calculations.47,59 PBE-optimized coordinates of the nanocluster were used as a starting structure for the molecular dynamics simulation. Molecular dynamics (MD) was performed using a Langevin thermostat with a 2 fs time step and a 0.01 fs friction parameter. Masses of hydrogen atoms were treated as those of deuterium atoms. The total length of the MD run was 14.3 ps, from which heating to the target temperature of 300 K took ∼3 ps was performed. To reveal the possible fragmentation mechanism, the minimum distance between Ag6 and Ag10 parts of the metal core was analyzed from the MD trajectory. The last snapshot structure at 14.3 ps was then used for electronic structure analysis using the GLLB-SC xc-functional.60 Full details regarding DFT and MD calculations are provided in the ESI.†Data availability
The data supporting this article have been included as part of the ESI† in the form of mass spectral data graphs and tables.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by AFOSR FA9550-21-1-0163 and DURIP FA9550-22-1-0206 and by the Society of Hellman Fellows Program. M. R. acknowledges a UC Irvine Engineering Pathway to the PhD Fellowship. A. G.-R. acknowledges support from a “la Caixa” Foundation Fellowship (ID LCF/BQ/EU22/11930078) and Balsells Graduate Fellowship. H. H., S. M. and M. K. acknowledge the Research Council of Finland (former Academy of Finland, project 355083) and CSC supercomputing centre for computing time.References
- A. Gonzàlez-Rosell, C. Cerretani, P. Mastracco, T. Vosch and S. M. Copp, Nanoscale Adv., 2021, 3, 1230–1260 RSC.
- R. Guha, M. Rafik, A. Gonzàlez-Rosell and S. M. Copp, Chem. Commun., 2023, 59, 10488–10491 RSC.
- Y.-A. Chen, J. M. Obliosca, Y.-L. Liu, C. Liu, M. L. Gwozdz and H.-C. Yeh, J. Am. Chem. Soc., 2015, 137, 10476–10479 CrossRef CAS PubMed.
- X. Yan, J. Sun, X. E. Zhao, R. Wang, X. Wang, Y. N. Zuo, W. Liu, R. Kong and S. Zhu, Microchim. Acta, 2018, 185, 403 CrossRef PubMed.
- R. Guha and S. M. Copp, in Modern Avenues in Metal-Nucleic Acid Chemistry, ed. J. Müller and B. Lippert, CRC Press, 2023, ch. 12, pp. 291–342 Search PubMed.
- S. A. Bogh, M. R. Carro-Temboury, C. Cerretani, S. M. Swasey, S. M. Copp, E. G. Gwinn and T. Vosch, Methods Appl. Fluoresc., 2018, 6, 024004 CrossRef PubMed.
- V. A. Neacşu, C. Cerretani, M. B. Liisberg, S. M. Swasey, E. G. Gwinn, S. M. Copp and T. Vosch, Chem. Commun., 2020, 56, 6384–6387 RSC.
- V. Rück, N. K. Mishra, K. K. Sørensen, M. B. Liisberg, A. B. Sloth, C. Cerretani, C. B. Mollerup, A. Kjaer, C. Lou, K. J. Jensen and T. Vosch, J. Am. Chem. Soc., 2023, 145, 16771–16777 CrossRef PubMed.
- X. Wang, M. B. Liisberg, G. L. Nolt, X. Fu, C. Cerretani, L. Li, L. A. Johnson, T. Vosch and C. I. Richards, ACS Nano, 2023, 17, 12862–12874 CrossRef CAS PubMed.
- J. Sharma, H. C. Yeh, H. Yoo, J. H. Werner and J. S. Martinez, Chem. Commun., 2011, 47, 2294–2296 RSC.
- J. M. Obliosca, C. Liu, R. A. Batson, M. C. Babin, J. H. Werner and H.-C. Yeh, Biosensors, 2013, 3, 185–200 CrossRef CAS PubMed.
- C. J. Setzler, C. A. Arrington, D. Lewis and J. T. Petty, J. Phys. Chem. B, 2023, 127, 10851–10860 CrossRef CAS PubMed.
- P. Chakraborty, S. Malola, M. Neumaier, P. Weis, H. Häkkinen and M. M. Kappes, Angew. Chem., Int. Ed., 2023, 62, e202305836 CrossRef CAS PubMed.
- L. Zhang, M. Guo, J. Zhou, C. Fang and X. Sun, Small, 2023, 19, e2301633 CrossRef PubMed.
- T. Chen, Q. Yao, R. R. Nasaruddin and J. Xie, Angew. Chem., Int. Ed., 2019, 58, 11967–11977 CrossRef CAS PubMed.
- H. Gholipour-Ranjbar, Deepika, P. Jena and J. Laskin, Commun. Chem., 2022, 5, 130 CrossRef CAS PubMed.
- Z. Wu, D.-e. Jiang, E. Lanni, M. E. Bier and R. Jin, J. Phys. Chem. Lett., 2010, 1, 1423–1427 CrossRef CAS.
- A. Baksi, E. K. Schneider, P. Weis, K. R. Krishnadas, D. Ghosh, H. Hahn, T. Pradeep and M. M. Kappes, J. Phys. Chem. C, 2019, 123, 28477–28485 CrossRef CAS.
- M. Neumaier, A. Baksi, P. Weis, E. K. Schneider, P. Chakraborty, H. Hahn, T. Pradeep and M. M. Kappes, J. Am. Chem. Soc., 2021, 143, 6969–6980 CrossRef CAS PubMed.
- S. Biswas, S. Das and Y. Negishi, Coord. Chem. Rev., 2023, 492, 215255 CrossRef CAS.
- R. Jin, Nanoscale, 2010, 2, 343–362 RSC.
- R. H. Adnan, J. M. L. Madridejos, A. S. Alotabi, G. F. Metha and G. G. Andersson, Adv. Sci., 2022, 9, 2105692 CrossRef CAS PubMed.
- E. L. Albright, T. I. Levchenko, V. K. Kulkarni, A. I. Sullivan, J. F. DeJesus, S. Malola, S. Takano, M. Nambo, K. Stamplecoskie, H. Häkkinen, T. Tsukuda and C. M. Crudden, J. Am. Chem. Soc., 2024, 146, 5759–5780 CrossRef CAS PubMed.
- D. Schultz and E. G. Gwinn, Chem. Commun., 2012, 48, 5748–5750 RSC.
- K. Koszinowski and K. Ballweg, Chem. – Eur. J., 2010, 16, 3285–3290 CrossRef CAS PubMed.
- D. Schultz, K. Gardner, S. S. R. Oemrawsingh, N. Markešević, K. Olsson, M. Debord, D. Bouwmeester and E. Gwinn, Adv. Mater., 2013, 25, 2797–2803 CrossRef CAS PubMed.
- S. M. Copp, D. Schultz, S. Swasey, J. Pavlovich, M. Debord, A. Chiu, K. Olsson and E. Gwinn, J. Phys. Chem. Lett., 2014, 5, 959–963 CrossRef CAS PubMed.
- E. Largy, A. König, A. Ghosh, D. Ghosh, S. Benabou, F. Rosu and V. Gabelica, Chem. Rev., 2021, 122, 7720–7839 CrossRef PubMed.
- A. Gonzàlez-Rosell, R. Guha, C. Cerretani, V. Rück, M. B. Liisberg, B. B. Katz, T. Vosch and S. M. Copp, J. Phys. Chem. Lett., 2022, 13, 8305–8311 CrossRef PubMed.
- R. Guha, A. Gonzàlez-Rosell, M. Rafik, N. Arevalos, B. B. Katz and S. M. Copp, Chem. Sci., 2023, 14, 11340–11350 RSC.
- J. T. Petty, O. O. Sergev, A. G. Kantor, I. J. Rankine, M. Ganguly, F. D. David, S. K. Wheeler and J. F. Wheeler, Anal. Chem., 2015, 87, 5302–5309 CrossRef CAS PubMed.
- J. T. Petty, O. O. Sergev, M. Ganguly, I. J. Rankine, D. M. Chevrier and P. Zhang, J. Am. Chem. Soc., 2016, 138, 3469–3477 CrossRef CAS PubMed.
- K. G. Stamplecoskie and P. Aminfar, Chem. Mater., 2024, 36(19), 9003–9012 CrossRef CAS.
- C. Cerretani, J. Kondo and T. Vosch, RSC Adv., 2020, 10, 23854–23860 RSC.
- P. Mastracco, A. Gonzàlez-Rosell, J. Evans, P. Bogdanov and S. M. Copp, ACS Nano, 2022, 16, 16322–16331 CrossRef CAS PubMed.
- S. M. Copp, P. Bogdanov, M. Debord, A. Singh and E. Gwinn, Adv. Mater., 2016, 28, 3043 CrossRef CAS PubMed.
- S. M. Swasey, S. M. Copp, H. C. Nicholson, A. Gorovits, P. Bogdanov and E. G. Gwinn, Nanoscale, 2018, 10, 19701–19705 RSC.
- S. M. Copp, S. M. Swasey, A. Gorovits, P. Bogdanov and E. G. Gwinn, Chem. Mater., 2020, 32, 430–437 CrossRef CAS.
- C. Cerretani, H. Kanazawa, T. Vosch and J. Kondo, Angew. Chem., Int. Ed., 2019, 58, 17153–17157 CrossRef CAS PubMed.
- C. Cerretani, J. Kondo and T. Vosch, CrystEngComm, 2020, 22, 8136–8141 RSC.
- A. Gonzàlez-Rosell and S. M. Copp, Acc. Chem. Res., 2024, 57, 2117–2129 CrossRef PubMed.
- E. Bethur, R. Guha, Z. Zhao, B. B. Katz, P. D. Ashby, H. Zeng and S. M. Copp, ACS Nano, 2024, 18, 3002–3010 CrossRef CAS PubMed.
- M. S. Blevins, D. Kim, C. M. Crittenden, S. Hong, H.-C. Yeh, J. T. Petty and J. S. Brodbelt, ACS Nano, 2019, 13, 14070–14079 CrossRef CAS PubMed.
- D. J. E. Huard, A. Demissie, D. Kim, D. Lewis, R. M. Dickson, J. T. Petty and R. L. Lieberman, J. Am. Chem. Soc., 2019, 141, 11465–11470 CrossRef CAS PubMed.
- A. Gonzàlez-Rosell, S. Malola, R. Guha, N. R. Arevalos, M. F. Matus, M. E. Goulet, E. Haapaniemi, B. B. Katz, T. Vosch, J. Kondo, H. Häkkinen and S. M. Copp, J. Am. Chem. Soc., 2023, 145, 10721–10729 CrossRef PubMed.
- S. Malola and H. Häkkinen, Chem. Commun., 2024, 60, 3315–3318 RSC.
- S. Malola, M. F. Matus and H. Häkkinen, J. Phys. Chem. C, 2023, 127, 16553–16559 CrossRef CAS.
- N. Bossert, D. de Bruin, M. Götz, D. Bouwmeester and D. Heinrich, Sci. Rep., 2016, 6, 37897 CrossRef CAS PubMed.
- S. M. Copp and A. Gonzàlez-Rosell, Nanoscale, 2021, 13, 4602–4613 RSC.
- J. M. Obliosca, M. C. Babin, C. Liu, Y. L. Liu, Y. A. Chen, R. A. Batson, M. Ganguly, J. T. Petty and H. C. Yeh, ACS Nano, 2014, 8, 10150–10160 CrossRef CAS PubMed.
- Y.-A. Kuo, O. S. Zhao, S. Hong, T. D. Nguyen, Y.-I. Chen, H.-C. Li and T. Yeh, Biophys. J., 2021, 120, 272a CrossRef.
- Y.-A. Chen, H. T. Vu, Y.-L. Liu, Y.-I. Chen, T. D. Nguyen, Y.-A. Kuo, S. Hong, Y.-A. Chen, S. Carnahan, J. T. Petty and H.-C. Yeh, Chem. Commun., 2019, 55, 462–465 RSC.
- E. Lopez-Martinez, D. Gianolio, S. Garcia-Orrit, V. Vega-Mayoral, J. Cabanillas-Gonzalez, C. Sanchez-Cano and A. L. Cortajarena, Adv. Opt. Mater., 2022, 10, 2101332 CrossRef CAS.
- S. Gregersen, T. Vosch and K. J. Jensen, Chem. – Eur. J., 2016, 22, 18492–18500 CrossRef CAS PubMed.
- S. C. Scott, J. A. Cadge, G. K. Boden, J. F. Bower and C. A. Russell, Angew. Chem., Int. Ed., 2023, 62, e202301526 CrossRef CAS PubMed.
- J. J. Mortensen, A. H. Larsen, M. Kuisma, A. V. Ivanov, A. Taghizadeh, A. Peterson, A. Haldar, A. O. Dohn, C. Schäfer, E. Jónsson, E. D. Hermes, F. A. Nilsson, G. Kastlunger, G. Levi, H. Jónsson, H. Häkkinen, J. Fojt, J. Kangsabanik, J. Sødequist, J. Lehtomäki, J. Heske, J. Enkovaara, K. T. Winther, M. Dulak, M. M. Melander, M. Ovesen, M. Louhivuori, M. Walter, M. Gjerding, O. Lopez-Acevedo, P. Erhart, R. Warmbier, R. Würdemann, S. Kaappa, S. Latini, T. M. Boland, T. Bligaard, T. Skovhus, T. Susi, T. Maxson, T. Rossi, X. Chen, Y. L. A. Schmerwitz, J. Schiøtz, T. Olsen, K. W. Jacobsen and K. S. Thygesen, J. Chem. Phys., 2024, 160(9), 092503 CrossRef CAS PubMed.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Møller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens. Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Held and M. Walter, J. Chem. Phys., 2014, 141, 174108 CrossRef PubMed.
- M. Kuisma, J. Ojanen, J. Enkovaara and T. T. Rantala, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115106 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Materials and experimental methods; mass spectra and associated calculated mass distributions; details of simulation and modelling. See DOI: https://doi.org/10.1039/d4nr03533j |
| This journal is © The Royal Society of Chemistry 2024 |