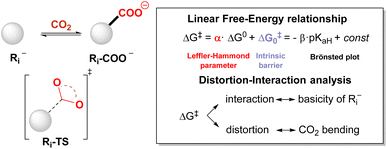
Unveiling the reactivity of CO₂ with carbanions: a theoretical analysis of the carboxylation step

Abstract

The synthetic insertion of carbon dioxide into organic scaffolds typically requires the reaction of CO₂ with a carbanion (carboxylation step), with the latter being generated through chemical, electrochemical, or photochemical routes. Still, little is known about the energetic and structural requirements of this step. In this work, we unveil the reactivity of CO₂ with a selected set of 28 carbanions through DFT calculations and provide linear free-energy relationships that correlate the ΔG⁰ and the ΔG^‡ of the carboxylation step. These reveal a Leffler–Hammond parameter α = 0.26 ± 0.02 and an intrinsic barrier ΔG^‡₀ = 12.7 ± 0.3 kcal mol⁻¹ (ωb97XD/aug-cc-pvtz//ωb97XD/def2tzvp level of theory), indicative of smooth reactivity of carbanions with CO₂. This reactivity is further associated with the basicity of the carbanions (expressed as the pK_aH of the conjugate acid), in a linear Brønsted plot between calculated ΔG^‡ and experimental pK_aH (slope β = 0.40 ± 0.04 kcal mol⁻¹). According to the Mayr–Patz equation, calculations allow the extrapolation of electrophilicity values for CO₂ in the range from −15.3 to −18.7, in good agreement with a single reported experimental value of −16.3. Concerning the structural changes occurring in the transition state, the major energy penalty comes from the distortion of CO₂. These findings can be useful in designing novel reactivity targeting carbon dioxide fixation.

---

Introduction

Carbon dioxide is a by-product of many anthropogenic activities, and its current increase in the atmosphere is causing severe climate changes.¹ On the other hand, CO₂ is a cheap, non-toxic and renewable single carbon atom building block that can be exploited for fuel production or for organic synthesis. Strategies to capture and reconvert CO₂ into fuels or chemicals are thus important targets for achieving carbon neutrality,² in line with the United Nations sustainable development goals.³ Current carbon dioxide capturing technologies exploit amine solutions, with the formation of carbamate salts;^4,5 CO₂ is then released by an energy demanding thermal step involving heating of the solution up to 100–125 °C. Electrochemical methods are considered as possible alternatives to avoid the need for an external high temperature energy source; they can operate through electrochemically induced displacement reactions (such as in the case of electrochemically modulated amine regeneration) or through CO₂ binding to electrochemically reduced nucleophilic capturing agents, such as quinones.^4,6

Concerning carbon dioxide reconversion, some strategies target CO₂ reduction to C₁ or C₂₊ products.^7–9 For instance, a cobalt phthalocyanine molecular catalyst was exploited to mediate CO₂ to CO formation in a zero-gap membrane flow reactor with selectivity >95% at an impressive current density of 150 mA cm⁻².¹⁰ Examples of reduction of CO₂ to C₂ products include the use of a 3D dendritic copper–cuprous oxide composite for acetic acid and ethanol production¹¹ and the use of single site metal catalysts. In this field, the use of DFT calculations for a thermodynamic and kinetic analysis of the relevant steps is considered a powerful tool for catalyst design.^8,12

Finally, carbon dioxide is a single carbon atom building block to be exploited in organic synthesis.^13–18 In this regard, processes involving CO₂ are already industrialised for the preparation of linear and cyclic carbonates (from alkynes or epoxides), for urea synthesis,¹⁹ and in the Kolbe–Schmitt reaction^20,21 for the preparation of salicylic acid and 3-hydroxy-2-naphthoic acid (from sodium phenolate and 2-naphtholate, respectively).

CO₂ is however a thermodynamic sink of the carbon cycle and its conversion requires highly reactive chemicals, transition metal catalysis^22,23 and/or severe reaction conditions.^13,24 An appealing strategy is the formation of new C–C bonds through the polar reaction of CO₂ with nucleophilic carbanions generated through chemical,^25,26 electrochemical,^27,28 or photochemical routes.^29–31 This strategy enabled the preparation of products of pharmaceutical interest – although obtained as racemic mixtures – such as amino acids,^32,33 the anti-epilepsy and absence seizure drug ethosuximide precursor (synthesised via electrochemical hydrocarboxylation in flow),³⁴ and benzylic carboxylic acids such as fenoprofen, flurbiprofen, ibuprofen and naproxen.³⁵

However, while earlier reports rationalised the conversion of CO₂ to formate using metal and organic hydrides,³⁶ its reactivity with carbanion nucleophiles is still poorly understood, due to very limited kinetic data available.³⁷ In a seminal work by Ofial and Mayr, a rate constant for the carboxylation step was reported only for the indenide anion (bimolecular k = 2.09 ± 0.07 10⁵ M⁻¹ s⁻¹, in dimethylsulfoxide at 20 °C).³⁷ Therefore, the rationalisation of the thermodynamic, kinetic and structural requirements that govern the reactivity of carbanions with CO₂ is an important target, from the perspective of designing novel carboxylation processes. In particular, the prediction of free energy barriers and reaction rates on the basis of physical parameters of carbanions would be a powerful tool for an a priori evaluation of the envisaged reactivity.

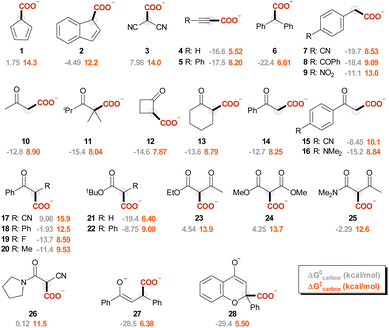
In this work, we sought to unveil the reactivity of CO₂ with carbanions by exploiting DFT calculations. We thus considered a selected set of 28 organic carbanions (R_i⁻) and calculated both the standard free energy (ΔG⁰) and the activation free energy (ΔG^‡) of the carboxylation step (eqn (1) and Scheme 1). Products and transition states will be denoted as R_i-COO⁻ and R_i-TS, respectively.

R_i⁻ + CO₂ ⇌ R_i-COO⁻ ΔG⁰, ΔG^‡ (1)

We will show that ΔG⁰ and ΔG^‡ correlate in linear free-energy relationships (also known as rate-equilibrium relationships³⁸), whose slope α provides the Leffler–Hammond parameter (describing the fraction of the change in the Gibbs energy of the reaction reflected in the change of the Gibbs energy of activation³⁹) and the intercept ΔG^‡₀ is the intrinsic barrier (i.e. the activation free energy for an isoergonic reaction). Compared to other organic reactions, these parameters indicate low ΔG^‡ for the carboxylation step with a slight dependence on ΔG⁰, identifying CO₂ as a powerful electrophile. The reactivity of the carbanions in terms of ΔG^‡ correlates with their basicity, in a Brønsted plot. Distortion/interaction analysis using the model developed by Bickelhaupt and Houk groups⁴⁰ reveals that the carboxylation step is controlled by both carbanion/CO₂ interaction and distortion of the reactants. The interaction is correlated to the basicity of the carbanion; concerning the distortion, the most important contribution to the activation energy penalty is made by the distortion of CO₂, in terms of the reduction of the O–C–O angle and the C(R_i⁻)⋯C(CO₂) distance in the transition states. Both these geometric parameters linearly correlate indeed with ΔG^‡.

Scheme 1 Schematic representation of the carboxylation step of a carbanion R_i⁻ to R_i-COO⁻, and representation of the transition state R_i-TS. Linear free-energy relationship and distortion–interaction analysis explored in this work.

Computational methods

Calculations were performed with Gaussian16 software.⁴¹ Most carbanions included in this study possess few rotatable bonds. In the cases of anions with possible multiple conformations that may impact the target C-site reactivity (i.e. anions R₂₃⁻, R₂₄⁻, R₂₅⁻, and R₂₇²⁻), an initial conformational search was performed with a semiempirical pm3 method^42–44 including a solvation model for acetonitrile to identify the most stable conformers that were then optimized with DFT methods (see ESI, Fig. S1–S4†). In the manuscript and in the correlations presented, we report ΔG^‡ and ΔG⁰ data for the most stable conformer of these anions. We have corroborated this assumption by performing calculations and analysing the ΔG^‡ and ΔG⁰ data also for the second most stable conformer of R₂₃⁻, R₂₄⁻ and R₂₅⁻. From the results reported in Table S1 in the ESI,† the variations of the calculated activation and standard free energy of carboxylation resulting from changes in the nature of the initial conformer are in a range of 0.16–0.65 and 0.73–2.14 kcal mol⁻¹, respectively, minimally impacting the correlations presented in this work.

Structures were optimized with DFT methods including a continuum solvation model for acetonitrile (or dimethylsulfoxide) using the integral equation formalism variant (IEFPCM).^45–47 Analysis of the frequencies was performed to assess the nature of the stationary points; in particular, for the transition states, the presence of a single imaginary frequency was confirmed, and the reliability of the transition states was corroborated by intrinsic reaction coordinate (IRC) analysis. For all calculations, a pruned (99 590) integration grid was used. For all the species, a correction of +1.90 kcal mol⁻¹ was applied to the computed free energy values to convert the standard state from 1 atmosphere to a 1 M solution.^37,48 When specified, corrections for entropy were applied according to the Truhlar model,⁴⁹ using a frequency cut-off value of 100.0 wavenumber.

The following levels of theory were employed:

ωb97XD/def2tzvp//ωb97XD/def2tzvp: geometries optimised using the ωb97XD⁵⁰ hybrid functional taking advantage of Grimme's dispersion model with Ahlrichs' triple-zeta basis set def2tzvp;^51,52

ωb97XD/aug-cc-pvtz//ωb97XD/def2tzvp: geometries optimized at the ωb97XD/def2tzvp level, followed by a single point energy calculation performed using the same functional and the aug-cc-pvtz basis set^53,54 including diffuse functions;

b2plypd/aug-cc-pvtz//ωb97XD/def2tzvp: geometries optimized at the ωb97XD/def2tzvp level, followed by a single point energy calculation performed using the double hybrid b2plypd functional,⁵⁵ with the aug-cc-pvtz basis set;

b3lyp/6–311g(d,p)//b3lyp/6–311g(d,p): geometries optimised using the b3lyp functional (without dispersion correction) with a Pople⁵⁶ 6–311g(d,p) basis set (not including diffuse functions).

Results and discussion

Evaluation of the level of theory

The availability of an experimental ΔG^‡ value of 10.0 kcal mol⁻¹ for the carboxylation of the indenide anion R₂⁻ from a bimolecular rate constant of 2.09 ± 0.07 10⁵ M⁻¹ s⁻¹ (in dimethylsulfoxide at 20 °C)³⁷ allowed the evaluation and the selection of the suitable level of theory among the four levels discussed in the “Computational methods” section. The four levels of theory (continuum model for dimethylsulfoxide solvent) provided calculated ΔG^‡ for the carboxylation of R₂⁻ in the range 11.9–15.2 kcal mol⁻¹, in good agreement with the experimental value (Table S2 in the ESI†). The best match was found at the ωb97XD/aug-cc-pvtz//ωb97XD/def2tzvp level (calculated ΔG^‡ = 11.9 kcal mol⁻¹), which was chosen as the level for the calculations discussed in this work. Corrections for entropy according to the Truhlar model⁴⁹ lead to an increase of +0.7 kcal mol⁻¹ in the calculated activation free energies and thus were not further applied.

Calculations of ΔG⁰ and ΔG^‡ for the carboxylation step

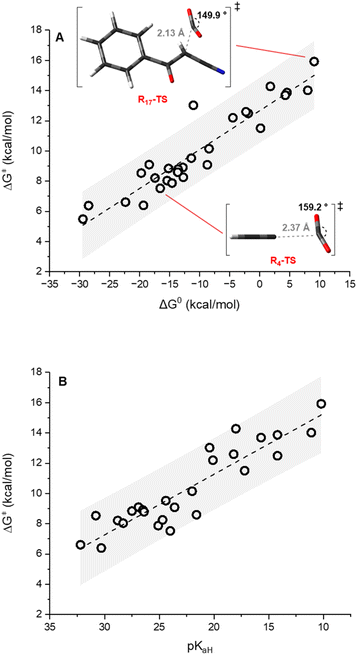
The carbanions R_i⁻ were selected from our previous investigation,⁵⁷ and the corresponding carboxylated species R_i-COO⁻ are represented in Fig. 1. Since several reports exploit acetonitrile as the solvent for carboxylation reactions, this was chosen as the medium for the calculations presented in this work. Fig. 2A reports the plot of ΔG^‡vs. ΔG⁰ values for the carboxylation step (ωb97XD/aug-cc-pvtz//ωb97XD/def2tzvp level of theory, including a continuum model for acetonitrile solvent; data including the calculations at the other levels are reported in Tables S3–S7 and Fig. S5 in the ESI†). The geometries of the transition states R₄-TS and R₁₇-TS are also shown in Fig. 2A as representative cases.

Fig. 1 Representation of R_i-COO⁻ considered in this work (i is indicated below each structure), together with ΔG⁰ and ΔG^‡ values for the carboxylation step at the ωb97XD/aug-cc-pvtz//ωb97XD/def2tzvp level of theory.

Fig. 2 (A) Plot of ΔG^‡vs. ΔG⁰ values for the carboxylation of carbanions R_i⁻ (ωb97XD/aug-cc-pvtz//ωb97XD/def2tzvp level of theory, including a continuum model for acetonitrile solvent). The shaded ranges represent the 95% confidence interval of the correlations. Geometries of R₄-TS and R₁₇-TS (ωb97xd/def2tzvp level) are shown as representative cases of transition states with low and high ΔG^‡. (B) Plot of ΔG^‡ (ωb97XD/aug-cc-pvtz//ωb97XD/def2tzvp) vs. experimental pK_aH of carbanions R_i⁻.

Clearly, considering that charged species are involved in eqn (1), solvation impacts the ΔG⁰ and ΔG^‡ values. While this was addressed by the inclusion of an implicit solvation model, any possible deviation from an ideal explicit solvation could be neglected assuming that such an effect would be similar through the anion series, thus preserving the sought-after linear correlations. Also, the impact of cations possibly present under real reaction conditions could impact the structure and the reactivity of carbanions; this is particularly relevant for the case of enolate like anions in the presence of small alkali cations.⁵⁸

The data plot of ΔG^‡vs. ΔG⁰ values shows a good linear trend according to eqn (2) (R² = 0.88).

ΔG^‡ = α × ΔG⁰ + ΔG^‡₀ (2)

α = 0.26 ± 0.02; ΔG^‡₀ = 12.7 ± 0.3 kcal mol⁻¹

The slope α of 0.26 ± 0.02 corresponds to the Leffler–Hammond parameter α = δΔG^‡/δΔG⁰, describing the fraction of the change in the Gibbs energy of the reaction reflected in the change of the Gibbs energy of activation.³⁹ It is worth noting that α has long been exploited as an indication of the position of the transition state along the reaction coordinate (with α close to 0 indicating an early transition state and α close to 1 indicating a late transition state), until Bordwell's observation of an α value of 1.31 for the deprotonation of substituted 1-nitro-1-phenylethanes (nitroalkane anomaly)⁵⁹ evidenced that the former interpretation was wrong and that α cannot be a measure for the position of the transition state.

The intercept of the fitting in Fig. 2 ΔG^‡₀ = 12.7 ± 0.3 kcal mol⁻¹ provides the intrinsic barrier, i.e. the activation free energy for an isoergonic reaction (with ΔG⁰ = 0).‡ Importantly, quadratic fitting of the data in Fig. 2 according to the Marcus model for group transfer reactions (eqn (3)) leads to consistent values of ΔG^‡₀ of 14.2 ± 0.4 kcal mol⁻¹, see ESI Fig. S6.† According to the Marcus model for group transfer in bimolecular reactions, the ΔG^‡₀ is associated with the reorganization energy λ (λ = 4 × ΔG^‡₀), with λ being estimated to be 50.8 ± 1.2 kcal mol⁻¹.

ΔG^‡ = ΔG^‡₀ + 0.5 × ΔG⁰ + {(ΔG⁰)²/(16 × ΔG^‡₀)} (3)

Comparable α and ΔG^‡₀ values were found with the other levels of theory employed (Fig. S5 in the ESI†). Importantly, α and ΔG^‡₀ parameters determined from the fittings are in line with those reported for the decarboxylation reaction of organic carboxylates in water (i.e. the microscopically reverse reaction of eqn (1));⁶⁰ the value of α reported in this case was 0.76/0.78 (experimental/computed; note that the sum of α for the forward and for the backward step must be 1.00,³⁹ while the intrinsic barrier was 15.5/16.8 kcal mol⁻¹ (experimental/computed).⁶⁰ The α and ΔG^‡₀ parameters extrapolated from the data in Fig. 2A indicate smooth reactivity of carbanions with CO₂,⁶¹ characterised by low energy barriers and by a slight dependence on ΔG⁰; these identify CO₂ as a powerful electrophile, comparable to carbonyl compounds^37,62 and support the recent observation of the exchange of the COO group from carboxylate salts, occurring under an atmosphere of CO₂ at room temperature and in the absence of catalysts.^63,64 As a comparison, in nucleophilic substitutions α values between 0.48 and 0.73 were found for the reaction of several types of nucleophiles with benzhydrylium ions,³⁹ while the intrinsic barriers ΔG^‡₀ reach up to 45 kcal mol⁻¹ for carbanion nucleophiles.^65,66 An intrinsic barrier of 14.1 kcal mol⁻¹ was reported for the addition of enolate ions to the carbonyl group of benzaldehyde.⁶⁷ Lower intrinsic barriers have been observed for proton and hydride transfer (1–10 kcal mol⁻¹).^68–70

Four further points are worth mentioning.

(i) We previously reported a linear correlation between variations in ΔG⁰ and the change of the basicity of the carbanion R_i⁻ expressed as the pK_aH of the conjugate acid (eqn (4));⁵⁷ combination of eqn (2) and (4) allows the direct correlation of variations in ΔG^‡ with pK_aH, in a Brønsted type plot (eqn (5)). Indeed, a good linear correlation of calculated ΔG^‡ with experimental pK_aH⁷¹ is observed in Fig. 2B (R² = 0.83), providing a powerful prediction tool of ΔG^‡.

δ(ΔG⁰) = −1.30 kcal mol⁻¹ × δ(pK_aH) (4)

ΔG^‡ = −β × pK_aH + const (5)

with β = 0.40 ± 0.04 kcal mol⁻¹ and const = 19.3 ± 0.9 kcal mol⁻¹.

(ii) The calculated ΔG^‡ values can be exploited to contextualise the carboxylation step on a more general nucleophilic/electrophilic scale, exploiting the Mayr–Patz equation (eqn (6)),⁷²

log k (20 °C) = s_N(N + E) (6)

where k (20 °C) is the reaction rate constant at 20 °C, N is the nucleophilicity parameter, E is the electrophilicity parameter, and s_N is a nucleophile-specific sensitivity parameter. By obtaining log k (20 °C) from ΔG^‡ through the Eyring equation and exploiting the reported S_N and N parameters for carbanions R₂⁻, R₃⁻, R₁₇⁻, R₂₃⁻ and R₂₄⁻,⁷³ it is possible to extrapolate electrophilicity values for CO₂ in the range from −15.3 to −18.7, while a value of −16.3 was reported according to a single experimental kinetic data with the indenide anion (R₂⁻)³⁷ (Table S8 in the ESI†). Many reports have discussed the theoretical prediction of nucleophilicity/electrophilicity.^48,74–76

(iii) The variations of ΔG⁰ and ΔG^‡ values for the carboxylation step represented in Fig. 2 are mainly related to enthalpic contributions, while the TΔS⁰ and TΔS^‡ terms are found to be almost constant in the carbanion series (Tables S4–S7 and Fig. S7 in the ESI†), with average values of −10.6 ± 0.8 and −9.95 ± 0.8 kcal mol⁻¹, respectively (the error is given as the standard deviation).

(iv) In the reactivity investigated, the formation of a reactant complex between the anion and carbon dioxide could in principle occur,^63,77 in particular for highly basic carbanions. Based on our calculations and IRC analysis, we do not have evidence for the formation of such a reactant complex; the calculated energy barriers refer then to the isolated reactants.

Distortion interaction analysis

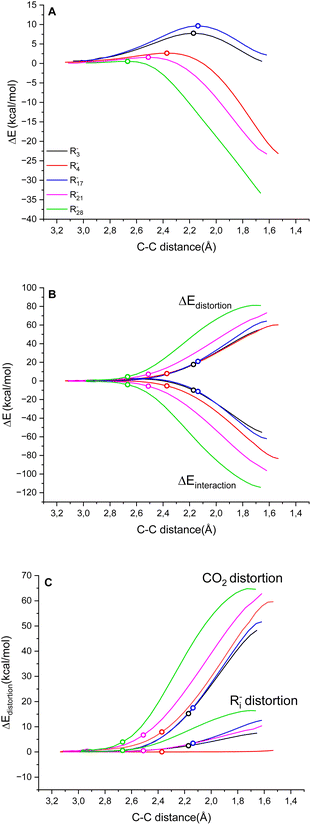
We rationalised the molecular factors that impact the energetic barrier of the carboxylation step by employing the distortion/interaction model (also known as the activation/strain model) for bimolecular reactions, developed independently by the Bickelhaupt and Houk groups.⁴⁰ Accordingly, the potential energy ΔE along the reaction coordinate is given by the sum of the energy due to the distortion of the reactants (ΔE_distortion > 0) and the energy given by the interaction of the two reactants (ΔE_interaction < 0), eqn (7).

ΔE = ΔE_distortion + ΔE_interaction (7)

Fig. 3A reports the ΔE versus the C(R_i⁻)⋯C(CO₂) distance as the reaction coordinate for the carboxylation step of R₃⁻, R₄⁻, R₁₇⁻, R₂₁⁻ and R₂₈²⁻ as representative cases, spanning the entire range of ΔG^‡ explored. As can be visually perceived, the profiles show a switch from a late to an early transition state along the series R₁₇⁻ ∼ R₃⁻ → R₄⁻→ R₂₁⁻ → R₂₈²⁻, consistent with the progressive decrease of activation energy. When the ΔE is dissected into the ΔE_distortion and ΔE_interaction contributions (Fig. 3B and Table S9 in the ESI†), the profiles suggest that the carboxylation step is both distortion- and interaction-controlled,^78,79 with an evident contribution from the interaction of the carbanions with CO₂.

Fig. 3 (A) Plot of ΔE vs. the C(R_i⁻)⋯C(CO₂) distance as the reaction coordinate for R₃⁻, R₄⁻, R₁₇⁻, R₂₁⁻ and R₂₈²⁻ as representative cases. (B) Dissection of ΔE into ΔE_distortion and ΔE_interaction. (C) Dissection of ΔE_distortion into ΔE^‡_distortion (R_i⁻) and ΔE^‡_distortion (CO₂). In all graphs, the empty dots indicate the transition states.

According to energy decomposition analysis, with some software the ΔE_interaction could be dissected into separate contributions from electrostatic interaction, Pauli repulsion, orbital interaction and dispersion interaction.⁷⁹ In the present case, the previous correlation between the activity and basicity of carbanions (Fig. 2B) identifies pK_aH as the physical parameter impacting the interaction. This is also supported by a smooth correlation between nucleophilicity and proton affinity among nucleophiles belonging to the same class.⁷⁵

Concerning the distortion, the ΔE_distortion can be decomposed into the contributions of the carbanion R_i⁻ and CO₂ reactants (eqn (8)); the ΔE_distortion for each reactant along the reaction coordinate is given by the single point energy difference between the geometry of the reactant at each point and the geometry of the isolated reactant.^40,78,79

ΔE_distortion = ΔE_distortion (R_i⁻) + ΔE_distortion (CO₂) (8)

Splitting the ΔE_distortion along the reaction coordinate according to eqn (8) shows that the major energy penalty arises from CO₂ for the five cases investigated, Fig. 3C. Consistently, by expanding the analysis by evaluating the ΔE_distortion (R_i⁻) and ΔE_distortion (CO₂) contributions with the transition state geometries of all R_i⁻ species, it is observed that the ΔE_distortion of CO₂ exceeds the ΔE_distortion of carbanions by ca. 5 times (Fig. S8 in the ESI;† note that for rigid “sp” carbanions such as R₄⁻ and R₅⁻ the ΔE_distortion (R_i⁻) is almost negligible).

From a structural point of view, the distortion of carbon dioxide in the transition states is obviously described by the bending of CO₂ and by the contraction of the O–C–O angle, while the carbanion nucleophile approaches and the C(R_i⁻)⋯C(CO₂) distance decreases. Calculations show indeed a linear trend in the carbanion series between the ΔG^‡ of carboxylation and the O–C–O angle (see Fig. S9 in the ESI†), predicting that one kcal mol⁻¹ of penalty in the ΔG^‡ is associated with a decrease of 1.41 ± 0.09° of the O–C–O angle in the transition state.

Fig. 4 shows the ΔG^‡, the O–C–O angle and the C⋯C distance in a single graph, demonstrating that the higher the free energy of activation, the higher the required distortion of CO₂ in a “late” transition state, with a small O–C–O angle and a short C(R_i⁻)⋯C(CO₂) distance.

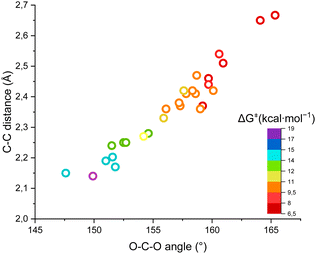Fig. 4 Plot of the ΔG^‡ for the carboxylation of the carbanions versus the O–C–O angle and the C(R_i⁻)⋯C(CO₂) distance in the transition states.

Conclusions and perspectives

In conclusion, we have reported energy and structural correlations for the carboxylation step of carbanions with CO₂. These allow linking the basicity of the carbanion (pK_aH), the standard and activation free energies of the carboxylation step (ΔG⁰ and ΔG^‡) and the distortion of CO₂ in the transition state (O–C–O angle and C(R_i⁻)⋯C(CO₂) distance), deriving reactivity descriptors such as the Leffler–Hammond coefficient, the intrinsic barrier and the electrophilicity of CO₂.

These tools are instrumental for the design of experimental chemical, electrochemical or photochemical fixation of CO₂ into organic compounds. The a priori evaluation of the reaction barrier (and consequently the rate constant) between a carbanion and CO₂ should be pivotal in driving the envisaged carboxylation reactivity with respect to undesired competitive pathways. In particular, these may include irreversible protonation of the carbanion or its reactivity with other electrophiles (as documented in the case of electrochemical carboxylation of α,β-unsaturated ketones⁵⁷). The regioselectivity of the carboxylation step could also be a challenge and should be considered when involving extended organic scaffolds, as in the case of electrochemical carboxylation of dienes⁸⁰ and naphthalene derivatives.⁸¹ Thus, we hope to provide a guide for future studies on carbon dioxide reconversion.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

All authors conceptualised the research and contributed to the discussion of the results. C. N., M. O. and A. S. performed the calculations. C. N. and A. S. co-wrote the manuscript. L. D. A. and A. S. were responsible for funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are indebted to Prof. Herbert Mayr (Department Chemie Ludwig-Maximilians-Universität München) for very constructive and useful discussions. Financial support from the Italian Ministero dell’Università e della Ricerca (Grants “PROMETEO” 2022KPK8WM and 2020927WY3) and from the European Union – Next Generation EU – Bando PRIN 2022 – M4.C2.1.1 (Grants “PHOTOCORE” P2022ZSPWF and P2022WLAY7) is greatly acknowledged.

Notes and references

1. (a) D. I. A. McKay, A. Staal, J. F. Abrams, R. Winkelmann, B. Sakschewski, S. Loriani, I. Fetzer, S. E. Cornell, J. Rockström and T. M. Lenton, Science, 2022, 377, eabn7950; (b) S. I. Zandalinas, F. B. Fritschi and R. Mittler, Trends Plant Sci., 2021, 26, 588–599.
2. (a) IEA International Energy Agency, Carbon Capture, Utilisation and Storage, https://www.iea.org/energy-system/carbon-capture-utilisation-and-storage; (b) K. Kohse-Höinghaus, Chem. Rev., 2023, 123, 5139–5219; (c) P. Friedlingstein and M. O. Sullivan, et al. , Earth Syst. Sci. Data, 2023, 15, 5301–5369; (d) L. Chen, G. Msigwa, M. Yang, A. I. Osman, S. Fawzy, D. W. Rooney and P.-S. Yap, Environ. Chem. Lett., 2022, 20, 2277–2310.
3. United Nations 17, Sustainable Development Goals, https://www.un.org/sustainabledevelopment/.
4. (a) T. L. Biel-Nielsen, T. A. Hatton, S. N. B. Villadsen, J. S. Jakobsen, J. L. Bonde, A. M. Spormann and P. L. Fosbøl, ChemSusChem, 2023, e202202345; (b) R. J. Detz, C. J. Ferchaud, A. J. Kalkman, J. Kemper, C. Sanchez-Martinez, M. Saric and M. V. Shinde, Sustainable Energy Fuels, 2023, 7, 5445–5472.
5. K. M. Diederichsen, R. Sharifian, J. S. Kang, Y. Liu, S. Kim, B. M. Gallant, D. Vermaas and T. A. Hatton, Nat. Rev. Methods Primers, 2022, 2, 68.
6. A. Hasanzadeh, S. Ghazanfari, M. Janbazvatan, H. Rashidpour, A. Chitsaz and M. Khalilian, J. CO₂ Util., 2023, 67, 102306.
7. J. Albero, Y. Peng and H. García, ACS Catal., 2020, 10, 5734–5749.
8. B. Chang, H. Pang, F. Raziq, S. Wang, K.-W. Huang, J. Ye and H. Zhang, Energy Environ. Sci., 2023, 16, 4714–4758.
9. S. Fang, M. Rahaman, J. Bharti, E. Reisner, M. Robert, G. A. Ozin and Y. H. Hu, Nat. Rev. Methods Primers, 2023, 3, 61.
10. S. Ren, D. Joulié, D. Salvatore, K. Torbensen, M. Wang, M. Robert and C. P. Berlinguette, Science, 2019, 365, 367–369.
11. Q. Zhu, X. Sun, D. Yang, J. Ma, X. Kang, L. Zheng, J. Zhang, Z. Wu and B. Han, Nat. Commun., 2019, 10, 3851.
12. M. Han, X. Fu, A. Cao, C. Guo, W. Chu and J. Xiao, Adv. Theory Simul., 2019, 2, 1800200.
13. Q. Liu, L. Wu, R. Jackstell and M. Beller, Nat. Commun., 2015, 6, 5933.
14. Q. W. Song, R. Ma, P. Liu, K. Zhang and L. N. He, Green Chem., 2023, 25, 6538–6560.
15. S. Pimparkar, A. K. Dalvi, A. Koodan, S. Maiti, S. A. Al-Thabaiti, M. Mokhtar, A. Dutta, Y. R. Lee and D. Maiti, Green Chem., 2021, 23, 9283–9317.
16. S. Bierbaumer, M. Nattermann, L. Schulz, R. Zschoche, T. J. Erb, C. K. Winkler, M. Tinzl and S. M. Glueck, Chem. Rev., 2023, 123, 5702–5754.
17. M. M. F. Hasan, L. M. Rossi, D. P. Debecker, K. C. Leonard, Z. Li, B. C. E. Makhubela, C. Zhao and A. Kleij, ACS Sustainable Chem. Eng., 2021, 9, 12427–12430.
18. P. K. Sahoo, Y. Zhang and S. Das, ACS Catal., 2021, 11, 3414–3442.
19. J. Ding, R. Ye, Y. Fu, Y. He, Y. Wu, Y. Zhang, Q. Zhong, H. H. Kung and M. Fan, Nat. Commun., 2023, 14, 4586.
20. H. Kolbe, Adv. Cycloaddit., 1860, 113, 125–127.
21. R. Schmitt, J. Prakt. Chem., 1885, 2, 397–410.
22. A. Tortajada, F. Juliá-Hernández, M. Börjesson, T. Moragas and R. Martin, Angew. Chem., Int. Ed., 2018, 57, 15948–15982.
23. J. Davies, J. R. Lyonnet, B. Carvalho, B. Sahoo, C. S. Day, F. Juliá-Hernández, Y. Duan, N. Álvaro Velasco-Rubio, M. Obst, P. O. Norrby, K. H. Hopmann and R. Martin, J. Am. Chem. Soc., 2024, 146, 1753–1759.
24. C. Qiao, W. Shi, A. Brandolese, J. Benet-Buchholz, E. C. Escudero-Adán and A. W. Kleij, Angew. Chem., Int. Ed., 2022, 61, e202205053.
25. Y. Yan, J. Hao, F. Xie, F. Han, L. Jing and P. Han, J. Org. Chem., 2023, 88, 14640–14648.
26. S. Zheng, T. Zhang and H. Maekawa, J. Org. Chem., 2022, 87, 7342–7349.
27. J. Wang, Z. F. Wei, Y. X. Luo, C. H. Lu and R. J. Song, SynOpen, 2024, 8, 116–124.
28. H. Senboku, Chem. Rec., 2021, 21, 2354–2374.
29. P. Franceschi, E. Rossin, G. Goti, A. Scopano, A. Vega-Penaloza, M. Natali, D. Singh, A. Sartorel and L. Dell'Amico, J. Org. Chem., 2023, 88, 6454–6464.
30. M. Schmalzbauer, T. D. Svejstrup, F. Fricke, P. Brandt, M. J. Johansson, G. Bergonzini and B. König, Chem, 2020, 6, 2658–2672.
31. Z. Zhang, J. H. Ye, T. Ju, L. L. Liao, H. Huang, Y. Y. Gui, W. J. Zhou and D. G. Yu, ACS Catal., 2020, 10, 10871–10885.
32. H. Seo, M. H. Katcher and T. F. Jamison, Nat. Chem., 2017, 9, 453–456.
33. Y. Naito, Y. Nakamura, N. Shida, H. Senboku, K. Tanaka and M. Atobe, J. Org. Chem., 2021, 86, 15953–15960.
34. A. Sheta, A. Alkayal, M. Mashaly, S. Said, S. Elmorsy, A. V Malkov and B. R. Buckley, Angew. Chem., Int. Ed., 2021, 60, 21832–21837.
35. Q. Y. Meng, T. E. Schirmer, A. L. Berger, K. Donabauer and B. König, J. Am. Chem. Soc., 2019, 141, 11393–11397.
36. K. M. Waldie, A. L. Ostericher, M. H. Reineke, A. F. Sasayama and C. P. Kubiak, ACS Catal., 2018, 8, 1313–1324.
37. Z. Li, R. J. Mayer, A. R. Ofial and H. Mayr, J. Am. Chem. Soc., 2020, 142, 8383–8402.
38. F. G. Bordwell and D. L. Hughes, J. Org. Chem., 1980, 45, 3314–3320.
39. H. Mayr and A. R. Ofial, Acc. Chem. Res., 2016, 49, 952–965.
40. F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
42. J. J. P. Stewart, J. Comput. Chem., 1989, 10, 209–220.
43. J. J. P. Stewart, J. Comput. Chem., 1989, 10, 221–264.
44. E. Anders, R. Koch and P. Freunscht, J. Comput. Chem., 1993, 14, 1301–1312.
45. S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129.
46. S. Miertuš and J. Tomasi, Chem. Phys., 1982, 65, 239–245.
47. J. L. Pascual-Ahuir, E. Silla and I. Tuñón, J. Comput. Chem., 1994, 15, 1127–1138.
48. J. N. Harvey, F. Himo, F. Maseras and L. Perrin, ACS Catal., 2019, 9, 6803–6813.
49. R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562.
50. J. Da Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
51. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
52. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
53. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
54. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371.
55. T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406.
56. J. A. Pople, P. M. W. Gill and B. G. Johnson, Chem. Phys. Lett., 1992, 199, 557–560.
57. P. Franceschi, C. Nicoletti, R. Bonetto, M. Bonchio, M. Natali, L. Dell'Amico and A. Sartorel, Front. Chem., 2021, 9, 783993.
58. O. Larrañaga, A. De Cõzar, F. M. Bickelhaupt, R. Zangi and F. P. Cossío, Chem.–Eur. J., 2013, 19, 13761–13773.
59. F. Bordwell, W. J. J. Boyle, J. A. Hautala and K. C. Yee, J. Am. Chem. Soc., 1969, 91, 4002–4003.
60. S. Zhou, Y. Wang and J. Gao, JACS Au, 2021, 1, 233–244.
61. Y. Fu, X. Suo, Z. Yang, S. Dai and D. E. Jiang, J. Phys. Chem. B, 2022, 126, 6979–6984.
62. F. M. Bickelhaupt and I. Fernández, Chem. Sci., 2024, 15, 3980–3987.
63. D. Kong, P. J. Moon, E. K. J. Lui, O. Bsharat and R. J. Lundgren, Science, 2020, 369, 557–561.
64. G. Destro, K. Horkka, O. Loreau, D. A. Buisson, L. Kingston, A. Del Vecchio, M. Schou, C. S. Elmore, F. Taran, T. Cantat and D. Audisio, Angew. Chem., Int. Ed., 2020, 59, 13490–13495.
65. H. Mayr, M. Breugst and A. R. Ofial, Angew. Chem., Int. Ed., 2011, 50, 6470–6505.
66. S. Hoz, H. Basch, J. L. Wolk, T. Hoz and E. Rozental, J. Am. Chem. Soc., 1999, 121, 7724–7725.
67. J. P. Richard, T. L. Amyes and M. M. Toteva, Acc. Chem. Res., 2001, 34, 981–988.
68. A. Kresge, Acc. Chem. Res., 1975, 8, 354–360.
69. C. R. Reinhardt, T. C. Jaglinski, A. M. Kastenschmidt, E. H. Song, A. K. Gross, A. J. Krause, J. M. Gollmar, K. J. Meise, Z. S. Stenerson, T. J. Weibel, A. Dison, M. R. Finnegan, D. S. Griesi, M. D. Heltne, T. G. Hughes, C. D. Hunt, K. A. Jansen, A. H. Xiong, S. Hati and S. Bhattacharyya, J. Mol. Model., 2016, 22, 199.
70. C. F. Bernasconi and P. J. Wenzel, J. Am. Chem. Soc., 2001, 123, 7146–7153.
71. Bordwell pKa table, collected by prof. Hans Reich (UW-Madison) https://organicchemistrydata.org/hansreich/resources/pka/last update April 2024.
72. H. Mayr and M. Patz, Angew. Chem., Int. Ed., 1994, 33, 938–957.
73. H. Mayr and A. R. Ofial, Mayr's Database of Reactivity Parameters, https://www.cup.lmu.de/oc/mayr/reaktionsdatenbank2/.
74. C. Wang, Y. Fu, Q. X. Guo and L. Liu, Chem.–Eur. J., 2010, 16, 2586–2598.
75. M. Orlandi, M. Escudero-Casao and G. Licini, J. Org. Chem., 2021, 86, 3555–3564.
76. M. Vahl and J. Proppe, Phys. Chem. Chem. Phys., 2023, 25, 2717–2728.
77. M. A. Zambri and R. Kluger, J. Am. Chem. Soc., 2024, 146, 1403–1409.
78. I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953–4967.
79. P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649–667.
80. A. M. Sheta, M. A. Mashaly, S. B. Said, S. S. Elmorsy, A. V Malkov and B. R. Buckley, Chem. Sci., 2020, 11, 9109–9114.
81. V. K. Rawat, H. Hayashi, H. Katsuyama, S. R. Mangaonkar and T. Mita, Org. Lett., 2023, 25, 4231–4235.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of calculations and additional tables and figures. See DOI: https://doi.org/10.1039/d4se01065e

‡ The existence of a linear correlation between ΔG^‡ and ΔG⁰ is indicative of a constant ΔG₀^‡ throughout the reaction series or of a ΔG^‡₀ varying proportionally to ΔG⁰.

---