Open Access Article
Open Access ArticleAnomalous mass dependence of phonon thermal transport in lanthanum monopnictides and its origin in the nature of chemical bonding†
Safoura
Nayeb Sadeghi
 a and
Keivan
Esfarjani
*bc
a and
Keivan
Esfarjani
*bc
aDepartment of Mechanical and Aerospace Engineering, University of Virginia, Charlottesville, VA, USA. E-mail: safoura@virginia.edu
bDepartment of Materials Science and Engineering, University of Virginia, Charlottesville, VA, USA
cDepartment of Physics, University of Virginia, Charlottesville, VA, USA. E-mail: k1@virginia.edu
First published on 7th August 2024
Abstract
In certain compounds of binary lanthanum monopnictides exhibiting a rocksalt crystal structure, a phenomenon arises: larger average atomic mass, smaller acoustic phonon velocities, and smaller acoustic optical frequency gap do not necessarily result in lower lattice thermal conductivity. In this study, we present an analysis of the lattice thermal conductivity of both LaP and LaBi compounds using a first-principles approach to calculate force constants and to solve the linearized phonon Boltzmann transport equation. Through a comparison of phonon dispersions, interatomic force constants, and Grüneisen parameters, we infer that long-range interactions stemming from the electronic polarizability in the lighter compound, LaP, are stronger than those in LaBi. This leads to heightened anharmonicity and phonon scattering of transverse optical (TO) modes in LaP, which is the primary contributor to its lower lattice thermal conductivity. Additionally, we examined the electron density distribution and the anti-bonding character of the valence bands in order to gain a better chemical understanding of the increased anharmonicity and bond softening in the case of LaP. Our findings show that the lighter compound, LaP, with a more delocalized electron density distribution due to the stronger antibonding character of La-p and P-p orbitals, exhibits softer and more anharmonic TO modes, thereby resulting in weakened bonds and lower lattice thermal conductivity compared to LaBi. Next, it was found that the polarizability, Born charges and the Grüneisen parameters of LaP have a much stronger dependence on pressure compared to LaBi. These are signatures of the metavalent nature of the bonds in LaP, leading to its lower lattice thermal conductivity.
1 Introduction
Lanthanum monopnictides such as LaAs, LaSb, and LaBi with a rocksalt crystal structure have recently garnered attention due to their extreme magnetoresistance (XMR) resulting from electron–hole compensation1–3 and potential topological states.4–10 These materials are promising candidates for magnetic sensor and spintronics applications. The measured bulk band structure of LaBi, using angle-resolved photoemission spectroscopy (ARPES), has revealed a clear band inversion, while LaSb is near a band inversion and LaAs is clearly non-inverted, exhibiting weaker magnetoresistance than the heavier compounds.Pressure-induced phase transitions for LaX (X = P, As, and Sb) at room temperature have been reported both experimentally using synchrotron radiation powder X-ray diffraction11 and theoretically.12–15 These compounds exhibit a first-order phase transition from an FCC NaCl-type structure to a tetragonal structure (distorted cubic CsCl-type) at approximately 24 GPa for LaP, 20 GPa for LaAs, and 14 GPa for LaSb.11 This structural transition has also been studied in LaBi, both experimentally at 11 GPa (ref. 16) and theoretically at 7 GPa.17 Lanthanum monopnictides may thus provide a rich playground for exploring novel phases and phase transitions driven by temperature and pressure.
Little attention has however been devoted to understanding thermal transport in these compounds. Recent studies have found that LaP is theoretically semiconducting with a narrow band gap and exhibits high thermoelectric performance18 that can be tuned by strain.19 The thermoelectric properties of semimetallic LaBi have also been investigated.20 These studies used relaxed lattice constants close to the actual experimental values, within the local density approximation (LDA) and generalized gradient approximation (GGA) approximations. However, no study has yet been conducted to cross-compare the lattice thermal conductivity of these materials which have the same structure but only differ in the atomic mass. It is well-known that using elements with large atomic mass lead to smaller speeds of sounds and thus to lower lattice thermal conductivity. Nevertheless, anomalous mass dependence of lattice thermal conductivity has already been observed in some materials, such as the IV–VI compounds,21,22 and ternary chalcopyrites (space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d).23 In the former, the unusually low intrinsic lattice thermal conductivity of the IV–VI semiconductor family with rocksalt crystal structures has been attributed to soft optical phonon modes arising from long-range interatomic interactions due to resonant (now called metavalent) bonding.21 These soft optical modes can strongly scatter heat-carrying low-frequency acoustic phonons. In the latter, this phenomenon has been related to metavalent bonding in the studied diamond-like structure materials, AInC2 (A = Cu, Ag; C = Te or Se).23,24
2d).23 In the former, the unusually low intrinsic lattice thermal conductivity of the IV–VI semiconductor family with rocksalt crystal structures has been attributed to soft optical phonon modes arising from long-range interatomic interactions due to resonant (now called metavalent) bonding.21 These soft optical modes can strongly scatter heat-carrying low-frequency acoustic phonons. In the latter, this phenomenon has been related to metavalent bonding in the studied diamond-like structure materials, AInC2 (A = Cu, Ag; C = Te or Se).23,24
Recently, J. Zhang et al.25 successfully investigated the giant anharmonicity of soft low-lying transverse phonon modes and the unexpectedly low thermal conductivity of InTe by combining chemical bonding analysis, inelastic X-ray, neutron scattering, and first-principles phonon calculations. Their findings revealed that the In1+ 5s2 states in InTe are highly delocalized and hybridized with the Te 5p states to form anti-bonding states at the valence band maximum (VBM). The delocalized s2 lone pair electrons on the rattling In1+ ions show a strong tendency to deform along the weak bonding direction (the z-axis) to stabilize the electronic structure. This leads to anharmonic soft low-lying transverse phonon modes and the suppression of κl in InTe. J. He et al. have recently highlighted that antibonding hybridization of p–d orbitals can effectively weaken interatomic interactions, leading to ultralow thermal conductivity in Cu/Ag-based compounds.26
More recently, J. Yuan et al.27 conducted a comprehensive analysis of chemical bonds and thermal transport in the XS family, where X = K, Rb, and Cs representing alkaline metals. They attributed the ultralow thermal conductivity, less than 1 (W mK−1) at room temperature, to weakened bonds and increased phonon anharmonicity arising from valence bands composed of anti-bonding π* states formed by S-px and S-py orbitals. Additionally, they demonstrated that strong anti-bonding valence bands (ABVBs) underlie the ultra-low lattice thermal conductivity in well-studied materials like PbTe and CsPbBr3. The presence of 6s2 lone pair electrons on Pb2+ ions enables efficient hybrid interaction between fully occupied Pb-6s states and Te-5p states, resulting in the highest-occupied valence band possessing strong antibonding character. Consequently, the anti-bonding valence bands are accountable for weakened chemical bonds and soft optical phonons, thus leading to abnormally low lattice thermal conductivities in both compounds. Other studies have also indicated that ultra-low thermal conductivities in various materials are triggered by anti-bonding chemical bonds.28–31 Our recent study explored how doping in cubic GeTe affects its transport properties. It has been revealed that weak s–p interactions in Bi-, Sb-, and Pb-doped GeTe improves electronic performance by modifying electronic density of states (DOS) whereas weak p–p interactions in them reduce thermal transport by diminishing the strength of chemical bonding, explaining the experimentally observed high power factor and enhanced zT in Bi, Sb, and Pb doping in contrast to In doping by reinforcing the chemical bonds.32
In this study, the low lattice thermal conductivity of LaP rather than LaBi is explored from vibrational and electronic structure perspectives. As mentioned above, the intrinsic lattice thermal conductivity of crystalline materials is heavily influenced by the strength of chemical bonding, which notably affects the velocity of heat-conducting acoustic phonons. Hence, the chemical properties of both compounds and their impact on thermal transport properties are thoroughly investigated. Given that physical properties directly stem from bonding nature, we proceed to examine the relative changes in select properties, including phonon frequency, Grüneisen parameter γTO, optical dielectric constant, and Born effective charge, under varying pressure conditions.
2 Computational methods
In this study, we performed first-principles calculations utilizing the Vienna ab initio simulation package (VASP)33,34 employing the projector augmented-wave (PAW) method35 and the PBEsol form of the generalized gradient approximation (PBEsol-GGA) for the exchange–correlation energy functional. A plane-wave cutoff energy of 500 eV was employed. For electronic structure calculations, the Monkhorst–Pack scheme was used to sample the Brillouin Zone (BZ) for integrations in reciprocal space, employing a k-mesh of 20 × 20 × 20, while considering spin–orbit interaction. To alleviate the under-estimated band gap problem, we incorporated the hybrid density functional of Heyd, Scuseria, and Ernzerhof, aka HSE06 (ref. 36) (with parameters α = 25 Fock exchange μ = 0.2 Å−1). Experimental lattice constants of a = 6.025 Å (ref. 11 and 37) for LaP and a = 6.5799 Å (ref. 2) for LaBi were selected for the bulk phase lattice parameters.The determination of lattice thermal conductivity and phonon scattering rates through ab initio methods involves acquiring interatomic force constants (IFCs), determining phonon frequencies and group velocities, ωλ, vλ, phonon transition probabilities using density functional theory (DFT) calculations, and finally solving the linearized Boltzmann transport equation (BTE). Harmonic and anharmonic interatomic force constants (IFCs) were obtained utilizing the direct supercell approach. Harmonic IFCs were computed using a 4 × 4 × 4 supercell with a 4 × 4 × 4 Γ-centered Monkhorst–Pack k mesh by utilizing the Phonopy package.38–40 Convergence of the phonon dispersions with respect to the supercell size and the k-grid sampling was tested. The phonon dispersions included the non-analytic Born charge corrections. Anharmonic IFCs were determined utilizing plane-wave cutoff energy of 500 eV and Γ-point calculations with 4 × 4 × 4 supercells, considering the cutoff for cubic IFCs up to the seventh nearest neighbors. Various neighbor interaction cutoffs were tested to ensure convergence. Subsequently, after obtaining second-order harmonic and third-order anharmonic IFCs, the thermal conductivities of both compounds, LaP and LaBi, were calculated on a converged q-space grid of 30 × 30 × 30 by iteratively solving the phonon Boltzmann transport equation as implemented in the Sheng-BTE software package.41 Within the framework of the BTE, the thermal conductivity tensor (κ) at temperature T can be expressed as:
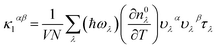 | (1) |
To gain insights about the chemical bonding and bond strengths between different pairs of atoms, we have performed the crystal orbital Hamilton population (COHP) analysis.42,43 The COHP method partitions the one-particle band energies into interactions between pairs of atomic orbitals between adjacent atoms. It is a measure of the electronic density of states (DOS) weighted by the Hamiltonian matrix elements, enabling the identification of the bonding and antibonding interactions. The bonding strength is quantified by the integrated COHP (ICOHP) values. The bonding interaction is indicated by a positive COHP value, while a negative value denotes the antibonding character. Here, we have performed COHP analysis for nearest neighbor atom pairs of both compounds LaP and LaBi using the LOBSTER code.42–44 For the projection, we employed the local basis function as given by pbeVaspFit2015. Specifically, the orbitals included are 5s, 5p, 5d, 6s, and 4f for La, as well as 3s, 3p and 6s, 6p for P and Bi respectively.
3 Results
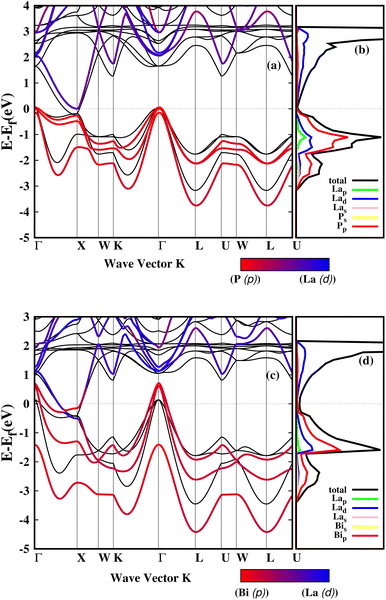
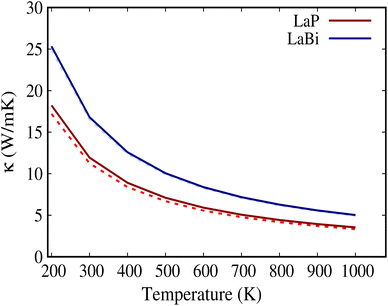
For both LaP and LaBi compounds, the experimental lattice parameters a = 6.025 Å (ref. 11) for LaP and a = 6.5799 Å (ref. 2) for LaBi were used. Fig. 1 shows the calculated orbital-projected electronic band structure of LaP (a) and LaBi (c) along the high-symmetry directions of the Brillouin zone using the HSE06 functional. It also displays the electronic band structure of both compounds at the GGA-PBESOL level along with their corresponding orbital-projected density of states (PDOS). As depicted in Fig. 1, both compounds exhibit similar band structures, with the three-fold degenerate valence band maximum (VBM) located at the Γ point. Both compounds turn out to be semimetallic, with a larger conduction-valence overlap for LaBi. In the projected bands, blue denotes d orbital-dominated bands, while red denotes p orbital-dominated bands. The p orbitals of P and Bi predominantly contribute to the valence band, while the d orbitals of La mostly contribute to the unoccupied conduction bands. However, the La-d and Bi-p bands cross only once along the Γ–X direction, indicating a clear band inversion at X, which reveals that LaBi is a topologically non-trivial semimetal. This finding aligns with experimental results obtained by angle-resolved photoemission spectroscopy (ARPES) measurements, which have shown that LaBi is a non-trivial topological semimetal with a 450 meV direct gap.4 The electronic projected DOS of both materials indicates that the valence bands are predominantly composed of d and p orbitals of La and p orbitals of P and Bi. As both the lattice constant and spin–orbit coupling decrease in the lighter pnictogen species, the LaP bands are clearly non-inverted, implying its topological triviality.Fig. 2 shows the calculated natural lattice thermal conductivity of both LaP and LaBi as a function of temperature, using both the relaxation time approximation (RTA) and the full iterated solution to the phonon Boltzmann equation. Despite following the same trend, the room temperature κl value of LaP is 40% lower than that of LaBi, even though LaBi has a twice larger average atomic mass and 1.5 times smaller acoustic group velocities (Fig. 4(b)). To understand the relationship between lattice thermal conductivity and atomic masses, it is essential to analyze the various factors contributing to the total lattice thermal conductivity in eqn (1).
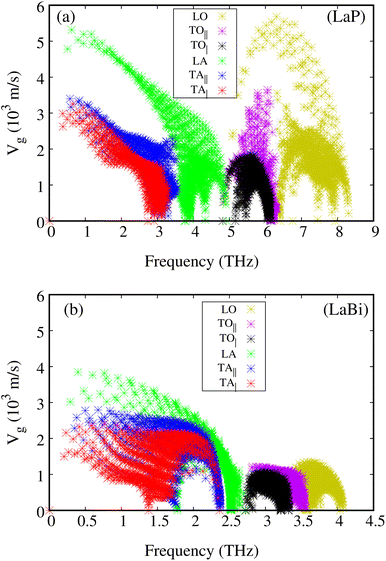
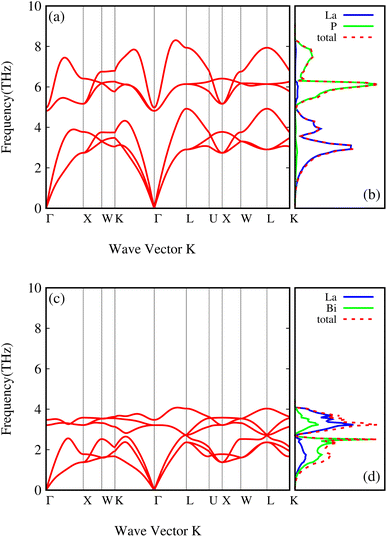
The phonon dispersions of both compounds, LaP and LaBi, are plotted in Fig. 3(a and c), which align with other theoretical calculations.45 As can be seen in these figures, the frequencies of all phonon modes are positive, attesting to the dynamical stability of both compounds. The corresponding phonon density of states with contributions from each element of both compounds, LaP and LaBi, are illustrated in Fig. 3(b and d). Phonon modes at frequencies lower than the acoustic optical frequency gap are dominantly due to vibrations of heavier atoms (La in LaP and Bi in LaBi), while optical phonon modes at frequencies higher than acoustic optical frequency gap are dominantly due to vibrations of lighter atoms (P in LaP and La in LaBi). As can be seen, the compound with lighter atomic masses (LaP) exhibits higher phonon frequency bandwidth (Fig. 3(a)) and higher acoustic velocities (Fig. 4(a)) compared to LaBi (Fig. 3(c) and 4(b)) This is expected since vibrational frequencies scale inversely with atomic masses.
 | ||
| Fig. 3 Phonon dispersion curves and atom-projected phonon density of states of LaP (a and b) and LaBi (c and d). | ||
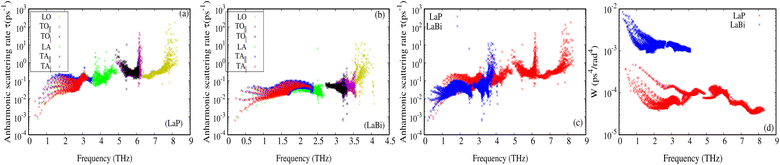
The larger mass difference in LaP results in a more significant gap between the acoustic and optical phonon bands compared to LaBi, as shown in the Fig. 3(a and c). The high phonon-frequency scale and the large acoustic-optical phonon gap in LaP reduce the phase space for three-phonon scatterings, contributing to a tendency for higher lattice thermal conductivity in LaP. This indicates that the lower lattice thermal conductivity of LaP, as shown in Fig. 2, should be solely due to the phonon anharmonicity reflected in the relaxation time. The Grüneisen parameter is a good indicator of anharmonicity strength. Fig. 5 shows Grüneisen parameters for both compounds LaP and LaBi, indicating that LaP is more anharmonic than LaBi. This is consistent with the anharmonic phonon scattering rates of LaP and LaBi, which are plotted for each mode in Fig. 6(a and b), and they are compared in Fig. 6(c). It shows that the anharmonic phonon scattering rates of LaP are stronger than those of LaBi. This hold for both acoustic as well as the optical modes. The softening of the TO mode has caused strong 3-phonon scatterings. Therefore, anharmonicity is the primary factor contributing to the lower lattice thermal conductivity of LaP.
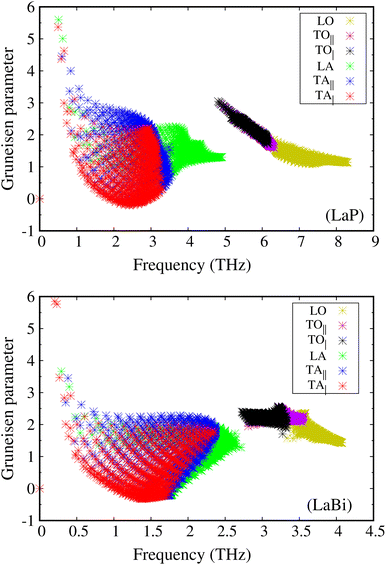 | ||
| Fig. 5 Mode Grüneisen parameters as a function of phonon frequency for LaP are larger than those for LaBi, attesting to stronger anharmonicity strength in LaP. | ||
The weighted phase spaces of phonon–phonon scattering for both LaP and LaBi are compared in Fig. 6(d), where it can be seen that even the 3-phonon scattering phase space is larger for LaBi than for LaP, producing another justification that only anharmonicity strength is the cause of reduced lattice thermal conductivity in LaP.
Fig. 7 shows the calculated harmonic force constants for both compounds LaP and LaBi as a function of the reduced pair distance. As can be seen, interactions along the 〈100〉 direction are of longer range for the lighter compound (LaP). For both compounds LaP and LaBi force constants have been calculated up to the fourteenth-nearest neighbours.
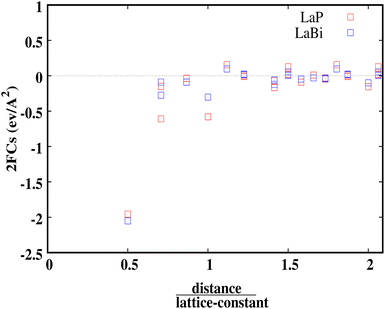 | ||
| Fig. 7 Harmonic forces constants for LaP and LaBi versus distance over lattice constant. LaP is seen to have consistently larger force constants. | ||
This behavior is similar to the long-ranged and non-monotonically decreasing interactions due to the long-ranged electronic polarizability in rocksalt structures for IV–VI materials, as discussed in ref. 21. In this paper, lead chalcogenides and SnTe were compared with other materials such as NaCl and InSb as prototypes of ionic and sp-hybridized covalently-bonded materials, respectively. The long-ranged and non-monotonically decreasing interactions of LaP and LaBi, are then due to their electronic polarizability, which is more pronounced in LaP (see also data on dielectric constant in Table 1). Both compounds, LaP and LaBi, also have positive force constants (in their 5th and 8th neighbor shells), giving them the behavior of ‘anti-springs’. The positive force constants for the lighter compound (LaP) are stronger than those of LaBi.
| Strain | p (GPa) | ω TO (THz) | Z* | ε ∞ | γ TO | κ (W mK−1) | |
|---|---|---|---|---|---|---|---|
| LaP | −5% | −9.4 | 2.84 | 4.8 | 19 | 9 | 1.9 |
| −3.5% | −7.7 | 3.42 | 5 | 38.7 | 5.2 | 2.9 | |
| 0% | −1.8 | 4.81 | 5.7 | 657 | 3 | 11.8 | |
| 3.5% | 7.6 | 6.08 | 6.4 | 1047 | 2.4 | 35.5 | |
| LaBi | −3.5% | −4.7 | 2.53 | 4.6 | 73 | 3.5 | 8.8 |
| 0% | 0.5 | 3.21 | 4.4 | 82 | 2.5 | 16 | |
| 3.5% | 6.3 | 3.96 | 4 | 66.7 | 2.2 | 28 |
This directional long-ranged interaction was also considered as a main reason for the ferroelectric instability-induced phonon softening in perovskite BaTiO3 and PbTiO3.46,47 In ref. 21, it has also been shown that the long-ranged interactions along the 〈100〉 direction in rocksalt structures are related to the existence of a soft TO mode, leading to strong anharmonicity and phonon scattering by the TO modes. The mode Gruneisen parameters are good indicators of the anharmonicity of the modes. As can be seen in Fig. 3(a and c), the TO modes of LaBi are not as soft as those of LaP, resulting in larger TO mode Gruneisen parameters in LaP compared to LaBi (Fig. 5(a and b)).
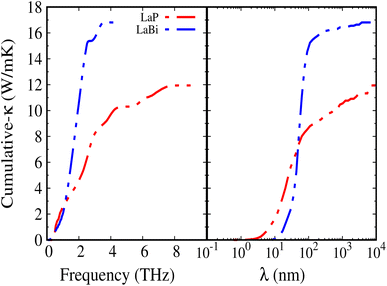
Fig. 8 shows the accumulated lattice thermal conductivity as a function of the phonon mean-free path at 300 K. It is clearly seen that LaP exhibits shorter mean-free paths compared to LaBi.
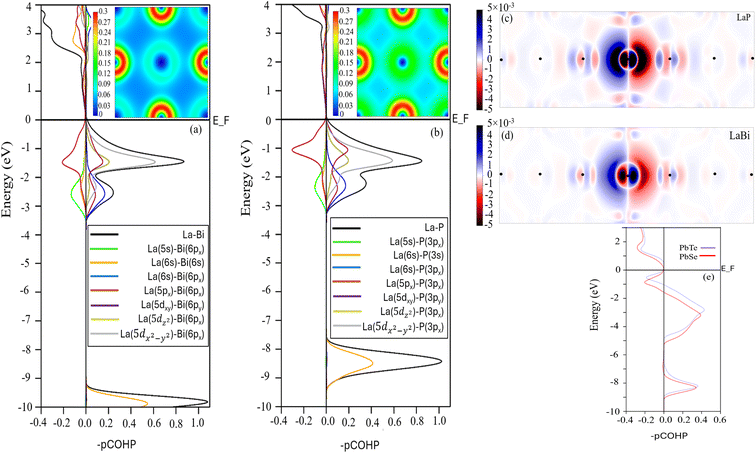
Materials properties can be traced back, to a significant extent, to the nature of interatomic bonding. To gain a better chemical understanding of the origin of anharmonicity increase in the lighter compound LaP, we further calculated the projected crystal orbital Hamilton population (pCOHP) and valence electron density distribution for LaP and LaBi, as shown in Fig. 9. The COHP diagram attributes the anti-bonding states of the valence band to the interactions between p orbitals of both atoms, while interactions between La-d and P-p (Bi-p) orbitals result in the formation of bonding states. This is consistent with PDOS in Fig. 1(b and d) which indicates that the valence bands of both materials are dominated by p, d orbitals of La and p orbitals of P and Bi. As can be seen, the interaction of La-p and P-p orbitals of LaP displays a larger antibonding peak in the valence band range than that formed by the La-p and Bi-p orbitals of LaBi. These anti-bonding states result in a weakening or softening of the La–P bonds, and a more delocalized electron density distribution (see Fig. 9 (insets (a) and (b))) as well as longer range interactions in LaP (Fig. 7).
This is also evident in Fig. 9(c and d), where the electron polarization in LaP is longer-ranged and more pronounced than in LaBi. LaBi electrons having more states at the Fermi level provide better screening of the interatomic interactions leading to a reduced Hamiltonian overlap integral in LaBi and thus a weaker antibonding character.
As mentioned above, the long-range electron polarizability and interactions have been observed in IV–VI materials with rocksalt structures, such as PbTe and PbSe.21 To compare with PbTe and PbSe, which are also low thermal conductivity materials with anomalous mass dependence of their lattice thermal conductivity, we display in Fig. 9(e) the strong antibonding nature of their valence bands in both compounds, leading to their long-range polarizability and interactions. In Fig. 9(e), it is evident that the integrated COHP (ICOHP) value below the Fermi level of PbSe is higher than that of PbTe, indicating weaker bonding in PbSe compared to PbTe.48 This weaker bonding contributes to the slightly lower lattice thermal conductivity of the lighter compound (PbSe) compared to PbTe, as previously reported.21,22
It is well known that materials with delocalized electron density distributions exhibit large electronic polarizability, optical dielectric constants. For example, materials previously referred to as “resonantly” bonded,21 now termed metavalent,49 including chalcogenide phase-change materials (PCMs)50 and IV–VI semiconductors,21,51 possess delocalized electron density due to high effective coordination numbers that exceed those prescribed by the 8 − N rule. In rocksalt structures with 6 nearest neighbors, when the average valence is 3, there is 1/2 of an electron per bond, as opposed to the one electron per bond in the case of purely covalent bonds. This half-filling leads to the resonant nature, delocalization and larger polarizability of these compounds.
Metavalent bonding is characterized as a distinct region intermediate between covalent and metallic realms, or between localized and delocalized electron distributions. Compared to semiconductors, these materials have a smaller bandgap, larger dielectric constant, larger electronic conductivity, and larger Born effective charges due to chemical bond polarizability, and displaying stronger electron-phonon coupling effects. They also exhibit significant vibrational changes, including unusual phonon softening and large Grüneisen parameters for the transverse optical modes49,52,53 as shown for LaP in this study.
It has furthermore been shown that these physical properties strongly change with external pressure in the case of metavalent materials.49 In our study, we examined these properties for both LaP and LaBi under pressure. As shown in Fig. 10, the transverse optical (TO) modes of LaP change significantly with external pressure, leading to large Grüneisen parameters. Table 1 presents the properties of both compounds under different pressures. It is clear that the properties of LaP change more strongly than LaBi under pressure. This implies the stronger metavalent nature of the bonding in LaP, compared to LaBi which just a semimetal. In terms of electron sharing both compounds have the same number of valence electrons, 3 electrons per atom with 6 bonds leading to 1/2 electron per atom or 1 shared electron per bond, with no appreciable difference between LaP and LaBi. Both P and Bi contribute 3p electrons to the bonds. Bi may have a slightly larger contribution from hybridization with the s2 electrons as they are closer in energy, but the hybridization is still very weak.
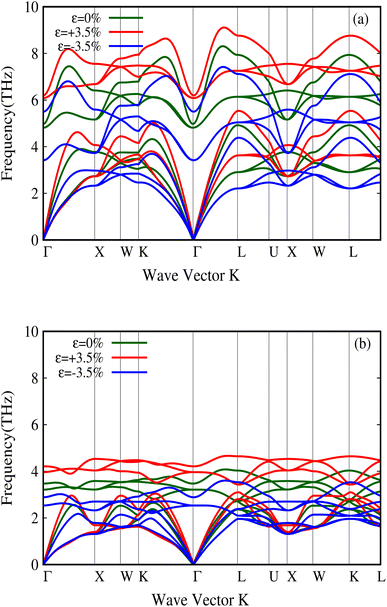 | ||
| Fig. 10 Change in the phonon dispersion of LaP (a) and LaBi (b) with pressure. One can note a relatively large change in the TO mode frequency at Γ for LaP. | ||
The electron localization function (ELF) has also been proposed as a support to metavalency,51,54 but no quantitative relationship has been established between the two. In some works ELF value of near 0.4 has been observed for some metavalent materials, but this is not universal as far as we know. We show ELF for both compounds in the ESI,† and, again, see no discernible difference between the two. It seems that, in addition to their strong pressure dependence, the relatively large values of properties such as dielectric constant, Gruneisen parameter and Born effective charges, which we have summarized in Table 1, are a better indicator of metavalency, and imply LaP tends to be more metavalent than LaBi.
4 Conclusion
Phonons and thermal transport properties of two binary lanthanum monopnictides with rocksalt crystal structures, LaP and LaBi, have been investigated. It is found that unexpectedly, the twice lighter compound, LaP, possesses 1.5 times lower lattice thermal conductivity than the heavier LaBi. This is traced back to the larger scattering rate and anharmonicity in the lighter compound. From a chemical and electronic perspective, this is explained by the more antibonding character of the valence band states of LaP compared to LaBi. In turn, this leads to a more delocalized and polarizable electronic distribution, which is corroborated by the ion-clamped dielectric constant. Additionally, we have shown that the LaP has a more metavalent bonding character because of its large Born effective charges and Gruneisen parameters, as well as a stronger dependence of these properties on the pressure. As a result, we conclude that the antibonding nature of the valence states is responsible for the stronger metavalency of LaP, and stronger anharmonicity of its bonds, leading to its lower lattice thermal conductivity when compared to the heavier LaBi, which is merely a semimetal.Understanding the root reason of the unusual thermal transport properties of these materials, which are also known for their extreme magnetoresistance, topologically non-trivial phases, and structural phase transitions, can guide the search and design of new potential applications, including low dissipation devices.
Data availability
This study was carried out using the following publicly available software packages. All specific parameters and data used in this study are detailed in the main text. Additional data related to this paper are available from the corresponding author upon reasonable request. (1) Vienna Ab initio Simulation Package (VASP): https://www.vasp.at/. (2) Phonopy: https://phonopy.github.io/phonopy/. (3) Sheng-BTE: https://www.shengbte.org/. (4) LOBSTER: http://www.cohp.de/.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to acknowledge the support of the School of Engineering and Applied Sciences of the University of Virginia for allocating computational resources on the Rivanna supercomputer. The authors also gratefully acknowledge financial support from the NSF-CSSI program, award #2103989.Notes and references
- F. Tafti, Q. Gibson, S. Kushwaha, N. Haldolaarachchige and R. Cava, Nat. Phys., 2016, 12, 272–277 Search PubMed
.
- F. Fallah Tafti, Q. Gibson, S. Kushwaha, J. W. Krizan, N. Haldolaarachchige and R. J. Cava, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E3475–E3481 CrossRef
.
- J. Jiang, N. Schröter, S.-C. Wu, N. Kumar, C. Shekhar, H. Peng, X. Xu, C. Chen, H. Yang and C.-C. Hwang,
et al.
, Phys. Rev. Mater., 2018, 2, 024201 CrossRef CAS
.
- T. J. Nummy, J. A. Waugh, S. P. Parham, Q. Liu, H.-Y. Yang, H. Li, X. Zhou, N. C. Plumb, F. F. Tafti and D. S. Dessau, npj Quantum Mater., 2018, 3, 24 CrossRef
.
- J. Nayak, S.-C. Wu, N. Kumar, C. Shekhar, S. Singh, J. Fink, E. E. Rienks, G. H. Fecher, S. S. Parkin and B. Yan,
et al.
, Nat. Commun., 2017, 8, 13942 CrossRef CAS
.
- Y. Wu, T. Kong, L.-L. Wang, D. D. Johnson, D. Mou, L. Huang, B. Schrunk, S. L. Bud'ko, P. C. Canfield and A. Kaminski, Phys. Rev. B, 2016, 94, 081108 CrossRef
.
- X. Niu, D. Xu, Y. Bai, Q. Song, X. Shen, B. Xie, Z. Sun, Y. Huang, D. Peets and D. Feng, Phys. Rev. B, 2016, 94, 165163 CrossRef
.
- L.-K. Zeng, R. Lou, D.-S. Wu, Q. Xu, P.-J. Guo, L.-Y. Kong, Y.-G. Zhong, J.-Z. Ma, B.-B. Fu and P. Richard,
et al.
, Phys. Rev. Lett., 2016, 117, 127204 CrossRef PubMed
.
- R. Lou, B.-B. Fu, Q. Xu, P.-J. Guo, L.-Y. Kong, L.-K. Zeng, J.-Z. Ma, P. Richard, C. Fang and Y.-B. Huang,
et al.
, Phys. Rev. B, 2017, 95, 115140 CrossRef
.
- H.-Y. Yang, T. Nummy, H. Li, S. Jaszewski, M. Abramchuk, D. Dessau and F. Tafti, Phys. Rev. B, 2017, 96, 235128 CrossRef
.
- I. Shirotani, K. Yamanashi, J. Hayashi, N. Ishimatsu, O. Shimomura and T. Kikegawa, Solid State Commun., 2003, 127, 573–576 CrossRef CAS
.
- Y. Zhou, L.-T. Shi, A.-K. Liang, Z.-Y. Zeng, X.-R. Chen and H.-Y. Geng, RSC Adv., 2021, 11, 3058–3070 RSC
.
- G. Pagare, S. P. Sanyal and P. Jha, J. Alloys Compd., 2005, 398, 16–20 CrossRef CAS
.
- X. Yan, Y. Chen, X. Kuang and S. Xiang, J. Appl. Phys., 2014, 116, 083707 CrossRef
.
- Z. Charifi, A. H. Reshak and H. Baaziz, Solid State Commun., 2008, 148, 139–144 CrossRef CAS
.
- F. F. Tafti, M. S. Torikachvili, R. L. Stillwell, B. Baer, E. Stavrou, S. T. Weir, Y. K. Vohra, H.-Y. Yang, E. McDonnell and S. K. Kushwaha,
et al.
, Phys. Rev. B, 2017, 95, 014507 CrossRef CAS
.
- J.-F. Zhang, P.-J. Guo, M. Gao, K. Liu and Z.-Y. Lu, Phys. Rev. B, 2020, 101, 155139 CrossRef CAS
.
- Y. Zhou, W.-L. Tao, Z.-Y. Zeng, X.-R. Chen and Q.-F. Chen, J. Appl. Phys., 2019, 125, 045107 CrossRef
.
- C.-M. Lin, W.-C. Chen and C.-C. Chen, Phys. Chem. Chem. Phys., 2021, 23, 18189–18196 RSC
.
- H. S. Saini, N. Kumar, S. Singhmar, J. Thakur, S. Srivastava, M. K. Kashyap and A. H. Reshak,
et al.
, Phys. Lett. A, 2020, 384, 126789 CrossRef
.
- S. Lee, K. Esfarjani, T. Luo, J. Zhou, Z. Tian and G. Chen, Nat. Commun., 2014, 5, 3525 CrossRef PubMed
.
- Z. Tian, J. Garg, K. Esfarjani, T. Shiga, J. Shiomi and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184303 CrossRef
.
- L. Elalfy, D. Music and M. Hu, Phys. Rev. B, 2021, 103, 075203 CrossRef CAS
.
- M. Al-Fahdi, X. Zhang and M. Hu, J. Mater. Sci., 2021, 56, 18534–18549 CrossRef CAS
.
- J. Zhang, D. Ishikawa, M. M. Koza, E. Nishibori, L. Song, A. Q. Baron and B. B. Iversen, Angew. Chem., 2023, 135, e202218458 CrossRef
.
- J. He, Y. Xia, W. Lin, K. Pal, Y. Zhu, M. G. Kanatzidis and C. Wolverton, Adv. Funct. Mater., 2022, 32, 2108532 CrossRef CAS
.
- J. Yuan, Y. Chen and B. Liao, J. Am. Chem. Soc., 2023, 145, 18506–18515 CrossRef CAS
.
- J. Zhang, H. Jiang, X. Xia, Y. Gao and Z. Huang, ACS Appl. Energy Mater., 2022, 5, 15566–15577 CrossRef CAS
.
- K. Yuan, X. Zhang, Z. Chang, D. Tang and M. Hu, J. Mater. Chem. C, 2022, 10, 15822–15832 RSC
.
- A. Das, K. Pal, P. Acharyya, S. Das, K. Maji and K. Biswas, J. Am. Chem. Soc., 2023, 145, 1349–1358 CrossRef CAS PubMed
.
- C. Hu, L. Zhou, X. Hu, B. Lv and Z. Gao, Appl. Surf. Sci., 2023, 613, 156064 CrossRef CAS
.
- S. S. Das, S. Nayeb Sadeghi, K. Esfarjani and M. Zebarjadi, J. Mater. Chem. A, 2024, 12(23), 14072–14086 RSC
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS
.
- M. Shoaib, G. Murtaza, R. Khenata, M. Farooq and R. Ali, Comput. Mater. Sci., 2013, 79, 239–246 CrossRef CAS
.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS
.
- A. Togo, L. Chaput, T. Tadano and I. Tanaka, J. Phys.: Condens. Matter, 2023, 35, 353001 CrossRef CAS
.
- A. Togo, J. Phys. Soc. Jpn., 2023, 92, 012001 CrossRef
.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS
.
- R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624 CrossRef CAS
.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed
.
- R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940 CrossRef CAS PubMed
.
- W.-C. Chen, C.-M. Lin, J. Maciejko and C.-C. Chen, Comput. Mater. Sci., 2021, 200, 110779 CrossRef CAS
.
- W. Zhong, D. Vanderbilt and K. Rabe, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 6301 CrossRef CAS PubMed
.
- P. Ghosez, E. Cockayne, U. Waghmare and K. Rabe, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 836 CrossRef CAS
.
- P. M. Konze, R. Dronskowski and V. L. Deringer, Phys. Status Solidi RRL, 2019, 13, 1800579 CrossRef
.
- M. Wuttig, V. L. Deringer, X. Gonze, C. Bichara and J.-Y. Raty, Adv. Mater., 2018, 30, 1803777 CrossRef PubMed
.
- B. J. Kooi and M. Wuttig, Adv. Mater., 2020, 32, 1908302 CrossRef CAS PubMed
.
- J.-Y. Raty and M. Wuttig, J. Phys. D: Appl. Phys., 2020, 53, 234002 CrossRef CAS
.
- J.-Y. Raty, M. Schumacher, P. Golub, V. L. Deringer, C. Gatti and M. Wuttig, Adv. Mater., 2019, 31, 1806280 CrossRef PubMed
.
- Y. Yu, M. Cagnoni, O. Cojocaru-Mirédin and M. Wuttig, Adv. Funct. Mater., 2020, 30, 1904862 CrossRef CAS
.
- M. Xu, S. Jakobs, R. Mazzarello, J.-Y. Cho, Z. Yang, H. Hollermann, D. Shang, X. Miao, Z. Yu and L. Wang,
et al.
, J. Phys. Chem. C, 2017, 121, 25447–25454 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta04146a |
| This journal is © The Royal Society of Chemistry 2024 |